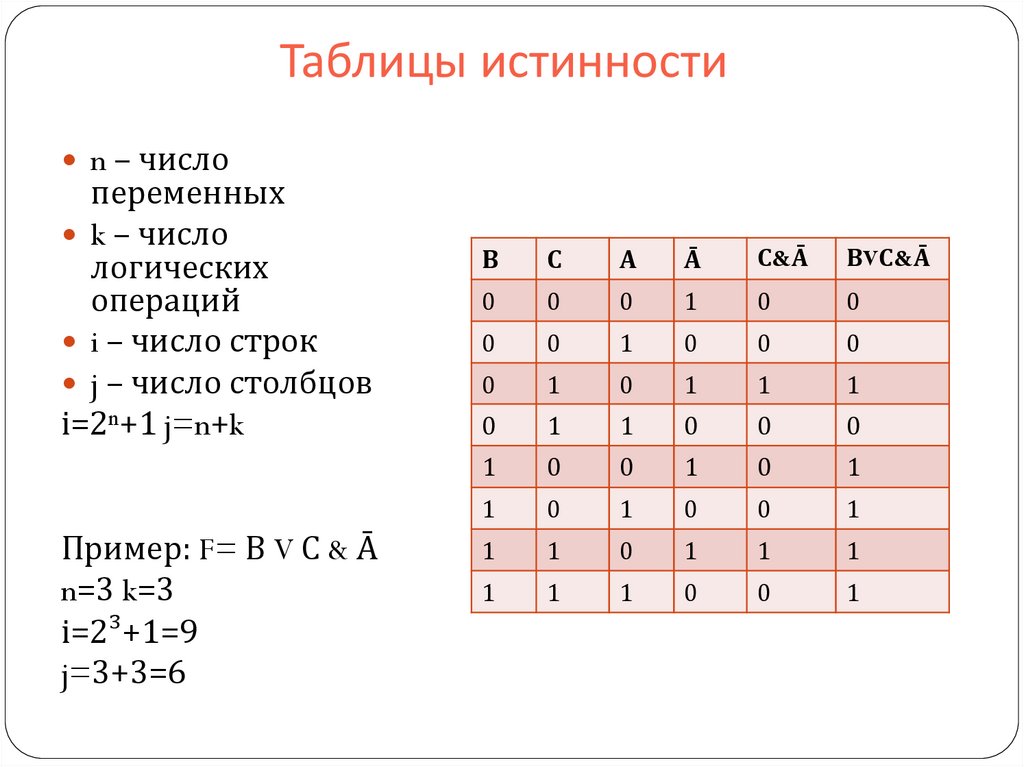
определение и методика её построения
Содержание:
-
Таблица истинности — это…
- Символы
- Значение таблицы истинности
- Таблицы истинности для основных двоичных логических функций
- Таблицы истинности для троичных логических функций
- Алгоритм построения таблицы истинности
Содержание
-
Таблица истинности — это.
- Символы
- Значение таблицы истинности
- Таблицы истинности для основных двоичных логических функций
- Таблицы истинности для троичных логических функций
- Алгоритм построения таблицы истинности
Таблица истинности — это…
Таблица истинности в логике является диаграммой, показывающей значение истинности определенного числа составных предлогов для каждой возможной комбинации.
Ее можно использовать для проверки обоснованности аргументов.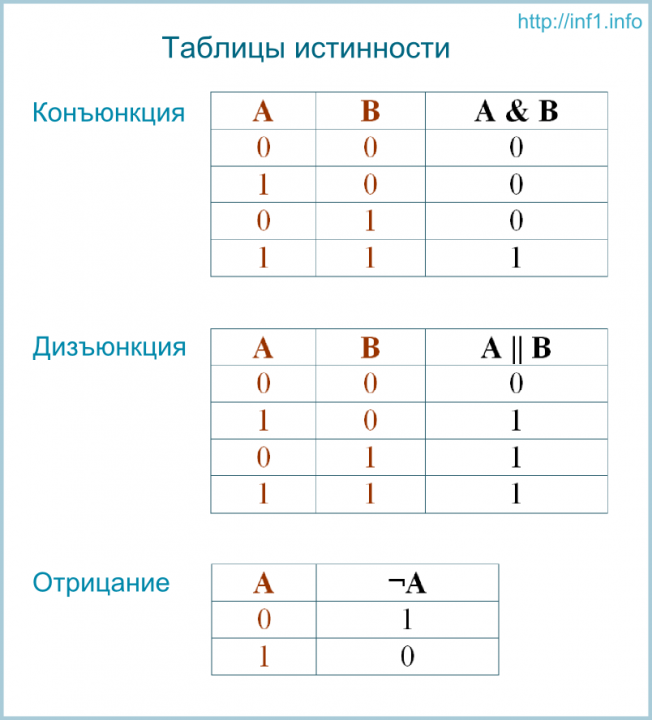
Предполагается, что каждое суждение либо истинно, либо ложно, и истинность или ложность каждого суждения считается его истинностной ценностью. Все строки такой таблицы представляют возможные комбинации значений истинности для составных предложений составного, и строк должно быть достаточно, чтобы охватить все возможные комбинации. Например, если составное предложение содержит только два составных предложения, в таблице будет четыре возможности и четыре строки. Значение истинности соединения указывается в каждой строке под функциональным оператором истинности. Таблица для «p или q» использует специальные обозначения (например, знак ∨, обозначающий «или»).
| p | q | p∨q |
| T | T | T |
| T | F | T |
| F | T | |
| F | F | F |
Здесь показывается, что «p или q» является ложным только тогда, когда оба p и q являются ложными.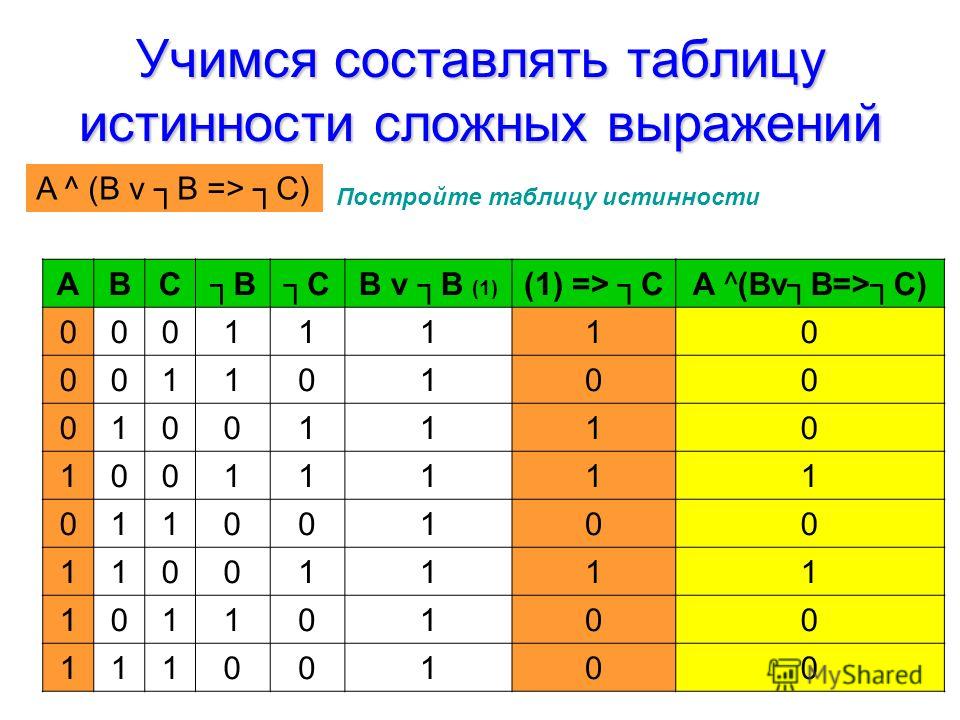
Таблицы истинности для соединений большой сложности, имеющих более одного функционального оператора истинности, могут быть построены с помощью компьютеров.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Символы
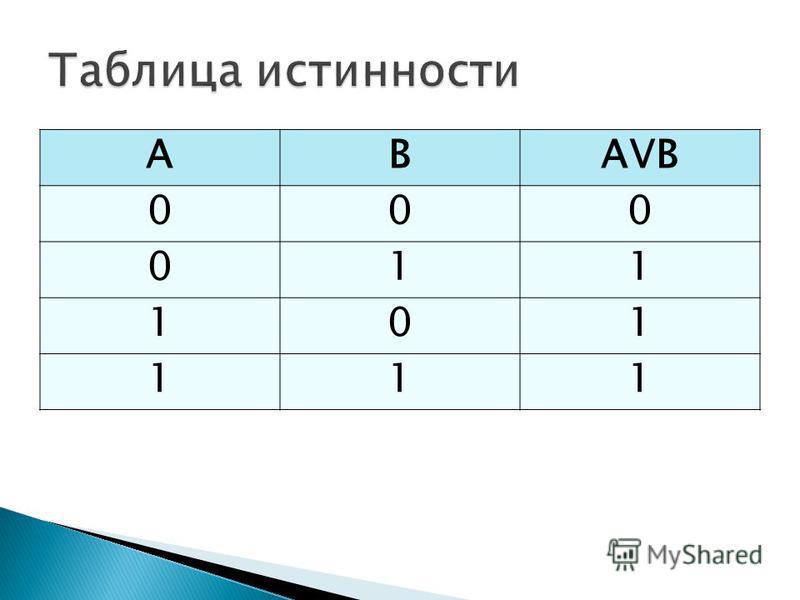
Символ ⋀ используется для и: A и B обозначаются A ⋀ B.
Символ ⋁ используется для обозначения или: A или B обозначается A ⋁ B.
Символ ~ используется для обозначения не: горячий A обозначается ~A.
Нужно запомнить первые два символа, связав их с фигурами для объединения и пересечения. A ⋀ B будут элементами, которые существуют в обоих наборах, в A ⋂ B. Аналогично, A ⋁ B будут элементами, которые существуют в любом наборе, в A ⋃ B.
Значение таблицы истинности
Таблица истинности отображает логические операции над входными сигналами в табличном формате. Каждое логическое выражение можно рассматривать как таблицу истинности.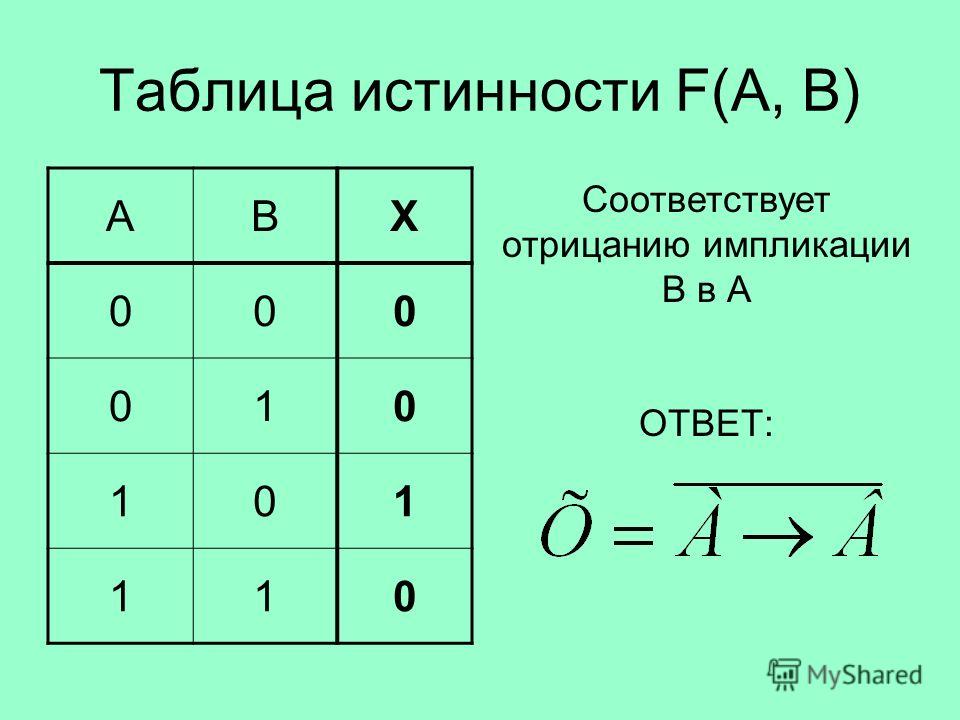
Таблица истинности определяет все возможные комбинации входных данных и выходные данные для каждой из них. Обычно таблицу создают таким образом, чтобы входные комбинации приводили к увеличению числа двоичных файлов без знака.
Таблица истинности — это разбивка логической функции путем перечисления всех возможных значений, которые может получить функция. Такая таблица обычно содержит несколько строк и столбцов, причем верхняя строка представляет логические переменные и комбинации с возрастающей сложностью, ведущей к конечной функции.
В логической функции есть три основные операции: НЕ (также называемые инверсией или отрицанием и обозначенные символом -), ИЛИ (также называемые дизъюнкцией или сложением и обозначенные символом +) и И (также называемые соединением или умножением и обозначенные символом *). Значения функций обычно присваиваются как логические 0 = false и логические 1 = true. Таким образом, применяются следующие правила:
- Если A = 0, то -A = 1.
- Если A = 1, то -A = 0.
- A+B = 1, за исключением случаев, когда A = 0 и B = 0.
- A+B = 0, если A = 0 и B = 0.
- A*B = 0, за исключением случаев, когда A = 1 и B = 1.
- A*B = 1, если A = 1 и B = 1.
Данная таблица является средством, которое представляет все возможные значения логических переменных / операторов вместе со всеми возможными результатами заданных комбинаций значений. С помощью таблицы истинности можно узнать все возможные комбинации значений и результатов логических утверждений.
Пример 1
Английское утверждение «Если идет дождь, значит, на небе есть облака» является логическим следствием. Это веский аргумент, потому что если предшествующее «идет дождь» верно, то следствие «на небе облака» также должно быть истинным. Однако это утверждение ничего не говорит нам о том, чего ожидать, если дождя нет. Если антецедент ложен, то импликация становится неуместной.
Друг говорит вам, что «Если ты загрузишь эту фотографию, то потеряешь работу».
Есть четыре возможных исхода:
- Вы загружаете фотографию и сохраняете свою работу.
- Вы загружаете фотографию и теряете работу.
- Вы не загружаете фотографию и не сохраняете свою работу.
- Вы не загружаете фотографию и не теряете работу.
Есть только один возможный случай, когда ваш друг лгал — первый вариант, когда вы загружаете фотографию и сохраняете свою работу. В последних двух случаях друг ничего не сказал о том, что произойдет, если вы не загрузите фотографию, поэтому вы не можете сделать вывод, что это заявление недействительно, даже если вы не загрузили фотографию и все равно потеряли работу.
В традиционной логике импликация считается действительной (истинной) до тех пор, пока нет случаев, в которых антецедент истинен, а следствие ложно. Важно иметь в виду, что символическая логика не может охватить все тонкости языка.
Пример 3
Обратным выражению «Если идет дождь, значит, на небе есть облака» было бы: «Если на небе облака, значит, идет дождь».
Также могут сказать: «Если нет дождя, значит, на небе нет облаков». Точно так же это не всегда верно.
Противопоставление было бы таким: «Если на небе нет облаков, значит, дождя нет». Это утверждение действительно и эквивалентно первоначальному подтексту.
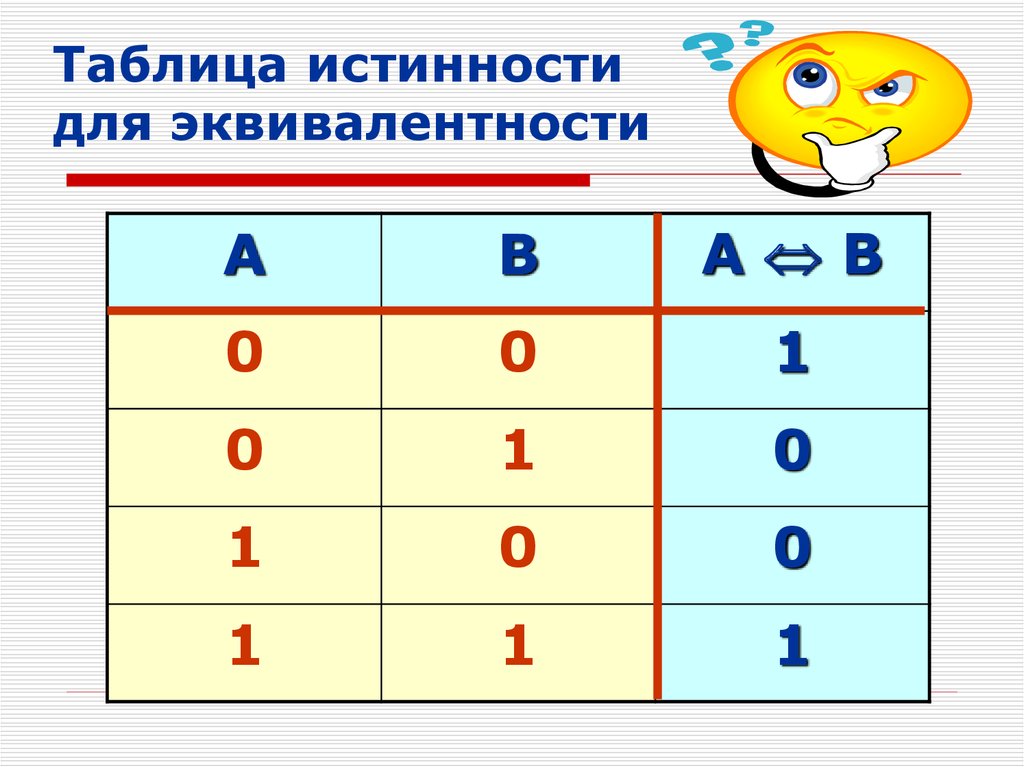
Глядя на таблицы истинности, мы можем видеть, что исходное условное и противоположное логически эквивалентны, и что обратное и обратное логически эквивалентны.
Пример 4
Аргумент «каждый день в течение последнего года самолет пролетает над моим домом в 2 часа дня. Самолет будет пролетать над моим домом каждый день в 2 часа дня» — это более сильный индуктивный аргумент, поскольку он основан на большем наборе доказательств.
Пример 5
Аргумент «Все кошки — млекопитающие, а тигр — это кошка, поэтому тигр является млекопитающим» является обоснованным дедуктивным аргументом.
Посылки таковы:
- все кошки — млекопитающие;
- тигр — это кошка.
Вывод: Тигр — это млекопитающее.
Обе предпосылки верны. Из первой предпосылки можно заключить, что множество кошек является подмножеством множества млекопитающих. Исходя из второй предпосылки, нам говорят, что тигр находится внутри множества кошек. Исходя из этого, тигр также находится внутри множества млекопитающих, так что вывод верен.
Таблицы истинности для основных двоичных логических функций
Кроме обычного логического выражения, входная и выходная информация любого логического элемента или схемы может быть отображена в стандартной таблице, чтобы дать визуальное представление о функции переключения системы.
Рассмотрим единственную логическую схему с 2 входами с входными переменными, обозначенными как A и B. Существует четыре возможных входных комбинации или 22 «ВЫКЛ.» и «ВКЛ.» для двух входов.
Тогда 4 возможные комбинации A и B для логического элемента с 2 входами задаются как:
- Комбинация ввода 1. — ВЫКЛ. – ВЫКЛ. или ( 0, 0 ).
- Комбинация ввода 2. — ВЫКЛ. – ВКЛ. или ( 0, 1 ).
- Комбинация ввода 3. — ВКЛ. – ВЫКЛ. или (1, 0 ).
- Комбинация ввода 4. — ВКЛ. – ВКЛ. или ( 1, 1 ).
– ВЫКЛ. или ( 0, 0 ).Следовательно, логическая схема с 3 входами будет иметь 8 возможных комбинаций входных сигналов или 23, а логическая схема с 4 входами будет иметь 16 или 24, и так далее по мере увеличения числа входов. Тогда логическая схема с числом входов «n» будет иметь 2n возможных входных комбинаций как «ВЫКЛ.», так и «ВКЛ.».
Тогда таблицы истинности для элемента с 2 входами И, элемента с 2 входами ИЛИ и элемента с одним входом НЕ задаются как:
Логические вентили
2-вход И вентиль
Для элемента с 2 входами И выход Q имеет значение истины, если ОБА входа A «И» вход B имеют значение истина, что дает логическое выражение: ( Q = A и B ).
Источник: electronics-tutorials.wsЛогическое выражение Q = A.B
| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2-входной элемент ИЛИ (включительно ИЛИ)
Для элемента с 2 входами ИЛИ выход Q имеет значение истины, если либо вход A, ИЛИ вход B имеет значение истины, что дает логическое выражение: ( Q = A или B ).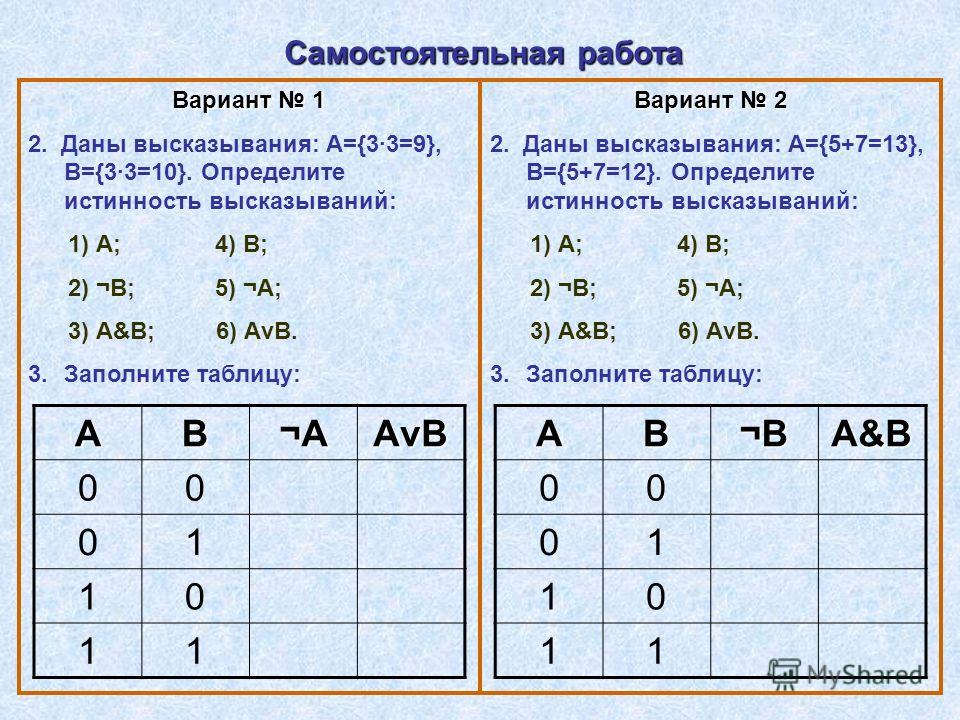
| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
«НЕ» вентиль (Инвертор)
Для одного входного элемента NOT выходной сигнал Q имеет значение истины только тогда, когда входной сигнал имеет значение НЕ истина, выходной сигнал является обратным или дополнением к входному сигналу, дающему логическое выражение: ( Q = NOT A ).
Источник: electronics-tutorials.ws| A | Q |
| 0 | 1 |
| 1 | 0 |
Элементы NAND (НЕ И) и НЕ представляют собой комбинацию элементов И и ИЛИ соответственно с элементом НЕ (инвертор).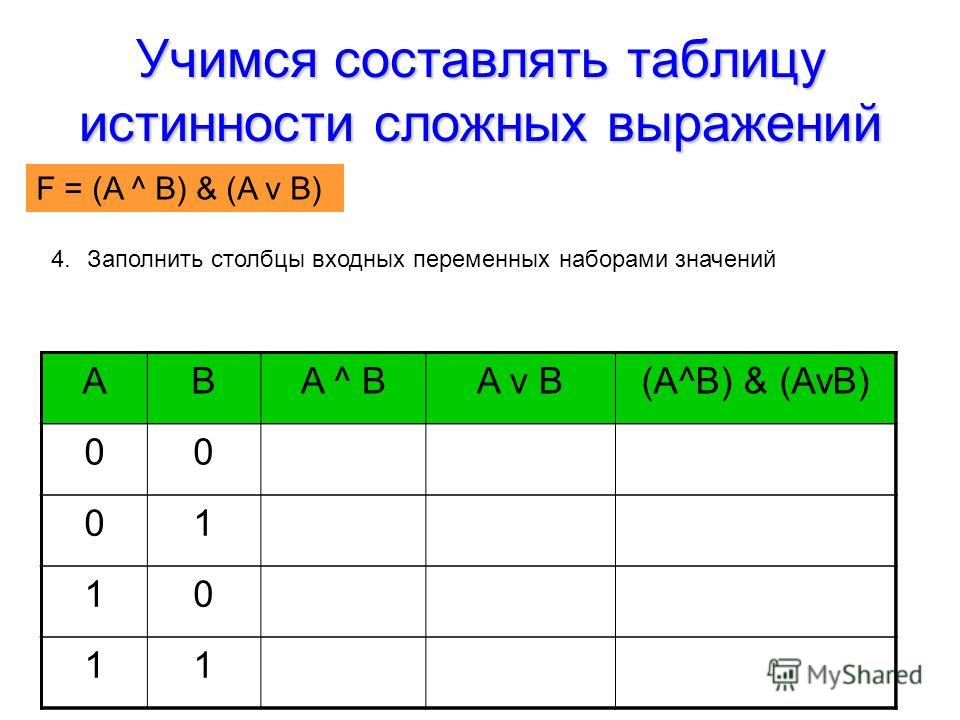
2-входной элемент NAND (Не И)
Для элемента NAND с 2 входами выход Q НЕ является истинным, если ОБА входа A и вход B имеют значение истины, что дает логическое выражение: ( Q = not(A И B)).
Источник: electronics-tutorials.ws| A | B | Q |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
2-входной элемент NOR (Не ИЛИ)
Для элемента NOR с 2 входами выход Q имеет значение истины, если ОБА входа A и вход B НЕ имеют значения истина, что дает логическое выражение: ( Q = not(A ИЛИ B)).
Источник: electronics-tutorials.ws| A | B | Q |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Помимо стандартных логических элементов, существуют также два специальных типа функций логических элементов, называемых элементом Исключающего ИЛИ и элементом Исключающего ИЛИ.
Логическое выражение для обозначения функции Исключающего-ИЛИ или Исключающего-НЕ относится к символу со знаком плюс внутри круга (⊕).
Действия переключения обоих этих типов элементов могут быть созданы с использованием вышеуказанных стандартных логических элементов.
2-входной элемент EX-OR (Исключающее ИЛИ)
Для элемента Ex-OR с 2 входами вывод Q имеет значение true, если либо вход A, либо вход B имеет значение true, но НЕ оба, дающие логическое выражение: ( Q = (A, а НЕ B) или (НЕ A и B)).
Источник: electronics-tutorials.ws| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
2-входной элемент EX-NOR (Исключающий NOR)
Для элемента Ex-NOR с 2 входами выход Q равен true, если ОБА входа A и вход B одинаковы, либо истина, либо ложь, что дает логическое выражение: ( Q = (A и B) или (НЕ A и НЕ B)).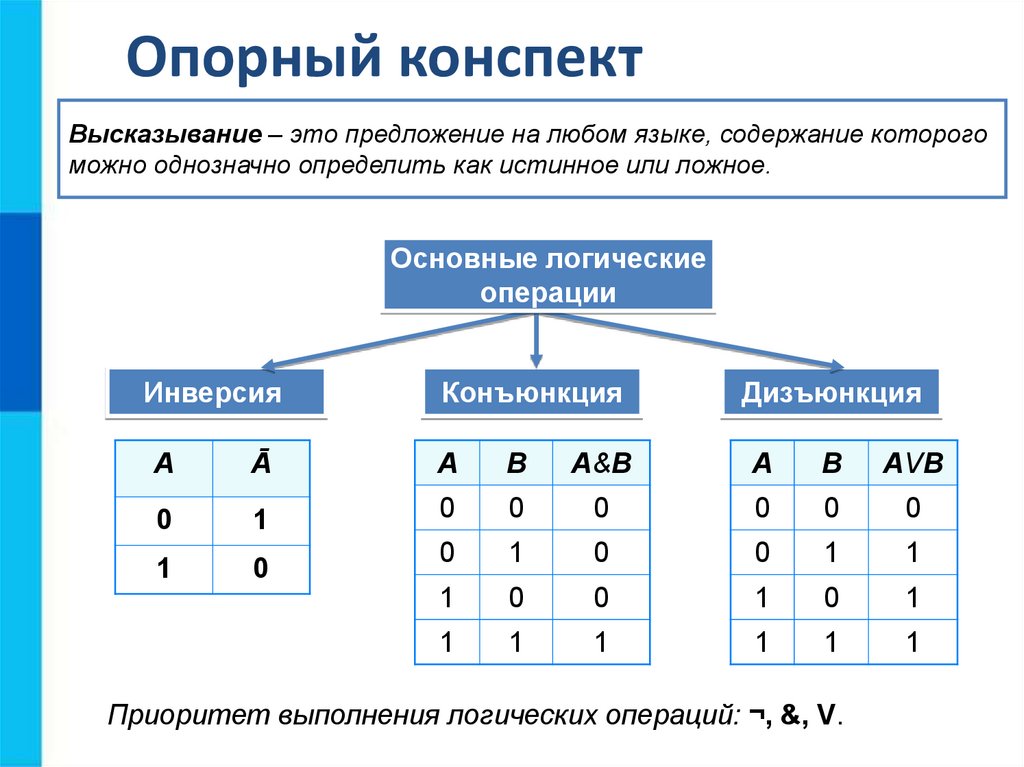
| A | B | Q |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Краткое описание логических элементов с 2 входами
В следующей таблице истинности сравниваются логические функции приведенных выше логических элементов с 2 входами.
| Входы | Выходы таблицы истинности для каждого элемента | ||||||
| A | B | И | HAND | И | NOR | EX-OR | EX-NOR |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
Таблицы истинности для троичных логических функций
В логике трехзначная логика (также трехвалентная, троичная или тройная логика, иногда сокращенно 3VL) — это любая из нескольких многозначных логических систем, в которых есть три значения истинности, указывающие на истинное, ложное и некоторое неопределенное третье значение.
Это контрастирует с более широко известными бивалентными логиками (такими как классическая сентенциальная или булева логика), которые предусматривают только истина и ложь.
Примеры операторов троичной логики в таблицах истинности:
не a
| ¬ | |
| правда | ложь |
| может быть | может быть |
| ложь | правда |
a и b
| ∧ | правда | может быть | ложь |
| правда | правда | может быть | ложь |
| может быть | может быть | может быть | ложь |
| ложь | ложь | ложь | ложь |
a или b
| ∨ | правда | может быть | ложь |
| правда | правда | правда | правда |
| может быть | правда | может быть | может быть |
| ложь | правда | может быть | ложь |
если a, то b
| ⊃ | правда | может быть | ложь |
| правда | правда | может быть | ложь |
| может быть | правда | может быть | может быть |
| может быть | правда | правда | правда |
| ложь | может быть | может быть | может быть |
a эквивалентно b
| ≡ | правда | может быть | ложь |
| правда | правда | может быть | ложь |
| может быть | может быть | может быть | может быть |
| ложь | ложь | может быть | правда |
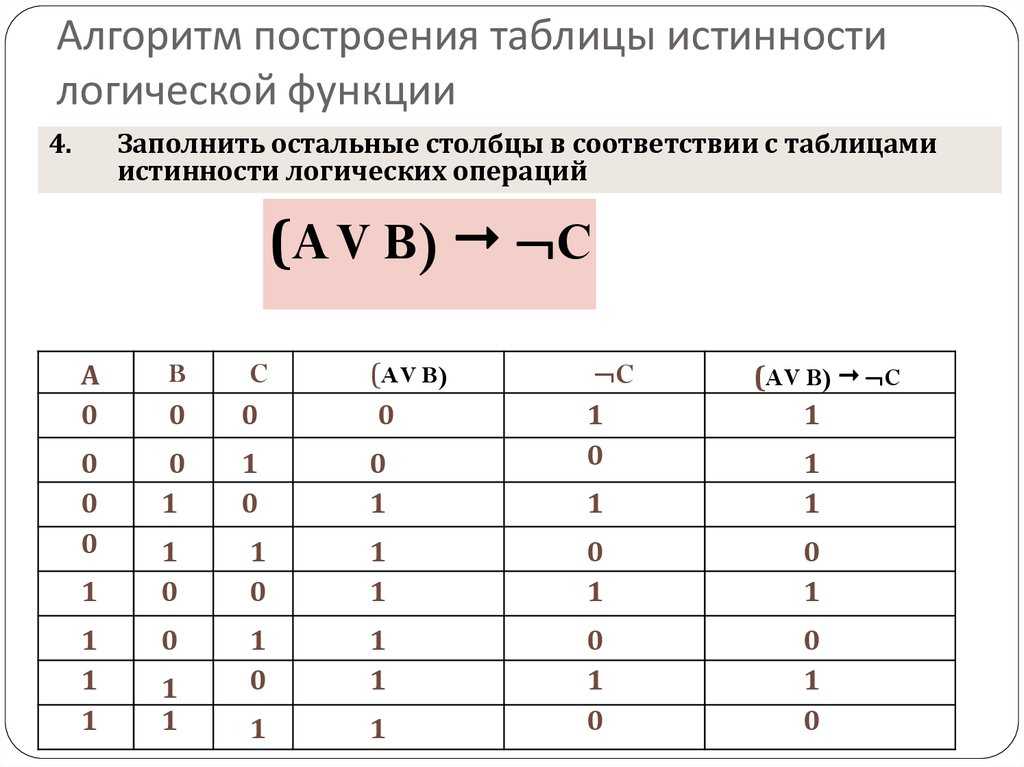
Алгоритм построения таблицы истинности
Учитывая сложное предложение с несколькими связками и задачу построения таблицы истинности для этого предложения, нужно начать с определения того, как предложение составлено из его частей.
Сначала следует пронумеровать связки, чтобы четко указать, как составлено предложение. Есть способ определить номера, которые нужно присвоить соединительным элементам.
- Начать с левой части предложения и двигаться вправо, повторяя предложение столько раз, сколько потребуется, чтобы пронумеровать все связки. На каждом проходе останавливаться на ненумерованных соединениях и задавать следующий вопрос: «Применима ли эта соединительная связь, на которую я смотрю, к (или соединяющим) предложениям, которые содержат ненумерованные соединения?» Ответ да: Пропустить его и перейти к следующему соединению. Ответ нет: Присвоить соединительному слову число, на единицу большее, чем наибольшее число, присвоенное соединительным словам в связанных предложениях. (Если связные предложения вообще не содержат связных слов, то число равно 1.)
- Номер 1 будет присвоен тем соединениям, которые применимы только к предложениям в ссылочной колонке. Число 2 будет применяться к предложениям, по крайней мере, одно из которых содержит соединительное слово, которому присвоен номер 1. Число 3 будет применяться к предложениям, по крайней мере, одно из которых содержит соединительную связь, присвоенную номеру 2. И так далее.
- Меньшие числа относятся к меньшим фрагментам предложения, а большие числа — к большим фрагментам. Помните, что эти предложения составлены из более мелких фрагментов в более крупные, и это порядок, которому вы должны следовать при создании таблиц истинности.
- При заполнении таблицы истинности для предложения вам нужно будет сначала сгенерировать столбцы «T» и «F» под «1», а затем перейти к «2», а затем к «3» и т.д. При создании столбцов под номером 1 входные значения истинности берутся только из справочных столбцов; при создании столбцов под номером 2 нужно будет взять входные значения истинности по крайней мере из одного столбца под номером 1; при создании столбцов под номером 3 нужно будет принять входные значения истинности. Значения истинности по крайней мере из одного столбца под номером 2; и т.д.
Число 3 будет применяться к предложениям, по крайней мере, одно из которых содержит соединительную связь, присвоенную номеру 2. И так далее.Суть таблиц истинности: Создавая таблицы истинности, мы узнаем, как структура предложений ограничивает и помогает определить их значения.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
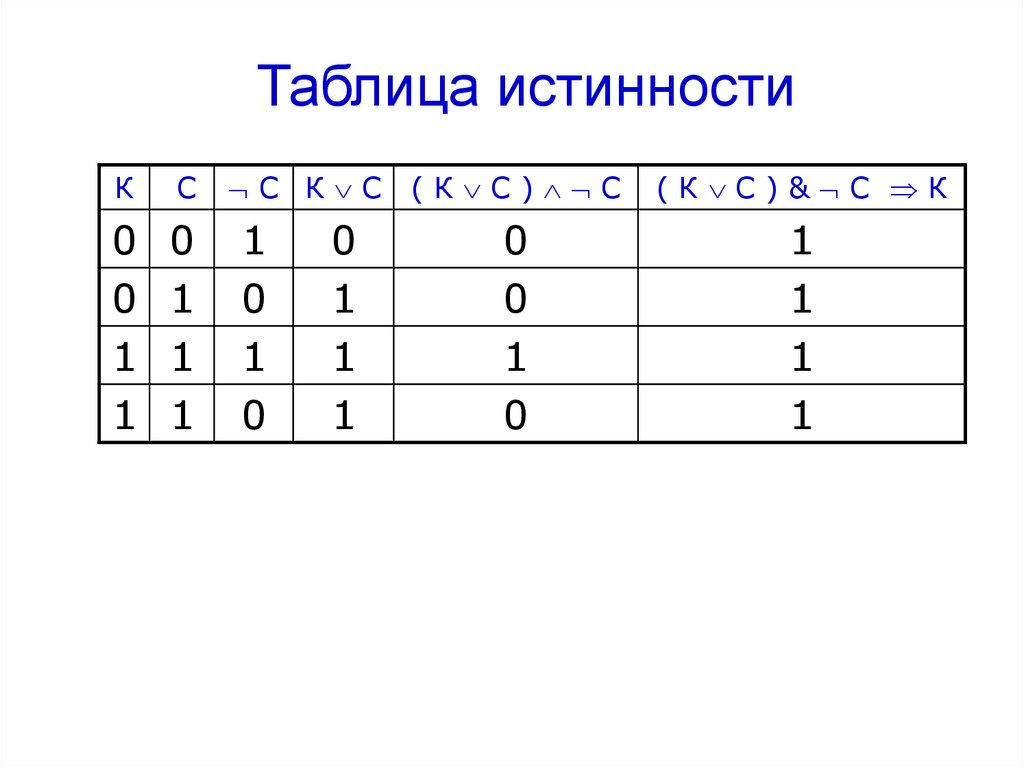
4. Логические выражения и таблицы истинности
13
4.1.Логические выражения
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.
Запишем в форме логического выражения составное высказывание
«(2·2=5 или 2·2=4) и (2·2≠5 или 2·2≠4)».
Проанализируем составное высказывание. Оно содержит два простых высказывания:
А = «2•2=5»—ложно (0), В = «2•2=4»—истинно (1).
Тогда составное высказывание можно записать в следующей форме: «(А или В) и (Ā или В)».
Теперь необходимо записать высказывание в форме логического выражения с учётом последовательности выполнения логических операций.
При выполнении логических операций определён следующий порядок их выполнения:
инверсия, конъюнкция, дизъюнкция.
Для изменения указанного порядка могут использоваться скобки:
F = (A v В) & (Ā v В).
Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.
Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:
F = (A v В) & (Ā v В) = (0 v 1) & (1 v 0) = 1 & 1 = 1.
14
4.2.Таблицы истинности
Таблицы, в которых логические операции отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний, называются таблицами истинности.
Простые высказывания обозначаются переменными (например, A и B).
При построении таблиц истинности целесообразно руководствоваться определённой последовательностью действий:
1) необходимо определить количество строк в таблице истинности.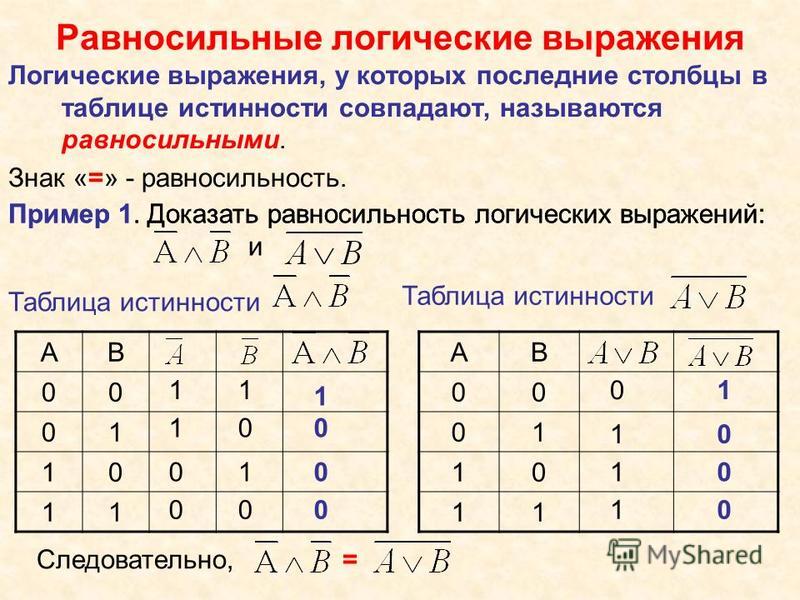
Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:
количество строк = 2n.
В нашем случае логическая функция имеет 2 переменные и, следовательно, количество строк в таблице истинности должно быть равно 4;
2)необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум: А и В, а количество логических операций — пяти (таблица 8), то есть количество столбцов таблицы истинности равно семи;
3)необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных;
4)необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.
Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
15
Таблица 8 – Таблица истинности логической функции
4.3.Равносильные логические выражения
Логические выражения, у которых последние столбцы таблиц истинности сов-
падают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».
Докажем, что логические выражения равносильны. Построим сначала таблицу истинности логического выражения (табли-
ца 9).
Таблица 9 – Таблица истинности логического выражения
А | В |
|
|
|
|
|
|
|
|
0 | 0 | 1 | 1 | 1 |
|
|
|
|
|
0 | 1 | 1 | 0 | 0 |
|
|
|
|
|
1 | 0 | 0 | 1 | 0 |
|
|
|
|
|
1 | 1 | 0 | 0 | 0 |
|
|
|
|
|
Теперь построим таблицу истинности логического выражения (таблица 10).
Таблица 10 – Таблица истинности логического выражения
А | В | А v В |
|
|
|
|
|
0 | 0 | 0 | 1 |
|
|
|
|
0 | 1 | 1 | 0 |
|
|
|
|
1 | 0 | 1 | 0 |
|
|
|
|
1 | 1 | 1 | 0 |
|
|
|
|
Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны:
=.
16
5. Построение таблиц истинности для сложных выражений
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений
переменных всего четыре: |
| ||
(0, 0), | (0, 1), | (1, 0), | (1, 1). |
Если формула содержит три переменные, то возможных наборов значений
переменных восемь: |
|
|
|
|
|
| |
(0, 0, 0), | (0, 0, 1), | (0, 1, 0), | (0, 1, 1), | (1, 0, 0), | (1, 0, 1), | (1, 1, 0), | (1, 1, 1). |
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Пример 1 1. Составим таблицу истинности для формулы, которая содержит две пере-
менные X и Y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу 11:
Таблица 11 – Таблица истинности для формулы с переменными Х и У
Пример 2
Cоставить таблицу истинности сложного логического выражения: D = неA & (B+C).
А, В, С – три простых высказывания, поэтому:
количество строк = 23 +2 = 10 (n=3, т.к. на входе три элемента А, В, С) количество столбцов (таблица 12):
1)А,
2)В,
таблиц истинности | Математика для гуманитарных наук
Результаты обучения
- Объединение наборов с использованием булевой логики и соответствующих обозначений
- Использование операторов и условий для написания и интерпретации выражений
- Используйте таблицу истинности для интерпретации сложных утверждений или условий
- Напишите таблицы истинности с учетом логического следствия и связанных с ним утверждений — обратных, обратных и контрапозитивных
- Определить, являются ли два оператора логически эквивалентными
- Использовать законы ДеМоргана для определения логических эквивалентностей утверждения
Поскольку сложные логические утверждения могут быть сложными для понимания, мы можем создать таблицу истинности , чтобы разбить сложное утверждение на простые утверждения и определить, истинны они или ложны.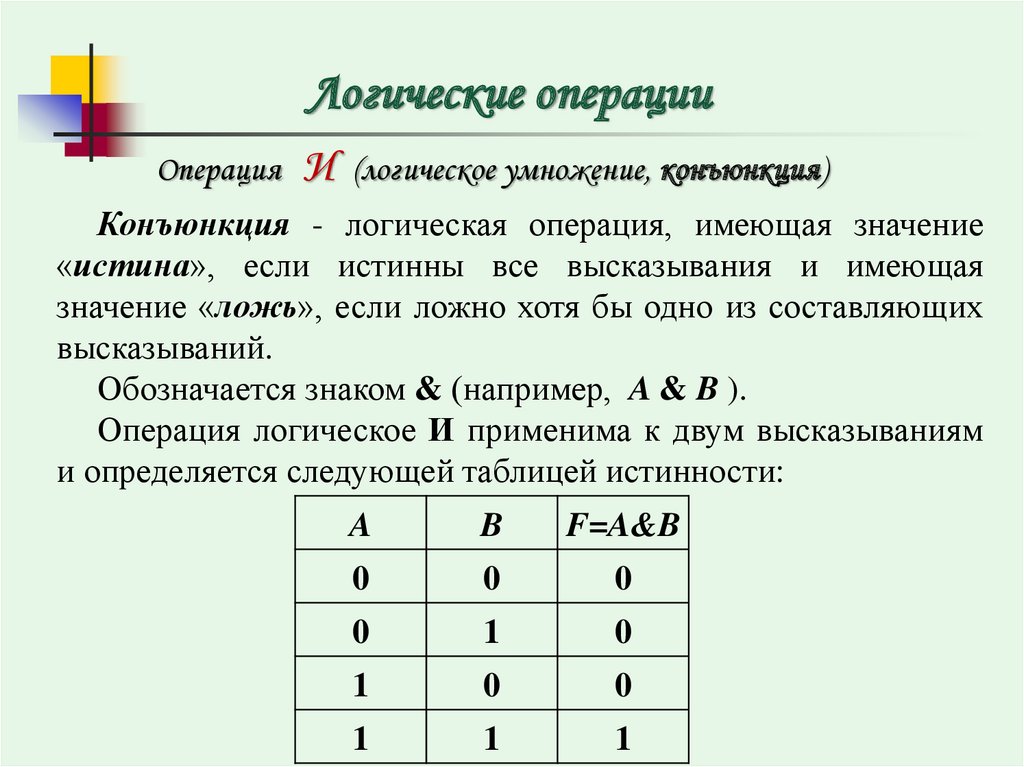
Таблица поможет отслеживать все значения истинности простых утверждений, составляющих сложное утверждение, что приведет к анализу всего утверждения.
Таблица истинности
Таблица, показывающая результирующее значение истинности сложного утверждения для всех возможных значений истинности простых утверждений.
Пример
Предположим, вы выбираете новый диван, и ваша вторая половинка говорит: «Купите секционный или что-нибудь с шезлонгом». Постройте таблицу истинности, описывающую элементы условий этого утверждения и соблюдение условий.
Показать решение
Некоторые символы, которые обычно используются для и , или и , а не , облегчают использование таблицы истинности.
Символы
Символ [латекс]\клин[/латекс] используется для и : A и B обозначается как [латекс]А\клин {В}[/латекс].
Символ [латекс]\vee[/латекс] используется для или : A или B обозначается как [латекс]A\vee{B}[/латекс]
Символ [латекс]\ sim[/latex] используется для не : не A обозначается как [latex]\sim{A}[/latex]
Вы можете запомнить первые два символа, связав их с фигурами для объединения и пересечения .
[latex]A\wedge{B}[/latex] – это элементы, существующие в обоих наборах, в [latex]A\cap{B}[/latex]. Точно так же [latex]A\vee{B}[/latex] будет элементами, которые существуют в любом наборе, в [latex]A\cup{B}[/latex].
В предыдущем примере таблица истинности просто обобщала то, что мы уже знаем о том, как работают операторы или . Ниже показаны таблицы истинности для основных утверждений и , или и , а не .
Основные таблицы истинности
| А | Б | [латекс]A\клин {B}[/латекс] |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Ф |
| Ф | Ф | Ф |
| А | Б | [латекс]A\vee{B}[/латекс] |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Т |
| Ф | Т | Т |
| Ф | Ф | Ф |
| А | [латекс]\sim{A}[/латекс] |
|---|---|
| Т | Ф |
| Ф | Т |
Попробуйте
Таблицы истинности очень полезны при анализе более сложных логических выражений.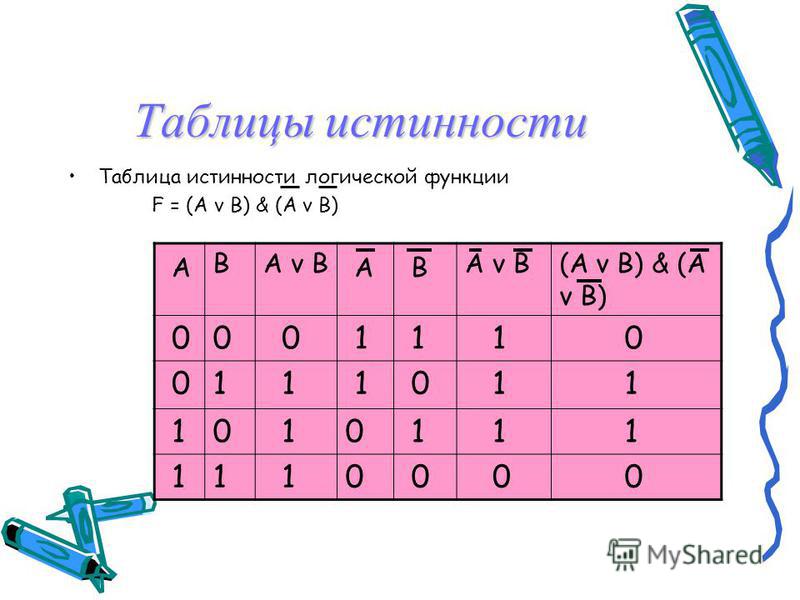
Пример
Создать таблицу истинности для утверждения [latex]A\wedge\sim\left(B\vee{C}\right)[/latex]
Показать решение
Попробуйте
Когда мы обсуждали условия ранее, мы обсуждали тип, при котором мы предпринимаем действие на основе значения условия. Теперь мы поговорим о более общей версии условного предложения, иногда называемой импликацией .
Импликации
Импликации — это логические условные предложения, утверждающие, что утверждение p , называемое антецедентом, подразумевает следствие q .
Импликации обычно записываются как [latex]p\rightarrow{q}[/latex]
Импликации аналогичны условным операторам, которые мы рассматривали ранее; [latex]p\rightarrow{q}[/latex] обычно записывается как «если p, то q» или «p, следовательно, q». Разница между импликациями и условными предложениями заключается в том, что условные предложения, которые мы обсуждали ранее, предполагают действие — если условие истинно, то в результате мы предпринимаем какое-то действие.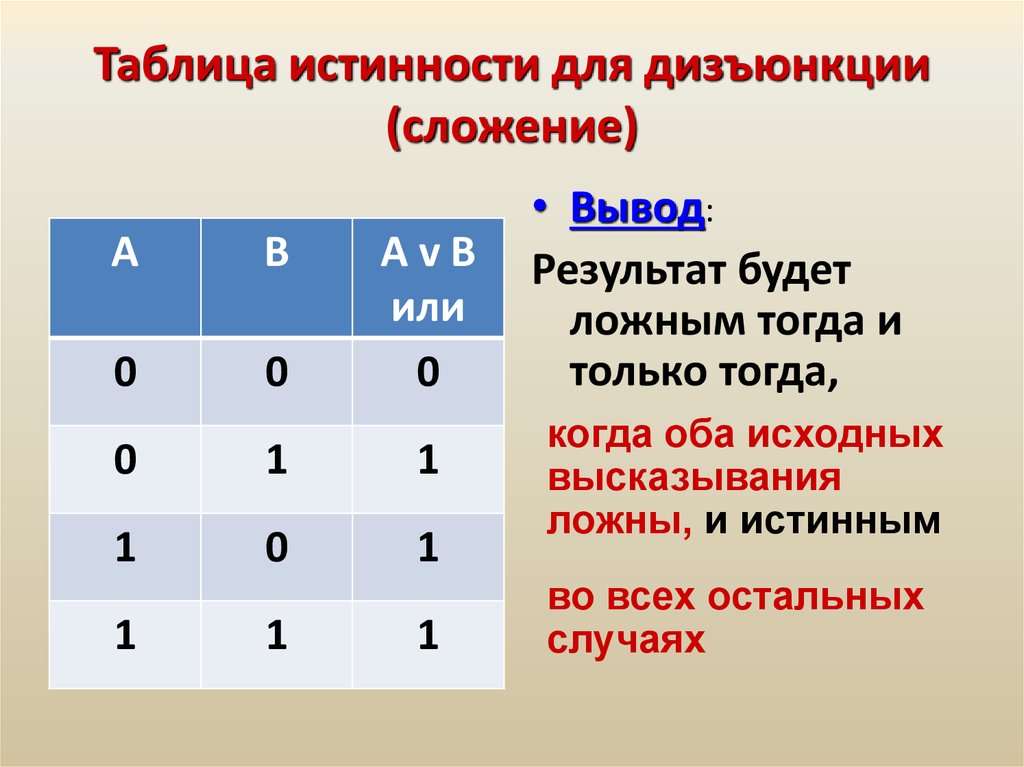
Импликации — это логическое утверждение, предполагающее, что следствие должно логически следовать, если антецедент истинен.
Пример
Английское высказывание «Если идет дождь, то облака — это небо» является логическим следствием. Является ли это веским аргументом, почему или почему нет?
Показать решение
Обратите внимание, что это утверждение ничего не говорит нам о том, чего ожидать, если не идет дождь. Если антецедент ложен, то импликация становится нерелевантной.
Пример
Друг говорит вам, что «если вы загрузите это изображение на Facebook, вы потеряете работу». Опишите возможные результаты, связанные с этим утверждением, и определите, является ли утверждение вашего друга недействительным.
Показать решение
В традиционной логике импликация считается достоверной (истинной), если нет случаев, в которых антецедент истинен, а следствие ложно. Важно помнить, что символическая логика не может охватить все тонкости английского языка.
Значения истинности для следствий
| р | q | р → q |
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Т |
| Ф | Ф | Т |
Пример
Построить таблицу истинности для утверждения [latex]\left(m\wedge\sim{p}\right)\rightarrow{r}[/latex]
Показать решение
Попробуйте
Для любого следствия есть три связанных утверждения: обратное, обратное и противоположное.
Связанные операторы
Первоначальный вывод: «если p , то q »: [latex]p\rightarrow{q}[/latex]
Обратное: «if q then p »: [latex]q\rightarrow{p}[/latex]
Обратное: «если не p , то не q »: [latex]\sim{p}\rightarrow\sim{q}[/latex]
Противоположный вариант «если не q , то не p »: [latex]\sim{q}\rightarrow{p}[/latex]
Пример
Рассмотрим еще раз верный вывод: «Если идет дождь, значит, в небе облака».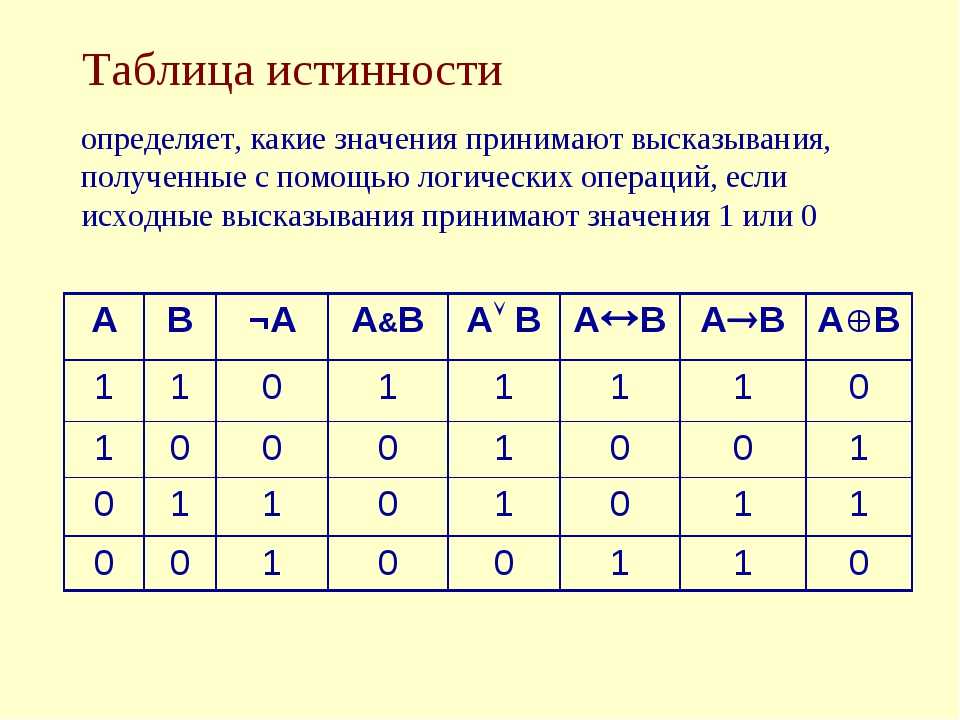
Напишите соответствующие обратные, обратные и противоположные утверждения.
Показать решение
Попробуйте
Глядя на таблицы истинности, мы видим, что исходное условное и контрапозитивное логически эквивалентны, а обратное и обратное логически эквивалентны.
| Значение | Конверс | Инверсия | Противоположный | ||
|---|---|---|---|---|---|
| р | q | [латекс]p\стрелка вправо{q}[/латекс] | [латекс] q {\ rightarrow} р [/латекс] | [латекс]\sim{p}\стрелка вправо\sim{q}[/латекс] | [латекс]\sim{q}\стрелка вправо\sim{p}[/латекс] |
| Т | Т | Т | Т | Т | Т |
| Т | Ф | Ф | Т | Т | Ф |
| Ф | Т | Т | Ф | Ф | Т |
| Ф | Ф | Т | Т | Т | Т |
Эквивалентность
Условное утверждение и его противоположность логически эквивалентны.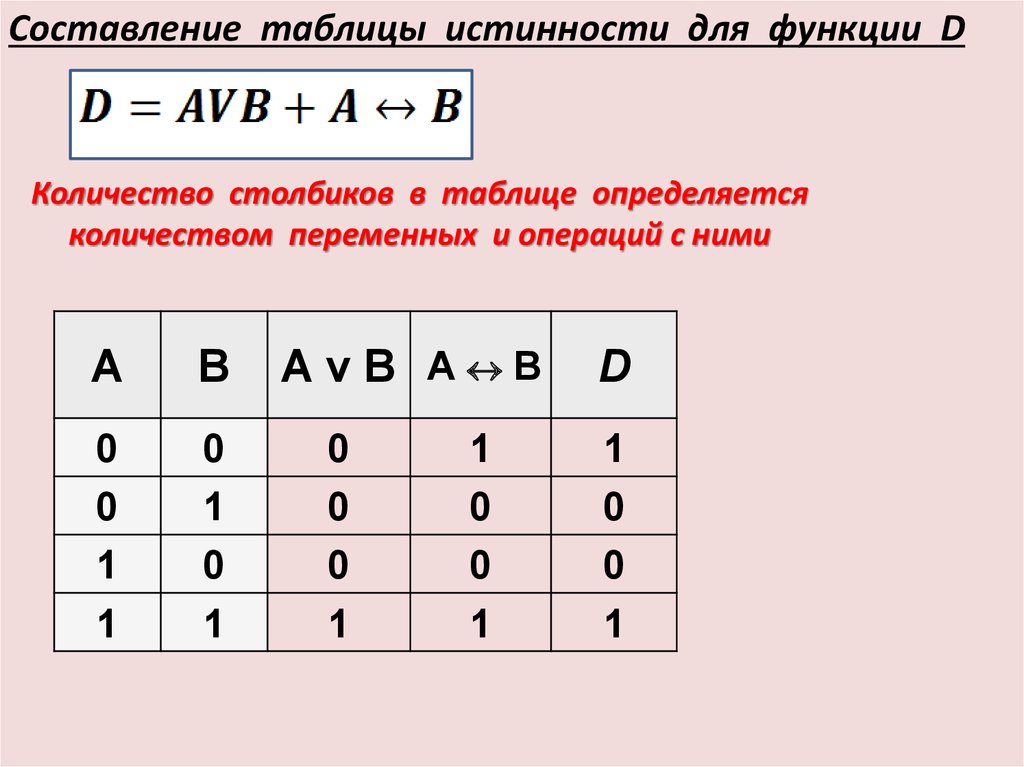
Обратное и обратное утверждения логически эквивалентны.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Домашняя страница > Логика > Символика Логика > Логические связки | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Философия 103: Введение в логику Конъюнкция, отрицание и дизъюнкция Аннотация: Логические операции конъюнкции, отрицания и дизъюнкции (альтерации) обсуждаются относительно их табличных определений истинности.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Присылайте исправления или предложения по адресу webmaster@philosophy.  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
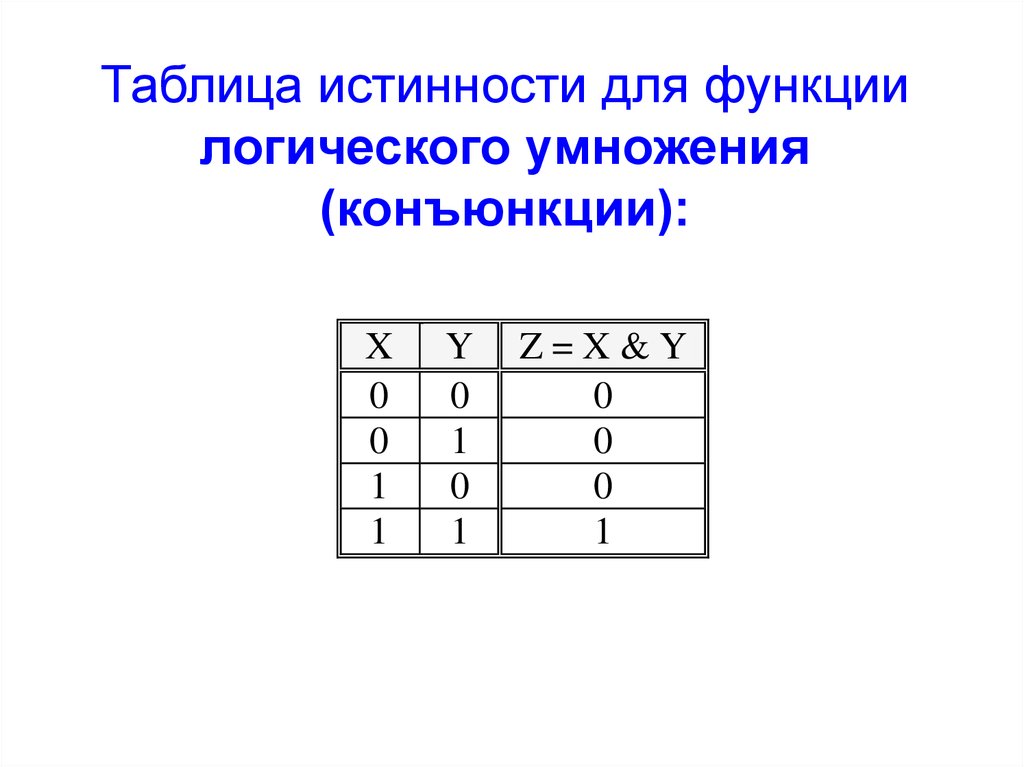
Эти случаи могут быть
перечислены ниже в том, что называется таблица истинности .
Его можно рассматривать как «минимальный
общее логическое значение» для соединенных утверждений.
которые ложны, только если оба утверждения (дизъюнкты) ложны.
» Если в этом примере Джон не на
библиотека и Джон не учится, то истинность сложного утверждения
неверно:
