Мультиплексоры, демультиплексоры. Основные положения, таблицы истинности, синтез. План

1. Мультиплексор.

2. Демультиплексор.

3. Примеры использования ИМС .

Ход лекции

1. Мультиплексор

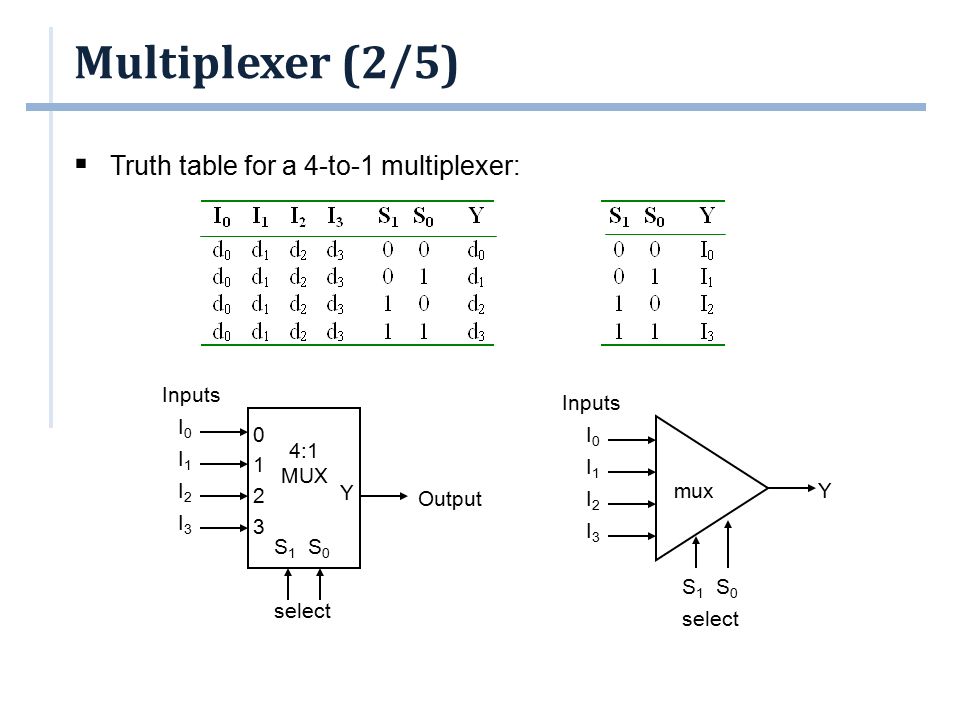
М ультиплексор является устройством, которое осуществляет выборку одного из нескольких информационных входов и подключает его к выходу в соответствии с заданным кодом на управляющих входах.

D₀, D₁, D₂, D₃ – информационные входы;

А₀, А₁ – адресные входы;

С – вход для подачи стробирующего сигнала;

Q – выход;

Каждому информационному входу присваивается адрес. При подаче стробирующего сигнала на вход С мультиплексор выбирает один из входов, адрес которого задается двоичным кодом на адресных входах, и подключает его к выходу.

Н

Адресные входы		Строб. сигнал	Выходы
А1	А0	С	Q
X	X	0	O
0	0	1	D0
0	1	1	D1
1	0	1	D2
1	1	1	D3

апример, для восьмиразрядного мультиплексора если подать на адресные входы код 0001₂ = 1₁₀, то на выход будет передана информация с 1-го входа. Если адресный сигнал будет иметь вид 0110₂ = 6₁₀ – на выход будет передана информация с 6-го входа.

Число информационных входов n

инф. и число адресных n_адр. связаны:

n_инф. = 2^nадр.

При отсутствии стробирующего сигнала (С = 0) связь между информационными входами и выходом отсутствует (Q = 0). При подаче стробирующего сигнала (С = 1) на выход передается логический уровень того из информационных входов D_i, номер I которого в двоичной форме задан на адресных входах. Так, при задании адреса А₁А₀ = 11₂ = 3₁₀ на выход Q будет передаваться сигнал информационного входа D₃.

По табл. можно записать следующее логическое выражение для Q:

Можно заметить, что для каждого входа D комбинации сигналов управления А₁, А₂ в мультиплексоре такие же, как в дешифраторе. Следовательно, составной частью мультиплексора является дешифратор.

В случаях, когда требуется передавать на выходы многоразрядные входные данные в параллельной форме, то используется параллельное включение мультиплексоров. Количество необходимых мультиплексоров определяется по числу разрядов передаваемых данных.

Пример: Пусть требуется реализовать функцию, записанную в СДНФ: F = . Т.к. управляющими сигналами 101, 011 и 100 активизируются информационные входы D

5, D₃ и D₄, то подадим на них константу 1, а на остальные – 0. При наличии синхронизирующего входа, на него также необходимо подать 1.

2. Демультиплексор

В функциональном отношении противоположны мультиплексорам. Здесь сигналы с одного информационного входа распределяются в желаемой последовательности по нескольким выходам. Выбор нужной выходной шины обеспечивается кодом на адресных входах.

А – адресный вход

При А = 1 верхний элемент И заперт и на выходе F₀ = 0, нижний открыт и работает как повторитель информационных сигналов.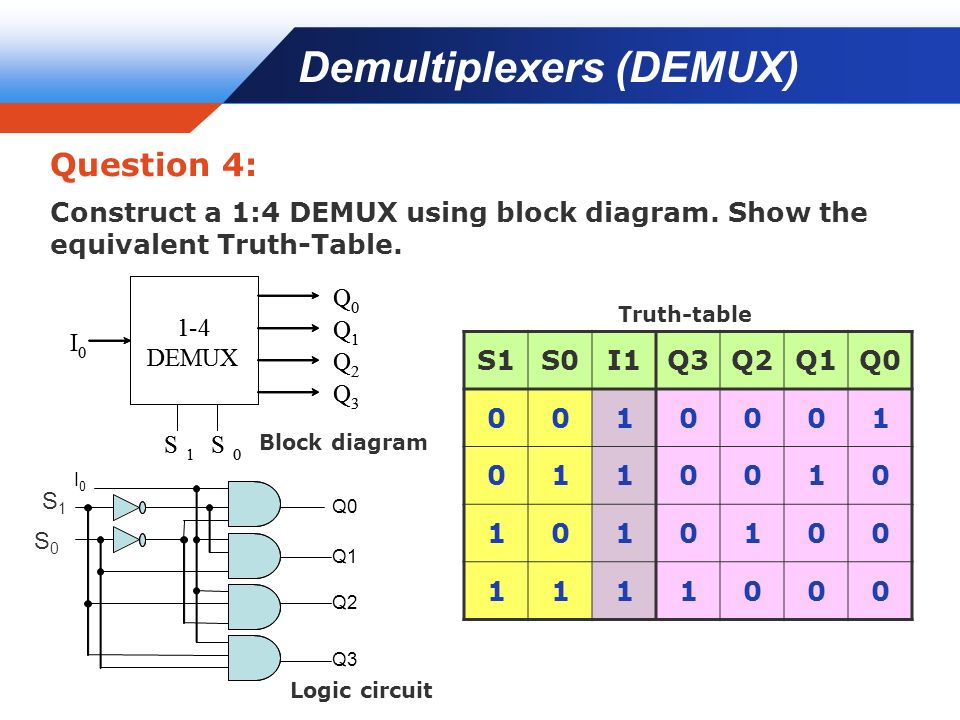

При А = 0 – наоборот.

входы				выходы
А2	А1	Х	С	F0	F1	F2	F3
0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0/1 0/1 0/1 0/1 х х х х	0 0 0 0 1 1 1 1	0/1 1 1 1 0 1 1 1	1 0/1 1 1 1 0 1 1	1 1 0/1 1 1 1 0 1	1 1 1 0/1 1 1 1 0

Исследование комбинационных схем | Лаборатория Электронных Средств Обучения (ЛЭСО) СибГУТИ

Лабораторная работа выполняется с помощью учебного лабораторного стенда LESO2.

1 Цель работы

Целью работы является изучение принципов действия комбинационных схем: дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.

2 Краткие теоретические сведения

2.1 Дешифратор (декодер)

Дешифратор (декодер) служит для преобразования n-разрядного позиционного двоичного кода в единичный выходной сигнал на одном из 2n выходов. При каждой входной комбинации сигналов на одном из выходов появляется 1. Таким образом, по единичному сигналу на одном из выходов можно судить о входной кодовой комбинации. Таблица истинности для декодера с двумя входами изображена в таблице 2.1.

Таблица 2.1 – Таблица истинности двухразрядного дешифратора

x1	x2	y0	y1	y2	y3
0	0	1	0	0	0
0	1	0	1	0	0
1	0	0	0	1	0
1	1	0	0	0	1

Для построения схемы декодера по таблице истинности воспользуемся методикой, изложенной в лабораторной работе №1, выполняемой на стенде LESO2. Например, устройство должно иметь 4 выхода. Для каждого выхода записываем логическое выражение. На основе СДНФ:

y0 = x1·x2

y1 = x1·x2

y2 = x1·x2

y3 = x1·x2

По этой системе выражений несложно построить схему требуемого дешифратора (рисунок 2.1).

Рисунок 2.1 – Схема дешифратора

Условное графическое обозначение такого дешифратора изображено на рисунке 2.2.

Рисунок 2.2 – Условное графическое обозначение дешифратора

2.2 Шифратор (кодер)

Шифратор выполняет функцию, обратную декодеру (дешифратору), то есть преобразует непозиционный (унитарный) двоичный 2n разрядный код в n разрядный позиционный код. При подаче на один из входов единичного сигнала на выходе формируется соответствующий двоичный код. Составим таблицу истинности шифратора при n = 2.

Таблица 2.2 – Таблица истинности шифратора при n = 2

x1	x2	x3	x4	y1	y0
1	0	0	0	0	0
0	1	0	0	0	1
0	0	1	0	1	0
0	0	0	1	1	1

Синтезируем шифратор. 4 = 16, что больше 10). Составим таблицу истинности работы такого преобразователя.

Таблица 2.3 – Таблица истинности преобразователя

Цифра	Двоичный код 8-4-2-1				a	б	в	г	д	е	ж
0	0	0	0	0	1	1	1	1	1	1	0
1	0	0	0	1	0	1	1	0	0	0	0
2	0	0	1	0	1	1	0	1	1	0	1
3	0	0	1	1	1	1	1	1	0	0	1
4	0	1	0	0	0	1	1	0	0	1	1
5	0	1	0	1	1	0	1	1	0	1	1
6	0	1	1	0	1	0	1	1	1	1	1
7	0	1	1	1	1	1	1	0	0	0	0
8	1	0	0	0	1	1	1	1	1	1	1
9	1	0	0	1	1	1	1	1	0	1	1

По ТИ несложно составить систему собственных функций для всех выходов, т. n информационных входов X на один выход Y под действием n управляющих (адресных) сигналов. На рисунке. 2.7 изображена упрощенная функциональная схема мультиплексора на идеализированных электронных ключах.

Рисунок 2.7 – Схема мультиплексора на идеализированных электронных ключах

В цифровых схемах требуется управлять ключами при помощи логических уровней. Поэтому желательно подобрать устройство, которое могло бы выполнять функции электронного ключа с управлением цифровым сигналом. Попробуем «заставить» работать в качестве электронного ключа уже знакомые нам логические элементы. Рассмотрим ТИ логического элемента «И». При этом один из входов логического элемента «И» будем рассматривать как информационный вход электронного ключа, а другой вход – как управляющий. Так как оба входа логического элемента «И» эквивалентны, то не важно какой из них будет управляющим входом. Пусть вход X будет управляющим, а Y – информационным. Для простоты рассуждений, разделим ТИ на две части в зависимости от уровня логического сигнала на управляющем входе X.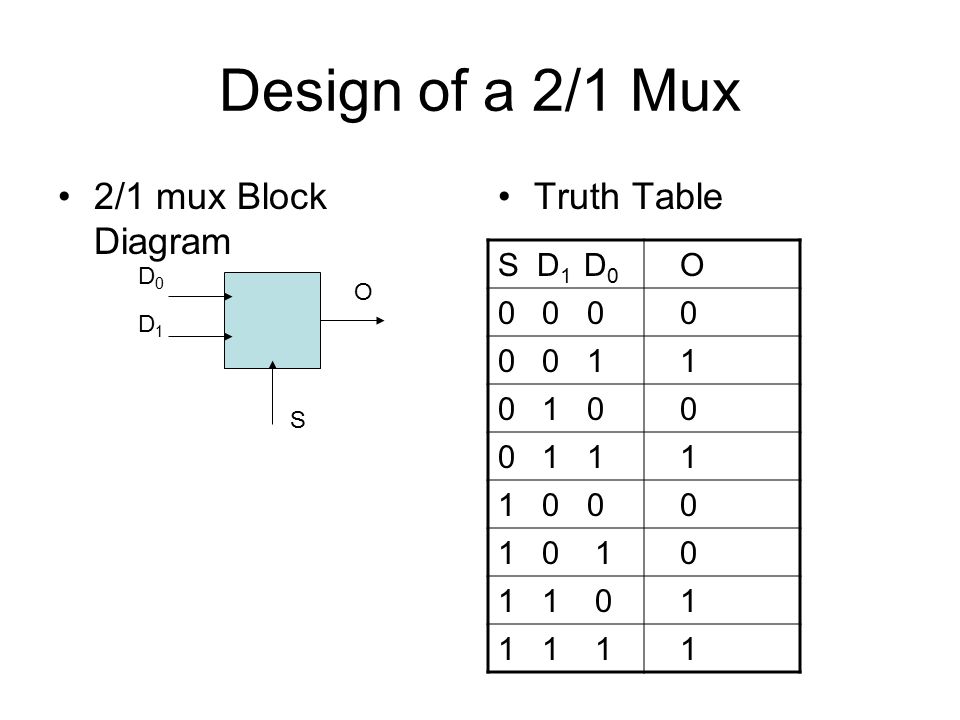

Таблица 2.4 – Таблица истинности

y	x	Out
0 0	0 1	0 0
1 1	0 1	0 1

По таблице истинности отчётливо видно, что если на управляющий вход X подан нулевой логический уровень, сигнал, поданный на вход Y, на выход Out не проходит. При подаче на управляющий вход X логической единицы, сигнал, поступающий на вход Y, появляется на выходе Out. Это означает, что логический элемент «И» можно использовать в качестве электронного ключа. При этом не важно, какой из входов элемента «И» будет использоваться в качестве управляющего входа, а какой – в качестве информационного. Остается только объединить выходы элементов «И» на один общий выход. Это делается при помощи логического элемента «ИЛИ» точно так же как и при построении схемы по произвольной таблице истинности. Получившийся вариант схемы коммутатора с управлением логическими уровнями приведён на рисунке 2.8.

Рисунок 2.8 – Принципиальная схема мультиплексора, выполненная на логических элементах

В схемах, приведенных на рисунках 2.7 и 2.8, можно одновременно включать несколько входов на один выход. Однако обычно это приводит к непредсказуемым последствиям. Кроме того, для управления таким коммутатором требуется много входов, поэтому в состав мультиплексора обычно включают двоичный дешифратор, как показано на рисунке 2.9. Такая схема позволяет управлять переключением информационных входов мультиплексора при помощи двоичных кодов, подаваемых на его управляющие входы. Количество информационных входов в таких схемах выбирают кратным степени числа два.

Рисунок 2.9 – Принципиальная схема мультиплексора, управляемого двоичным кодом

Условное графическое обозначение 4–х входового мультиплексора с управлением двоичным кодом приведено на рисунке 2. 10. Входы A0 и A1 являются управляющими входами мультиплексора, определяющими адрес информационного входного сигнала, который будет соединён с выходным выводом мультиплексора Y. Информационные входные сигналы обозначены: X0, X1, X2 и X3.

Рисунок 2.10 – Условное графическое обозначение 4-х входового мультиплексора

В условном графическом обозначении названия информационных входов A, B, C и D заменены названиями X0, X1, X2 и X3, а название выхода Out заменено на название Y. Такое обозначение входов и выходов мультиплексора более распространено в отечественной литературе. Адресные входы обозначены как A0 и A1.

Об особенностях реализации мультиплесоров на языке Verilog можно почитать в статье:
Архитектура ПЛИС. Часть 2. Мультиплексор

2.5 Сумматор

Сумматор – узел компьютера, предназначенный для сложения двоичных чисел. Построение двоичных сумматоров обычно начинается с сумматора по модулю 2.

Сумматор по модулю 2

Схема сумматора по модулю 2 совпадает со схемой исключающее «ИЛИ».

Таблица 2.5 – Таблица истинности сумматора по модулю 2

x1	x2	y
0	0	0
0	1	1
1	0	1
1	1	0

Логическое выражение, описывающее сумматор по модулю 2:

y = x1 · x2 + x1 · x2

Рисунок 2.11 – Условное графическое обозначение сумматора по модулю 2

На основе логического уравнения, описывающего этот элемент можно синтезировать схему:

Рисунок 2.12 – Схема сумматора по модулю 2

Сумматор по модулю 2 выполняет суммирование без учёта переноса. В обычном двоичном сумматоре требуется учитывать перенос, поэтому требуются схемы, позволяющие формировать перенос в следующий двоичный разряд. Таблица истинности такой схемы, называемой полусумматором, приведена в таблице 2.6.

Таблица 2.6 – Таблица истинности полусумматора

A	B	S	P0
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Здесь A и B – слагаемые;
S – сумма;
P0 – перенос в старший разряд (выход переноса Pout).
Запишем систему собственных функций для полусумматора:

S = A · B + A · B
P0 = A · B

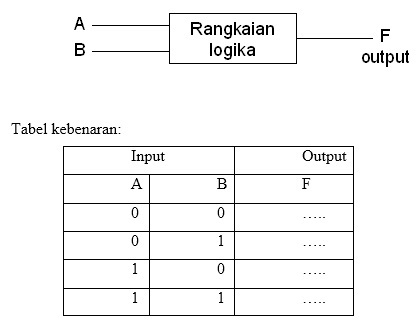Рисунок 2.13 – Принципиальная схема, реализующая таблицу истинности полусумматора Рисунок 2. 14 – Изображение полусумматора на схемах

Полный сумматор.

Схема полусумматора формирует перенос в старший разряд, но не может учитывать перенос из младшего разряда. При сложении многоразрядных двоичных чисел необходимо складывать три цифры в каждом разряде – 2 слагаемых и единицу переноса из предыдущего разряда PI.

Таблица 2.7 – Таблица истинности полного сумматора

PI	A	B	S	PO
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

 
PI – вход 1 переноса из предыдущего разряда,
PO – выход 1 переноса в старший разряд.

На основании таблицы истинности запишем систему собственных функций для каждого выхода:

S = A · B · PI + A · B · PI + A · B · PI + A · B · PI

PO = A · B · PI + A · B · PI + A · B · PI + A · B · PI

В результате получим схему полного сумматора (рисунок 2.15).

Рисунок 2.15 – Принципиальная схема, реализующая таблицу истинности полного двоичного одноразрядного сумматора 

Рисунок 2.16 – Изображение полного двоичного одноразрядного сумматора на схемах

Теория Вопросы

3 Задание к работе

3.1 Исследовать принцип работы дешифратора 2 x 4

Сконфигурировать ПЛИС в соответствии с рисунком 3.1. Подключить к входам X0 и X1 переключатели S7 и S8, а к выходам Y0, Y1, Y2, Y3 светодиодные индикаторы LED5, LED6, LED7, LED8. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС.

Рисунок 3.1 – Схема дешифратора

Подавая все возможные комбинации логических уровней на входы X0, X1 с помощью ключей S7, S8 и наблюдая за состояниями светодиодных индикаторов LED5, LED6, LED7, LED8, заполните таблицу истинности дешифратора.

Таблица 3.1 – Таблица дешифратора

x1	x2	y0	y1	y2	y3
0	0
0	1
1	0
1	1

3. 2 Исследовать принцип работы шифратора 4×2
Сконфигурировать ПЛИС в соответствии с рисунком 3.2.

Рисунок 3.2 – Схема шифратора 4×2

Подключить к входам X1, X2, X3, X4 переключатели S8, S7, S6, S5, а к выходам Y0, Y1 светодиодные индикаторы LED8, LED7. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС. Подавая все возможные комбинации логических уровней на входы X1, X2, X3, X4 с помощью ключей S8, S7, S6, S5 и наблюдая за состояниями светодиодных индикаторов LED7, LED8, заполните таблицу истинности шифратора.

Таблица 3.2 – Таблица истинности шифратора

x1	x2	x3	x4	y1	y0
1	0	0	0
0	1	0	0
0	0	1	0
0	0	0	1

3. 3 Исследовать работу преобразователя кода для семисегментного индикатора.

Составить таблицу истинности преобразователя кода (таблица. 3.3).
Собрать схему, изображенную на рисунке 3.3.

Таблица 3.3 – Таблица истинности преобразователя

x3	x2	x1	x0	A	B	C	D	E	F	G
0	0	0	0
0	0	0	1
0	0	1	0
0	0	1	1
0	1	0	0
0	1	0	1
0	1	1	0
0	1	1	1
1	0	0	0
1	0	0	1

 Рисунок 3. 3 – Схема преобразователя кода для семисегментного индикатора

Подавая с помощью ключей S8, S7, S6, S5 различные кодовые комбинации на входы X0, X1, X2, X3 определить цифры, высвечиваемые на индикаторе. По результатам эксперимента заполнить таблицу 3.4.

Таблица 3.4 – Таблица, описывающая работу преобразователя кода для семисегментного индикатора

x3	x2	x1	x0	Показание индикатора
0	0	0	0
0	0	0	1
0	0	1	0
0	0	1	1
0	1	0	0
0	1	0	1
0	1	1	0
0	1	1	1
1	0	0	0
1	0	0	1

3.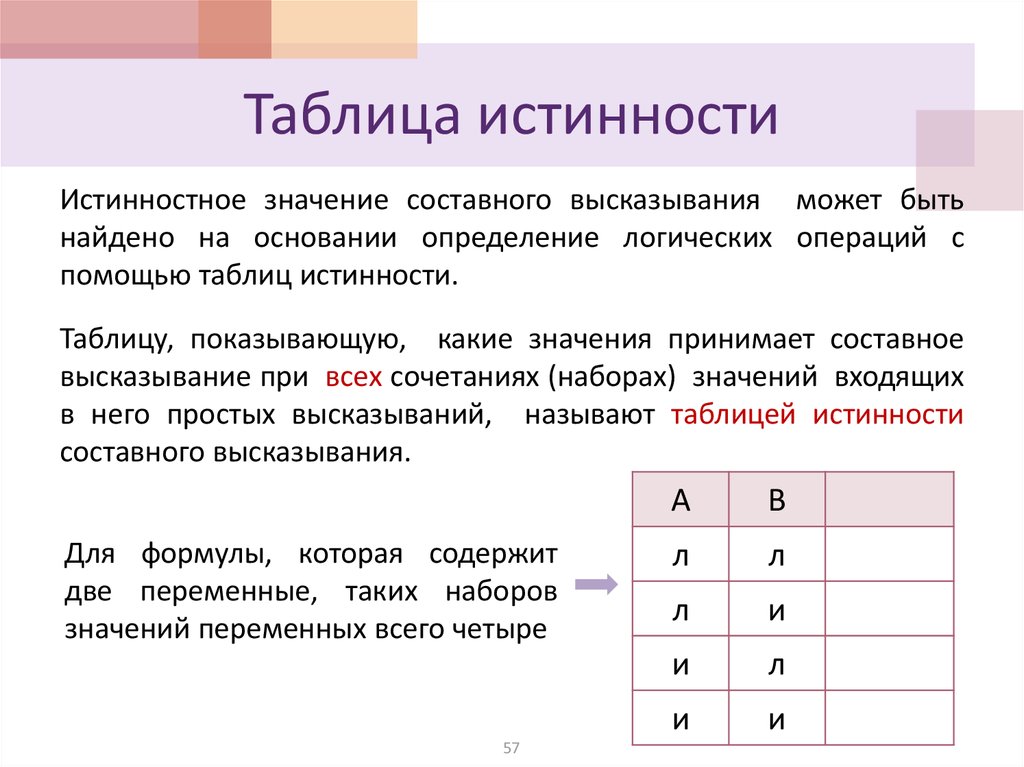 4 Исследовать работу мультиплексора 4×1

Сконфигурировать ПЛИС в соответствии с рисунком 3.4.

Рисунок 3.4 – Схема мультиплексора 4×1

Поочередно устанавливая все возможные кодовые комбинации на адресных входах A и B, определите номера коммутируемых каналов. Номер коммутируемого канала определяется путем поочерёдного подключения к входам X0, X2, X3, X4 уровня логической единицы и наблюдения за выходом Y. Заполните таблицу 3.5.

Таблица 3.5 – Таблица, описывающая работу мультиплексора

B	A	Номер коммутируемого канала
0	0
0	1
1	0
1	1

3.5 Исследовать схему сумматора

Сконфигурировать ПЛИС в соответствии с рисунком 3. 5. Здесь Pin, Pout соответственно вход и выход единицы переноса, A и B – слагаемые, S – сумма.

Рисунок 3.5 – Схема сумматора

Заполнить таблицу истинности сумматора (таблица 3.6).

Таблица 2.7 – Таблица истинности полного сумматора

Pin	B	A	Pout
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

 

4 Содержание отчета

1. Цель работы.
2. Схемы исследования дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.
3. Таблицы истинности для каждой схемы.
4. Выводы по каждому заданию.

5 Контрольные вопросы

1. Принцип работы дешифратора?
2. Как синтезировать дешифратор с произвольной разрядностью?
3. Как работает шифратор?
4. Изобразите таблицу истинности шифратора.
5. Как работает преобразователь кода для семисегментного индикатора?
6. Как устроен семи сегментный индикатор?
7. Как работает мультиплексор?
8. Как в лабораторной работе проводилось исследование мультиплексора?
9. Как работает сумматор?
10. Изобразите таблицу истинности шифратора.
11. Что такое единица переноса?

Работа мультиплексора 4 в 1, таблица истинности и приложения

A Мультиплексор 4 в 1 представляет собой составную схему с максимум 2 ² входными данными; где «2» — строка выбора.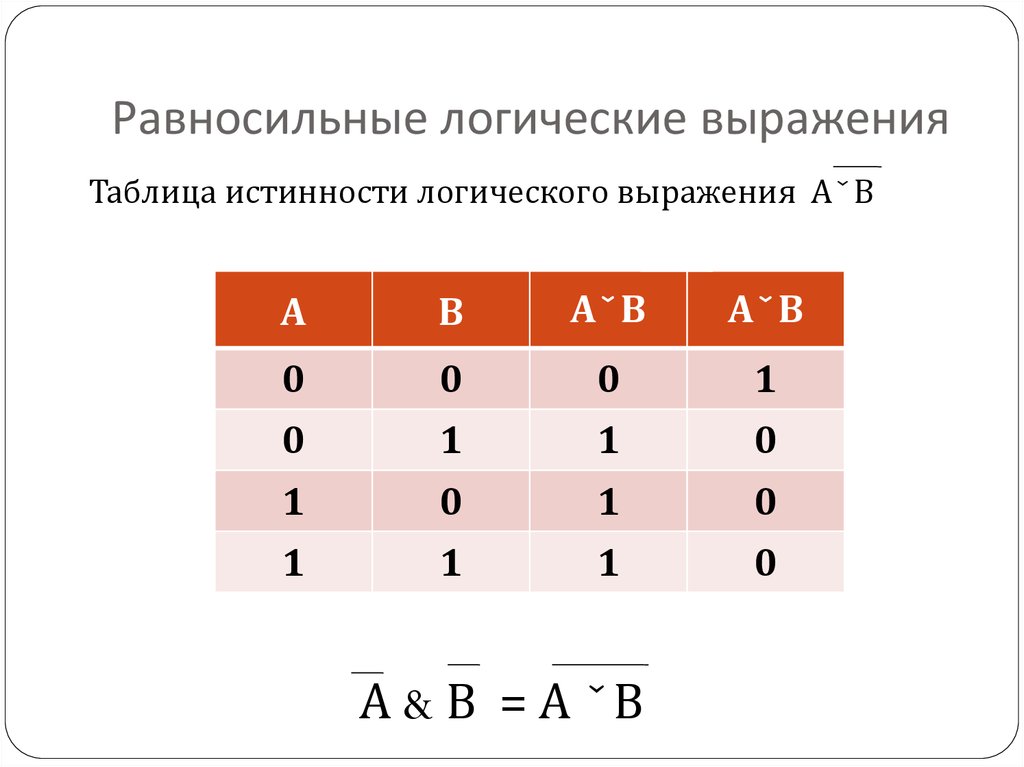 Один из этих входов данных будет подключен к выходу с выбранными строками. Поскольку имеется n строк выбора, будет примерно 2 ⁿ комбинаций «1» и «0». Мультиплексор 4 в 1 также известен как мультиплексор 4 в 1.

В этом руководстве мы рассмотрим поведение мультиплексора 4 к 1. В предыдущей лекции мы уже узнали о мультиплексоре, работе и его таблице истинности. Мультиплексор представляет собой комбинационную схему без памяти. Это означает, что текущий ввод не зависит от прошлого ввода.

Что такое мультиплексирование?

Мультиплексирование – это процесс объединения одного или нескольких сигналов и передачи по общему каналу. В аналоговых системах связи канал связи является наиболее ценной частью, которую следует использовать надлежащим образом. Для недорогого и эффективного использования канала очень полезна концепция мультиплексирования, поскольку она позволяет нескольким пользователям логически использовать один канал.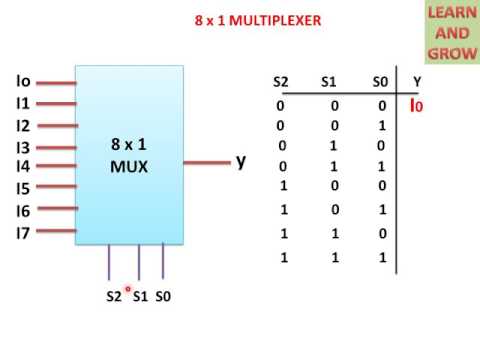
Три наиболее распространенных типа методов мультиплексирования:

• Время
• Обычно
• Космос

Два превосходных примера систем мультиплексирования, используемых в нашей повседневной жизни, — домашняя телефонная сеть и кабельное телевидение. Мультиплексоры знакомы как с аналоговыми сигналами, так и с цифровыми сигналами. Давайте сосредоточимся на цифровых сигналах в этом исследовании, чтобы не усложнять задачу. Мультиплексор является широко используемой комбинированной схемой и важным строительным блоком для многих цифровых систем.

Они широко используются для построения выбранного маршрута между несколькими источниками и одним пунктом назначения. Базовый мультиплексор имеет несколько линий ввода данных и одну исходящую линию. Применение мультиплексора в цифровых схемах — выбор данных и маршруты данных, цифровые вычислители с индикаторами мультиплексирования, телефонная сеть, системы связи, генераторы сигналов и т.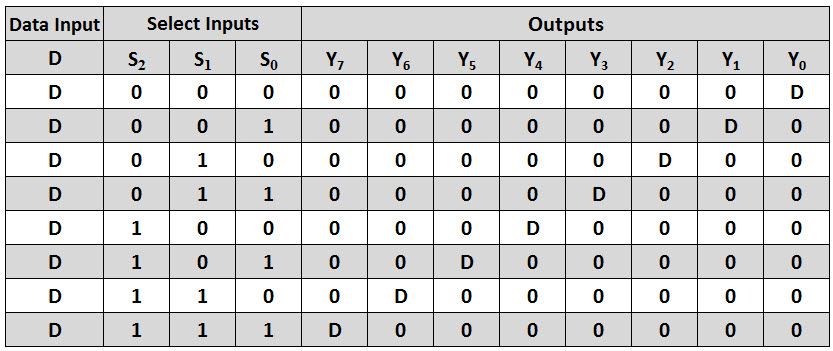 д.

Мультиплексор — комбинированная схема. Он имеет 2 ⁿ 2 входа и одну выходную линию. Другими словами, мультиплексор — это несколько входов и один выход. Двоичная информация размещается на входной линии и направляется на выходную. Выбор выходной строки зависит от выбранной строки.
В отличие от кодировщика и декодера, имеется «n» входных строк и «m» входных строк. Мультиплексор также рассматривается как MUX.

Обычно количество входных линий зависит от степени двойки, например 2, 4, 8, 16 и т. д. Некоторые из наиболее часто используемых мультиплексоров: 1 мультиплексор.
Мультиплексор также доступен в виде ИС различных конфигураций входа и выбора линии. Некоторые микросхемы мультиплексора перечислены ниже.

1. 74157 = Четырехканальный мультиплексор 2-в-1
2. 8158 = Четырехканальный мультиплексор 2-к-1
3. 74153 = мультиплексор 4-в-1
4. 74152 = мультиплексор 8-к-1
5. 74150 = мультиплексор 16:1.

Мультиплексор 4 на 1

Мультиплексор 4 на 1 содержит «ЧЕТЫРЕ» входные линии: D0 D1 D2 и D3, две выбранные линии S0 и S1 и одну выходную Y-линию. Выбранные линии S0 и S1 выбирают одну из четырех входных линий для подключения исходящей линии. На рисунке ниже показана блок-схема MUX 4:1, где мультиплексор определяет вход по выбранной линии.

Блок-схема мультиплексора 4 в 1

Ниже на рисунке показана блок-схема мультиплексора 4 в 1. В этом типе мультиплексора есть только четыре входа и одна выходная линия и линии выбора.

Принципиальная схема мультиплексора 4 на 1

Логическая схема мультиплексора 4 на 1 показана ниже. В этой логической схеме выход четырех вентилей, объединенных по схеме ИЛИ, объединен по схеме ИЛИ. Которые наглядно показаны на рисунке.

Ниже приведенной таблицы истинности мультиплексора 4 к 1, в этом типе MUX есть четыре различных комбинации входов 00, 10, 01 и 11, а две линии выбора переключают входы A0, A2, D1 и A3 на выход соответственно. . Таблица истинности выходных конфигураций мультиплексора 4 к 1.

Таблица истинности мультиплексора 4 к 1

S0	С1	А0	А1	А2	А3	Д (ВЫХОД)
0	0	0	х	х	х	0
0	0	1	х	х	х	1
0	1	х	0	х	х	0
0	1	х	1	х	х	1
1	0	х	х	0	х	0
1	0	х	х	1	х	1
1	1	х	х	х	0	0
1	1	х	х	х	1	1

 

Из приведенной выше таблицы истинности мы можем легко получить следующие выходные выражения:0255 1 ‘S ₀ A ₁ +S ₁ S ₀ ‘ A ₂ +S ₁ S ₀ A ₃ S ₀ A ₃ S ₀ A ₃ S ₀ A ₃ S _{0 3} S _{0 3} S _{0 3} . N: 1 с ‘ 9N входов. Другими словами, мультиплексор соединяет выход с одним из своих входов на основе значения, содержащегося в выбранных линиях. Мультиплексор (или обычно называемый MUX) также называется селектором данных. Общие функции мультиплексора включают концентрацию нескольких строк данных в одной строке. Его также можно использовать в качестве селектора данных или селектора часов.

Мультиплексоры можно классифицировать по количеству входов:

• Мультиплексор с 2 входами : Мультиплексор 2:1 имеет 2 линии ввода данных и 1 линию выбора. Состояние строки выбора определяет, какой из входов распространяется на выход. Таблица истинности мультиплексора 2×1 приведена ниже. Как видно, когда SEL равен 1, OUT следует за IN2, а когда SEL равен 0, OUT следует за IN1.

Логическая схема и символ мультиплексора 2×1 показаны на рисунке 2. Предположим, что логическая область мультиплексора 2:1 равна A. Рисунок 2(b): Схематическое обозначение мультиплексора 2×1

• Мультиплексор с 3 входами : Мультиплексор 3:1 имеет 2 линии выбора и 3 входа. Поскольку мультиплексор с 2 линиями выбора может представлять максимум 4 входа, мультиплексор 3:1 повторяет некоторые входы для 2 комбинаций. Таблица истинности для 3-входового мультиплексора приведена ниже. Как видно, при значениях SEL «10» и «11» на выходе выбирается IN2 (это один из 3-х возможных сценариев, также возможно повторение IN0 или IN1).

Рисунок 3: Таблица истинности для мультиплексора 3×1

Схематический символ и структурное представление (в терминах мультиплексоров 2×1) для мультиплексора 3:1 показаны на рисунке 4 ниже. Как можно понять, 1 мультиплексор 3×1 можно построить, используя 2 мультиплексора 2×1.

Рисунок 4 (A): Схематический символ для 3×1 MUX Рис. мультиплекс : Мультиплексор 4:1 имеет 2 линии выбора и 4 входа. Таблица истинности для мультиплексора 4×1 показана ниже: На рисунке 6 ниже показаны схематический символ и структурный символ мультиплексора 4:1 с использованием мультиплексоров 2:1. Как видно, мультиплексор 4:1 можно построить из 3 мультиплексоров 2:1. Рисунок 6(a): Схематическое обозначение мультиплексора 4×1    0292 Мультиплексор с 8 входами : Мультиплексор 8×1 имеет 3 линии выбора и 8 входов. Таблица истинности для мультиплексора 8×1 показана ниже: Структурное представление с использованием мультиплексоров 2×1 и их условное обозначение показано ниже на рисунке 8. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника