Принципы построения таблиц истинности
Оглавление
Время чтения: 5 минут
546
Логическая функция одно из основополагающих понятий математической логики. Она зависит от логических переменных и принимает значения из множества, от которого находится в зависимости. Логические функции булевых переменных могут принимать только два значения – 1 или 0.
Понятие таблиц истинности
Задаваться логическая функция может числовым способом, словесным описанием, картами Карно, аналитическим выражением и с помощью таблиц истинности. В последнем случае все аргументы функции следует записать в левой части таблицы, а значения, которые им соответствуют, в правой.
Определения 1 — 2
Таблица истинности – это таблица, просто и наглядно показывающая, какие значения будут у логического выражения при всевозможных наборах переменных функции.
Равносильными именуют те логические выражения с совпадающими последними столбцами таблицы истинности. Обозначают равносильные функции знаком «=».
Обозначают равносильные функции знаком «=».
Правила того, как следует проводить построение таблицы истинности
Несоблюдение хотя бы одного из них ведёт к очень грубой ошибке. Вот эти правила:
- Число строк таблицы должно совпадать с числом комбинаций всевозможных n логических переменных, то есть быть равным 2n;
- Количество столбцов таблицы должно равняться сумме числа логических переменных и числа логических операций;
- В построенный шаблон таблицы истинности должны вписываться все значения исходных переменных;
- Построение таблицы истинности выражения происходит по её столбцам, при этом обязательно учитываются правила логических операций.
Порядок действий при построении таблицы истинности для логических выражений
Порядок действий при построении таблицы истинности, какой бы ни была логическая функция, следующий:
- Определить, какое число строк и столбцов будет в будущей таблице. Делается подобное по формулам
X = n + m, Y = 2n+1.
Где n – число переменных, m – чило логических операций. - Заполнить самую верхнюю строку таблицы переменными и логическими операциями, идя слева направо. При этом приоритетность логических операций следует учитывать обязательно, иначе получится совсем не то, что нужно;
- В первых столбцах перечислить всевозможные комбинации входных значений;
- Выполняя заданные логические операции, заполнить все оставшиеся ячейки;
Ответом следует считать последний заполненный столбец таблицы.
О порядке логических операций
Лучше его представить списком. Логические операции выполняют в следующей последовательности: сначала идёт инверсия, затем конъюнкция, после этого дизъюнкция, после неё импликация, по её выполнении эквиваленция.
После них идут Штрих Шеффера и Стрелка Пирса. Первым может быть выполнено как то, так и другое.
Далее приведём несколько поучительных задач на построение таблиц истинности
Задачи 1 — 3
Сделать построение таблицы истинности для функции ((A→B) ∧ A) ↔ B
Решение:
- Определяем сколько будет у нас столбцов.
 Количество переменных у нас 2, логических операций 4, число столбцов равно сумме 2+4 = 6.
Количество переменных у нас 2, логических операций 4, число столбцов равно сумме 2+4 = 6. - Определяем, сколько будет у на строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций. У нас будет 2n+1 = 22 + 1= 5;
- Заполняем первую строку. Прописываем символы переменные и логических операций;
- В двух первых столбцах записываем возможные значения переменных;
- В далее идущих столбцах записываем, какие значения принимают промежуточные функции;
- В самом последнем из столбцов записываем итоговые значения функции.
- Определяем сколько будет у нас столбцов.
В результате всего этого у нас должно получиться:
Провести построение таблицы истинности функции (A ∨ B) ∧ – C
Решение:
- Определяем сколько будет столбцов. Количество переменных у нас 3, количество логических операций 3.
 Складываем то и другое: 3+3 = 5.
Складываем то и другое: 3+3 = 5. - Определяем, количество строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций.В итоге будет 2n+1 = 23 + 1= 9;
- Заполняем первую строку. Прописываем символы переменные и логических операций;
- В два первые столбца вносим возможные значения наших переменных;
- В далее следующие столбцы записываем, какие значения принимают промежуточные функции;
- В последнем столбце записываем итоговые значения функции.
В итоге получим таблицу:
Сделать таблицу истинности для
(A ∧ B ↔ B ∧ C) ∨ (C → A)
Функция посложнее и таблица получится значительно больше, чем предыдущая.
- Считаем столбцы. Количество переменных 3, количество логических операций 6. Значит столбцов будет 3+6=9;
- Считаем строки. Их количество будет 23+1= 9;
- Заполняем первую строку таблицы;
- В первых столбцах записываем все допустимые значения наших переменных;
- В остающихся столбцах пишем, какие наша функция принимает промежуточные значения
- В последний столбец пишем итоговые значения данной нам функции.

В итоге у нас получается таблица:
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Построения функции, если известна её таблица истинности
Совершенной дизъюнктивной нормальной формой считают такую нормальную форму, в которой отсутствуют одинаковые элементарные конъюкции и все конъюкции включают один и тот же набор переменных, куда каждая из них входит не более одного раза.
Алгоритм действий для получения СДНФ по таблице истинности:
- Отметьте в таблице строки, в которых значение функции равняется 1
- Выпишете для каждой отмеченной строки конъюкцию всех переменных. Если переменная равна 1, в конъюкцию следует включить саму эту переменную. Если переменная равняется 0, то её отрицание;
- Все полученные конъюкции свяжите в дизъюкцию.
Аналогичным образом определяется СКНФ
В строках, в последнем столбце которых функция равна 0, запишите дизъюкции всех переменных. Если значение переменной в данной строке будет 0, в дизъюкцию следует включить саму эту переменную. Если значение функции равно 1, то включить нужно её отрицание.
Если значение переменной в данной строке будет 0, в дизъюкцию следует включить саму эту переменную. Если значение функции равно 1, то включить нужно её отрицание.
Правило + задача
СДНФ всегда равно СКНФ. СДНФ = СКНФ.
Дана таблица истинности:
Выделяем в ней цветом строку
Заполняем столбцы с СДНФ и с СКНФ
Записываем СДНФ
СДНФ = A & B
Записываем СКНФ
СКНФ = (A ∨ B) & (A ∨ B) & (A ∨ B)
Оценить статью (79 оценок):
Поделиться
Жанна Ивановна Конева — Магистр прикладной информатики
Популярные статьи
Выполнение любых работ по информатике
Таблицы истинности — интернет энциклопедия для студентов
ОПРЕДЕЛЕНИЕ
Логическая функция — это функция, в которой значения переменных и значение функции выражают логическую истину.
Они могут быть либо истинными, либо ложными (1 или 0). Для функции, содержащей две переменные, существует только четыре набора переменных значений:
\(\ (1,1),(1,0),(0,1),(0,0) \)
Значения логических функций определяются с помощью таблицы истинности.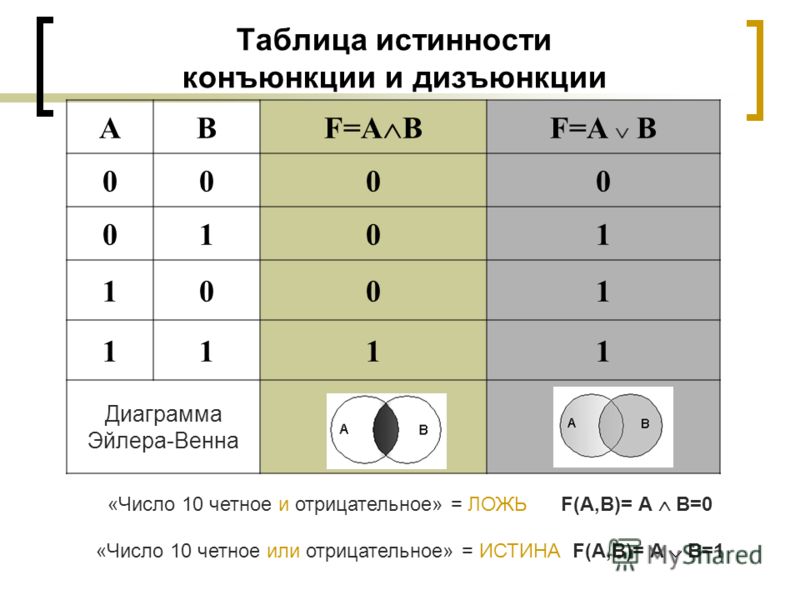
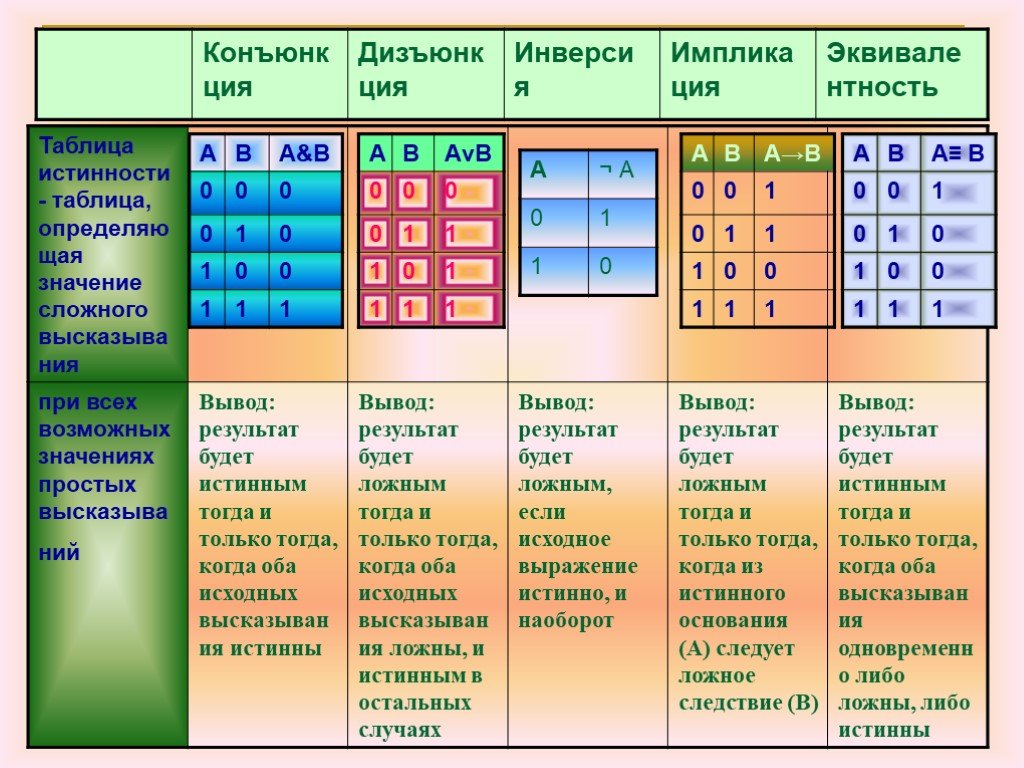
Таблицы истинности для основных двоичных логических функций
1. Конъюнкция (логическое умножение) представляет собой сложное логическое выражение, которое истинно, только если оба простых выражения истинны.
Обозначение:\(\ A \wedge B \)
\(\ \begin{array}{|c|c|c|} \hline A&B&A \wedge B\\ \hline 1&1&1\\ \hline 1&0&0\\ \hline 0&1&0\\ \hline 0&0&0\\ \hline \end{array} \)
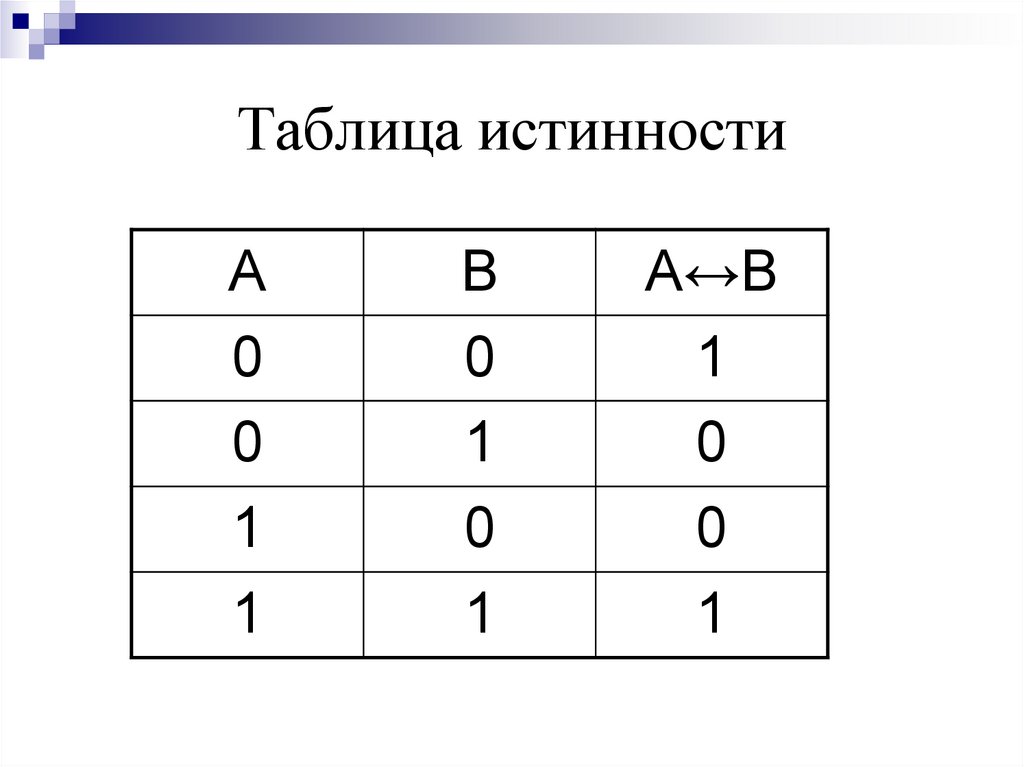
2. Дизъюнкция (логическое добавление) представляет собой сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений является истинным и ложным, если оба простых логических выражения являются ложными.
Обозначение: \(\ A \vee B \)
\(\ \begin{array}{|c|c|c|} \hline А&В&A \vee B\\ \hline 1&1&1\\ \hline 1&0&1\\ \hline 0&1&1\\ \hline 0&0&0\\ \hline \end{array} \)
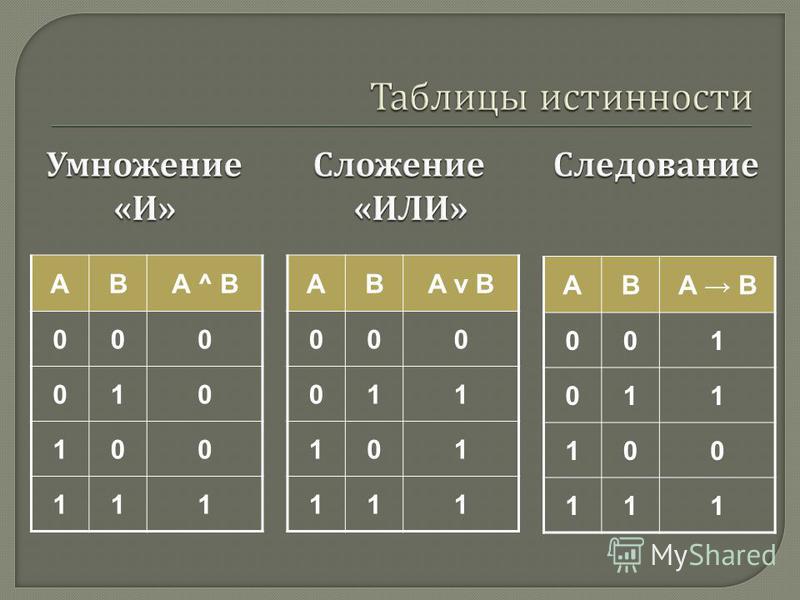
3. Импликация (логическое следствие) представляет собой сложное логическое выражение, которое является ложным тогда и только тогда, когда условие истинно и следствие является ложным.
Обозначение:\(\ A \rightarrow B \)
\(\ \begin{array}{|c|c|c|} \hline А&В&A \rightarrow B\\ \hline 1&1&1\\ \hline 1&0&0\\ \hline 0&1&1\\ \hline 0&0&1\\ \hline \end{array} \)
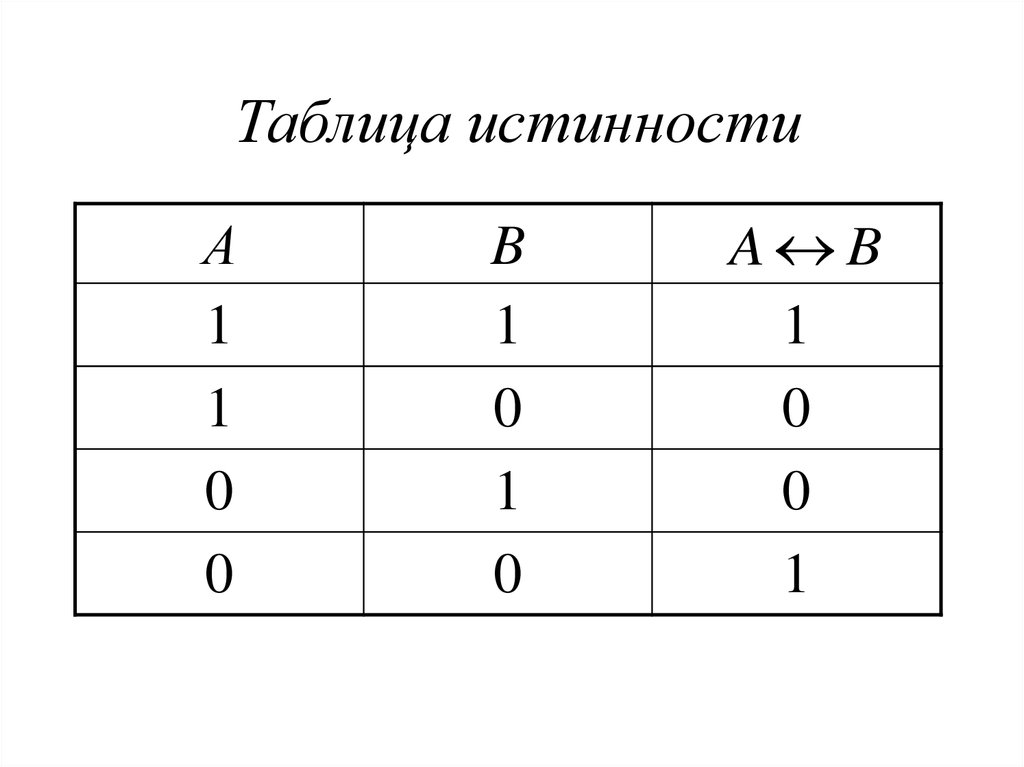
4. Эквивалентность — это сложное логическое утверждение, которое верно только для тех же значений истинности простых выражений, включенных в него.
Обозначение:\(\ A \leftrightarrow B \)
\(\ \begin{array}{|c|c|c|} \hline A&B&A \leftrightarrow B\\ \hline 1&1&1\\ \hline 1&0&0\\ \hline 0&1&0\\ \hline 0&0&1\\ \hline \end{array} \)
5. Логическое отрицание (инверсия) делает истинное утверждение ложным и, наоборот, ложное утверждение истинно.
\(\ \begin{array}{|c|c|} \hline A&\neg A\\ \hline 1&0\\ \hline 0&1\\ \hline \end{array} \)
6. Ход Шаффера — это операция, которая отрицает конъюнкцию, т. е. Значение ложно тогда и только тогда, когда оба простых выражения истинны.
Обозначение:\(\ A | B \)
\(\ \begin{array}{|c|c|c|} \hline A&B&A | B\\ \hline 1&1&0\\ \hline 1&0&1\\ \hline 0&1&1\\ \hline 0&0&1\\ \hline \end{array} \)
7. Стрелка Пирса — это операция, которая отрицает соединение, т. е. Значение истинно тогда и только тогда, когда оба простых выражения являются ложными.
Обозначение: \(\ A \downarrow B \)
\(\ \begin{array}{|c|c|c|} \hline А&В&A \downarrow B\\ \hline 1&1&0\\ \hline 1&0&0\\ \hline 0&1&0\\ \hline 0&0&1\\ \hline \end{array} \)
Процедура выполнения логических операций
При построении таблицы истинности необходимо учитывать порядок логических операций:
1. Инверсия
2. Конъюнкция
3. Дизъюнкция
4. Последствия
5. Эквивалентность
6. Шеффирский удар
7. Стрелка Пирс
Для двух последних операций приоритет не определен.
Комментарий. Если вам необходимо изменить указанный порядок логических операций, используются скобки.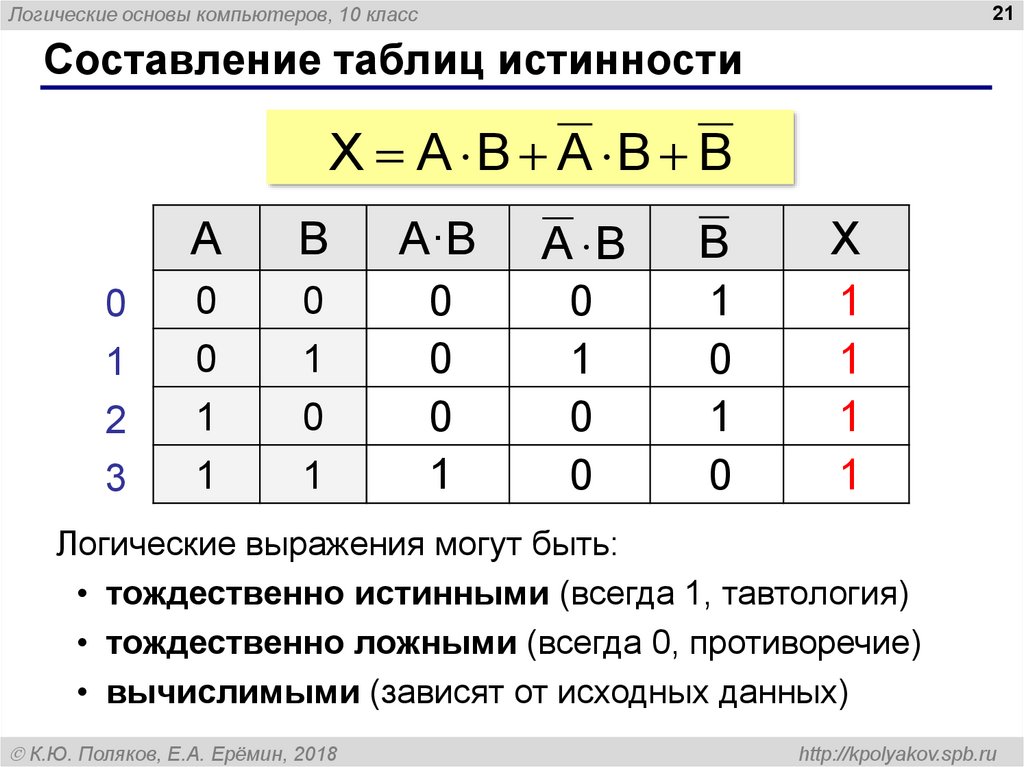
Примеры решения проблем
ПРИМЕР 1
Задача Создать таблицу истинности для функции \(\ ((A \rightarrow B) \wedge A) \leftrightarrow \overline{B} \)
Решение. Давайте сделаем таблицу истинности для данной функции, которая содержит две переменные \(\ A \) и \(\ В \). В первых двух столбцах таблицы мы пишем четыре возможные пары значений этих переменных, в последующих столбцах — значения промежуточные функции и в последнем столбце — значение функций. В результате мы получаем таблицу:
\(\ \begin{array}{|c|c|c|c|c|c|} \hline A&B&A \rightarrow B&(A \rightarrow B) \wedge A&\overline{B}&((A \rightarrow B) \wedge A) \leftrightarrow \overline{B}\\ \hline 1&1&1&1&0&0\\ \hline 1&0&0&0&1&0\\ \hline 0&1&1&0&0&1\\ \hline 0&0&1&0&1&0\\ \hline \end{array} \)
ПРИМЕР 2
\(\ (A \wedge B \leftrightarrow B \wedge C) \vee(C \rightarrow A) \)
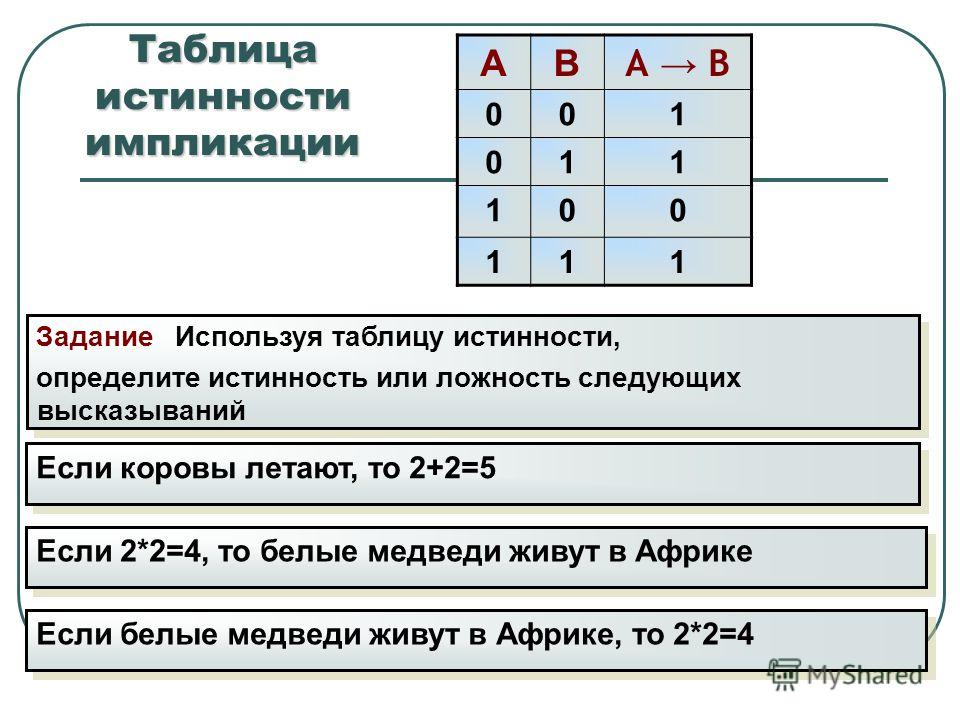
Давайте создадим таблицу истинности для данной функции, которая содержит три переменные \(\ A \), \(\ B \) и \(\ C \). Множества возможных переменных будут 8, и мы напишем их в первых трех столбцах таблицы, в последующих столбцах значения Промежуточных функций, а в последнем столбце — значения функций.
Промежуточные функции:
I — \(\ A \wedge B \)
II — \(\ B \wedge C \)
III — \(\ (A \wedge B \leftrightarrow B \wedge C) \)
IV — \(\ C \)
V — \(\ C \rightarrow A \)
VI — \(\ (A \wedge B \leftrightarrow B \wedge C) \vee(C \rightarrow A) \)
\(\ \begin{array}{|c|c|c|c|c|c|c|c|c|} \hline A&B&C&I&II&III&\mathrm{IV}&\mathrm{V}&\mathrm{VI}\\ \hline 1&1&1&1&1&1&0&1&1\\ \hline 1&1&0&1&0&0&1&1&1\\ \hline 1&0&1&0&0&1&0&1&1\\ \hline 1&0&0&0&0&1&1&1&1\\ \hline 0&1&1&0&1&0&0&1&1\\ \hline 0&1&0&0&0&1&1&0&1\\ \hline 0&0&1&0&0&1&0&1&1\\ \hline 0&0&0&0&0&1&1&0&1\\ \hline \end{array} \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Таблица котангенсов Таблица тангенсов Таблица Брадиса Таблица факториалов
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПодпишись на рассылку, чтобы не пропустить информацию об акциях
Таблица истинности | логика | Британика
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Обзор недели
- Инфографика
- Демистификация
- Списки
- #WTFact
- Товарищи
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
- Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории. - Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
- Студенческий портал
Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
- Britannica Beyond
Мы создали новое место, где вопросы находятся в центре обучения. Вперед, продолжать. Просить. Мы не будем возражать. - Спасение Земли
Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать! - SpaceNext50
Britannica представляет SpaceNext50. От полёта на Луну до управления космосом — мы исследуем широкий спектр тем, которые подпитывают наше любопытство к космосу!
Содержание
- Введение
Краткие факты
- Связанный контент
Таблицы истинности ADS и предложения, сгенерированные набором
Подраздел 3.
 2.1 Таблицы истинности
2.1 Таблицы истинностиРассмотрим сложное предложение \(c= (p \land q)\lor (\neg q \land r)\text{,}\), где \(p\text{,}\) \(q\text{, }\) и \(r\) являются предложениями. Это пример предложения, порожденного \(p\text{,}\) \(q\text{,}\) и \(r\text{.}\). Мы определим эту терминологию позже в этом разделе. Поскольку каждое из трех простых утверждений имеет два возможных значения истинности, отсюда следует, что существует восемь различных комбинаций значений истинности, которые определяют значение для \(c\text{.}\). Эти значения могут быть получены из таблицы истинности для \ (c\text{.}\) Чтобы построить таблицу истинности, мы строим \(c\) из \(p\text{,}\) \(q\text{,}\) и \(r\) и от логических операторов. Результатом является приведенная ниже таблица истинности. Строго говоря, первые три столбца и последний столбец составляют таблицу истинности для \(c\text{.}\). Остальные столбцы представляют собой рабочее пространство, необходимое для построения до \(c\text{.}\)
Таблица 3.2.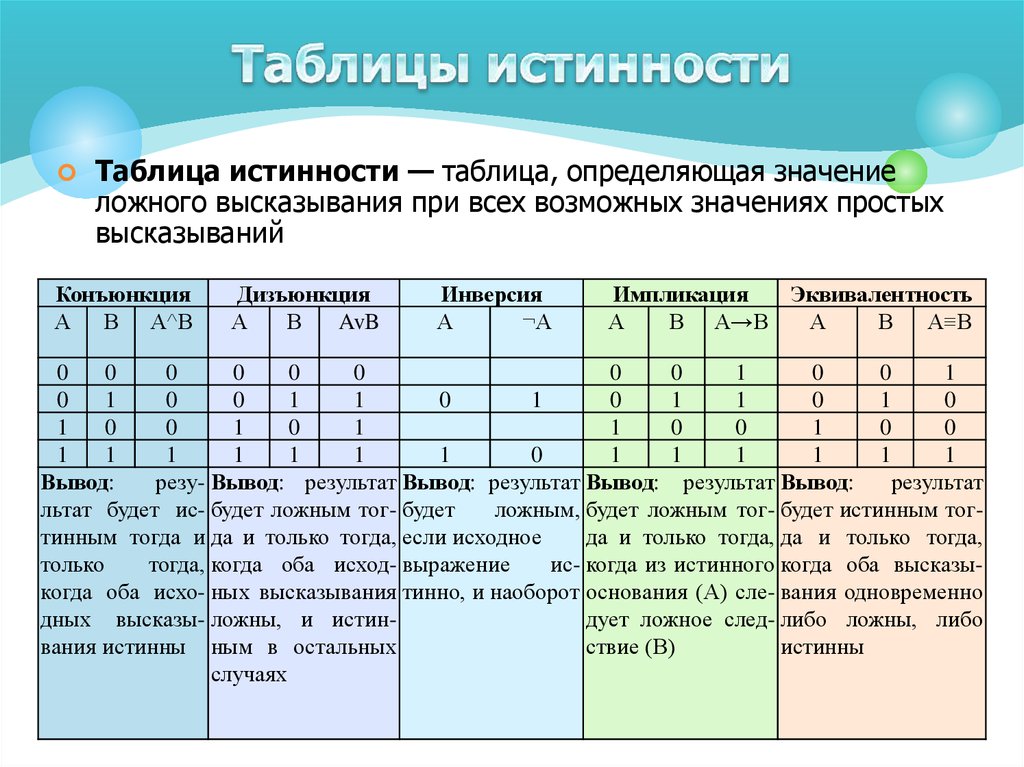 1. Таблица истинности для \(c= (p \land q)\lor (\neg q \land r)\)
1. Таблица истинности для \(c= (p \land q)\lor (\neg q \land r)\)| \(p\) | \(к\) | \(р\) | \(р\земля д\) | \(\отрицательный д\) | \(\neg q\land r\) | \((p\land q)\lor (\neg q\land r)\) |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 |
Обратите внимание, что первые три столбца таблицы истинности представляют собой перечисление восьми трехзначных двоичных целых чисел.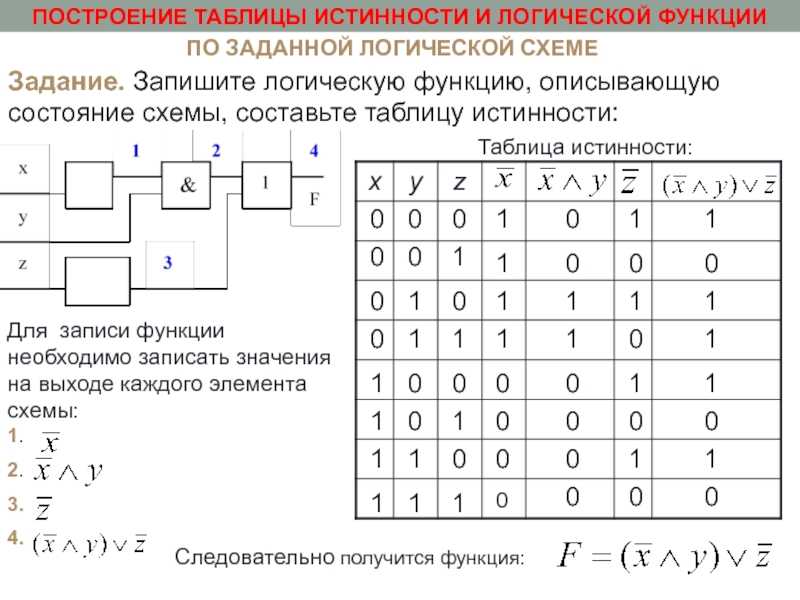 n\) строк с первыми \(n\) столбцами перечисление \(n\) цифр двоичных целых чисел. В нашем примере мы можем с первого взгляда увидеть, что ровно в четырех из восьми случаев \(с\) будет истинным. Например, если \(p\) и \(r\) истинны, а \(q\) ложно (шестой случай), то \(c\) истинно.
n\) строк с первыми \(n\) столбцами перечисление \(n\) цифр двоичных целых чисел. В нашем примере мы можем с первого взгляда увидеть, что ровно в четырех из восьми случаев \(с\) будет истинным. Например, если \(p\) и \(r\) истинны, а \(q\) ложно (шестой случай), то \(c\) истинно.
Пусть \(S\) — любое множество предложений. Мы дадим два определения предложения, порожденного S. Первое немного неточно, но должно быть ясным. Второе определение называется рекурсивным определением . Если это вас сбивает с толку, используйте первое определение и вернитесь ко второму позже.
Подраздел 3.2.2 Предложения, порожденные множеством
Определение 3.2.2. Предложение, порожденное множеством.
Пусть \(S\) — любое множество предложений. Предложение, порожденное \(S\), представляет собой любую допустимую комбинацию предложений в \(S\) с конъюнкцией, дизъюнкцией и отрицанием. Или, если быть более точным,
Если \(p \in S\text{,}\), то \(p\) является предложением, порожденным \(S\text{,}\) и
Если \(x\) и \(y\) являются предложениями, порожденными \(S\text{,}\), то таковыми являются \((x)\text{,}\) \(\neg x\text {,}\) \(x\lor y\) и \(x\land y\text{.
 }\)
}\)
Примечание. Мы не включили в определение условное и биусловное предложения, потому что они оба могут быть получены из конъюнкции, дизъюнкции и отрицания, как мы увидим позже.
Если \(S\) — конечное множество, то мы можем использовать несколько иную терминологию. Например, если \(S = \{p, q, r\}\text{,}\), мы можем сказать, что предложение порождено \(p, q\text{,}\) и \(r\ ) вместо \(\{p, q, r\}\text{.}\)
Обычно для интерпретации предложений используется следующая иерархия, при этом круглые скобки преобладают над этим порядком:
Внутри любого уровня иерархии работайте слева направо. Используя эти правила, \(p \land q \lor r\) означает \((p \land q)\lor r\text{.}\) Эти правила приоритета являются универсальными и в точности языки для интерпретации логических выражений.
Пример 3.2.3. Примеры иерархии логических операций.
Несколько сокращенных выражений и их полностью заключенных в скобки версий:
\(p \land q \land r\) is \((p \land q) \land r\text{.
 }\)
}\)\(\neg p \lor \neg r\) is \((\neg p) \lor (\neg r)\text{.}\)
\(\neg \neg p\) равно \(\neg (\neg p)\text{.}\)
\(p \leftrightarrow q\land r\rightarrow s \) is \(p \leftrightarrow ((q\land r)\rightarrow s)\text{.}\)
Предложение, порожденное множеством \(S\), не обязано включать в свое выражение каждый элемент \(S\). Например, \(\neg q \land r\) является предложением, порожденным \(p, q\text{,}\) и \(r\text{.}\)
Упражнения 3.2.3 Упражнения
1.
Построить таблицы истинности:
\(\displaystyle p\lor p\)
\(\displaystyle p\land (\neg p)\)
\(\displaystyle p\lor (\neg p)\)
\(\displaystyle p \land p\)
Ответ.
\(\displaystyle \begin{массив}{cc} р & р \ лор р \\ \hline 0 и 0 \\ 1 и 1 \\ \конец{массив}\)
\(\displaystyle \begin{массив}{ccc} p & \neg p & p\land (\neg p) \\ \hline 0 и 1 и 0 \\ 1 и 0 и 0 \\ \конец{массив}\)
\(\displaystyle \begin{массив}{ccc} p & \neg p & p\lor (\neg p) \\ \hline 0 и 1 и 1 \\ 1 и 0 и 1 \\ \конец{массив}\)
\(\displaystyle \begin{массив}{cc} р&р\земля р\\ \hline 0 и 0 \\ 1 и 1 \\ \конец{массив}\)
2.
Построить таблицы истинности:
\(\displaystyle \neg (p\land q )\)
\(\displaystyle p \land (\neg q)\)
\(\displaystyle (p \land q)\land r\)
\(\displaystyle (p \land q) \lor (q \land r)\lor (r \land p)\)
\(\displaystyle \text{ }\neg p\lor \neg q\)
\(\displaystyle p \lor q \lor r \lor s\)
3.
Перепишите следующее, убрав как можно меньше лишних скобок:
\(\displaystyle (\neg ((p) \land (r))) \lor (s)\)
\(\displaystyle ((p) \lor (q)) \land ((r) \lor (q))\)
Ответ.
\(\displaystyle \neg (p\land r) \lor s\)
\(\displaystyle (p\lor q) \land (r\lor q)\)
4.
В каком порядке выполняются операции в следующих предложениях?
\(\displaystyle p \lor \neg q \lor r\land \neg p\)
\(\displaystyle p \land \neg q \land r \land \neg p\)
5.



 Количество переменных у нас 2, логических операций 4, число столбцов равно сумме 2+4 = 6.
Количество переменных у нас 2, логических операций 4, число столбцов равно сумме 2+4 = 6. Складываем то и другое: 3+3 = 5.
Складываем то и другое: 3+3 = 5.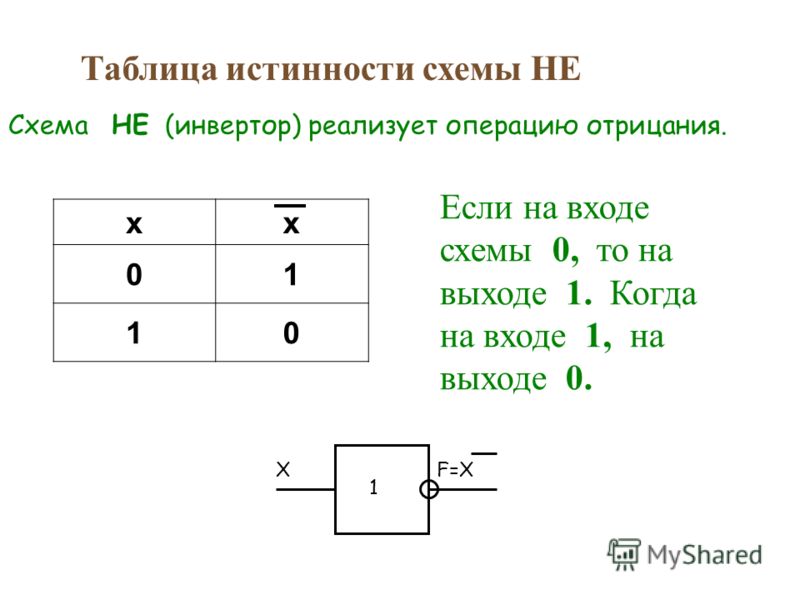
 }\)
}\) }\)
}\)