НОУ ИНТУИТ | Лекция | Минимизация логических схем

Аннотация: Рассматривается взаимосвязь различных способов описания работы логических схем и принципы их минимизации.

Ключевые слова: диаграмма Вейча, представление, выражение, Произведение, значение, переменная, решение обратной задачи, метод минимизации, логическая схема, КНФ

Составление логических выражений по таблице истинности

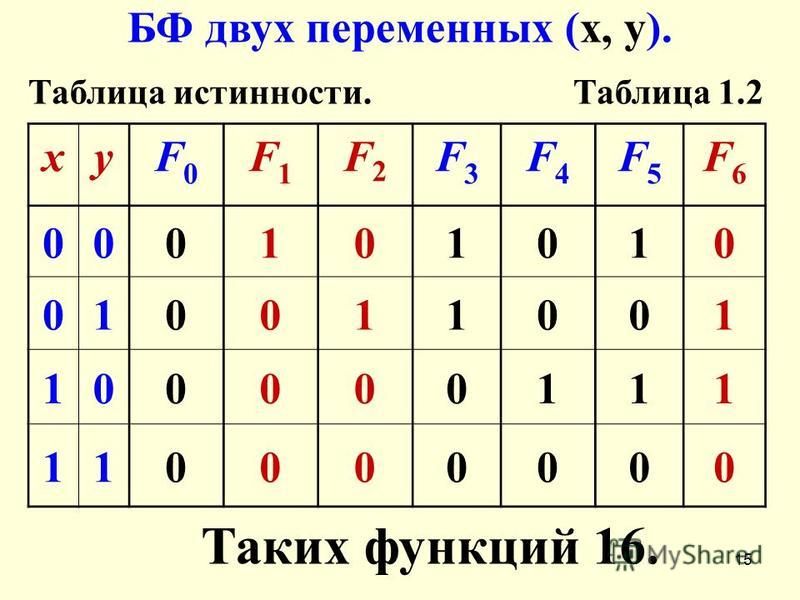
Каноническая сумма минтермов

Минтерм — это полное произведение всех входных переменных, соответствующее одной строке таблицы истинности, в которой значение выходной переменной (значение функции) равно логической 1. Переменная входит в минтерм с инверсией, если ее значение в данной строке таблицы равно 0, и без инверсии, если ее значение в данной строке таблицы равно 1.

Каноническая сумма минтермов — это логическая сумма всех минтермов, которая представляет собой максимальное логическое выражение, соответствующее таблице истинности. Она составляется в следующей последовательности:

1. В заданной таблице истинности подсчитывается — количество строк таблицы, в которой значение функции равно 1.
2. Затем записывается логическая сумма полных произведений.
3. Далее в каждом произведении расставляются инверсии над переменными в соответствии с их значением в строке таблицы.

Для примера, представленного на рис. 1.6, каноническая сумма минтермов будет выглядеть так:

( 2.1)

Из сравнения (1.1) и (2.1) видно, что одной и той же таблице истинности (рис.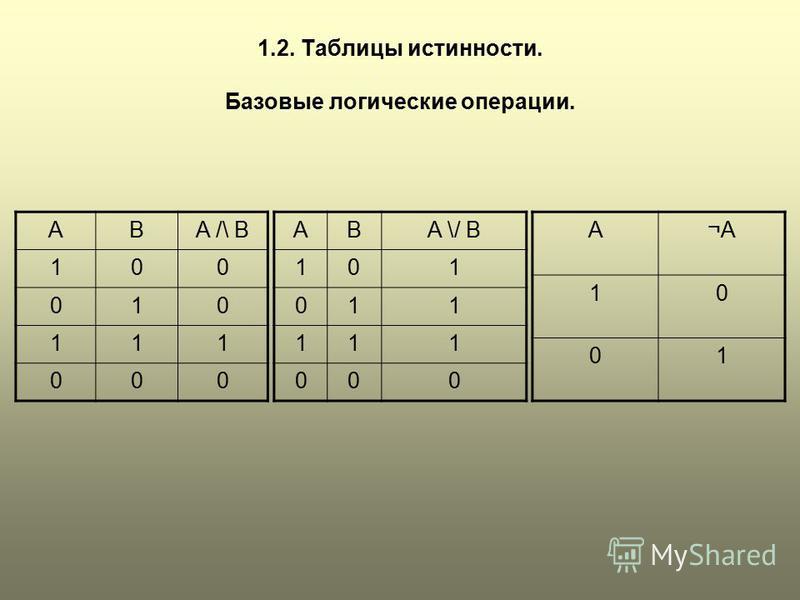

1.6,б) соответствуют два разных логических выражения, причем (1.1) записывается более компактно, но возможности минимизации для него еще есть. Следовательно, есть возможность минимизировать и логическую схему, представленную на рис. 1.6, a.

Минимизация логических выражений может осуществляться с помощью различных методов на основе правил булевой алгебры, в частности, диаграммы Вейча, диаграммы Венна и табличным методом, но наиболее простым и наглядным является графический способ минимизации с помощью карт Карно, опубликованный в 1953 г. Морисом Карно.

Минимизация с помощью карт Карно

Карта Карно — графическое представление таблицы истинности. Каждой клетке карты Карно соответствует строка таблицы истинности

. По осям карты расставляются сочетания переменных, а внутри карты — значения функции.

Назначение карты Карно — найти логические суммы прямого и инверсного значения переменных. Для любой переменной, например, , такая сумма равна при любом значении : при это будет , при это . Поэтому при вынесении за скобки в выражении:

— сумму можно отбросить, при этом результат выражения не изменится. В этом и заключается минимизация логических выражений с помощью

карт Карно. Для достижения поставленной цели минимизации нужно соблюдать правила разметки осей карты:

1. Вертикальная ось размечается независимо от горизонтальной.
2. Начинать разметку можно с любого сочетания переменных.
3. Все сочетания переменных должны быть перечислены.
4. Для соседних клеток карты сочетание переменных должно отличаться не более чем одним знаком, причем соседними являются крайние клетки строки (столбца).

intuit.ru/2010/edi»>Для функции двух переменных карта Карно — это квадрат 2×2 клетки. В этих клетках размещаются 4 значения функции из последнего столбца таблицы истинности (рис. 2.2).

Рис. 2.2. Таблица истинности (а) и карта Карно (б) для функции 2 переменных.

Для функции трех переменных карта Карно — это прямоугольник 2×4 или 4×2 клетки. В этих клетках размещаются 8 значений функции из последнего столбца таблицы истинности (рис. 2.3). При разметке большей из осей нужно четко придерживаться последнего,

четвертого правила разметки и следить за тем, чтобы соседними не оказались сочетания и , либо и , в которых одновременно меняются обе переменные.

Для функции четырех переменных карта Карно — это квадрат 4×4 клетки. В этих клетках размещаются 16 значений функции из последнего столбца таблицы истинности (рис. 2.4). При разметке обеих осей нужно также четко придерживаться последнего, четвертого правила разметки и следить за тем, чтобы

по одной оси соседними не оказались сочетания и , либо и , в которых одновременно меняются обе переменные.

Для функции пяти переменных карта Карно представляет собой уже объемную фигуру — куб 4x4x4 клетки, поэтому для минимизации логических выражений она не применяется.

увеличить изображение
Рис. 2.3. Таблица истинности (а) и примеры заполнения карты Карно (б, в, г, д) для логической функции 3 переменных.

увеличить изображение
Рис. 2.4.

Таблица истинности (а) и примеры заполнения карты Карно (б, в) для логической функции 4 переменных.

В конкретных случаях вместо значений функций в общем виде в клетки карты проставляются конкретные значения (логические 0 и 1) из соответствующих строк таблицы истинности.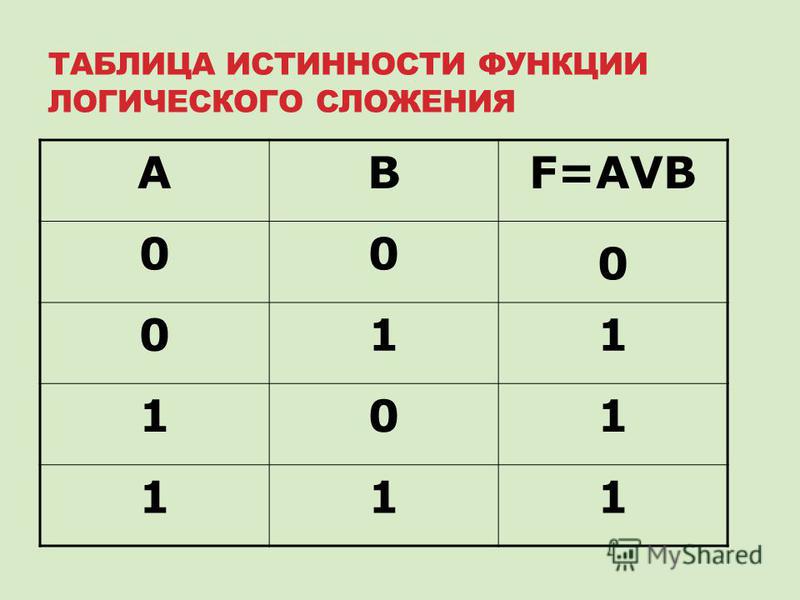 Затем рассматриваются только те клетки, которые заполнены единицами. Все эти единицы должны быть обведены контурами по следующим правилам составления контуров:

1. Контуры должны быть прямоугольными и содержать количество единиц, равное , где — целое число. Таким образом, в контуре может быть либо одна, либо две, либо четыре, либо восемь единиц.
2. Количество единиц в контуре должно быть максимальным, при этом контуры могут пересекаться между собой. Нужно учитывать, что крайние строки являются соседними и крайние столбцы также являются соседними, поэтому контуры могут быть «разорванными».
3. Количество контуров должно быть минимальным, но все единицы должны быть охвачены контурами. Нельзя забывать об отдельно стоящих единицах. Каждая такая единица — это контур, которому соответствует полное логическое произведение всех переменных.

После обведения контуров нужно записать минимальное выражение как логическую сумму логических произведений. Каждому произведению соответствует один контур карты Карно. В произведение входят только те переменные, которые остаются в данном контуре неизменными.При этом переменная входит в произведение с инверсией, если ее значение в данном контуре равно 0, и без инверсии, если ее значение равно 1.

Пример 1. Написать минимальное выражение для таблицы истинности, представленной на рис. 2.5,а и нарисовать по нему логическую схему.

При одном варианте разметки осей (рис. 2.5,б) первый контур, состоящий из четырех единиц, получается разорванным. Если же принять разметку, показанную на рис. 2.5,в, то контур будет иметь нормальные очертания, а выражение, ему соответствующее, останется без изменений. Учитывая, что при данном горизонтальном начертании карты Карно крайние столбцы являются соседними, ее можно представить себе как цилиндр, развернутый на плоскости. На рис. 2.5,б представлена развертка такого цилиндра, «разрезанная» между комбинациями , равными и . А на рис. 2.5,в представлена развертка этого же цилиндра, «разрезанная» между произведениями , равными и .

Первый контур охватывает четыре единицы, ему соответствует сумма минтермов: , в которой не изменяется только переменная . Второй контур охватывает две единицы. Ему соответствует сумма минтермов , в которой переменная принимает оба возможных значения, а произведение остается неизменным. Таким образом, получаем минимальное выражение:

( 2.2)

Ему соответствует логическая схема на рис. 2.5,г.

Рис. 2.5. Минимизация функции трех переменных

Для сравнения запишем максимальное выражение:

( 2.3)

Разница между (2.2) и (2.3) очевидна и в комментариях не нуждается, за исключением того, что схема, реализованная по (2.3), будет на порядок сложнее и, соответственно, менее надежна, чем схема, показанная на рис. 2.5,г.

Пример 2. Написать минимальное выражение для таблицы истинности, представленной на рис. 2.6,а, и нарисовать по нему логическую схему.

Рис. 2.6. Минимизация функции четырех переменных

intuit.ru/2010/edi»>При первоначально выбранной разметке осей (рис. 2.6,б) первый контур, состоящий из четырех единиц с номерами 1.1, 1.2, 1.3 и 1.4, расположенных по углам карты, получается разорванным. Если же принять разметку, показанную на рис. 2.7, то контур будет иметь очертания квадрата, а выражение, ему соответствующее, останется без изменений. Учитывая, что крайние столбцы являются соседними и крайние строки являются соседними, карту Карно для функции четырех переменных можно представить себе как торроид, развернутый на плоскости. Проще представить себе обратный процесс получения торроида из плоской фигуры — квадрата. Для этого надо сначала соединить мысленно крайние строки — получим цилиндр. После этого основания цилиндров надо мысленно соединить. Получится торроид. На рис. 2.6,б представлена развертка такого торроида, «разрезанная» между комбинациями , равными и и между сочетаниями , равными и . А на рис. 2.7 представлена развертка этого же торроида, «разрезанная» между комбинациями , равными и и между произведениями , равными и .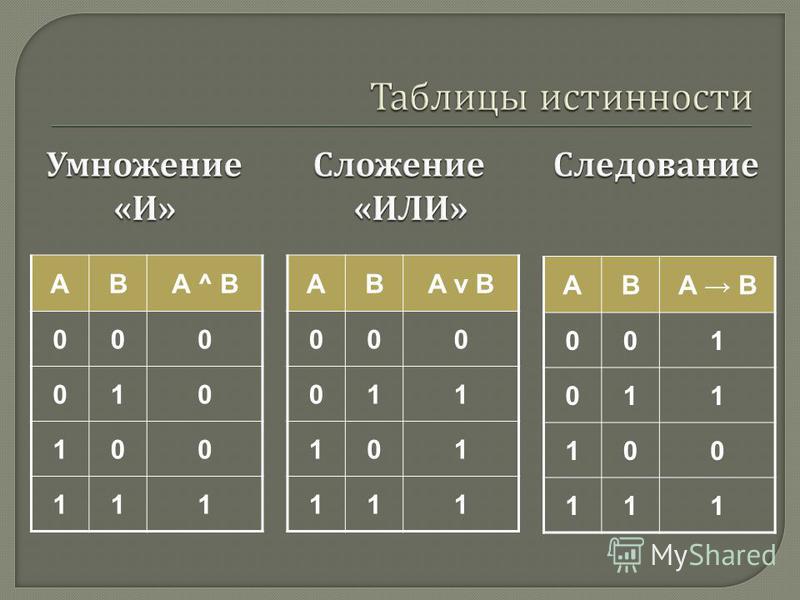 После анализа контуров получим минимальное выражение . Соответствующая ему схема приведена на рис. 2.8.

Рис. 2.7. К минимизации логической функции четырех переменных

Рис. 2.8. Логическая схема для минимизированного логического выражения

Таблицы истинности

Таблицы истинности

---

Приоритет логических операций:

1) инверсия 2) конъюнкция 3) дизъюнкция 4) импликация и эквивалентность

Как составить таблицу истинности?

Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.

Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре: (0, 0), (0, 1), (1, 0), (1, 1). Если формула содержит три переменные, то возможных наборов значений переменных восемь (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1). Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д. Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.

Примеры.

1. Составим таблицу истинности для формулы , которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу:

Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.

2. Таблица истинности для формулы

Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 0, то есть является тождественно ложной.

3. Таблица истинности для формулы :

Из таблицы видно, что формулав некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.

Пример1:

Вася спросил у мамы: «Можно пойти в кино или на футбол?» Мама ответила отрицательно. Как поступить мальчику?

Проверим правильность этого закона с помощью таблицы истинности.

Пример2:

В классе оказалось разбито стекло. Учитель объясняет директору: это сделал Коля или Саша. Но Саша этого на делал, т.к. в это время сдавал мне зачет. Следовательно, это сделал Коля

Решение: Формализуем данное сложное высказывание.

К — это сделал Коля

С — это сделал Саша

Кол-во простых высказываний n = 2.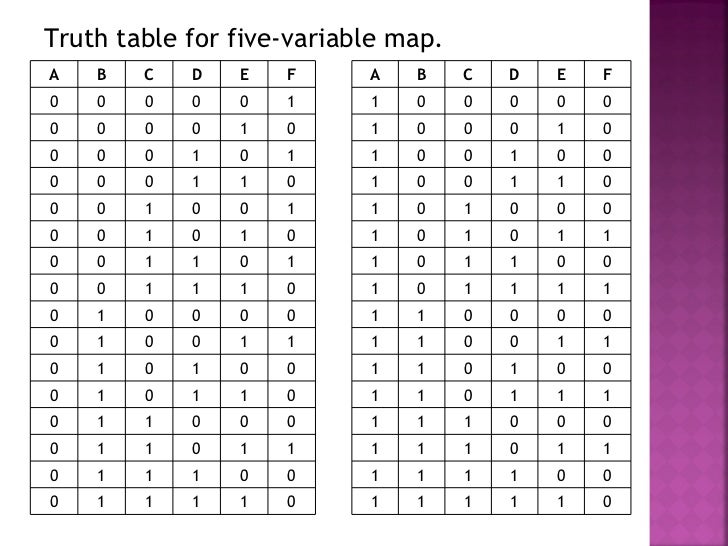

1) Определить количество строк и столбцов в таблице истинности.

Т.к. каждое из простых высказываний может принимать всего два значения (0 или 1), то количество разных комбинаций значений n высказываний — 2 n . Количество строк в таблице = 2 n + строка на заголовок. Количество столбцов в таблице равно сумме количества простых высказываний (n) и количества разных логических операций, входящих в сложное высказывание. В нашем примере: количество строк — 2*2 + 1 = 5 , столбцов — 2 + 4 = 6

2) Начертить таблицу и заполнить заголовок

Первая строка — номера столбцов. Вторая строка промежуточные формулы и соответствующие им условные записи операций над значениями .

3) Заполнить первые n столбцов.

В нашем примере сначала заполняем 1-й и 2-й столбцы.

4) Заполнить остальные столбцы.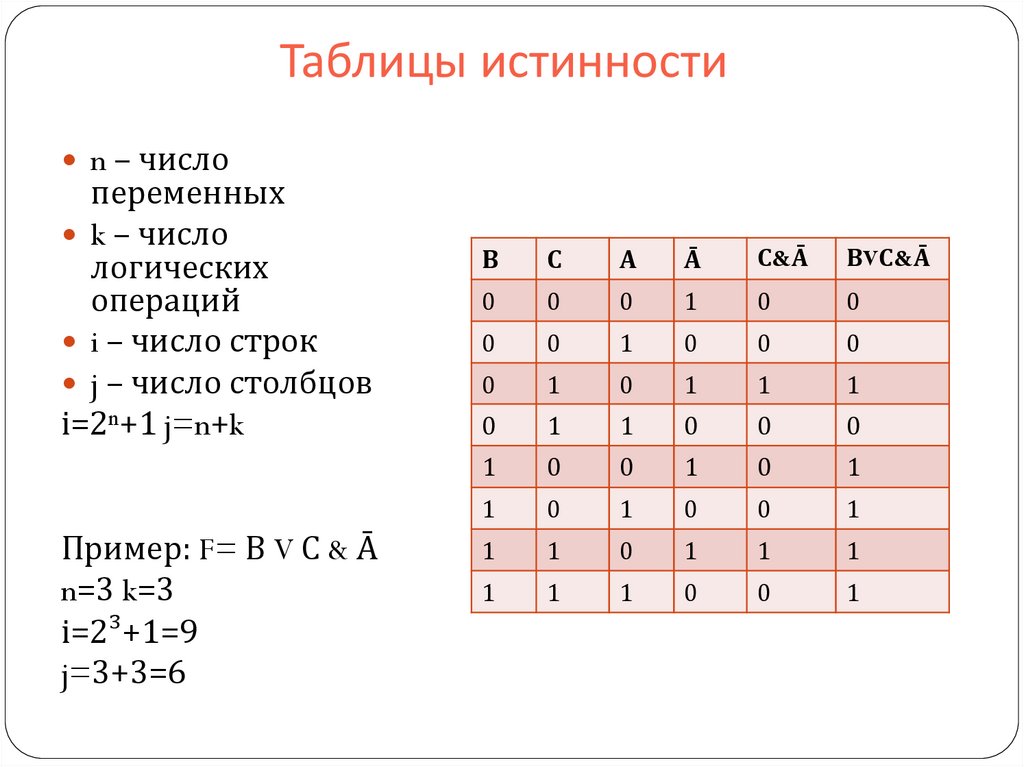

В соответствии с таблицами истинности соответствующих логических операций, причем при заполнении каждого столбца операции выполняются над значениями одного или двух столбцов, расположенных левее заполняемого. Итак, вычисляем значения 3-го столбца по значениям 2-го, потом значения 4-го — по значениям 1-го и 2-го…

Вывод: получили в последнем столбце все единицы. Значит, значение сложного высказывания истинно при любых значениях простых высказываний К и С. Следовательно, учитель рассуждал логически правильно.

---

K-Map с 5 переменными в Digital Logic

Предварительное условие – присутствует в K-Map 

Карта Карно или K-Map — это альтернативный способ записи таблицы истинности, который используется для упрощения логических выражений. До сих пор мы знакомы с K-Map с 3 переменными и K-Map с 4 переменными. Теперь давайте подробно обсудим K-карту с 5 переменными. Любое логическое выражение или функция, состоящая из 5 переменных, может быть решена с использованием K-карты с 5 переменными. K-карта для выражения с 5 переменными может быть обозначена двумя картами с 4 переменными, расположенными рядом друг с другом. Такая K-карта с 5 переменными должна содержать

 *** QuickLaTeX не может скомпилировать формулу:
 
*** Сообщение об ошибке:
Ошибка: Нечего показывать, формула пуста
 

2 ⁵ = 32 ячейки для заполнения каждого минтерма. По мере увеличения числа переменных эффективность карты Карно снижается. Пусть булева функция с 5 переменными представлена ​​в виде f (P Q R S T) , где P, Q, R, S и T — переменные, P — старшая битовая переменная, а T — наименее значащая битовая переменная. Структура такой K-карты для экспрессии SOP приведена ниже: Cell no. написанное, соответствующее каждой ячейке, можно понять из примера, описанного здесь:

  

Здесь для переменной P=0 имеем Q = 0, R = 1, S = 1, T = 1, т.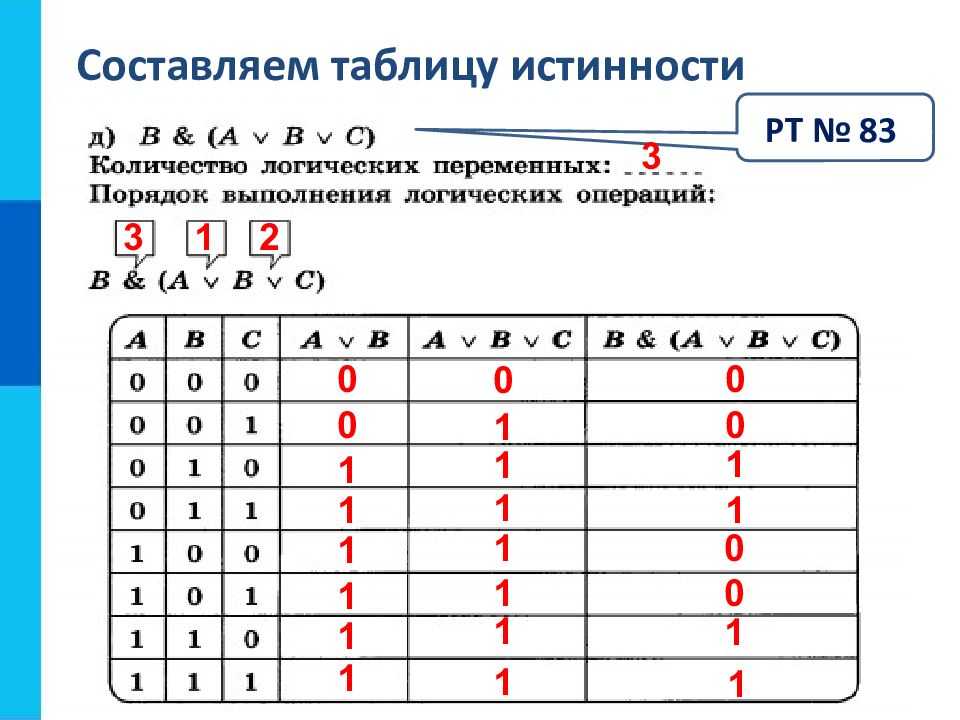 е. (PQRST)=(00111) . В десятичной форме это эквивалентно 7 . Итак, для ячейки, показанной выше, соответствующая ячейка №. = 7. Аналогичным образом мы можем записать номера ячеек, соответствующие каждой ячейке, как показано на рисунке выше. Теперь давайте обсудим, как использовать K-карту с 5 переменными для минимизации булевой функции.

Правила, которым нужно следовать: 

1. Если функция задана в компактной канонической форме SOP (сумма произведений), то мы пишем «1» , соответствующий каждому минтерму (указанному в вопросе) в соответствующих номерах ячеек. Например: For мы напишем «1», соответствующее номерам ячеек (0, 1, 5, 7, 30 и 31).
2. Если функция задана в компактной канонической форме POS (произведение сумм), то мы пишем «0» , соответствующее каждому максимальному термину (указанному в вопросе) в соответствующих номерах ячеек. Например: For мы напишем «0», соответствующий номерам ячеек (0, 1, 5, 7, 30 и 31).

Шаги, которые необходимо выполнить: 

1. Создайте вложенный куб максимально возможного размера, охватывающий все отмеченные 1 в случае SOP или все отмеченные 0 в случае POS на K-карте. Важно отметить, что каждый подкуб может содержать члены только в степени 2. Также вложенный куб ячеек возможен тогда и только тогда, когда в этом вложенном кубе для каждой ячейки мы удовлетворяем тому, что «m» число ячеек составляет соседних ячеек .
2. Все Essential Prime Implicants (EPI) должны присутствовать в минимальных выражениях.

I. Решение SOP-функции: Для ясности давайте решим пример минимизации SOP-функции 5 Variable K-Map, используя следующее выражение: В приведенной выше K-Map у нас есть 4 подкуба:

• Подкуб 1: Отмеченный красным содержит ячейки ( 0, 4, 8, 12, 16, 20, 24, 28)
• Подкуб 2: Отмеченный синим содержит ячейки (7, 23 )
• Подкуб 3: Отмеченный розовым цветом включает в себя ячейки (0, 2, 8, 10, 16, 18, 24, 26)
• Подкуб 4: Отмеченный желтым цветом содержит ячейки (24, 25, 26, 27)

Теперь, записывая минимальное выражение каждого из подкубов, мы будем искать литерал, общий для всех ячеек, присутствующих в этом подкубе.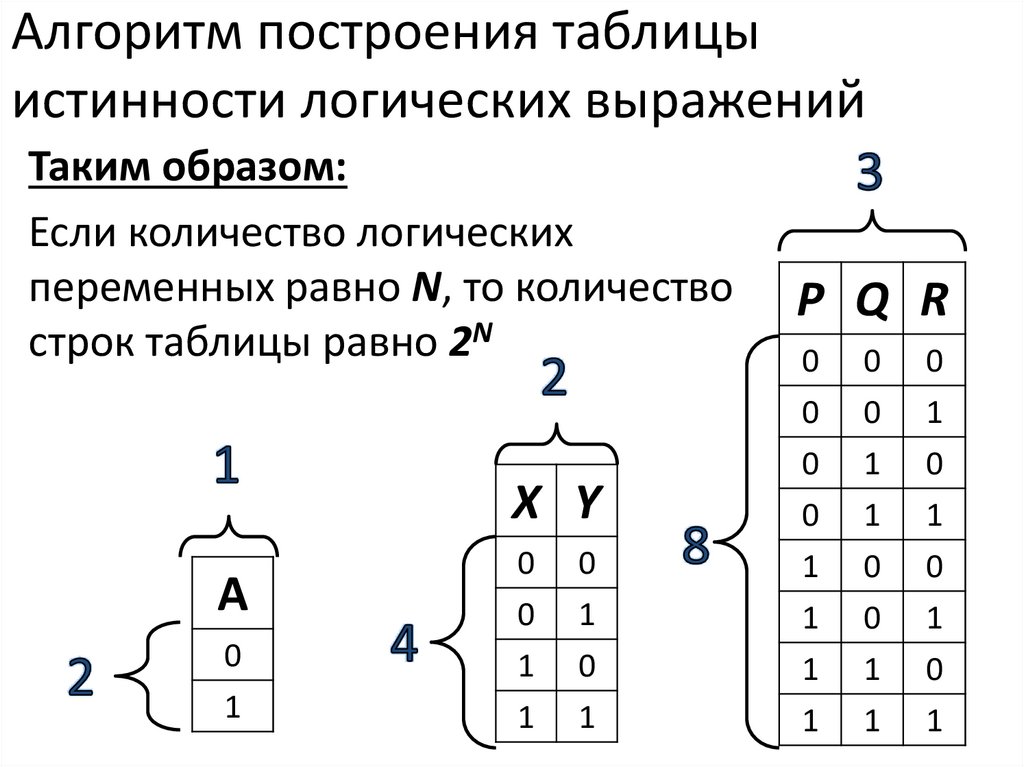

• Подкуб 1 :  [Tex]\bar T [/Tex]
• Подкуб 2 :  [Tex]R  [/Tex][Tex]T 9 [/Tex][Tex]T 
• Подкуб 3 : [Tex]\bar T [/Tex]
• Подкуб 4 : [Tex]Q [/Tex]

90 выражается следующим образом: [Tex]\bar T  [/Tex][Tex]R  [/Tex][Tex]T  [/Tex][Tex]\bar T  [/Tex][Tex]Q  [/Tex]

II. Решение функции POS: Теперь давайте решим пример минимизации функции POS для K-карты с 5 переменными, используя следующее выражение: В приведенной выше K-карте у нас есть 4 подкуба:

• Подкуб 1: Отмеченный красным включает ячейки (0, 4, 8, 12, 16, 20, 24, 28)
• Подкуб 2: Отмеченный синим (7, 23)
• Подкуб 3: Отмеченный розовым цветом содержит ячейки ( 0, 2, 8, 10, 16, 18, 24, 26)
• Подкуб 4: Отмеченный

  желтым цветом содержит ячейки (24, 25, 26, 27)

Теперь, записывая минимальное выражение каждого из подкубов, мы будем искать литерал, общий для всех ячеек, присутствующих в этом подкубе.

• Subcube 1 : 
• Subcube 2 :  [Tex]+ \bar S  [/Tex]
• Subcube 3 : 
• Subcube 4 :  [Tex ]+ R [/Tex]

Наконец, минимальное выражение данной логической функции может быть выражено следующим образом:

ПРИМЕЧАНИЕ:

1. Для 5-переменной K-Map диапазон номеров ячеек будет от 0 до -1, т. е. от 0 до 31,
2. Вышеупомянутый термин «Смежные ячейки» означает «любые две ячейки, отличающиеся только одной переменной».

оптимизация — Таблица истинности с 5 входами и 3 выходами

Мне нужно составить таблицу истинности с 5 входами и 3 выходами, примерно так:

A B C D E красный зеленый синий
0 0 0 0 0 0 0 0
0 0 0 0 1 0 0 1
0 0 0 1 0 0 0 1 . . . . 1 1 0 1 0 0 1 1
. . . 1 1 1 1 1 1 0 1

и т. д.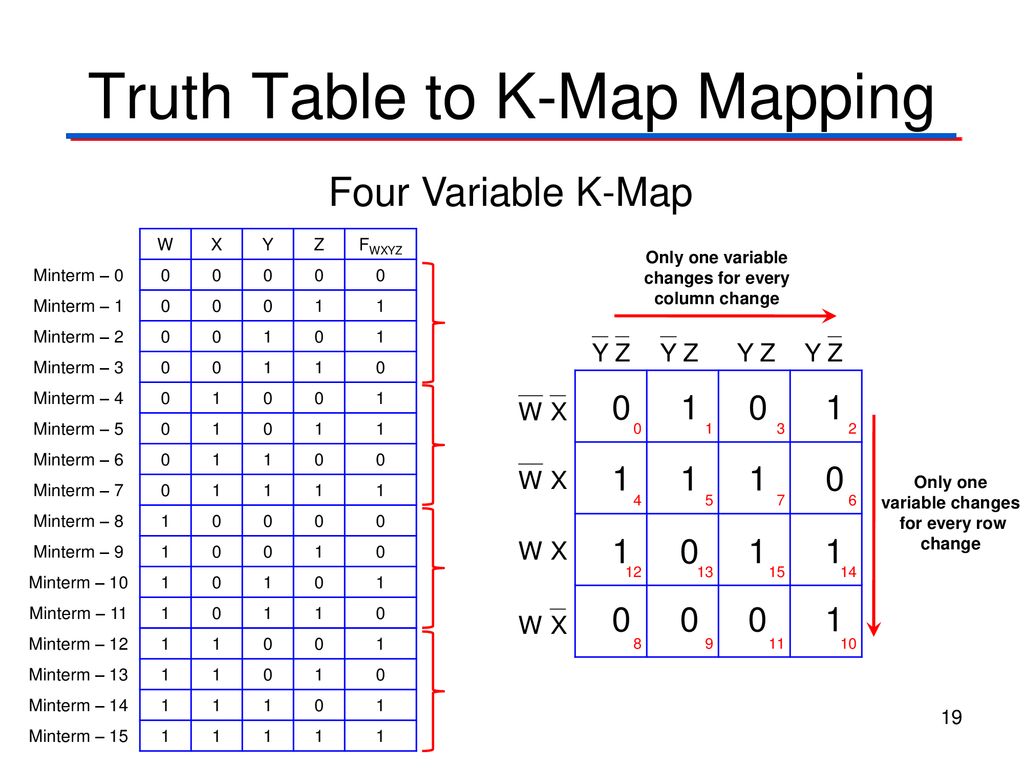 (всего 32 строки, числа в таблице rgb представляют количество единиц в каждой строке в двоичном формате, т.е. в строке 1 1 0 1 0 есть три единицы, поэтому три в двоичном формате равны 0 1 1).

Я хотел бы представить результат этого в инструменте Atanua (http://sol.gfxile.net/atanua/index.html) (например, когда я нажимаю кнопку E, загорается синий свет, при нажатии A B D будут светиться зеленый и синий свет и так далее). Но есть требование, что я могу использовать только И, ИЛИ, НЕ операнды, и каждый операнд может иметь только два входа. Хотя я использую карту Карно, чтобы свести ее к минимуму, все же для такого количества записей результаты для каждого вывода очень длинные (особенно для последнего).

Я попытался еще больше упростить его, добавив все три выходные булевы функции в одну, и процесс минимизации закончился вполне прилично: только один выходной свет, он работает только в красной зеленой синей колонке отдельно). Меня беспокоит тот факт, что я хотел бы иметь три выхода (три источника света, а не один), и возможно ли это вообще после такой минимизации? Есть ли хорошее решение сделать это в Атануа? Или мне надо сделать 3 отдельные булевы функции, какой бы длины они ни были (а их очень много даже после минимизации)?

Изменить: таблица всей истины 🙂

A B C D E R G B

0 0 0 0 0 0 0
0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0 1
.