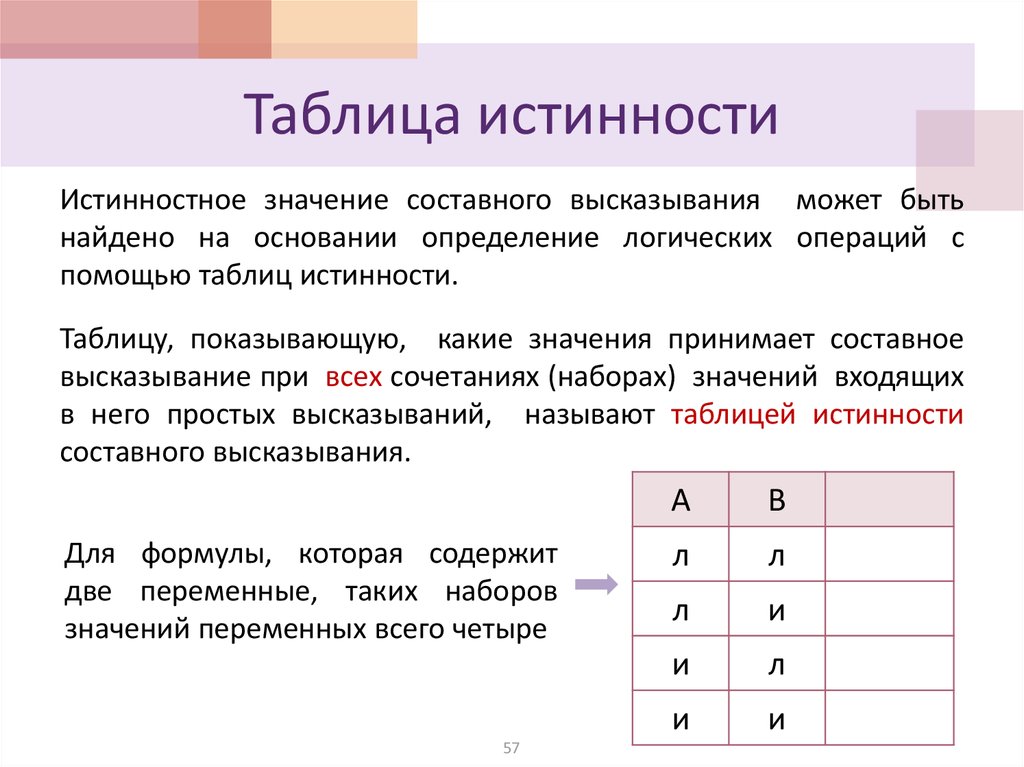
2и не таблица истинности
Простейшим логическим элементом является инвертор, который просто изменяет входной сигнал на прямо противоположное значение. Его логическая функция записывается в следующем виде:. Так как вход у инвертора только один, то его таблица истинности состоит всего из двух строк. В качестве логического инвертора можно использовать простейший усилитель с транзистором, включенном по схеме с общим эмиттером или истоком для полевого транзистора.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Логические схемы и таблицы истинности
- Логические схемы и таблицы истинности
- Логические элементы
- Базовые логические элементы
- Volt-info | Электроника, электротехника.
Профессионально-любительские решения.
- Интегральные микросхемы и работа с ними
Профессионально-любительские решения.ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Логические выражения, таблицы истинности ,структурная логическая схема
Логические схемы и таблицы истинности
Нетрудно заметить см. На рис. Реализация смешивания двух сигналов. Схемы совпадения двух сигналов. Например, возьмем логический элемент 2И-НЕ. Пусть по тем или иным причинам вследствие передачи по проводам, вследствие разных задержек элементов и т. Он может успеть переключиться, и тогда сформируется короткий импульс.
Схема, выполняющая такую функцию, довольно проста рис. В ее основе — многовходовые элементы И-НЕ. А сигналы, соответствующие разрядам кода, в которых должны быть нули, подаются на входы элементов И- НЕ через инверторы.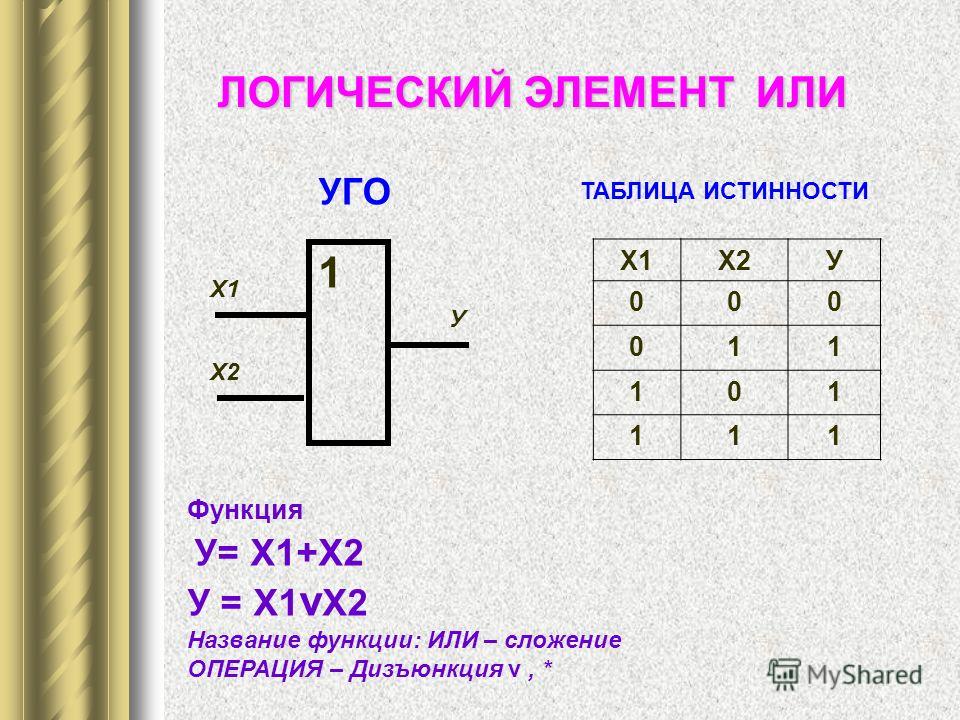
Формирователи коротких импульсов по фронту входного сигнала. При любой полярности входных сигналов выходные сигналы элемента будут положительными. Таблица 2. Примеры применения элементов И и ИЛИ. Появление лишнего фронта при запрещении входного сигнала. Поделиться ссылкой: Twitter Facebook.
Понравилось это: Нравится Загрузка Опубликовать в Отмена. Политика конфиденциальности и использования файлов сookie: Этот сайт использует файлы cookie. Продолжая пользоваться сайтом, вы соглашаетесь с их использованием. Дополнительную информацию, в том числе об управлении файлами cookie, можно найти здесь: Политика использования файлов cookie.
Логические схемы и таблицы истинности
Поиск по сайту. Главная страница. Лекционный материал. Лабораторный практикум. Тестовый комплекс. Самостоятельная работа. Программа подготовки к экзамену.
Основные логические элементы. Логическая «1»: +2,5 ÷ +5 В. Логический «0» : 0 ÷ +0,2 В. «И». Лог. элемент. Таблица истинности. Временная диаграмма.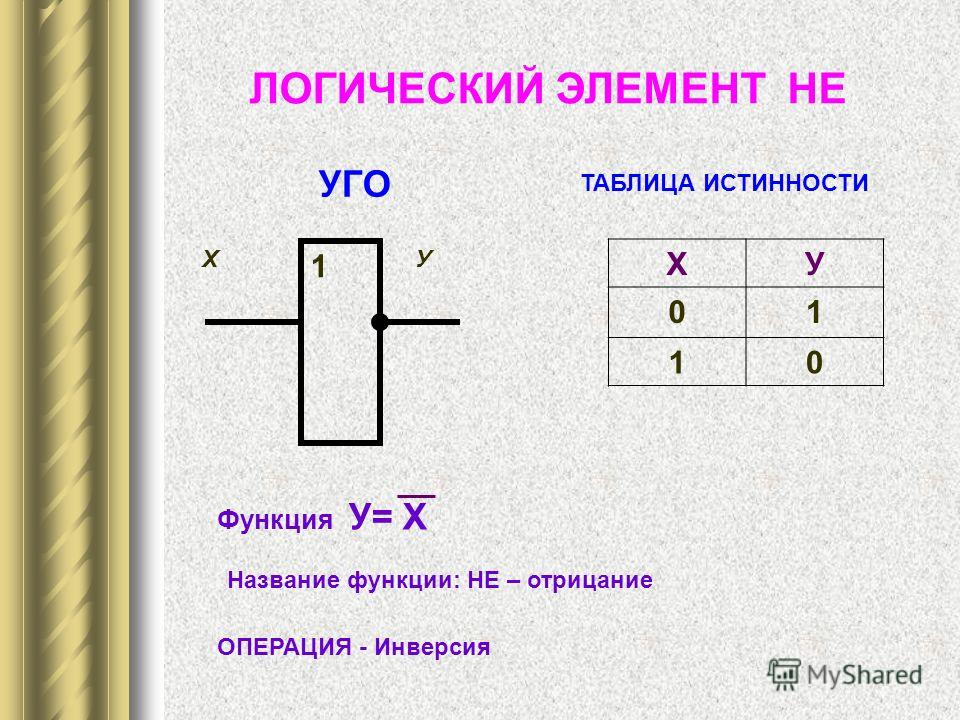
Логические элементы
Нетрудно заметить см. На рис. Реализация смешивания двух сигналов. Схемы совпадения двух сигналов. Например, возьмем логический элемент 2И-НЕ. Пусть по тем или иным причинам вследствие передачи по проводам, вследствие разных задержек элементов и т. Он может успеть переключиться, и тогда сформируется короткий импульс.
Базовые логические элементы
Вернуться к оглавлению. Наиболее простой логический элемент получается при помощи диодов. Схема такого элемента приведена на рисунке 1. Рисунок 1. Принципиальная схема логического элемента «2И», выполненного на диодах.
Различают комбинационные схемы и цифровые автоматы.
Volt-info | Электроника, электротехника. Профессионально-любительские решения.
Данная статья имеет ознакомительный характер. Если Вы ещё ни чего не знаете о диодах , она введёт Вас в курс. Данный пример предлагает простой вариант реализации ждущего одновибратора на базе микрокотроллера PIC16FA. Сама по себе схема практического значения не имеет и представлена для рассмотрения в качестве образовательного материала.
Интегральные микросхемы и работа с ними
Физически логические элементы могут быть выполнены механическими, электромеханическими на электромагнитных реле , электронными в частности, на диодах или транзисторах , пневматическими, гидравлическими , оптическими и другими. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами. Логические элементы выполняют логическую функцию операцию над входными сигналами операндами, данными. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы. Логические операции булева функция своё теоретическое обоснование получили в алгебре логики. Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков.
По таблице истинности следует, что на выходе элемента «2И-НЕ» будет логический ноль только в том случае, если на обоих входах.
Вот о них мы и поговорим сейчас. Логический элемент — это такая схемка, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе.
Логические схемы создаются для реализации в цифровых устройствах булевых функций функций алгебры логики. В цифровой схемотехнике цифровой сигнал — это сигнал, который может принимать два значения, рассматриваемые как логическая «1» и логический «0». Первые три логических элемента позволяют реализовать любую, сколь угодно сложную логическую функцию в булевом базисе. Мы будем решать задачи на логические схемы, реализованные именно в булевом базисе. Для обозначения логических элементов используется несколько стандартов. На рисунке ниже приведены обозначения логических элементов в этих стандартах для увеличения можно нажать на рисунок левой кнопкой мыши.
В Булевой алгебре, на которой базируется вся цифровая техника, электронные элементы должны выполнять ряд определённых действий.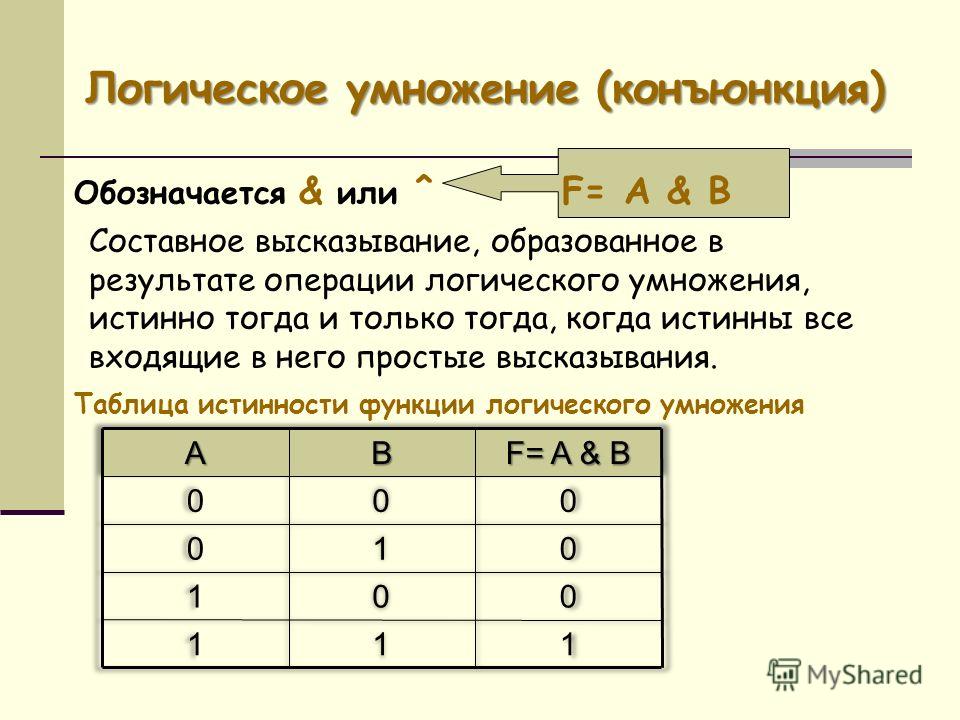
В отличие от аналоговых электронных устройств, в цифровых устройствах ЦУ входные и выходные сигналы могут принимать ограниченное количество состояний. В соответствии с логическим соглашением ГОСТ 2. Такое соглашение называется положительной логикой. Обратное соотношение называется отрицательной логикой. Теоретической основой проектирования ЦУ является алгебра-логики или булева алгебра, оперирующая логическими переменными. Для логических переменных, принимающих только два значения,существуют 4 основных операции. Операция логическое «НЕ» NOT , изменение значения, инверсия или отрицание, обозначается чертой над логическим выражением.
Оказывается помощью логических элементов НЕ, И, ИЛИ можно реализовать любые логические функции, абсолютно любой сложности. Может лишь потребоваться большее или меньшее количество элементов этих типов. Первым и самым простым логическим элементом является инвертор, выполняющий логическую операцию НЕ — инверсию или логическое отрицание.
2.
Логические элементы и, или, не. Таблицы истинности, принципиальные схемы.Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис.1, а таблица истинности в таблице 1.
Таблица 1
у | х * у | |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 |
Единица
на выходе схемы И будет тогда и только
тогда, когда на всех входах будут единицы.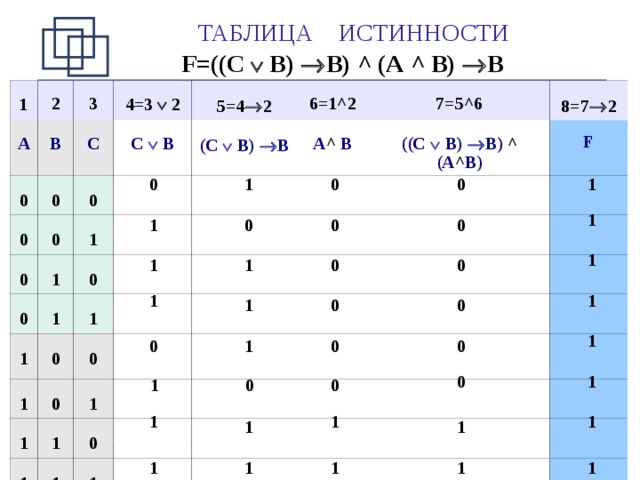
Когда хотя бы на одном входе будет ноль,
на выходе также будет ноль.
Связь между выходом z этой схемы и входами х и у описывается отношением z = х * у (читается как «х и у»).
Операция конъюнкции на функциональных схемах обозначается знаком & (читается как «амперсэнд»), являющимся сокращенной записью английского слова and.
Схема ИЛИ реализует дизъюнкцию двух или более логических значений.
Когда хотя бы на одном входе схемы ИЛИ будет единица, на ее выходе также будет единица.
Условное обозначение схемы ИЛИ знак «1». Связь между выходом z этой схемы и входами х и у описывается соотношением z = х + у (читается как «х или у»). Рис.2 и таблица 2.
Таблица 2
х | у | х + у |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
Схема
НЕ (инвертор) реализует операцию
отрицания.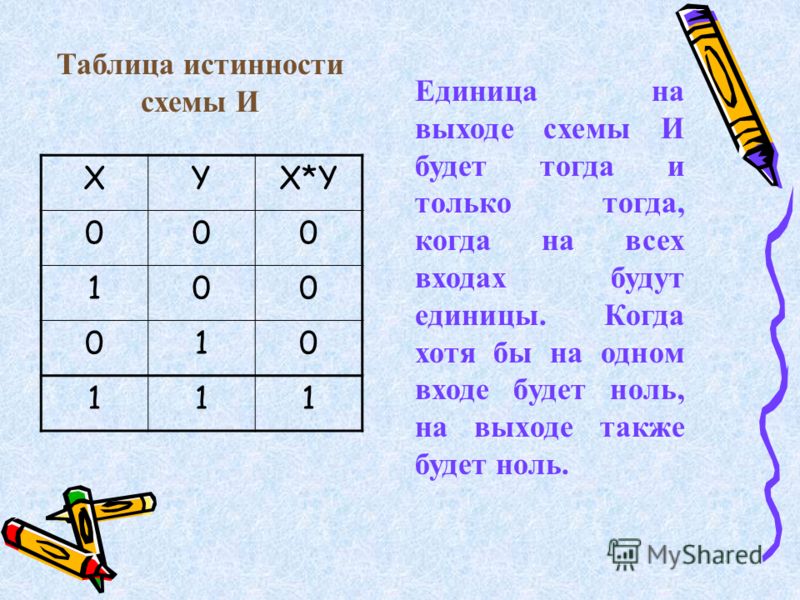
Связь между входом х этой схемы и выходом z можно записать соотношением z = , где читается как «не х» или «инверсия х».
Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение инвертора — на рис.3, а таблица истинности – в таблице 3
.
Таблица 3
x | |
0 | 1 |
1 | 0 |
3.Логические элементы и — не, или — не. Таблицы истинности. Графическое представление элементов. Графики работы.
Связь между выходом z и входами х и у схемы записывают следующим образом:
z = , где читается как «инверсия х и у».
рис. 4
Таблица 4
х | у | |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Условное
обозначение схемы И-НЕ представлено на
рис.
4, а таблица истинности схемы И-НЕ
– в таблице 4.
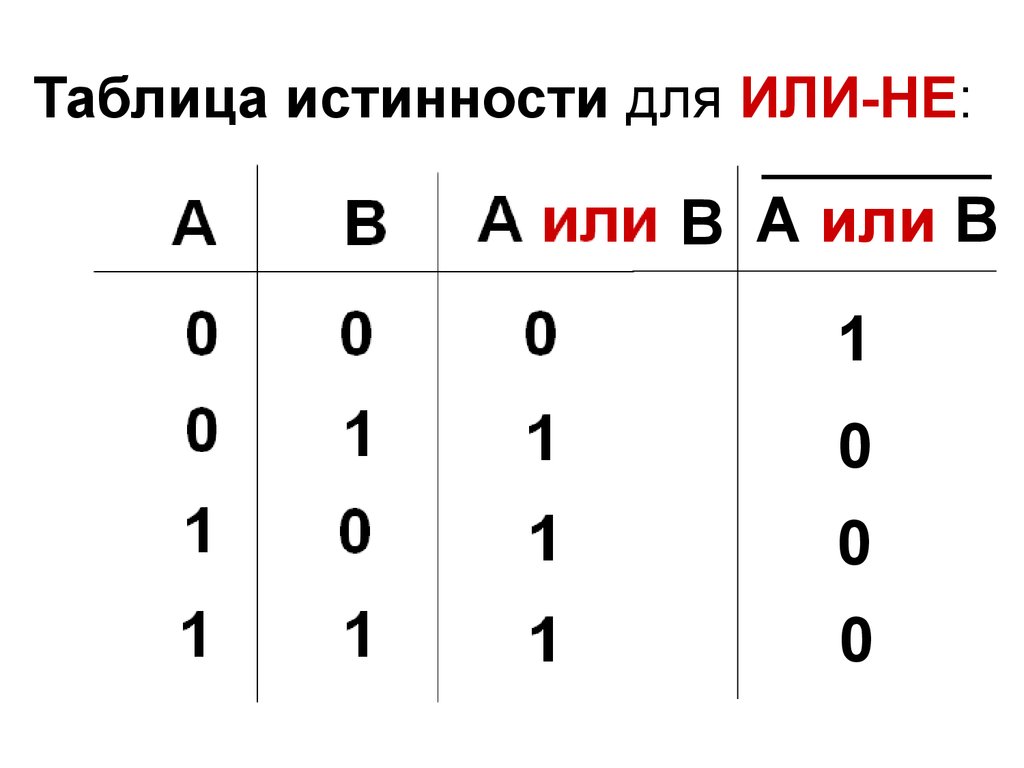
Схема ИЛИ-НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ.
Связь между выходом z и входами х и у схемы записывают следующим образом:
z = , где читается как «инверсия х или у».
Таблица 5
х | у | |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 0 |
Условное
обозначение схемы ИЛИ-НЕ представлено
на рис.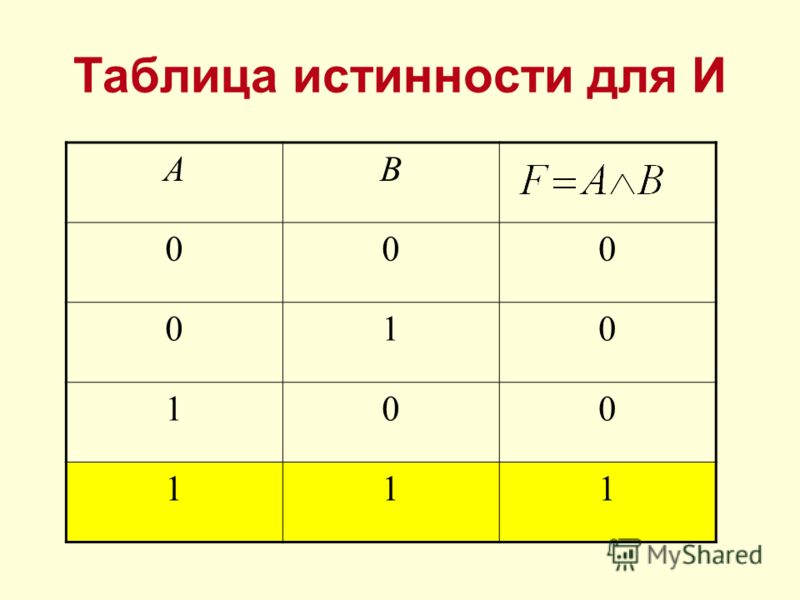
5, а таблица истинности схемы
ИЛИ-НЕ – в таблице 5
4.Исключающие или, исключающие или — не. Таблицы истинности. Графическое представление элементов.
лементы Исключающее ИЛИ (по-английски — Exclusive-OR) также можно было бы отнести к простейшим элементам, но функция, выполняемая ими, несколько сложнее, чем в случае элемента И или элемента ИЛИ. Все входы элементов Исключающее ИЛИ равноправны, однако ни один из входов не может заблокировать другие входы, установив выходной сигнал в уровень единицы или нуля.
Таблица 4.1. Таблица истинности двухвходовых элементов И, И-НЕ, ИЛИ, ИЛИ-НЕ
Вход 1 | Вход 2 | Выход |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Рис.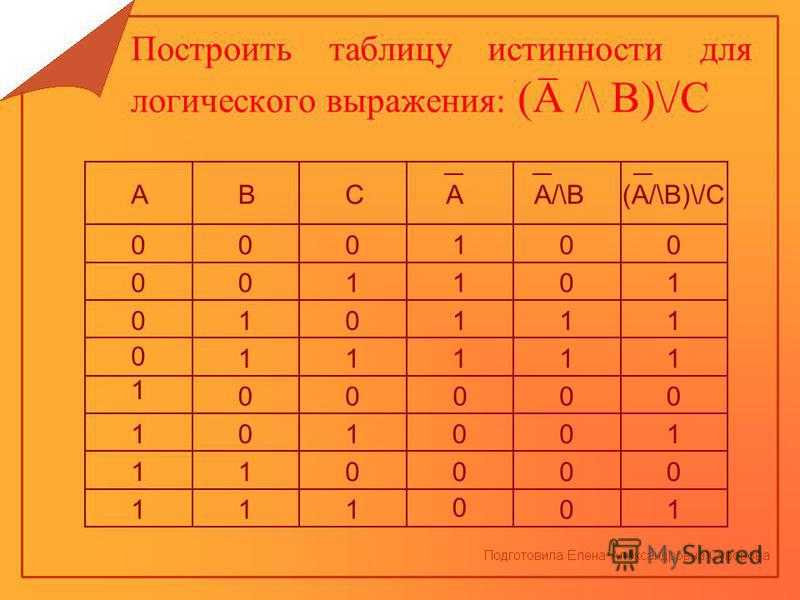
4.1.
Обозначения элементов Исключающее ИЛИ:
зарубежные (слева) и отечественные
(справа)
Под функцией Исключающее ИЛИ понимается следующее: единица на выходе появляется тогда, когда только на одном входе присутствует единица. Если единиц на входах две или больше, или если на всех входах нули, то на выходе будет нуль. Таблица истинности двухвходового элемента Исключающее ИЛИ приведена в табл. 4.1. Обозначения, принятые в отечественных и зарубежных схемах, показаны на рис. 4.1. Надпись на отечественном обозначении элемента Исключающее ИЛИ “=1″ как раз и обозначает, что выделяется ситуация, когда на входах одна и только одна единица.
Элементов Исключающее ИЛИ в стандартных сериях немного. Отечественные серии предлагают микросхемы ЛП5 (четыре двухвходовых элемента с выходом 2С), ЛЛ3 и ЛП12, отличающиеся от ЛП5 выходом ОК. Слишком уж специфическая функция реализуется этими элементами.
С
точки зрения математики, элемент
Исключающее ИЛИ выполняет операцию так
называемого суммирования по модулю 4.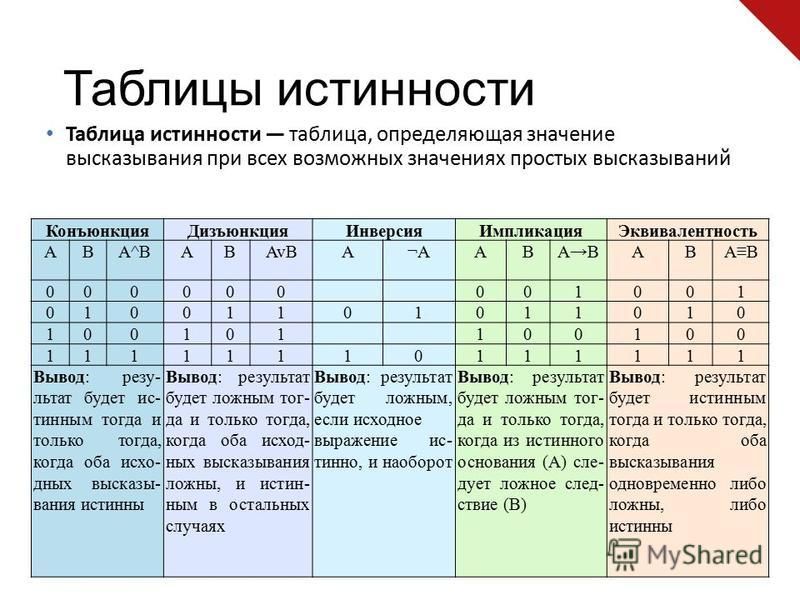
Поэтому эти элементы также называются
сумматорами по модулю два. Как уже
отмечалось в предыдущей лекции,
обозначается суммирование по модулю 2
знаком плюса, заключенного в кружок.
Основное применение элементов Исключающее ИЛИ, прямо следующее из таблицы истинности, состоит в сравнении двух входных сигналов. В случае, когда на входы приходят две единицы или два нуля (сигналы совпадают), на выходе формируется нуль (см. табл. 4.1). Обычно при таком применении на один вход элемента подается постоянный уровень, с которым сравнивается изменяющийся во времени сигнал, приходящий на другой вход. Но значительно чаще для сравнения сигналов и кодов применяются специальные микросхемы компараторов кодов, которые будут рассмотрены в следующей лекции.
В
качестве сумматора по модулю 2 элемент
Исключающее ИЛИ используется также в
параллельных и последовательных
делителях по модулю 2, служащих для
вычисления циклических контрольных
сумм. Но подробно эти схемы будут
рассмотрены в лекциях 14,15.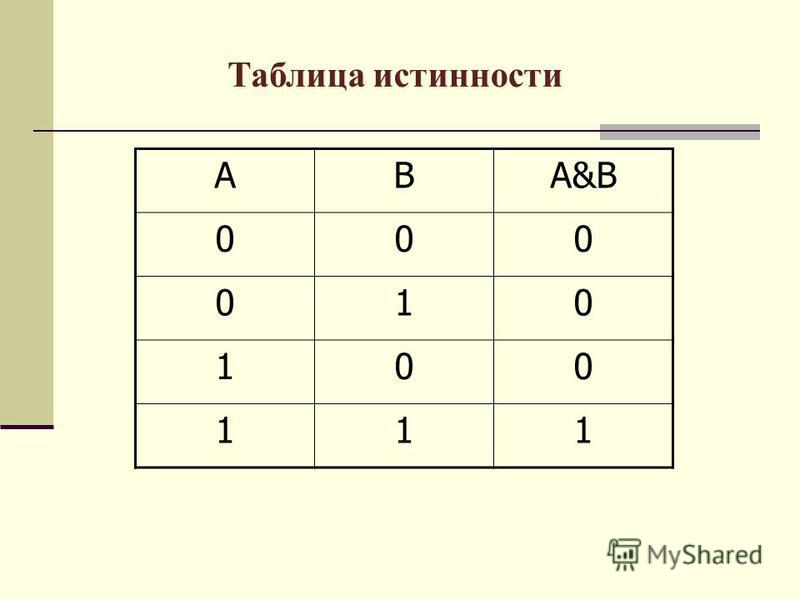
Важное применение элементов Исключающее ИЛИ — это управляемый инвертор (рис. 4.2). В этом случае один из входов элемента используется в качестве управляющего, а на другой вход элемента поступает информационный сигнал. Если на управляющем входе единица, то входной сигнал инвертируется, если же нуль — не инвертируется. Чаще всего управляющий сигнал задается постоянным уровнем, определяя режим работы элемента, а информационный сигнал является импульсным. То есть элемент Исключающее ИЛИ может изменять полярность входного сигнала или фронта, а может и не изменять в зависимости от управляющего сигнала.
Рис. 4.2. Элемент Исключающее ИЛИ как управляемый инвертор
В
случае, когда имеется два сигнала
одинаковой полярности (положительные
или отрицательные), и при этом их
одновременный приход исключается,
элемент Исключающее ИЛИ может быть
использован для смешивания этих сигналов
(рис. 4.3). При любой полярности входных
сигналов выходные сигналы элемента
будут положительными.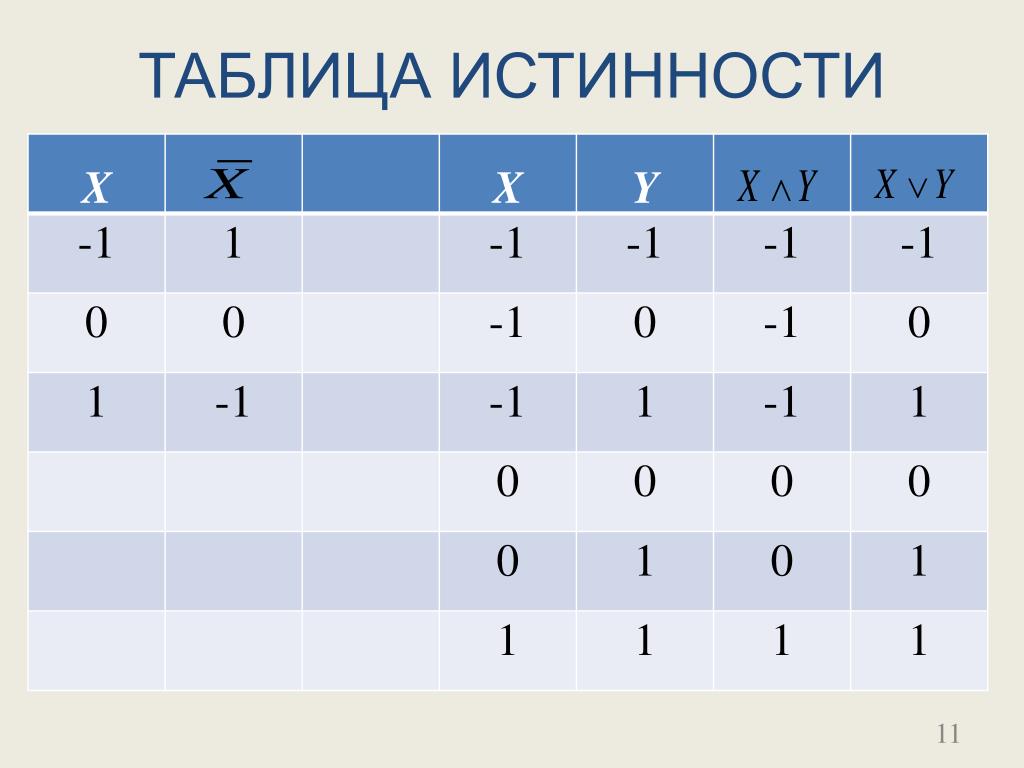
При положительных
входных сигналах элемент Исключающее
ИЛИ будет работать как элемент 2ИЛИ, а
при отрицательных он будет заменять
элемент 2И-НЕ. Такие замены могут быть
полезны в тех случаях, когда в схеме
остаются неиспользованными некоторые
элементы Исключающее ИЛИ. Правда, при
этом надо учитывать, что задержка
распространения сигнала в элементе
Исключающее ИЛИ обычно несколько больше
(примерно в 1,5 раза), чем задержка в
простейших элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ.
Рис. 4.3. Применение элемента Исключающее ИЛИ для смешивания двух неодновременных сигналов
Рис. 4.4. Выделение фронтов входного сигнала с помощью элемента Исключающее ИЛИ
Еще
одно важнейшее применение элемента
Исключающее ИЛИ — формирование коротких
импульсов по любому фронту входного
сигнала (рис. 4.4). В данном случае не
важно, положительный фронт входного
сигнала или отрицательный, на выходе
все равно формируется положительный
импульс.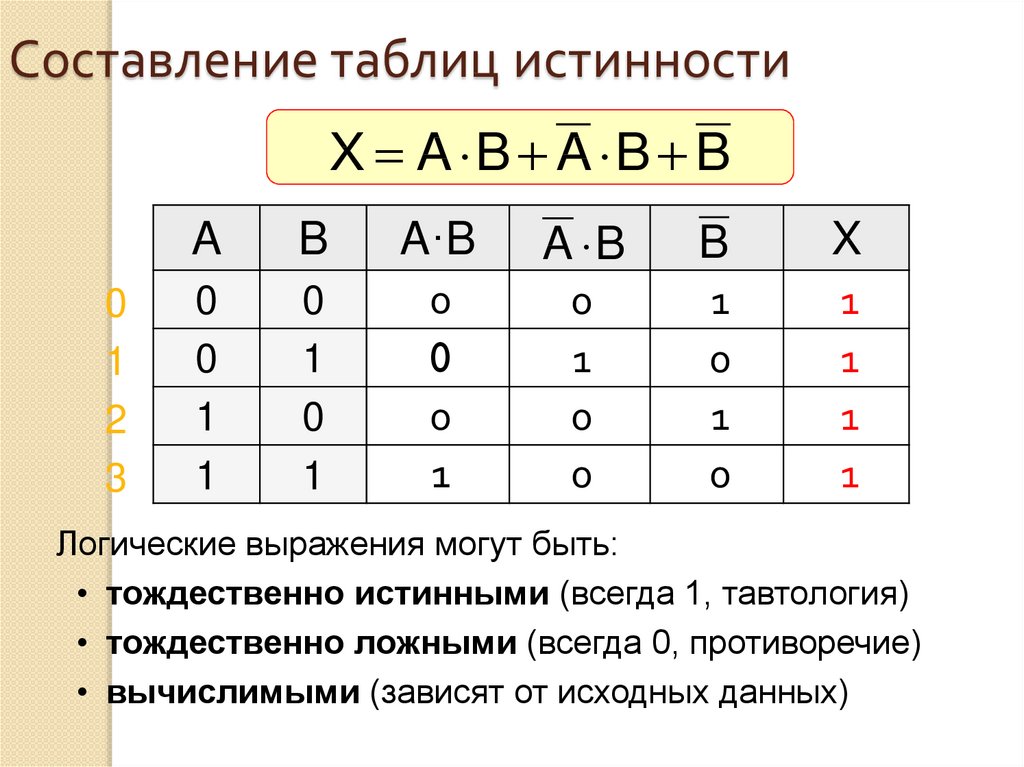
Входной сигнал задерживается
с помощью конденсатора или цепочки
элементов, а затем исходный сигнал и
его задержанная копия поступают на
входы элемента Исключающее ИЛИ. В обеих
схемах в качестве элементов задержки
используются также двувходовые элементы
Исключающее ИЛИ в неинвертирующем
включении (на неиспользуемый вход
подается нуль). В результате такого
преобразования можно говорить об
удвоении частоты входного сигнала, так
как выходные импульсы следуют вдвое
чаще, чем входные.
Данную особенность элементов Исключающее ИЛИ надо учитывать в том случае, когда на оба входа элемента поступают изменяющиеся одновременно сигналы. При этом на выходе элемента возможно появление коротких паразитных импульсов по любому из фронтов входных сигналов. Исключить их влияние на дальнейшую схему можно, например, с помощью синхронизации, подобной рассмотренной в предыдущем разделе.
Сообщество Экспонента
- вопрос
- 22.09.2022
Математика и статистика, Системы управления, Изображения и видео, Робототехника и беспилотники, Глубокое и машинное обучение(ИИ), Другое
Коллеги, добрый день.
Необходимо использовать corrcoef, а массивы разной длины.
Как сделать кол-во элементов одинаково?
Коллеги, добрый день. Необходимо использовать corrcoef, а массивы разной длины. Как сделать кол-во элементов одинаково?
8 Ответов
- вопрос
- 20.09.2022
Другое, Встраиваемые системы, Цифровая обработка сигналов, Системы управления
Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…
Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…
1 Ответ
- MATLAB
20.09.2022
- Публикация
- 15.09.2022
Системы управления, Другое
Видел видос на канале экспоненты по созданию топливной системы.
Вопрос заключается в наличии более полного описания готового примера или соответсвующее документации. Я новичок в симулинке и ещё многого не знаю. Адекватных и раскрытых пособий по созданию гидрав…
Моделирование гидравлических систем в simulink
- Публикация
- 10.09.2022
Системы управления, Электропривод и силовая электроника, Другое
Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов. В этой книге в научно-практическо-методической форме я план…
Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов.
- Публикация
- 24.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
&.
..
Здесь собрана литература по комбинированным методам множественного доступа, в которых используется разделение пользователей в нескольких ресурсных пространствах.
- вопрос
- 23.08.2022
Математика и статистика, Радиолокация, Цифровая обработка сигналов
Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?
Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?
4 Ответа
- ЦОС
- цифровая обработка сигналов
23.08.2022
- Публикация
- 23.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
&…
Здесь соборана литература по методам множественного доступа с поляризационным разделением и разделением по орбитальном угловому моменту.
- Публикация
- 16.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
Здесь собрана литература по методам множественного доступа с пространственным разделением.
- вопрос
- 22.07.2022
Изображения и видео, Цифровая обработка сигналов, Математика и статистика, Биология, Встраиваемые системы, Глубокое и машинное обучение(ИИ), Автоматизация испытаний, ПЛИС и СнК, Системы управления, Другое
Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1.txt file_1_2.txt file_1_3.txt file_1_4.txt fil…
Здравствуйте.
Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например:
file_1_1.
txt
file_1_2.txt
file_1_3.txt
file_1_4.txt
fil…
2 Ответа
- чтение
22.07.2022
- вопрос
- 17.07.2022
Математика и статистика, Цифровая обработка сигналов
Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
- MATLAB
- Signal Processing
17.07.2022
n$ конечно работает, но хотелось бы понять почему и как это работает.Кто может помочь? Спасибо!
- комбинаторика
- логика
$\endgroup$
1
$\begingroup$
Проблема со счетом.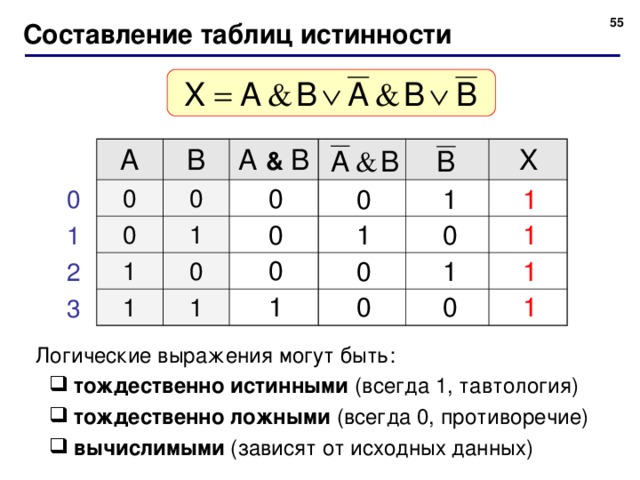
n$. 9н$.
Следовательно, всегда нужно брать возможное количество состояний (2 для таблиц истинности) и возводить его в степень количества входных данных.
Надеюсь, это поможет.
$\endgroup$
1
$\begingroup$
Хотя Артуро Магидин, безусловно, прав в своем ответе, есть еще один простой способ проиллюстрировать это. То есть по аналогии с десятичными числами через двоичные числа.
Точно так же, как десятичные числа идут от $k$ цифр до $k + 1$ цифр (например, от $9n$ строк, чтобы покрыть все возможные комбинации.
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
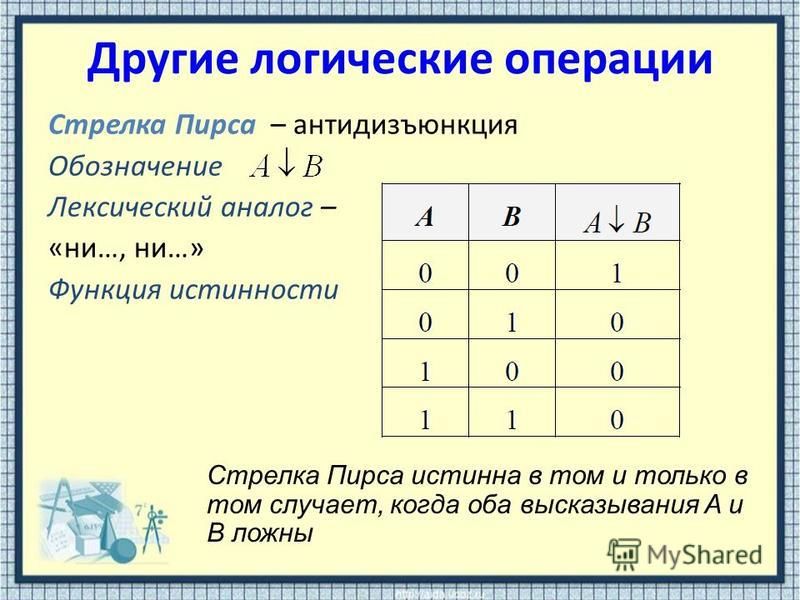n строками, которую сложно построить, когда число переменных превышает 4.Таблица истинности
В этой статье я покажу вам, как SQL может помочь построить таблицу истинности. Чтобы построить таблицу истинности, я написал хранимую процедуру:
.
создать PROC Usp_BuildTruthTable ( @variables xml,
@выражения xml)
В КАЧЕСТВЕ
DECLARE @docHandle int,
@ВЫБРАТЬ varchar(8000),
@ОТ varchar(8000),
@SQL nvarchar(4000)
EXEC sp_xml_preparedocument @docHandle ВЫВОД, @variables
ВЫБЕРИТЕ @FROM=isnull( @FROM +char(13)
+' перекрестное соединение (выберите приведение (0 как бит) объединение всех
выберите приведение (1 как бит)) как '+value+'('+value+')'+char(13)
, '(выберите приведение (0 как бит) объединение всех выберите приведение (1 как бит)) как'
+значение+'('+значение+')')
ОТ OPENXML(@docHandle, N'/Variables/var')
с (значение символа (1))
EXEC sp_xml_removedocument @docHandle
--создание предложения Select
EXEC sp_xml_preparedocument @docHandle ВЫВОД, @expressions
SELECT @SELECT=isnull(@SELECT+' ,['+col+']='+col, '['+col+']='+col)
ОТ OPENXML(@docHandle, N'/expressions/exp')
С (столбец VARCHAR(8000) '@val')
SET @SQL='выбрать *,'+@SELECT+ 'из '+char(13) +@FROM
ВЫПОЛНИТЬ( @SQL)
EXEC sp_xml_removedocument @docHandle
Как видите, он принимает два параметра, которые объявлены как тип данных XML, новый для SQL Server 2005.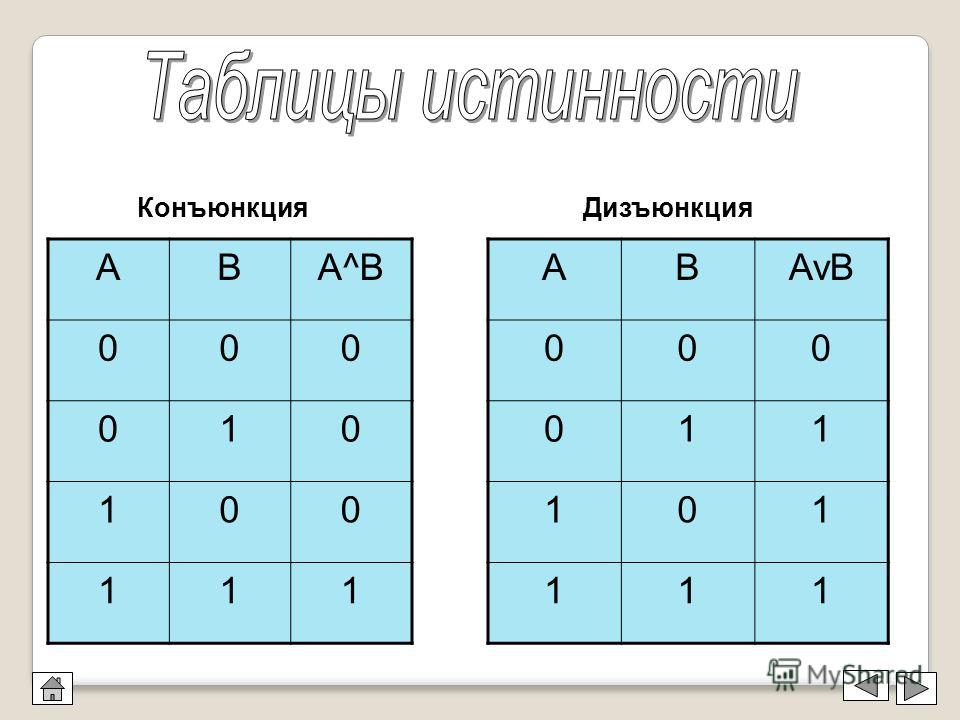
Если вы не знакомы с процедурой XML, которую я использовал в Usp_BuildTruthTable , вы можете обратиться к документации BOL.
Основным ядром хранимой процедуры является оператор «(выберите приведение (0 как бит) объединение всех выбранных приведения (1 как бит))», который присваивает все возможные значения переменным и CROSS JOIN, который используется для создания все возможные комбинации переменных. @SELECT будет оценивать выражение, и логика этого проста: SQL Server имеет побитовый оператор, поэтому он может оценивать побитовые выражения. По этой причине я преобразовал ноль и единицу в битовый тип данных. В SQL SERVER есть 4 побитовых оператора: 9
Now I want to show you how to use these bitwise operators in logical connectives:
| Logical operator | Expression | Bitwise |
| Not | P | ~P |
| И | P И Q | P & Q |
| Включительно или | P OR Q | P | Q |
| Исключительно или 9Q | ||
| Подразумевается | P IMP Q | ~P | Q |
| Эквивалентность | P EQU Q ==( P IMP Q) & (Q IMP P) | (~P | Q ) & (~Q | P ) |
Вы должны передавать переменные и выражения в следующем формате:
<Переменные> . Проверим сложное выражение: ((P imp Q) и (Q imp R)) imp (P imp R) == ~ ((~P |Q) & (~Q | R)) | (~П | Р) У нас есть три переменные и выражение, поэтому мы вызываем хранимую процедуру следующим образом: exec usp_BuildTruthTable '<Переменные> <вар значение = "R" /> ', '<выражения> И вот результат: P Q R ~((~p |Q) & (~Q |R)) | (~П|Р) ----- ----- ----- ---------------- 0 0 0 1 0 1 0 1 1 0 0 1 1 1 0 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1 1 код можно скачать отсюда Раздел 2: Полные таблицы истинности
Значение истинности предложений, содержащих только одну связку, определяется характеристической таблицей истинности для этой связки. В предыдущей главе мы написали характеристические таблицы истинности, где «T» означает «истина», а «F» — ложь. Однако важно отметить, что речь идет не об истине в каком-либо глубоком или космическом смысле. Поэты и философы могут долго спорить о природе и значении истины , но функции истинности в SL — это просто правила, которые преобразуют входные значения в выходные значения. Чтобы подчеркнуть это, в этой главе мы будем писать «1» и «0» вместо «T» и «F». Хотя мы интерпретируем «1» как значение «истинно», а «0» — как «ложно», компьютеры можно запрограммировать на заполнение таблиц истинности чисто механическим способом. В машине «1» может означать, что регистр включен, а «0» — что регистр выключен. Математически это всего лишь два возможных значения, которые может иметь предложение SL. Вот таблицы истинности для связок SL, записанные в единицах и нулях.
Таблица 3. Характеристическая таблица истинности для соединения, например, дает условия истинности для любого предложения формы (\(\mathcal{A}\)&\(\mathcal{B}\)). Даже если союзы \(\mathcal{A}\) и \(\mathcal{B}\) являются длинными сложными предложениями, союз истинен тогда и только тогда, когда и \(\mathcal{A}\), и \( \mathcal{B}\) верны. Рассмотрим предложение (\(H\)&\(I\)) → \(H\). Мы рассматриваем все возможные комбинации истинного и ложного для \(H\) и \(I\), что дает нам четыре строки. Затем мы копируем значения истинности для букв предложения и пишем их под буквами в предложении.
Теперь рассмотрим подпредложение \(H\)&\(I\).
Все предложение является условным \(\mathcal{A}\)→\(\mathcal{B}\) с (\(H\)&\(I\)) как \(\mathcal{A }\) и с \(H\) как \(B\).
Столбец с единицами под условным предложением говорит нам, что предложение (\(H\)&\(I\)) → \(I\) истинно независимо от значений истинности \(H\) и \(Я\). В этом примере мы не повторили все записи в каждой последующей таблице. Однако при написании таблиц истинности на бумаге нецелесообразно стирать целые столбцы или переписывать всю таблицу для каждого шага. Хотя он более людный, таблицу истинности можно записать так:
Большинство столбцов под предложением предназначены только для бухгалтерских целей. В полной таблице истинности есть строка для всех возможных комбинаций 1 и 0 для всех букв предложения. Размер полной таблицы истинности зависит от количества различных букв предложения в таблице. Предложение, содержащее только одну букву предложения, требует только двух строк, как в характеристической таблице истинности для отрицания. Это верно, даже если одна и та же буква повторяется много раз, как в предложении [(\(C\) ↔ \(C\)) → \(C\)]&¬(\(C\) → \(C \)). Полная таблица истинности требует всего две строки, потому что есть только две возможности: \(C\) может быть истинным или ложным. Одна буква предложения никогда не может быть отмечена как 1, так и 0 в одной и той же строке.
Глядя на столбец под главной связкой, мы видим, что предложение ложно в обеих строках таблицы; т. е. оно ложно независимо от того, истинно или ложно \(С\). Предложение, содержащее две буквы предложения, требует четырех строк для полной таблицы истинности, как в характеристических таблицах истинности и таблице для (\(H\)&\(I\)) → \(I\). Предложение, содержащее три буквы предложения, занимает восемь строк. Например:
Из этой таблицы мы знаем, что предложение \(M\) &(\(N\)∨\(P\)) может быть истинным или ложным, в зависимости от значений истинности \(M\) , \(N\) и \(P\). Полная таблица истинности предложения, состоящего из четырех разных букв, занимает 16 строк. Пять букв, 32 строки. Шесть букв, 64 строки. И так далее. Чтобы быть совершенно общим: если полная таблица истинности имеет \(\mathcal{n}\) различных букв предложения, то она должна иметь 2 п рядов. Чтобы заполнить столбцы полной таблицы истинности, начните с самой правой буквы предложения и чередуйте 1 и 0. В следующем столбце слева напишите две единицы, напишите два нуля и повторите. В третьем предложении напишите четыре единицы, а затем четыре нуля. Это дает восьмистрочную таблицу истинности, подобную приведенной выше. Для 16-строчной таблицы истинности в следующем столбце букв предложения должно быть восемь единиц, за которыми следуют восемь нулей. Для 32-строчной таблицы в следующем столбце будет 16 единиц, за которыми следуют 16 нулей. И так далее. Эта страница под названием «Раздел 2: Полные таблицы истинности» распространяется по лицензии CC BY-SA, автором, ремиком и/или куратором которой является П.  |
b)" />
D. Магнус
1: Характеристические таблицы истинности для связок SL.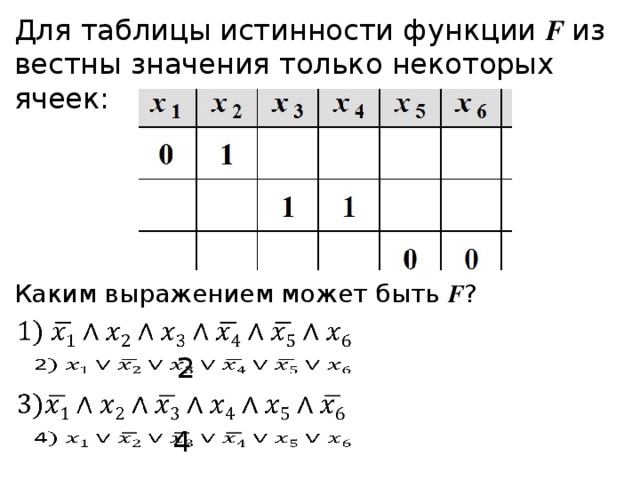
Это конъюнкция \(\mathcal{A}\)&\(\mathcal{B}\) с \(H\) как \(\mathcal{A}\) и с \(I\) как \(\ математический{B}\). \(H\) и \(I\) верны в первой строке. Поскольку конъюнкция истинна, когда оба конъюнкта истинны, мы пишем 1 под символом конъюнкции. Продолжаем остальные три ряда и получаем вот это:
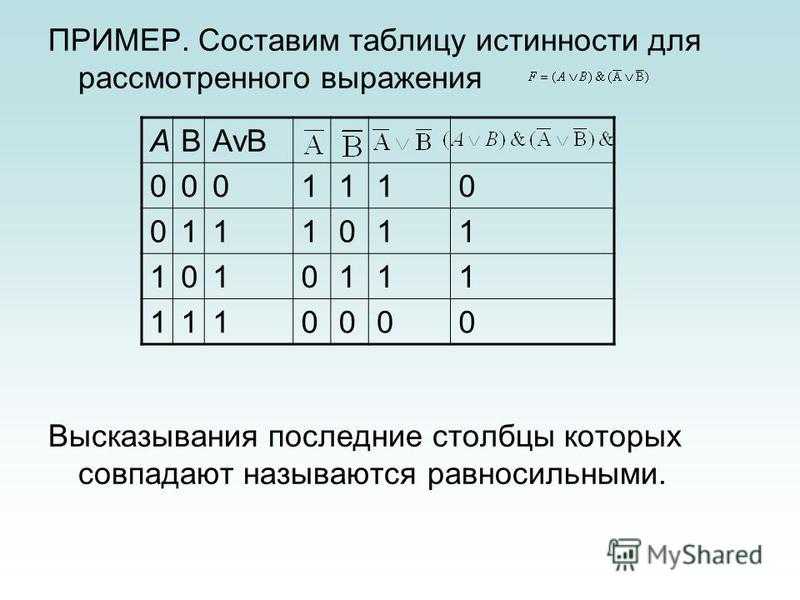Например, во второй строке (\(H\)&\(I\)) ложно, а \(H\) истинно. Поскольку условие истинно, когда антецедент ложен, мы пишем 1 во второй строке под условным символом. Продолжаем остальные три ряда и получаем вот это:
Они могут быть истинными или ложными в любой комбинации, и составное предложение все равно будет истинным. Крайне важно, чтобы мы рассмотрели все возможные комбинации. Если бы у нас была только двухстрочная таблица истинности, мы не могли бы быть уверены, что предложение не будет ложным для какой-либо другой комбинации значений истинности.
Когда вы станете лучше разбираться в таблицах истинности, вам, вероятно, больше не потребуется копировать столбцы для каждой буквы предложения. В любом случае истинностное значение предложения в каждой строке — это просто столбец под основным логическим оператором предложения; в этом случае столбец под условным.
Таблица истинности для этого предложения выглядит так:
