Логические выражения и таблица истинности в примерах решения задач

Теория по этой теме по этой теме Пройти тестирование по этой теме Контрольная по этой теме

 №1.

Докажите, что А <=> В равносильно (A\/ ¬B) /\ (¬A\/ B)

 Для доказательства равносильности двух высказываний достаточно построить таблицу истинности для высказывания (A\/ ) /\ (\/ B) и сравнить ее с таблицей истинности эквивалентности:

А	В	¬B	A\/¬B	¬A	¬AVB	(A\/¬B) /\ (¬A \/B)
0	0	1	1	1	1	1
0	1	0	0	1	1	0
1	0	1	1	0	0	0
1	1	0	1	0	1	1

Последние столбцы этих функций совпадают, значит, они равносильны. ЧТД.

 

№2.

Укажите, какое логическое выражение равносильно выражению 

A /\ ¬ (¬B \/ C)

   1) ¬A \/ ¬B \/ ¬C

   2) A /\ ¬B /\ ¬C  

   3) A /\ B /\ ¬C 

   4) A /\ ¬B /\ C

Ответ:  3

№3.

Постройте таблицу истинности для логического выражения:

1)A=>B<=> ¬А \/  B 

Ответ:

А	В	A=>B	¬А	A → B<=> ¬А	A → B<=> ¬А \/  B
0	0	1	1	1	1
0	1	1	0	0	1
1	0	0	0	1	1
1	1	1	0	0	1

2)F=A<=>B<=>(¬А \/  B) /\ (¬B\/  А)

Ответ:

 

 

 

 

 

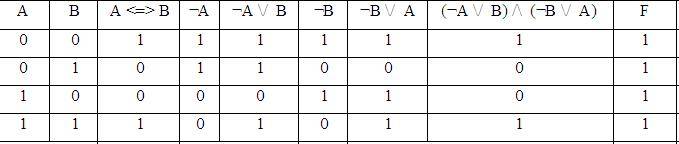
№4.

Определите истинность следующего высказывания: «За окном светит солнце, и нет дождя».

Решение:

Нам дано сложное составное высказывание. Выделим из него простые высказывания:

А = «За окном светит солнце»

В = «За окном дождь»

 Составим логическую функцию, соответствующую данному высказыванию.

F(A, B) = A /\ ¬B

построим таблицу истинности для данной логической функции.

A	B	¬B	A /\ ¬B
0	0	1	0
0	1	0	0
1	0	1	1
1	1	0	0

 Ответ: логическое выражение принимает значение истина только при наборе F(1,0)=1.Следовательно, данное нам высказывание истинно только тогда, когда первое простое высказывание истинно, а второе ложно.

 

№5.

Определите истинность следующего высказывания: «Гости смеялись, шутили и не расходились по домам».

Решение:

Выделим из данного сложного высказывания простые высказывания:

А = «Гости смеялись»

В = «Гости шутили»

С = «Гости расходились по домам»

Составим логическую функцию, соответствующую данному высказыванию.

F(A, B, С) = A/\ B /\¬C

Построим таблицу истинности для данной логической функции.

 

A	B	C	¬C	A /\ B/\¬C
0	0	0	1	0
0	0	1	0	0
0	1	0	1	0
0	1	1	0	0
1	0	0	1	0
1	0	1	0	0
1	1	0	1	1
1	1	1	0	0

Ответ: логическое выражение принимает значение истина только при наборе F(1,1,0)=1.Следовательно, данное нам высказывание истинно только тогда, когда первое и второе простые высказывания истинны, а второе ложно.

 

№6.

На языке алгебры логики составьте истинное тождество, соответствующее заданному условию задачи:

Школьника, Миша, остававшийся в классе на перемене, был вызван к директору по поводу разбитого в это время окна в кабинете. На вопрос директора о том, кто это сделал, мальчик ответили следующее: «Я не бил окно, и Коля тоже…»

Известно, что он либо сказал чистую правду, либо в одной части заявления соврал, а другое его высказывание истинно, либо оба факта исказил.

Решение:

Пусть

А = «Окно разбил Миша»

В = «Окно разбил Коля»

Если Миша сказал чистую правду, то¬А /\ ¬В = 1.

Если в одной части заявления Миша соврал, а другое его высказывание истинно, то (¬А /\ В) \/ (А /\¬В) = 1

Если Миша оба факта исказил, то А /\ В = 1.

Ответ:

Истинное тождество, соответствующее условию задачи будет выглядеть так: ¬А /\ ¬В  \/¬А /\ В \/А /\ ¬ В \/ А /\ В = 1.

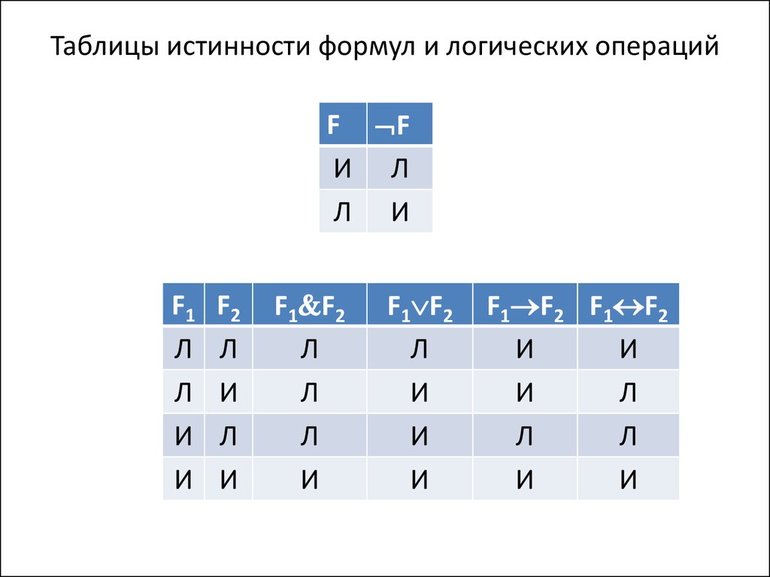
Таблицы истинности, с формулами и примерами

Они могут принимать значения «истина» или «ложь» (1 или 0). Для функции, содержащей две переменные, наборов значений переменных всего четыре:

   

Значения логических функций определяются с помощью таблица истинности.

Таблицы истинности для основных двоичных логических функций

1. Конъюнкция (логическое умножение) – сложное логическое выражение, которое является истинным только в том случае, когда истинны оба входящих в него простых выражения.

Обозначение:

2. Дизъюнкция (логическое сложение) – это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно, если оба простых логических выражения ложны.

Обозначение:

3. Импликация (логическое следствие) – это сложное логическое выражение, которое является ложным тогда и только тогда, когда условие истинно, а следствие ложно.

Обозначение:

4. Эквиваленция – это сложное логическое высказывание, которое является истинным только при одинаковых значениях истинности простых выражений, входящих в него.

Обозначение:

5. Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным.

Обозначение:

6. Штрих Шеффера – операция, отрицающая конъюнкцию, т.е. значение ложно тогда и только тогда, когда оба простых выражения истинны.

Обозначение:

7. Стрелка Пирса – операция, отрицающая конъюнкцию, т.е. значение истинно тогда и только тогда, когда оба простых выражения ложны.

Обозначение:

Порядок выполнения логических операций

При построении таблицы истинности необходимо учитывать порядок выполнения логических операций:

1. Инверсия
2. Конъюнкция
3. Дизъюнкция
4. Импликация
5. Эквиваленция
6. Штрих Шеффера
7. Стрелка Пирса

Для последних двух операций приоритет не определен.

Замечание. Если необходимо изменить указанный порядок выполнения логических операций используются скобки.

Примеры решения задач

Логические выражения и логическая таблица истинности. Правила построения

Примеры задач с решениями по этой теме Пройти тестирование по теме Контрольная по теме

 Таблица истинности — таблица, показывающая,  какие значения принимает составное высказывание при  всех сочетаниях (наборах)  значений  входящих в него простых высказываний.

Логическое выражение — составные высказывания в виде формулы.

Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».

Алгоритм построения  таблицы  истинности:

1.    подсчитать количество переменных n в логическом выражении;

2.   определить число строк в таблице по формуле m=2ⁿ, где n — количество переменных;

3.   подсчитать количество логических операций в формуле;

4.   установить последовательность выполнения логических операций с учетом скобок и приоритетов;

5.   определить количество столбцов: число переменных + число операций;

6.   выписать наборы входных переменных;

7.   провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.

Заполнение таблицы:

1.      разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;

2.      разделить колонку  значений  второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;

3.      продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.

 

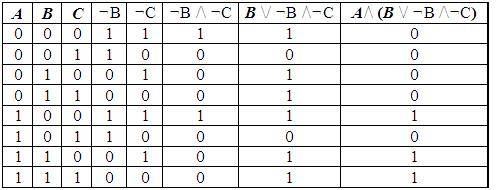
Пример 1. Для формулы  A/\ (B \/ ¬B /\¬C) постройте  таблицу истинности.

 Количество логических переменных 3, следовательно, количество строк — 2³ = 8.

Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.

 

 

 

 

 

 

Пример 2. Определите истинность  логического выражения  F(А, В) = (А\/ В)/\(¬А\/¬В) .

1. В выражении две переменные А и В (n=2).

2.  m_строк=2ⁿ, m=2²=4 строки.

3. В формуле 5 логических операций.

4. Расставляем порядок действий

1) А\/ В;  2) ¬А;  3) ¬В;  4) ¬А\/¬В;  5) (А\/ В)/\(¬А\/¬В).

5. К_{столбцов}=n+5=2+5=7 столбцов.

 

А	В	А\/ В	¬А	¬В	¬А\/¬В	F
0	0	0	1	1	1	0
0	1	1	1	0	1	1
1	0	1	0	1	1	1
1	1	1	0	0	0	0

 Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.

 

Пример 3. Построёте таблицу истинности для логического выражения

F = (A\/ B) /\ ¬С

1. В данной функции три логические переменные – А, В, С
2. количество строк таблицы = 2³ =8
3. В формуле 3 логические операции.
4. Расставляем порядок действий

1) А\/ В;  2) ¬С; 3) (AVB) /\ ¬С  .

5. количество столбцов таблицы = 3 + 3 = 6

А	В	С	A\/B	¬С	(A\/B) /\ ¬С
0	0	0	0	1	0
0	0	1	0	0	0
0	1	0	1	1	1
0	1	1	1	0	0
1	0	0	1	1	1
1	0	1	1	0	0
1	1	0	1	1	1
1	1	1	1	0	0

 

Пример 4.  Определите истинность формулы: F = ((С \/В) =>  В) /\ (А /\ В) => В.

Построим таблицу истинности этой формулы.

 

 

 

 

 

 

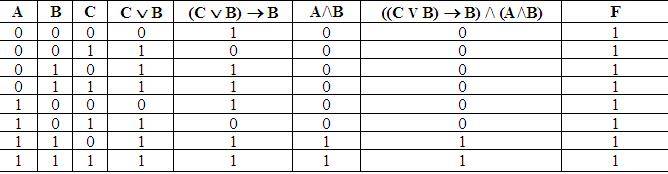
Ответ: формула является тождественно истинной.

Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.

Дан фрагмент таблицы истинности выражения F:

 

 

Какое выражение соответствует F?

 1) ¬X/\¬Y/\Z                      2) ¬X\/¬Y\/Z                  3) X\/Y\/¬Z              4) X\/Y\/Z

 Решение (вариант 1, через таблицы истинности):

Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:

X	Y	Z	F	¬X	¬Y	¬Z	¬X/\¬Y/\Z	¬X\/¬Y\/Z	X\/Y\/¬Z	X\/Y\/Z
0	0	0	1	1	1	1	0	1	1	0
0	0	1	0	1	1	0	1	1	0	1
0	1	0	1	1	0	1	0	1	1	1

 Очевидно, что значения заданной функции F совпадают со значениями выражения X\/Y\/¬Z. Следовательно, правильный ответ – 3.

Ответ: 3

 Решение (Вариант 2):

Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y  и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.

 Рассмотрим данный конкретный пример:

1)      первое заданное выражение  ¬X/\¬Y/\Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;

2)      второе заданное выражение ¬X\/¬Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует  второй строке таблицы;

3)      третье выражение   X\/Y\/¬Z    соответствует F при всех предложенных комбинациях X,Y и Z;

4)      четвертое выражение X\/Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.

Ответ: 3

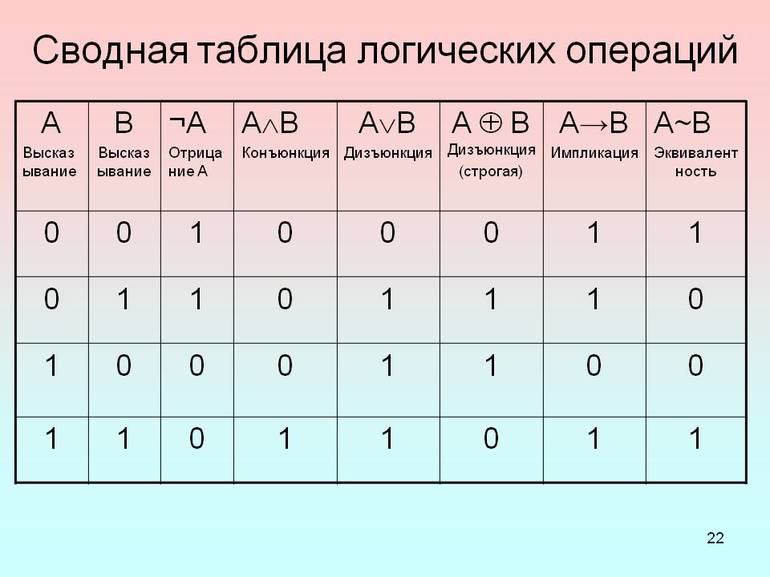
Таблицы истинности логических операций ✔️ алгоритм построения и решение задач с помощью таблиц, примеры

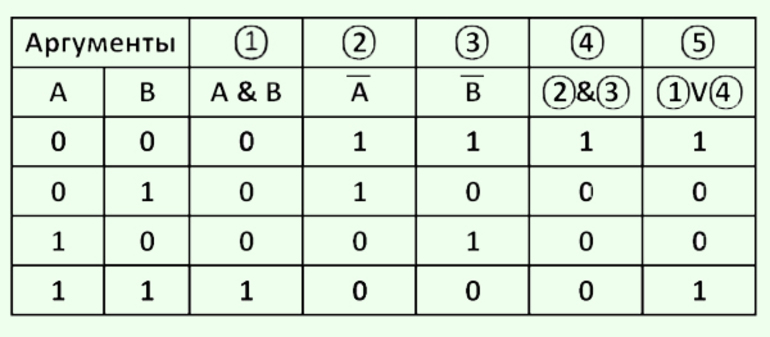
Определения и понятия

Под таблицей истинности понимают свод значений, которые может принять высказывание при сочетании различных входящих комбинаций. Другими словами, каждому набору функций или сигналам, присутствующим на входе чего-либо, соответствует строго определённые показатели на выходе. Все значения, являющиеся всевозможными высказываниями, называют логическими выражениями. Если в таблице последние столбцы логичных выражений идентичны, то рассматриваемый объект считается равносильным.

Любое выражение можно описать формулой, в которую будут включаться переменные, характеризующие состояния, и обозначающие функции знаки логических операций. Поэтому используя язык математики, в частности, алгебры, любое сложное высказывание можно разделить на несколько простых, а затем объединить логической связью.

Обычно значениями истинности описывают логическую функцию, у которой показатели параметров определяют верность. Раздел математики рассматривающий их на правдивость или ложность называется булевым. В 1854 году английский учёный Джордж Буль предложил метод, позволяющий проводить анализ классов и высказываний. Согласно ему, любое значение может принимать одно из двух состояний — истина или ложь.

Эти состояния принято обозначать арабскими цифрами один либо ноль или словами true и false. Это возможно из-за того, что для математики важна только истинность высказываний, а конкретное содержание второстепенно. Простые высказывания принято считать логическими переменными, а сложные — функциями логики. Выражения для упрощения записи обозначают латинскими буквами A, B, C.

Применение двух цифр подчёркивает соответствие между двоичной системой счисления и математической логикой. В итоге с помощью последней стало удобным описывать работу цифровых схем радиоэлектронной аппаратуры, алгоритмы в программировании, проводить синтез и анализ результата выполнения операций.

Суждение о правильности построения таблиц истинности для логических выражений основано на учёте всех переменных и операций, последовательно выполняющихся в рассматриваемой функции. Обычно для начертания используют 2ⁿ+1 строк, где n обозначает количество входных переменных, и n+m столбцов, m — число значений на выходе.

Виды логических операций

В качестве наименьшей единицы измерения объёма данных принято считать бит. В него заносится одно из двух значений — ложь (0) или правда (1). Каждая ячейка, соответствующая биту, находится лишь в одном из этих состояний.

Существуют определённые операции, используемые для действий с ячейками:

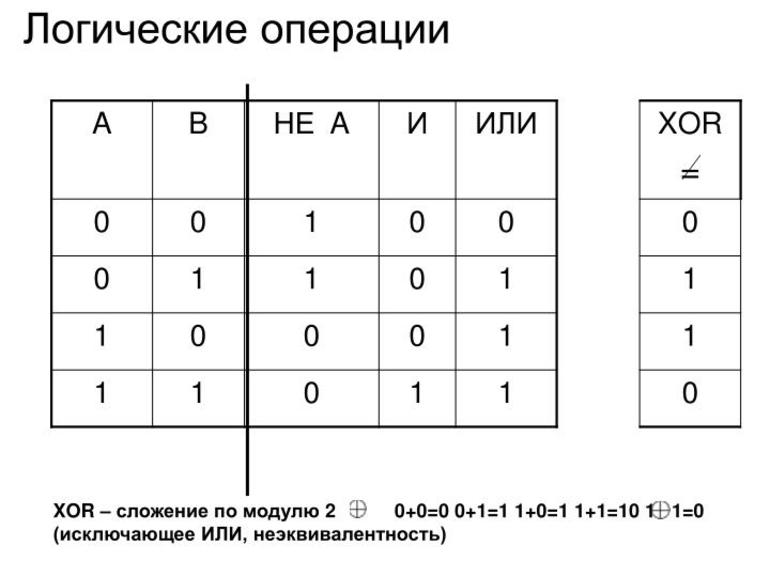
1. AND (И) — применяется для сравнения двух бит. Результатом действия будет единица, но лишь в том случае, если значения двух ячеек одинаковое. При остальных вариантах итог будет иметь устойчивое нулевое состояние.
2. OR (ИЛИ) — по сути, операция обратная AND. Результат становится нулевым, если содержимое двух сравниваемых бит одинаковое. В остальных случаях он равный единице.
3. XOR (ИЛИ) — если значения, содержащиеся в двух сравниваемых битах противоположны, при выполнении логического действия результат будет равный единице. Во всех остальных случаях он будет равняться нулю.
4. NOT (НЕ) — действие, используемое для одного бита. Если первоначально ячейка находилась в нулевом состоянии, то после выполнения над ней операции она станет равной единице и наоборот. Фактические это логическая инверсия.

Эти операции являются основными элементами при составлении таблиц истинности и получения возможного результата. На основании их построена алгебра Буля. Некоторые элементы получаются путём объединения нескольких операций. Так, существует состояние: NAND (И-НЕ) и NOR (ИЛИ-НЕ). Первый элемент является инверсией операции «И», а второй — «ИЛИ». На основании рассмотренных операторов строится работа всех цифровых интегральных схем.

В информатике существует своя терминология, обозначающая то или иное логическое действие. Так, AND называют операцией конъюнкции, OR — дизъюнкции, XOR — сложение по модулю 2, NOT — отрицание. Задача инженера при анализе схем или алгоритма сводится к выполнению булевой арифметики и упрощению выражений. Для этого используют различные правила и положения не требующих доказательства.

Аксиомы и законы

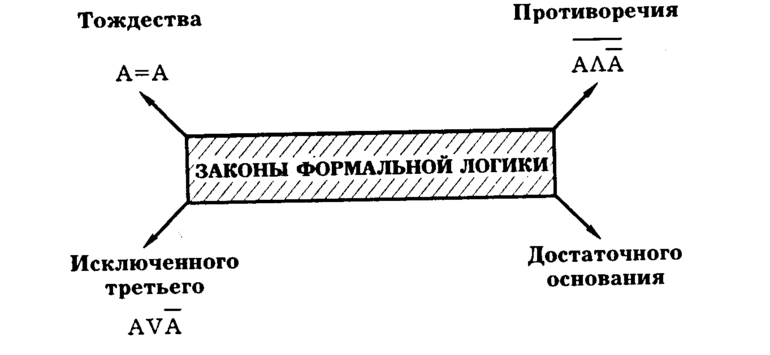
Построение таблиц в удобной форме позволяет определить, когда определённое действие или высказывание принимает верное значение, а в каком случае нет. В верхней строчке записывают логическую форму высказывания, а в столбцах — истинные значения. Некоторые комбинации высказываний всегда будут истинными или ложными, независимо от содержания. Поэтому и были сформулированы следующие законы:

1. Торжества. Записывается в виде утверждения: А = А. В этом случае таблица будет состоять из двух комбинаций: ложной и правдивой. Бинарная логическая связка «Если А, то А» является материальной импликацией. Для такого варианта всегда можно сказать, что А есть А. Этот закон обозначает то, что нельзя подменять одно понятие другим, иначе возникнут логические ошибки.
2. Противоречия. Согласно ему, утверждение, что А и НЕ-А, неверно: A & A = 0. Другими словами, если А истинное значение, то его отрицание не может быть ложным. То есть их перемножение будет всегда фальшивой операцией. Этот закон довольно часто применяется для упрощения сложных логических суждений.
3. Третьего исключённого. Закон записывается в виде A v A = 1 и обозначает, что в один и тот же момент высказывание может быть только правдивым или ложным. То есть третьего не дано.

Эти три закона фундаментальны. Без их соблюдения сделать любое правильное утверждение невозможно.

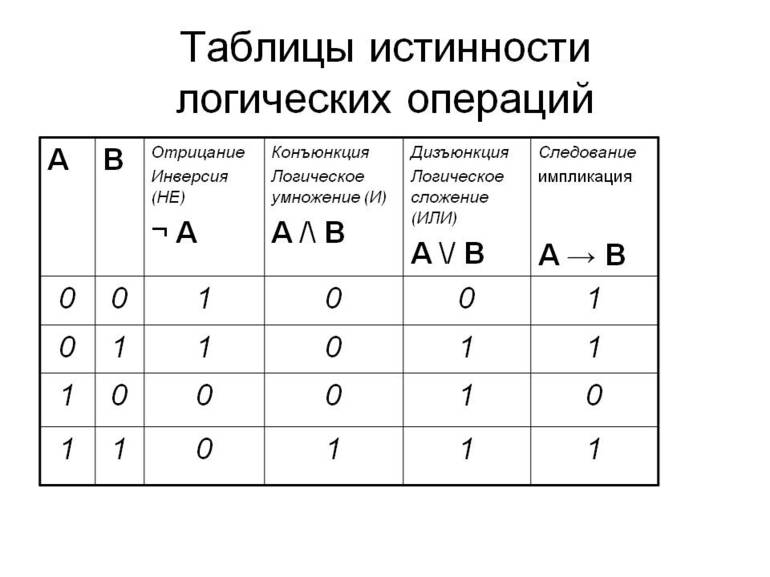
Для решения логических задач с помощью таблиц истинности используют различные формулы, соответствующие разного вида операциям. Одно из них логическое умножение (конъюнкция). В этом случае считается, что функция истинная лишь тогда, когда оба выражения являются верными: F = A & B. Другое логическое сложение (дизъюнкция). Оно гласит, что если оба выражения ложны, то и логическая функция будет неверной.

Кроме того, используется закон:

• инверсии (отрицания) — если логическое высказывание истинно, то отрицание его будет ложным выражением;
• импликации (следования) — для всегда истинного сложного логического выражения ложь будет тогда, когда из верности следует отрицание;
• эквивалентности (равнозначности) — выражение будет истинным лишь тогда, когда оба высказывания имеют одинаковое значение.

При построении таблиц нужно придерживаться установленного порядка выполнения упрощения операций. Вначале считают инверсию и конъюнкцию, а затем дизъюнкцию, импликацию и эквиваленцию. При изменении же порядка выполнения действий в описании логических операций используют скобки.

Алгоритм построения

Таблицы истинности показывают, какой вид может принять выражение при различных входящих в него значениях переменных. Для того чтобы их правильно построить и выполнить вычисление логического выражения нужно придерживаться установленного алгоритма. Построение таблиц выполняют в следующей последовательности:

• подсчитывают количество переменных n;
• вычисляют число строк для будущей таблицы используя формулу m = 2n+1;
• определяют число логических операций;
• устанавливают порядок выполнения операций в соответствии со скобками и приоритетами;
• строят таблицу с указанием столбцов и наборов значений, заданных логических операций;
• заполняют оставшиеся ячейки в таблице.

Для заполнения таблиц нужно упрощать выражения с учётом последовательности выполнения операций. При этом учитывать, что если значение какого-то из аргументов функции в соответствующей строке таблицы будет равное нулю, то записывать его нужно в виде отрицания.

Пример задания

Пусть необходимо построить таблицу для логического выражения F = (A → B) * (A + B). Эта формула состоит из двух логических переменных A и B и нескольких операций. Начинают построение с определения строк. Используя формулу 2n+1 для рассматриваемого примера можно установить, что их число будет: x = 22 + 1 = 5.

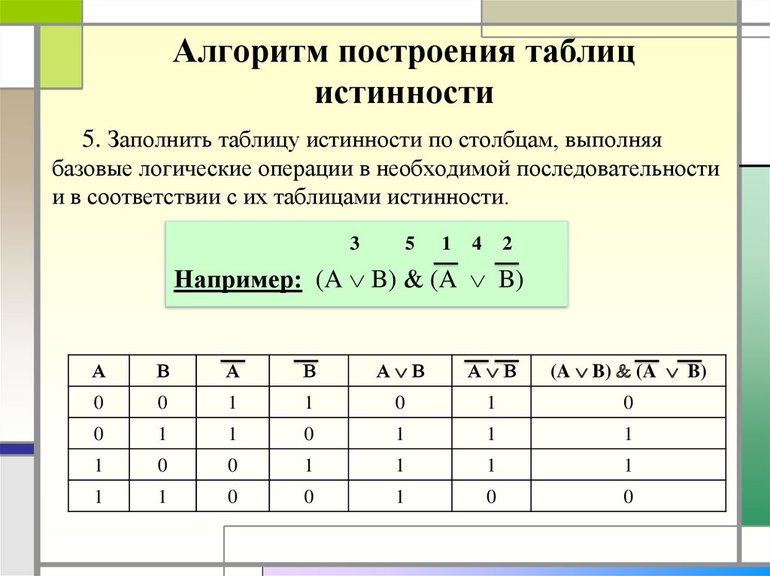
Теперь следует определить число столбцов. Для этого используется формула, в которой учитывается количество переменных и операций. Последние можно просто посчитать, сложив количество разных знаков, используемых в записи формулы. Но правильней сначала расставить порядок операций, а затем посчитать. Согласно порядку действия над операциями их нумерацию можно представить в следующей очерёдности:

1. Импликация в первой скобке.
2. Инверсия во второй скобке переменной A.
3. Отрицание во второй скобке неизвестной B.
4. Сложение во втором члене.
5. Конъюнкция.

В итоге получится, что столбцов будет: Y = 2 + 5 = 7. Теперь нужно построить таблицу 7Х5. В шапку первого и второго столбца вписывают переменные, а затем операции над ними. Затем в строках, соответствующих A и B нужно записать всё, что с ними может произойти. В итоге останется только правильно посчитать последний столбец.

Для этого нужно использовать законы. Необходимо выполнить логическое умножение значений в скобках. Первой и второй строчке будет соответствовать операция произведения один на один, что в ответе даст единицу. Третьей и четвёртой — ноль на один, что в итоге даст ноль. Последний столбец является главным для рассматриваемой логической функции. По нему можно узнать значение логической функции для любых форм переменных A и B.

Это довольно простая задача, содержащая всего две переменных. Но в реальности, например, в программировании, их может быть намного больше. Решать такие задания методом перебора проблематично. Поэтому при решении сложных примеров функцию вначале пытаются упростить.

Например, заданно выражение (x + y + z) * (x + y). По сути, оно записано в совершенно нормальной конъюнктивной форме. Но для приведения его к этому виду нужно, чтобы во втором выражении стояла z. Для того чтобы её добавить необходимо обратить внимание на то, что внутри скобок стоит логическое сложение. Поэтому дописав к нему ноль, результат не изменится. Добавить ноль через z можно, как ноль умножить на НЕ z. В итоге получится выражение (x + y + z) * (x + y + z + z), для которого, используя алгоритм составить таблицу уже не так и сложно.

Вычисления онлайн

В интернете есть сервисы, автоматически строящие таблицы истинности. Такие сайты предлагают свои услуги бесплатно и доступны даже тем, кто слабо ориентируется в теме. С их помощью можно находить таблицы для довольно сложных выражений, решение которых требует скрупулёзности в расчёте. В основе онлайн-вычислений заложены принципы логических законов, поэтому за достоверность результата можно не переживать. Тем более расчёт занимает совсем небольшое количество времени.

Для того чтобы воспользоваться сайтами-калькуляторами пользователю необходимо знать обозначение операций, иметь подключение к интернету и установленный веб-обозреватель, поддерживающий Flash-технологию. Регистрацию, указание личных данных сервисы, предлагающие такого рода услуги, не требуют.

Из различных порталов можно отметить три наиболее популярных калькулятора:

1. Allcalc.
2. Programforyou.
3. Uchim.

Эти сайты имеют интуитивно понятный интерфейс и что довольно полезно, на своих страницах содержат краткую теорию, используемую для составления таблиц истинности и даже примеры решений.

Таблица истинности онлайн с примерами

Таблица истинности — это таблица, которая описывает логическую функцию. Логическая функция здесь — это функция, у которой значения переменных и значение самой функции выражают истинность. Например, они принимают значения «истина» либо «ложь» (true либо false, 1 либо 0).

Таблицы истинности применяются для определения значения какого-либо высказывания для всех возможных случаев значений истинности высказываний, которые его составляют. Количество всех существующих комбинаций в таблице находится по формуле N=2*n; где N — общее количество возможных комбинаций, n — число входных переменных. Таблицы истинности нередко используются в цифровой технике и булевой алгебре, чтобы описать работу логических схем.

Таблицы истинности для основных функций

Примеры: конъюнкция — 1&0=0, импликация — 1→0=0.

Порядок выполнения логических операций

Инверсия; Конъюнкция; Дизъюнкция; Импликация; Эквиваленция; Штрих Шеффера; Стрелка Пирса.

Последовательность построения (составления) таблицы истинности:

https://uchim.org/matematika/tablica-istinnosti — uchim.org

1. Определить количество N используемых переменных в логическом выражении.
2. Вычислить количество всевозможных наборов значений переменных M = 2^N , равное количеству строк в таблице.
3. Подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество логических операций.
4. Озаглавить столбцы таблицы названиями переменных и названиями логических операций.
5. Заполнить столбцы логических переменных наборами значений, например, от 0000 до 1111 с шагом 0001 в случае для четырех переменных.
6. Заполнить таблицу истинности по столбцам со значениями промежуточных операций слева направо.
7. Заполнить окончательный столбец значений для функции F.

Таким образом, можно составить (построить) таблицу истинности самостоятельно.

Составить таблицу истинности онлайн

Заполните поле ввода и нажмите OK. T — истина, F — ложь. Рекомендуем добавить страницу в закладки или сохранить в социальной сети.

Обозначения

1. Множества или выражения большими буквами латинского алфавита: A, B, C, D…
2. A’ — штрих — дополнения множеств
3. && — конъюнкция («и»)
4. || — дизъюнкция («или»)
5. ! — отрицание (например, !A)
6. \cap — пересечение множеств \cap
7. \cup — объединение множеств (сложение) \cup
8. A&!B — разность множеств A∖B=A-B
9. A=>B — импликация «Если …, то»
10. AB — эквивалентность

Всё для учебы » Математика в школе » Таблица истинности онлайн с примерами — логика

Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):

Таблица истинности — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 октября 2016; проверки требуют 26 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 октября 2016; проверки требуют 26 правок.

Таблица истинности — таблица, описывающая логическую функцию.

Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» (true{\displaystyle true} либо false{\displaystyle false}, 1{\displaystyle 1} либо 0{\displaystyle 0}).

Табличное задание функций встречается не только в логике, но и в логических функциях. Таблицы оказались довольно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики.

Таблицы истинности для основных двоичных логических функций[править | править код]

В программировании:

• Конъюнкция = AND = И = ∧{\displaystyle \land } = &
• Дизъюнкция = OR = ИЛИ = ∨{\displaystyle \lor } = |
• Сложение по модулю 2 = XOR = ИСКЛЮЧАЮЩЕЕ ИЛИ = ⊕{\displaystyle \oplus } = ~
• Отрицание = NOT = НЕ = ¬{\displaystyle \neg } = !

Таблицы истинности для некоторых троичных логических функций[править | править код]

x	2	1	0	2	1	0	2	1	0
y	2	2	2	1	1	1	0	0	0
min(x,y)	2	1	0	1	1	0	0	0	0

x	2	1	0	2	1	0	2	1	0
y	2	2	2	1	1	1	0	0	0
max(x,y)	2	2	2	2	1	1	2	1	0

x	2	1	0	2	1	0	2	1	0
y	2	2	2	1	1	1	0	0	0
F2TN22310	0	0	0	0	2	2	0	2	1

• Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б. Функции алгебры логики и классы Поста. — М.: Наука, 1966. — (Математическая логика и основания математики).

5.10. Как составить таблицу истинности?

Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.

Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре: (0,0),   (0,1),   (1,0),   (1,1).

Если формула содержит три переменные, то возможных наборов значений переменных восемь:

(0,0,0),   (0,0,1),   (0,1,0),   (0,1,1),

(1,0,0),   (1,0,1),   (1,1,0),   (1,1,1).

Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.

Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.

Примеры.

1. Составим таблицу истинности для формулы , которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце - значение формулы. В результате получим таблицу:

Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.

2. Таблица истинности для формулы :

Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 0, то есть является тождественно ложной.

3. Таблица истинности для формулы :

Из таблицы видно, что формула в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.