4.3. Логические выражения и таблицы истинности

Логические выражения. Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.

Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.

Запишем в форме логического выражения составное выска­зывание «(2 — 2 = 5 или 2-2 = 4) и (2 • 2 ≠ 5 или 2-2≠ 4)». Проанализируем составное высказывание. Оно содержит два простых высказывания:

А = «2 • 2 = 5» — ложно (0),

В = «2 • 2 = 4>> — истинно (1).

Тогда составное высказывание можно записать в следующей форме:

«(А или В) и (⌐А или (⌐В)».

Теперь необходимо записать высказывание в форме логи­ческого выражения с учетом последовательности выполнения логических операций. При выполнении логических операций определен следующий порядок их выполнения: инверсия, конъюнкция, дизъюнкция. Для изменения указанного порядка могут использоваться скобки:

F = (A v В) & (⌐A v ⌐В).

Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.

Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых ло­гических операций, получим значение логической функции:

F = (AvB)&( ⌐Av⌐B) = (0v1)&(1v0) = 1 & 1 = 1.

Таблицы истинности. Для каждого составного высказывания (логического выражения) можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний (логических переменных).

При построении таблиц истинности целесообразно руко­водствоваться определенной последовательностью действий.

Во-первых, необходимо определить количество строк в таблице истинности. Оно равно количеству возможных ком­бинаций значений логических переменных, входящих в ло­гическое выражение. Если количество логических переменных равно n, то:

количество строк = 2ⁿ.

В нашем случае логическая функция F = (AvB)&( ⌐Av⌐B) имеет 2 переменные и, следовательно, количество строк в таблице истинности должно быть равно 4.

Во-вторых, необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.

В нашем случае количество переменных равно двум, а количество логических операций — пяти, то есть количество столбцов таблицы истинности равно семи.

В-третьих, необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных.

В-четвертых, необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности (табл. 4.4). Теперь мы можем определить значение логической функции для любого набора значений логических переменных.

Таблица 4.4. Таблица истинности логической функции

F=(AvB)&( ⌐Av⌐B)

А	В	AvB	А	В	AvB	(AvB)&( ⌐Av⌐B)
0	0	0	1	1	1	0
0	1	1	1	0	1	1
1	0	1	0	1	1	1
1	1	1	0	0	0	0

Равносильные логические выражения. Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».

Докажем, что логические выражения ⌐А &⌐В и ⌐(AvB) равносильны. Построим сначала таблицу истинности логическое выражения

⌐А &⌐ В (табл. 4.5).

Таблица 4.5. Таблица истинности логического выражения ⌐А & ⌐В

А	В	А	В	⌐А&⌐В
0	0	1	1	1
0	1	1	0	0
1	0	0	1	0
1	1	0	0	0

Теперь построим таблицу истинности логического выражения ⌐(AvB) (табл. 4.6).

Таблица 4.6. Таблица истинности логического выражения ⌐(AvB)

А	В	AvB	⌐(AvB)
0	0	0	1
0	1	1	0
1	0	1	0
1	1	1	0

Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны:

⌐А & ⌐В = ⌐(AvB).

Логические выражения и таблицы истинности

Цели урока:

Обучающие:

• Научить составлять логические выражения из высказываний
• Ввести понятие “таблица истинности”
• Изучить последовательность действий построения таблиц истинности
• Научить находить значение логических выражений посредством построения таблиц истинности
• Ввести понятие равносильности логических выражений.

Развивающие:

• Развивать логическое мышление
• Развивать внимание
• Развивать память
• Развивать речь учащихся

Воспитательные:

• Воспитывать умение слушать учителя и одноклассников
• Воспитывать дисциплинированность
• Формировать интеллектуальную и эмоциональную активность учащихся.
• Воспитывать чувства ответственности за результаты своего труда.

Вид урока: Урок — деловая игра.

Тип урока: проверка знаний и изучение нового материала

Методы организации учебной деятельности: фронтальная, групповая, метод проектов.

Система оценивания: по ходу урока руководитель группы на “Оценочных листах» отмечает долю участия ученика на уроке при выполнении каждого задания

Оборудование урока: Презентация урока, плакаты “Таблица истинности функции логического сложения”, “Таблица истинности функции логического умножения”, “Таблица истинности функции логического отрицания”, маркеры, “Оценочный лист”, карточки с заданиями, карточка “Вопросники” для “Собеседования”, файл “Логические микросхемы”, мультимедийный проектор.

Место проведения урока: компьютерный класс

Участники: ученики 10-х классов.

Ход урока

1. Организационный момент

(2 минуты)

На экране проецируется первый слайд презентации – надпись “Логические выражения. Таблицы истинности”.

— Здравствуйте, ребята. Мы продолжаем изучать основы логики и тема нашего сегодняшнего урока “Логические выражения. Таблицы истинности”. Изучив данную тему, вы научитесь, как  из высказываний составляются логические выражения, и определять их истинность посредством составления таблиц истинности. ( Второй слайд презентации)

Эпиграфом к уроку являются слова Б.Паскаля: “ВЕЛИЧИЕ ЧЕЛОВЕКА — В ЕГО СПОСОБНОСТИ МЫСЛИТЬ”. ( Третий слайд презентации)

— Сегодня мы проведем с вами необычный урок, урок — деловая игра “Устраиваюсь на работу”.

Дадим волю нашим фантазиям:

завод “Микрон” объявил набор агентов для проведения рекламной кампании по продвижению своих чипов на рынке. Но нужно пройти несколько ступенек проверки профессиональной пригодности:

1. Проверка умения презентовать своё выступление. (Презентация. 10 минут)
2. Проверка знания в области логических микросхем. (Собеседование. 5 минут)
3. Проверка умения слушать других и поддерживать разговор. (Объяснение новой темы.15 минут)
4. Проверка умения применять полученные знания на практике. (Закрепление изученного материала. 10 минут)

И все эти умения и знания нужно показать за 40 минут!

2. Проверка домашнего задания (10 минут)

Перейдём к 1 проверке — демонстрации групповых домашних работ на экране. Каждая группа подготовила презентацию по теме “Базовые логические операции”.

Слово предоставляется 1 группе.

Первую группу меняет вторая, вторую группу – третья.

Оценивается групповая работа учеников.

— Ребята, вы прошли первую проверку, все приглашаетесь к 2 испытанию – к “Собеседованию”.

— Для предварительной подготовки каждая группа получает “Вопросник”

Образец вопросника

Работа за компьютером!

Юный друг!

Наше агентство от завода “Микрон” объявляет набор специалистов для проведения рекламной кампании по продвижению своих чипов на рынок. Мы рады видеть тебя в своих рядах, но сначала ответь, пожалуйста, на следующие вопросы:

Что знаешь о заводе “Микрон”?

Знаешь ли, что такое чип?

Что знаешь о чипах?

Используются ли знания в области алгебры логики при разгадке схемы “чипа”?

Информацию можешь найти в файле “Логические микросхемы”.

Путь к файлу:

Рабочий стол – К уроку – Логические микросхемы

Текст в файле “Логические микросхемы”

ВСЁ О ЧИПАХ

Еще несколько лет назад различные электронные устройства собирали из отдельных элементов электронных ламп, реле, трансформаторов, резисторов, конденсаторов, долго и ненадежно, да и размеры аппаратуры получались весьма внушительными. Например, электронная вычислительная машина (ЭВМ) первого поколения содержала около 10 000 электронных ламп и, хотя срок службы каждой лампы составлял 2000 ч, работала с постоянными сбоями, каждые 6 мин одна из ламп выходила из строя. К тому же эта аппаратура занимала площадь огромного цеха и потребляла столько же электроэнергии, сколько небольшой завод. На смену электронным лампам пришел более долговечный транзистор. Электронные вычислительные машины (теперь уже второго поколения) заметно похудели и стали работать без остановки 56 дней, хотя срок службы транзисторов миллионы часов. Такая ненадежность ЭВМ объяснялась недостаточно высоким качеством паяных соединений. Миллионы таких соединений в блоках ЭВМ стали главной причиной отказов. Перед конструкторами встали две задачи: как увеличить надежность ЭВМ и уменьшить ее объем. Решить их, создать высоконадежные, миниатюрные и экономичные устройства позволила микроэлектроника — новое направление электроники. Теперь отдельные детали, соединяемые друг с другом проводами, заменили микросхемы: на маленьком полупроводниковом кристалле размером несколько квадратных миллиметров (его еще часто называют чипом, от англ. chip, что означает чешуйка) размещают тончайший узор микроячеек. Каждая микро ячейка представляет собой законченную радиоэлектронную схему, состоящую из множества элементов, транзисторов, резисторов, конденсаторов и, конечно, межсоединений…

Цифровые микросхемы. Типы логики, корпуса. Ну сначала скажем так: микросхемы делятся на два больших вида: аналоговые и цифровые. Аналоговые микросхемы работают с аналоговым сигналом, а цифровые, соответственно – с цифровым.

От chip – щепка

Центральные процессоры: первые ЦП, Intel 4004, Intel 8008

В 1959 г. Роберт Нойс, 31-летний директор и научный руководитель фирмы Fairchild Semiconductors, разработал первую в мире интегральную схему – совокупность нескольких планарных транзисторов. До этого каждый компонент электронной схемы изготавливался отдельно, а затем они спаивались вручную. С 1962 г. интегральные схемы, прозванные “чипами”, были пущены в массовое производство.

В Зеленограде на заводе микрочипов «Микрон» произошло знаменательное событие: с официальным визитом приехал Владимир Путин. Руководство завода торжественно встретило президента. Хотелось показать все, чем богат завод. А гордиться действительно есть чем. Крупнейший производитель чипов в России и СНГ, образованный в 1964 году, «Микрон» выполняет полный цикл их изготовления. На «Микроне» делают микросхемы для ракет «Тополь» и «Булава», компоненты для МКС. Еще недавно чипы для банковских и SIМ-карт или биометрических паспортов были для производства неподвластны, но теперь святая святых завода, так называемая «чистая комната» модернизируется. Предприятие уже выпускает и SIМ-карты, и жидкокристаллические экраны. В «чистой комнате» поддерживается полная стерильность, одного белого халата мало, так что Путину показывали ее через специальное стеклянное окно.

«Чип» или, другими словами, логическая микросхема. И, конечно, много усилий нужно приложить для того, чтобы разгадать секрет и выяснить устройство этого «чипа». При разгадке схемы такого устройства используется алгебра логики. И на сегодняшнем уроке мы и познакомимся с методами помогающими решить такого рода задачи.

— Какие будут ответы? (Ученики высказывают своё мнение)

— “Собеседование” показало, что вы осведомлены о логических микросхемах и о заводе “Микрон”. Какая связь между алгеброй логики и компьютером? Как используются элементы алгебры логики в вычислительной технике? – вы частично ответили на эти вопросы. Логические основы устройства мы будем затрагивать позже, когда научимся решать логические задачи разными способами.

А вторую проверку вы прошли, перейдём к следующей – умеете ли вы слушать других и поддерживать разговор.

С помощью рассуждений мы умеем решать логические задачи с первого класса. А вот с помощью таблиц истинности научимся решать сегодня.

3. Решение задач с помощью рассуждения

Пример. Для формулы

— Сколько переменных содержит данная формула? 3

— Сколько строк и столбцов будет в таблице? 

8 строк (Логических переменных 3, следовательно, 2³ =8) и 8 столбцов (Логических операций в формуле 5, следовательно, 3+5=8)

— Какова будет в нашем примере последовательность операций? (инверсия, операции в скобках, операцию за скобкой)

Мы уже несколько уроков подряд используем понятие “таблица истинности”, а что же такое таблица истинности, как вы думаете?

Таблица истинности – это таблица, устанавливающая соответствие между возможными наборами значений логических переменных и значениями функций.

При построении таблиц истинности есть определенная последовательность действий.

1. Необходимо определить количество строк в таблице истинности.
   количество строк = 2ⁿ,  где n – количество логических переменных
2. Необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.
3. Необходимо построить таблицу истинности с указанным количеством строк и столбцов, ввести названия столбцов таблицы в соответствии с последовательностью  выполнения   логических  операций  с  учетом скобок и приоритетов;
4. Заполнить столбцы входных переменных наборами значений
5. Провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью.

Всё это найдёте на 130 странице учебника. Откройте, ребята, эту страницу. Найдите этот алгоритм. Он нужен нам при решении задач.

Решение задач

Пример 1. Получить таблицы истинности логической функции

Записали. Строим таблицу истинности

— Что мы делаем во-первых?

Определить количество столбцов в таблице

— Как мы это делаем?

Считаем количество переменных. В нашем случае логическая функция  содержит 2 переменных.

— Какие?

А и В

— Значит сколько строк будет в таблице?

Количество строк в таблице истинности должно быть равно 4.

— А если 3 переменных?

Количество строк = 2³ = 8

— Верно. Что делаем дальше?

Определяем количество столбцов = количеству логических переменных плюс количество логических операций.

— Сколько будет в нашем случае?

В нашем случае количество переменных равно двум, а количество логических операции — пяти, то есть количество столбцов таблицы истинности равно семи.

— Хорошо. Дальше?

Строим таблицу с указанным количеством строк и столбцов, обозначаем столбцы и вносим в таблицу возможные наборы значений исходных логических переменных и заполняем таблицу истинности по столбцам.

— Какую операцию будем выполнять первой? Только учитывайте скобки и приоритеты.

Можно сначала выполнить логическое отрицание или найти значение сначала в первой скобке, затем инверсию и значение во второй скобке, затем значение между этими скобками

Пример 2. Получить таблицу истинности логического выражения

Теперь построим таблицу истинности логического выражения .

Сколько строк будет в таблице? 4

Сколько столбцов  будет в таблице? 5

Пример 3. Получить таблицу истинности логического выражения

Построили таблицы. Теперь давайте, сравним значения в последних столбцах таблиц истинности примера 2 и 3, т.к. именно последние столбцы являются результирующими.

Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными. Таким образом, вы доказали равносильность каких выражений?

=

Домашнее задание

. Получить таблицу истинности логического выражения

Итог урока.

— Вы познакомились с новым способом решения логических задач – с помощью таблиц истинности. Справились и с заданиями.

— Поднимите оценочные листы те учащиеся, у кого общий балл больше или равно 12. Поздравляю Вас – Вы приняты на работу. Значит, Вы хорошо работали на уроке и поняли тему.

ВЫВОД В КОНЦЕ УРОКА.

Кем бы вы ни стали после окончания школы, вам всегда будут нужны знания и хорошая память, сообразительность и аккуратность, наблюдательность и фантазия, внимательность, умение логически мыслить, умение анализировать, сопоставлять и обобщать факты.

При проведении рефлексии следует попросить ребят выразить свое мнение о работе на уроке, путем ответов на вопросы:

• Довольны ли вы своей работой на уроке?
• Работой группы?

Логические функции с таблицами истинности

Логические функции

Импликация (логическое следование) — это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

·в естественном языке — если …, то …; когда …,тогда;коль скоро…,то и т.п.;

  ·обозначения=>

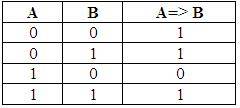
Например, дано сложное высказывание: «Если выглянет солнце, то станет тепло». Для того, чтобы преобразовать высказывание к логической формуле, необходимо выделить простые высказывания: А = «выглянет солнце», В = «станет тепло».

Тогда логическая форма имеет вид А => В.

 

Эквивалентность (равнозначность) – это логическая операция,ставящаяв соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.

·в естественном языке — тогда и только тогда; в том и только в том случае; если и только если;

·обозначения<=>, ~.

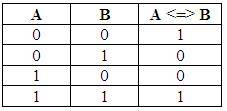
       Например, дано сложное высказывание: «Людоед голоден тогда и только тогда, когда он давно не ел». Чтобы преобразовать его к логической формуле, необходимо выделить простые высказывания А = «людоед голоден», В = «он давно не ел».

Тогда логическая формула имеет вид А <=>В.

 Приоритет логических операций: действия в скобках, ¬, /\, \/,=>,

Логические высказывания и логические операции над ними, приоритет их выполнения

Алгебра высказываний

Высказывание – повествовательное предложение, о котором можно сказать истинно оно или ложно. В алгебре простым высказываниям ставятся в соответствии логические переменные (А, В, С и т.д.)

Логическая переменная – это простое высказывание.
 Логические переменные обозначаются прописными и строчными латинскими буквами (a-z, A-Z) и могут принимать всего два значения – 1, если высказывание истинно, или 0, если высказывание ложно.

 Пример высказываний:

 

 

 

 

 

 

 

 

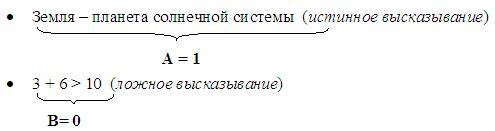
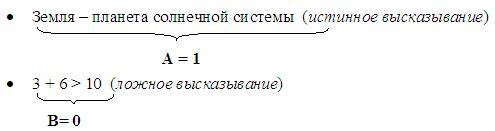
Логическая функция – это сложное высказывание, которое получается в результате проведения логических операций над простыми высказываниями.

Для образования сложных высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «и», «или», «не».
Например,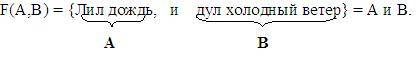

 

 

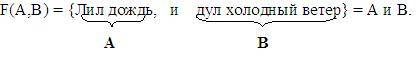
Многие люди  не любят сырую погоду.

Пусть А = «Многие люди любят сырую погоду». Получаем логическую функцию F(A) = не А.

Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.

Логическая формула (логическое выражение) — формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА (1) или ЛОЖЬ (0).

Значение логической функции зависит от значений входящих в нее логических переменных. Поэтому значение логической функции можно определить с помощью специальной таблицы (таблицы истинности), в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.

 

                                                                      Основные (базовые) логические операции:

1. Логическое умножение (конъюнкция), от лат. konjunctio – связываю:
•    Объединение двух (или нескольких) высказываний в одно с помощью союза И;
•     в языках программирования — And.
•    Принятые обозначения: /\ , •, и, and.
•    В алгебре множеств конъюнкции соответствует операция пересечения множеств.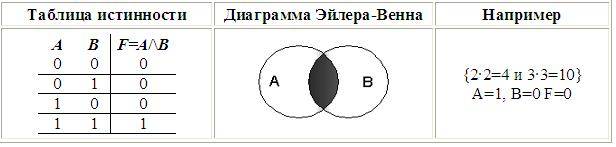

 

 

 

 

 

 

Конъюнкция истинна тогда и только тогда, все, входящие в нее высказывания истинны.

Пример:
Рассмотрим составное высказывание  «2 • 2 = 4 и 3 • 3 = 10». Выделим простые высказывания:
А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)
В = «3 • 3 = 10» = 0 (т.к. это ложное высказывание)
Поэтому, логическая функция F(A, B) = A /\ B = 1 /\ 0 = 0 (в соответствии с таблицей истинности), то есть данное составное высказывание ложное.

2. Логическое сложение (дизъюнкция), от лат. disjunctio – различаю:
•    Объединение двух (или нескольких) высказываний в одно с помощью союза ИЛИ;
•     в языках программирования — Or.
•    Обозначение:  \/, +, или, or.
•    В алгебре множеств дизъюнкции соответствует операция объединения множеств.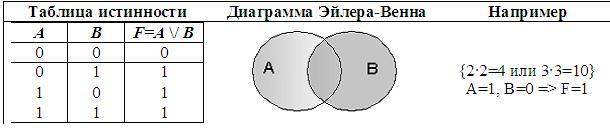

 

 

 

 

 

 

Дизъюнкция ложна тогда и только тогда, все, входящие в нее высказывания ложны.

Пример:
Рассмотрим составное высказывание  «2 • 2 = 4 или 2 • 2 = 5». Выделим простые выска-зывания:
А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)
В = «2 • 2 = 5» = 0 (т.к. это ложное высказывание)
Поэтому, логическая функция F(A, B) = A \/ B = 1 \/ 0 = 1 (в соответствии с таблицей истинности), то есть данное составное высказывание истинно.

3. Отрицание (инверсия), от лат. InVersion – переворачиваю:

•    Соответствует частице НЕ, словосочетаниям НЕВЕРНО, ЧТО или НЕ ЯВЛЯЕТСЯ ИСТИНОЙ, ЧТО;
•    в языках программирования — Not;
•    Обозначение: не А, ¬А, not
•    В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества.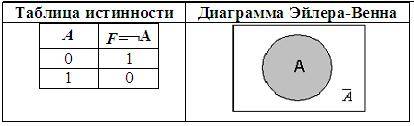

 

 

 

 

 

 

Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.

 Пример:

А = {два умножить на два равно четырем} = 1.

 ¬A= {Неверно, что два умножить на два равно четырем}= 0.

Рассмотрим высказывание А : «Луна — спутник Земли«;  тогда   ¬А будет формулироваться так:  «Луна — не спутник Земли«.

Рассмотрим высказывание: «Неверно, что 4 делится на 3». Обозначим через А простое высказывание «4 делится на 3». Тогда логическая форма отрицания этого высказывания имеет вид ¬А

 

Приоритет логических операций:

Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке:
     1. инверсия;
     2. конъюнкция;
     3. дизъюнкция;
Для изменения указанного порядка выполнения логических операций используются круглые скобки.

Составные логические выражения алгебры высказываний называют формулами.
Истинно или ложно значение формулы можно определить законами алгебры логики, не обращаясь к смыслу:
F = (0 \/ 1) /\ (¬0 \/ ¬1) = (0 \/ 1) /\ (1 \/ 0) =1 /\ 1=1 — истина
F = (¬0 /\ ¬1) \/ (¬1 \/ ¬1) = (1 /\ 0) \/ (0 \/ 0) = 0 \/ 0 = 0 — ложь

Логические выражения и таблицы истинности

Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинностисоставного высказывания.

Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности.

Алгоритм построения таблицы истинности:

1) подсчитать количество переменныхnв логическом выражении;

2) определить число строк в таблице, которое равноm = 2ⁿ;

3) подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций;

4) ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;

5) заполнить стобцы входных переменных наборами значений;

6) провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в п.4 последовательностью.

Наборы входных переменных, во избежание ошибок, рекомендуют перечислять следующим образом:

а) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю единицами;

б) разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами нулей и единиц , начиная с группы нулей;

в) продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами нулей или единиц до тех пор, пока группы нулей и единиц не будут состоять из одного символа.

Пример 3.9. Для формулыA&(B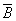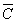&) построить таблицу истинности алгебраически и с использованием электронных таблиц.

Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 2³= 8.

Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3 + 5 = 8.

A	B	C			&	B  ( & )	A&(B  & )
0	0	0	1	1	1	1	0
0	0	1	1	0	0	0	0
0	1	0	0	1	0	1	0
0	1	1	0	0	0	1	0
1	0	0	1	1	1	1	1
1	0	1	1	0	0	0	0
1	1	0	0	1	0	1	1
1	1	1	0	0	0	1	1

Алгебра высказываний, логические выражения и таблицы истинности

Инверсия – это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, то есть множеству, получившемуся в результате отрицания множества А, соответствует множество 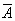, дополняющее его до универсального множества.

4. Для закрепления теоретического материала данной части урока проводится практическая работа с использованием программы Microsoft Excel, которая изучалась ранее. Именно поэтому необходимо повторить знания по теме Microsoft Excel в виде опроса по основным понятиям:

а) для чего предназначены электронные таблицы; 
б) из каких элементов состоит электронная таблица;
в) как можно определить адрес ячейки;
г) как ввести нужную информацию в любую ячейку;
д) как исправить или отредактировать данные в ячейке;
е) что значит выделить ячейку ли сделать её активной;
ж) как можно скопировать формулу в другие ячейки;
з) как осуществить ввод функции с помощью мастера функций.

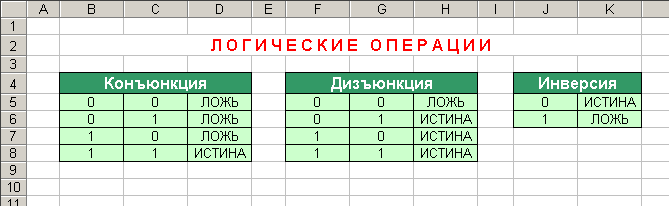
5. Практическое задание по теме “Логические функции в Excel”

1. Откройте программу Microsoft Excel.

2. Выделите ячейки A1, B1, C1 (для этого нажав на кнопку мыши внутри ячейки А1, протяните мышь до ячейки С1).

3. Нажмите на панели инструментов кнопку “Объединить и поместить в центре”:  (если этой кнопки не видно, нажмите )

4. Напишите в объединенной ячейке слово “Конъюнкция”.

5. В столбцах А и В введите значения логических аргументов (см. рис. ниже).

6. Аналогично объедините ячейки E1, F1, G1 и напишите слово “Дизъюнкция”. Введите также значения логических аргументов.

7. Аналогично сделайте для Инверсии (см. рис.).

8. Сделайте активной ячейку С2 и выполните команду Вставка – Функция. В разделе “Категория” выберите “Логические”, а в разделе “Функция” – “И”, нажмите ОК. Сдвиньте вниз серую панель (взявшись за нее в любом месте и потянув вниз), так, чтобы были видны заполненные ячейки.

9. Щелкните по ячейке А2 – в окне “Логическое1” появится адрес А2, затем поставьте курсор в окошко “Логическое2” и щелкните по ячейке В2 – в окошке появится адрес В2, нажмите ОК.

10. В ячейке С2 появилось значение ЛОЖЬ, а в строке формул (наверху) мы видим формулу =И(А2;В2). Теперь эту формулу надо скопировать в нижние три ячейки. Для этого ухватите за маркер в правом нижнем углу ячейки (при этом курсор приобретет форму маленького черного крестика) и потяните вниз на три ячейки (там тоже появятся значения логической функции).Аналогично проделайте для Дизъюнкции (в столбце G) и для Инверсии (в столбце J).

11. Теперь займемся оформлением таблиц. Выделите диапазон ячеек А1:С5 и нажмите кнопку “Границы”: . Аналогично сделайте границы для остальных таблиц.

12. Выделите строки со 2-й по 5-ю (протянув мышкой по номерам строк — с левой стороны) и нажмите кнопку “По центру”: .

13. Раскрасим таблицы. Выделите диапазон А2:С5 и нажмите кнопку “Цвет заливки”: , выберите бледно-зеленый цвет. Заголовок таблицы раскрасьте в изумрудный цвет, а цвет текста в заголовке сделайте белым (с помощью кнопки “Цвет шрифта”: ). Увеличьте размер шрифта в заголовке до 12 и сделайте его полужирным.

14. Аналогичные операции проделайте с остальными таблицами.

15. Выделите первую таблицу и, взявшись за рамку этой таблицы, перетащите ее вниз-вправо так, чтобы ее верхний левый угол был в ячейке В4. Вторую таблицу перетяните в ячейку F4, а третью – в J4.

16. Уменьшите ширину столбца А (для этого возьмитесь за границу между названиями столбцов А и В и потяните ее влево). Аналогично уменьшите ширину столбцов Е и I.

17. Объедините ячейки В2:К2 и напишите (заглавными буквами) общий заголовок “ЛОГИЧЕСКИЕ ОПЕРАЦИИ”. Сделайте его красного цвета, размером 12, полужирным.

18. У вас должно получиться следующее:

6. Решение задачи с использованием программы NumLock Calculator 3.2.

Примеры представлены в приложении (Приложение)

9. Самостоятельная работа по всей теме урока проводится на компьютере и состоит из двух заданий. Всего – три варианта карточек.(Приложение 1).

10. Домашнее задание.

11. Подведение итогов урока.

Оценка знаний учащихся по новой теме с учётом знаний по предыдущим темам (повторение), а также краткое сообщение о теме следующего урока.

12. Список используемой литературы:

1. Информатика и информационные технологии.10-11:Учебник для 10-11 классов. Угринович Н.Д. – М.: БИНОМ. Лаборатория знаний, 2007;

2. Практикум по информатике и информационным технологиям: Учебное пособие. Угринович Н.Д. и др. – М.: БИНОМ. Лаборатория знаний, 2007;

Прил 1

Приложение 1

Самостоятельная работа

Вариант № 1

Задание 1

.Даны простые высказывания:

А = {Принтер – устройство ввода информации},

В = {Процессор – устройство обработки информации},

С = {Монитор – устройство хранения информации},

D = {Клавиатура – устройство ввода информации}.

Определите истинность составного высказывания А & 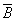 (C  D), используя таблицы истинности логических операций, а правильность полученного результата проверить с использованием программы NumLock Calculator.

Задание 2

Для формулы (А 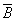 )  C & 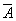построить таблицу истинности алгебраически и с использованием электронных таблиц.

Вариант №2

Задание 1

.Даны простые высказывания:

А = {Принтер – устройство ввода информации},

В = {Процессор – устройство обработки информации},

С = {Монитор – устройство хранения информации},

D = {Клавиатура – устройство ввода информации}.

Определите истинность составного высказывания (АВ) 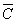 &D, используя таблицы истинности логических операций, а правильность полученного результата проверить с использованием программы NumLock Calculator.

Задание 2

Для формулы B & (A 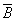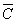 & ) построить таблицу истинности алгебраически и с использованием электронных таблиц.

Вариант № 3

Задание 1

.Даны простые высказывания:

А = {Принтер – устройство ввода информации},

В = {Процессор – устройство обработки информации},

С = {Монитор – устройство хранения информации},

D = {Клавиатура – устройство ввода информации}.

Определите истинность составного высказывания (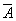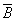 )  (C  D), используя таблицы истинности логических операций, а правильность полученного результата проверить с использованием программы NumLock Calculator.

Задание 2

Для формулы B & ( 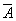 C ) 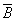 построить таблицу истинности алгебраически и с использованием электронных таблиц.

Прил 2

Пример1. Определите истинность составного высказывания: (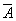&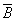)  (CD), состоящего из простых высказываний с использованием программы NumLock Calculator 3.2.

А = {Принтер – устройство вывода информации},

В = {Процессор – устройство хранения информации},

С = {Монитор – устройство вывода информации},

D = {Клавиатура – устройство обработки информации}.

  Сначала на основании знания устройства компьютера устанавливаем истинность простых высказываний: А = 1, В = 0, С = 1, D = 0.

Определим теперь истинность составного высказывания, используя таблицы истинности логических операций:

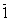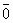(& ) (1 0) = (0&1)  (1 0) = 0

Составное высказывание ложно.

  Проверим правильность полученного результата с использованием NumLock Calculator — это специальная программа, позволяющая проверить совпадение правильности значения составного логического выражения с вычисленным алгебраически.  

7.Лекция – беседа.

Логические выражения и таблицы истинности.

Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.

Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности.

Алгоритм построения таблицы истинности:

1)       подсчитать количество переменных n в логическом выражении;

2)       определить число строк в таблице, которое равно m = 2ⁿ;

3)       подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций;

4)       ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;

5)       заполнить столбцы входных переменных наборами значений;

6)       провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в п.4 последовательностью.

  Наборы входных переменных рекомендую перечислять следующим образом:

а)       разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю единицами;

б)       разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами нулей и единиц , начиная с группы нулей;

в)       продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами нулей или единиц до тех пор, пока группы нулей и единиц не будут состоять из одного символа.

8. Решение задач на построение таблиц истинности.

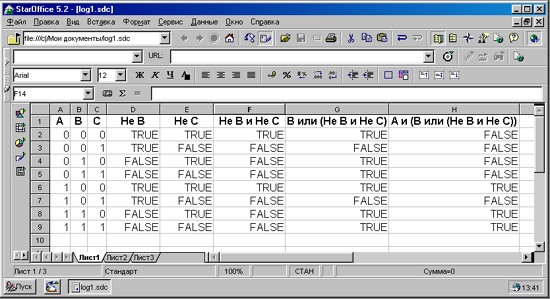
Пример2. Для формулы A & (B 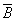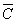 & ) построить таблицу истинности алгебраически и с использованием электронных таблиц. (алгебраическое решение выполняет учащийся на доске, с использованием электронных таблиц – все вместе на компьютерах).

Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 2³ = 8. Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3 + 5 = 8.

5

Переименовать лист Лист1 в Таблицу истинности и сохранить в файле log.xlc .

Таблицы истинности. Логические функции. Основные логические операции

Приведем примеры, предложений не являющихся высказываниями: «Посмотрите в окно.» «Который час?»

«2x+7>12»

Еще раз подчеркнем, что отличительным признаком любого высказывания является его свойство быть истинным или ложным, а этим свойством три вышеприведенных предложения не обладают.

Используя простые высказывания, можно образовывать сложные, или составные, высказывания, в которые простые входят в качестве элементарных составляющих. В образовании сложных высказываний используются слова: и, или, тогда и только тогда, когда (в том и только в том случае), если …, то …, нет. Рассмотрим несколько примеров сложных высказываний. Рассмотрим несколько примеров сложных высказываний:

«Если идет дождь, то солнце не светит.» « Если ветер дует, то нет дождя.»

Основная задача логики высказываний заключается в том, чтобы на основании истинности или ложности простых высказываний определить истинность или ложность сложных высказываний.

Условимся, простые высказывания называть логическими переменными и обозначать большими буквами и, если высказывание истинно, будем писать A=1, а если ложно, то A=0.

Использование 0 и 1 подчеркивает некоторое соответствие между значениями логических переменных и функций в алгебре логики и цифрами в двоичной системе счисления. Это позволяет описывать работу логических схем ЭВМ и проводить их анализ и синтез с помощью математического аппарата алгебры логики.

Любое устройство ЭВМ, выполняющее действия над двоичными числами, можно рассмотреть как некоторый функциональный преобразователь. Причем числа на входе — значения входных логических переменных, а число на выходе — значение логической функции, которое получено в результате выполнения определенных операций. Таким образом, этот преобразователь реализует некоторую логическую функцию.

Значения	логической	функции для разных	X				F(X, Y, Z)
			Y
сочетаний значений входных			Z
переменных	— или, как	это иначе называют,

наборов входных переменных — обычно задаются специальной таблицей. Такая таблица называется таблицей истинности. Количество наборов входных переменных (Q) можно определить по формуле:

Q=2n, где n — количество входных переменных.

Простейшим примером логической функции является функция одной переменной .

Аргумент			Функция
X	F0 ( X )	F1 (X )		F2 (X )	F3 ( X )
0	0	0		1	1
1	0	1		0	1

F0 (X ) — константа 0;

F1 (X ) — переменная X;

F2 (X ) — инверсия X;

F3 ( X ) — константа 1.
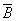
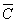
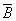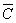
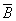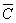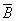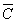