Таблиц истинности составление: Построение таблиц истинности — Информатика в школе – Построение таблицы истинности онлайн | СКНФ | СДНФ | Полином Жегалкина | Таблица истинности булевой функции онлайн — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Построение СКНФ и СДНФ по таблице истинности

Нормальная форма логической формулы не содержит знаков импликации, эквивалентности и отрицания неэлементарных формул.

Нормальная форма существует в двух видах:

конъюнктивная нормальная форма (КНФ) — конъюнкция нескольких дизъюнкций, например, $\left(A\vee \overline{B}\vee C\right)\wedge \left(A\vee C\right)$;
дизъюнктивная нормальная форма (ДНФ) — дизъюнкция нескольких конъюнкций, например, $\left(A\wedge \overline{B}\wedge C\right)\vee \left(B\wedge C\right)$.

СКНФ

Совершенная конъюнктивная нормальная форма (СКНФ) — это КНФ, удовлетворяющая трем условиям:

не содержит одинаковых элементарных дизъюнкций;
ни одна из дизъюнкций не содержит одинаковых переменных;
каждая элементарная дизъюнкция содержит каждую переменную из входящих в данную КНФ.

Любая булева формула, которая не является тождественно истинной, может быть представлена в СКНФ.

Правила построения СКНФ по таблице истинности

Для каждого набора переменных, при котором функция равна 0, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием.

СДНФ

Совершенная дизъюнктивная нормальная форма (СДНФ) — это ДНФ, удовлетворяющая трем условиям:

не содержит одинаковых элементарных конъюнкций;
ни одна из конъюнкций не содержит одинаковых переменных;
каждая элементарная конъюнкция содержит каждую переменную из входящих в данную ДНФ, к тому же в одинаковом порядке.

Любая булева формула, которая не является тождественно ложной, может быть представлена в СДНФ, к тому же единственным образом.

Правила построения СДНФ по таблице истинности

Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные, которые имеют значение 0 берут с отрицанием.

Примеры нахождения СКНФ и СДНФ

Пример 1

Записать логическую функцию по ее таблице истинности:

Рисунок 1.

Решение:

Воспользуемся правилом построения СДНФ:

Рисунок 2.

Получим СДНФ:

\[F\left(x_1,\ x_2,\ x_3\right)=\left(\overline{x_1}\wedge \overline{x_2}\wedge \overline{x_3}\right)\vee \left(\overline{x_1}\wedge \overline{x_2}\wedge x_3\right)\vee \left(x_1\wedge \overline{x_2}\wedge \overline{x_3}\right)\vee \left(x_1\wedge \overline{x_2}\wedge x_3\right)\vee \left(x_1\wedge x_2\wedge x_3\right)\]

Воспользуемся правилом построения СКНФ:

Рисунок 3.

Получим СКНФ:

\[F\left(x_1,\ x_2,\ x_3\right)=\left(x_1\vee \overline{x_2}\vee x_3\right)\wedge \left(x_1\vee \overline{x_2}\vee \overline{x_3}\right)\wedge \left(\overline{x_1}\vee \overline{x_2}\vee x_3\right)\]

Пример 2

Функция задана таблицей истинности:

Рисунок 4.

Представить эту функцию в виде СДНФ и СКНФ.

Решение:

Запишем логическую функцию в СДНФ. Для удобства решения добавим к таблице вспомогательный столбец.
Используя правило составления СДНФ не забываем вводить знак отрицания для переменных со значением 0. Инвертировать нулевые значения переменных обязательно, т.к. иначе они превратят значения конъюнкций в нули основной функции.
Рисунок 5.
Полученные во вспомогательном столбце конъюнкции соединим знаком дизъюнкции и получим искомую логическую функцию в виде СДНФ:
\[F\left(x_1,x_2,x_3,x_4\right)=\left(\overline{x}\wedge \overline{y}\wedge z\wedge f\right)\vee \left(\overline{x_1}\wedge x_2\wedge \overline{x_3}\wedge \overline{x_4}\right)\vee \left(\overline{x_1}\wedge x_2\wedge x_3\wedge x_4\right)\vee \left(x_1\wedge \overline{x_2}\wedge \overline{x_3}\wedge \overline{x_4}\right).\]

Запишем логическую функцию в СКНФ.
Используя правило составления СКНФ не забываем вводить знак отрицания для переменных со значением 1. Инвертировать единичные значения переменных обязательно, т.к. иначе они превратят значения дизъюнкций в единицы основной функции.
Рисунок 6.
Полученные во вспомогательном столбце дизъюнкции соединим знаком конъюнкции и получим искомую логическую функцию в виде СКНФ:
\[F\left(x_1,x_2,x_3,x_4\right)=\left(x_1\vee x_2\vee x_3\vee x_4\right)\wedge \left(x_1\vee x_2\vee x_3\vee \overline{x_4}\right)\wedge \left(x_1\vee x_2\vee \overline{x_3}\vee x_4\right)\wedge \left(x_1\vee \overline{x_2}\vee x_3\vee \overline{x_4}\right)\wedge \left(x_1\vee \overline{x_2}\vee \overline{x_3}\vee x_4\right)\wedge \left(\overline{x_1}\vee x_2\vee x_3\vee \overline{x_4}\right)\wedge \left(\overline{x_1}\vee x_2\vee \overline{x_3}\vee x_4\right)\wedge \left(\overline{x_1}\vee x_2\vee \overline{x_3}\vee \overline{x_4}\right)\wedge \left(\overline{x_1}\vee \overline{x_2}\vee x_3\vee x_4\right)\wedge \left(\overline{x_1}\vee \overline{x_2}\vee x_3\vee \overline{x_4}\right)\wedge \left(\overline{x_1}\vee \overline{x_2}\vee \overline{x_3}\vee x_4\right)\wedge \left(\overline{x_1}\vee \overline{x_2}\vee \overline{x_3}\vee \overline{x_4}\right).\]

Построить таблицу истинности следующих логических выражений

Проблема определения истинности выражения встаёт перед многими науками. Любая доказательная дисциплина должна опираться на некоторые критерии истинности доказательств. Наука, изучающая эти критерии, называется алгеброй логики. Основной постулат алгебры логики заключается в том, что любое самое витиеватое утверждение может быть представлено в виде алгебраического выражения из более простых утверждений, истинность или ложность которых легко определить.

Для любого «алгебраического» действия над утверждением задаётся правило определения истинности или ложности измененного утверждения, исходя из истинности или ложности исходного утверждения. Эти правила записываются через таблицы истинности выражения. Прежде, чем составлять таблицы истинности, надо поближе познакомиться с алгеброй логики.

Алгебраические преобразования логических выражений

Любое логическое выражение, как и его переменные (утверждения), принимают два значения: ложь или истина. Ложь обозначается нулём, а истина — единицей. Разобравшись с областью определения и областью допустимых значений, мы можем рассмотреть действия алгебры логики.

Отрицание

Отрицание и инверсия

— самое простое логическое преобразование. Ему соответствует частица «не.» Это преобразование просто меняет утверждение на противоположное. Соответственно, значение утверждения тоже меняется на противоположное. Если утверждение А истинно, то «не А» — ложно. Например, утверждение «прямой угол — это угол, равный девяносто градусов» — истина. Тогда его отрицание «прямой угол не равен девяноста градусам» — ложь.

Таблица истинности для отрицания будет такова:

Конъюнкция

Конъюнкция аналогична умножению и соответствует союзу «и». Такое выражение будет верно, только если верны все утверждения, объединённые конъюнкцией. То есть, утверждение «А и Б» будет истинным, только если А — истина и Б — истина. Во всех остальных случаях выражение «А и Б» ложно. Например, высказывание «Земля круглая и плоская» будет ложно, так как первая часть истина, а вторая — ложь.

Таблица истинности конъюнкции

А	Б	А и Б
Л	Л	Л
Л	И	Л
И	Л	Л
И	И	И

Дизъюнкция

Эта операция может быть

обычной или строгой, их результаты будут различаться.

Обычная дизъюнкция или логическое сложение соответствует союзу «или». Она будет истинной если хотя бы одно из утверждений, входящих в неё — истина. Например, выражение «Земля круглая или стоит на трёх китах» будет истинным, так как первое утверждение — истинно, хоть второе и ложно.В таблице это будет выглядеть так:

А	Б	А или Б
Л	Л	Л
Л	И	И
И	Л	И
И	И	И

Строгую дизъюнкцию или сложение по модулю также называют «исключающим или». Эта операция может принимать вид грамматической конструкции «одно из двух: либо …, либо …». Здесь значение логического выражения будет ложным, если все утверждения, входящие в него, имеют одинаковую истинность. То есть, оба утверждения либо вместе истинны, либо вместе ложны.

Таблица значений исключающего или

А	Б	либо А, либо Б
Л	Л	Л
Л	И	И
И	Л	И
И	И	Л

Импликация и эквивалентность

Импликация представляет собой следствие и грамматически может быть выражена как «из А следует Б». Здесь утверждение А будет называться предпосылкой, а Б — следствием. Импликация может быть ложной, только в одном случае: если предпосылка истинна, а следствие ложно. То есть, ложь не может следовать из истины. Во всех остальных случаях импликация истинна. Варианты, когда оба утверждения имеют одинаковую истинность, вопросов не вызывают. Но почему верное следствие из неверной предпосылки — истина? Дело в том, что из ложной предпосылки может следовать что угодно. Это и отличает импликацию от эквивалентности.

В математике (и других доказательных дисциплинах) импликация используется для указания необходимого условия. Например, утверждение А — «точка О — экстремум непрерывной функции», утверждение Б — «производная непрерывной функции в точке О обращается в ноль». Если О, действительно, точка экстремума непрерывной функции, то производная в этой точке будет, и вправду, равна нулю. Если же О не является точкой экстремума, то производная в этой точке может быть нулевой, а может не быть. То есть Б необходимо для А, но не достаточно.

Таблица истинности для импликации выглядит следующим образом:

А	Б	из А следует Б
Л	Л	И
Л	И	И
И	Л	Л
И	И	И

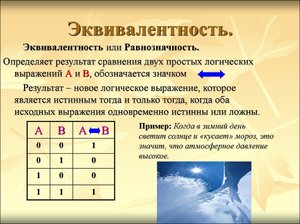
Логическая операция эквивалентность, по сути, является взаимной импликацией. «А эквивалентно Б» означает, что «из А следует Б» и «из Б следует А» одновременно. Эквивалентность верна, когда оба утверждения либо одновременно верные, либо одновременно неверные.

А	Б	А эквивалентно Б
Л	Л	И
Л	И	Л
И	Л	Л
И	И	И

В математике эквивалентность используется для определения необходимого и достаточного условия. Например, утверждение А — «Точка О является точкой экстремума непрерывной функции», утверждение Б — «В точке О производная функции обращается в ноль и меняет знак». Эти два утверждения эквивалентны. Б содержит необходимое и достаточное условие для А. Обратите внимание, что в данном примере утверждений Б на самом деле является конъюнкцией двух других: «производная в точке О обращается в ноль» и «производная в точке О меняет знак».

Прочие логические функции

Выше были рассмотрены основные логические операции, которые часто используются. Есть и другие функции, которые используются:

Штрих Шеффера или несовместимость представляет собой отрицание конъюнкции А и Б
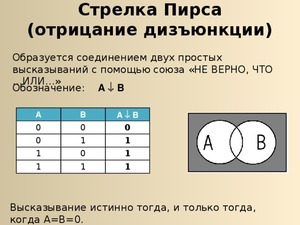
Стрелка Пирса представляет сбой отрицание дизъюнкции.

Построение таблиц истинности

Чтобы построить таблицу истинности для какого-либо логического выражения, надо действовать в соответствии с алгоритмом:

Разбить выражение на простые утверждения и обозначить каждое из них как переменную.
Определить логические преобразования.
Выявить порядок действий этих преобразований.
Сосчитать строки в будущей таблице. Их количество равно два в степени N, где N — число переменных, плюс одна строка для шапки таблицы.
Определить число столбцов. Оно равно сумме количества переменных и количества действий. Можно представлять результат каждого действия в виде новой переменной, если так будет понятней.
Шапка заполняется последовательно, сначала все переменные, потом результаты действий в порядке их выполнения.
Заполнение таблицы надо начать с первой переменной. Для неё количество строк делится пополам. Одна половина заполняется нулями, вторая — единицами.
Для каждой следующей переменной нули и единицы чередуются вдвое чаще.
Таким образом заполняются все столбцы с переменными и для последней переменной значение меняется в каждой строке.
Потом последовательно заполняются результаты всех действий.

В итоге последний столбец отобразит значение всего выражения в зависимости от значения переменных.

Отдельно следует сказать о порядке логических действий. Как его определить? Здесь, как и в алгебре, есть правила, задающие последовательность действий. Они выполняются в следующем порядке:

выражения в скобках;
отрицание или инверсия;
конъюнкция;
строгая и обычная дизъюнкция;
импликация;
эквивалентность.

Примеры

Для закрепления материала можно попробовать составить таблицу истинности для ранее упомянутых логических выражений. Рассмотрим три примера:

Штрих Шеффера.
Стрелка Пирса.
Определение эквивалентности.

Штрих Шеффера

Штрих Шеффера — это логическое выражение, которое можно записать в виде «не (А и Б)». Здесь две переменные, и два действия. Конъюнкция в скобках, значит, она выполняется первой. В таблице будет шапка и четыре строки со значениями переменных, а также четыре столбца. Заполним таблицу:

А	Б	А и Б	не (А и Б)
Л	Л	Л	И
Л	И	Л	И
И	Л	Л	И
И	И	И	Л

Отрицание конъюнкции выглядит как дизъюнкция отрицаний. Это можно проверить, если составить таблицу истинности для выражения «не А или не Б». Проделайте это самостоятельно и обратите внимание, что здесь будет уже три операции.

Стрелка Пирса

Рассматривая Стрелку Пирса, которая представляет собой отрицание дизъюнкции «не (А или Б)», сравним её с конъюнкцией отрицаний «не А и не Б». Заполним две таблицы:

А	Б	А или Б	не (А или Б)
Л	Л	Л	И
Л	И	И	Л
И	Л	И	И
И	И	И	Л

А	Б	не А	не Б	не А и не Б
Л	Л	И	И	И
Л	И	И	Л	Л
И	Л	Л	И	И
И	И	Л	Л	Л

Значения выражений совпали. Изучив два эти примера, можно прийти к выводу, как раскрывать скобки после отрицания: отрицание применяется ко всем переменным в скобках, конъюнкция меняется на дизъюнкцию, а дизъюнкция — на конъюнкцию.

Определение эквивалентности

Про утверждения А и Б можно сказать, что они эквивалентны, тогда и только тогда, когда из А следует Б и из Б следует А. Запишем это как логическое выражение и построим для него таблицу истинности. «(А эквивалентно Б) эквивалентно (из А следует Б) и (из Б следует А)».

Здесь две переменных и пять действий. Строим таблицу:

А	Б	В = (из А следует Б)	Г = (из Б следует А)	Д = А эквивалентно Б	Е = В и Г	Д эквивалентно Е
Л	Л	И	И	И	И	И
Л	И	И	Л	Л	Л	И
И	Л	Л	И	Л	Л	И
И	И	И	И	И	И	И

В последнем столбце все значения истинные. Это значит, что приведенное определение эквивалентности верно при любых значениях А и Б. Значит, оно всегда истинно. Именно так с помощью таблицы истинности можно проверить корректность любых определений и логических построений.

НОУ ИНТУИТ | Лекция | Минимизация логических схем

Аннотация: Рассматривается взаимосвязь различных способов описания работы логических схем и принципы их минимизации.

Составление логических выражений по таблице истинности

Каноническая сумма минтермов

Минтерм — это полное произведение всех входных переменных, соответствующее одной строке таблицы истинности, в которой значение выходной переменной (значение функции) равно логической 1. Переменная входит в минтерм с инверсией, если ее значение в данной строке таблицы равно 0, и без инверсии, если ее значение в данной строке таблицы равно 1.

Каноническая сумма минтермов — это логическая сумма всех минтермов, которая представляет собой максимальное логическое выражение, соответствующее таблице истинности.Она составляется в следующей последовательности:

В заданной таблице истинности подсчитывается — количество строк таблицы, в которой значение функции равно 1.
Затем записывается логическая сумма полных произведений.
Далее в каждом произведении расставляются инверсии над переменными в соответствии с их значением в строке таблицы.

Для примера, представленного на рис. 1.6, каноническая сумма минтермов будет выглядеть так:

( 2.1)

Из сравнения (1.1) и (2.1) видно, что одной и той же таблице истинности (рис. 1.6,б) соответствуют два разных логических выражения, причем (1.1) записывается более компактно, но возможности минимизации для него еще есть. Следовательно, есть возможность минимизировать и логическую схему, представленную на рис. 1.6, a.

Минимизация логических выражений может осуществляться с помощью различных методов на основе правил булевой алгебры, в частности, диаграммы Вейча, диаграммы Венна и табличным методом, но наиболее простым и наглядным является графический способ минимизации с помощью карт Карно, опубликованный в 1953 г. Морисом Карно.

Минимизация с помощью карт Карно

Карта Карно — графическое представление таблицы истинности. Каждой клетке карты Карно соответствует строка таблицы истинности. По осям карты расставляются сочетания переменных, а внутри карты — значения функции.

Назначение карты Карно — найти логические суммы прямого и инверсного значения переменных. Для любой переменной, например, , такая сумма равна при любом значении : при это будет , при это . Поэтому при вынесении за скобки в выражении:

— сумму можно отбросить, при этом результат выражения не изменится. В этом и заключается минимизация логических выражений с помощью карт Карно. Для достижения поставленной цели минимизации нужно соблюдать правила разметки осей карты:

Вертикальная ось размечается независимо от горизонтальной.
Начинать разметку можно с любого сочетания переменных.
Все сочетания переменных должны быть перечислены.
Для соседних клеток карты сочетание переменных должно отличаться не более чем одним знаком, причем соседними являются крайние клетки строки (столбца).

Для функции двух переменных карта Карно — это квадрат 2×2 клетки. В этих клетках размещаются 4 значения функции из последнего столбца таблицы истинности (рис. 2.2).

Рис. 2.2. Таблица истинности (а) и карта Карно (б) для функции 2 переменных.

Для функции трех переменных карта Карно — это прямоугольник 2×4 или 4×2 клетки. В этих клетках размещаются 8 значений функции из последнего столбца таблицы истинности (рис. 2.3). При разметке большей из осей нужно четко придерживаться последнего, четвертого правила разметки и следить за тем, чтобы соседними не оказались сочетания и , либо и , в которых одновременно меняются обе переменные.

Для функции четырех переменных карта Карно — это квадрат 4×4 клетки. В этих клетках размещаются 16 значений функции из последнего столбца таблицы истинности (рис. 2.4). При разметке обеих осей нужно также четко придерживаться последнего, четвертого правила разметки и следить за тем, чтобы по одной оси соседними не оказались сочетания и , либо и , в которых одновременно меняются обе переменные.

Для функции пяти переменных карта Карно представляет собой уже объемную фигуру — куб 4x4x4 клетки, поэтому для минимизации логических выражений она не применяется.

увеличить изображение
Рис. 2.3. Таблица истинности (а) и примеры заполнения карты Карно (б, в, г, д) для логической функции 3 переменных.
увеличить изображение
Рис. 2.4. Таблица истинности (а) и примеры заполнения карты Карно (б, в) для логической функции 4 переменных.

В конкретных случаях вместо значений функций в общем виде в клетки карты проставляются конкретные значения (логические 0 и 1) из соответствующих строк таблицы истинности. Затем рассматриваются только те клетки, которые заполнены единицами. Все эти единицы должны быть обведены контурами по следующим правилам составления контуров:

Контуры должны быть прямоугольными и содержать количество единиц, равное , где — целое число. Таким образом, в контуре может быть либо одна, либо две, либо четыре, либо восемь единиц.
Количество единиц в контуре должно быть максимальным, при этом контуры могут пересекаться между собой. Нужно учитывать, что крайние строки являются соседними и крайние столбцы также являются соседними, поэтому контуры могут быть «разорванными».
Количество контуров должно быть минимальным, но все единицы должны быть охвачены контурами. Нельзя забывать об отдельно стоящих единицах. Каждая такая единица — это контур, которому соответствует полное логическое произведение всех переменных.

После обведения контуров нужно записать минимальное выражение как логическую сумму логических произведений. Каждому произведению соответствует один контур карты Карно. В произведение входят только те переменные, которые остаются в данном контуре неизменными.При этом переменная входит в произведение с инверсией, если ее значение в данном контуре равно 0, и без инверсии, если ее значение равно 1.

Пример 1. Написать минимальное выражение для таблицы истинности, представленной на рис. 2.5,а и нарисовать по нему логическую схему.

При одном варианте разметки осей (рис. 2.5,б) первый контур, состоящий из четырех единиц, получается разорванным. Если же принять разметку, показанную на рис. 2.5,в, то контур будет иметь нормальные очертания, а выражение, ему соответствующее, останется без изменений. Учитывая, что при данном горизонтальном начертании карты Карно крайние столбцы являются соседними, ее можно представить себе как цилиндр, развернутый на плоскости. На рис. 2.5,б представлена развертка такого цилиндра, «разрезанная» между комбинациями , равными и . А на рис. 2.5,в представлена развертка этого же цилиндра, «разрезанная» между произведениями , равными и .

Первый контур охватывает четыре единицы, ему соответствует сумма минтермов: , в которой не изменяется только переменная . Второй контур охватывает две единицы. Ему соответствует сумма минтермов , в которой переменная принимает оба возможных значения, а произведение остается неизменным. Таким образом, получаем минимальное выражение:

( 2.2)

Ему соответствует логическая схема на рис. 2.5,г.

Рис. 2.5. Минимизация функции трех переменных

Для сравнения запишем максимальное выражение:

( 2.3)

Разница между (2.2) и (2.3) очевидна и в комментариях не нуждается, за исключением того, что схема, реализованная по (2.3), будет на порядок сложнее и, соответственно, менее надежна, чем схема, показанная на рис. 2.5,г.

Пример 2. Написать минимальное выражение для таблицы истинности, представленной на рис. 2.6,а, и нарисовать по нему логическую схему.

Рис. 2.6. Минимизация функции четырех переменных

При первоначально выбранной разметке осей (рис. 2.6,б) первый контур, состоящий из четырех единиц с номерами 1.1, 1.2, 1.3 и 1.4, расположенных по углам карты, получается разорванным. Если же принять разметку, показанную на рис. 2.7, то контур будет иметь очертания квадрата, а выражение, ему соответствующее, останется без изменений. Учитывая, что крайние столбцы являются соседними и крайние строки являются соседними, карту Карно для функции четырех переменных можно представить себе как торроид, развернутый на плоскости. Проще представить себе обратный процесс получения торроида из плоской фигуры — квадрата. Для этого надо сначала соединить мысленно крайние строки — получим цилиндр. После этого основания цилиндров надо мысленно соединить. Получится торроид. На рис. 2.6,б представлена развертка такого торроида, «разрезанная» между комбинациями , равными и и между сочетаниями , равными и . А на рис. 2.7 представлена развертка этого же торроида, «разрезанная» между комбинациями , равными и и между произведениями , равными и . После анализа контуров получим минимальное выражение . Соответствующая ему схема приведена на рис. 2.8.

Рис. 2.7. К минимизации логической функции четырех переменных
Рис. 2.8. Логическая схема для минимизированного логического выражения

Построение таблицы истинности online | Полезная информация

Что такое таблица истинности?

Таблица, описывающая логическую функцию, называется таблицей истинности.

В таблице истинности перечислены все возможные наборы входных переменных.

В последнем столбце таблицы истинности выводится число, соответствующее значению функции, по которой строилась данная таблица истинности.

Рассмотрим пример:

Допустим, у нас есть две булевых переменных x₁ и x₂. От этих переменных зависит логическая функция f(x₁,x₂)

Для примера возьмем f(x₁,x₂)=x₁∧x₂∨x₁.

Так как x₁,x₂ булевы, то они принимают значния 0 или 1 (Истина или Ложь, True или False, сокращенно можно писать T или F).

Все возможные варианты входных переменных x₁ и x₂ можно представить в таблице:

x₁	x₂	f(x₁,x₂)
0	0
0	1
1	0
1	1

Подставим значения переменных x₁ и x₂ в каждой строчке в функцию f(x₁,x₂).

f(0,0)= 0∧0∨0=0

f(0,1)= 0∧1∨0=0

f(1,0)= 1∧0∨1=1

f(1,1)= 1∧1∨1=1

Получившиеся значения запишем в последний столбец нашей таблицы:

x₁	x₂	f(x₁,x₂)
0	0	0
0	1	0
1	0	1
1	1	1

Мы получили таблицу истинности функции f(x₁,x₂)=x₁∧x₂∨x₁.

На нашем сайте вы можете построить таблицу истинности online.

Для этого вам всего лишь нужно ввести функцию в поле и нажать вычислить.

Таблицы истинности основных булевых функций:

Унарные функции:

Бинарные функции