Пара сил и моменты сил
Часто в прикладных задачах механики приходится определять моменты сил, приложенных к телу, относительно его оси. Покажем, что в сечениях тела под действием внешних сил всегда возникают внутренние силы.
Рассмотрим устройство для подъема грузов, состоящее из вала ABC, на который насажены барабан АВ с радиусом r и зубчатое колесо С с радиусом R.
Вал приводится во вращение от электродвигателя D через зубчатую передачу. Вес поднимаемого груза Q передается через трос на обод барабана, а от шестерни K, насаженной на вал электродвигателя, передается движущая

При равномерном подъеме груза моменты внешних сил, приложенных к валу, должны уравновешиваться, т. е.
Реакции опор А и В не войдут в уравнение моментов, так как они пересекают ось z и, следовательно, не создают относительно этой оси моментов.
Из составленного уравнения равновесия следует, что PR = Qr или Мz (Р) = Мz
Участок вала между сечениями приложения вращающих моментов, как уже отмечалось, находится в равновесии. Естественно, что любая часть, мысленно отсеченная от этого вала, также должна быть в равновесии. На рисунке внизу проведено сечение
Естественно, что любая часть, мысленно отсеченная от этого вала, также должна быть в равновесии. На рисунке внизу проведено сечение
Чтобы отсеченная часть ЕС находилась в равновесии, в сечении Е должен действовать какой-то момент, равный и противоположный по направлению вращающему моменту, приложенному к колесу С. Этот момент называется крутящим (его обозначают Мк ) и является моментом внутренних сил, возникающих в сечении тела.
Использованный здесь метод установления внутренних сил в сечении вала называется методом сечений (более подробно о методе сечений — см. здесь).
Момент внутренних сил в сечении —крутящий момент— равен алгебраической сумме моментов внешних сил, т. е. вращающих моментов, приложенных к отсеченной части вала:
е. вращающих моментов, приложенных к отсеченной части вала:
,
где n — число вращающих моментов, приложенных к отсеченной части рассматриваемого вала.
Знак крутящего момента в поперечном сечении вала можно установить, исходя из направления внешних вращающих моментов. 
При возрастании веса поднимаемого груза соответственно увеличиваются вращающие моменты. Будут возрастать также крутящие моменты в сечениях вала. Очевидно, что при данных размерах вала нельзя допускать безграничного возрастания вращающего, а следовательно, и крутящего моментов, так как вал может разрушиться или сильно деформироваться. Поэтому определение крутящих моментов имеет очень большое практическое значение для расчетов на прочность.
7. Основные понятия и определения статики. Момент силы. Пара сил.
- Основные понятия и определения статики. Аксиомы статики.
- Связи и их реакции.
- Момент силы относительно центра и оси.
- Пара сил. Векторный и алгебраический момент пары сил (Свойства пар сил на плоскости).

- Условия эквивалентности пар сил.
- Сложение пар сил, лежащих в пересекающихся плоскостях.
- Условия равновесия системы пар сил.
1. Основные понятия и определения статики.
Материальные объекты в статике:
материальная точка,
система материальных точек,
абсолютно твердое тело.
Системой материальных точек, или механической системой, называется такая совокупность материальных точек, в которой положение и движение каждой точки зависит от положения и движения других точек этой системы.
Абсолютно твердое тело – это тело, расстояние между двумя точками которого не изменяется.
Твердое тело может находиться в состоянии покоя или движения определенного характера.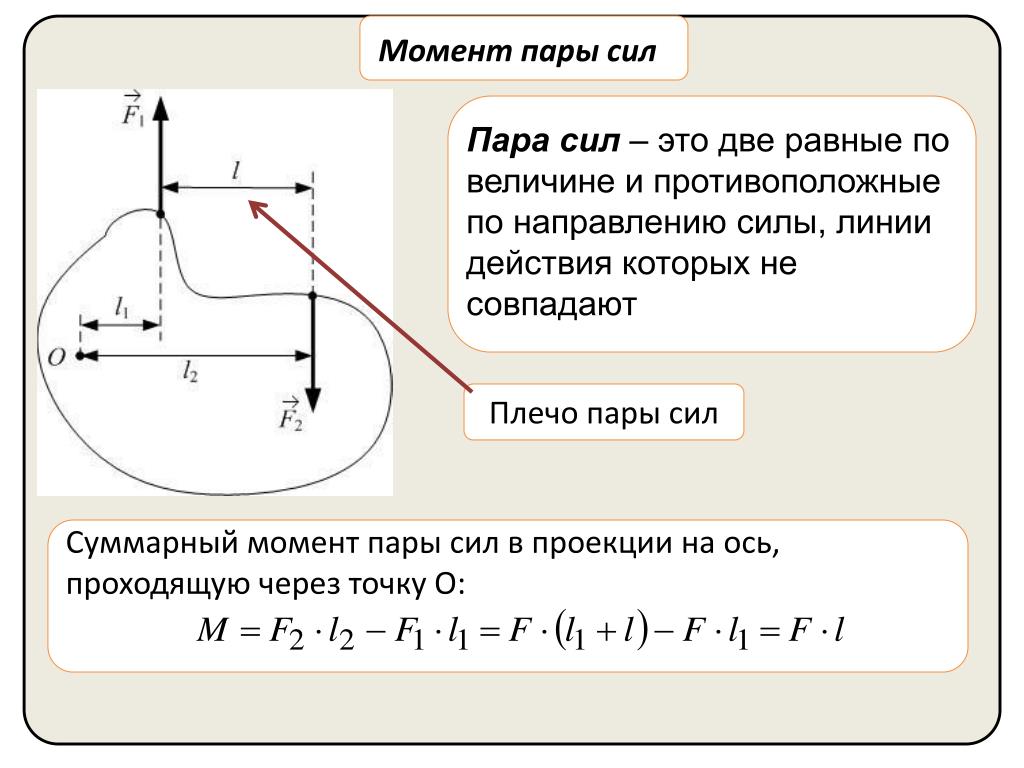 Каждое их этих состояний будем называть кинематическим состоянием тела.
Каждое их этих состояний будем называть кинематическим состоянием тела.
|
|
Сила — мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия. Сила может быть приложена в точке, тогда эта сила – сосредоточенная. Сила может действовать на все точки данного объема или поверхности тела, тогда эта сила – распределенная. |
|
Система сил — совокупность сил, действующих на данное тело. |
|
|
Равнодействующей называется сила, эквивалентная некоторой системе сил. |
|
|
Уравновешивающей силой называется сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону. |
|
|
Системой взаимно уравновешивающихся сил называется система сил, которая будучи приложенной к твердому телу, находящемуся в покое, не выводит его из этого состояния.
|
Внутренние силы – это силы, которые действуют между точками или телами данной системы.
Внешние силы – это силы, которые действуют со стороны точек или тел, не входящих в данную систему.
— преобразование систем сил, действующих на твердое тело в эквивалентные им системы;
— исследование условий равновесия тел под действием приложенных к ним сил.
|
1.
2. Аксиома равновесия двух сил. Две силы, приложенные к твердому телу взаимно уравновешиваются только в том случае, если их модули равны и они направлены по одной прямой в противоположные стороны.
|
|
|
3. Аксиома присоединения и исключения уравновешивающихся сил. Действие системы сил на твердое тело не изменится, если к ней присоединить или из нее исключить систему взаимно-уравновешивающихся сил. Следствие. Не изменяя кинематического состояния абсолютно твердого тела, силу можно переносить вдоль линии ее действия, сохраняя неизменным ее модуль и направление. Сила — скользящий вектор.
|
|
|
|
4. Аксиома параллелограмма сил. Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.
|
|
5. Аксиома равенства действия и противодействия. Всякому действию соответствует равное и противоположно направленное противодействие.
2. Связи и их реакции
Твердое тело называется свободным, если оно может перемещаться в пространстве в любом направлении.
Тело, ограничивающее свободу движения данного твердого тела, является по отношению к нему связью.
Твердое тело, свобода движения которого ограничено связями, называется несвободным.
Все силы, действующие на несвободное твердое тело, можно разделить на:
- задаваемые (активные)
- реакции связей
Задаваемая сила выражает действие на данное тело других тел, способных вызвать изменение его кинематического состояния.
Реакция связи – это сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям.
Принцип освобождаемости твердых тел от связей — несвободное твердое тело можно рассматривать как свободное, на которое кроме задаваемых сил, действуют реакции связей.
|
|
|
|
|
|
Как определить направление реакции?
Если существует два взаимно перпендикулярных направления на плоскости, в одном из которых связь препятствует перемещению тела, а в другом нет, то направление ее реакции противоположно первому направлению.
В общем случае направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу.
|
|
Неподвижный шарнир
Подвижный шарнир
|
|
|
3.
Момент силы относительно центраМоментом силы F относительно некоторого неподвижного центра О называется вектор, расположенный перпендикулярно к плоскости, проходящей через вектор силы и центр О, направленный в ту сторону, чтобы смотря с его конца можно было видеть поворот силы F относительно центра О против часовой стрелки.
Свойства момента силы относительно центра:
|
|
1) Модуль момента силы относительно центра может быть выражен удвоенной площадью треугольника ОАВ (1.1)
2) Момент силы относительно центра равен нулю в том случае, если линия действия силы проходит через эту точку, то есть h = 0.
|
|
|
3) Если из точки О в точку приложения силы А провести радиус вектор , то вектор момента силы можно выразить векторным произведением
(1. |
|
|
4) При переносе силы по линии ее действия вектор ее момента относительно данной точки не изменяется.
|
|
|
5) Если через центр О провести оси координат Охуz то выражение (4.2) позволяет вычислить момент МО аналитически относительно координатных осей.
(1.3)
|
Если к твердому телу приложено несколько сил, лежащих в одной плоскости, можно вычислить алгебраическую сумму моментов этих сил относительно любой точки этой плоскости
Момент МО, равный алгебраической сумме моментов данной системы относительно какой-либо точки в той же плоскости, называют главным моментом системы сил относительно этой точки.
3. Момент силы относительно оси
Чтобы определить момент силы относительно оси необходимо:
1) провести плоскость, перпендикулярную к оси Z;
2) определить точку О пересечения оси с плоскостью;
3) спроецировать ортогонально силу F на эту плоскость;
4) найти момент проекции силы F относительно точки О пересечения оси с плоскостью.
(1.4)
Правило знаков:
Момент силы относительно оси считается положительным, если, смотря навстречу оси Z, можно видеть проекцию , стремящейся вращать плоскость I вокруг оси Z в сторону, противоположную вращению часовой стрелки.
|
|
Свойства момента силы относительно оси 1) Момент силы относительно оси изображается отрезком, отложенным по оси Z от точки О в положительном направлении, если > 0 и в отрицательном направлении, если < 0. 2) Значение момента силы относительно оси может быть выражено удвоенной площадью Δ (1.5)
3) Момент силы относительно оси равен нулю в двух случаях:
|
4. Пара сил. Векторный и алгебраический момент пары сил
Система двух равных по модулю, параллельных и противоположно направленных сил и , называется парой сил.
Плоскость, в которой находятся линии действия сил и , называется плоскостью действия пары сил.
Кратчайшее расстояние hмежду линиями действия сил, составляющих пару, называется плечом пары сил.
Момент пары сил определяется произведением модуля одной из сил пары на плечо.
(1.6)
|
|
Правило знаков
Вектор момента М пары и направляют перпендикулярно к плоскости действия пары сил в такую сторону, что бы смотря навстречу этому вектору, видеть пару сил стремящейся вращать плоскость ее действия в сторону, обратную вращению часовой стрелки.
- 4. Свойства пар сил на плоскости
Свойство 1. Вектор-момент M пары по модулю и направлению равен векторному произведению радиуса вектора АВ на ту из сил этой пары, к началу которой направлен радиус-вектор АВ, то есть
(1.7)
|
|
Если пары сил лежат в одной плоскости
|
|
Свойство 2. Главный момент сил, составляющих пару относительно произвольной точки на плоскости действия пары, не зависит от положения этой точки и равняется моменту этой пары сил.
|
|
5. Условия эквивалентности пар сил
Теорема об условии эквивалентности пар сил,
лежащих в одной плоскости.
Пары сил, лежащие в одной плоскости, эквивалентны, если их моменты равны численно и одинаковы по знаку.
|
|
следовательно, их можно исключить из этой системы сил. Тогда получим пару с плечом NK=CD=h2, эквивалентную паре с плечом KZ = h1 = AB. Из подобия треугольников
|
Сравнивая (*) и (**) получим, что пару сил, не изменяя ее действия на твердое тело можно переносить в любое место плоскости ее действия, поворачивать ее плечо на любой угол, а также изменять это плечо и модули сил, не изменяя величины ее момента и направления вращения.
Следовательно, основной характеристикой пары является ее момент.
Теорема об условии эквивалентности пар сил в пространстве
Пары сил в пространстве эквивалентны, если их моменты геометрически равны.
|
|
Имеем :
|
|
|
|
Из рассмотренных теорем следует:
- не изменяя действия пары сил на твердое тело, пару сил можно переносить в любую плоскость, параллельную плоскости ее действия, а так же изменять ее силы и плечо, сохраняя неизменным модуль и направление ее момента.
- вектор момента пары сил определяет все три ее элемента: положение плоскости действия пары, направление вращения и численное значение момента.
Таким образом, вектор момента пары сил можно переносить в любую точку пространства, то есть
момент пары сил является свободным вектором
6. Сложение пар сил, лежащих в пересекающихся плоскостях
Теорема о сложении пар сил, лежащих в пересекающихся плоскостях
Система пар сил, лежащих в пересекающихся плоскостях эквивалентна одной паре с вектором-моментом, равным геометрической сумме векторов –моментов слагаемых пар.
|
|
то есть вектор-момент равнодействующей пары по модулю и направлению изображается диагональю параллелограмма, построенного из векторов-моментов слагаемых пар.
Если на тело действует nпар, лежащих в разных плоскостях, то складывая эти пары в последовательном порядке и применяя каждый раз теорему о сложении двух пар сил, установим, что эта система пар заменится одной равнодействующей парой с вектором-моментом
(1.8)
|
|
|
|
7
. Условия равновесия системы пар сил
— векторная форма (1.9)
— в проекциях на оси координат (1.10)
Момент пары сил — Энциклопедия по машиностроению XXL
Приведенной силой или приведенным моментом называют условные силу или момент (пары сил), которые, будучи приложены к звену приведения, развивают мощность iV , равную сумме мощностей SiV/,, развиваемых приводимыми силами и моментами. [c.124]При статическом размещении масс не удовлетворяется уравнение (12.11), так как момент инерции звена с размещенными массами, вообще говоря, не равен действительному моменту инерции Js звена. Следовательно, при этом будет допускаться ошибка в моменте пары сил инерции. Этой ошибкой можно пренебречь, если угловое ускорение е невелико. [c.244]
I. ПАРА СИЛ И АЛГЕБРАИЧЕСКИЙ МОМЕНТ ПАРЫ СИЛ [c.30]
Для количественной характеристики действия пары сил на твердое тело и указания направления, в котором пара сил стремится вращать тело в плоскости действия, введем понятие алгебраического момента пары сил. [c.31]
Алгебраическим моментом пары сил называют взятое со знаком плюс или минус произведение одной из сил пары на плечо пары сил. [c.31]
Алгебраический момент пары сил имеет знак плюс, если пара сил стремится вращать тело против часовой стрелки, и знак минус, если пара сил стремится вращать тело по часовой стрелке. [c.31]
Алгебраический момент пары сил не зависит от переноса сил пары вдоль своих линий действия и может быть равен нулю, если линии действия сил пары совпадают, т. е. в случае двух равных по модулю, но противоположных по направлению сил, действующих вдоль одной прямой. Такая система двух сил, как известно, эквивалентна нулю. Алгебраический момент парь[ сил численно равен площади параллелограмма, построенной на силах пары [c.31]
Векторный момент пары сил можно выразить в виде векторного произведения двух векторов [c.34]
Последовательно применяя правило параллелограмма ко всем векторным моментам пар сил, можно любое количество пар сил в общем случае заменить одной парой сил, векторный [c.37]
Пример 1. Определить векторный момент пары сил, которая получается при сложении двух пар сил с моментами М,=40Н м и Л/2 = 30Н м, действующих на одно и то же твердое тело. Пары сил расположены в пересекающихся плоскостях, двугранный угол между которыми равен 60″. [c.38]
Решение. Сложим сначала алгебраически моменты пар сил, расположенных в параллельных плоскостях. Получим пару сил с моментом М,2 = Л/,— [c.38]
Н м, так как моменты пар сил имеют противоположные [c.38]
Таким образом, для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций векторных моментов пар сил па каждую UJ трех координатных осей была равна нулю. [c.39]
Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующей качению [c.74]
Наибольший момент пары сил, препятствующей качению, в довольно широких пределах не зависит от радиуса катка. [c.74]
Задача считается решенной, если определены проекции неи- вестных си-jH.i и момента пары сил М, на какие-либо прямоугольные оси коор-дина , [c.85]
У регулятора с переменным размахом крыльев 1 при вращении вала 2 создается момент пары сил инерции (Рц, —Рц), который, преодолевая сопротивление пружины 3, разворачивает крылья вокруг оси 4. За счет увеличения размаха крыльев резко возрастает тормозной момент регулятора, что обеспечивает лучшее регулирование скорости. [c.116]
Г. в задачу силового расчета входит определение всех сил и моментов пар сил, которые приложены к каждому отдельному звену механизма. Эти силы нлн oмellты надо знать, например, для расчета на прочность отдельных звеньев механизм или их частей (деталей). [c.103]Момент силы, момент пары сил Нъютон- метр Нм I Нм ir ОД кгс-м I кН — 0,1 тс-м [c.4]
Учет сил инерции звеньев механизма при различных видах движения. Все силы инерции звена АВ (рис. 4.13), совершающего плос-конарал.пельное двпл- с 1ие и имеющего плоскость симметрии, параллельную плоскости движения, могут быть приведены к глав1Ю.му вектору сил инерции / приложенному в центре масс звена, и главному моменту пары сил инерции Мц. [c.139]
Силу Р, действующую на рычаг, приводим (по правилам статики) к центру тяжести болтового соединения (точке С), как показз1ю на рис. 5.36, а. В ре- ультате получаем силу Ру = Р п момент М = Р1 (в плоскости стыка). Сила и момент должны быть уравновешены силами трения, вызванными затяжкой болтов. Условно примем, что точки приложения равнодействующих сил трения совпадают с центрами тяжести болтовых отверстий рычага. Действие силы Р- и момента рассматриваем раздельно. Сила Р уравгювешивается силами Тр, каждая из которых равна 0,5Pi = 0,5Р (рис. 5.36, б). Момент М уравновешивается моментом пар сил (см. рис. 5.36, б) [c.81]
А1пебраический момент пары сил выражается в тех же единицах, что и алгебраический момент силы относительно гочки. [c.31]
Векторным моментом пары сил назовем вектор, числовое значение которого равно произведению силы пары на ее плечо. Векторный момот пары сил направлен перпендикулярно плоскости действия пары сил так. чтобы с его нanpaвJleнuя мо.жно выло видеть стрем.гение пары u.i вращать тело против часовой стрелки. Векторный момент нары сил условимся временно прикладывать посередине отрезка, соединяющего точки приложения сил пары (рис. 29). Его можно нрикладывагь также, как будег доказано ниже, в любой точке тела, на которое действует пара сил. Векторный момент пары сил (Z ,, F2) обозначим М или М F ). [c.34]
Отмегим простейшие свойства векторного момента пары сил его числовое значение не зависит ог переноса сил пары вдоль своих линий действия, и он может быть равен нулю, если одна из сторон параллелограмма А B D превратится в точку, т. е. плечо пары или сила пары становится равной нулю. [c.34]
Известно, что пару сил можно как угодно поворачивать и переноси II) в плоскости ее действия действие пары сил на твердое тело не изменяется, если алгебраический момент пары сил остается таким же. Следовательно, векторный момент пары сил можно переносить параллельно самому себе в любую точку твердого тела, лежащую в плоскости действия пары сил. Так как к юму же пару сил можно переносить в параллельную плоскость, то векторный момент пары сил можно переносить параллельно самому себе в любую точку тела, не изменяя действия пары сил на твердое тело. Поэтому векторный момент пары сил. действующей на твердое тело, есть свободный вектор, т. е. он характеризуется только модулем и направлением, а точкой приложения у него может быть любая точка тела следовательно, векторный момент пары сил не обязательно прикладывать посередине отрезка, соеди-няюп(его точки приложения сил пары. [c.35]
Если моментная точка О выбирается в плоскости действия сил пары как частный случай, справедлива теорема о сумме алгебраических моментов сил пары сумма алгебраических моментов сил, входящих в состав пары сил, относительно точки, лежащей в плоскости действия пары сил, равна алгебраическому моменту пары сил и, следователмю, не зависит от выбора моментной точки, г. е. [c.36]
Итак, при сложении двух пар сил, лежащих в пересекающихся плоскостях, получается MeueajieitmnaM пара сил. Обозначим М векторный момент пары сил R, R ). Тогда на основании формул (4) и (7) [c.37]
Если это сложение выполня1ь графически, особенно когда векторные моменты пар сил находятся в одной плоскости, то векторный момент эквивалент-32 ной пары сил изобразится замыкающей [c.38]
Величины тгих реакций равны. Их можно пайги приравняв момент пары сил опорных реакций сумме алгебраических моментов пар сил, дейсгвуюпшх па гело. Таким образом, [c.40]
Очевидно, если рассмотреть любую часть балки, расчленив ее мысленно по сечению тп, то в месте расчленения надо приложить неизвестные силу и пару сил, заменяющие действие отброн1енной части балки на рассматриваемую ее часть, причем сила и момент пары сил, действующие на различные части балки, будут иметь противоположные направления дейспвия и вращения соответстветшо, как всякое действие и противодействие. [c.60]
Реакции залслки в точке А в общем случае дают >ри неизвестные две составляющие силы по осям координап и момент пары сил одна неизвестная сила имеется и точке В. Ее дает шарнирный стержень. Таким образом, имеем четыре неизвестные, а независимых уравнений для их определения -голько три. Систему тел следует расчленить на отдельные тела (рис. 51), приложив к каждому из них в точке С силы действия одного тела на другое, которые равны по величине, но противоположны по направлению. [c.63]
Пара вращений аналогична паре сил, действующей на твердое тело. YrjmBbie скорости вращения гела, аналогично силам, являются векторами скользящими. Векторный момент пары сил является вектором свободным. Аналогичным свой-сгвом обладает и векторный момент пары вращений. [c.298]
Краткий курс теоретической механики (1995) — [ c.34 , c.42 ]
Курс теоретической механики Ч.1 (1977) — [ c.39 ]
Курс теоретической механики 1973 (1973) — [ c.64 ]
Курс теоретической механики 1981 (1981) — [ c.150 ]
Теоретическая механика (1976) — [ c.121 ]
Курс теоретической механики. Т.1 (1972) — [ c.265 ]
Курс теоретической механики. Т.1 (1982) — [ c.43 ]
Физические основы механики и акустики (1981) — [ c.67 ]
Теоретическая механика (1999) — [ c.134 ]
Теоретическая механика Изд2 (1952) — [ c.235 , c.242 , c.282 ]
Справочное руководство по физике (0) — [ c.72 ]
Курс теоретической механики Изд 12 (2006) — [ c.41 ]
Справочник по Международной системе единиц Изд.3 (1980) — [ c.29 ]
Пара сил и ее свойства [wiki.eduVdom.com]
Определение. Парой называется система двух сил, которые равны по
модулю, параллельны и направлены в противоположные стороны.
Пара, приложенная к ТТ, стремится вызвать его вращение. Вращательное
действие пары определяется ее моментом, который равен произведению одной из
сил пары на ее плечо, то есть расстояние между линиями действия сил пары:
$$M(P,\,P’) = P\cdot d = P’\cdot d$$
Нетрудно убедиться в справедливости следующих утверждений:
Сумма проекций сил пары на любую ось равна нулю;
Сумма моментов сил пары относительно любой точки равна моменту этой пары.
В общем случае действие пары сил на ТТ определяется тремя факторами:
плоскостью действия;
направлением вращения в этой плоскости;
величиной момента.
Чтобы однозначно определить все эти факторы, вводят понятие вектор-момента пары.
Определение. Вектор-моментом пары сил называется вектор, который:
перпендикулярен плоскости действия пары;
направлен по правилу правого винта;
равен по модулю моменту пары (
Рис.1).
Нетрудно убедиться, что вектор-момент пары сил можно представить в виде векторных произведений:
$$\vec{М} (\vec{P}, \vec{P’}) = \vec{AB} \times \vec{P’} = \vec{BA}\times\vec{P}$$
Рис.1
Примечание:
subjects/termeh/statics/пара_сил_и_ее_свойства.txt · Последние изменения: 2013/04/06 01:09 — ¶
Пара сил и момент силы относительно точки
1. Пара сил и момент силы относительно точки
Преподаватель «Основы технической механики»Шингисова Макпал Байшотовна
КГКП «Павлодарский химико-механический колледж»
г. Павлодар
2020 год
2. Пара сил, момент пары сил
• Парой сил называется система двух сил, равных по модулю,параллельных и направленных в разные стороны, приложенных к телу в
двух разных точках.
• Плечом пары h называется кратчайшее расстояние между линиями
действия сил, составляющих пару.
• Моментом пары сил называется взятое со знаком «плюсом» или
«минусом» произведение модуля одной из сил на плечо пары.
Пара сил вызывает вращение тела и ее действие на тело оценивается
моментом. Силы, действующие на пару, не уравновешиваются, т.к. они
приложены к двум точкам. Их действие на тело не может быть заменено одной
силой (равнодействующей)
Момент пары сил численно равен произведению модуля силы на расстояние
между линиями действия сил (плечо пары).
Момент считается положительным, если пара вращает тело по часовой стрелке
и наоборот.
М
М>0
4. Свойства пар
• Пару можно перемещать в плоскости ее действия• Эквивалентность пар. Две пары моменты которых равны, эквивалентны
(действие их на тело аналогично).
• Сложение пар сил. Систему пар сил можно заменить равнодействующей
парой. Момент равнодействующей пары равен алгебраической сумме
моментов пар, составляющих систему
• Равновесие пар.
Для равновесия пар необходимо и достаточно, чтобы алгебраическая сумма
моментов пар системы равнялась нулю:
7. Момент пары
В результате силы тяжести все конструкции имеют опору. Если кконструкции приложить активные силы, то на опоре возникает такая же, но
реактивная противоположно направленная. Если две силы || то они
обозначают пару.
При подсчёте момента пары достаточно видеть одну силу и расстояние
до второй. Поэтому решая задачи подсчитывают момент силы
относительно точки, вокруг которой эта сила стремится повернуть тело.
8. Момент силы относительно точки
9. Решение задач
10. Пример 1
11. Контрольные вопросы и задания
Тема: «Пара сил и момент силыотносительно точки»
12. Контрольные вопросы и задания
5. Ответьте на вопросы тестового задания.Вопросы
1. Какие силы из заданной системы сил,
действующих на тело, образуют пару сил?
Ответы
а) 7 Н; 7 Н
б) 7 Н; 10 Н
в) 10 Н; 10 Н
г) 15 Н; 15 Н;
2. Определить момент заданной пары сил.
а) 0,35 Н·м
б) -35,35 Н·м
в) 50 Н·м
г) -70,7 Н·м
Вопросы
3. Укажите пару сил, эквивалентную заданной.
Ответы
а)
б)
в)
г)
Вопросы
Ответы
4. Найдите момент уравновешивающей пары сил.
а) -0,4 Н·м
б) 0,4 Н·м
в) -0,8 Н·м
г) 0,8 Н·м
5. Определить сумму моментов сил относительно
точки С.
а) 7 Н·м
б) 47 Н·м
в) 19 Н·м
г) 77 Н·м
17. Благодарю за внимание!
Как найти момент пары сил. Момент пары как вектор
position:relative; z-index:2″> ПАРА СИЛ И МОМЕНТЫ СИЛ
Пара сил и ее действие на тело
Две равные и параллельные силы, направленные в противоположные стороны и не лежащие на одной прямой, называются парой сил. Примером такой системы сил могут служить усилия, передаваемые руками шофера на рулевое колесо автомобиля. Пара сил имеет большое значение в практике. Именно поэтому свойства пары как специфической меры механического взаимодействия тел изучаются отдельно.
Сумма проекций сил пары на ось х и на ось у равна нулю (рис. 19, а), поэтому пара сил не имеет равнодействующей. Несмотря на это тело под действием пары сил не находится в равновесии.
Действие пары сил на твердое тело состоит в том, что она стремится вращать это тело. Способность пары сил производить вращение определяется моментом пары, равным произведению силы на кратчайшее расстояние (взятое по перпендикуляру к силам) между линиями действия сил. Обозначим момент пары М , а кратчайшее расстояние между силами а, тогда абсолютное значение момента (рис. 19, а):
font-size:12.0pt»>Кратчайшее расстояние между линиями действия сил называется плечом пары, поэтому можно сказать, что момент пары сил по абсолютному значению равен произведению одной из сил на ее плечо.
Эффект действия пары сил полностью определяется ее моментом. Поэтому момент пары сил можно показывать дугообразной стрелкой, указывающей направление вращения. Так как font-size:12.0pt»>пара сил не имеет равнодействующей, ее нельзя уравновесить одной силой. Момент пары в СИ измеряется в ньютонометрах (Нм) или в единицах, кратных ньютонометру: кНм, МНм и т. д.
Момент пары сил будем считать положительным, если пара стремится повернуть тело по направлению хода часовой стрелки (рис. 19, а), и отрицательным, если пара стремится вращать тело против хода часовой стрелки (рис. 19, б). Принятое правило знаков для моментов пар условно: можно было бы принять противоположное правило.
Упражнение 1.
1. Определить, на каком рисунке изображена пара сил:
А. Рис. 20, а. Б. Рис. 20, б. В. Рис. 20, в. Г. Рис. 20, г.
font-size:12.0pt»>2. Что определяет эффект действия пары сил?
А. Произведение силы на плечо. Б. Момент пары и направление поворота.
3. Чем можно уравновесить пару сил?
А. Одной силой. Б. Парой сил.
Эквивалентность пар
font-size:12.0pt»>Две пары сил считаются эквивалентными в том случае, если после замены одной пары другой парой механическое состояние тела не изменяется, т. е. не изменяется движение тела или не нарушается его равновесие.
Эффект действия пары сил на твердое тело не зависит от ее положения в плоскости. Таким образом, пару сил можно переносить в плоскости ее действия в любое положение.
Рассмотрим еще одно свойство пары сил, которое является основой для сложения пар.
Не нарушая состояния тела, можно как угодно изменять модули сил и плечо пары, только бы момент пары оставался неизменным.
Заменим пару сил https://pandia.ru/text/79/460/images/image007_8.gif»> с плечом b (рис. 21, б) так, чтобы момент пары оставался тем же.
Момент заданной пары сил font-size:12.0pt»>Если, изменив значения сил и плечо новой пары, мы сохраним равенство их моментов М1 = М2 или F1a = F2b, то состояние тела от такой замены не нарушится. Итак, вместо заданной пары с плечом а мы получили эквивалентную пару EN-US»>b .
Упражнение 2
1. Зависит ли эффект действия пары сил на тело от ее положения в плоскости?
А. Да. Б. Нет.
2. Какие из приведенных ниже пар эквивалентны?
А. а) сила пары 100 кН, плечо 0,5 м; б) сила пары 20 кН, плечо 2,5 м; в) сила пары 1000 кН, плечо 0,05 м. Направление всех трех пар одинаково.
Б. а) Мг = -300 Нм; б) М2 = 300 Нм.
3. Момент пары сил равен 100 Нм, плечо пары 0,2 м. Определить значение сил пары. Как изменится значение сил пары, если плечо увеличить в два раза при сохранении численного значения момента.
Сложение и равновесие пар сил на плоскости
Подобно силам, пары можно складывать. Пара, заменяющая собой действие данных пар, называется результирующей.
Как показано выше, действие пары сил полностью определяется ее моментом и направлением вращения. Исходя из этого сложение производится алгебраическим суммированием их моментов, т. е. момент результирующей пары равен алгебраической сумме моментов составляющих пар.
Это применимо к любому количеству пар, лежащих в одной плоскости. Поэтому при произвольном числе слагаемых пар, лежащих в одной плоскости или параллельных плоскостях, момент результирующей пары определится по формуле
font-size:12.0pt»>где моменты пар, вращающие по часовой стрелке принимаются положительными, а против часовой стрелки — отрицательными.
На основании приведенного правила сложения пар устанавливается условие равновесия системы пар, лежащих в одной плоскости, а именно: для равновесия системы пар необходимо и достаточно, чтобы момент результирующей пары равнялся нулю или чтобы алгебраическая сумма моментов пар равнялась нулю:
a0″>Пример .
Определить момент результирующей пары, эквивалентной системе трех пар, лежащих в одной плоскости. Первая пара образована силами F1 = F»1 = 2 кН, имеет плечо h 1 = 1,25 м и действует по часовой стрелке; вторая пара образована силами F2 = F»2 = 3 кН, имеет плечо h3 =. 2 м и действует против часовой стрелки; третья пара образована силами F 3 = F»3 = 4,5 кН, имеет плечо h4 = 1,2 м и действует по часовой стрелке (рис. 22).
font-size:12.0pt»>Решение.
Вычисляем моменты составляющих пар:
font-size:12.0pt»>Для определения момента результирующей пары складываем алгебраически моменты заданных пар
font-size:12.0pt»>Момент сил относительно точки и оси
Момент силы относительно точки определяется произведением модуля силы на длину перпендикуляра, опущенного из точки на линию действия силы (рис. 23, а).
При закреплении тела в точке О сила стремится поворачивать его вокруг этой точки. Точка О, относительно которой берется момент, называется центром момента, а длина перпендикуляра а называется плечом силы относительно центра момента.
Момент силы font-size:12.0pt»>font-size:12.0pt»>Измеряют моменты сил в ньютонометрах (Нм) или в соответствующих кратных и дольных единицах, как и моменты пар.
font-size:12.0pt»>Момент принято считать положительным, если сила стремится вращать тело по часовой стрелке (рис. 23, а), а отрицательным — против часовой стрелки (рис. 23, б). Когда линия действия силы проходит через данную точку, момент силы относительно этой точки равен нулю, так как в рассматриваемом случае плечо а = 0 (рис. 23, в).
Между моментом пары и моментом силы есть одно существенное различие. Численное значение и направление момента пары сил не зависят от положения этой пары в плоскости. Значение и направление (знак) момента силы зависят от положения точки, относительно которой определяется момент.
Рассмотрим, как определяется момент силы относительно оси.
Из опыта известно, что ни сила (рис. 24), линия действия которой пересекает ось Oz , ни сила F2, параллельная оси, не смогут повернуть тело вокруг этой оси, т. е. не дают момента.
Пусть на тело в какой-то точке (рис. 25) действует сила . Проведем плоскость H , перпендикулярную оси Oz и проходящую через начало вектора силы..gif»> расположенную в плоскости H , и , параллельную оси Oz .
Составляющая EN-US»>Oz и момента относительно этой оси не создает. Составляющая EN-US»>H и создает момент относительно оси Oz или, что то же самое, относительно точки О. Момент силы измеряется произведением модуля самой силы на длину а перпендикуляра, опущенного из точки О на направление этой силы, т. е.: font-size:12.0pt»>Знак момента по общему правилу определяется направлением вращения тела: плюс (+) – при движении по часовой стрелке, минус (-) – при движении против часовой стрелки. Для определения знака момента наблюдатель должен непременно находиться со стороны положительного направления оси. На рис. 25 момент силы EN-US»>Oz положителен, так как для наблюдателя, смотрящего со стороны положительного направления оси (сверху), тело под действием заданной силы представляется вращающимся вокруг оси по ходу часовой стрелки.
Если сила EN-US»>H , перпендикулярной оси О z , момент этой силы определится произведением полной ее величины на плечо l относительно точки пересечения оси О и плоскости H :
Следовательно, для определения момента силы относительно оси нужно спроецировать силу на плоскость, перпендикулярную оси, и найти момент проекции силы относительно точки пересечения оси с этой плоскостью.
ПЛЕЧО ПАРЫ СИЛ кратчайшее расстояние между линиями действия сил, составляющих пару
(Болгарский язык; Български) — рамо на двоица сили
(Чешский язык; Čeština) — rameno dvojice sil
(Немецкий язык; Deutsch) — Hebelarm eines Kräftepaares
(Венгерский язык; Magyar) — erőpár karja
(Монгольский язык) — xoc хүчний мөр
(Польский язык; Polska) — ramię pary sił
(Румынский язык; Român) — braţ al cuplului de forţe
(Сербско-хорватский язык; Српски језик; Hrvatski jezik) — krak sprega sila
(Испанский язык; Español) — brazo del par
(Английский язык; English) — arm of couple of forces
(Французский язык; Français) — bras de couple des forces
Строительный словарь .
Смотреть что такое «ПЛЕЧО ПАРЫ СИЛ» в других словарях:
Расстояние между прямыми, по которым направлены силы, образующие пару сил. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь
плечо пары сил — Кратчайшее расстояние между линиями действия сил, составляющих пару [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] EN arm of couple of forces DE Hebelarm eines Kräftepaares FR bras de couple des forces …
плечо пары сил — jėgų dvejeto petys statusas T sritis fizika atitikmenys: angl. arm of couple; moment arm vok. Arm des Kräftepaares, f rus. плечо пары сил, n pranc. bras de levier du couple, m; bras du couple, m; bras du couple de forces, m … Fizikos terminų žodynas
плечо внутренней пары сил — z — [Англо русский словарь по проектированию строительных конструкций. МНТКС, Москва, 2011] Тематики строительные конструкции Синонимы z EN lever arm of internal forces … Справочник технического переводчика
плечо внутренней пары сил в сечении армокаменного элемента при действии изгибающего момента или внецентренном сжатии — z — [Англо русский словарь по проектированию строительных конструкций. МНТКС, Москва, 2011] Тематики строительные конструкции Синонимы z EN lever arm … Справочник технического переводчика
плечо пары — Расстояние между линиями действия сил пары. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика Обобщающие термины кинетика EN… … Справочник технического переводчика
плечо пары — Расстояние между линиями действия сил пары … Политехнический терминологический толковый словарь
П. момента силы (см. соотв. статью) или количества движения вокруг данной точки кратчайшее расстояние силы или направления скорости от этой точки. П. пары сил есть длина кратчайшего расстояния между силами пары. П. инерции какого нибудь тела… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Две равные по величине и противоположные по направлению параллельные силы, приложенные к одному телу. Пара сил не имеет равнодействующей. Кратчайшее расстояние между линиями действия сил, образующих пару сил, называют плечом пары. Действие пары… … Энциклопедический словарь
1. Плоская система сходящихся сил
Система сходящихся сил находится в равновесии , когда алгебраические суммы проекций ее слагаемых на каждую из двух координатных осей равны нулю.
Проекция силы на ось.
Осью называют прямую линию, которой приписано определенное направление. Проекция вектора на ось является скалярной величиной.
Проекция вектора считается положительной (+), если направление от начала к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной (-), если направление от начала проекции к ее концу противоположно положительному направлению оси.
Если сила совпадает с положительным направлением оси, но угол будет тупой – тогда проекция силы на ось будет отрицательною.
Итак, проекция силы на ось координат равна произведению модуля силы на косинус или синус угла между вектором силы и положительным направлением оси.
Силу, расположенную на плоскости хОу, можно спроецировать на две координатные оси Ох и Оу:
; ; .Проекция векторной суммы на ось.
Геометрическая сумма, или равнодействующая, этих сил
определяется замыкающей стороной силового многоугольника: ,где п – число слагаемых векторов.
Итак, проекция векторной суммы или равнодействующей на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.
2. Пара сил
Сумма проекций пары сил на ось х и на ось у равна нулю, поэтому пара сил не имеет равнодействующей. Несмотря на это тело под действием пары сил находится в равновесии.
Способность пары сил производить вращение определяется моментом пары , равным произведению силы на кратчайшее расстояние между линиями действия сил. Обозначим момент пары М , а кратчайшее расстояние между силами а , тогда абсолютное значение момента:
Кратчайшее расстояние между линиями действия сил называется – плечом пары , поэтому можно сказать, что момент пары сил по абсолютному значению равен произведению одной из сил на ее плечо.
Момент пары сил можно показывать дугообразной стрелкой, указывающей направление вращения.
Две пары сил считаются эквивалентными в том случае, если после замены одной пары другой механическое состояние тела не изменяется, т.е. не изменяется движение тела или не нарушается его равновесие.
Эффект действия пары сил на твердое тело не зависит от ее положения в плоскости. Таким образом, пару сил можно переносить в плоскости ее действия в любое положение.
Еще одно свойство пары сил, которое является основой для сложения пар:
− не нарушая состояния тела, можно как угодно изменять модули сил и плечо пары, только бы момент пары оставался неизменным.
По определению пары сил эквивалентны, т.е. производят одинаковое действие, если их моменты равны.
Если, изменив значения сил и плечо новой пары, мы сохраним равенство их моментов М 1 = М 2 или F 1 a = F 2 b, то состояние тела от такой замены не нарушится.
Подобно силам пары можно складывать. Пара, заменяющая собой действие данных пар, называется результирующей. Действие пары сил полностью определяется ее моментом и направлением вращения. Исходя из этого, сложение пар производится алгебраическим суммированием их моментов, т.е. момент результирующей пары равен алгебраической сумме моментов составляющих пар.
Момент результирующей пары определится по формуле:
М= М 1 + М 2 +... + М п. =
М і ,Где моменты пар, вращающие по часовой стрелке, принимаются положительными, а против часовой стрелки – отрицательными. На основании приведенного правила сложения пар устанавливается условие равновесия системы пар лежащих в одной плоскости, а именно: для равновесия системы пар необходимо и достаточно, чтобы момент результирующей пары равнялся нулю или чтобы алгебраическая сумма моментов пар равнялась нулю:
Момент силы относительно точки и оси.
Момент силы относительно точки определяется произведением модуля силы на длину перпендикуляра, опущенного из точки на линию действия силы.
При закреплении тела в точке О сила
стремится поворачивать его вокруг этой точки. Точка О, относительно которой берется момент, называется центром момента , а длина перпендикуляра а – плечом относительно центра момента .Момент силы
относительно О определяется произведением силы на плечо: .Момент принято считать положительным, если сила стремится вращать тело по часовой стрелке, а отрицательным — против часовой стрелки. Между моментом пары и моментом силы есть одно существенное различие. Численное значение и направление момента пары сил не зависит от положения этой пары в плоскости. Значение и направление (знак) момента силы зависит от положения точки, относительно которой определяется момент.Следовательно, для определения момента силы относительно оси нужно спроектировать силу на плоскость, перпендикулярную оси, и найти момент проекции силы относительно точки пересечения оси с этой плоскостью.
3. Метод кинетостатики
Представим себе материальную точку массой т, движущуюся с ускорением а под действием какой-то системы активных и реактивных сил, равнодействующая которых равна F.
Воспользуемся одной из известных нам формул (основным уравнением динамики) для того, чтобы уравнения движения записать в форме уравнений равновесия (метод кинетостатики):
Перепишем это уравнение в следующем виде:
Выражение обозначается К ин и называется силой инерции:
Сила инерции есть вектор, равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению.
Это равенство, являющееся математическим выражением принципа, который носит имя французского ученого Даламбера (1717-1783), можно рассматривать как уравнение равновесия материальной точки. Следует подчеркнуть, что полученное равенство, хотя и названо уравнением равновесия, в действительности является видоизмененным уравнением движения материальной точки.
Принцип Даламбера формулируется гак: активные и реактивные силы, действующие на материальную точку, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющую всем условиям равновесия.
Следует помнить, что сила инерции приложена к рассматриваемой материальной точке условно, но для связи, вызывающей ускорение, она в определенном смысле является реальной. Обладая свойством инерции, всякое тело стремится сохранять свою скорость по модулю и направлению неизменной, в результате чего оно будет действовать на связь, вызывающую ускорение, с силой, равной силе инерции. В качестве примера действия сил инерции можно привести случаи разрушения маховиков при достижении ими критической угловой скорости. Во всяком вращающемся теле действуют силы инерции, так как каждая частица этого тела имеет ускорение, а соседние частицы являются для нее связями. Отметим, что весом тела называется сила, с которой тело вследствие притяжения Земли действует на опору (или подвес), удерживающую его от свободного падения. Если тело и опора неподвижны, то вес тела равен его силе тяжести.
4. Момент силы относительно точки
Рассмотрим гайку, которую затягивают гаечным ключом определенной длины, прикладывая к концу ключа мускульное усилие. Если взять гаечный ключ в несколько раз длиннее, то прилагая то же усилие, гайку можно затянуть значительно сильнее. Из этого следует, что одна и та же сила может оказывать различное вращательное действие. Вращательное действие силы характеризуется моментом силы.
Понятие момента силы относительно точки ввел в механику итальянский ученый и художник эпохи Возрождения Леонардо да Винчи (1452-1519).
Моментом силы относительно точки называется произведение модуля силы на ее плечо:
М 0 (¥) = РИ.
Точка, относительно которой берется момент, называется центром момента. Плечом силы относительно точки называется кратчайшее расстояние от центра момента до линии действия силы.
Пару сил в механике рассматривают как одно из основных понятий, наряду с понятием силы.
Пара сил – система двух параллельных, противоположно направленных и равных по модулю сил, не лежащих на одной прямой.
Плоскость действия пары сил – плоскость, в которой находятся линии действия сил.
Плечо пары сил – кратчайшее расстояние (длина перпендикуляра) между линиями действия сил, составляющих пару сил.
На рис. 1.34 изображена пара сил, плоскость действия которой лежит в плоскости OXY системы отсчёта OXY.
Силы F 1 , F 2 образуют пару сил. F 1 = F 2 ; F 1 = – F 2 . Однако силы пары не уравновешиваются, так как они направлены не по одной прямой. Пара сил стремится произвести вращение тела, к которому она приложена. Действие пары сил на тело характеризуется её моментом.
Для количественной характеристики действия пары сил на тело и указания направления, в котором пара сил стремится вращать тело, вводится понятие алгебраического момента пары сил .
Алгебраический момент пары сил – величина, равная взятому с соответствующим знаком произведению модуля одной из сил на её плечо.
M = ± F 1 ·h = ± F 2 ·h.
Алгебраический момент пары сил считают положительным, если пара сил стремится повернуть тело против вращения часовой стрелки, и отрицательным, если в сторону вращения часовой стрелки. i , M = F 1 ×h = F 2 ·h. Таким образом, пара сил полностью характеризуется её моментом M .
Теорема . Пары сил, лежащие в одной плоскости, эквивалентны, если их алгебраические моменты численно равны и одинаковы по знаку.
Доказательство этой теоремы несложно и здесь оно не приводится.
Следствия из теоремы:
1.Пару сил, не изменяя её действия на тело, можно как угодно поворачивать и переносить в любое место плоскости её действия.
2.У пары сил можно изменять плечо и модуль силы, сохраняя при этом алгебраический момент пары и плоскость действия.
Суть теоремы и её следствий иллюстрируется рис. 1.36, на котором приведены пары сил с эквивалентными алгебраическими и векторными моментами. Плоскости действия пар сил совпадают с плоскостью YOZ.
Теорема . Пары сил в пространстве эквивалентны, если их моменты геометрически равны.
Доказательство этой теоремы также достаточно просто и здесь не приведено.
Из теорем о парах сил следует вывод: не изменяя действия пары сил на тело, пару сил можно переносить в любую плоскость, параллельную плоскости её действия, а также изменять её силу и плечо, сохраняя неизменными модуль и направление её момента.
Таким образом, вектор момента пары сил можно переносить в любую точку, то есть момент пары сил является свободным вектором .
Вектор момента пары сил определяет три элемента: положение плоскости действия пары; направление вращения; числовое значение (модуль) момента.
Отметим аналогию: если точку приложения вектора силы можно помещать где угодно на линии действия этой силы (скользящий вектор ), то векторный момент пары сил можно приложить в любой точке тела (свободный вектор ).
Система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело. Действие пары сил на твердое тело сводится к некоторому вращательному эффекту, который характеризуется величиной — момент пары.
Он определяется:
Его модулем = F*d. d — расстояние между линиями действия сил пары, называется плечом пары.
Положением в пространстве плоскости действия пары.
Направлением поворота пары в этой плоскости.
Момент пары сил — вектор m(или M), модуль которого равен произведению модуля одной из сил пары, на ее плечо, и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.
Две пары, лежащие в || плоскостях и имеющие одинаковый момент эквивалентны.
Все пары в пересекающихся плоскостях можно заменить одной парой с моментом, равным сумме моментов этих пар. Для абсолютно твердого тела пара — свободный вектор, определяемы только моментом. Момент перпендикулярен плоскости образуемой парой.
Пару можно заменить параллельной ей равной силе и парой с моментом, равным произведению этой силы на расстояние до новой точки приложения.
Теоремы о парах .1) Две пары, лежащие в одной плоскости, можно заменить одной парой, лежащей в той же плоскости, с моментом, равным сумме моментов данных двух пар. .
2) Две пары, имеющие геометрически равные моменты, эквиваленты.
3) Не нарушая состояния твердого тела, пару сил можно переносить в плоскости ее действия. Т.е. момент пары сил является свободным вектором.
4) Система нескольких пар сил эквивалента одной паре, момент которой равен векторной сумме моментов данных пар. Т.е. система пар приводится к одной паре, момент которой равен сумме моментов всех пар. Условие равновесия пар сил: — геометрическая сумма их моментов равна 0. Пары сил, расположенные в одной плоскости, взаимно уравновеш-тся, если алгебраическая сумма их моментов åМ i =0.
Момент силы относительно точки — вектор, численно равный произведению модуля силы на плечо и направленный перпендикулярно плоскости, содержащей силу и точку, в такую сторону, чтобы смотря ему навстречу, видеть силу стремящейся повернуться против хода час.стрелки. Плечо «h»- кратчайшее расстояние от точки до линии действия силы. — момент силы равен векторному произведению вектора на вектор . Модуль векторного произведения: R×F×sina = F×h. Для плоской сист. сил обычно находят не вектор момента, а только его модуль: ± F×h, >0 — против час.стр.; x, F y , F z — проекции силы на оси координат и точка 0 — начало координат, то
= (yF z — zF y) + (zF x — xF z) + (xF y — yF x) , откуда проекции момента силы на оси коорд.: М 0 x () = yF z — zF y ; М 0 y () = zF x — xF z ; М 0 z () = xF y — yF x .
Главный вектор — векторная сумма всех сил, приложенных к телу. Главный момент относительно центра — векторная сумма моментов всех сил, приложенных к телу относительно того же центра.
Теорема (лемма) о параллельном переносе силы : сила приложенная в какой-либо точке тверд. тела, эквивалента такой же силе, приложенной в любой др. точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения.
Плоская система пар сил.
Плоская система пар сил
Пара сил и момент пары
В предыдущей статье мы рассматривали сложение пары антипараллельных сил, не равных по модулю и пришли к выводу, что равнодействующая таких сил существует и ее величина равна алгебраической сумме сил; точка приложения равнодействующей пары антипараллельных сил находится в пропорциональной зависимости от соотношения между модулями сил пары.
Если пара антипараллельных сил состоит из одинаковых по модулю сил, то такая система сил называется парой сил или просто парой.
Понятие пары сил введено в механику в начале XIX века французским ученым Л. Пуансо (1777-1859), который разработал теорию пар.
Плоскость, в которой расположена пара, называется плоскостью действия пары. Расстояние между линиями действия сил, составляющих пару, называется плечом пары.
Эффект действия пары состоит в том, что она стремится вращать тело, к которому приложена. Ее вращающее действие определяется моментом пары.
Моментом пары называется произведение модуля одной из сил, составляющих пару, на плечо:
M(F1, F2) = F1h =F2h = m .
Момент пары и момент силы имеют одинаковую размерность — ньютон×метр (Нм).
Правило знаков для моментов пары.
Условимся считать момент пары положительным, если она стремится вращать свое плечо против часовой стрелки, и наоборот.
Если сделать геометрические построения (см. рисунок 1), то можно сделать вывод, что момент пары численно равен удвоенной площади треугольника, у которого основанием является вектор одной из сил пары, а высотой – плечо пары (как известно, площадь треугольника равна половине произведения основания на высоту).
Очевидно, что перенос любой из сил пары вдоль линии ее действия не влияет на вращающее действие всей пары, т. е. не изменяет момент пары, поскольку и основание треугольника (модуль силы) и его высота (плечо пары) в этом случае не меняются (перенос сил, составляющих пару вдоль линий их действия приводит к образованию равновеликих треугольников).
***
Основные свойства пары сил
Основные свойства пары сил характеризуются следующими тремя теоремами.
Теорема I. Пара сил не имеет равнодействующей.
Дана пара сил (F1, F2) с плечом h. (см. рисунок 2а).
Ранее мы доказали, что равнодействующая пары антипараллельных сил может быть определена, как алгебраическая сумма сил, составляющих такую пару, т. е., с учетом направленности векторов сил в разные стороны: FΣ = |F1| — |F2|.
Применим это утверждение к случаю, когда силы равны между собой по модулю, и получим, что равнодействующая будет равна нулю: F1 – F2 = 0.
Из этого следует, что пара силы не имеет равнодействующей (или равнодействующая пары равна нулю).
Теорема II. Алгебраическая сума моментов сил, составляющих пару, относительно любой точки плоскости действия пары есть величина постоянная, равная моменту пары.
Дана пара сил (F1, F2) с плечом h. (см. рисунок 2b).
Момент пары: m = F1h = F2h.
Выберем в плоскости действия пары произвольную точку А и примем ее за центр моментов:
MA(F1) = -F1a; MA(F2) = F2(a+h).
Сложим правые и левые части этих равенств (не забываем, что |F1| = |F2|):
MA(F1) + MA(F2) = -F1а + F2(a+h) = -F1а + F2а + F2h = F2h = m .
Теорема доказана.
Из этой теоремы следует, что при любом центре моментов пара сил войдет в уравнение моментов с одним и тем же знаком и одной и той же величиной.
***
Теорема III. Алгебраическая сумма проекций сил пары на любую ось всегда равна нулю.
Дана пара сил (F1, F2) и ось z, лежащая в плоскости действия пары (см. рисунок 3). Из равенства заштрихованных треугольников видно, что F1z = F2z, при этом проекция одной из сил положительная, проекция другой силы – отрицательная, следовательно, сумма этих проекций равна нулю.
Теорема доказана.
Из теорем I и III следует, что пара сил не может входить ни в уравнение сил, ни в уравнение проекций сил, поскольку ее нельзя заменить ни равнодействующей, ни проекцией силы.
***
Эквивалентные пары
Две пары называют эквивалентными, если одну из них можно заменить другой, не нарушая механического состояния свободного твердого тела.
Теорема об эквивалентных парах формулируется так: если моменты двух пар алгебраически равны, то эти пары эквивалентны.
Пусть даны две пары (F1, F2) и (Q1, Q2), моменты которых алгебраически равны (см. рисунок 4), т. е.:
M(F1, F2) = M(Q1, Q2), или Fa = Qh.
Продолжим линии действия сил пары до их взаимного пересечения в точках А и В. На основании следствия из III и IV аксиом статики перенесем силы F и F1 вдоль линий их действия в точки А и В.
Соединим эти точки прямой линией и разложим силы F и F1 по направлению АВ и вдоль линий действия сил Q и Q1.
Из равенства треугольников Akd и Bmn вытекет, что T = T1 и S = S1.
Силы T и Т1 представляют собой уравновешенную систему, так как они равны по модулю и действуют по одной прямой в противоположные стороны. На основании аксиомы IV такую систему можно отбросить.
Силы S и S1 представляют собой пару сил с плечом b.
Таким образом, пара (F1, F2) ≡ паре (S1, S2).
Рассмотрим треугольники AmB и AnB.
Они имеют общее основание АВ, и высоты их равны, следовательно площади тоже будут равны.
Поскольку площадь треугольника AnB равна половине момента пары (F1, F2), а площадь треугольника AmB равна половине момента пары (S1, S2), то можно записать:
М(F, F1) = М(S, S1) или Fa = Sb.
По условиям теоремы Fa = Qb, следовательно Sb = Qb, отсюда S = Q, S1 = Q1.
Силы S и Q равны по модулю, действуют вдоль одной прямой в одном направлении, следовательно они эквивалентны друг другу; на этом же основании можно сделать вывод об эквивалентности сил S1 и Q1. Очевидно, что тогда пара (Q,O1) ≡ паре (S,S1).
Так как две пары порознь эквивалентны одной и той же третьей паре, то эти пары тоже будут эквивалентны между собой:
М(F, F1) = М(Q, Q1), что и требовалось доказать.
Из доказательства теоремы об эквивалентных парах вытекает четыре следствия:
- не изменяя механического состояния тела, пару можно переносить как угодно в плоскости ее действия;
- не изменяя механического состояния тела, можно менять силы и плечо пары, но так, чтобы ее момент оставался неизменным;
- чтобы задать пару, достаточно задать ее момент, поэтому иногда слово «пара» заменяют словом «момент»;
- условия равновесия плоской системы параллельных сил будут справедливы, если вместе с такой системой действуют и пары сил, так как их можно повернуть в плоскости действия и поставить силы пары параллельно другим силам системы.
***
Теорема о сложении пар
Теорема: Всякая плоская система пар эквивалентна одной результирующей паре, момент которой равен алгебраической сумме моментов данных пар.
Пусть даны три пары с моментами m1, m2 и m3, действующие в одной плоскости (рис. 1а).
На основании следствия из теоремы об эквивалентных парах преобразуем эти пары так, чтобы их плечи стали равными d, и перенесем к произвольно взятому на плоскости отрезку АВ длиной d.
Тогда вместо заданной системы пар получим новую систему, эквивалентную данной, причем моменты данных и новых пар будут равны, т. е.
m1 = -P1d ; m2 = F1d ; m3 = -Qd .
Сложив три силы в точке А, получим равнодействующую R1, модуль которой R1 = P1 + Q1 – F1.
Сложив три силы в точке В (рис. 4b) , получим равнодействующую R2, модуль которой R2 = P2 + Q2 – F2, причем очевидно, что силы R1 и R2 равны по модулю, параллельны и противоположно направлены.
Значит, система (R1, R2) представляет собой пару с плечом d, эквивалентную данной системе пар.
Момент этой результирующей пары:
m = -R1d = -( P1 + Q1 – F1)d = -P1d – Q1d + F1d, или
m = m1 +m2 + m3.
Аналогичное доказательство можно привести для любой плоской системы пар, т. е. в общем виде можно записать:
m = Σmi, что и требовалось доказать.
***
Условие равновесия плоской системы пар
Применяя доказанную ранее теорему о сложении пар к плоской системе пар, находящихся в равновесии, запишем:
m = Σmi = 0.
Следовательно, условие равновесия плоской системы пар в общем виде будет выглядеть так:
Σmi = 0,
а формулируется следующим образом: для равновесия плоской системы пар необходимо и достаточно, чтобы алгебраическая сумма моментов данных пар равнялась нулю.
***
Опоры и опорные реакции балок
Опоры балок по их устройству могут быть разделены на три основных типа (см. рисунок 6): шарнирно-подвижная (опора А), шарнирно-неподвижная (опора В) и жесткая заделка (опора С). На приведенном рисунке показаны два способа условного изображения шарнирно-неподвижной опоры (опора А).
Применим правило для определения направления реакций связей и определим, какое направление могут иметь реакции представленных опор в зависимости от ограничений, накладываемых на балку.
Шарнирно-подвижная опора допускает поворот вокруг оси шарнира и линейное перемещение параллельно опорной плоскости. Если пренебречь трением на опоре и в шарнире, то реакция такой связи будет направлена перпендикулярно опорной плоскости, и неизвестна только по модулю (одно неизвестное).
Шарнирно-неподвижная опора допускает только поворот вокруг оси шарнира, и не допускает никаких линейных перемещений. Реакция такой опоры будет направлена перпендикулярно оси шарнира; модуль и направление ее заранее не известны (два неизвестных).
Жесткая заделка (защемление) не допускает ни линейных перемещений, ни поворотов защемленного конца балки. Жесткую заделку заменяют реактивной силой, неизвестной по модулю и направлению, и реактивным моментом (три неизвестных).
Реактивную силу, неизвестную по направлению, раскладывают на две взаимно-перпендикулярные составляющие. Если при решении задачи реактивная сила или реактивный момент получаются отрицательными, то их действительное направление противоположно принятому.
Кроме перечисленных выше трех основных типов опор балок в конструкциях нередко балка свободно опирается на плоскость (поверхность) или ребро призмы (угол). В этих случаях направление реакций определяют, как для аналогичных типов связей, рассмотренных здесь.
***
Пример решения задачи по определению реакций опор балки
Пусть горизонтальная балка длиной l = 4 м закреплена на опорах, как показано на рисунке 7, и нагружена парой сил с моментом m = 420 Нм.
Не учитывая силу тяжести балки, определим реакции R опор А и В.
Решение.
Отбросим опоры, заменив их реакциями, и рассмотрим равновесие балки.
Так как пару сил можно уравновесить только парой, то реакции R опор А и В должны образовывать пару сил, причем реакция шарнирно подвижной опоры В перпендикулярна опорной плоскости.
Применим условие равновесия плоской системы пар и составим уравнение равновесия:
Σmi = 0; -m + Rh = 0, где h = lcos30˚ .
Подставив известные значения, получим: R = m/h = m/(l cos30˚) = 420/(4×0,866) ≈ 120 Н.
Задача решена.
***
Пример решения задачи по определению реакции в жесткой заделке
Пусть консольная балка длиной l = 2 м нагружена на свободном конце силой F = 3000 Н (рис. 8).
Не учитывая силу тяжести балки, определим реакцию заделки.
Решение.
Отбросим заделку, заменив ее реакциями, и рассмотрим равновесие балки.
Реакция заделки представляет собой реактивную силу R и реактивный момент m.
Так как реактивный момент m может быть уравновешен только парой сил, то нагрузка F и реакция R должны образовывать пару, следовательно:
R = F = 3000 Н .
Далее применим условие равновесия плоской системы пар и составим уравнение равновесия:
Σmi = 0; m – F1 – 0, откуда получим:
m = Fl = 3000×2 = 6000 Нм.
Задача решена.
***
Плоская система произвольно расположенных сил
Главная страница
Дистанционное образование
Специальности
Учебные дисциплины
Олимпиады и тесты
Объяснитель урока: Момент пары
В этом объяснении мы узнаем, как вычислить момент пары двух сил и результат двух или более пар.
Давайте сначала определим пару в механике.
Определение: пара
Пара — это пара сил, действующих на одно и то же тело, которые параллельны, но не совпадают. линии действия и которые действуют в противоположных направлениях и имеют равные величины.
Хотя сумма сил равна нулю, имеется ненулевой чистый момент (т.е.е., сумма моментов обеих сил) потому что у сил разное направление действий. Разберемся с чистым моментом.
Рассмотрим пару сил ⃑𝐹 и ⃑𝐹 воздействуя на стержень, перпендикулярно длине стержня. Пусть 𝐹 будет величиной обеих сил. У нас есть ⃑𝐹 = −⃑𝐹, а также ‖‖⃑𝐹‖‖ = ‖‖⃑𝐹‖‖ = 𝐹.
Найдем моменты сил ⃑𝐹 и ⃑𝐹 относительно точки 𝐴, середина между точками применения и ⃑𝐹.Напомним, что момент силы относительно точки определяется выражением 𝑀 = ± 𝐹𝑑, ⟂ где 𝐹 — величина силы, а 𝑑⟂ — расстояние по перпендикуляру между силой и точкой около который момент взят. Если сила производит вращение по часовой стрелке, момент отрицательный. Момент положительный, когда сила производит движение против часовой стрелки. вращение.
Обе силы производят вращение по часовой стрелке (отрицательное), и их точки приложения находятся на перпендикулярном расстоянии 2 от 𝐴.Момент по часовой стрелке относительно точки точки, следовательно, определяется выражением 𝑀 = −𝐹𝑑2, и момент около из ⃑𝐹 равен 𝑀 = −𝐹𝑑2.
Чистый момент пары определяется выражением 𝑀 = 𝑀 + 𝑀𝑀 = −2𝐹𝑑2 = −𝐹𝑑.netnet
Теперь найдем чистый момент ⃑𝐹 и ⃑𝐹 относительно 𝐵. Пусть 𝑙 — длина стержня. Момент около 𝐵 из ⃑𝐹 отрицательный, потому что ⃑𝐹 производит вращение по часовой стрелке (отрицательное) на 𝐵. Следовательно, момент определяется выражением 𝑀 = −𝑙⋅𝐹.
Напротив, момент ⃑𝐹 около 𝐵 положителен, поскольку ⃑𝐹 производит вращение против часовой стрелки (положительное) на 𝐵.Мы находим, что 𝑀 = (𝑙 − 𝑑) ⋅𝐹.
Чистый момент около 𝐵 пары определяется выражением 𝑀 = 𝑀 + 𝑀𝑀 = −𝑙𝐹 + (𝑙 − 𝑑) 𝐹𝑀 = 𝐹 (−𝑙 + 𝑙 − 𝑑) 𝑀 = −𝐹𝑑.netnetnet
Заметим, что момент пары имеет одинаковое значение в обоих случаях . Это общее: момент пары примерно одинаков. любая точка тела, на которую пара воздействует. Стоит отметить разницу между точками А и Б. Точка А находится между двумя точки приложения сил, и силы производят вращение в одном и том же смысле.Точка B находится за пределами области между две точки приложения обеих сил пары, и моменты двух сил в паре имеют противоположные знаки, поскольку они производить вращение в противоположных смыслах.
Свойство: Момент пары
Момент пары не зависит от того, какие моменты пары снимаются.
Силы в паре не обязательно действуют перпендикулярно линии, соединяющей точки, из которых они действуют.Следующие На рисунке показаны три примера пар, где силы в паре не действуют перпендикулярно линии, соединяющей точки. откуда они действуют.
В этом случае перпендикулярное расстояние, также называемое плечом пары, обозначенное 𝐿 на приведенном выше рисунке, это не расстояние между двумя точками приложения сил. Мы видим, что на двух диаграммах справа рука пары дается Осином. На диаграмме слева, где больше чем 90∘, мы видим, что 𝐿 = 𝑑𝜃 ′ = 𝑑 (180 − 𝜃) = 𝑑𝜃sinsinsin∘, так как грех (180 − 𝑥) = 𝑥∘.Следовательно, мы видим, что плечо пары, перпендикулярное расстояние между силами, всегда определяется выражением 𝐿 = 𝑑𝜃.sin
Таким образом, момент пары 𝑀 = ± 𝐹𝐿 = ± 𝐹𝑑𝜃.sin
Мы также можем интерпретировать 𝐹𝑑𝜃sin как (𝐹𝜃) 𝑑sin, то есть произведение абсолютного значения составляющей силы, перпендикулярной стержню, и расстояния между двумя точками приложения сил.
Свойство: Момент пары
Момент действия пары в точках и определяется выражением 𝑀 = ± 𝐹𝑑𝜃𝑀 = ± 𝐹𝐿𝑀 = ± | 𝐹 | ⋅𝑑, sin⟂ где 𝐹 — величина обеих сил в паре, 𝑑 — расстояние между 𝐴 а 𝐵, 𝜃 — угол между любой силой и сегментом 𝐴𝐵, 𝐿 — рука пары, а 𝐹⟂ — составляющая силы, перпендикулярная 𝐴𝐵.
Давайте посмотрим на пример о моменте пары.
Пример 1: Определение руки пары, эквивалентной системе двух сил
Если нормой момента пары является 750 Нм, и величина одного из двух силы составляет 50 Н, определить длину плеча момента.
Ответ
Нормой момента является величина момента. Величина момента пары — произведение величины любой из сил в паре и 𝐿, длина плеча момента.Поскольку момент указан в ньютон-метры а сила дана в ньютонах, 750 = 50𝐿𝐿 = 75050 = 15 м
В предыдущем примере мы видим, что величина момента просто определяется произведением величины одного из силы и рука пары.
Свойство: Величина момента пары
Величина момента пары определяется как | 𝑀 | = 𝐹𝐿, где 𝐹 — величина любой из сил в паре, а 𝐿 — плечо пара.
Давайте рассмотрим пример с моментом пары, когда силы не перпендикулярны линии, соединяющей их точки приложения.
Пример 2: Определение величины пары двух наклонных сил, действующих на двух концах линии
На рисунке ниже 𝐹 = 3N а 𝐹 и 𝐹 образуют пара. Найдите алгебраическую меру момента этой пары.
Ответ
Силы в паре должны иметь равные величины.Если ⃑𝐹 имеет величину 3 Н, тогда ⃑𝐹 также имеет величину 3 Н. Угол между ⃑𝐹 и ⃑𝐹 и линия, соединяющая точки that и ⃑𝐹 действовать от 45∘.
Пара вращается против часовой стрелки и, следовательно, положительно. Величина момента определяется выражением 𝑀 = 𝐹𝜃⋅𝑑sin быть 𝑀 = 3 × 45 × 7√2𝑀 = 3 × √227√2𝑀 = 21⋅.sinNcm
Правильное математическое определение момента силы дается перекрестным произведением.
Определение: Момент пары с использованием перекрестного произведения
Момент силы ⃑𝐹 относительно точки можно найти с помощью перекрестного произведения. Вектор ⃑𝑟 представляет положение вектор от точки, вокруг которой передается момент, до любой точки на линии действия силы. 𝑀 = ⃑𝑟 × ⃑𝐹
Для пары, образованной двумя силами; ⃑𝐹 действующий в точке 𝐴 и ⃑𝐹 действующий в точке 𝐵 момент пары определяется выражением 𝑀 = 𝐵𝐴 × ⃑𝐹 = 𝐴𝐵 × ⃑𝐹
Обратите внимание, что в приведенном выше уравнении для момента пары, ⃑𝑟 был заменен вектором между точками приложения сил.Мы можем думать об этом как о том, чтобы взять моменты, связанные с точкой в первом случае, и взять моменты о точке 𝐴 во втором случае.
Полезный способ оценить перекрестное произведение — рассмотреть определитель матрицы 3 × 3. 𝑀 = ⃑𝑟 × ⃑𝐹 = ||||| ⃑𝑖⃑𝑗⃑𝑘𝑟𝑟𝑟𝐹𝐹𝐹 |||||
Хотя этот метод в основном используется, когда векторы ⃑𝐹 и ⃑𝑟 существуют в трех измерениях, иногда он может быть полезен для 2-х мерные системы. Давайте посмотрим на один такой пример.
Пример 3: Нахождение перпендикулярного расстояния между двумя векторами силы, образующими Пара
Учитывая, что две силы ⃑𝐹 = −⃑𝑖 + 2⃑𝑗 и ⃑𝐹 действуют в двух точках (2,2) и (−2, −2) соответственно, чтобы образовать пару, найти перпендикулярное расстояние между двумя силами.
Ответ
Поскольку силы образуют пару, они должны быть в сумме 0. Для полноты мы можем использовать это, чтобы найти ⃑𝐹, однако это не требуется для достижения решения. ⃑𝐹 + ⃑𝐹 = 0⃑𝐹 = −⃑𝐹⃑𝐹 = ⃑𝑖 − 2⃑𝑗
Перпендикулярное расстояние между линиями действия ⃑𝐹 и ⃑𝐹 — это длина линии, перпендикулярной обеим. Мы можем определить это расстояние как 𝑑.
Момент пары можно найти по следующей формуле, где 𝐹 — величина любого из силы, 𝑑 — перпендикулярное расстояние между линиями действия сил, а знак момента обозначает направление вращения.𝑀 = ± 𝐹𝑑
Чтобы лучше понять нашу систему, мы можем переключиться на векторные обозначения и напомнить себе, где эта формула происходит от. Момент силы равен величине силы, умноженной на ее перпендикулярное расстояние от точки, вокруг которой снимается момент.
Представим себе моменты, связанные с точкой 𝐵. Поскольку в точке действует сила ⃑𝐹, определим вектор ⃑𝑟 как: ⃑𝑟 = 𝐵𝐴.
Определив 𝜃 как положительный острый угол между линией действия ⃑𝐹 и ⃑𝑟 мы можем выполнить полезное упрощение, используя геометрию прямоугольного треугольника.Здесь мы выразили перпендикулярное расстояние через величину ⃑𝑟 и угол 𝜃. 𝑑 = ‖‖⃑𝑟‖‖𝜃sin
Обратите внимание, что в этой конкретной системе мы находим расстояние 𝑑, которое является неотрицательным скаляром. Это означает, что нас не интересует знак в нашем уравнении, и, следовательно, направление вращения можно игнорировать.
Именно по этой причине мы можем определить 𝜃 как положительный острый угол, по сути, отбрасывая любые отрицательные решения. При этом мы упростили нашу систему до учитывайте только величину момента, которая может быть выражена как: ‖‖𝑀‖‖ = ‖‖⃑𝐹‖‖‖‖⃑𝑟‖‖𝜃 = ‖‖⃑𝐹‖‖𝑑.sin
Преобразование этого уравнения показывает, что если мы сможем найти величины момента и силы ⃑𝐹 мы сможем найти перпендикулярное расстояние 𝑑. 𝑑 = ‖‖𝑀‖‖‖‖⃑𝐹‖‖
В продолжение напомним, что момент пары можно найти с помощью векторного произведения. В качестве дополнительного бонуса, если мы вспомним определение перекрестного произведения, мы подтвердим нашу предыдущую логику, хотя мы не будем вдаваться в подробности здесь. 𝑀 = ⃑𝑟 × ⃑𝐹 = ‖‖⃑𝐹‖‖‖‖⃑𝑟‖‖𝜃⃑𝑛sin
Напомним, что мы, по сути, берем момент относительно точки.Это означает, что мы будем рассматривать силу ⃑𝐹 и вектор ⃑𝑟 определяется от точки 𝐵 до точки 𝐴. ⃑𝑟 = 𝐵𝐴 = (2,2) — (- 2, −2) = (4,4)
Стандартный метод для 3-х мерного векторного произведения включает в себя нахождение определителя матрицы 3 × 3, однако, поскольку ⃑𝐹 и ⃑𝑟 являются двумерными векторами, наши вычисления можно упростить. 𝑀 = ⃑𝑟 × ⃑𝐹 = 𝑟, 𝑟, 0 × 𝐹, 𝐹, 0 = 𝑟𝐹 − 𝑟𝐹⃑𝑘 = (4⋅2−4⋅ (−1)) ⃑𝑘 = (8 + 4) ⃑𝑘 = 12⃑𝑘
Теперь найдем величину 𝑀 и ⃑𝐹. ‖‖𝑀‖‖ = ‖‖12⃑𝑘‖‖ = 12‖‖⃑𝐹‖‖ = ‖‖ − ⃑𝑖 + 2⃑𝑗‖‖ = (−1) + 2 = √5
И, наконец, у нас есть все компоненты, необходимые для нахождения расстояния 𝑑.𝑑 = ‖‖𝑀‖‖‖‖⃑𝐹‖‖ = 12√5 = 12√55
Это перпендикулярное расстояние между линиями действия сил в паре.
Несколько пар могут воздействовать на тело одновременно. Когда несколько пар действуют на тело, результирующий момент, связанный с парами, является суммой моментов, создаваемых парами. Давайте посмотрим на пример с участием нескольких пар.
Пример 4: Анализ системы четырех сил, действующих на горизонтальный стержень, эквивалентный паре
𝐴𝐵 — горизонтальный световой стержень, имеющий длина 60 см, где действуют две силы величиной 45 Н каждая. вертикально на 𝐴 и 𝐵 в двух противоположных направлениях.Две другие силы, каждая магнитудой 120 Н, действуют в двух противоположных направлениях. направления в точках 𝐶 и 𝐷 стержня, где 𝐶𝐷 = 45см. Если они образуют пару, эквивалентную паре, образованной первыми двумя силами, найдите меру угла наклона, который две вторые силы образуют со стержнем.
Ответ
Пара 𝑐 образована силами, которые действуют в, а given задается формулой 𝑐 = — (45 × 60) ⋅.Ncm
Пара 𝑐, образованная силами, действующими на 𝐶 и 𝐷 задается 𝑐 = — (120𝜃 × 45) ⋅.sinNcm
В вопросе указано, что пары эквивалентны, поэтому 𝑐 = 𝑐.
Угол 𝜃 находится перестановкой: (45 × 60) = (120𝜃 × 45) 60120 = 𝜃𝜃 = 30.sinsin∘
Ключевые моменты
- Пара — это пара сил, которые имеют параллельные и четкие линии действия и равные величины, но противоположные направления.
- Момент, связанный с парой, определяется выражением 𝑀 = ± 𝐹𝑑𝜃sin, где 𝐹 — величина любой из сил в паре, 𝑑 — длина линии, соединяющей точки, из которых действуют силы, и 𝜃 — это угол между ⃑𝐹 и этой линией.
- Величина момента пары определяется как | 𝑀 | = 𝐹𝐿, где 𝐹 — величина либо сил, а 𝐿 — рука пары.
- Момент пары можно найти с помощью векторного произведения. 𝑀 = ⃑𝑟 × ⃑𝐹
- Для пары, образованной двумя силами; ⃑𝐹 действующий в точке 𝐴 и ⃑𝐹 действующий в точке 𝐵: 𝑀 = 𝐵𝐴 × ⃑𝐹 = 𝐴𝐵 × ⃑𝐹
- Несколько пар могут воздействовать на тело одновременно. Когда несколько пар действуют на тело, результирующий момент из-за пары — это сумма моментов, связанных с парами.
Определение пар сил взаимодействия
Согласно третьему закону Ньютона, для каждой действующей силы существует равная (по величине) и противоположная (по направлению) сила противодействия. Силы всегда приходят парами — известными как «пары сил действие-противодействие». Идентификация и описание пар сил действие-противодействие — это простой вопрос идентификации двух взаимодействующих объектов и создания двух утверждений, описывающих , кто на кого толкает, и в каком направлении.Например, рассмотрим взаимодействие между бейсбольной битой и бейсбольным мячом.
Бейсбол толкает биту влево; бита толкает мяч вправо. Вместе эти две силы, действующие на два разных объекта, образуют пару сил действие-противодействие. Обратите внимание, что в описании двух сил существительные в предложении, описывающем силы, просто меняются местами.
Рассмотрим следующие три примера. Описана одна из сил во взаимном взаимодействии; описать другую силу в паре сил действие-противодействие.Нажмите кнопку, чтобы просмотреть ответ.
Бейсбол сдвигает перчатку влево.
Шар для боулинга толкает штифт влево.
Закрытые частицы воздуха выталкивают стенку воздушного шара наружу.
Проверьте свое понимание
1.Рассмотрим взаимодействие, изображенное ниже между ступней A, мячом B и ступней C. Три объекта взаимодействуют одновременно (в одно и то же время). Определите две пары сил действия-противодействия. Используйте в своих утверждениях обозначения «ступня A», «ступня C» и «мяч B». Нажмите кнопку, чтобы просмотреть ответ.
2. На следующей диаграмме обозначьте как минимум шесть пар сил действие-противодействие.
(решено) — Определите момент, связанный с парой сил 400-Н … — (1 ответ)
Заключения Верховного суда Калифорнии доступны на ряде веб-сайтов, в том числе…
Мнения Верховного суда Калифорнии доступны на нескольких веб-сайтах, в том числе http://www.courtinfo.ca.gov/. 26 мая 2009 г. Верховный суд Калифорнии вынес решение по делу Штраус против Хортона, 207 P.3d 48 (Cal. 2009). Дело содержало три …
Опубликовано 4 дня назад1.Было ли постановление судьи Стампа судебным актом? Объяснять. 2. Судебная неприкосновенность снова была проверена в …
1. Было ли постановление судьи Стампа судебным актом? Объяснять. 2. Судебная неприкосновенность снова была проверена в Верховном суде США в 1988 г. в деле Forrester v. White, 108 S. Ct. 538, в котором судья Уайт уволил женщину-офицера службы пробации…
Опубликовано 4 дня назад1.Юридическая школа Уошберна поддерживает известный веб-сайт Washlaw Web, доступный по адресу …
1. Юридическая школа Уошберна поддерживает хорошо известный веб-сайт Washlaw Web, доступный по адресу http://www.washlaw.edu/. Используйте этот веб-сайт для доступа к информации о федеральных агентствах и федеральных постановлениях.
Опубликовано 4 дня назадОднополые браки — горячая тема, поскольку государства рассматривают эту тему в соответствии с положениями штата…
Однополые браки — горячая тема, поскольку штаты рассматривают эту тему в соответствии с положениями конституций штатов, законодательными актами и прецедентным правом. Много информации об однополых браках доступно на http://www.freedomtomarry.org/. Используя этот сайт, …
Опубликовано 4 дня назад1.Почему коммунальные предприятия подчиняются регулирующим органам? 2. Какую особую роль может выполнять помощник юриста ..
1. Почему коммунальные предприятия подчиняются регулирующим органам? 2. Какую особую роль может играть помощник юриста в административном праве, чего нет в делах частного права? 3. Откуда взялась «презумпция возможности проверки»? 4.Какие…
Опубликовано 4 дня назад1.Что определяет, является ли государственное агентство независимым регулирующим органом? 2. Почему …
1. Что определяет, является ли государственный орган независимым регулирующим органом? 2. Почему курсы административного права сосредоточены почти исключительно на административных процедурах? 3.Каков законный источник полномочий для федеральных …
Опубликовано 4 дня назадЗаключения Верховного суда Коннектикута доступны на ряде веб-сайтов, в том числе.
Заключения Верховного суда Коннектикута доступны на нескольких веб-сайтах, включая http://www.jud.ct.gov/. 28 октября Верховный суд Коннектикута постановил, что Керриган против Комиссара общественного здравоохранения, 957 A.2d 407 (Коннектикут, 2008 г.) …
Опубликовано 4 дня назад1.Когда возможен устный аргумент в нормотворчестве § 553? 2. Может ли человек подать в суд на город в возрасте до 42 лет США. §
1. Когда возможен устный аргумент в нормотворчестве § 553? 2. Может ли человек подать в суд на город до 42 лет США? § 1983? 3. Зачем нам административное право? 4. Должны ли решения государственных органов быть пересмотрены в суде?
Опубликовано 19 часов назад1.Какую информацию не предоставила компания «Юнистар»? 2. Почему суд решил, что комиссия была.
1. Какую информацию не предоставила компания «Юнистар»? 2. Почему суд счел, что комиссия действовала в соответствии с правилами, а Unistar не оспаривала эти правила? 3.Может ли город через своих избранных представителей отменить полицию …
Опубликовано 4 дня назад1.Согласованы ли эти два случая? 2. Был ли судья мотивирован политическими соображениями? Объяснять..
1. Согласованы ли эти два случая? 2. Был ли судья мотивирован политическими соображениями? Поясните свой ответ. 3. Почему суд указал, что комиссия разбила общественные слушания на четыре заседания, которые проходили в течение нескольких месяцев, и детали…
Опубликовано 4 дня назадрычагов — повествование о физике | IOPSpark
Силы и движение
Повествование о физике для 11-14
Стабильность
Устойчивость может быть связана с действием сил поворота.Вот как это сделать.
Размышление о поворачивающем эффекте силы также может пролить свет на то, почему одни вещи стабильны, а другие нет. Наклоните игрушечный строительный кирпич вдоль одной из его длинных сторон, затем отпустите. Как далеко вы можете наклонить его, чтобы он не вернулся в исходное положение?
Повторите попытку с более длинной стороной.
Падение
Простая и полезная мера устойчивости — это максимальный угол, на который вы можете наклонить что-либо, когда оно вернется в исходное состояние после того, как вы отпустите его.Если вы наклоните объект только на небольшую величину, сила тяжести, действующая на объект, все равно вернет его в исходное положение. Однако, если вы наклонитесь больше определенного угла, сила тяжести теперь поворачивает объект в новое положение. Объект больше не будет падать на основание, а теперь будет падать на бок.
Подумайте об этих ситуациях для трех автомобилей, просматриваемых с конца. Какой из автомобилей перевернется?
Центр масс
Полезный способ взглянуть на этот вопрос — сказать, что вещи стабильны, пока их центр масс (через который действует сила тяжести, действующая на объект) находится в пределах их следа
.
Если объект наклоняется и линия действия силы тяжести выходит за пределы его отпечатка, объект опрокидывается.
Итак, центр масс объекта связан с вращающим действием сил.
Попробуйте протолкнуть книгу по гладкому столу, не заставляя книгу вращаться. У вас получилось? Затем вы указываете на центр масс. Попробуйте еще раз подтолкнуть край под прямым углом к первому. Если вам удастся выполнить еще один успешный акт наведения, то центр тяжести книги окажется на линии, где эти две точки пересекаются.Это должна быть линия, потому что книга трехмерная, и вам нужно будет провести измерение по третьей оси, чтобы выбрать, где на этой линии находится точка, являющаяся центром масс.
Этот центр масс — особое место для книги. Ранее в этом разделе вы работали с силами, действующими только вдоль одной линии. Если силы заставляют объект двигаться без вращения, то эта линия должна проходить через центр масс. Поэтому, когда мы упрощаем мир до сил, действующих на точечные частицы, точки должны находиться в центре масс объектов, которые они представляют.
Центр масс книги — это место, где частица, представляющая всю книгу, свернулась в одну точку.
Момент пары — Вопросы и ответы по инженерной механике
Этот набор вопросов и ответов по инженерной механике с множественным выбором (MCQ) посвящен теме «Момент пары».
1. Пара имеет сочетание двух сил.Они разные по величине.
a) Верно
b) Неверно
Посмотреть ответ
Ответ: b
Пояснение: Пара представляет собой комбинацию двух сил одинаковой величины. Они действуют в одном направлении вращения. То есть они действуют в противоположном направлении, но дают телу вращение в том же направлении. Будь то по часовой стрелке или против часовой стрелки.
2. Определите момент пары, действующий на показанную балку.
а) 500 Нм
б) 1500 Нм
в) 740 Нм
г) 50 Нм
Посмотреть ответ
Ответ: с
Пояснение: Поскольку мы знаем, что момент — это векторная величина, их суммирование требует векторной математики.Момент пары тоже такой же. То есть они тоже векторы и требуют векторной математики. Таким образом, результирующий момент пары является векторной суммой различных пар, действующих в теле.
3. Расстояние между силами, действующими в паре, составляет ____________
a) Бесконечность
b) Ноль
c) Конечное расстояние
d) Круговая петля
Посмотреть ответ
Ответ: c
Пояснение: Расстояние между силами действующая в паре имеет конечное расстояние.Пара — это комбинация двух сил, действующих в одном направлении вращения. То есть они действуют в противоположном направлении, чтобы обеспечить вращение в том же направлении.
4. Результирующая сила, действующая в паре, равна _________
a) Нулевая
b) Бесконечная
c) Удвоенная величина одиночной силы
d) Половина величины одиночной силы
Посмотреть ответ
Ответ: a
Объяснение : Результирующая силы, действующей на пару, всегда равна нулю.Поскольку силы действуют в противоположных направлениях. Итак, если мы сложим силы алгебраически, то сумма будет равна нулю. Или, другими словами, они отменяют друг друга.
5. Мужчина едет в машине. Он ведет машину. Если он поворачивает на дороге. Он прилагает силу к рулевому колесу, удерживая его обеими руками. Рулевое колесо сталкивается с моментом силы.
a) Верно
b) Неверно
Посмотреть ответ
Ответ: b
Объяснение: Человек пытается повернуть колесо, применяя силу.Усилие прилагается к рулевому колесу. Которая вращает колесо, но это момент пары. Поскольку человек держал колесо обеими руками, значит, это не момент силы.
6. Что из следующего верно для момента пары M, вызванного двумя силами одинаковой величины F, разделенными расстоянием r?
a) M = rxF
b) M = r.F
c) M = — (rxF)
d) M = — (r.F)
Посмотреть ответ
Ответ: a
Объяснение: Ответ M = rxF.Момент — это произведение расстояния и сил. Это направление, определяемое сгибанием руки. Большой палец показывает направление момента. А движение пальца, то есть вращение, дает направление вращения, вызванное силами.
7. Момент пары — это вектор _______.
a) Градиент
b) Скаляр
c) Del
d) Бесплатно
Посмотреть ответ
Ответ: d
Пояснение: Пара моментов — это свободный вектор. Он может действовать где угодно между силами.В паре действуют две силы, действующие в противоположных направлениях. Эти силы разделены, скажем, расстоянием r, тогда вызываемый ими момент может действовать где угодно между этими силами.
8. Определите момент пары, действующий на показанную балку.
a) 20KNm
b) 21KNm
c) 22KNm
d) 19KNm
Посмотреть ответ
Ответ: a
Объяснение: Поскольку мы знаем, что момент — это векторная величина, их суммирование требует векторной математики. Момент пары тоже такой же.То есть они тоже векторы и требуют векторной математики. Таким образом, результирующий момент пары является векторной суммой различных пар, действующих в теле.
9. Что из перечисленного верно?
a) Момент пары зависит от оси вращения
b) Момент пары напрямую зависит от радиус-вектора сил
c) Момент пары зависит только от вектора расстояния между силами
d) Дано направление момента пары по правилу левой руки
Посмотреть ответ
Ответ: c
Пояснение: Момент пары зависит только от вектора расстояния между силами.Радиус-вектор сил не делает пару зависимой от него. Но вектор расстояния определяется путем вычитания радиус-векторов сил. Это означает, что момент пары не зависит напрямую от радиус-вектора сил.
10. Если силы, действующие на пару, имеют одинаковое направление, то есть они не имеют противоположного направления, как всегда, тогда?
a) Направление сил не определяет момент
b) Момент пары будет максимальным
c) Пара невозможна
d) Никаких изменений не происходит
Посмотреть ответ
Ответ: c
Пояснение: Силы в этот момент всегда в противоположном направлении.Но если они не будут вести себя одинаково, то есть меняют направление и выравниваются в одном направлении, пара невозможна.
11. Определите момент пары, действующий на показанную трубу.
а) -130 Нм
б) 130 Нм
в) -120 Нм
г) 120 Нм
Посмотреть ответ
Ответ: а
Объяснение: Поскольку мы знаем, что момент — это векторная величина, их суммирование требует векторной математики. Момент пары тоже такой же. То есть они тоже векторы и требуют векторной математики.Таким образом, результирующий момент пары является векторной суммой различных пар, действующих в теле.
12. Результирующий момент пары равен ____________ сумме различных пар, действующих на тело.
a) Векторная
b) Скалярная
c) Скалярная тройная
d) Точка
Посмотреть ответ
Ответ: a
Объяснение: Поскольку мы знаем, что момент — это векторная величина, их суммирование требует векторной математики. Момент пары тоже такой же. То есть они тоже векторы и требуют векторной математики.Таким образом, результирующий момент пары является векторной суммой различных пар, действующих в теле.
13. Определите момент пары, действующий на показанную треугольную плоскость.
a) 1600 Нм
b) 100 Нм
c) 2600 Нм
d) 600 Нм
Посмотреть ответ
Ответ: c
Пояснение: Нет.
14. Если две силы величиной F каждая действуют в декартовой системе координат и действуют в точках A (3,3) и B (-3,3). Они движутся в отрицательном направлении z и положительном направлении z соответственно.Расстояние между ними задается как r. Радиус-векторы силы в точках A и B равны Ra и Rb соответственно. Тогда момент задается как:
a) (Ra-Rb) .F
b) (Rb-Ra) .F
c) (Ra-Rb) xF
d) (Rb-Ra) xF
Посмотреть ответ
Ответ: d
Пояснение: Как мы знаем, момент пары — это произведение силы и расстояния между ними. Но в этом случае нам заданы радиус-векторы сил. Итак, когда мы применяем векторную математику, чтобы найти расстояние между силами, мы получаем, что расстояние r = Rb-Ra.Теперь, когда у нас есть расстояние, мы пересекаем его с силой.
15. Определите момент пары, действующий на показанную трубу.
a) 108j + 144k Нм
b) -108j + 144k Nm
c) 108j — 144k Nm
d) -108j — 144k Nm
Посмотреть ответ
Ответ: a
Объяснение: Как мы знаем, момент — это векторная величина , их суммирование требует векторной математики. Момент пары тоже такой же. То есть они также являются векторами и требуют векторной математики. Таким образом, результирующий момент пары является векторной суммой различных пар, действующих в теле.
Sanfoundry Global Education & Learning Series — Инженерная механика.
Чтобы практиковать все области инженерной механики, представляет собой полный набор из 1000+ вопросов и ответов с несколькими вариантами ответов .
Примите участие в конкурсе сертификации Sanfoundry, чтобы получить бесплатную Почетную грамоту. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!
Конференция по строительному бизнесу и технологиям
Конференция по строительному бизнесу и технологиям — Основы поперечных стенПереворачивание
Когда приложенная нагрузка мала, опрокидывающий момент мала, и склонность стены к опрокидыванию мала.Может быть что вес самой стеновой панели уравновешивает систему без необходимость дополнительных подключений. Способность стены противостоять опрокидыванию рассчитывается аналогично опрокидывающему моменту путем сложения суммы вес стены на удалении от общей точки опрокидывания. Этот вес на расстоянии создает момент, в частности, сопротивляется момент . Один момент хочет толкнуть стену, другой сопротивляется Это.
| Основная стенка, работающая на сдвиг Схема | |
| Этот первый пример предназначен для стен с низкой нагрузкой на сдвиг.
без учета материала , действительно устойчивого к сдвигу. |
Mot = Момент перелома. Это значение включает все нагрузки, которые хотят толкнуть стену по часовой стрелке относительно в положение контрольной точки.Мистер = Момент сопротивления. Это значение включает все нагрузки, которые хотят толкнуть стену против часовой стрелки относительно в точку отсчета.
| Результирующие силы | |
| Треугольная силовая пара является результатом поперечного
нагрузки, приложенные на расстоянии над контрольной точкой (см. также внизу страницы). Равномерная горизонтальная сила сжатия представляет собой
вес стены Две диаграммы сил можно сложить вместе, чтобы получить
распределение |
Для боковых нагрузок (треугольная пара сил)…
Mot = (Vroof * H) + (Vwall * H / 2)
Для вертикальных нагрузок (прямоугольная сила) …
Mr = (Общий вес * л / 2)
И наконец…
«a» = (Mr-Mot) / (Общий вес)макс. комп. = (2/3) * (Общий вес / год)
| Альтернативный результат | |
| Когда «a» больше, чем (L / 3), следующие формулы
следует использовать : макс.комп. = (4L-6a) (Ш / (Д * Д)) |
Поначалу треугольная схема загрузки может сбивать с толку. Может быть полезно посмотреть на аналогичный результат в знакомой системе …
| Изгиб балки | |
| Сечение балки выше показывает силы, которые
от приложенных нагрузок, вызывающих изгиб балки.Силы натяжения возникают из-за растяжения древесных волокон на стороне, противоположной приложенным нагрузкам. Сжимающие силы создаются волокнами, которые прижимаются друг к другу на нагруженной стороне. Эта согласованная и противоположная пара треугольных сил являются типичным результатом для материалов, подвергаемых изгибу. |
«Изгибающий момент» в балке равен сумме силы сжатия и растяжения, умноженные на расстояние до центральной линии луч.
МОМЕНТ = [(глубина / 2) * (2/3)] * [(макс. сила) * (глубина / 2) * (1/2)] * [2]
- [(глубина / 2) * (2/3)] = моментный рычаг
- [(макс. Сила) * (глубина / 2) * (1/2)] = общая сила
- [2] = два треугольника
Coplanar Force — обзор
Поскольку тело жесткое и внутренняя виртуальная работа, следовательно, равна нулю, мы можем рассматривать тело как большую частицу.Отсюда следует, что если тело находится в равновесии под действием набора сил, F 1 , F 2 , … , F k , … , F r , общая виртуальная работа, выполняемая внешними силами во время произвольного виртуального перемещения тела, равна нулю.
Принцип виртуальной работы, по сути, является альтернативой формуле. (2.10) для задания необходимых условий равновесия системы компланарных сил.Чтобы проиллюстрировать это, мы рассмотрим расчет опорных реакций в некоторых простых балках.
Пример 15.1Рассчитайте опорные реакции в консольной балке, показанной на рис. 15.4 (а).
Рисунок 15.4. Луч Ex. 15.1.
Сосредоточенная нагрузка W вызывает вертикальную реакцию R A , а также момент M A в A. Предположим, что балке дано небольшое воображаемое, т.е. виртуальный, вращение, θ v, A , в точке A, как показано на рис.15.4 (б). Поскольку здесь нас интересуют только внешние силы, мы можем рассматривать балку как твердое тело, так что балка остается прямой, а B смещается к B ‘. Вертикальное смещение B, Δ v, B , тогда определяется как
Δv, B = θv, AL
или(i) θv, A = Δv, B / L
Общая виртуальная работа, Вт. t , создаваемое всеми силами, действующими на балку, определяется как
(ii) Wt = WΔv, B − MAθv, A
Обратите внимание, что вклад M A в общую виртуальную работу равен отрицательное, поскольку предполагаемое направление M A противоположно виртуальному смещению, θ v, A .Также обратите внимание, что в точке A нет линейного движения балки, поэтому R A не работает. Подставляя в уравнение. (ii) для θ v, A из уравнения. (i) имеем
(iii) Wt = WΔv, B − MAΔv, B / L
Поскольку балка находится в равновесии, W t = 0 из принципа виртуальной работы. Следовательно,
0 = WΔv, B — MAΔv, B / L
, так чтоMA = WL
, что является результатом, который был бы получен при рассмотрении моментного равновесия балки относительно A.Предположим теперь, что всей балке задано виртуальное смещение Δ v , как показано на рис. 15.4 (c). Вращение балки отсутствует, поэтому M A не работает. Общая проделанная виртуальная работа тогда равна
(iv) Wt = WΔv − RAΔv
Вклад R A отрицателен, поскольку его направление противоположно направлению Δ v . Балка находится в равновесии, так что W t = 0. Следовательно, из уравнения.(iv)
RA = W
, что является результатом, который мы получили бы при разрешении сил по вертикали. Пример 15.2Рассчитайте опорные реакции в консольной балке, показанной на рис. 15.5 (a).
Рисунок 15.5. Луч Ex. 15.2.
В этом случае мы получаем решение, одновременно задавая балке виртуальное смещение, Δ v, A , в точке A и виртуальное вращение, θ v, A , в точке A . Полное отклонение в точке B тогда составляет Δ v, A + θ v, A L , а на расстоянии x от A составляет Δ v, A + θ v, A x .Поскольку балка несет равномерно распределенную нагрузку, мы находим виртуальную работу, выполняемую нагрузкой, сначала рассматривая элементную длину, δ x , нагрузки на расстоянии x от A. Нагрузка на элемент составляет w δ. x , а виртуальная работа, выполняемая этой элементарной нагрузкой, равна
δW = wδx (Δv, A + θv, Ax)
Общая виртуальная работа, выполненная на балке, тогда составляет
Wt = ∫0Lw (Δv, A + θv, Ax) dx − MAθv, A − RAΔv, A
, который упрощается до(i) Wt = (wL − RA) Δv, A + [(wL2 / 2) −MA] θv, A = 0
, поскольку балка находится в равновесии.Уравнение (i) действительно для всех значений Δ v, A и θ v, A , так чтоwL − RA = 0 и (wL2 / 2) −MA = 0
Следовательно,
RA = wLandMA = wL2 / 2
, которые являются результатами, которые были бы получены при разрешении сил по вертикали и принятии моментов около A. Пример 15.3Рассчитайте реакции на встроенном конце консольной балки, показанной на рис. 15.6.
Рисунок 15.6. Луч Ex. 15.3.
В этом примере нагрузка W вызывает реакции вертикальной силы, момента и крутящего момента на встроенном конце.Вертикальная реакция и момент такие же, как в Пр. 15.1. Чтобы определить реакцию крутящего момента, мы налагаем небольшое виртуальное смещение Δ v, C , вертикально вниз в точке C. Это заставляет балку AB вращаться как твердое тело на угол, θ v, AB , который равен задается формулой
(i) θv, AB = Δv, C / a
В качестве альтернативы мы могли бы наложить небольшое виртуальное вращение, θ v, AB , на балку, которое привело бы к виртуальному смещению C равно aθ v, AB : очевидно, что оба подхода дают идентичные результаты.
Общая виртуальная работа, проделанная с балкой, тогда определяется как
(ii) Wt = WΔv, C − TAθv, AB = 0
, поскольку балка находится в равновесии. Подставляя θ v, AB в уравнении. (ii) из уравнения. (i) у нас естьTA = Wa
, что является результатом, который был бы получен с учетом статического равновесия балки. Пример 15.4Рассчитайте опорные реакции в балке без опоры, показанной на рис. 15.7.
Рисунок 15.7. Использование принципа виртуальной работы для расчета опорных реакций.
К балке прикладывается только вертикальная нагрузка, поэтому возникают только вертикальные реакции, R A и R C .
Предположим, что лучу в точке C задано небольшое воображаемое, то есть виртуальное смещение, Δ v, C , в направлении R C , как показано на рис. 15.7 (b). Поскольку здесь нас интересуют исключительно внешние силы , действующие на балку, мы можем рассматривать балку как твердое тело.Таким образом, луч вращается вокруг A, так что C перемещается в C ‘, а B перемещается в B’. Из аналогичных треугольников мы видим, что
(i) Δv, B = aa + bΔv, C = aLΔv, C
Затем задается общая виртуальная работа, W t , выполненная всеми силами, действующими на балку. by
(ii) Wt = RCΔv, C − WΔv, B
Обратите внимание, что работа, выполняемая нагрузкой, W , отрицательна, поскольку Δ v, B находится в направлении, противоположном его линии действия. Также обратите внимание, что опорная реакция R A не работает, поскольку луч вращается только вокруг A.Теперь заменяя Δ v, B в уравнении. (ii) из уравнения. (i) имеем
(iii) Wt = RCΔv, C − WaLΔv, C
Поскольку луч находится в равновесии, W t равно нулю из принципа виртуальной работы. Следовательно, из уравнения. (iii)
RCΔv, C − WaLΔv, C = 0
, что даетRC = WaL
, что является результатом, который был бы получен при рассмотрении моментного равновесия балки около A. R A следует аналогичным образом. Предположим теперь, что вместо одиночного смещения Δ v, C всей балке дается виртуальное вертикальное смещение Δ v вместе с виртуальным вращением, θ v , примерно на A, как показано на рис.

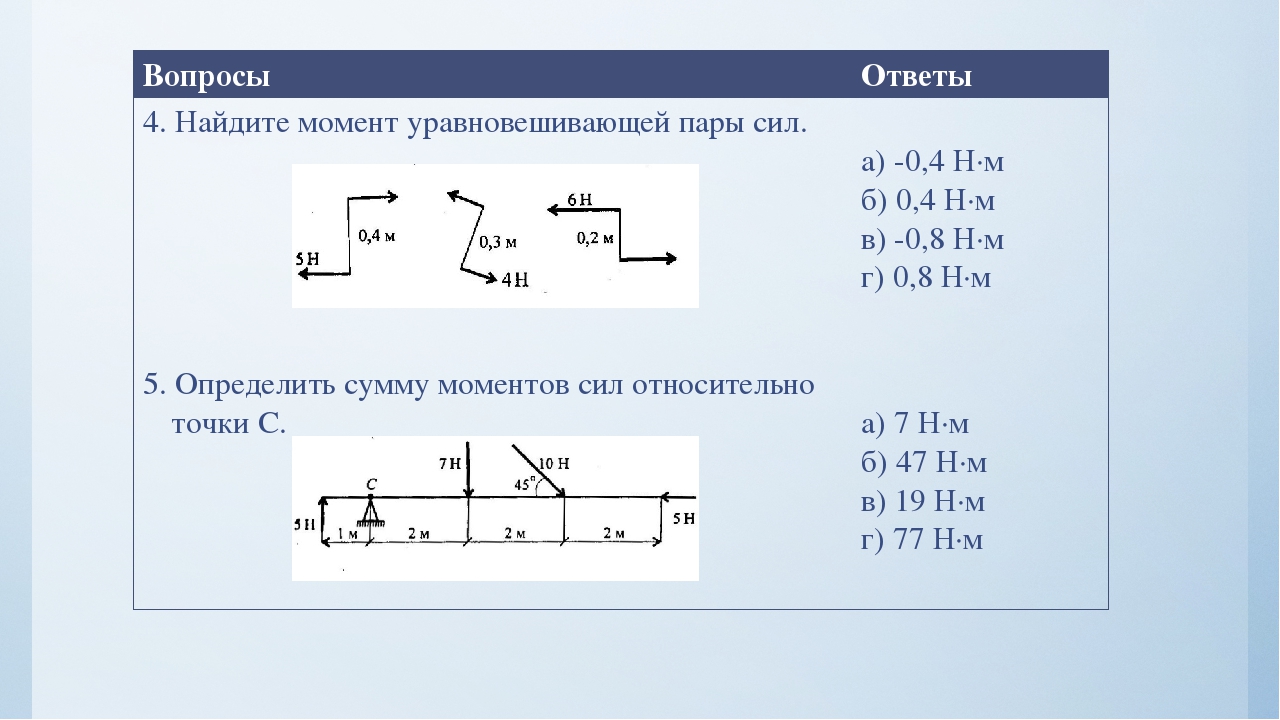

 Аксиома инерции. Под действием взамно-уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно.
Аксиома инерции. Под действием взамно-уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно.
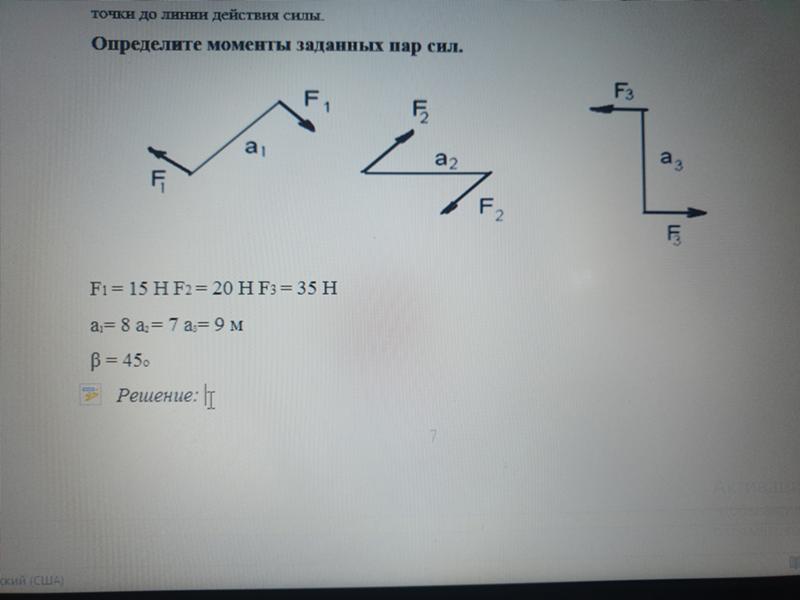 2)
2)