Алгебра свободных и скользящих векторов

Алгебра свободных и скользящих векторов

Меркин Д.Р. Алгебра свободных и скользящих векторов. М: изд-во «Физматгиз», 1962 — 165 с. В книге дается подробное изложение алгебры свободных и скользящих векторов. Содержание первой главы соответствует в основном программе по векторной алгебре курса высшей математики втузов. Во второй главе рассматривается теория преобразования системы скользящих векторов и приведения их к простейшему виду. Эта теория имеет важное значение в различных вопросах физики и техники; она может рассматриваться также, как вводная глава винтового исчисления. В книге большое внимание уделено примерам и разъяснению некоторых деталей и особенностей векторного исчисления, весьма важных в приложениях. Книга может служить учебным пособием для студентов и преподавателей втузов и университетов. Она рассчитана также на инженеров, желающих повысить свою теоретическую подготовку. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА 2. Определение вектора. 3. Классификация векторов. 4. Равенство векторов. 5. Перенос вектора. 6. Нуль-вектор. 7. Компланарность и коллинеарность векторов. 8. Прямопротивоположные векторы. § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ 2. Сумма векторов. 3. Свойства суммы векторов. 4. Правила параллелограмма и параллелепипеда. 5. Разность двух векторов. 6. Свойства модуля суммы векторов. § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО 2. Свойства произведения. 3. Деление вектора на число. 4. Единичные векторы. 5. Орт оси. 6. Коллинеарность двух векторов. § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ 3. Разложение вектора по трем другим векторам. 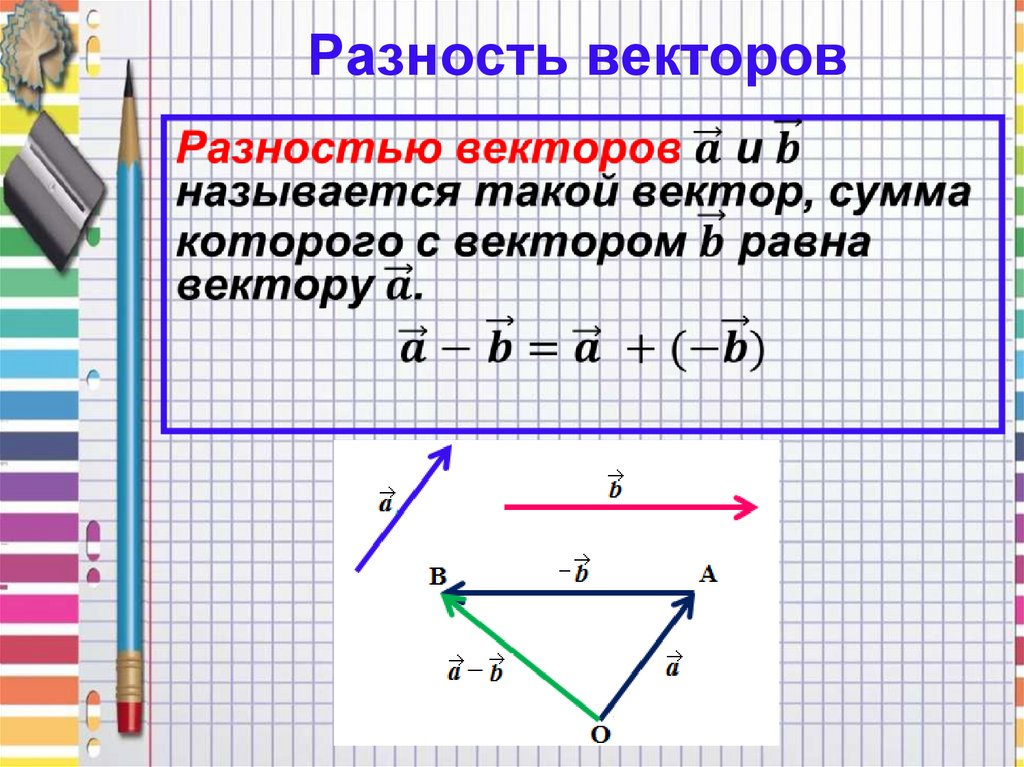4. Разложение вектора по ортам базиса. § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ 2. Условие коллинеарности двух векторов. 3. Условие компланарности трех векторов. 4. Линейная зависимость четырех векторов. § 6. ПРОЕКЦИИ ВЕКТОРА 2. Свойства составляющих вектора. 3. Проекция вектора на ось. 4. Свойства проекций. 5. Угол между векторами. 6. Вычисление проекций вектора. 7. Теорема о проекции сумммы векторов. 8. Псевдоскаляры. § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА 2. Естественный способ задания свободного вектора. 3. Задание свободного вектора с помощью его проекций (координатный метод). 4. Связь между естественным и координатным способами задания вектора. 5. Задание несвободного вектора. 6. Задание скользящего вектора. 7. Некоторые приложения. § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ 2. Свойства скалярного произведения. 3. Выражение скалярного произведения через проекции векторов. 4. Векторные уравнения геометрических мест. 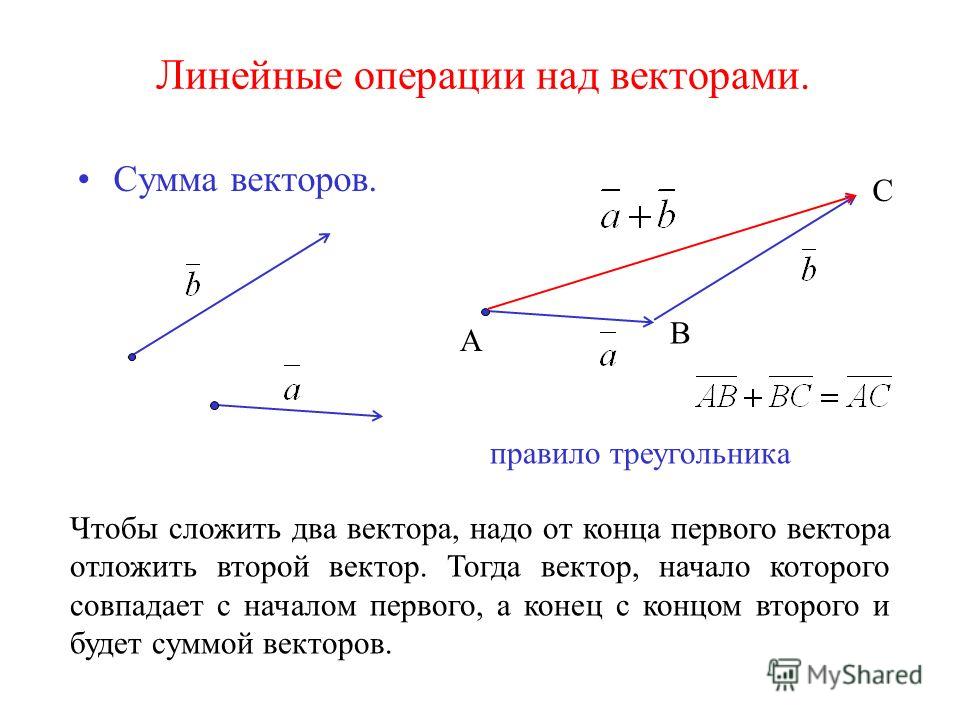5. Уравнение плоскости. 7. Изменение проекций вектора при преобразовании координат. 8. Другое определение вектора. § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ 2. Примеры из физики. 3. Способ Н. Е. Жуковского построения векторного произведения. 4. Свойства векторного произведения. 5. Разложение вектора-произведения по координатным ортам. 6. Условие коллинеарности двух векторов. 7. Тождество Лагранжа. 8. Полярные и аксиальные векторы. § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 2. Двойное векторное произведение. 3. Разложение вектора по трем другим векторам. 4. Скалярное произведение двух векторных произведений. 5. Векторное произведение двух векторных произведений. 6. Произведение двух смешанных произведений. 7. Взаимные реперы. § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ 2. Уравнение прямой, проходящей через две заданные точки. 3. Плюкерово уравнение прямой в пространстве. 4. Прямая как пересечение двух плоскостей. § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ ГЛАВА II. 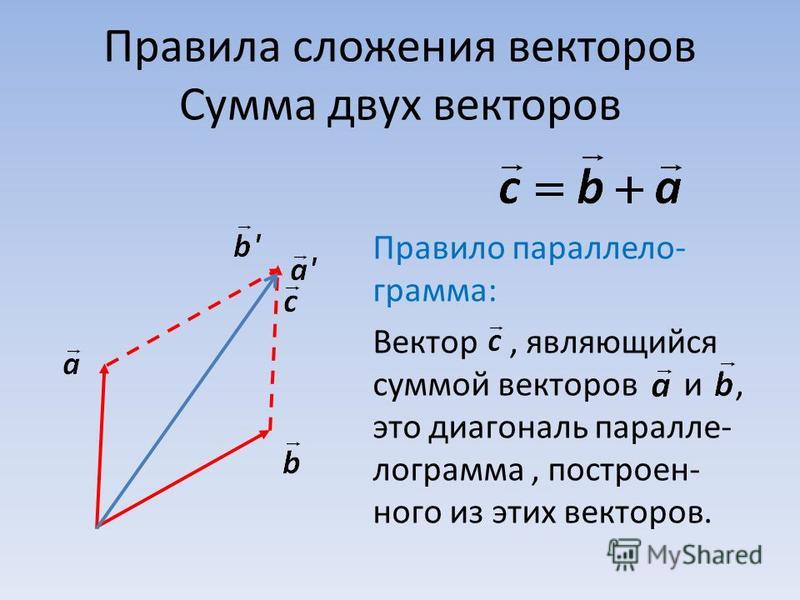АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА 2. Момент вектора относительно точки. 3. Проекции момента. 4. Момент вектора относительно оси. 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей. § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ 2. Главный вектор системы векторов. 3. Главный момент системы векторов. 4. Система двух равнопротивоположных векторов. 5. Первая теорема Вариньона. 6. Изменение главного момента с изменением полюса. 7. Инварианты системы векторов. 8. Минимальный момент и центральная ось системы. 9. Распределение главных моментов в пространстве. 10. Понятие о винте. 11. Винт системы векторов. § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ 2. Основные определения и аксиомы. § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ 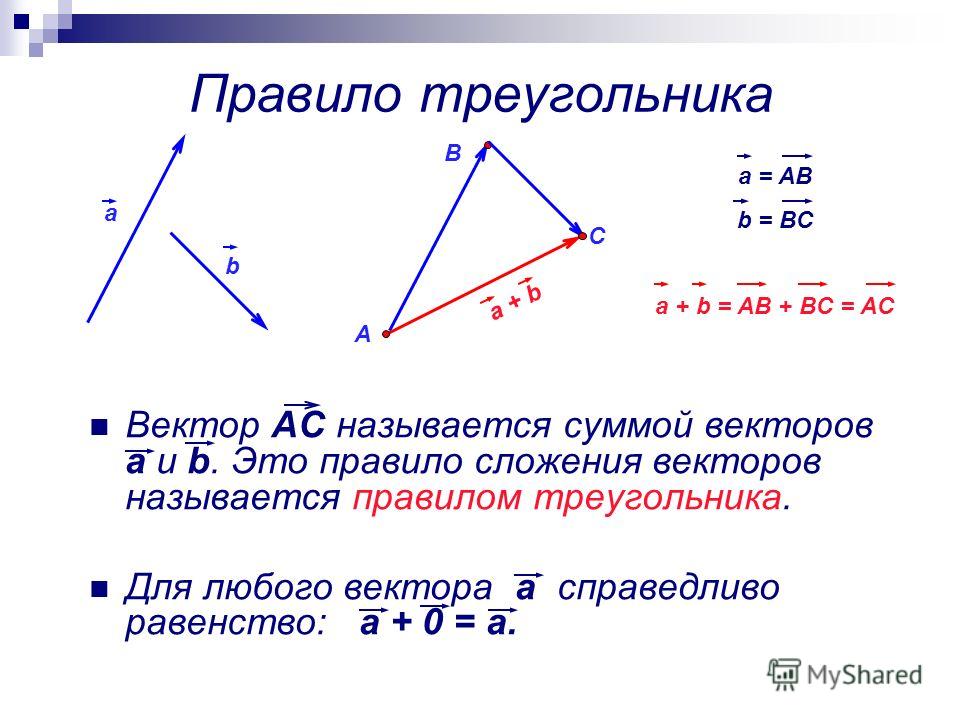2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение). § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Условия эквивалентности двух систем скользящих векторов. 3. Преобразование эквивалентных систем. § 19. ТЕОРИЯ ПАР 1. Пара векторов и ее момент. 2. Свойства пар. 3. Винт § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение). 3. Приведение системы скользящих векторов к вектору и паре. 4. Пример из кинематики. 5. Приведение системы скользящих векторов к винту. 6. Примеры. 7. Уравнения равновесия векторов. 8. Вторая теорема Вариньона. § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ 2. Плоская система скользящих векторов. 3. Система параллельных скользящих векторов. 4. Центр системы параллельных векторов.

Может ли длина суммы двух ненулевых векторов быть равна длине разности этих векторов? Вопрос №10 к 4 главе, Геометрия, 10-11 класс, Атанасян Л.

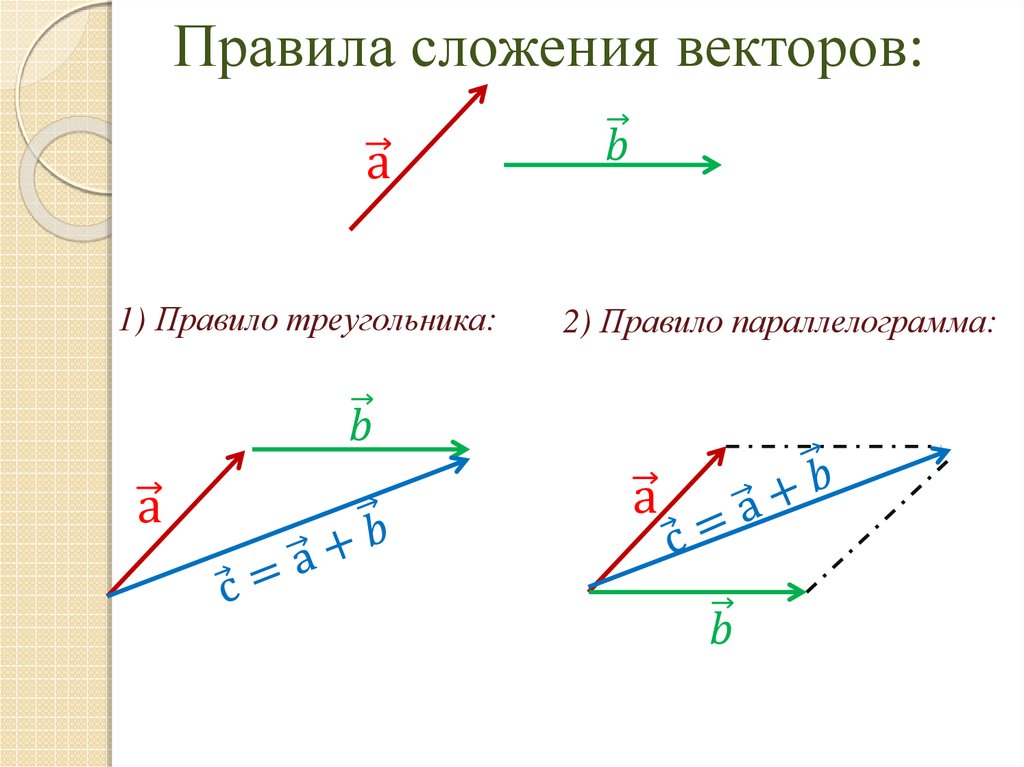С. Может ли длина суммы двух ненулевых векторов быть равна длине разности этих векторов? Вопрос №10 к 4 главе, Геометрия, 10-11 класс, Атанасян Л.С. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Может ли длина суммы двух ненулевых векторов быть равна длине разности этих векторов? — у кого какой ответ на этот вопрос к параграфу?

Лучший ответ

У меня такой
Пусть  коллинеарны. Для них сложение и вычитание производится как для обычных чисел,  а сумма двух ненулевых чи­сел не равна их разности. Рассмотрим особый случай, когда угол между векторами 

по свойству диагоналей прямоугольника.
Ответ: да.

еще ответы

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Юмор

Олимпиады

ЕГЭ

Компьютерные игры

похожие вопросы 5

Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.

Привет. Запуталась при решении, нужна помощь знатоков!!!
 
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)

ГДЗГеометрия11 класс10 классАтанасян Л.С.

Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос

Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
 

ГДЗЭкзаменыГеометрия9 классЗив Б. Г.

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь 

Новости10 классБезопасность

Какой был проходной балл в вузы в 2017 году?

Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее…)

Поступление11 классЕГЭНовости

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Замечание о нормах сумм векторов со знаком

Ключевые слова: Выпуклые тела; балансирующие векторы; подписанные суммы; гипотеза Комлоса; случайные вращения; гауссова мера; Вероятность малого мяча

1. Сообщение: М. Хенк

Благодарности

Мы хотели бы поблагодарить Апостолоса Яннопулоса за полезные обсуждения и анонимных рецензентов за их комментарии и ценные предложения, которые помогли улучшить представление результатов Эта статья.

Литература

[1] Артштейн-Авидан С., Яннопулос А., Мильман В.Д., Асимптотический геометрический анализ. Часть I , том 202 из Математические обзоры и монографии . амер. Мат. соц. 2015. MR3331351 Zbl 1337.5200110.1090/surv/202Search in Google Scholar

[2] В. Банащик, Балансирующие векторы и выпуклые тела. Студия Математики . 106 (1993), 93–100. MR1226426 Zbl 0810.4600910.4064/sm-106-1-93-100Поиск в Google Scholar

[3] В. Банащик, Балансирующие векторы и гауссовы меры n -мерных выпуклых тел. Алгоритмы случайных структур 12 (1998), 351–360. MR1639752 Zbl 0958.5200410.1002/(SICI)1098-2418(199807)12:4<351::AID-RSA3>3.0.CO;2-SПоиск в Google Scholar

[4] Н. Бансал, Д. Дадуш, С. Гарг, Алгоритм гипотезы Комлоша, согласующийся с границей Банащика. В: 57 -й ежегодный симпозиум IEEE по основам компьютерных наук — FOCS 2016, 788–79.9, IEEE Computer Soc., Los Alamitos, CA 2016. MR3631042 Zbl 0705139810.1109/FOCS.2016.89Search in Google Scholar

[5] I. Bárány, О силе линейных зависимостей. В: Строительство мостов , том 19 из Bolyai Soc. Мат. Stud ., 31–45, Springer 2008. MR2484636 Zbl 1160.1500110.1007/978-3-540-85221-6_1Search in Google Scholar

[6] Барвинок А. Измерение концентрации. Конспект лекций, Мичиганский университет, 2005 г., доступно на сайте www.math.lsa.umich.edu/barvinok/total710.pdf. Поиск в Google Scholar

[7] Бекнер В., Неравенства в анализе Фурье. Энн. по математике . (2) 102 (1975), 159–182. MR0385456 Zbl 0338.4201710.2307/1970980Search in Google Scholar

[8] HJ Brascamp, E.H. Lieb, Наилучшие константы в неравенстве Юнга, его обращение и его обобщение более чем на три функции.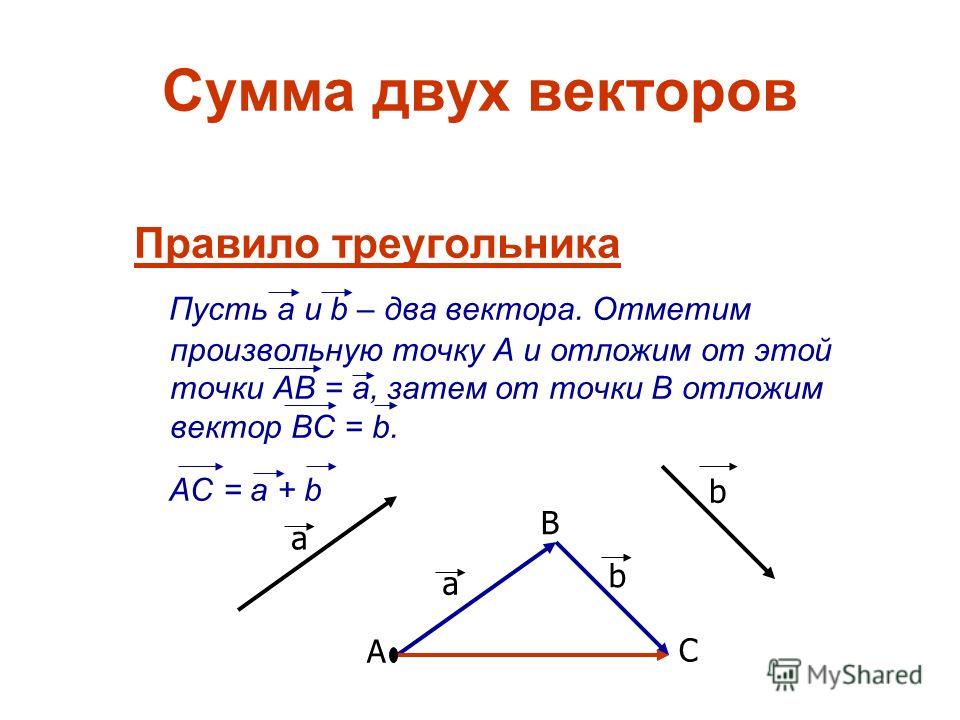 Успехи в математике . 20 (1976), 151–173. MR0412366 Zbl 0339.2602010.1007/978-3-642-55925-9_35Поиск в Google Scholar

[9] С. Бразитикос, А. Яннопулос, П. Валеттас, Б.-Х. Врициу, Геометрия изотропных выпуклых тел , том 196 из Математические обзоры и монографии . амер. Мат. соц. 2014. MR3185453 Zbl 1304.5200110.1090/surv/196Search in Google Scholar

[10] Глускин Э., Мильман В. Геометрическая вероятность и случайный котип 2. В: Геометрические аспекты функционального анализа , том 1850 из Lecture Notes in Math ., 123–138, Springer 2004. MR2087156 Zbl 1087.4600610.1007/978-3-540-44489-3_12Search in Google Scholar

[11] Глускин Е. Д., Экстремальные свойства ортогональных параллелепипедов и их приложения к геометрии банаховых пространств. (Русский) Мат. Сб . ( NS .) 136 (178) (1988), 85–96. Английский перевод: Math. СССР–Сб . 64 (1989), вып.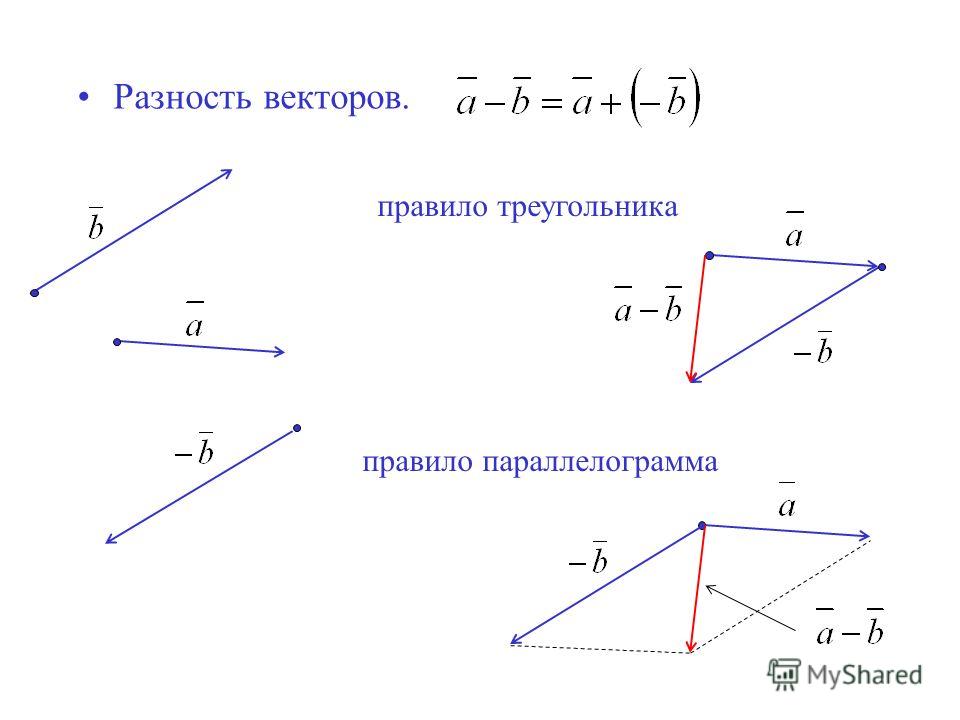 1, 85–96. MR945901 Zbl 0668.52002Search in Google Scholar

[12] Д. Хайела, О гипотезе Кёмлоса о знаковых суммах векторов внутри сферы. Европейский Дж. Комбин . 9 (1988), 33–37. MR938820 Zbl 0646.0501310.1016/S0195-6698(88)80024-6Search in Google Scholar

[13] Б. Клартаг, Р. Вершинин, Вероятность малого шара и теорема Дворецкого. Исраэль Дж. Математика . 157 (2007), 193–207. MR2342445 Zbl 1120.4600310.1007/s11856-006-0007-1Поиск в Google Scholar

[14] Р. Латала, К. Олешкевич, Оценки вероятности малого мяча с точки зрения ширины. Студия Математики . 169 (2005), 305–314. MR2140804 Zbl 1073.6004310.4064/sm169-3-6Поиск в Google Scholar

[15] М. Леду, М. Талагран, Вероятность в банаховых пространствах . Springer 1991. MR1102015 Zbl 0748.6000410.1007/978-3-642-20212-4Search in Google Scholar

[16] Литова А., Тихомиров К. Дисперсия ℓpn-норма гауссова вектора и теорема Дворецкого. Алгебра и анализ 30 (2018), 107–139 и Санкт-Петербург. Мат. Дж . 30 (2019), вып. 4, 699–722. MR3851373 Zbl 07063280Search in Google Scholar

[17] В. Д. Мильман, Г. Шехтман, «Изоморфная» версия теоремы Дворецкого. ЧР Академ. науч. Париж сер. Я Математика . 321 (1995), 541–544. MR1356550 Zbl 0836.46007Search in Google Scholar

[18] Г. Паурис, П. Валеттас, Гауссово неравенство малого уклонения для выпуклых функций. Энн. Вероятно . 46 (2018), 1441–1454. MR3785592 Zbl 0689477810.1214/17-AOP1206Поиск в Google Scholar

[19] Г. Паурис, П. Валеттас, Дж. Зинн, Случайная версия теоремы Дворецкого в ℓпн. Стохастический процесс. Заявка . 127 (2017), 3187–3227. MR3692312 Zbl 1397.4601110.1016/j.spa.2017.02.007Поиск в Google Scholar

[20] Дж. Спенсер, Шести стандартных отклонений достаточно. Пер. амер. Мат. Соц . 289 (1985), 679–706. MR784009 Zbl 0577.0501810.1090/S0002-9947-1985-0784009-0Поиск в Google Scholar

[21] Дж. Спенсер, Балансировка векторов в максимальной норме. Combinatorica 6 (1986), 55–65. MR856644 Zbl 0593.10.1007/BF02579409Search in Google Scholar

[22] J. Spencer, Десять лекций по вероятностному методу , том 64 из серии региональных конференций CBMS-NSF по прикладной математике . SIAM, Philadelphia, PA 1994. MR1249485 Zbl 0822.05060Search in Google Scholar

[23] A. Szankowski, О теореме Дворецкого о почти сферических сечениях выпуклых тел. Исраэль Дж. Математика . 17 (1974), 325–338. MR0350388 Zbl 0288.5200210.1007/BF02756881Поиск в Google Scholar

решеток — Нахождение подмножества векторов, сумма которых близка к заданному вектору

спросил 1 год, 6 месяцев назад

Изменено 1 год, 6 месяцев назад

Просмотрено 192 раза 9d$ и вектор $y$, найдите подмножество $I\subset\{1,2,. ..,n\}$ такое, что $\|\sum_{i\in I} x_i-y\|$ как можно меньше. Здесь $\|.\|$ может быть любой нормой, и $I$ не обязательно должно быть оптимальным множеством. Эта проблема тесно связана с задачами о сумме подмножеств и задачах о рюкзаке, но мне нужен только эффективный алгоритм для нахождения достаточно хорошего множества $I$. Любые соответствующие ссылки приветствуются.

• решетки
• комбинаторно-оптимизационные

$\endgroup$

4

$\begingroup$

Это можно свести к ближайшей векторной задаче, добавляя к каждому $x_i$ $2M\cdot e_i$, что приводит к $(d+n)$-мерному вектору $x’_i$, и добавляя $y$ к $ (M,M,\dots,M)$, что приводит к $(d+n)$-мерному вектору $y’$. Если константа $M$ достаточно велика, то решение задачи CVP для $y’$ в решетка, натянутая на $x’_i$, будет иметь коэффициенты 0-1 и даст решение исходной задачи.