4.1.1 Одноразрядные сумматоры

В цифровых устройствах применяются одноразрядные сумматоры на два и на три входа. Сумматор на два входа называют полусумматором (ПС), а на три входа – полным одноразрядным сумматором (ПОС).

Полусумматорами называют устройства с двумя входами и двумя выходами, на которых вырабатываются сигналы суммы и переноса согласно формулам

 

Полусумматор реализует лишь часть задачи суммирования, так как не учитывает третьей входной величины – переноса из соседнего младшего разряда в данный.

Учитывая, что ПС реализует только часть задачи, в цифровой технике ПОС обычно называют одноразрядными сумматорами.

Одноразрядные сумматоры (ОС) имеют три входа и обеспечи­вают сложение разрядов слагаемы a_i и b_i с переносом из преды­дущего разряда p_i-1

(таблица 4.1).

Таблица 4.1 – Схема переноса

В таблице скобками объединены строки, отличающиеся инвер­тированием аргументов. Видно, что при этом инвертируются и значения функций суммы и переноса. Обозначив вектор аргументов X, можно записать

 

 

Функции, обладающие указанным свойством, называются само­двойственными.

Функции, реализуемые ПС и КОС, представлены выражениями и в таблицах истинности соответственно:

 

 

Таблица 4.2 – Таблица состояния ПС Таблица 4.3 – Таблица состояния ПОС

a	b	S?	p?
0	0	0	0
1	0	1	0
0	1	1	0
1	1	0	1

 

a	b	c	S	p	a	b	c	S	p
0	0	0	0	0	1	1	0	0	1
1	0	0	1	0	0	1	1	0	1
0	1	0	1	0	1	0	1	0	1
0	0	1	1	0	1	1	1	1	1

 

 

 

где a, b, c – суммируемые числа; S? и S – сумма ПС и ПОС Р? и P – перенос ПС и ПОС

На рисунке 4.2 показана реализация ПОС на элементах И-ИЛИ-НЕ. Пользуясь законами алгебры логики, можно по-разному преобразовывать выражения IIOС и получить много вари­антов реализации функций суммы и переноса:

(4.1)

 

В зависимости от вида базовой функции, выполняемой цифровой интегральной микросхемой И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ и т.д., для реализации сумматора могут быть взяты за основу различные выражения. Так последнее выражение может быть положено в основу ПОС на элементах И-НЕ, при этом

,где .

Рисунок 4.2 – Одноразрядный сумматор с парофазными входами: а) – на элементах

И-ИЛИ-НЕ; б) – на элементах И-НЕ; в) – на элементах И-ИЛИ-НЕ и И-НЕ

 

Быстродействие ПОС характеризуется временем установления выходных сигналов суммы S и переноса P после установления сигналов на входе. На рисунке 4.2, б приведена фундаментальная схема ПОС на элементах И-НЕ. Задержка формирования cyммы S и переноса составляет 5t_зд.ср

Применяя элементы И-ИЛИ-НЕ, можно построить ПОС, схема которого показана на рисунке 4.1, в. Быстродействие этой cxeмы определяется временем задержки формирования суммы, равной 4t_зд.ср, а переноса – 3t_зд.ср.

В качестве примечания можно отметить следующее, что многовариантность реализации функций суммы и переноса (4.1) нужно учитывать особенности конкретной серии ИМС (типа используемой схемотехники). При построении ОС на элементах ТТЛ сигнал переноса можно получить всего на одном элементе (например, К155ЛР3) типа 2-2-2-3И-4ИЛИ-НЕ. Будет реализовано соотношение, соответствующее выработке инвертного значения переноса

.

Выражение для S_i непосредственно быть реализовано не может, если в серии элементов нет микросхемы типа 3-3-3-3И-4ИЛИ-НЕ. Поэтому следует попытаться уменьшить число букв в конъюнкциях, входящих в формулу для S_i. Идея в том, чтобы использовать полученное значение переноса как вспомогательный аргумент при вычислении S_i.

Составим таблицу для S_i как функции четырех аргументов – a_i, b_i, p_-1 и p_i (таблица 4.4).

 

ai bi pi-1 pi	si
1 0 0 1   1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1	0 0 1

Таблица 4.4 – Таблица для суммы s_i

ai bi pi-1 pi	si
0 0 0 0   0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0	0   1 1 0 1

 

В таблице против наборов аргументов, являющихся нереальными (например, единичное значение переноса p_i при нулевых значениях всех входных переменных), проставлены неопределенные значения функции, которые можно трактовать произвольно.

Так из таблицы 4.1 следует

 

(4.2)

 

А при использовании полученного выражения значения переноса как вспомогательный аргумент, построив карту Карно (рисунок 4.3), получим:

 

(4.3)

 

Схема ОС, построенного по формулам (4.2) и (4.3) показана на рисунке 4.4, а, а условное обозначение одноразрядного сумматора на рисунке 4.4, б.

 

Рисунок 4.3 – Карта Карно для суммы как функции четырех аргументов

Рисунок 4.4 – Схемная реализация (а) и условное обозначение (б)

одноразрядного сумматора

 

Быстродействие одноразрядных сумматоров оценивают задержками распространения сигналов по четырем трактам: «слагаемое – сумма», «слагаемое – перенос», «перенос – сумма» н «перенос – перенос».

Для рассмотренного ОС справедливо

 

,

 

Быстродействующие ОС можно получить па элементах типа ЭСЛ. Функции суммы и переноса зависят от трех аргументов, поэтому осуществима их реализация на многоярусном переключателе тока. Для непосредственной реализацин функции па многоярусном переключателе их следует выразить в виде инверсии логической суммы наборов аргументов, соответствующих нулевым значениям функции.

 

В данном случае

 

Наряду с каноническим решением, состоящим в реализации полученных выражений на двух трехъярусных переключателях, можно применить более экономичную по числу транзисторов структуру ЭСЛ.

 

Одноразрядный сумматор — Студопедия

Сумматоры выполняют арифметическое сложение чисел, которое производится начиная с младших разрядов чисел. В каждом разряде сумматора выполняются одинаковые действия, т. е. суммируются две двоичные цифры в со­ответствии с правилами сложе­ния двоичных цифр.

При сложении двух единиц возникает единица переноса в старший разряд, которую нужно учесть при сложении цифр следующего разряда. Поэтому в каждом разряде сумматора необходимо предусмотреть возможность суммирования трех цифр: двух цифр слагаемых и единицы переноса из младшего разряда. В свою очередь, в каждом разряде необходимо сформировать не только значение одного разряда суммы, но и значение единицы переноса в соседний старший разряд. Таким образом, сумматор для сложения многоразрядных чисел можно построить из одинаковых схем, каждая из которых выполняет сложение двух цифр слагаемых и переноса из младшего разряда. Такая схема называется одноразрядным сумматором. Одноразрядный сумматор представляет собой комбинационную схему с тремя входами и двумя выходами, логика работы которой соответствует следующей таблице истинности (табл. 2.13).

Таблица 2.13. Логика одноразрядного сумматора

Входы	Выходы
ai	bi	pi-1	si	pi

В соответствии с таблицей истинности уравнения выходов после минимизации имеют следующий вид:

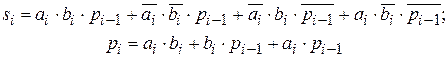
Схемы одноразрядного сумматора и его условное графическое обозначение показаны на рис. 2.25.

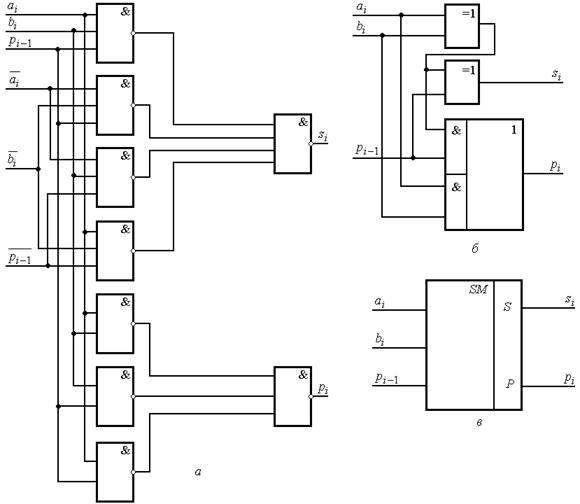
Рис. 2.25. Одноразрядные сумматоры:

а – схема сумматоров на элементах И-НЕ;

б – схема сумматора с использованием элементов сложения по модулю 2;

в – условное графическое обозначение

Принцип работы сумматора

Сумматоры. Устройство, принцип работы

Сумматоры — это комбинационные устройства, предназначенные для сложения чисел. 

Сумматорами называют логические устройства, выполняющие арифметические суммирование кодов двоичного числа. Символическое изображение одноразрядного двоичного сумматора показано на рис.10.29. Сумматор имеет три входа, где — слагаемые одинакового разряда, – слагаемое переноса; на выходе формируется – сумма cлагаемых и – слагаемое переноса в старший разряд.

Функционирование однозарядного сумматора показано в таблице, приведённой на рис.10.30. В этом случае при сложении слагаемых используется перевод десятичных чисел в двоичные числа.

Pиc.10.29. Символическое изображение одноразрядного двоичного сумматора

Рассмотрим пример:

При сложении слагаемых или 0+1+0 получается десятичное число 1. Такому числу соответствует двоичное число 01, при этом Аналогично, 1+1+0 = 2, которому соответствует двоичное число 10, при этом . При сложении чисел 1+1+1 = 3, которому соответствует двоичное число 11, при этом и так далее.

Сумматоры могут быть последовательного и параллельного действия. В сумматорах последовательного действия коды двоичных чисел вводятся в последовательной форме слагаемое за слагаемым, начиная с младшего разряда.

На рис.10.31 изображена схема сумматора последовательного действия, предназначенного для суммирования четырёхразрядных двоичных чисел. Сумматор построен на трёх регистрах сдвига, D-триггере и на одноразрядном сумматоре.

Рис.10.30. Таблица функционирования одноразрядного сумматора

Рис.10.31. Схема сумматора последовательного действия

Функционирование сумматора приведено в таблице рис.10.32, где слагаемое pi для первого разряда всегда равно нулю.

Рис.10.32. Таблица функционирования сумматора

Для ускорения операции сложения используются сумматоры параллельного действия, которые состоят из нескольких однозарядных сумматоров. В таких сумматорах слагаемые поступают одновременно на соответствующие входы однозарядных сумматоров, при этом каждый из однозарядных сумматоров формирует на своих выходах суммы соответствующих разрядов и слагаемые переноса, передаваемых на входы старших разрядов. Схема четырёхразрядного сумматора параллельного действия приведена на рис.10.33.

Рис.10.33. Схема четырёхразрядного сумматора параллельного действия

• 5 Компенсационный резистор в схеме сумматора
• 6 Симуляция работы сумматора на ОУ в Proteus

• 6.1 Симуляция инвертирующего сумматора
• 6.2 Симуляция неинвертирующего сумматора

• 7 АЧХ и ФЧХ сумматора
• 8 Сравнение неинвертирующих сумматоров
• 9 Плюсы и минусы инвертирующего и неинвертирующего сумматора
• 10 Применение аналогового сумматора

Что такое сумматор

В общем смысле слова, сумматор – это какое-либо устройство, которое что-либо суммирует и выдает на выходе сумму этих воздействий. Сумматор можно представить в виде какого-либо неизвестного нам ящика, на который поступает входные воздействия и на выходе такого ящика выдается их сумма.

В электронике сумматоры делятся на две группы:

• сумматоры аналоговых сигналов
• сумматоры цифровых сигналов

В этой статье мы будем разбирать аналоговые сумматоры.

Аналоговый сумматор

Многие помнят осциллограмму постоянного напряжения.

Если, допустим, цена нашего квадратика 1 В, то на данной картинке мы видим постоянное напряжение амплитудой в 1 В. Суммировать постоянное напряжение – одно удовольствие. Для этого достаточно сложить амплитуды этих сигналов в любой момент времени.

На рисунке ниже мы видим два сигнала A и B и сумму этих сигналов: A+B. Если сигнал A = 2 В, сигнал B = 1 В, то сумма этих сигналов составит 3 В.

Все то же самое касается и сигналов с отрицательной полярностью.

При сложении сигналов с равной амплитудой, но разной полярности, в сумме получаем 0. То есть эти два сигнала взаимно себя скомпенсировали: 1 +(-1)=0. Все становится намного веселее, если мы начинаем складывать сигналы, которые меняются во времени, то есть переменные сигналы. Они могут быть как периодические, так и непериодические. 

Рассмотрим самый простой пример. Есть два синусоидальных сигнала с одинаковыми амплитудами, частотами и фазами. Подадим их на сумматор. Что получится в итоге?

Получим синусоиду с амплитудой в два раза больше. Как вообще она получилась? Вычисления производятся довольно просто. Каждая точка синусоиды A+B  – это сложение точек в одинаковый момент времени синусоид А и B. Для наглядности взяли 3 точки: t1 , t2  и t3 .

В момент времени t1 у нас амплитуда сигнала А была равна 1 В, амплитуда сигнала В тоже 1 В.

В сумме их результат в момент времени t1 будет равен 2 В, что мы и видим на сигнале A+B

В момент времени t2 амплитуда сигнала A была 0 В, амплитуда сигнала В тоже 0 В. Как нетрудно догадаться, 0+0=0, что мы и видим на сигнале A+B в момент времени t2 .

Ну а в момент времени t3 амплитуда сигнала А = -1 В, амплитуда сигнала В = -1 В, в результате их сумма -1+(-1) = – 2 В, что мы как раз и видим на синусоиде А+B в момент времени t3 . Отсюда вывод: для сложения сигналов надо суммировать амплитуды сигналов в одинаковые моменты времени.

Если сместить фазу одного из сигналов на 180 градусов, относительно другого, а амплитуды и частоты сигналов оставить без изменения, то чему будет равняться их сумма? Сместим второй сигнал на 180 градусов и суммируем их амплитуды в каждый момент времени. Сумма будет равняться нулю, что и видно на рисунке ниже.

Сложение двух сигналов в Proteus

Если надо сложить в теории два каких-нибудь два сложных сигнала с разными фазами, амплитудами, частотами, то проще всего прибегнуть к различным симуляторам.

Один из них – это Proteus. С помощью него можно сложить два любых сигнала и посмотреть их сумму.

Для этого надо выбрать синусоидальный генератор.

Затем виртуальный осциллограф.

Собрать схему.

Задать параметры генератору.

Теперь можно сложить два синусоидальных сигнала с одинаковыми амплитудами, фазами и частотами.

Прописать амплитуду и частоту каждого сигнала и нажать «пуск».

Нажать правой кнопкой мыши на виртуальный осциллограф и нажать Digital Oscilloscope.

Для того, чтобы найти их сумму, достаточно нажать на кнопку A+B.

Получаем сумму двух сигналов.

В таком виртуальном осциллографе можно складывать любые два сигнала.

Источники:

Понравилась статья? Расскажите друзьям: Оцените статью, для нас это очень важно:

Проголосовавших: 1 чел.
Средний рейтинг: 5 из 5.

Одноразрядные сумматоры — Студопедия

В цифровой вычислительной технике используются одноразрядные суммирующие схемы с двумя и тремя входами, причём первые называютсяполусумматорами, а вторые — полными одноразрядными сумматорами. Полусумматоры могут использоваться только для суммирования младших разрядов чисел. Полные одноразрядные сумматоры имеют дополнительный третий вход, на который подаётся перенос из предыдущего разряда при суммировании многоразрядных чисел.

На рисунке 21, а) приведена таблица истинности полусумматора, на основании которой составлена его структурная формула в виде СДНФ (Рисунок 21, б). Функциональная схема, составленная на элементах основного базиса в соответствии с этой структурной формулой, приведена на рисунке 21, в).

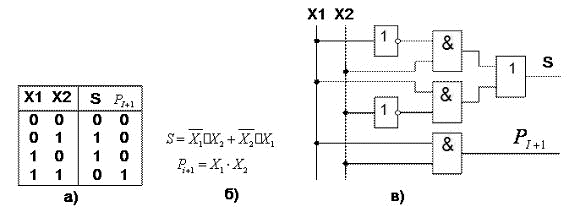
Рисунок 21 Одноразрядный полусумматор: а) таблица истинности, б) структурная формула, в) функциональная схема.

Основными параметрами, характеризующими качественные показатели логических схем, являются быстродействие и количество элементов, определяющее сложность схемы.

Быстродействие определяется суммарным временем задержки сигнала при прохождении элементов схемы. В приведённой выше схеме быстродействие определяется задержкой в трёх логических элементах.

Кроме количества элементов сложность схемы, как было отмечено выше, определяется количеством входов элементов, по которым выполняются логические операции. Этот параметр называется «Число по Квайну». Приведённая выше схема содержит 6 элементов и имеет 10 входов (Число по Квайну равно 10).

Недостатком схемы рисунок 21, в) является то, что на её входы необходимо подавать и прямые и инверсные значения операндов. Применяя законы алгебры логики схему можно преобразовать, исключив инверсии над отдельными операндами. Порядок минимизации показан на рисунке 22, а), функциональная схема — на рисунке 22, б), а её УГО — на рисунке 22, в).

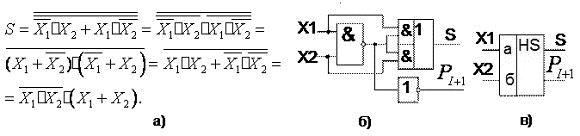
Рисунок 22 Пример минимизации а), функциональная схема б) и УГО одноразрядного полусумматора в).

Минимизированная схема является более быстродействующей, так как вместо 6 содержит 3 элемента, а число по Квайну уменьшилось с 10 до 7. Учитывая огромное количество используемых суммирующих схем, выигрыш можно считать весьма ощутимым.

Схему полного одноразрядного сумматора можно получить на основе двух схем полусумматоров и схемы «ИЛИ», как показано на рисунке 23,а).

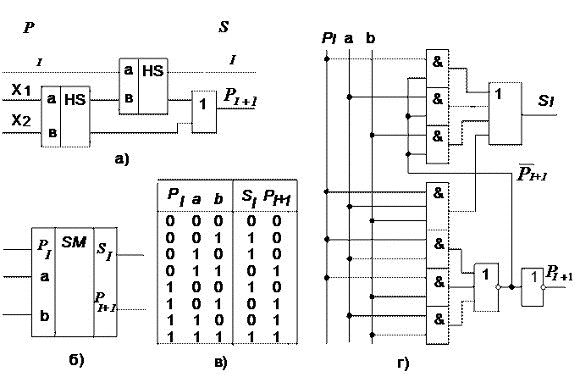
Рисунок 23 Одноразрядный полный сумматор: а) — функциональная схема на двух полусумматорах; б) — УГО; в) — таблица истинности: г) — минимизированная схема.

Из рассмотрения принципа работы функциональной схемы рисунок 23,а) составлена её таблица истинности, анализ которой показывает, что данная схема выполняет функции полного одноразрядного сумматора. Однако схема не является оптимальной по быстродействию, поскольку в ней сигнал проходит последовательно через две схемы полусумматоров и схему ИЛИ.

Представляется целесообразным разработка сумматора как устройства, имеющего три входа и два выхода. СДНФ такой функции записывается в виде:

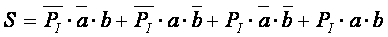
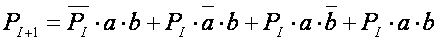
Минимизированные значения, используемые в интегральной схемотехнике:

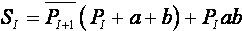
P_I+1 = P_Ia + P_Ib + ab

Первое из уравнений минимизируется аналитическим методом, используя законы алгебры логики, а второе — методом минимизирующих карт Карно.

Функциональная схема, составленная по этим уравнениям, приведена на рисунке 23, г). По сравнению со схемой рисунок 23, а) эта схема является более быстродействующей. Условное графическое обозначение (УГО) схемы полного одноразрядного сумматора приведено на рисунке 23, б).

Одноразрядные двоичные сумматоры

Реализация логических схем на компьютере с использование программы

Electronics Workbench

Правила сложения двоичных и десятичных чисел одинаковы:

1. сложение производиться поразрядно — от младшего разряда к старшему;

2. в младшем разряде вычисляется сумма младших разрядов слагаемых А; и Bj. Эта сумма в данной системе счисления может быть записана однозначным числом Si либо двухзначным числом PiS,. Функция Р называется переносом;

3. во всех последующих разрядах находиться сумма данных разрядов слагаемых А; и В„ причем при Ри-1 к этой сумме добавляется единица (в числовых примерах, приведенных выше, этот случай выделен жирным шрифтом, результат сложения в i-м разряде записывается в виде однозначного Si или двухзначного PjSi числа.

Таким образом, в каждом разряде необходимо найти сумму A;, Bi иР_м (если Рм=1), т.е. определить Si и Pj. По числу входов различают полусумматоры, одноразрядные сумматоры (ОС) и многоразрядные сумматоры.

Полусумматоры

 

Рис. 6.10 Схема полусумматора

 

Рис. 6.11 Схема полусумматора с использованием стандартной схемы сложения по

модулю 2

Таблица 6.4 Таблица истинности полусумматора

Рис. 6.12 Диаграмма работы полусумматора Логические уравнения: S=x^A*y+x*y^A P=x*y 6.6.2 Одноразрядный двоичный сумматор

Рис. 6.13 Схема одноразрядного двоичного сумматора

Рис. 6.14 Диаграмма работы одноразрядного двоичного сумматора

Таблица 6.4 Таблица истинности сумматора

 

в Electronics Workbench.

Рис. 6.15 Схема последовательного сумматора

Рис. 6.16 Диаграмма работы последовательного сумматора

Цифровые схемы сравнения

Рис. 6.17 Цифровая схема сравнения

Цифровые схемы сравнения формируют на выходе F=l при равенстве подаваемых на вход двух двоичных чисел А (поразрядно записываем а и Ь) и В (с и d). Цифровая схема сравнения это цифровой аналог компаратора (см. рисунок 6.17), являющегося одним из важнейших устройств импульсной техники, временная диаграмма сумматоров приведена рисунке 6.18, приложения. На основе таблицы истинности для компаратора составим уравнения (для А>В, А<В, А^В), минимизируем их используя законы алгебры логики.

Рис. 6.18 Диаграмма работы цифровой схемы сравнения

Таблица 6.5 — Таблица истинности цифровой схемы сравнения

Приложение 2

Микросхемы представляют собой четырехразрядный (двоичный) полный сумматор. Содержат 781 интегральный элемент. Корпус К155ИМЗ типа 238.16-2, масса не более 2 г., КМ155ИМЗ типа 201.16-6, масса не более 2,5 г.

Корпус ИМС К155ИМЗ

238.16-1 238.16-2

Условное графическое обозначение вход слагаемого А4; выход суммы S3;

3 — вход слагаемого A3;

4 — вход слагаемого ВЗ;

5 — напряжение питания;

6 — выход суммы S2;

7— входслагаемого В2;

8— входслагаемого A3;

9 — выход суммы S1;

 

10— вход слагаемого А1;

11 — вход слагаемого В1;

12 — общий;

13 — вход переноса РО;

14 — выход переноса четвкртого разряда Р4;

15 — выход суммы S4;

16 — вход слагаемого В4; Электрические параметры

 

 

к-:-»»:-:-:-:-:-:.:-»:-:-»:-:-»

Время задержки распространения по цепи переноса Зарубежные аналоги

SN7483N, SN7483J

Устройство.

Работа выполняется на плате П6 с использованием одной технологической карты VI-1.

Карта VI-1 позволяет исследовать АЛУ. При не нажатой кнопке SB2 общая шина подключается к выходу счетчика 10. Набирая любую необходимую информацию (кнопкой -SB1), контролируемую по индикатору HG-1 переписывают ее в регистры кода операций или операндов. Выход информации из АЛУ на индикатор HG-1 осуществляют сигналом, подаваемым на вход V микросхемы счетчика.

Стандартное АЛУ типа К155ИПЗ, как известно [2] , может выполнять 64 логических или арифметическо-логических операции, в зависимости от сигналов, подаваемых на управляющие входы S, М и вход переноса Р₍₎.

Для знакомства с принципом действия АЛУ можно ограничиться значительно меньшим набором операций. Список этих операций и соответствующие им коды приведены в таблице 2.

Таблица входных кодов и выполняемых операций.

Таблица 7.2

I

При работе со стендом карта (VI-1) удобнее пользоваться, шестнадцатеричным

кодом операции, который набирается кнопкой, SB1 с контролем по индикатору

HG1.

Приложение 1

Приложение

Микросхема представляет собой арифметико-логическое устройсво (АЛУ). Корпус К155ИПЗ типа 201.14-1, масса не более 1 г.

Корпус ИМС К155ИПЗ

Условное графическое обозначение информационный вход младшего разряда ВО; информационный вход младшего разряда АО;

 

Одноразрядные двоичные сумматоры

Вцифровых устройствах применяются одноразрядные суммирующие схемы на два и три входа, причем первую называют полусумматором, вторую — полным

одноразрядным сумматором. 6.3.1 Полусумматоры

Простейшим суммирующим элементом является полусумматор. Он имеет (рис.6.3) два входа А и В для двух слагаемых и два выхода : Б(сумма) и РО (перенос). Обозначением полусумматора служат буквы HS (HalfSum — полусумма), работу прибора отражает таблица истинности таблица 6.1

 

Рис. 6.3 Полусумматор Полусумматор имеет два входа и пригоден для использования только в младших разряде.

Рассмотрим синтез полусумматоров, имеющихдва входа А и В. Выходными сигналами такого устройства являются сумма S и перенос РО, которые вырабатываются согласно таблице 1 функционирования данного устройства.

Таблица 6.1

 

Рис. 6.4 Реализация полусумматора на элементах И-НЕ, И-ИЛИ-НЕ (а) и его

условное обозначение (б)

Сумматор в отличие от полусумматорадолжен воспринимать не два, а три

входных сигнала: два слагаемых А, В и сигнал переноса с предыдущего разряда Р.

Вообще говоря, сумматор можно построить из двух полусумматоров и одной схемы

ИЛИ (рис. 6.5).

 

Рис.6.5 Полный одноразрядный сумматор на основе полусумматоров (а) и его

условное обозначение (б)
Составим таблицу функционирования полного одноразрядного сумматора
(табл. 6.2). Таблица 6.2

Рассмотрим работу сумматора состоящего из двух полусумматоров, (рис 6.6)

 

Таблица 6.3

Рис. 6.7 Схема одноразрядного сумматора с парафазными входными сигналами 6.4 Параллельные многоразрядные сумматоры

Параллельные многоразрядные сумматоры предназначены для одновременного суммирования двух многоразрядных чисел и характеризуются различными способами передачи сигналов переноса от младших разрядов сумматора к старшим. Различают параллельные комбинационные сумматоры с последовательным, одновременным и комбинированным переносом. Выбор типа переноса между разрядами суммирующего устройства определяется требованиями к быстродействию.

Простейшими из параллельныхсумматоров (ПС) являются ПС с последовательной передачей сигналов переноса (рис. 6.8).

При последовательном вводе используется один,общий для всех разрядов полный сумматор с дополнительной цепью задержки. Оба слагаемых кодируются последовательностями импульсов, которые синхронно вводятся в сумматор через входы А и В, начиная с младших разрядов. Цепь задержки обеспечивает хранение импульса переноса Р на время одного такта, т.е. до прихода пары слагаемых следующего разряда, с которыми он будет просуммирован. Задержку обеспечивает D-триггер (триггер задержки). Для хранения и ввода слагаемых А и В, а так же для преобразования последовательного кода выходных импульсов в параллельный применяют регистры сдвига. Работа регистров и схемы задержки синхронизируется общим генератором тактовых импульсов.

Сигнал переноса, образованный в младшем разряде, распространяется

последовательно по цепям переноса к старшим разрядам. Время распространения переноса определяется суммарной задержкой этих цепей.

Ь2 Ьп

Рис. 6.8 Комбинационный n-разрядный сумматор с последовательным переносом

Быстродействие сумматора при сложении двух n-разрядных чисел характеризуется временем суммирования, которое в наихудшем случае равно

t_s=(n-l)t_P+t_iS

где t_is, t_P — задержки формирования одноразрядным сумматором суммы и переноса соответственно. Следовательно, сумматоры с последовательным переносом обладают низким быстродействием. С целью повышения быстродействия (сокращения времени сложения) применяются сумматоры с одновременным переносом.

Серьезным недостатком сумматоров с одновременным переносом является значительный рост аппаратурных затрат при построении схем межразрядных переносов. Поэтому на практике применяют метод построения сумматоров с комбинированным переносом.

В сумматорах с комбинированным переносом полные одноразрядные сумматоры объединяются в группы. Внутри группы, как правило, осуществляется одновременный перенос. Между группами перенос может быть как последовательный, так и одновременный. На рис.6.9 в качестве примера приведена схема 16-разрядного двоичного сумматора с комбинированным переносом на базе четырехразрядных схем сумматоров АЛУ (микросхем ИГО). Здесь внутри групп организован одновременный перенос, между группами -последовательный.

Рис.6.9 16-разрядный сумматор с комбинированным переносом Для удобства построения сумматоров с одновременным переносом в ряде серий микросхем логические функции, формирующие переносы, реализуются в виде отдельной микросхемы.

6.5ЛАБОРАТОРНАЯ РАБОТА № 6 Цель работы: Исследовать четырехразрядный параллельный сумматор. Объем заданий к работе:

1. На примерах рассмотрения арифметических действий над двоичными числами обоснуйте утверждение, что наиболее часто встречающейся операцией над числами в вычислительных устройствах и в ЭВМ является операция сложения.

2. Ответить, чем отличаются операции параллельного и последовательного суммирования.

3. По таблице вариантов, возникающих при сложении двух одноразрядных чисел, составить и объяснить буревые выражения для описания одноразрядного сумматора.

4. Продумать и зарисовать в тетради рабочие схемы для изучения работы параллельного 4-х разрядного сумматора. Зарисовать условно-графическое обозначение изучаемого устройства.

5. Продумать формы отчетных таблиц.
При выполнении работы:

1. Собрать схему стенда для исследования работы 4-х разрядного параллельного сумматора (карта Ш-3).

2. Провести исследование работы 4-х разрядного параллельного сумматора. В процессе исследования провести суммирование 4-5 пар 4-х разрядных двоичных чисел (операндов). Формирование и промежуточное хранение операндов выполнять соответственно с помощью регистра RG и тумблеров SA4…SA1. Суммирование производить с учетом сигнала переноса (SB3).

Результаты суммирования проверить при переводе значений операндов в десятичный код.

3. Провести вычисление 3-4 пар 4-х разрядных операндов, используя перевод вычитаемого в дополнительный код. Результаты вычитания проверить при переводе значений операндов в десятичный код.

4. Результаты исследования представить соответствующими таблицами.

5. Просмотр состояний входов и выходов SM производить с помощью устройства цифровой индикации в режимах представления информации в двоичном и шестнадцатеричном кодах.

При зачете:

1. Произвести сравнительную оценку используемых ИС для построения сумматоров.

2. Указать, возможно, ли создание на базе ИС К155ИМЗ сумматоров большой разрядности.

Работа выполняется на плате ПЗ с использованием технологической карта Ш-3

Карта Ш-3предназначена для исследования работы сумматора двух 4-х разрядных двоичных чисел на ИМС типа К155ИМЗ (D2). Для задания двух 4-х разрядных слагаемых используются тумблеры SA1 — SA4 (слагаемое А) и регистр D1 (слагаемое В). Ввод слагаемого В в регистр может осуществляться как в параллельном (с тумблеров SA1-SA4), так и в последовательном (с кнопки SB2) режимах. Сигнал начального переноса Р₀ подается с кнопки.SB3 через инвертор D 2.3, имеющийся в основном блоке. Индикация входных операндов А и В осуществляется двоичным восьмиразрядным индикатором HL2 — HL9, Сигнал переноса в сстарший (пятый) разряд подается на индикатор HL1. Сумма в четырех первых разрядах дешифруется в блоке индикации и высвечивается в виде шестнадцатеричного числа на семисегментном индикаторе. Приложение 1 Технологическая карта (шаблон) Ш-3

---

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Одноразрядный двоичный сумматор — Студопедия

Рис. 3.17. Асинхронный реверсивный счетчик

Здесь при наличии единичного сигнала на управляющей шине I счетчик работает как суммирующий, а при наличии единичного сигнала на управляющей шине II – как вычитающий.

Одноразрядный двоичный сумматор является комбинационной схемой с тремя входами и двумя выходами (рис.3.18).

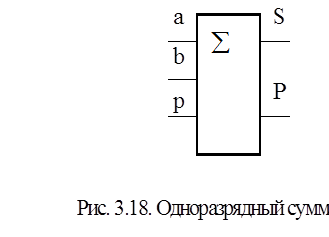
При параллельном суммировании на входы каждого разряда сумматора поступают значения цифр а и b соответствующих разрядов слагаемых и значение переноса p с младших разрядов сумматора. На выходе одноразрядного сумматора формируются значения цифры соответствующего разряда суммы Sи переноса в старший разряд сумматора P.

Значения S и P таблицы истинности одноразрядного сумматора построена на основе сложения и умножения для двоичной системы счисления.

Таблица истинности выходов одноразрядного сумматора
№	Входы	Выходы
a	b	p	S	P

Для каждого выходного сигнала составляются все комбинации входных сигналов, при которых выходные сигналы S и P принимают единичные значения:

,

.

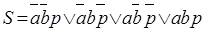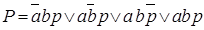Эти уравнения являются совершенной дизъюнктивной нормальной формой логических функций (СДНФ). В этой форме логическая функция (ЛФ) представляется в виде дизъюнкций конституэнт единицы.

Конституэнта единицы – это конъюнкция всех значений входных переменных: в прямой форме для единичных значений переменных, или в инверсной форме для нулевых значений переменных.

СДНФ позволяет записывать любые переключательные функции от двух переменных, используя только три основных логических операции И, ИЛИ, НЕ.

Следующим этапом проектирования является минимизация логических функций (не всегда возможна).

Из таблицы истинности видно, что переменная P принимает значение только для таких комбинаций входных переменных, когда хотя бы две переменные имеют единичные значения. Это можно записать в виде:

.

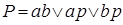Анализируя функцию S можно заметить, что значение S равно единице, если в комбинациях входных сигналов присутствует хотя бы один единичный сигнал, и нет одновременно двух единичных значений переменных (компонента: 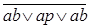=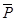) или есть совпадение трех входных единичных сигналов (компонента abp), т.е.:

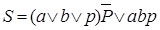
Построение функциональной схемы по ПФ:

.

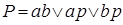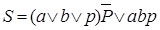
Для реализации ПФ для выхода Р требуется :

· три конъюнктора (схемы И) на два входа,

· дизъюнктор (схема ИЛИ) на 3 входа.

Для реализации ПФ для выхода S требуются:

· дизъюнктор (схема ИЛИ) на 3 входа,

· инвертор (схема НЕ),

· конъюнкторы (схемы И) на 2 и 3 входа.

· дизъюнктор (схема ИЛИ) на 2 входа.

Функциональная схема одноразрядного сумматора представлена на рис.3.19.

В этой схеме использована совместная минимизация уравнений, при которой для формирования разных выходных значений (S и P) используются общие логические схемы. Совместная минимизация позволяет получать схемы с минимальным количеством используемых элементарных вентилей, которое определяется по общему количеству входов. Такие схемы, как правило, имеют большую задержку выходных сигналов, которая определяется по максимальному количеству элементов пути его формирования.

По этой причине часто одноразрядный сумматор строят без совместной минимизации схем формирования выходных сигналов по уравнениям:

,

.

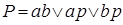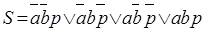Многоразрядные сумматоры

Обычно в ЭВМ используют обработку данных параллельно по разрядам. Для такой обработки используются многоразрядные (параллельные) сумматоры.

Сумматор для параллельной обработки данных получают на основе поразрядного соединения одноразрядных схем.

Пример построения многоразрядного сумматора представлен на рис. 3.20.

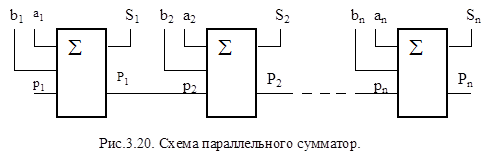
Сумматор имеет 2n входных разрядных линий a_i и b_i для приема цифр слагаемых, n выходных линий S_n разрядов суммы, выход переноса Р_n из старшего разряда и вход переноса р₀ на младший разряд сумматора.

На функциональных схемах многоразрядные функциональные узлы обозначаются в виде прямоугольников с тремя полями (рис.3.21).

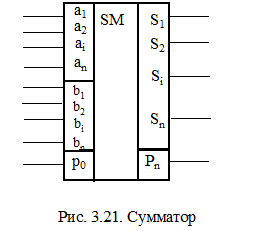
В основном поле обозначается функциональное назначение схемы. Для сумматора это SM (СМ,å).

Боковые поля предназначены для обозначения данных: левое поле для входных данных, правое – для выходных.

Сумматор — Википедия

Сумма́тор — в кибернетике — устройство, преобразующее информационные сигналы (аналоговые или цифровые) в сигнал, эквивалентный сумме этих сигналов^[1]; устройство, производящее операцию сложения.

История

Классификация сумматоров

В зависимости от формы представления информации различают сумматоры аналоговые и цифровые^[1].

По способу реализации

По принципу действия

• На счётчиках, считающие количества импульсов входного сигналах.
• Функциональные, выдающие на выходах значения логической функции суммы по модулю и логической функции разряда переноса:
  • логические, каждый раз вычисляющие функцию разряда суммы по модулю и функцию разряда переноса
  • табличные, с таблицами заранее вычисленных значений функции разряда суммы по модулю и значений функции разряда переноса записанных:
    • в ПЗУ, ППЗУ (аппаратные) (надёжнее и дешевле логических, так как вместо полупроводников, выполняющих логические вычисления, в ПЗУ используются проводники и изоляторы («прошивки»))^[4] или
    • в ОЗУ (аппаратные и программные).
      

Табличные сумматоры впервые были применены в калькуляторах построенных на реле в США до второй мировой войны.

По архитектуре

• Четвертьсумматоры — бинарные (двухоперандные) сумматоры по модулю без разряда переноса, характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма по модулю.
• Полусумматоры — бинарные (двухоперандные) сумматоры по модулю с разрядом переноса, характеризующиеся наличием двух входов, на которые подаются одноимённые разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма по модулю в данном разряде, а на другом — перенос в следующий (старший) разряд.
• Полные сумматоры — тринарные (трёхоперандные) сумматоры по модулю с разрядом переноса, характеризующиеся наличием трёх входов, на которые подаются одноимённые разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма по модулю в данном разряде, а на другом — перенос в следующий (более старший разряд). Такие сумматоры изначально ориентированы только на показательные позиционные системы счисления^{[источник не указан 2874 дня]}.
• Накапливающие сумматоры — снабжённые собственной внутренней памятью.

По способу действия

• Последовательные (одноразрядные), в которых обработка разрядов чисел ведётся поочерёдно, разряд за разрядом, на одном и том же одноразрядном оборудовании.
• Параллельнопоследовательные, в которых одновременно параллельно последовательно складываются разряды нескольких пар чисел.
• Параллельные (многоразрядные), в которых слагаемые складываются одновременно по всем разрядам, и для каждого разряда имеется своё оборудование.

По способу организации переноса^[5][6]

По системе счисления

Двоичный сумматор

Двоичный сумматор может быть описан тремя способами:

1. табличным, в виде таблицы истинности,
2. аналитическим, в виде формулы (СДНФ),
3. графическим, в виде логической схемы.

Так как формулы и схемы могут тождественно преобразовываться, то, одной таблице истинности двоичного сумматора могут соответствовать множества различных логических формул и логических схем. Поэтому, с точки зрения получения результата без учёта затрат времени на вычисление суммы, табличный способ определения двоичного сумматора является основным. Обычное табличное и обычное формульное описание сумматора не учитывают времена задержек в реальных логических элементах и не годятся для определения быстродействия реальных сумматоров.

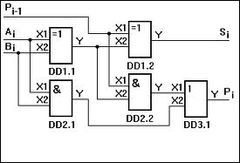Рис.1. Логическая схема трёхступенчатого двоичного сумматора на двух полусумматорах и логическом элементе 2ИЛИ.

x0=A	1	0	1	0	1	0	1	0
x1=B	1	1	0	0	1	1	0	0
x2= P i − 1 {\displaystyle P_{i-1}}	1	1	1	1	0	0	0	0	Название действия (функции)	Номер функции
S i {\displaystyle S_{i}}	1	0	0	1	0	1	1	0	Бит суммы по модулю 2	F3,150
P i {\displaystyle P_{i}}	1	1	1	0	1	0	0	0	Бит переноса	F3,232

Единица переноса возникает в 4-х случаях из 8-ми.

СДНФ суммы по модулю 2:
S i = f ( x 2 , x 1 , x 0 ) = ( x 2 ¯ ⋅ x 1 ¯ ⋅ x 0 ) ∨ ( x 2 ¯ ⋅ x 1 ⋅ x 0 ¯ ) ∨ ( x 2 ⋅ x 1 ¯ ⋅ x 0 ¯ ) ∨ ( x 2 ⋅ x 1 ⋅ x 0 ) {\displaystyle S_{i}=\mathbf {f} (x_{2},x_{1},x_{0})=({\overline {x_{2}}}\cdot {\overline {x_{1}}}\cdot {x_{0}})\vee ({\overline {x_{2}}}\cdot {x_{1}}\cdot {\overline {x_{0}}})\vee ({x_{2}}\cdot {\overline {x_{1}}}\cdot {\overline {x_{0}}})\vee ({x_{2}}\cdot {x_{1}}\cdot {x_{0}})}

СДНФ бита переноса:
P i = f ( x 2 , x 1 , x 0 ) = ( x 2 ¯ ⋅ x 1 ⋅ x 0 ) ∨ ( x 2 ⋅ x 1 ¯ ⋅ x 0 ) ∨ ( x 2 ⋅ x 1 ⋅ x 0 ¯ ) ∨ ( x 2 ⋅ x 1 ⋅ x 0 ) {\displaystyle P_{i}=\mathbf {f} (x_{2},x_{1},x_{0})=({\overline {x_{2}}}\cdot {x_{1}}\cdot {x_{0}})\vee ({x_{2}}\cdot {\overline {x_{1}}}\cdot {x_{0}})\vee ({x_{2}}\cdot {x_{1}}\cdot {\overline {x_{0}}})\vee ({x_{2}}\cdot {x_{1}}\cdot {x_{0}})}

Схема, которая обеспечивает сложение двух однобитных чисел А и В без получения бита переноса из предыдущего разряда называют полусумматором. Полусумматор имеет 4 сигнальных линии: два входа для сигналов, представляющих одноразрядные двоичные числа А и В, и два выхода: сумма А и В по модулю 2 (S) и сигнал переноса в следующий разряд (P). При этом S наименее значимый бит, а P наиболее значимый бит.

Объединив два полусумматора и добавив дополнительную схему ИЛИ, можно создать трёхступенчатый полный сумматор с дополнительным входом P_i-1 (на рисунке 1), который принимает сигнал переноса из предыдущей схемы. Первая ступень на полусумматоре осуществляет сложение двух двоичных чисел и вырабатывает первый частный бит переноса, вторая ступень на полусумматоре осуществляет сложение результата первой ступени с третьим двоичным числом и вырабатывает второй частный бит переноса, третья ступень на логическом элементе 2ИЛИ вырабатывает результирующий бит переноса в старший разряд.

Схема полного сумматора может быть использована в качестве «строительных блоков» для построения схем многоразрядных сумматоров, путём добавления одноразрядных полных сумматоров. Для каждой цифры, которую схема должна быть в состоянии обрабатывать, используется один полный сумматор.

В сумматоре на рис.1 время вычисления суммы по модулю 2 равно 2dt, время вычисления переноса равно 3dt, где dt — время задержки в одном типовом логическом элементе. В m-разрядном сумматоре в худшем случае (единицы переноса во всех разрядах) до последнего разряда сигнал переноса проходит через m-1 разряд, а сумма будет готова ещё через 2dt, поэтому максимальное время сложения равно:

3 d t ( m − 1 ) + 2 d t = ( 3 m − 1 ) d t {\displaystyle 3dt(m-1)+2dt=(3m-1)dt} .

Максимальные времена выполнения сложения и вычисления переноса для большего числа разрядов приведены в таблице 1:
Таблица 1.

число разрядов сумматора	1	2	4	8	16	32	64
время выполнения сложения, dt	2	5	11	23	47	95	191
время вычисления переноса, dt	3	6	12	24	48	96	192

Двоичный одноразрядный полный сумматор является полной тринарной (трёхоперандной) двоичной логической функцией с бинарным (двухразрядным) выходом. Все три операнда и оба выходных разряда однобитные.

Десятичный сумматор

Десятичный сумматор можно задать в виде двух таблиц:
с нулём в переносе из предыдущего разряда:

+	0	0	0	0	0	0	0	0	0	0
+	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9	10
2	2	3	4	5	6	7	8	9	10	11
3	3	4	5	6	7	8	9	10	11	12
4	4	5	6	7	8	9	10	11	12	13
5	5	6	7	8	9	10	11	12	13	14
6	6	7	8	9	10	11	12	13	14	15
7	7	8	9	10	11	12	13	14	15	16
8	8	9	10	11	12	13	14	15	16	17
9	9	10	11	12	13	14	15	16	17	18

и с единицей в переносе из предыдущего разряда:

+	1	1	1	1	1	1	1	1	1	1
+	0	1	2	3	4	5	6	7	8	9
0	1	2	3	4	5	6	7	8	9	10
1	2	3	4	5	6	7	8	9	10	11
2	3	4	5	6	7	8	9	10	11	12
3	4	5	6	7	8	9	10	11	12	13
4	5	6	7	8	9	10	11	12	13	14
5	6	7	8	9	10	11	12	13	14	15
6	7	8	9	10	11	12	13	14	15	16
7	8	9	10	11	12	13	14	15	16	17
8	9	10	11	12	13	14	15	16	17	18
9	10	11	12	13	14	15	16	17	18	19

или в виде одной таблицы, в которой единица переноса из предыдущего разряда смещает на одну колонку вправо:

+	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10	11
2	2	3	4	5	6	7	8	9	10	11	12
3	3	4	5	6	7	8	9	10	11	12	13
4	4	5	6	7	8	9	10	11	12	13	14
5	5	6	7	8	9	10	11	12	13	14	15
6	6	7	8	9	10	11	12	13	14	15	16
7	7	8	9	10	11	12	13	14	15	16	17
8	8	9	10	11	12	13	14	15	16	17	18
9	9	10	11	12	13	14	15	16	17	18	19

C соответствующей прошивкой как десятичный сумматор (десятеричный) могут работать шестнадцатеричный сумматор и двадцатисемиричный сумматор-вычитатель на ПЗУ.

Направления развития сумматоров

Быстродействия параллельных сумматоров вполне достаточно для быстрого сложения небольшого количества чисел фиксированной длины.
Так как поразрядное сложение по природе своей последовательно, то при очень большом количестве сложений более выгодно перенастроить то же самое оборудование (АЛУ) для одновременного или не очень одновременного параллельного выполнения нескольких последовательных сложений.

Например, параллельный 64-х разрядный двоичный сумматор из 64-х двоичных сумматоров со сложными схемами ускоренного переноса сложит 1 пару 64-х битных чисел в лучших схемах приблизительно за 5dt, а 32 пары 64-х битных чисел приблизительно за 32*5dt=160dt.
32 последовательных двоичных сумматора без схем ускоренного переноса бит за битом сложат 32 пары 64-х битных чисел приблизительно за 64*2dt=128dt.
32 последовательных четверичных сумматора без схем ускоренного переноса сложат 32 пары 64-х битных чисел приблизительно за (64/lg₂4)*2dt=64dt.
32 последовательных шестнадцатиричных сумматора без схем ускоренного переноса сложат 32 пары 64-х битных чисел приблизительно за (64/lg₂16)*2dt=32dt.
32 последовательных двухсотпятидесятишестиричных сумматора без схем ускоренного переноса сложат 32 пары 64-х битных чисел приблизительно за (64/lg₂256)*2dt=16dt, т.е. приблизительно в десять раз быстрее, чем параллельный 64-х битный сумматор со схемами ускоренного переноса.
32 последовательных четыретысячидевяностошестиричных сумматора без схем ускоренного переноса сложат 32 пары 64-х битных чисел приблизительно за (64/lg₂4096)*2dt=10,67dt.

См. также

Примечания

Литература

• Угрюмов Е. П. Элементы и узлы ЭЦВМ. М.: Высшая школа, 1976. — 232 с.
• Угрюмов Е. П. Цифровая схемотехника. — СПб.: БХВ-Петербург, 2001. — 528 с.
• Жан М. Рабаи, Ананта Чандракасан, Боривож Николич. 11. Проектирование арифметических блоков: Сумматор // Цифровые интегральные схемы. Методология проектирования = Digital Integrated Circuits. — 2-е изд. — М.: Вильямс, 2007. — С. 912. — ISBN 0-13-090996-3.

Ссылки

однозначный сумматор — это … Что такое однозначный сумматор?

одноразрядный сумматор — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl. сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

однозначный сумматор — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl.сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

добавочный однозначный — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl. сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

одноколонный сумматор — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl.сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

Сумматор с сохранением переноса — Мотивация Сумматор с сохранением переноса — это тип цифрового сумматора, используемый в компьютерной микроархитектуре для вычисления суммы трех или более n-битных чисел в двоичном формате. Он отличается от других цифровых сумматоров тем, что выводит два числа той же размерности, что и… Wikipedia

Сумматор с упреждающим переносом — 4-битный сумматор с упреждающим переносом Сумматор с упреждающим переносом (CLA) — это тип сумматора, используемый в цифровой логике.Сумматор упреждающего переноса повышает скорость за счет сокращения времени, необходимого для определения битов переноса. Его можно противопоставить более простому… Wikipedia

Сумматор с упреждающим переносом — Сумматор с упреждающим переносом — это тип сумматора, используемый в цифровой логике. Его можно сравнить с более простым, но обычно более медленным сумматором переноса пульсаций (см. Сумматор для получения подробной информации о сумматорах переноса пульсаций). Сумматор с волновым переносом работает так же, как карандаш… Wikipedia

Список отдельных томов Ace — Ace Books начали издавать жанровую фантастику в 1952 году.Первоначально они были в основном в привлекательном формате dos à dos, но в первые годы они также опубликовали несколько отдельных томов, и это число росло, пока двойники не перестали появляться примерно в…… Wikipedia

Ein-Bit-Addierer — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl. сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

einstelliges Addierwerk — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl.сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

vienskiltis sudėtuvas — statusas T sritis automatika atitikmenys: angl. сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

,

однозначный сумматор — это … Что такое однозначный сумматор?

одноразрядный сумматор — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl. сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

однозначный сумматор — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl.сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

добавочный однозначный — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl. сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

одноколонный сумматор — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl.сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

Сумматор с сохранением переноса — Мотивация Сумматор с сохранением переноса — это тип цифрового сумматора, используемый в компьютерной микроархитектуре для вычисления суммы трех или более n-битных чисел в двоичном формате. Он отличается от других цифровых сумматоров тем, что выводит два числа той же размерности, что и… Wikipedia

Сумматор с упреждающим переносом — 4-битный сумматор с упреждающим переносом Сумматор с упреждающим переносом (CLA) — это тип сумматора, используемый в цифровой логике.Сумматор упреждающего переноса повышает скорость за счет сокращения времени, необходимого для определения битов переноса. Его можно противопоставить более простому… Wikipedia

Сумматор с упреждающим переносом — Сумматор с упреждающим переносом — это тип сумматора, используемый в цифровой логике. Его можно сравнить с более простым, но обычно более медленным сумматором переноса пульсаций (см. Сумматор для получения подробной информации о сумматорах переноса пульсаций). Сумматор с волновым переносом работает так же, как карандаш… Wikipedia

Список отдельных томов Ace — Ace Books начали издавать жанровую фантастику в 1952 году.Первоначально они были в основном в привлекательном формате dos à dos, но в первые годы они также опубликовали несколько отдельных томов, и это число росло, пока двойники не перестали появляться примерно в…… Wikipedia

Ein-Bit-Addierer — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl. сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

einstelliges Addierwerk — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl.сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

vienskiltis sudėtuvas — statusas T sritis automatika atitikmenys: angl. сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

,Сумматоры

, Синтез одноразрядного сумматора, Последовательный многозначный сумматор, Параллельные сумматоры

Сумматоры

Синтез однозначного сумматора

Как известно, все разнообразие математических операций можно свести к одной операции сложения прямого и обратного кодов чисел, сдвинутых влево или вправо на определенное количество цифр. Поэтому одним из основных узлов вычислительных устройств является сумматор (СМ). Любые многозначные целые числа могут быть построены на основе однозначного сумматора, складывающего три однозначных двоичных числа — a и b с с учетом перехода от младшего разряда суммы.Результат его работы — одна выплата суммы и сигнал о переводе в более высокий ранг. В табл. 3.11 показаны все возможные варианты цифры i суммы s i и переход в старший разряд < p i + i, которые возникают при сложении a i , b i с переносом p i.

Таблица 3.11

Перенести предыдущую цифру p i	Термин		Сумма с i	Перевод на старшую цифру pi + 1
	и и	b i
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Скомпилированные данные для сигнала передачи:

Выполняя неполную склейку первого соединения с четвертым, второго с четвертым и третьего с четвертым, получаем:

(3.1)

Для получения булевой сигнальной функции суммы s i можно использовать обычный метод на основе SovDNF, но в интегральной схеме для этого используется другой вид функции s i, который использует Результирующее выражение для сигнала j + l p . Следует отметить, что во всех строках таблицы истинности, кроме первой и последней,. Использовать сигнал

p i + 1, вам нужно получить из него выражение, удовлетворяющее первой и последней строкам.Выражение равно нулю только в первой строке таблицы, а во всех остальных равно единице. Итак, конъюнкция с выражением сохраняет все отдельные значения, кроме первой строки. Чтобы добавить единицу к последней строке, выполните операцию ИЛИ полученного выражения с конъюнкцией a i b i strong> p i Таким образом, выражение для сигнала суммы s приму окончательную форму:

Поскольку в интегральной схеме базовый элемент обычно обеспечивает инвертирование, схема сумматора имеет вид, показанный на рис.3.22, а. Для получения прямых значений сигналов si и p <+ i + 1 необходимы еще два инвертора. Условное обозначение одноразрядного сумматора показано на рис. 3.22, b.

Рис. 3.22. Сумматор:

и — функциональная схема; b — символ

Последовательный многобитовый сумматор

Используя однобитовый сумматор, вы можете построить суммирующее устройство для сложения многобитовых двоичных чисел.Различают многобитовые последовательные и параллельные сумматоры.

Последовательный сумматор состоит из однобитового сумматора, входы которого из сдвиговых регистров, хранящих члены A и B, , обозначены полосами после разряда кодов этих чисел, начиная с младшей цифры (рисунок 3.23). Если время элемента задержки равно одному тактовому циклу (например, используется триггер D), сигнал переноса из предыдущей цифры, сформированной в предыдущем тактовом цикле, поступит на нижний вход сумматора только в следующих тактах, когда входы a и b , будет сообщена следующая цифра позиций.В результате на выходе s strong> B будет сгенерировано двоичное число, равное сумме чисел A и , которое будет восприниматься регистром суммы сдвига.

Рис. 3.23. Последовательный многобитовый сумматор

Параллельные сумматоры

Недостатком последовательного сумматора является то, что операция сложения растягивается на набор мер, превышающий количество цифр.Параллельный сумматор имеет значительно меньшее время выполнения. В этом устройстве операция сложения выполняется одновременно для всех цифр номеров A и B, , поступающих в параллельном коде. Для этого схема состоит из одноразрядного сумматора n , соединяющего выход передачи i-го разряда с входом передачи соседнего разряда (i + 1) (см. Рисунок 3). ,24). Такой сумматор называется последовательным сумматором переноса. После того, как результат сформирован на выходах всех однозначных сумматоров, он сохраняется в параллельном регистре.

Чтобы результат формировался на выходах одноразрядных сумматоров, на входах должны присутствовать все три сигнала: a i , b i и p i. Но сигнал перехода от разряда к разряду генерируется предыдущим однобитовым сумматором, причем каждый последующий сумматор должен ждать, пока результат не сформируется во всех предыдущих.В крайнем случае возможно, что сигнал передачи будет передаваться последовательно по всей цепочке от младшего разряда до старшего, например, при сложении чисел A = 11 … 11 и In = 00 … 01. Следовательно, время формирования результата наихудшего случая включает в себя временные задержки, вносимые всеми однозначными сумматорами.

Рис. 3.24. Параллельный секвенсор с последовательной передачей

Без учета продолжительности распространения позволяет сумматор с параллельной передачей. Идея состоит в том, что сигналы переноса для всех цифр формируются чисто логически на основе терминов A и B. Подумайте, как это сделать.

Сигнал передачи на первую цифру p 1 = a 0 b 0. Сигнал передачи на второй бит можно определить по формуле (3.1):

Как видите, сигнал переноса p 2 может быть получен из значений предыдущих цифр A и In без сигнала переноса p 1, сгенерировано сумматором.Подставляя выражение для сигнала передачи p 2 в формулу (3.1), можно получить логическое выражение для сигнала передачи третьей цифры, в котором также значения только предыдущих цифр чисел < strong> A и В и т. д. Таким образом, транспортные сигналы для любой цифры могут быть сформированы чисто логически по значениям термов. Следовательно, нет необходимости ждать, пока сигналы передачи будут сгенерированы однозначными сумматорами.Очевидно, однако, другое. Чем больше разрядов числа, тем выше сложность булевых функций сигналов передачи, особенно для самой старшей цифры. Следовательно, сумматоры с параллельным переносом подходят для чисел небольшой разрядности — не более восьми.

Структура сумматора с параллельным транспортом показана на рис. 3.25. Сигналы передачи генерируются специальной логикой быстрой передачи CR

.

однозначный сумматор — это … Что такое однозначный сумматор?

одноразрядный сумматор — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl. сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

однозначный сумматор — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl.сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

добавочный однозначный — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl. сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

одноколонный сумматор — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl.сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

Сумматор с сохранением переноса — Мотивация Сумматор с сохранением переноса — это тип цифрового сумматора, используемый в компьютерной микроархитектуре для вычисления суммы трех или более n-битных чисел в двоичном формате. Он отличается от других цифровых сумматоров тем, что выводит два числа той же размерности, что и… Wikipedia

Сумматор с упреждающим переносом — 4-битный сумматор с упреждающим переносом Сумматор с упреждающим переносом (CLA) — это тип сумматора, используемый в цифровой логике.Сумматор упреждающего переноса повышает скорость за счет сокращения времени, необходимого для определения битов переноса. Его можно противопоставить более простому… Wikipedia

Сумматор с упреждающим переносом — Сумматор с упреждающим переносом — это тип сумматора, используемый в цифровой логике. Его можно сравнить с более простым, но обычно более медленным сумматором переноса пульсаций (см. Сумматор для получения подробной информации о сумматорах переноса пульсаций). Сумматор с волновым переносом работает так же, как карандаш… Wikipedia

Список отдельных томов Ace — Ace Books начали издавать жанровую фантастику в 1952 году.Первоначально они были в основном в привлекательном формате dos à dos, но в первые годы они также опубликовали несколько отдельных томов, и это число росло, пока двойники не перестали появляться примерно в…… Wikipedia

Ein-Bit-Addierer — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl. сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

einstelliges Addierwerk — vienskiltis sudėtuvas statusas T sritis automatika atitikmenys: angl.сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

vienskiltis sudėtuvas — statusas T sritis automatika atitikmenys: angl. сумматор на один столбец; одноразрядный сумматор; однозначный сумматор вок. Эйн Бит Аддирер, м; einstelliges Addierwerk, рус. одноразрядный сумматор, м пранц. extraneur mono digit, m… Automatikos terminų žodynas

,