Электрические величины. Напряжение, ток, мощность. Переменный и постоянный ток, полярность.

Содержание

Электричество – это движение электронов по проводам. Ток – это скорость движения электронов, измеряемая в Амперах, напряжение – сила заставляющая их двигаться, измеряемая в Вольтах. Для того, чтобы ток протекал в цепи, она должна быть замкнута и в ней должен присутствовать источник электрического напряжения. Вот почему любое устройство подключается к сети как минимум двумя проводами, а каждая батарейка имеет как минимум два контакта. Любой проводник, либо электроприбор, включенный в сеть, создает в цепи сопротивление движению электронов, измеряемое в Омах. Чем меньше напряжение и больше сопротивление, тем меньше будет ток. Это и есть главный закон электричества – закон Ома. Записывается он следующим образом:

Рисунок 1 — Закон Ома.

Наглядно можно представить себе закон Ома в виде трех граждан с характером:

Рисунок 2 — Закон Ома (наглядное представление).

Ток и напряжение бывают как постоянными, так и переменными.
Постоянное напряжение всегда направлено в одну сторону, соответственно и ток будет всегда направлен туда же. Для постоянного тока характерна полярность, обозначаемая значками «+» и «-». Полярность обозначает направление протекания тока, и для многих устройств, включая светодиоды, это направление очень важно не перепутать.Постоянное напряжениеочень удобно в плане хранения, поэтому трудится оно в автомобилях и во всех портативных устройствах на батарейках и аккумуляторах. А вот передача на большие расстояние постоянного напряжения невозможна из-за слишком больших потерь.

Рисунок 3 — Постоянный ток.

И вот в этом, нам на помощь приходит переменное напряжение. Оно названо так, потому что меняет свое направление много раз в секунду (50 раз в обычной российской розетке), соответственно и ток тоже будет протекать то в одну, то в другую сторону. У такого тока нет полярности, а провода обозначаются как «L» и «N».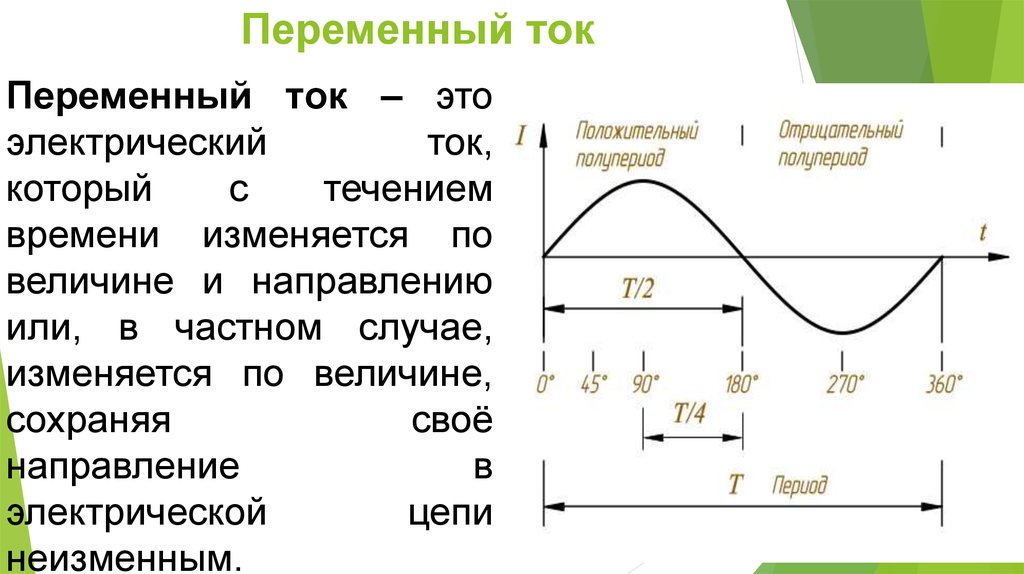

Переменное напряжение удобно для его выработки при помощи различных генераторов, передачи на любые расстояния, повышения или понижения при помощи обычных трансформаторов. Его можно встретить в любом доме, магазине и офисе, в каждой розетке, в линиях электропередач.

Рисунок 4 — Переменный ток.

Каждый электрический прибор имеет мощность, которая измеряется в Ваттах (Вт). Чем больше ток и напряжение, тем больше мощность. Рассчитать ее можно по формуле:

Рисунок 5 — Формула мощности.

Как видим из формулы, это произведение напряжения и тока, а значит при одинаковой мощности, лампочка на 100Вт в автомобиле при 12В питания, будет потреблять гораздо больший ток, чем 10Вт лампочка на 220В в домашней люстре.
Соединяя формулу мощности и закон Ома, мы получим еще две удобные формулы для вычисления мощности при известном сопротивлении нагрузки:

Рисунок 6 — Формула вычисления мощности.Рисунок 7 — Формула вычисления мощности.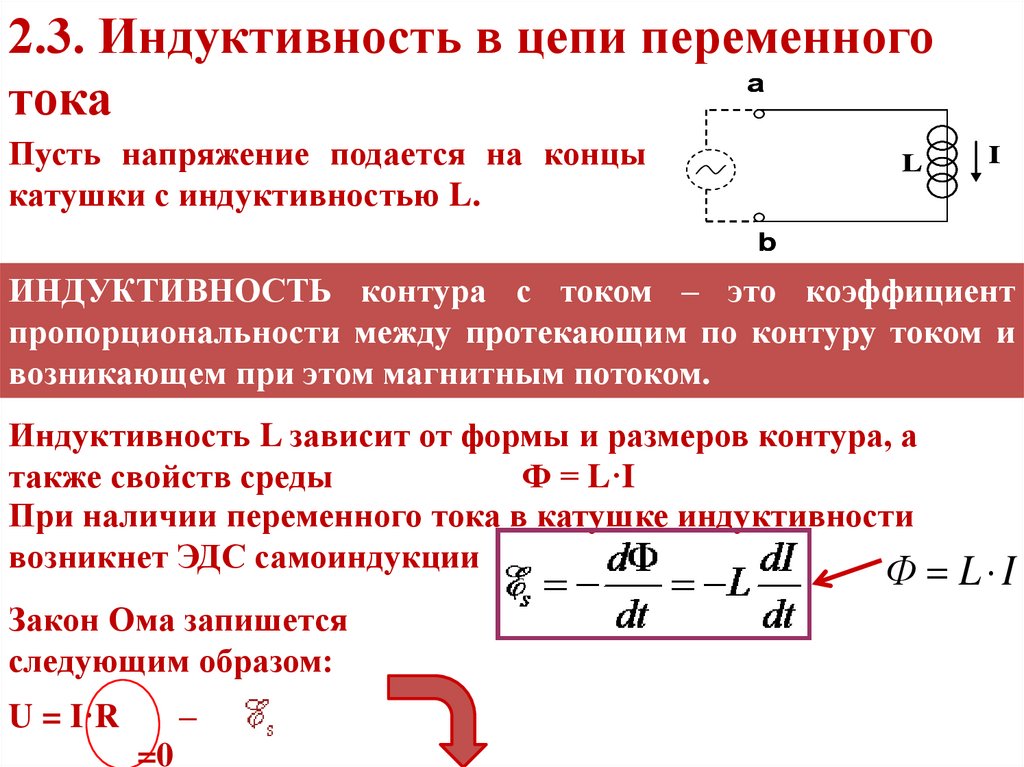

Тэги:

#основы #вольты_и_ватты

• Почему постоянный ток не используется в городских электросетях?
• Что обозначают метки + и – у батарейки?
• У вас есть блок питания 12В 200Вт. Какой ток он способен отдавать в цепь? А блок на 24В 200Вт?
• У вас есть батарейка на 3В, и вы подключили к ней резистор с сопротивлением 10 Ом. Какой ток потечет через резистор? Какая мощность будет на нем выделяться?

10.26.2022

Наша компания участвует в выставке Art Dom 2022

Новости

06.03.2022

Светодиодные модули. Устройство. Виды модулей. Монтаж и подключение

Освещение в квартире

06.03.2022

ТОП 6 идей по использованию светодиодной ленты SWG в интерьере

Освещение в квартире

06.03.2022

220В лента, особенности подключения и монтажа

Освещение в квартире

06.03.2022

Освещение для большого офиса в центре Москвы: подбор и особенности

Освещение в квартире

06. 03.2022

НЕСКУЧНОЕ ОСВЕЩЕНИЕ ЗАГОРОДНОГО ДОМА

Освещение в квартире

06.03.2022

ОСВЕЩЕНИЕ ФИТНЕС ЦЕНТРА

Освещение в квартире

06.02.2022

Почему нет бина на RGB ленте?

Освещение в квартире

04.29.2022

Сколько светильников нужно в офис, размеры которого заставляют сотрудников ездить на самокатах?

Вопрос-ответ

04.29.2022

Традиционные источники света (лампы). Их питание и диммирование

Освещение в квартире

04.28.2022

Слои освещения на примере кухонной зоны

Освещение в квартире

04.27.2022

Блоки питания. Требования по безопасности, особенности подключения и монтажа

Освещение в квартире

Спасибо,
ваша заявка принята!

Подписаться на рассылку

Ваш e-mail*

Согласен на обработку персональных данных

Спасибо,
за подписку!

Основы электротехники 4 – Переменный ток

Этим постом мы продолжаем серию публикаций, посвящённых основам электротехники. В нём мы поговорим о переменном токе. Основные задачи электротехники – это произвести, передать и распределить энергию, по пути её к тому же приходится, преобразовывать. Всё это проще делать на переменном токе, чем на постоянном. Вообще говоря, переменный – это всё, что не постоянно, но мы будем говорить о синусоидальных токах и напряжениях, потому что именно их используют на практике.

Почему это пошло от генераторов электроэнергии? Их проще всего сделать так, чтобы они выдавали синусоидальное напряжение, а синусоидальное напряжение по природе своей точно такое же, как постоянное, только его значение изменяется во времени по закону синуса.  Вообще переход от вращения к синусоиде очень простой.  Поэтому, например, синусоиду удобно описывать с помощью угловой частоты Ω. Об этом мы поговорим ещё позже. Раз уж мы заговорили об описании синусоиды, то остановимся пока на этом и дадим несколько определений.

Мгновенное значение – это значение в данный момент времени.

Амплитудное значение – наибольшее значение которого достигает сигнал.

Действующее значение – это такое значение постоянного напряжения, которое производит такой же тепловой эффект, как и рассматриваемые синусоидальные.

Период – наименьший период времени между двумя одинаковыми значениями сигнала. 

Частота линейная – это величина обратная периоду, угловая – 2 π f. Об этом поговорим чуть позже.

Фаза – это то, насколько синусоида сдвинута относительно начала координат в момент времени 0.

Когда говорят о переменном напряжении или токе, говорят обычно действующее значение и частоту. Например, в розетке 220 Вольт, 50 Герц. Это значит, что действующее значение 220 Вольт, а линейная частота 50 Герц, период 20 миллисекунд кстати.

Теперь о том, как ведут себя элементы цепи на переменном токе. С резистором ничего нового, но появляются два новых элемента: ёмкость и индуктивность.  

Начнём с ёмкости, то есть конденсатора. Конденсатор представляет из себя две пластины, разделенные диэлектриком. Прикладываем напряжение, побежали электроны, то есть потек ток. Бежать они могут только до пластины, дальше некуда. На пластинах место ограничено, поэтому чем больше электронов там уже есть, тем медленнее прибегают новые, то есть ток постепенно спадает.

Из-за того, что напряжение у нас синусоидальное, ток спадает до 0 ровно в тот момент, когда напряжение достигает максимума. Не будем сейчас лезть в математику, просто примем это на веру. Напряжение у нас теперь начинает уменьшаться, значит электроны на пластине ему уже удерживать сложнее. Они начинают бежать обратно, то есть ток меняет знак. Быстрее всего они бегут тогда, когда напряжение равно нулю, ток становится максимальным. Дальше всё повторяется в обратную сторону и так далее.

Если посмотреть теперь на график тока и напряжения, можно увидеть, что ток достигает какого-то значения раньше, чем напряжение.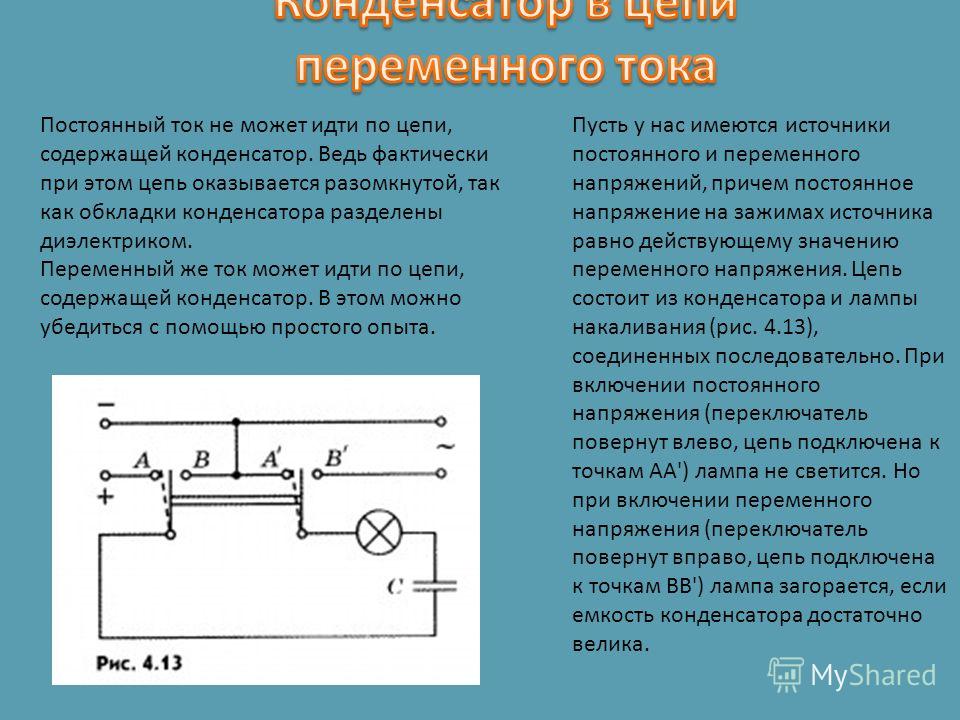 Например, в нулевой момент времени напряжение ещё равно нулю, а ток уже максимальный. Поэтому говорят, что на ёмкости ток опережает напряжение. В идеальном случае это опережение составляет четверть периода или π/2 (если переходят в угловые меры).

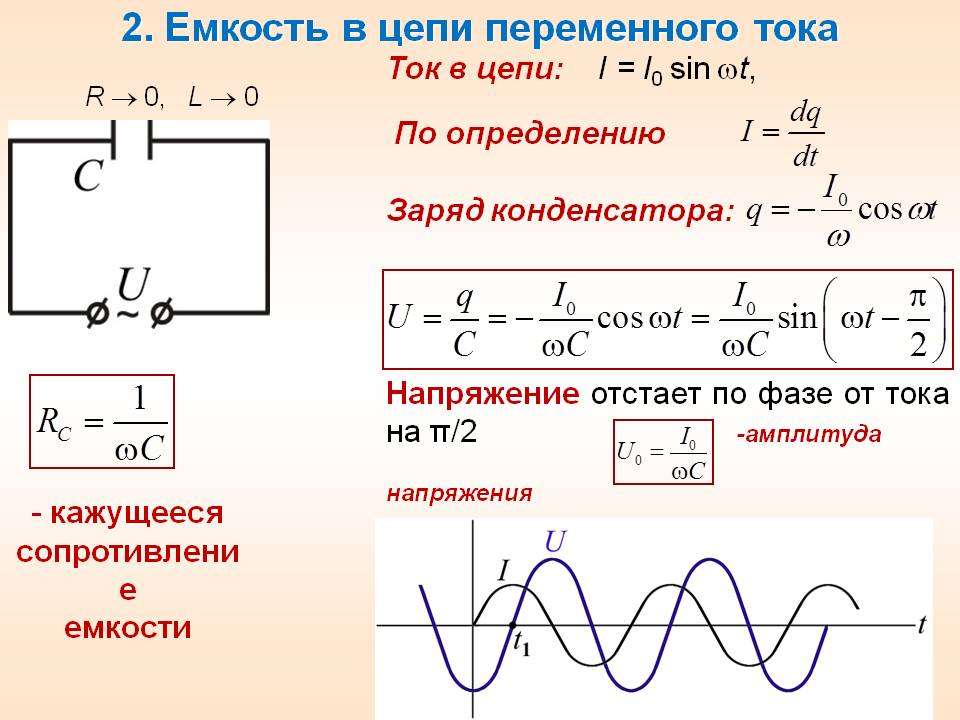
Чтобы определить какой ток потечёт через конденсатор, нам понадобится сделать некоторые математические выкладки. Сначала охарактеризуем конденсатор численно и введем для этого понятия ёмкости. Ёмкость – это отношение заряда на пластинах к напряжению, при котором оно возникает.

Теперь вспоминаем что ток – это производная заряда по времени. Отсюда получаем выражение для тока через напряжение. Подставим теперь переменное напряжение, пропустим скучноватую математику и получим выражение для тока.  Осталось поделить напряжение для тока и получаем выражение для ёмкостного сопротивления.

Второй новый элемент – индуктивность. Самый простой индуктивный элемент – это катушка из провода.

Для понимания её работы нам понадобится еще один вспомогательный закон (закон электромагнитной индукции). На нём строится почти вся теория электрических машин, но для нас сейчас это не более чем вспомогательный факт. Суть этого закона в том, что переменное магнитное поле порождает электрическое и главное наоборот. То есть вокруг любого проводника с переменным током есть магнитное поле, но, когда провод сворачивается в катушку почти всё порождаемое им поле концентрируется внутри катушки и начинает влиять на неё саму.

Влияние это заключается в том, что магнитное поле, порождённое катушкой, начинает создавать в ней самой поле электрическое. Звучит так, как будто “Мюнхаузен вытаскивает сам себя за волосы”, но всё дело в направлении этого наведённого поля. Его можно вывести математически, для синусоиды это несложно, но мы воспользуемся очень удобным и простым правилом Ленца, которое есть не что иное как красиво сформулированный закон зловредства. Наведённое ЭДС всегда направлено так, чтобы противодействовать полю её породившему. То есть наведенное ЭДС направлено навстречу напряжению на катушке и мешает току протекать через неё. Иногда для того, чтобы лучше запоминалось, говорят, что ток запутывается в витках катушки. Как бы то ни было, приводит это к тому, что ток через катушку отстаёт от напряжения и тоже на четверть периода, те π/2.

Индуктивное сопротивление математически выводится похоже на то, как выводится ёмкостное, только исходная характеристика здесь не ёмкость, а индуктивность, отношение магнитного потока в катушке к току, которой её породил. Затем берем закон электромагнитной индукции и связываем ток с напряжением через дифференциальные уравнения. Дальше опять немного скучная, но простая математика, и в результате несложных выкладок получаем выражение для напряжения при синусоидальном токе, делим одно на другое, получаем выражение для индуктивного сопротивления.

Вообще говоря, ёмкость и индуктивность очень похожи по своим свойствам, но с точностью до наоборот. Поэтому если вы затрудняетесь вспомнить что-то касающееся одного из них, попробуйте вспомнить для одного из них и сделать всё наоборот. Почти наверняка не ошибетесь.

Для цепей переменного тока справедливы все законы, что мы с вами рассмотрели раньше. Поскольку эти законы фундаментальные и следуют из самой природы вещества.

Однако считать по ним становится уже весьма трудно, приходится делить и умножать синусы, да ещё и с разными фазами. Для того чтобы уйти от всей этой тригонометрии, пользуются так называемыми векторными диаграммами.

Векторные диаграммы. Разберёмся что это и для начала введём понятие вектора для некоторой синусоиды. Для определённости пусть это будет ток с амплитудой Im и фазой φ, для общности берем произвольную фазу. Теперь строим плоскость координат и проводим из её центра вектор, длина которого равна Im, а угол с осью абсцисс равен φ.

То, что у нас получилось, как раз и есть вектор, соответствующий переменному току, амплитудой Im и фазой φ. Если теперь у нас появится ток с другой амплитудой и фазой, то его мы сможем тоже изобразить на этой же плоскости. Теперь понятно зачем мы переходили в угловые величины, когда говорили об отставании, опережении тока, это углы между векторами на плоскости координат.

Следующий шаг, перейдя в декартовы координаты, мы смогли избавиться от тригонометрических функций, операции над векторами уже стали чисто алгебраическими, привычным. Сделаем ещё один небольшой шаг и заметим, что если принять, что ось абсцисс действительная, а ось ординат – мнимая, то мы сможем пользоваться хорошо разработанным математическим аппаратом для комплексных чисел.

 

Именно в виде векторов на комплексной плоскости чаще всего анализируют переменные токи и напряжения. Они позволяют не только наглядно изобразить их, но и применить для расчёта цепей множество вычислительных приёмов, упрощающих и ускоряющих расчёт. Сейчас мы не будем их касаться, это предмет рассмотрения скорее строго академического курса, посмотрим вещь более простую и практическую: активную, реактивную и полной мощности.

Не давая строгого определения, рассмотрим, что они означают практически. Активная мощность – это та мощность, которая совершает полезную работу. Иначе говоря, что-то греет, крутит, двигает и так далее. Но посмотрим ещё раз на процесс, происходящий в конденсаторе. Заряды к нему то приходят, то уходят, ток создается, идёт в разные стороны. Но обратите внимание, все эти перемещения происходят в пределах одного узла цепи, то есть потенциал не меняется. Значит, хотя ток и есть, но работа не совершается.

Для разрешения этого противоречия вводят понятие реактивной мощности – эта мощность не совершает работы, а нужна только для создания электромагнитного поля. Обратимся ещё раз немного к математике. Вспомним как смещены друг относительно друга ток и напряжение конденсатора – на 90°.

А теперь то же самое для резистора – на нём ток и напряжение совпадают по фазе. Ток, текущий через конденсатор, как мы уже видели, работы не совершает. Его называют реактивным током. Он создаёт реактивную мощность. На векторной диаграмме он направлен по мнимой оси.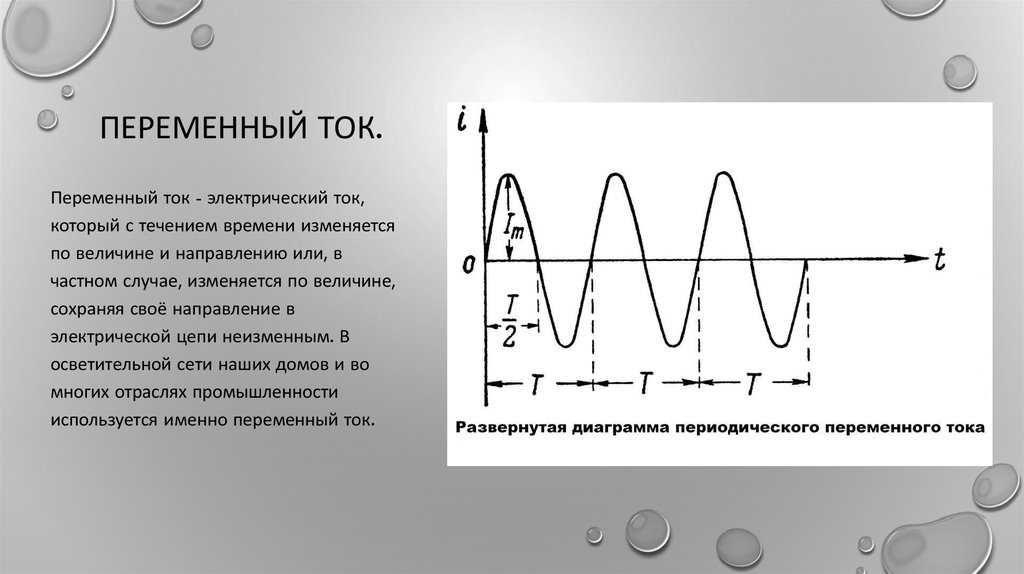

Ток, текущий через резистор, работу как раз-таки завершает, его поэтому называют активным. На векторной диаграмме он направлен уже по действительной оси. Поскольку реальные элементы цепи – это всегда комбинация активных и реактивных векторов, то и реальные токи – это всегда комбинация активных и реактивных.

Их векторная сумма называется полным током, векторная сумма активной и реактивной мощностей – полной мощностью. В полной мере эти понятия используется не столько в электротехнике, сколько в электроэнергетике, поэтому сейчас мы на них подробно останавливаться не будем. Посмотрим лучше, как описанные ранее эффекты выглядят на моделях.

Начнем с модели первой. Здесь одно и тоже переменное напряжение, мы прикладываем к ёмкости и индуктивности. Источник здесь собран из блоков Simulink, чтобы можно было на ходу менять частоту. Начнём её менять и увидим изменения тока. На индуктивности он падает, потому что сопротивление индуктивности прямо пропорционально частоте, а на емкости растёт, потому что емкостное сопротивление обратно пропорционально частоте приложенного напряжения.

Теперь вторая модель. Здесь у нас, как мы видим, резистор, токоограничивающий, по сути, батарея конденсаторов. Если мы включаем резистор без конденсаторов, то мы увидим, что ток и напряжение совпадает по фазе. Как только начинаем конденсаторы подключать, увидим, как ток постепенно смещается относительно напряжения, изменяется его фаза. 

На этом мы завершаем наш рассказ об элементах цепи переменного тока. В следующей публикации мы ненадолго отвлечемся от классической теории электротехники и поговорим о полупроводниковых элементах: диодах и транзисторах.

 

Другие публикации по данной теме:

Основы электротехники, введение

Основы электротехники 2 — Электрическая цепь

Основы электротехники 3 — Расчет режима цепи

Переменное напряжение Определение и значение

• Основные определения
• Викторина
• Примеры

Показывает уровень оценки в зависимости от сложности слова.

Сохрани это слово!

Показывает уровень сложности слова.

---

сущ. Электричество.

напряжение, которое меняет направление в регулярных циклах.

ВИКТОРИНА

ВСЕ ЗА(U)R ЭТОГО БРИТАНСКОГО ПРОТИВ. АМЕРИКАНСКИЙ АНГЛИЙСКИЙ ВИКТОРИНА

Существует огромная разница между тем, как люди говорят по-английски в США и Великобритании. Способны ли ваши языковые навыки определить разницу? Давай выясним!

Вопрос 1 из 7

Правда или ложь? Британский английский и американский английский различаются только сленговыми словами.

Слова рядом с переменным напряжением

переменный ток, переменно-градиентная фокусировка, переменная группа, переменный свет, переменный ряд, переменное напряжение, чередование, чередование поколений, альтернатива, альтернативное соединение, альтернативная учебная программа

Dictionary.com Unabridged На основе Random House Unabridged Dictionary, © Random House, Inc.

, 2023 г.

Как использовать переменное напряжение в предложении

• Она добавила высоким, громким голосом, как будто попеременно сосала гелий и бонг.

  Ким Кардашьян Конундрум из SNL: почему уход Назима Педрада так болезненно|Джейсон Линч|26 сентября 2014 г.|DAILY BEAST

• Они также сбивали с толку, чередуя большие надежды и разочарования.

  Progressive-palooza: Об Обаме, Occupy и моральном понедельнике|Джедедайя Парди|5 июля 2014 г.|DAILY BEAST

• С чередующимися главами роман отправляет нас в лихорадочное путешествие через перспективы этих маловероятных апокалиптов.

  В новом романе апатичные подростки возвещают апокалипсис|Эллиот Акерман|9 июня 2014|DAILY BEAST

• Он преуспевает в пределах своих собственных параметров, но никогда не вызывает максимальное напряжение искреннего удивления.

  Герой дебютного романа Теда Томпсона — 1 процент|Стефан Бек|6 мая 2014 г.|DAILY BEAST

• В чередующихся главах два рассказчика романа описывают свою жизнь с Исааком из двух разных периодов времени.

  Горячие чтения этой недели: 3 марта 2014 г.|Николас Манкузи|3 марта 2014 г.|DAILY BEAST

• Он оглянулся – посмотрел вниз – на прежние эмоции и действия; и отсюда сбивающее с толку чередование ревности и прощения.

  Волна|Алджернон Блэквуд

• Многие приятные утра могут быть проведены в гостях, когда одна дама читает вслух, пока другая шьет, чередуя работу.

  Книга женского этикета и Руководство по вежливости|Флоренс Хартли

• Фоном галереи была масса тропических растений, чередующихся с решетчатыми окнами и длинными стеклянными дверями.

  Предки|Гертруда Атертон

• В средней части вы сделали что-то новое и хорошее; чередующиеся аккорды над точкой педали, скорее, как у Руслана.

  Жизнь и жизнь Письма Петра Ильича Чайковского|Модеста Чайковского

• Очень распространена строфа, состоящая из четырехстопного стиха, чередующегося с трехстопным.

  Английский язык: композиция и литература|W. Ф. (Уильям Франклин) Вебстер

20,5: переменный ток в сравнении с постоянным током

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

2683

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Объяснять различия и сходства между переменным и постоянным током.
• Рассчитать среднеквадратичное значение напряжения, тока и средней мощности.
• Объясните, почему переменный ток используется для передачи энергии.

Переменный ток

Большинство примеров, рассмотренных до сих пор, и особенно те, в которых используются батареи, имеют источники постоянного напряжения. Как только ток установлен, он, таким образом, также является постоянным. Постоянный ток (DC) представляет собой поток электрического заряда только в одном направлении. Это устойчивое состояние цепи постоянного напряжения. Однако в большинстве известных приложений используется источник переменного напряжения. Переменный ток (AC) представляет собой поток электрического заряда, который периодически меняет направление. Если источник периодически меняется, особенно синусоидально, цепь известна как цепь переменного тока. Примеры включают коммерческую и жилую энергию, которая удовлетворяет многие из наших потребностей. На рисунке \(\PageIndex{1}\) показаны графики зависимости напряжения и тока от времени для типичного питания постоянного и переменного тока. Напряжение и частота переменного тока, обычно используемые в домах и на предприятиях, различаются по всему миру.

Рисунок \(\PageIndex{1}\): (a) Напряжение постоянного тока и ток постоянны во времени после установления тока. (b) График зависимости напряжения и тока от времени для сети переменного тока с частотой 60 Гц. Напряжение и ток синусоидальны и находятся в фазе для простой цепи сопротивления. Частоты и пиковые напряжения источников переменного тока сильно различаются.

На рисунке \(\PageIndex{2}\) показана схема простой цепи с источником переменного напряжения. Напряжение между клеммами колеблется, как показано, с напряжением переменного тока определяется как \[V = V_{0} sin 2 \pi ft, \label{20.6.1}\], где \(V\) — напряжение в момент времени \(t\), \(V_{0}\ ), \(V_{0}\) — пиковое напряжение, а \(f\) — частота в герцах. Для этой простой цепи сопротивления \(I = V/R\), поэтому переменный ток равен

\[I = I_{0} sin 2 \pi ft, \label{20.6.2}\]

, где \(I\) — ток в момент времени \(t\), а \(I_{0} = V_{0} / R\) — пиковый ток. В этом примере говорят, что напряжение и ток совпадают по фазе, как показано на рисунке \(\PageIndex{1b}\).

Рисунок \(\PageIndex{2}\): Разность потенциалов \(В\) между клеммами источника переменного напряжения колеблется, как показано.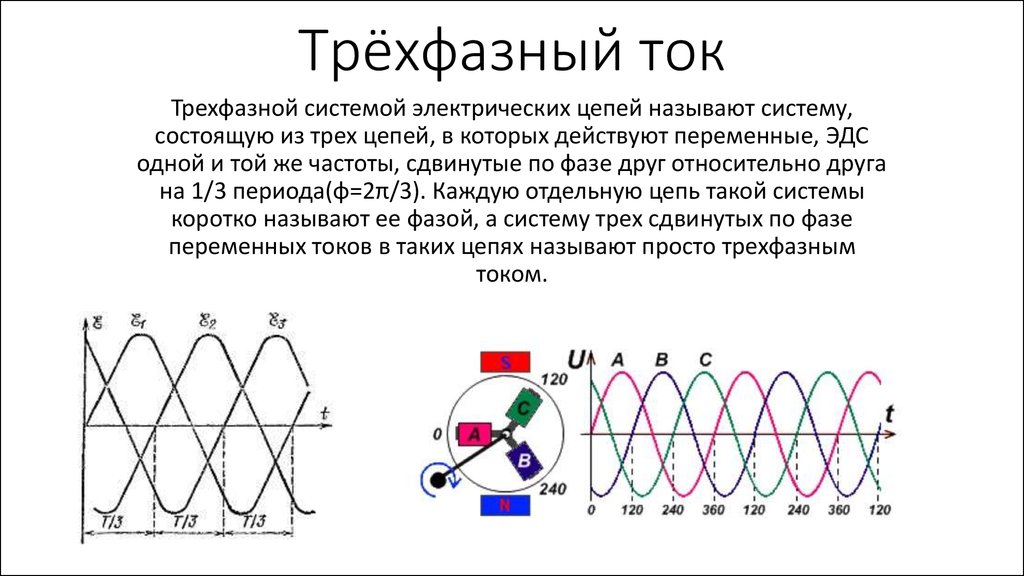 {2}2\pi ft\), как показано на рисунке \(\PageIndex{3}\).

Рисунок \(\PageIndex{3}\): Мощность переменного тока как функция времени. Поскольку здесь напряжение и ток совпадают по фазе, их произведение неотрицательно и колеблется между нулем и \(I_{0}V_{0}\). Средняя мощность равна \( \left( 1/2 \right) I_{0} V_{0}\).

Установление связей: домашний эксперимент — освещение переменного/постоянного тока

Проведите рукой вперед и назад между лицом и флуоресцентной лампочкой. Наблюдаете ли вы то же самое с фарами на вашем автомобиле? Объясните, что вы наблюдаете. Внимание! Не смотрите прямо на очень яркий свет.

Чаще всего нас интересует средняя мощность, а не ее колебания — например, 60-ваттная лампочка в вашей настольной лампе потребляет в среднем 60 Вт. Как показано на рисунке 3, средняя мощность \(P_{ave}\) равна \[P_{ave} = \frac{1}{2}I_{0}V_{0}. \label{20.6.3}\] Это видно из графика, так как площади выше и ниже линии \(\left(1/2\right)I_{0}V_{0}\) равны, но это также можно доказать с помощью тригонометрических тождеств.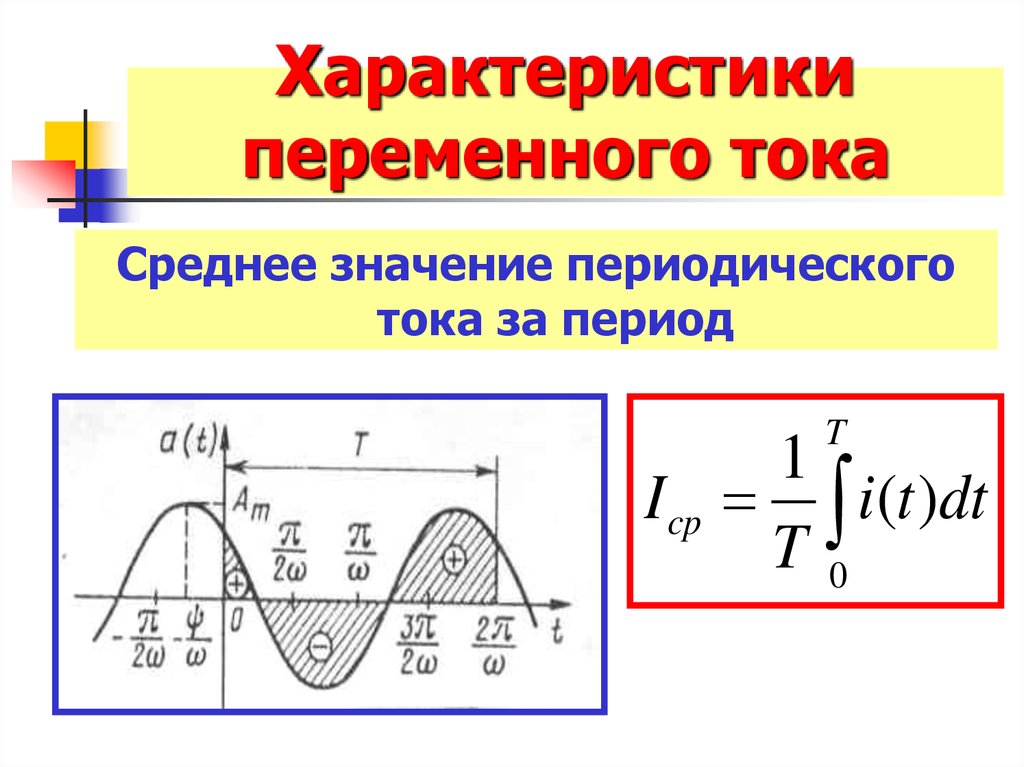 Точно так же мы определяем среднее или действующее значение тока \(I_{rms}\) и среднее значение или действующее значение напряжения \(V_{rms}\) должно быть, соответственно,

\[I_{rms} = \frac{I_{0}}{ \sqrt{2}}\label{20.6.4}\]

и

\[V_{rms} = \frac{V_{0}}{\sqrt{2}}.\label{20.6.5} \]

, где rms означает среднеквадратичное значение, особый вид среднего значения. В общем, для получения среднеквадратичного корня конкретную величину возводят в квадрат, находят ее среднее (или среднее) и извлекают квадратный корень. Это полезно для переменного тока, так как среднее значение равно нулю. Теперь \[P_{ave} = I_{rms}V_{rms}, \label{20.6.6}\], что дает

\[P_{ave} = \frac{I_{0}}{\sqrt{2}} \cdot \frac{V_{0}}{\sqrt{2}} = \frac{1}{2} I_{0}V_{0}, \label{20.6.7}\]

, как указано выше. Стандартной практикой является указывать \(I_{rms}\), \(V_{rms}\) и \(P_{ave}\), а не пиковые значения. Например, в большинстве бытовых электросетей напряжение переменного тока составляет 120 В, а это означает, что \(V_{rms}\) равно 120 В.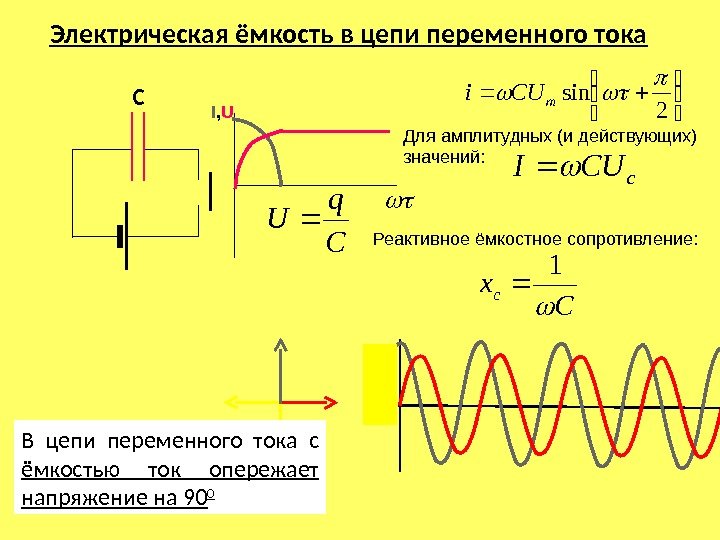 Обычный автоматический выключатель на 10 А отключит устойчивое напряжение \(I_{rms}\), превышающее 10 А. Ваша микроволновая печь мощностью 1,0 кВт потребляет \(P_{ave} = 1,0 кВт\) и так далее. Вы можете думать об этих среднеквадратичных и средних значениях как об эквивалентных значениях постоянного тока для простой резистивной цепи. 9{2}_{rms}R.\label{20.6.11}\]

Пример \(\PageIndex{1}\): Пиковое напряжение и мощность для переменного тока

(a) Каково значение пикового напряжения для сети переменного тока 120 В?

Стратегия

Нам говорят, что \(V_{rms}\) равно 120 В, а \(P_{ave}\) равно 60,0 Вт. Мы можем использовать \(V_{rms} = \frac{V_{0 }}{\sqrt{2}}\), чтобы найти пиковое напряжение, и мы можем манипулировать определением мощности, чтобы найти пиковую мощность из заданной средней мощности.

Решение
Решение уравнения \(V_{rms}=\frac{V_{0}}{\sqrt{2}}\) для пикового напряжения \(V_{0}\) и подстановка известного значения для \(V_{rms}\) дает \[V_{0} = \sqrt{2} V_{rms} = 1,414\left(120 V\right) = 170 V. \]

Обсуждение

Это означает, что переменное напряжение колеблется от 170 В до \(-170 В\) и обратно 60 раз в секунду. Эквивалентное постоянное напряжение равно 120 В.

(b) Какова пиковая потребляемая мощность лампочки переменного тока мощностью 60,0 Вт?

Решение

Пиковая мощность представляет собой произведение пикового тока на пиковое напряжение. Таким образом, \[P_{0} = I_{0}V_{0} = 2\left(\frac{1}{2} I_{0} V_{0} \right) = 2P_{ave}.\] Мы известно, что средняя мощность равна 60,0 Вт, поэтому \[P_{0} = 2\left(60,0 Вт\right) = 120 Вт.\]

Обсуждение

Итак, мощность колеблется от нуля до 120 Вт сто двадцать раз в секунду (дважды за цикл), а средняя мощность составляет 60 Вт.

Зачем использовать переменный ток для распределения электроэнергии?

Большинство крупных систем распределения электроэнергии работают на переменном токе. Кроме того, мощность передается при гораздо более высоких напряжениях, чем 120 В переменного тока (240 В в большинстве стран мира), которые мы используем дома и на работе. Экономия за счет масштаба делает строительство нескольких очень крупных электростанций дешевле, чем строительство множества мелких. Это требует передачи энергии на большие расстояния, и, очевидно, важно, чтобы потери энергии в пути были сведены к минимуму. Как мы увидим, высокое напряжение может передаваться с гораздо меньшими потерями мощности, чем низкое напряжение. (См. рис. 4.) Из соображений безопасности напряжение у пользователя снижено до привычных значений. Решающим фактором является то, что переменное напряжение намного проще увеличивать и уменьшать, чем постоянное, поэтому переменный ток используется в большинстве крупных систем распределения электроэнергии.

Рисунок \(\PageIndex{4}\): Энергия распределяется на большие расстояния при высоком напряжении для уменьшения потерь мощности в линиях передачи. Напряжения, генерируемые на электростанции, повышаются пассивными устройствами, называемыми трансформаторами (см. Трансформаторы), до 330 000 вольт (или более в некоторых местах по всему миру). В точке использования трансформаторы снижают напряжение

Пример \(\PageIndex{2}\): Потери мощности меньше при высоковольтной передаче

(a) Какой ток необходим для передачи 100 МВт мощности при 200 кВ ? 9{2} \left(1,00 \Omega\right) = 250 кВт.\]

(c) Какой процент мощности теряется в линиях электропередачи?

Решение

Потери в процентах представляют собой отношение этой потерянной мощности к общей или входной мощности, умноженное на 100: \[% потерь = \frac{250kW}{100 МВт} \times 100 = 0,250 %.\ ]

Обсуждение

Одна четвертая процента — допустимая потеря. Заметим, что если бы передавалось 100 МВт мощности при напряжении 25 кВ, то понадобился бы ток 4000 А. Это приведет к потере мощности в линиях 16,0 МВт, или 16,0%, а не 0,250%. Чем ниже напряжение, тем больше требуется тока и тем больше потери мощности в линиях передачи с фиксированным сопротивлением. Конечно, можно построить линии с меньшим сопротивлением, но для этого нужны более крупные и дорогие провода. Если бы сверхпроводящие линии можно было производить экономично, то в линиях передачи вообще не было бы потерь. Но, как мы увидим в одной из последующих глав, в сверхпроводниках также существует предел тока. Короче говоря, высокое напряжение более экономично для передачи мощности, а напряжение переменного тока гораздо легче повышать и понижать, поэтому переменный ток используется в большинстве крупномасштабных систем распределения электроэнергии.

Широко известно, что высокое напряжение представляет большую опасность, чем низкое. Но на самом деле некоторые высокие напряжения, например, связанные с обычным статическим электричеством, могут быть безвредны. Так что не только напряжение определяет опасность. Не так широко признано, что разряды переменного тока часто более вредны, чем аналогичные разряды постоянного тока. Томас Эдисон считал, что удары переменного тока более вредны, и в конце 1800-х годов создал систему распределения электроэнергии постоянного тока в Нью-Йорке. Были ожесточенные споры, в частности, между Эдисоном и Джорджем Вестингаузом и Николой Теслой, которые выступали за использование переменного тока в первых системах распределения электроэнергии. Переменный ток преобладает во многом благодаря трансформаторам и меньшим потерям мощности при передаче высокого напряжения.

ИССЛЕДОВАНИЯ PHET: ГЕНЕРАТОР

Генерировать электричество с помощью стержневого магнита! Откройте для себя физику этого явления, исследуя магниты и то, как вы можете использовать их, чтобы зажечь лампочку.

Рисунок \(\PageIndex{5}\): Генератор

Резюме

• Постоянный ток (DC) представляет собой поток электрического тока только в одном направлении. Это относится к системам, в которых напряжение источника постоянно.
• Источник напряжения системы переменного тока (AC) выдает \(V= V_{0} \sin{2\pi} ft\), где \(V\) — напряжение в момент времени \(t\), \(V_{0}\) — пиковое напряжение, а \(f\) — частота в герцах.
• В простой цепи \(I = V/R\), а переменный ток равен \(I = I_{0} \sin{2\pi}ft\), где \(I\) — ток в момент времени \ (t\), а \(I_{0} = V_{0}/R\) — пиковый ток.
• Средняя мощность переменного тока равна \(P_{ave} = \frac{1}{2} I_{0}V_{0}\).
• Средний (среднеквадратический) ток \(I_{rms}\) и среднее (среднеквадратичное) напряжение \(V_{rms}\) и \(I_{rms} = \frac{I_{0}}{\sqrt{2} }\) и \(V_{rms} = \frac{V_{0}}{\sqrt{2}}\), где rms обозначает среднеквадратичное значение.
• Таким образом, \(P_{ave} = I_{rms} V_{rms}\). 9{2}R\), аналогично выражениям для цепей постоянного тока.

Глоссарий

постоянный ток

(DC) поток электрического заряда только в одном направлении

переменный ток

(AC) поток электрического заряда, который периодически меняет направление на противоположное

Напряжение переменного тока

напряжение, которое синусоидально колеблется во времени, выражается как В = В ₀ sin 2 πft , где В — напряжение в момент времени t, В ₀ — пиковое напряжение, а f — частота в герцах

Переменный ток

ток, синусоидально колеблющийся во времени, выраженный как I = I ₀ sin 2 πft , где I — ток в момент времени t, I ₀ — пиковый ток3, а 42 — пиковый ток3 частота в герцах

действующее значение тока

среднеквадратичное значение тока, \(I_{rms}=I_0/\sqrt{2}\), где I ₀ пиковое значение тока в системе переменного тока

среднеквадратичное напряжение

среднеквадратичное значение напряжения, \(V_{rms}=V_0/\sqrt{2}\), где В ₀ — пиковое напряжение в системе переменного тока

---

Эта страница под названием 20.