Момент силы | Физика
Моментом силы относительно оси вращения называется физическая величина, равная произведению силы на ее плечо.
Момент силы определяют по формуле:
М — FI , где F — сила, I — плечо силы.
Плечом силы называется кратчайшее расстояние от линии действия силы до оси вращения тела.
На рис. 1.33, а изображено твердое тело, способное вращаться вокруг оси. Ось вращения этого тела перпендикулярна плоскости рисунка и проходит через точку, обозначенную буквой О. Плечом силы F здесь является расстояние 1Хот оси вращения до линии действия силы. Находят его следующим образом. Сначала проводят линию действия силы. Затем из точки О, через которую проходит ось вращения тела, опускают на линию действия силы перпендикуляр. Длина этого перпендикуляра является плечом данной силы.
Момент силы характеризует вращающее действие силы. Это действие зависит как от силы, так и от плеча. Чем больше плечо, тем меньшую силу надо приложить, чтобы получить желаемый результат, т. е. один и тот же момент силы (см. (1.33)). Именно поэтому открыть дверь, толкая ее возле петель, гораздо труднее, чем берясь за ручку, а гайку отвернуть гораздо проще длинным, чем коротким гаечным ключом.
За единицу момента силы в СИ принимается момент силы в 1 Н, плечо которой равно 1м — ньютон-метр (Н • м).
Правило моментов
Твердое тело, способное вращаться вокруг неподвижной оси, находится в равновесии, если момент силы М,, вращающей его по часовой стрелке, равен моменту силы М2, вращающей его против часовой стрелки:
М1 = -М2 или F 1 ll = — F 2 l 2 .
Момент силы принято считать положительным, если тело вращается по часовой стрелке, и отрицательным, если — против.
Пара сил
Если на тело действуют две равные и противоположно направленные силы, не лежащие на одной прямой, то такое тело не находится в равновесии, поскольку результирующий момент этих сил относительно любой оси не равен нулю, т. к. обе силы имеют моменты, направленные в одну сторону. Две такие силы, одновременно действующие на тело, называют парой сил. Если тело закреплено на оси, то под действием пары сил оно будет вращаться. Если пара сил приложена ксвободному телу, то оно будет вращаться вокруг оси, проходящей через центр тяжести тела, рис. 1.33, б.
Момент пары сил одинаков относительно любой оси, перпендикулярной к плоскости пары. Суммарный момент М пары всегда равен произведению одной из сил F на расстояние I между силами, которое называется плечом пары,независимо от того, на какие отрезки и /2 разделяет положение оси плечо пары:
M = Fll + Fl2=F(l1 + l2) = Fl.
Момент нескольких сил, равнодействующая которых равна нулю, будет одинаковым относительно всех осей, параллельных друг другу, поэтому действие всех этих сил на тело можно заменить действием одной пары сил с тем же моментом.
Формула момента силы в физике
Определение и формула момента силы
На рис.1 точка О и вектор силы ( )и радиус – вектор находятся в плоскости рисунка. В таком случае вектор момента силы () перпендикулярен плоскости рисунка и имеет направление от нас. Вектор момента силы является аксиальным. Направление вектора момента силы выбирается таким образом, что вращение вокруг точки О в направлении силы и вектор создают правовинтовую систему. Направление момента сил и углового ускорения совпадают.
Величина вектора равна:
где – угол между направлениями радиус – вектора и вектора силы, – плечо силы относительно точки О.
Момент силы относительно оси
Моментом силы по отношению к оси является физическая величина, равная проекции вектора момента силы относительно точки избранной оси на данную ось. При этом выбор точки значения не имеет.
Главный момент сил
При этом точку О называют центром приведения системы сил.
Если имеются два главных моменты ( и )для одной системы сил для разных двух центров приведение сил (О и О’), то они связаны выражением:
где — радиус-вектор, который проведен из точки О к точке О’, – главный вектор системы сил.
В общем случае результат действия на твердое тело произвольной системы сил такое же, как действие на тело главного момента системы сил и главного вектора системы сил, который приложен в центре приведения (точка О).
Основной закон динамики вращательного движения
где – момент импульса тела находящегос
Момент силы — определение и свойства
Момент силы относительно точки
Определение момента
- Момент силы относительно точки O
- – это векторное произведение вектора , проведенного из точки O в точку приложения силы A, на вектор силы :
(1) .
Если выбрать прямоугольную систему координат Oxyz с центром в точке O, то момент силы будет иметь следующие компоненты:
(1.1) ;
(1.2) ;
(1.3) .
Здесь – координаты точки A в выбранной системе координат:
.
Компоненты представляют собой значения момента силы относительно осей , соответственно.
Определение плеча силы
- Плечо силы относительно точки
- – это расстояние между линией действия силы и точкой, относительно которой определяется плечо. То есть плечо силы – это длина перпендикуляра, опущенного из точки на линию действия силы.
Свойства
Если точку приложения силы переместить вдоль линии ее действия, то момент, при таком перемещении, не изменится.
Доказательство ⇓
Абсолютная величина момента силы относительно некоторой точки равна произведению абсолютного значения силы на плечо этой силы относительно выбранной точки.
Доказательство ⇓
Момент относительно точки O, от силы, линия действия которой проходит через эту точку, равен нулю.
Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:
.
Доказательство ⇓
Тоже самое относится и к силам, чьи линии продолжения пересекаются в одной точке. При этом в качестве точки приложения суммы сил берется точка пересечения линий их действия.
Если векторная сумма сил равна нулю:
,
то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:
.
Доказательство ⇓
Момент силы является псевдовектором или, что то же самое, аксиальным вектором.
Это свойство следует из свойства векторного произведения. Поскольку векторы и являются
Но если бы мы определили направление по правилу левого винта, то векторное произведение было бы направлено в противоположную сторону. При этом никакого противоречия не возникает. То есть фактически, аксиальные векторы могут иметь два взаимно противоположных направления. Чтобы не усложнять математические формулы, мы выбираем одно из них, применяя правило правого винта. По этой причине, псевдовекторы нельзя геометрически складывать с истинными векторами. Но их можно перемножать, используя скалярное или векторное произведение.
Момент силы относительно оси
Определение
Часто встречаются случаи, когда нам не нужно знать все компоненты момента силы относительно выбранной точки, а нужно знать только момент силы относительно выбранной оси.
- Момент силы относительно оси
- – это проекция вектора момента силы относительно произвольной точки, принадлежащей этой оси, на направление оси.
Пусть – единичный вектор, направленный вдоль оси. И пусть O – произвольная точка, принадлежащая ей. Тогда момент силы относительно оси является скалярным произведением:
.
Такое определение возможно, поскольку для любых двух точек O и O′, принадлежащих оси, проекции моментов относительно этих точек на ось равны. Покажем это.
Воспользуемся векторным уравнением :
;
.
Умножим это уравнение скалярно на единичный вектор , направленный вдоль оси:
.
Поскольку вектор параллелен оси, то . Отсюда
.
То есть проекции моментов на ось, относительно точек O и O′, принадлежащих этой оси, равны.
Свойства
Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
Доказательство ⇓
Момент относительно оси от силы, параллельной этой оси равен нулю.
Доказательство ⇓
Доказательство свойств
Перемещение точки приложения силы вдоль линии ее действия
Все свойства ⇑ Если точку приложения силы переместить вдоль линии действия силы, то момент, при таком перемещении, не изменится.
Доказательство
Пусть сила приложена в точке A. Через точку A проведем прямую, параллельную вектору силы. Эта прямая является линией ее действия. Переместим точку A приложения силы в точку A′, принадлежащую линии действия. Тогда
Вектор проведен через две точки линии действия. Поэтому его направление совпадает или противоположно направлению вектора силы . Тогда , где λ – параметр; . , если точка A′ смещена относительно A в направлении вектора . В противном случае .
Таким образом, вектор, проведенный из O в A′, имеет вид:
.
Найдем момент силы, приложенной в точке A′, применяя свойства векторного произведения:
.
Мы видим, что момент не изменился:
.
Свойство доказано.
Абсолютная величина момента силы
Все свойства ⇑ Абсолютная величина момента силы относительно некоторой точки равна произведению абсолютного значения силы на плечо этой силы относительно выбранной точки.
Доказательство

Абсолютное значение момента M относительно точки O равно произведению силы F на ее плечо d = |OD|.
Пусть мы имеем силу , приложенную в точке A. Рассмотрим момент этой силы относительно некоторой точки O. Заметим, что точки O, A и вектор лежат в одной плоскости. Изобразим ее на рисунке. Через точку A, в направлении вектора проводим прямую AB. Эта прямая называется линией действия силы . Через точку O опустим перпендикуляр OD к линии действия. И пусть D является точкой пересечения линии действия и перпендикуляра. Тогда – плечо силы относительно центра O. Обозначим его буквой . Воспользуемся предыдущим свойством ⇑, согласно которому точку приложения силы можно перемещать вдоль ее линии действия. Переместим ее в точку D. Момент силы:
.
Поскольку векторы и перпендикулярны, то по свойству векторного произведения, абсолютное значение момента:
,
где – абсолютное значение силы.
Заметим, что вектор момента перпендикулярен плоскости рисунка. Его направление определяется по правилу правого винта. Если мы будем вращать винт, проходящий через точку O перпендикулярно плоскости рисунка, в направлении силы F, то он будет перемещаться на нас. Поэтому вектор момента перпендикулярен плоскости рисунка и направлен на нас.
Свойство доказано.
Момент относительно точки от силы, проходящей через эту точку
Все свойства ⇑ Момент относительно точки O, от силы, линия действия которой проходит через эту точку, равен нулю.
Доказательство
Пусть линия действия силы проходит через точку O. Тогда плечо этой силы относительно O равно нулю: . Согласно предыдущему свойству ⇑, абсолютное значение момента силы относительно выбранной точки равно нулю:
.
Свойство доказано.
Момент суммы сил, приложенных в одной точке
Все свойства ⇑ Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:
.
Доказательство
Пусть силы приложены в одной точке A. Пусть – векторная сумма этих сил. Находим момент относительно некоторой точки O от векторной суммы , приложенной в точке A. Для этого применяем свойства векторного произведения:
.
Свойство доказано.
Момент системы сил, векторная сумма которых равна нулю
Все свойства ⇑ Если векторная сумма сил равна нулю:
,
то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:
.
Доказательство
Пусть силы приложены в точках , соответственно. И пусть точки O и C обозначают два центра, относительно которых мы будем вычислять моменты. Тогда имеют место следующие векторные уравнения:
.
Используем их при вычислении суммы моментов относительно точки O:
.
Здесь мы воспользовались тем, что по условию,
.
Свойство доказано.
Момент относительно оси от силы, проходящей через эту ось
Все свойства ⇑ Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
Доказательство
В определении ⇑ указано, что момент силы относительно оси – это проекция вектора момента силы относительно произвольной точки, принадлежащей этой оси, на направление оси. В качестве такой точки возьмем точку пересечения линии действия силы с осью. Но, согласно доказанному выше ⇑, момент относительно этой точки равен нулю. Поэтому равна нулю и его проекция на эту ось.
Свойство доказано.
Момент относительно оси от силы, параллельной этой оси
Все свойства ⇑ Момент относительно оси от силы, параллельной этой оси равен нулю.
Доказательство
Пусть O – произвольная точка на оси. Рассмотрим момент силы относительно этой точки. Согласно определению:
.
Согласно свойству векторного произведения, вектор момента перпендикулярен вектору силы . Поскольку вектор силы параллелен оси, то вектор момента ей перпендикулярен. Поэтому проекция момента относительно точки O на ось равна нулю.
Свойство доказано.
Автор: Олег Одинцов. Опубликовано:
Суммарный момент — сила — Большая Энциклопедия Нефти и Газа, статья, страница 1
Суммарный момент — сила
Cтраница 1
Суммарный момент сил будет равен нулю. [1]
Суммарный момент сил М, под действием которого вращается диск, равен М Fr — Мтр. [2]
Мт — суммарный момент сил трения, зависящий от вязкости среды, который мало изменяется при изменении расхода газонефтяной смеси. Момент Мв измеряется по величине приращения тока, потребляемого электродвигателем ( на фиг. [3]
Для определения суммарного момента сил трения пяты это равенство необходимо проинтегрировать в пределах изменения независимых переменных: а — от 0 до 2я и р — от г до К. [4]
Известно, что суммарные моменты сил, порождающих центростремительные ускорения, равны нулю, так как оба вращения происходят относительно главных осей инерции волчка. Момент сил, вызывающих кориолисовы ускорения, был вычислен в предыдущем пункте. [5]
Отличный от нуля суммарный момент сил Кориолиса, действующих на частицы жидкости, обозначим через М г. В случае установившегося движения этот момент легко вычисляется. [6]
Мс элемента называют суммарный момент сил трения элемента, возникающий при его вращении в соответствующих направляющих. [7]
Таким образом, суммарный момент сил тяжести относительно произвольной точки О совпадает с моментом силы mg, приложенной к точке С. Итак, равнодействующая сил тяжести равна Р / ng и приложена к центру инерции тела. Точка, относительно которой момент сил тяжести равен нулю, называется центром тяжести тела. Таким образом, в случае, когда поле тяготения в пределах тела однородно, центр тяжести совпадает с центром инерции. [8]
Из равенства нулю суммарного момента сил можно вывести открытое Koran правило парности напряжений isv тух. Используя снова прием Эйлера, можно установить, что всегда найдутся два взаимно перпендикулярных направления 1 и 2, относительно которых происходит только двуосное сжатие — растяжение без сдвига. Соответствующие напряжения GI и 02 называются главными напряжениями, а оси 1 и 2 — главными осями. [10]
Из условия равенства нулю суммарного момента сил относительно оси, проходящей через точку О приложения искомой силы РП, имеем УУ т / 2, где / V — сила реакции опоры. [11]
Из выражения (3.7) следует, что суммарный момент сил сопротивления возрастает от турбобура до нейтрального сечения колонны по кубическому закону. [12]
Как показывает опыт, под действием суммарного момента сил угловая скорость вращения тела меняется и вместе с этим меняется его кинетическая энергия. [13]
Как показывает опыт, под действием суммарного момента сил угловая скорость вращения тела меняется и вместе с этим меняется его кинетическая энергия. Если в момент времени tl тело имеет угловую скорость cot и кинетическую энергию К. [14]
Как показывает опыт, под действием суммарного момента сил угловая скорость вращения тела меняется и вместе с этим меняется его кинетическая энергия. [15]
Страницы: 1 2 3 4
1.4 Определение приведенного момента сил сопротивления
Момент приведенный от сил сопротивления определяется из соотношения:
 ,
где Vqc– передаточная
функция.
,
где Vqc– передаточная
функция.
Значения передаточных функций и приведенного момента сил сопротивления приведены в таблицах 1.2, 1.3, 1,4.
1.5 Определение суммарного приведенного момента
Суммарный приведенный момент определяется как сумма приведенного момента движущих сил и приведенного момента сил сопротивления:

Значения суммарного приведенного момента приведены в таблицах 1.2, 1.3, 1.4.
Таблица 1.4 Суммарный приведенный момент
величина | размерн | 0 | 1 | 2 | 3 | 4 | 5 |
Мпр Fд | Н*м | 0 | 4039,415 | 2547,464 | 1221,474 | 565,4937 | 99,32211 |
Мпр Fк | Н*м | 489,7959 | 371,0204 | 192,5633 | 0 | -32,0939 | -371,02 |
Мпр сум | Н*м | 489,7959 | 4410,436 | 2740,027 | 1221,474 | 533,3998 | -271,698 |
величина | размерн | 6 | 7 | 8 | 9 | 10 | 11 |
Мпр Fд | Н*м | 0 | -49,6611 | -76,5474 | -229,011 | -822,284 | -1479,37 |
Мпр Fк | Н*м | -1469,39 | -3440 | -3441,8 | 0 | 1147,265 | 480 |
Мпр сум | Н*м | -1469,39 | -3489,66 | -3518,34 | -229,011 | 324,9813 | -999,368 |
Вычисляем масштаб графика суммарного приведенного момента и масштаб этого графика по оси абсцисс:


Моментами, от действия сил тяжести звеньев пренебрегаем, так как их величина очень незначительна – менее 5 % от максимального суммарного приведенного момента.
1.6 Построение графика суммарной работы
Построение графика работы движущих сил производится путем графического интегрирования графика приведенного момента движущих сил.

Отрезок интегрирования ОК выбираем равным 50 мм.
Построение графика работы сил сопротивления производится путем графического интегрирования графика приведенного момента сил сопротивления.

Отрезок интегрирования ОК выбираем равным 50 мм.
Построение графика суммарной работы производится путем графического интегрирования графика суммарного приведенного момента.

Отрезок интегрирования ОК выбираем равным 50 мм.
Масштаб графика работы определим по соотношению:

1.7 Определение приведенного момента инерции II группы звеньев механизма двс
Приведение моментов инерции осуществили на основе метода приведения масс. В основу метода положено равенство кинетической энергии всех звеньев механизма и звена динамической модели. В этом случае закон движения последнего будет таким же, как и закон движения начального звена реального механизма.
Суммарный приведенный момент инерции всего механизма равен сумме приведенных моментов инерции всех его звеньев. Суммарный приведенный момент инерции второй группы звеньев (поршней 3 и 5 и шатунов 2 и 4) рассчитывается по формуле:
 ,
,
где I3Ппр — приведенный момент инерции поршня ДВС при его поступательном движении;
где I5Ппр — приведенный момент инерции поршня компрессора при его поступательном движении;
I2Ппр — приведенный момент инерции шатуна 2 при его поступательном движении;
I4Ппр — приведенный момент инерции шатуна 4 при его поступательном движении;
I2Врпр — приведенный момент инерции шатуна 2 при его вращательном движении;
I4Врпр — приведенный момент инерции шатуна 4 при его вращательном движении.
Приведенные моменты инерции элементов при поступательном движении рассчитываются по формулам:
 , где
, где
Vi— скорость поступательного движения звена [м/с];
1 — угловая скорость кривошипа 1 [рад/с];
mi — масса звена [кг].
Приведенные моменты инерции шатунов 2 и 4 при их вращательном движении рассчитываются по формуле:
 ,
где
,
где
i— угловая скорость звена [рад/с];
Iis -момент инерции звена относительно оси, проходящей через центр тяжести [кгм2].
Суммарный приведенный
момент инерции всего механизма  =
=  +
+  , где
, где  — приведенный момент инерции первой
группы звеньев. Результаты расчетов
представлены в таблице 1.5.
— приведенный момент инерции первой
группы звеньев. Результаты расчетов
представлены в таблице 1.5.
Таблица 1.5 Суммарный приведенный момент инерции II группы звеньев
величина | размер | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
I2 пр пост | кг*м^2 | 0,08467 | 0,11005 | 0,16116 | 0,1728 | 0,14123 | 0,10156 | 0,08467 |
I2 пр вр | кг*м^2 | 0,01919 | 0,01461 | 0,00502 | 0 | 0,00502 | 0,01461 | 0,01919 |
I2 пр сум | кг*м^2 | 0,10386 | 0,12467 | 0,16618 | 0,1728 | 0,14625 | 0,11618 | 0,10386 |
I4 пр пост | кг*м^2 | 0,1728 | 0,13516 | 0,08342 | 0,06220 | 0,08342 | 0,13516 | 0,1728 |
I4 пр вр | кг*м^2 | 0 | 0,00502 | 0,01463 | 0,01919 | 0,01461 | 0,00502 | 0 |
I4 пр сум | кг*м^2 | 0,1728 | 0,14018 | 0,09803 | 0,0814 | 0,09803 | 0,14018 | 0,1728 |
I3 пр сум | кг*м^2 | 0 | 0,04937 | 0,13829 | 0,144 | 0,08262 | 0,02225 | 0 |
I5 пр сум | кг*м^2 | 0,216 | 0,12394 | 0,03338 | 0 | 0,03338 | 0,12394 | 0,216 |
I пр Сум ll | кг*м^2 | 0,49266 | 0,43817 | 0,43591 | 0,3982 | 0,36031 | 0,40256 | 0,49266 |
Вычислим масштаб графика суммарного приведенного момента инерции II группы звеньев:

2. Момент силы
Моментом силы F относительно точки О называется физическая величина, определяемая векторным произведением радиус-вектора r, проведенного из точки О в точку приложения силы F. Направление M совпадает с направлением поступательного движения буравчика при его вращения от r к F.
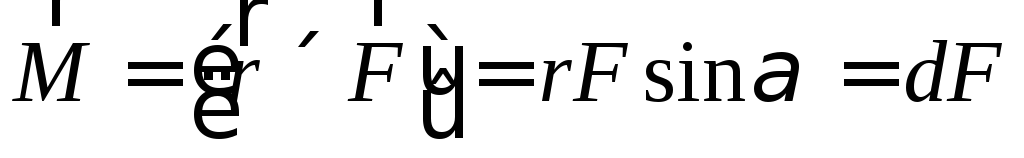 ,
, 
где α
– между векторами 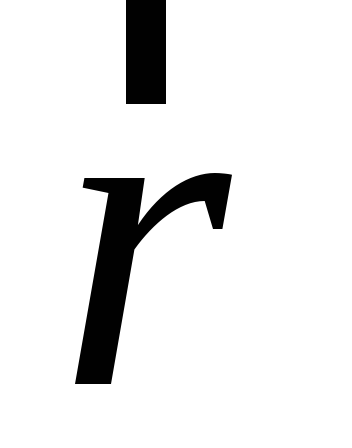 и
и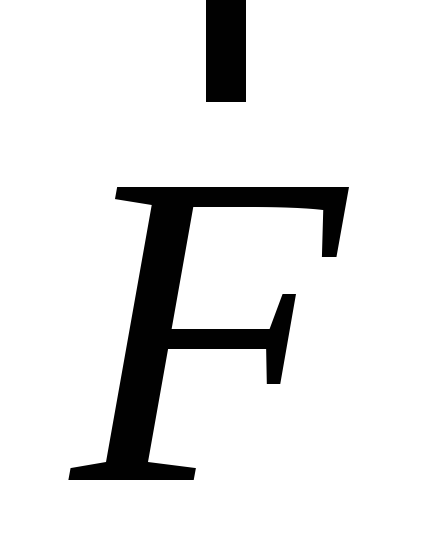 ,d – плече силы – кратчайшее расстояние
от оси вращения до прямой вдоль которой
действует сила.
,d – плече силы – кратчайшее расстояние
от оси вращения до прямой вдоль которой
действует сила.
IV.Законы динамики вращательного движения.
В основе динамики вращательного движения лежат законы Ньютона.
I закон | Тело вращается равномерно или находится в покое, если суммарный момент всех действующих на тело сил равен нулю: |
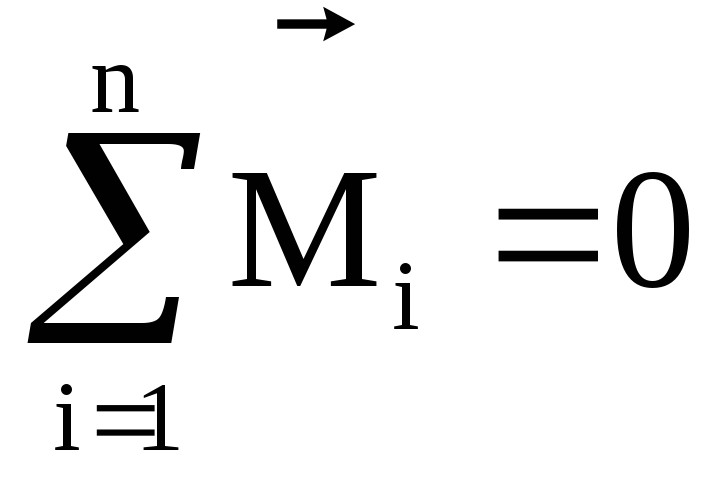
II закон | Угловое ускорение,
приобретаемое телом под действием
силы |
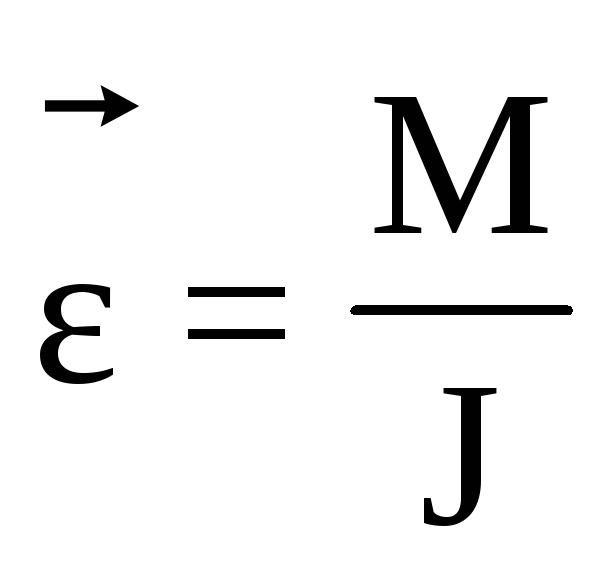 – основной закон динамики вращательного
движения.
– основной закон динамики вращательного
движения.
Опытной проверкой этого закона служит прибор – крестообразный маятник Обербека.
III закон | Моменты сил, с которыми два тела действуют друг на друга равны по величине и противоположны по направлению: |
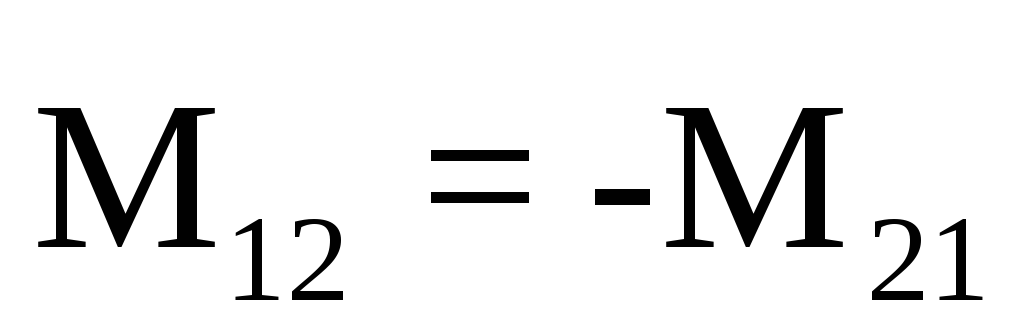
Согласно этому закону, два взаимодействующих тела всегда вращаются в разных направлениях относительно своих осей вращения.
Закон сохранения момента импульса.
В замкнутой системе момент внешних сил отсутствует т.е.
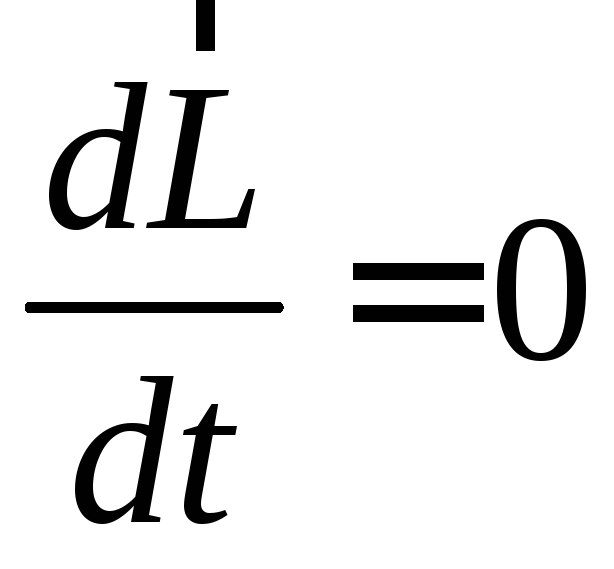
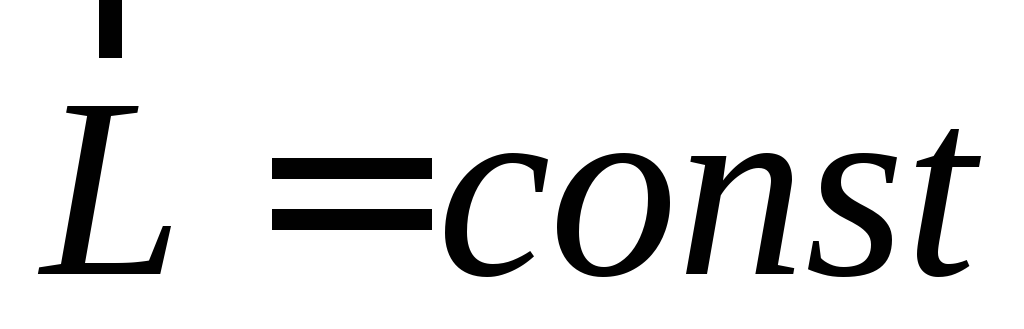
Закон сохранения момента импульса — момент импульса замкнутой системы относительно любой неподвижной точки не изменяется с течением времени.
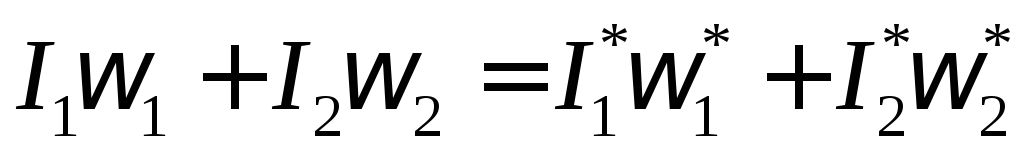
Закон сохранения момента импульса | Если суммарный момент всех внешних сил относительно произвольной неподвижной оси равен нулю, то момент импульса системы не изменяется с течением времени. |
Пример:
Скамья Жуковского: скамья раскручена, и руки человека опущены. Человек расставляет руки с гантелями в стороны, скорость движения резко уменьшается.
(Jω=const=mr2ω) → увеличениеrприводит к уменьшениюω, чтобы произведениеmr2ωоставалось постоянным.
Кинетическая энергия вращающегося твёрдого тела.
Кинетическая энергия твердого тела конечных размеров равна сумме кинетических энергий элементов, на которые разбито тело. Рассмотрим частный случай вращения твердого тела вокруг неподвижной оси.
Кинетическая энергия каждого элемента, движущегося с линейной скоростью:
Vi=ωri
равна: 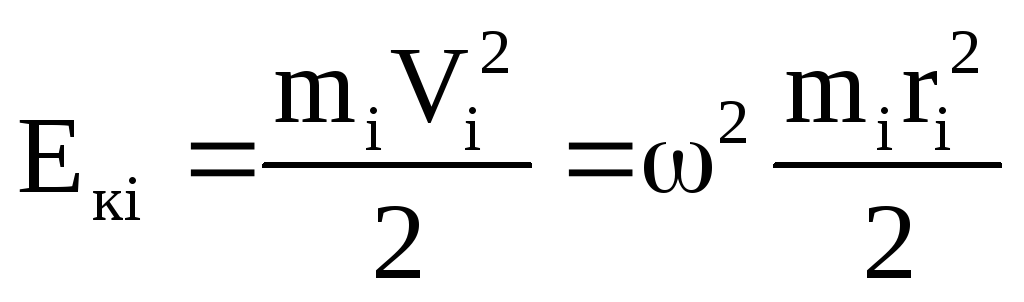
Просуммировав по всем элементам, получим:
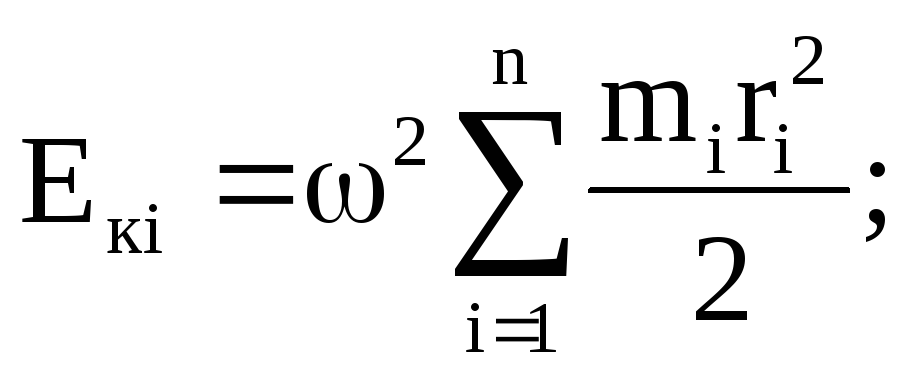
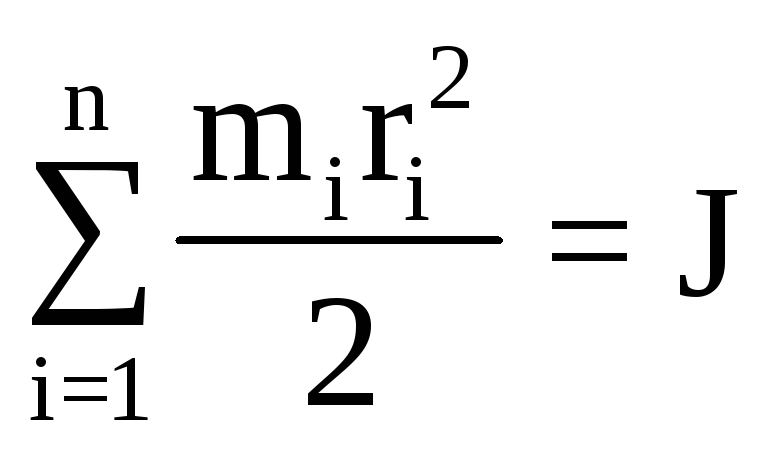 – момент инерции тела, относительно
оси вращения.
– момент инерции тела, относительно
оси вращения.
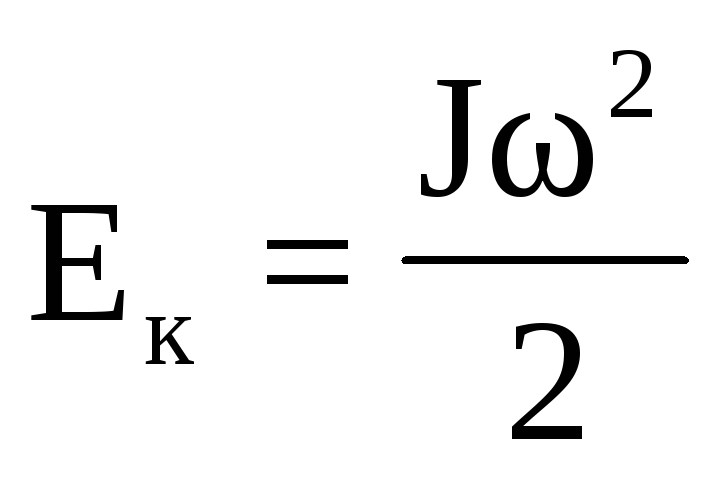 (11)
(11)
Если твердое тело одновременно участвует
в двух движениях: поступательном со
скоростью  и вращательном со скоростью
и вращательном со скоростью ,
то
,
то
|
|
Полная кинетическая энергия твердого тела равна сумме кинетической энергии Еппоступательного движения центра масс тела и кинетической энергии вращения Ев. |
Задача: полый цилиндр и сплошной скатываются с наклонной плоскости
Работа силы при вращении

Условие равновесия тела.
Пусть до приложения сил тело покоилось.
Для того, чтобы тело не двигалось поступательно необходимо, чтобы сумма сил проходящих через центр масс тела была равна нулю.
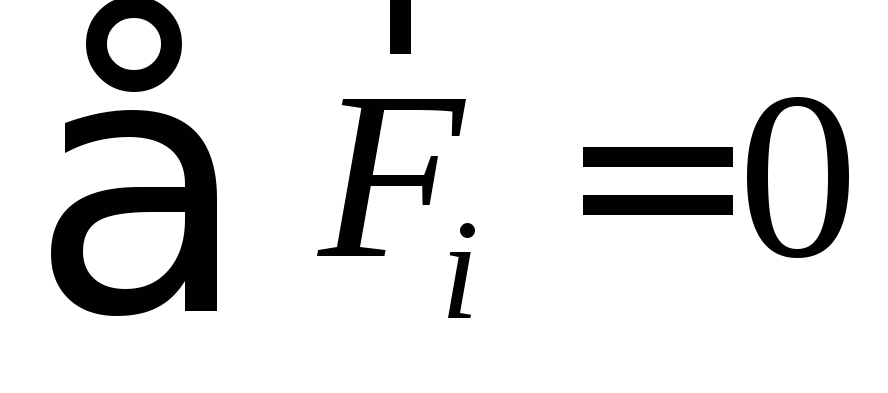 или
или 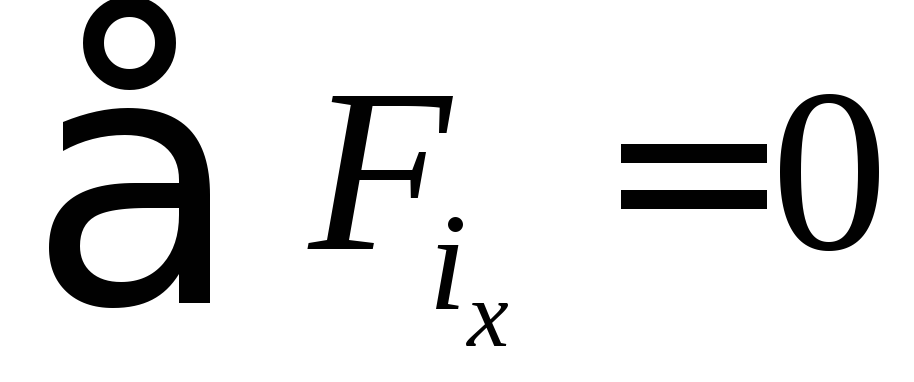
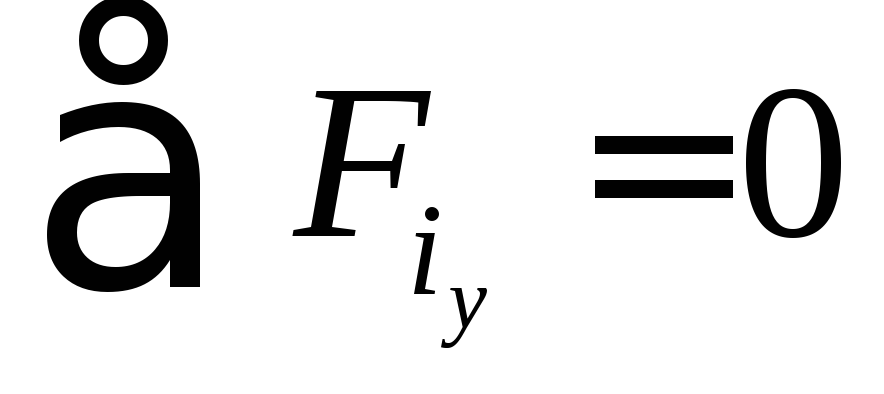
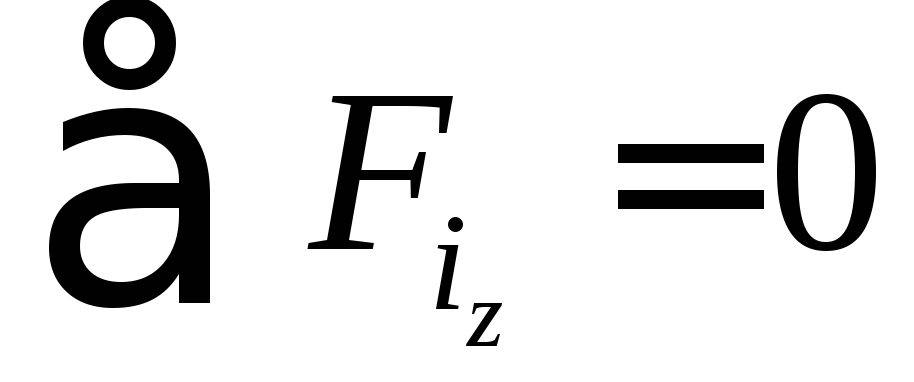
Для того, чтобы тело не вращалось, требуется исчезновение вращающих моментов внешних сил:
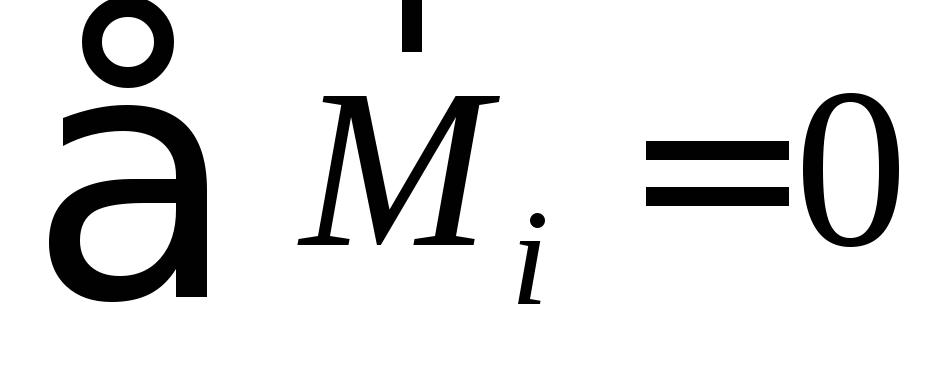 или
или 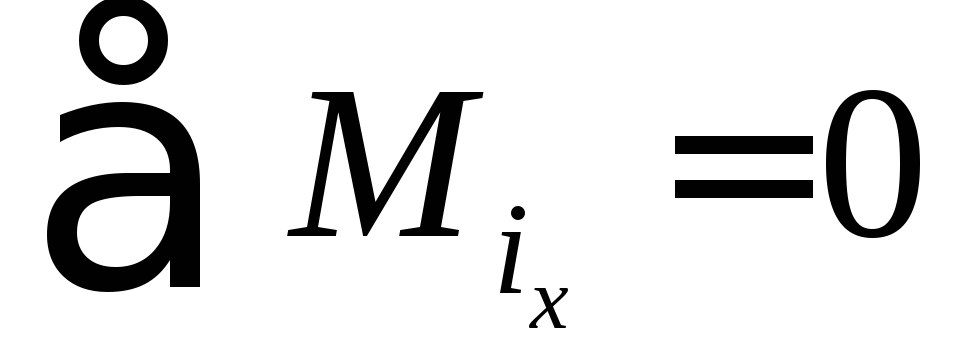
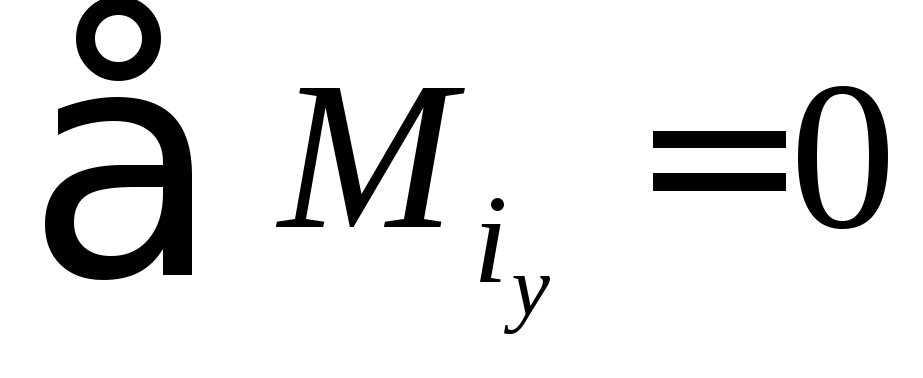
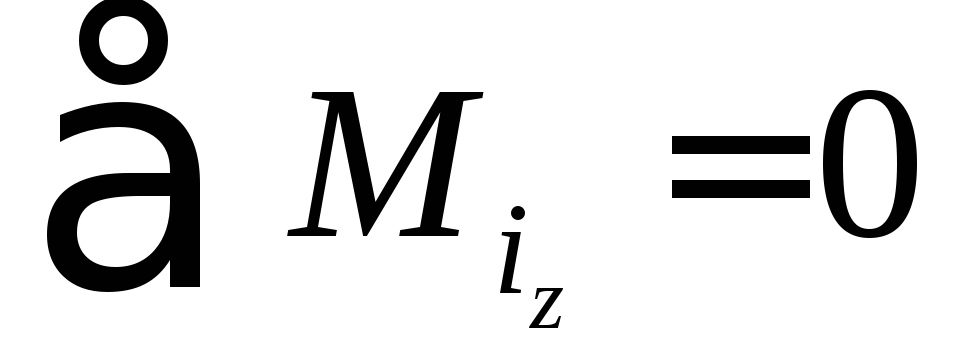
Если тело немного сместить из положения равновесия и предоставить его самому себе возможны три случая:
а) Оно самопроизвольно возвратится в положение равновесия (устойчивое равновесие)
б) оно остается в новом положении (безразличное равновесие)
в) оно еще дальше отходит от положения равновесия (неустойчивое равновесие).
Задача: мост на опорах найти силу давления на каждую опору
7. Определение суммарного приведенного момента внешних сил
В основе метода приведения сил лежит равенство элементарных работ или мгновенных мощностей, с одной стороны сил и моментов, приложенных к реальному механизму, а с другой – от приведенного момента, действующего на динамическую модель.
Мощность приведенного момента, приложенного к модели
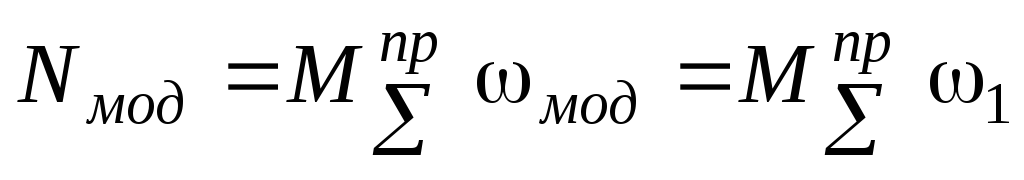 .
.
Мощность сил и моментов, приложенных к механизму
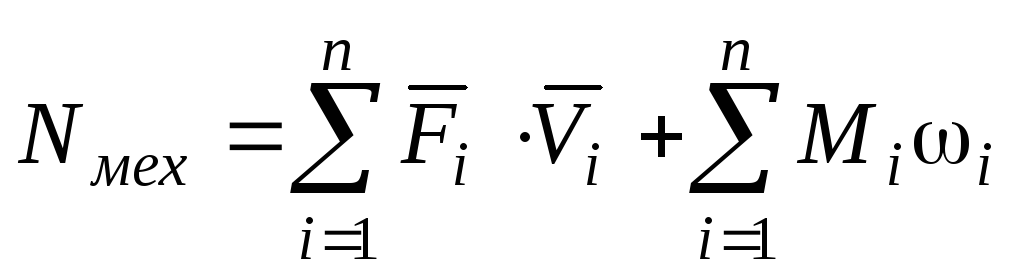 .
.
Так как 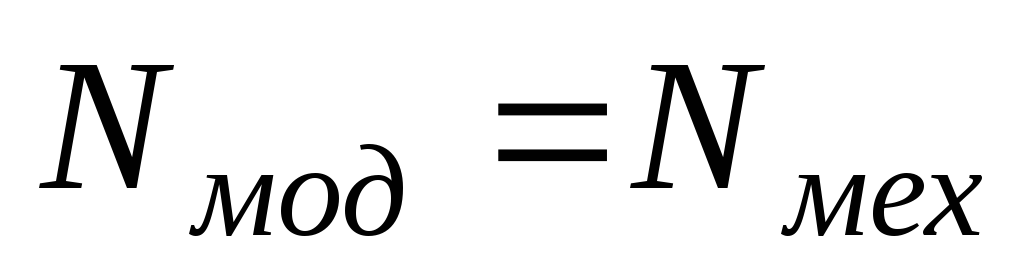 ,
то
,
то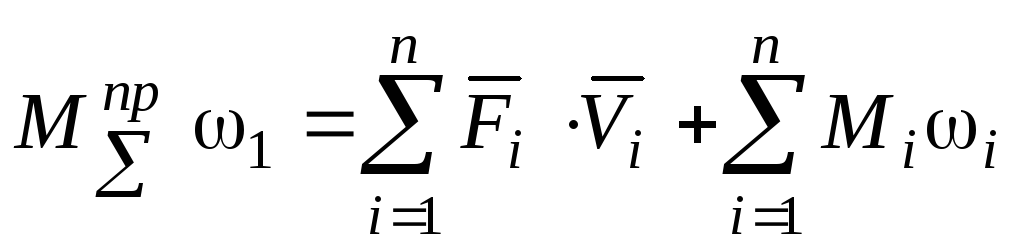 ,
,
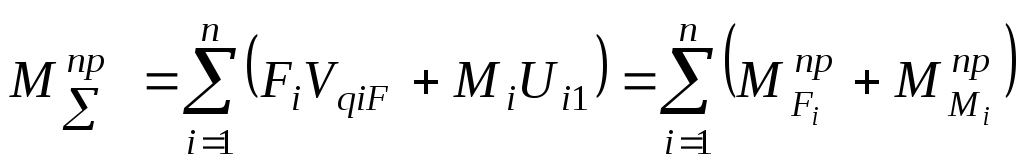 ,
то есть
,
то есть
суммарный приведенный момент – это алгебраическая сумма приведенных моментов от отдельных сил и моментов.
Рассмотрим построение графиков суммарного приведенного момента некоторых механизмов, характерных для заданий на курсовой проект.
7.1. Двигатель внутреннего сгорания
В ДВС с одним цилиндром движущая сила действует на поршень цилиндра, а полезное сопротивление снимается с кривошипа в виде постоянного момента сил.
Таким образом, суммарный приведенный момент:
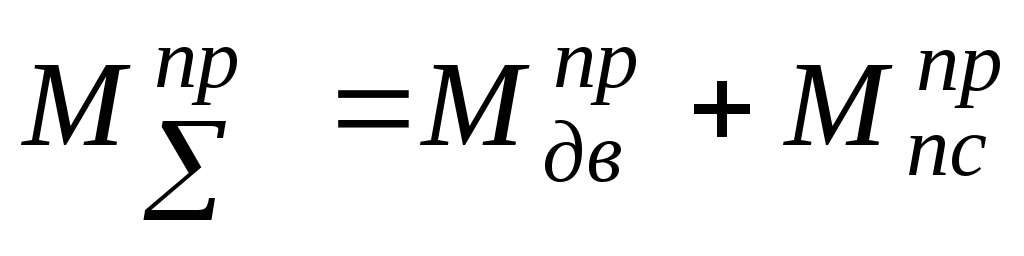 ,
при этом:
,
при этом:
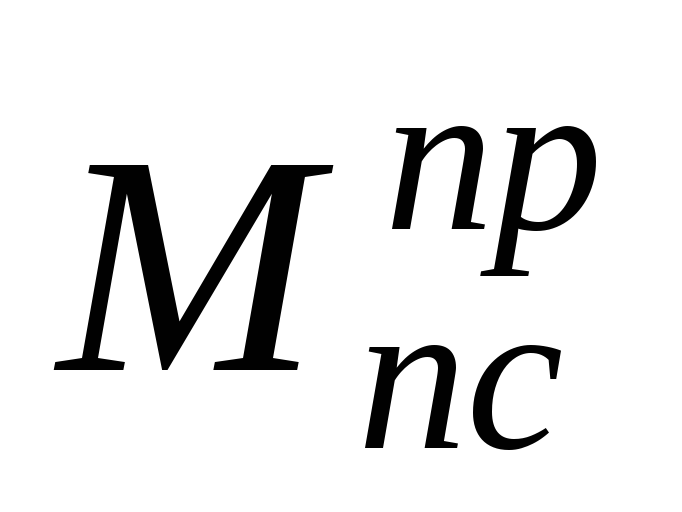 –постоянный,
отрицательный момент сил полезного
сопротивления, который приложен к
кривошипу и неизвестен по величине;
–постоянный,
отрицательный момент сил полезного
сопротивления, который приложен к
кривошипу и неизвестен по величине;
приведенный момент
движущих сил вычисляется по формуле 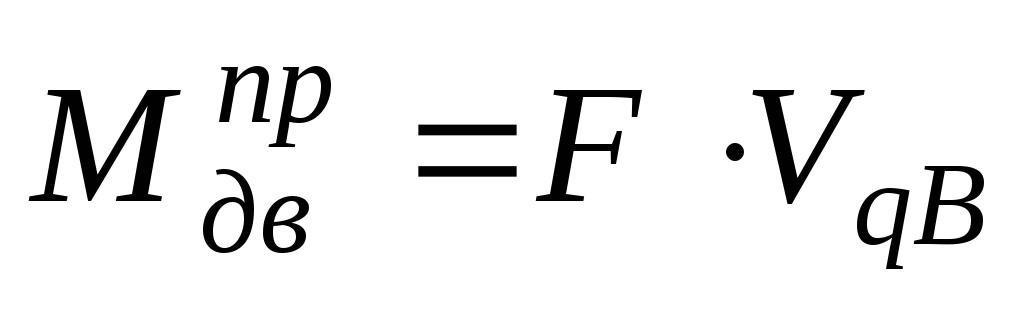 на основе диаграмм
на основе диаграмм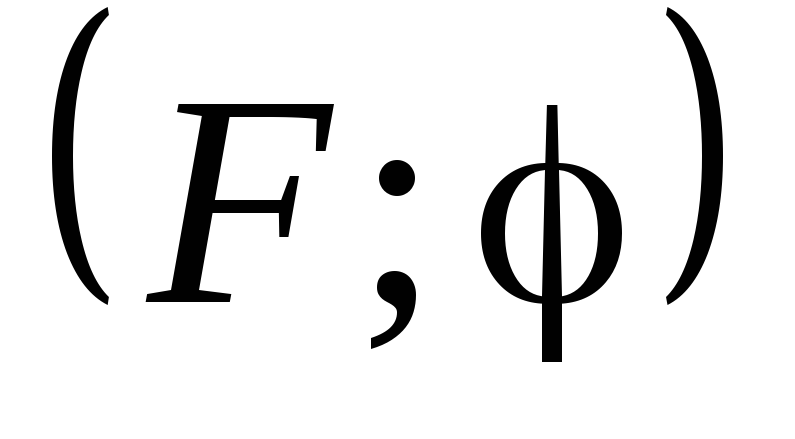 (Рис. 9б) и
(Рис. 9б) и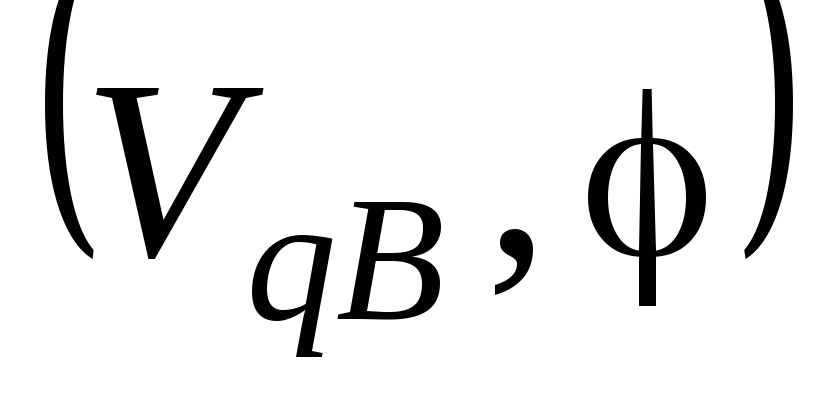 (Рис. 14в) и может быть получен аналитически
или графически. Знак приведенного
момента совпадает со знаком движущей
силы.
(Рис. 14в) и может быть получен аналитически
или графически. Знак приведенного
момента совпадает со знаком движущей
силы.
Масштабы: 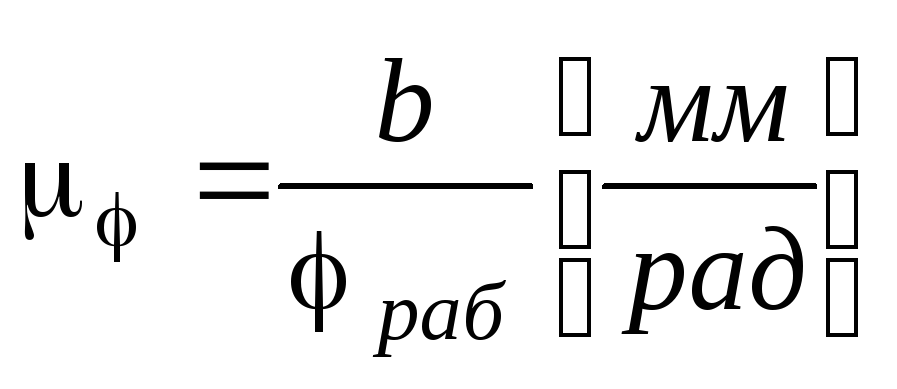 ,
,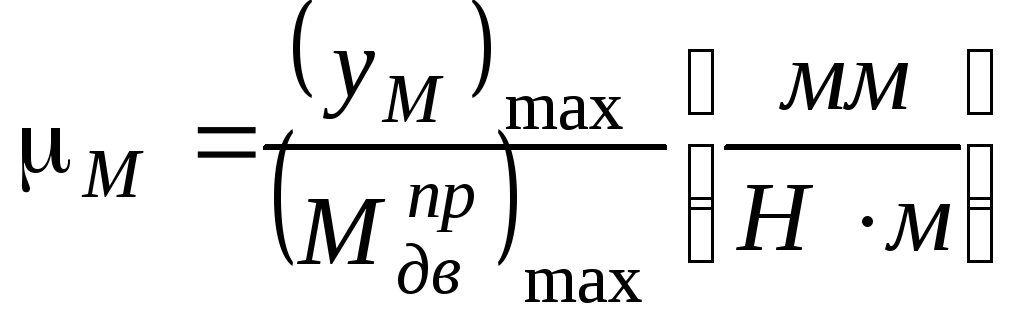 ,
,
где: 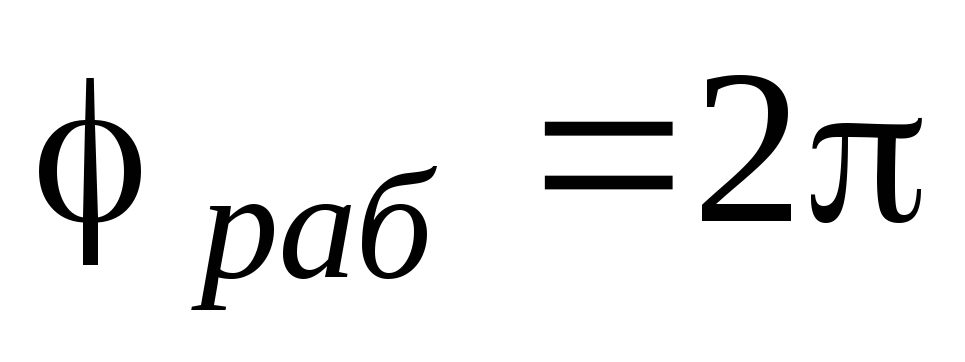 –
для двухтактного двигателя,
–
для двухтактного двигателя,
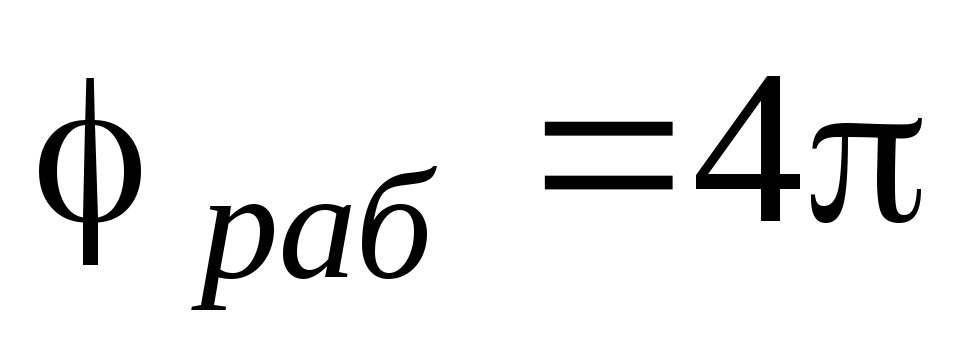 –для четырехтактного
двигателя.
–для четырехтактного
двигателя.
 Рис.
16. Диаграммы для ДВС:
Рис.
16. Диаграммы для ДВС:
а) диаграмма приведенных моментов;
б) диаграмма работ моментов
Когда момент
полезного сопротивления будет определен,
суммарный момент может быть получен
как алгебраическая сумма 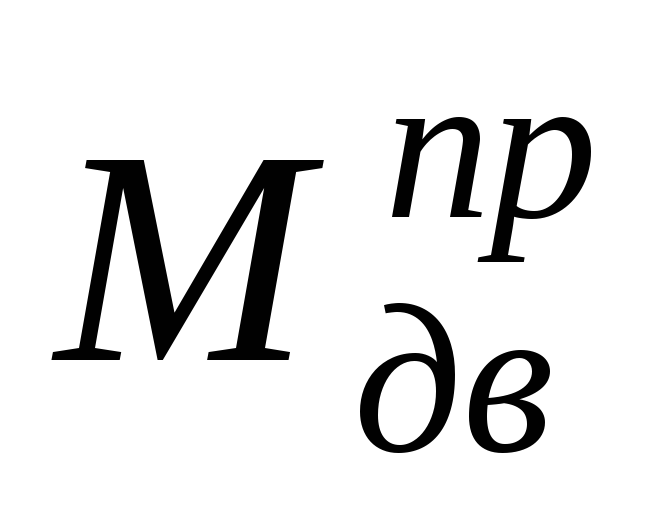 и
и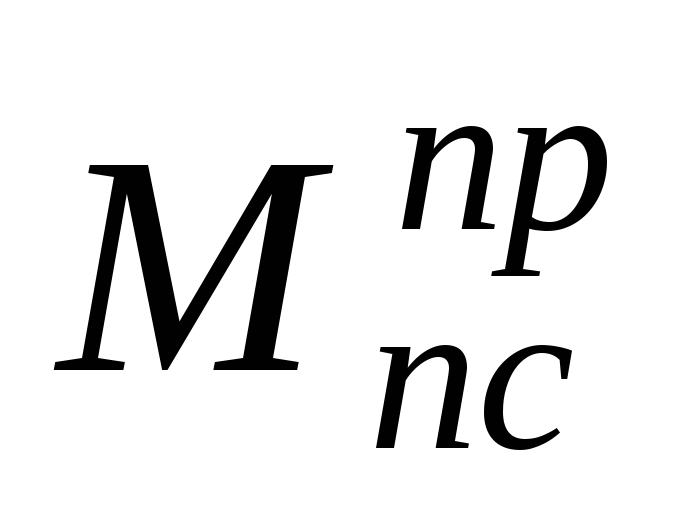 .
.
График 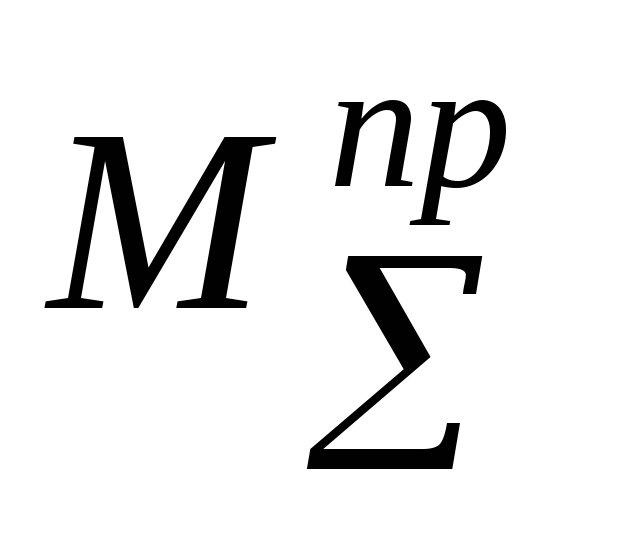 может быть получен одним из двух способов:
может быть получен одним из двух способов:
7.2. Поперечно-строгальный станок
Для поперечно-строгального
станка приведенный момент сил полезного
сопротивления вычисляется на основе
диаграмм силы полезного сопротивления 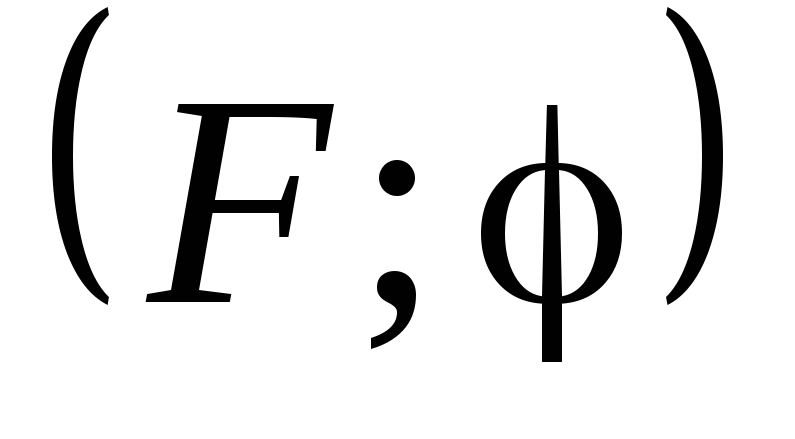 (Рис. 11) и передаточной функции
(Рис. 11) и передаточной функции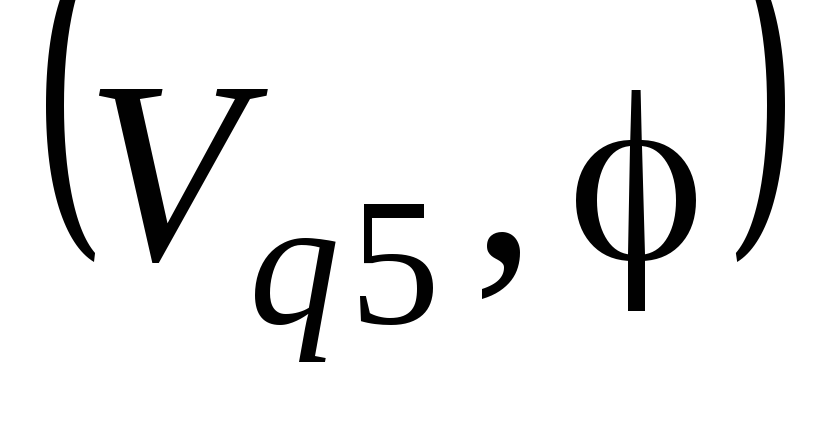 (Рис. 13в) и может быть получен аналитически
или графически, а движущий момент
снимается с кривошипа в виде постоянного
момента сил.
(Рис. 13в) и может быть получен аналитически
или графически, а движущий момент
снимается с кривошипа в виде постоянного
момента сил.
Таким образом, суммарный приведенный момент:
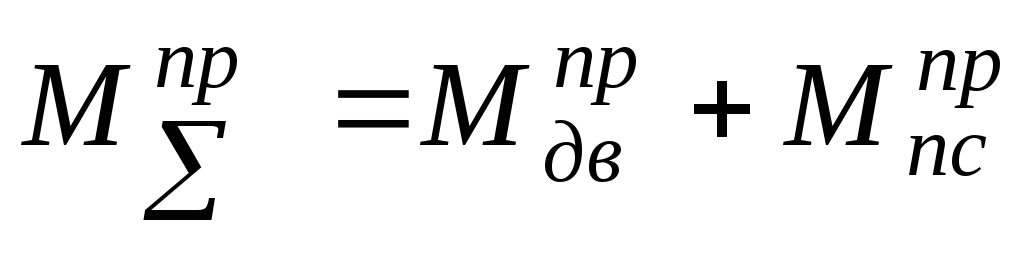 ,
при этом
,
при этом
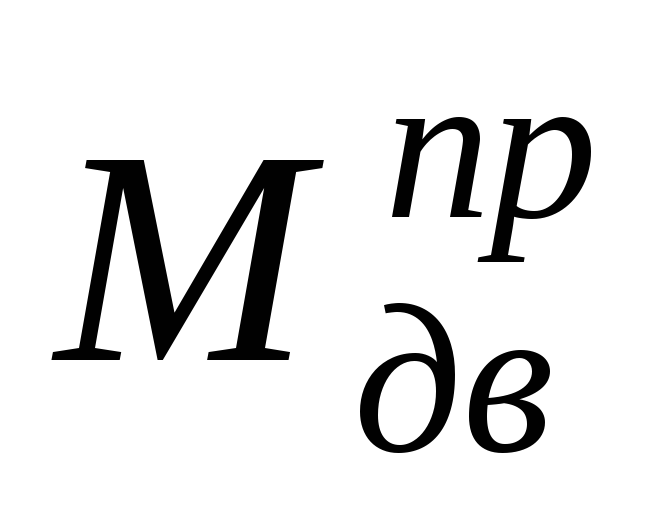 –постоянный,
положительный движущий момент, который
приложен к кривошипу и неизвестен по
величине;
–постоянный,
положительный движущий момент, который
приложен к кривошипу и неизвестен по
величине;
момент сил полезного
сопротивления вычисляется по формуле 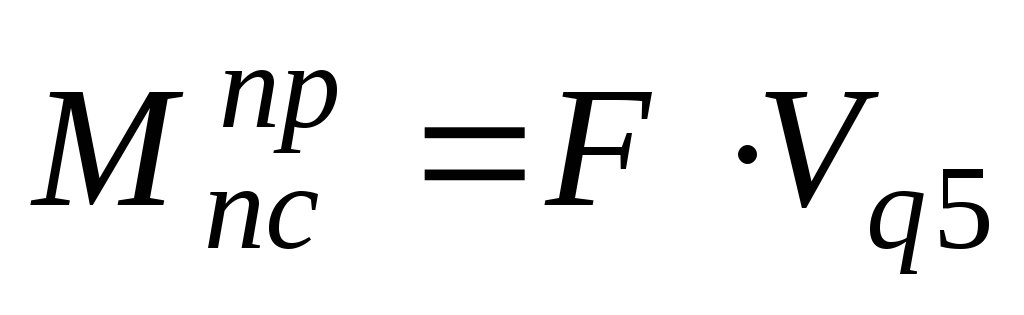 .
.
Знак приведенного момента совпадает со знаком силы полезного сопротивления.
Масштабы: 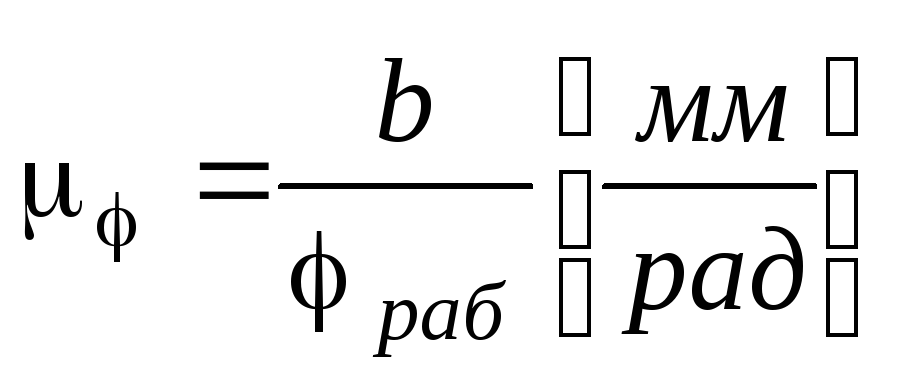 ,
,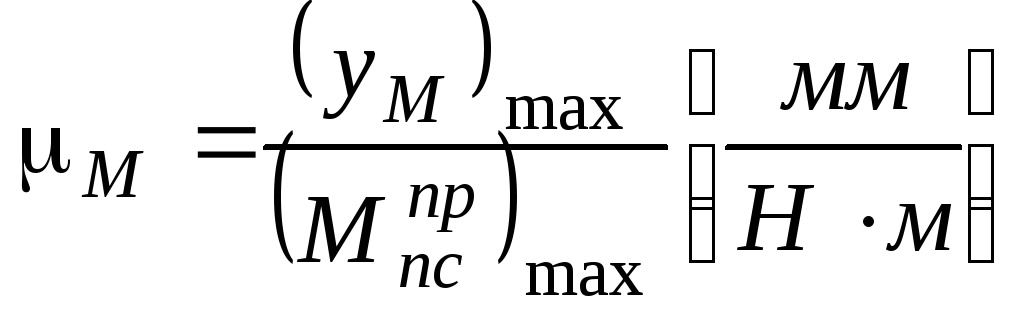 ,
,
где: 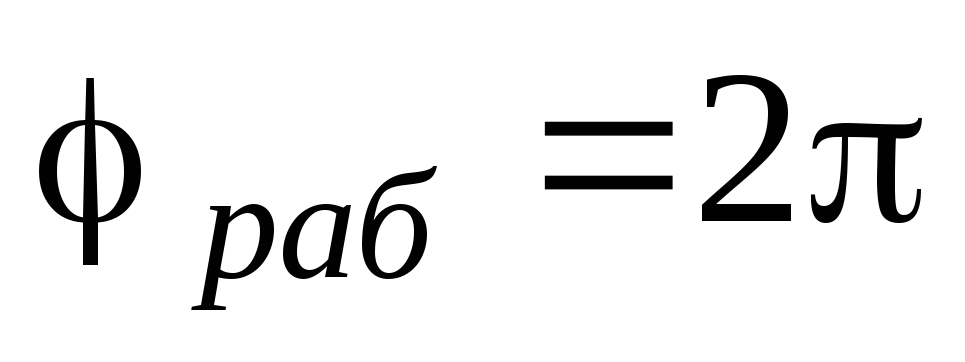 .
.
Когда момент
полезного сопротивления будет определен,
суммарный момент может быть получен
как алгебраическая сумма 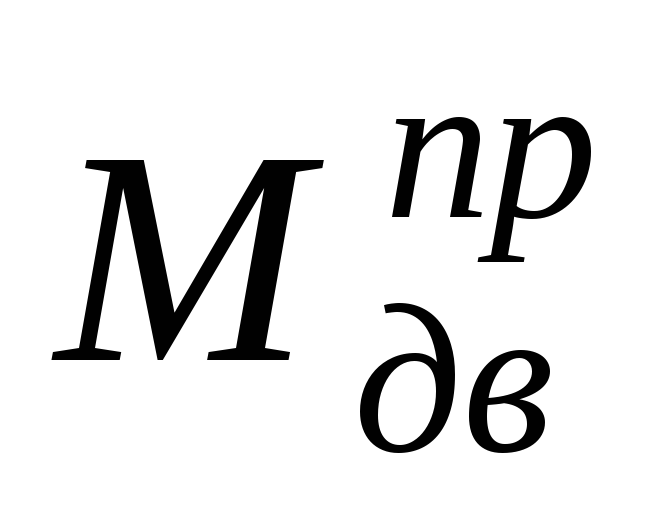 и
и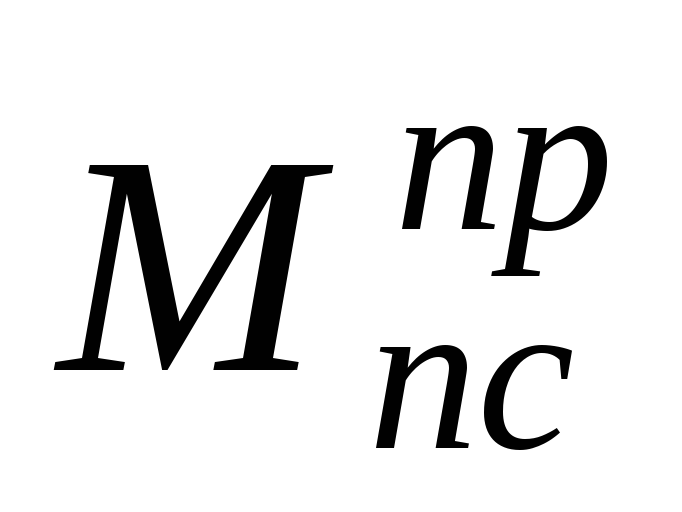 .
.
 Рис.
17. Диаграммы для поперечно-строгального
станка:
Рис.
17. Диаграммы для поперечно-строгального
станка:
а) диаграмма приведенных моментов;
б) диаграмма работы моментов
График 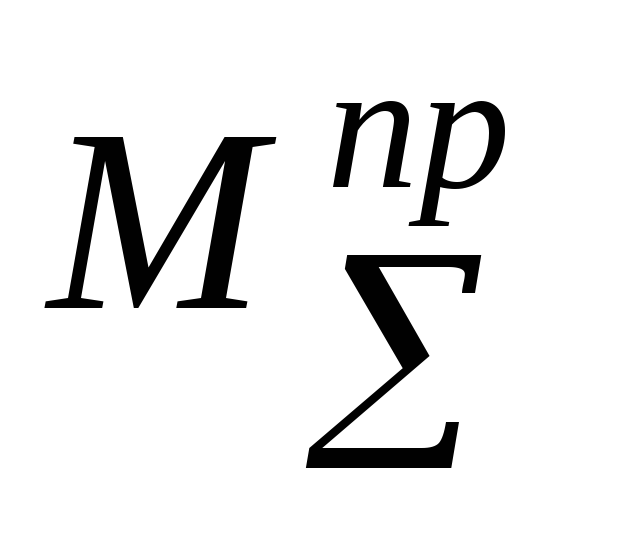 может быть получен одним из двух способов:
может быть получен одним из двух способов:
8. Диаграмма работ
Работа может быть подсчитана по формулам
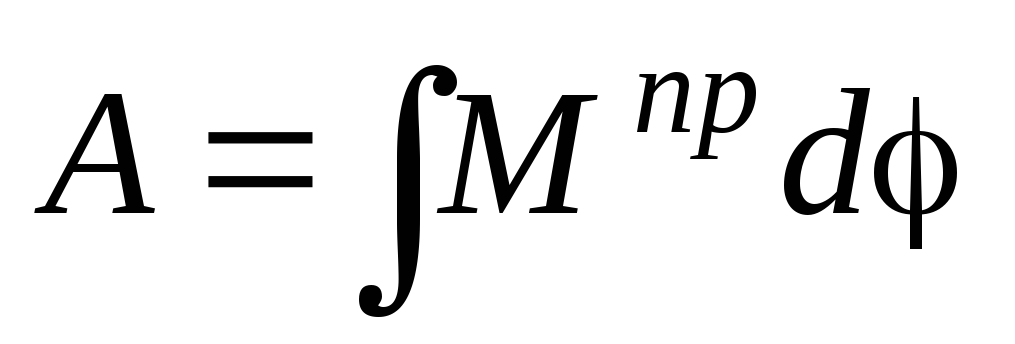 ,
если
,
если 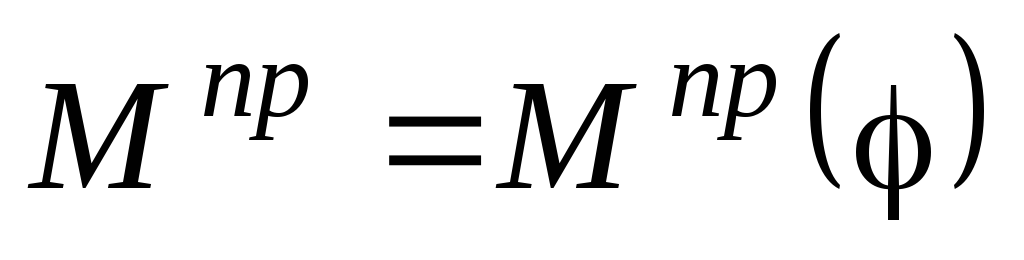 ;
;
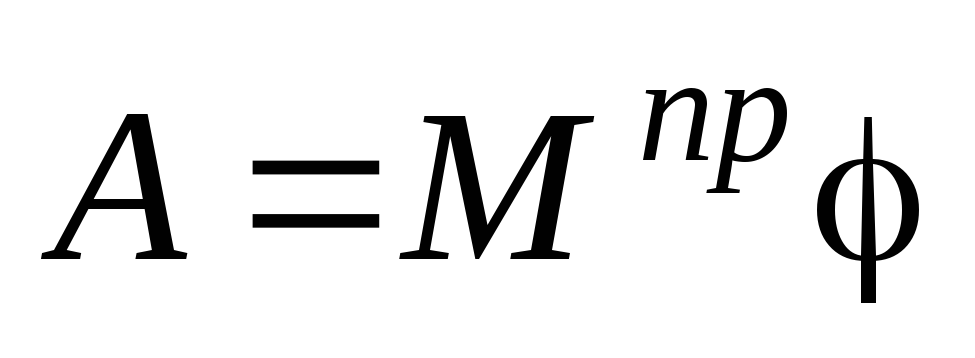 ,
если
,
если 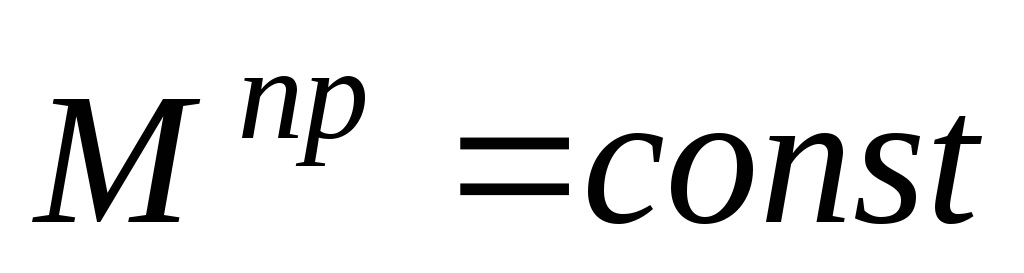 .
.
Если интегрирование
проводится графически, необходимо
выбрать полюс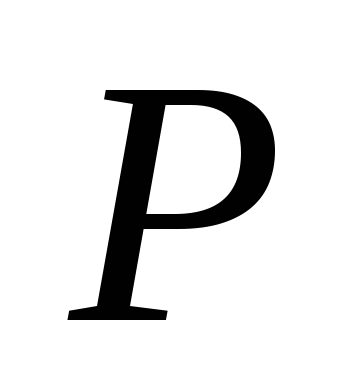 ,
определить
,
определить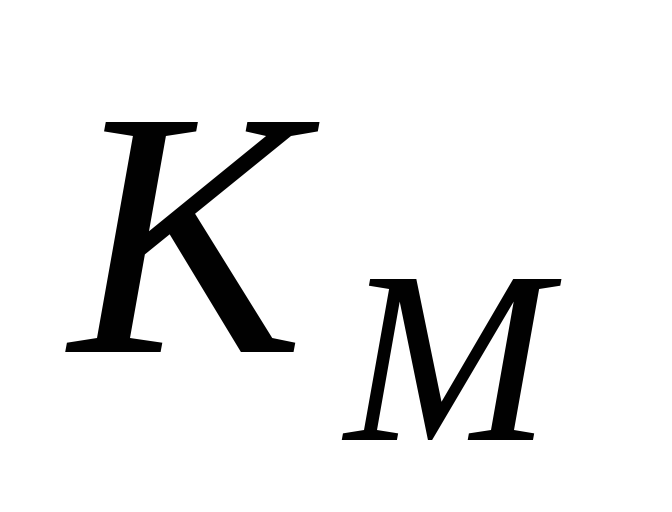 – постоянную интегрирования, масштаб
диаграммы работ
– постоянную интегрирования, масштаб
диаграммы работ
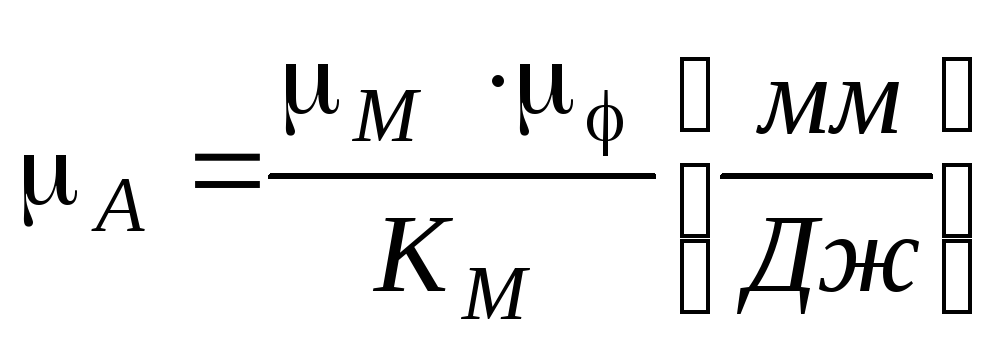 .
.
Рассмотрим построение диаграммы работ некоторых механизмов, характерных для заданий на курсовой проект.


 ,
прямо пропорционально моменту силы
и обратно пропорционально моменту
инерции тела:
,
прямо пропорционально моменту силы
и обратно пропорционально моменту
инерции тела:
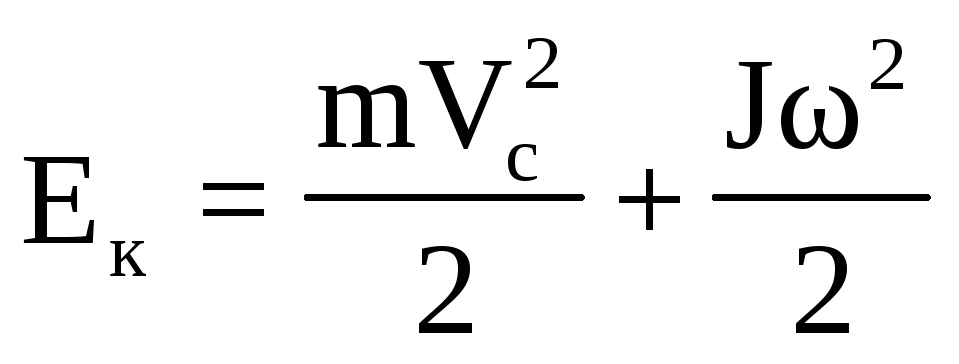 (12)
(12)