Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Физика
| Похожие вопросы |
ЗНАЧОК ОБОЗНАЧЕНИЯ «ЧАСТОТЫ»
В однородном магнитном поле с индукцией 1 Тл
Решено
жесткость пружины
Помогите пожалуйста с решением задачи
Куда деваются фотоны?
Пользуйтесь нашим приложением
Сумма трех векторов равна нулю
Содержание
- тЕЫЕОЙЕ
- пФЧЕФ
- йУФПЮОЙЛЙ Й РТЕГЕДЕОФЩ ЙУРПМШЪПЧБОЙС
- Правило треугольника
- Сумма противоположных векторов
- Свойство переместительности
- Правило параллелограмма
- Сложение векторов.
 Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор
Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор
нПЦОП МЙ ТБУРПМПЦЙФШ ОБ РМПУЛПУФЙ ФТЙ ЧЕЛФПТБ ФБЛ, ЮФПВЩ НПДХМШ УХННЩ ЛБЦДЩИ ДЧХИ ЙЪ ОЙИ ВЩМ ТБЧЕО 1, Б УХННБ ЧУЕИ ФТЈИ ВЩМБ ТБЧОБ ОХМЕЧПНХ ЧЕЛФПТХ?
тЕЫЕОЙЕ
ъБНЕФЙН, ЮФП ЕУМЙ УХННБ ФТЈИ ЕДЙОЙЮОЩИ ЧЕЛФПТПЧ ТБЧОБ ОХМА, ФП УХННБ ЛБЦДЩИ ДЧХИ ЙЪ ОЙИ ТБЧОБ ФТЕФШЕНХ У ПВТБФОЩН ЪОБЛПН, ФП ЕУФШ ЕЈ НПДХМШ ТБЧЕО 1. фТЙ ФБЛЙИ ЕДЙОЙЮОЩИ ЧЕЛФПТБ НПЦОП ТБУРПМПЦЙФШ РП ТБЪОПНХ.
рЕТЧЩК УРПУПВ. тБУУНПФТЙН РТБЧЙМШОЩК ФТЕХЗПМШОЙЛ бчу УП УФПТПОБНЙ ЕДЙОЙЮОПК ДМЙОЩ (УН. ТЙУ.). фПЗДБ ЙУЛПНЩК РТЙНЕТ: , Й .
чФПТПК УРПУПВ. йУЛПНЩНЙ СЧМСАФУС ФТЙ ЕДЙОЙЮОЩИ ЧЕЛФПТБ , Й , ПВТБЪХАЭЙЕ РПРБТОП ХЗМЩ 120° (УН. ЪБДБЮХ 55373 Б).
пФЧЕФ
йУФПЮОЙЛЙ Й РТЕГЕДЕОФЩ ЙУРПМШЪПЧБОЙС
| ПМЙНРЙБДБ | |
| оБЪЧБОЙЕ | нПУЛПЧУЛБС НБФЕНБФЙЮЕУЛБС ТЕЗБФБ |
| ЗПД | |
| зПД | 2012/13 |
| ЛМБУУ | |
| 1 | |
| лМБУУ | 10 |
| ЪБДБЮБ | |
| оПНЕТ | 10. 1.2 1.2 |
рТПЕЛФ ПУХЭЕУФЧМСЕФУС РТЙ РПДДЕТЦЛЕ Й .
Правило треугольника
Сумма векторов a и b это третий вектор с , получаемый следующим построением: из произвольного начала О строим вектор OL , равный а ; из точки L , как из начала строим вектор LM , равный b . Вектор с = ОМ есть сумма векторов a и b («правило треугольника»).
При сложении векторов справедливы неравенства
Эти неравенства показывают, что сторона OM треугольника OML меньше суммы и больше разности двух других сторон.
В формуле (1) знак равенства имеет место только для равнонаправленных векторов, в формуле (2) – только для противоположного направленных векторов.
Сумма противоположных векторов
Из определения следует, что сумма противоположных векторов равна нуль-вектору.
Свойство переместительности
От перестановки слагаемых сумма не изменяется.
Правило параллелограмма
Если слагаемые a и b не коллинеарны, то сумму a + b можно найти следующим построением:
из любого начала О строим векторы ОА = а и ОВ = b ; на отрезках ОА , ОВ строим параллелограмм ОАСВ . Вектор диагонали ОС = с есть сумма векторов a и b (так как АС = OB = b и ОС = ОА + АС ).
Вектор диагонали ОС = с есть сумма векторов a и b (так как АС = OB = b и ОС = ОА + АС ).
К коллинеарным векторам это построение неприменимо.
Определение сложения векторов установлено в соответствии с физическими законами сложения векторных величин (например, сил, приложенных к материальной точке).
Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор
В механике существуют два типа величин:
- скалярные величины,
- векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д..
Рассмотрим сначала алгебраический подход к сложению векторов.
Покоординатное сложение векторов.
Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.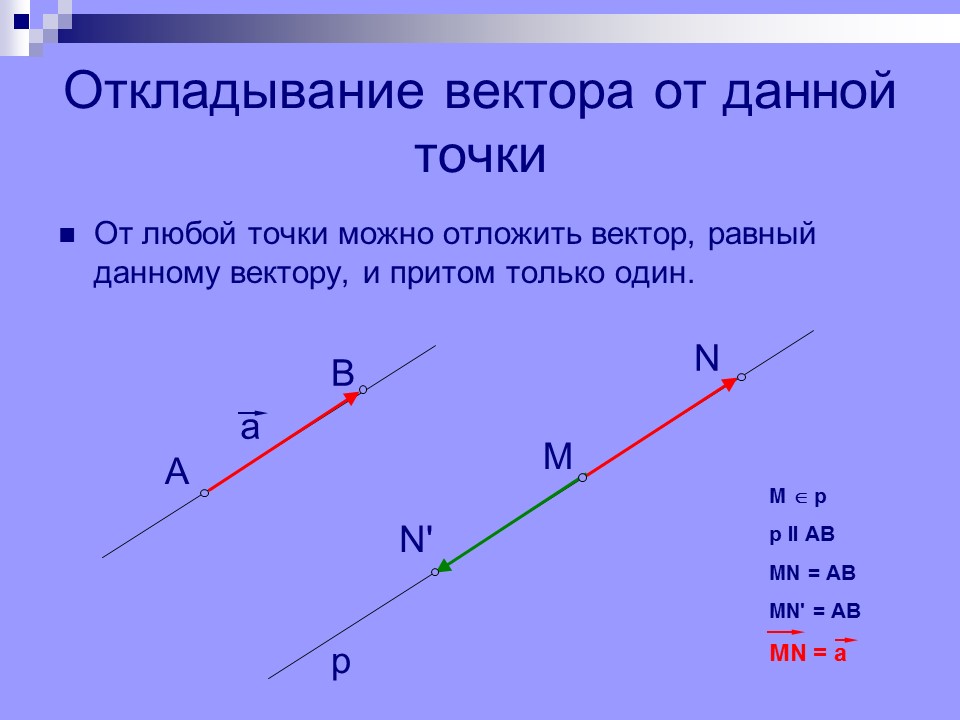 е. из первой координаты — первую, из второй — вторую и т.д.):
е. из первой координаты — первую, из второй — вторую и т.д.):
Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:
В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.
Теперь перейдем к геометрическому смыслу сложения двух векторов: .
При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:
- правило параллелограмма
- правило треугольника
- тригонометрический способ
Правило параллелограмма.
Процедура сложения векторов по правилу параллелограмма заключается в следующем:
- нарисовать первый вектор, учитывая его величину и направление
- от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление
- дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны
- результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.

Правило треугольника
Сложение векторов по правилу треугольника заключается в следующем:
- нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении
- от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление
- результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом второго.
Тригонометрический способ
Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов:
F = числовое значение вектора
α = угол между векторами 1 и 2
Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов:
α = угол между исходными векторами
Пример — сложение векторов.
Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.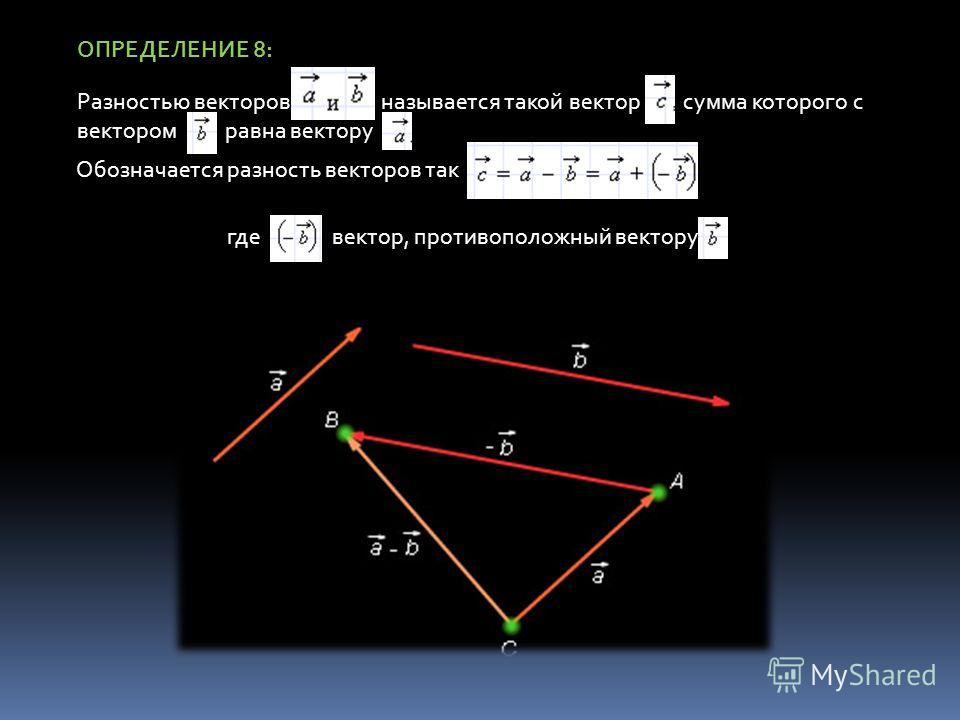
Результирующая сила вычисляется следующим образом:
Fрез = [ (5 кН) 2 + (8 кН) 2 — 2 (5 кН)(8 kН) cos(180 o — (80 o )) ] 1/2
Угол между результирующей силой и первой силой равен:
А угол между второй и результирующей силой можно посчитать следующим образом: as
α = arcsin [ (5 кН) sin(180 o — (80 o )) / (10,2 кН) ]
Он-лайн калькулятор сложения векторов.
Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.
Консультации и техническая
поддержка сайта: Zavarka Team
Векторы на плоскости и в пространстве. Основные понятия
1. Векторы на плоскости и в пространстве. Основные понятия.
2. Понятие вектора в пространстве
Вектор(направленный отрезок) –отрезок, для которого указано какой из его
концов считается началом, а какой – концом.

В
А
AB
a
M
MM 0
Длина вектора AB – длина отрезка AB.
AB AB
0 0
Нулевым вектором называется вектор, начало и конец
которого совпадают.
Единичным вектором называется вектор, длина которого
равна единице.
Векторы называются коллинеарными, если они лежат на
одной прямой или параллельных прямых.
Векторы называются компланарными, если они лежат в одной
плоскости или в параллельных плоскостях.
4. Коллинеарные векторы
Среди коллинеарных различают:• Сонаправленные векторы
• Противоположно направленные векторы
5. Равные векторы
Равные векторы — сонаправленные векторы,длины которых равны.
a
a b a b, a b
b
От любой точки можно отложить вектор,
равный данному, и притом только один.
6. Противоположные векторы
Противоположные векторы – противоположнонаправленные векторы, длины которых равны.
a
a b a b, a b
b
Вектором, противоположным нулевому,
считается нулевой вектор.

7. Признак коллинеарности
Если существует такое число k при которомвыполняется равенство a k b и при том
вектор b 0 , то векторы a и b коллинеарн ы.
вектор k a b, если k 0
вектор k a b, если k 0
8. Действия с векторами
• Сложение• Вычитание
• Умножение вектора на число
9. Сложение векторов
Правило треугольника
Правило параллелограмма
Правило многоугольника
Правило параллелепипеда
10. Правило треугольника
Для сложения двух векторов необходимо :1. отложить от какой нибудь точки А вектор
AB, равный а
2. от точки В отложить вектор BC , равный b
3. вектор AC называется суммой векторов a и b
B
a
a
А
b
a b
b
C
11. Правило треугольника
Ba
А
a b
b
C
Для любых трех точек А, В и С справедливо равенство:
AB BC AC
12. Правило параллелограмма
Для сложения двух векторов необходимо :1. отложить от какой нибудь точки А
вектор AB, равный а
2.
 от точки А отложить вектор AC, равный b
от точки А отложить вектор AC, равный b3. достроить фигуру до параллелограмма , проведя
дополнительные линии параллельно данным
векторам
4. диагональ параллелограмма сумма векторов
B
a
a
b
А
с
b
с a b
C
13. Правило многоугольника
Сумма векторов равна вектору, проведенномуиз начала первого в конец последнего(при
последовательном откладывании).
a
B
b
C
A
a b c d e
e
c
E
d
Пример
D
AB BC CD DE AE
14. Пример
B1A1
C1
D1
B
A
C
D
AA1 D1C1 A1 D BA CB 0
15. Правило параллелепипеда
Вектор, лежащий на диагонали параллелепипеда,равен сумме векторов, проведенных из той же
точки и лежащих на трех измерениях
параллелепипеда.
B
A1
C1
1
d
AB b
D1
с bB
C
А
a
AD a
D
AC1 AD AB AA1
AA1 c
AC1 d
16. Свойства
B1A1
C1
d
D1
с aB
А
C
b
D
d a b c для любого параллелепипеда
d 2 a 2 b 2 c 2 для прямоуголь ного
параллелепипеда
17.
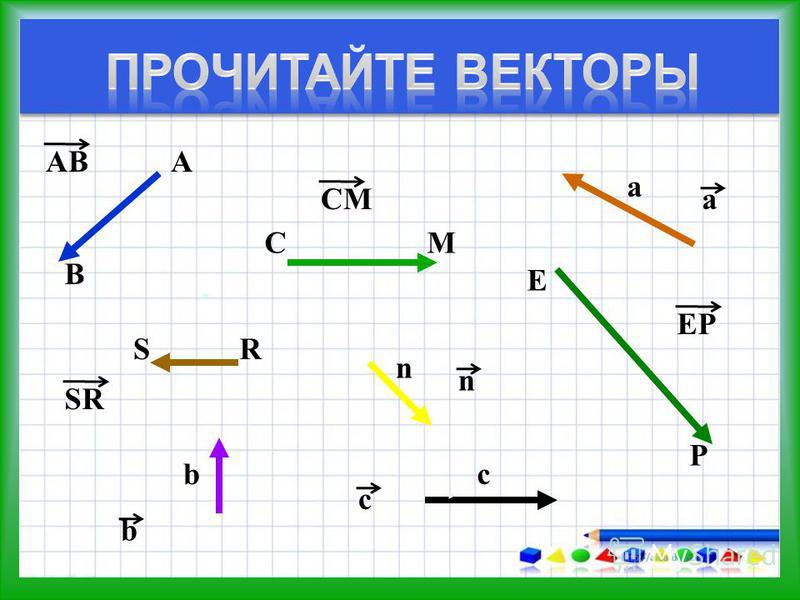 ВычитаниеРазностью векторов a и b называется такой
ВычитаниеРазностью векторов a и b называется такойвектор, сумма которого с вектором b равна
вектору a .
18. Вычитание
Для вычитания одного вектора из другого необходимо :1. отложить от какой нибудь точки А
вектор AB, равный а
2. от этой же точки А отложить вектор AC,
равный b
3. вектор CB называется разностью векторов a и b
B
a
b
Правило трех точек
a
a b
A
b
C
19. Умножение вектора на число
Произведением ненулевог о вектора a на число kназывается такой вектор b , длина которог о
равна к а , при чем векторы a и b сонаправле ны
при k 0 и противоположно направлены при k 0.
a
2a
b
1
b
3
20. Свойства
Для любыхвект оровa и b и любыхчисел k, l справедливы равенст ва:
(kl)a k(la )
сочет ат ельный закон
k( a b ) k a k b
1 ый распределит ельный
закон
(k l)a k a l a
2 ой распределит ельный
закон
21. Определение компланарных векторов
Компланарные векторы – векторы, приоткладывании которых от одной и той же точки
пространства, они будут лежать в одной
плоскости.
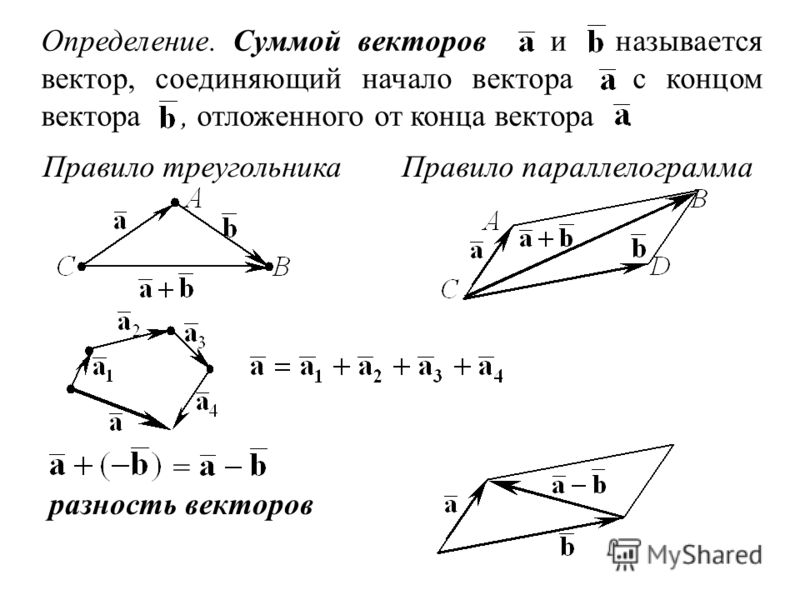
Пример:
B1
A1
C1
D1
B
А
C
D
BB1 , AC,AC 1 компланарн ы, т.к.
BB1 AA1 , а векторы AA1 , AC , AC1
лежат в плоскости (AA1C)
22. О компланарных векторах
Любые два вектора всегда компланарны.α
a
b
a
b
a
b
a и b компланарн ы
Три вектора, среди которых имеются два
коллинеарных, компланарны.
a, b и c
компланарн ы
если
a, b, c
a kb
23. Признак компланарности
Если вектор c можно разложить по векторама и b, т.е. представить в виде
с xa yb
где х и у некоторые числа, то векторы a, b
и c компланарн ы.
24. Разложение вектора
• По двум неколлинеарным векторам• По трем некомпланарным векторам
25. Разложение вектора по двум неколлинеарным векторам
Теорема.Любой вектор можно разложить по двум
данным неколлинеарным векторам, причем
коэффициенты разложения определяются
единственным образом.
26. Разложение вектора по трем некомпланарным векторам
Если вектор p представлен в видеp xa yb z c
где x, y, z – некоторые числа, то говорят, что вектор
p разложен по векторам a , b и c .

Числа x, y, z называются коэффициентами разложения.
Теорема
Любой вектор можно разложить по трем данным
некомпланарным векторам, причем коэффициенты
разложения определяются единственным образом.
27. Доказательство теоремы
Сс
P
p
b
O
B
P2
P1
aA
Доказательство :
О произвольн ая точка
Дано :
abc
некомпланр ные
векторы
p x a yb z c
OA a OB b OC c OP p
AP OC AP (AOB) P1 P2 P1 OB
OP OP2 P2 P1 P1 P
OP2 , и OA , PP1 и OB , P1 P , OC коллинеарны
OP2 x OA , P2 P1 y OB , P1 P z OC
OP x OA y OB z OC
p x a yb z c ч.т.д.
Скалярное произведение векторов
Скалярным произведением двух векторов называется число
ab a b cos
Замечание. Если два вектора являются перпендикулярными, то
их скалярное произведение равно нулю, и наоборот.
Теорема. Скалярное произведение двух векторов
a X1 , Y1 , Z1 , b X 2 , Y2 , Z 2
вычисляется по формуле
ab X1 X 2 YY
1 2 Z1Z 2
Следствие 1.
 Косинус угла между векторами
Косинус угла между векторамиa X1 , Y1 , Z1 , b X 2 , Y2 , Z 2
вычисляется по формуле
cos
ab
a b
X 1 X 2 Y1Y2 Z1Z 2
X 12 Y12 Z12 X 2 2 Y2 2 Z 2 2
Следствие 2. Необходимое и достаточное условие
перпендикулярности двух векторов выражается равенством
ab X1 X 2 YY
1 2 Z1Z 2 0
30. Базисные задачи
31. Вектор, проведенный в середину отрезка,
равен полусумме векторов, проведенных из той жеточки в его концы.
С
A
B
O
1
1
1
OC ( OA OB ) OA OB
2
2
2
Доказательство
32. Доказательство
СA
B
O
Доказательство :
OC OA AC
OC OB BC
Дано :
AB отрезок
AC CB
Доказать :
1
OC ( OA OB )
2
2OC OA AC OB BC OA OB (
AC
BC
)
o
2OC OA OB 2
1
OC ( OA OB ) ч.т.д.
2
33. Вектор, соединяющий середины двух отрезков,
равен полусумме векторов, соединяющих их концы.С
N
D
B
С
N
D
B
M
M
A
A
1
1
MN ( AD BC ) ( AC BD )
2
2
Доказательство
34.
 ДоказательствоС
ДоказательствоСN
D
B
M
A
Доказатель ство :
MN MA AC CN
MN MB BD DN
2 MN AC BD
1
MN ( AC BD ) ч.т.д.
2
Дано :
AB; CD
BM AM
CN ND
Доказать :
1
MN ( AC BD )
2
35. Вектор, проведенный в точку пересечения диагоналей параллелограмма,
равен одной четверти суммы векторов, проведенныхиз этой точки в вершины параллелограмма.
O
C
B
M
A
D
1
OM ( OA OB OC OD )
4
Доказательство
36. Доказательство
OB
C
M
Дано :
ABCD пар м
BD AC M
Доказать :
1
OM ( OA OB OC OD )
4
A
D
1
OM ( OA OC )
2
1
OM ( OB OD )
2
1
1
1
1
2OM OA OB OC OD
2
2
2
2
1
1
1
1
OM OA OB OC OD
4
4
4
4
1
( OA OB OC OD ) ÷.ò.ä.
4
37. Задача 1. Разложение векторов
Разложите вектор по a, b и c :D
N точка пересечения
медиан ABC
a
A
а) DB
б) CB
в) DC
г) DN
Решение
b
B
N
c
C
38.
 Решениеа) DB b a
Решениеа) DB b aб) CB b c
в) DC c a
г) DN a 1 AN a 1 ( 1 ( b c ))
3
1
1
a b c
6
6
3 2
39. Задача 2. Сложение и вычитание
Упростите выражения:а)
б)
в)
г)
д)
е)
CM MK
DM MA
SD ST
PL PK
AC BC PM AP BM
AD MP EK EP MD
Решение
40. Решение
а) CM MK CKб) DM MA DA
в) SD ST TD
г) PL PK KL
д) AC BC PM AP BM
AC CB MP PA BM
AB MA BM AM MA 0
е) AD MP EK EP MD
AD DM MP PE EK
AK
Проекция вектора онлайн
Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:Прab = |b|cos(a,b) или
где a•b — скалярное произведение векторов,|a| — модуль вектора a.
Инструкция. Для нахождения проекции вектора Пpab в онлайн режиме необходимо указать координаты векторов a и b. При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word. Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор.
При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word. Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор.
две координаты вектора
три координаты вектора
a: ; ;
b: ; ;
Классификация проекций вектора
Виды проекций по определению проекция вектора
- Геометрическая проекция вектора AB на ось (вектор) называется вектор A’B’, начало которого A’ есть проекция начала A на ось (вектор), а конец B’ – проекция конца B на ту же ось.
- Алгебраическая проекция вектора AB на ось (вектор) называется длина вектора A’B’, взятая со знаком + или -, в зависимости от того, имеет ли вектор A’B’ то же направление, что и ось (вектор).
Виды проекций по системе координат
- проекции на плоскости (система координат OX,OY).
 Пример: a(2;-3), a=2i-3j
Пример: a(2;-3), a=2i-3j
- проекции в пространстве (система координат OX,OY, OZ). Пример: a(2;-3;1), a=2i-3j+k
- проекции в N-мерном пространстве
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).
- Алгебраическая проекция вектора есть число.
Теоремы о проекциях вектора
Теорема 1. Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.AC’=AB’+B’C’
Теорема 2. Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Прab = |b|·cos(a,b)
Виды проекций вектора
- проекция на ось OX.
- проекция на ось OY.
- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак.
| Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак.
| Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак.
|
| Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак.
| Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак.
| Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак.
|
| Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB.
| Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB.
| Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB.
|
| Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор).
| Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор).
| Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор).
|
1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор). Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Пример 1. Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60о. Если OE есть единица масштаба, то |b|=4, так что .
Если OE есть единица масштаба, то |b|=4, так что .
Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.
Пример 2. Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120o. Длина |b| вектора b равна 4, поэтому прab=4·cos120o = -2.
Действительно, длина вектора равна 2, а направление противоположно направлению оси.
Пример 3. Пусть вектор b задан через координаты точек M(1;1), N(4;5).
Координаты вектора: MN(4-1;5-1) = MN(3;4)
Тогда модуль вектора MN равен:
Направляющий вектор для оси OX равен вектору M’N’, где координаты точек M’(1;0) N’(4;0). Следовательно, вектор M’N’ имеет координаты: x = 4-1, y = 0-0 = 0.
M’N’(3;0)
Пример 4. Найти проекцию вектора c на вектор d;
с = АС = (-2;-1;3), d = CB(-5;-3;3)
Найдем проекцию вектора AC на вектор BC
Пример 5. Найти проекцию прb(-2a+4b)
Найти проекцию прb(-2a+4b)
где a=2m+3n и b=4m-n, |m|=k, |n|=l, угол между ∠(m,n)= π
Тогда -2a+4b = -4m+6n + 16m-4n = 12m+2n
а) Рассмотрим треугольник со сторонами a,b,c. По теореме косинусов:
a2 = b2 + c2 – 2bc∙cos(b,c), откуда
или б) Рассмотрим второй вариант решения.
Поскольку угол между векторами π, т.е. 180о, то векторы лежат на одной оси.
Таким образом, 4m-n = 4*1 – 1 = 3.
Находим проекцию.
прb(-2a+4b) = прb(12m+2n) =
Сумма векторов — Энциклопедия по экономике
Буквенное обозначение В. принято выделять жирным шрифтом (хотя не всегда это соблюдается). Суммой векторов х = (хр…, л )и У = (Ур > > ) является также В. (х + у) = = (х, + ух,. .., х»+у). [c.42]Разбиение единичного тензора (3.102) используется для построения проекций на касательную плоскость и нормаль.
 Например, вектор с компонентами Т1 можно представить в виде суммы вектора, касательного к поверхности, и вектора, направленного по нормали,
[c.55]
Например, вектор с компонентами Т1 можно представить в виде суммы вектора, касательного к поверхности, и вектора, направленного по нормали,
[c.55]Регрессионный анализ зависимости производительности труда от значений основных факторов заключается в нахождении такой функции y=f(x), где х — вектор с компонентами х — хь, при которой суммы квадратов отклонений от выборочных значений производительности труда были бы минимальными. [c.82]
Матрица С согласно (2.8) удовлетворяет соотношению С = А + 4 Аг + А3 +. . . Смысл матрицы С легко понять из следующих соображений. Вектор Ау показывает, какие прямые затраты необходимы для выпуска конечного продукта у. Поэтому вектор А2у = А(Ау) описывает прямые затраты, необходимые для обеспечения выпуска продукта Ау, вектор А3у = А(А2у] показывает, какие прямые затраты необходимо сделать для выпуска продукта Агу, и т. д. Таким образом, сумма Azy + А3у + А у +. . . показывает, какое количество продукции каждой отрасли необходимо выделить на производство конечного продукта у не напрямую, а косвенно, через производство продукции других отраслей.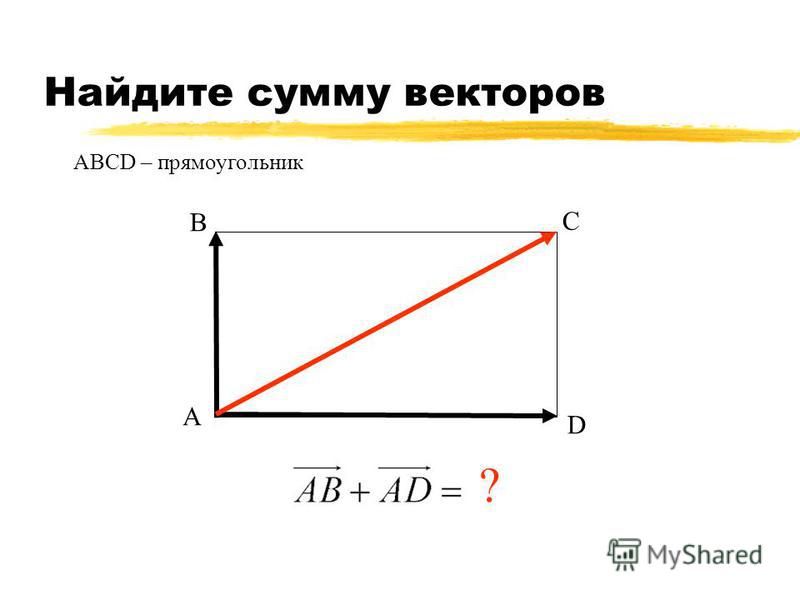 Поа-
[c.266]
Поа-
[c.266]
Если отказаться от предположения о том, что запасы отсутствуют, то тогда вектор чистой конечной продукции можно представить в виде суммы двух составляющих — потребления w(t и изменения запасов q(t+ 1) — q(t), т. е. [c.272]
Таким образом, каждый столбец матрицы Z представляет собой вектор, координаты которого в сумме равны нулю, а длина этого вектора — единице. Матрица Z является исходной для расчета комплексной оценки. Далее методика расчета полностью совпадает с методикой метода расстояний. [c.29]
РМ 2 = PN2 + NM , где вертикальными чертами отмечены длины векторов. Это равенство соответствует разложению (3.41) общей суммы Q квадратов отклонений зависимой переменной Y от средней у на сумму квадратов Qg, обусловленную регрессией, и остаточную сумму квадратов Qe, т. e. Q=QR+Qe- Поэтому коэффициент детерминации Л2, определяемый по (3.47), примет вид [c.78]
Следует, однако, отметить и недостаток такой замены переменных, связанный с тем, что вектор оценок b получается не из условия минимизации суммы квадратов отклонений для исходных переменных, а из условия минимизации суммы квадратов отклонений для преобразованных переменных, что не одно и то же. В связи с этим необходимо определенное уточнение полученных оценок.
[c.125]
В связи с этим необходимо определенное уточнение полученных оценок.
[c.125]
Богданов сделал попытку сформулировать основные понятия и методы организационной науки. Анализируя сущность организации, он высказал идею о необходимости системного подхода к ее изучению, впервые показав, что организованное целое оказывается больше суммы его частей, а дезорганизованное — меньше. Роль организации, по его мнению, в данном случае сводится к выстраиванию векторов активности в нужном направлении и к преодолению возникающего при этом организационного сопротивления. Организованное целое оказывается больше про- [c.8]
При заданных координатных значениях п, т (натуральные числа) и сложившемся векторе цен Р /-и потребитель тратит деньги с учетом своего уровня дохода х. таким образом, чтобы достичь максимально возможного для него уровня потребления. Другими словами, потребитель становится обладателем определенной потребительной ценности (стоимости) при сложившейся цене набора и общей фиксированной сумме расходов, находясь в рамках соответствующего жизненного стандарта, и эта ситуация может быть охарактеризована своей кривой безразличия.
 [c.237]
[c.237]При умножении матрицы на вектор-столбец мы умножаем все элементы первого столбца матрицы на первый элемент вектора, все элементы второго столбца матрицы на второй элемент вектора, и так далее. Если бы вектор был вектор-строка, мы бы умножили все элементы первой строки матрицы на первый элемент вектора, все элементы второй строки матрицы на второй элемент вектора, и так далее. Так как речь идет о векторе-столбце и последние четыре элемента нули, нам надо умножить первый столбец обратной матрицы на Е (ожидаемая прибыль портфеля) и второй столбец обратной матрицы на S (сумма весов). Мы получим следующий набор уравнений, в которые можно подставить значения Е и S и получить оптимальные веса. [c.201]
Используя иерархический синтез для взвешивания собственных векторов матриц весами критериев, вычисляется сумма по всем соответствующим взвешенным компонентам собственных векторов матриц целей уровня иерархии, лежащего ниже. [c.98]
Множество А, А с R», называют выпуклым, если оно вместе с каждой парой своих точек содержит и весь отрезок, соединяющий эти точки.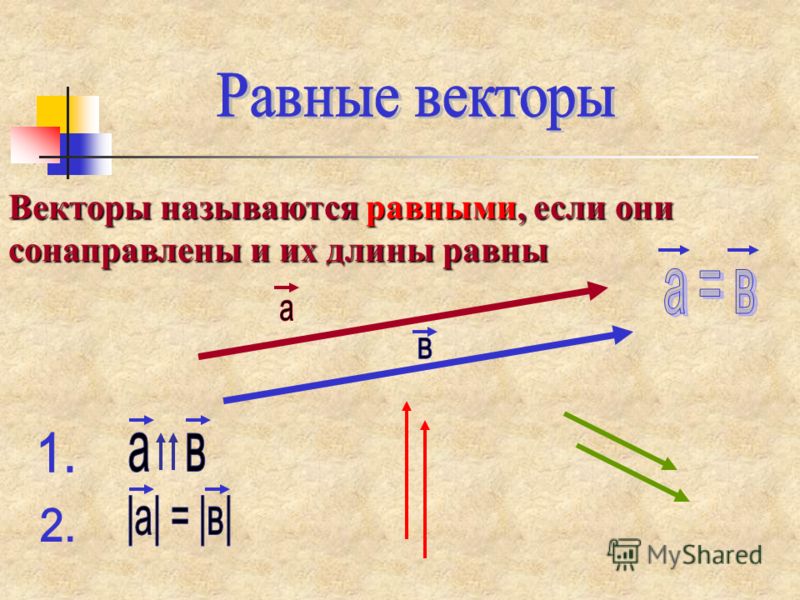 Иными словами, подмножество А пространства Rm выпукло, если для всех пар точек у, у» е А и любого числа А е [0, 1] выполнено соотношение у + (1 — А) у» е А. Множество К, К с Rm, называется конусом, если для каждой точки у е К и любого положительного числа а выполняется включение ау е К. Конус, являющийся выпуклым, именуют выпуклым конусом. Иначе говоря, выпуклое множество является выпуклым конусом, если оно вместе с каждой своей точкой содержит и весь луч, исходящий их начала координат (в общем случае без самого начала) и проходящий через данную точку. При этом начало координат (вершина конуса) может как принадлежать, так и не принадлежать данному конусу. Можно проверить, что сумма любых двух (и более) элементов выпуклого конуса всегда принадлежит данному конусу. Конус К называют острым, если не существует такого ненулевого вектора у е К, для которого выполняется включение -у е К. Не являющийся острым конус обязательно содержит, по крайней мере, одну прямую, проходящую через начало координат (вместе с самим началом или же без него).
Иными словами, подмножество А пространства Rm выпукло, если для всех пар точек у, у» е А и любого числа А е [0, 1] выполнено соотношение у + (1 — А) у» е А. Множество К, К с Rm, называется конусом, если для каждой точки у е К и любого положительного числа а выполняется включение ау е К. Конус, являющийся выпуклым, именуют выпуклым конусом. Иначе говоря, выпуклое множество является выпуклым конусом, если оно вместе с каждой своей точкой содержит и весь луч, исходящий их начала координат (в общем случае без самого начала) и проходящий через данную точку. При этом начало координат (вершина конуса) может как принадлежать, так и не принадлежать данному конусу. Можно проверить, что сумма любых двух (и более) элементов выпуклого конуса всегда принадлежит данному конусу. Конус К называют острым, если не существует такого ненулевого вектора у е К, для которого выполняется включение -у е К. Не являющийся острым конус обязательно содержит, по крайней мере, одну прямую, проходящую через начало координат (вместе с самим началом или же без него). [c.52]
[c.52]
Проверим транзитивность отношения предпочтения. Для этой цели выберем произвольную тройку векторов у, у», у » Г, удовлетворяющих соотношениям у «Sly» и у» Яу «. Последние два соотношения можно переписать в виде у — у» е К и у» — у » g К, откуда следует, что имеются два определенных элемента конуса К. Поскольку сумма любых двух элементов выпуклого конуса принадлежит данному конусу, из двух последних соотношений получаем у — у» е К, или, что то же самое, у Шу». Полученное доказывает транзитивность отношения 3 . [c.56]
В соответствии с этим рассуждением сумму у + Ау + А2у +. .. называют вектором полных затрат, а сделанное выше заключение формулируется так вектор валового выпуска х совпадает с вектором полных затрат. [c.261]
Поскольку р > 0, вектор у не может быть неотрицательным. Действительно, если у > 0, то все слагаемые в левой части (1.4) неотрицательны и, по крайней мере, одно слагаемое положительно (напомним, что у — собственный вектор, поэтому уФО), что противоречит равенству нулю всей суммы. Таким образом, мы доказали, что все неотрицательные собственные векторы положительны и принадлежат только максимальному по модулю собственному значению.
[c.264]
Таким образом, мы доказали, что все неотрицательные собственные векторы положительны и принадлежат только максимальному по модулю собственному значению.
[c.264]
Так, мы получим Q = QD. Опять-таки при условии, что С и Q — невырожденные матрицы, мы сможем записать С = QDQ»1. Однако если длина собственных векторов равна единице, т. е. сумма квадратов компонент собственных векторов равна единице, то матрицей, обратной Q, будет сама матрица Q, тогда можно записать, что С = QDQ [c.305]
Доля совокупной дисперсии, которая приходится на счет каждой комбинации переменных, равна доле соответствующего собственного значения в сумме всех собственных значений. Сумма собственных значений задается суммой элементов главной диагонали в матрице D. В нашем примере сумма собственных значений равна 0,0(30400. Таким образом, собственный вектор с собственным значением, равным 0,000271, отвечает за 0,000271/0,000400, или 67,75% совокупной дисперсии. [c.306]
Поскольку переменные были стандартизованы перед анализом, сумма собственных значений будет равна четырем, так как мы имеем четыре переменные. Принимая это во внимание, соответствующий вклад каждого из собственных векторов в совокупную дисперсию составит Я j=44,09 Я 2 =26,26 Я3 = 22,22 Я4= 7,44.
[c.309]
Принимая это во внимание, соответствующий вклад каждого из собственных векторов в совокупную дисперсию составит Я j=44,09 Я 2 =26,26 Я3 = 22,22 Я4= 7,44.
[c.309]
Скалярным произведением векторов х и у называется число, равное сумме произведений соответствующих компонент этих В. [c.42]
В экономико-математическом моделировании (в вероятностных моделях, экономико-статистических моделях) В. отражается стохастическим членом модели, который называется «ошибкой», «вектором помех», а также «остатком». Этот член, во-первых, улавливает неучтенные моделью факторы, поскольку в модель можно включать лишь ограниченное число существенных переменных (хотя эффект каждого из неучтенных факторов — иначе он был бы признан существенным — невелик, в сумме они оказывают определенное воздействие на выходы модели) во-вторых, он включает непредсказуемый элемент случайности человеческих поступков и реакций и в-третьих, ошибки измерения или наблюдения, следствия неточности информации, имеющейся при разработке модели. [c.52]
[c.52]
Функцией П.в. некоторые авторы называют зависимость набора товаров, выбираемых потребителем, от вектора цен и суммы его дохода (платежеспособности его бюджета). [c.271]
Hn — вычисление суммы компонент вектора ]Г]и = xt [c.47]
Пусть для определенности при вычислении матрицы B-Q по формуле (4.4.8) использовался единичный вектор ( , т), направленный из области Р в область Р . Тогда, с учетом сделанных обозначений и замечаний, сумма вариантов очевидного нуля , записанных для областей Р и Р[c.342]
В этой таблице /-е строки отражают виды КПТ, а /-е столбцы — соответствующие отрасли промышленности и народного хозяйства (см. п. 4.4.1). При этом каждому /(/=1,. .., 10) соответствуют три соседних столбца, из которых средний х) служит для представления переменных х) при меняющемся /, а крайние — соответствующих ограничений из условий (4.53). Таким образом, переменная х) отображается клеткой на пересечении своих /-й строки и /-го столбца. При этом левая часть условия (4.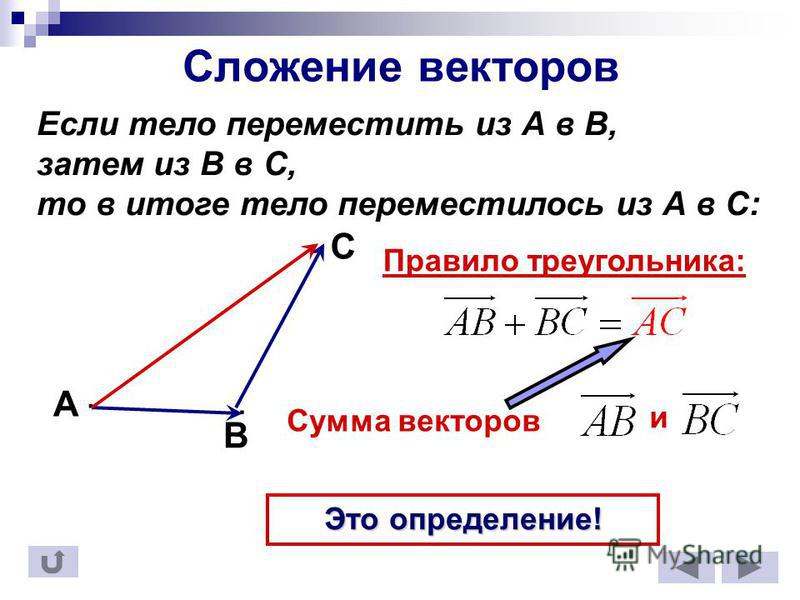 51) отображается суммой значений х) во всех заполненных клетках /-й строки, а значение х) из правой части условия (4.51) представлено на пересечении /-й строки и столбца 5 и определяется при решении подзадач, реализующих модели 01, 02, 04 и 06. В этих моделях задаются и ограничения из. условий (4.55). Левая часть условий (4.52) формально представима как скалярное произведение соответствующих векторов, представленных столбцами 7 и x) i. Значение х пт из правой части условия (4.52) в других моделях не определялось. Оно заносится после расчета в 0-ю строку табл. 4.2 как выходного документа над столбцом ху ,. В две соседние клетки этой строки могут быть априорно занесены ограничения из условий (4.54), которые ранее также не вводились.
[c.104]
51) отображается суммой значений х) во всех заполненных клетках /-й строки, а значение х) из правой части условия (4.51) представлено на пересечении /-й строки и столбца 5 и определяется при решении подзадач, реализующих модели 01, 02, 04 и 06. В этих моделях задаются и ограничения из. условий (4.55). Левая часть условий (4.52) формально представима как скалярное произведение соответствующих векторов, представленных столбцами 7 и x) i. Значение х пт из правой части условия (4.52) в других моделях не определялось. Оно заносится после расчета в 0-ю строку табл. 4.2 как выходного документа над столбцом ху ,. В две соседние клетки этой строки могут быть априорно занесены ограничения из условий (4.54), которые ранее также не вводились.
[c.104]
Денежные потоки в любой организации, без преувеличения, можно назвать ее кровеносной системой. В то же время этот показатель, как никакой другой, труден для прогнозирования. Эта глава посвящена проблеме управления активами и пассивами Министерства финансов Голландии (далее — MoF).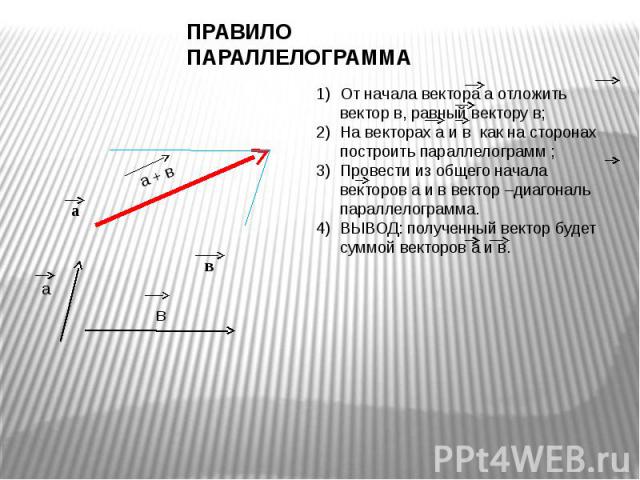 Особое внимание будет уделено оценке суммы ежемесячного валового сбора налогов. Мы рассмотрим и сравним различные методы, в том числе, и модель ARIMA — собственную разработку MoF. Так как нейронные сети превосходят другие методы по показателю среднеквадратичной ошибки (MSE) на вновь предъявляемых образцах, мы будем выделять различные типы индивидуального и совместного поведения переменных с помощью анализа первичных весов, тестов на чувствительность и выделения кластеров среди векторов весов-состояния.
[c.94]
Особое внимание будет уделено оценке суммы ежемесячного валового сбора налогов. Мы рассмотрим и сравним различные методы, в том числе, и модель ARIMA — собственную разработку MoF. Так как нейронные сети превосходят другие методы по показателю среднеквадратичной ошибки (MSE) на вновь предъявляемых образцах, мы будем выделять различные типы индивидуального и совместного поведения переменных с помощью анализа первичных весов, тестов на чувствительность и выделения кластеров среди векторов весов-состояния.
[c.94]
С 1889 г. вплоть до 1933 г. торговый баланс США неизменно сводился с положительным сальдо, хотя сумма последнего значительно колебалась в отдельные периоды. После Великой депрессии в течение 1934—1939 гг. импорт превышал экспорт. Однако Вторая мировая война снова повернула вектор на 180° торговый баланс, вплоть до 1971 г., стал сводиться с активом1. За счет огромных ежегодных поступлений от экспорта Соединенным Штатам удавалось иметь активное сальдо платежного баланса в первые послевоенные годы, а затем значительно компенсировать величину дефицита. Такое положение дел считалось само собой разумеющимся, и на этом строилась вся концепция платежного баланса.
[c.379]
Такое положение дел считалось само собой разумеющимся, и на этом строилась вся концепция платежного баланса.
[c.379]
ЛИНЕЙНАЯ КОМБИНАЦИЯ ВЕКТОРОВ [linear ombination] — вектор, представленный в виде д = а а. +… + а а, где коэффициенты а. — произвольные числа а. — рассматриваемые векторы (г = 1,…, п). Если сумма коэффициентов равна единице и 0 [c.169]
Рассмотрим частный случай, когда вектор цен остается неизменным, а изменяется только доход. Для двух групп товаров этот случай представлен на рис. 25.5. Если по оси абсцисс отложить количество единиц товара у, которое можно приобрести на имеющийся доход Z (точка В), а по оси ординат — количество товара у тотл же стоимости (точка А), то прямая линия АВ, называемая бюджетной линией, показывает любую комбинацию количеств этих двух товаров, которую можно купить за сумму денег Z. При увеличении дохода бюджетные ли- [c.551]
Основная предпосылка возможного применения данной модели состоит в том, что любой происходящий производственный процесс можно представить в виде линейной комбинации с не-отри-цательными коэффициентами некоторых основных (или базовых) производственных процессов. В свою очередь, каждый из этих процессов задается при помощи вектора выпуск—затраты , размерность которого определяется суммой количества видов производимых продуктов и потребляемых ресурсов. Коэффициенты в разложении данного производственного процесса по базовым производственным процессам назовем, как и выше, интенсивнос-тями основных способов.
[c.58]
В свою очередь, каждый из этих процессов задается при помощи вектора выпуск—затраты , размерность которого определяется суммой количества видов производимых продуктов и потребляемых ресурсов. Коэффициенты в разложении данного производственного процесса по базовым производственным процессам назовем, как и выше, интенсивнос-тями основных способов.
[c.58]
Проекция вектора на ось (Лекция №16)
Пусть в пространстве даны два вектора и . Отложим от произвольной точки O векторы и . Углом между векторами и называется наименьший из углов . Обозначается .
Рассмотрим ось l и отложим на ней единичный вектор (т.е. вектор, длина которого равна единице).
Под углом между вектором и осью l понимают угол между векторами и .
Итак, пусть l – некоторая ось и – вектор.
Обозначим через A1 и B1 проекции на ось lсоответственно точек A и B. Предположим,
что A1 имеет координату x1, а B1 – координату x2 на оси l.
Предположим,
что A1 имеет координату x1, а B1 – координату x2 на оси l.
Тогда проекцией вектора на ось l называется разность x1 – x2 между координатами проекций конца и начала вектора на эту ось.
Проекцию вектора на ось l будем обозначать .
Ясно, что если угол между вектором и осью l острый, то x2> x1, и проекция x2 – x1> 0; если этот угол тупой, то x2< x1 и проекция x2 – x1< 0. Наконец, если вектор перпендикулярен оси l, то x2= x1 и x2– x1=0.
Таким образом, проекция вектора на ось l – это длина отрезка A1B1,
взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр.
Следовательно, проекция вектора на ось это число или скаляр.
Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор.
Рассмотрим некоторые основные свойства проекций.
- Проеция вектора на ось l равна
произведению модуля вектора на косинус угла между
вектором и осью:
Доказательство. Ясно, что проекция вектора не изменится при его параллельном переносе, поэтому достаточно рассмотреть случай, когда начало вектора совпадает с началом отсчёта O оси l. Так как координата проекции начала равна нулю, то обозначим .
- Если угол φ острый, то из прямоугольного получаем . Откуда или
- Если угол φ тупой, то x< 0, . Тогда из или . Т.е. .
- Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось: .

Доказательство. Пусть . Обозначим через x1, x2 и x3 координаты проекций A1, B1, C1 на ось l точек A, B и C. Тогда . Но .
Это свойство можно обобщить на случай любого числа слагаемых.
- Если вектор умножается на число λ, то его проекция на ось
также умножается на это число:
.
Доказательство. Пусть угол между вектором и осью .
Если λ > 0, то вектор имеет то же направление, что и , и составляет с осью такой же угол .
При λ > 0 .
Если же λ < 0, то и имеют противоположные направления и вектор составляет с осью угол π – φ и .
Следствие. Проекция разности двух векторов на ось равна разности проекций этих векторов на ту же ось.
ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ
Рассмотрим несколько векторов .
Линейной комбинацией данных векторов называется любой вектор вида , где — некоторые числа. Числа называются коэффициентами линейной комбинации. Говорят также, что в этом случае линейно выражается через данные векторы , т.е. получается из них с помощью линейных действий.
Например, если даны три вектора то в качестве их линейной комбинации можно рассматривать векторы:
Если вектор представлен как линейная комбинация каких-то векторов, то говорят, что он разложен по этим векторам.
Векторы называются линейно зависимыми, если существуют такие числа, не все равные нулю, что . Ясно, что заданные векторы будут линейно зависимыми, если какой-либо из этих векторов линейно выражается через остальные.
В противном случае, т.е. когда соотношение выполняется только при , эти векторы называются линейно независимыми.
Теорема 1. Любые два вектора линейно зависимы тогда и
только тогда, когда они коллинеарны.
Доказательство:
- Действительно, пусть имеем два коллинеарных вектора и . Тогда либо оба они равны нулю, и следовательно, любая их линейная комбинация при любых λ1 и λ2, либо один из них не нуль, тогда другой отличается от него на числовой множитель, например, . Но отсюда , а это и означает линейную зависимость векторов и .
- Докажем обратное, т.е. если два вектора
линейно зависимы, то они коллинеарны. Пусть векторы и линейно зависимы.
Тогда найдутся числа λ1 и λ2 такие, что , причём, например, λ2 ≠ 0. Тогда , т.е. векторы коллинеарны.
Таким образом, теорема утверждает, что линейно независимыми на плоскости могут быть только те векторы, которые неколлинеарны.
Аналогично можно доказать следующую теорему.
Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Доказательство.
- Пусть три вектора линейно зависимы, т.е.
, где, например, λ3 ≠ 0. Тогда .
Отнесём векторы и к одному началу и проведём через них плоскость. Тогда и будут лежать в той же плоскости, а потому и их сумма, т.е. будет лежать в той же плоскости, т.е. – компланарны.
- Пусть теперь векторы – компланарны. Тогда
они будут лежать в одной плоскости. Отнесём все три вектора к одному началу.
Если векторы и не коллинеарны, то очевидно, вектор можно предствить в виде . Действительно из рисунка видно, что , где и , а значит найдутся числа и такие, что .
Если же вектор коллинеарен вектору , то один из них линейно выражен через другой, т.е. . Что и требовалось доказать.
Таким образом, три некомпланарных вектора всегда линейно независимы. Кроме того, можно показать, что каждые четыре вектора линейно зависимы.
БАЗИС
Базисом называется совокупность
отличных от нулей линейно независимых векторов. Элементы базиса будем обозначать
.
Элементы базиса будем обозначать
.
В предыдущем пункте мы видели, что два неколлинеарных вектора на плоскости линейно независимы. Поэтому согласно теореме 1, из предыдущего пункта, базисом на плоскости являются любые два неколлинеарных вектора на этой плоскости.
Аналогично в пространстве линейно независимы любые три некомпланарных вектора. Следовательно, базисом в пространстве назовём три некомпланарных вектора.
Справедливо следующее утверждение.
Теорема. Пусть в пространстве задан базис . Тогда любой вектор можно представить в виде линейной комбинации , где x, y, z – некоторые числа. Такое разложение единственно.
Доказательство.
- Докажем сначала существование такого представления.
- Предположим, что коллинеарен
какому-либо из векторов базиса, например, . Тогда по доказанному выше . Следовательно, , где x = l, y = z = 0.

- Пусть компланарен с какой-либо парой базисных векторов, например, с и . Отложим три вектора от одной точки O. Через точку A проведём прямые, параллельные векторам и . Тогда , причём векторы и коллинеарны соответственно векторам и . Поэтому найдутся числа x и y такие, что , а значит .
- Пусть некомпланарен ни с одной парой базисных векторов. Отложим от одной точки и проведём через конец вектора прямую, параллельную вектору . Она пересечёт плоскость в точке A1. Очевидно, что . Но вектор компланарен векторам и , следовательно, по доказанному выше, , а вектор коллинеарен , поэтому . Таким образом, .
- Предположим, что коллинеарен
какому-либо из векторов базиса, например, . Тогда по доказанному выше . Следовательно, , где x = l, y = z = 0.
- Докажем теперь единственность такого представления.
Допустим, что возможны два представления вектора и . Причём, например, . Тогда должны иметь , т.к. иначе мы имели бы две прямые, проходящие через точку A1 параллельно .
 Из последнего равенства вытекает, что . Получили противоречие с нашим предположением, что и
доказывает теорему.
Из последнего равенства вытекает, что . Получили противоречие с нашим предположением, что и
доказывает теорему.В качестве частного случая из этой же теоремы можно сформировать следующее утверждение:
Если задан базис на плоскости, то любой вектор, компланарный с векторами можно представить в виде , причём такое разложение единственно.
Таким образом, базис позволяет однозначно сопоставить каждому вектору тройку чисел – коэффициенты разложения этого вектора по векторам базиса: . Верно и обратное, каждой тройке чисел x, y, z при помощи базиса можно сопоставить вектор, если составить линейную комбинацию .
Если базис и , то числа x, y, z называются координатами вектора в данном базисе. Координаты вектора обозначают .
ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Пусть в пространстве задана точка O и три некомпланарных вектора .
Декартовой системой координат в пространстве (на плоскости) называется совокупность точки и базиса, т. е.
совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки.
е.
совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки.
Точка O называется началом координат; прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат – осью абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называют координатными плоскостями.
Рассмотрим в выбранной системе координат произвольную точку M. Введём понятие координаты точки M. Вектор , соединяющий начало координат с точкой M. называется радиус-вектором точки M.
Вектору в выбранном базисе можно сопоставить тройку чисел – его координаты: .
Координаты радиус-вектора точки M. называются координатами точки M. в рассматриваемой системе координат. M(x,y,z). Первая координата называется абсциссой, вторая – ординатой, третья – аппликатой.
Аналогично определяются декартовы координаты на плоскости. Здесь точка имеет только две координаты – абсциссу и ординату.
Здесь точка имеет только две координаты – абсциссу и ординату.
Легко видеть, что при заданной системе координат каждая точка имеет определённые координаты. С другой стороны, для каждой тройки чисел найдётся единственная точка, имеющая эти числа в качестве координат.
Если векторы, взятые в качестве базиса, в выбранной системе координат, имеют единичную длину и попарно перпендикулярны, то система координат называется декартовой прямоугольной системой координат. В этом случае основные векторы принято обозначать буквами , а оси координат Ox, Oy и Oz.
Таким образом, любой вектор в декартовой прямоугольной системе координат можно записать в виде: .
Примеры.
- Построить на плоскости в декартовой системе координат вектор . Вектор примем в качестве радиус-вектора точки
М(-1;3).
- Построить вектор . Вектор примем в качестве радиус-вектора точки N(2; -1; 3).
В дальнейшем мы в основном будем использовать только декартову прямоугольную систему координат.

НАПРАВЛЯЮЩИЕ КОСИНУСЫ ВЕКТОРА
Пусть в декартовой прямоугольной системе координат задан вектор . Направление вектора в пространстве определяется углами α, β, γ которые вектор составляет с осями координат. Косинусы этих углов cos α, cos β, cos γ называются направляющими косинусами вектора.
Найдем выражение для направляющих косинусов вектора.
Пусть вектор задан в координатной форме .
Тогда , откуда.
Несложно показать, что .
Направляющие косинусы вектора полностью определяют его направление, но ничего не говорят о его длине.
Может ли сумма двух векторов равняться 0? – Книга Vea
сообщите об этом объявлении
Содержание
Может ли сумма двух векторов равняться 0?
Результат двух векторов разной величины может быть равен нулю.
Что значит, когда вектора складываются в ноль?
Это связано с тем, что единственное требование к векторам в сумме с нулевым вектором состоит в том, что сумма всех компонентов в одном и том же направлении друг относительно друга равна нулю. Таким образом, если сумма значений x равна нулю, сумма значений y равна нулю, а сумма значений z {если вы находитесь в трех измерениях} равна нулю.
Таким образом, если сумма значений x равна нулю, сумма значений y равна нулю, а сумма значений z {если вы находитесь в трех измерениях} равна нулю.
Как равнодействующая двух векторов может быть равна нулю?
Таким образом, два векторных результата могут быть равны нулю , если они имеют одинаковую величину, но противоположны по направлению.
При сложении двух векторов сумма равна?
результирующий
Можно ли сложить два вектора одинаковой величины и получить ноль?
Да, можно сложить три вектора одинаковой величины и получить ноль. Возьмем три вектора равных величин A, B и C, учитывая, что эти три вектора составляют угол 120xb0 друг с другом.
Чему равна сумма двух векторов?
Сумма двух или более векторов называется равнодействующей. Равнодействующую двух векторов можно найти либо методом параллелограмма, либо методом треугольника.
Может ли равнодействующая двух векторов быть нулевым вектором?
да, если два вектора одинаковы по величине и направлению.
Что означает, что сумма векторов равна 0?
Так как сумма векторов равна нулю Значит что начальная и конечная точки набора векторов совпадают.
Можно ли добавить ноль к вектору?
Да, мы можем добавить нулевой вектор или нулевой вектор к нулевому вектору. Мы также можем умножить нулевой вектор на ноль.
Что означает, что результирующий вектор равен нулю?
Результант трех векторов будет равен нулю, если применимы все следующие условия: Если направление результирующего этих двух векторов точно противоположно направлению третьего вектора. 3. Если модуль равнодействующей двух векторов точно равен модулю третьего вектора.
Могут ли два равных вектора дать нулевую равнодействующую?
Если у нас есть два вектора, результирующая этих двух векторов равна нулю, когда направления этих двух векторов противоположны друг другу. Кроме того, результирующая будет равна нулю, если и только , если они имеют одинаковую величину. Итак, мы можем сказать, что два ненулевых вектора с одинаковой величиной дают нулевой результирующий.
Итак, мы можем сказать, что два ненулевых вектора с одинаковой величиной дают нулевой результирующий.
Может ли равнодействующая двух неравных векторов равняться нулю?
Да, два вектора одинаковой величины, направленные в противоположных направлениях, в сумме будут равны нулю. Два вектора из неравная величина никогда не может в сумме равняться нулю. Если они указывают на одну и ту же прямую, то сумма не будет равна нулю, так как их величины различны.
При сложении двух векторов сумма называется?
Результат представляет собой векторную сумму двух или более векторов. Это результат сложения двух или более векторов вместе.
Что произойдет, если сложить два вектора?
Можно сложить два вектора вместе, чтобы определить результат (или результирующую). То есть результирующая сила была результатом (или равнодействующей) сложения всех векторов сил.
Что означает сумма двух векторов?
Определение векторной суммы: сумма ряда векторов, которая для суммы двух векторов геометрически представлена диагональю параллелограмма, стороны которого представляют два складываемых вектора.
Является ли сумма двух векторов вектором?
Сумма двух математических векторов равна третьему вектору, лежащему в том же векторном подпространстве, что и первый и второй. Сложение коммутативно и ассоциативно.
Можно ли сложить два вектора одинаковой величины и получить ноль Можно ли сложить три вектора одинаковой величины и получить ноль?
Нет, невозможно получить ноль, сложив два вектора неравных величин. Сумма двух векторов может быть равна нулю только в том случае, если они равны по величине и противоположны по направлению.
Может ли сложение двух векторов быть равным нулю?
Если сумма двух векторов равна нулю, то величины равны, но векторы указывают в противоположном направлении.
Когда сумма двух векторов может быть равна нулю?
Когда два вектора равны и противоположны по направлению, то их сумма будет равна нулю.
Два вектора с одинаковой величиной равны?
Когда два вектора равны? Два или более вектора на равны, если они имеют одинаковую длину и указывают в одном направлении. Любые два или более вектора будут равны, если они коллинеарны, сонаправлены и имеют одинаковую величину. Если два вектора равны, их векторы-столбцы также будут равны.
Любые два или более вектора будут равны, если они коллинеарны, сонаправлены и имеют одинаковую величину. Если два вектора равны, их векторы-столбцы также будут равны.
Что такое формула векторной суммы?
Сумма p p + q q представлена по величине и направлению диагональю параллелограмма, проходящей через их общую точку. Это закон параллелограмма сложения векторов. Следовательно, мы можем заключить, что треугольные законы сложения векторов и параллелограммный закон сложения векторов эквивалентны друг другу.
Как результирующий вектор мог быть равен нулю?
они могут сократить до нуля только , если величины А и В равны и они направлены в противоположные стороны. В случае трех векторов, если три вектора, действующие на точечный объект одновременно, представлены по величине и направлению тремя сторонами треугольника, взятыми в одном и том же порядке, их результирующая равна нулю.
Что такое нулевой результирующий вектор?
Да, два вектора одинаковой величины, направленные в противоположных направлениях, в сумме будут равны нулю. Два вектора неравных величин никогда не могут в сумме равняться нулю. Если они указывают на одну и ту же прямую, то сумма не будет равна нулю, так как их величины различны.
Два вектора неравных величин никогда не могут в сумме равняться нулю. Если они указывают на одну и ту же прямую, то сумма не будет равна нулю, так как их величины различны.
Что значит, если сумма двух векторов равна 0?
Если сумма двух векторов равна нулю, то величины равны, но векторы указывают в противоположном направлении.
Что значит, когда вектор равен 0?
Нулевой вектор — это вектор, величина которого равна нулю. нулевой вектор не имеет направления или может иметь любое направление. как правило, нулевой вектор либо равен равнодействующей двух равных векторов, действующих в противоположных направлениях на несколько векторов в разных направлениях.
сообщите об этом объявлении
Может ли сумма векторов равняться нулю? – Fast-Advices
Содержание
- 1 Может ли сумма векторов равняться нулю?
- 2 Может ли вектор иметь нулевую величину?
- 3 Можно ли объединить три вектора разной величины, чтобы получить нулевой результирующий? Объясните?
- 4 Можно ли для трех векторов одинаковой величины добавить к нулю, если да, набросать графический ответ, если не объяснить, почему?
- 5 Могут ли два вектора неравных величин в сумме дать нулевой вектор Могут ли три неравных вектора в сумме дать нулевой вектор?
- 6 Могут ли три неравных вектора в сумме дать нулевой вектор?
- 7 Что произойдет, если три неравных вектора образуют треугольник?
Может ли сумма векторов равняться нулю?
Да, два вектора одинаковой величины, направленные в противоположные стороны, в сумме будут равны нулю. Два вектора разной величины никогда не могут в сумме равняться нулю. Если они указывают на одну и ту же прямую, то сумма не будет равна нулю, так как их величины различны.
Два вектора разной величины никогда не могут в сумме равняться нулю. Если они указывают на одну и ту же прямую, то сумма не будет равна нулю, так как их величины различны.
Могут ли три вектора одинаковой величины?
Да, можно сложить три вектора одинаковой величины и получить ноль. Это может произойти, если равнодействующая двух векторов равна и противоположна по направлению третьему вектору. Таким образом, векторная сумма трех векторов равна нулю.
Может ли вектор иметь нулевую величину?
Ответ: Величина не может быть отрицательной. Нулевой вектор (вектор, все значения которого равны 0) имеет величину 0, но все остальные векторы имеют положительную величину.
Если сложить n векторов разной величины, получится нулевой вектор?
Могут ли два вектора неравной величины в сумме дать нулевой вектор? Да, два вектора одинаковой величины, направленные в противоположные стороны, в сумме будут равны нулю. Два вектора разной величины никогда не могут в сумме равняться нулю. Если они указывают на одну и ту же прямую, то сумма не будет равна нулю, так как их величины различны.
Если они указывают на одну и ту же прямую, то сумма не будет равна нулю, так как их величины различны.
Можно ли объединить три вектора разной величины, чтобы получить нулевой результат? Объясните?
Нет, два вектора разной величины не могут давать нулевой равнодействующий. Три вектора могут дать нулевую результирующую, а два вектора — нет. Это связано с тем, что влияние векторов компенсируется только тогда, когда они действуют в противоположном направлении и имеют одинаковую величину.
Объясните, может ли сумма трех векторов равняться нулю?
Если разложить все три вектора, то либо получится треугольник, либо, если два вектора идут в одну сторону, то третий будет направлен в противоположную сторону. Третья возможность состоит в том, что все векторы имеют величину 0,9.0003
Можно ли для трех векторов одинаковой величины добавить к нулю, если да, набросать графический ответ, если нет, то почему?
Нет, невозможно получить ноль, сложив два вектора неравных величин. Возьмем три вектора одинаковой величины →A, →B и →C, учитывая, что эти три вектора составляют угол 120° друг с другом.
Возьмем три вектора одинаковой величины →A, →B и →C, учитывая, что эти три вектора составляют угол 120° друг с другом.
Может ли вектор нулевой величины иметь ненулевые значения?
Вектор с нулевой величиной не может иметь ненулевые компоненты. Поскольку модуль заданного вектора ˉV=√V2x+V2y должен быть равен нулю. Это возможно только тогда, когда V2x и V2y равны нулю.
Могут ли два вектора неравных величин в сумме дать нулевой вектор Могут ли три неравных вектора в сумме дать нулевой вектор?
№ . Два неравных вектора никогда не могут дать нулевой вектор путем сложения. Но три неравных вектора при сложении могут дать нулевой вектор.
Возможно ли иметь три вектора одинаковой величины?
Да, возможно иметь три вектора одинаковой величины, сумма которых равна нулю. Они будут сторонами равностороннего треугольника. Например, вы можете добавить A+B+C, если A=i, B=-0,5i +086j и C=-0,5i-0,86j, это даст A+B+C=i-0,5i +0,86j -0,5i-0,86j=0, где i и j — унитарные векторы в любом направлении x соответственно.
Могут ли три неравных вектора в сумме дать нулевой вектор?
Возьмите любые два неравных вектора. Назовем их Первый и Второй вектор. Добавьте их. Вы получите результирующий вектор. Возьмем третий вектор, равный результирующему вектору в противоположном направлении. Теперь первый, второй и третий вектор, если их сложить вместе, дадут вам нулевой вектор.
Может ли сумма двух векторов равняться нулю?
Мне нужна помощь в том, как сумма определенного количества векторов может равняться нулю. Я знаю, что сумма двух векторов с одинаковыми величинами, но противоположными направлениями, будет равна нулю; 2 вектора неравной величины никогда не могут иметь сумму, равную нулю; и что три вектора неравной величины могут иметь сумму, равную нулю, если они образуют замкнутый треугольник.
9к(п-1)+1$. Это, безусловно, точно: можно выбрать наше множество, состоящее из $n-1$ копий множества $(a_1,…,a_k)$, где каждая $a_i=0$ или $1$. Случай $k=1$ — это какой-то математический конкурсный вопрос (кажется, но не могу вспомнить точную ссылку). Кто-нибудь знает какие-то ссылки? Спасибо.
Кто-нибудь знает какие-то ссылки? Спасибо.
Всем спасибо! Хотел бы я принять все ответы, они очень полезны!
- кокомбинаторика
$\endgroup$
4
$\begingroup$
Ваша догадка верна для k=1 и 2, но когда k больше, все становится сложнее. Например, когда k=n=3, N=19. Краткое изложение некоторых известных результатов см.:
Elsholtz, C. Нижние границы для многомерных нулевых сумм. Combinatorica 24 , 351–358 (2004).
$\endgroup$
$\begingroup$
Случай k = 1 — это теорема Эрдёша-Гинзбурга-Зива. Взгляните на эту статью в Википедии, в которой есть ссылки на некоторые обзоры большой литературы с аналогичными результатами. (Конкретные обобщения, о которых я знаю, требуют набора векторов, суммирующихся с 0, размер которых равен мощности группы, а не ее показателю.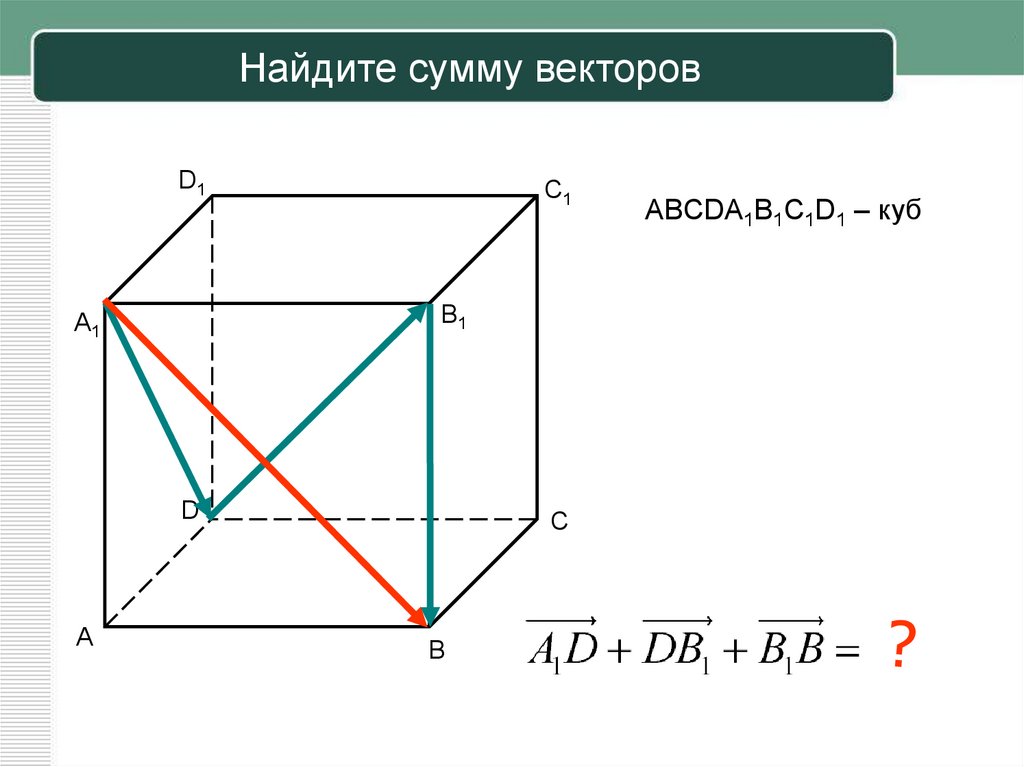 ) 94$. Раздается несколько карт, и ваша задача состоит в том, чтобы идентифицировать тройки карт, называемые наборами, которые образуют линию или эквивалентно, что в сумме дает нулевой вектор. Естественный вопрос заключается в том, сколько точек вы можете раздать без существования линии. Несложно построить 9 различных точек в аффинном трехмерном пространстве или 20 различных точек в аффинном четырехмерном пространстве над $\mathbb Z/3$ так, чтобы в этих точках не было прямых, и это максимумы. Они соответствуют $N=19$ для $(n,k) = (3,3)$ и $N=41$ для $(n,k) = (3,4)$, как в ссылке Рики Лю , повторив каждый пункт дважды. 92:$
$\{(0,0,0),(\pm1,0,1),(0,\pm1,1),(\pm1,\pm1,-1)\}$
и это множество не содержит строк.
) 94$. Раздается несколько карт, и ваша задача состоит в том, чтобы идентифицировать тройки карт, называемые наборами, которые образуют линию или эквивалентно, что в сумме дает нулевой вектор. Естественный вопрос заключается в том, сколько точек вы можете раздать без существования линии. Несложно построить 9 различных точек в аффинном трехмерном пространстве или 20 различных точек в аффинном четырехмерном пространстве над $\mathbb Z/3$ так, чтобы в этих точках не было прямых, и это максимумы. Они соответствуют $N=19$ для $(n,k) = (3,3)$ и $N=41$ для $(n,k) = (3,4)$, как в ссылке Рики Лю , повторив каждый пункт дважды. 92:$
$\{(0,0,0),(\pm1,0,1),(0,\pm1,1),(\pm1,\pm1,-1)\}$
и это множество не содержит строк.
$\endgroup$
1
$\begingroup$
Хотя я не знаю ответа на ваш конкретный вопрос, похоже, он связан с хорошо известной проблемой, когда вы настаиваете только на том, что количество simmand не равно нулю. О ней известно много и есть интересные открытые проблемы. Когда n простое число, вам нужно (n-1)k+1 векторов (и это точно). Это «теорема Олсона», и ее можно доказать с помощью теорем Шевале о ненулевых решениях для полиномиальных уравнений, когда число переменных превышает степень. Возможно, подобные методы (по крайней мере, для случая n=prime) сработают для вашей проблемы.)
О ней известно много и есть интересные открытые проблемы. Когда n простое число, вам нужно (n-1)k+1 векторов (и это точно). Это «теорема Олсона», и ее можно доказать с помощью теорем Шевале о ненулевых решениях для полиномиальных уравнений, когда число переменных превышает степень. Возможно, подобные методы (по крайней мере, для случая n=prime) сработают для вашей проблемы.)
Ссылка на Олсона: Дж. Э. Олсон, Комбинаторная проблема на конечных абелевых группах I, J. Теория чисел 1 (1969), 8-10.
Непростую степень смотрите в статье Р. Мешулама: Неравенство неопределенности и нулевые подсуммы. Дискретная математика. 84 (1990), вып. 2, 197—200.
Для общего релевантного метода: Н. Алон, Комбинаторный Nullstellensatz. комбин. Вероятно. вычисл. 8 (1999), вып. 1-2, 7—29.
$\endgroup$
$\begingroup$
9{k-1}$ наборов возможных значений, поэтому один набор этих координат должен иметь $2n-1$ элементов, мы можем выбрать $n$ из них, у которых сумма координат $k$ равна нулю по теореме Эрдёша–Гинзбурга–Зива, тогда поскольку первые $k-1$ координат фиксированы, их сумма также будет равна нулю, и у нас есть желаемый набор векторов, сумма которых равна нулю.
Для $k=2$ существует гипотеза Кемница, что это $4n-3$.
Теперь я вижу, что эта гипотеза доказана. См.:
Reiher, C. О гипотезе Кемница относительно точек решетки на плоскости. 9{k-2}(4n-4)+1$.
Для продолжения шаблона следующий случай будет для $k=3$ это будет $8m-7$ есть контрпример на самом деле для всех нечетных $k$ и $n$ больше $3$ это неверно . Следующая статья была упомянута в другом ответе; последнее предложение реферата имеет общий результат.
Эльсгольц, К. Нижние границы для многомерных нулевых сумм. Combinatorica 24 , 351–358 (2004).
В степени $d/3$ есть множитель $1,125$, поэтому в качестве нижней границы используется показатель степени больше двух.
$\endgroup$
0
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
4. При каком условии три вектора дают нуль результат?
1 ответ
Хамид Пау8 класс |
Когда все три вектора лежат в одной плоскости и образуют треугольник, а сумма двух сторон треугольника больше третьей стороны или сумма любых двух векторов равна третьей, тогда все три вектора лежат на одной прямой производят их результирующий нуль.
| 0 | Поделитесь этим ответом |
Похожие вопросы
2. Могут ли три некомпланарных вектора давать нулевую равнодействующую?
… Могут ли три некомпланарных вектора давать нулевую равнодействующую?
… |
Минимальное количество векторов, имеющих разные плоскости, которые можно сложить, чтобы получить нулевой результирующий: .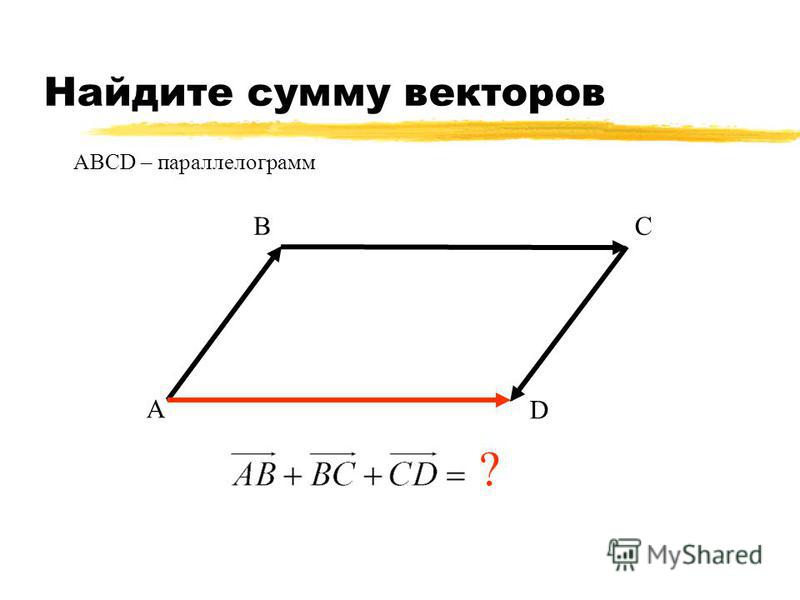 .. .. |
Сколько минимального числа ненулевых векторов может 2. добавить, чтобы получить нулевой результирующий? (2) 3 (4) 5 (3) 4 … |
(г) Может ли равнодействующая двух векторов быть равной нулю . .. .. |
является ДОМАШНЯЯ РАБОТА 1. Какое из следующих утверждений НЕВЕРНО? Когда A умножается на -3, направление A меняется на противоположное, и величина увеличивается в три раза. (2) Угол между A+B и AB может (1) очень между 0° и 180° 3) e минимальное количество векторов величина, необходимая для получения нулевого результирующего, равна 3. (д’ ) является единичным вектором . .. .. |
2. Можно ли сложить два вектора неравных величин и получить ноль? Можно ли сложить три вектора равных величин и получить ноль? … |
В. 5
Два вектора А и В действуют в одной плоскости
а вектор Č перпендикулярен плоскости.
равнодействующая этих векторов —
[1] может быть нулевым
[2] не может быть нулем
Хануман Нагар.
… 5
Два вектора А и В действуют в одной плоскости
а вектор Č перпендикулярен плоскости.
равнодействующая этих векторов —
[1] может быть нулевым
[2] не может быть нулем
Хануман Нагар.
… |
СВИДАНИЕ 1 СТРАНИЦА . Сумма Что это три вектора, показанные на рисунке, равны нулю. величины векторов OB и OC ? та «А=ИОН .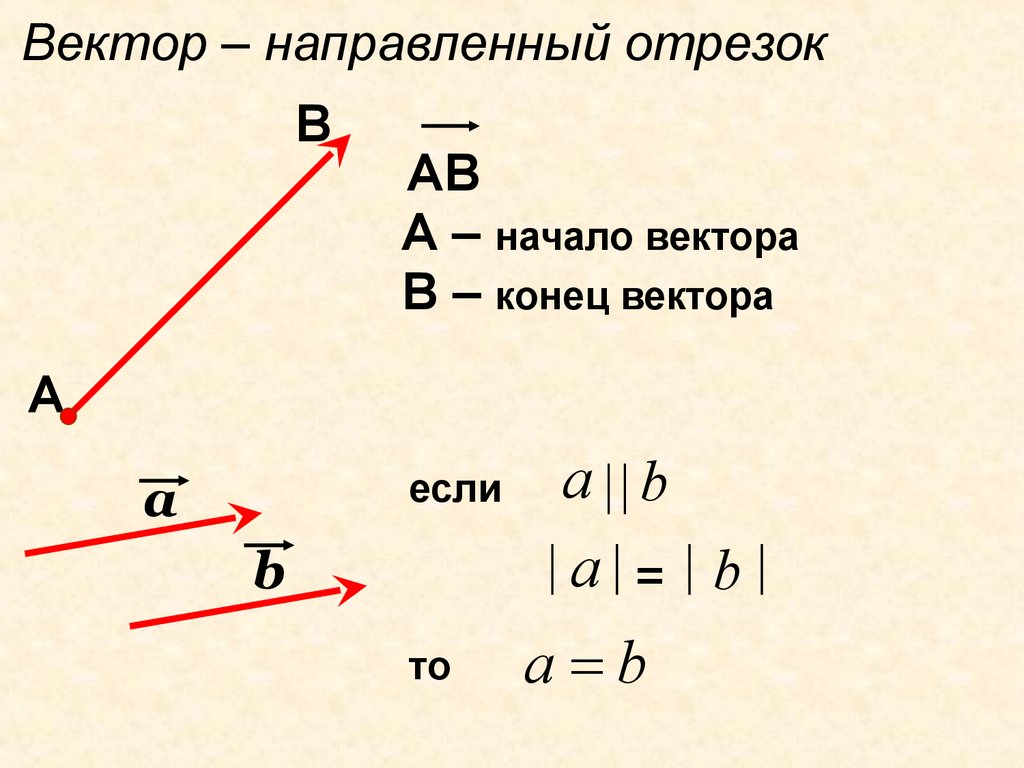 .. .. |
Равнодействующая трех векторов OA, OB и OC имеет величину (R = радиус круга) 1) В2Р 2) (1+√2R 3) (√2-1) 4) 2р А 0 р … |
Sholr — крупнейшая в Индии платформа для обмена знаниями. Отправляйте свои вопросы на
Эксперты.
Отправляйте свои вопросы на
Эксперты.
Если векторная сумма трех векторов дает нулевую равнодействующую, то какой может быть ориентация векторов?
Копировать
Думаю, если векторы имеют одинаковую величину и все действуют в 120 градусов друг к другу, то равнодействующая будет равна нулю.
также, если три вектора представлены как три стороны треугольника, взятого в том же порядке, результирующая равна нулю
Этот ответ:
Учебные пособия
Заработок +
20
pts
Q:
Если векторная сумма трех векторов дает нулевую результирующую направление векторов?
Напишите ответ…
Отправить
Остались вопросы?
Продолжить изучение физики
Какая операция дает результирующий вектор?
добавление двух или более векторов
Что дает вам система отсчета для вашей скорости при поездке на поезде?
Векторы смещения 10 м на запад и 14 м на запад составляют результирующую вектор, который равен
Каково направление равнодействующей после сложения двух равных и противоположных векторов?
Направление после сложения двух равных и противоположных векторов равно
«Направление» двух векторов. V=aНаправление и противоположность V = OV =
— Направление. Сложение двух дает V + OV= (a-a)Direction = 0
Направление.
V=aНаправление и противоположность V = OV =
— Направление. Сложение двух дает V + OV= (a-a)Direction = 0
Направление.
Может ли единица работы быть отрицательной?
Да. Работа — это скалярное произведение векторов, силы f и
водоизмещение р. Отрицательная работа называется эксергией, а положительная работа
называется энергией. Эксергия означает работу, а энергия означает работу
поглощается.
Есть аспекты этого вопроса, которые прояснят физику и
научное образование. Отрицательная работа является результатом смещения
вектор в направлении вектора силы. w= f.r = — fvcos(x).
Примером этого является падение мяча. Водоизмещение
вниз, по радиусу земли, -r и сила направлена вниз по
радиус земли, гравитация -f. это дает отрицательную работу,
которую мы называем эксергией, то есть выходной энергией, w=-f.-r= — frcos(x).
Поднятие мяча дает w= -f.r= frcos(x) пример положительного
работа, энергия в.
Векторы f и r являются векторами, математически комплексными числами,
и их квадраты отрицательны.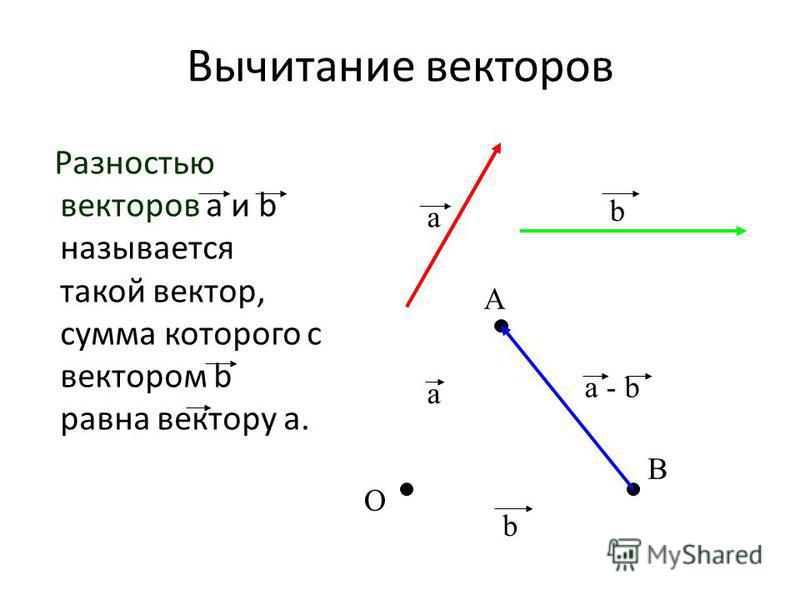 2= ijk= -1. Этот
формулировка сохраняет «ассоциативность» и свойство групп
для векторного умножения. Текущая формулировка векторов Гиббса
в физике математически и физически дефектен. Хорошая физика
зависит от хорошей математики, вектора кватерниона!
2= ijk= -1. Этот
формулировка сохраняет «ассоциативность» и свойство групп
для векторного умножения. Текущая формулировка векторов Гиббса
в физике математически и физически дефектен. Хорошая физика
зависит от хорошей математики, вектора кватерниона!
Четвёртое измерение — реальность или создано руками человека?
4-е измерение — это реальность, а не созданная человеком. 4-е измерение
не похож на остальные три измерения. Математика и физика
размеры непонятны большинству людей.
Первые три измерения являются векторными размерами и описывают
три измерения пространства говорят, x, y и z. Эти размеры
были открыты первые измерения, и они считаются
реальные размеры. Реальные размеры подобны реальным числам, их
квадрат — положительное число. Правда первые три
размеры являются векторами и являются геометрическими размерами. Векторы есть
отношения как параллельные и перпендикулярные. поэтому v1 и v2 могут быть
параллельны друг другу или перпендикулярны друг другу.
отношение между векторами включает в себя угол между ними, поэтому
v1. v2 = v1v2cos(a), и если cos(a) равен нулю, угол является нечетным
кратно 90 градусов, перпендикулярно. cos(a) равен единице, если
угол четно кратен 90 градусам. Минус единица означает
векторы параллельны и указывают в одном направлении. Плюс единство
означает, что векторы антипараллельны, векторы указывают в
противоположные направления.
Все примерно знакомы с векторными размерностями, кроме
что ученые и математики хотят, чтобы квадрат векторов был
положительный не отрицательный. Это математический дефект, который разрушает
векторы.
4-е измерение — это не вектор, это простое старое действительное число
иногда называется скалярным числом. Sclars или eeal имеют положительный
квадраты. Скаляры не являются векторами. Скаляры критически важны
в естественных науках и математике. Причина лучше всего понятна, когда вы
задать вопрос «Что происходит с векторами при умножении двух
параллельны два вектора v1 и v2? Ответ: произведение двух
параллельные векторы — это не вектор! Это как разбить два апельсина
вместе, и апельсины исчезают и превращаются в бананы.
v2 = v1v2cos(a), и если cos(a) равен нулю, угол является нечетным
кратно 90 градусов, перпендикулярно. cos(a) равен единице, если
угол четно кратен 90 градусам. Минус единица означает
векторы параллельны и указывают в одном направлении. Плюс единство
означает, что векторы антипараллельны, векторы указывают в
противоположные направления.
Все примерно знакомы с векторными размерностями, кроме
что ученые и математики хотят, чтобы квадрат векторов был
положительный не отрицательный. Это математический дефект, который разрушает
векторы.
4-е измерение — это не вектор, это простое старое действительное число
иногда называется скалярным числом. Sclars или eeal имеют положительный
квадраты. Скаляры не являются векторами. Скаляры критически важны
в естественных науках и математике. Причина лучше всего понятна, когда вы
задать вопрос «Что происходит с векторами при умножении двух
параллельны два вектора v1 и v2? Ответ: произведение двух
параллельные векторы — это не вектор! Это как разбить два апельсина
вместе, и апельсины исчезают и превращаются в бананы. Это
называется отсутствием замыкания в математике. Замыкание говорит, что если A и B
являются векторами, то AB является вектором. Вы могли бы сказать, что человек родился
Люди и рыбы порождают рыб. Это идея Закрытия. Векторы
не имеют закрытия. В физике сказали бы, что векторы
преобразовать в действительное число. Физики составили бы таблицу
«частицы Realtionships». Два реалов производят реал; настоящий и
вектор создать вектор; два вектора дают отрицательное вещественное число, если
параллель или положительное вещественное число, если оно антипараллельно; два вектора дают
вектор, если он перпендикулярен; и обычно два вектора дают реальный
и вектор, если не параллельный или перпендикулярный!
Это может открыть целую новую область «физики элементарных частиц».
простой ответ — 4-е измерение! 4-е измерение реально
измерение. Это реальное измерение удовлетворяет Замыканию. Два вектора
произвести реальное, и это в 4-м реальном измерении. Этот
размер сохраняет Closure, потому что теперь элементы называются
кватернионы.
Это
называется отсутствием замыкания в математике. Замыкание говорит, что если A и B
являются векторами, то AB является вектором. Вы могли бы сказать, что человек родился
Люди и рыбы порождают рыб. Это идея Закрытия. Векторы
не имеют закрытия. В физике сказали бы, что векторы
преобразовать в действительное число. Физики составили бы таблицу
«частицы Realtionships». Два реалов производят реал; настоящий и
вектор создать вектор; два вектора дают отрицательное вещественное число, если
параллель или положительное вещественное число, если оно антипараллельно; два вектора дают
вектор, если он перпендикулярен; и обычно два вектора дают реальный
и вектор, если не параллельный или перпендикулярный!
Это может открыть целую новую область «физики элементарных частиц».
простой ответ — 4-е измерение! 4-е измерение реально
измерение. Это реальное измерение удовлетворяет Замыканию. Два вектора
произвести реальное, и это в 4-м реальном измерении. Этот
размер сохраняет Closure, потому что теперь элементы называются
кватернионы. Кватернион — это сумма вещественного числа и трех векторов,
таким образом, делая четыре измерения таким образом quater, латинское для 4.
Если А и В — кватернионы, то АВ — кватернион. 4-й
Dimesnsion имеет единицы измерения, подобные трем пространственным измерениям — метры, r=ct
— четвертое измерение, где c — скорость света, а t —
время. оба c и t являются действительными числами, а реальные значения реального времени дают
реалы. Скорость света c является действительным числом, а не вектором, поэтому
скорость света неверна, потому что скорость означает вектор, не
настоящий.
Четвёртое измерение человек не создавал. Можно сказать 4-й
измерение было создано, когда Бог сказал: «Да будет Свет!»
Кватернион — это сумма вещественного числа и трех векторов,
таким образом, делая четыре измерения таким образом quater, латинское для 4.
Если А и В — кватернионы, то АВ — кватернион. 4-й
Dimesnsion имеет единицы измерения, подобные трем пространственным измерениям — метры, r=ct
— четвертое измерение, где c — скорость света, а t —
время. оба c и t являются действительными числами, а реальные значения реального времени дают
реалы. Скорость света c является действительным числом, а не вектором, поэтому
скорость света неверна, потому что скорость означает вектор, не
настоящий.
Четвёртое измерение человек не создавал. Можно сказать 4-й
измерение было создано, когда Бог сказал: «Да будет Свет!»
Похожие вопросы
Люди также спрашивали
Остались вопросы?
3.5: Векторы с геометрической точки зрения
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7115
- Тед Сандстром и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @ Государственный университет Гранд-Вэлли
Основные вопросы
Следующие вопросы предназначены для того, чтобы направлять наше изучение материала в этом разделе. Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
- Что такое вектор?
- Как с помощью геометрической формы векторов найти сумму двух векторов?
- Как мы используем геометрическую форму векторов, чтобы найти скалярное число, кратное вектору?
- Как мы используем геометрическую форму векторов, чтобы найти разность двух векторов?
- Чему равен угол между двумя векторами?
- Почему сила является вектором и как мы используем векторы и треугольники для определения сил, действующих на объект?
Всем нам приходилось что-то ронять и смотреть, как оно падает на землю. Происходит, конечно, то, что сила тяжести заставляет объект падать на землю. На самом деле, мы каждый день испытываем силу гравитации, просто находясь на Земле. Вес каждого человека является мерой силы тяжести, поскольку фунты являются единицей силы. Поэтому, когда человек весит 150 фунтов, это означает, что гравитация оказывает прямое воздействие на этого человека силой в 150 фунтов. Обратите внимание, что мы описали это количеством и направлением (прямо вниз). Такая величина (с величиной и направлением) называется вектором.
Поэтому, когда человек весит 150 фунтов, это означает, что гравитация оказывает прямое воздействие на этого человека силой в 150 фунтов. Обратите внимание, что мы описали это количеством и направлением (прямо вниз). Такая величина (с величиной и направлением) называется вектором.
Теперь предположим, что человек весом 150 фунтов стоит на холме. В математике мы упрощаем ситуацию и говорим, что человек стоит на наклонной плоскости, как показано на рис. 3.20. (Сделав холм прямой линией, мы упростим математику.) На рисунке \(\PageIndex{1}\) объект находится на наклонной плоскости в точке \(P\). Наклонная плоскость составляет угол \(\тета\) с горизонтом. Вектор \(\textbf{w}\) показывает вес объекта (сила тяжести, направленная прямо вниз). На диаграмме также показаны два других вектора. Вектор \(\textbf{b}\) перпендикулярен
Рисунок \(\PageIndex{1}\): Наклонная плоскость
к плоскости представляет силу, с которой объект действует на плоскость. Вектор \(\textbf{a}\) перпендикулярен \(\textbf{b}\) и параллелен наклонной плоскости.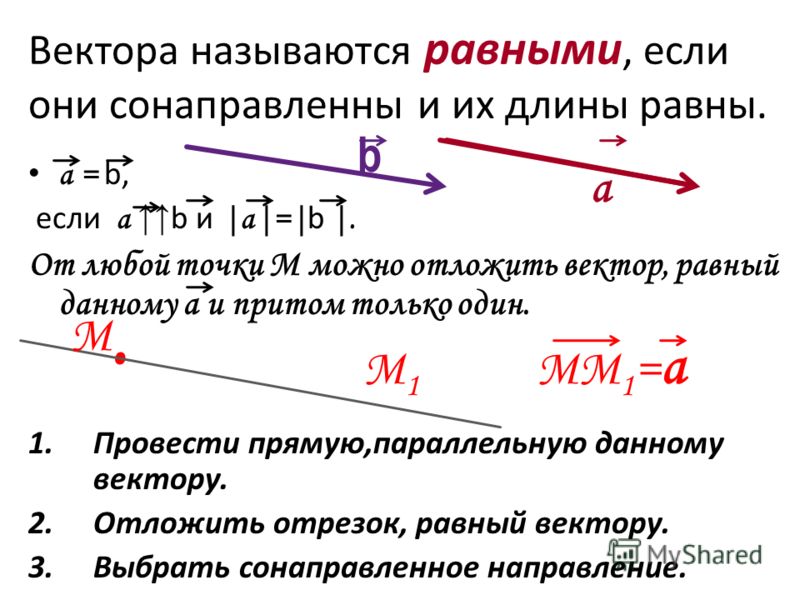 Этот вектор представляет собой силу тяжести вдоль плоскости. В этом и следующем разделах мы узнаем больше об этих векторах и о том, как определить величины этих векторов. Мы также увидим, что с нашим определением сложения двух векторов \(\textbf{w} = \textbf{a} + \textbf{b}\).
Этот вектор представляет собой силу тяжести вдоль плоскости. В этом и следующем разделах мы узнаем больше об этих векторах и о том, как определить величины этих векторов. Мы также увидим, что с нашим определением сложения двух векторов \(\textbf{w} = \textbf{a} + \textbf{b}\).
Определения
Существуют некоторые величины, для описания которых требуется только число. Мы называем это число величиной количества. Одним из таких примеров является температура, поскольку мы описываем ее только числом, таким как 68 градусов по Фаренгейту. Другими такими величинами являются длина, площадь и масса. Эти типы величин часто называют скалярными величинами . Однако есть и другие величины, требующие как величины, так и направления. Одним из таких примеров является сила, а другим — скорость. Мы бы описали скорость примерно 45 миль в час к северо-западу. Скорость и сила являются примерами векторная величина . Другими примерами векторов являются ускорение и перемещение.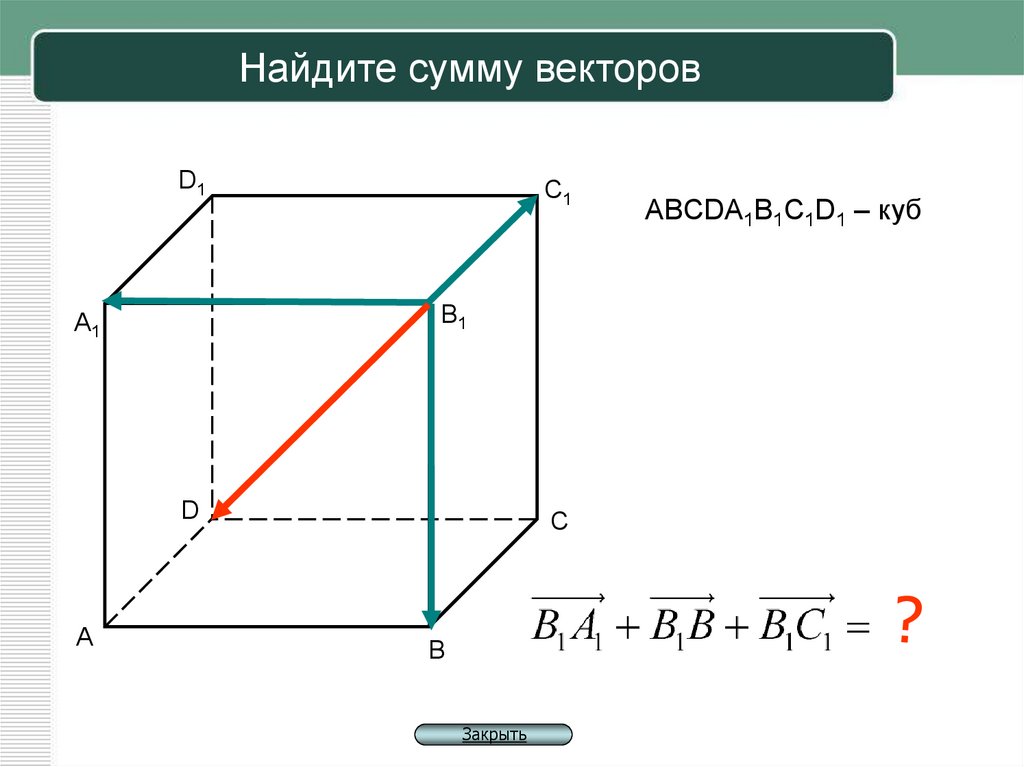
Некоторые векторы тесно связаны со скалярами. В математике и естественных науках мы делаем различие между скоростью и скоростью . Скорость — это скаляр, и мы бы сказали, что наша скорость равна 65 милям в час. Однако, если бы мы использовали скорость, мы бы сказали что-то вроде 65 миль в час на восток. Это отличается от скорости \(65\) миль в час на север, хотя в обоих случаях скорость равна 65 милям в час.
Определения: Векторы и скаляры
- Вектор — это величина, которая имеет как величину, так и направление.
- Скаляр — это величина, которая имеет только величину.
Геометрическое представление векторов
Векторы могут быть представлены геометрически в виде стрелок (направленных отрезков). Наконечник стрелки указывает направление вектора, а длина стрелки описывает величину вектора.
Вектор с начальной точкой \(P\) (конец стрелки) и конечной точкой \(Q\) (конец стрелки) может быть представлен как
\[\overrightarrow{PQ}, \textbf{v} или \overrightarrow{v}. \]
\]
Мы часто пишем \(v = \overrightarrow{PQ}\). В этом тексте мы будем использовать полужирный шрифт для обозначения вектора. При письме карандашом и бумагой мы всегда используем стрелку над буквой (например, \(\overrightarrow{v}\)) для обозначения вектора. звездная величина (или норма или длина ) вектора \(\textbf{v}\) обозначается \(\textbf{|v|}\). Важно помнить, что \(|\textbf{v}|\) — это число, представляющее величину или длину вектора \(\textbf{v}\).
Согласно нашему определению, вектор обладает атрибутами длины (величины) и направления, но положение не упоминается. Таким образом, мы будем считать два вектора равными, если они имеют одинаковую величину и направление. Например, если два разных автомобиля движутся со скоростью \(45\) миль в час на северо-запад (но в разных местах), они имеют равные векторы скорости. Дадим более формальное определение.
Определение: равные векторы
Два вектора равны тогда и только тогда, когда они имеют одинаковую величину и одно и то же направление.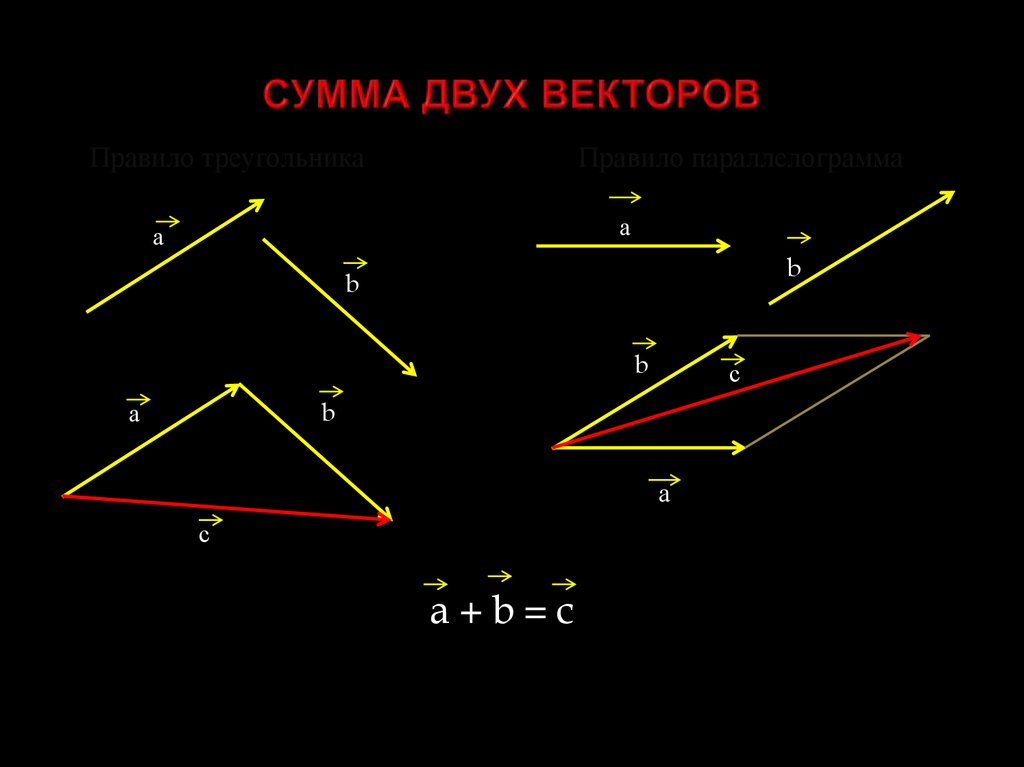 Когда векторы \(\textbf{v}\) и \(\textbf{w}\) равны, мы пишем \(\textbf{v} = \textbf{v}\).
Когда векторы \(\textbf{v}\) и \(\textbf{w}\) равны, мы пишем \(\textbf{v} = \textbf{v}\).
Упражнение \(\PageIndex{1}\)
На следующих диаграммах вектор \(\textbf{v}\) показан рядом с четырьмя другими векторами. Какие (если есть) из этих четырех векторов равны вектору \(\textbf{v}\)?
- Ответить
Вектор \(\textbf{w}\) является единственным вектором, равным вектору \(\textbf{v}\). Вектор \(\textbf{u}\) имеет то же направление, что и \(\textbf{v}\), но другую величину. Вектор \(\textbf{a}\) имеет ту же величину, что и \(\textbf{v}\), но другое направление (обратите внимание, что направление a противоположно вектору \(\textbf{v}\)) . Вектор \(\textbf{b}\) имеет другое направление и другую величину, чем вектор \(\textbf{v}\).
Операции над векторами
Скалярное кратное вектору
Удвоение скалярной величины — это просто умножение ее величины на \(2\). Например, если в контейнере \(20\) унций воды, а количество воды удвоено, в нем будет \(40\) унций воды. Что мы подразумеваем под удвоением вектора? Основная идея состоит в том, чтобы сохранить то же направление и умножить величину на \(2\). Таким образом, если объект имеет скорость \(5\) футов в секунду на юго-восток, а второй объект имеет скорость в два раза больше, второй объект будет иметь скорость \(10\) футов в секунду в юго-восточном направлении. В этом случае говорят, что мы умножили вектор на скаляр \(2\). Теперь мы делаем определение, которое также учитывает, что скаляр может быть отрицательным.
Что мы подразумеваем под удвоением вектора? Основная идея состоит в том, чтобы сохранить то же направление и умножить величину на \(2\). Таким образом, если объект имеет скорость \(5\) футов в секунду на юго-восток, а второй объект имеет скорость в два раза больше, второй объект будет иметь скорость \(10\) футов в секунду в юго-восточном направлении. В этом случае говорят, что мы умножили вектор на скаляр \(2\). Теперь мы делаем определение, которое также учитывает, что скаляр может быть отрицательным.
Определение
Для любого вектора \(\textbf{v}\) и любого скаляра \(c\) вектор \(c\textbf{v}\) (называемый скаляром, кратным вектору \(\textbf {v}\) — это вектор, величина которого в \(|c|\) умножается на величину вектора \(\textbf{v}\).
- Если \(c > 0\), то направление \(c\textbf{v}\) совпадает с направлением \(\textbf{v}\).
- Если \(c < 0\), то направление \(c\textbf{v}\) противоположно направлению \(\textbf{v}\).
- Если \(c = 0\), то \(c\textbf{v} = 0 \textbf{v} = 0\).

Вектор \(\textbf{0}\) называется нулевым вектором , а нулевой вектор не имеет ни величины, ни направления. Иногда мы пишем \(\overrightarrow{0}\) для нулевого вектора.
В этом определении \(|c|\) является абсолютным значением скаляра \(c\). Следует соблюдать осторожность, чтобы не спутать это с обозначением \(\textbf{|v|}\), которое является величиной вектора \(\textbf{v}\). Это одна из причин, по которой важно иметь обозначения, которые четко указывают, когда мы работаем с вектором или скаляром.
Сложение векторов
Мы покажем, как складывать векторы с двумя векторами смещения. Как и в случае скорости и скорости, существует различие между смещением и расстоянием. Расстояние является скаляром. Таким образом, можно сказать, что мы проехали 2 мили. Смещение , с другой стороны, представляет собой вектор, состоящий из расстояния и направления. Таким образом, векторы 2 мили на север и 2 мили на восток являются разными векторами смещения.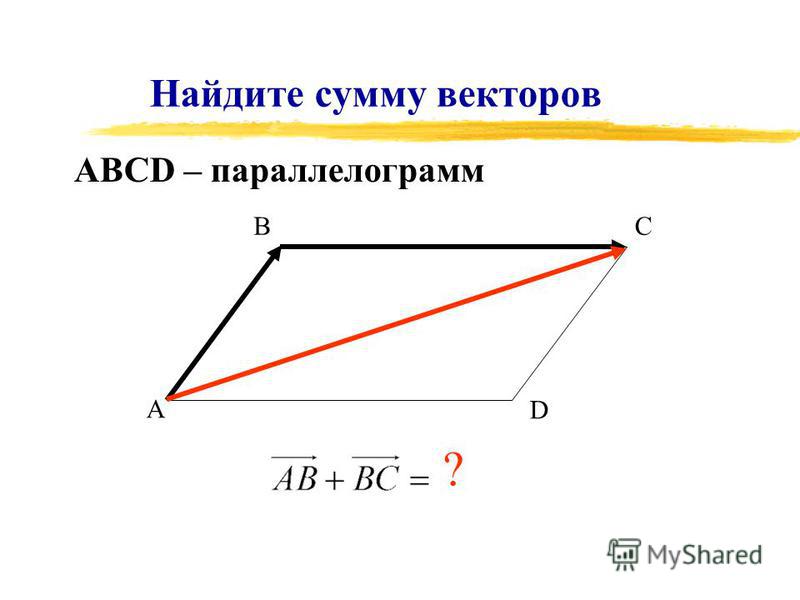
Теперь, если мы проедем 3 мили на север, а затем проедем 2 мили на восток, мы закончим в точке, определяющей новый вектор смещения. См. схему справа. На этой диаграмме \(\textbf{u}\) — это «3 мили на север», а \(\textbf{v}\) — «2 мили на восток». Векторная сумма \(\textbf{u} + \textbf{v}\) идет от начальной точки \(\textbf{u}\) до конечной точки \(\textbf{v}\).
Определение: сумма двух векторов
Сумма двух векторов определяется следующим образом: мы располагаем векторы так, чтобы начальная точка \(\textbf{w}\) совпадала с конечной точкой \ (\textbf{v}\). Вектор \(\textbf{v} + \textbf{w}\) — это вектор, начальная точка которого совпадает с начальной точкой \(\textbf{v}\), а конечная точка совпадает с конечной точкой \( \textbf{ш}\).
Вектор \( \textbf{v} + \textbf{w}\) называется суммой или равнодействующей векторов \(\textbf{v}\) и \(\textbf{w}\).
В определении обратите внимание, что векторы \(\textbf{v}\), \(\textbf{w}\) и \(\textbf{v} + \textbf{w} \) размещаются так, чтобы в результате получился треугольник.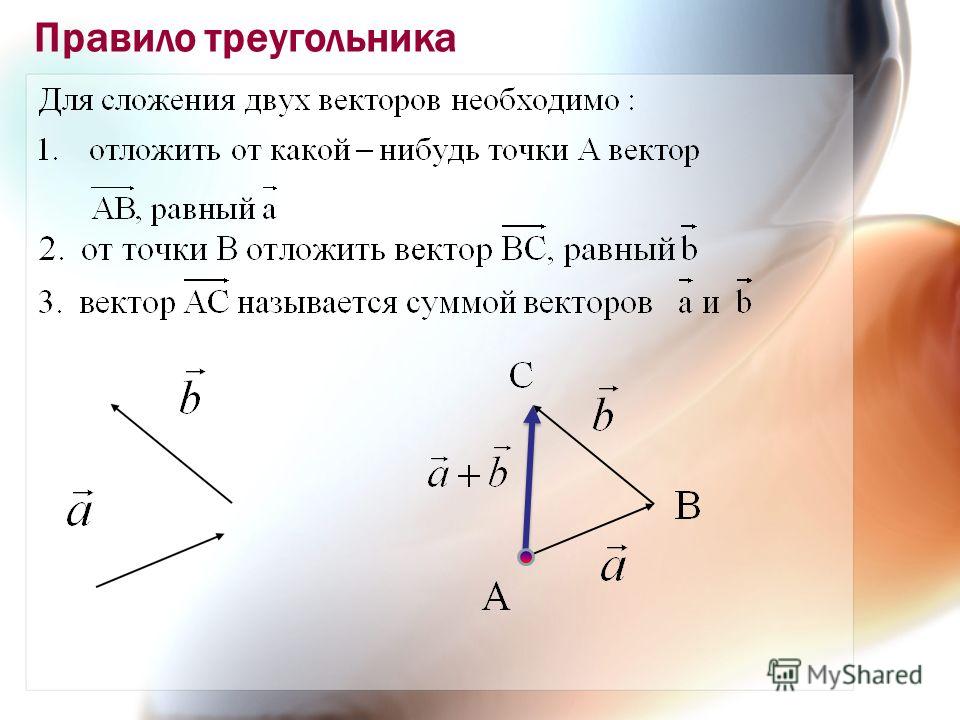 Длины сторон этого треугольника равны величинам этих сторон \(|\textbf{v}|\), \(|\textbf{w}|\) и \(|\textbf{v} + \textbf {ж}|\). Если мы поместим два вектора \(\textbf{v}\) и \(\textbf{w}\) так, чтобы их начальные точки совпадали, мы можем использовать параллелограмм для сложения двух векторов. Это показано на рисунке \(\PageIndex{2}\).
Длины сторон этого треугольника равны величинам этих сторон \(|\textbf{v}|\), \(|\textbf{w}|\) и \(|\textbf{v} + \textbf {ж}|\). Если мы поместим два вектора \(\textbf{v}\) и \(\textbf{w}\) так, чтобы их начальные точки совпадали, мы можем использовать параллелограмм для сложения двух векторов. Это показано на рисунке \(\PageIndex{2}\).
Рисунок \(\PageIndex{2}\): сумма двух векторов с использованием параллелограмма
Обратите внимание, что вектор \(\textbf{v}\) образует пару противоположных сторон параллелограмма, как и вектор \(\textbf{ш}\).
Упражнение \(\PageIndex{2}\)
На следующей диаграмме показаны два вектора, \(\textbf{v}\) и \(\textbf{w}\). Нарисуйте следующие векторы:
- \(\textbf{v} + \textbf{w}\)
- \(2\textbf{v}\)
- \(2\textbf{v} + \textbf{w}\)
- \(-2\textbf{ш}\)
- \(-2\textbf{ш + v}\)
- Ответить
Вычитание векторов
Прежде чем объяснять, как вычитать векторы, мы сначала объясним, что подразумевается под «отрицательным вектором».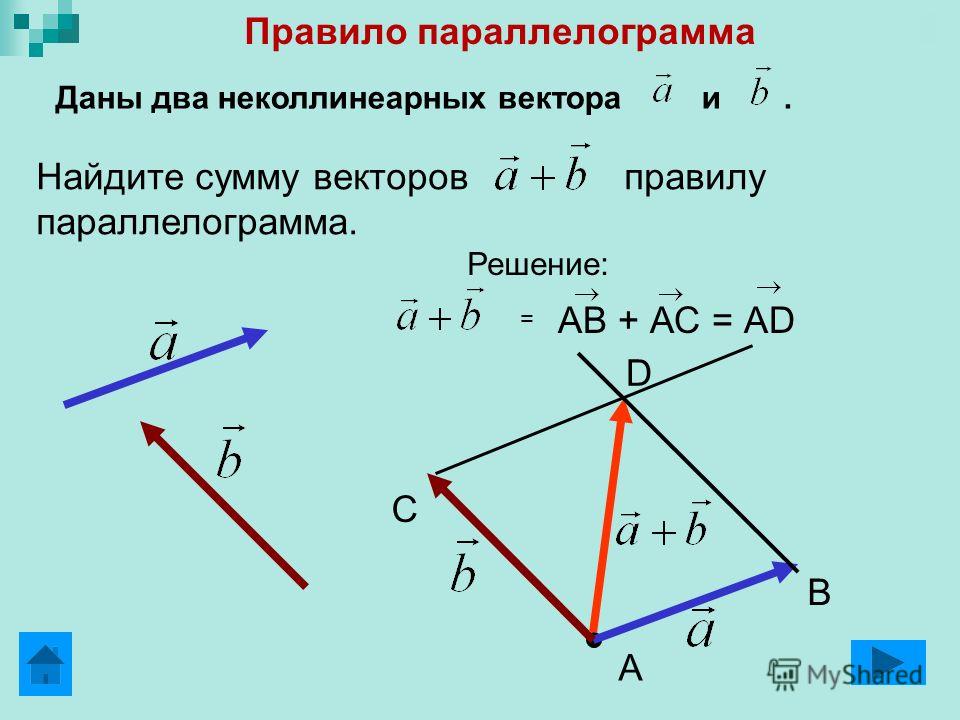 Это работает аналогично отрицательному вещественному числу. Например, мы знаем, что когда мы добавляем \(-3\) к \(3\), результатом будет \(0\). То есть \(3 + (-3) = 0\)
Это работает аналогично отрицательному вещественному числу. Например, мы знаем, что когда мы добавляем \(-3\) к \(3\), результатом будет \(0\). То есть \(3 + (-3) = 0\)
Нам нужно нечто подобное для векторов. Для вектора \(\textbf{w}\) идея состоит в том, чтобы использовать скалярное число \((-1)\textbf{w}\). Вектор \((-1)\textbf{w}\) имеет ту же величину, что и \(\textbf{w}\), но имеет направление, противоположное вектору \(\textbf{w}\). Мы определяем \(-\textbf{w}\) как \((-1)\textbf{w}\). На рисунке показано, что когда мы добавляем \(-\textbf{w}\) к \(\textbf{w}\), конечная точка суммы совпадает с начальной точкой суммы, и поэтому результатом является ноль вектор. То есть \(\textbf{w} + (-\textbf{w}) = \textbf{0}\).
Рисунок \(\PageIndex{3}\): сумма вектора и его отрицательного значения
Теперь мы можем определить вычитание векторов. Идея почти такая же, как вычитание действительных чисел в том, что для любых двух действительных чисел \(a\) и \(b\), \(a — b = a + (-b)\).
Определение: разность между векторами
Для любых двух векторов \(\textbf{v}\) и \(\textbf{w}\) разность между \(\textbf{v}\) и \(\textbf{w}\) обозначается \(\textbf{v} — \textbf{w}\) и определяется следующим образом:
\[ \textbf{v} — \textbf{w} = \textbf{v} + (-\textbf{w}).\]
Мы также говорим, что вычитаем вектор \(\textbf{w}\ ) из вектора \(\textbf{v}\).
Упражнение \(\PageIndex{3}\)
На следующей диаграмме показаны два вектора, \(\textbf{v}\) и \(\textbf{w}\). Нарисуйте следующие векторы:
- \(-\textbf{w}\)
- \(\textbf{v — w}\)
- \(-\textbf{v}\)
- \(\textbf{ш — v}\)
- Ответить
Угол между двумя векторами
Мы видели, что мы можем использовать треугольники, чтобы помочь нам сложить или вычесть два вектора. Длины сторон треугольника — это величины некоторых векторов. \circ — \theta\). Мы рассмотрим это в следующей проверке прогресса.
\circ — \theta\). Мы рассмотрим это в следующей проверке прогресса.
Рисунок \(\PageIndex{3}\): Угол между двумя векторами
Упражнение \(\PageIndex{4}\)
Предположим, что векторы \(\textbf{a}\) и \(\ textbf{b}\) имеют величины 80 и 60 соответственно, а угол \(\theta\) между двумя векторами равен 53 градусам. На рис. 3.24 мы нарисовали параллелограмм, определяемый этими двумя векторами, и пометили вершины для справки.
Рисунок 3.24: Диаграмма для проверки выполнения 3.27
Помните, что вектор определяется его величиной и направлением. Определим \(|\textbf{a + b}|\) и меру угла между \(\textbf{a}\) и \(\textbf{a + b}\)
Определим меру \(\угол АВС\).
В \(\треугольнике ABC\) длина стороны \(AB\) равна \(|\textbf{a}| = 80\), а длина стороны \(BC\) равна \(|\textbf {b}|=60\). Используйте этот треугольник и закон косинусов, чтобы определить длину третьей стороны, которая равна \(|\textbf{a + b}|\). 9\круг\).
Сила
Важной векторной величиной является сила. В физике сила, действующая на объект, определяется как любое взаимодействие, которое, если ему не противостоять, изменит движение объекта. Таким образом, сила заставит объект изменить свою скорость, то есть объект ускорится. Говоря более неформально, сила — это толчок или притяжение объекта.
В физике сила, действующая на объект, определяется как любое взаимодействие, которое, если ему не противостоять, изменит движение объекта. Таким образом, сила заставит объект изменить свою скорость, то есть объект ускорится. Говоря более неформально, сила — это толчок или притяжение объекта.
Сила гравитации влияет на нашу жизнь. Величина силы тяжести, действующей на человека, равна его весу. Направление силы тяжести прямо вниз. Итак, если человек весом 150 фунтов стоит неподвижно на земле, то земля также оказывает на человека силу в 150 фунтов в направлении вверх. Чистая сила, действующая на неподвижного человека, равна нулю. Это пример того, что известно как 9\circ)}\]
\[|\textbf{a}| \примерно 53,21\]
Величина вектора a (и вектора b) приблизительно равна \(53,21\) фунта.
Наклонные плоскости
В начале этого раздела мы обсудили силы, возникающие при размещении объекта на наклонной плоскости. Рисунок 3.25 — это схема, которую мы использовали, но теперь мы добавили метки для некоторых углов.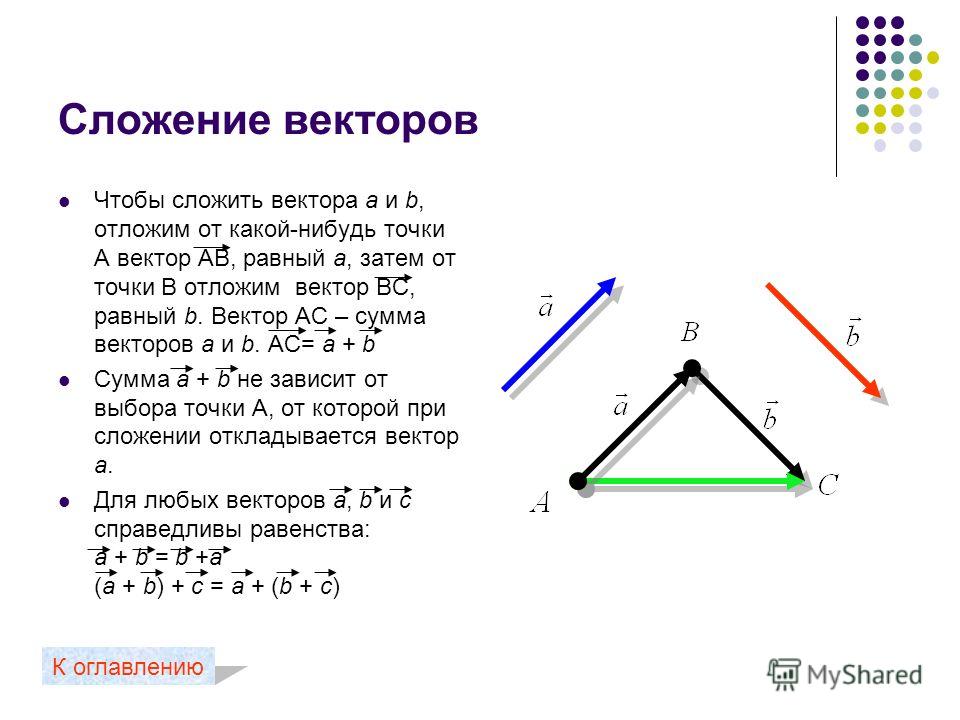 Напомним, что вектор \(\textbf{w}\) показывает вес объекта (сила тяжести, направленная прямо вниз), вектор \(\textbf{b}\) перпендикулярен плоскости и представляет силу, с которой объект давит на плоскость, а вектор \(\textbf{a}\) перпендикулярен \(\textbf{b}\) и параллелен наклонной плоскости. Этот вектор представляет собой силу тяжести вдоль плоскости. Обратите внимание, что мы также добавили вторую копию вектора a, которая начинается с вершины вектора \(\textbf{b}\). 9\circ\), так как это два острых угла прямоугольного треугольника. Отсюда делаем вывод, что \(\beta = \theta\). Это дает нам окончательный вариант диаграммы сил на наклонной плоскости, показанной на рис. 3.26. Обратите внимание, что векторы \(\textbf{a}\),
Напомним, что вектор \(\textbf{w}\) показывает вес объекта (сила тяжести, направленная прямо вниз), вектор \(\textbf{b}\) перпендикулярен плоскости и представляет силу, с которой объект давит на плоскость, а вектор \(\textbf{a}\) перпендикулярен \(\textbf{b}\) и параллелен наклонной плоскости. Этот вектор представляет собой силу тяжести вдоль плоскости. Обратите внимание, что мы также добавили вторую копию вектора a, которая начинается с вершины вектора \(\textbf{b}\). 9\circ\), так как это два острых угла прямоугольного треугольника. Отсюда делаем вывод, что \(\beta = \theta\). Это дает нам окончательный вариант диаграммы сил на наклонной плоскости, показанной на рис. 3.26. Обратите внимание, что векторы \(\textbf{a}\),
Рис. 3.26: Наклонная плоскость
\(\textbf{b}\) и \(\textbf{w}\) образуют прямоугольный треугольник, и поэтому мы можем использовать тригонометрию прямоугольного треугольника для задач, связанных с силами на наклонной плоскости.
Упражнение \(\PageIndex{6}\) 9\circ\) градусов по горизонтали.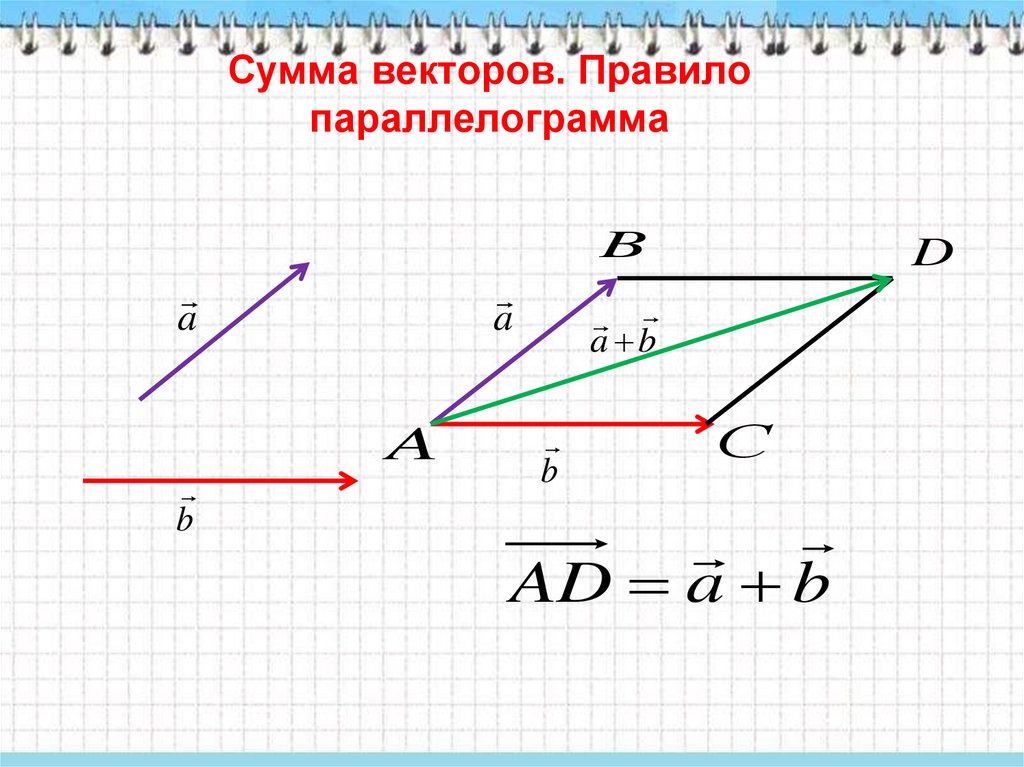 Используя диаграмму, подобную той, что изображена на рис. 3.26, определите величину силы, приложенной к плоскости со стороны объекта, и величину силы, действующей на плоскость, действующую на объект из-за гравитации.
Используя диаграмму, подобную той, что изображена на рис. 3.26, определите величину силы, приложенной к плоскости со стороны объекта, и величину силы, действующей на плоскость, действующую на объект из-за гравитации.
Примечание : Величина силы, направленной вниз по плоскости, будет силой в направлении вверх по плоскости, необходимой для удержания объекта в неподвижном состоянии.
- Ответить
Используя обозначения на рис. 3.26, получаем следующее: 9\circ)\]
\[|\textbf{b}| \приблизительно 244,54\]
\[|\textbf{a}| \около 51,98\]Объект действует с силой около \(244,54\) фунтов, перпендикулярной плоскости, а сила тяжести вниз по плоскости на объект составляет около \(51,98\) фунтов. Таким образом, чтобы удерживать объект неподвижным, к объекту должна быть приложена сила около \(51,98) фунта, направленная вверх по плоскости.
Резюме
В этом разделе мы изучили следующие важные концепции и идеи:
- Векторы и скаляры
- Вектор — это величина, которая имеет как величину, так и направление.

- Скаляр — это величина, которая имеет только величину.
- Два вектора равны тогда и только тогда, когда они имеют одинаковую величину и одно и то же направление.
- Вектор — это величина, которая имеет как величину, так и направление.
- Скалярное кратное вектора
Для любого вектора \(\textbf{v}\) и любого скаляра \(c\) вектор \(c\textbf{v}\) (называемый скаляром, кратным вектору \(\textbf{v} \) — это вектор, величина которого в \(|c|\) умножается на величину вектора \(\textbf{v}\).0003
- Если \(c > 0\), то направление \(c\textbf{v}\) совпадает с направлением \(\textbf{v}\).
- Если \(c < 0\), то направление \(c\textbf{v}\) противоположно направлению \(\textbf{v}\).
- Если \(c = 0\), то \(c\textbf{v} = 0\textbf{v} = 0\).
Вектор \(\(\textbf{0}\)\) называется нулевым вектором, а нулевой вектор не имеет ни величины, ни направления. Иногда мы пишем \(\overrightarrow{0}\) для нулевого вектора.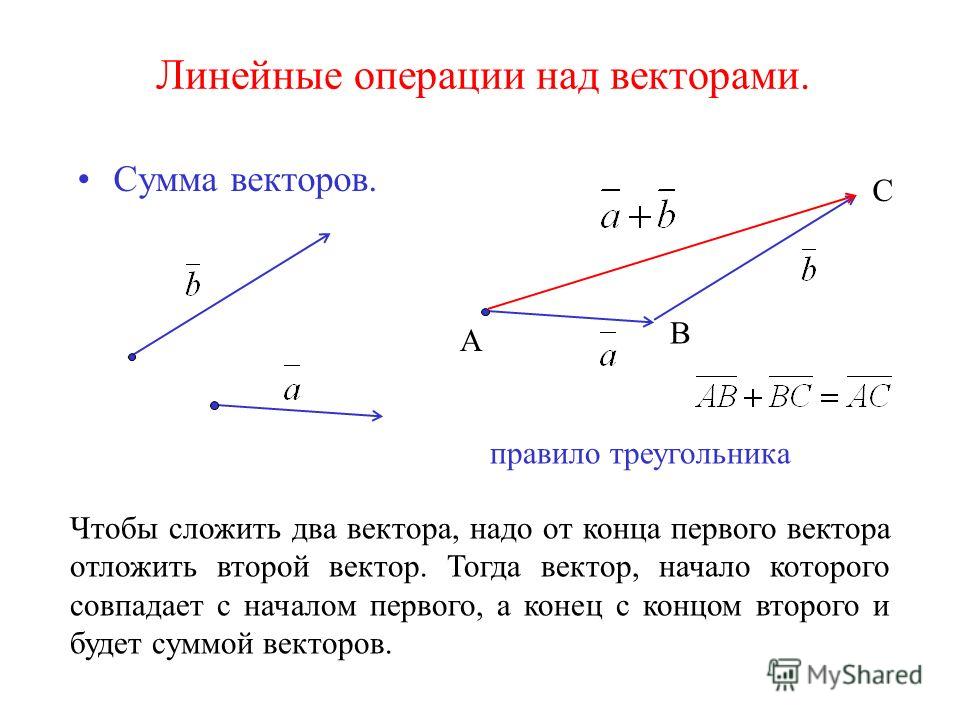
- Сумма двух векторов
Сумма двух векторов определяется следующим образом: мы располагаем векторы так, чтобы начальная точка \(\textbf{w}\) совпадала с конечной точкой \(\textbf{v}\). Вектор \(\textbf{v} + \textbf{w}\) — это вектор, начальная точка которого совпадает с начальной точкой \(\textbf{v}\), а конечная точка совпадает с конечной точкой \( \textbf{ш}\).
Вектор \( \textbf{v} + \textbf{w}\) называется суммой или равнодействующей векторов \(\textbf{v}\) и \(\textbf{w}\ ). 9\circ\)) когда они имеют одинаковую начальную точку.
Эта страница под названием 3.5: Векторы с геометрической точки зрения распространяется под лицензией CC BY-NC-SA 3.0, автором, ремиксом и/или куратором являются Тед Сандстром и Стивен Шликер (ScholarWorks @Grand Valley State University) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.



 Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор
Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор
 Пример: a(2;-3), a=2i-3j
Пример: a(2;-3), a=2i-3j


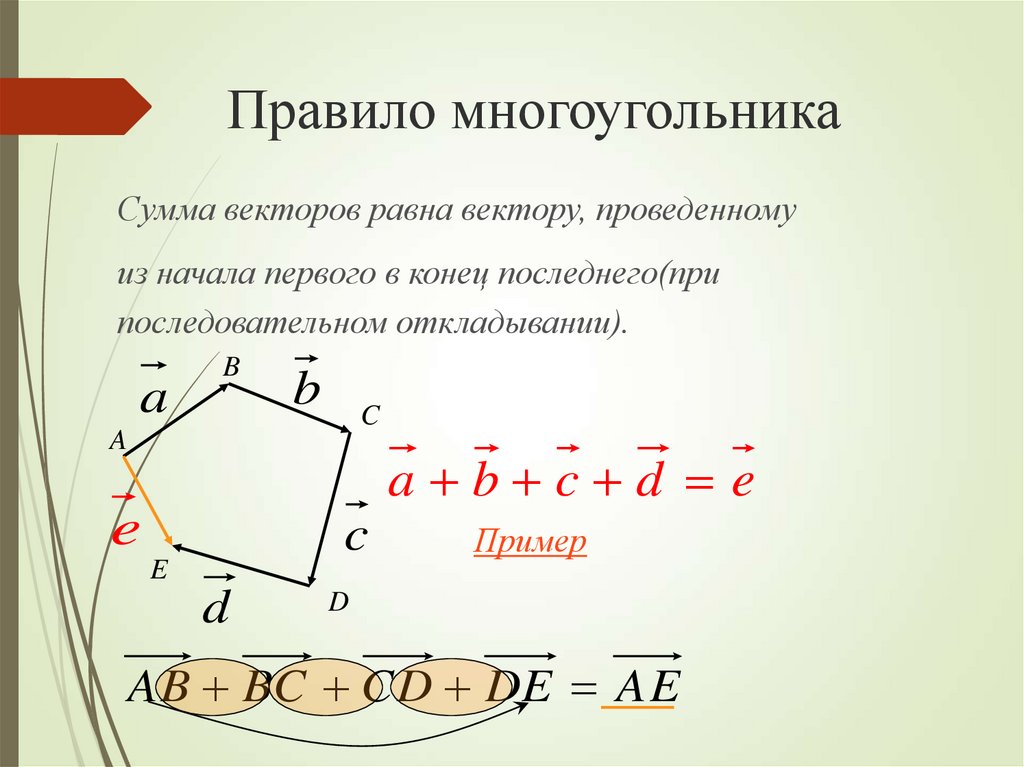 Из последнего равенства вытекает, что . Получили противоречие с нашим предположением, что и
доказывает теорему.
Из последнего равенства вытекает, что . Получили противоречие с нашим предположением, что и
доказывает теорему.

