Векторы — что это, определение и ответ
ОСНОВНЫЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
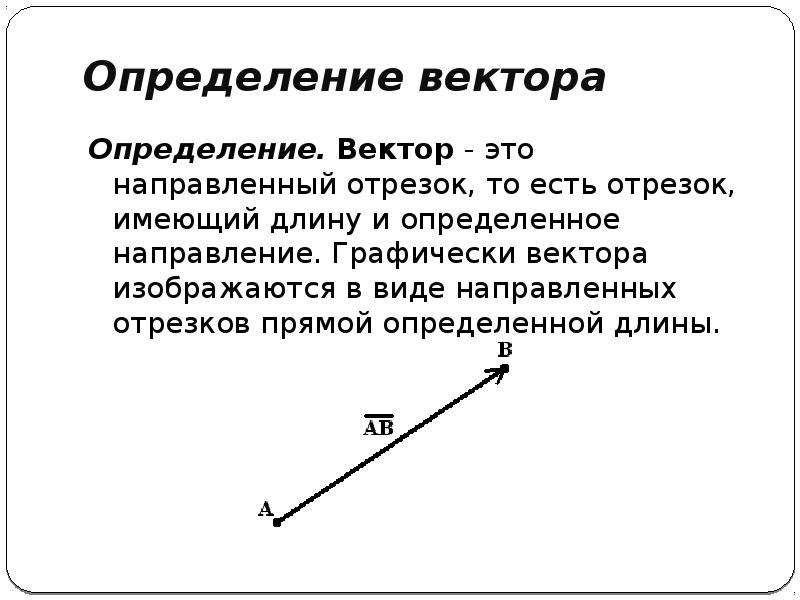
Вектор – отрезок, у которого есть начало и конец, то есть указано его направление.
Вектор обозначается через точки начала и конца вектора, например \(\overrightarrow{АВ}\) (первая буква – начало вектора, вторая – конец) или, если мы хотим обозначить вектор без указания точек, пишем просто \(\overrightarrow{a}\).
Точка тоже может быть вектором, в таком случае вектор называют нулевым, т.к. его началом и концом является одна и та же точка. Обозначаем нулевой вектор как, например, \(\overrightarrow{\text{MM}}\) или \(\overrightarrow{0}\).
Длина или модуль вектора – это длина отрезка (как если бы у него не было направления).
Длина вектора \(\overrightarrow{АВ}\) обозначается как \(\left| \overrightarrow{АВ} \right|\), длина вектора \(\overrightarrow{a}\ \)как \(\left| \overrightarrow{a} \right|\), а длина нулевого вектора всегда равна нулю:
\(\left| \overrightarrow{АВ} \right| = 7\)
\(\left| \overrightarrow{a} \right| = 3\)
\(\left| \overrightarrow{\text{MM}} \right| = \left| \overrightarrow{0} \right| = 0\)
РАСПОЛОЖЕНИЕ ВЕКТОРОВ
Коллинеарные векторы – это векторы, которые лежат на параллельных прямых или на одной прямой. Нулевой вектор коллинеарен любому вектору.
Нулевой вектор коллинеарен любому вектору.
Сонаправленные векторы – это коллинеарные векторы, которые направлены в одну сторону.
Обозначается как \(\overrightarrow{a} \upuparrows \overrightarrow{b}\) (вектор \(\overrightarrow{a}\) сонаправлен вектору \(\overrightarrow{b}\))
Противоположно направленные векторы – это коллинеарные векторы, которые направлены в противоположные стороны.
Обозначаются как \(\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}\) (вектор \(\overrightarrow{a}\) противоположно напрвлен вектору \(\overrightarrow{b}\))
Равные векторы – это сонаправленные векторы, у которых равны длины, т.е. у них одинаковые и направление, и длина.
Например:
\(\overrightarrow{АВ}\) и \(\overrightarrow{a}\) – коллинеарны, при этом противоположно направлены, т.к. лежат параллельных прямых и направлены в разные стороны:
\(\overrightarrow{АВ} \uparrow \downarrow \overrightarrow{a}\)
\(\overrightarrow{\text{CD}}\) и \(\overrightarrow{b}\) – коллинеарны, при этом сонаправлены, т.
 к. лежат параллельных прямых и направлены в одну сторону:
к. лежат параллельных прямых и направлены в одну сторону:
\(\overrightarrow{\text{CD}} \upuparrows \overrightarrow{b}\)
\(\overrightarrow{\text{CD}}\) и \(\overrightarrow{b}\) – равны, т.к. сонаправлены (из п.2) и равны по модулю:
\(\left. \ \frac{\overrightarrow{\text{CD}} \upuparrows \overrightarrow{b}}{\overrightarrow{\left| \text{CD} \right|} = 5 = \left| \overrightarrow{b} \right|} \right\} \Longrightarrow \overrightarrow{\text{CD}} = \overrightarrow{b}\)
\(\overrightarrow{М}\) коллинеарен всем векторам, и может являться им как сонаправленным, так и противоположно направленным, т.к. \(\overrightarrow{М} = \overrightarrow{0}\).
СВОЙСТВА НЕНУЛЕВЫХ КОЛЛИНЕАРНЫХ ВЕКТОРОВ:
\(\left. \ \frac{\overrightarrow{a} \upuparrows \overrightarrow{b}}{\overrightarrow{b} \upuparrows c} \right\} \Longrightarrow \overrightarrow{a} \upuparrows \overrightarrow{c}\)
Если \(\overrightarrow{a} \upuparrows \overrightarrow{b}\) и \(\overrightarrow{b} \upuparrows c\), то \(\overrightarrow{a} \upuparrows \overrightarrow{c}\)
\(\left. \ \frac{\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}}{\overrightarrow{b} \uparrow \downarrow c} \right\} \Longrightarrow \overrightarrow{a} \upuparrows \overrightarrow{c}\)
\ \frac{\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}}{\overrightarrow{b} \uparrow \downarrow c} \right\} \Longrightarrow \overrightarrow{a} \upuparrows \overrightarrow{c}\)
Если \(\overrightarrow{a} \uparrow \downarrow \overrightarrow{b}\) и \(\overrightarrow{b} \uparrow \downarrow c\), то \(\overrightarrow{a} \upuparrows \overrightarrow{c}\)
\(\left. \ \frac{\overrightarrow{a} \upuparrows \overrightarrow{b}}{\overrightarrow{a} \uparrow \downarrow \overrightarrow{c}} \right\} \Longrightarrow \overrightarrow{b} \uparrow \downarrow \overrightarrow{c}\)
Если \(\overrightarrow{a} \upuparrows \overrightarrow{b}\) и \(\overrightarrow{a} \uparrow \downarrow \overrightarrow{c}\), то \(\overrightarrow{b} \uparrow \downarrow \overrightarrow{c}\)
ОТКЛАДЫВАЕНИЕ ВЕКТОРА ОТ ТОЧКИ:
Говорят, что вектор отложен от точки, если она является его началом. Например, \(\overrightarrow{АВ}\) отложен от точки А, \(\left| \text{CD} \right|\) отложен от точки С и так далее. Можно откладывать абсолютно любые векторы абсолютно из любых точек. Это описывается следующим правилом:
Можно откладывать абсолютно любые векторы абсолютно из любых точек. Это описывается следующим правилом:
От любой точки можно отложить вектор, равный данному и при том только один.
Например, возьмем точку М и два вектора \(\overrightarrow{a}\) и \(\overrightarrow{b}\). Мы можем отложить от точки М вектора, равные \(\overrightarrow{a}\) и \(\overrightarrow{b}\) всего один раз. Делается это параллельным переносом:
Таким образом \(\overrightarrow{a} = \overrightarrow{a’}\), и \(\overrightarrow{b} = \overrightarrow{b’}\), при этом \(\overrightarrow{a’}\ и\ \overrightarrow{b’}\) отложены от точки М.
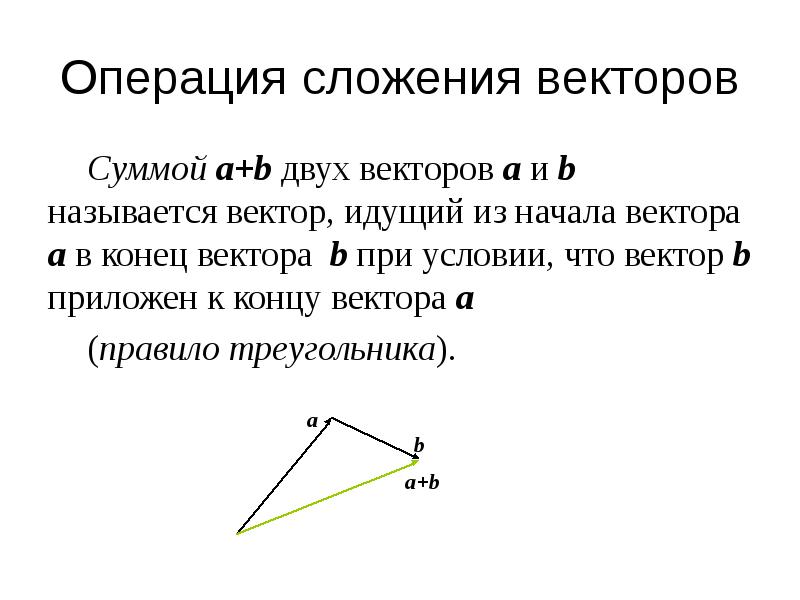
СЛОЖЕНИЕ ВЕКТОРОВ:
При сложении векторов нужно учитывать их направления, поэтому проще всего складывать вектора визуально. Существуют два самых простых способа сложить два вектора – это правило треугольника и правило параллелограмма.
ПРАВИЛО ТРЕУГОЛЬНИКА
Если нужно найти сумму двух векторов, по правилу треугольника нужно:
Параллельным переносом перенести начало одного вектора в конец другого.

Пусть эти векторы будут сторонами треугольника, тогда третья его сторона – их сумма.
Обозначить направление получившегося вектора суммы – от начала первого вектора в конец второго (стрелка к стрелке).
Пример №1:
Найдите сумму векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) по правилу треугольника:
Перенесем вектор \(\overrightarrow{b}\) так, чтобы он начинался там, где заканчивается вектор \(\overrightarrow{a}\).
Соединим эти векторы в треугольник, третьей стороной которой будет вектор \(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}\).
Направление вектора \(\overrightarrow{c}\) будет идти от начала \(\overrightarrow{a}\) до конца \(\overrightarrow{b}\) (стрелка к стрелке)
ПРАВИЛО ПАРАЛЛЕЛОГРАММА:
Если нужно найти сумму двух векторов, по правилу параллелограмма нужно:
Параллельным переносом перенести начала этих векторов в одну точку.

Пусть эти векторы будут сторонами параллелограмма, тогда диагональ этого параллелограмма – их сумма.
Обозначить направление получившегося вектора суммы – от начала векторов в противоположный конец параллелограмма (по диагонали).
Пример №2:
Найдите сумму векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) по правилу параллелограмма:
Перенесем оба вектора параллельным переносом так, чтобы они начинались из одной точки.
Представим, что они являются сторонами параллелограмма.
Диагональ этого параллелограмма, которая начинается в точке начала векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) – это вектор \(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}\).
СВОЙСТВА СЛОЖЕНИЯ ВЕКТОРОВ:
Переместительное свойство:
\(\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}\)
Сочетательное свойство:
\((\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c})\)
СЛОЖЕНИЕ НЕСКОЛЬКИХ ВЕКТОРОВ:
Чтобы сложить несколько векторов, нужно ставить их друг за другом, сохраняя их направление (используя параллельный перенос), тогда их суммой будет являться вектор, начала которого – это начало первого вектора, а конец – конец последнего вектора (как в правиле треугольника).
Пример №3:
Найдите сумму векторов \(\overrightarrow{a}\), \(\overrightarrow{b}\), \(\overrightarrow{c}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\):
Поставим эти векторы как бы по порядку сохраняя их длину и направление. По переместительному свойству неважно, в каком порядке мы будем располагать вектора. Соединим их, например, в таком порядке — \(\overrightarrow{d}\), \(\overrightarrow{e}\), \(\overrightarrow{b}\), \(\overrightarrow{c}\), \(\overrightarrow{a}\).
Проведем вектор их суммы от начала первого вектора в конец второго:
ВЫЧИТАНИЕ ВЕКТОРОВ:
Вычесть вектор – это то же самое, что прибавить отрицательный вектор:
\(\overrightarrow{a}\ –\ \overrightarrow{b} = \overrightarrow{a} + (–\overrightarrow{b})\)
То есть и при вычитании можно использовать правила сложения. Главное – найти противоположный вектор.
Главное – найти противоположный вектор.
Само словосочетание «противоположный вектор» говорит о том, что такие вектора направлены в разные стороны.
Значит вычесть вектор – значит прибавить вектор с противоположным ему направлением.
Мы можем проверить это свойство алгебраически. Мы знаем, что противоположные числа в сумме дают 0:
\(a + (–a) = a\ –\ a = 0\)
Тогда и сумма противоположных векторов дадут 0 (т.е. если мы «пойдем» от начала до конца \(\overrightarrow{a}\) и обратно по –\(\overrightarrow{a}\), то мы вернемся снова в начало \(\overrightarrow{a}\)):
Значит и для векторов справедливо это свойство:
\(\overrightarrow{a}\ + (–\ \overrightarrow{a}) = 0\)
Пример №4:
Найдите \(\overrightarrow{f} = \overrightarrow{a}\ –\ \overrightarrow{b} + \overrightarrow{c}\ –\ \overrightarrow{d}\ –\ \overrightarrow{e}\), если
Можем использовать сложение векторов, если мы найдем отрицательные векторы.
 В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие:
В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие:
Теперь сложим все векторы, учитывая отрицательные:
ПРОИЗВЕДЕНИЕ ВЕКТОРА И ЧИСЛА:
Произведением ненулевого вектора и числа является вектор, коллинеарный данному, длина которого равна произведению длины данного вектора и числа:
\(k \bullet \overrightarrow{a} = \overrightarrow{\text{ka}}\)
где k – это число, при этом:
\(\overrightarrow{a} \upuparrows \overrightarrow{\text{ka}}\) при \(k > 0\)
\(\overrightarrow{a} \uparrow \downarrow \overrightarrow{\text{ka}}\) при \(k < 0\)
Произведением любого вектора на ноль является нулевой вектор.
Пример №5:
Найдите 5\(\overrightarrow{a}\) и –2\(\overrightarrow{a}\) , если:
1. Также можно представить произведение вектора и числа как сложение этого вектора несколько раз:
Также можно представить произведение вектора и числа как сложение этого вектора несколько раз:
\(5\overrightarrow{a} = \overrightarrow{a} + \overrightarrow{a} + \overrightarrow{a} + \overrightarrow{a} + \overrightarrow{a}\):
\(5\overrightarrow{a} \upuparrows \overrightarrow{a}\), т.к 5 > 0
2. Аналогично поступим и с отрицательным числом, только теперь уже складываем противоположные векторы:
\(–2\overrightarrow{a} \uparrow \downarrow \overrightarrow{a}\), т.к –2 < 0
СВОЙСТВА ПРОИЗВЕДЕНИЯ ВЕКТОРА И ЧИСЛА:
Сочетательное свойство:
\(kl \bullet \overrightarrow{a} = k(l\overrightarrow{a}) \)
Распределительный закон:
\(\overrightarrow{a}(k + l) = k\overrightarrow{a} + l\overrightarrow{a}\)
и
\(k(\overrightarrow{a} + \overrightarrow{b}) = k\overrightarrow{a} + k\overrightarrow{b}\)
ПРИМЕНЕНИЕ ВЕКТОРОВ К РЕШЕНИЮ ЗАДАЧ:
Используя векторы и связанные с ними свойства можно решать различные геометрические задачи.
Пример №6:
Точка С – середина отрезка АВ, О – произвольная точка на плоскости. Докажите, что
\(ОС = \frac{1}{2}(АО + ОВ)\)
По правилу треугольника:
\(\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{АС}\)
\(\overrightarrow{ОС} = \overrightarrow{ОВ} + \overrightarrow{ВС}\)
Сложим два этих выражения, получим:
\(2\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{ОВ} + \overrightarrow{АС} + \overrightarrow{ВС}\)
При этом \(\overrightarrow{АС}\) и \(\overrightarrow{ВС}\) – противоположные векторы, т.к. равны по модулю (точка С середина АВ), и имеют противоположное направление, значит:
\(2\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{ОВ} + \overrightarrow{АС} + \overrightarrow{ВС}\)
\(2\overrightarrow{ОС} = \overrightarrow{ОА} + \overrightarrow{ОВ} + 0\)
\(ОС = \frac{1}{2}(АО + ОВ)\)
Что и требовалось доказать.
Пример №7:
ABCD – трапеция. Точки M и N середины оснований BC и AD соответственно. Точка О – точка пересечения прямых AB и CD. Докажите, что О, M и N лежат на одной прямой.
Треугольники OAD и OBC подобны по двум углам:
\(\left. \ \frac{\angle\text{OBC} = \angle OAD\ как\ соответствующие\ углы}{\angle O\ — \ общий} \right\}\Delta\text{OAD}\sim\text{ΔOBC}\)
\(\frac{\text{OA}}{\text{OB}} = \frac{\text{OD}}{\text{OC}} = k\)
При этом соответствующие стороны коллинеарны, значит можем выразить их как произведение числа и вектора:
\(\overrightarrow{\text{OA}} \upuparrows \overrightarrow{\text{OB}} \Longrightarrow \overrightarrow{\text{OA}} = k\overrightarrow{\text{OB}}\)
\(\overrightarrow{\text{OD}} \upuparrows \overrightarrow{\text{OC}} \Longrightarrow \overrightarrow{\text{OD}} = k\overrightarrow{\text{OC}}\)
В данной задаче можем выразить \(\overrightarrow{\text{OM}}\) и \(\overrightarrow{ON}\) как
\(\overrightarrow{\text{OM}} = \frac{1}{2}\left( \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right)\)
\(\overrightarrow{\text{ON}} = \frac{1}{2}(\overrightarrow{\text{OA}} + \overrightarrow{\text{OD}})\)
т. к. М – середина BC, а N – середина AD (аналогично вектору \(\overrightarrow{\text{OC}}\) из Примера №6).
к. М – середина BC, а N – середина AD (аналогично вектору \(\overrightarrow{\text{OC}}\) из Примера №6).
Соединим выразим вектор \(\overrightarrow{\text{ON}}\) через \(\overrightarrow{\text{OA}}\) и \(\overrightarrow{\text{OD}}\) из пункта 3:
\(\overrightarrow{\text{ON}} = \frac{1}{2}\left( \overrightarrow{\text{OA}} + \overrightarrow{\text{OD}} \right)\)
\(\overrightarrow{\text{ON}} = \frac{1}{2}\left( k\overrightarrow{\text{OB}} + k\overrightarrow{\text{OC}} \right)\)
\(\overrightarrow{\text{ON}} = \frac{1}{2}k\left( \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right)\)
\(\overrightarrow{\text{ON}} = k(\frac{1}{2}\left( \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right)) = k\overrightarrow{\text{OM}}\)
Если вектор \(\overrightarrow{\text{ON}}\) можно представить как произведение числа k с вектором \(\overrightarrow{\text{OM}}\), значит \(\overrightarrow{\text{ON}}\) и \(\overrightarrow{\text{OM}}\) коллинеарны, а значит лежат на одной прямой (они не могут быть параллельны, т.
 к. уже пересекаются в точке О).
к. уже пересекаются в точке О).
Что и требовалось доказать.
Геометрия Сложение и вычитание векторов
Материалы к уроку
Конспект урока
3. Сложение и вычитание векторов
|
Введем правило сложения двух векторов. Пусть нам даны два неколлинеарных вектора a и b. Отложим от произвольной точки пространства А вектор АВ, равный вектору а. Затем от точки В отложим вектор ВС, равный вектору b. Вектор АС называется суммой векторов а и b. Нужно отметить, что сумма векторов не зависит от выбора точки А. Это правило сложения векторов называется правилом треугольника. |
Текст Сложение двух векторов Рисунок двух неколлинеарных векторов, треугольник, две стороны параллельны данным векторам
|
|
При сложении неколлинеарных векторов можно воспользоваться правилом параллелограмма. Пусть даны векторы а и b. От произвольной точки А отложим векторы АВ и АС, равные соответственно а и b. Достроим до параллелограмма, проведя дополнительные линии, параллельно данным векторам. Вектор AD являющийся диагональю параллелограмма, выходящий из точки А есть сумма векторов а и b. |
Текст Правило треугольника Рисунок параллелепипеда
|
|
Решим задачу №327 под буквой а. На рисунке изображен параллелепипед ABCDA1B1 Воспользуемся правилом параллелограмма. К вектору АВ прибавим вектор АD, равный вектору A1D1. Суммой этих векторов будет диагональ основания параллелепипеда, то есть вектор АС. |
Текст №327(а) Рисунок параллелепипеда
По правилу параллелограмма , |
|
Напомним свойства сложения векторов, так как они ни чем не отличаются от свойств сложения векторов в планиметрии: Для любых трех векторов а, бэ и це, выполняются равенства 1) переместительный закон 2) сочетательный закон |
|
|
Введем определение противоположных векторов. Два вектора называются противоположными, если их длины равны и они противоположно направлены Вектор минус а противоположен вектору а
Вектор DF противоположен вектору FD, и равен минус вектор FD
|
Противоположные векторы
Если и – противоположные, то | |=| |, .
и – противоположные, = – |
|
Определим вычитание векторов
|
Текст Вычитание векторов Разностью векторов a и b называется такой вектор, сумма которого с вектором b равна вектору a.
|
|
Разность можно найти как сумму вектора с противоположным вектором вектору . |
|
|
Существует правило для трех точек.
Любой вектор можно представить как разность двух векторов, проведенных из одной точки. Добавляем третью точку (любую) и задаем разность из вектора, проведенного из этой точки в конец данного вектора минус вектор, проведенный в начало. |
Текст Правило трех точек
Рисунок разности векторов
(по ходу правила строить сначала вектор ВК затем вектор АК и АВ) |
|
Решим задачу №332 На рисунке изображен параллелепипед ABCDA1B1C1D1 Представьте векторы АВ1 и DK в виде разности двух векторов, начала и концы которых совпадают с отмеченными на рисунке точками.
|
Текст Задача №332 Рисунок параллелепипеда
|
|
Решение. Рассмотрим вектор АВ1 и воспользуемся правилом трех точек. Третьей точкой удобно взять точку А1. Вектор, проведенный в конец то есть в точку В1 будет А1В1 и в начало точку А – вектор А1А. |
Текст Решение. Рисунок прежний
|
|
Выполним это же задание для вектора DK. Здесь третьей точкой удобно взять точку D1. Вектор в конец — D1K, в начало — D1D. Получим вектор DK равен D1K минус D1D. |
Текст Задача №332
|
Комментарий, было упущено свойства сложения векторов, и определение противоположного вектора.
Остались вопросы по теме? Наши педагоги готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать педагогаОставить заявку на подбор
4.
 3: Геометрический смысл сложения векторов
3: Геометрический смысл сложения векторов- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14519
- Кен Каттлер
- Университет Бригама Янга via Lyryx 9{n}\) — это упорядоченный список чисел. В конкретном случае \(n=2,3\) это можно использовать для определения точки в двух- или трехмерном пространстве. Эта точка задается относительно некоторых осей координат.
Рассмотрим случай \(n=3\). Напомним, что перемещение вектора без изменения его длины или направления не меняет вектор. Это важно в геометрическом представлении сложения векторов.
Предположим, у нас есть два вектора, \(\vec{u}\) и \(\vec{v}\) в \(\mathbb{R}^{3}\).
 Каждый из них можно изобразить геометрически, поместив хвост каждого вектора в \(0\) и его точку в \(\left( u_{1}, u_{2}, u_{3}\right)\) и \ (\left(v_{1}, v_{2}, v_{3}\right)\) соответственно. Предположим, мы сдвинем вектор \(\vec{v}\) так, чтобы его хвост оказался в точке \(\vec{u}\). Мы знаем, что это не меняет вектор \(\vec{v}\). Теперь нарисуйте новый вектор от хвоста \(\vec{u}\) до точки \(\vec{v}\). Этот вектор равен \(\vec{u}+\vec{v}\). 9n\) для любого \(n\) дается в следующем определении.
Каждый из них можно изобразить геометрически, поместив хвост каждого вектора в \(0\) и его точку в \(\left( u_{1}, u_{2}, u_{3}\right)\) и \ (\left(v_{1}, v_{2}, v_{3}\right)\) соответственно. Предположим, мы сдвинем вектор \(\vec{v}\) так, чтобы его хвост оказался в точке \(\vec{u}\). Мы знаем, что это не меняет вектор \(\vec{v}\). Теперь нарисуйте новый вектор от хвоста \(\vec{u}\) до точки \(\vec{v}\). Этот вектор равен \(\vec{u}+\vec{v}\). 9n\) для любого \(n\) дается в следующем определении.Определение \(\PageIndex{1}\): геометрия сложения векторов
Пусть \(\vec{u}\) и \(\vec{v}\) — два вектора. Сдвиньте \(\vec{v}\) так, чтобы хвост \(\vec{v}\) оказался на точке \(\vec{u}\). Затем нарисуйте стрелку, которая идет от хвоста \(\vec{u}\) к точке \(\vec{v}\). Эта стрелка представляет собой вектор \(\vec{u}+\vec{v}\).
Рисунок \(\PageIndex{1}\)Это определение проиллюстрировано на следующем рисунке, на котором \(\vec{u}+\vec{v}\) показан для особого случая \(n=3\) .
Рисунок \(\PageIndex{2}\)
Обратите внимание на параллелограмм, созданный \(\vec{u}\) и \(\vec{v}\) на приведенной выше диаграмме. Тогда \(\vec{u} + \vec{v}\) — направленная диагональ параллелограмма, определяемая двумя векторами \(\vec{u}\) и \(\vec{v}\).
Если у вас есть вектор \(\vec{v}\), его аддитивным обратным \(-\vec{v}\) будет вектор, имеющий ту же величину, что и \(\vec{v}\), но противоположное направление. Когда кто-то пишет \(\vec{u}-\vec{v,}\), это означает \(\vec{u} + \left(-\vec{v}\right)\), как и в случае с действительными числами. Следующий пример иллюстрирует эти определения и соглашения.
Пример \(\PageIndex{1}\): графическое сложение векторов
Рассмотрим следующее изображение векторов \(\vec{u}\) и \(\vec{v}\).
Рисунок \(\PageIndex{3}\)Эскиз рисунка \(\vec{u}+\vec{v},\vec{u}-\vec{v}.\)
Решение
Мы Сначала нарисуйте \(\vec{u}+\vec{v}.\) Начните с рисования \(\vec{u}\), а затем в точке \(\vec{u}\) поместите хвост из \(\vec{v}\), как показано.
Рисунок \(\PageIndex{4}\) Тогда \(\vec{u}+\vec{v}\) — это вектор, полученный в результате рисования вектора от хвоста \(\vec{u}\) до кончика \(\vec{v}\ ).
Тогда \(\vec{u}+\vec{v}\) — это вектор, полученный в результате рисования вектора от хвоста \(\vec{u}\) до кончика \(\vec{v}\ ).Далее рассмотрим \(\vec{u}-\vec{v}.\) Это означает \(\vec{u}+\left( -\vec{v} \ вправо). Вот картинка.
Рисунок \(\PageIndex{5}\)Эта страница под названием 4.3: Геометрическое значение сложения векторов распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) через исходный контент это было отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Кен Каттлер
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- source@https://lyryx.
 com/first-course-linear-алгебра
com/first-course-linear-алгебра - сложение векторов
- source@https://lyryx.
Сложение и вычитание векторов — Club Z! Репетиторство
В математике вектор — это объект, который имеет как величину, так и направление. Векторы можно складывать и вычитать друг из друга. Процесс сложения и вычитания векторов называется соответственно сложением и вычитанием векторов. В этой статье мы рассмотрим определения и примеры сложения и вычитания векторов. Мы также рассмотрим различные типы векторного сложения и вычитания, такие как покомпонентное сложение и скалярное умножение.
Что такое вектор?
Вектор — это математический объект, который имеет как величину, так и направление. Векторы часто используются в физике и технике для представления таких вещей, как сила, скорость и ускорение.
Векторы можно складывать и вычитать друг из друга. Когда два вектора складываются вместе, результат называется суммой векторов.
 Сумма двух векторов — это вектор, который имеет ту же величину, что и исходные векторы, но его направление определяется углом между исходными векторами.
Сумма двух векторов — это вектор, который имеет ту же величину, что и исходные векторы, но его направление определяется углом между исходными векторами.Когда два вектора вычитаются друг из друга, результат называется разностью векторов. Разность двух векторов — это вектор, который имеет ту же величину, что и исходные векторы, но его направление противоположно углу между исходными векторами.
В чем разница между скаляром и вектором?
Скаляры — это отдельные числа, такие как 1, 2, 3, 4 и т. д. Векторы — это математические величины, которые имеют как величину, так и направление. Другими словами, векторы можно рассматривать как стрелки.
Величина вектора равна длине стрелки. Направление вектора — это направление, на которое указывает стрелка. Векторы можно складывать и вычитать так же, как отдельные числа (скаляры).
При сложении или вычитании векторов необходимо учитывать как величину, так и направление векторов.
Как добавить векторы?
Есть несколько способов добавления векторов.
 Самый распространенный способ — просто сложить компоненты вместе. Итак, если у вас есть вектор A с компонентами (2,1) и другой вектор B с компонентами (-3,4), то вы можете найти результирующий вектор C, складывая компоненты каждого вектора: 92)
Самый распространенный способ — просто сложить компоненты вместе. Итак, если у вас есть вектор A с компонентами (2,1) и другой вектор B с компонентами (-3,4), то вы можете найти результирующий вектор C, складывая компоненты каждого вектора: 92)
Где R — результирующий вектор, а A и B — складывающиеся отдельные векторы.Как вычитать векторы?
В векторной математике вычитание — это процесс нахождения разницы между двумя векторами. Результат вычитания одного вектора из другого называется разностным вектором.
Чтобы вычесть один вектор из другого, нам сначала нужно найти компоненты каждого вектора. Компонент вектора — это величина этого вектора в заданном направлении. Например, если у нас есть вектор с величиной 5 в положительном направлении x, то его компонент в положительном направлении x будет равен 5.
Зная компоненты каждого вектора, мы можем вычесть их, чтобы найти разностный вектор. Например, если у нас есть вектор с величиной 4 в положительном направлении x и другой вектор с величиной 2 в отрицательном направлении x, то их разность будет вектором с величиной 6 в положительном направлении x.
 -направление.
-направление.Как складывать и вычитать векторы?
Существует несколько различных способов сложения и вычитания векторов. Наиболее распространенным способом является использование метода компонентов, который включает в себя разбиение векторов на их компоненты x и y. Чтобы сложить два вектора с помощью метода компонентов, просто сложите вместе соответствующие компоненты x и соответствующие компоненты y. Например, если вы сложите векторы (3,4) и (-2,5), вы получите (3+-2=1, 4+5=9).), поэтому сумма этих двух векторов равна (1,9).
Чтобы вычесть один вектор из другого с помощью метода компонентов, вы должны вычесть компонент x одного вектора из компонента x другого вектора, и аналогично для компонентов y. Итак, если вы вычитаете вектор (-2,5) из (3,4), вы получите (3-(-2)=5, 4-5=-1), и разница между этими двумя векторами равна (5,-1).
Существует также графический метод сложения и вычитания векторов, который может помочь визуализировать происходящее. Чтобы сложить два вектора с помощью этого метода, просто поместите их лицом к хвосту, чтобы они образовали параллелограмм.
 Диагональ этого параллелограмма и есть результирующий вектор.
Диагональ этого параллелограмма и есть результирующий вектор.Графическое сложение и вычитание векторов в одном измерении
Чтобы сложить или вычесть два вектора, мы объединяем их, соединяя начало второго вектора с хвостом первого вектора (или наоборот). Результирующий вектор идет от свободного хвоста к свободной голове. Величина равнодействующей представляет собой сумму (или разность) величин отдельных векторов, а направление определяется углом между ними.
Мы можем изобразить это графически, используя стрелки, чтобы указать направление каждого вектора, и прямую линию, чтобы показать их соединение. Величина затем представлена длиной каждого вектора:
В этом примере у нас есть два вектора, A и B, которые мы хотим сложить. Начнем с рисования буквы А на бумаге, убедившись, что ее стрелка указывает правильное направление. Затем мы рисуем B так, чтобы его наконечник указывал в том же направлении, что и хвост A. Чтобы найти результирующий вектор, мы просто проводим линию от хвоста А к голове Б.
 Длина этой линии равна сумме длин A и B, а ее направление определяется углом между A и B.
Длина этой линии равна сумме длин A и B, а ее направление определяется углом между A и B.Математическое сложение и вычитание векторов в одном измерении
Когда мы складываем или вычитаем векторы, мы на самом деле просто складываем или вычитаем компоненты, составляющие эти векторы. В одном измерении это довольно просто. Допустим, у нас есть два вектора, A и B. Вектор A имеет величину 5 и указывает в положительном направлении, а вектор B имеет величину 3 и указывает в отрицательном направлении. Чтобы найти результирующий вектор (C), мы должны просто сложить величины отдельных векторов и использовать знак результирующего вектора, чтобы указать его направление. В этом случае C будет иметь величину 2 и указывать в положительном направлении.
Если бы мы вычли вектор B из вектора A, результирующий вектор имел бы величину 8 и был бы направлен в положительном направлении.
Графическое сложение и вычитание векторов в двух измерениях
Графическое сложение и вычитание векторов в двух измерениях — это процесс сложения или вычитания векторов путем их графического отображения на координатной плоскости.
 Для этого каждый вектор изображается стрелкой, проведенной от начала координат к его конечной точке. Хвосты векторов помещаются в одну и ту же точку, а голова добавляемого вектора помещается в конец вектора, к которому он добавляется. Результирующий вектор затем рисуется из хвоста первого вектора в голову последнего вектора. Этот результирующий вектор представляет собой сумму или разность исходных векторов, в зависимости от того, были ли они добавлены или вычтены. 92). Это известно как величина векторов.
Для этого каждый вектор изображается стрелкой, проведенной от начала координат к его конечной точке. Хвосты векторов помещаются в одну и ту же точку, а голова добавляемого вектора помещается в конец вектора, к которому он добавляется. Результирующий вектор затем рисуется из хвоста первого вектора в голову последнего вектора. Этот результирующий вектор представляет собой сумму или разность исходных векторов, в зависимости от того, были ли они добавлены или вычтены. 92). Это известно как величина векторов.B. Пример 2
В этом примере мы будем складывать и вычитать векторы, которые не находятся под прямым углом друг к другу. Это может быть немного сложнее визуализировать, но может быть полезно думать о векторах как о стрелках. Начало первого вектора (стрелка) будет начинаться с хвоста второго вектора (стрелка). Затем мы нарисуем новый вектор от начала первого вектора до начала второго вектора. Этот новый вектор и есть наш ответ.
Давайте рассмотрим пример. Скажем, у нас есть два вектора, вектор A и вектор B.
 Вектор A имеет длину 5 единиц и указывает строго на север. Вектор B имеет длину 4 единицы и направлен строго на восток. Чтобы сложить эти векторы вместе, мы должны начать с хвоста вектора B и провести стрелку к голове вектора A. Нашим ответом будет новый вектор длиной 9 единиц, указывающий строго на северо-восток.
Вектор A имеет длину 5 единиц и указывает строго на север. Вектор B имеет длину 4 единицы и направлен строго на восток. Чтобы сложить эти векторы вместе, мы должны начать с хвоста вектора B и провести стрелку к голове вектора A. Нашим ответом будет новый вектор длиной 9 единиц, указывающий строго на северо-восток.Если бы мы хотели вычесть вектор B из вектора A, мы бы сделали то же самое — начали с хвоста вектора B и нарисовали стрелку к началу вектора A — но нашим ответом был бы новый вектор, равный 1 единице. длинный и направленный строго на северо-запад.
Когда вы используете сложение и вычитание векторов?
Сложение и вычитание векторов — это две математические операции, которые используются для нахождения результирующего вектора двух или более векторов. Результирующий вектор — это вектор, полученный в результате сложения или вычитания двух или более векторов.
Заключение
В заключение отметим, что векторы являются очень важной частью математики и физики.



 к. лежат параллельных прямых и направлены в одну сторону:
к. лежат параллельных прямых и направлены в одну сторону:

 В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие:
В данном случае отрицательны векторы \(\overrightarrow{b}\), \(\overrightarrow{d}\) и \(\overrightarrow{e}\). Тогда \(\overrightarrow{–b}\), \(–\overrightarrow{d}\) и \(–\overrightarrow{e}\) следующие: к. уже пересекаются в точке О).
к. уже пересекаются в точке О).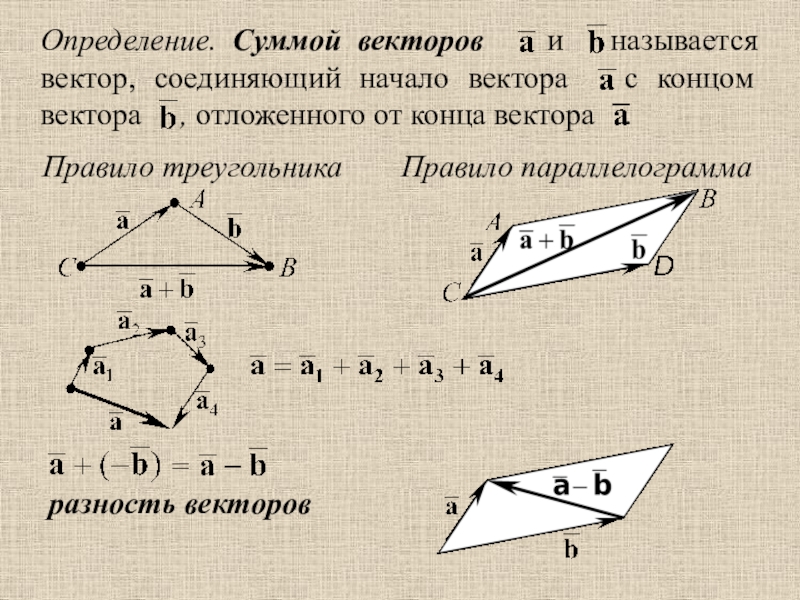



 Получаем АВ1 равно А1В1 минус А1А.
Получаем АВ1 равно А1В1 минус А1А. Каждый из них можно изобразить геометрически, поместив хвост каждого вектора в \(0\) и его точку в \(\left( u_{1}, u_{2}, u_{3}\right)\) и \ (\left(v_{1}, v_{2}, v_{3}\right)\) соответственно. Предположим, мы сдвинем вектор \(\vec{v}\) так, чтобы его хвост оказался в точке \(\vec{u}\). Мы знаем, что это не меняет вектор \(\vec{v}\). Теперь нарисуйте новый вектор от хвоста \(\vec{u}\) до точки \(\vec{v}\). Этот вектор равен \(\vec{u}+\vec{v}\). 9n\) для любого \(n\) дается в следующем определении.
Каждый из них можно изобразить геометрически, поместив хвост каждого вектора в \(0\) и его точку в \(\left( u_{1}, u_{2}, u_{3}\right)\) и \ (\left(v_{1}, v_{2}, v_{3}\right)\) соответственно. Предположим, мы сдвинем вектор \(\vec{v}\) так, чтобы его хвост оказался в точке \(\vec{u}\). Мы знаем, что это не меняет вектор \(\vec{v}\). Теперь нарисуйте новый вектор от хвоста \(\vec{u}\) до точки \(\vec{v}\). Этот вектор равен \(\vec{u}+\vec{v}\). 9n\) для любого \(n\) дается в следующем определении.
 Тогда \(\vec{u}+\vec{v}\) — это вектор, полученный в результате рисования вектора от хвоста \(\vec{u}\) до кончика \(\vec{v}\ ).
Тогда \(\vec{u}+\vec{v}\) — это вектор, полученный в результате рисования вектора от хвоста \(\vec{u}\) до кончика \(\vec{v}\ ). com/first-course-linear-алгебра
com/first-course-linear-алгебра Сумма двух векторов — это вектор, который имеет ту же величину, что и исходные векторы, но его направление определяется углом между исходными векторами.
Сумма двух векторов — это вектор, который имеет ту же величину, что и исходные векторы, но его направление определяется углом между исходными векторами. Самый распространенный способ — просто сложить компоненты вместе. Итак, если у вас есть вектор A с компонентами (2,1) и другой вектор B с компонентами (-3,4), то вы можете найти результирующий вектор C, складывая компоненты каждого вектора: 92)
Самый распространенный способ — просто сложить компоненты вместе. Итак, если у вас есть вектор A с компонентами (2,1) и другой вектор B с компонентами (-3,4), то вы можете найти результирующий вектор C, складывая компоненты каждого вектора: 92)  -направление.
-направление. Диагональ этого параллелограмма и есть результирующий вектор.
Диагональ этого параллелограмма и есть результирующий вектор.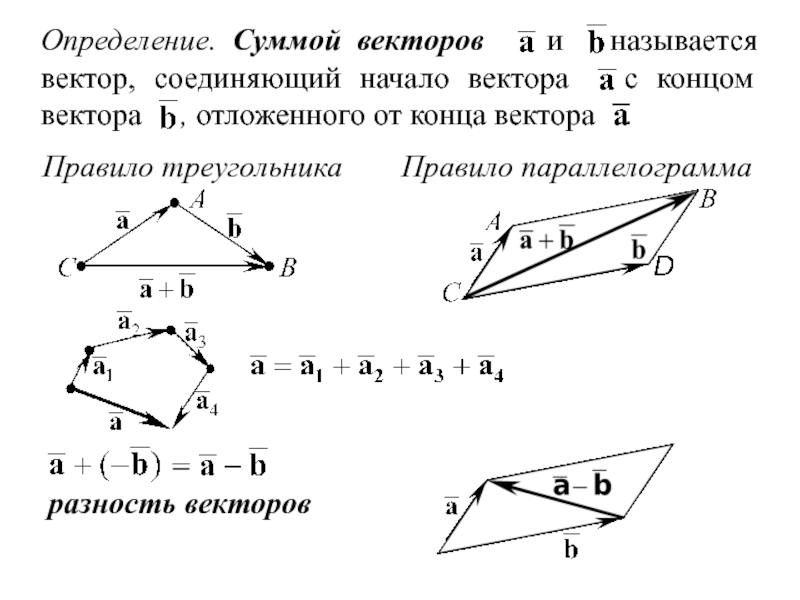 Длина этой линии равна сумме длин A и B, а ее направление определяется углом между A и B.
Длина этой линии равна сумме длин A и B, а ее направление определяется углом между A и B. Для этого каждый вектор изображается стрелкой, проведенной от начала координат к его конечной точке. Хвосты векторов помещаются в одну и ту же точку, а голова добавляемого вектора помещается в конец вектора, к которому он добавляется. Результирующий вектор затем рисуется из хвоста первого вектора в голову последнего вектора. Этот результирующий вектор представляет собой сумму или разность исходных векторов, в зависимости от того, были ли они добавлены или вычтены. 92). Это известно как величина векторов.
Для этого каждый вектор изображается стрелкой, проведенной от начала координат к его конечной точке. Хвосты векторов помещаются в одну и ту же точку, а голова добавляемого вектора помещается в конец вектора, к которому он добавляется. Результирующий вектор затем рисуется из хвоста первого вектора в голову последнего вектора. Этот результирующий вектор представляет собой сумму или разность исходных векторов, в зависимости от того, были ли они добавлены или вычтены. 92). Это известно как величина векторов. Вектор A имеет длину 5 единиц и указывает строго на север. Вектор B имеет длину 4 единицы и направлен строго на восток. Чтобы сложить эти векторы вместе, мы должны начать с хвоста вектора B и провести стрелку к голове вектора A. Нашим ответом будет новый вектор длиной 9 единиц, указывающий строго на северо-восток.
Вектор A имеет длину 5 единиц и указывает строго на север. Вектор B имеет длину 4 единицы и направлен строго на восток. Чтобы сложить эти векторы вместе, мы должны начать с хвоста вектора B и провести стрелку к голове вектора A. Нашим ответом будет новый вектор длиной 9 единиц, указывающий строго на северо-восток.