Стационарное электрическое поле уравнения — Справочник химика 21
УРАВНЕНИЯ СТАЦИОНАРНОГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ [c.49]Стационарное электрическое поле описывается следующими двумя уравнениями [c.446]
В электротехнике такая задача эквивалентна расчету стационарного электрического поля. При нахождении первичного распределения тока задача сводится к решению уравнения Лапласа при следующих граничных условиях [c.87]
Как уже было сказано, уравнение (VI. ) было выведено при условии стационарного режима, т. е. равенства электрической силы, действующей на частицу, и силы трения. Следует, однако, учитывать, что иа движение частицы в электрическом поле оказывают влияние эффекты электрофоретического торможения и электрической релаксации, которые не учитываются классической теорией Смолуховского. [c.97]
Релаксационные методы исследования кинетики химических реакций основаны на том принципе, что при быстром внешнем воздействии на систему (изменение температуры, давления, электрического поля) время, которое нужно системе для достижения нового равновесного (или стационарного) состояния, зависит от скорости химической реакции (или иногда от скорости диффузии реагентов).

Предположим, что мы имеем ориентированный по оси л капилляр радиуса г и длины I, наполненный жидкостью, к концам которого приложена разность потенциалов Е (рис. 30). Под влиянием электрического поля происходит электроосмотический перенос жидкости с некоторой скоростью причем в результате такого течения жидкости создается некоторая разность давлений Р. Описание движения вязкой, несжимаемой жидкости под влиянием электрического поля и при наличии гидростатического давления может быть сделано с использованием гидродинамических уравнений Навье—Стокса. Для данного случая — ламинарного потока жидкости в направлении оси л — в стационарном состоянии в соединении с уравнением несжимаемости жидкости уравнение Навье—Стокса сводится к следующему выражению  54]
54]
В стационарных условиях при наличии электрического поля уравнение для Се принимает вид [c.60]
Если к раствору электролита приложено переменное электрическое поле с частотой порядка этого времени релаксации, то атмосфера не успевает сделаться асимметричной и изменение подвижности ионов, связанное с асимметричностью их атмосфер, будет меньше, чем в стационарном случае. Эта идея лежит в основе развитой Дебаем и Фалькенгагеном теории влияния высоких частот на электропроводность ионных растворов. Отправным пунктом этой теории является уравнение (39) для нестационарного случая.
Для того чтобы составить тепловой баланс на спаях термопары, прежде всего необходимо рассмотреть распределение температуры в ее ветвях. Каждая ветвь термопары представляет собой однородный стержень с постоянным сечением з, по которому проходит электрический ток I. Если считать, что физические свойства материала стержня не зависят от температуры, то температурное поле стержня в стационарном состоянии описывается уравнением [c. 10]
10]
В теории зонда Ленгмюра [35] содержится вся информация, необходимая для понимания простых процессов, происходящих па мишени, помещенной в плазму низкого давле тя. Условия в газоразрядной трубке и в высоковакуумной электронной лампе совершенно различны. Плазма имеет такую высокую электропроводность, что напряжение, приложенное к зонду (мишени), не приводит к изменению электрического поля во всей трубке, а изменяет его только в непосредственной близости от зонда. Так, например, когда к электроду прикладывается отрицательное напряжение относительно плазмы (или относительно анода, поскольку потенциал плазмы обычно близок к потенциалу анода), электроны плазмы, находящиеся вблизи электрода, отталкиваются от него и в приэлектродной области образуется оболочка из положительных ионов, сквозь которую ионы плазмы устремляются к электроду. Причем большая часть приложенного напряжения падает именно на этой ионной оболочке. После установления стационарного состояния толщина оболочки ё определяется уравнением Ленгмюра для области пространственного заряда  364]
364]
Влияние постоянного электрического поля на профиль диффузионного слоя при направленной кристаллизации расплава рассмотрели Пфанн и Вагнер [56, с. 95]. Подход этих авторов может быть распространен и на поле центробежных сил. Решение уравнения непрерывности для примеси в диффузионном слое при стационарном режиме кристаллизации полубесконечного слитка приводит к следующему выражению
Напряженность электрического поля во внешней зоне стационарной униполярной короны в цилиндрическом конденсаторе при допущении о постоянстве подвижности приближенно описывается уравнением [Л. 3] [c.88]
Итак, свободные, диффузионные потоки, описываемые уравнением (I. 1. 42), в плазме не реализуются. На самом деле стационарная диффузия ионных, нейтральных и электронной компонент происходит совместно. Результирующие амбиполярные потоки компонент можно получить в слу-чае частично ионизованной многокомпонентной плазмы, исключая напряженность внутреннего электрического поля, возникающего вследствие разделения заряда, из уравнений (1.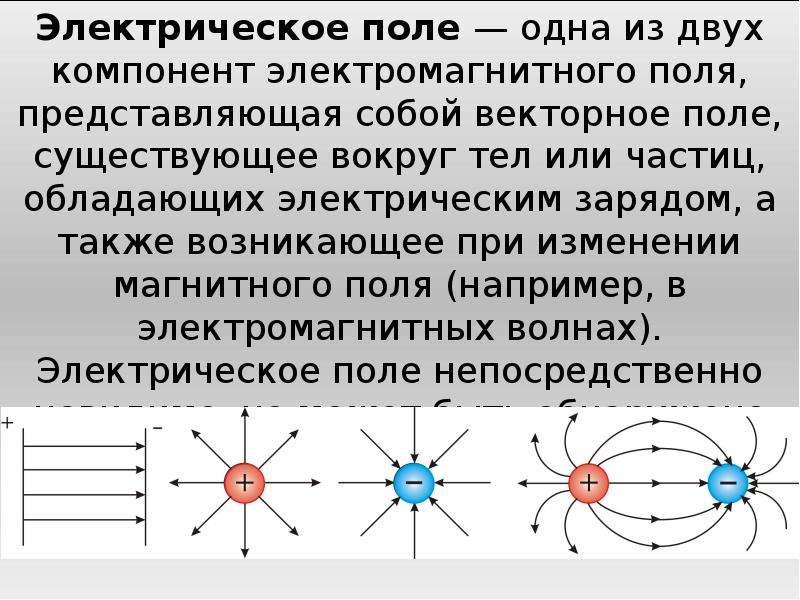
Перейдем к рассмотрению стационарного волнового уравнения (И1. 6. 6). Так как длина волны в волноводе велика по сравнению с радиусом трубки, электромагнитное поле является квазистационарным [217], и напрянэлектрического поля во всех точках поверхности можно считать одинаковой [201]. Из условий симметрии следует, что величины Е и е зависят только от расстояния до оси цилиндра г. Стационарное волновое уравнение (III. 6. 6) в цилиндрической системе координат имеет вид
В последнее время широкое применение получили также релаксационные методы исследования кинетики ферментативных реакций. Они основаны на принципе, предполагающем, что при быстром внешнем воздействии на систему (изменение температуры, давления, электрического поля) время, необходимое системе для достижения нового стационарного состояния, зависит от скорости химической реакции (или иногда от скорости диффузии реагентов). Переход системы к новым стационарным концентрациям реагентов называется химической релаксацией . Если отклонение от равновесия, вызванное внешним воздействием, невелико, то кинетику релаксации можно описать с помощью дифференциальных уравнений с постоянными коэффициентами. Релаксационные методы, используемые для исследования быстрых химических реакций в растворах, имеют высокую разрешающую способность. Так, например, метод поглощения ультразвука обнаруживает время разрешения вплоть до наносекундного диапазона. Именно поэтому релаксационная кинетика широко используется при исследовании механизмов ферментативных реакций.
Если отклонение от равновесия, вызванное внешним воздействием, невелико, то кинетику релаксации можно описать с помощью дифференциальных уравнений с постоянными коэффициентами. Релаксационные методы, используемые для исследования быстрых химических реакций в растворах, имеют высокую разрешающую способность. Так, например, метод поглощения ультразвука обнаруживает время разрешения вплоть до наносекундного диапазона. Именно поэтому релаксационная кинетика широко используется при исследовании механизмов ферментативных реакций.
Вторая составляющая связана с возникающим в результате наложения градиента температуры ЧТ градиентом электрического поля УЕ. Последний можно найти из уравнения (Х.98), учтя условия стационарности (г = 0) и отсутствие перепада давления (ЛР = 0). При этих условиях и ведутся как раз измерения скоростей течения жидкости в порах под действием УГ. Из (Х.98) получим
Из уравнения (4. 1.56) видно, что деформационная поляризация в отличие от ориентационной не зависит от температуры. При диэлектрических измерениях величина диэлектрической проницаемости уменьшается с увеличением частоты поля / по сравнению со своим стационарным значением (при / = 0) в определенной области частот (дисперсионной области) до величины = п. Дисперсия характеризуется зависимостью показателя преломления от длины волны. Обычно показатель преломления возрастает с уменьшением длины волны. Так как в данном случае показатель преломления уменьшается с уменьшением длины волны, эту область называют областью аномальной диэлектрической дисперсии. При этом фактор диэлектрических потерь, тангенс б, характеризующий энергию, получаемую диэлектриком, проходит через максимум при (еоэо — еоо)/2, так как потребление энергии особенно велико, когда время, проходящее между изменением поля, соизмеримо с временем релаксации (резонанс рис. 4.10), [19, 20]. При низких частотах ориентационная поляризация еще безынерционно следует изменению электрического поля.
1.56) видно, что деформационная поляризация в отличие от ориентационной не зависит от температуры. При диэлектрических измерениях величина диэлектрической проницаемости уменьшается с увеличением частоты поля / по сравнению со своим стационарным значением (при / = 0) в определенной области частот (дисперсионной области) до величины = п. Дисперсия характеризуется зависимостью показателя преломления от длины волны. Обычно показатель преломления возрастает с уменьшением длины волны. Так как в данном случае показатель преломления уменьшается с уменьшением длины волны, эту область называют областью аномальной диэлектрической дисперсии. При этом фактор диэлектрических потерь, тангенс б, характеризующий энергию, получаемую диэлектриком, проходит через максимум при (еоэо — еоо)/2, так как потребление энергии особенно велико, когда время, проходящее между изменением поля, соизмеримо с временем релаксации (резонанс рис. 4.10), [19, 20]. При низких частотах ориентационная поляризация еще безынерционно следует изменению электрического поля.
Диодная модель нелинейного сопротивления. Релаксационное уравнение. Рассмотрим (рис. 7.1) электрическую цепь, состоящую из нелинейного резистора и емкости С. Последняя может быть паразитной емкостью нелинейного резистора или суммой емкости конденсатора и паразитной. Нелинейный резистор будем представлять себе как вакуумный диод (рис. 7.2), причем предполагаем, что в пространстве между электродами имеется стационарный ( закрепленный ) отрицательный пространственный заряд. Он создает электрическое поле, описываемое электрическим потенциалом ср (х), где х — координата, перпендикулярная поверх- [c.57]
При наличии возмущения V волновые функции 1д и i 2д уже не являются стационарными. Происходят быстрые переходы из одного состояния в другое. Эти переходы вызваны взаимодействиями между моментами переходов двух мономеров [уравнение (7. 51)]. Колебания электрического поля одного мономера воспринимаются другими, вызывая перенос возбуждения. Заметим, что взаимодействие между двумя мономерами пропорционально Л,2 , так что оно быстро убывает с увеличением расстояния между ними. [c.49]
51)]. Колебания электрического поля одного мономера воспринимаются другими, вызывая перенос возбуждения. Заметим, что взаимодействие между двумя мономерами пропорционально Л,2 , так что оно быстро убывает с увеличением расстояния между ними. [c.49]
Характерным примером аналогии в более широком смысле является так называемая электро-тепловая аналогия, сущность которой заключается в замещении стационарного температурного поля (подлежащего изучению) стационарным полем электрического потенциала. Уравнения, определяющие оба поля в безразмерном представлении, совершенно тождественны. Безразмерные граничные условия также тождественны только в том случае, если ими непосредственно определяется поле искомой величины на границах системы (т. е. в случае, если тепловая задача поставлена в граничных условиях первого или второго рода). Для граничных условий третьего рода невозможно найти электрическую аналогию. Соответственно, критерий B — не имеет электрического ана- [c. 214]
214]
Прямые задачи в замкнутой области решаются с помощью интеграла Грина. Гармоническая функция V определяется значением этой функции и ее первой производной на замкнутой поверхности [9]. При электрохимической обработке поверхность анода никогда не бывает замкнутой. Эксперименты показывают, что поле потенциала в зазоре определяется только близлежащими участками анодной поверхности. Поверхность корректированного инструмента совпадает с поверхностью эквипотенциальной линии поля, на которой V = —ф . Формулировка задач для неравномерного распределения величины х в зазоре достаточно сложна. Должны быть приняты во внимание распределение скоростей раствора электролита в зазоре, уравнение конвективного теплопереноса (19), уравнение поля с учетом температурного коэффициента электропроводности и граничные условия для тока, потенциала и температуры. Возможна постановка ряда упрощенных задач, например, в предположении, что линии тока в зазоре не искривляются и что температура в зазоре распределена по определенному закону.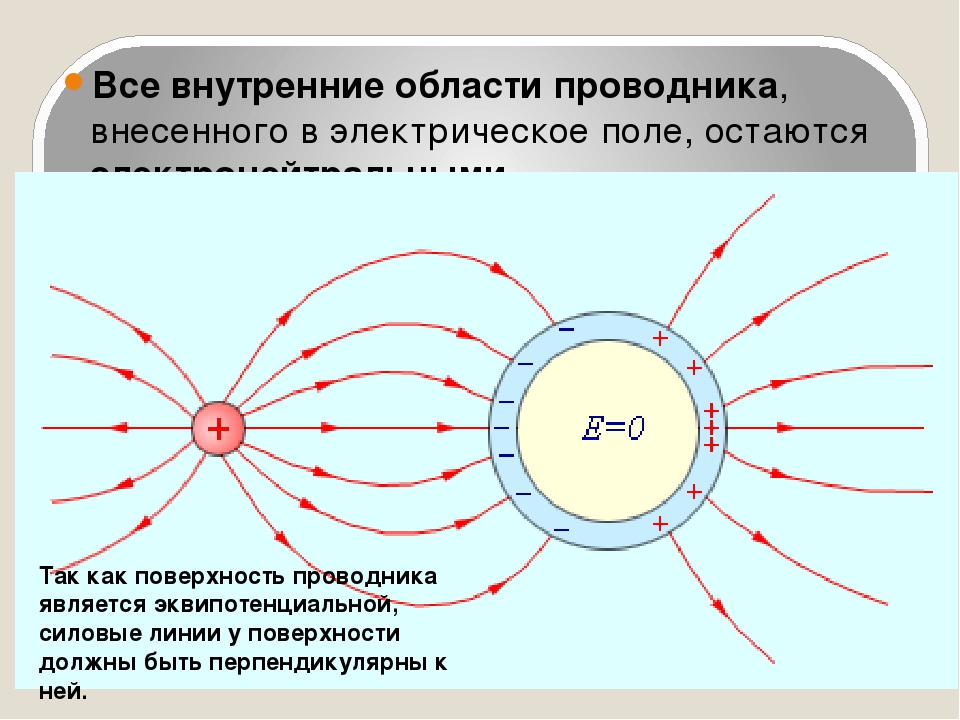 Анализ процессов, происходящих при электрохимической обработке в проточном электролите, показывает, что некоторые стационарные процессы анодного формообразования можно описать уравнениями теории электрического поля в среде с равномерной удельной электропроводностью. Поэтому можно аналитически определить ту форму инструмента — катода, при 58 [c.58]
Анализ процессов, происходящих при электрохимической обработке в проточном электролите, показывает, что некоторые стационарные процессы анодного формообразования можно описать уравнениями теории электрического поля в среде с равномерной удельной электропроводностью. Поэтому можно аналитически определить ту форму инструмента — катода, при 58 [c.58]
Абсолютные электрические заряды протона и электрона равны. Площадь поверхности сферы протона, с гравитационным радиусом К = 2,81 10 » см также равна площади сферы электрона. Поэтому напряженности электромагнитного поля вблизи этих сферических поверхностей, согласно уравнению (9), также равны. Следовательно, одинаковы и количества силовых линий электромагнитного поля, распространяемых электроном и протоном. В центральной силовой трубке, заканчивающейся электроном и протоном, количество силовых линий электрона и протона также одинаково ( 7). На I стационарной орбите электрон в атоме водорода проходит расстояние з, = 387,2 10 » см с линейной скоростью 2,2 [c. 25]
25]
Дифференциальные уравнения. Законы природы, которые управляют течением химически реагирующей жидкости, можно разделить на два класса законы сохранения и законы для потоков. Первый класс включает первый закон термодинамики, принцип сохранения массы и закон сохранения индивидуальных химических элементов второй класс включает закон теплопроводности Фурье и закон диффузии Фика. Здесь будем пользоваться той же системой обозначений и теми же приемами, что и в предыдущей статье Л. 50], и сосредоточим внимание на двух дифференциальных уравнениях для стационарного течения газа со средними скоростями без учета эффектов гравитации, электрического, магнитного и электромагнитного полей. Это дает [c.186]
Ряд свойств гетерогенных систем можно объединить в группе свойств под общим названием обобщенной проводимости (электропроводность, теплопроводность, диэлектрическая проницаемость). Это объединение основывается на известном формальном совпадении дифференциальных уравнений скалярных и векторных полей для стационарных потоков тепла, электрического тока, электрической и магнитной индукции и т. д. [c.68]
д. [c.68]
Особый случай электроосмоса представляет электроосмотиче-ское давление. Если капилляр С (рис. 33) расположен не горизонтально, а наклонно или вертикально, то при электроосмосе уровень жидкости в нем изменится и появится гидростатическое давление, направление действия которого противоположно электроосмоти-ческому течению. В результате создаются условия для обратного переноса жидкости через пористую перегородку. В конце концов уровень мениска остановится в положении, соответствующем постоянной разности гидростатических давлений, т. е. электроосмоти-ческому давлению АР. Возникающее состояние на первый взгляд похоже на равновесие в осмотической ячейке. В действительности же оно не имеет ничего общего с равновесием, а представляет собой стационарное состояние. Это обстоятельство часто не учитывается, что иногда приводит к грубым ошибкам. На самом деле и при стационарном уровне мениска под влиянием приложенного электрического поля продолжается электроосмотический перенос жидкости вдоль стенок капилляров пористой перегородки. В то же время внутри капилляра существует обратное течение, вызванное гидростатическим давлением. Так как стационарному состоянию отвечает не равенство давлений (электроосмотического и гидростатического), а равенство количеств жидкости, перенесенных за 1 с путем электроосмоса [уравнение (5.7а) ] и под действием гидростати- [c.138]
В то же время внутри капилляра существует обратное течение, вызванное гидростатическим давлением. Так как стационарному состоянию отвечает не равенство давлений (электроосмотического и гидростатического), а равенство количеств жидкости, перенесенных за 1 с путем электроосмоса [уравнение (5.7а) ] и под действием гидростати- [c.138]
Пуазейль при анализе полученных им результатов опытов, в которых электрическое поле отсутствовало, указывает на влияние концевых эффектов, которое возрастает при уменьшении длины. Концевые эффекты учитываются в гидравлике как добавочные сопротивления при переходе к трубам различного сечения, возникающие вследствие перемены режима течения (возникновение завихрений и турбулизации потока) в стыках труб, но вопрос о распространении этих возмущений по длине потока недостаточно выяснен. Ранее мы объясняли наличие определенных минимальных соотношений Ijd в электроосмосе тем, что не учитывался инерционный член в основном гидродинамическом уравнении злектроосмоса, данном Гельмгольцем, поскольку им рассматривался стационарный процесс, протекающий с постоянной скоростью. Однако в последнее время К- П. Тихомоловой был проведен расчет сил инерции, который показал, что [c.68]
Однако в последнее время К- П. Тихомоловой был проведен расчет сил инерции, который показал, что [c.68]
Определению измеряемого потенциала посвящено достаточно много работ [2, 24—27]. Анализ этих работ показывает, что определить исследуемый потенциал без значительного числа допущений нельзя. Так, Бонхе-форер, Ена и Кэше, исследуя частные реакции коррозии металлов с помощью наложенного тока, допускают равенство анодных и катодных плотностей тока и равенство их суммы внешнему току, учитывая точность измерений методом Хиклинга и Пирсона. Стационарный потенциал, как это было уже показано, есть потенциал, установившийся на границе раздела фаз сооружение—грунт без влияния внешнего источника, поэтому, как бы ни были точны измерения, наложенное электрическое поле внесет коррективы в электрохимический процесс на границе фаз металл—грунт. Вагнер [10], например, принимает, что если концентрация корродирующего металла в непосредственной близости от электрода не превышает 10 моль/л, то током д можно пренебречь (т. е. / =0). В соответствии с уравнением (9) двухвалентный металл при этой концентрации приобретает потенциал на 0,2 В отрицательнее стандартного потенциала этого металла. [c.17]
е. / =0). В соответствии с уравнением (9) двухвалентный металл при этой концентрации приобретает потенциал на 0,2 В отрицательнее стандартного потенциала этого металла. [c.17]
В общем случае функция 1 может иметь более сложную зависимость от времени Это бывает, когда на молекулу наложено внешнее переменное электрическое или магнитное поле, когда происходит сближение молекул или атомов при химических реакциях и др Решение уравнения Шредш1гера в таких ситуациях оказывается нередко очень сложным Важно, однако, что имеются частные случаи, когда поиск решения существенно упрощается Это относится, например, к случаю, когда атом или молекула взаимодействует с электромагнитным полем Тогда в соответствии со вторым постулатом Н Бора атом или молекула может изменить свое стационарное состояние и перейти в другое, также стационарное Результат решения уравнения Шредингера позволяет найти вероятность такого перехода (см гл 8) и интенсивность соответствующей линии в спектре поглощения или излучения В дальнейшем офаничимся проблемами, которые описываются стационарным уравнением Шредингера [c.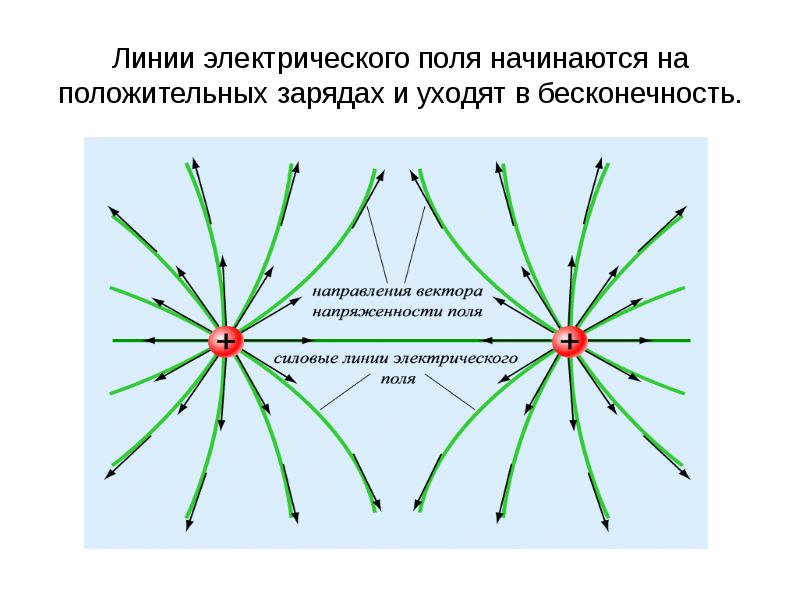 17]
17]
Уравнение (1) выведено для стационарного состояния, характеризуемого равенством конвективного потока зарядов диффузной части двойного эле1стрического слоя (ДЭС) и противоположно направленного миграционного потока, обусловленного электропроводностью жидкости. Однако используемый для вывода этого уравнения механизм переноса зарядов является сильно упрощенным. Так, Бикерманом [1] было указано на необходимость учета поверхностной проводимости Хм обусловленной ионами ДЭС, что особенно существенно в случае электрохимически активных капиллярных систем, т. е. таких систем, где толщина ДЭС соизмерима со средним радиусом капилляров при значительном заряде поверхности. Наряду с этим существенное значение имеет и так называемый фильтрационный эффект , заключающийся в изменении концентрации раствора электролита при фильтрации его через капиллярную систему (диафрагму) [2—6]. Этот эффект обусловлен тем, что потоки противоионов и коионов, равные по величине (условие электронейтральности), задерживаются зарядом ДЭС и возникающим электрическим полем, что приводит к повышению концентрации электролита в области входа В настоящее время фильтрационный эффект находит широкое практическое применение для обессоливания воды [7]. [c.90]
[c.90]
Определение концентрации железа (Ш) в зоне в стационарном состоянии позволило оценить вклад различных заряженных Ьонных форм железа в миграцию зоны, так как под действием электрического поля движутся только заряженные частицы. Для этого составляем уравнения материального баланса по ионам хлора и железа [c.20]
Основными процессами, формирующими функцию распределения электронов при воздействии внешнего поля на плазму, являются упругие столкновения электронов друг с другом, с тяжелыми частицами плшмы, а также неупругие соударения. Функция распределения находится из решения уравнения Больцмана. В общем виде задача решения этого уравнения для произвольной среды в настоящее время практически невыполнима. Детальный обзор различных приближений, используемых при решении уравнения Больцмана, проведен в /31-34/. Исследование кинетики электронов 8 электрическом поле представлено в /35/, где было получено решение стационарного уравнения Больцмана и качественно выяснена роль различных факторов для нестационарного случая. В /36/ развит приближенный метод, позволяющий определить эффективность возбуждения дискретных уровней атомов свободными электронами. и рассмотрены конкретные примеры двух-, трех-, четырехуровневых атомов в интеграле столкновений. [c.255]
В /36/ развит приближенный метод, позволяющий определить эффективность возбуждения дискретных уровней атомов свободными электронами. и рассмотрены конкретные примеры двух-, трех-, четырехуровневых атомов в интеграле столкновений. [c.255]
Таким образом последовательное уменьшение влажности грунтового массива приводит не только к изменению скорости образования гидроксил-ионов за счет восстановления растворенного в грунтовом электролите кислорода, но, вблизи стационарного значения потенциала коррозии (фкорр.), приводит к изменению закона, определяющего кинетику катодного направления коррозионного процесса. При этом, как показывает диаграмма АОО С рис. 36, при изменении кинетических законов восстановительного процесса скорость коррозии (1 корр.) слабо зависит от потенциала. Т.е. переход с одной кинетической зависимости восстановительного процесса на другую зависимость гораздо больше связан со смещением значения стационарного потенциала в анодную область, чем с изменением значения тока коррозии, поскольку ток восстановительного процесса ограничен преимущественно не электрохимическими условиями. А поскольку смещение потенциала в область анодных значений обусловливает уменьшение отрицательного заряда на поверхности металла, что связано с уменьшением параметра (пз) уравнения (20), то при этом уменьшается и вероятность осуществления восстановительной реакции. Кроме того, уменьшение потенциала электрического поля двойного слоя, адекватно анодному перенапряжению Г]А для катодного процесса восстановления кислорода, что резко (экспоненциально ) увеличивает яктивяционное сопротивление восстановительному процессу, т.е. уменьшает скорость образования гидроксил-ионов. [c.38]
А поскольку смещение потенциала в область анодных значений обусловливает уменьшение отрицательного заряда на поверхности металла, что связано с уменьшением параметра (пз) уравнения (20), то при этом уменьшается и вероятность осуществления восстановительной реакции. Кроме того, уменьшение потенциала электрического поля двойного слоя, адекватно анодному перенапряжению Г]А для катодного процесса восстановления кислорода, что резко (экспоненциально ) увеличивает яктивяционное сопротивление восстановительному процессу, т.е. уменьшает скорость образования гидроксил-ионов. [c.38]
Задача, связанная с определением трехмерной формы катода, ставится следующим образом. Требуется найти такую поверхность катода г = (ху), имеющую потенциал фк, для которой при заданных параметрах и, А, к, (1а, 8д потенциал электрического поля V (хуг), удовлетворяющий в межэлектродном пространстне уравнению Лапласа ДУ = О, на заданной стационарной поверхности анода 2 = /а (ху) принимает определенные граничные условия для себя и для своей первой производной. [c.139]
[c.139]
Интенсивность поглощения. Внутримолекулярные переходы из одного стационарного состояния т в другое п могут возбуждаться электромагнитным полем только тогда, когда эти переходы сопровождаются изд1енением распределения электрических зарядов в молекуле. Во время колебательных переходов изменяется межъядерное расстояние г и — как следствие этого — дипольный момент молекулы [Хв. Этот факт является решающим для интегральной интенсивности поглощения, которая численно равна площади полосы поглощения основного колебания см. стр. 230 и уравнение (5.3.20)] [c.220]
Рассмотрим подробно уравнение Шредингера для простейшей системы, представляющей собой микрочастицу ( микроволницу ), которая находится в центральном поле, создаваемом электрическим зарядом. Будем считать систему стационарной, т. е. не изменяющейся во времени. Такой системой является атом водорода. В нем электрон движется в центральном поле, создаваемом протоном. Для электрона [c. 19]
19]
Стационарное электрическое поле — Энциклопедия по машиностроению XXL
Эффект Штарка в стационарном электрическом поле состоит в расщеплении и смещении спектральных линий под действием внешнего электрического поля. В большинстве практически важных случаев внешнее поле мало по сравнению с внутренним полем атома, и влияние его на атомную систему можно рассматривать как малое возмущение. Получение электрических полей, близких к напряженности внутреннего поля атома ([c.264]Для вектора электрической напряженности Е стационарного электрического поля из уравнений Максвелла имеем [c.268]
Ввиду высокой электропроводности металлов внутри анодов и катодов не может возникнуть никакой разности потенциалов. Для оценки сопротивлений и плотностей тока в растворах электролита можно, например, измерить в электролитической ванне па переменном токе первичное распределение потенциалов без учета поляризации [31], если на электродах нет никаких покрытий, создающих помехи, или же в простейших случаях рассчитать стационарное электрическое поле [32]. В общем случае фактическое распределение потенциалов после наступившей поляризации будет более равномерным, чем первичное распределение.
[c.350]
В общем случае фактическое распределение потенциалов после наступившей поляризации будет более равномерным, чем первичное распределение.
[c.350]
РАСПРЕДЕЛЕНИЕ ТОКА И НАПРЯЖЕНИЯ В СТАЦИОНАРНОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ [c.446]
Стационарное электрическое поле описывается следующими двумя уравнениями [c.446]
Станции катодной защиты 215— 219, 252, 255, 256, 261, 364, 421 Старение покрытий 158 Стационарные потенциалы 174,187 Стационарное электрическое поле, уравнения 446 [c.495]
Известно, что электростатическое поле, постоянное магнитное поле, стационарное электрическое поле тока в проводящей среде, стационарное тепловое поле (без источников тепла), поле функций тока при движении невихревых потоков идеальной жидкости и многие другие поля описываются уравнением Лапласа, имеющим следующий вид [c.90]
Стационарное электрическое поле тока в проводящей среде
[c. 91]
91]
Метод электрического моделирования (электрической аналогии) основан на той закономерности, что одними и теми же дифференциальными уравнениями описываются как электрические поля, так и поля совершенно другой физической природы — гидродинамические, электростатические, магнитные, температурные и т. д. В частности, стационарное температурное поле, так же как и стационарное электрическое поле, характеризуется уравнением Лапласа нестационарные поля (и температурные, и электрические) описываются уравнением типа уравнения Фурье и т. д. [c.14]
В электротехнике такая задача эквивалентна расчету стационарного электрического поля. При нахождении первичного распределения тока задача сводится к решению уравнения Лапласа при следующих граничных условиях [c.87]
Множество инженерных задач, связанных, в частности, с медленным стационарным обтеканием корпуса корабля, стационарной фильтрацией подземных вод, возникновением поля вокруг электромагнита, а также стационарного электрического поля в окрестности фарфорового изолятора или заглубленного в землю электрического кабеля переменного поперечного сечения, сводится к решению трехмерных уравнений Лапласа или Пуассона. Соответствующее дифференциальное уравнение в системе координат Xi с осями, направленными вдоль главных осей тензора проводимости , в случае однородной среды принимает вид
[c.143]
Соответствующее дифференциальное уравнение в системе координат Xi с осями, направленными вдоль главных осей тензора проводимости , в случае однородной среды принимает вид
[c.143]
ДИЭЛЕКТРИКИ В СТАЦИОНАРНОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ [c.5] С физической точки зрения понятно, что неоднородность температуры и химического потенциала вызывает необратимые потоки, в конечном счете приводящие систему к состоянию равновесия. Мы предположим, что стационарное неоднородное распределение температуры и химического потенциала поддерживается за счет контакта с соответствующим образом подобранными резервуарами. В таком случае требуется найти потоки (например, поток тепла) при заданных функциях Т г) и /х(г). Для того, чтобы рассмотреть перекрестные эффекты, связанные с одновременным присутствием термических и механических возмущений, будем считать, что система помещена в стационарное электрическое поле Е.
 Соответствующий гамильтониан взаимодействия с полем имеет вид
[c.406]
Соответствующий гамильтониан взаимодействия с полем имеет вид
[c.406]Если Ex есть стационарное электрическое поле, то мы имеем непрерывную суперпозицию токов, определяемых уравнениями [c.109]
Методы моделирования. Сущность метода моделирования заключается в использовании аналогии описания различных процессов статического и стационарного электрических полей, электрического поля и поля скоростей жидкости, движущейся в капиллярно-пористом теле (фильтрационный аналог) н так далее. [c.102]
При рещении задач в плоскопараллельных полях широкое распространение получил метод электрической аналогии, в котором математической моделью рассматриваемого поля служит стационарное электрическое поле в проводящей среде. По этому методу экспериментально исследуется движение постоянного электрического тока, а результаты исследования при помощи дифференциальных уравнений переносятся на моделируемое поле. [c.267]
Решение двухмерной задачи теплопроводности проводилось методом моделирования температурного поля на электроинтеграторе ЭГДА-9/60. Этот метод основан на существующей аналогии между стационарным электрическим полем тока в проводящей среде и стационарным полем температур.
[c.122]
Этот метод основан на существующей аналогии между стационарным электрическим полем тока в проводящей среде и стационарным полем температур.
[c.122]
Электрооптические эффекты наблюдаются в неподвижных материалах, помещенных в сильное стационарное электрическое поле, когда по такому фоновому состоянию (отличающемуся от естественного в отсутствие поля) пропускается электромагнитная волна (свет), К таким эффектам относится электрический эффект Керра (используемый в так называемых ячейках Керра). Очевидно, существование таких эффектов в материальной среде свидетельствует, что уравнения для электромагнитного поля в этой материальной среде в отличие от подобных уравнений в вакууме нелинейны, так как сумма двух решений не является решением. [c.64]
Электрическим полем называется одна из частей электромагнитного поля, особенностью которой является то, что это поле создается электрическими зарядами или заряженными телами, а также воздействует на эти объекты незави-си. мо от того, движутся они или неподвижны. Электрическое поле описывается определенными силовыми и энергетическими характеристиками (III.1.8. Г). Если электрически заряженные частицы или тела неподвижны в данной системе отсчета, то их взаимодействие осуществляется посредством электростатического поля. Электростатическое поле является не изменяющимся во времени стационарным) электрическим полем. В общем случае электрическое и электромагнитное поля могут изменяться с течением времени переменное, нестационарное электрическое и электромагнитное поля).
[c.181]
мо от того, движутся они или неподвижны. Электрическое поле описывается определенными силовыми и энергетическими характеристиками (III.1.8. Г). Если электрически заряженные частицы или тела неподвижны в данной системе отсчета, то их взаимодействие осуществляется посредством электростатического поля. Электростатическое поле является не изменяющимся во времени стационарным) электрическим полем. В общем случае электрическое и электромагнитное поля могут изменяться с течением времени переменное, нестационарное электрическое и электромагнитное поля).
[c.181]
При проектировании и расчете ионно-оптических систем необходимо учитывать закономерности интенсивных ионных течений в стационарных электрических полях в условиях вакуума. [c.75]
Проанализируем полученное соотношение для критерия 8Ь (т). Выражение в правой части (6. 7. 27), заключенное в квадратные скобки, представляет собой значение критерия Шервуда для стационарного массообмена между пузырьком газа и жидкостью при тех же условиях обтекания в отсутствие электрического поля [99]
[c. 275]
275]
Отметим, что соотношение (6. 7. 33) определяет значение критерия Шервуда для стационарного массообмена между пузырьком газа и жидкостью при наличии постоянного внешнего электрического поля. Используя (6. 7. 29) и (6. 7. 33), получим [c.277]
Здесь м — фазовый угол, величина которого зависит от угловой частоты изменения электрического поля со и от свойств жидкости, окружаюш ей газовый пузырек Уд п 7 определяют соответственно стационарный и зависящий от времени вклады в скорость течения жидкости и имеют вид [100] [c.278]
Нетрудно убедиться в том, что при со оо оба вклада в скорость жидкости V стремятся по своему значению к нулю. При этом, как следует из (6. 8. 6), (6. 8. 7), первый из них (т. е. стационарный) уменьшается как о) , а второй (нестационарный) — как со . Это связано с тем, что при увеличении угловой частоты колебаний напряженности электрического поля локальный заряд, индуцированный этим полем на поверхности пузырька, уменьшается. [c.278]
[c.278]
Потенциальный барьер возрастает до такой величины, при которой возникающее на переходе электрическое поле создает такие электрические токи электронов и дырок, которые полностью компенсируют диффузионные потоки соответствующих носителей через переход, в результате чего достигается стационарное состояние. В и-области электрический ток обусловливается движением электронов, которые там являются основными носителями. В /г-области основными носителями служат дырки. Следовательно, электрическое поле на переходе создает электрический ток, состоящий из дырок, которые движутся из и-области в /j-область, и из электронов, которые движутся из />-области в -область. Образующийся суммарный электрический ток является током неосновных носителей, направленным из и-области в / -область его плотность обозначим (рис. 119). Диффузионные потоки электронов и дырок составляют на переходе диффузионный ток основных носителей, направленный из р-области в -область его плотность обозначим В состоянии равновесия = 0. Для дальней-
[c.357]
Для дальней-
[c.357]
Рассмотрим задачу о стационарном течении невязкого проводящего газа в канале с заданным поперечным сечением А (лс). При этом будем считать, что параметры потока в любом сечении канала одинаковы т. е. являются функциями лишь координаты х, направленной вдоль оси канала магнитное и электрическое поля приложены к потоку извне, причем направлены они перпендикулярно движению газа и друг к другу (рис. XV.3). [c.410]
Рассмотрим диэлектрик, помещенный в HeoAiHqpo№Hoe стационарное электрическое поле. Тогда согласно уравнению ( 6) на некоторый о1бъам будет действовать сила. В результате начнется перемещение внутри жидкости моли, обладающие большими значениями х, будут перемещаться в область с большей напряженностью, вытесняя оттуда моли жидкости с меньшей и. [c.283]
Заметим, что, кроме мембранной аналогии, в теории кручения стержней известны гидродинамические аналогии, а также электродинамическая аналогия. Последняя является следствием той аналогии, которая присуща уравнениям теории упругости и уравнениям стационарных электрических полей в диэлектрических или токопрово-ДЯЩ.ИХ линейных средах.
[c.221]
Последняя является следствием той аналогии, которая присуща уравнениям теории упругости и уравнениям стационарных электрических полей в диэлектрических или токопрово-ДЯЩ.ИХ линейных средах.
[c.221]
Известны попытки применить эллипсометрию для температурных измерений в газоразрядной плазме [4.35]. Поскольку в процессе плазменного воздействия происходит модификация и зарядка поверхности, требуется выделять ту часть сигнала, которая связана с температурой. Для этого необходимы дополнительные данные о состоянии поверхности в разряде, что существенно усложняет задачу. В частности, не изучено влияние стационарных электрических полей, возникающих в приповерхностном слое образца, на эллипсометрические параметры. Толщина этого слоя в полупроводниковом кристалле сравнима с глубиной формирования отраженного светового пучка. Аналогом измерений в плазме является электроотражение света от поверхности, к которой приложен потенциал относительно опорного электрода.
[c. 106]
106]
Предлагаемое устройство основано на фазовой устойчивости некоторых орбит в циклотроне. Рассмотрим, например, частицу, энергия которой такова, что ее угловая скорость как раз соответствует круговой частоте электрического поля. Назовем эту энергию равновесной. Пусть, далее, частица пересекает ускоряющий зазор как раз в тот момент, когда электрическое поле проходит через нуль, изменяясь в таком направлении, что более ранний подход частицы вызвал бы ее ускорение. Такая орбита является безусловно стационарной. Чтобы это показать предположим, что сдвиг по фазе таков, что частица подходит к зазору слишком рано. Тогда она получает ускорение рост энергии вызывает уменьшение угловой скорости, что задерживает подход к зазору Аналогичное рассуждение доказывает, что и отклонение энергии от равновесного значения вызывает самокоррекцию. [c.411]
Стационарный эффект заключается в том, что сверхпроводящий ток может течь в отсутствие электрического поля чер,ез щель между двумя сверхпроводниками, заполненную изолятором, если Толщина слоя изолятора достаточно мала (1—2 нм). Это означает, что сверхпроводящие электроны способны туннелировать через тонкие изолирующие слои.
[c.265]
Это означает, что сверхпроводящие электроны способны туннелировать через тонкие изолирующие слои.
[c.265]
Эти результаты Пайерлс использовал при исследовании электропроводности при низких температурах. Электрическое поле стремится увеличить J с постоянной скоростью, и поскольку электрон-фононные взаимодействия сохраняют J, равновесие может быть достигнуто только за счет взаимодействия фононов между собой, при котором не сохраняется q, т. е. за счет того же взаимодействия, которое обусловливает тепловое сопротивление (п. 7). Таким образом, в стационарном состоянии Ь /= О, а » gp (время релаксации электронов, обусловленное взаимодействием с фононами), согласно (21.4), возрастает, превышая значение, вычисленное по теории Блоха. Если ад — проводимость, рассчитанная по теории Блоха в предположенип = 0, то, согласно (21.4), а равно [c.285]
Клеменс [124] оценил упомянутый дополнительный тепловой поток следующим образом.
 Поток состоит из двух частей из добавки к Qn, возникающей вследствие условия Ф О, и теплоты, вызванной тем, что при переходе электронов из сверхпроводящего в нормальное состояние поглощается некоторая энергия, которая затем высвобождается при обратном процессе. В (25.6) последним эффектом мы пренебрегли, воспользовавшись в (25.5) выражением для справедливость такого пренебрежения вытекает из следующих рассуждений. Так как / = 0, / = / и так как в сверхпроводниках в стационарном состоянии электрическое поле 7 = 0 или по крайней мере мало ), то / будет порядка L,j (/sTr/QгдеЬ — коэффициент переноса (14.11), в котором учтено рассеяние статическими дефектами и вклад токов только в нормальных областях. Тепло, переносимое / порядка КТ, т. е. меньше на множитель(isTT/Q . Вторая добавка к имеет порядок так как скрытая теплота перехода из нормального в сверхпроводящее состояние на один электрон Эта добавка равна примерно Ь КТ IQ К Т рУТ, что значительно больше тенла, переносимого В свою очередь меньше на множитель порядка КТи-р.
Поток состоит из двух частей из добавки к Qn, возникающей вследствие условия Ф О, и теплоты, вызванной тем, что при переходе электронов из сверхпроводящего в нормальное состояние поглощается некоторая энергия, которая затем высвобождается при обратном процессе. В (25.6) последним эффектом мы пренебрегли, воспользовавшись в (25.5) выражением для справедливость такого пренебрежения вытекает из следующих рассуждений. Так как / = 0, / = / и так как в сверхпроводниках в стационарном состоянии электрическое поле 7 = 0 или по крайней мере мало ), то / будет порядка L,j (/sTr/QгдеЬ — коэффициент переноса (14.11), в котором учтено рассеяние статическими дефектами и вклад токов только в нормальных областях. Тепло, переносимое / порядка КТ, т. е. меньше на множитель(isTT/Q . Вторая добавка к имеет порядок так как скрытая теплота перехода из нормального в сверхпроводящее состояние на один электрон Эта добавка равна примерно Ь КТ IQ К Т рУТ, что значительно больше тенла, переносимого В свою очередь меньше на множитель порядка КТи-р. 1%, поэтому циркуляционный механизм не дает заметного вклада в полную электронную теплопроводность ) отсюда вытекает, что в (25.5) должна фигурировать именно С .
[c.298]
1%, поэтому циркуляционный механизм не дает заметного вклада в полную электронную теплопроводность ) отсюда вытекает, что в (25.5) должна фигурировать именно С .
[c.298]Уравнение (I) утверждает, что электрическое поле в стационарных условиях внутри сверхпроводника должно быть равно нулю. В односвяз-ном теле этот вывод единственный не может существовать никаких токов в отсутствие внешнего магнитного поля. В многосвязном теле, например в кольце, существуют разные решения, соответствующие различным стационарным токам, текущим по кольцу даже в случае отсутствия внешнего поля. Магнитное по.пе, создающее ток сверхпроводпмостп, самоопре-ляется им. Это справедливо и для тока, текущего в сверхпроводящей проволоке между контактами с нормальным металлом ток создает магнитное поле, которое в свою очередь определяет ток сверхпроводимости в прово- [c.693]
В случае стационарного двумерного электрического поля, со-г.часно (25), имеем
[c. 219]
219]
На рис. 98 схематически показана простейшая атомная система с одним электроном (атом водорода или водородоподобный ион), какой она представляется в теории Бора. Поле в атоме водорода можно считать число кулоновским. Состояния с различными значениями побочного квантового числа I и одинаковыми главными квантовыми числами и в атоме водорода вырождены и обладают практически одинаковыми энергиями. Орбита электрона в кулоновском поле не совершает прецессии вокруг ядра, а имеет вполне определенное положение. Электрон, обращаясь по орбите, наиболее медленно движется вдали от ядра. Поэтому электрический центр тяжести орбиты электрона находится в точке С. Такая атомная система обладает стационарным дипольным моментом. В этом случае наблюдается линейный игтарк-эффект — линейная зависимость расщепления линий от величины электрического поля. [c.264]
Стационарные двумерные поля температуры и электрического потенциала в однородной среде с постоянным коэффициентом теплопроводности (Я,= onst) и в токопроводящей среде с постоянной электрической проводимостью (а = onst) описываются дифференциальным уравнением Лапласа
[c. 76]
76]
Пример 27.1. Найти волновые функции стационарных состояний и уровни энергии гармонического осциллятора, находящегося в однородном электрическом поле напряжен-Н0С1И i. [c.173]
Такое состояние не может быть равновесным, и электроны начнут диффундировать со стороны металла с большей концентрацией свободных электронов в сторону металла с меньшей концентрацией. В результате этого концентрация электронов в некоторой области вблизи границы со стороны металла с большей энергией Ферми уменьшается и эта область заряжается положительно, а с другой стороны границы концентрация электронов увеличивается и эта область заряжается отрицательно. Благодаря возникновению зарядов по разные стороны границы образуется электрическое поле, напряженность которого направлена со стороны металла с большей энергией Ферми в сторону металла с меньшей энергией Ферми. Сила, действующая со стороны этого поля на электроны, направлена против диффундирующего потока электронов и создает упорядоченное движение электронов в противоположном диффузии направлении, т. е. электрический ток. Когда диффузионный поток электронов и электрический ток электронов уравновесят друг друга, наступает стационарное состояние. Изменение концентрации элек-
[c.347]
е. электрический ток. Когда диффузионный поток электронов и электрический ток электронов уравновесят друг друга, наступает стационарное состояние. Изменение концентрации элек-
[c.347]
Течение между неподвижными параллельными стенками (плоская труба). Рассмотрим плоское стационарное течение несжимаемой элект- X ропроводящей вязкой жидкости между параллельными бесконечными изолированными стенками в однородном внешнем магнитном и электрическом полях. [c.416]
Стационарное электрическое поле уравнения — Энциклопедия по машиностроению XXL
Станции катодной защиты 215— 219, 252, 255, 256, 261, 364, 421 Старение покрытий 158 Стационарные потенциалы 174,187 Стационарное электрическое поле, уравнения 446 [c.495]Для вектора электрической напряженности Е стационарного электрического поля из уравнений Максвелла имеем [c.268]
Стационарное электрическое поле описывается следующими двумя уравнениями
[c. 446]
446]
Известно, что электростатическое поле, постоянное магнитное поле, стационарное электрическое поле тока в проводящей среде, стационарное тепловое поле (без источников тепла), поле функций тока при движении невихревых потоков идеальной жидкости и многие другие поля описываются уравнением Лапласа, имеющим следующий вид [c.90]
Метод электрического моделирования (электрической аналогии) основан на той закономерности, что одними и теми же дифференциальными уравнениями описываются как электрические поля, так и поля совершенно другой физической природы — гидродинамические, электростатические, магнитные, температурные и т. д. В частности, стационарное температурное поле, так же как и стационарное электрическое поле, характеризуется уравнением Лапласа нестационарные поля (и температурные, и электрические) описываются уравнением типа уравнения Фурье и т. д. [c.14]
В электротехнике такая задача эквивалентна расчету стационарного электрического поля. При нахождении первичного распределения тока задача сводится к решению уравнения Лапласа при следующих граничных условиях
[c.87]
При нахождении первичного распределения тока задача сводится к решению уравнения Лапласа при следующих граничных условиях
[c.87]
Множество инженерных задач, связанных, в частности, с медленным стационарным обтеканием корпуса корабля, стационарной фильтрацией подземных вод, возникновением поля вокруг электромагнита, а также стационарного электрического поля в окрестности фарфорового изолятора или заглубленного в землю электрического кабеля переменного поперечного сечения, сводится к решению трехмерных уравнений Лапласа или Пуассона. Соответствующее дифференциальное уравнение в системе координат Xi с осями, направленными вдоль главных осей тензора проводимости , в случае однородной среды принимает вид [c.143]
Если Ex есть стационарное электрическое поле, то мы имеем непрерывную суперпозицию токов, определяемых уравнениями [c.109]
При рещении задач в плоскопараллельных полях широкое распространение получил метод электрической аналогии, в котором математической моделью рассматриваемого поля служит стационарное электрическое поле в проводящей среде. По этому методу экспериментально исследуется движение постоянного электрического тока, а результаты исследования при помощи дифференциальных уравнений переносятся на моделируемое поле.
[c.267]
По этому методу экспериментально исследуется движение постоянного электрического тока, а результаты исследования при помощи дифференциальных уравнений переносятся на моделируемое поле.
[c.267]
Электрооптические эффекты наблюдаются в неподвижных материалах, помещенных в сильное стационарное электрическое поле, когда по такому фоновому состоянию (отличающемуся от естественного в отсутствие поля) пропускается электромагнитная волна (свет), К таким эффектам относится электрический эффект Керра (используемый в так называемых ячейках Керра). Очевидно, существование таких эффектов в материальной среде свидетельствует, что уравнения для электромагнитного поля в этой материальной среде в отличие от подобных уравнений в вакууме нелинейны, так как сумма двух решений не является решением. [c.64]
Здесь большой практический интерес представляет даже простейший случай стационарного движения в электрическом поле жидкости, содержащей электрические заряды (ионы). Уравнения гидродинамики, электростатики и постоянного тока, относящиеся к вопросу, таковы
[c.277]
Уравнения гидродинамики, электростатики и постоянного тока, относящиеся к вопросу, таковы
[c.277]
Данная глава посвящена теории пассивных оптических резонаторов. Под пассивным оптическим резонатором мы понимаем замкнутую полость, состоящую из отражающих поверхностей и содержащую внутри себя однородную, изотропную и пассивную диэлектрическую среду. Напомним, что мода резонатора была определена в разд. 2.2 как стационарная конфигурация электромагнитного поля, которая удовлетворяет как уравнениям Максвелла, так и граничным условиям. При этом электрическое поле такой конфигурации можно записать в виде [c.160]
Пусть ось X перпендикулярна плоским граням образца, а начало координат помещено в центр кристалла так, чтобы поверхности находились при x = =ta. Поскольку в стационарных условиях V (8р) не может иметь у- и 2-компонент, а электрическое поле не имеет л—компоненты, то член Е V (бр) в уравнении непрерывности обращается в нуль. Кроме того, в стационарных условиях д (8p)idt = 0. Падающий свет создает постоянное количество электронно-дырочных пар g в единице объема за единицу времени во всех точках внутри образца. Наконец, симметрия образца такова, что избыточная концентрация носителей не изменяется вдоль направлений у или г, поэтому
[c.358]
Падающий свет создает постоянное количество электронно-дырочных пар g в единице объема за единицу времени во всех точках внутри образца. Наконец, симметрия образца такова, что избыточная концентрация носителей не изменяется вдоль направлений у или г, поэтому
[c.358]
Теперь мы хотим решить уравнение (4Б.8) и найти зависимость функции распределения /(р) от поля. Однако мы сталкиваемся с новой проблемой. Дело в том, что в изолированной электронно-примесной системе, находящейся во внешнем электрическом поле, не может установиться стационарное состояние из-за выделения джоулева тепла. В реальном кристалле энергия, получаемая электронами от поля, поглощается затем термостатом (атомами кристаллической решетки), но при выводе кинетического уравнения взаимодействие с термостатом не учитывалось. Поэтому физический смысл решения кинетического уравнения (4Б.8) и возможность его использования для вычисления проводимости вовсе не очевидны. Так как джоулево тепло пропорционально квадрату напряженности электрического поля, то фактически уравнение (4Б. 8) применимо лишь для вычисления линейной реакции электронов на электрическое поле.
[c.331]
8) применимо лишь для вычисления линейной реакции электронов на электрическое поле.
[c.331]
В случае постоянного электрического поля левые части уравнений (7.1.78) равны нулю, и, следовательно, из этих уравнений можно найти стационарную скорость дрейфа и электронную температуру = 1/ как функции электрического поля Е при заданной температуре решетки Т = 1//5, а затем вычислить стационарный ток в системе. Для этого нужно, конечно, иметь явные выражения для кинетических коэффициентов. Если рассматривать подсистемы электронов и фононов как квантовые газы, то кинетические коэффициенты легко вычисляются (см. [167]). Однако даже в этом простейшем приближении зависимость кинетических коэффициентов от Е и Т оказывается весьма сложной, и уравнения баланса приходится решать численными методами. Результаты таких расчетов, приведенные в работах [115, 118, 167], хорошо согласуются с экспериментальными данными. [c.104]
Из приведенных в п. 3.122 уравнений полуклассической теории можно найти полностью определенные во времени функции электрического поля, поляризации, электромагнитной энергии или чисел фотонов сказанное справедливо также и для величин ЛЛ и Q, входящих в уравнения баланса полной квантовой теории, поскольку эти уравнения применяются к квантовомеханическим математическим ожиданиям скоростей изменений вероятностей переходов. Эту теорию можно использовать для описания непрерывно протекающих процессов так, например, ею можно воспользоваться для получения стационарных и нестационарных решений для среднего числа фотонов и средней инверсии в лазере. Однако следует помнить, что в действительности эти процессы протекают дискретно вследствие квантовой природы как атомов, так и излучения. Поэтому неизбежны стохастические отклонения от названных выше средних значений. Они оказываются ответственными за некоторые другие свойства лазера, такие, как минимальная достижимая ширина линии и когерентные свойства излучаемого света.
[c.300]
Эту теорию можно использовать для описания непрерывно протекающих процессов так, например, ею можно воспользоваться для получения стационарных и нестационарных решений для среднего числа фотонов и средней инверсии в лазере. Однако следует помнить, что в действительности эти процессы протекают дискретно вследствие квантовой природы как атомов, так и излучения. Поэтому неизбежны стохастические отклонения от названных выше средних значений. Они оказываются ответственными за некоторые другие свойства лазера, такие, как минимальная достижимая ширина линии и когерентные свойства излучаемого света.
[c.300]
Уравнение (4-10) характеризует кинетику изменения концентрации дефектов в отсутствие электрического поля в том случае, если их концентрация в данный момент времени / = О не равна стационарной. Согласно решению уравнения (4-10), это изменение концентрации является экспоненциальной функцией времени [c.
 149]
149]Появление электрического поля обязательно приводит к не-стационарности, т. е. к зависимости величин от времени. Как уже отмечалось, нестационарные уравнения теории сверхпроводимости весьма сложны, даже в пределе медленных временных н пространственных изменений. Поэтому мы воспользуемся модельным уравнением (19.47) для окрестности Т . [c.485]
Рассмотрим теперь применение уравнения (28.6.4). Пусть в проводнике, находящемся в стационарном состоянии, существует поток электронов, вызванный электрическим полем Ш. [c.628]
Чтобы перейти от плотности тока к выражению для электропроводимости, надо найти связь функции распределения т) с напряженностью электрического поля Е. Это можно сделать, решая кинетическое уравнение, которое для стационарных полей имеет вид [22] [c.22]
Создадим в резонаторе электромагнитное поле с частотой V при этом возбуждение создает электрическое поле, параллельное оси Ог. Исходя из уравнения для электромагнитной волны и условий, налагаемых на волновое поле на стенках, покажите, что можно получить стационарные состояния, в которых поле Е параллельно оси Ог и имеет значение, не зависящее от г, для которого существует соотношение между длиной резонатора Е и длиной волны Яо в вакууме для плоской волны с частотой V. Примем
[c.77]
Исходя из уравнения для электромагнитной волны и условий, налагаемых на волновое поле на стенках, покажите, что можно получить стационарные состояния, в которых поле Е параллельно оси Ог и имеет значение, не зависящее от г, для которого существует соотношение между длиной резонатора Е и длиной волны Яо в вакууме для плоской волны с частотой V. Примем
[c.77]
Необходимость учитывать наряду с движением электронов также движение ядер кристалла, вообще говоря, существенно усложняет проблему отыскания стационарных состояний в невозмущенной задаче (т. е. в задаче, в которой не учтено макроскопическое электрическое поле). Еще далеко не все аспекты теории этих состояний достаточно полно изучены и вся проблема, несомненно, нуждается в дальнейшем обсуждении. Однако в настоящей книге мы делать этого не имеем возможности, и в последующем изложении стационарные состояния в невозмущенной задаче считаются известными ). Эти состояния по самой постановке вопроса характеризуются лишь приближенными собственными функциями оператора энергии системы, поскольку всегда в действительности имеется такое взаимодействие (например, ангармонические члены в уравнениях колебаний решетки), которое приводит к переходам между указанными приближенными состояниями системы даже при отсутствии внешнего возмущения. Такие переходы делают время жизни возбужденных состояний кристалла и, в частности, время жизни нормальных электромагнитных волн, конечным ). Для того чтобы учесть эти переходы при
[c.325]
Такие переходы делают время жизни возбужденных состояний кристалла и, в частности, время жизни нормальных электромагнитных волн, конечным ). Для того чтобы учесть эти переходы при
[c.325]
Стационарное решение кинетического уравнения при наличии электрического и магнитного полей и градиента температуры. [c.51]
Достаточно найти плотность тока в виде выражения, пропорционального электрическому полю. Для однородного стационарного случая уравнение Больцмана принимает вид [c.397]
Вычислить теплопроводность металла, предполагая, что в уравнении Больцмана, рассмотренном в примере 4, электрическое поле положено равным нулю, а вместо него введен однородный и стационарный градиент температуры. Рассмотреть случай е р) = р 12т т — эффективная масса) и т = Л г , где Л > О и 5 > —7— постоянные. [c.404]
Если К системе одновременно приложены однородное электрическое поле Е и однородное магнитное поле Д, то уравнение Больцмана для стационарного случая приобретает вид
[c. 418]
418]
Согласно знаку а в (3.44) уравнение (3.46) может иметь стационарное трехмерное решение, если плазменная частота больше циклотронной, когда вклад в энергию (3.48) от поперечного электрического поля положителен. Ищем стационарное решение (3.46) в виде [c.60]
В случае диффузии внедренных атомов во внешнем электрическом поле из уравнения (I.IO) следует, что когда t oo, устанавливается стационарное распределение концентрации, которой удовлетворяет выражению [c.67]
Под модой поля излучения понимают стационарную конфигурацию электромагнитного поля, которая удовлетворяет уравнениям Максвелла и граничным условиям. Электрическое поле такой моды можно записать в виде [c.168]
Рассмотрим диэлектрик, помещенный в HeoAiHqpo№Hoe стационарное электрическое поле. Тогда согласно уравнению ( 6) на некоторый о1бъам будет действовать сила. В результате начнется перемещение внутри жидкости моли, обладающие большими значениями х, будут перемещаться в область с большей напряженностью, вытесняя оттуда моли жидкости с меньшей и. [c.283]
[c.283]
Заметим, что, кроме мембранной аналогии, в теории кручения стержней известны гидродинамические аналогии, а также электродинамическая аналогия. Последняя является следствием той аналогии, которая присуща уравнениям теории упругости и уравнениям стационарных электрических полей в диэлектрических или токопрово-ДЯЩ.ИХ линейных средах. [c.221]
Пусть в образце в направлении х приложено электрическое поле Е и имеется температурный градиент йх1йх. Наша цель состоит в том, чтобы приближенно найти из уравнения Больцмана функцию распределения и затем определить поток электрического заряда и энергии, причем далее мы ограничимся стационарным случаем, так что дЦд1=0. Тогда для частиц с зарядом д и массой т, находящихся в электрическом поле, уравнение переноса (12) приобретает вид [c.332]
Уравнение (I) утверждает, что электрическое поле в стационарных условиях внутри сверхпроводника должно быть равно нулю. В односвяз-ном теле этот вывод единственный не может существовать никаких токов в отсутствие внешнего магнитного поля. В многосвязном теле, например в кольце, существуют разные решения, соответствующие различным стационарным токам, текущим по кольцу даже в случае отсутствия внешнего поля. Магнитное по.пе, создающее ток сверхпроводпмостп, самоопре-ляется им. Это справедливо и для тока, текущего в сверхпроводящей проволоке между контактами с нормальным металлом ток создает магнитное поле, которое в свою очередь определяет ток сверхпроводимости в прово-
[c.693]
В многосвязном теле, например в кольце, существуют разные решения, соответствующие различным стационарным токам, текущим по кольцу даже в случае отсутствия внешнего поля. Магнитное по.пе, создающее ток сверхпроводпмостп, самоопре-ляется им. Это справедливо и для тока, текущего в сверхпроводящей проволоке между контактами с нормальным металлом ток создает магнитное поле, которое в свою очередь определяет ток сверхпроводимости в прово-
[c.693]
Стационарные двумерные поля температуры и электрического потенциала в однородной среде с постоянным коэффициентом теплопроводности (Я,= onst) и в токопроводящей среде с постоянной электрической проводимостью (а = onst) описываются дифференциальным уравнением Лапласа [c.76]
В газовом разряде электроны могут получать энергию, ускоряясь в электрическом поле, и от возбужденных молекул при ударах второго рода. Эта энергия расходуется при упругих и неупругих столкновениях с атомами и молекулами. В зависимости от соотношения между направленным действием электрического поля и хаотизи-рующими движение упругими взаимодействиями могут установиться различные распределения скоростей электронов от строго направленного до совершенно хаотического. Распределение скоростей электронов можно найти, решая кинетическое уравнение. Однако из-за математических трудностей, связанных с необходимостью учета неупругих и кулоновских столкновений, это решение удается получить строго лишь в ряде простых частных случаев. Стационарное распределение скоростей электронов Ve получено лишь для случая постоянного слабого электрического поля Е при малой концентрации электронов. При = 0 распределение электронов является максвелловским с температурой и средней тепло-
[c.79]
В зависимости от соотношения между направленным действием электрического поля и хаотизи-рующими движение упругими взаимодействиями могут установиться различные распределения скоростей электронов от строго направленного до совершенно хаотического. Распределение скоростей электронов можно найти, решая кинетическое уравнение. Однако из-за математических трудностей, связанных с необходимостью учета неупругих и кулоновских столкновений, это решение удается получить строго лишь в ряде простых частных случаев. Стационарное распределение скоростей электронов Ve получено лишь для случая постоянного слабого электрического поля Е при малой концентрации электронов. При = 0 распределение электронов является максвелловским с температурой и средней тепло-
[c.79]
Рассмотрим однородный образец полупроводника, в котором постоянное поле о создается приложенной извне э. д. с. так, что в образце устанавливается поток электронов и дырок. В стационарном состоянии df/dt = 0. Если поле Ео однородно, то V/ = 0 и сила F, действующая на дырки и электроны, равна еЕо (знак плюс относится к дыркам, минус —к электронам). Не теряя общности, можно выбрать систему координат так, чтобы ось 2 совпадала с направлением электрического поля, тогда Ео = 1гЕо. Используя эти условия и вводя в (13.8.1) время релаксации Тр с учетом того, что pg = tripV , можно получить для функции распределения дырок следующее уравнение
[c.327]
Не теряя общности, можно выбрать систему координат так, чтобы ось 2 совпадала с направлением электрического поля, тогда Ео = 1гЕо. Используя эти условия и вводя в (13.8.1) время релаксации Тр с учетом того, что pg = tripV , можно получить для функции распределения дырок следующее уравнение
[c.327]
Близкой к рассматриваемым задачей является определение поля температур по заданным температурам на границе, так как распределение температур внутри области при источниках тепла на поверхности подчинено уравнению Лапласа. Эта задача должна решаться при определении температурных напряжений. Для определения температур в плоском поле применяется плоская электрическая модель со сплошным полем или сеточная модель. Пространственная модель для определения температур внутри детали объемной формы может быть изготовлена из электролита или дисперсной массы. Пространственная модель должна иметь резервуар, дно и стенки которого выполнены из диэлектрика по форме подобной исследуемой области. Замеры внутри объемной модели производятся по плоскостям сечений модели с помощью иглы, передвигаемой по точкам. Трехразмерная модель для решения уравнения Лапласа в трех координатах может быть выполнена также в виде сеточной модели из сопротивлений, соединенных в узловых точках по всем трем направлениям. Определение с применением электрических моделей стационарных температурных полей по заданным температурам на границах рассмотрено, например, в работах [9], [12], [38], [42], [50].
[c.273]
Замеры внутри объемной модели производятся по плоскостям сечений модели с помощью иглы, передвигаемой по точкам. Трехразмерная модель для решения уравнения Лапласа в трех координатах может быть выполнена также в виде сеточной модели из сопротивлений, соединенных в узловых точках по всем трем направлениям. Определение с применением электрических моделей стационарных температурных полей по заданным температурам на границах рассмотрено, например, в работах [9], [12], [38], [42], [50].
[c.273]
Описание вынужденного рассеяния Бриллюэна основано на дифференциальных уравнениях (2.51-16) и (2.52-1) для давления и электрического поля. Решение этой системы дифференциальных уравнений в частных производных в общем случае очень затруднено. Поэтому мы рассмотрим решения при некоторых упрощающих предположениях. Прежде всего мы ограничимся стационарными решениями. Они позволяют получить приближенное описание реальных фактов, если длительность световых импульсов очень велика по сравнению с временем установления колебаний в среде. Это время задается обратны. значением константы затухания Г, которая равна удвоенному ароизведению скорости звука V и коэффициента поглощения звуковой мощности и для жидкостей п,ри комнатной температуре и%1еет порядок величины 10″ с. При рассмотрении стационарных процессов можно исходить из обыкновенных дифференциальных уравнений (2.52-3), (2.52-5) и из соответствующего уравнению (2.52-5) уравнения для амплитуды лазерной волны. Будем снова а,реиебрегать вторыми производными от амплитуды, а в правой части уравнения (2.52-3) также и первой производной. Условия применимости такого приближения обсуждались в разд. 1.322. Тогда мы получим систему
[c.217]
Это время задается обратны. значением константы затухания Г, которая равна удвоенному ароизведению скорости звука V и коэффициента поглощения звуковой мощности и для жидкостей п,ри комнатной температуре и%1еет порядок величины 10″ с. При рассмотрении стационарных процессов можно исходить из обыкновенных дифференциальных уравнений (2.52-3), (2.52-5) и из соответствующего уравнению (2.52-5) уравнения для амплитуды лазерной волны. Будем снова а,реиебрегать вторыми производными от амплитуды, а в правой части уравнения (2.52-3) также и первой производной. Условия применимости такого приближения обсуждались в разд. 1.322. Тогда мы получим систему
[c.217]
Еще в начальной стадии развития электротехники были попытки найти аналогию между электрическими и другими физическими явлениями. Так, Максвелл в своем Трактате об электричестве и магнетизме (1881 г.) указывает на существование электротепловой аналогии. Согласно общим замечаниям Максвелла применение электротепловой аналогии ограничено областью установившихся во времени процессов [Л. 72]. В 1929 г. С. А. Гершгорин (Л. 8 предложил применить для решения уравнения Лапласа электрические сетки из сопротивлений. Идея, высказанная С. А. Гершгориным, показала возможность применения сосредоточенных элементов электрических цепей для решения дифференциального уравнения Лапласа, т. е. был показан путь отыскания стационарных полей.
[c.11]
72]. В 1929 г. С. А. Гершгорин (Л. 8 предложил применить для решения уравнения Лапласа электрические сетки из сопротивлений. Идея, высказанная С. А. Гершгориным, показала возможность применения сосредоточенных элементов электрических цепей для решения дифференциального уравнения Лапласа, т. е. был показан путь отыскания стационарных полей.
[c.11]
Раздел 3. Стационарное электрическое поле
3.1. Электростатическое
поле в вакууме. Электрический заряд. Дискретность
заряда. Закон сохранения заряда. Закон
Кулона. Электрическое поле, напряженность
поля. Принцип суперпозиции. Поле
электрического диполя. Поток вектора
напряженности. Теорема Гаусса для
электростатического поля в вакууме.
Применение теоремы Гаусса к расчету
полей. Работа сил электростатического
поля. Циркуляция вектора напряженности
электростатического поля. Потенциал.
Связь напряженности электростатического
поля с потенциалом. Эквипотенциальные
поверхности.
Потенциал.
Связь напряженности электростатического
поля с потенциалом. Эквипотенциальные
поверхности.
3.2. Электрическое поле в веществе. Свободные и связанные заряды в диэлектриках. Типы диэлектриков. Диполь в однородном и неоднородном электрических полях. Поляризация диэлектриков. Виды поляризации. Поляризованность. Диэлектрическая восприимчивость и ее зависимость от температуры. Поляризационные заряды на поверхности и внутри диэлектрика. Теорема Гаусса для электрического поля в диэлектрике. Электрическое смещение. Диэлектрическая проницаемость среды. Условия на границе раздела двух диэлектрических сред. Сегнетоэлектрики. Электреты. Поле внутри проводника и вблизи его поверхности. Распределение зарядов в проводнике. Электростатическая защита. Генератор Ван-дер-Граафа.
3.3. Энергия
электрического поля. Электрическая
емкость проводников и конденсаторов. Электроемкость уединенного проводника.
Взаимная емкость двух проводников
Конденсаторы и их соединение. Энергия
системы зарядов. Энергия заряженного
проводника. Энергия заряженного
конденсатора. Плотность энергии
электростатического поля. Работа и
энергия поляризации.
Энергия
системы зарядов. Энергия заряженного
проводника. Энергия заряженного
конденсатора. Плотность энергии
электростатического поля. Работа и
энергия поляризации.
3.4. Постоянный электрический ток. Характеристики и условия существования постоянного электрического тока. Закон Ома в локальной и интегральной формах. Сторонние силы. Закон Ома для неоднородного участка цепи. Разветвленные цепи. Правила Кирхгофа. Работа и мощность тока. Закон Джоуля – Ленца в интегральной и локальной формах. Классическая теория электропроводности металлов и ее опытное обоснование. Вывод законов Ома, Джоуля – Ленца, Видемана-Франца на основе классических представлений. Затруднения классической электронной теории электропроводности металлов. Границы применимости закона Ома. Ток в газах и электролитах. Плазма. Дебаевский радиус экранирования.
Раздел 4. Электромагнетизм
4.1. Магнитное
поле в вакууме. Взаимодействие токов. Магнитное поле.
Вектор магнитной индукции. Поле
движущегося заряда. Закон Био-Савара-Лапласа.
Принцип суперпозиции. Примеры расчета
магнитных полей. Циркуляция вектора
магнитной индукции. Магнитное поле
тороида и длинного соленоида. Магнитный
поток. Теорема Гаусса.
Поле
движущегося заряда. Закон Био-Савара-Лапласа.
Принцип суперпозиции. Примеры расчета
магнитных полей. Циркуляция вектора
магнитной индукции. Магнитное поле
тороида и длинного соленоида. Магнитный
поток. Теорема Гаусса.
4.2. Действие магнитного поля на проводники с током и движущиеся заряды. Сила Ампера. Контур с током в магнитном поле. Магнитный момент. Момент сил, действующих на контур в однородном поле. Работа перемещения проводника и контура в магнитном поле. Взаимодействие контура с неоднородным полем. Сила Лоренца. Движение заряженной частицы в магнитном и электрическом полях. Принцип действия циклических ускорителей заряженных частиц, масс-спектрометров. Эффект Холла. МГД-генератор. ЭДС при движении проводников в магнитном поле.
4.3. Магнитное
поле в веществе. Магнитные моменты атомов. Орбитальный
и спиновый моменты. Магнитомеханические
явления. Намагниченность. Микро- и
макротоки. Теорема о циркуляции
напряженности магнитного поля. Магнитная
восприимчивость и магнитная проницаемость
среды. Элементарная теория диа- и
парамагнетизма. Ферромагнетики. Опыты
Столетова. Кривая намагничивания.
Магнитный гистерезис. Точка Кюри.
Спиновая природа ферромагнетизма.
Домены. Условия на границе раздела двух
сред. Магнитные цепи.
Магнитная
восприимчивость и магнитная проницаемость
среды. Элементарная теория диа- и
парамагнетизма. Ферромагнетики. Опыты
Столетова. Кривая намагничивания.
Магнитный гистерезис. Точка Кюри.
Спиновая природа ферромагнетизма.
Домены. Условия на границе раздела двух
сред. Магнитные цепи.
4.4. Явление электромагнитной индукции. Энергия магнитного поля. Опыты Фарадея. Закон электромагнитной индукции. Вихревое электрическое поле. Токи Фуко. Явление самоиндукции. Индуктивность. Скин-эффект. Переходные процессы в электрической цепи при подключении и отключении источника. Явление взаимной индукции. Энергия контура с током. Энергия магнитного поля. Плотность энергии магнитного поля.
Стационарное электрическое поле — презентация онлайн
1. Физико-технические основы электроэнергетики
Лекция 2Профессор Е.Ю.Клименко
Стационарное электрическое поле
Уравнения Максвелла
Первое уравнение: электрический заряд порождает
электрическое поле
Второе уравнение: изменяющееся магнитное поле
порождает вихревое электрическое поле
Третье уравнение: магнитных зарядов не существует
Четвертое уравнение: электрический ток и изменение
электрической индукции порождают вихревое
магнитное поле
Исключив зависимость от времени, получаем:
Из второго следует, что Е можно представить в виде
— скалярный потенциал
Минус выбран для того, чтобы выполнить общепринятое условие:
«вектор Е направлен от положительного заряда к отрицательному»
2
Электростатическая энергия
Точечный заряд – конечный заряд, сконцентрированный в столь
малой области, что ее размерами можно пренебречь по сравнению с
другими характерными размерами рассматриваемой задачи.
Сила, действующая на заряд, равна
, где E- поле,
создаваемое другими стационарно распределенными зарядами.
Работа, совершаемая над зарядом при перемещении из точки r1
в другую точку r2 равна
Работа, произведенная при медленном перемещении заряда по
замкнутому пути равна нулю. Поля, в которых работа зависит только от
конечных положений, но не от пути, называются консервативными
3
Потенциал определен с точностью до постоянной
, поскольку
Устраним неоднозначность, договорившись, что потенциал равен
работе, совершаемой при перемещении единичного положительного
заряда из бесконечности в точку
Поверхности
Вектор
называют эквипотенциальными
лежит на эквипотенциальной поверхности
— компоненты градиента
То, что
означает, что электрическое поле
перпендикулярно эквипотенциальной поверхности.
Линии, касающиеся в каждой точке Е названы силовыми.
Чтобы малое смещение вдоль силовой линии
Совпадало с Е должно быть
4
Дифференциальные уравнения силовых линий
Примеры силовых линий и эквипотенциальных поверхностей
1.
 Два точечных заряда
Два точечных зарядаразных знаков.
2. Два одинаковых
точечных заряда
3. Три отрицательных и два
положительных заряда
1
2
3
5
Соотношение между компонентами D и Е обычно линейны:
Получаем связь потенциала с зарядами:
В однородной среде потенциал описывается уравнением Пуассона
В точках, где нет зарядов это уравнение сводится к уравнению Лапласа
6
Основная задача электростатики
Определение функции
, удовлетворяющей в каждой точке
пространства уравнению Пуассона, а на заданных поверхностях –
граничным условиям.
7
Граничные условия
Рассматривается малый, (такой что
на каждом из торцов индукция не
меняется) цилиндр высотой
Пусть плавно меняется по высоте,
а заряд сохраняется. Когда
боковая поверхность уменьшится до
нуля
.
— плотность зарядов на
поверхности.
Наличие зарядов на поверхности приводит к
скачку индукции, равном поверхностной
плотности заряда в кулонах на кв.
 метр
метрРассмотрим контур L с нормалью
— нормаль к поверхности.
-вектор вдоль E.
Проекция E на
При переходе через поверхность
разрыва тангенциальная
компонента эл. поля непрерывна
8
Граничные условия для потенциала
Из
Из
следует
следует
Из консервативности поля следует непрерывность потенциала
на границе
9
Лапласиан в различных системах координат
В декартовых
В цилиндрических
В сферических
10
Определение поля по заданному распределению зарядов
Потенциал в заданной точке (x’,y’,z’)
внутри объема V можно выразить через
объемный интеграл по объему V и
поверхностный интеграл по S.
Заряд распределен в объеме с конечной
плотностью
.
Воспользуемся теоремой Грина
Примем
удовлетворяет уравнению Лапласа
, но в точке r=0 особенность.
Избавимся от нее, окружив точку (x’,y’,z’) малой сферой S2.
11
Подставляя
в уравнение Грина получим
На сферической поверхности S2
поэтому
Если заменить
и
средними значениями, то получим
при
.
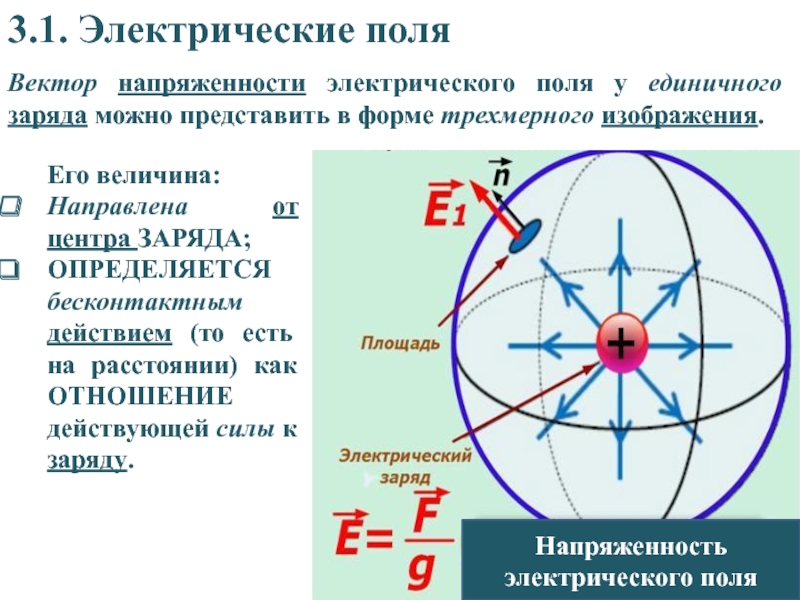 Это значение
Это значениеинтеграла по S2. Тогда
Можем выразить потенциал через плотность заряда (без особенностей)
12
Если в V1 нет зарядов, то
Это значит, что интеграл по поверхности выражает вклад в потенциал в
точке
от зарядов, расположенных вне объема V1.
Если вне этого объема нет зарядов, то поверхностный интеграл должен
равняться нулю.
Интеграл
Пуассона.
частное решение уравнения
Если точка
лежит вне области, содержащей заряды на
расстоянии R от какой-либо точки этого объема то при R много большем
линейных размеров этой области
Определение: Потенциальная функция регулярна на бесконечности, если
при
произведение
остается ограниченным.
На больших расстояниях распределение потенциала зависит только от R
E направлен по радиусу и
тоже ограничено.
13
Поверхность S1 делит пространство
на две области внутреннюю V1 и
внешнюю V2 . Теорему Грина можно
применить в этом случае, считая ,
что S2 удалена на бесконечность.
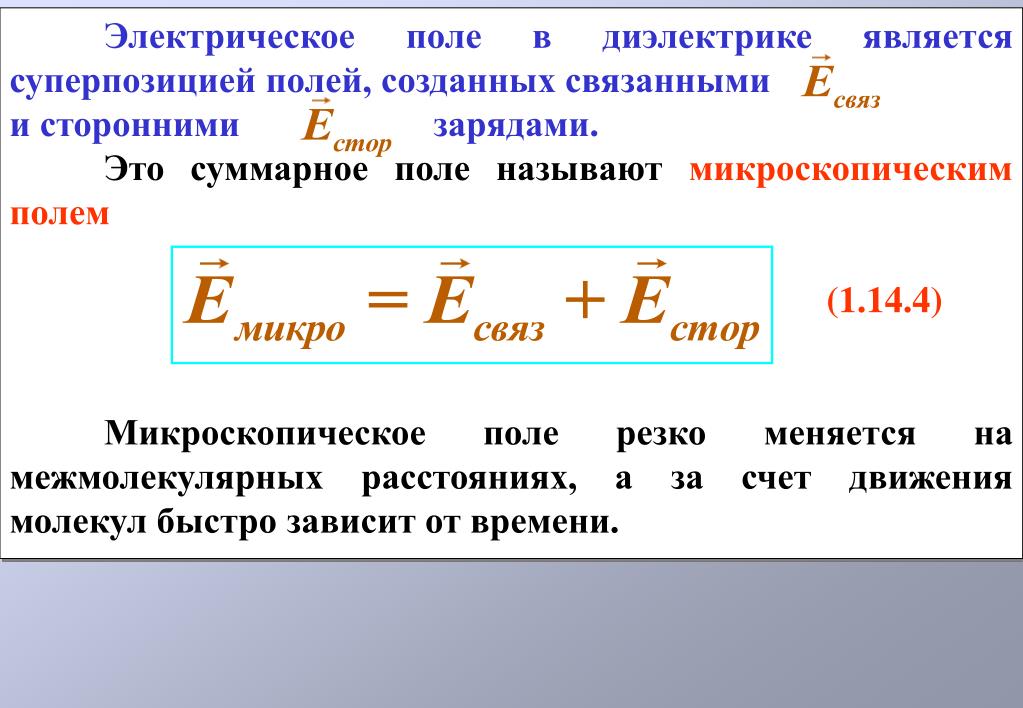
Величины
к нулю
и
исчезают, как
и интеграл по S2 стремится
Если в области V2 нет зарядов, то повторив преобразования,
проделанные выше получим
и
Поле точечного заряда обратно пропорционально квадрату расстояния
и направлено по радиусу от заряда q, если заряд положителен.
Так получили закон Кулона!
14
Точка r=0 особая. Полагать, что где-то в природе поле становится
бесконечным никаких оснований нет. Это лишь математика.
Если в каком-то объеме распределен электрический заряд с
плотностью
, то потенциал и электрическое поле можно
получить интегрированием:
Может возникнуть вопрос, можно ли использовать эти формулы
внутри объема с зарядом, поскольку там возникают особенности
при r=0.
Интегралы оказываются сходящимися. Если особую точку
окружить сферой, то при уменьшении ее радиуса знаменатель
стремится к нулю, как квадрат радиуса, а заряд, как его куб,
поэтому вклад в поле особой точки оказывается нулевым.

15
Спасибо за внимание
16
17
18
19
20
21
22
Электрическое поле.
13.1. Электростатическое поле. Потенциал поля . . . . . . . . . . . . . . . . . . . .
13.2. Уравнения Лапласа и Пуассона. Метод разделения переменных . .
13.3. Метод комплексного потенциала . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.4. Электростатическое поле проводов круглого сечения . . . . . . . . . .
13.5. Метод зеркальных изображений. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.6. Потенциальные коэффициенты, коэффициенты электростатической
индукции и частичные емкости в системе заряженных тел . . . . . .
13.7. Емкость линий электропередачи . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.8. Электрическое поле в диэлектрике. . . . . . . . . . . . . . . . . . . . . . . . . . .
13.9. Электрическое поле постоянных токов . . . . . . . . . . . . . . . . . . . . . .
13.10.Энергия и силы в электрическом поле.
 2}+\frac{\pi r_0}{2}\sqrt{\frac{A}{{\lambda }_0}}\right).$
2}+\frac{\pi r_0}{2}\sqrt{\frac{A}{{\lambda }_0}}\right).$Постоянный электрический ток. Направление тока, формула
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: постоянный электрический ток, сила тока, напряжение.Электрический ток обеспечивает комфортом жизнь современного человека. Технологические достижения цивилизации — энергетика, транспорт, радио, телевидение, компьютеры, мобильная связь — основаны на использовании электрического тока.
Электрический ток — это направленное движение заряженных частиц, при котором происходит перенос заряда из одних областей пространства в другие.
Электрический ток может возникать в самых различных средах: твёрдых телах, жидкостях, газах. Порой и среды никакой не нужно — ток может существовать даже в вакууме! Мы поговорим об этом в своё время, а пока приведём лишь некоторые примеры.
• Замкнём полюса батарейки металлическим проводом. Свободные электроны провода начнут направленное движение от «минуса» батарейки к «плюсу».
Это — пример тока в металлах.
• Бросим в стакан воды щепотку поваренной соли . Молекулы соли диссоциируют на ионы, так что в растворе появятся свободные заряды: положительные ионы и отрицательные ионы . Теперь засунем в воду два электрода, соединённые с полюсами батарейки. Ионы начнут направленное движение к отрицательному электроду, а ионы — к положительному.
Это — пример прохождения тока через раствор электролита.
• Грозовые тучи создают столь мощные электрические поля, что оказывается возможным пробой воздушного промежутка длиной в несколько километров. В результате сквозь воздух проходит гигантский разряд — молния.
Это — пример электрического тока в газе.
Во всех трёх рассмотренных примерах электрический ток обусловлен движением заряженных частиц внутри тела и называется током проводимости.
• Вот несколько иной пример. Будем перемещать в пространстве заряженное тело. Такая ситуация согласуется с определением тока! Направленное движение зарядов — есть, перенос заряда в пространстве — присутствует. Ток, созданный движением макроскопического заряженного тела, называется конвекционным.
Будем перемещать в пространстве заряженное тело. Такая ситуация согласуется с определением тока! Направленное движение зарядов — есть, перенос заряда в пространстве — присутствует. Ток, созданный движением макроскопического заряженного тела, называется конвекционным.
Заметим, что не всякое движение заряженных частиц образует ток. Например, хаотическое тепловое движение зарядов проводника — не направленное (оно совершается в каких угодно направлениях), и потому током не является (при возникновении тока свободные заряды продолжают совершать тепловое движение! Просто в этом случае к хаотическим перемещениям заряженных частиц добавляется их упорядоченный дрейф в определённом
направлении).
Не будет током и поступательное движение электрически нейтрального тела: хотя заряженные частицы в его атомах и совершают направленное движение, не происходит переноса заряда из одних участков пространства в другие.
Направление электрического тока
Направление движения заряженных частиц, образующих ток, зависит от знака их заряда. Положительно заряженные частицы будут двигаться от «плюса» к «минусу», а отрицательно заряженные — наоборот, от «минуса» к «плюсу». В электролитах и газах, например, присутствуют как положительные, так и отрицательные свободные заряды, и ток создаётся их встречным движением в обоих направлениях. Какое же из этих направлений принять за направление электрического тока?
Положительно заряженные частицы будут двигаться от «плюса» к «минусу», а отрицательно заряженные — наоборот, от «минуса» к «плюсу». В электролитах и газах, например, присутствуют как положительные, так и отрицательные свободные заряды, и ток создаётся их встречным движением в обоих направлениях. Какое же из этих направлений принять за направление электрического тока?
Направлением тока принято считать направление движения положительных зарядов.
Попросту говоря, по соглашению ток течёт от «плюса» к «минусу» (рис. 1; положительная клемма источника тока изображена длинной чертой, отрицательная клемма — короткой).
Рис. 1. Направление тока
Данное соглашение вступает в некоторое противоречие с наиболее распространённым случаем металлических проводников. В металле носителями заряда являются свободные электроны, и двигаются они от «минуса» к «плюсу». Но в соответствии с соглашением мы вынуждены считать, что направление тока в металлическом проводнике противоположно движению свободных электронов. Это, конечно, не очень удобно.
Это, конечно, не очень удобно.
Тут, однако, ничего не поделаешь — придётся принять эту ситуацию как данность. Так уж исторически сложилось. Выбор направления тока был предложен Ампером (договорённость о направлении тока понадобилась Амперу для того, чтобы дать чёткое правило определения направления силы, действующей на проводник с током в магнитном поле. Сегодня эту силу мы называем силой Ампера, направление которой определяется по правилу левой руки) в первой половине XIX века, за 70 лет до открытия электрона. К этому выбору все привыкли, и когда в 1916 году выяснилось, что ток в металлах вызван движением свободных электронов, ничего менять уже не стали.
Действия электрического тока
Как мы можем определить, протекает электрический ток или нет? О возникновении электрического тока можно судить по следующим его проявлениям.
1. Тепловое действие тока. Электрический ток вызывает нагревание вещества, в котором он протекает. Именно так нагреваются спирали нагревательных приборов и ламп накаливания. Именно поэтому мы видим молнию. В основе действия тепловых амперметров лежит тепловое расширение проводника с током, приводящее к перемещению стрелки прибора.
Именно поэтому мы видим молнию. В основе действия тепловых амперметров лежит тепловое расширение проводника с током, приводящее к перемещению стрелки прибора.
2. Магнитное действие тока. Электрический ток создаёт магнитное поле: стрелка компаса, расположенная рядом с проводом, при включении тока поворачивается перпендикулярно проводу. Магнитное поле тока можно многократно усилить, если обмотать провод вокруг железного стержня — получится электромагнит. На этом принципе основано действие амперметров магнитоэлектрической системы: электромагнит поворачивается в поле постоянного магнита, в результате чего стрелка прибора перемещается по шкале.
3. Химическое действие тока. При прохождении тока через электролиты можно наблюдать изменение химического состава вещества. Так, в растворе положительные ионы двигаются к отрицательному электроду, и этот электрод покрывается медью.
Электрический ток называется постоянным, если за равные промежутки времени через поперечное сечение проводника проходит одинаковый заряд.
Постоянный ток наиболее прост для изучения. С него мы и начинаем.
Сила и плотность тока
Количественной характеристикой электрического тока является сила тока. В случае постоянного тока абсолютная величина силы тока есть отношение абсолютной величины заряда , прошедшего через поперечное сечение проводника за время , к этому самому времени:
(1)
Измеряется сила тока в амперах (A). При силе тока в А через поперечное сечение проводника за с проходит заряд в Кл.
Подчеркнём, что формула (1) определяет абсолютную величину, или модуль силы тока.
Сила тока может иметь ещё и знак! Этот знак не связан со знаком зарядов, образующих ток, и выбирается из иных соображений. А именно, в ряде ситуаций (например, если заранее не ясно, куда потечёт ток) удобно зафиксировать некоторое направление обхода цепи (скажем, против часовой стрелки) и считать силу тока положительной, если направление тока совпадает с направлением обхода, и отрицательной, если ток течёт против направления обхода (сравните с тригонометрическим кругом: углы считаются положительными, если отсчитываются против часовой стрелки, и отрицательными, если по часовой стрелке).
В случае постоянного тока сила тока есть величина постоянная. Она показывает, какой заряд проходит через поперечное сечение проводника за с.
Часто бывает удобно не связываться с площадью поперечного сечения и ввести величину плотности тока:
(2)
где — сила тока, — площадь поперечного сечения проводника (разумеется, это сечение перпендикулярно направлению тока). С учётом формулы (1) имеем также:
Плотность тока показывает, какой заряд проходит за единицу времени через единицу площади поперечного сечения проводника. Согласно формуле (2), плотность тока измеряется в А/м2.
Скорость направленного движения зарядов
Когда мы включаем в комнате свет, нам кажется, что лампочка загорается мгновенно. Скорость распространения тока по проводам очень велика: она близка к км/с (скорости света в вакууме). Если бы лампочка находилась на Луне, она зажглась бы через секунду с небольшим.
Однако не следует думать, что с такой грандиозной скоростью двигаются свободные заряды, образующие ток.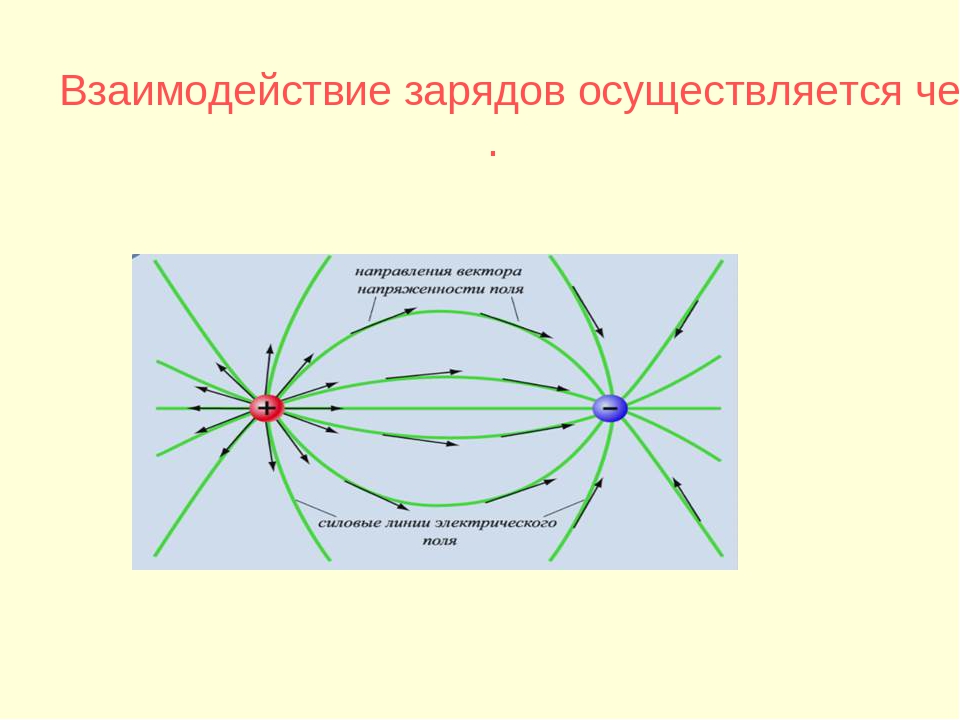 Оказывается, их скорость составляет всего-навсего доли миллиметра в секунду.
Оказывается, их скорость составляет всего-навсего доли миллиметра в секунду.
Почему же ток распространяется по проводам так быстро? Дело в том, что свободные заряды взаимодействуют друг с другом и, находясь под действием электрического поля источника тока, при замыкании цепи приходят в движение почти одновременно вдоль всего проводника. Скорость распространения тока есть скорость передачи электрического взаимодействия между свободными зарядами, и она близка к скорости света в вакууме. Скорость же, с которой сами заряды перемещаются внутри проводника, может быть на много порядков меньше.
Итак, подчеркнём ещё раз, что мы различаем две скорости.
1. Скорость распространения тока. Это — скорость передачи электрического сигнала по цепи. Близка к км/с.
2. Скорость направленного движения свободных зарядов. Это — средняя скорость перемещения зарядов, образующих ток. Называется ещё скоростью дрейфа.
Мы сейчас выведем формулу, выражающую силу тока через скорость направленного движения зарядов проводника.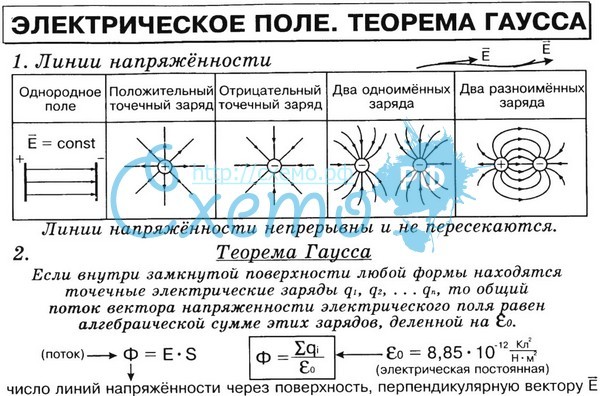
Пусть проводник имеет площадь поперечного сечения (рис. 2). Свободные заряды проводника будем считать положительными; величину свободного заряда обозначим (в наиболее важном для практики случая металлического проводника это есть заряд электрона). Концентрация свободных зарядов (т. е. их число в единице объёма) равна .
Рис. 2. К выводу формулы
Какой заряд пройдёт через поперечное сечение нашего проводника за время ?
С одной стороны, разумеется,
(3)
С другой стороны, сечение пересекут все те свободные заряды, которые спустя время окажутся внутри цилиндра с высотой . Их число равно:
Следовательно, их общий заряд будет равен:
(4)
Приравнивая правые части формул (3) и (4) и сокращая на , получим:
(5)
Соответственно, плотность тока оказывается равна:
Давайте в качестве примера посчитаем, какова скорость движения свободных электронов в медном проводе при силе тока A.
Заряд электрона известен: Кл.
Чему равна концентрация свободных электронов? Она совпадает с концентрацией атомов меди, поскольку от каждого атома отщепляется по одному валентному электрону. Ну а концентрацию атомов мы находить умеем:
м
Положим мм . Из формулы (5) получим:
м/с.
Это порядка одной десятой миллиметра в секунду.
Стационарное электрическое поле
Мы всё время говорим о направленном движении зарядов, но ещё не касались вопроса о том, почему свободные заряды совершают такое движение. Почему, собственно, возникает электрический ток?
Для упорядоченного перемещения зарядов внутри проводника необходима сила, действующая на заряды в определённом направлении. Откуда берётся эта сила? Со стороны электрического поля!
Чтобы в проводнике протекал постоянный ток, внутри проводника должно существовать стационарное (то есть — постоянное, не зависящее от времени) электрическое поле. Иными словами, между концами проводника нужно поддерживать постоянную разность потенциалов.
Иными словами, между концами проводника нужно поддерживать постоянную разность потенциалов.
Стационарное электрическое поле должно создаваться зарядами проводников, входящих в электрическую цепь. Однако заряженные проводники сами по себе не смогут обеспечить протекание постоянного тока.
Рассмотрим, к примеру, два проводящих шара, заряженных разноимённо. Соединим их проводом. Между концами провода возникнет разность потенциалов, а внутри провода — электрическое поле. По проводу потечёт ток. Но по мере прохождения тока разность потенциалов между шарами будет уменьшаться, вслед за ней станет убывать и напряжённость поля в проводе. В конце концов потенциалы шаров станут равны друг другу, поле в проводе обратится в нуль, и ток исчезнет. Мы оказались в электростатике: шары плюс провод образуют единый проводник, в каждой точке которого потенциал принимает одно и то же значение; напряжённость
поля внутри проводника равна нулю, никакого тока нет.
То, что электростатическое поле само по себе не годится на роль стационарного поля, создающего ток, ясно и из более общих соображений. Ведь электростатическое поле потенциально, его работа при перемещении заряда по замкнутому пути равна нулю. Следовательно, оно не может вызывать циркулирование зарядов по замкнутой электрической цепи — для этого требуется совершать ненулевую работу.
Ведь электростатическое поле потенциально, его работа при перемещении заряда по замкнутому пути равна нулю. Следовательно, оно не может вызывать циркулирование зарядов по замкнутой электрической цепи — для этого требуется совершать ненулевую работу.
Кто же будет совершать эту ненулевую работу? Кто будет поддерживать в цепи разность потенциалов и обеспечивать стационарное электрическое поле, создающее ток в проводниках?
Ответ — источник тока, важнейший элемент электрической цепи.
Чтобы в проводнике протекал постоянный ток, концы проводника должны быть присоединены к клеммам источника тока (батарейки, аккумулятора и т. д.).
Клеммы источника — это заряженные проводники. Если цепь замкнута, то заряды с клемм перемещаются по цепи — как в рассмотренном выше примере с шарами. Но теперь разность потенциалов между клеммами не уменьшается: источник тока непрерывно восполняет заряды на клеммах, поддерживая разность потенциалов между концами цепи на неизменном уровне.
В этом и состоит предназначение источника постоянного тока. Внутри него протекают процессы неэлектрического (чаще всего — химического) происхождения, которые обеспечивают непрерывное разделение зарядов. Эти заряды поставляются на клеммы источника в необходимом количестве.
Количественную характеристику неэлектрических процессов разделения зарядов внутри источника — так называемую ЭДС — мы изучим позже, в соответствующем листке.
А сейчас вернёмся к стационарному электрическому полю. Каким же образом оно возникает в проводниках цепи при наличии источника тока?
Заряженные клеммы источника создают на концах проводника электрическое поле. Свободные заряды проводника, находящиеся вблизи клемм, приходят в движение и действуют своим электрическим полем на соседние заряды. Со скоростью, близкой к скорости света, это взаимодействие передаётся вдоль всей цепи, и в цепи устанавливается постоянный электрический ток. Стабилизируется и электрическое поле, создаваемое движущимися зарядами.
Стационарное электрическое поле — это поле свободных зарядов проводника, совершающих направленное движение.
Стационарное электрическое поле не меняется со временем потому, что при постоянном токе не меняется картина распределения зарядов в проводнике: на место заряда, покинувшего данный участок проводника, в следующий момент времени поступает точно такой же заряд. По этой причине стационарное поле во многом (но не во всём) аналогично полю электростатическому.
А именно, справедливы следующие два утверждения, которые понадобятся нам в дальнейшем (их доказательство даётся в вузовском курсе физики).
1. Как и электростатическое поле, стационарное электрическое поле потенциально. Это позволяет говорить о разности потенциалов (т. е. напряжении) на любом участке цепи (именно эту разность потенциалов мы измеряем вольтметром).
Потенциальность, напомним, означает, что работа стационарного поля по перемещению заряда не зависит от формы траектории. Именно поэтому при параллельном соединении проводников напряжение на каждом из них одинаково: оно равно разности потенциалов стационарного поля между теми двумя точками, к которым подключены проводники.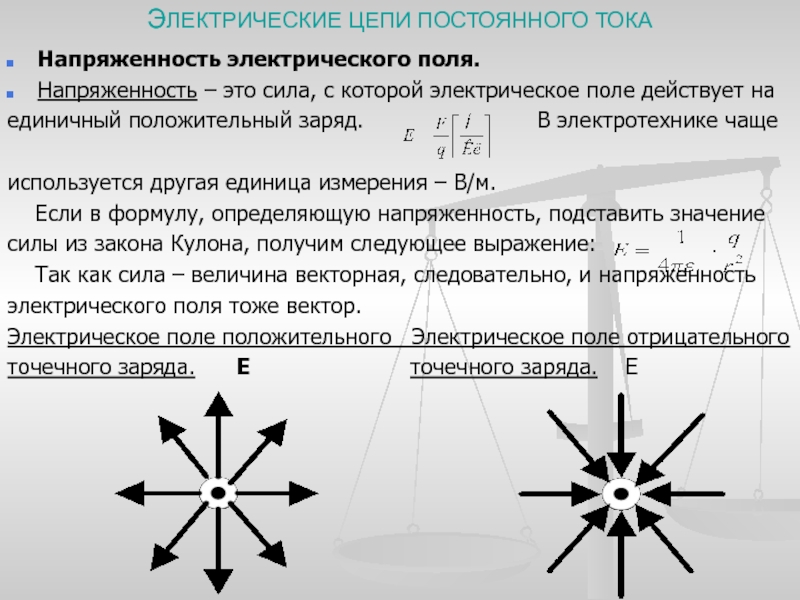
2. В отличие от электростатического поля, стационарное поле движущихся зарядов проникает внутрь проводника (дело в том, что свободные заряды, участвуя в направленном движении, не успевают должным образом перестраиваться и принимать «электростатические» конфигурации).
Линии напряжённости стационарного поля внутри проводника параллельны его поверхности, как бы ни изгибался проводник. Поэтому, как и в однородном электростатическом поле, справедлива формула , где — напряжение на концах проводника, — напряжённость стационарного поля в проводнике, — длина проводника.
Электрическое поле — Energy Education
Электрическое поле — один из фундаментальных результатов электромагнетизма, созданный статическим (стационарным) зарядом или динамическим (изменяющимся во времени) магнитным полем. Электрическое поле определяется как сила на единицу заряда, определяемая уравнением:
- [math] E = \ frac {F} {q} [/ math],
где [math] q [/ math] — это заряд в кулонах (Кл).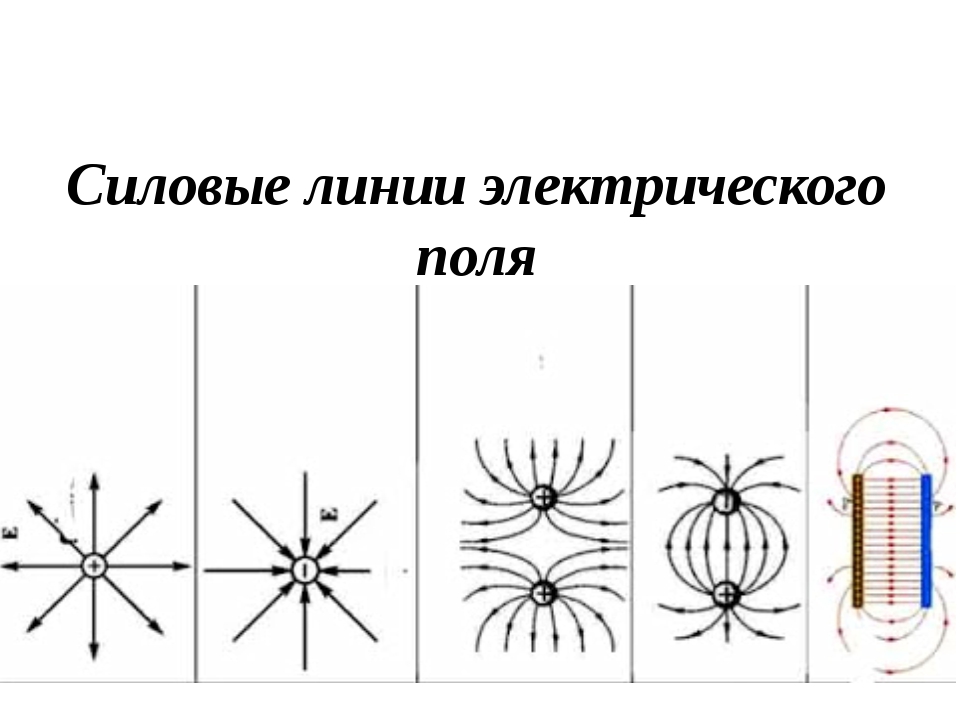 Таким образом, когда заряд находится в присутствии электрического поля, он испытывает силу, заставляющую заряженную частицу перемещаться, что можно получить, переписав приведенное выше уравнение так, чтобы:
Таким образом, когда заряд находится в присутствии электрического поля, он испытывает силу, заставляющую заряженную частицу перемещаться, что можно получить, переписав приведенное выше уравнение так, чтобы:
- [математика] \ vec {F} = q \ vec {E} [/ математика].2 [/ math] в простых случаях. Для сложных распределений заряда электрическое поле может иметь несколько различных соотношений, см. Галерею рисунков ниже (более полное обсуждение см. В разделе «Гиперфизика».
Однако есть одно существенное отличие: гравитационные поля ограничены притяжением (притягиванием объектов), тогда как электрические поля могут быть либо притягивающими, либо отталкивающими, в зависимости от заряда объекта в поле. По определению, положительный заряд в приведенном выше уравнении силы будет испытывать силу отталкивания (он будет двигаться от источника поля), а отрицательный заряд будет ощущать силу притяжения.
Из-за этой притягивающей / отталкивающей природы электрических полей существует обозначение для их рисования.
 Линии электрического поля положительного стационарного заряда направлены радиально от него (перпендикулярные линии от его поверхности во всех направлениях), а линии отрицательного стационарного заряда направлены радиально к нему.
Линии электрического поля положительного стационарного заряда направлены радиально от него (перпендикулярные линии от его поверхности во всех направлениях), а линии отрицательного стационарного заряда направлены радиально к нему.- Линии электрического поля
Рис. 1. Отрицательный заряд с полевыми линиями, направленными в сторону . [2]
Рисунок 2.Показано, что взаимодействие положительных и отрицательных силовых линий электрического поля является привлекательным. [3]
Рис. 3. Взаимодействие двух положительных силовых линий электрического поля, показанное как отталкивающее. [4]
Для дальнейшего чтения
Список литературы
- ↑ Р. Чабай и Б. Шервуд, «Электрическое поле диполя», в Matter & Interactions, 3-е изд., Хобокен, штат Нью-Джерси: Wiley, 2011, глава 14, раздел 6, стр. 556-560
- ↑ [GFDL (http: // www.gnu.
 org/copyleft/fdl.html) или CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)] через Wikimedia Commons
org/copyleft/fdl.html) или CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)] через Wikimedia Commons - ↑ «Дипольные электрические многолинии VFPt» Лицензия CC BY-SA 3.0 через Wikimedia Commons — http://commons.wikimedia.org/wiki/File:VFPt_dipole_electric_manylines.svg#mediaviewer/File:VFPt_dipole_electric_manylines.svg
- ↑ «Плата за VFPt плюс плюс» Лицензия CC BY-SA 3.0 через Wikimedia Commons — http://commons.wikimedia.org/wiki/File:VFPt_charges_plus_plus.svg#mediaviewer/File:VFPt_charges_plus_plus.svg
В чем разница между электрическим и магнитным полем?
Виктор де Шванберг / Библиотека научных фотографий
В чем, помимо происхождения, разница между магнитным полем и электрическим?
Адам Грей , Манчестер, Великобритания
Электрическое и магнитное поля являются составляющими электромагнитного поля.
Эти два компонента занимают разные плоскости относительно причины электромагнитного поля, например движущегося электрического заряда.
 Это единственное различие, а также то, является ли заряд, генерирующий поле, неподвижным или движущимся.
Это единственное различие, а также то, является ли заряд, генерирующий поле, неподвижным или движущимся.Брайан Поллард , Лонсестон, Корнуолл, Великобритания
Между электрическим и магнитным полями существует взаимосвязь, в которой изменение одного приводит к изменению другого. Электромагнитная волна состоит из полей обоих типов, которые колеблются вперед и назад.
Связь между электрическим и магнитным полями — это то, что позволяет формировать электромагнитные волны, включая свет и тепло.Эти отношения имеют фундаментальное значение для работы Вселенной в ее нынешнем виде.
Помимо этих аспектов электромагнетизма, электрическое поле образуется между положительным и отрицательным потенциалами напряжения. Пример магнитного поля, с которым знаком большинство людей, создается снаружи между северным и южным магнитными полюсами стержневого магнита и продолжается внутри магнита между полюсами, образуя петлю.
Все магнитные поля образуют эти петли — свойство, обнаруженное английским ученым 19 века Майклом Фарадеем.Он применил петли в предметах повседневного обихода, таких как электрические трансформаторы и двигатели.
Джейсон Дикер , Лонсестон, Тасмания, Австралия
И электрическое, и магнитное поля являются следствием притяжения и отталкивания электрических зарядов. Однако магнитный эффект вызывается движущимися электрическими зарядами, а электрическое поле — неподвижными зарядами.
Например, магнитное поле, наблюдаемое в простом стальном стержневом магните, является результатом орбитальных и вращающихся зарядов субатомных частиц.
Однако движение относительное, поэтому, например, человек, движущийся с линией зарядов, не будет воспринимать магнитное поле, которое было бы у неподвижного человека рядом с движущимися зарядами.
Этот эффект полностью объясняется специальной теорией относительности Эйнштейна, которая появилась в 1905 году, почти через полвека после того, как шотландский физик Джеймс Клерк Максвелл объединил электричество и магнетизм в единую теорию электромагнетизма в 1860-х годах.
Хотя многие люди говорят, что релятивистские эффекты Эйнштейна можно увидеть только при высоких скоростях, таких как движение объектов в пространстве, электроны в проводе, которые движутся как ток, создавая магнитную силу, перемещаются со скоростью около миллиметра в секунду, даже если электромагнитная волна в электрическом токе движется намного быстрее.
Чтобы ответить на этот вопрос или задать новый, напишите на [email protected].
Вопросы должны быть научными вопросами о повседневных явлениях, и как вопросы, так и ответы должны быть краткими. Мы оставляем за собой право редактировать элементы для ясности и стиля. Пожалуйста, укажите почтовый адрес, номер телефона в дневное время и адрес электронной почты.
New Scientist Ltd сохраняет полный редакторский контроль над опубликованным контентом и оставляет за собой все права на повторное использование материалов вопросов и ответов, представленных читателями, на любом носителе и в любом формате.
Вы также можете отправить ответы по почте по адресу: The Last Word, New Scientist, 25 Bedford Street, London WC2E 9ES.
Применяются правила и условия.
Постоянный электрический заряд на теле производит физику A класса 11 JEE_Main
Подсказка: Катушка с током также имеет собственное магнитное поле вокруг себя.Магнитное поле создается только тогда, когда заряд находится в движении. Это похоже на протекание тока в материале. Любой проводник, в котором протекает ток, сопровождается электрическим полем, а также магнитным полем вокруг него. Это происходит только тогда, когда заряд движется или находится в движении.Полное пошаговое решение:
Стационарный электрический заряд — это не что иное, как статическое электричество.
Мы знаем, что магнитное поле присутствует везде, где есть ток. Это говорит нам о том, что когда заряд течет, вместе с ним присутствует магнитное поле.
В случае неподвижного заряда в заряде нет движения, следовательно, не создается магнитное поле. Итак, создается только электрическое поле.Следовательно, вариант (B) только электрическое поле является правильным ответом.
Дополнительная информация Это концепция, которая используется в индукторе. Индукторы представляют собой проводники в форме катушек, по которым протекает электричество. Катушки усиливают магнитное поле. Чем больше количество катушек, тем больше магнитное поле.Опять же, для этого требуется ток. Стационарный заряд не создает магнитного поля.
Примечание: если стационарный заряд действительно создавал магнитное поле, то каждый раз, когда возникает молния, магнитное поле должно возникать вместе с ней, потому что молния возникает из-за статического электричества. Но в реальной жизни этого не происходит, потому что стационарный заряд не создает магнитного поля.
Вы в одном шаге от ответа!
Подпишитесь бесплатно!
Регистрируясь, вы также получаете БЕСПЛАТНЫЙ доступ к тысячам решенных вопросов, викторин
и загружаемым PDF-файлам!Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследовать
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О Массачусетском технологическом институте
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О Массачусетском технологическом институте
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатовПредложения или отзывы?
Электростатика
Работа — это изменение потенциальной энергии: U B — U A = q ′ Ed .
В общем, разность электростатических потенциалов , иногда называемая разностью электрических потенциалов , определяется как изменение энергии на единицу положительного заряда, или В B — В A = ( U B — U A ) / q ′. Для определенных конфигураций электрического поля может потребоваться интегральное определение электростатического потенциала:
, где испытательный заряд движется по интегральной линии от точки A к точке B по пути s в электрическом поле ( E ).
Для особого случая параллельных пластин:
, где В — разность потенциалов между пластинами, измеренная в вольтах (В):
Электрический потенциал из-за точечного заряда (q) на расстоянии (r) от точечного заряда равен
Следующая задача иллюстрирует расчеты электрического поля и потенциала точечных зарядов.
Пример 3: Для двух зарядов +3 Q и — Q , на расстоянии X друг от друга, найдите следующее: (1) В какой точке (точках) на линии электрическое поле равно нулю? (2) В какой точке (точках) электрический потенциал равен нулю? (См. Рисунок 11.)
Рисунок 11
Расположение двух точечных зарядов для примера.
Первая задача — найти области, где электрическое поле равно нулю. Электрическое поле является вектором, и его направление можно определить с помощью пробного заряда. Рисунок разделен на три области. Между противоположными зарядами направление силы на испытательный заряд будет одинаковым для каждого заряда; следовательно, в области II невозможно иметь нулевое электрическое поле.Несмотря на то, что силы, действующие на пробный заряд от двух зарядов в области I, имеют противоположные направления, сила и, следовательно, электрическое поле никогда не могут быть нулевыми в этой области, потому что пробный заряд всегда ближе к наибольшему заданному заряду. Следовательно, область III — единственное место, где E может быть равно нулю. Выберите произвольную точку (r) справа от — Q и установите два электрических поля равными. Поскольку поля расположены в противоположных направлениях, векторная сумма в этой точке будет равна нулю.
Если дано X , найти r .
Потенциал не является вектором, поэтому потенциал равен нулю, если выполняется следующее уравнение:
, где r м — расстояние от контрольной точки до +3 Q и r 2 — расстояние до — Q .
Этот пример иллюстрирует разницу в методах анализа при нахождении векторной величины ( E ) и скалярной величины (V). Обратите внимание, что если бы заряды были либо положительными, либо отрицательными, можно было бы найти точку с нулевым электрическим полем между зарядами, но потенциал никогда не был бы равен нулю.
Электрическая потенциальная энергия пары точечных зарядов, разделенных расстоянием r , равно
Эквипотенциальные поверхности — это поверхности, на которых не требуется работать для перемещения заряда из одной точки в другую. Эквипотенциальные поверхности всегда перпендикулярны силовым линиям электрического поля. Эквипотенциальные линии — это двумерные представления пересечения поверхности с плоскостью диаграммы. На рисунке эквипотенциальные линии показаны для (а) однородного поля, (б) точечного заряда и (в) двух противоположных зарядов.
% PDF-1.5 % 1 0 объект > эндобдж 4 0 obj > эндобдж 2 0 obj > поток 2013-01-09T07: 55: 08 + 01: 002013-01-04T10: 47: 25 + 01: 002013-01-09T07: 55: 08 + 01: 00uuid: 1859cafc-0395-4a7e-880b-3b7bcf4e28d6uuid: 2072d25a- a40f-4158-9e32-d2b728b41a08application / pdf Adobe Acrobat 9.2 Подключаемый модуль захвата бумаги конечный поток эндобдж 3 0 obj > эндобдж 5 0 obj > >> / Ресурсы> / ProcSet [/ PDF / Text / ImageB] / XObject> >> / Повернуть 0 / Тип / Страница / Аннотации [34 0 R] >> эндобдж 6 0 obj > >> / Ресурсы> / ProcSet [/ PDF / Text / ImageB] / XObject> >> / Повернуть 0 / Тип / Страница >> эндобдж 7 0 объект > >> / Ресурсы> / ProcSet [/ PDF / Text / ImageB] / XObject> >> / Повернуть 0 / Тип / Страница >> эндобдж 8 0 объект > >> / Ресурсы> / ProcSet [/ PDF / Text / ImageB] / XObject> >> / Повернуть 0 / Тип / Страница >> эндобдж 9 0 объект > >> / Ресурсы> / ProcSet [/ PDF / Text / ImageB] / XObject> >> / Повернуть 0 / Тип / Страница >> эндобдж 10 0 obj > >> / Ресурсы> / ProcSet [/ PDF / Text / ImageB] / XObject> >> / Повернуть 0 / Тип / Страница >> эндобдж 11 0 объект > >> / Ресурсы> / ProcSet [/ PDF / Text / ImageB] / XObject> >> / Повернуть 0 / Тип / Страница >> эндобдж 12 0 объект > >> / Ресурсы> / ProcSet [/ PDF / Text / ImageB] / XObject> >> / Повернуть 0 / Тип / Страница >> эндобдж 13 0 объект > поток HT [@ ~ ϯ-9gnXb] bkk +! 络 | KARJ «e> _ ‘jYM> &} ~ [& 8bns;: @ 4 [‘ 7E3Wj} MJ & ?, {v {˷YrqT! G * zS (: D #..% PV: T2GQgRgRA ~ BW ܍ G.5qVH} U _] & MdpP?Q~839o.-Br@g*zh2] m 庐 pϭVF2s8Q ~} T ~ zL / «HNSuQxM1 ~ f ] 66 \
Электростатика — Uni Study Guides
Это тема из Высшей физики 1B
Введение
Электростатика — это исследование стационарных электрических зарядов и полей (в отличие от движущихся зарядов и токов).
Свойства электрических зарядов
Электромагнитная сила между заряженными частицами — фундаментальное явление в природе, и заряды, которые создают эти силы, обладают следующими свойствами:
- Обозначение заряда — q или Q
- Начисления бывают двух видов: положительные и отрицательные.
- Единицей электрического заряда является кулон, обозначаемый символом C
- Электрический заряд квантуется в «пакеты» энергии, равные основной единице заряда, обозначаемые символом «e», где e = 1.-19 C следующим образом:
- Q = ne
- Где n — целое положительное число (натуральное число)
- Заряд квантуется, потому что существуют частицы, которые несут наименьшую величину заряда (основная единица заряда), так что все количества заряда должны быть кратны этой единице.
- Эти частицы представляют собой протоны и электроны, которые несут заряд «+ e» и «-e» соответственно.
- Отношение протонов к электронам, присутствующим в данной точке материала, определяет, имеет ли эта точка положительный, отрицательный или нейтральный заряд.
Проводники и изоляторы
- Проводники — это материалы, в которых некоторые электроны являются «свободными электронами», что означает, что некоторые электроны не связаны с атомами, но могут относительно свободно перемещаться через материал.Когда проводник заряжается в одной области, заряд распространяется по всему проводнику.
- Изоляторы, с другой стороны, обладают противоположными свойствами, в результате чего электроны с большим трудом движутся через материал, так что, если одна область заряжена, заряд остается изолированным от этой области. Это означает, что поверхность изолятора может быть заряжена, и его внутренняя часть может оставаться нетронутой.
Закон Кулона
Определение
Этот закон был экспериментально обнаружен (не выведен математически) Шарлем-Огюстеном де Кулоном путем измерения величин электрических сил между заряженными сферами в контролируемой среде.В нем говорится, что сила была пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между центрами масс сфер, как показано ниже:
- F e = k e q 1 q 2 / r 2
Где F e представляет силу в Ньютонах (Н)
- k e представляет собой постоянную Кулона, равную 8.9875 x 10 9 в квадрате Ньютон-метров на квадрат кулон (Нм 2 C -2 )
- q 1 и q 2 представляют два заряда, участвующие в кулонах (C)
- r представляет собой расстояние между центрами масс двух заряженных частиц в метрах (м)
Обратите внимание на структуру этого уравнения, аналогичную закону тяготения Ньютона, описанному в Physics 1A. Две массы заменяются двумя зарядами, и, конечно, постоянная другая.Это сходство может помочь в осмыслении и запоминании этой формулы
Дальность свободного пространства
Постоянная Кулонасвязана с другой полезной постоянной, ε o , известной как проницаемость свободного пространства, следующим уравнением:
- ε o = 1 / 4πk e
Где ε o = 8,8542 x 10 -12 C 2 N -1 м -2
Примечания к применению
Учитывая, что силы являются векторными величинами (в отличие от скалярных величин), при использовании уравнения необходимо учитывать направление:
- При аналогичных знаках зарядов произведение q 1 q 2 положительное, а сила положительная (отталкивающая)
- С противоположными знаками для зарядов произведение q 1 q 2 отрицательно, а сила отрицательна (притягивающая)
- Результирующая сила различных электрических сил равна векторной сумме этих сил.
- Электрические силы подчиняются Третьему закону Ньютона, так что F 12 = — F 21
Электрические поля
Определение
Считается, что в области пространства вокруг заряженного объекта существует электрическое поле, известное как источник заряда.Когда другой заряженный объект, известный как тестовый заряд, входит в поле, он испытывает силу. Таким образом, электрическое поле определяется как электрическая сила, действующая на пробный заряд на единицу заряда:
- E = F e / q o → F e = Eq o
Где E представляет электрическое поле (NC -1 )
- q o представляет собой испытательный заряд
Вектор электрического поля в точке пространства определяется как электрическая сила, действующая на положительный тестовый заряд — тот факт, что тестовый заряд считается положительным, будет важен, когда дело доходит до рисования и интерпретации силовых линий при экзамене и домашние задания
Плотность заряда
Заряд может быть распределен в одном, двух или трех измерениях — по линии, по площади или по всему объему соответственно.
- Если общий заряд «q» равномерно распределен по линии длиной «l», то плотность заряда «λ» определяется следующим образом:
- λ = q / l
- Если общий заряд «q» равномерно распределен по поверхности площади «A», то плотность заряда «σ» определяется следующим образом:
- σ = q / A
- Если общий заряд «q» равномерно распределен по объекту объемом «V», то плотность заряда «ρ» определяется следующим образом:
- ρ = q / V
Получение электрического поля однородно заряженного объекта
- Напоминая, что заряд объекта является результатом избытка протонов или нейтронов по всему объекту или на его поверхности, электрическое поле объекта на самом деле является результирующей векторной суммой электрических полей его субатомных частиц.
- Однако непрактично рассматривать электрические поля в таком микроскопическом масштабе, поэтому для решения проблем, связанных с заряженными объектами, в более разумном масштабе, мы суммируем электрические поля из-за малых зарядов, Δq
- Этот подход действителен только для объектов с однородным зарядом, как в следующем примере с достаточно тонким стержнем, который считается линией в одном измерении:
- Заряд Δq в точке стержня на рисунке выше оказывает на испытательный заряд q o силу следующим образом:
- F e = k e Δqq o / r 2 (Закон Кулона)
- Подстановка в определение электрического поля дает:
- E = F e / q o
- = k e Δq / r 2
- Суммирование электрических полей, вызванных этими небольшими зарядами, Δq может дать электрическое поле в целом стержень:
- E ≈ k e Σ i Δq i / r 2
- Принятие предела, поскольку размер этих зарядов стремится к нулю, дает точное решение:
- Следующим шагом в вычислении электрического поля на расстоянии «b» от стержня вдоль его оси является поиск выражения для dq через расстояние.Это делается с использованием уравнений для плотности заряда, в данном случае для заряда, равномерно распределенного по линии:
- λ = q / л
- q = λL
- dq = λdL (помните, что λ — постоянная величина, а расстояние (x или L) — переменная)
- Если кто-то хочет проверить достоверность этого результата, ему нужно только рассмотреть, что произойдет, если длина стержня L будет все короче и короче, пока не приблизится к нулю.Тогда полученный результат, приведенный выше, даст уравнение для электрического поля вокруг точечной частицы, которым стержень стал бы
Поле в заряженном объекте
Для замкнутой поверхности с однородной плотностью заряда по всему объему электрическое поле в центре равно нулю, увеличиваясь линейно, пока не достигнет максимума на поверхности объекта, после чего затухает по закону обратных квадратов. Причина, по которой электрическое поле равно нулю, заключается в том, что силы, возникающие от окружающих зарядов, компенсируют друг друга, так что результирующая сила равна нулю.По мере того как пробный заряд перемещается от центра к поверхности, с одной стороны заряда больше, чем с другой, и поэтому возникает чистое электрическое поле. Это выражено на рисунке ниже:
Линии электрического поля
Линии электрического поля — это графический инструмент, используемый для обозначения относительного направления и силы электрического поля в данной точке.
- Тренд линии выражает направление
- Концентрация линий в заданной области выражает силу
- Никакие две силовые линии электрического поля не могут пересекать друг друга
Ниже приведены некоторые иллюстративные и общие примеры линий поля:
.
- [математика] \ vec {F} = q \ vec {E} [/ математика].2 [/ math] в простых случаях. Для сложных распределений заряда электрическое поле может иметь несколько различных соотношений, см. Галерею рисунков ниже (более полное обсуждение см. В разделе «Гиперфизика».


 Линии электрического поля положительного стационарного заряда направлены радиально от него (перпендикулярные линии от его поверхности во всех направлениях), а линии отрицательного стационарного заряда направлены радиально к нему.
Линии электрического поля положительного стационарного заряда направлены радиально от него (перпендикулярные линии от его поверхности во всех направлениях), а линии отрицательного стационарного заряда направлены радиально к нему.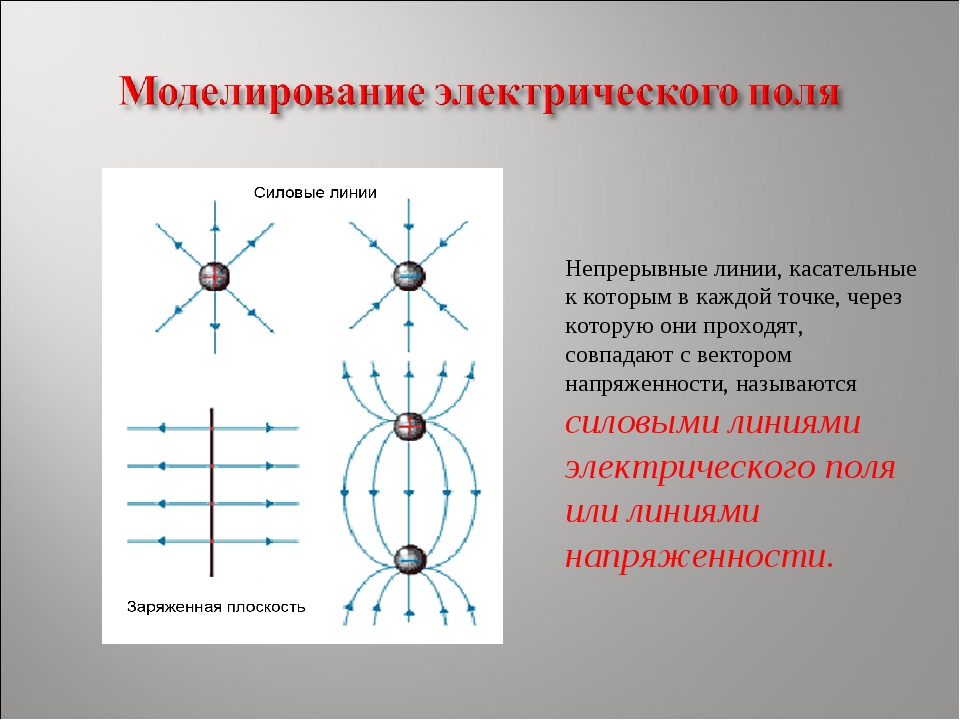 org/copyleft/fdl.html) или CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)] через Wikimedia Commons
org/copyleft/fdl.html) или CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0)] через Wikimedia Commons Это единственное различие, а также то, является ли заряд, генерирующий поле, неподвижным или движущимся.
Это единственное различие, а также то, является ли заряд, генерирующий поле, неподвижным или движущимся.