Исчисление средней из интервального ряда, относительных величин. Средняя гармоническая, порядок исчисления. Средняя геометрическая. Средняя квадратическая.
Пример: Требуется определить средний возраст студента заочной формы обучения по данным, заданным в следующей таблице:
Возраст студентов, лет (х) | Число студентов, чел (f) | среднее значение интервала (x’,xцентральн) | xi*fi |
1 | 2 | 3 | 4 |
до 20 | 65 | (18+20)/2=19 | 19*65=1235 |
20-22 | 125 | 21 | 2625 |
22-24 | 190 | 23 | 4370 |
24-26 | 80 | 25 | 2000 |
26 и старше | 40 | 27 | 1080 |
Итого: | 500 |
| 11310 |
Для вычисления средней в интервальных рядах сначала определяют среднее значение интервала как полу-сумму верхней и нижней границы, а затем рассчитывается средняя величина по формуле средне арифметическая взвешенная.
Выше дан пример с равными интервалами, причем 1-й и последний являются открытыми.

Ответ: средний возраст студента составляет 22,6 года или примерно 23 года.
Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Используется в тех случаях, когда статистическая информация не содержит частот по отдельным значениям признака, а представлена произведением значения признака на частоту. Средняя гармоническая как вид степенной средней выглядит следующим образом: 
В зависимости от формы представления исходных данных средняя гармоническая может быть рассчитана как простая и как взвешенная. Если исходные данные несгруппированны, то применяется средняя гармоническая простая:

К ней прибегают в случаях определения, например, средних затрат труда, материалов и т. д. на единицу продукции по нескольким предприятиям.
При работе со сгруппированными данными используется средняя гармоническая взвешенная:

Средняя геометрическая применяется в тех случаях, когда общий объем усредняемого признака является мультипликативной величиной, т.е. определяется не суммированием, а умножением индивидуальных значений признака.

Форма средней геометрической взвешенной в практических расчётах не применяется.
Средняя квадратическая используется в тех случаях, когда при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин.
Главная
Средняя квадратическая рассчитывается в двух формах:

Все степенные средние различаются между собой значениями показателя степени. При этом, чем выше показатель степени, тем больше количественное значение среднего показателя:

Это свойство степенных средних называется свойством мажорантности средних.
16. Средние величины в статистике. Степенная средняя. Средняя квадратическая. Простая и взвешенная.
Средняя величина – это обобщающий показатель, характеризующий типический уровень явления. Он выражает величину признака, отнесенную к единице совокупности.
Общих принципах применения средних величин. 1. Средняя должна определяться для совокупностей, состоящих из качественно однородных единиц.
2. Средняя должна исчисляться для совокупности, состоящей из достаточно большого числа единиц.
3. Средняя должна рассчитываться для совокупности, единицы которой находятся в нормальном, естественном состоянии.
4. Средняя должна вычисляться с учетом экономического содержания исследуемого показателя.
Средние величины делятся на два больших класса: степенные средние, структурные средние.
К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая.
В качестве структурных средних рассматриваются мода и медиана.
Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.
Простая
средняя: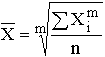 ,
,
где Xi – варианта (значение) осредняемого признака; m – показатель степени средней; n – число вариант.
Взвешенная
средняя 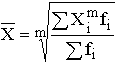 ,
,
где Xi – варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта; m – показатель степени средней; fi – частота, показывающая, сколько раз встречается i-e значение осредняемого признака.
Виды степенных средних: средняя гармоническая, если m = -1; средняя геометрическая, если m –> 0; средняя арифметическая, если m = 1; средняя квадратическая, если m = 2; средняя кубическая, если m = 3.
Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:
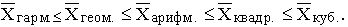
В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные.
Средняя квадратическая простая
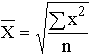
Взвешенная
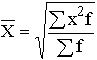
17. Средние величины в статистике. Степенная средняя. Средняя геометрическая. Простая и взвешенная.
Средняя величина – это обобщающий показатель, характеризующий типический уровень явления. Он выражает величину признака, отнесенную к единице совокупности.
Общих принципах применения средних величин. 1. Средняя должна определяться для совокупностей, состоящих из качественно однородных единиц.
2. Средняя должна исчисляться для совокупности, состоящей из достаточно большого числа единиц.
3. Средняя должна рассчитываться для совокупности, единицы которой находятся в нормальном, естественном состоянии.
4. Средняя должна вычисляться с учетом экономического содержания исследуемого показателя.
Средние величины делятся на два больших класса: степенные средние, структурные средние.
К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая.
В качестве структурных средних рассматриваются мода и медиана.
Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.
Простая
средняя: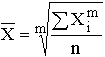 ,
,
где Xi – варианта (значение) осредняемого признака; m – показатель степени средней; n – число вариант.
Взвешенная
средняя 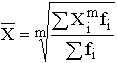 ,
,
где Xi – варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта; m – показатель степени средней; fi – частота, показывающая, сколько раз встречается i-e значение осредняемого признака.
Виды степенных средних:
средняя гармоническая, если m = -1; средняя геометрическая, если m –> 0;
средняя арифметическая, если m = 1; средняя квадратическая, если m = 2;
средняя кубическая, если m = 3.
В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные.
Средняя геометрическая
простая
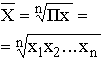
взвешенная
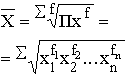
Средняя геометрическая применяется, если задана последовательность цепных относительных величин динамики, указывающих, например, на рост объема производства по сравнению с уровнем предыдущего года: i1, i2, i3,…, in.
Геометрическая простая
Для расчетов средней геометрической простой используется формула:
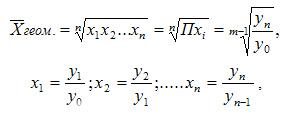
где:
 —цепной коэффициент
роста
—цепной коэффициент
роста —число этих
коэффициентов роста
—число этих
коэффициентов ростаП — знак произведения
 —количество уровней
ряда
—количество уровней
ряда —значение начального
уровня ряда
—значение начального
уровня ряда —значение конечного
уровня ряда
—значение конечного
уровня ряда
Геометрическая взвешенная
Для определения средней геометрической взвешенной применяется формула:
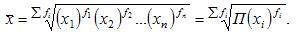
редние диаметры колес, труб, средние стороны квадратов определяются при помощи средней квадратической.
Среднеквадратические величины используются для расчета некоторых показателей, например коэффициент вариации, характеризующего ритмичность выпуска продукции. Здесь определяют среднеквадратическое отклонение от планового выпуска продукции за определенный период по следующей формуле:
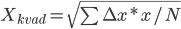
Эти величины точно характеризуют изменение экономических показателей по сравнению с их базисной величиной, взятое в его усредненной величине.
Квадратическая простая
Средняя квадратическая простая вычисляется по формуле:
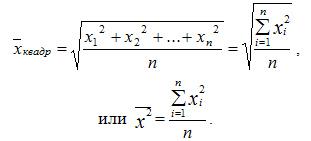
Квадратическая взвешенная
Средняя квадратическая взвешенная равна:
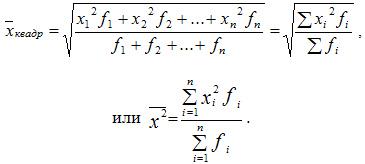
22. Абсолютные показатели вариации включают:
размах вариации 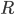
среднее линейное
отклонение 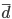
дисперсию 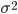
среднее квадратическое
отклонение 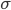
Размах вариации (r)
Размах вариации — это разность между максимальным и минимальным значениями признака

Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности.
Пример
Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет. Решение: размах вариации = 9 — 2 = 7 лет.
Для
обобщенной характеристики различий в
значениях признака вычисляют средние
показатели вариации, основанные на
учете отклонений от средней арифметической.
За отклонение от средней принимается
разность 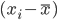 .
.
При
этом во избежании превращения в нуль
суммы отклонений вариантов признака
от средней (нулевое свойство средней)
приходится либо не учитывать знаки
отклонения, то есть брать эту сумму по
модулю 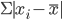 ,
либо возводить значения отклонений в
квадрат
,
либо возводить значения отклонений в
квадрат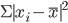
Среднее линейное и квадратическое отклонение
Среднее
линейное отклонение 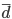 —
этосредняя
арифметическая
из абсолютных отклонений отдельных
значений признака от средней.
—
этосредняя
арифметическая
из абсолютных отклонений отдельных
значений признака от средней.
Среднее линейное отклонение простое:
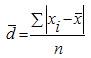
Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.
В
нашем примере: 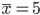 лет;
лет;
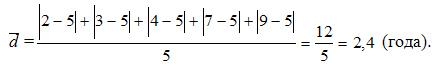
Ответ: 2,4 года.
Среднее линейное отклонение взвешенное применяется для сгруппированных данных:
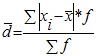
Среднее линейное отклонение в силу его условности применяется на практике сравнительно редко (в частности, для характеристики выполнения договорных обязательств по равномерности поставки; в анализе качества продукции с учетом технологических особенностей производства).
Среднее квадратическое отклонение
Наиболее
совершенной характеристикой вариации
является среднее квадратическое
откложение, которое называют стандартом
(или стандартным отклонение). Среднее квадратическое отклонение (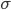 )
равно квадратному корню из среднего
квадрата отклонений отдельных значений
признака отсредней
арифметической:
)
равно квадратному корню из среднего
квадрата отклонений отдельных значений
признака отсредней
арифметической:
Среднее квадратическое отклонение простое:
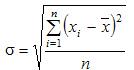

Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:
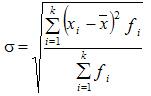
Между
средним квадратическим и средним
линейным отклонениями в условиях
нормального распределения имеет место
следующее соотношение: 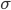 ~
1,25.
~
1,25.
Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.
Среднее квадратичное Википедия
Среднее квадратическое (квадратичное)[1] — число s{\displaystyle s}, равное квадратному корню из среднего арифметического квадратов данных чисел a1,a2,…,an{\displaystyle a_{1},a_{2},…,a_{n}}:
- s=a12+a22+…+an2n{\displaystyle s={\sqrt {\frac {a_{1}^{2}+a_{2}^{2}+\ldots +a_{n}^{2}}{n}}}}
Среднее квадратическое — частный случай среднего степенного и потому подчиняется неравенству о средних. В частности, для любых чисел оно не меньше среднего арифметического:
- a1+a2+…+ann⩽a12+a22+…+an2n{\displaystyle {\frac {a_{1}+a_{2}+\ldots +a_{n}}{n}}\leqslant {\sqrt {\frac {a_{1}^{2}+a_{2}^{2}+\ldots +a_{n}^{2}}{n}}}}
Среднее квадратическое находит широкое применение во многих науках. В частности, через него определяется основное понятие теории вероятностей и математической статистики — дисперсия (квадратный корень из которой называется среднеквадратическим отклонением). Также тесно связан с этим понятием метод наименьших квадратов, имеющий общенаучное значение.
Примечания[ | ]
Свойства[ | ]
- Среднее квадратическое набора неотрицательных чисел лежит между минимальным и максимальным числами из этого набора.
Средняя геометрическая, средняя гармоническая, средняя квадратичная и средняя кубическая
Понятие средней геометрической
Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т. е. характеризует средний коэффициент роста.
В контрольных по статистике она исчисляется извлечением корня степени n из произведений отдельных значений — вариантов признака Х по формуле:
где П — оператор умножения, знак произведения;
n — число вариантов.
Средняя геометрическая в частности рассчитывается тогда, когда данные даны в процентах.
Рассчитаем среднюю величину инфляции
Исходные данные взяты из справочника «Краткосрочные экономические показатели Российской Федерации за 2012 г.». Сайт www.gks.ru
| год | квартал | Индекс потребительских цен, y |
| 2008 | 1 | 104,8 |
| 2 | 103,8 | |
| 3 | 101,7 | |
| 4 | 102,5 | |
| 2009 | 1 | 105,4 |
| 2 | 101,9 | |
| 3 | 100,6 | |
| 4 | 100,7 | |
| 2010 | 1 | 103,2 |
| 2 | 101,2 | |
| 3 | 101,8 | |
| 4 | 102,4 | |
| 2011 | 1 | 103,8 |
| 2 | 101,1 | |
| 3 | 99,7 | |
| 4 | 101,4 |
Среднемесячный индекс потребительских цен определяется по формуле средней геометрической, т.к. в основе расчета лежит индекс. Перемножим данные и разделим на число кварталов за 4 года:
Вывод: в период с 2008 по 2011 года средний квартальный прирост инфляции составил 2,24%
Средняя гармоническая
Определяющее свойство средней гармонической заключается в том, чтобы при осреднении оставалась неизменной сумма величин, обратных осредняемым.
Формула средней геометрической взвешенной применяется в тех случаях, когда статистическая информация не содержит частот f по отдельным вариантам х совокупности и представлена как их произведение xf. Для того чтобы исчислить среднюю геометрическую, необходимо обозначить: xf = w, откуда f = w/x.
Преобразуем формулу средней арифметической так, чтобы по имеющимся данным х и w можно было вычислить среднюю. В формулу средней арифметической взвешенной вместо xn подставим w, а вместо n — отношение w/x и таким образом получим формулу средней гармонической взвешенной:
Средняя гармоническая простая применяется в тогда, когда вес каждого варианта равен единице. Она вычисляется по формуле:
где 1/x — отдельные варианты обратного признака, встречающиеся по одному разу;
n — число вариантов.
Средняя квадратичная
Средняя квадратичная применяется, например, для вычисления средней величины сторон n квадратных участков, средних диаметров стволов, труб и т. д. Она подразделяется на два вида.
Средняя квадратичная простая. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратичной средней величиной.
Она является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:
Средняя квадратичная взвешенная вычисляется по формуле:
где f — признак веса.
Средняя кубическая
Средняя кубическая применяется, например, при определении средней длины стороны и кубов. Она подразделяется на два вида.
Средняя кубическая простая:
Средняя кубическая взвешенная:
Средняя квадратическая и средняя кубическая имеют неширокое применение в практической статистике. Часто в статистике используют среднюю квадратическую, но не из самих факторов х, и из их отклонений от средней при расчете показателей вариации.
Средняя может быть рассчитана не для всей, а для какой-либо части данных совокупности. Примером может быть средняя прогрессивная как одна из частных средних, рассчитанная не для всех, а только для «лучших» (например, для показателей выше или ниже средних индивидуальных).
Структурные средние
Для характеристики центральной тенденции в статистических распределениях рационально вместе со средней арифметической использовать некое значение признака X, которое в силу определенных особенностей расположения в ряду распределения может характеризовать его уровень.
Это особенно важно тогда, когда в ряду распределения крайние значения признака имеют нечеткие границы. В связи с этим точное определение средней арифметической, как правило, невозможно, либо очень сложно. В таких случаях средний уровень можно определить, взяв, например, значение признака, которое расположено в середине ряда частот или которое чаще всего встречается в текущем ряду.
Такие значения зависят только от характера частот т. е. от структуры распределения. Они типичны по месту расположения в ряду частот, поэтому такие значения рассматриваются в качестве характеристик центра распределения и поэтому получили определение структурных средних.
Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.
Мода и медиана очень часто рассчитывают в задачах статистики и они являются дополнительными к средней характеристиками совокупности и используются в математической статистике для анализа типа рядов распределения, которое может нормальным, асимметричным, симметричным и т.д.
Также как и медиану вычисляются значения признака, делящего совокупность на четыре равные части — квартели, на пять частей — квинтели, на десять равных частей — децели, на сто равных частей — перцентели. Использование при анализе вариационных рядов распределения рассмотренных характеристик в статистике позволяет более глубоко и детально охарактеризовать изучаемую совокупность.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
6.4. Средняя квадратическая погрешность суммы измеренных величин
Рассмотрим функцию, представляющую собой алгебраическую сумму двух величин:

где х и у- — независимые слагаемые.
Случайные погрешности слагаемых и их суммы при однократном из-мерении обозначим соответственно х, у и z, тогда
С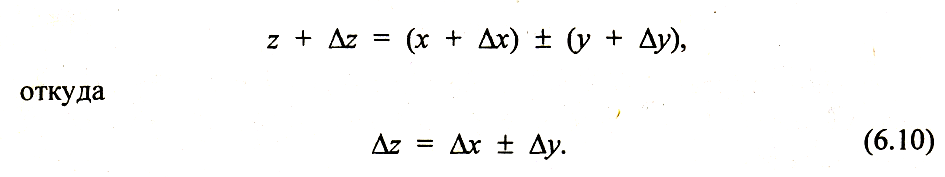 ложив
левые и правые части п таких
уравнений и разделив затем обе части
равенства на п, получим:
ложив
левые и правые части п таких
уравнений и разделив затем обе части
равенства на п, получим:
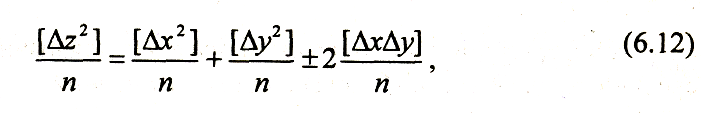
В соответствии с формулой (6.6) можно
написать:
соответствии с формулой (6.6) можно
написать:
г де
[ху]
есть сумма произведений случайных
погрешностей, которая согласно четвертому
свойству случайных погрешностей’
стремится к нулю
при значительном числе измерений.
Тогда, отбросив последнее слагаемое
равенства (6.12), окончательно получим:
де
[ху]
есть сумма произведений случайных
погрешностей, которая согласно четвертому
свойству случайных погрешностей’
стремится к нулю
при значительном числе измерений.
Тогда, отбросив последнее слагаемое
равенства (6.12), окончательно получим:
средние квадратические погрешности функции и аргу-
ментов.
По аналогии для алгебраической суммы п независимых величин
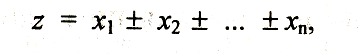
можно записать
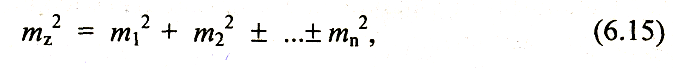
Т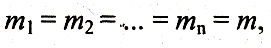 .
е. квадрат средней квадратической
погрешности алгебраической сум-мы
аргумента равен сумме квадратов средних
квадратических погрешно-стей
слагаемых.
.
е. квадрат средней квадратической
погрешности алгебраической сум-мы
аргумента равен сумме квадратов средних
квадратических погрешно-стей
слагаемых.
В частном случае, когда формула (6.15) примет формула (6.15) примет вид:
Если каждое слагаемое было измерено п раз, то, написав п соотноше-ний типа (6.10) и возведя каждое в квадрат, получим п выражений:

5

т. е. средняя квадратическая погрешность алгебраической суммы равно-точных измерений в п раз больше средней квадратической погрешности одного слагаемого.
Например, если измерено 9 углов 30-секундным теодолитом, то средняя квадратическая погрешность угловых измерений составит
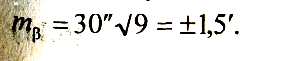
6
6.5. Средняя квадратическая погрешность арифметического среднего
Арифметическое среднее определятся выражением (6.3), которое можно представить как:
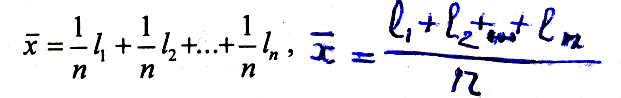
где 1/n некоторое постоянное число. Если среднюю квадратическую по-
грешность арифметического среднего обозначить через М, а среднюю квадратическую погрешность одного измерения через т, то согласно (6.15) можно записать:

т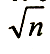 .
е. средняя квадратическая погрешность
арифметического среднего в раз
меньше средней квадратической погрешности
одного измерения.
Это свойство средней квадратической
погрешности арифметического среднего
позволяет повысить точность измерений
путем увёличения числа
измерений. Например, требуется определить
величину угла с точностью
± 15″ при наличии 30-секундного теодолита.
Очевидно, что если измерить
угол 4 раза и определить арифметическое
среднее, то его средняя квадратическая
погрешность согласно (6.17) составит ±
15″.
.
е. средняя квадратическая погрешность
арифметического среднего в раз
меньше средней квадратической погрешности
одного измерения.
Это свойство средней квадратической
погрешности арифметического среднего
позволяет повысить точность измерений
путем увёличения числа
измерений. Например, требуется определить
величину угла с точностью
± 15″ при наличии 30-секундного теодолита.
Очевидно, что если измерить
угол 4 раза и определить арифметическое
среднее, то его средняя квадратическая
погрешность согласно (6.17) составит ±
15″.
Средняя квадратическая погрешность арифметического среднего М показывает, в какой мере снижается влияние случайных погрешностей при многократных измерениях.
6.6. Веса результатов неравноточных измерений
При неравноточных измерениях, когда результаты каждого измере-ния нельзя считать одинаково надежными, уже нельзя обойтись опреде-лением простого арифметического среднего. В таких случаях учитывают достоинство (или надежность) каждого результата измерений.
Д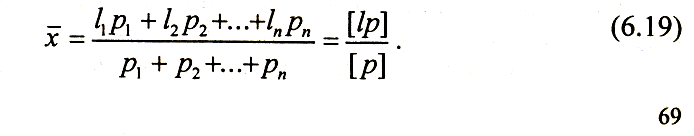 остоинство
результатов измерений выражают некоторым
числом, называемым весом этого
измерения. Очевидно, что арифметическое
среднее
будет иметь больший вес по сравнению
с единичным измерени-
остоинство
результатов измерений выражают некоторым
числом, называемым весом этого
измерения. Очевидно, что арифметическое
среднее
будет иметь больший вес по сравнению
с единичным измерени-
ем, а измерения, выполненные при использовании более совершенного и точного прибора, будут иметь большую степень доверия, чем те же из-мерения, выполненные прибором менее точным.
Поскольку условия измерений определяют различную величину средней квадратической погрешности, то последнюю и принято прини-мать в качестве основы оценки весовых значений проводимых измере-ний. При этом веса результатов измерений принимают обратно пропорциональными квадратам соответствующих им средних квадратических погрешностей. Так, если обозначить через р и Р веса измерений, имею-щие средние квадратические погрешности соответственно т и М, то можно записать сротношение пропорциональности:

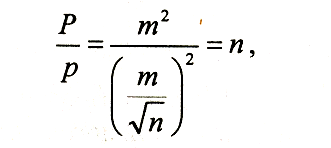 Например, если
М средняя квадратическая погрешность
арифметиче-ского
среднего, а т
— соответственно,
одного измерения, то, как следует из
(6.17), можно записать:
Например, если
М средняя квадратическая погрешность
арифметиче-ского
среднего, а т
— соответственно,
одного измерения, то, как следует из
(6.17), можно записать:
т. е. вес арифметического среднего в п раз больше веса единичного изме-рения.
Аналогичным образом можно установить, что вес углового измере-ния, выполненного 15-секундным теодолитом, в четыре раза выше веса углового измерения, выполненного 30-секундным прибором.
При практических вычислениях обычно вес одной какой-либо вели-чины принимают за единицу и при этом условии вычисляют веса осталь-ных измерений. Так, в последнем примере если принять вес результата углового измерения 30-секундным теодолитом за р = 1, то весовое значе-ние результата измерения 15-секундным теодолитом составит Р = 4.
§ 23. Средняя квадратическая погрешность
где (∂f/∂хi) — частная производная функции по аргументу хi . Правила определения СКП функций следующие.
1.Выполнить последовательно дифференцирование функции отдельно по каждому из аргументов, считая остальные аргументы постоянными числами (коэффициентами).
2.Полученные выражения умножить на СКП аргументов, по которым производилось дифференцирование функции и возвести полученные выражения каждое отдельно в квадрат.
3.Записать полученные выражения в виде суммы под знаком квадратного корня.
Рассмотрим несколько примеров определения СКП функций.
Пример 3.1. Средняя квадратическая погрешность среднего арифметического. Очевидно, что значение среднего арифметического является функцией суммы
измеренных величин хi (3.1). Представим это выражение в виде
хо = (х1 + х2 + … + хn ) / n (3.14) Поскольку 1/n является постоянным коэффициентом, то при почленном
дифференцировании и после умножения на mi и возведения в квадрат пролучим:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| , |
| ||||
m | x | = M = |
| [(m / n) | 2 + (m | 2 | / n)2 | + …+ (m | n | / n)2 | ] | (3.15) | |||||||||
| o | 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| mxo = M = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (3.16) | |||
|
| (m1 | 2 | + m2 | 2 |
| + … + | mn | 2 )/ n |
|
|
|
| ||||||||
Полагая измерения равноточными, т.е. m1 |
| = m2 | = … = mn | = | m, выражение (3.16) | ||||||||||||||||
преобразуем к виду |
|
|
|
|
| m |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| M = |
|
|
|
|
|
|
|
|
|
|
|
|
| (3.17) | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
| n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т.е. СКП среднего арифметического в корень из числа измерений меньше СКП одного измерения.
С учетом (3.10)
M | = |
| [ν | 2 ] |
| (3.18) |
| n(n — 1) | |||||
|
|
|
|
| ||
Очевидно, что, если при увеличении числа измерений значение СКП одного измерения стремится к предельному значению, отличному от нуля, то значение СКП среднего арифметического стремится при увеличении числа измерений к нулю, а само среднее арифметическое – к истинному значению.
Пример 3.2. Объем пирамиды, | основанием которой является прямоугольник, | |
определен по формуле | hab |
|
V = | (3.19) | |
| 3 |
|
где h – высота пирамиды, а и b – стороны основания.
Требуется определить СКП объема пирамиды, вычисленного по формуле (3.19), если известно, что h = 12,34 м, а = 23,46 м, b = 39,63 м и их СКП равны соответственно: mh = 0,07 м, ma = 0,02 м, mb = =0,04 м.
Решение.
Выполняем последовательное дифференцирование по аргументам h, a и b:


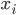 —цепной коэффициент
роста
—цепной коэффициент
роста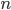 —число этих
коэффициентов роста
—число этих
коэффициентов роста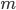 —количество уровней
ряда
—количество уровней
ряда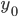 —значение начального
уровня ряда
—значение начального
уровня ряда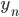 —значение конечного
уровня ряда
—значение конечного
уровня ряда