Переменный ток
Переменный ток все время изменяет свое направление в отличие от постоянного, который протекает только в одном направлении. Постоянный ток вырабатывают батареи и источники постоянного тока, а переменный – генераторы сигналов и государственные энергетические системы.
Синусоидальные колебания
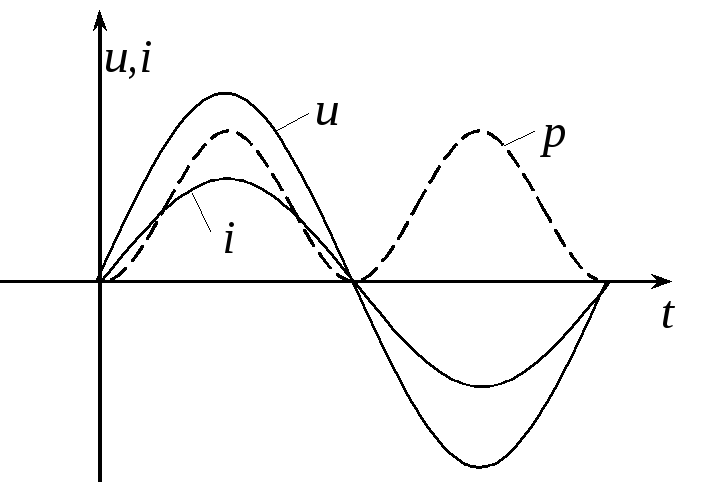
Форма переменного тока или напряжения может принимать самые различные виды. Наиболее распространенной является синусоидальная форма переменного напряжения или тока (рис. 2.1). Синусоидальное колебание имеет два максимальных значения, или пика: положительный пик и отрицательный. Пиковое значение называется также амплитуде синусоиды. Значение синусоидального напряжения, измеренное от пика до пика (размах), является разностью потенциалов между положительным пиком и отрицательным.
Размах = Положительная амплитуда + Отрицательная амплитуда = Удвоенная амплитуда.

Рис. 2.1. Синусоидальные колебания переменного тока
Среднеквадратическое значение
Постоянный ток имеет постоянное значение, и это значение можно использовать во всех вычислениях. Значение же переменного тока изменяется во времени. Чтобы преодолеть эту трудность, за «постоянное» значение переменного тока приняли и используют его среднеквадратическое значение.
Среднеквадратическое значение переменного тока является эквивалентом значения постоянного тока, при котором вырабатывается такая же мощность, что и при исходном значении переменного тока. Если известно среднеквадратическое значение переменного тока, то его можно использовать для вычисления мощности так же, как если бы это было постоянное напряжение или ток. Например:
Мощность пост. тока = Постоянный ток х Постоянное напряжение;
Мощность перем. Тока = Среднеквадр. значение тока х Среднеквадр. значение напряжения.
Значения переменного тока и напряжения всегда задают в виде среднеквадратической величины, за исключением специально оговоренных случаев.
Пример 1
Какое сопротивление имеет домашний электрический обогреватель мощностью 1 кВт?
Решение
Домашние обогреватели работают от сетевого напряжения, имеющего среднеквадратическое значение 240 В (в России 220 В. — Прим. перев.). Мощность, потребляемая обогревателем, составляет 1 кВт = 1000 Вт. Из формулы P = V2/R определяем
P = V2/R = 240*240/1000 = 57, б Ом.
Соотношение между пиковыми и среднеквадратическими значениями
Среднеквадратическое значение сигнала переменного тока зависит от его формы. Так, среднеквадратическое значение синусоидального сигнала составляет 0,707 его пикового значения (амплитуды). Заметим, что это справедливо только для синусоидального сигнала. Например, если амплитуда синусоидального сигнала Vр = 10 В, то его среднеквадратическое значение составит Vср.кв. = 0,707 * Vр = 0,707 * 10 = 7,07 В (см. рис. 2.2). Из соотношения Vср.кв. = 0,707 * Vр следует, что
Vр = 1/0,707 * Vср.кв. = 1,414 * Vср.кв.

Рис. 2.2. Среднеквадратическое значение синусоидального сигнала.

Рис. 2.3. Постоянная составляющая сигнала переменного тока.
Постоянная составляющая в сигнале переменного тока
До сих пор мы имели дело с сигналами переменного тока, которые не содержали постоянной составляющей. Рассмотрим два синусоидальных сигнала, изображенных на рис. 2.3. Левый сигнал не имеет постоянной составляющей, и его положительный пик равен отрицательному. Правый же сигнал содержит составляющую постоянного тока величиной 5 В.
Постоянная составляющая переменного тока называется также средним, или усредненным значением сигнала переменного тока.
Определим постоянную составляющую сигнала, имеющего прямоугольную форму (рис. 2.4).

Рис. 2.4.
1. Сначала определим положение нулевого уровня.
2. Вычислим площадь А1, лежащую выше нулевого уровня:
А1 = 4*1 = 4.
3. Вычислим площадь А2, лежащую ниже нулевого уровня:
А2 = 2*1 = 2.
4. Вычислим суммарную площадь:
А1 – А2 = 4 – 2 = 2.
5. Отсюда среднее значение напряжения за период равно
Суммарная площадь/Время периода = 2/3 = 0,67 В.
Среднеквадратическое значение сложных сигналов
Как уже говорилось, соотношение
Среднеквадратическое значение = 0,707 амплитуды
справедливо только для синусоидальных сигналов. Среднеквадратическое значение сигналов, имеющих другую форму, может быть определено следующим образом.
2. Определить среднее значение площади сигнала за период.
3. Вычислить квадратный корень из средней площади сигнала за период.
Определим среднеквадратическое значение сигнала, имеющего форму меандра (рис. 2.5(а)). Площадь положительного полупериода этого сигнала равна 3 * 3 = 9. Площадь отрицательного полупериода составля¬ет (-3) * (-3) = 9. Среднее значение площади за период, следовательно, равно 9. Отсюда среднеквадратическое значение напряжения будет

Рис. 2.5. Сравнение среднеквадратических значений
прямоугольного и синусоидального сигналов.
Для сравнения определим среднеквадратическое значение синусоидального напряжения, имеющего значение положительной и отрицательной амплитуды +3 В и –3 В соответственно (рис. 2.5(б)): 0,707 * 3 В = 2,12 В.
Как видим, прямоугольный сигнал имеет большее среднеквадратическое значение. Это объясняется тем, что площадь под прямоугольной огибающей больше, чем площадь под синусоидой, хотя оба сигнала имеют одинаковые значения положительного и отрицательного пиков. В данном случае среднеквадратическое значение прямоугольного сигнала равно его пиковому значению.
На рис. 2.6 изображен прямоугольный сигнал, имеющий только положительные значения. Среднеквадратическое значение этого сигнала меньше его пикового значения.
При однополупериодном выпрямлении среднеквадратическое значение напряжения равно половине его амплитуды.
При двухполупериодном выпрямлении среднеквадратическое значение такое же, как у полной синусоиды, т. е. 0,707 амплитуды (рис. 2.7), поскольку при вычислении среднеквадратического значения положительная полуволна сигнала идентична отрицательной, положительный полупериод идентичен отрицательному.

Рис. 2.6. Среднеквадратическое значение прямоугольного сигнала, имеющего только положительную полярность.


Рис. 2.7. (а) При однополупериодном выпрямлении синусоидального напряжения его среднеквадратическое значение равно 0,5 амплитуды.
(б) При двухполупериодном выпрямлении синусоидального напряжения его среднеквадратическое значение равно 0,707 амплитуды.
В этом видео наглядно рассказывается о типах тока, в том числе о переменном токе:
Добавить комментарий
Среднеквадратичное значение сигнала — это… Что такое Среднеквадратичное значение сигнала?
- Среднеквадратичное значение сигнала
11. Среднеквадратичное значение сигнала
Корень квадратный из среднего значения квадрата сигнала
Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.
- среднеквадратичное значение корректированного ускорения aw
- среднеквадратичное рабочее напряжение
Смотреть что такое «Среднеквадратичное значение сигнала» в других словарях:
среднеквадратичное значение — 3.4 среднеквадратичное значение: Эффективное значение тока. Источник: ГОСТ Р 52506 2005: Совместимость технических средств электромагнитная. Лифты, эскалаторы и пассажирские конв … Словарь-справочник терминов нормативно-технической документации
Среднеквадратичное значение сигналя — 1. Корень квадратный из среднего значения квадрата сигнала Употребляется в документе: ГОСТ 16465 70 Сигналы радиотехнические измерительные. Термины и определения … Телекоммуникационный словарь
Максимальное среднеквадратичное значение — 1. Наибольшее кратковременное среднеквадратичное значение напряжения модулированного радиочастотного сигнала на интервале наблюдения, равном одному периоду модулирующего сигнала Употребляется в документе: ГОСТ Р 51317.4.3 99 Устойчивость к… … Телекоммуникационный словарь
действующее значение тока — Среднеквадратичное значение периодического электрического тока за период. Примечание — Аналогично определяют действующие значения периодических электрического напряжения, электродвижущей силы, магнитного потока и т. д. [ГОСТ Р 52002 2003]… … Справочник технического переводчика
максимальный уровень излучаемого сигнала — 2.1.15 максимальный уровень излучаемого сигнала (Peak Radiated Power; PRP): Величина, представляющая собой среднеквадратичное значение непрерывного синусоидального сигнала, удвоенная амплитуда (полный размах) колебаний которого равна удвоенной… … Словарь-справочник терминов нормативно-технической документации
ГОСТ 16465-70: Сигналы радиотехнические измерительные. Термины и определения — Терминология ГОСТ 16465 70: Сигналы радиотехнические измерительные. Термины и определения оригинал документа: 40. Абсолютное отклонение сигналов Максимальное значение разности мгновенных значений сигналов, взятых в один и тот же момент времени на … Словарь-справочник терминов нормативно-технической документации
допуск — 01.01.65 допуск [ tolerance]: Максимальный допустимый интервал отклонений значений параметра системы, вызванных любым воздействием со стороны системы или окружающей среды. Примечание 1 Допуск обычно выражается в частях на миллион (ч/млн)2).… … Словарь-справочник терминов нормативно-технической документации
ГОСТ 31418-2010: Методы испытаний на стойкость к механическим внешним воздействующим факторам машин, приборов и других технических изделий. Испытания на удар с воспроизведением ударного спектра — Терминология ГОСТ 31418 2010: Методы испытаний на стойкость к механическим внешним воздействующим факторам машин, приборов и других технических изделий. Испытания на удар с воспроизведением ударного спектра оригинал документа: 3.28 вейвлет… … Словарь-справочник терминов нормативно-технической документации
ГОСТ Р 53190-2008: Методы испытаний на стойкость к механическим внешним воздействующим факторам машин, приборов и других технических изделий. Испытания на удар с воспроизведением ударного спектра — Терминология ГОСТ Р 53190 2008: Методы испытаний на стойкость к механическим внешним воздействующим факторам машин, приборов и других технических изделий. Испытания на удар с воспроизведением ударного спектра оригинал документа: 3.28 вейвлет… … Словарь-справочник терминов нормативно-технической документации
допуск на сигнал — 3.21 допуск на сигнал (signal tolerance): Величина, выражаемая в процентах и определяемая формулой где NF среднеквадратичное значение задающего сигнала; F среднеквадратичное значение сигнала, воспроизведенного на вибростоле. Примечание 1 Данный… … Словарь-справочник терминов нормативно-технической документации
Среднее и действующее значение синусоидальных функций
Средним
значением за период любой периодической
функции 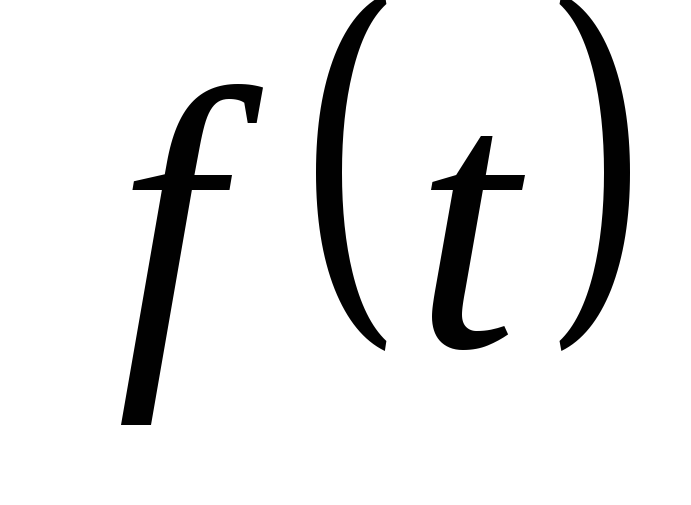 называется интеграл
называется интеграл
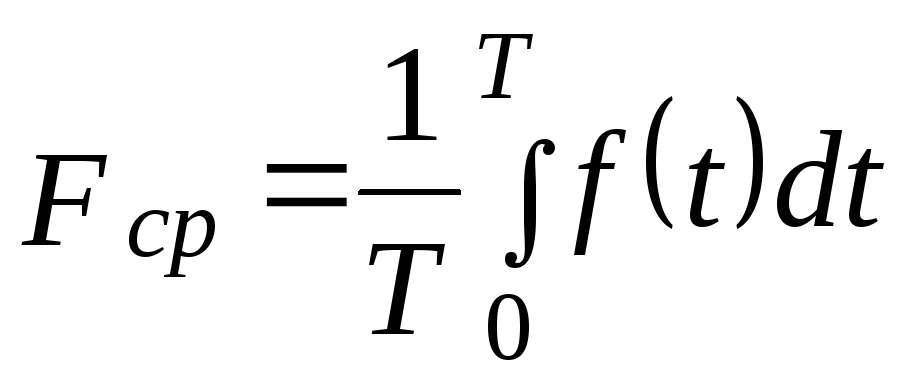 ,
где T —
период
,
где T —
период
У любой гармонической функции среднее значение за период равно нулю, так как площадь положительной полуволны компенсируется площадью отрицательной. В этом случае пользуются средним значением за полупериод.
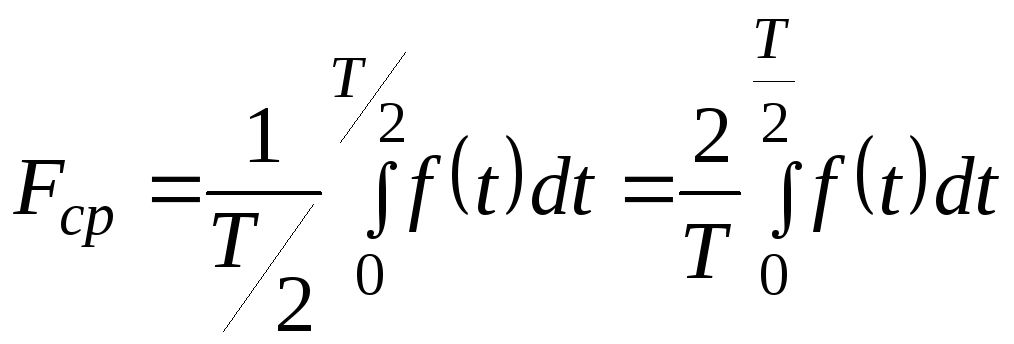
С последним значением совпадают среднее значение функции за период, взятой по абсолютной величине.
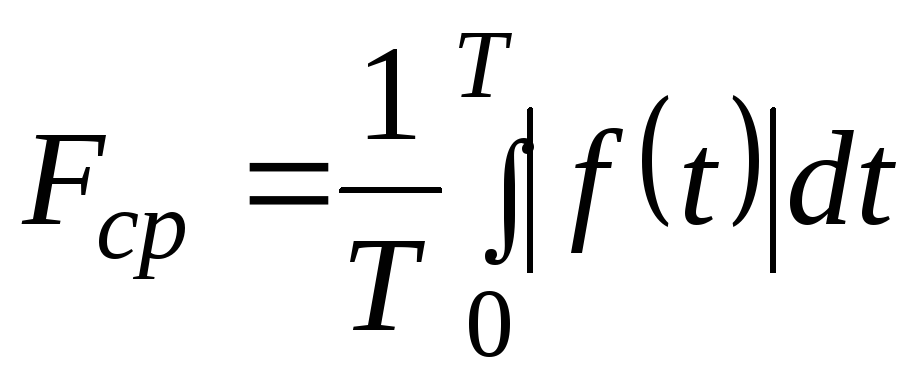 .
.
Пусть 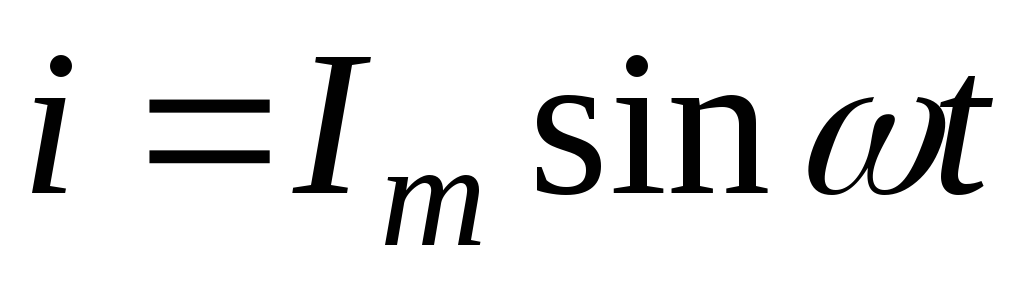 ,
тогда:
,
тогда: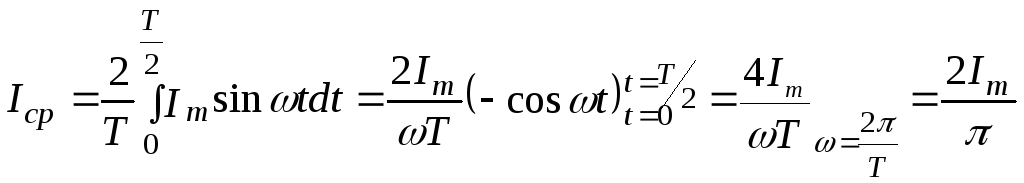
Приборы выпрямительной системы показывают среднее значение величин.
Приборы магнитоэлектрической системы, предназначены для измерения постоянного напряжения и тока.
Тепловое действие тока пропорционально квадрату тока и поэтому часто о величине переменного тока судят по так называемому средне квадратичному или действующему значению тока.
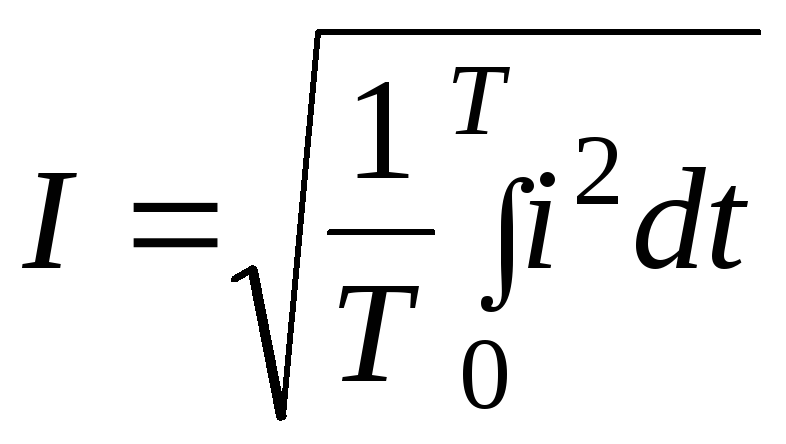 ,
, 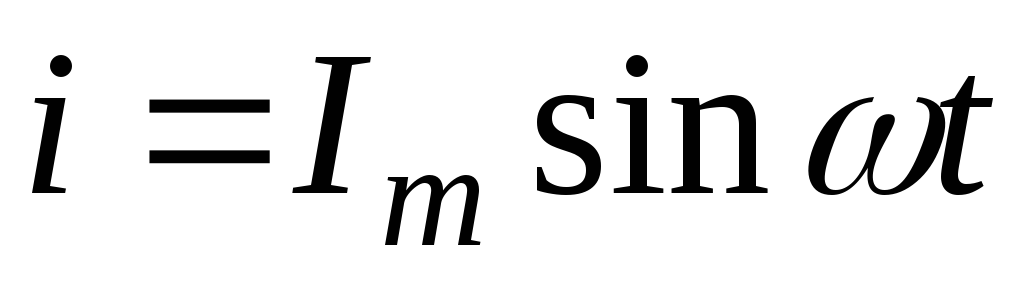 ,
тогда:
,
тогда: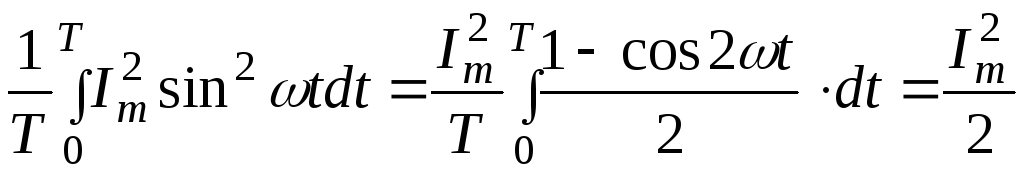 ;
;
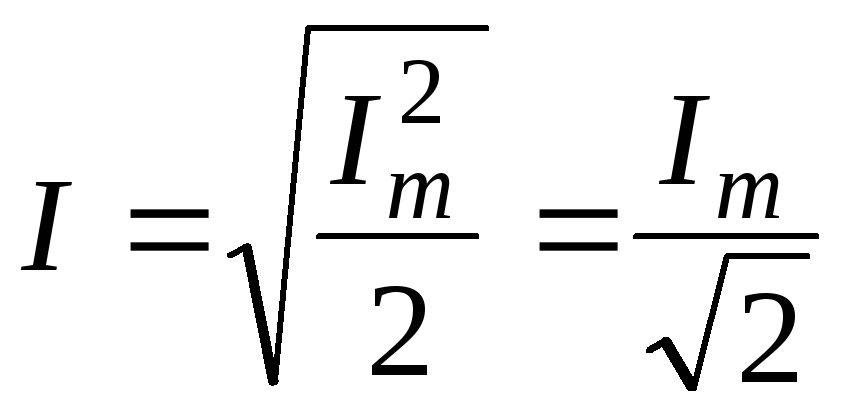 —
действующее значение тока
—
действующее значение тока
Действующее значение показывают приборы электромагнитной, электродинамической, ферродинамической, электростатической систем.
Синусоидальный ток в сопротивлении
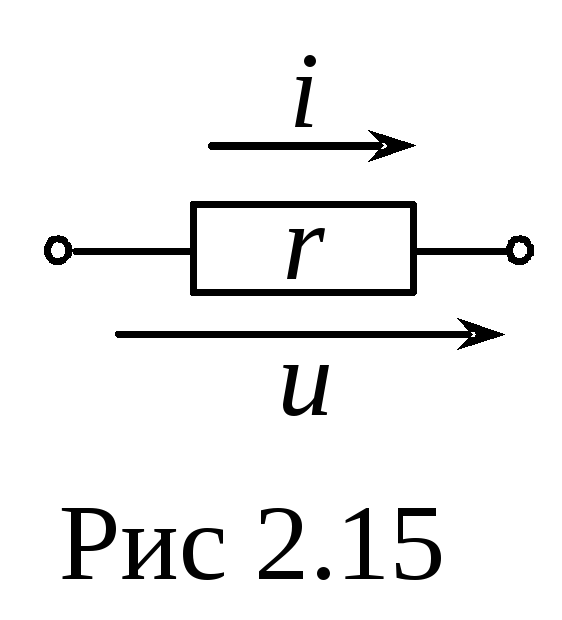
Дано: 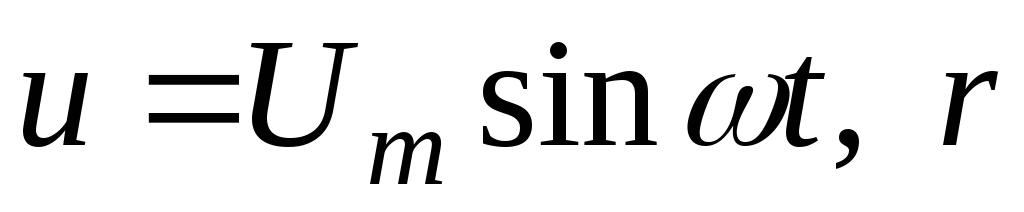 (рис 2.15).
(рис 2.15).
Найти: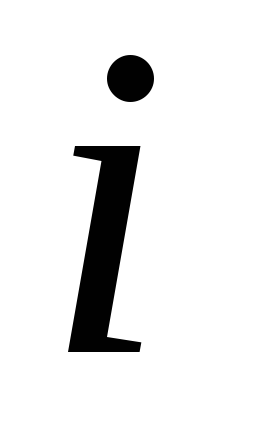
Только в частном случае сопротивления выполняется закон Ома для мгновенных значений напряжений и тока.
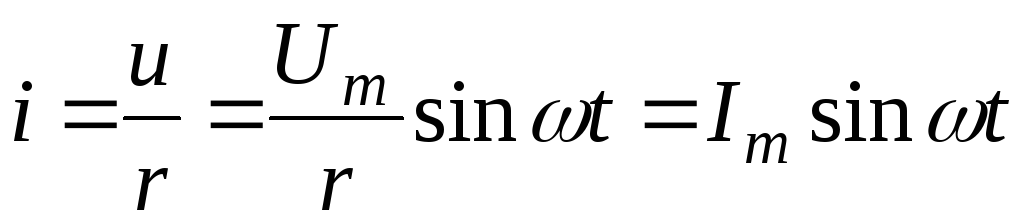
В сопротивлении напряжение и ток совпадают по фазе (рис 2.16).
|
Рис. 2.16 |
Мгновенная мощность в сопротивлении.
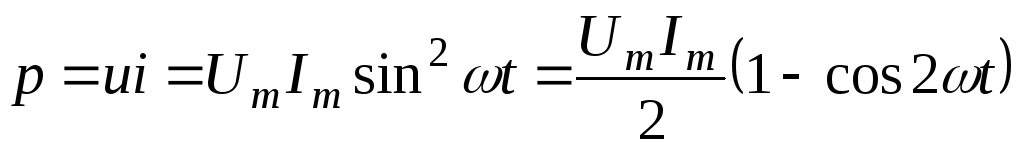 .
.
Среднее значение за период мгновенной мощности называется активной мощностью.
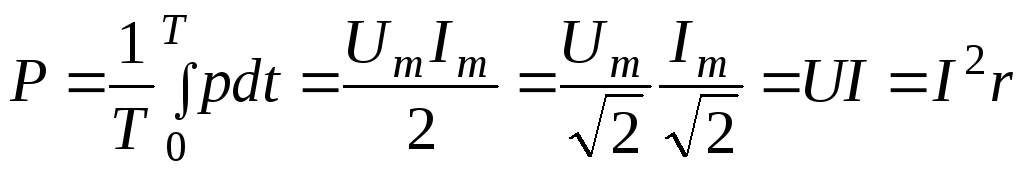 .
.
Синусоидальный ток в индуктивности.
Д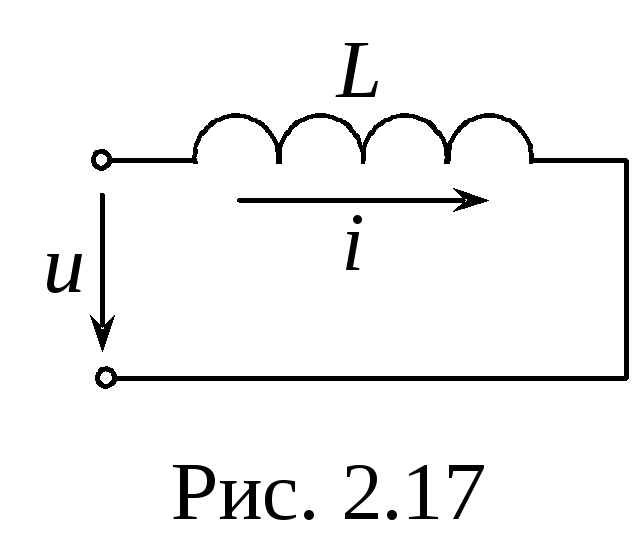 ано:
ано: ,
, 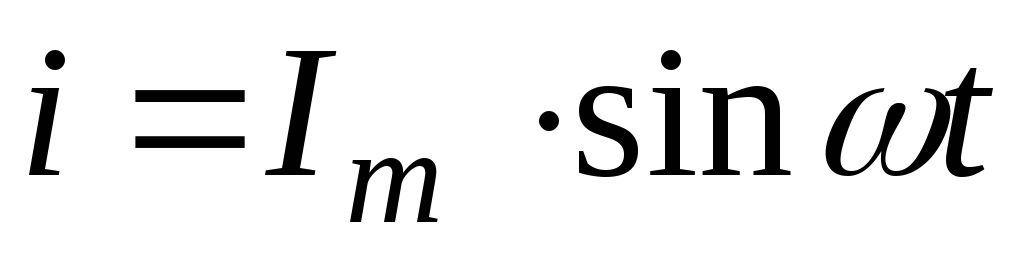 (рис.
2.17)
(рис.
2.17)
Найти: 
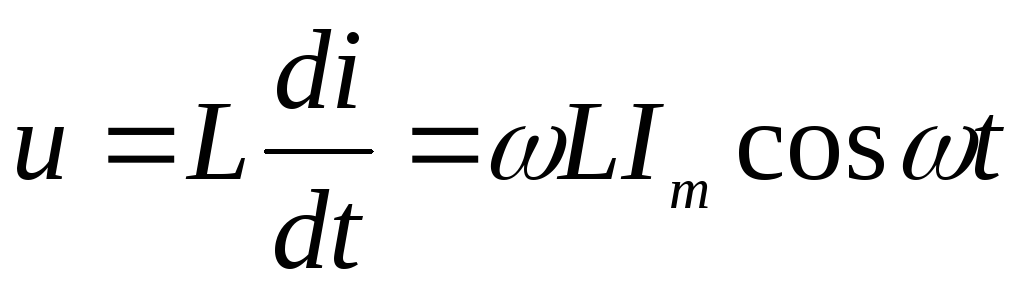 ;
; 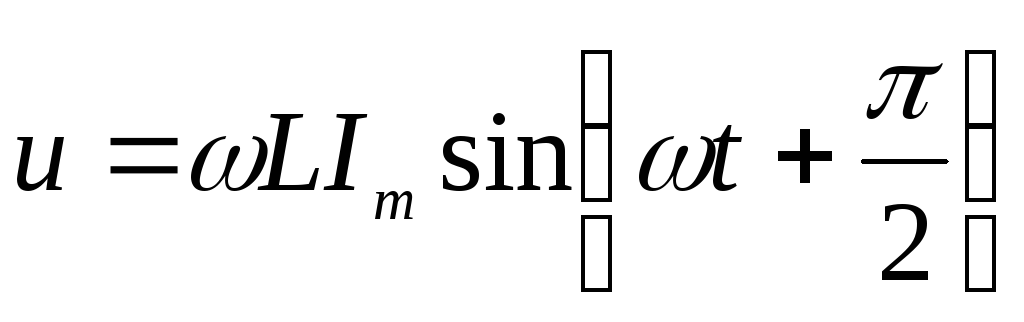
Напряжение
на индуктивности опережает ток на  .
Обозначим
.
Обозначим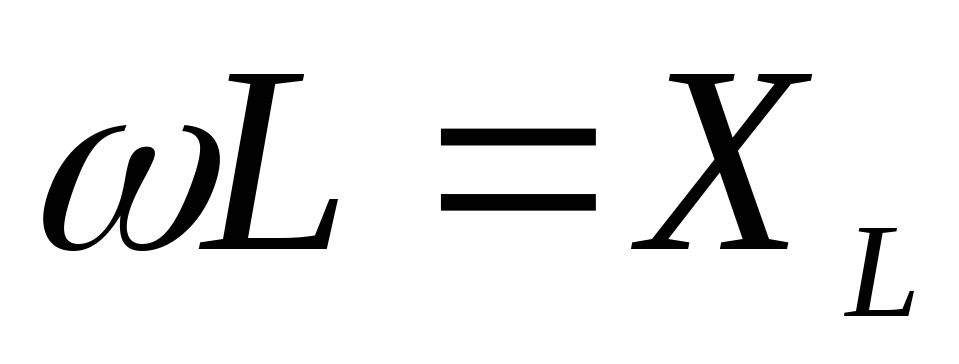 —
реактивное сопротивление индуктивности.
—
реактивное сопротивление индуктивности.
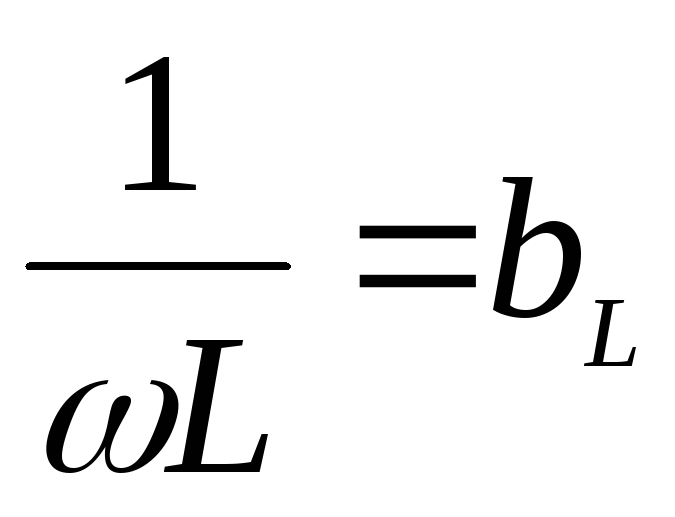 —
реактивная проводимость индуктивности,
тогда
—
реактивная проводимость индуктивности,
тогда
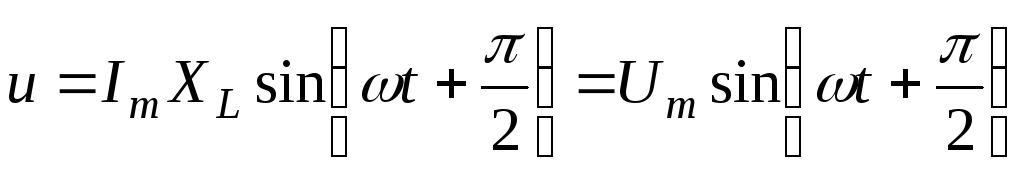 .
.
О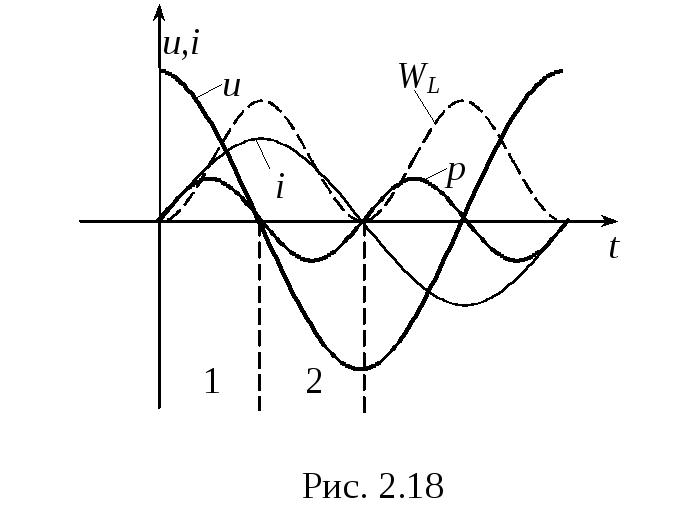 тсюда
следует, что амплитуда (действующее
значение) напряжения и тока на индуктивности
связаны соотношением подобным закону
Ома.
тсюда
следует, что амплитуда (действующее
значение) напряжения и тока на индуктивности
связаны соотношением подобным закону
Ома.
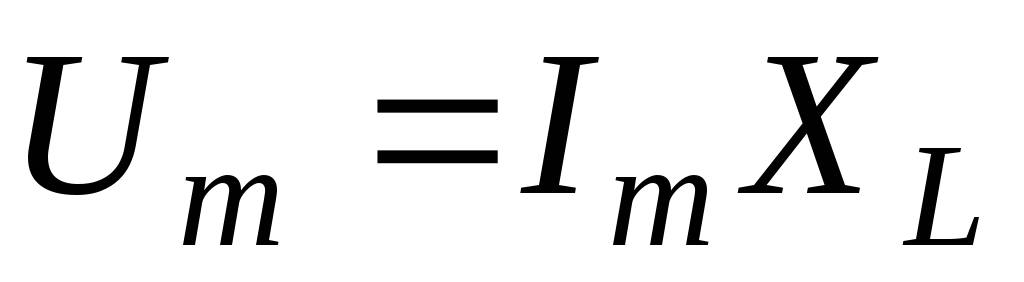 ;
; 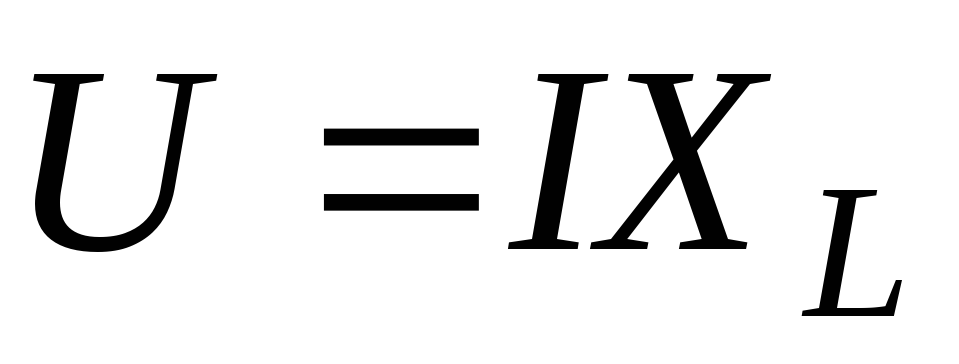 .
.
Частное деления напряжения на ток даёт некоторую функцию времени не имеющую физического смысла и практического применения (рис.2.18).
Мгновенная мощность в индуктивности:
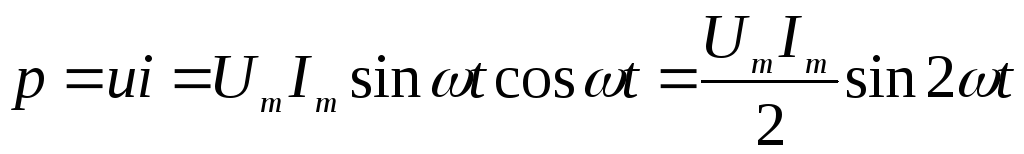 .
.
Активная
мощность в индуктивности: 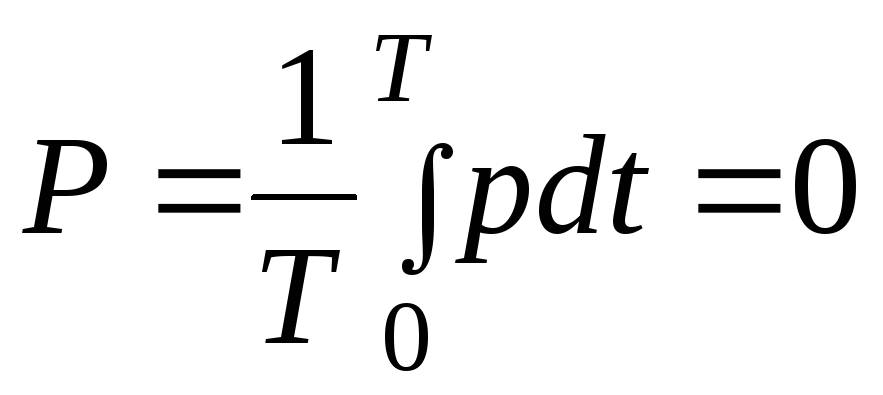 .
.
Энергия магнитного поля индуктивности:
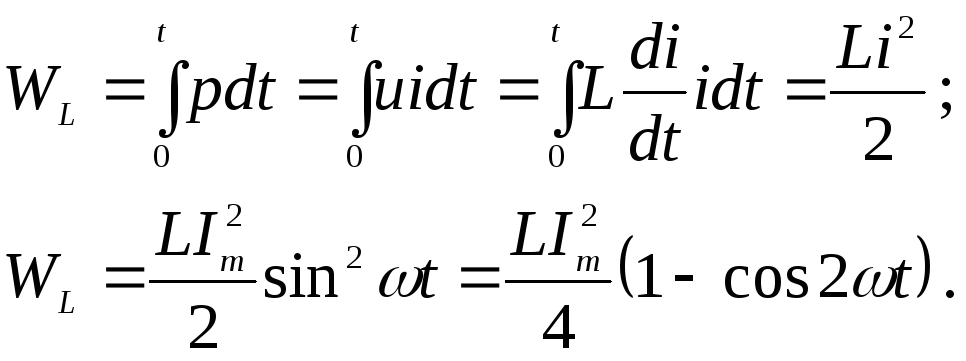
На первом интервале энергия поступает в цепь и временно запасается в магнитном поле индуктивности. На втором интервале энергия возвращается в источник. Таким образом, в цепях с индуктивностью происходит непрерывный колебательный процесс обмена энергией.
Синусоидальный ток в ёмкости
Д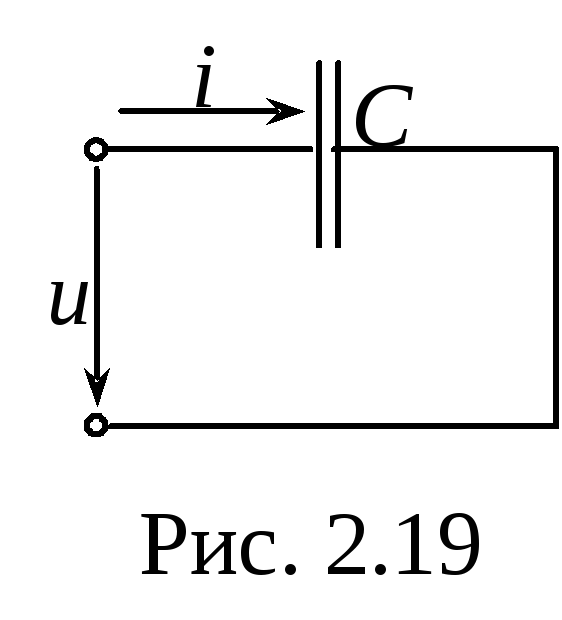 ано:
ано: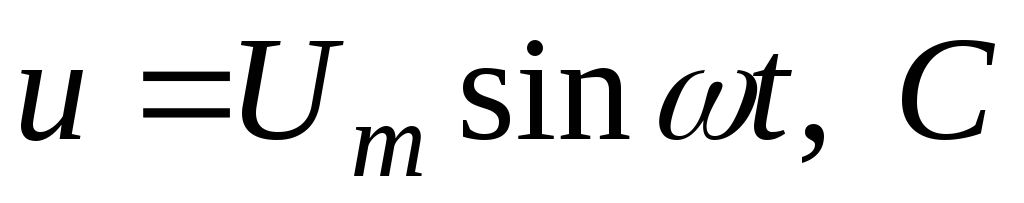 (рис.2.19).
(рис.2.19).
Найти: 

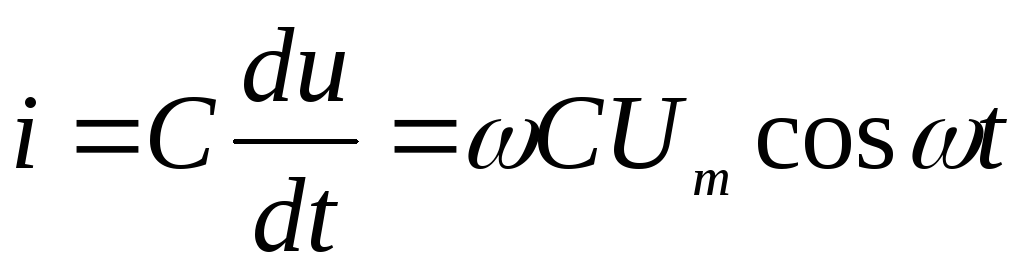 ;
; 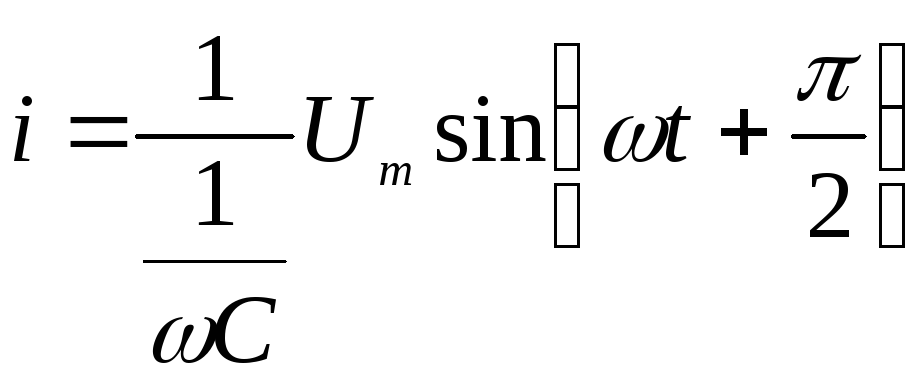 .
.
Ток в ёмкости опережает напряжение на 90º (рис. 2.20)
Обозначим 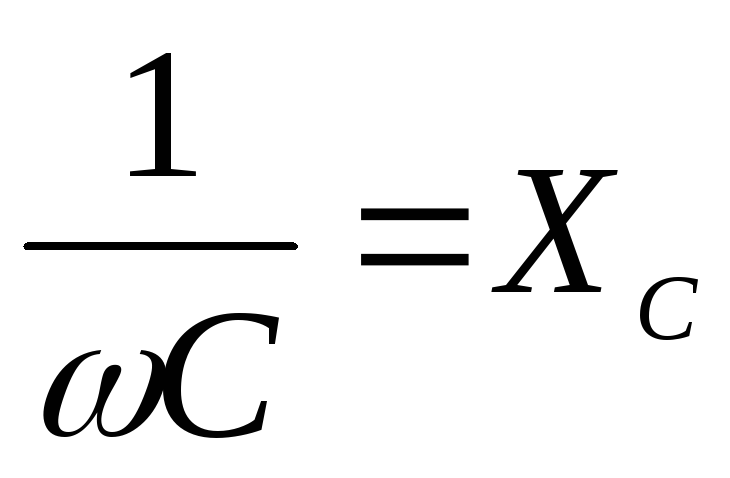 — реактивное сопротивление емкости
— реактивное сопротивление емкости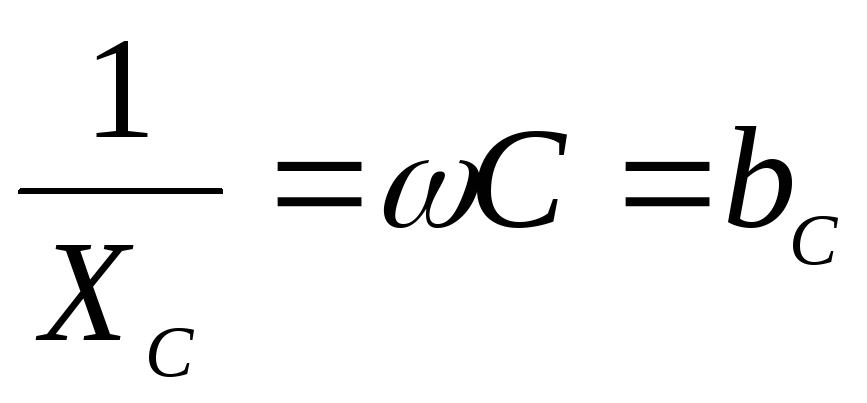 — реактивная проводимость ёмкости.
— реактивная проводимость ёмкости.
Тогда: 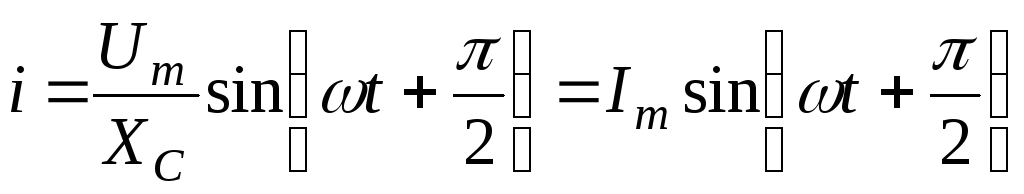 .
.
Амплитуды (действующие значения) напряжения и тока в ёмкости связаны соотношением подобным закону Ома.
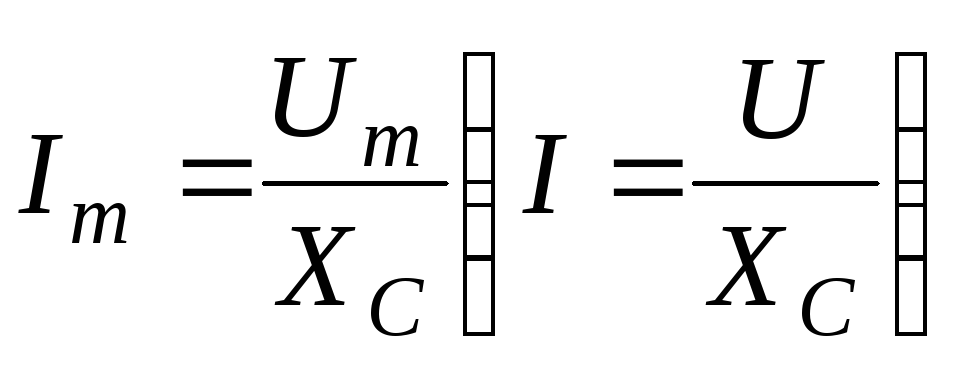
Мгновенная
мощность 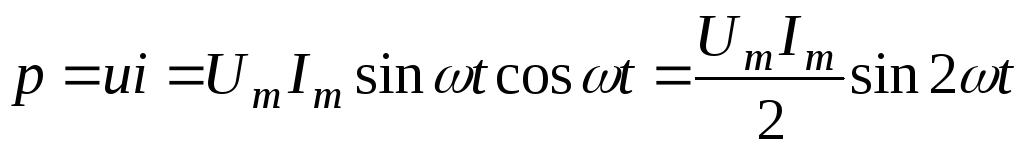 .
.
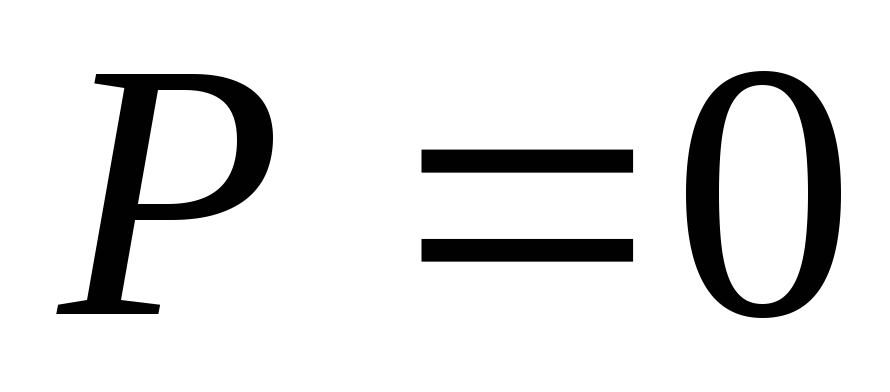
Энергия
электрического поля  ;
;
Синусоидальный ток в цепи r, l, c
Д ано:
ано:
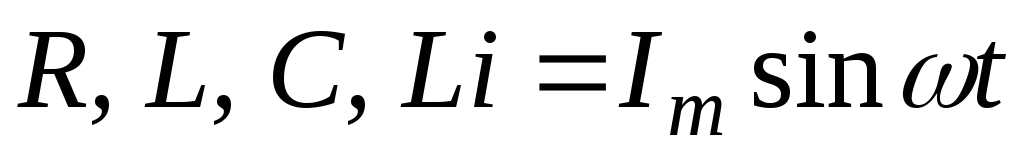 (рис.
2.21).
(рис.
2.21).
Найти: 
Напряжение будем искать в виде
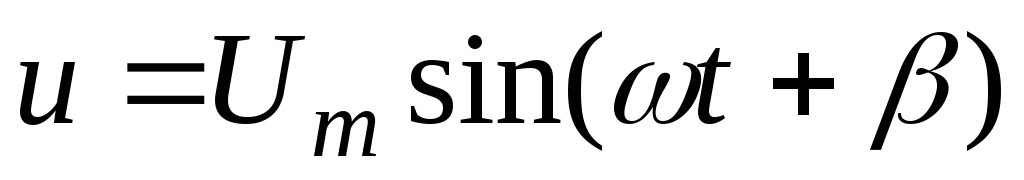 ,
, 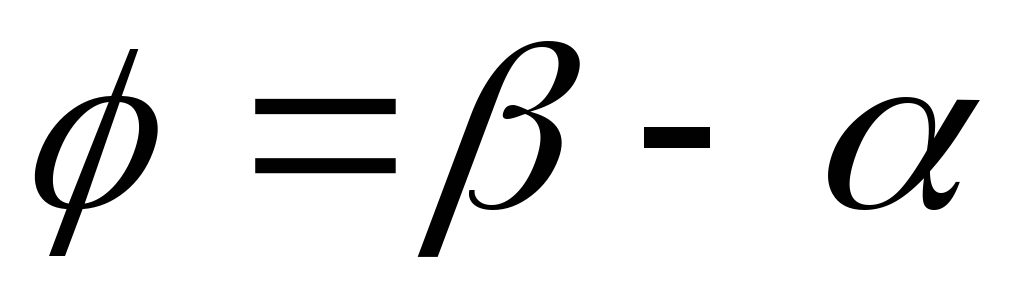 ,
,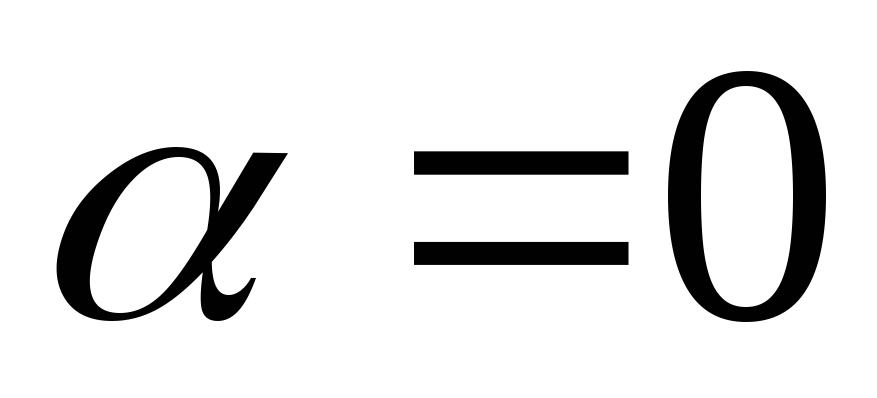 ,
, 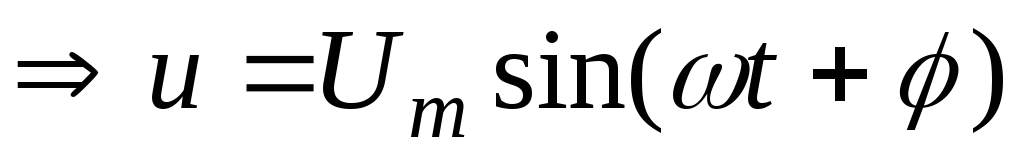
На основании второго закона Кирхгофа:
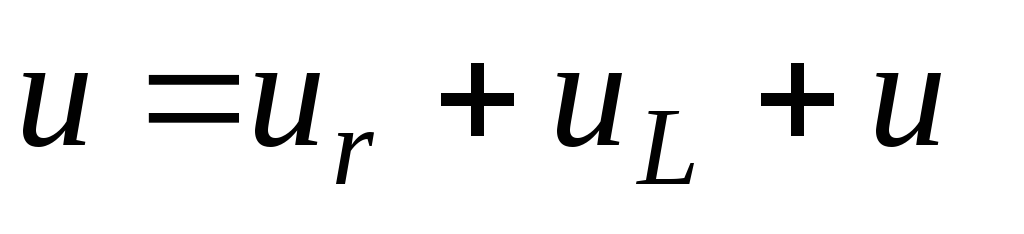
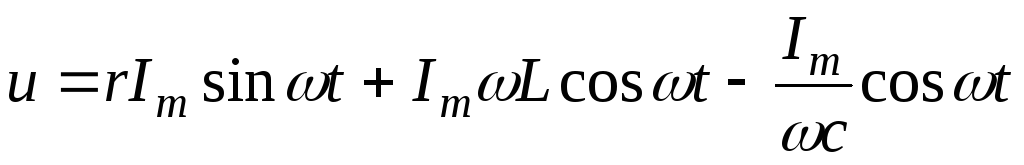 ,
, 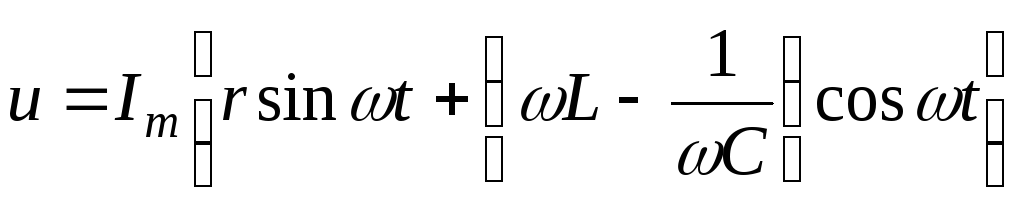 .
.
из тригонометрии:
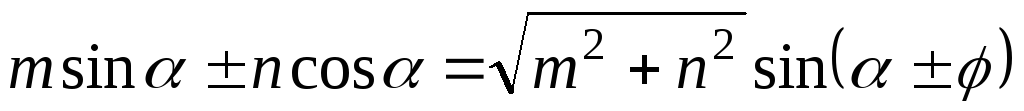 ,
, 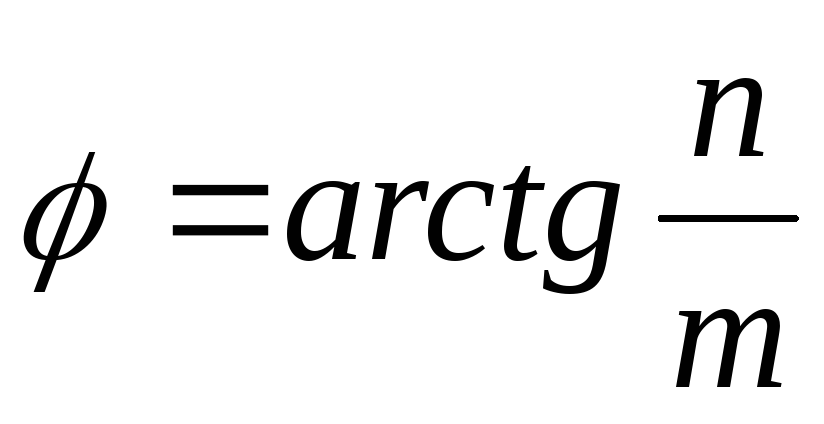 ;
;
Обозначим 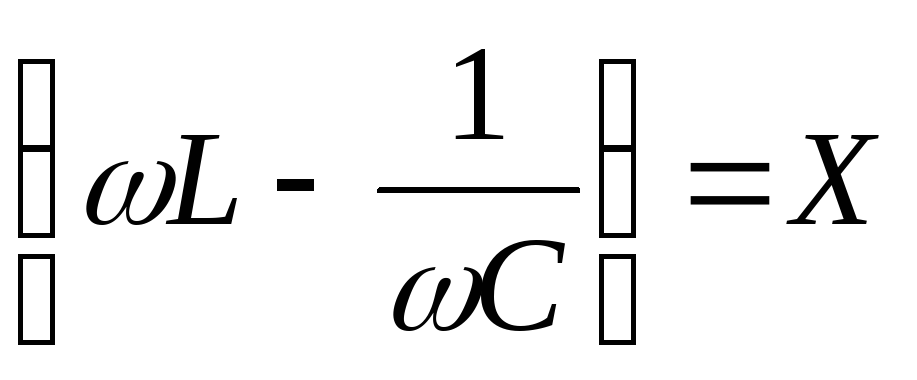 — реактивное сопротивление цепи.
— реактивное сопротивление цепи.
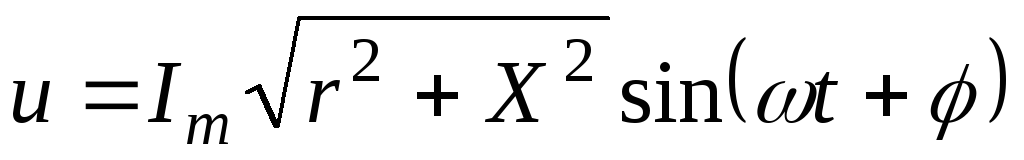 ,
, 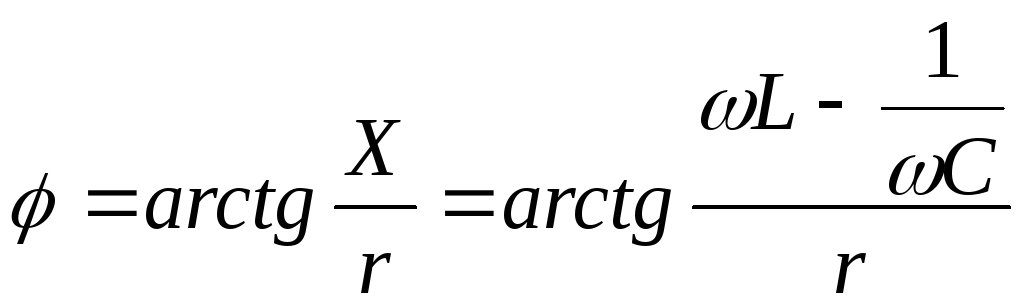 .
.
Отсюда
видно, что 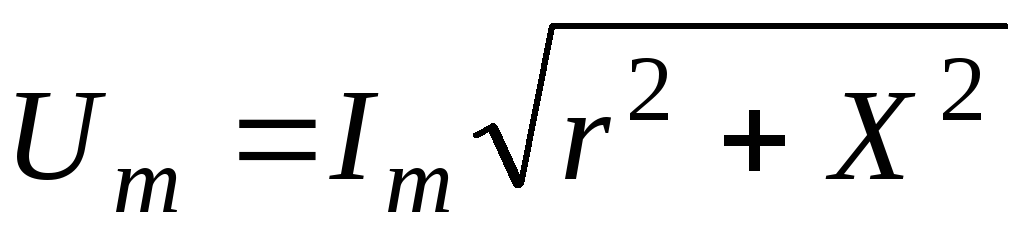 .
Обозначим
.
Обозначим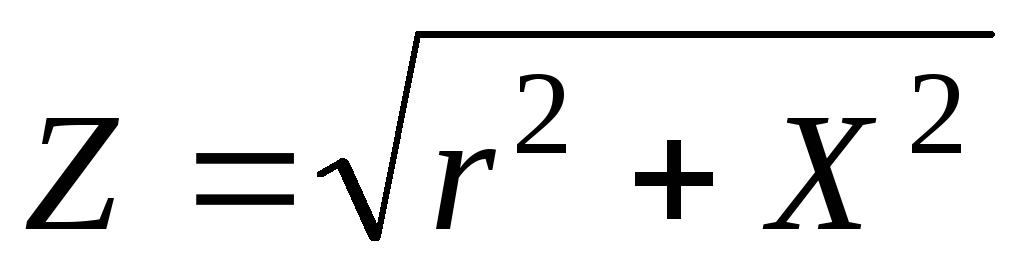 -полное сопротивление цепи, тогда:
-полное сопротивление цепи, тогда:
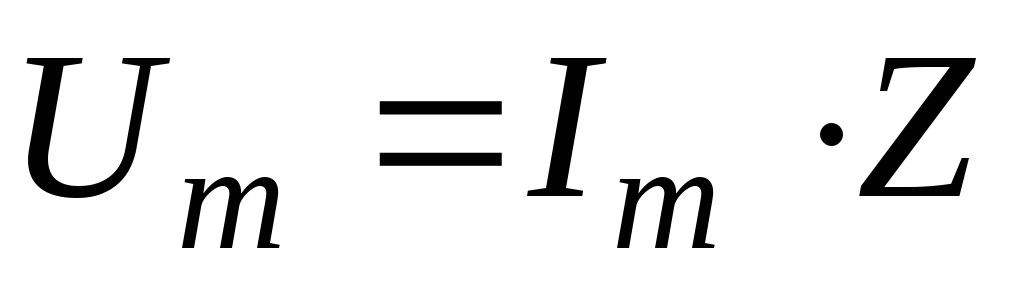 -соотношение
подобное закону Ома.
-соотношение
подобное закону Ома.
т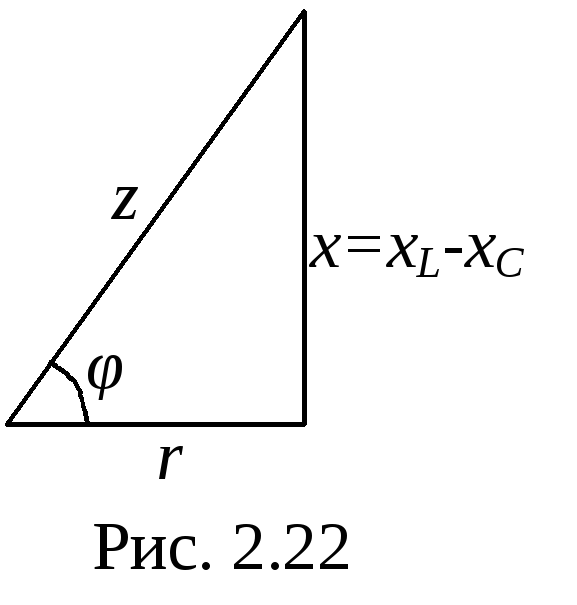 реугольник
сопротивлений (рис. 2.22)
реугольник
сопротивлений (рис. 2.22)
 ;
; 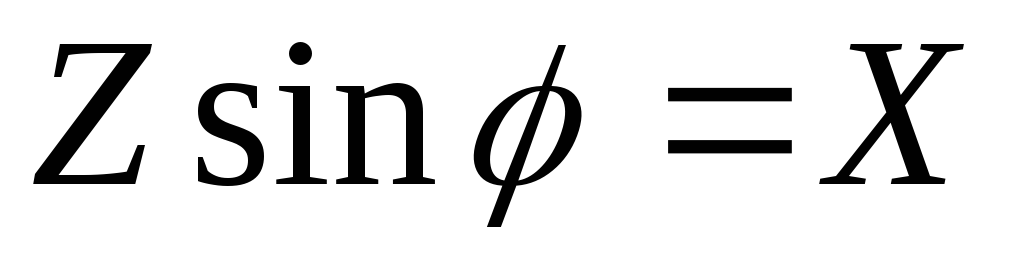
Ели умножить все стороны треугольника сопротивлений на действующее (амплитудное) значение тока, то мы получим треугольник напряжений, в котором катеты – активная и реактивная составляющие входного напряжения (рис. 2.23).
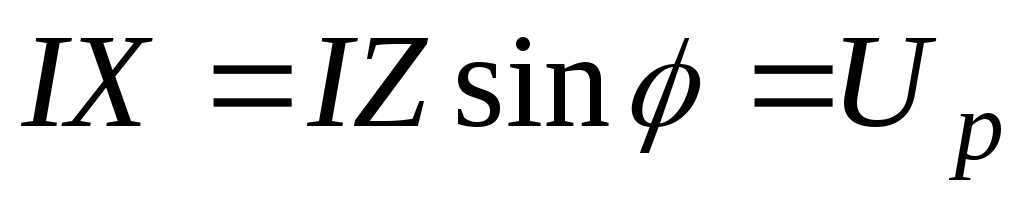 —
реактивная составляющая
—
реактивная составляющая
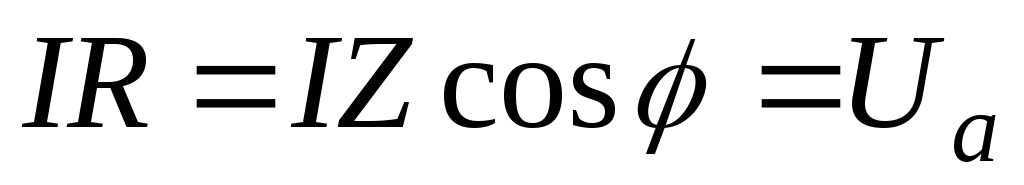 —
активная составляющая
—
активная составляющая
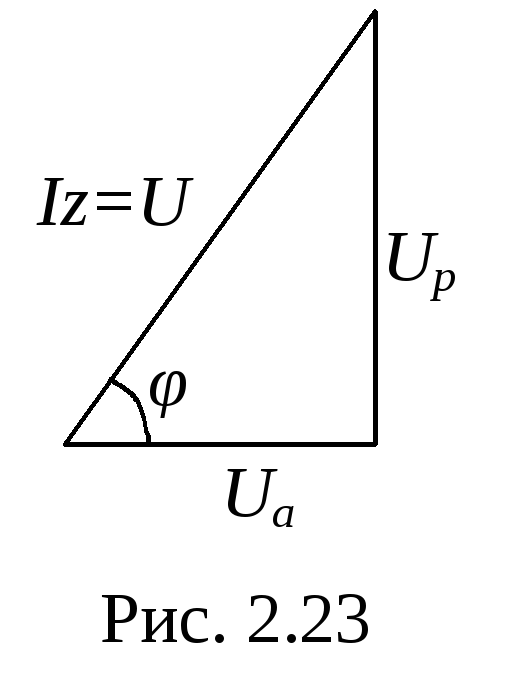
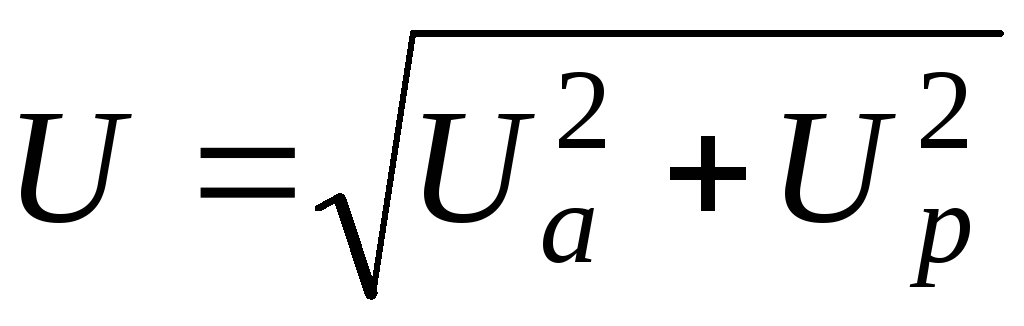
Расчет среднего и среднеквадратичного значений тока и напряжения: формулы и калькулятор
Расчет среднего и среднеквадратичного значений тока и напряжения: формулы и калькулятор
03.04.18
Данный текст является расширенным и углубленным вариантом моей старой заметки на сайте we.easyelectronics.ru.
Введение
В рамках данной заметки рассмотрим способы вычисления среднего и среднеквадратичного значений тока и напряжения. При этом для простоты ограничимся формами сигнала, характерными для импульсных источников питания. Обращаю ваше внимание – все формулы, приводимые в заметке, даются без выводов, дабы не забивать головы читателей мутной и не особо нужной херней. С другой стороны, если кому-то интересно, откуда данные формулы взялись – можно скачать файл, в котором приведены все необходимые выводы с пояснениями.
Основные определения
Будучи в недавнем прошлом яростным разработчиком всевозможных импульсных источников питания (ИИП), интересовался всяким по данной теме (да и сейчас, бывает, трясу стариной). В частности, весьма важными мне всегда казались такие характеристики сигнала, как среднее и среднеквадратичное значение токов и напряжений в различных точках схемы, поскольку при расчетах ИИП данные параметры используются сплошь и рядом. Чтобы понять, где могут быть полезны данные характеристики, сначала определимся с тем, что мы под ними понимаем.
Естественно, существуют строгие «математические» определения как для среднего, так и для среднеквадратичного значений физических величин, периодически изменяющихся во времени по некоторому закону. Однако, больно уж они мутные и абстрактные, и, на мой взгляд, нужны только при выводе формул. Разработчику же гораздо важнее понимать физический смысл используемых в расчетах величин, поэтому приводимые ниже определения среднего и среднеквадратичного значений будут носить сугубо прикладной характер.
Среднее значение переменного тока или напряжения (во вражеских терминах AVG) – это просто их постоянная составляющая. Поэтому вполне очевидно, что среднее значение широко применяется при расчетах схем, выделяющих из переменного сигнала постоянный уровень. Простейший понижающий преобразователь (Step-Down) с LC-фильтром на выходе, RC-цепочка, призванная выделить постоянное напряжение из поступающего на вход ШИМ-сигнала – всё это примеры того, где без использования среднего значения физической величины ничего толком не посчитаешь.
Среднеквадратичное (действующее, эффективное) значение определяется немного сложнее. Как известно, любой переменный ток (напряжение), проходя через активную линейную нагрузку (например, резистор), выделяет на ней некоторое количество тепла. Но так поступает не только переменный сигнал – постоянный ток тоже будет греть резистор.
Так вот, среднеквадратичное значение переменного тока или напряжения (во вражеских терминах RMS) – это такой постоянный ток (напряжение), который за одинаковый промежуток времени нагреет один и тот же резистор точно так же, как и исходный переменный сигнал. Поэтому одно из важнейших применений среднеквадратичного значения – расчет потерь и соответствующего нагрева для различных элементов силовых цепей ИИП. Хочешь узнать статические потери на ключе флайбэка – будь добр посчитать среднеквадратичное значение тока первички. Надо узнать мощность токосчитывающего резистора – туда же. Даже потери (и приблизительный нагрев) в обмотках трансов и дросселей для хиленьких источников и невысоких частот преобразования в первом приближении можно посчитать при помощи среднеквадратичного значения тока, через эти обмотки протекающего.
В общем, среднее и среднеквадратичное значения используются довольно часто. Поэтому неплохо было бы уметь их рассчитывать для любого сигнала, который может нам встретиться в импульсном источнике питания. При этом лично я разделяю токи и напряжения в ИИП на две большие группы: сигналы с простой формой (элементарные) и сигналы со сложной формой (т.е. те, которые могут быть представлены в виде суммы нескольких элементарных). И поскольку принципы расчета среднего и среднеквадратичного значений для этих двух групп немного отличаются, предлагаю рассмотреть их по отдельности.
Сигналы простой формы
У сигналов простой формы вычислить среднее и среднеквадратичное значение довольно легко – для этого надо всего лишь взять соответствующую формулу и подставить в нее нужные значения. Чтобы постоянно не шариться по различным справочникам, я завел себе специальную табличку, в которую свел расчетные формулы для наиболее часто встречающихся элементарных сигналов:
• прямоугольника:
• треугольника:
• трапеции:
• и пилы:
(данные формулы, кстати, взяты не с потолка – их вывод при желании можно посмотреть в специальной заметке-пояснении).
Здесь хотелось бы заострить внимание на нескольких моментах. Во-первых, на приведенных выше рисунках рассматривается по два варианта каждого из простейших сигналов: «в общем виде» и «без смещения». При этом с точки зрения разработчика импульсных источников питания наиболее интересным обычно является именно второй вариант, поэтому для него и даны отдельные формулы (чтобы постоянно не подставлять С=0 в «общие» выражения). Во-вторых, пилообразное напряжение, вообще говоря, является сложным сигналом, поскольку может быть представлено в виде суммы двух простых (либо трапеций, либо треугольников). Однако, пила настолько часто встречается при расчетах ИИП, а выражения AVG и RMS для нее настолько лаконичны и красивы, что я в результате включил-таки ее в список сигналов, среднее и среднеквадратичное значение которых вычисляется тупо всего по одной формуле. Ну и в-третьих, вышеприведенная таблица, в принципе, могла бы состоять всего из одной трапеции, ибо из нее легко получить как прямоугольник, так и треугольник, поставляя соответствующие значения «H», «L» и «C». Однако практика показала, что постоянно этим заниматься весьма муторно, ибо мы рассчитываем источник, а не тренируем математические навыки. Поэтому в итоге я себе выписал готовые формулы AVG и RMS для прямоугольника и треугольника, что оказалось весьма и весьма удобным. Ну а в целом – как ни странно, представленные выше формулы для элементарных сигналов покрывают, наверное, 75-80% всех потребностей разработчика импульсных источников питания, что весьма немало. Однако, всё многообразие токов и напряжений в ИИП отнюдь не ограничивается вышеупомянутыми четырьмя (и даже тремя, если не учитывать пилу) формами. Поэтому рано или поздно любой разработчик импульсников сталкивается с необходимостью вычисления среднего и среднеквадратичного значения сложного сигнала (яркий пример – расчет пуш-пула).
Сигналы сложной формы
Как было сказано выше, сигналы сложной формы – это такие, которые могут быть представлены в виде суммы нескольких элементарных сигналов. Применительно к импульсным источникам питания в качестве последних выступают прямоугольник, треугольник или трапеция, и значительно реже – синус, косинус и прочая «плавная» херня. Отметим, что в данном случае, в отличие от простейших форм, нахождение аналитических выражений для среднего и среднеквадратичного значений обычно превращается в неблагодарное занятие. Например, для вывода «среднеквадратичной» формулы нам надо разбить сложный сигнал на несколько простейших, а затем извлечь квадратный корень из суммы квадратов «элементарных» среднеквадратичных значений (думаю, даже понять, о чем говорится в данном предложении, у вас получится далеко не сразу). Найти среднее значение сложного сигнала немного проще (надо просто просуммировать средние «элементарные» значения), однако поверьте – сделать из этого удобоваримую формулу в подавляющем большинстве случаев не удается:
К счастью, готовая формула для нахождения AVG и RMS сложного сигнала обычно не требуется. Чаще всего нам надо просто узнать среднее или среднеквадратичное значение тока (напряжения) именно для нашего конкретного случая, а не вывести аналитическое выражение на все случаи жизни. А это существенно упрощает задачу, ибо посчитать числовое значение AVG или RMS для каждого элементарного сигнала на соответствующем временно́м интервале не так уж и сложно. В качестве примера можно рассмотреть нахождение среднего и среднеквадратичного значения напряжения, характерного для пушпульной, полумостовой и полномостовой схем (данный расчет есть и в специальной заметке-пояснении):
Как следует из предпоследнего рисунка, для начала нам надо разбить исходный сигнал на элементарные. Очевидно, что это будут три трапеции и один прямоугольник:
Дальше нам надо посчитать среднее и среднеквадратичное значение каждого из четырех элементарных сигналов, для чего воспользуемся формулами из вышеприведенной таблицы. Начнем с первого из них — трапеции №1. Как видно из последнего рисунка, это трапеция без смещения с параметрами
H1=11;
L1=9;
C1=0;
tИ1=0,15∙T.
Поэтому в соответствии с формулами для трапеции, приведенными выше, будем иметь:
Сигнал №2 – это тоже трапеция без смещения. Параметры данной трапеции будут таковы:
H2=21;
L2=19;
C2=0;
tИ2=0,50∙T – 0,15∙T = 0,35∙T.
Поэтому среднее и среднеквадратичное значение второго сигнала составят соответственно
Трапеция №3 полностью совпадает с трапецией №1, просто она сдвинута вправо на полпериода. Поэтому как параметры третьего сигнала, так и его среднее и среднеквадратичное значения будут равны соответствующим значениям первого сигнала:
H3= H1=11;
L3= L1=9;
C3= C1=0;
tИ3= tИ1= 0,65∙T – 0,50∙T = 0,15∙T.
Ну и остался сигнал №4. Данный сигнал представляет собой прямоугольник с параметрами
H4=0,5;
C4=0;
tИ4=1,00∙T – 0,65∙T = 0,35∙T.
И после использования формул для вычисления среднего и среднеквадратичного значения сигнала №4, получим следующее:
Теперь у нас есть все данные для нахождения AVG и RMS исходного сигнала. Как было сказано выше, среднее значение находится как сумма средних значений элементарных сигналов, на которые был разложен «исходник», а среднеквадратичное – как квадратный корень из суммы квадратов «элементарных» среднеквадратичных значений. То есть в нашем случае будем иметь
Для проверки полученного результата используем широко распространенное бесплатное ПО LTSpice IV от компании Linear Technology Corporation (LTC). Сгенерировав сигнал с требуемыми параметрами, измерим в эмуляторе среднее и среднеквадратичное его значение за 5 периодов:
Как видим, результаты работы эмулятора полностью совпадают с расчетными AVG и RMS, т.е. предложенный способ вычисления среднего и среднеквадратичного значений для сложного сигнала вполне имеет право на жизнь. Более того, способ этот довольно прост и не требует от разработчика ИИП никаких особых математических навыков. С другой стороны, муторность рассмотренного алгоритма также налицо. Лично меня дичайше бесит постоянно считать на калькуляторе и выписывать на бумажку средние и среднеквадратичные значения для всех элементарных сигналов, на которые раскладывается исходный, а пото́м складывать их на том же калькуляторе (и это в лучшем случае, ибо если требуется RMS, всё становится еще волшебнее). Поэтому я принял решение сделать себе некий инструмент, упрощающий жизнь разработчика ИИП, которым и хотел бы поделиться с читателями.
Калькулятор
Данный инструмент – это такая специальная «программа» (cko4aTb бесплатно). «Программа» представляет собой обычный экселовский файл (т.к. программист я тот еще), поэтому для работы нам потребуется «Excel» (у меня вот такой: Microsoft® Excel 2002 (10.4302.2625)). Изначальная и основная задача рассматриваемой «программы» – отрисовка формы трапецеидального сигнала с заданными параметрами (рисуется один период), а также вычисление среднего и среднеквадратичного значений для этого сигнала. Также «программа» умеет рисовать переменную составляющую заданной трапеции (она получается если из исходного сигнала вычесть постоянную составляющую) и вычислять ее RMS-значение (это уж так, чисто на всякий случай). Ну и еще предлагаемый софт позволяет быстро посчитать среднее и среднеквадратичное значения для сложного сигнала, состоящего максимум из 16-ти различных элементарных (большее количество в реальной жизни вряд ли потребуется):
Почему в качестве основы взята именно трапеция? Потому что, как было сказано выше, из нее легко получить все основные формы сигналов, встречающихся в импульсных источниках питания, а именно – прямоугольник и треугольник:
Ну а уж на основе этих базовых сигналов можно сляпать и пилу, и напряжение на стоке ключа во флайбэке, и то, что творится на вторичке пушпула и многое другое.
Пользоваться «программой» очень просто. Исходные данные для трапеции вводятся слева в ячейки, выделенные зеленым цветом. После этого чуть ниже можно посмотреть на форму сигнала с введенными параметрами, а еще ниже отобразятся рассчитанные среднее и среднеквадратичное значения этого сигнала. За переменную составляющую трапеции отвечает правый нижний угол экрана (здесь рисуется ее график и рассчитывается значение RMS). Ну а для работы со сложным сигналом предназначен правый верхний угол. Здесь в ячейки, выделенные зеленым цветом, вводятся средние и среднеквадратичные значения элементарных сигналов, из которых состоит «исходник», а ниже рассчитываются уже́ его собственные AVG и RMS.
Отмечу, что на всю «программу» наложена магическая защита, позволяющая редактировать только те ячейки, которые можно. При необходимости защита снимается элементарно («Сервис» => «Защита» => «Снять защиту листа»), однако делать это не рекомендую: можно по дури снести какую-нибудь нужную формулу, восстанавливать которую – лишний геморрой.
Вот, в принципе, и всё описание представленной «программы». Несмотря на свою простоту и очевидность, данный софт довольно существенно помогает и экономит время при расчетах ИИП (ну, во всяком случае, у меня происходит именно так). Например, на расчет среднего и среднеквадратичного значения сложного сигнала, приведенного в предыдущем пункте, понадобится менее минуты. Последовательность действий проста – вводим параметры первой трапеции, затем переписываем рассчитанные для нее значения AVG и RMS в ячейки секции сложного сигнала. Затем то же самое проделываем для остальных трех элементарных функций, из которых состоит «исходник». Всё, остальное «программа» сделает сама, не надо никаких шаманств с бумажками и калькуляторами:
Ну а у меня на сегодня всё. Желаю удачи при проектировании и изготовлении импульсных (и не только) источников питания!
Обсудить эту заметку можно здесь
Ссылки по теме, документация
Заметка-пояснение с выводом формул и примером расчета среднего и среднеквадратичного значений сложного сигнала:
• AVG_RMS.pdf;
Калькулятор для упрощения вычислений среднего и среднеквадратичного значений простых и сложных сигналов:
• AVG_RMS_Calc.xls;
Расчет среднего и среднеквадратичного значений тока/напряжения
..
Вот здесь есть расширенный и углубленный вариант данной заметки
.
.
Будучи в очень недавнем прошлом яростным разработчиком всевозможных импульсных источников питания, интересовался всяким по данной теме. В частности – вычислением среднего (AVG, Average) и среднеквадратичного (действующего, эффективного, RMS) значений напряжений и (особенно) токов, живущих в разрабатываемом источнике. Для тех, кто не помнит/не знает – напомню определение среднеквадратичного значения тока/напряжения из Википедии:
Действующим (эффективным) значением силы переменного тока называют величину постоянного тока, действие которого произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток за время одного периода. В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение силы переменного тока
Посему, хочешь узнать статические потери на ключе флайбэка – будь добр посчитать среднеквадратичное значение тока первички. Надо узнать мощность токосчитывающего резистора – туда же. И про выпрямители во вторичной цепи – та же песня. Даже потери (и приблизительный нагрев) в обмотках трансов и дросселей для хиленьких источников и невысоких частот преобразования в первом приближении можно посчитать при помощи среднеквадратичного значения тока, через эти обмотки протекающего.
Или, например, делаем могучий источник с высоким КПД. Чтобы оптимально спроектировать обмотку магнитного элемента требуются уже среднее значение тока и среднеквадратичное значение переменной составляющей. В общем – куда ни плюнь, везде фигурируют RMS и AVG (среднее значение, а не антивирус, это важно). Поэтому было принято решение сделать себе некий инструмент, упрощающий жизнь разработчика импульсных источников питания. Вот этим инструментом я и хочу поделиться с общественностью – вдруг кому пригодится.
Как нетрудно заметить, данный инструмент («программа») представляет собой обычный Экселовский файл, поскольку в «компьютерном» программировании я вообще ничего не понимаю. В задачу рассматриваемой «программы» входит отрисовка формы трапецеидального сигнала с заданными параметрами (рисуется один период) и отрисовка формы переменной составляющей заданного сигнала. Также «программа» умеет вычислять среднее и среднеквадратичное значения заданного сигнала и RMS-значение его переменной составляющей. Исходные данные вводятся слева в ячейки, выделенные зеленым цветом (на рисунке обведены красным). Рассчитанные значения AVG и RMS, а также среднеквадратичное значение переменной составляющей заданного сигнала отображаются в правой стороне экрана (обведены синим). Ну а картинки рисуются в нижней части экрана: слева – исходный сигнал, справа – его переменная составляющая.
В нагрузку к «программе» идет короткая заметка, в которой выводятся (а не берутся невесть откуда) расчетные формулы для основных форм сигналов в импульсных источниках питания (трапеции, прямоугольника, треугольника, пилы). Также в этой короткой заметке рассмотрен пример расчета AVG и RMS значений сложного сигнала.
Почему в качестве основы взята именно трапеция? Потому, что из нее легко получить все основные формы сигналов, встречающихся в импульсных источниках питания, а именно – прямоугольник
и треугольник
А уж на основе этих базовых сигналов можно сляпать и пилу
и даже то, что творится на вторичке пушпула:
И еще много чего. Пример же расчета среднего и среднеквадратичных значений для сложных (т.е., составленных из простейших) сигналов, повторюсь, есть в короткой заметке-нагрузке. Хотя, если кого-то заинтересует данный аспект, могу впоследствие осветить его и в этом топике.
Вот, в принципе, и всё описание представленной «программы». Желаю удачи при проектировании и изготовлении импульсных (и не только) источников питания!
Примечание: все вопросы лучше валить в камменты после заметки, так как не факт, что я смогу на них на все ответить. А вот шансы на то, что в сообществе найдется более прошаренный человек по твоей теме — довольно хорошие. Но уж если зарегистрироваться на сайте совсем никак — можно воспользоваться возможностями электрической почты: [email protected]
Содержание архива (также прилеплен к заметке):
AVG_RMS.zip:
Среднее_и_среднеквадратичное_Трапеция.xls – собственно, «программа» для расчета AVG и RMS в формате Microsoft Excel;
Среднее и среднеквадратичное.pdf – короткая заметка-нагрузка с выводом расчетных формул и с примером расчета AVG и RMS значений сложного сигнала.
среднеквадратичное значение — это… Что такое среднеквадратичное значение?
- среднеквадратичное значение
3.4 среднеквадратичное значение: Эффективное значение тока.
3.30 среднеквадратичное значение (root-mean-square value): Квадратный корень из среднего значения квадрата функции на заданном интервале (для спектральной плотности таким интервалом является полоса частот между f1 и f2 — см. рисунок 1).
Примечание — В данном методе испытаний среднеквадратичное значение может быть рассчитано для разных видов возбуждения: чисто широкополосного случайного процесса, совокупности широкополосного случайного и гармонического процессов (SoR) или совокупности двух случайных процессов (RoR) — см. В.2.4 (приложение В).
3.30 среднеквадратичное значение (root-mean-square value): Квадратный корень из среднего значения квадрата функции на заданном интервале (для спектральной плотности таким интервалом является полоса частот между f1 и f2 — см. рисунок 1).
Примечание — В данном методе испытаний среднеквадратичное значение может быть рассчитано для разных видов возбуждения: чисто широкополосного случайного процесса, совокупности широкополосного случайного и гармонического процессов (SoR) или совокупности двух случайных процессов (RoR) — см. В.2.4 (приложение В).
Смотри также родственные термины:
3.1.5.1 среднеквадратичное значение корректированного ускорения aw: Усредненная по времени поступательная или угловая вибрация, определяемая формулой
(1)
где aw(x) — текущее значение корректированного ускорения (поступательного или углового) как функция времени;
Т — период измерений.
Определения термина из разных документов: среднеквадратичное значение корректированного ускорения aw
11. Среднеквадратичное значение сигнала
Ндп. Среднеквадратичное значение. Действующее значение. Эффективное значение
Корень квадратный из среднего значения квадрата сигнала
Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.
- среднеквадратическое отклонение повторяемости (сходимости) результатов испытаний
- среднеквадратичное значение корректированного ускорения aw
Смотреть что такое «среднеквадратичное значение» в других словарях:
СРЕДНЕКВАДРАТИЧНОЕ ЗНАЧЕНИЕ — СРЕДНЕКВАДРАТИЧНОЕ ЗНАЧЕНИЕ, в математике величина, получаемая определением СРЕДНЕГО ЗНАЧЕНИЯ множества возведенных в квадрат величин. Предоставляет значение периодически изменяющейся величины и была разработана в начале XX в. для точного… … Научно-технический энциклопедический словарь
среднеквадратичное значение — vidutinė kvadratinė vertė statusas T sritis automatika atitikmenys: angl. root mean square value vok. Effektivwert, m; quadratischer Mittelwert, m rus. среднеквадратичное значение, n pranc. valeur moyenne quadratique, f … Automatikos terminų žodynas
среднеквадратичное значение — efektinis vidurkis statusas T sritis radioelektronika atitikmenys: angl. effective mean value; mean square value; root mean square value vok. quadratischer Mittelwert, m rus. среднеквадратичное значение, n pranc. valeur effective, f; valeur… … Radioelektronikos terminų žodynas
среднеквадратичное значение — kvadratinis vidurkis statusas T sritis fizika atitikmenys: angl. mean effective value; root mean square value vok. quadratischer Mittelwert, m; quadratisches Mittel, n rus. среднеквадратичное значение, n pranc. valeur moyenne quadratique, f … Fizikos terminų žodynas
Среднеквадратичное значение сигнала — 11. Среднеквадратичное значение сигнала Ндп. Среднеквадратичное значение. Действующее значение. Эффективное значение Корень квадратный из среднего значения квадрата сигнала Источник: ГОСТ 16465 70: Сигналы радиотехнические измерительные. Термины… … Словарь-справочник терминов нормативно-технической документации
среднеквадратичное значение корректированного ускорения aw — 3.1.5.1 среднеквадратичное значение корректированного ускорения aw: Усредненная по времени поступательная или угловая вибрация, определяемая формулой (1) где aw(x) текущее значение… … Словарь-справочник терминов нормативно-технической документации
среднеквадратичное значение шума — efektinė triukšmo vertė statusas T sritis radioelektronika atitikmenys: angl. noise root mean square value vok. Mittelquadratrauschwert, m rus. среднеквадратичное значение шума, n pranc. valeur moyenne quadratique de bruit, f … Radioelektronikos terminų žodynas
Среднеквадратичное значение сигналя — 1. Корень квадратный из среднего значения квадрата сигнала Употребляется в документе: ГОСТ 16465 70 Сигналы радиотехнические измерительные. Термины и определения … Телекоммуникационный словарь
текущее среднеквадратичное значение корректированного ускорения aw, — 3.1.5.3 текущее среднеквадратичное значение корректированного ускорения aw, q(t): Среднеквадратичное значение корректированного ускорения в момент времени t, определяемое формулой (3) где aw(x)… … Словарь-справочник терминов нормативно-технической документации
максимальное кратковременное среднеквадратичное значение (корректированного ускорения) MTVV — 3.1.5.4 максимальное кратковременное среднеквадратичное значение (корректированного ускорения) MTVV: Максимальное значение текущего среднеквадратичного значения корректированного ускорения для периода интегрирования q, равного 1 с. Источник: ГОСТ … Словарь-справочник терминов нормативно-технической документации
| На главную | База 1 | База 2 | База 3 |
| Поиск по реквизитамПоиск по номеру документаПоиск по названию документаПоиск по тексту документа |
| Искать все виды документовДокументы неопределённого видаISOАвиационные правилаАльбомАпелляционное определениеАТКАТК-РЭАТПЭАТРВИВМРВМУВНВНиРВНКРВНМДВНПВНПБВНТМ/МЧМ СССРВНТПВНТП/МПСВНЭВОМВПНРМВППБВРДВРДСВременное положениеВременное руководствоВременные методические рекомендацииВременные нормативыВременные рекомендацииВременные указанияВременный порядокВрТЕРВрТЕРрВрТЭСНВрТЭСНрВСНВСН АСВСН ВКВСН-АПКВСПВСТПВТУВТУ МММПВТУ НКММПВУП СНЭВУППВУТПВыпускГКИНПГКИНП (ОНТА)ГНГОСТГОСТ CEN/TRГОСТ CISPRГОСТ ENГОСТ EN ISOГОСТ EN/TSГОСТ IECГОСТ IEC/PASГОСТ IEC/TRГОСТ IEC/TSГОСТ ISOГОСТ ISO GuideГОСТ ISO/DISГОСТ ISO/HL7ГОСТ ISO/IECГОСТ ISO/IEC GuideГОСТ ISO/TRГОСТ ISO/TSГОСТ OIML RГОСТ ЕНГОСТ ИСОГОСТ ИСО/МЭКГОСТ ИСО/ТОГОСТ ИСО/ТСГОСТ МЭКГОСТ РГОСТ Р ЕНГОСТ Р ЕН ИСОГОСТ Р ИСОГОСТ Р ИСО/HL7ГОСТ Р ИСО/АСТМГОСТ Р ИСО/МЭКГОСТ Р ИСО/МЭК МФСГОСТ Р ИСО/МЭК ТОГОСТ Р ИСО/ТОГОСТ Р ИСО/ТСГОСТ Р ИСО/ТУГОСТ Р МЭКГОСТ Р МЭК/ТОГОСТ Р МЭК/ТСГОСТ ЭД1ГСНГСНрГСССДГЭСНГЭСНмГЭСНмрГЭСНмтГЭСНпГЭСНПиТЕРГЭСНПиТЕРрГЭСНрГЭСНсДИДиОРДирективное письмоДоговорДополнение к ВСНДополнение к РНиПДСЕКЕНВиРЕНВиР-ПЕНиРЕСДЗемЕТКСЖНМЗаключениеЗаконЗаконопроектЗональный типовой проектИИБТВИДИКИМИНИнструктивное письмоИнструкцияИнструкция НСАМИнформационно-методическое письмоИнформационно-технический сборникИнформационное письмоИнформацияИОТИРИСОИСО/TRИТНИТОсИТПИТСИЭСНИЭСНиЕР Республика КарелияККарта трудового процессаКарта-нарядКаталогКаталог-справочникККТКОКодексКОТКПОКСИКТКТПММ-МВИМВИМВНМВРМГСНМДМДКМДСМеждународные стандартыМетодикаМетодика НСАММетодические рекомендацииМетодические рекомендации к СПМетодические указанияМетодический документМетодическое пособиеМетодическое руководствоМИМИ БГЕИМИ УЯВИМИГКМММНМОДНМонтажные чертежиМос МУМосМРМосСанПинМППБМРМРДСМРОМРРМРТУМСанПиНМСНМСПМТМУМУ ОТ РММУКМЭКННАС ГАНБ ЖТНВННГЭАНДНДПНиТУНКНормыНормы времениНПНПБНПРМНРНРБНСПНТПНТП АПКНТП ЭППНТПДНТПСНТСНЦКРНЦСОДМОДНОЕРЖОЕРЖкрОЕРЖмОЕРЖмрОЕРЖпОЕРЖрОКОМТРМОНОНДОНКОНТПОПВОПКП АЭСОПНРМСОРДОСГиСППиНОСНОСН-АПКОСПОССПЖОССЦЖОСТОСТ 1ОСТ 2ОСТ 34ОСТ 4ОСТ 5ОСТ ВКСОСТ КЗ СНКОСТ НКЗагОСТ НКЛесОСТ НКМОСТ НКММПОСТ НКППОСТ НКПП и НКВТОСТ НКСМОСТ НКТПОСТ5ОСТНОСЭМЖОТРОТТПП ССФЖТПБПБПРВПБЭ НППБЯПВ НППВКМПВСРПГВУПереченьПиН АЭПисьмоПМГПНАЭПНД ФПНД Ф СБПНД Ф ТПНСТПОПоложениеПорядокПособиеПособие в развитие СНиППособие к ВНТППособие к ВСНПособие к МГСНПособие к МРПособие к РДПособие к РТМПособие к СНПособие к СНиППособие к СППособие к СТОПособие по применению СППостановлениеПОТ РПОЭСНрППБППБ-АСППБ-СППБВППБОППРПРПР РСКПР СМНПравилаПрактическое пособие к СППРБ АСПрейскурантПриказПротоколПСРр Калининградской областиПТБПТЭПУГПУЭПЦСНПЭУРР ГазпромР НОПРИЗР НОСТРОЙР НОСТРОЙ/НОПР РСКР СМНР-НП СРО ССКРазъяснениеРаспоряжениеРАФРБРГРДРД БГЕИРД БТРД ГМРД НИИКраностроенияРД РОСЭКРД РСКРД РТМРД СМАРД СМНРД ЭОРД-АПКРДИРДМРДМУРДПРДСРДТПРегламентРекомендацииРекомендацияРешениеРешение коллегииРКРМРМГРМДРМКРНДРНиПРПРРТОП ТЭРС ГАРСНРСТ РСФСРРСТ РСФСР ЭД1РТРТМРТПРУРуководствоРУЭСТОП ГАРЭГА РФРЭСНрСАСанитарные нормыСанитарные правилаСанПиНСборникСборник НТД к СНиПСборники ПВРСборники РСН МОСборники РСН ПНРСборники РСН ССРСборники ценСБЦПСДАСДАЭСДОССерияСЗКСНСН-РФСНиПСНиРСНККСНОРСНПСОСоглашениеСПСП АССП АЭССправочникСправочное пособие к ВСНСправочное пособие к СНиПСправочное пособие к СПСправочное пособие к ТЕРСправочное пособие к ТЕРрСРПССНССЦСТ ССФЖТСТ СЭВСТ ЦКБАСТ-НП СРОСТАСТКСТМСТНСТН ЦЭСТОСТО 030 НОСТРОЙСТО АСЧМСТО БДПСТО ВНИИСТСТО ГазпромСТО Газпром РДСТО ГГИСТО ГУ ГГИСТО ДД ХМАОСТО ДОКТОР БЕТОНСТО МАДИСТО МВИСТО МИСТО НААГСТО НАКССТО НКССТО НОПСТО НОСТРОЙСТО НОСТРОЙ/НОПСТО РЖДСТО РосГеоСТО РОСТЕХЭКСПЕРТИЗАСТО САСТО СМКСТО ФЦССТО ЦКТИСТО-ГК «Трансстрой»СТО-НСОПБСТПСТП ВНИИГСТП НИИЭССтП РМПСУПСССУРСУСНСЦНПРТВТЕТелеграммаТелетайпограммаТематическая подборкаТЕРТЕР Алтайский крайТЕР Белгородская областьТЕР Калининградской областиТЕР Карачаево-Черкесская РеспубликаТЕР Краснодарского краяТЕР Мурманская областьТЕР Новосибирской областиТЕР Орловской областиТЕР Республика ДагестанТЕР Республика КарелияТЕР Ростовской областиТЕР Самарской областиТЕР Смоленской обл.ТЕР Ямало-Ненецкий автономный округТЕР Ярославской областиТЕРмТЕРм Алтайский крайТЕРм Белгородская областьТЕРм Воронежской областиТЕРм Калининградской областиТЕРм Карачаево-Черкесская РеспубликаТЕРм Мурманская областьТЕРм Республика ДагестанТЕРм Республика КарелияТЕРм Ямало-Ненецкий автономный округТЕРмрТЕРмр Алтайский крайТЕРмр Белгородская областьТЕРмр Карачаево-Черкесская РеспубликаТЕРмр Краснодарского краяТЕРмр Республика ДагестанТЕРмр Республика КарелияТЕРмр Ямало-Ненецкий автономный округТЕРпТЕРп Алтайский крайТЕРп Белгородская областьТЕРп Калининградской областиТЕРп Карачаево-Черкесская РеспубликаТЕРп Краснодарского краяТЕРп Республика КарелияТЕРп Ямало-Ненецкий автономный округТЕРп Ярославской областиТЕРрТЕРр Алтайский крайТЕРр Белгородская областьТЕРр Калининградской областиТЕРр Карачаево-Черкесская РеспубликаТЕРр Краснодарского краяТЕРр Новосибирской областиТЕРр Омской областиТЕРр Орловской областиТЕРр Республика ДагестанТЕРр Республика КарелияТЕРр Ростовской областиТЕРр Рязанской областиТЕРр Самарской областиТЕРр Смоленской областиТЕРр Удмуртской РеспубликиТЕРр Ульяновской областиТЕРр Ямало-Ненецкий автономный округТЕРррТЕРрр Ямало-Ненецкий автономный округТЕРс Ямало-Ненецкий автономный округТЕРтр Ямало-Ненецкий автономный округТехнический каталогТехнический регламентТехнический регламент Таможенного союзаТехнический циркулярТехнологическая инструкцияТехнологическая картаТехнологические картыТехнологический регламентТИТИ РТИ РОТиповая инструкцияТиповая технологическая инструкцияТиповое положениеТиповой проектТиповые конструкцииТиповые материалы для проектированияТиповые проектные решенияТКТКБЯТМД Санкт-ПетербургТНПБТОИТОИ-РДТПТПРТРТР АВОКТР ЕАЭСТР ТСТРДТСНТСН МУТСН ПМСТСН РКТСН ЭКТСН ЭОТСНэ и ТЕРэТССЦТССЦ Алтайский крайТССЦ Белгородская областьТССЦ Воронежской областиТССЦ Карачаево-Черкесская РеспубликаТССЦ Ямало-Ненецкий автономный округТССЦпгТССЦпг Белгородская областьТСЦТСЦ Белгородская областьТСЦ Краснодарского краяТСЦ Орловской областиТСЦ Республика ДагестанТСЦ Республика КарелияТСЦ Ростовской областиТСЦ Ульяновской областиТСЦмТСЦО Ямало-Ненецкий автономный округТСЦп Калининградской областиТСЦПГ Ямало-Ненецкий автономный округТСЦэ Калининградской областиТСЭМТСЭМ Алтайский крайТСЭМ Белгородская областьТСЭМ Карачаево-Черкесская РеспубликаТСЭМ Ямало-Ненецкий автономный округТТТТКТТПТУТУ-газТУКТЭСНиЕР Воронежской областиТЭСНиЕРм Воронежской областиТЭСНиЕРрТЭСНиТЕРэУУ-СТУказУказаниеУказанияУКНУНУОУРврУРкрУРррУРСНУСНУТП БГЕИФАПФедеральный законФедеральный стандарт оценкиФЕРФЕРмФЕРмрФЕРпФЕРрФормаФорма ИГАСНФРФСНФССЦФССЦпгФСЭМФТС ЖТЦВЦенникЦИРВЦиркулярЦПИШифрЭксплуатационный циркулярЭРД |
| Показать все найденныеПоказать действующиеПоказать частично действующиеПоказать не действующиеПоказать проектыПоказать документы с неизвестным статусом |
| Упорядочить по номеру документаУпорядочить по дате введения |