2.1.3.Среднее значение переменного тока и напряжения

Среднее значение переменного напряжения, ЭДС и тока за период равно нулю, так как площадь отрицательных и положительных полуволн синусоид равны по величине и различны по знаку (рис.2.6).

е,u,i e

u i

0t

0

T/2

T

Рис.2.6

Поэтому, когда говорят о среднем значении переменного тока i, напряжения u или ЭДС е, под ним подразумевается среднее значение за половину периода Т/2 между двумя нулевыми значениями величины 0 и .

Например, среднее значение переменной ЭДС любого вида определяется так:

Если ЭДС изменяется по синусоидальному закону е , то можно установить простую зависимость между средним значением ЭДС E_ср и его амплитудным значением Е

m_.

а так как ,

то =0,637.

Аналогично получим средние значения напряжения и тока:

2.1.4. Действующее значение переменного тока и напряжения.

В электротехнике часто приходится иметь дело с тепловыми и механическими действиями переменного тока.

Механическая сила взаимодействия двух проводников с одинаковыми токами и тепловое действие тока пропорциональны квадрату мгновенных значений тока. Для переменного тока тепловое или механическое действие определяется средним значением квадратов токов за период, называемым действующим значением тока.

Иначе говоря, действующее значение переменного тока равняется постоянному току, выделяющему за время, равное периоду, в каком-либо проводнике такое же количество тепла, что и данный переменный ток.

Количество теплоты, выделяемое постоянным током в резисторе с активным сопротивлением r за промежуток времени Т, равный периоду переменного тока, составляет:

=0,24

Количество теплоты, выделяемое переменным током в том же эелементе за промежуток времени dt, равно:

Количество теплоты, выделяемое за период Т, равно:

Приравнивая количество теплоты, выделяемое постоянным и переменным током, получим:

=

Отсюда получим действующее значение тока:

Аналогично для напряжений и ЭДС переменного тока имеем:

Выражения для I,U и Е определяют в общем виде действующие периодические токи, напряжение и ЭДС при любом законе их изменения.

Для синусоидального переменного тока i= будем иметь:

Второй интеграл равен нулю, и для действующего синусоидального тока имеем:

Аналогично получим выражение для действующих синусоидальных ЭДС и напряжения:

.

Градация вольтметров и амперметров, предназначенных для работы в цепи синусоидального тока, обычно показывает непосредственно действующие значения напряжения или тока.

2.1.5.Векторные диаграммы переменного тока.

Как было установлено, гармонически изменяющееся напряжение в общем виде определяется выражением:

Зная амплитуду напряжения и аргумент синусоидальной функции , можно с помощью несложных математических операций определить мгновенные значения напряжения u в любой момент времени.

Наряду с аналитическим способом расчета получить u можно графически, например, по временной диаграмме гармонической переменной (рис.2.7).

Однако при различных расчетах бывает удобнее пользоваться методом векторных диаграмм. Применение векторных диаграмм при исследовании цепей переменного тока позволяет наглядно представить рассматриваемые процессы и упрощать производимые расчеты.

Y U

u Х u

0

u=0

Рис.2.7

Синусоидальный ток и напряжение можно представить как вектор, движущийся по окружности со скоростью Мгновенные значения будут равны проекции этого вектора на ось Y.

Суть данного метода заключается в следующем: если какая-нибудь точка движется с постоянной скоростью по окружности, то её проекция на любой диаметр (горизонтальный- воображаемая ось Х или вертикальная- ось Y) совершает гармонические(синусоидальные колебания). Радиус-вектор ( в дальнейшем для краткости будем называть просто вектор) этой точки вращается с постоянной угловой скоростью

Y U_{m U}

X 0

U_m

Рис.2.8

Если этот вектор (рис.2.8) в известном, произвольно выбранном масштабе изображающий амплитуду напряжения ( тока и ЭДС), занимает в начальный момент времени (t=0) горизонтальное положение, вправо от центра вращения 0 и вращается против часовой стрелки с угловой скоростью , то в произвольный момент времени t, когда он образует с горизонталью угол

, проекция его на вертикальную ось Y в том же масштабе покажет соответствующее мгновенное напряжение:

Если же вектор в начальный момент расположен не горизонтально, а образует с осью абсцисс Х угол , то проекция на ось Y покажет мгновенное значение напряжения опережающее предыдущее на часть периода . Представим этот случай графически. Расположим под углом относительно положительной оси абсцисс вектора ,длина которого в заранее выбранном масштабе равна амплитуде изображаемой гармонической величины (рис.2.9).

Y

U

0 X

Рис.2.9

Положительные углы ( начальные фазы напряжения , а так же только принято откладывать в направлении против часовой стрелки, а отрицательные( )-по часовой стрелке ( рис.2.9, показана положительная начальная фаза напряжения ).

Предположим, что вектор , начиная с момента времени t=0, вращается вокруг начала координат против часовой стрелки с постоянной частотой вращения , равной угловой частоте изображаемого напряжения.

В момент времени t вектор повернется на угол и будет расположен под углом по отношению к оси абсцисс X.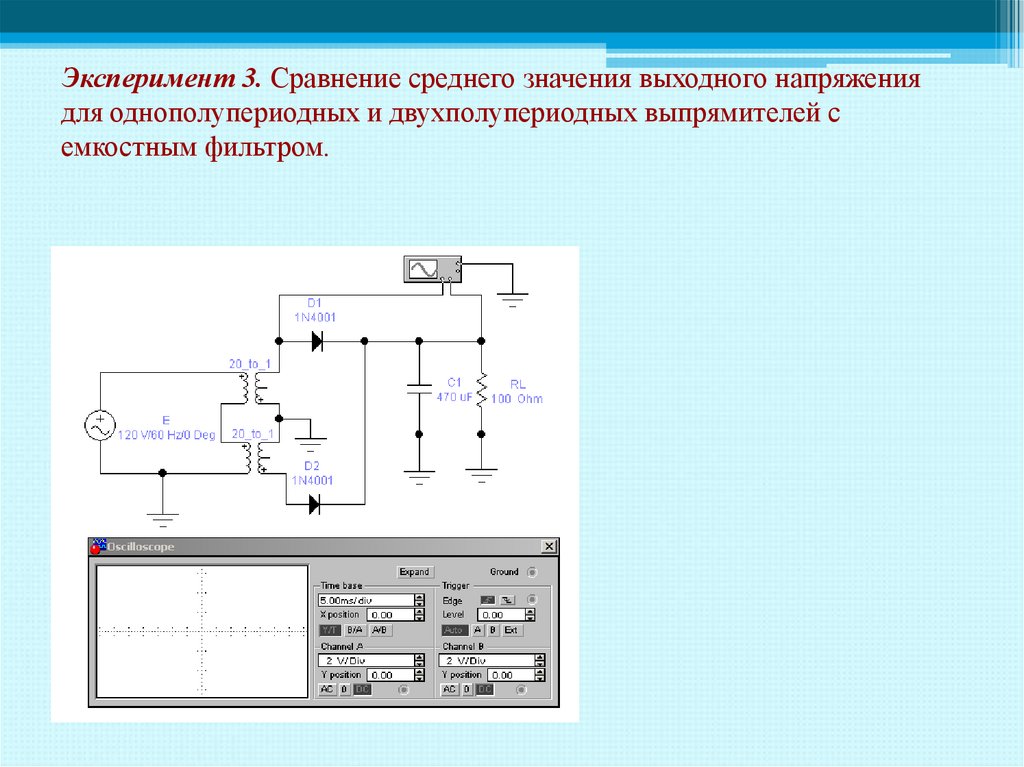

Проекция этого вектора на ось координат Y в выбранном масштабе равна мгновенному значению изображаемого напряжения .

Следовательно, величину, изменяющуюся гармонически во времени, можно изображать вращающимся вектором. При начальной фазе, равной нулю ( когда , вектор для t=0. (рис.2.8) расположен на оси абсцисс.

При больше или меньше 0 положение вектора для t=0 определяется знаком и величиной начальной фазы напряжения.

Обычно при расчете цепи используются действующие ЭДС, напряжения и токи( или амплитуды этих величин), а так же их сдвиг по фазе относительно друг друга. Поэтому рассматриваются неподвижные векторы для некоторого момента времени, который выбирается так, чтобы диаграмма была наглядней. Такая диаграмма называется векторной. Иными словами векторная диаграмма является совокупностью векторов, изображающих движущие синусоидальные ЭДС, напряжение и токи или их амплитудные значения. Углы сдвига по фазе откладываются в направлении вращении векторов (против часовой стрелки), если они положительны (например,

, и в обратном направлении, если они отрицательны (. Если, например, начальный фазовый угол ЭДС больше начального фазового угла (см.временную диаграмму на рис.2.10), то соответственно сдвиг по фазе и этот угол откладывается в положительном направлении от вектора тока (рис.2.10).

Мгновенные значения ЭДС и тока в начальный момент отсчета ( для определяются проекциями амплитудных значений их векторов на ось ординат Y в заданном масштабе расчетных параметров e и i.

Рассмотрим сложение ЭДС, токов и напряжений на векторной диаграмме. При исследовании цепи переменного тока часто приходится складывать ЭДС, токи и напряжения одной и той же частоты.

Y

e₀ E_me,i

e i

I_m X

0

Рис. 2.10

Предположим, что требуется сложить две ЭДС:

Такое сложение можно осуществить аналитически ( путем математических вычислений) и графически с помощью векторных диаграмм. Последний способ более нагляден и прост. Две складываемые ЭДС е₁ и е₂ в определенном масштабе представлены векторами и

Y e e₁ e₂

e E_m

e₁ E₁

E_2m Ψ_2e E_1m E_2m

e₂ Ψ_e Ψ_1e

0 Ψ_1e Ψ_e Ψ_2e

Рис. 2.11

При вращении этих векторов с одинаковой частотой вращения, равной угловой частоте переменного тока , взаимное расположение вращающихся векторов относительно друг друга остается неизменным. Сумма проекций вращающихся векторов и на ось ординат (е₁ и е₂) равна проекции на ту же ось Y вектора , равного геометрической сумме векторов и :

.

Указанный способ сложения двух ЭДС универсален, его можно применить для сложения и вычитания любого числа ЭДС, напряжений и токов одной частоты. При этом операцию вычитания можно представить в виде сложения, проведя элементарные преобразования.

Например, , то есть уменьшаемая величина складывается с вычитаемой, взятой с обратным знаком.

На практике векторные диаграммы, как правило, строятся не для амплитудных значений переменных ЭДС, напряжений и токов, а для действующих величие E,U и I, пропорциональных амплитудных значениям так как все расчеты цепей выполняются для действующих значений ЭДС, напряжений и токов.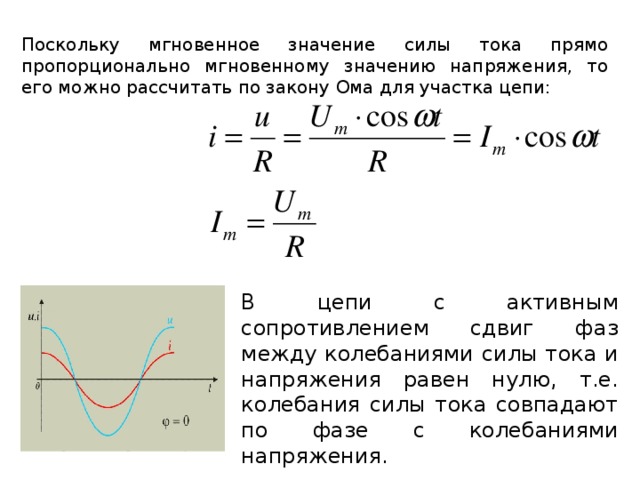

Электротехника

Электротехника

Евсюков А. А. Электротехника: Учеб. пособие для студентов физ. спец. пед. ин-тов.— М.: Просвещение, 1979.— 248 с. В пособии описаны линейные цепи переменного тока, трехфазные цепи, электрические измерения и приборы, трансформаторы, электрические машины переменного и постоянного токов, элементы автоматики, а также техника безопасности. Приведены основные правила работы в учебной электротехнической лаборатории. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ ГЛАВА I. ЛИНЕЙНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА 1. ОДНОФАЗНЫЕ ЦЕПИ § 1.2. ПРИНЦИП ПОЛУЧЕНИЯ ПЕРЕМЕННОЙ СИНУСОИДАЛЬНОЙ ЭДС § 1.3. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ ТОКА И НАПРЯЖЕНИЯ § 1.4. СРЕДНЕЕ ЗНАЧЕНИЕ ПЕРЕМЕННОГО ТОКА § 1. 5. МЕТОД ВЕКТОРНЫХ ДИАГРАММ § 1.6. СОПРОТИВЛЕНИЯ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА § 1.7. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ СОПРОТИВЛЕНИЕМ § 1.8. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ИНДУКТИВНОСТЬЮ § 1.9. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНО-ИНДУКТИВНОЙ НАГРУЗКОЙ § 1.10. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ЕМКОСТЬЮ § 1.11. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНО-ЕМКОСТНОЙ НАГРУЗКОЙ § 1.12. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ R, L И С. КОЭФФИЦИЕНТ МОЩНОСТИ § 1.13. РЕЗОНАНС НАПРЯЖЕНИЙ § 1.14. РЕЗОНАНС ТОКОВ § 1.15. СПОСОБЫ ПОВЫШЕНИЯ КОЭФФИЦИЕНТА МОЩНОСТИ § 1.16. ПРОВОДИМОСТЬ И РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ § 1.17. СИМВОЛИЧЕСКИЙ МЕТОД 2. ТРЕХФАЗНЫЕ ЦЕПИ § 1.19. ПРИНЦИП ПОСТРОЕНИЯ ТРЕХФАЗНОЙ СИСТЕМЫ § 1.20. СОЕДИНЕНИЕ ЗВЕЗДОЙ § 1.21. СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ § 1.22. МОЩНОСТЬ ТРЕХФАЗНОЙ СИСТЕМЫ ГЛАВА II. ЭЛЕКТРИЧЕСКИЕ ИЗМЕРЕНИЯ И ПРИБОРЫ § 2.3. ПОГРЕШНОСТИ ЭЛЕКТРИЧЕСКИХ ИЗМЕРЕНИЙ § 2.4. ОСНОВНЫЕ ДЕТАЛИ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ § 2.5. МАГНИТОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ § 2. 6. ЭЛЕКТРОМАГНИТНЫЕ ПРИБОРЫ § 2.7. ЭЛЕКТРОДИНАМИЧЕСКИЕ ПРИБОРЫ § 2.8. ФЕРРОДИНАМИЧЕСКИЕ ПРИБОРЫ § 2.9. ЭЛЕКТРОДИНАМИЧЕСКИЕ ВАТТМЕТРЫ § 2.10. ОДНОФАЗНЫЙ ФАЗОМЕТР § 2.11. ОДНОФАЗНЫЙ ИНДУКЦИОННЫЙ СЧЕТЧИК ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ § 2.12. ОММЕТРЫ § 2.13. ЛОГОМЕТРЫ § 2.14. ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ § 2.15. ДЕТЕКТОРНЫЕ ПРИБОРЫ § 2.16. ШКОЛЬНЫЕ ДЕМОНСТРАЦИОННЫЕ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ § 2.17. ПОНЯТИЕ О ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ ПРИБОРАХ § 2.18. ИЗМЕРЕНИЕ МОЩНОСТИ ТРЕХФАЗНОЙ СИСТЕМЫ § 2.19. ИЗМЕРЕНИЕ ЭНЕРГИИ ТРЕХФАЗНОЙ СИСТЕМЫ § 2.20. СПОСОБЫ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА МОЩНОСТИ § 2.21. ПОНЯТИЕ ОБ ИЗМЕРЕНИЯХ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН ЭЛЕКТРИЧЕСКИМИ МЕТОДАМИ ГЛАВА III. ТРАНСФОРМАТОРЫ § 3.2. УСТРОЙСТВО И ПРИНЦИП РАБОТЫ ТРАНСФОРМАТОРА § 3.3. ХОЛОСТОЙ РЕЖИМ РАБОТЫ ТРАНСФОРМАТОРА § 3.4. РАБОЧИЙ РЕЖИМ ТРАНСФОРМАТОРА § 3.5. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ТРАНСФОРМАТОРА § 3.6. ТРЕХФАЗНЫЕ ТРАНСФОРМАТОРЫ § 3.7. КОНСТРУКЦИИ ТРАНСФОРМАТОРОВ § 3. 8. АВТОТРАНСФОРМАТОР § 3.9. ИЗМЕРИТЕЛЬНЫЕ ТРАНСФОРМАТОРЫ Глава IV. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ВЫПРЯМИТЕЛИ 4.1. ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ И ЭЛЕМЕНТОВ § 4.2. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ § 4.3. ТИРИСТОРЫ § 4.4. ОСНОВНЫЕ СХЕМЫ ВЫПРЯМЛЕНИЯ ПЕРЕМЕННОГО ТОКА § 4.5. ПРИМЕНЕНИЕ ТИРИСТОРОВ ДЛЯ ВЫПРЯМЛЕНИЯ И РЕГУЛИРОВАНИЯ ТОКА § 4.6. СГЛАЖИВАЮЩИЕ ФИЛЬТРЫ § 4.7. ПОНЯТИЕ ОБ ИНВЕРТОРАХ § 4.8. ФЕРРОРЕЗОНАНС В НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ § 4.9. ФЕРРОРЕЗОНАНСНЫЙ СТАБИЛИЗАТОР НАПРЯЖЕНИЯ § 4.10. ШКОЛЬНЫЕ ВЫПРЯМИТЕЛИ ГЛАВА V. МАШИНЫ ПЕРЕМЕННОГО ТОКА § 5.1. КЛАССИФИКАЦИЯ МАШИН ПЕРЕМЕННОГО ТОКА § 5.2. ПРИНЦИП РАБОТЫ И УСТРОЙСТВО АСИНХРОННОГО ДВИГАТЕЛЯ § 5.3. СОЗДАНИЕ ВРАЩАЮЩЕГОСЯ МАГНИТНОГО ПОЛЯ ТРЕХФАЗНОЙ СИСТЕМОЙ § 5.4. СКОРОСТЬ ВРАЩЕНИЯ МАГНИТНОГО ПОЛЯ. ТИПЫ ОБМОТОК СТАТОРА § 5.5. СКОЛЬЖЕНИЕ АСИНХРОННЫХ ДВИГАТЕЛЕЙ § 1.6. МАГНИТНЫЙ ПОТОК ЭДС И ТОКИ АСИНХРОННОГО ДВИГАТЕЛЯ § 5.7. ВЕКТОРНАЯ ДИАГРАММА АСИНХРОННОГО ДВИГАТЕЛЯ § 5. 8. АСИНХРОННЫЙ ДВИГАТЕЛЬ С КОНТАКТНЫМИ КОЛЬЦАМИ § 5.9. РАБОЧИЕ ХАРАКТЕРИСТИКИ АСИНХРОННОГО ДВИГАТЕЛЯ § 5.10. ПУСК В ХОД АСИНХРОННЫХ ДВИГАТЕЛЕЙ § 5.11. РЕВЕРСИРОВАНИЕ И РЕГУЛИРОВАНИЕ СКОРОСТИ АСИНХРОННЫХ ДВИГАТЕЛЕЙ § 5.12. ОДНОФАЗНЫЕ АСИНХРОННЫЕ ДВИГАТЕЛИ § 5.13. ПРИМЕНЕНИЕ ТРЕХФАЗНЫХ АСИНХРОННЫХ ДВИГАТЕЛЕЙ § 5.14. УСТРОЙСТВО И ПРИНЦИП РАБОТЫ СИНХРОННОГО ГЕНЕРАТОРА § 5.15. ЭДС СИНХРОННОГО ГЕНЕРАТОРА § 5.16. РЕАКЦИЯ ЯКОРЯ § 5.17. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СИНХРОННОГО ГЕНЕРАТОРА § 5.18. УПРОЩЕННАЯ ВЕКТОРНАЯ ДИАГРАММА СИНХРОННОГО ГЕНЕРАТОРА § 5.19. РАБОТА СИНХРОННОГО ГЕНЕРАТОРА ПАРАЛЛЕЛЬНО С СЕТЬЮ § 5.20. ОБРАТИМОСТЬ СИНХРОННЫХ МАШИН. ПРИНЦИП РАБОТЫ СИНХРОННОГО ДВИГАТЕЛЯ § 5.21. ПУСК И ОСТАНОВКА СИНХРОННОГО ДВИГАТЕЛЯ § 5.22. ВЛИЯНИЕ ТОКА ВОЗБУЖДЕНИЯ НА РАБОТУ СИНХРОННОГО ДВИГАТЕЛЯ. СИНХРОННЫЙ КОМПЕНСАТОР § 5.23. РЕАКТИВНЫЕ СИНХРОННЫЕ ДВИГАТЕЛИ § 5.24. ПРИМЕНЕНИЕ СИНХРОННЫХ ДВИГАТЕЛЕЙ ГЛАВА VI. МАШИНЫ ПОСТОЯННОГО ТОКА § 6. 2. ПРИНЦИП РАБОТЫ И УСТРОЙСТВО ГЕНЕРАТОРА ПОСТОЯННОГО ТОКА. ТИПЫ ОБМОТОК ЯКОРЯ § 6.3. ЭДС И ЭЛЕКТРОМАГНИТНЫЙ МОМЕНТ ГЕНЕРАТОРА ПОСТОЯННОГО ТОКА § 6.4. РЕАКЦИЯ ЯКОРЯ § 6.5. КОММУТАЦИЯ § 6.6. СПОСОБЫ ВОЗБУЖДЕНИЯ ГЕНЕРАТОРОВ ПОСТОЯННОГО ТОКА § 6.7. ОБРАТИМОСТЬ МАШИН ПОСТОЯННОГО ТОКА. ДВИГАТЕЛИ § 6.8. ДВИГАТЕЛЬ ПАРАЛЛЕЛЬНОГО И НЕЗАВИСИМОГО ВОЗБУЖДЕНИЯ § 6.9. ДВИГАТЕЛЬ ПОСЛЕДОВАТЕЛЬНОГО ВОЗБУЖДЕНИЯ § 6.10. ДВИГАТЕЛЬ СМЕШАННОГО ВОЗБУЖДЕНИЯ § 6.11. КОЛЛЕКТОРНЫЕ ДВИГАТЕЛИ ПЕРЕМЕННОГО ТОКА ГЛАВА VII. ЭЛЕМЕНТЫ АВТОМАТИКИ § 7.2. РЕЛЕ § 7.3. ДАТЧИКИ § 7.4. АВТОМАТИЧЕСКИЙ КОНТРОЛЬ § 7.5. АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ § 7.6. АВТОМАТИЧЕСКОЕ РЕГУЛИРОВАНИЕ § 7.7. ТЕЛЕМЕХАНИКА § 7.8. КОМПЛЕКСНАЯ АВТОМАТИЗАЦИЯ ГЛАВА VIII. ПРОИЗВОДСТВО, ПЕРЕДАЧА И ИСПОЛЬЗОВАНИЕ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ В НАРОДНОМ ХОЗЯЙСТВЕ § 8.1. ЭЛЕКТРИЧЕСКИЕ СТАНЦИИ § 8.2. ЭНЕРГЕТИЧЕСКИЕ СИСТЕМЫ § 8.3. ПЕРЕДАЧА ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ ПОСТОЯННЫМ ТОКОМ § 8.4. АВТОМАТИЗАЦИЯ ЭЛЕКТРИЧЕСКИХ СТАНЦИЙ И ПОДСТАНЦИЙ ГЛАВА IX. СОВРЕМЕННЫЕ ТЕНДЕНЦИИ РАЗВИТИЯ ЭЛЕКТРОЭНЕРГЕТИКИ ГЛАВА X. ЭЛЕМЕНТЫ ТЕХНИКИ БЕЗОПАСНОСТИ § 10.1. ОПАСНОСТЬ ПОРАЖЕНИЯ ЭЛЕКТРИЧЕСКИМ ТОКОМ ДЛЯ ОРГАНИЗМА ЧЕЛОВЕКА § 10.2. ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ ТЕЛА ЧЕЛОВЕКА § 10.3. ОСНОВНЫЕ ПРИЧИНЫ ПОРАЖЕНИЯ ЭЛЕКТРИЧЕСКИМ ТОКОМ § 10.4. ЗАЩИТНОЕ ЗАЗЕМЛЕНИЕ И ЗАЗЕМЛЕНИЕ НА НЕЙТРАЛЬ (ЗАНУЛЕНИЕ) § 10.5. ЗАЩИТНЫЕ СРЕДСТВА И КОНТРОЛЬ СОСТОЯНИЯ ИЗОЛЯЦИИ ЭЛЕКТРОУСТАНОВОК § 10.6. ОКАЗАНИЕ ПЕРВОЙ ПОМОЩИ ПОРАЖЕННОМУ ЭЛЕКТРИЧЕСКИМ ТОКОМ § 10.7. ОСНОВНЫЕ ПРАВИЛА ТЕХНИКИ БЕЗОПАСНОСТИ В УЧЕБНЫХ ЛАБОРАТОРИЯХ ЛИТЕРАТУРА

Среднее значение

и среднеквадратичное значение — важные понятия и советы для JEE

Среднее значение

и среднеквадратичное значение являются важными выражениями для синусоидальных волн. Как мы знаем, существует два типа источников и токов: источник переменного тока и источник постоянного тока; переменного и постоянного тока. Переменный ток или переменный ток — это тот, который повторяется через 2π, тогда как источник постоянного тока — это тот, который не меняется. Некоторые важные термины, связанные как с переменным, так и с постоянным током: среднеквадратичное значение, мгновенное значение и среднее значение.

Среднеквадратичное значение — это количество тепла, выделяемое резистором, когда через него одновременно проходят как переменный, так и постоянный ток. Среднее значение представляет собой площадь одного цикла синусоидальной волны за период времени. Однако мгновенное значение — это значение в конкретный момент времени. Давайте подробнее разберемся в этих концепциях ниже.

Среднеквадратичное значение тока

Среднеквадратичное значение тока или среднеквадратичное значение — это количество тепла, выделяемое резистором или цепью при прохождении через них переменного и постоянного тока. Если мы примем среднеквадратичное значение токов как Irms, а его пиковое значение равно Im, то формула среднеквадратичного значения задается как: 

$ I_{r m s}=\dfrac{I_{m}}{\sqrt{2}}$ 

Также называется среднеквадратичным значением переменного тока, где Im — максимальное значение синусоиды.

Среднеквадратичное значение синусоиды

Мы уже видели выражения для среднеквадратичных значений, но теперь мы получим среднеквадратичное значение с помощью аналитического метода. Давайте сначала получим среднеквадратичное значение тока, а затем мы можем обобщить его и для напряжения. Поскольку синусоида симметрична, мы можем рассчитать среднеквадратичное значение, учитывая только полупериод. 9{2}}{2}} \\ &I_{RM S}=\dfrac{I_{m}}{\sqrt{2}} \end{align}$

Это выражение для среднеквадратичного тока. Весь этот вывод можно повторить и для напряжения, и среднеквадратичное значение напряжения также будет

$V_{RM S}=\dfrac{V_{m}}{\sqrt{2}}$

Как обсуждалось выше, среднеквадратичное значение значение синусоиды обозначается как $I_{rm s}=\dfrac{I_{m}}{\sqrt{2}}$ или для синусоидального напряжения $V_{rm s}=\dfrac{V_{m}} {\sqrt{2}}$

Переменный ток или переменный ток

Im и Vm здесь пиковое значение тока и напряжения соответственно. Vm или Im  можно рассчитать как Vrms $\cdot \sqrt{2}$

Среднеквадратичное значение прямоугольной волны

Поскольку мы рассчитали среднеквадратичное значение синусоидальных волн, аналогичным образом мы рассчитаем среднеквадратичное значение квадратной волны. волна. Среднеквадратичное значение — это просто корень из среднеквадратичного значения. Предположим, у нас есть прямоугольная волна, как показано ниже.

 

Прямоугольная волна
9{2}} \\ &V_{RM S}=V_{0} \end{align}$

Это означает, что среднеквадратичное значение прямоугольной волны совпадает с ее амплитудой. Предположим, что величина прямоугольной волны равна A, тогда ее среднеквадратичное значение также будет равно A. 

Прямоугольная волна

Среднее значение переменного тока

Когда переменный ток преобразуется в постоянный с помощью выпрямителя, это преобразованное значение переменного тока называется средним значением переменного тока. Среднее значение синусоидальной волны можно рассчитать графически или с помощью стандартного уравнения синусоидальности. Используя стандартное синусоидальное уравнение, среднее значение переменного тока получается равным $I_{\text {average}}=\dfrac{2 I_{m}}{\pi}$, где Im — пиковое значение синусоидального волна. 9{T} \\ &\bar{i}=\dfrac{I_{m}}{\omega}[-\cos \omega T-(-\cos 0)]\end{align}$

Теперь мы знаем что период времени связан с угловой частотой как

$T=\dfrac{2\pi}{\omega}$

Подставляя это в приведенное выше выражение, получаем

$\begin{align} &\bar{ i}=\dfrac{I_{m}}{\omega}[-\cos 2 \pi+1] \\ &\bar{i}=0 \end{align}$

Таким образом, среднее значение AC для полный цикл равен нулю.

Точно так же для полупериода мы можем найти среднее значение как 9{\dfrac{T}{2}} \end{align}$

$\begin{align} &\bar{i}=\dfrac{I_{m}}{\omega}\left[-\cos \ влево(\omega \dfrac{T}{2}\right)-(-\cos 0)\right]\\ &\bar{i}=\dfrac{I_{m}}{\omega}\left[- \cos \left(\omega \dfrac{2 \pi}{2 \omega}\right)+1\right] \\&\bar{i}=\dfrac{I_{m}}{\omega}[- \cos (\pi)+1] \\&\bar{i}=\dfrac{I_{m}}{\omega}[-(-1)+1] \\ &\bar{i}=\dfrac {2 I}{\omega} \end{align}$

Таким образом, среднее значение формулы переменного тока задается как $I_{\text {average}}=\dfrac{2 I_{m}}{\pi} $. Мы подсчитали, что среднее значение для полной синусоиды равно нулю. Поскольку в положительном и отрицательном циклах имеется одинаковое количество тока, и, таким образом, течет в противоположных направлениях, это нейтрализует эффект, и среднее значение полной синусоидальной волны равно нулю. Та же формула справедлива и для переменного напряжения. Таким образом, среднее значение формулы напряжения задается как $V_{\text {average}}=\dfrac{2 V_{m}}{\pi}$.

Вт

Верно для полупериода, для полного цикла, однако среднее значение напряжения равно нулю.

Мгновенное значение

Мгновенное значение переменного тока, с другой стороны, является его значением в конкретный момент времени. В одном цикле есть несколько экземпляров волны. Посмотрите на рисунок ниже.

Мгновенное значение синусоиды

Теперь мы знаем, что ток синусоиды можно выразить через ее амплитуду Im как

$i=I_{m} \sin \omega t$

Для любого значения t можно найти значение тока. Это означает, что это формула мгновенного тока при конкретном значении t. Если мы хотим найти значение тока для определенного угла $\theta=\omega t$, то мы можем использовать соотношение между периодом времени и угловой частотой, которое задается как

$T=\dfrac{2\pi }{\омега}$.

Таким образом, мы можем найти мгновенное значение переменного тока.

Вывод

Переменный и постоянный ток являются основными источниками питания в электрической цепи, будь то соответствующее напряжение или ток. Переменный ток, как мы знаем, важен, поскольку питание наших домов осуществляется переменным током, а также бытовой техникой. Тем не менее, он не пренебрегает источником постоянного тока, поскольку он также используется для различных приложений. Электронные схемы, такие как часы телевизора, ноутбук, светодиодная лента и т. д., используют источник постоянного тока. Более того, сами солнечные батареи производят постоянный ток. С разными источниками приходят способы их обозначения. Таким образом, средние, среднеквадратичные и мгновенные значения играют важную роль. Каждая из этих величин имеет свое собственное значение, как обсуждалось выше.

Среднее значение волны переменного тока

Вычисление величины переменных величин, таких как ток или напряжение, при переменном токе не является простой задачей, как при постоянном токе, где значения остаются постоянными во времени. Существует несколько способов представления амплитуды формы переменного сигнала. В случае синусоидальной формы волны переменного тока величины напряжения и тока могут быть представлены как

[adsense1]

• Пиковое значение
• От пика до пикового значения
• Среднеквадратичное значение
• Мгновенное значение

(Эти значения могут использоваться для представления амплитуды любой другой периодической формы сигнала)
Существует еще один способ представления амплитуды сигнала переменного тока. Он известен как среднее значение.

Значения среднего напряжения и среднего тока синусоиды переменного тока могут быть полезны во многих операциях анализа цепей. Фактически, мультиметры выпрямительного типа измеряют среднее напряжение переменного тока, а затем выполняют некоторые вычисления и отображают выходное значение как среднеквадратичное значение.

Краткое описание

Среднее напряжение

Среднее напряжение, как следует из названия, представляет собой среднее значение мгновенных напряжений, выбранных через соответствующие временные интервалы в полупериоде синусоидальной (или любой другой периодической) волны переменного тока. Среднее значение представляет собой отношение площади под формой волны переменного тока к времени.

Чтобы найти среднее напряжение формы волны переменного тока, один полупериод делится на равноотстоящие ординаты. Рассчитываются мгновенные напряжения на этих средних ординатах. Вычисляя среднее значение этих мгновенных значений напряжения, мы получаем среднее значение формы сигнала переменного тока (будь то напряжение или ток).

[adsense2]

Определение среднего значения напряжения сигнала переменного тока аналогично определению среднеквадратичного значения напряжения сигнала переменного тока. Но в процессе нахождения среднего напряжения нет необходимости находить квадраты мгновенных напряжений. Мы можем найти среднее значение напряжения любой формы волны.

Среднее значение напряжения можно назвать «отношением площади под кривой (синусоидальной, прямоугольной или любой другой периодической волной) в любой момент времени» или мы также можем сказать «среднее значение всех мгновенных значений напряжения». значения известны как среднее напряжение».

Форма каждой периодической волны симметрична, т. е. будет положительный полупериод и отрицательный полупериод. Площадь под положительным полупериодом всегда равна и противоположна по знаку площади под отрицательным полупериодом.

Сумма площадей под обоими полупериодами возвращается к нулю, так как отрицательная и положительная площади нейтрализуют каждую из них. Следовательно, среднее значение рассчитывается с учетом только половины периода.

Среднее значение напряжения измеряется только за один полупериод полного периодического сигнала. Среднее напряжение также называют «средним напряжением сигнала».

Среднее значение можно найти для анализа и расчетов цепей переменного и постоянного тока. Среднее значение представлено VAVG для среднего напряжения и IAVG для среднего тока.

Понятие мгновенного значения

Мгновенное значение (напряжение или ток) переменного сигнала представляет собой значение в любой конкретный момент времени. Напряжение сигнала в данный момент времени называется «мгновенным напряжением».

На приведенной выше диаграмме V1, V2, V3, V4 … — мгновенные напряжения синусоидальной волны. Чтобы найти мгновенное значение напряжения синусоидальной волны, мы зависим от максимального напряжения синусоидальной волны.

Мгновенное напряжение = Максимальное напряжение x sin θ

В _INST = В _{МАКС. Например, в случае синусоидальной волны переменного тока максимальный угол составляет 180° для положительного полупериода. Если мы разделим полупериод на 10 средних ординат, то θ будет кратным 1800 / 10 = 180, т. е. θ занимает 180, 360, 540….до 1800.}

Среднее напряжение сигнала в графическом методе

среднее значение переменного сигнала, такого как синусоидальная волна, при взятии полного цикла равно 0. Это связано с тем, что синусоидальная форма волны, которая является переменной волной, т.е. она симметрична относительно оси X, и значения в положительной половине отменяют значения в отрицательной половине, когда берется среднее значение.

Но средние значения синусоидальных напряжений и токов не могут быть равны 0 в реальном времени. Следовательно, среднее значение переменного значения можно рассчитать, взяв средние значения равноотстоящих мгновенных значений полупериода переменного сигнала.

Этот процесс аналогичен процессу определения среднеквадратичного значения напряжения. Положительный полупериод делится поровну на n частей с равными промежутками между ними. Равномерно разделенные части называются «средними ординатами», а это частное значение каждой части называется «мгновенным значением».

Каждое среднее значение ординаты переменного сигнала добавляется к его следующему значению ординаты, а полученная сумма делится на общее количество средних ординат. Это значение среднего напряжения. Среднее напряжение определяется по представленной ниже формуле.

Например, если мы разделили полупериод на 10 равных ординат, то среднее напряжение можно рассчитать как

среднее напряжение можно рассчитать следующим образом.

Разделите кривую на 10 средних ординат и рассчитайте мгновенные напряжения в этих точках.

Используя приведенную выше формулу, среднее напряжение можно рассчитать как

Vavg = 2146 / 10 = 214,6 вольт

Следовательно, среднее значение напряжения составляет 214,6 вольт.

Среднее напряжение формы волны в аналитическом методе

Как мы уже знаем, каждая периодическая форма волны имеет свое среднее значение как сумму нулей, поскольку она имеет равные доли положительных и отрицательных полупериодов. Среднее значение можно рассчитать, рассматривая мгновенное значение только половины периода вместо всех мгновенных значений.

Это применимо только к симметричным сигналам, таким как синусоидальные волны. В несимметричных напряжениях мы должны вычислить среднее значение мгновенных напряжений для полного цикла периодического сигнала, чтобы найти точное значение.

Аппроксимация площади

Чтобы найти среднее значение, нам нужно вычислить приблизительную площадь сигнала или кривой через несколько интервалов. Чтобы найти площадь кривой, ее делят на множество маленьких прямоугольников или треугольников. Путем аппроксимации площадей этих отдельных прямоугольников и сложения всех этих площадей можно рассчитать среднее значение.

Точность среднего значения можно повысить, рассматривая бесконечное (очень большое) количество маленьких прямоугольников. Следующий график представляет собой среднее значение площади, покрытой кривой, с небольшими прямоугольниками через равные интервалы формы сигнала.

Рассчитав среднее значение площади под кривой, мы можем найти точное значение среднего значения напряжения. Наиболее точное значение будет получено, когда значение приблизится к 2П.

Существует множество способов приблизить значение площади под кривой. Это правило трапеций, правило средней ординаты, правило Симпсона и т. д. Если мы рассмотрим синусоиду переменного напряжения, она будет представлена ​​как V (t) = Vp.cos (ωt). Площадь под кривой в каждом случае математически определяется как

Area = V _p Sin(wt)dt

Здесь T — период времени периодической формы волны, а пределы интегрирования равны 0 и Π, поскольку мы рассматриваем только полупериод.

Используя приведенную выше формулу, мы можем рассчитать площадь под сигналом, и мы получим это как

Площадь = 2V _P .

Теперь, когда мы знаем площадь под положительным полупериодом (или отрицательным полупериодом), мы можем легко вычислить среднее значение (напряжение или ток) периодической переменной синусоидальной волны, интегрируя синусоидальную величину по положительному (или отрицательному) периоду. и разделить его на период.

Например, если у нас есть мгновенное напряжение переменной волны как V = Vp.sinθ с периодом времени 2Π, тогда среднее напряжение формы волны переменного тока составляет

В _AV =1/Π В _p Sin(Φ)dΦ

В _AV =V _p /Π -cos(Φ)

=2 В _p /Π = 0,673 В _p

Среднее значение напряжения переменный сигнал задается как

В _AV =2 В _p /Π = 0,673 В _p

Таким образом, среднее значение синусоидальной волны переменного тока равно произведению пикового значения напряжения на 0,637.
Как и в приведенном выше примере, если у нас есть синусоида с максимальным (пиковым) напряжением 340 Вольт, то среднее значение напряжения можно найти с помощью аналитического метода, приведенного ниже.

В _AV = В _{ПИКОВОЕ} x 0,637 = 340 x 0,637 = 216,5 В.

Среднеквадратичное значение напряжения в пересчете на пиковое напряжение составляет В _{Среднеквадратичное значение} = 0,707 x V _{ПИК . Сравнение среднего и среднеквадратичного напряжения показано ниже.}

ПРИМЕЧАНИЕ. Умножение пикового значения на 0,637 применимо только для синусоидальной волны, но не для других форм волны, таких как пилообразная волна и треугольная волна.

Важность среднего значения при измерении формы синусоидального сигнала переменного тока

Мультиметры выпрямительного типа показывают среднеквадратичное значение (напряжение или ток) только для синусоидального сигнала. Среднеквадратичное значение вычисляется путем вычисления среднего значения, а затем умножения на 1,11. Если мы используем этот мультиметр для измерения среднеквадратичного значения любых других сигналов переменного тока, результатом будет ошибочное среднеквадратичное значение.