Тест по физике Закон всемирного тяготения 9 класс

Тест по физике Закон всемирного тяготения для учащихся 9 класса с ответами. Тест состоит из 10 заданий и предназначен для проверки знаний к главе Законы взаимодействия и движения тел.

1. Кто впервые сформулировал закон всемирного тяготения?

1) Аристотель
2) Галилей
3) Ньютон
4) Архимед

2. Закон всемирного тяготения справедлив

1) для тел пренебрежимо малых размеров по сравнению с расстоянием между ними
2) если оба тела однородны и имеют шарообразную форму
3) если одно из взаимодействующих тел -шар, размеры и масса которого значительно больше, чем у второго тела (любой формы), находящегося на поверхности этого шара или вблизи него
4) во всех трех случаях

3. Какая из приведенных формул выражает закон всемирного тяготения?

4. Космический корабль массой 8 т приближается к орбиталь­ной станции массой 20 т на расстояние 100 м. Найдите силу их взаимного притяжения. Гравитационная постоянная

1) 1 × 10^-6 н
2) 1 × 10^-8 Н
3) 1 × 10⁶ н
4) 1 × 10⁸ Н

5. Определите значение силы взаимного тяготения двух кораблей, удаленных друг от друга на 100 м, если мас­са каждого из них 10 000 т. Гравитационная постоянная

1) 6,67 мН
2) 0,667 Н
3) 6,67 мкН
4) 6,67 кн

6. При увеличении массы одного из взаимодействующих тел в 5 раз сила всемирного тяготения

1) увеличится в 5 раз
2) уменьшится в 5 раз
3) увеличится в 2 5 раз
4) уменьшится в 25 раз

7. При увеличении массы каждого из взаимодействующих тел в 2 раза сила всемирного тяготения

1) увеличится в 2 раза
2) уменьшится в 2 раза
3) увеличится в 4 раза
4) уменьшится в 4 раза

8. При увеличении в 3 раза расстояния между центрами шаро­образных тел сила гравитационного притяжения

1) увеличивается в 3 раза

2) уменьшается в 3 раза
3) увеличивается 9 раз
4) уменьшается в 9 раз

9. Если массу одного тела увеличить в 4 раза, а расстояние между телами уменьшить в 2 раза, то сила всемирного тяготения

1) увеличится в 2 раза
2) уменьшится в 2 раза
3) увеличится в 8 раз
4) увеличится в 16 раз

10. По какой из приведенных формул можно рассчитать силу гравитаци­онного притяжения между двумя кораблями одинаковой массы m (см. рис.)?

1) F = Gm²/b²
2) F = Gm²/4b²
3) F = Gm²/16b²
4) Ни по одной из указанных формул

Ответы на тест по физике Закон всемирного тяготения
1-3
2-4
3-3
4-1
5-2
6-1
7-3
8-4
9-4
10-3

Закон всемирного тяготения. Видеоурок. Физика 9 Класс

Открыл закон всемирного тяготения английский ученый Исаак Ньютон (рис. 1) в 1667 году. Свое открытие И. Ньютон обосновал на астрономических наблюдениях.

Рис. 1. Исаак Ньютон (1642-1727)

Эти астрономические наблюдения были сделаны датским астрономом Тихо Браге (рис. 2). Тихо Браге измерил положение всех на тот момент известных планет и записал их координаты, но вывести окончательно, создать закон движения планет относительно Солнца Тихо Браге не удалось. Это сделал его ученик Иоганн Кеплер (рис. 3).

Рис. 2. Тихо Браге (1546-1601)

Рис. 3. Иоганн Кеплер (1571-1630)

Иоганн Кеплер воспользовался не только измерениями Тихо Браге, но и к тому времени уже достаточно обоснованной, используемой везде и всюду гелиоцентрической системой мира Коперника (рис. 4). Той системой, в которой считается, что в центре нашей системы находится Солнце и вокруг него обращаются планеты.

Рис. 4. Гелиоцентрическая система мира (система Коперника)

Три эмпирических соотношения, интуитивно подобранных Иоганном Кеплером на основе анализа астрономических наблюдений Тихо Браге, описывают идеализированную гелиоцентрическую орбиту планеты:

1. Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.
2. Каждая планета движется в плоскости, проходящей через центр Солнца, причем за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.
3. Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосейорбит планет.

Одновременно с выводом закона всемирного тяготения появилось несколько вопросов, например почему те или иные тела притягиваются друг к другу и каким свойствам должны отвечать эти тела? Почему они создают вокруг себя нечто, что заставляет другие тела двигаться относительно них с тем условием, которое мы рассматриваем? Отвечать на эти вопросы пришлось Ньютону, и он быстро нашел ответы. В первую очередь Ньютон предположил, что все тела обладают свойством притяжения, т. е. те тела, которые обладают массами, притягиваются друг к другу. Это явление стали называть

всемирным тяготением. Силу, с которой тела притягиваются, стали называть гравитационной (от слова gravitas – «тяжесть») (рис. 5).

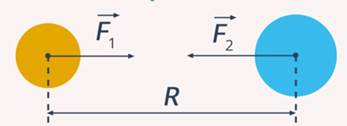
Рис. 5. Сила гравитационного взаимодействия

Ньютону удалось получить формулу для вычисления силы взаимодействия тел, обладающих массами. Обычно именно эту формулу и называют законом всемирного тяготения. Сам

закон всемирного тяготения обычно звучит так: два тела притягиваются друг к другу с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.

Запись закона всемирного тяготения выглядит следующим образом:

 

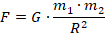
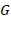             – гравитационная постоянная. Ее физический смысл заключается в том, что она показывает, с какой силой взаимодействуют два тела массой каждое в 1 кг, расположенные на расстоянии 1 м (рис. 6).

Рис. 6. Физический смысл гравитационной постоянной

Эта величина очень маленькая, по порядку величины составляет

:

Такое ее значение говорит о том, с какой силой взаимодействуют тела, находящиеся рядом. Даже если они будут достаточно близко располагаться (например, два стоящих человека), они абсолютно не почувствуют этого взаимодействия, поскольку порядок силы  не даст значительного ощущения. Действие гравитационной силы начинает сказываться только тогда, когда масса тел велика.

 

Когда Ньютон открыл закон всемирного тяготения, значения гравитационной постоянной он еще не знал. Точное измерение этой величины произошло только в конце XVIII века, в 1788 году. Это сделал английский ученый Генри Кавендиш (рис. 7).

Рис. 7. Генри Кавендиш (1731-1810)

Эксперимент Кавендиша – первое экспериментальное измерение гравитационной постоянной. Первоначально эксперимент был предложен Джоном Мичеллом. Именно он сконструировал главную деталь в экспериментальной установке – крутильные весы, однако умер в 1793, так и не поставив опыта. После его смерти экспериментальная установка перешла к Генри Кавендишу. Кавендиш модифицировал установку, провел опыты и описал их в Philosophical Transactions в 1798. Установка представляла собой деревянное коромысло с прикрепленными к его концам небольшими свинцовыми шарами диаметром 5 см и массой 775 г. Оно было подвешено на нити из посеребренной меди длиной 1 м. К шарам подносили шары большего размера диаметром 20 см и массой 49,5 кг, сделанные так же из свинца. В результате действия гравитационных сил коромысло закручивалось на некий угол. В «Британнике» утверждается, что Г. Кавендиш получил значение

В той форме, в которой мы используем закон всемирного тяготения, он справедлив не всегда, а только в некоторых случаях (рис. 8).

1. Расстояние между телами. Закон всемирного тяготения будет справедлив для точечных тел. Это означает, что расстояние между телами такое большое, что размерами самих тел мы можем пренебречь.
2. Форма тел. Закон всемирного тяготения применим, когда тела обладают сферической формой. Расстояния между телами определяются как расстояния между центрами рассматриваемых тел.
3. Одно тело – материальная точка, второе имеет шарообразную форму. Это как раз случай, когда вокруг Земли по своим орбитам движутся спутники.

Рис. 8. Границы применимости закона всемирного тяготения

 

Рассмотрим еще один интересный момент. По третьему закону Ньютона, два взаимодействующих тела обладают действием друг на друга. В данном случае можно говорить о том, что сила взаимодействия между этими телами одинакова, а вот направление этих сил противоположное (рис. 9).

Рис. 9. Иллюстрация третьего закона Ньютона

В данном случае важно понимать, что если мы имеем дело с небольшим телом, например со спутником Земли (рис. 10), то Земля и спутник притягивают (действуют на) друг друга с равной силой. Но ускорение у Земли будет значительно меньше, так как масса Земли в огромное количество раз превосходит массу спутника.

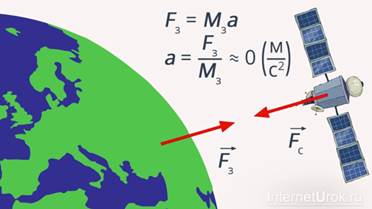
Рис. 10. Взаимодействие Земли и спутника

Заключение

На следующих уроках мы рассмотрим частные случаи применения закона всемирного тяготения: ускорение свободного падения на небесных телах и движение искусственных спутников.

 

Список литературы

1. Белонучкин В.Е. Кеплер, Ньютон и все-все-все. – М.: Библиотечка Квант, 1990.
2. Элементарный учебник физики./Под ред. Г.С. Ландсберга. Т. 1. Механика. Теплота. Молекулярная физика. – М., 1974.
3. Городецкий Е.Е. Закон всемирного тяготения //Квант. – 1987. – № 11. – С. 36-38.
4. Смородинский Я. Закон всемирного тяготения //Квант. – 1990. – № 12. – С. 8-13, 51. Физика: Механика. 10 кл.: Учеб. для углубленного изучения физики / М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др.; Под ред. Г.Я. Мякишева. – М.: Дрофа, 2002. – 496 с.
5. Перышкин А.В., Гутник Е.М. Физика. 9 кл.: учебник для общеобразоват. учреждений / А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300.
6. Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание, передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «eduspb.com» (Источник)
2. Интернет-портал «fizmat.by» (Источник)
3. Интернет-портал «phisiki.com» (Источник)

 

Домашнее задание

1. Сформулируйте закон всемирного тяготения, запишите его формулу. Кто открыл этот закон? Какие константы входят в эту формулу?
2. Расстояние между двумя шариками 10 см, сила притяжения между ними 1·10^-13 Н. определите массу первого шарика, если масса второго – 10 г?
3. На каком расстоянии r сила притяжения между двумя телами (масса каждого тела 100 кг) будет равна 5·10^-12 Н?

Закон всемирного тяготения и его следствия

1. Закон тяготения. Причина движения планет оставалась неизвестной до конца XVIIв. — до открытия Ньютоном закона всемирного тяготения. Этот закон состоит в том, что все тела во Вселенной (как и вообще все частицы материи) притягиваются друг к другу с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. В виде формулы это можно записать так:

где т1 и m2 — массы двух рассматриваемых тел, r — расстояние между ними, а f — коэффициент, численная величина которого зависит от единиц, в которых выражены масса и расстояние. Эта величина называется постоянной тяготения. Позднее стало известно из опыта, что две массы, каждая по одному грамму, притягиваются одна к другой на расстоянии 1 см с силой, равной 6,673*10-8 дины. Поэтому, выражая массы в граммах, а r — в сантиметрах, мы, чтобы получить F в динах, должны положить

2. Движение Луны и земное притяжение. Ньютон доказал, что притяжение Земли, под действием которого все предметы падают на Землю, распространяется и за пределы земной атмосферы, ослабевая обратно пропорционально квадрату расстояния от центра Земли. Это значит, что действие тяготения, или силы земной тяжести, простирается в бесконечность. Сила земной тяжести удерживает и Луну на ее орбите, иначе Луна оторвалась бы от Земли и унеслась бы по касательной к своей орбите.

Исаак Ньютон (1643-1727).

Это притяжение Луны к Земле и является той центростремительной силой, которой соответствует наблюдаемое центростремительное ускорение в движении Луны.

На рисунке 28 Луна из точки L1, двигаясь по касательной, через некоторое время пришла бы в точку L’1. Но за это время она падает к Земле на величину отрезка L1 L 2 и оказывается в точке L2 и т. д. В результате Луна все время обращается вокруг Земли.

Рисунок 28 — «Падение» Луны к Земле.

Величайшая заслуга Ньютона еще и в том, что он доказал тождество открытой им силы тяготения между мировыми телами с силой земного притяжения, давно знакомой людям из опыта. Ньютон доказал, что и та и другая сила изменяется обратно пропорционально квадрату расстояния и что, в частности, ускорение, с которым Луна «падает» к Земле (оно составляет 0,27 см/сек2), в точности равняется ускорению, с которым падал бы камень, если бы мы его поместили на расстоянии Луны от Земли.

3. Движение небесных тел и определение их масс. Масса Земли. Действие тяготения к Солнцу все время искривляет пути Земли и планет. Строго говоря, все планеты и Солнце обращаются вокруг их общего центра масс.

Спутники планет обращаются вокруг своих планет под действием тяготения к ним так же, как Луна обращается под действием тяготения к Земле.

За пределами солнечной системы встречаются системы двойных звезд: каждая из двух звезд данной пары обращается вокруг их общего центра масс также под действием тяготения, поэтому закон, открытый Ньютоном, и называется законом всемирного тяготения.

Ньютон доказал, что существование всемирного тяготения подтверждает справедливость законов Кеплера; эти законы были Ньютоном уточнены. Он доказал, что при определенных условиях одно тело под действием притяжения другого может двигаться не только по эллипсу, но и по окружности, по параболе и по гиперболе (Рисунок 29).

Рисунок 29 — Различные формы орбит.

Затем Ньютон доказал, что третий закон Кеплера не вполне точен и что период взаимного обращения двух тел, отстоящих друг от друга на определенном расстоянии, зависит еще и от суммы масс этих тел. Это дает возможность определять массы небесных тел, зная расстояние между ними и период обращения друг около друга.

Масса Солнца не только больше массы любой из планет, но в 750 раз больше массы всех планет, взятых вместе (Рисунок 31). Поэтому все планеты и обращаются вокруг Солнца, испытывая к нему центростремительное ускорение — ускорение тяготения. Массу Земли приближенно можно определить, измерив угол, на который отклоняется отвес вследствие притяжения его горой, расстояние до которой и масса которой известны. Этот угол отклонения зависит от отношения массы Земли к массе горы и от отношения расстояний отвеса от центра Земли и от центра горы, к которым притягивается отвес. Точнее массу Земли можно определить другими способами. Масса Земли равна 6-1027 г, а ее средняя плотность 5,5 г/см3.

4. Приливы и отливы. У берегов морей и океанов каждые сутки наблюдается колебание уровня воды. Два раза в сутки уровень воды поднимается — это приливы. И два раза в сутки уровень ее падает — это отливы. Отлив наступает приблизительно через 6 часов после прилива, а еще через 6 часов наступает прилив, так что от одного прилива до другого проходит 12 часов (более точно — 12 ч 25 мин). Таким образом, в среднем за 24 ч 50 мин бывает два прилива и два отлива. Но как раз такой же промежуток времени проходит между двумя соседними одноименными кульминациями Луны. Ньютон доказал, что приливы и отливы вызваны притяжением Луны. Луна притягивает к себе разные точки земного шара с неодинаковой силой: более близкие — сильнее, а более далекие — слабее. Это различие сил притяжения вызывает растяжение водной оболочки Земли вдоль линии, направленной к Луне (Рисунок 30). Там, где водная оболочка растянута, уровень воды выше — происходит прилив. При суточном вращении Земли в полосу прилива будут последовательно попадать разные места Земли, а в одном и том же месте приливы и отливы будут чередоваться. Если в точке А (Рисунок 30) прилив, то, вращаясь в сторону С, точка А через полсуток придет опять в полосу прилива, в которой на рисунке находится точка В.

Рисунок 30 — Прилив и отлив в водной оболочке Земли (схема).

5. Возмущения в движении планет. Открытие планеты Нептун. Если бы вокруг Солнца обращалась только одна планета, то она двигалась бы в точности по законам Кеплера. Но так как вокруг Солнца обращается не одна планета, а несколько и все они взаимно притягивают друг друга, то их движения несколько отклоняются от движений по законам Кеплера. Эти, вообще говоря, очень небольшие отклонения в движениях планет от движений по законам Кеплера называются возмущениями.

Вследствие возмущений планеты движутся то быстрее, то медленнее, чем следует из второго закона Кеплера; поэтому и орбиты их не являются правильными эллипсами и постепенно изменяются. Современной наукой возмущения учитываются очень точно на основании теории всемирного тяготения и знания массы Солнца и планет, а также расстояний между ними.

В 1781 г. английский астроном Вильям Гершель (1738-1822), в ту пору еще безвестный любитель астрономии, наблюдая небо в телескоп, построенный им собственноручно, открыл никому до этого не известную планету — седьмую по расстоянию от Солнца. Планета получила название Уран.

Рисунок 31 — Сравнение массы Солнца и планет: 1 — Меркурий; 2 — Марс; 3 — Плутон; 4 – Венера; 5 — Земля; 6 — Уран; 7 — Нептун; 8 — Сатурн; 9 — Юпитер.

В начале XIXв. окончательно убедились, что движение планеты Уран немного не согласуется с ее движением, вычисленным на основании учета притяжения ее как Солнцем, так и всеми остальными известными тогда планетами. Как ни ничтожны были эти отклонения наблюдений от теории, астрономы не могли с ними примириться. Ученые предположили, что отклонение в движении Урана вызвано притяжением неизвестной планеты, находящейся от Солнца еще дальше, чем Уран. Ученые Леверрье и Адамc вычислили положение этой планеты на небе. Согласно их расчетам, эта неизвестная планета была найдена в 1846 г. Ее назвали Нептуном.

Открытие планеты, сделанное, как говорят, на «кончике пера», в кабинете, является одним из величайших достижений человеческой мысли. Оно демонстрирует могущество научного предвидения, блестяще доказывает познаваемость природы, вопреки религиозным воззрениям, по которым человеческое познание будто бы ограниченно.

Упражнение 2.

Вычислить, на каком расстоянии от Земли находится та точка, в которой притяжения Земли и Луны одинаковы, зная, что расстояние между Луной и Землей равно 60 радиусам Земли, а массы Земли и Луны относятся как 81 : 1.

Закон всемирного тяготения

.

Исаак Ньютон смог объяснить движение тел в космическом пространстве с помощью закона всемирного тяготения. Ньютон пришел к своей теории в результате многолетних исследований движения Луны и планет.

Закон всемирного тяготения.

Если m1 и m2 – массы двух точечных тел, а r – расстояние между ними, то закон всемирного тяготения записывается в виде

где G = 6,67∙10–11 Н∙м2/кг2 – гравитационная постоянная. Этот закон справедлив также для сферически симметричных тел (при расстояниях между центрами больше суммы их радиусов), а приближенно он выполняется для любых тел, если расстояние между ними велико по сравнению с их размерами. Ускорение, которое испытывает тело m, находящееся на расстоянии r от тела M, равно

В частности, ускорение свободного падения в поле Земли равно , где – масса Земли, r – расстояние до ее центра. Вблизи поверхности Земли ускорение свободного падения равно g = 9,8 м/с2. Сплюснутость Земли и ее вращение приводят к отличию силы тяжести на экваторе и возле полюсов: ускорение свободного падения в точке наблюдения может приближенно высчитываться по формуле g = 9,78 ∙ (1 + 0,0053 sin φ), где φ – широта этой точки.

Гравитация внутри Земли.

Внутри Земли, если принять ее за однородный шар, сила тяжести убывает пропорционально расстоянию до центра:

Поскольку размеры Земли не бесконечно малы по сравнению с расстояниями до Луны и Солнца, то силы лунного и солнечного притяжения в разных точках Земли разные. Так, самая близкая точка будет притягиваться сильнее, чем самая далекая точка. Действие возмущающих сил на отдельные части земной поверхности вызывает приливы и отливы. При этом приливное влияние Луны в 2,2 раза сильнее, чем Солнца.

Квадратурные и сизигийные приливы.

Каждый день уровень океанских вод поднимается и снижается, причем в устьях некоторых рек и отдельных заливах на несколько метров. Эти явления носят название приливов и отливов. Гидросфера, как и всякое жидкое тело, способна деформироваться, что и происходит каждый день в результате притяжения Луны и Солнца. В полнолуние и новолуние тяготение Луны и Солнца усиливают действие друг друга, и приливы бывают выше средних. Когда же Луна находится в фазах первой и последней четверти, силы тяготения светил гасят друг друга, и уровень приливов ниже среднего. Перегородив дамбой залив, приливы можно использовать для получения электроэнергии.

Луна каждые 24 часа 50 минут вызывает приливы не только в океанах, но и в коре Земли, и в атмосфере. Под воздействием приливных сил литосфера вытягивается примерно на полметра. Тяготение Луны вызывает также прецессию земной оси. Из-за океанских приливов и отливов возникает сила трения между литосферой и гидросферой, замедляющая скорость вращения Земли вокруг своей оси. Каждое столетие продолжительность суток увеличивается приблизительно на 0,002 с. Два миллиарда лет назад продолжительность земных суток составляла всего 10 часов, а в отдаленном будущем они будут равны одному месяцу. Уже теперь благодаря приливным силам Луна постоянно обращена к Земле одной и той же стороной. Кроме того, притяжение приливных выступов Земли увлекает Луну по орбите вперед, в результате чего она удаляется от Земли со скоростью около 3 см в год. Именно приливные силы, возникшие в гравитационном поле Юпитера, разорвали ядро кометы Шумейкеров – Леви на множество частей, после чего несколько лет назад она упала на Юпитер. Закон всемирного тяготения справедлив только в рамках классической механики. Он, по-видимому, нарушается на малых расстояниях (порядка планковской длины). В 1916 году Альберт Эйнштейн в теории относительности показал, что свойства пространства и времени изменяются вблизи больших масс.

Это не обсуждается: Закон всемирного тяготения

В нашем мире противоречий и сомнений есть вещи, которые не обсуждаются — аксиомы и законы. К таким относятся законы Ньютона, объясняющие силы тяготения и притяжения. Давайте вспомним, как они работают и почему знания о них так важны.

Однажды Исаак Ньютон гулял по яблоневому саду и вдруг увидел Луну в дневном небе. Тут возле него упало яблоко, и он связал эти два факта — Луну и яблоко — воедино. Ученый тогда исследовал законы движения и знал, что яблоко падает из-за гравитационного поля Земли.

Знал он и о том, что Луна не просто висит в небе, а вращается по орбите вокруг Земли, и, следовательно, на нее воздействует какая-то сила, которая удерживает ее от того, чтобы сорваться с орбиты и улететь по прямой прочь, в открытый космос. Тут ему и пришло в голову, что, возможно, это одна и та же сила заставляет и яблоко падать на землю, и Луну оставаться на околоземной орбите.

Сегодня это может быть в порядке вещей, но более чем 300 лет назад сэр Исаак Ньютон предложил революционную идею: два любых объекта, независимо от их массы, притягиваются друг к другу. До Ньютона считалось, что на Земле и в космосе действуют разные физические законы. То есть, яблоко падает на землю по одним причинам, а планеты вращаются вокруг Солнца — совершенно по другим. Преимущество универсального закона тяготения в том, что он позволяет вычислить гравитационное притяжение между двумя любыми объектами. Эта способность крайне полезна, когда ученые, например, запускают спутник на орбиту или определяют курс Луны. Двигатель космического корабля должен быть достаточно мощным, чтобы преодолеть земное притяжение. Приливы и отливы морей и рек тоже происходят благодаря силе тяготения, они вызваны действием силы тяготения Луны. Земное притяжение (сила тяготения) заставляет течь реки.

Закон Ньютона: сила притяжения двух тел прямо пропорциональна массе каждого тела и обратно пропорциональна квадрату расстояния между ними.

Так что при увеличении расстояния эта сила убывает, но она никогда не равна в точности нулю. Конечно, если массы малы, а расстояние велико, то сила настолько мала, что она просто незаметна, и мы считаем ее равной нулю. Сила тяготения не возникает, она всегда есть, но заметна только при больших массах (или если хотя бы одна из масс велика) и небольших расстояниях. Правда, «небольшое» расстояние в космических масштабах может показаться нам огромным, например, от Солнца до Земли 149000000 км, а сила притяжения настолько велика, что Земля (с нашей точки зрения, огромный шар) не улетает прочь, а всегда вращается вокруг Солнца.

Закон Ньютона существует и работает в своей неизменной форме. То же самое относится к выбору скоростного режима на дороге. Значение скорости, указанную на дорожном знаке, следует понимать однозначно, без лишних интерпретаций — это всегда максимально разрешенная скорость. Соблюдайте ее и путешествуйте безопасно!

ЧИТАЙТЕ ТАКЖЕ:

Это не обсуждается: Скоростной режим

Это не обсуждается: Число Пи

Это не обсуждается: Таблица умножения

Это не обсуждается: Золотое сечение

Это не обсуждается: Таблица Менделеева

Это не обсуждается: Закон Архимеда