4 Энергия и мощность сигнала

Если к резистору с сопротивлением R приложено постоянное напряжение U, то выделяющаяся в резисторе мощность будет равна:

За время Т в этом резисторе выделяется тепловая энергия:

Пусть теперь к тому же резистору приложено не постоянное напряжение, а сигнал S(t). Рассеивающаяся в резисторе мощность при этом тоже будет зависеть от времени (речь идет о мгновенной мощности).

Чтобы вычислить теряющуюся за время T энергию, мгновенную мощность необходимо проинтегрировать:

Можно ввести и понятие средней мощности за заданный промежуток времени, разделив энергию на длительность временного интервала:

Во все приведенные формулы входит сопротивление нагрузки R. Если энергия и мощность интересуют нас не как физические величины, а как средние сравнения различных сигналов, этот параметр можно из формул исключить (принять R=1).

Тогда мы получим определение энергии мгновенной мощности и средней мощности, принятой в теории сигналов

— энергия сигнала

— мгновенная мощность

(1)

Данные параметры иногда называются удельной мощностью и энергией, чтобы подчеркнуть, подразумевая при этом единичное значение сопротивления нагрузки.

Энергия сигнала может быть конечной или бесконечной. Любой сигнал конечной длительности будет иметь конечную энергию, а любой периодический – бесконечную. Если энергия сигнала бесконечна, можно определить его среднюю мощность на всей временной оси. Для этого из формулы (1) путем предельного перехода, устремив интервал усреднения в бесконечность

(2)

Квадратный корень из Рср даст среднеквадратичное значение мощности сигнала

(3)

Для периодического сигнала с периодом Т выполняется соотношение:S(t+nT) = S(t) при любом t.

где n — произвольное целое число; Т – период сигнала.Величина обратная периоду называется частотой повторения сигнала (

f = 1/T). Используют понятие круговой частоты. (ω = 2πf)

Разложению в ряд Фурье могут подвергаться периодические сигналы.

Чтобы такое разложение существовало, фрагмент сигнала длительностью в один период должен удовлетворять условиям Дирихле:

1. не должно быть разрывов 2-го рода (с уходящими в бесконечность ветвями функции)

2. число разрывов 1-го рода (скачков) должно быть конечным

3. число экстремумов должно быть конечным

Различают несколько форм записи ряда Фурье:

1. синусно – косинусная

2. вещественная

3. комплексная

Синусно-косинусная форма записи ряда Фурье

Входящие в формулу кратные основной частоте (ω₁) частоты называются гармониками. Гармоники нумеруются в соответствии с индексом k, частота ω _k = k ω ₁ называется к-ой гармоникой сигнала.

Коэф-ты, входящие в данный ряд определяются след образом:

; ;

a₀/2 – среднее значение с-ла на периоде.

Если S(t) — чётная ф-ция, то все b_к

= 0 и в ф-ле ряда Фурье будут только косинусные слагаемые. Если S(t) — нечётная ф-ция, то все а_к = 0 и в ф-ле ряда Фурье будут только синусные слагаемые.

Вещественная форма записи

Некоторое неудобство синусно-косинусной формы ряда Фурье состоит в том, что для каждого значения индекса суммирования к в формуле фигурируют два слагаемых синус и косинус.

, где ;- фазаk—ой гармоники.

Если S(t) является чётной функцией фазы φ_к могут принимать значения 0 и π, а если S(t) функция нечётная, то возможны значения фазы ±π/2.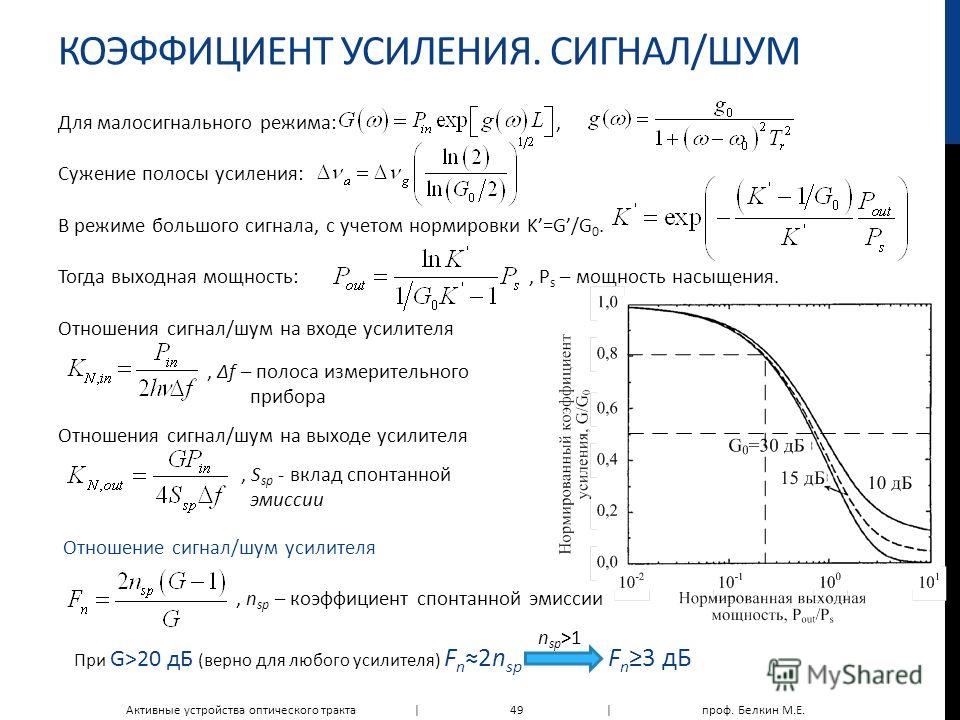

Комплексная форма записи

Данная форма представления является наиболее употребимой в радиотехнике. Она получается из вещественной формы представления косинуса в виде полусуммы комплексных экспонент. Вытекает из формулы Эйлера: е^jx = cos(x) + jsin(x), cos(x) = ½ ( e^jx + e^—jx ).

Применив данное преобразование к вещественной форме ряда Фурье получим:

.

Учитывая, что ,получим . Формулы называются парой преобразований Фурье. Вторая формула из них позволяет найти спектр, т.е. совокупность гармонических составляющих, образующих в сумме колебание.

Спектр периодической последовательности импульсов состоит из постоянной составляющей и множества гармонических составляющих, частоты которых образуют дискретный ряд значений () кратных основной частоте колебаний. Амплитуды гармонических составляющих или сокращенно гармоник равны, а начальные фазы. Такой спектр называется дискретным или линейчатым. Постоянную составляющую можно рассматривать как гармонику с нулевой частотой колебания и амплитудой_.

Методы и техника обработки сигналов при физических измерениях, Т.1

Макс Ж. Методы и техника обработки сигналов при физических измерениях: В 2-х томах. Пер. с франц. — М.: Мир, 1983. — Т. 1. 312 с. Первый том книги французских специалистов посвящен математическим методам обработки сигналов, основанным на идеях корреляционного и спектрального анализа. Изложены вопросы фильтрации и дискретизации сигналов, свойства корреляционных функций и спектральных плотностей и способы их измерения для различных типов сигналов. Специальное внимание уделяется анализу погрешностей, возникающих на всех этапах обработки. Для специалистов, создающих системы автоматизации физических экспериментов, инженеров, аспирантов и студентов, специализирующихся в области измерительной техники, радиофизики и квантовой оптики. Оглавление ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА ВВЕДЕНИЕ Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ 2.2. Преобразование Фурье непериодических функций 2.3. Преобразование Фурье физических функций 2.4. Физический смысл преобразования Фурье 2.5. Условия существования преобразования Фурье 2.6. Некоторые свойства преобразования Фурье 2.7. Несколько функций и их фурье-образы 2.8. Частный случай вещественных сигналов 2.9. Отрицательные частоты 2.10. Аналитический сигнал 2.11. Почему выбрано преобразование Фурье? 2.12 Физическая реализация фурье-образа. Преобразование Фурье в оптике 2.13. Свойства функции sin х/х 2. 14. Лямбда-функция Глава 3. МОЩНОСТЬ И ЭНЕРГИЯ СИГНАЛОВ 3.2. Частотная мощность. Спектральная плотность мощности. Спектр мощности 3.3. Общее определение спектральной плотности 3.4. Теорема Парсеваля 3.5. Понятие скалярного произведения и нормы Глава 4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА 4.2. Связь между фурье-образом и изображением Лапласа Глава 5. СВЕРТКА 5.2. Уравнение свертки 5.3. Несколько замечаний относительно свертки 5.4. Физическая интерпретация свертки 5.5. Прямая и обратная задачи, связанные с операцией свертки 5.6. Свертка и преобразование Фурье. Теорема Планшереля Глава 6. ФИЛЬТРАЦИЯ 6.2. Временная фильтрация 6.3. Частотная фильтрация («линейная фильтрация» в смысле Блан-Лапьера) 6.4. Связь между фильтрацией и сверткой 6.5. Физически реализуемые линейные фильтры частоты 6.6. Идеальный фильтр 6.7. Реализуемые непрерывные аналоговые фильтры [3] 6.8. Фильтры с линейным сдвигом фаз 6.9. Узкополосные фильтры 6. 10. Обобщение понятия фильтрации Глава 7. ДИСКРЕТИЗАЦИЯ 7.2. Теоремы дискретизации 7.3. Дискретизация сигналов конечной длительности 7.4. Дискретизация фурье-образов 7.5. Выбор частоты дискретизации на практике 7.6. Противомаскировочный фильтр 7.7. Физическая дискретизация. Комбинированная дискретизация 7.8. Субдискретизация. Обобщение теоремы Шеннона [9] 7.9. Заключение Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ 8.2. Величина, характеризующая «связь» между двумя физическими процессами. Случай, когда известна одна реализация физического процесса, наблюдаемая в течение большого интервала времени 8.3. Эргодичность 8.4. Коэффициент корреляции и теория информации 8.5. Практические замечания 8.6. Характеристические функции 8.7. Спектральная плотность случайного сигнала 8.8. Связь между временными представлениями сигналов и спектральными плотностями. Теорема Винера — Хинчина 8.9. Функция связи 8.10. Распределение Гаусса, или нормальное распределение 8. 11. Спектральная плотность и центрирование сигналов Глава 9. ОЦЕНКА ОШИБОК ИЗМЕРЕНИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ 9.2. Оценка корреляционных функций 9.3. Оценка спектральных плотностей 9.4. Оценка одномерной плотности вероятности 9.5. Последовательное вычисление среднего значения и дисперсии 9.6. Физическая интерпретация дисперсии 9.7. Идеальный интегратор и низкочастотный фильтр 9.8. Дискретные сигналы Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ 10.2. Коррелометры с вспомогательными шумами 10.3. Условия на вспомогательные шумы, при которых отсутствует смещение оценки корреляционной функции 10.4. Вычисление дисперсии. Состоятельность оценки 10.5. Практические приложения 10.6. Важное замечание 10.7. Замечание относительно генераторов вспомогательных шумов Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ 11.2. Периодические функции 11.3. Переходные функции 11. 4. Дистрибутивность операций вычисления корреляции и спектральной плотности 11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ 12.2. Обнаружение периодического сигнала с известным периодом на фоне шума 12.3. Выделение сигнала на фоне шума. Усреднение 12.4. Обнаружение скрытых периодичностей 12.5. Получение спектральных плотностей по корреляционным функциям 12.6. Измерение динамических характеристик (переходных функций, импульсных характеристик) линейных систем. Идентификация процессов 12.7. Измерение когерентности 12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа 12.9. Измерение временного сдвига двух сигналов Глава 13. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ИЗМЕРЕНИЕ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ 13.2. Влияние фильтрации, обусловленной дискретизацией спектральной плотности 13.3. Дискретизация спектральной плотности, реализуемая на практике 13.4. Систематическая ошибка при измерении спектральной плотности 13.5. Измерение спектральной плотности 13.6. Спектральный анализ методом фильтрации 13.7. Измерение спектральной плотности методом фильтрации 13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7] 13.9. Вычисление автокорреляционных функций и взаимных корреляционных функций по спектральной плотности 13.10. Явление Гиббса 13.11. Корреляционный метод спектрального анализа 13.12. Корреляционный анализатор спектра 13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1] 13.14. Замечания по поводу применения спектральных анализаторов. Определение оптимальной частоты дискретизации Глава 14. ВЕСОВЫЕ ОКНА 14.2. Окна, связанные с преобразованием Фурье 14. 3. Окна, используемые в методе коррелограмм 14.4. Окна, применяемые в методе периодограмм 14.5. Окна, применяемые в методе фильтрации с возведением в квадрат и усреднением 14.6. Основные характеристики временных и спектральных окон 14.7. Первое семейство временных весовых окон 14.8. Второе семейство временных весовых окон (Метод периодограмм) 14.9. Исследование спектра в простом случае 14.10. Выбор весовой функции

Понимание расчетов диапазона беспроводной связи | Electronic Design

Загрузите эту статью в формате .PDF

Одним из ключевых расчетов в любой беспроводной конструкции является диапазон, максимальное расстояние между передатчиком и приемником для нормальной работы. В этой статье определяются факторы, связанные с расчетом дальности, и показано, как оценить дальность, чтобы обеспечить надежную связь.

Почему фактический диапазон может не совпадать с заявленным диапазоном

Вы когда-нибудь покупали беспроводную радиостанцию ​​для встраиваемого проекта и обнаруживали, что не достигли радиочастотного (РЧ) диапазона, указанного в техническом описании? Почему это? Вероятно, это связано с различиями между тем, как поставщик измерил дальность, и тем, как вы используете радио.

Поставщики обычно определяют диапазон, определяя его эмпирическим путем на основе реальных испытаний или путем расчета. Любой подход хорош, если вы учитываете все переменные. Однако эмпирическое решение может выявить реальные ситуации, которые не учитываются расчетами.

Прежде чем мы сравним подходы, давайте определим несколько терминов, чтобы понять цифры производителя или соответствующие переменные для диапазона.

Расчеты мощности и дБм

ВЧ-мощность чаще всего выражается и измеряется в децибелах с милливаттным эталоном или дБм. Децибел — это логарифмическая единица, представляющая собой отношение мощности системы к некоторому эталону. Значение в децибелах, равное 0, эквивалентно отношению 1. Децибел-милливатт — это выходная мощность в децибелах по отношению к 1 мВт.

Так как дБм основан на логарифмической шкале, это абсолютное измерение мощности. При каждом увеличении на 3 дБм выходная мощность увеличивается примерно вдвое, а каждое увеличение на 10 дБм соответствует десятикратному увеличению мощности. 10 дБм (10 мВт) в 10 раз мощнее 0 дБм (1 мВт), а 20 дБм (100 мВт) в 10 раз мощнее 10 дБм.

Вы можете преобразовать мВт в дБм, используя следующие формулы:

P(дБм) = 10 · log ₁₀ (P(мВт))

P(мВт) = 10 ^{(P(дБм)/10)}

Например, мощность 2,5 мВт в дБм:

дБм = 10log2,5 = 3,979

или около 4 дБм. Значение дБм, равное 7 дБм в мВт мощности:

P = 10 ^7/10 = 10 ^0,7 = 5 мВт

Потери в тракте

радиоволна распространяется на большое расстояние. Основным фактором потерь на трассе является уменьшение мощности сигнала на расстоянии самих радиоволн. Радиоволны подчиняются закону обратных квадратов плотности мощности: плотность мощности пропорциональна обратному квадрату расстояния. Каждый раз, когда вы удваиваете расстояние, вы получаете только одну четвертую мощности. Это означает, что каждое увеличение выходной мощности на 6 дБм удваивает достижимое расстояние.

Помимо мощности передатчика, еще одним фактором, влияющим на дальность действия, является чувствительность приемника. Обычно выражается в –дБм. Поскольку и выходная мощность, и чувствительность приемника указаны в дБм, вы можете использовать простое сложение и вычитание для расчета максимальных потерь на трассе, которые могут возникнуть в системе:

Максимальные потери на трассе = мощность передачи – чувствительность приемника + усиление – потери

Коэффициенты усиления включают любые усиления, возникающие в результате использования направленных передающих и/или приемных антенн. Усиление антенны обычно выражается в дБи относительно изотропной антенны. Потери включают затухание в фильтре или кабеле или известные условия окружающей среды. Это соотношение также может быть сформулировано как бюджет канала, который представляет собой учет всех выигрышей и потерь системы для измерения уровня сигнала в приемнике:

Принимаемая мощность = мощность передачи + усиление – потери

Цель состоит в том, чтобы принимаемая мощность превышала чувствительность приемника.

В свободном пространстве (в идеальных условиях) закон обратных квадратов является единственным фактором, влияющим на дальность.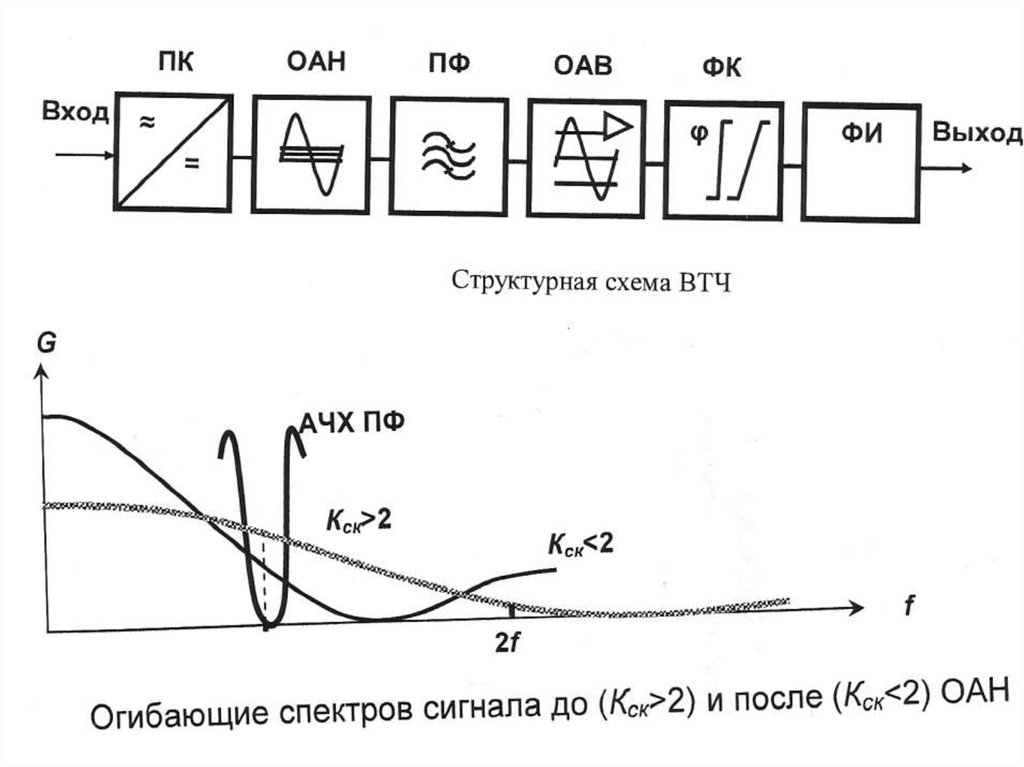 Однако в реальном мире радиус действия также может быть ограничен другими факторами:

• Препятствия, такие как стены, деревья и холмы, могут вызвать значительную потерю сигнала.

• Вода в воздухе (влажность) может поглощать радиочастотную энергию.

• Металлические предметы могут отражать радиоволны, создавая новые версии сигнала. Эти множественные волны достигают приемника в разное время и деструктивно (а иногда и конструктивно) интерферируют друг с другом. Это называется многолучевым распространением.

Fade Margin

Существует множество формул для количественной оценки этих препятствий. Однако, публикуя значения дальности, производители часто игнорируют препятствия и указывают только дальность прямой видимости (LOS) или идеальную дальность пути. Справедливости ради производитель, невозможно знать все среды, в которых может использоваться радио, поэтому невозможно рассчитать конкретный диапазон, которого можно достичь. Производители иногда включают в свои расчеты запас на выцветание, чтобы предусмотреть такие условия окружающей среды. Таким образом, уравнение для расчета расстояния принимает следующий вид:

Максимальные потери на трассе = мощность передачи – чувствительность приемника + усиление – потери – запас на замирание

Запас на замирание – это допуск, который проектировщик системы включает для учета неизвестных переменных. Чем выше запас на затухание, тем лучше будет общее качество связи. Если запас на затухание установлен равным нулю, бюджет канала по-прежнему действует, только в условиях прямой видимости, что не очень практично для большинства проектов. Величина запаса на затухание, которую необходимо включить в расчет, зависит от среды, в которой предполагается развертывание системы. Запас на затухание 12 дБмВт — это хорошо, но лучше от 20 до 30 дБмВт.

В качестве примера предположим мощность передачи 20 дБм, чувствительность приемника –100 дБм, усиление приемной антенны 6 дБи, усиление передающей антенны 6 дБи и запас на затухание 12 дБ. Потери в кабеле незначительны:

Максимальные потери на пути = мощность передачи – чувствительность приемника + усиление – потери – запас на затухание

В – максимальные потери на пути = 20 – (–100) + 12 – 12 = 120 дБ

Один раз на максимальном пути потеря найдена, диапазон можно найти по формуле:

Расстояние (км) = 10 ^{(максимальные потери на трассе – 32,44 – 20 log(f))/20}

, где f = частота в МГц. Например, если максимальные потери на трассе составляют 120 дБ на частоте 2,45 ГГц или 2450 МГц, диапазон будет равен:

Расстояние (км) = 10 ^{(120 – 32,44 – 67,78)/20} = 9,735 км

На рис. 1 показано соотношение между максимальными потерями на трассе и дальностью на частоте 2,45 ГГц.

1. Кривая показывает взаимосвязь между бюджетом канала или максимальными потерями на пути в дБм и предполагаемой дальностью в километрах.

Интерпретация эмпирических результатов

Несмотря на то, что эмпирические методы очень полезны при определении диапазона, часто бывает трудно достичь идеальной LOS для реальных измерений и трудно понять, какой запас на затухание должен быть заложен в систему. Результаты измерений могут помочь определить проблемы, выходящие за рамки распространения РЧ, которые могут повлиять на дальность действия системы, такие как многолучевое распространение, помехи и поглощение РЧ. Но не все тесты в реальном мире одинаковы, поэтому измерения в реальном мире должны использоваться в первую очередь для подтверждения значений бюджета канала, рассчитанных выше.

Факторы, которые могут повлиять на диапазон, достигнутый в эмпирическом тесте, включают усиление антенны, высоту антенны и помехи. Усиление антенны является ключевым источником усиления в системе. Часто производители сертифицируют свои радиостанции для работы с различными типами антенн, от Yagi с высоким коэффициентом усиления и патч-антенн до всенаправленных антенн с более умеренным коэффициентом усиления. Важно убедиться, что тесты проводились с тем же типом антенны, с которой вы сейчас используете радиостанцию. Замена антенны на 6 дБм на антенну на 3 дБм как на стороне передачи, так и на стороне приема вызовет разницу в 6 дБм в бюджете канала и уменьшит дальность вдвое.

Высота антенны и зона Френеля

Высота антенны — еще одна проблема, связанная с эмпирическими измерениями. Увеличение высоты антенны делает две основные вещи. Во-первых, это может помочь вам преодолеть любые возможные препятствия, такие как автомобили, люди, деревья и здания. Во-вторых, это может помочь получить ваш истинный путь сигнала RF LOS с зазором не менее 60% в зоне Френеля.

Зона Френеля представляет собой эллипсоид между передатчиком и приемником, площадь которого определяется длиной волны сигнала. Это рассчитанная площадь, которая стремится учесть блокировку или дифракцию радиоволн. Он используется для расчета надлежащего зазора, который сигнал должен иметь вокруг препятствий для достижения оптимальной мощности сигнала. Общее эмпирическое правило состоит в том, чтобы траектория прямой видимости была свободна от препятствий, высота которых не превышает 60% высоты антенны.

Кривизна Земли также может повлиять на LOS для беспроводных соединений дальнего действия. В таблице приведены некоторые примеры воздействия, когда высота Земли в средней точке трассы линии связи не учитывает холмы или другие особенности местности, а высота антенны обеспечивает сигнал, который составляет не менее 60 % в зоне Френеля.

Во многих практических условиях ваши приемопередатчики могут работать с меньшей высотой антенны, но стоит поспорить, что производители размещают свои антенны на соответствующей высоте. Для вашего приложения вы должны стремиться иметь подходящую высоту антенны для достижения наилучшего диапазона. На рис. 2 показано, как расстояние пути, высота препятствия и высота антенны связаны с зоной Френеля.

2. Требуемая высота антенны определяется по высоте препятствия и с учетом запаса 60% для компенсации условий зоны Френеля.

Наконец, шум и помехи могут отрицательно сказаться на радиусе действия беспроводной системы. Шум нельзя контролировать, но его следует учитывать в диапазоне, если он является проблемой. В промышленных, научных и медицинских (ISM) диапазонах частот от 902 до 928 МГц (Северная Америка) и 2,4 ГГц (во всем мире) часто можно ожидать помех, но их учет затруднен. Изготовители могут проводить эмпирические испытания только при отсутствии помех. Вполне вероятно, что в вашей среде больше помех, чем было во время тестирования производителя.

Резюме

Как узнать, применим ли диапазон, заявленный производителем, к вашей системе при таком количестве переменных в системе? Часто невозможно узнать, проводились ли тесты эмпирически или были рассчитаны числа диапазона. В любом случае, анализируя максимальную мощность передачи и чувствительность приемника, вы можете создать базовый уровень для сравнения одной радиостанции с другой. Используя эти числа вместе с установленным запасом на затухание и любым усилением из-за антенн или потерь из-за ВЧ-кабелей, вы можете рассчитать максимальный бюджет канала. Затем используйте приведенное выше уравнение расстояния, чтобы рассчитать собственный диапазон. Для различных радиоустройств это должно стать хорошей отправной точкой для сравнения двух или трех систем, отвечающих вашим потребностям.

Чтобы понять, будут ли радиостанции работать в вашем приложении, вы должны стремиться к точным реальным тестам, которые могут учитывать высоту антенны, многолучевое распространение, помехи и препятствия. Откладывание реальных испытаний вашего приложения и использование только дословных данных производителя может привести к тому, что вы спросите: «Каков мой диапазон?»

Крис Дауни работает в Laird Technologies с 2007 года. Он отвечает за проектирование сети и устранение неполадок в сети передачи данных уровня 1, а также системное администрирование в общенациональной корпоративной сети. Ранее он был инженером по внедрению встроенных беспроводных модулей. В настоящее время он является менеджером по продуктам для беспроводных модулей на предприятии в Ленексе, штат Канзас. Он имеет степень бакалавра в области электротехники.  

Что такое отношение сигнал/шум и как его рассчитать? | Блог Advanced PCB Design

 

Будучи подростком, изучая все тонкости автомобильной аудиосистемы, я часто наслаждался мельчайшими подробностями каждой ноты. Для меня музыка опьяняла почти так же сильно, как науки и электроника. Однако в это время на первый план выходит появление компакт-дисков и, конечно же, автомобильного сабвуфера.

До появления компакт-дисков винил был очевидным выбором для воспроизведения звука с точки зрения удовольствия от прослушивания. Тем не менее, многие утверждают, что это все еще так, при определенных условиях. Более того, компакт-диск в то время изменил правила игры, и его четкость по сравнению с кассетной лентой была неоспоримой. Точно так же, как существовал спрос на устройства для воспроизведения нового видеостандарта 4K, то же самое было и с компакт-дисками.

Что, конечно же, положило начало автомобильному аудио CD-ресиверу. Благодаря превосходной четкости и простоте использования CD-ресивер был полным. Однако там, где есть капитализм, вы обязательно найдете прямую конкуренцию. Это, безусловно, имело место в случае с CD-ресивером, и самым высмеивающим отличием, которое высококачественные автомобильные аудиокомпоненты могли использовать, чтобы повлиять на своих клиентов, была превосходная четкость. Четкость, о которой они говорили, была достижима только благодаря их превосходным характеристикам отношения сигнал/шум.

Единственной характеристикой, которая всегда была лучше, чем у младших брендов, было отношение сигнал/шум (SNR). Кроме того, даже для нетренированного уха разница в чистоте и музыкальном присутствии была неоспоримой. Таким образом, если SNR может иметь такое большое значение в чистоте музыкального звука, то его важность в приложениях для передачи сигналов экспоненциально более критична. Поэтому в следующих нескольких абзацах я расскажу об отношении SNR и о том, как его рассчитать для обеспечения проектной точности.

Что такое отношение сигнал/шум?

С точки зрения определения, SNR или отношение сигнал/шум – это соотношение между полезной информацией или мощностью сигнала и нежелательным сигналом или мощностью фонового шума.

Кроме того, SNR — это параметр измерения, используемый в областях науки и техники, который сравнивает уровень полезного сигнала с уровнем фонового шума. Другими словами, SNR представляет собой отношение мощности сигнала к мощности шума, и его единицей выражения обычно являются децибелы (дБ). Кроме того, отношение больше 0 дБ или больше 1:1 означает больше сигнала, чем шума.

Помимо технического определения отношения сигнал-шум, я определяю его в других терминах с помощью сравнительного анализа. Например, скажите, что вы и еще один человек находитесь в большой комнате и разговариваете. Однако в комнате полно других людей, которые тоже разговаривают. Кроме того, некоторые из других людей также имеют схожие с вами и другим человеком, участвующими в вашем обсуждении, голосовые паттерны. Как вы понимаете, было бы трудно разобрать, кто что говорит.

Почему важно соотношение сигнал/шум?

В предыдущем сравнении вы можете лучше понять, что подразумевается под нежелательным сигналом или шумом. Как вы также можете себе представить, было бы почти невозможно понять другую сторону, участвующую в вашем разговоре. Кроме того, в подобном сценарии мы бы считали это проблемой отношения сигнал-шум или эквивалентом отношения сигнал-шум, которое ниже допустимых параметров.

Теперь предположим, что полезный сигнал представляет собой важные данные со строгим или узким допуском на ошибки, и есть другие сигналы, нарушающие ваш желаемый сигнал. Опять же, это сделало бы задачу приемника экспоненциально более сложной по расшифровке полезного сигнала. Таким образом, именно это делает столь важным высокое отношение сигнал/шум. Кроме того, в некоторых случаях это также может означать разницу в функционировании устройства, и во всех случаях это влияет на производительность между передатчиком и приемником.

В беспроводной технологии ключом к производительности устройства является способность устройства отличать применяемые сигналы как достоверную информацию от любого фонового шума или сигналов в спектре. Это олицетворяет определение стандартов, для установления которых используются спецификации SNR. Кроме того, стандарты, о которых я говорю, также обеспечивают надлежащую работу беспроводной сети.

Основы расчета отношения сигнал-шум

Говоря простыми словами, ОСШ представляет собой разницу между полезным сигналом и уровнем шума. Кроме того, с точки зрения определения, минимальный уровень шума — это кажущиеся фоновые передачи, создаваемые другими устройствами или устройствами, которые непреднамеренно создают помехи на аналогичной частоте. Следовательно, чтобы установить отношение сигнал/шум, необходимо найти измеримую разницу между уровнем полезного сигнала и нежелательным шумом, вычитая значение шума из значения уровня сигнала.

Достижение желаемой целостности сигнала может быть затруднено на любом этапе проектирования.

 

Гипотетически, если радиоустройство вашего устройства принимает сигнал -65 дБм (децибел на милливатт), а минимальный уровень шума составляет -80 дБм, то результирующее отношение сигнал/шум составляет 15 дБ. Тогда это будет отражаться как мощность сигнала 15 дБ для этого беспроводного соединения. Как я уверен, вы знаете, что с точки зрения подключения к беспроводным сетям, эксперты заявляют о требовании отношения сигнал-шум не менее 20 дБ, чтобы, скажем, просматривать веб-страницы. Однако ниже приведены требования к SNR в сравнении со значениями SNR:

• от 5 дБ до 10 дБ : ниже минимального уровня для установления соединения из-за того, что уровень шума почти неотличим от полезного сигнала (полезная информация).

• от 10 дБ до 15 дБ : принятый минимум для установления ненадежного соединения.

• от 15 дБ до 25 дБ : обычно считается минимально приемлемым уровнем для установления плохой связи.

• от 25 дБ до 40 дБ : считается хорошим.

• 41 дБ или выше : считается отличным.

Хотя SNR обычно используется для количественной оценки четкости или мощности электрических сигналов, его также можно применять к любой форме сигнала (передачи). Например, он используется для описания уровней изотопов в ледяных ядрах, биохимических сигналов между клетками или чистоты звука для автомобильных усилителей и источников (DVD, CD или Digital). Однако для аудиокомпонентов значение SNR всегда положительное. Например, ОСШ 95 дБ означает, что уровень звукового сигнала на 95 дБ выше уровня шума. Что, в свою очередь, означает, что SNR 95 дБ лучше, чем 80 дБ.

Как рассчитать отношение сигнал/шум

Вычисления SNR могут быть как простыми, так и сложными, в зависимости от рассматриваемых устройств и имеющихся у вас данных. Таким образом, если ваши измерения SNR уже представлены в децибелах, вы можете вычесть количество шума из желаемого сигнала: SNR = S — N. Это потому, что вычитание логарифмов эквивалентно делению нормальных чисел. Кроме того, разница в числах равна SNR. Например, вы измеряете радиосигнал мощностью -10 дБ и шумовой сигнал -50 дБ. -10 — (-50) = 40 дБ.

Как я уже говорил ранее, вычисление SNR также может быть задействовано. Итак, для сложных вычислений вы делите значение полезного сигнала на количество шума, а затем берете десятичный логарифм результата, то есть log (S ÷ N). После этого, если измерения уровня сигнала выражены в ваттах (мощность), вы умножаете на 20. Однако, если они являются единицами напряжения, вы умножаете на 10.

Кроме того, для мощности SNR = 20 log ( S ÷ N), а для напряжения SNR = 10 log (S ÷ N). Кроме того, результирующий расчет представляет собой SNR в децибелах. Например, ваше измеренное значение шума (N) составляет 2 мкВ, а ваш сигнал (S) — 300 мВ. SNR составляет 10 log (0,3 ÷ 0,000002) или приблизительно 62 дБ.

Формула соотношения сигнал-шум и пропускная способность канала

Соотношение сигнал-шум влияет на все беспроводные сети, включая Bluetooth, Wi-Fi, 4G, 4G LTE и 5G, поскольку их работа зависит от радиосигналов. Кроме того, поскольку они функционируют за счет использования радиосигналов, каждый из упомянутых способов связи имеет максимальную пропускную способность канала. Более того, с увеличением SNR увеличивается и пропускная способность канала.

В целом пропускная способность канала, полоса пропускания и отношение сигнал/шум влияют на максимальную пропускную способность каналов связи. Причем это открытие принадлежит Клоду Шеннону, и он делает эту корреляцию во время Второй мировой войны. В современных областях электроники и науки инженеры и ученые называют его законом Шеннона или теоремой Шеннона-Хартли.

В соответствии с законом Шеннона следующая формула изображает эту корреляцию, которая формирует отношение, зависящее от пропускной способности:

C = W log2(1 + S/N)

В рамках этой формулы:

C равно пропускной способности канала (биты /s)

S равно средней мощности принимаемого сигнала

N равно средней мощности шума

Вт равно ширине полосы частот (Гц)

Теорема Шеннона-Хартли показывает, что значения S (средняя мощность сигнала), N ( средняя мощность шума), а W (полоса пропускания) устанавливает предел скорости передачи.

Достижение технических решений с учетом сложных требований к сигналу является полезным в современной развивающейся отрасли.

 

Важность точного расчета отношения сигнал/шум является обязательным условием эффективной и точной разработки. Кроме того, вычисление отношения сигнал-шум также позволит получить представление о функциональных возможностях и характеристиках конструкции. Время, чтобы осознать, что дизайн неосуществим, наступает до этапа производства. Поэтому важно оценивать параметры конструкции с помощью расчетов, а также моделирования.

К счастью, благодаря набору инструментов для проектирования и анализа Cadence ваши дизайнеры и производственные группы будут работать вместе над внедрением надлежащих методов расчета отношения сигнал/шум во всех ваших проектах печатных плат. Allegro PCB Designer — это решение для компоновки, которое вы искали, и оно, несомненно, может облегчить реализацию эффективных стратегий соотношения сигнал/шум в ваших текущих и будущих проектах печатных плат.

Если вы хотите узнать больше о том, какое решение может предложить Cadence, обратитесь к нам и нашей команде экспертов.