Тема 8.3.Составление формулы по заданной таблице истинности
Пример 8.4:
0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 |
0 | 1 | 0 | 0 |
0 | 1 | 1 | 1 |
1 | 0 | 0 | 0 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 1 |
1 | 1 | 1 | 1 |
Выбираем
строки, где
и выписываем конъюнкции всех переменных,
причём, если переменная в этом наборе
равна 1, то записываем её саму, а если
переменная = 0, то её отрицание.
Для данного примера:
конъюнкция этих дизъюнкций и будет искомой формулой:
Определение: Конъюнкция называетсяэлементарной, если в неё входят переменные и их отрицания. Количество различных переменных, входящих в элементарную конъюнкцию или элементарную дизъюнкцию, называетсярангом.
Константы считаются элементарной конъюнкцией ранга 0. Переменная считается элементарной конъюнкцией или элементарной дизъюнкцией ранга 1. Любую конъюнкцию переменных, не являющуюся тождественно ложной, можно привести к виду элементарной, а любую дизъюнкцию букв, не являющуюся тождественно истинной, также можно привести к виду элементарной. Для этого надо применить свойства коммутативности, идемпотентности и ассоциативности конъюнкции и дизъюнкции.
Строго
доказано, что любую формулу булевой
алгебры можно выразить с помощью операций
, &,.
Интуитивно этот факт очевиден, вспомним
алгоритм составления формулы по таблице
истинности.
Определение:ДНФ– это дизъюнкция различных элементарных конъюнкций (т.е. каждая конъюнкция состоит из элементарных высказываний или их отрицаний).
Аналогично определяется КНФ – коньюктивная нормальная форма.
Определение: Если в ДНФ все элементарные конъюнкции имеют один и тот же ранг, равный числу переменных, от которых зависит ДНФ, то она называетсясовершенной(СДНФ).
Теорема:Для любой логической формулы, не являющейся тождественно ложной, существует и притом единственная, с точностью до перестановки СДНФ.
Следствие:Любую булеву формулу, не являющуюся тождественно ложной можно представить в виде суперпозиции &,,, причём отрицание относится только к переменным.
Определение:Функцияназываетсядвойственнойк функции,
если.
Если взять отрицание обеих частей равенства и подставить вместо переменных, то получится искомое равенство. Это означает, что функциядвойственна к функции, и, таким образом, отношение двойственности является симметричным. Из определения двойственности ясно, что для любой функции двойственная ей функция определяется однозначно. В частности, может оказаться, что функция двойственна самой себе. В этом случае она называется
Пример 8.5:Если рассматривать логические функции, то, очевидно, дизъюнкция двойственна конъюнкции и наоборот (непосредственно следует из законов Де Моргана). Отрицание является самодвойственной функцией. Функция-константадвойственна функции. Ещё один традиционный пример самодвойственной функции – функция.
Пользуясь определением двойственности нетрудно доказать следующее утверждение, называемое принципом двойственности.
Теорема: Если в формуле

В булевой алгебре принцип двойственности имеет более конкретный вид, вытекающий из ранее приведённых примеров: если в формуле , представляющей функцию, все конъюнкции заменить дизъюнкциями и наоборот, все единицы заменить нулями и наоборот, то получим формулу, представляющую функцию, двойственную функции.
Если функции равны, то двойственные им функции также равны. Это позволяет с помощью принципа двойственности получать новые эквивалентные соотношения, переходя от равенства с помощью указанных замен к равенству. Примером могут служить соотношенияи, которые могут быть получены друг из друга по указанному принципу.
Построение таблиц истинности | Учебно-методический материал на тему:
Лекция 13
Тема : «Построение таблиц истинности»
Цель: закрепить умение строить истинные сложные высказывания из простых с использованием логических операций, сформировать навыки построения таблиц истинности
Ход урока
1. Орг. момент
2. Решение задач
Упражнение 1
Запишите следующие высказывания в виде логических выражений
- Число 17 нечетное и двузначное
- Неверно, что корова – хищное животное
- На уроке физики ученики выполняли лабораторную работу и сообщали результаты исследований учителю
- Если число делится на 2, то – нечетное.

- Переходи улицу только на зеленый свет
- На уроке информатики необходимо соблюдать особые правила поведения
- При замерзании воды выделяется тепло
- Если Маша – сестра Саши, то Саша – брат маши
- если компьютер включен, то можно на нем работать
- Водительские права можно получить тогда и только тогда, когда тебе исполниться 18 лет
- Компьютер выполняет вычисления, если он включен
- ты можешь купить в магазине продукты, если у тебя есть деньги
- Тише едешь – дальше будешь
Упражнение 2
Составьте и запишите истинные сложные высказывания из простух с использованием логических операций
1. Неверно, что и
2. Z является min(Z,Y)
3. А является max(A,B,C)
4.Любое из чисел А,В,С положительно
5. Любое из чисел А,В,С отрицательно
6. Хотя бы одно из чисел А,В,С не отрицательно
7. Хотя бы одно из чисел А,В,С не меньше 12
8. Все числа А,В,С равны 12
9. Если Х делится на 9 то Х делится на 3
10. (¬10)
(¬10)
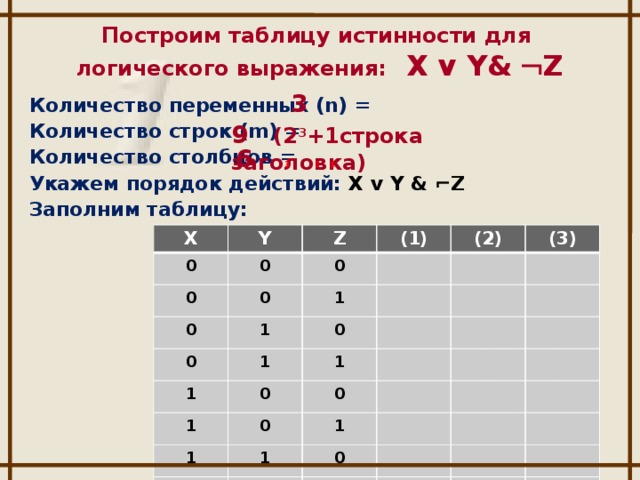
3. Построение таблиц истинности
Приоритет логических операций
1) инверсия 2) конъюнкция 3) дизъюнкция 4) импликация и эквивалентность
Как составить таблицу истинности?
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре:
(0, 0), (0, 1), (1, 0), (1, 1).
Если формула содержит три переменные, то возможных наборов значений переменных восемь (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Для составление таблицы истинности необходимо (алгоритм записать в тетрадь)
- выяснить количество сток в таблице (вычисляется как 2n, где n- количество переменных)
- выяснить количество столбцов = количеству переменных + количество логических операций
- установить последовательность логических операций
- построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных.

- заполнить таблицу истинности
Пример: В классе оказалось разбито стекло. Учитель объясняет директору: это сделал Коля или Саша. Но Саша этого на делал, т.к. в это время сдавал мне зачет. Следовательно, это сделал Коля.
Решение:
Формализуем данное сложное высказывание.
К – это сделал Коля
С – это сделал Саша
Кол-во простых высказываний n = 2.
Форма высказывания: Е = ( К ∨ C ) & ¬ С ⇒ К
- Определить количество строк и столбцов в таблице истинности.
Т.к. каждое из простых высказываний может принимать всего два значения (0 или 1), то количество разных комбинаций значений n высказываний – 2 n .
Количество строк в таблице = 2 n + строка на заголовок.
Количество столбцов в таблице равно сумме количества простых высказываний (n) и количества разных логических операций, входящих в сложное высказывание.
В нашем примере: количество строк — 22 + 1 = 5 ,
столбцов – 2 + 4 = 6
- Начертить таблицу и заполнить заголовок
Первая строка – номера столбцов.
Вторая строка промежуточные формулы и соответствующие им условные записи операций над значениями .
- Заполнить первые n столбцов.
В нашем примере сначала заполняем 1-й и 2-й столбцы.
- Заполнить остальные столбцы.
В соответствии с таблицами истинности соответствующих логических операций, причем при заполнении каждого столбца операции выполняются над значениями одного или двух столбцов, расположенных левее заполняемого.
Итак, вычисляем значения 3-го столбца по значениям 2-го, потом значения 4-го – по значениям 1-го и 2-го…
К | С | ¬ С | К ∨ C | ( К ∨ C ) & ¬ С | ( К ∨ C ) & ¬ С ⇒ К |
1 | 1 | 0 | 1 | 0 | 1 |
0 | 1 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 1 | 1 | 1 |
0 | 0 | 1 | 0 | 0 | 1 |
Вывод: получили в последнем столбце все единицы. Значит, значение сложного высказывания истинно при любых значениях простых высказываний К и С. Следовательно, учитель рассуждал логически правильно.
Значит, значение сложного высказывания истинно при любых значениях простых высказываний К и С. Следовательно, учитель рассуждал логически правильно.
Примеры.
1. Составим таблицу истинности для формулы , которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу:
Переменные | Промежуточные логические формулы | Формула | |||||
0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.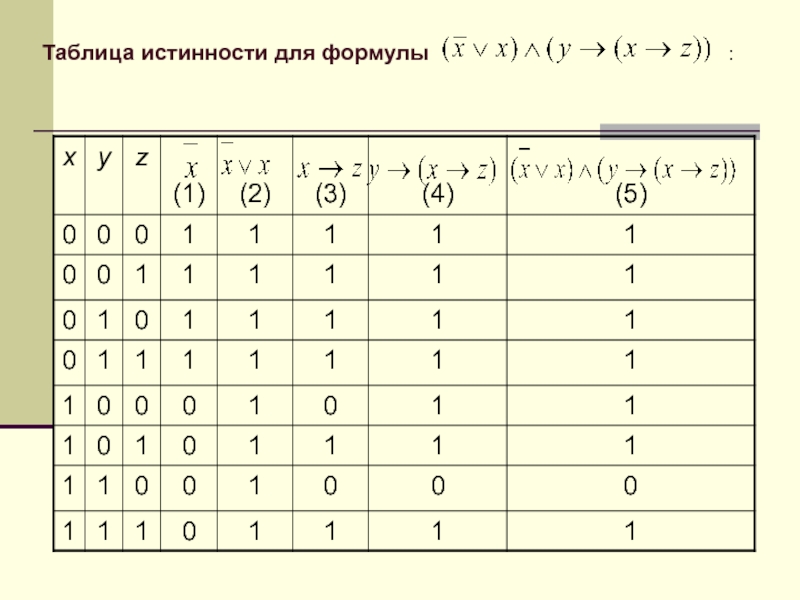
2. Таблица истинности для формулы :
Переменные | Промежуточные логические формулы | Формула | ||||
0 | 0 | 0 | 1 | 1 | 0 | 0 |
0 | 1 | 1 | 0 | 0 | 0 | 0 |
1 | 0 | 1 | 0 | 1 | 1 | 0 |
1 | 1 | 1 | 0 | 0 | 0 | 0 |
Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 0, то есть является тождественно ложной.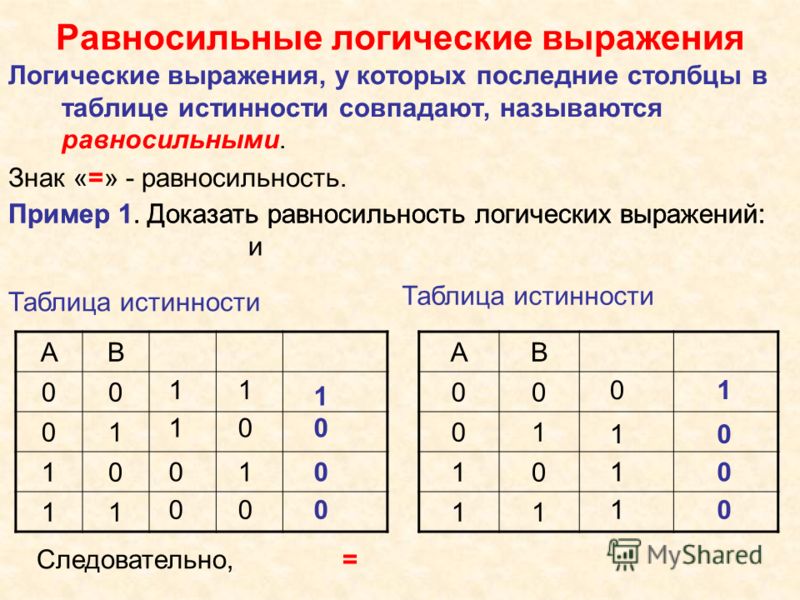
3. Таблица истинности для формулы :
Переменные | Промежуточные логические формулы | Формула | ||||||
0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
Из таблицы видно, что формула в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой. ¬Z
¬Z
5. Подведение итогов
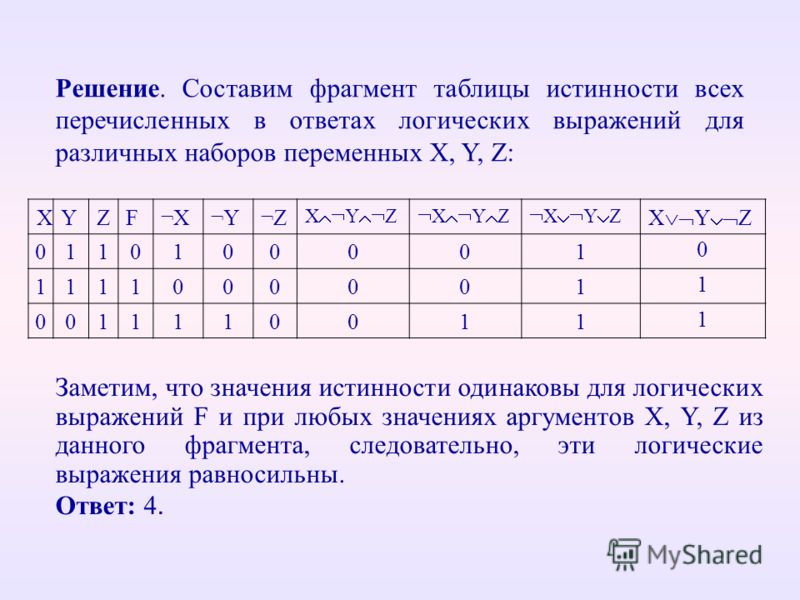
Логика— Как найти логическую формулу для данной таблицы истинности?
Задавать вопрос
спросил
Изменено 9 лет, 3 месяца назад
Просмотрено 27 тысяч раз
$\begingroup$
Допустим, у меня есть такая таблица истинности:
X Y A т т ф т ф т ф т т ф ф ф
Теперь мне нужно найти формулу для A. Этот случай довольно прост, потому что я сразу вижу, что это выглядит как перевернутые значения X~B, таким образом, ¬(X~B). Теперь для более сложной задачи я не знаю метода.
Х У З А т т т ф т т ж ф т ф т т т ф ф ф ф т т ф ж т ж ж ф ф т т ф ф ф ф
Есть ли подход, который я здесь упустил?
$\endgroup$
$\begingroup$
Я считаю, что Карты Карно полезны для этой цели.
$\endgroup$
0
$\begingroup$
Расширение ответа Мариано: чтобы получить формулу для таблицы истинности, которая имеет ровно одну t , а остальные строки f , посмотрите на строку и запишите значения переменных в этой строке. Например, если вам нужна формула для таблицы истинности с тремя переменными, как во втором примере, который имеет t в третьей строке (соответствующей $X$ и $Z$ истине и $Y$ ложно) и f во всех остальных строках, то, поскольку эта строка «$X$ истинна, $Y$ ложно, а $Z$ истинно», то вы используете формулу $X \клин (\neg Y)\клин Z$.
Теперь предположим, что у вас есть формула с t s в двух строках и f s везде. Скажем, три переменных: t в третьем ряду, t в пятом ряду и f везде. Формула, которая имеет
Формула, которая имеет t только в третьей строке — это, как и прежде, $X\wedge (\neg Y)\wedge Z$. Формула, которая имеет t только в пятой строке, это $(\neg X)\wedge (\neg Y)\wedge Z$. Таким образом, формула, которая как
Для произвольного числа t просто возьмите дизъюнкт достаточного количества формул, каждая из которых соответствует таблице только с одним т .
$\endgroup$
2
$\begingroup$
Выберите строки, в которых t появляются в крайнем правом столбце, и запишите дизъюнктивную нормальную форму. В вашем примере есть только две строки с t , и ваше выражение будет состоять из двух членов:
$ (X \cdot \bar{Y} \cdot Z) + (\bar{X} \cdot \bar{ Y} \cdot Z) $
Теперь у вас есть логическая формула для вашей таблицы истинности. Вы можете остановиться на этом или использовать законы булевой алгебры, чтобы получить более простое выражение. В этом случае можно использовать распределительный закон:
Вы можете остановиться на этом или использовать законы булевой алгебры, чтобы получить более простое выражение. В этом случае можно использовать распределительный закон:
$ (X \cdot \bar{Y} \cdot Z) + (\bar{X} \cdot \bar{Y} \cdot Z) = (X + \bar{X})\cdot (\bar{ Y} \cdot Z) = 1 \cdot (\bar{Y} \cdot Z) = \bar{Y} \cdot Z$
$\endgroup$
$\begingroup$
Сначала решите задачу поиска формулы для таблиц истинности, в крайней правой таблице которых имеется ровно одна буква T. Затем переходим к общему случаю.
$\endgroup$
Использование таблиц истинности для моделирования комбинаторной логики — MATLAB и Simulink
Использование таблиц истинности для моделирования комбинаторной логики
Таблицы истинности реализуют комбинаторную логику в табличном формате. Вы можете использовать
Таблицы истинности Stateflow ® для моделирования принятия решений для обнаружения и управления ошибками и
переключение режимов.
Вы можете использовать
Таблицы истинности Stateflow ® для моделирования принятия решений для обнаружения и управления ошибками и
переключение режимов.
Функции таблицы истинности в диаграмме Stateflow выполняются, только когда вы вызываете функцию таблицы истинности. Вы можете определить функция таблицы истинности в диаграмме Stateflow, состоянии или поддиаграмме. Расположение функции определяет множество состояния и переходы, которые могут вызвать функцию.
Если вы хотите вызвать функцию из одного состояния или поддиаграммы и ее подсостояния, поместите свою функцию таблицы истинности в это состояние или поддиаграмму. Эта функция переопределяет любые другие функции с тем же именем в родителях и предках этого состояние или подсхема.
Если вы хотите вызвать функцию в любом месте диаграммы, поместите функцию таблицы истинности на уровне диаграммы.
Если вы хотите вызвать функцию из любого графика в вашей модели, поместите свою таблицу истинности на уровне диаграммы и включить экспорт функций уровня диаграммы.
 Для дополнительной информации,
см. Экспорт функций Stateflow для повторного использования.
Для дополнительной информации,
см. Экспорт функций Stateflow для повторного использования.
Функция таблицы истинности может получить доступ к диаграмме и данным состояния над ней в Иерархия потоков состояний.
В качестве альтернативы, для более прямой реализации логики принятия решений, вы можете добавить Истина Блок таблицы непосредственно в вашу модель Simulink ® . Для реализации логики управления блоки таблицы истинности используют MATLAB ® в качестве языка действий.
Структура таблицы истинности
Эта функция таблицы истинности имеет имя ttable . Требуется три
аргументы ( x , y и z ) и возвращает
одно выходное значение ( r ).
Функция состоит из такого расположения условий, решений и действия.
. 0003 0003 | ||||
|---|---|---|---|---|
x == 1 | T | F | F | — |
y == 1 | F | T | F | — |
z == 1 | F | F | T | — |
Action | r = 1 | r = 2 | r = 3 | r = 4 |
Each of the conditions entered in the Условие столбец обязательно
оценить как true (ненулевое значение) или false (нулевое значение). Результаты для каждого условия
указывается как T (истина), F (ложь) или — (истина или ложь). Каждый из столбцов решений
объединяет результат для каждого условия с помощью логического И в составное условие, которое
называется решением.
Вы оцениваете таблицу истинности по одному решению за раз, начиная с Решение 1 . Решение 4 охватывает все возможные оставшиеся решения. Если одно из решений истинно, таблица выполняет соответствующее действие, а затем выполнение таблицы истинности завершено.
Например, если выполняются условия x == 1 и y == 1 .
false и условие z == 1 истинно, тогда Решение 3 верно, а переменная r устанавливается равным 3. Остальные решения
не проверено, и оценка таблицы истинности завершена. Если первые три решения
false, то решение по умолчанию автоматически становится истинным, и его действие
( r=4 ) выполняется. В этой таблице перечислены псевдокоды, соответствующие
оценка этого примера таблицы истинности.
Псевдокод | Описание |
|---|---|
если ((x == 1) & !(y == 1) & !(z == 1)) р = 1; | Если Решение 1 верно, то установить |
elseif (!(x == 1) & (y == 1) & !(z == 1)) г = 2; | Если Решение 2 верно, то установить |
elseif (!(x == 1) & !(y == 1) & (z == 1)) г = 3; | Если Решение 3 верно, то установить |
еще г = 4; конец | Если все остальные решения ложны, то решение по умолчанию истинно. Набор |
Определение функции таблицы истинности
Чтобы определить функцию таблицы истинности:
В палитре объектов щелкните значок функции таблицы истинности .
На холсте диаграммы щелкните место для новой функции таблицы истинности.

Введите метку подписи для функции.
Метка подписи функции указывает имя для вашего функция и формальные имена для ее аргументов и возвращаемых значений. Этикетка с подписью имеет это синтаксис:
[return_val1,return_val2,...] = имя_функции(arg1,arg2,...)
Вы может указывать несколько возвращаемых значений и несколько входных аргументов. Каждое возвращаемое значение и ввод аргумент может быть скаляром, вектором или матрицей значений. Для функций с одним возвращаемым значением опустить скобки в метке подписи.Вы можете использовать одно и то же имя переменной как для аргументов, так и для возвращаемые значения. Когда вы используете одну и ту же переменную для ввода и вывода, вы создаете оперативные данные . Например, функция с этой меткой подписи использует переменные
y1иy2как входные данные, так и выходы:[y1,y2,y3] = f(y1,u,y2)
Если вы экспортируйте эту функцию в код C, сгенерированный код обрабатываетy1иy2как аргументы на месте, передаваемые по ссылке. Использование данных на месте снижает
количество раз, которое сгенерированный код копирует промежуточные данные, что приводит к более
эффективный код.
Использование данных на месте снижает
количество раз, которое сгенерированный код копирует промежуточные данные, что приводит к более
эффективный код.В Панель символов и Model Explorer, аргументы и возвращаемые значения сигнатуры функции отображаются как элементы данных, принадлежащие функция. Аргументы имеют область действия
Вход. Возвращаемые значения имеют областьВыход.Укажите свойства данных для каждого аргумента и возвращаемого значения, как описано в Установите свойства данных. Когда аргумент и возвращаемое значение имеют того же имени, вы можете редактировать свойства только для аргумента. Свойства для возврата значение доступно только для чтения.
Чтобы запрограммировать функцию, откройте редактор таблицы истинности, дважды щелкнув функцию коробка.
В редакторе таблицы истинности добавьте условия, решения и действия.
 Для большего
информацию см. в разделе Программирование таблицы истинности.
Для большего
информацию см. в разделе Программирование таблицы истинности.Создайте любые дополнительные элементы данных, необходимые для вашей функции. Для дополнительной информации, см. Добавление данных через Model Explorer.
Ваша функция может обращаться к своим собственным данным или данным, принадлежащим родительским состояниям или диаграмма. Элементы данных в функции могут иметь одну из следующих областей:
Константа— Постоянные данные сохраняют свое начальное значение через все вызовы функций.Параметр— Данные параметра сохраняют исходное значение через все вызовы функций.Локальный— Локальные данные сохраняются от одного вызова функции до следующий вызов функции. Действительно только для таблиц истинности, которые используют C в качестве действия язык.
Temporary— Временные данные инициализируются в начале каждого вызов функции. Допустимо только для таблиц истинности, использующих C в качестве языка действий.
В функциях таблицы истинности, которые используют C в качестве языка действий, определяют локальные данные, когда вы хотите, чтобы ваши значения данных сохранялись при вызовах функций на протяжении всей симуляции. Определите временные данные, если вы хотите инициализировать значения данных в начале каждого вызов функции. Например, вы можете определить счетчик с помощью
Локальная область, если вы хотите отслеживать, сколько раз вы вызываете функцию. Напротив, вы можете назначить счетчику цикловВременный прицел, если счетчик не нужен значение, которое будет сохраняться после завершения функции.В функциях таблицы истинности, которые используют MATLAB в качестве языка действий, вам не нужно определять локальные или временные данные функции.
 Вместо этого в этих функциях вы можете использовать неопределенные переменные для хранения
значения, которые доступны только во время остальной части вызова функции. Для хранения значений
которые сохраняются при вызовах функций, используйте локальные данные на уровне диаграммы.
Вместо этого в этих функциях вы можете использовать неопределенные переменные для хранения
значения, которые доступны только во время остальной части вызова функции. Для хранения значений
которые сохраняются при вызовах функций, используйте локальные данные на уровне диаграммы.
Вызов функций таблицы истинности в состояниях и переходах
Вы можете вызывать функции таблицы истинности из действий любого состояния или перехода или из другие функции. Если вы экспортируете функцию таблицы истинности, вы можете вызвать ее из любой диаграммы в модель. Дополнительные сведения об экспорте функций см. в разделе Экспорт функций Stateflow для повторного использования.
Чтобы вызвать функцию таблицы истинности, используйте сигнатуру функции и включите фактический значение аргумента для каждого формального аргумента в сигнатуре функции.
[return_val1,return_val2,...] = имя_функции(arg1,arg2,...)
Если типы данных фактических и формальных аргументов различаются, функция приводит
фактический аргумент к типу формального аргумента.
Задание свойств функций таблицы истинности
Перечисленные ниже свойства определяют, как функция таблицы истинности взаимодействует с другими компоненты в вашей диаграмме Stateflow. Вы можете изменить эти свойства в свойстве . Инспектор , обозреватель моделей или диалоговое окно свойств таблицы истинности.
Для использования Property Inspector :
На вкладке Modeling в разделе Design Data , выберите Инспектор свойств .
В редакторе Stateflow выберите функцию таблицы истинности.
В инспекторе свойств отредактируйте функцию таблицы истинности характеристики.
Для использования обозревателя моделей:
На вкладке Modeling в разделе Design Data , выберите Обозреватель моделей .

В панели Model Hierarchy выберите таблицу истинности функция.
В диалоговом окне отредактируйте функцию таблицы истинности. характеристики.
Для использования диалогового окна свойств таблицы истинности:
В редакторе Stateflow щелкните правой кнопкой мыши функцию таблицы истинности.
Выберите .
В диалоговом окне свойств отредактируйте свойства функции таблицы истинности.
Эти свойства также можно изменять программно с помощью объектов Stateflow.TruthTable . Для получения дополнительной информации о программном интерфейсе Stateflow см. Обзор API Stateflow.
Имя
Имя функции. Щелкните ссылку с названием функции, чтобы вывести ее на передний план. на родной карте.
Встроенная опция функции
Управляет встраиванием вашей функции в сгенерированный код:
Auto— определяет, следует ли встраивать вашу функцию на основе внутреннего расчета.
Встроенный— Встраивает вашу функцию, если вы не экспортируете к другим диаграммам и не является частью рекурсии. (Рекурсия существует, если ваш функция вызывает себя прямо или косвенно через вызов другой функции.)Функция— не встраивает вашу функцию.
Это свойство недоступно в инспекторе свойств .
Ярлык
Ярлык для вашей функции. Метка сигнатуры функции задает имя для вашей функции и формальные имена для ее аргументов и возвращаемых значений. Это свойство недоступно в Property Inspector .
Заниженная спецификация
Управляет уровнем диагностики неполной спецификации в вашей функции таблицы истинности. Дополнительные сведения см. в разделе Исправление завышенных и недоопределенных таблиц истинности.
Превышение спецификации
Управляет уровнем диагностики завышения спецификации в вашей функции таблицы истинности.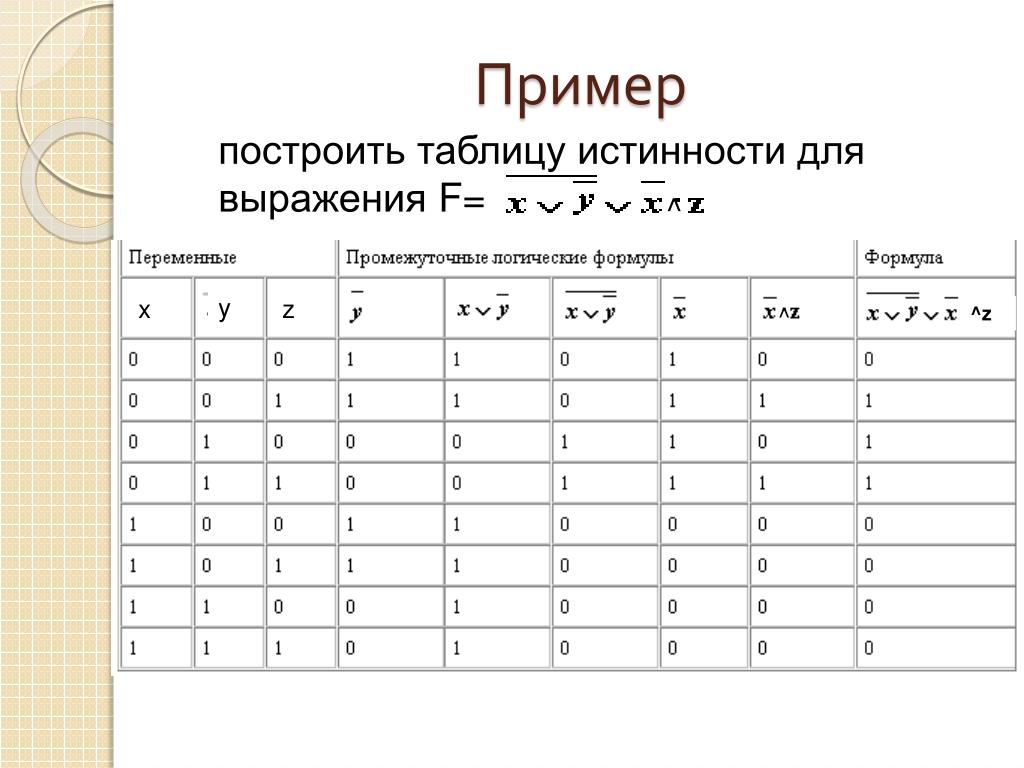 Дополнительные сведения см. в разделе Исправление завышенных и недоопределенных таблиц истинности.
Дополнительные сведения см. в разделе Исправление завышенных и недоопределенных таблиц истинности.
Язык действий
Управляет языком действий для вашей функции таблицы истинности Stateflow. Выберите между MATLAB или C. Это свойство доступно только в диаграммах, которые используют C в качестве действия. язык. Для получения дополнительной информации смотрите Различия Между MATLAB и C как Синтаксис Языка Действия.
Описание
Описание функции таблицы истинности.
Ссылка на документ
Ссылка на онлайн-документацию по функции таблицы истинности. Вы можете ввести веб-URL адрес или команду MATLAB, которая отображает документацию в виде файла HTML или в виде текста в Командное окно MATLAB. При нажатии на ссылку Документ гиперссылка, Stateflow оценивает ссылку и отображает документацию.
Задайте свойства для блоков таблицы истинности
Свойства блока таблицы истинности определяют, как ваша таблица истинности взаимодействует с
модель Симулинк.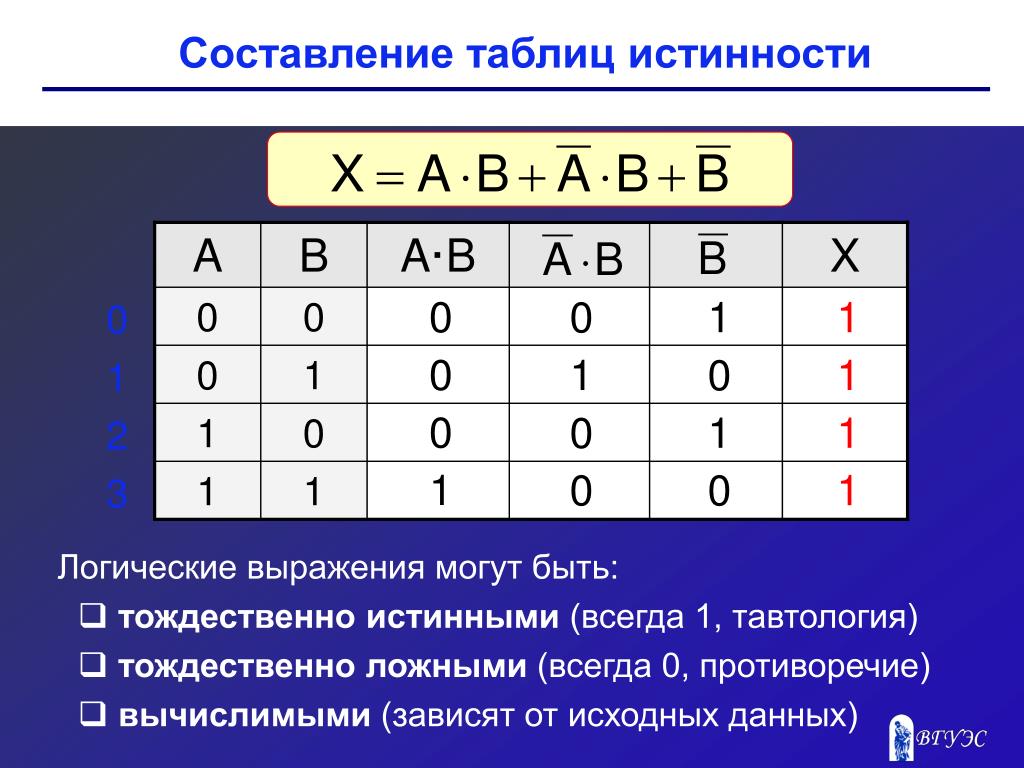 Вы можете изменить эти свойства в свойстве .
Inspector , Model Explorer или диалоговое окно свойств таблицы истинности.
Вы можете изменить эти свойства в свойстве .
Inspector , Model Explorer или диалоговое окно свойств таблицы истинности.
Для использования Property Inspector :
На вкладке Modeling в разделе Design Data , выберите Инспектор свойств .
В редакторе Stateflow щелкните таблицу истинности.
В Property Inspector отредактируйте таблицу истинности характеристики.
Для использования Model Explorer:
На вкладке Modeling в разделе Design Data , выберите Обозреватель моделей .
На панели Model Hierarchy выберите таблицу истинности.
В диалоговом окне отредактируйте свойства таблицы истинности.
Для использования диалогового окна свойств таблицы истинности:
Откройте редактор Stateflow.

На вкладке Моделирование щелкните Таблица Свойства .
В диалоговом окне свойств отредактируйте свойства таблицы истинности.
Эти свойства также можно изменить программно, используя объекты Stateflow.TruthTableChart .
Для получения дополнительной информации о программном интерфейсе Stateflow см. Обзор API Stateflow.
См. также
Блоки
- Таблица истинности
Объекты
-
Stateflow.TruthTable|Stateflow.TruthTableChart
Tools
- Model Explorer (Simulink)
Related Topics
- Program a Truth Table
- Differences Between MATLAB and C as Action Language Syntax
- Export Stateflow Functions for Reuse
- Reuse Функции с использованием атомарных блоков
Вы щелкнули ссылку, соответствующую этой команде MATLAB:
Запустите команду, введя ее в командном окне MATLAB.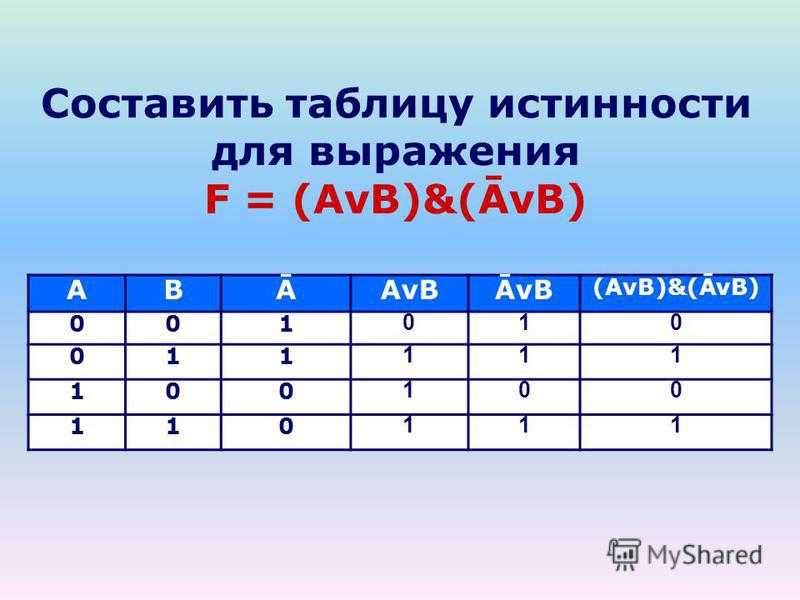




 Для дополнительной информации,
см. Экспорт функций Stateflow для повторного использования.
Для дополнительной информации,
см. Экспорт функций Stateflow для повторного использования.

 Использование данных на месте снижает
количество раз, которое сгенерированный код копирует промежуточные данные, что приводит к более
эффективный код.
Использование данных на месте снижает
количество раз, которое сгенерированный код копирует промежуточные данные, что приводит к более
эффективный код.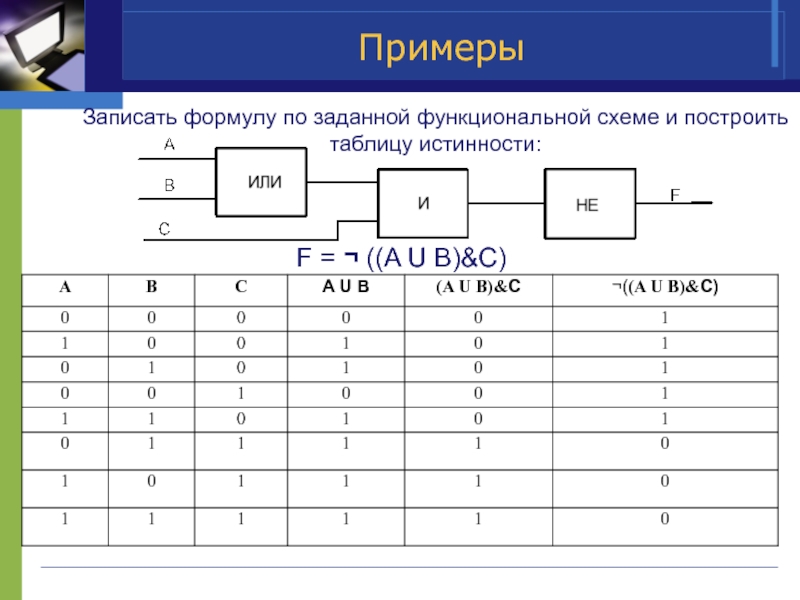 Для большего
информацию см. в разделе Программирование таблицы истинности.
Для большего
информацию см. в разделе Программирование таблицы истинности.
 Вместо этого в этих функциях вы можете использовать неопределенные переменные для хранения
значения, которые доступны только во время остальной части вызова функции. Для хранения значений
которые сохраняются при вызовах функций, используйте локальные данные на уровне диаграммы.
Вместо этого в этих функциях вы можете использовать неопределенные переменные для хранения
значения, которые доступны только во время остальной части вызова функции. Для хранения значений
которые сохраняются при вызовах функций, используйте локальные данные на уровне диаграммы.