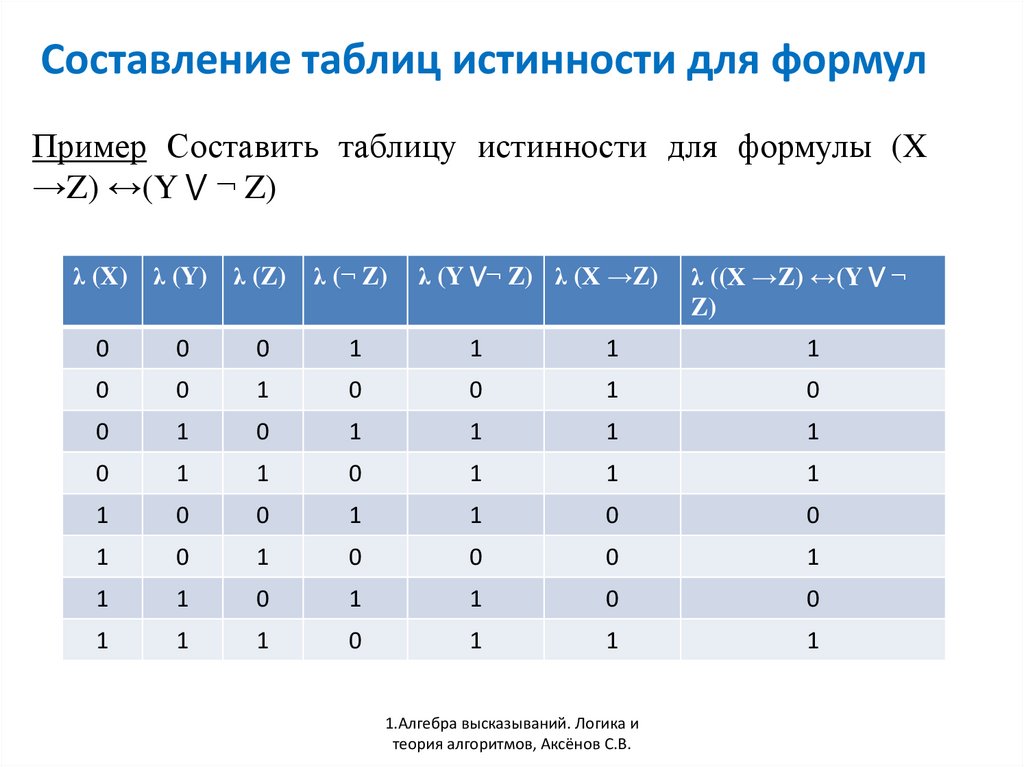
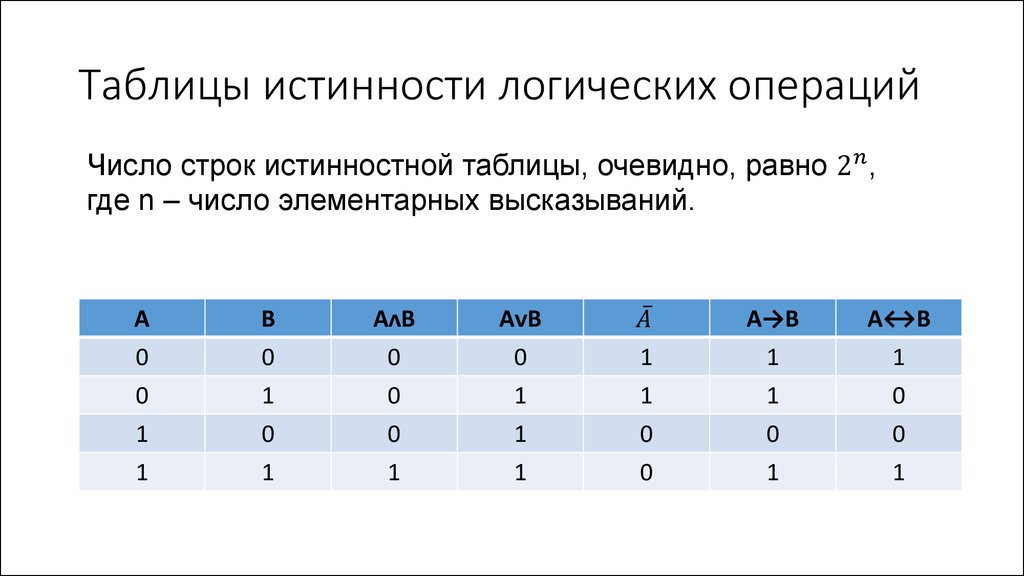
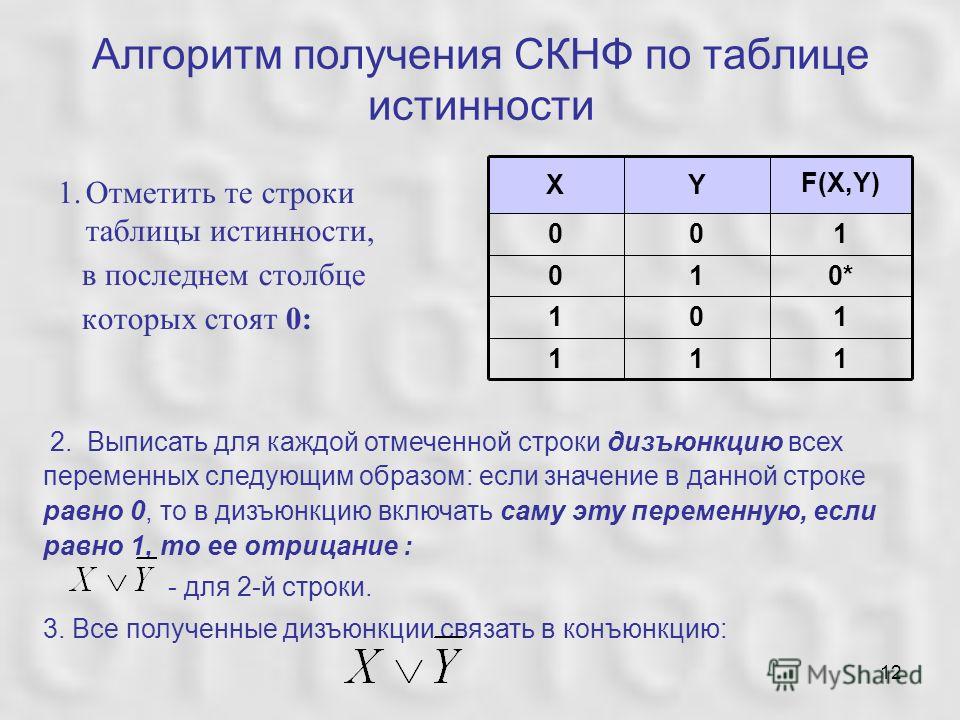
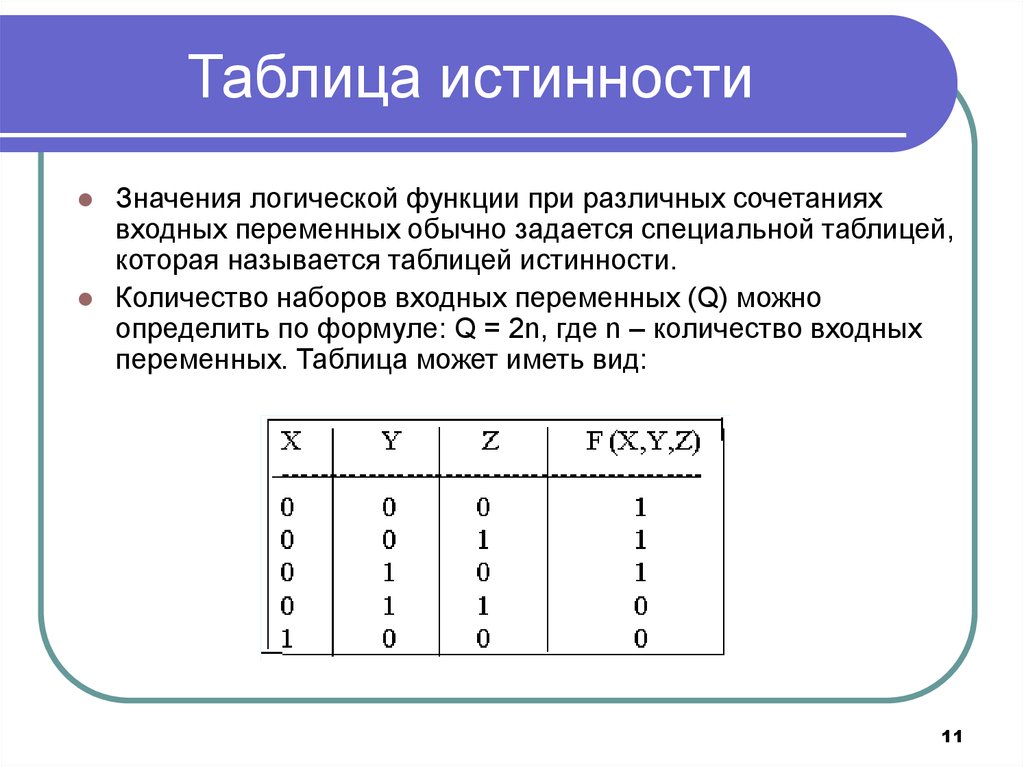
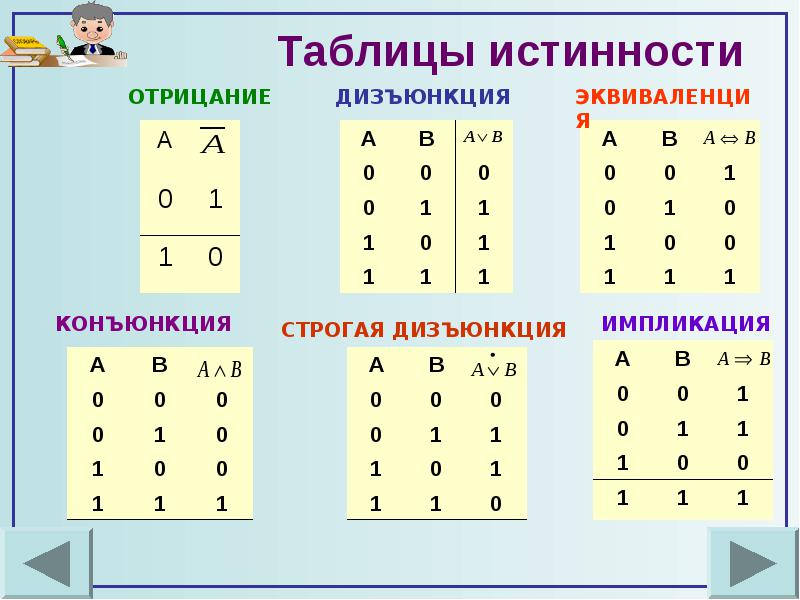
1.3 Построение таблицы истинности для логического выражения
При составлении таблицы истинности для логического выражения необходимо:
Выяснить количество строк в таблице (вычисляется как 2n, где n – количество переменных).
Выяснить количество столбцов (определяется как количество переменных + количество логических операций).
Установить последовательность выполнения логических операций.
Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных.
Заполнить таблицу истинности по столбцам.
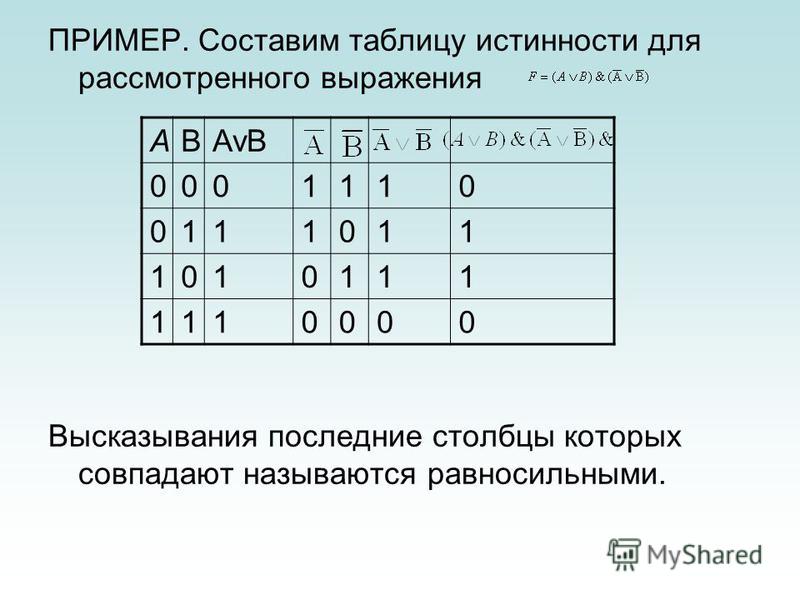
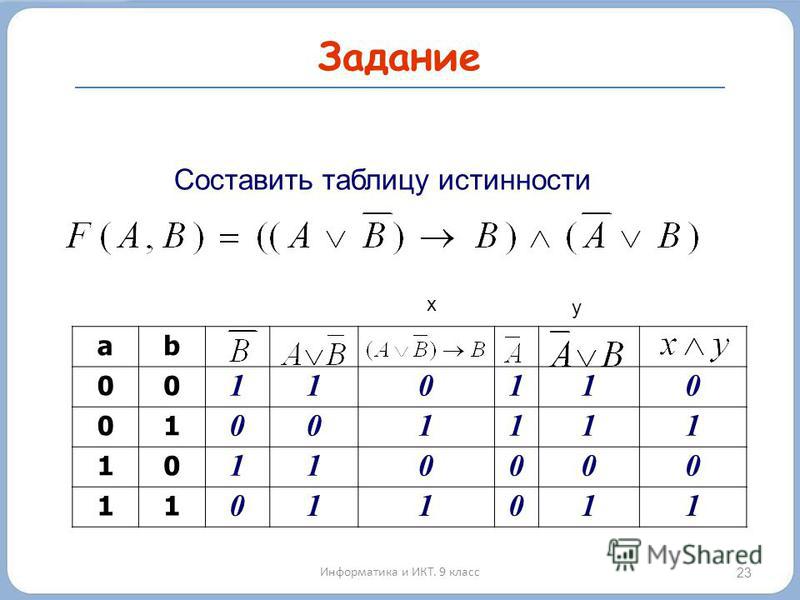
Контрольный пример. Построить таблицу истинности для выражения F = (A V B) & (¬A V ¬B).
Количество
строк в таблице определяется как 22 (2 переменных) + 1 (заголовок таблицы) = 5.
Расставим порядок выполнения операций:
(A V B) & (¬A V ¬B).
Построим таблицу истинности для данного логического выражения (таблица 5).
Таблица 5 – Таблица истинности для логического выражения
A | B | A V B | ¬A | ¬B | (A V B) & (¬A V ¬B) | |
0 | 0 | 0 | 1 | 1 | 1 | 0 |
0 | 1 | 1 | 1 | 0 | 1 | 1 |
1 | 1 | 0 | 1 | 1 | 1 | |
1 | 1 | 1 | 0 | 0 | 0 | 0 |
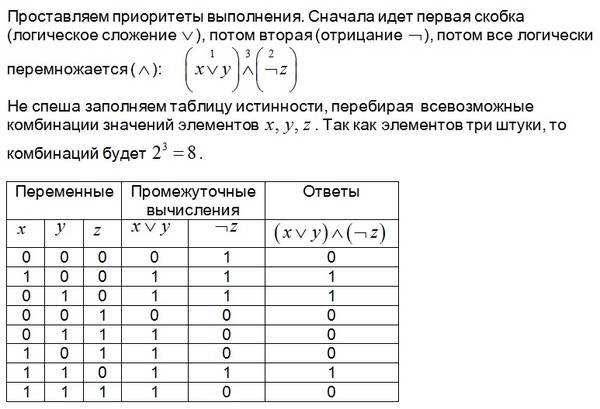
Контрольный
пример. Построить таблицу истинности для
логического выражения X
V
Y
& ¬Z.
Построить таблицу истинности для
логического выражения X
V
Y
& ¬Z.
Количество строк = 23+ 1 = 9.
Количество столбцов = 3 логические переменные + 3 логических операций = 6.
Укажем порядок действий:
3 2 1
X V Y & ¬Z.
Нарисуем и заполним таблицу 6:
Таблица 6 – Таблица истинности для логического выражения
X | Y | Z | Y & ¬Z | X V Y & ¬Z | |
0 | 0 | 0 | 1 | 0 | 0 |
0 | 0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 1 | 1 | 1 |
0 | 1 | 1 | 0 | 0 | 0 |
1 | 0 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 0 | 1 | |
1 | 1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 0 | 0 | 1 |
С
точки зрения логики электрический ток
либо течет, либо не течет; электрический
импульс есть или нет; электрическое
напряжение есть или нет.
A
A
A
B
B
Схема 1 – Конъюнкция Схема 2 – Дизъюнкция Схема 3 – Инверсия
(автоматический ключ)
Схема 4 – Конъюнктор Схема 5 – Дизъюнктор Схема 6 – Инвертор
Цепь
на схеме 1 с последовательным соединением
контактов соответствует логической
операции «И» и представляется конъюнктором
(схема 4). Цепь на схеме 2 с параллельным
соединением контактов соответствует
логической операции «ИЛИ» и представляется
дизъюнктором (схема 5). Цепь на схеме 3
(электромагнитное реле) соответствует
логической операции «НЕ» и представляется
инвертором (схема 6).
Цепь на схеме 3
(электромагнитное реле) соответствует
логической операции «НЕ» и представляется
инвертором (схема 6).
Именно такие электронные схемы нашли свое применение в качестве элементной базы ЭВМ. Элементы, реализующие базовые логические операции, назвали базовыми логическими элементами или вентилями и характеризуются они не состоянием контактов, а наличием сигналов на входе и выходе элемента. Их названия и условные обозначения являются стандартными и используются при составлении и описании логических схем компьютера.
Логические схемы необходимо строить из минимально возможного количества элементов, что, в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.
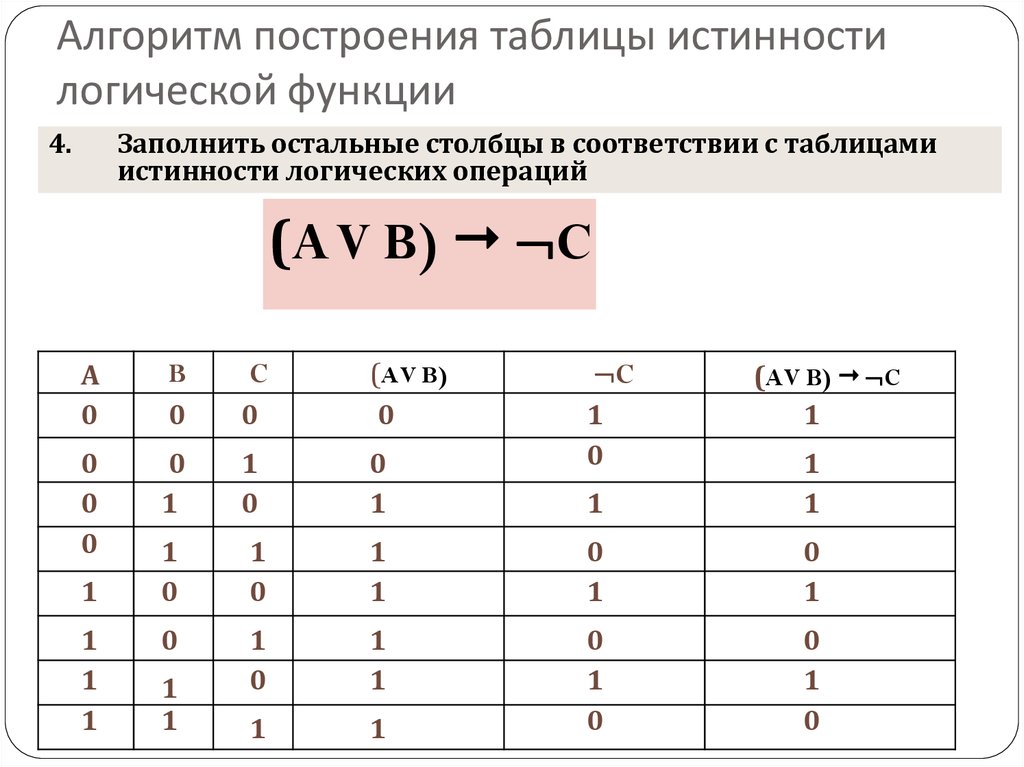
Правило построения логических схем:
Определить число логических переменных.
Определить количество базовых логических операций и их порядок.
Изобразить для каждой логической операции соответствующий ей вентиль.

Соединить вентили в порядке выполнения логических операций.
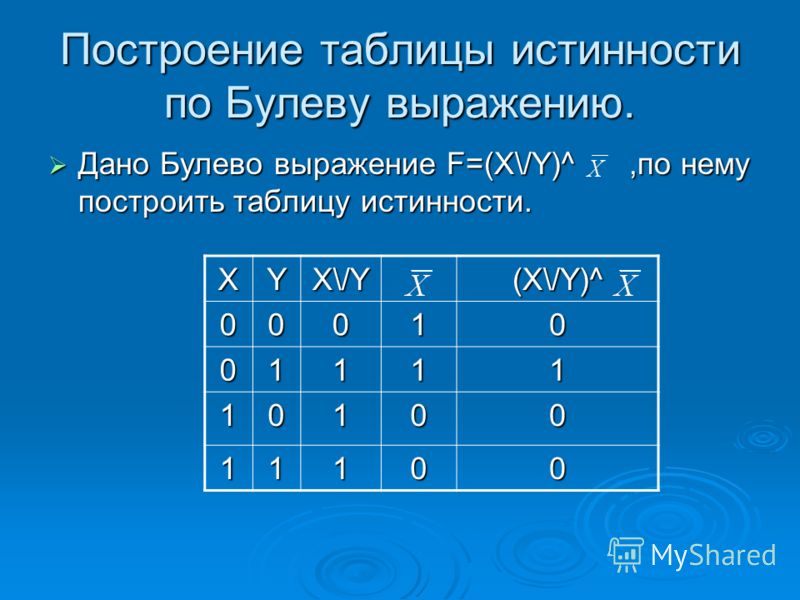
Контрольный пример. Пусть X = Истина (1), Y = Ложь (0). Составьте логическую схему для следующего логического выражения: F = X V Y & X.
1
2
1
2) Две логические операции: X V Y & X.
3) Строим схему (рисунок 3).
4) Ответ: 1 V 0 & 1 = 1.
X
Y
Рисунок 3 – Логическая схема для логического выражения F = X V Y & X
Таблицы истинности. Логические схемы. 10 класс
Похожие презентации:
Логические выражения и таблицы истинности
Логические выражения и таблицы истинности. Логика
Построение таблиц истинности для логических выражений
Таблицы истинности логических функций
Основы логики.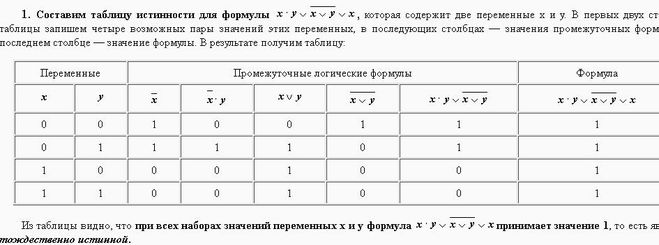
Формы мышления. Алгебра высказываний. (10 класс)
Логические выражения и таблицы истинности
Формы мышления. Логика
Логические схемы
Решение логических задач 10 класс
1. Таблицы истинности. Логические схемы
Урок информатики.10 класс.
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
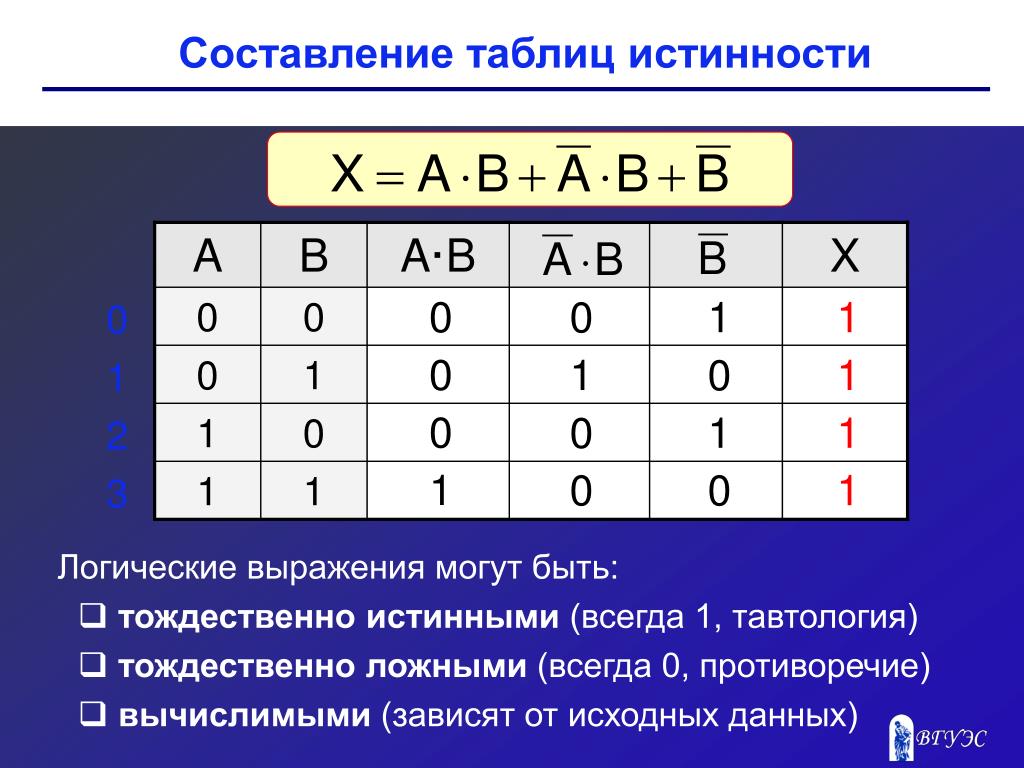
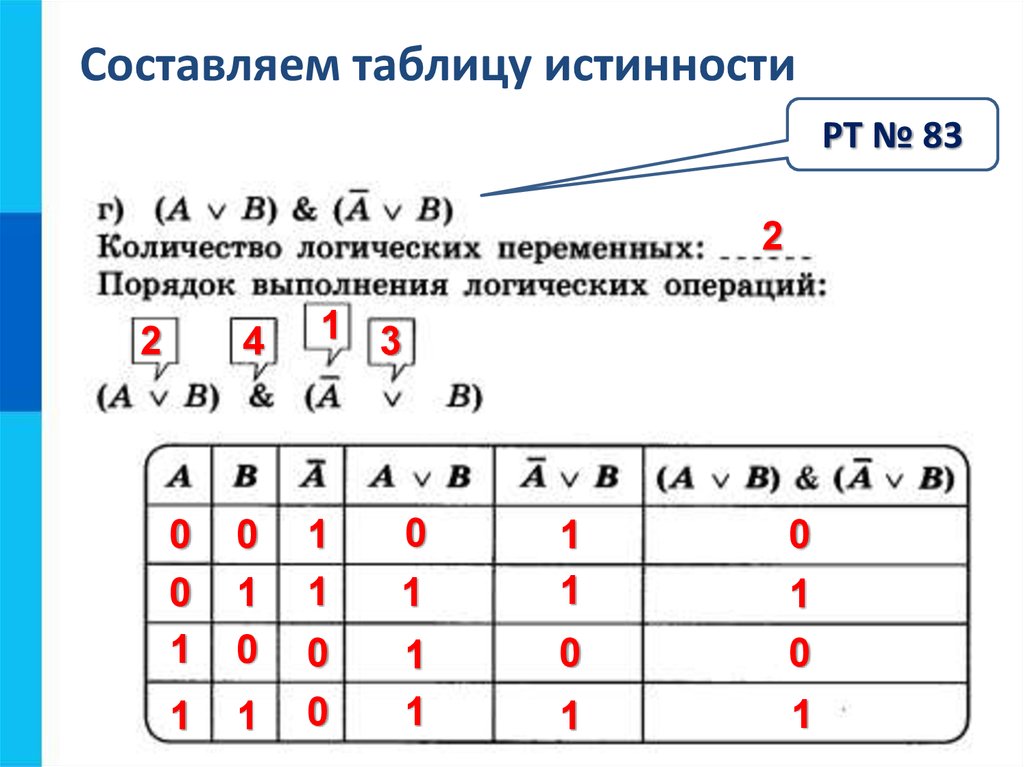
2. Построим таблицу истинности для выражения F = (AvB)&(¬Av¬B).
Построим таблицу истинности длявыражения F = (AvB)&(¬Av¬B).
Количество строк = 22 (2 переменных) + 1
(заголовки столбцов) = 5.
Количество столбцов = 2 логические переменные
(А, В) + 5 логических операций (v, &, ¬, v,) = 7.
Расставим порядок выполнения операций:
1 5 2 4 3
(A v B) & ( A v B)
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
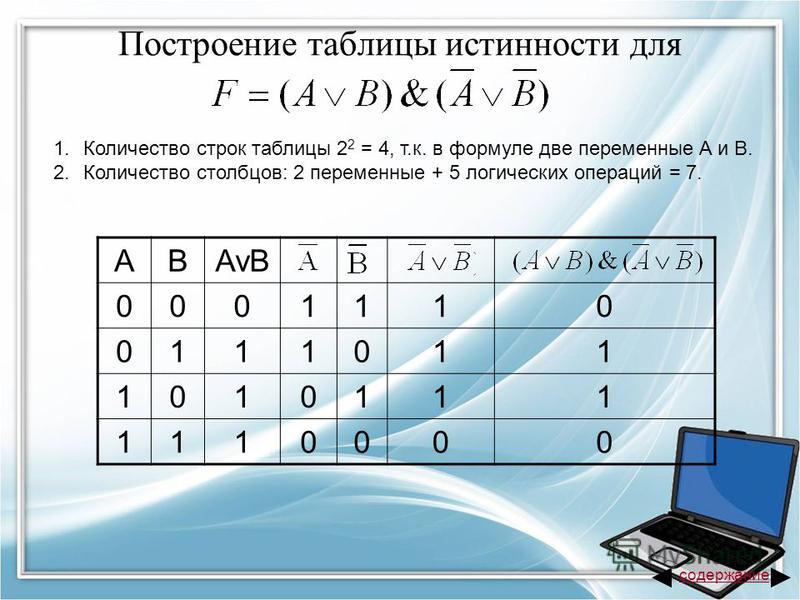
3. Построим таблицу истинности для выражения: F = (AvB)&(¬Av¬B).
Построим таблицу истинности длявыражения: F = (AvB)&(¬Av¬B).
A
B
A
B
:
AvB
Av B (AvB)&(¬Av¬B)
0
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
0
1
1
1
1
1
1
0
0
1
0
0
Сивова А.
B
v
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
9. Построение логических схем
Определить число логических переменных.Определить количество базовых логических операций и их
порядок.
Изобразить для каждой логической операции
соответствующий вентиль.
Соединить вентили в порядке выполнения логических
операций.
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
Пример 1
Пусть X = истина, Y = ложь.
Составить логическую схему для следующего логического
выражения: F = X v Y & X.
Две переменные — X и Y.
Две логические операции:
2 1
X v Y & X.
1
Х
Y
0
0
1
&
1
v
Ответ: 1v 0 & 1 = 1.
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
11. Пример 2 Постройте логическую схему, соответствующую логическому выражению F=X&Yv¬(YvX). Найдите значение логического выражения
Пример 2Постройте логическую схему, соответствующую логическому
выражению F=X&Yv¬(YvX).
Найдите значение логического выражения для
X=1, Y=0.

Переменных две: X и Y;
Логических операций четыре: конъюнкция, две дизъюнкции и
инверсия:
1 43 2
X&Yv ¬ (YvX)
Схему строим слева направо в соответствии с порядком
логических операций
1
0
1
0
0
&
11
v
0
¬
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
v
0
№1
Составьте таблицы истинности для следующих логических выражений:
1. F=(X& Y)vZ.
2. F=X&YvZ.
3. F= ¬ (XvY) & (YvX).
4. F= ¬ ((XvY) & (ZvX)) & (ZvY).
5. F= A&B&C& D.
6. F= (AvB) & ( BvAvB).
№2
Постройте логическое выражение по логической схеме:
А
&
А
¬¬
¬
В
С
1
ВВ
¬
¬
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
1
&
&
№3
Постройте логическую схему, соответствующую
логическому выражению, и найдите значение
логического выражения:
F = AvB& C, если А = 1, В=1, С=1 (1).
F = ¬ (AvB&C), если А=0, В=1, С=1 (1).
F = AvB&C, если А=1, В=0, С=1 (0).
F = (AvB) & (CvB), если А=0, В=1, С=0 (1).
F = ¬ (А&В&С), если А=0, В=0, С=1 (1).
F = ¬ (A&B&C) v (B & C v A), если А=1, В=1, С=0 (1).
F = B& Av B&A, если А=0, В=0 (0).
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
Домашнее задание
№1
Составьте таблицы истинности и определите истинность
формулы:
1) F = ((Av B)→B)&( AvB).
2)F = ¬(AvB)≡( AvB).
F = ¬ ((А В) ≡ ( B →Ā)).
№2
Составьте логические схемы к следующим логическим
выражениям:
A) F = Bv(C& A) v (A&B).
B) F= ¬ (A&B) vC&D.
№3
Постройте логические выражения к логическим схемам:
A
B
A
B
&
&
&&
11
&&
C
C
&&
11
D
D
Сивова А.Ю., МОУ «Лицей №31» г. Саранск
&&
English Русский Правила
Как составить таблицу истинности?
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре:
(0, 0), (0, 1), (1, 0), (1, 1).
Если формула содержит три переменные, то возможных наборов значений переменных восемь:
(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Примеры.
1. Составим таблицу истинности для формулы , которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу:
| Переменные | Промежуточные логические формулы | Формула | |||||
Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.
2. Таблица истинности для формулы :
| Переменные | Промежуточные логические формулы | Формула | ||||
Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 0, то есть является тождественно ложной.
3. Таблица истинности для формулы :
| Переменные | Промежуточные логические формулы | Формула | ||||||
Из таблицы видно, что формула в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.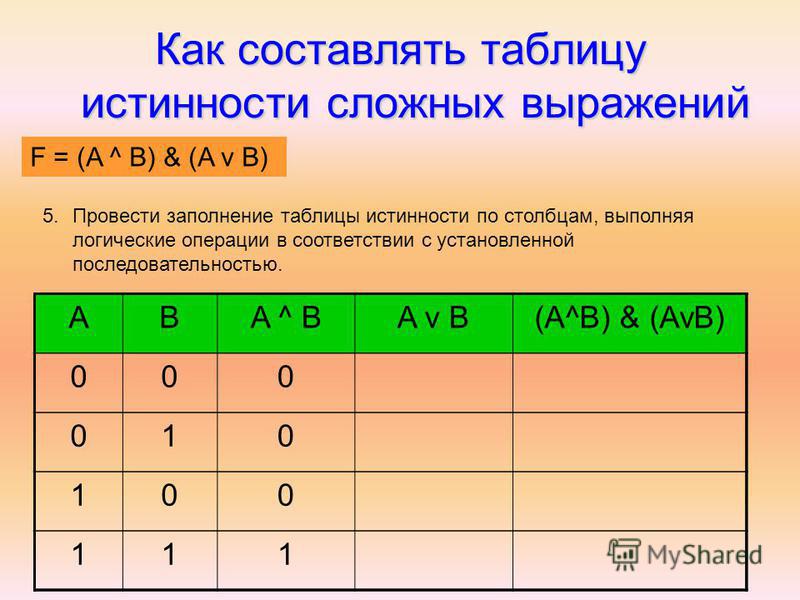
Дата добавления: 2016-05-31; просмотров: 1962; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Использование таблиц истинности для моделирования комбинаторной логики — MATLAB & Simulink
Использование таблиц истинности для моделирования комбинаторной логики
Таблицы истинности реализуют комбинаторную логику в табличном формате. Вы можете использовать Таблицы истинности Stateflow ® для моделирования принятия решений для обнаружения и управления ошибками и переключение режимов.
Функции таблицы истинности в диаграмме Stateflow выполняются, только когда вы вызываете функцию таблицы истинности. Вы можете определить функция таблицы истинности в диаграмме Stateflow, состоянии или поддиаграмме. Расположение функции определяет множество состояния и переходы, которые могут вызвать функцию.
Если вы хотите вызвать функцию из одного состояния или подграфика и его подсостояния, поместите свою функцию таблицы истинности в это состояние или поддиаграмму.
 Эта функция
переопределяет любые другие функции с тем же именем в родителях и предках этого
состояние или подсхема.
Эта функция
переопределяет любые другие функции с тем же именем в родителях и предках этого
состояние или подсхема.Если вы хотите вызвать функцию в любом месте диаграммы, поместите функцию таблицы истинности на уровне диаграммы.
Если вы хотите вызвать функцию из любого графика в вашей модели, поместите свою таблицу истинности на уровне диаграммы и включить экспорт функций уровня диаграммы. Чтобы получить больше информации, см. Экспорт функций Stateflow для повторного использования.
Функция таблицы истинности может получить доступ к диаграмме и данным состояния над ней в Иерархия потоков состояний.
В качестве альтернативы, для более прямой реализации логики принятия решений, вы можете добавить Истина
Блок таблицы непосредственно в вашу модель Simulink ® . Для реализации логики управления блоки таблицы истинности используют
MATLAB ® в качестве языка действий.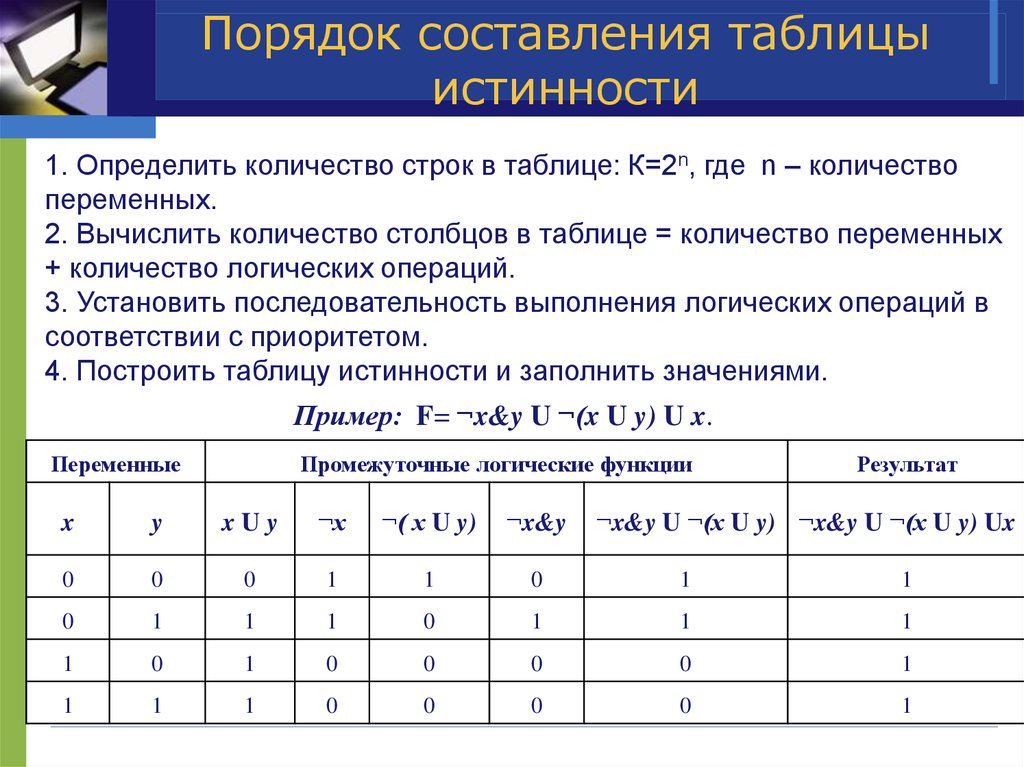
Структура таблицы истинности
Эта функция таблицы истинности имеет имя ttable . Требуется три
аргументы ( x , y и z ) и возвращает
одно выходное значение ( r ).
Функция состоит из такого расположения условий, решений и действия.
Состояние | Решение 1 | 2 | 3 | 40061 | 3 | 40061 | 0007 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
x == 1 | T | F | F | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
y == 1 | F | T | F | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
z == 1 | F | F | T | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Действие | r = 1 | R = 2 | R = 3 | RAIN | . | . | . Условие столбец обязательно
оценить как true (ненулевое значение) или false (нулевое значение). Результаты для каждого условия
указывается как T (истина), F (ложь) или — (истина или ложь). Каждый из столбцов решений
объединяет результат для каждого условия с помощью логического И в составное условие, которое
называется решением. Вы оцениваете таблицу истинности по одному решению за раз, начиная с Решение 1 . Решение 4 охватывает все возможные оставшиеся решения. Если одно из решений истинно, таблица выполняет соответствующее действие, а затем выполнение таблицы истинности завершено. Например, если выполняются условия
Определение функции таблицы истинностиЧтобы определить функцию таблицы истинности:
Вызов функций таблицы истинности в состояниях и переходах Вы можете вызывать функции таблицы истинности из действий любого состояния или перехода или из
другие функции. Чтобы вызвать функцию таблицы истинности, используйте сигнатуру функции и включите фактический значение аргумента для каждого формального аргумента в сигнатуре функции. [return_val1,return_val2,...] = имя_функции(arg1,arg2,...) Если типы данных фактических и формальных аргументов различаются, функция приводит фактический аргумент к типу формального аргумента. Указание свойств функций таблицы истинностиСвойства, перечисленные ниже, определяют, как функция таблицы истинности взаимодействует с другими компоненты в вашей диаграмме Stateflow. Вы можете изменить эти свойства в свойстве . Инспектор , обозреватель моделей или диалоговое окно свойств таблицы истинности. Для использования Property Inspector :
Для использования обозревателя моделей:
Чтобы использовать диалоговое окно свойств таблицы истинности:
Эти свойства также можно изменить программно, используя ИмяИмя функции. Щелкните ссылку с названием функции, чтобы вывести ее на передний план. на родной карте. Функция, встроенная ОпцияУправляет встраиванием вашей функции в сгенерированный код:
Это свойство недоступно в Инспекторе свойств . Ярлык Ярлык для вашей функции. Метка сигнатуры функции задает имя для
вашей функции и формальные имена для ее аргументов и возвращаемых значений. Заниженная спецификацияУправляет уровнем диагностики неполной спецификации в вашей функции таблицы истинности. Дополнительные сведения см. в разделе Исправление завышенных и недоопределенных таблиц истинности. Превышение спецификацииУправляет уровнем диагностики завышения спецификации в вашей функции таблицы истинности. Дополнительные сведения см. в разделе Исправление завышенных и недоопределенных таблиц истинности. Язык действийУправляет языком действий для вашей функции таблицы истинности Stateflow. Выберите между MATLAB или C. Это свойство доступно только в диаграммах, которые используют C в качестве действия. язык. Для получения дополнительной информации смотрите Различия Между MATLAB и C как Синтаксис Языка Действия. ОписаниеОписание функции таблицы истинности. Ссылка на документ Ссылка на онлайн-документацию по функции таблицы истинности. Задайте свойства для блоков таблицы истинностиСвойства блока таблицы истинности определяют, как ваша таблица истинности взаимодействует с модель Симулинк. Вы можете изменить эти свойства в свойстве . Inspector , Model Explorer или диалоговое окно свойств таблицы истинности. Для использования Property Inspector :
Для использования Model Explorer:
Чтобы использовать диалоговое окно свойств таблицы истинности:
Эти свойства также можно изменить программно, используя См. такжеБлоки
Объекты
Инструменты
Связанные темы
Вы щелкнули ссылку, соответствующую этой команде MATLAB: Запустите команду, введя ее в командном окне MATLAB. Веб-браузеры не поддерживают команды MATLAB. Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями. В зависимости от вашего местоположения мы рекомендуем вам выбрать: . Вы также можете выбрать веб-сайт из следующего списка: ЕвропаОбратитесь в местный офис 8.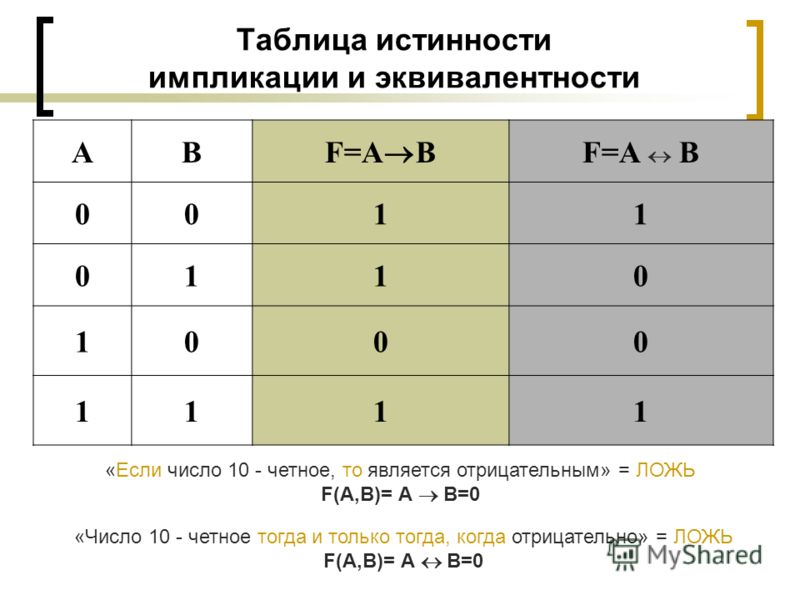 1 Расчет значений истинности утверждений 1 Расчет значений истинности утвержденийДо сих пор мы видели таблицы истинности, используемые для определения операторов. У них есть и другое применение: они позволяют классифицировать и сравнивать утверждения, оценивать их логические свойства, проверять аргументы на достоверность и определять правила вывода и замены. Таблица истинности показывает все значения истинности, которые может иметь данное утверждение или набор утверждений. Но давайте немного отступим. В предыдущем разделе мы ввели функциональные определения операторов. С этой информацией (представленной на таблицах истинности, которые показывают все возможные значения, которые могут иметь «p» и «q»), у нас есть достаточно информации, чтобы мы могли «вычислить» или определить истинностное значение составных утверждений, пока мы знаем истинностные значения составляющих их простых утверждений. Например, поскольку мы знаем, что «Бананы — это фрукты» верно и «Яблоки — это фрукты» верно и «Груши — это фрукты» верно, мы можем выяснить, что это утверждение: B ⊃ (A ∙ ~P) ложно. Как? Перечислите значения истинности под буквами, а затем объедините значения в соответствии с определениями пяти операторов, начиная с наименьшей единицы и заканчивая наибольшей.
В этой таблице показаны значения этих трех утверждений. Каждый из них верен, поэтому у нас есть буква «Т» под каждым утверждением; и поскольку происходит отрицание «Груши — это фрукты» («Груши — это не фрукты»), у нас есть «Ф» под тильдой. Самый простой или наименьший уровень, на котором могут быть выполнены любые «расчеты», — это отрицание простого утверждения. Следующий уровень находится в соединении отрицания с утверждением «Яблоки — это фрукты».
Это точечное утверждение является следствием условного предложения, а антецедент условного предложения истинен, поэтому само условие ложно; буква «F» идет под подковой. Я покрасил его в красный цвет, чтобы сделать его более заметным.
Теперь, в этом однострочном формате, единственный способ выровнять эти символы — это представить их в таблице. Таблицы, которые мы использовали для определения операторов, повторенные ниже, являются таблицами истинности. Для этих утверждений нет комбинаций значений истинности, которые не были бы показаны. Отрицание
Соединение
Разъединение
Материал Условный
Биусловный
Таблицы истинности обеспечивают функциональное определение пяти операторов. Джеймс Фармер преподавал Историю движения за гражданские права в Мэри Вашингтон. Мартин Лютер Кинг преподавал теологию в Мэри Вашингтон. Так как первое из них истинно, а второе ложно, то союз, составленный из них (F . K), ложен. Если Кинг преподавал теологию или Фармер преподавал Гражданские права в Мэри Вашингтон, то крупная фигура Движения за гражданские права была членом факультета UMW. У этого условного предложения есть дизъюнкция для предшествующего: (K v F) ⊃ M K = Кинг преподавал в UMW F = Фермер преподавал в UMW M = крупный деятель CRM был на факультете. (К в Ф) ⊃ М
Я отметил истинные значения: первое, которое мы можем ввести, выделено жирным шрифтом, потому что K v F — наименьшая единица; второй — наклонный, который объединяет значение из K v F со значением M. Вот еще несколько вариантов, на которых вы можете попрактиковаться: 1. Обама и Клинтон — демократы, если Кристи — республиканец. 2. Либо Клинтон будет баллотироваться, либо Кристи — демократ. 3. Если Клинтон баллотируется, то ей не менее 35 лет. 4. Обама является главнокомандующим тогда и только тогда, когда он президент. 5. Родиться в Америке — необходимое условие для того, чтобы стать президентом. 6. Если родиться здесь — необходимое условие для бега, то Шварценеггер не может бегать. 7. Быть здоровым является достаточным условием для того, чтобы быть действительным, а быть действительным является необходимым условием для того, чтобы быть здоровым; кроме того, дедуктивность является необходимым условием правильности и достоверности. 8. Если либо Юм не изобретал таблицы истинности, либо Витгенштейн не написал «Трактат», то парадокс Рассела был плохой новостью для Фреге; но Кант отрицал, что «существование» было предикатом только в том случае, если аристотелевская логика господствовала в течение двух тысяч лет. 9. Либо Юм не изобретал таблицы истинности, либо Витгенштейн написал «Трактат», и парадокс Рассела был плохой новостью для Фреге, только если Кант отрицал, что «существование» было предикатом, учитывая, что аристотелевская логика господствовала в течение двух тысяч лет. 10. Если неверно и то, что Юм изобрел таблицы истинности, и то, что Кант отрицал, что «существование» является предикатом, то, учитывая господство аристотелевской логики в течение двух тысяч лет, написание «Трактата» Витгенштейном подразумевает, что парадокс Рассела был плохой новостью для Фреге. Ответы: 1. Обама и Клинтон — демократы, если Кристи — республиканец. C > (O.C) 2. Либо Клинтон будет баллотироваться, либо Кристи — демократ. 3. Если Клинтон баллотируется, то ей не менее 35 лет. С > Т 4. Обама является главнокомандующим тогда и только тогда, когда он президент. O ≡ C 5. Родиться в Америке – необходимое условие для того, чтобы стать президентом. P > A 6. Если рождение здесь является необходимым условием для бега, то Шварценеггер не может бегать. (P > R) > ~S 7. Быть здоровым — это достаточное условие для того, чтобы быть действительным, а быть действительным — это необходимое условие для того, чтобы быть здоровым; кроме того, дедуктивность является необходимым условием правильности и достоверности. [(S > V) . (S > V)] . [(S v V) > D] 8. Если либо Юм не изобретал таблицы истинности, либо Витгенштейн не написал «Трактат», то парадокс Рассела был плохой новостью для Фреге; но Кант отрицал, что «существование» было предикатом только в том случае, если аристотелевская логика господствовала в течение двух тысяч лет. [(~H v W) > R] . (K > A) H = f ; Вт = т; Р = т; К= т; A= t 9. A > [(~H v W) . (R > K)] 10. Если неверно и то, что Юм изобрел таблицы истинности, и то, что Кант отрицал, что «существование» было предикатом, то, учитывая, что аристотелевская логика доминировала в течение двух тысяч лет, написание Витгенштейном «Трактата» подразумевает, что парадокс Рассела было плохой новостью для Фреге. ~(H . K) > [A > (W > R)] Канонические функции | CircuitVerseОглавление
Введение Логические функции состоят из двух компонентов: переменных и логических операций (И, ИЛИ, НЕ. Пример: Сокращенная запись, представляющая логическое выражение / F(A,B) = A + B //Это логическая функция, состоящая из переменных A и B F (А, В, С) = А (В + С (А + В)) \ Логическое выражение Формирование таблицы истинности Таблица истинности формируется путем оценки логического выражения для каждого значения истинности переменной. Теперь значения истинности переменной либо «истина», либо «ложь». Суть в том, чтобы оценить значение логического выражения для каждой комбинации истинностных значений
присутствуют переменные. Пример: F (А, В) = А + В Таблица истинности::
Здесь у вас есть 4 комбинации для 2 переменных, попробуйте понять следующий пример, где переменные 3, которые предполагает 8 комбинаций. Запишите, как истинные значения переменной записываются в каждом столбце для каждая переменная. Пример: F(A,B,C) = A + B.C Формирование таблицы истинности Таблица истинности показывает таблицу, содержащую все комбинации входных данных и соответствующие им результаты. Уравнение переключения также можно преобразовать в таблицу истинности. Например, рассмотрим уравнение переключения: F(A,B,C) = A + BC.
Сумма выражений продукта (SOP) Давайте рассмотрим более сложное выражение
В этом примере интересное наблюдение заключается в том, что вы выполняете оценку суммы продуктов, то есть Более того, оператор Продукт выражений суммы (POS) Давайте посмотрим на другое выражение
Судя по алгебраическому выражению, видно, что выражение является произведением сумм . Здесь условия суммы определяются с помощью операции ИЛИ , а условия произведения определяются с использованием операции И . Когда два или более членов суммы умножаются на логическое значение ИЛИ результирующее выходное выражение будет иметь форму произведения сумм или форму POS . Форма произведения сумм также называется конъюнктивной нормальной формой , так как сумма членов составляет И вместе, а операция конъюнкции является логическим И. Форма произведения сумм также называется стандартной POS. Канонические выраженияПрежде чем разбираться в канонических выражениях, давайте разберемся с Minterms и Maxterms первый. Минтермс Минтерм определяется как произведение n переменных, в котором каждая из n переменных встречается один раз либо в дополненной, либо в недополненной форме. Для булевой функции с двумя переменными (x и y) возможные minterms: Для булевой функции с 3 переменными (x, y и z) возможные minterms: 1 – Minterms = minterms, для которых функция F = 1. 0 – Minterms = minterms, для которых функция F = 0. Любая булева функция может быть выражена в виде суммы (ИЛИ) ее 1-минутных членов. Представление уравнения будет Пример: Обратная функция может быть выражена как сумма (ИЛИ) ее нулевых членов. Представление уравнения будет Примеры канонической формы выражения суммы произведений (каноническая форма минимального члена):
В стандартной форме СОП максимально возможные термины произведения для n переменных задаются как 2 n . МакстермсМаксимальный термин определяется как произведение n переменных в диапазоне 0 ≤ i < 2 n . Максимальный член обозначается как Mi. В максимальном термине каждая переменная является дополненной , если ее значение присвоено 1, и каждая переменная не дополнена , если ее значение присвоено 0. Для логической функции с 2 переменными (x и y) , возможные максимальные члены: х + у, х + у’, х’ + у и х’ + у’ Для булевой функции с тремя переменными (x, y и z) возможные maxterms: x + y + z, x + y + z', x + y' + z, x + y' + z ', x' + y + z, x' + y + z', x' + y' + z и x' + y' + z' 1 – Максимальное число членов = максимальное число членов, для которых функция F = 1. 0 – Максимальное число членов = максимальное число членов, для которых функция F = 0. Любая логическая функция может быть выражена произведением (И) ее 0 – максимальные сроки. Представление уравнения будет Пример: Обратное функции может быть выражена как произведение (И) ее 1 — максимальное количество членов. Представление уравнения будет следующим: Пример: Примеры канонической формы произведения выражений сумм (каноническая форма максимального члена): 1. Z = (X + Y).(X + Y′) 2. F = (X′ + Y + Z′).(X′ + Y + Z).(X′ + Y′ + Z′) В стандартной форме POS максимально возможные члены суммы для n переменных задаются как 2 n . Итак, для уравнений с 2 переменными сумма членов равна 2 2 = 4. Аналогично, для уравнений с 3 переменными сумма членов равна 2 3 = 8. . положение для понимания канонических форм. Любая булева функция, которая выражается как сумма minterms или как произведение maxterms, находится в своем каноническая форма . Когда форма SOP логического выражения находится в канонической форме, каждый из его терминов продукта называется minterm . Таким образом, каноническая форма функции суммы произведений также известна как minterm, каноническая форма , или Sum-of-minterms, или стандартная каноническая форма SOP. Аналогично, когда POS-форма логического выражения находится в канонической форме, каждый из его суммируемых членов называется maxterm . Итак, каноническая форма произведения сумм известна также как maxterm каноническая форма или произведение суммы или стандартная каноническая форма POS. Преобразование канонических форм Вы можете представить одно каноническое сформированное уравнение в другой канонической форме, т. Важно помнить о логических функциях: формы SOP и POS дублируют друг друга . Чтобы преобразовать каноническую форму уравнений, необходимо выполнить 2 шага. Они:-
Например:- Функция SOP
Запишите новое уравнение в виде формы POS , Функция POS
000 = A’B’C’, 001 = A’B’C, 100 = AB’C’, 110 = ABC’, 111 = ABC Запись нового уравнения в форме СОП, Преобразование из минимальных форм в каноническиеОт минимального POS до канонического POS Вы можете включить все переменные в каждое условие продукта уравнения формы POS, которое не содержит всех переменных, путем преобразования в стандартную форму POS.
С помощью этих трех шагов вы можете преобразовать функцию POS в стандартную функцию POS. Пример: В первом члене отсутствует переменная D или D’, поэтому добавьте к нему D*D’ = 1. Тогда Аналогично, во втором члене переменная A или A’ отсутствует, поэтому добавьте к ней A*A’ = 1. Третий член равен уже в стандартной форме, так как имеет все переменные. Теперь стандартное уравнение формы POS функции равно От минимальной СОП к канонической СОПВы можете включить все переменные в каждое условие продукта уравнения формы СОП, которое не содержит всех переменных, путем преобразования в стандартную форму СОП. Функцию нормальной формы SOP можно преобразовать в стандартную форму SOP, используя закон алгебры логики, (A + A’ = 1) , и выполнив следующие шаги.
С помощью этих двух шагов вы можете преобразовать функцию SOP в стандартную функцию SOP. Пример:
Преобразование нестандартной функции SOP Sol: F = x y + x z + y z = x y (z + z’) + x (y + y’) z + (x + x’) y z = x y z + x y z’ + x y z + x y’ z + x y z + x’ y z = x y z + x y z’ + x y’ z + x’ y z Стандартная форма СОП: Пример алгебраического упрощения Давайте упростим наше выражение из предыдущего примера с таблицей истинности. вы можете применить обычные алгебраические приемы, такие как факторинг. Помните, что 9Оператор 0035 + вызывает вентиль AB'C + BD + CD + D // Исходное выражение AB'C + BD + D // Применение закона поглощения к CD + D, что сводит его к D AB'C + D // Применение закона поглощения к BD + D, сводящее его к D => AB'C + D // Окончательное выражение В качестве упражнения для читателя заполните таблицу истинности, чтобы показать, что они логически эквивалентны. Неопределенный ввод и безразличие Определение «безразлично» — это комбинация неизвестных входных значений, которая может быть либо Рассмотрим следующую таблицу истинности:
Замечаем, что у нас есть пофиг . Рассмотрим различия в случаях для Случай 1: F(1, 0) = 0 => F(AB) = A'B' + A'B + AB Случай 2: F(1, 0) = 1 => F(AB) = A'B' + A'B + AB' + AB Упрощение случаев... F(АВ) = А'В' + А'В + АВ = А'(В' + В) + АВ = А' + АВ F(АВ) = А'В' + А'В + АВ' + АВ = А'(В' + В) + А (В' + В) = А' + А = 1 Как видно, если вы установите |


 Эта функция
переопределяет любые другие функции с тем же именем в родителях и предках этого
состояние или подсхема.
Эта функция
переопределяет любые другие функции с тем же именем в родителях и предках этого
состояние или подсхема.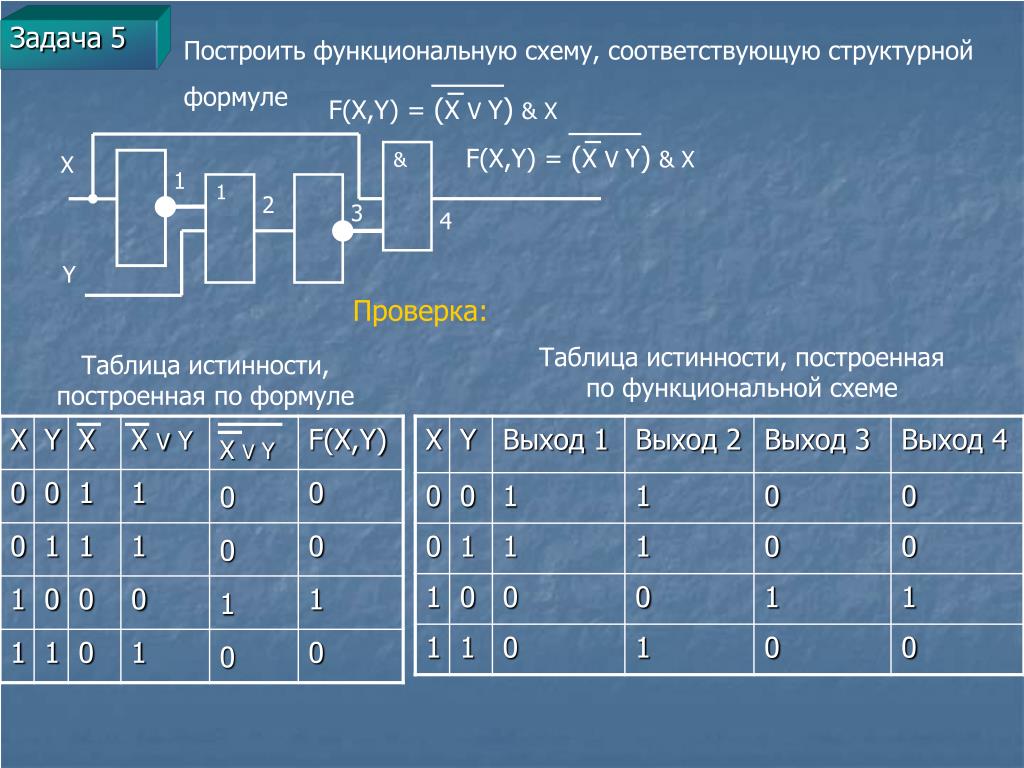 Остальные решения
не проверено, и оценка таблицы истинности завершена. Если первые три решения
false, то решение по умолчанию автоматически становится истинным, и его действие
(
Остальные решения
не проверено, и оценка таблицы истинности завершена. Если первые три решения
false, то решение по умолчанию автоматически становится истинным, и его действие
( 
 Для функций с одним возвращаемым значением
опустить скобки в метке подписи.
Для функций с одним возвращаемым значением
опустить скобки в метке подписи.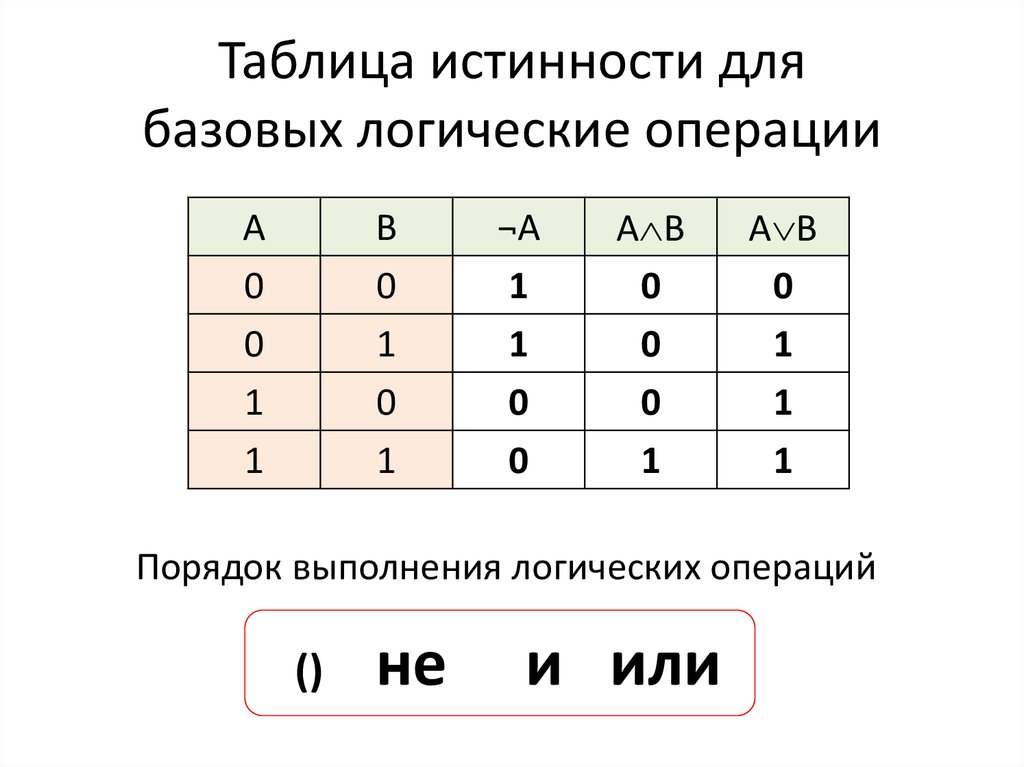 Аргументы имеют область действия
Аргументы имеют область действия 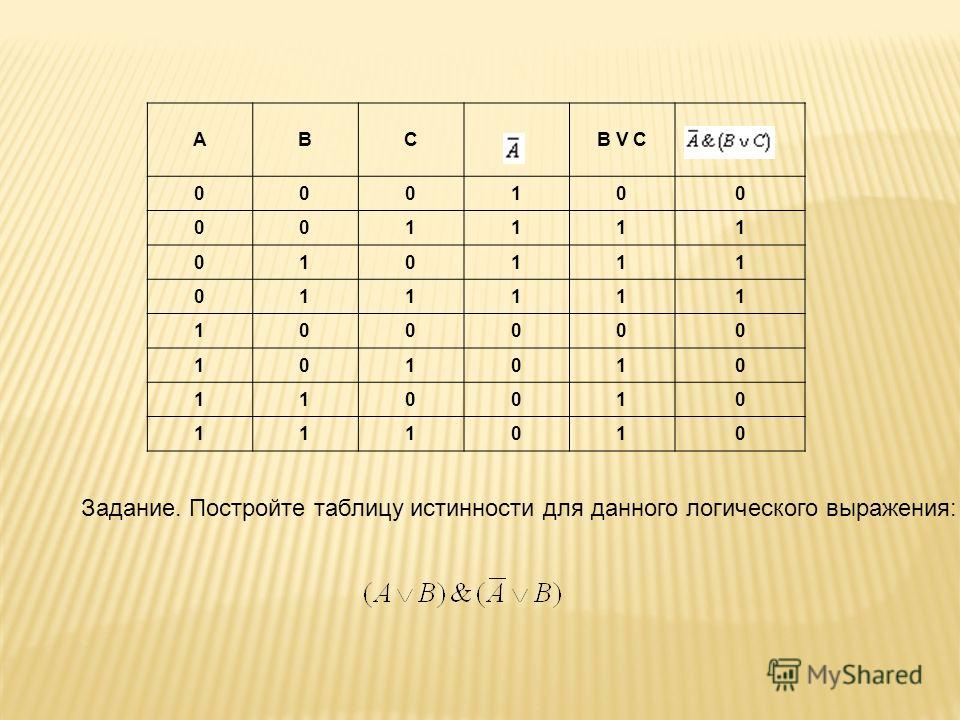 Элементы данных в функции могут иметь одну из следующих областей:
Элементы данных в функции могут иметь одну из следующих областей: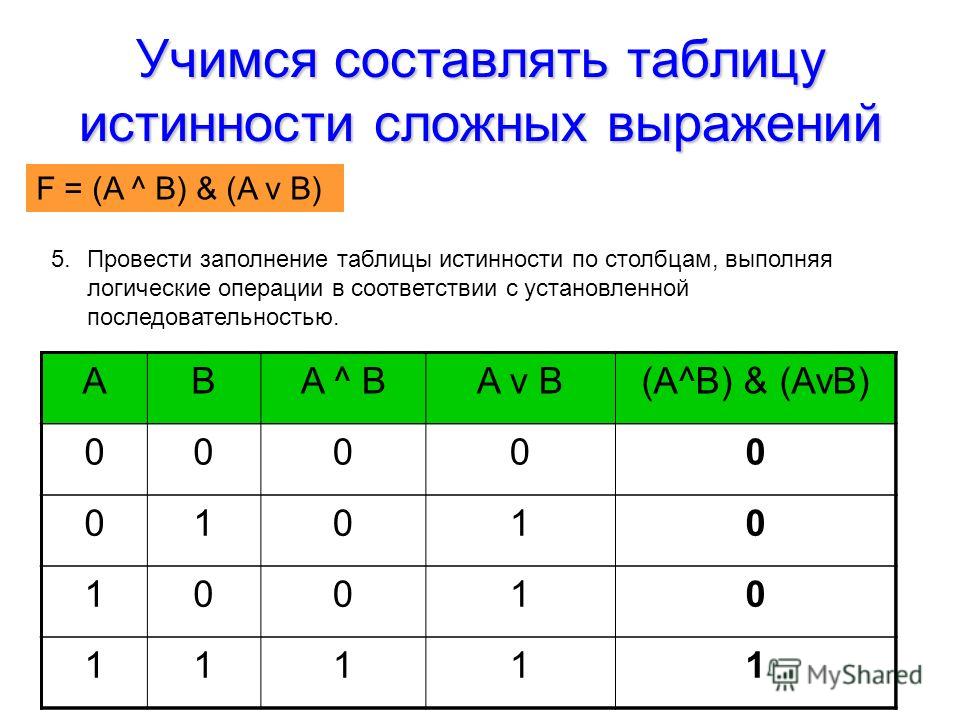 Определите временные данные, если вы хотите инициализировать значения данных в начале каждого
вызов функции. Например, вы можете определить счетчик с помощью
Определите временные данные, если вы хотите инициализировать значения данных в начале каждого
вызов функции. Например, вы можете определить счетчик с помощью  Если вы экспортируете функцию таблицы истинности, вы можете вызвать ее из любой диаграммы в
модель. Дополнительные сведения об экспорте функций см. в разделе Экспорт функций Stateflow для повторного использования.
Если вы экспортируете функцию таблицы истинности, вы можете вызвать ее из любой диаграммы в
модель. Дополнительные сведения об экспорте функций см. в разделе Экспорт функций Stateflow для повторного использования.
 TruthTable
TruthTable  Это свойство
недоступно в Property Inspector .
Это свойство
недоступно в Property Inspector .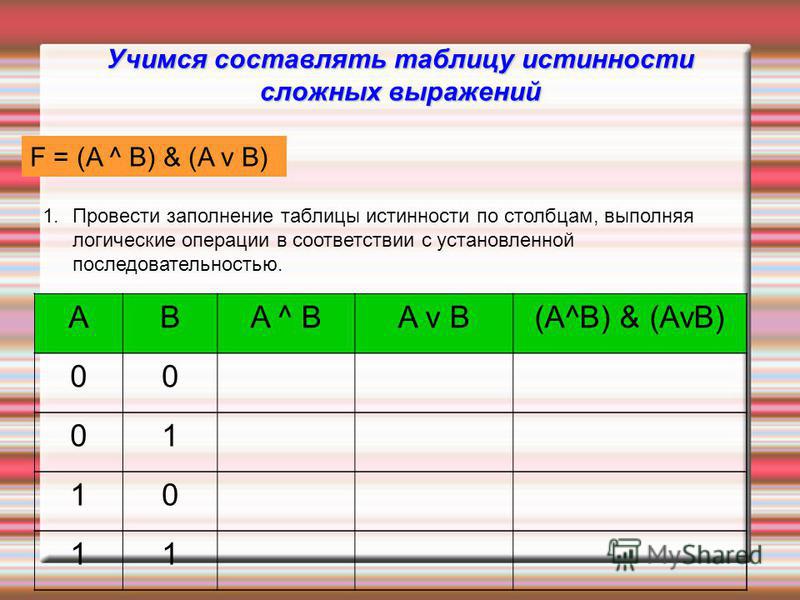 Вы можете ввести веб-URL
адрес или команду MATLAB, которая отображает документацию в виде файла HTML или в виде текста в
Командное окно MATLAB. При нажатии на ссылку Документ гиперссылка, Stateflow оценивает ссылку и отображает документацию.
Вы можете ввести веб-URL
адрес или команду MATLAB, которая отображает документацию в виде файла HTML или в виде текста в
Командное окно MATLAB. При нажатии на ссылку Документ гиперссылка, Stateflow оценивает ссылку и отображает документацию.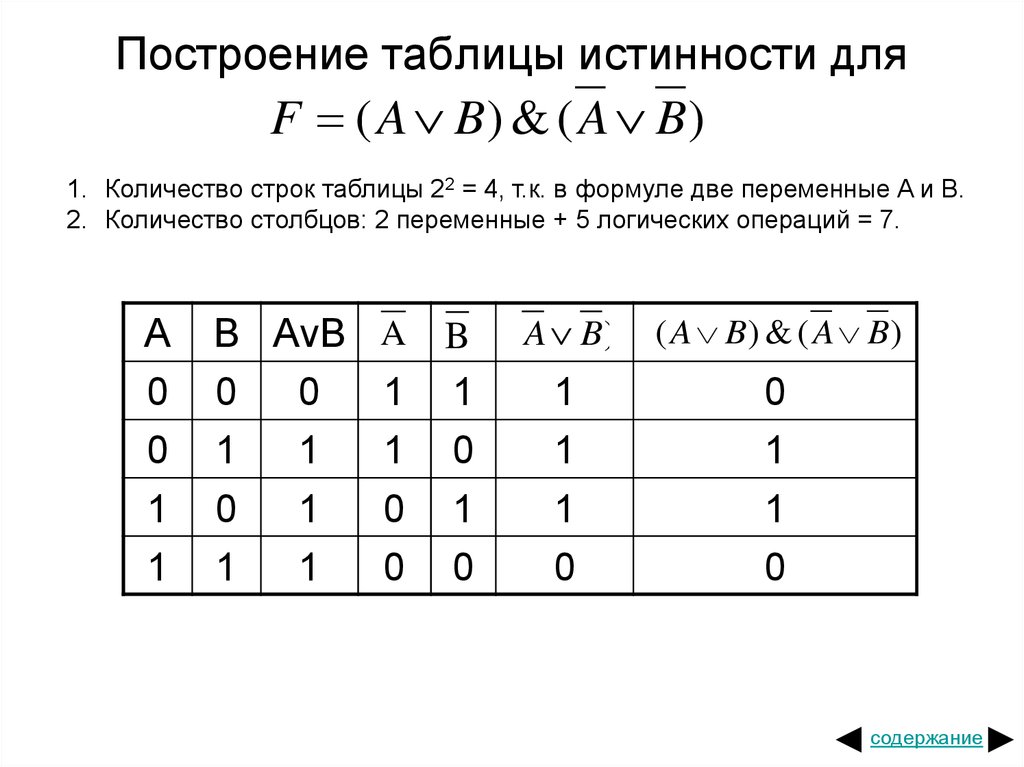
 Утверждение, что «яблоки — это фрукты, а груши — нет», неверно, поэтому буква «F» ставится под точкой.
Утверждение, что «яблоки — это фрукты, а груши — нет», неверно, поэтому буква «F» ставится под точкой. Но таблица, показывающая нам, что B ⊃ (A ∙ ~P) ложна, — это , а не , что мы назовем «таблицей истинности». Таблица истинности показывает все возможные значения истинности, которые могут иметь простые утверждения в составе или наборе соединений, и показывает результат этих значений; это всегда не менее двух строк. Пример, который мы здесь рассматриваем, просто вычисляет значение одного составного оператора, не демонстрируя всех возможностей, которые предоставляет форма этого оператора.
Но таблица, показывающая нам, что B ⊃ (A ∙ ~P) ложна, — это , а не , что мы назовем «таблицей истинности». Таблица истинности показывает все возможные значения истинности, которые могут иметь простые утверждения в составе или наборе соединений, и показывает результат этих значений; это всегда не менее двух строк. Пример, который мы здесь рассматриваем, просто вычисляет значение одного составного оператора, не демонстрируя всех возможностей, которые предоставляет форма этого оператора. С помощью этих определений мы можем вычислить истинностное значение составных утверждений, как только узнаем истинностные значения простых, из которых они состоят. Вот несколько примеров и несколько упражнений, в которых вы можете попрактиковаться.
С помощью этих определений мы можем вычислить истинностное значение составных утверждений, как только узнаем истинностные значения простых, из которых они состоят. Вот несколько примеров и несколько упражнений, в которых вы можете попрактиковаться.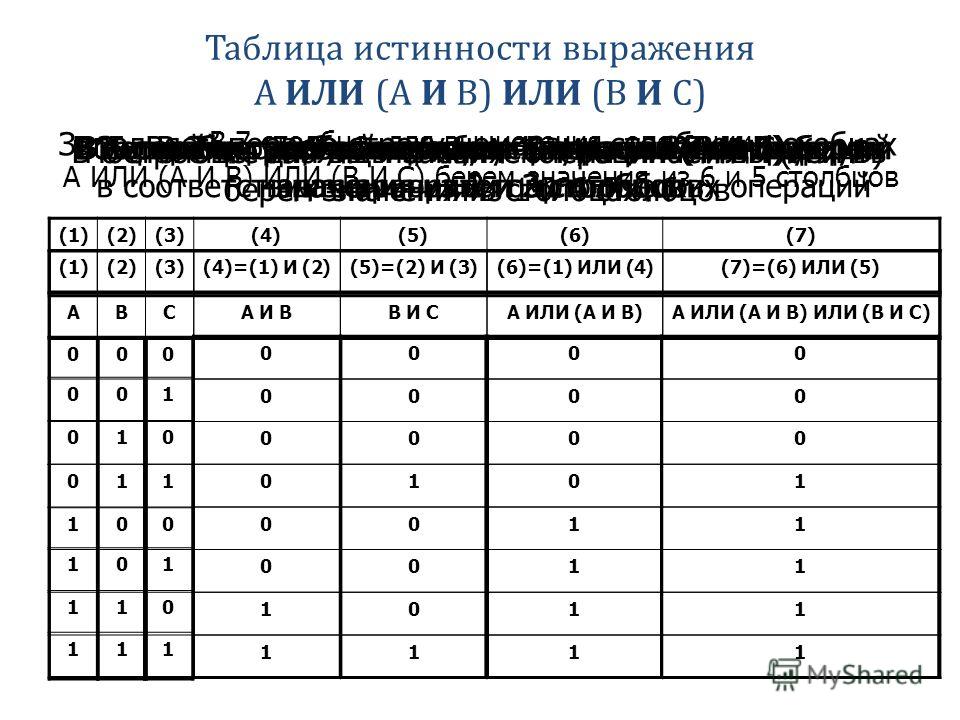 Кстати, не делайте вывод из этого примера, что первое значение, которое вы можете вычислить, всегда будет самым левым. Последнее значение, которое вы можете указать, — это то, что называется основным оператором: этот оператор является условным, его основной оператор — подкова.
Кстати, не делайте вывод из этого примера, что первое значение, которое вы можете вычислить, всегда будет самым левым. Последнее значение, которое вы можете указать, — это то, что называется основным оператором: этот оператор является условным, его основной оператор — подкова.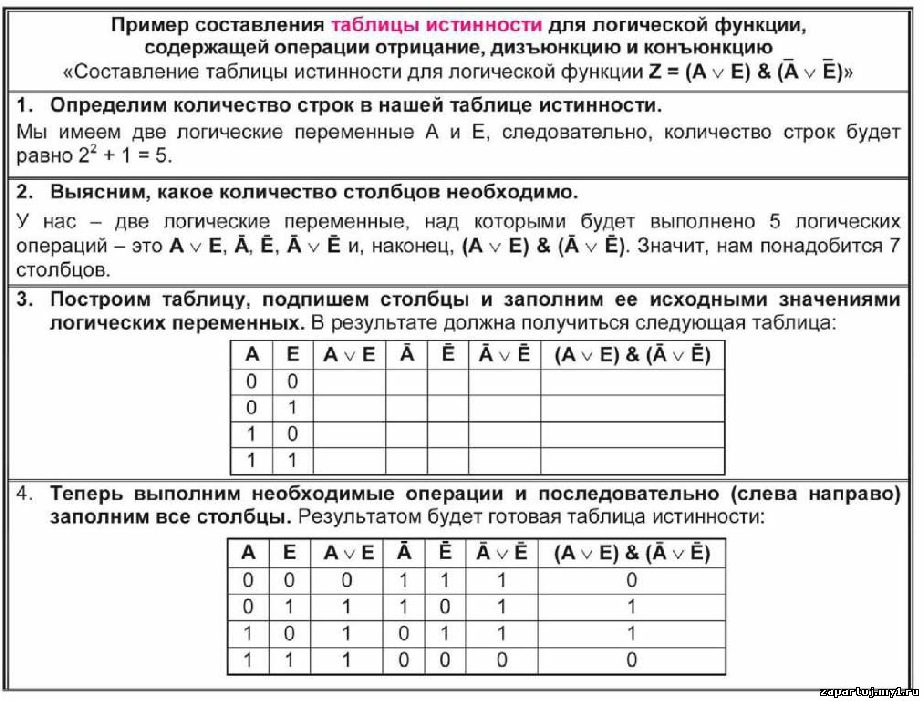
 C v D
C v D Либо Юм не изобретал таблицы истинности, либо Витгенштейн написал «Трактат», и парадокс Рассела был плохой новостью для Фреге, только если Кант отрицал, что «существование» было предикатом, учитывая, что аристотелевская логика господствовала в течение двух тысяч лет. .
Либо Юм не изобретал таблицы истинности, либо Витгенштейн написал «Трактат», и парадокс Рассела был плохой новостью для Фреге, только если Кант отрицал, что «существование» было предикатом, учитывая, что аристотелевская логика господствовала в течение двух тысяч лет. . .. и т. д.). Любое уравнение со смесью этих двух компонентов образует булеву функцию. Значение переменных может быть или не быть заранее определенным. Сокращенное обозначение булевой функции состоит в том, что она представлена заглавной буквой F, за которой следует скобка, состоящая из всех переменных этого уравнения, разделенных запятой (‘,’). Вы можете представить любое логическое выражение в виде таблицы истинности. Подпишитесь, чтобы узнать Как?
Рассмотрим следующий пример:
.. и т. д.). Любое уравнение со смесью этих двух компонентов образует булеву функцию. Значение переменных может быть или не быть заранее определенным. Сокращенное обозначение булевой функции состоит в том, что она представлена заглавной буквой F, за которой следует скобка, состоящая из всех переменных этого уравнения, разделенных запятой (‘,’). Вы можете представить любое логическое выражение в виде таблицы истинности. Подпишитесь, чтобы узнать Как?
Рассмотрим следующий пример: (количество переменных) комбинаций. Следуйте приведенным ниже примерам, чтобы узнать, как сопоставить эти значения.
(количество переменных) комбинаций. Следуйте приведенным ниже примерам, чтобы узнать, как сопоставить эти значения.
 Значение суммы произведения заключается в том, что когда вы выполняете
Значение суммы произведения заключается в том, что когда вы выполняете 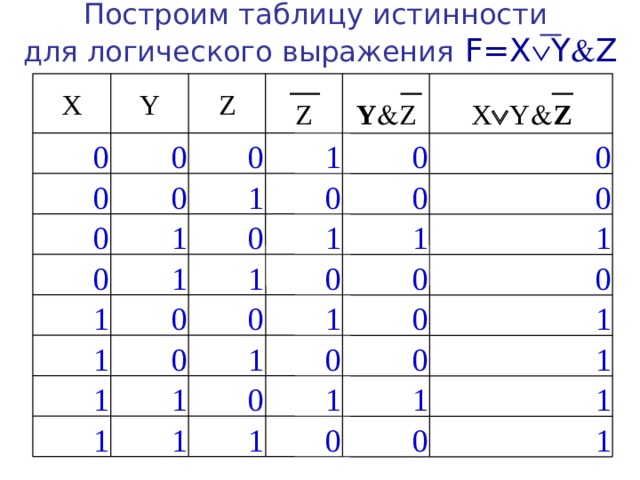 Такое выражение называется выражением Product of Sum или сокращенно POS .
Такое выражение называется выражением Product of Sum или сокращенно POS . Минимальный член обозначается как mi, где i находится в диапазоне 0 ≤ i < 2 n .
Минимальный член обозначается как mi, где i находится в диапазоне 0 ≤ i < 2 n .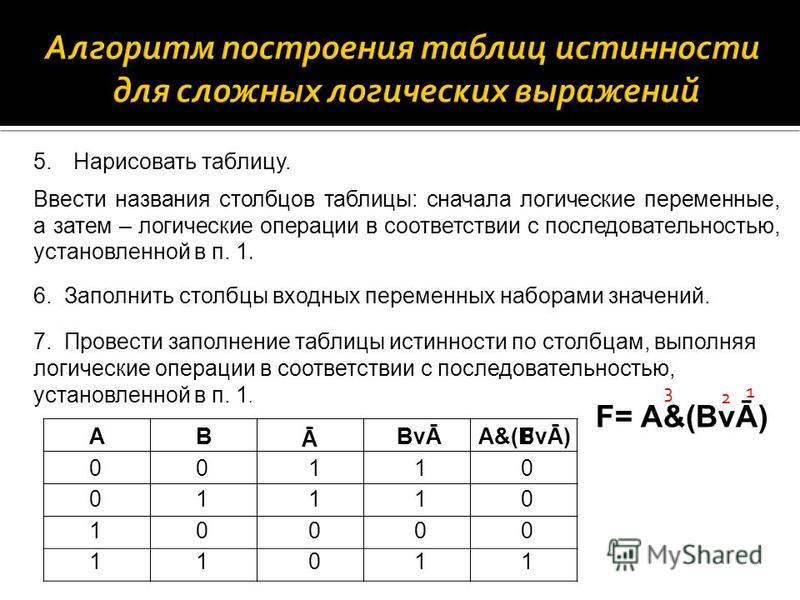 Таким образом, для уравнений с двумя переменными условия произведения равны 2 2 = 4. Аналогично, для уравнений с 3 переменными условия произведения равны 2 3 = 8.
Таким образом, для уравнений с двумя переменными условия произведения равны 2 2 = 4. Аналогично, для уравнений с 3 переменными условия произведения равны 2 3 = 8.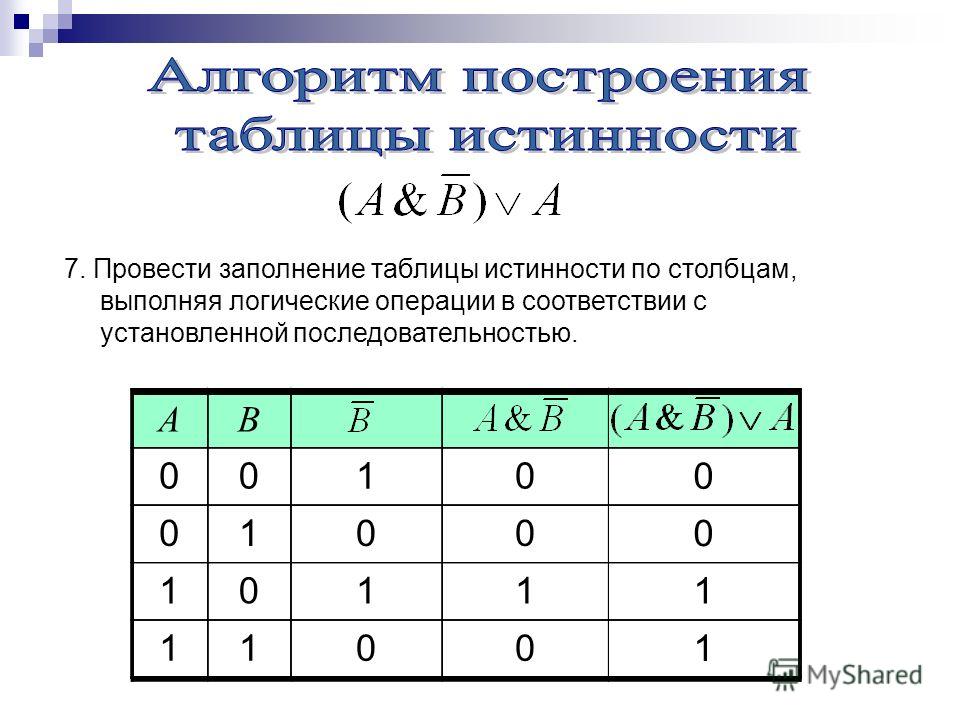
 е. вы можете представить форму уравнения SOP в форме POS и уравнение формы POS в форме SOP. Чтобы преобразовать канонические уравнения, вы поменяете местами символы Σ и Π после перечисления порядковых номеров уравнений, которые исключены из исходной формы уравнения.
е. вы можете представить форму уравнения SOP в форме POS и уравнение формы POS в форме SOP. Чтобы преобразовать канонические уравнения, вы поменяете местами символы Σ и Π после перечисления порядковых номеров уравнений, которые исключены из исходной формы уравнения. Теперь напишите форму суммы для этих отмеченных терминов.
Теперь напишите форму суммы для этих отмеченных терминов.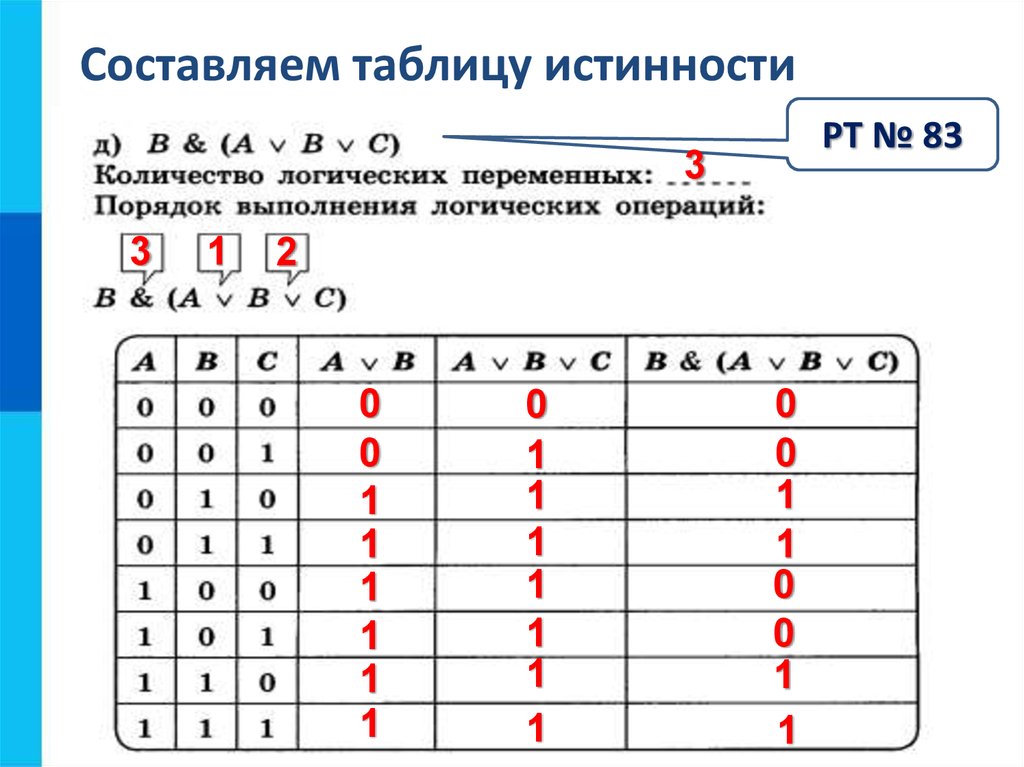 Обычная функция формы POS может быть преобразована в стандартную форму POS с помощью логического алгебраического закона 9.0150 (A * A’ = 0) и выполнив следующие действия.
Обычная функция формы POS может быть преобразована в стандартную форму POS с помощью логического алгебраического закона 9.0150 (A * A’ = 0) и выполнив следующие действия. Тогда
Тогда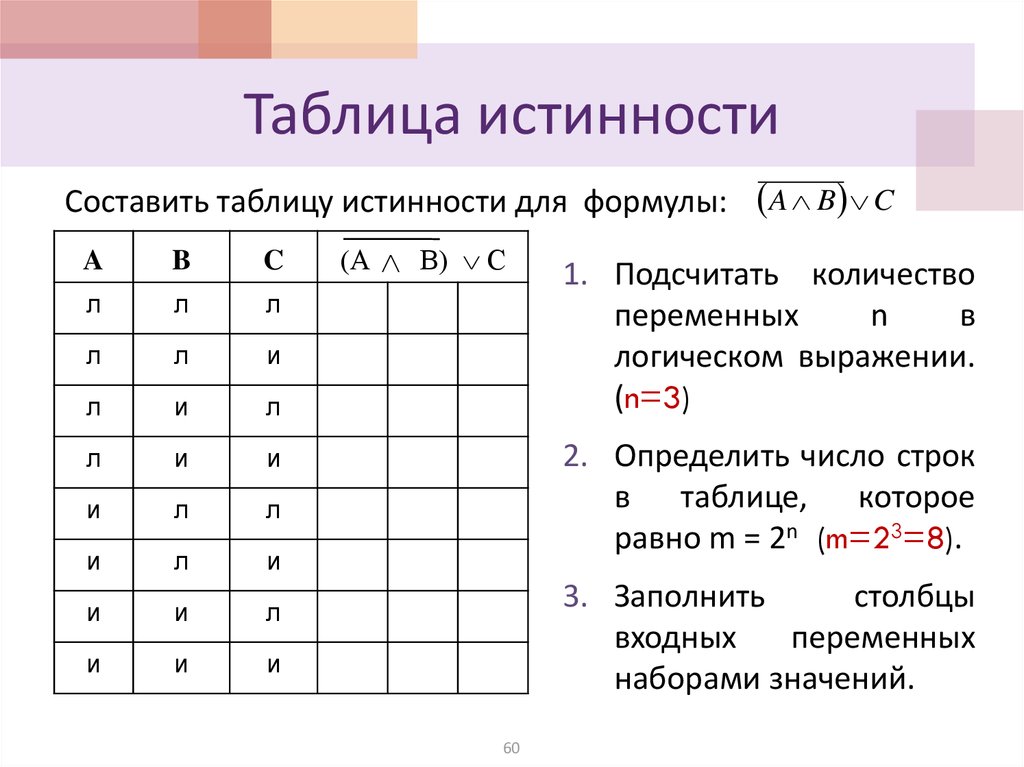 В этом процессе для каждой отсутствующей переменной в функции количество терминов продукта будет удваиваться.
В этом процессе для каждой отсутствующей переменной в функции количество терминов продукта будет удваиваться.