Физический смысл емкостного сопротивления в цепи переменного тока
Величины и единицы измерения ёмкости и индуктивности – для новичков в радиоделе
Ёмкость конденсатора, если его представить в виде двух металлических пластин с диэлектриком между ними, зависит от площади поверхности пластин, расстояния между ними и свойств диэлектрика Есть конденсаторы переменной ёмкости, где в качестве диэлектрика выступает воздух
Рис 418 Конденсатор переменной ёмкости
Чтобы увеличить ёмкость постоянного конденсатора его обкладки изготавливают, например, из алюминиевой фольги, проложенной тонким диэлектриком Поверхность получается достаточно большой, а свёрнутая фольга занимает мало места Чем тоньше диэлектрик, тем больше ёмкость
Но при этом тонкий диэлектрик легче пробивается напряжением То есть, рабочее напряжение конденсатора становится меньше
Переменные конденсаторы небольшой ёмкости служат для подстройки, их ещё называют триммерами
Рис 419 Подстроечный конденсатор
К единице ёмкости конденсаторов применяют приставки микро, нано, пико, что означает, почти все конденсаторы имеют ёмкость меньше основной единицы, фарады Часто это можно отнести и к единицам индуктивности, где основная единица генри
Есть один вид конденсаторов, отличающийся от других, которые называют электролитическими конденсаторами Это конденсаторы большой ёмкости, но для получения такой ёмкости их заполняют электролитом Такие конденсаторы, как правило, полярные, то есть, их правильная работа зависит от правильной полярности напряжения на них Чтобы при подключении конденсатора не произошла ошибка, на корпус наносят маркировку Если электролит в процессе работы конденсатора высыхает, то конденсатор теряет ёмкость
Хотя конденсатор не пропускает постоянный электрический ток, ток утечки всё-таки есть, то есть, у сопротивления конденсатора есть активная составляющая Электролитический конденсатор, выполненный из свёрнутой ленты фольги, похож на индуктивность, что подразумевает влияние этой индуктивности на высоких частотах Чтобы избежать этого влияния, параллельно электролитическому конденсатору можно поставить керамический конденсатор
Катушки индуктивности с номиналом в десятки миллигенри выглядят как катушки:
Рис 420 Катушка индуктивности 15 мГн
А катушки индуктивности в десятки микрогенри похожи, скорее, на резисторы
Рис 221 Катушка индуктивности 10 мкГн
Такие индуктивности называют ещё дросселями и используют в фильтрах, особенно в фильтрах цепей питания высокочастотных устройств Их можно намотать на обычном резисторе с большим сопротивлением, скажем в несколько мегаом Или намотать на тонком ферритовом стержне Катушки колебательных контуров карманных радиоприёмников наматывают на ферритовый стержень, который одновременно служит магнитной антенной приёмника
Индуктивность катушки зависит от количества витков, диаметра намотки и материала, на который наматывается катушка Чтобы уменьшить влияние сопротивления провода, его стараются выбрать достаточно большого диаметра Провод высокочастотных катушек, когда количество витков небольшое, применяют посеребрённый
На высоких частотах вполне можно применять изготовление катушки в виде спирали на печатной плате Такой способ изготовления очень технологичен и имеет хорошую повторяемость параметров
Для получения больших значений индуктивности используют такие сердечники, как кольца из ферритов или сердечники из трансформаторной стали
Для точной настройки величины индуктивности катушки индуктивности часто имеют сердечники, медные или ферритовые
Раньше карманные приёмники имели довольно большое количество фильтров промежуточной частоты, выполненных с использованием катушек индуктивности
Для уменьшения влияния катушек друг на друга их помещали в защитные экраны
Каждая из катушек имела ферритовый сердечник, который позволял настроить фильтр точно на промежуточную частоту
Позже в качестве фильтров стали применять ПАВ-фильтры (фильтры на поверхностных акустических волнах) и пьезо-фильтры
Рис 222 Катушки индуктивности с подстроечными сердечниками
Tweet Нравится
- Предыдущая запись: Как переводить с языка электрических схем
- Следующая запись: КОНВЕРТОРЫ В УСТРОЙСТВАХ НА МИКРОСХЕМАХ
Конденсаторы как элементы схем (0)
Конденсаторы в цепи переменного тока (0)
Индуктивности (0)
БУФЕРНОЕ УСТРОЙСТВО ДЛЯ АЦП I (0)
УСТРОЙСТВО ЗАЩИТЫ ПК C ПОМОЩЬЮ ПАРОЛЯ (0)
ЛИНЕЙНЫЙ УСИЛИТЕЛЬ МОЩНОСТЬЮ 1,2 KBT И ЧАСТОТОЙ 144 МГЦ (0)
УСТРОЙСТВО ДЛЯ ВЫБОРА ФИЛЬТРОВ HA Р1Н-ДИОДЕ (0)
Способы соединения элементов
Монтаж изделия на плату может быть вертикальным или горизонтальным. При использовании нескольких изделий они могут быть соединены между собой разными способами.
При использовании нескольких изделий они могут быть соединены между собой разными способами.
Параллельное соединение
Для его организации нужно подключить группу деталей к электроцепи так, чтобы обкладки всех деталей были подсоединены напрямую к местам включения. Поскольку все компоненты получают заряд от одного источника тока, у них будет одинаковая разность потенциалов. Но так как заряд копится на каждом изделии отдельно, количество электричества на группе можно выразить как сумму количеств на ее деталях.
Это справедливо и для емкостных данных – значение для конфигурации равно сумме значений каждой единицы. Поэтому такую группу можно считать равной одному конденсатору, емкостной параметр которого равен сумме таковых для всех частей.
Последовательное соединение
Эта схема подразумевает соединение устройств одно за другим, когда к местам подключения к цепи подсоединены только два крайних изделия. Количество электричества для каждой детали будет одинаковым. При этом, чем менее емкое устройство, тем большее значение напряжения на нем будет наблюдаться.
При этом, чем менее емкое устройство, тем большее значение напряжения на нем будет наблюдаться.
Последовательное подключение
Смешанное соединение
Такая сложная конструкция содержит фрагменты с двумя вышеприведенными типами соединений. Чтобы подсчитать полную емкость, схему делят на простые блоки, состоящие только из деталей, соединенных каким-то одним образом. Находят эквивалентные значения для каждого блока и затем рисуют схему заново в упрощенном виде. Рассчитывают данные для получившейся системы.
Чтобы суметь подобрать подходящий конденсаторный набор, нужно уметь узнавать емкостные данные
Важно также знать, как рассчитывается показатель для конфигурации из нескольких деталей, соединенных между собой тем или иным образом
Импеданс элемента
Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать.
Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.
Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где
- Xl — индуктивность;
- Xс — ёмкость;
- R — активная составляющая.
Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:
- X > 0, в элементе проявляются индуктивные свойства;
- X = 0, в ёмкости присутствует только активная величина;
- X < 0, в элементе проявляется ёмкостное сопротивление.
Ёмкостное сопротивление
Для понимания процесса следует представить конденсатор в электрической цепи, по которой течёт переменный ток. Причём в этой цепи нет других элементов. Значение тока, проходящего через конденсатор, и напряжения, приложенного к его обкладкам, изменяется по времени.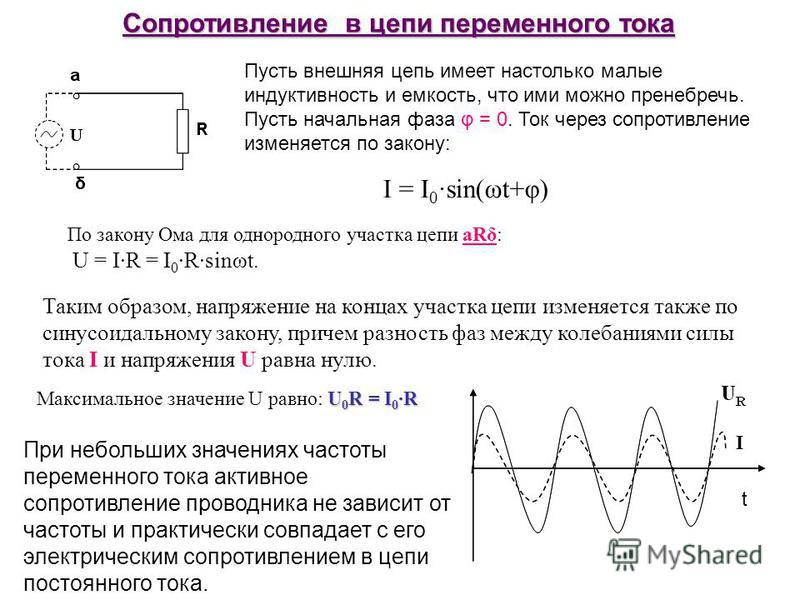 Зная любое из этих значений, можно найти другое.
Зная любое из этих значений, можно найти другое.
Пускай ток изменяется по синусоидальной зависимости I (t) = Im * sin (w*t+ f 0). Тогда напряжение можно описать как U (t) = (Im/C*w) *sin (w*t+ f 0 -p/2). При учёте в формуле сдвига фаз на 90 градусов, возникающего между сигналами, вводится комплексная величина j, называемая мнимой единицей. Поэтому формула для нахождения тока будет выглядеть как I = U /(1/j*w*C). Но учитывая, что комплексное число только обозначает смещение напряжения относительно тока, а на их амплитудные значения не влияет, его можно убрать из формулы, тем самым значительно её упростив.
Так как по закону Ома сопротивление прямо пропорционально напряжению на участке цепи и обратно пропорционально току, то преобразуя формулы, можно будет получить следующее выражение:
Xc = 1/w*C = ½*p*f*C. Единица измерения — ом.
Становится понятно, что ёмкостное сопротивление зависит не только от ёмкости, но и от частоты. При этом чем больше эта частота, тем меньшее сопротивление конденсатор будет оказывать проходимому через него току.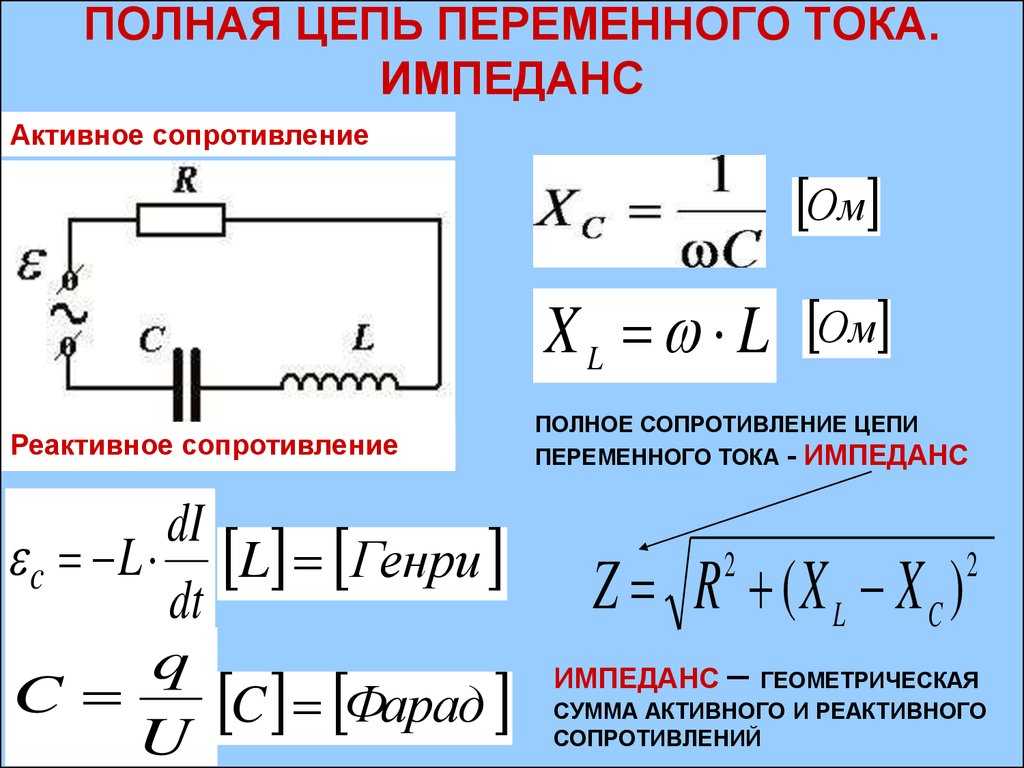 По отношению к ёмкости это утверждение будет обратным. Вот поэтому для постоянного тока, частота которого равна нулю, сопротивление накопителя будет бесконечно большим.
По отношению к ёмкости это утверждение будет обратным. Вот поэтому для постоянного тока, частота которого равна нулю, сопротивление накопителя будет бесконечно большим.
На практике всё немного по-другому. Чем ближе частота сигнала приближается к нулевому значению, тем больше становится сопротивление конденсатора, но при этом разрыв цепи наступить всё равно не может. Связанно это с током утечки. В случае когда частота стремится к бесконечности, сопротивление конденсатора должно становиться нулевым, но этого тоже не происходит — из-за присутствия паразитной индуктивности и всё того же тока утечки.
Индуктивная составляющая
При прохождении переменного сигнала через накопитель, его можно представить в виде последовательно включённой с источником питания катушки индуктивности.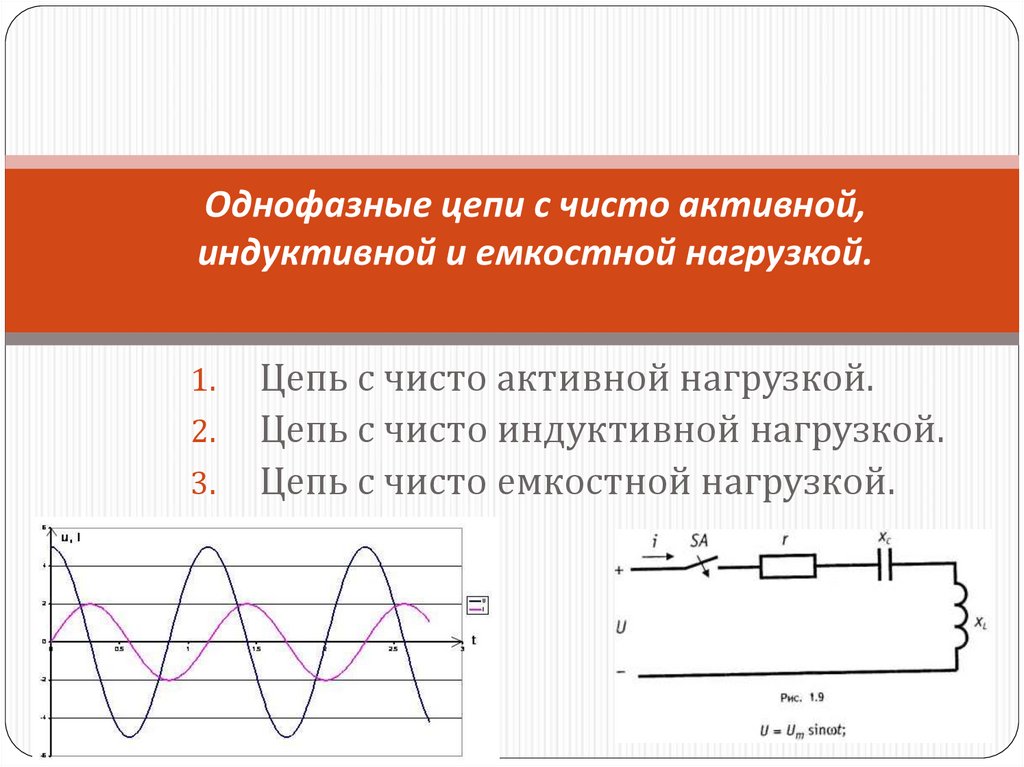
Приняв во внимание, что мгновенная величина напряжения U 0 обратна по знаку мгновенному значению ЭДС самоиндукции E 0, а также используя правило Ленца, можно получить выражение E = L * I, где L — индуктивность
Следовательно: U = L*w * I 0 *cosw*t = U 0 *sin (wt + p /2) , причём ток отстаёт от напряжения на p /2. Используя закон Ома и приняв, что сопротивление катушки равно w * L, получится формула для участка электрической цепи, имеющая только индуктивную составляющую: U 0 = I 0 / w * L.
Схема последовательного соединения
Когда применяется схема последовательного соединения конденсаторов, заряд каждой детали эквивалентен. С источником соединены только внешние пластины, другие – заряжаются перераспределением электрозарядов между ними. Все конденсаторы сохраняют аналогичное количество заряда на своих обкладках. Это объясняется тем, что на каждый последующий элемент поступает заряд от соседнего. Вследствие этого справедливо уравнение:
Это объясняется тем, что на каждый последующий элемент поступает заряд от соседнего. Вследствие этого справедливо уравнение:
q = q1 = q2 = q3 = …
Известно, что при последовательном соединении резисторных элементов их сопротивления суммируются, но емкость конденсатора, включенного в такую электроцепь, рассчитывается по-другому.
Падение напряжения на отдельном конденсаторном элементе зависит от его емкости. Если в последовательной электроцепи имеется три конденсаторных элемента, составляется выражение для напряжения U на основании закона Кирхгофа:
U = U1 + U2 + U3,
при этом U= q/C, U1 = q/C1, U2 = q/C2, U3 = q/C3.
Подставляя значения для напряжений в обе части уравнения, получается:
q/C = q/C1 + q/C2 + q/C3.
Так как электрозаряд q – величина одинаковая, на нее можно поделить все части полученного выражения.
Результирующая формула для емкостей конденсаторов:
1/С = 1/С1 + 1/С2 + 1/С3.
Важно! Если конденсаторы подключаются в последовательную электроцепь, показатель, обратный результирующей емкости, равен совокупности обратных значений единичных емкостей. Особенности последовательного соединения
Особенности последовательного соединения
Пример. Три конденсаторных элемента подключены в последовательную цепь и обладают емкостями: С1 = 0,05 мкф, С2 = 0,2 мкФ, С3 = 0,4 мкФ. Рассчитать общую емкостную величину:
- 1/С = 1/0,05 + 1/0,2 + 1/0,4 = 27,5;
- С = 1/27,5 = 0,036 мкФ.
Важно! Когда конденсаторные элементы включены в последовательную электроцепь, общее емкостное значение не превышает наименьшей емкости отдельного элемента. Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:. Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:
Если цепь состоит всего из двух компонентов, формула переписывается в таком виде:
С = (С1 х С2)/(С1 + С2).
В случае создания цепи из двух конденсаторов с идентичным емкостным значением:
С = (С х С)/(2 х С) = С/2.
Последовательно включенные конденсаторы имеют реактивное сопротивление, зависящее от частоты протекающего тока. На каждом конденсаторе напряжение падает из-за наличия этого сопротивления, поэтому на основе такой схемы создается емкостной делитель напряжения.
На каждом конденсаторе напряжение падает из-за наличия этого сопротивления, поэтому на основе такой схемы создается емкостной делитель напряжения.
Формула для емкостного делителя напряжения:
U1 = U x C/C1, U2 = U x C/C2, где:
- U – напряжение питания схемы;
- U1, U2 – падение напряжения на каждом элементе;
- С – итоговая емкость схемы;
- С1, С2 – емкостные показатели единичных элементов.
Вычисление падений напряжения на конденсаторах
К примеру, имеются сеть переменного тока 12 В и две альтернативных электроцепи подсоединения последовательных конденсаторных элементов:
- первая – для подключения одного конденсатора С1 = 0,1 мкФ, другого С2 = 0,5 мкФ;
- вторая – С1 = С2 = 400 нФ.
Первый вариант
- Итоговая емкость электросхемы С = (С1 х С2)/(С1 + С2) = 0,1 х 0,5/(0,1 + 0,5) = 0,083 мкФ;
- Падение напряжения на одном конденсаторе: U1 = U x C/C1 = 12 x 0,083/0,1 = 9,9 В
- На втором конденсаторе: U2 = U x C/C2 = 12 х 0,083/0,5 = 1,992 В.

Второй вариант
- Результирующая емкость С = 400 х 400/(400 + 400) = 200 нФ;
- Падение напряжения U1 = U2 = 12 x 200/400 = 6 В.
Согласно расчетам, можно сделать выводы, что если подключаются конденсаторы равных емкостей, вольтаж делится поровну на обоих элементах, а когда емкостные значения различаются, то на конденсаторе с меньшей емкостной величиной напряжение увеличивается, и наоборот.
Назначение и функции конденсаторов
Конденсатор играет огромную роль как в аналоговой, так и цифровой технике. Они бывают электролитическими и керамическими, и отличаются своими свойствами, но не общей концепцией. Примеры использования:
- Фильтрует высокочастотные помехи;
- Уменьшает и сглаживает пульсации;
- Разделяет сигнал на постоянные и переменные составляющие;
- Накапливает энергию;
- Может использоваться как источник опорного напряжения;
- Создает резонанс с катушкой индуктивности для усиления сигнала.

Примеры использования
В усилителях обычно используются для защиты сабвуферов, фильтрации питания, термостабилизации и разделение постоянной составляющей от переменной. А электролитические в автономных схемах с микроконтроллерами могут долго обеспечивать питание за счет большой емкости.
В данной схеме транзистор VT1 постоянно открыт, чтобы усиливать звук без искажений. Но если вход замнется или на него поступи постоянный ток, то транзистор откроется, перейдет в насыщение и перегреется. Чтобы этого не допустить, нужен конденсатор. С1 позволяет отделить постоянную оставляющую от переменной. Переменный сигнал легко проходит на базу транзистора, а постоянный сигнал не проходит.
С2 совместно с резистором R3 выполняет функцию термостабилизации. Когда усилитель работает, транзистор нагревается. Это может внести искажения в сигнал. Поэтому, резистор R3 помогает удержать рабочую точку при нагреве. Но когда транзистор холодный и стабилизации не требуется резистор может уменьшить мощность усилителя. Поэтому, в дело вступает С2. Он проводит через себя усиленный сигнал шунтируя резистор, тем самым, не снижая номинальную мощность схемы. Если его емкость будет ниже расчетной, он начнет вносить фазовые искажения в выходной сигнал.
Поэтому, в дело вступает С2. Он проводит через себя усиленный сигнал шунтируя резистор, тем самым, не снижая номинальную мощность схемы. Если его емкость будет ниже расчетной, он начнет вносить фазовые искажения в выходной сигнал.
Чтобы схема качественно работала, обязательно хорошее питание. Когда схема в пиковые значения потребляет больше тока, то это всегда сильная нагрузка на источник питания. С3 фильтрует помехи по питанию и помогает снизить нагрузку. Чем больше емкость — тем лучше звук, но до определенных значений, все зависит от схемы.
А в блоках питания используется тот же принцип, как и в предыдущей схеме по питанию, но здесь емкость нужна гораздо больше. На этой схеме емкость элеткролита может быть как 1000 мкФ, так и 10 000 мкФ.
Еще на диодный мост можно параллельно включить керамические конденсаторы, которые будут шунтировать схему от высокочастотных наводок и шума сети 220 В.
Фазовые искажения
Конденсатор может искажать переменный сигнал по фазе. Это происходит из-за неверного расчета емкости, общего сопротивления и взаимодействия с другими радиодеталями. Не стоит забывать и о том, что любая радиодеталь имеет как реактивное, так и активное сопротивление.
Это происходит из-за неверного расчета емкости, общего сопротивления и взаимодействия с другими радиодеталями. Не стоит забывать и о том, что любая радиодеталь имеет как реактивное, так и активное сопротивление.
Post Views:
1 363
История накопителей заряда
Самое раннее письменное свидетельство получения зарядов с помощью трения принадлежит учёному Фалесу из Милета (635—543 гг. до н. э.), который описал трибоэлектрический эффект от взаимодействия янтаря и сухой шерсти. Для приблизительно 2300 последующих лет любое получение электричества заключалось в трении двух различных материалов друг о друга.
Качественный рывок в знаниях о зарядах произошёл в эпоху Просвещения — период революционного развития научной мысли в образованных кругах. В это время электричество становится популярной темой, а энтузиастами было произведено немало опытов и экспериментов с генераторами на основе трения.
Открытие явления произошло во время опытов у обоих экспериментаторов, но с той разницей, что Мюссенбрук, во-первых, сделал немало усовершенствований первоначально созданного оборудования, а во-вторых, письменно сообщил коллегам о своих достижениях. Прошло совсем немного времени и учёные мира стали создавать накопители зарядов собственных конструкций. Это были первые шаги в эволюции конденсаторов, продолжающейся и в наши дни. Основные даты хронологии появления устройств для хранения зарядов:
Прошло совсем немного времени и учёные мира стали создавать накопители зарядов собственных конструкций. Это были первые шаги в эволюции конденсаторов, продолжающейся и в наши дни. Основные даты хронологии появления устройств для хранения зарядов:
- 1746 г. — изобретение лейденской банки в результате экспериментов по доработке устройства Клейста;
- 1750 г. — опыты Бенджамина Франклина с батареями конденсаторов;
- 1837 г. — публикация Майклом Фарадеем теории диэлектрической поляризации — научной основы работы накопителей;
- конец XIX в. — начало практического применения лейденских банок вместе с первыми устройствами постоянного тока;
- начало XX в. — изобретение слюдяных и керамических конденсаторов.
Емкостное сопротивление в цепи переменного тока
При включении конденсатора в цепь постоянного тока, на протяжении короткого периода времени будет наблюдаться течение по цепи зарядного тока. По окончании зарядки, когда напряжение конденсатора будет соответствовать напряжению источника тока, кратковременное течение тока в цепи прекратится. Таким образом, полностью при постоянном токе будет своеобразным разрывом цепи или сопротивлением с бесконечно большим значением. При переменном токе конденсатор будет вести себя совершенно иначе. Его зарядка в такой цепи будет осуществляться поочередно в разных направлениях. Течение переменного тока в цепи в это время не прерывается.
Таким образом, полностью при постоянном токе будет своеобразным разрывом цепи или сопротивлением с бесконечно большим значением. При переменном токе конденсатор будет вести себя совершенно иначе. Его зарядка в такой цепи будет осуществляться поочередно в разных направлениях. Течение переменного тока в цепи в это время не прерывается.
Более подробное рассмотрение этого процесса указывает на нулевое значение напряжения в конденсаторе в момент его включения. После поступления к нему переменного напряжения сети начнется зарядка. В это время сетевое напряжение будет возрастать на протяжении первой четверти периода. По мере того как на обкладках накапливаются заряды, происходит увеличение напряжения самого конденсатора. После того как сетевое напряжение в конце первой четверти периода станет максимальным, зарядка прекращается и значение тока в цепи станет равным нулю.
Существует формула для определения тока в цепи конденсатора: I = ∆q/∆t, где q является количеством электричества, протекающим по цепи в течение промежутка времени t. В соответствии с законами электростатики, количество электричества в устройстве составит: q = C x Uc = C x U. В этой формуле С будет емкостью конденсатора, U — напряжением сети, Uc — напряжением на обкладках элемента. В окончательном виде формула тока в цепи будет выглядеть следующим образом: i = C x (∆Uc/∆t) = C x (∆U/∆t).
В соответствии с законами электростатики, количество электричества в устройстве составит: q = C x Uc = C x U. В этой формуле С будет емкостью конденсатора, U — напряжением сети, Uc — напряжением на обкладках элемента. В окончательном виде формула тока в цепи будет выглядеть следующим образом: i = C x (∆Uc/∆t) = C x (∆U/∆t).
При наступлении второй четверти периода произойдет уменьшение сетевого напряжения и начнется разрядка конденсатора. Ток в цепи изменит свое направление и будет течь в обратную сторону. В следующей половине периода направление сетевого напряжения изменится, наступит перезарядка элемента, а потом он вновь начнет разряжаться. Ток, присутствующий в цепи с конденсаторной емкостью, будет опережать по фазе напряжение на обкладках на 90 градусов.
Установлено что изменения тока конденсатора происходят со скоростью, находящейся в пропорциональной зависимости с угловой частотой ω. Поэтому в соответствии с уже известной формулой тока в цепи i = C x (∆U/∆t), аналогично получается, что действующее значение тока также будет представлять собой пропорцию между скоростью изменения напряжения и угловой частотой ω: I = 2π x f x C x U.
Далее уже совсем несложно установить значение емкостного сопротивления или реактивного сопротивления емкости: xc = 1/2π x f x C = 1/ ω x C. Данный параметр вычисляется, когда конденсаторная емкость включается в цепь переменного тока. Поэтому в соответствии с законом Ома в цепи переменного тока с включенным конденсатором, значение силы тока будет следующим: I = U/xc, а напряжение на обкладках составит: Uc = Ic x xc.
Часть сетевого напряжения, приходящаяся на конденсатор, получила название емкостного падения напряжения. Она известна также, как реактивная слагающая напряжения, обозначаемая символом Uc. Величина емкостного сопротивления хс, так же, как и значение индуктивного сопротивления xi напрямую связана с частотой переменного тока.
ОПРЕДЕЛЕНИЕ
Конденсатор, в простейшем случае состоит из двух металлических проводников (обкладок), которые разделяет слой диэлектрика. Каждая из обкладок конденсатора имеет свой вывод и может быть подключена к электрической цепи.
Конденсатор характеризуют при помощи ряда параметров (емкость, рабочее напряжение и т. д), одной из таких характеристик является сопротивление. Конденсатор практически не пропускает постоянный электрический ток. То есть сопротивление конденсатора является бесконечно большим для постоянного тока, но это идеальный случай. Через реальный диэлектрик очень малый ток протекать может. Этот ток называют током утечки. Ток утечки является показателем качества диэлектрика, который применяется при изготовлении конденсатора. У современных конденсаторов ток утечки составляет некоторые доли микроампера. Сопротивление конденсатора в таком случае можно вычислить, используя закон Ома для участка цепи, зная величину напряжения, до которой заряжен конденсатор и ток утечки. Но обычно при решении учебных задач сопротивление конденсатора постоянному току считают бесконечно большим.
Последовательное соединение конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:
Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
Глава 15.
 Емкостные цепи переменного тока . Введение в электронику
Емкостные цепи переменного тока . Введение в электроникуЦЕЛИ
После изучения этой главы студент должен быть в состоянии:
• Описать фазовое соотношение между током и напряжением в емкостной цепи переменного тока.
• Дать определение емкостного сопротивления (реактивного сопротивления емкости) в емкостной цепи переменного тока.
• Описать, как резистивно-емкостные цепи могут использоваться для фильтрации, в качестве элементов согласования и фазового сдвига.
• Объяснить как работают RC фильтры верхних и нижних частот.
Конденсаторы являются ключевыми компонентами цепей переменного тока. Конденсаторы вместе с резисторами и катушками индуктивности образуют полезные электронные цепи.
15-1. КОНДЕНСАТОРЫ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА
Когда к конденсатору прикладывается переменное напряжение, создается впечатление, что во всей цепи есть поток электронов. Однако, электроны не проходят через диэлектрик конденсатора. При увеличении и уменьшении амплитуды переменного тока конденсатор заряжается и разряжается. Результирующее движение электронов от одной обкладки к другой представляет ток.
Однако, электроны не проходят через диэлектрик конденсатора. При увеличении и уменьшении амплитуды переменного тока конденсатор заряжается и разряжается. Результирующее движение электронов от одной обкладки к другой представляет ток.
В емкостной цепи переменного тока фазовое соотношение между током и приложенным напряжением не такое, как в чисто резистивной цепи. В чисто резистивной цепи ток находится в фазе с приложенным напряжением. В емкостной цепи переменного тока ток и напряжение находятся не в фазе друг с другом (рис. 15-1). Когда ток максимален, напряжение равно нулю. Это соотношение обусловлено сдвигом по фазе на 90 градусов. В емкостной цепи ток опережает приложенное напряжение.
Рис. 15-1. Обратите внимание на то, что ток и напряжение в емкостной цепи переменного тока находятся не в фазе. Ток опережает приложенное напряжение.
В емкостной цепи переменного тока приложенное напряжение постоянно изменяется, вынуждая конденсатор. заряжаться и разряжаться. После того как конденсатор первоначально зарядится, напряжение на его обкладках противодействует любому изменению приложенного напряжения. Противодействие, которое конденсатор оказывает приложенному переменному напряжению, называется емкостным сопротивлением. Емкостное сопротивление обозначается и измеряется в омах.
заряжаться и разряжаться. После того как конденсатор первоначально зарядится, напряжение на его обкладках противодействует любому изменению приложенного напряжения. Противодействие, которое конденсатор оказывает приложенному переменному напряжению, называется емкостным сопротивлением. Емкостное сопротивление обозначается и измеряется в омах.
Емкостное сопротивление может быть вычислено по формуле:
где π = 3,14, f — частота в герцах, С — емкость в фарадах.
Емкостное сопротивление является функцией частоты приложенного переменного напряжения и емкости. Увеличение частоты уменьшает емкостное сопротивление, что приводит к возрастанию тока. Уменьшение частоты увеличивает противодействие и приводит к уменьшению тока.
ПРИМЕР: Чему равно емкостное сопротивление конденсатора емкостью в 1 микрофараду при частоте 60 герц?
Дано:
π = 3,14; f = 60 Гц; С= 1 мкф = 0,000001 Ф
Хс =?
Решение:
Хс = 1/(2)(3,14)(60)(0,000001)
Хс = 1/0,000377 = 2653 Ом.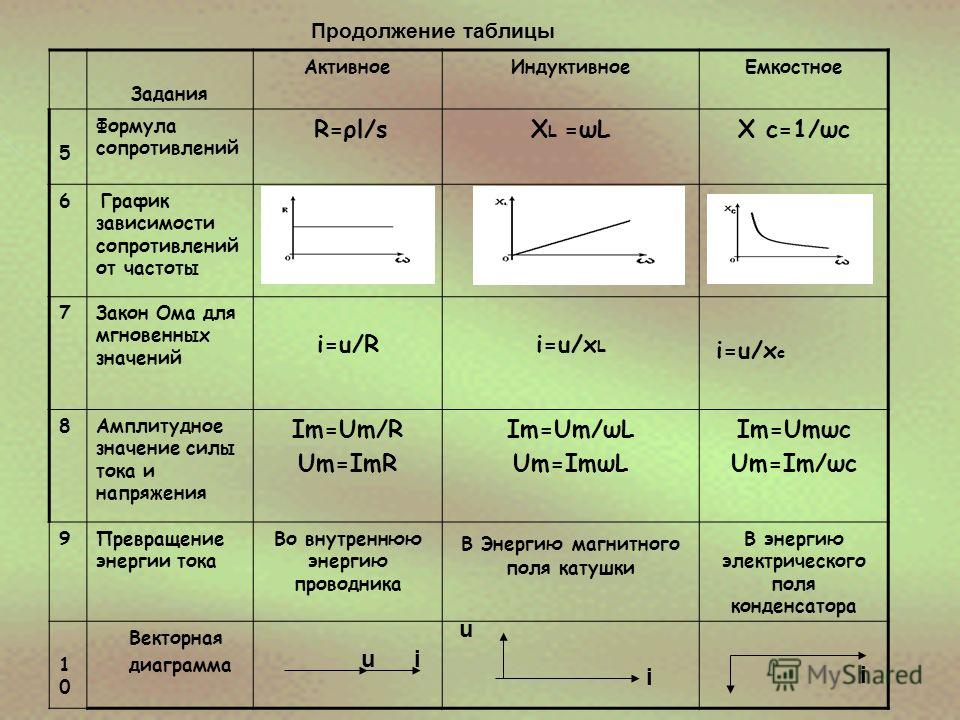
ПРИМЕР: Чему равно емкостное сопротивление конденсатора емкостью 1 мкФ на частоте 400 герц?
Дано:
π = 3,14; f = 400 Гц; С= 1 мкф = 0,000001 Ф
Хс =?
Решение:
Хс = 1/(2)(3,14)(400)(0,000001)
Хс = 1/0,00251 = 398 Ом.
ПРИМЕР: Чему разно емкостное сопротивление конденсатора емкостью в 0,1 микрофарад при частоте 60 герц?
Дано:
π = 3,14; f = 60 Гц; С= 0,1 мкф = 0,0000001 Ф
Хс =?
Решение:
Хс = 1/(2)(3,14)(60)(0,0000001)
Хс = 1/0,0000377 = 26,525 Ом.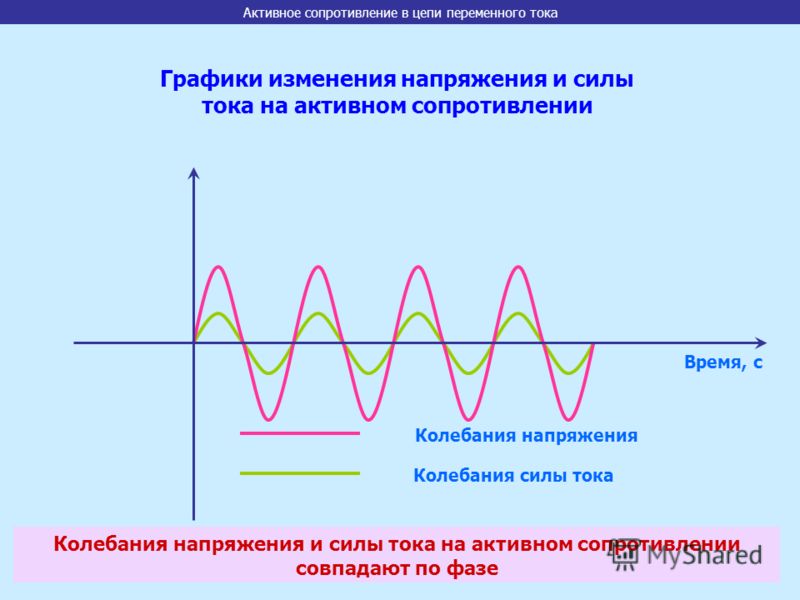
ПРИМЕР: Чему разно емкостное сопротивление конденсатора емкостью в 10 микрофарад при частоте 60 герц?
Дано:
π = 3,14; f = 60 Гц; С= 10 мкф = 0,00001 Ф
Хс =?
Решение:
Хс = 1/(2)(3,14)(60)(0,00001)
Хс = 1/0,00377 = 265 Ом.
Емкостное сопротивление есть ни что иное, как противодействие изменениям приложенного к конденсатору переменного напряжения. Следовательно, в цепи переменного тока конденсатор является эффективным способом управления током. Согласно закону Ома ток прямо пропорционален приложенному напряжению и обратно пропорционален емкостному сопротивлению. Это можно выразить с помощью формулы:
I = E/XC
Замечание: В законе Ома емкостное (реактивное) сопротивление XC заменило активное сопротивление R.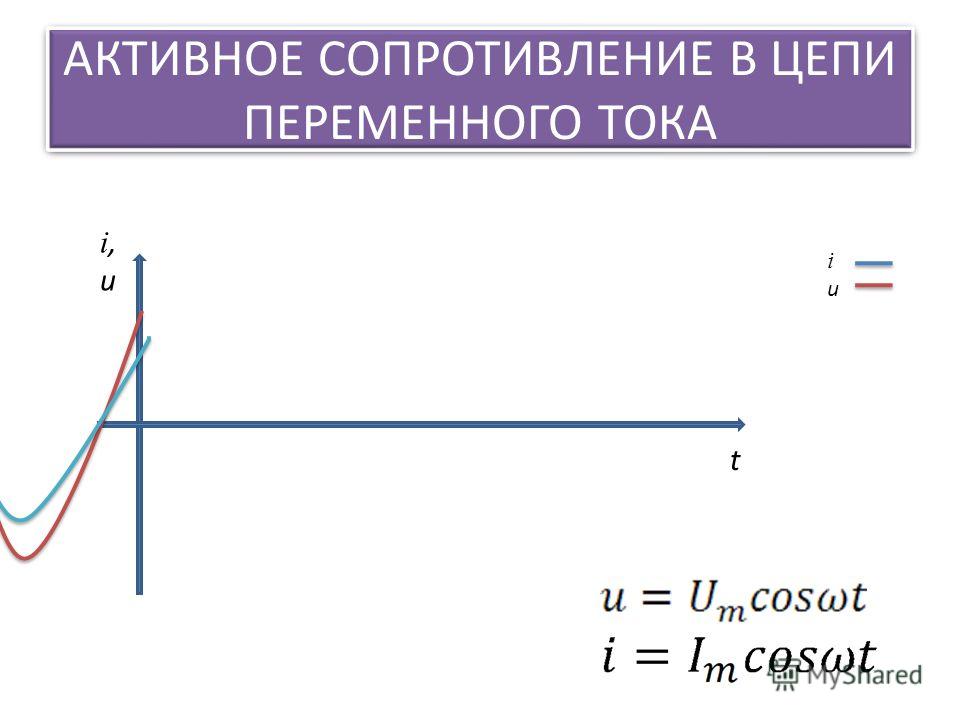
Важно помнить, что емкостное сопротивление зависит от частоты приложенного напряжения и емкости цепи.
ПРИМЕР: К конденсатору емкостью 100 мкФ приложено напряжение 12 вольт частотой 60 герц. Какова величина текущего через него тока?
Дано:
E = 12 В; π = 3,14; f = 60 Гц; С= 100 мкф = 0,0001 Ф
I =?
Решение:
Сначала найдем емкостное сопротивление (Хс)
Хс = 1/ 2πfC
Хс = 1/(2)(3,14)(60)(0,0001)
Хс = 1/0,0377 = 26,5 Ом
Теперь, зная Хс, найдем ток:
I = E/Хс = 12/26,5
I = 0,45 А или 450 мА.
ПРИМЕР: Через конденсатор емкостью 10 мкФ течет ток 250 мА. Какое напряжение частотой 60 Гц приложено к конденсатору?
Дано:
π = 3,14; f = 60 Гц; С = 10 мкф = 0,00001 Ф; I = 250 мА или 0,25 А
Хс =?; E =?
Решение:
Сначала найдем емкостное сопротивление (Хс):
Хс = 1/ 2πfC
Хс = 1/(2)(3,14)(60)(0,00001)
Хс = 1/0,00377 = 265 Ом
Теперь найдем падение напряжения (Е):
I = E/Хс
0,25 = E/265
E = 66,25 В
Когда конденсаторы соединены последовательно, общее емкостное сопротивление равно сумме емкостных сопротивлений отдельных конденсаторов:
XCT = XC1 + XC2 + XC3 +… + XCn
Когда конденсаторы соединены параллельно, обратная величина общего емкостного сопротивления равна сумме обратных величин емкостных сопротивлений отдельных конденсаторов.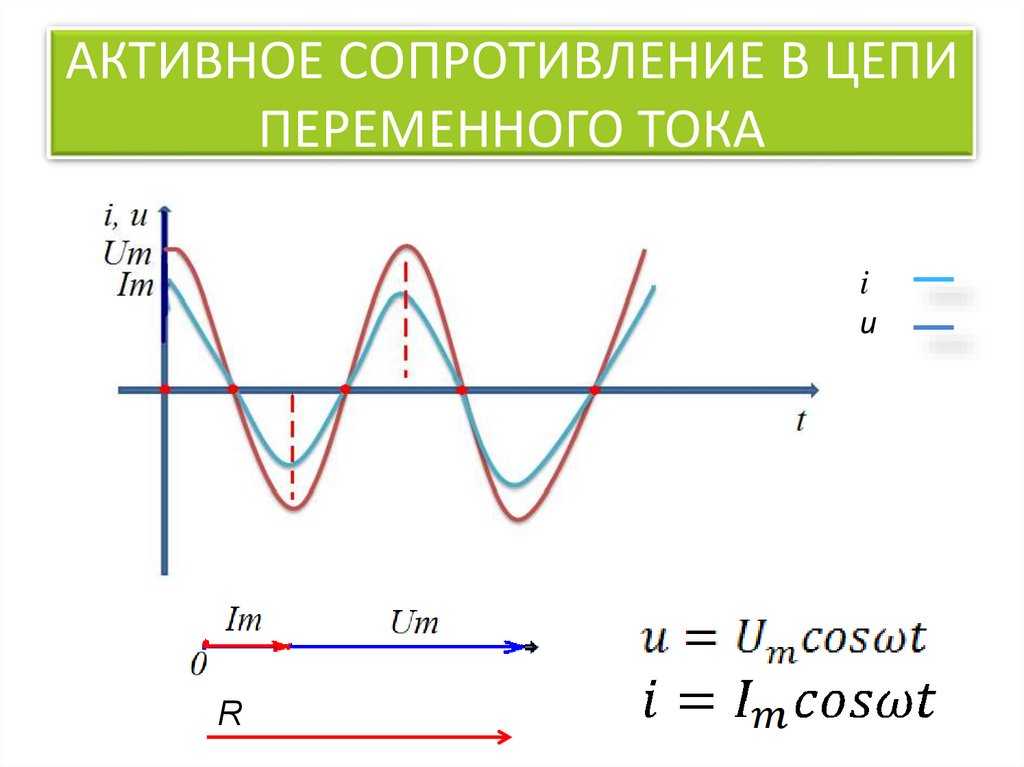
1/XCT = 1/XC1 + 1/XC2 + 1/XC3 +… + 1/XCn
15-1. Вопросы
1. Опишите, как переменное напряжение создает впечатление протекания тока через конденсатор.
2. Каково фазовое соотношение между током и напряжением в емкостной цепи?
3. Что такое емкостное сопротивление?
4. Чему равно емкостное сопротивление конденсатора емкостью 10 мкФ при частоте 400 герц?
15-2. ПРИМЕНЕНИЕ ЕМКОСТНЫХ ЦЕПЕЙ
Конденсаторы могут использоваться отдельно или в комбинации с резисторами, образуя RC (резистивно-емкостные) цепи. Одним из применений RC цепей является фильтрация.
Фильтром называется цепь, выделяющая некоторую область частот, ослабляя токи одних частот и пропуская другие.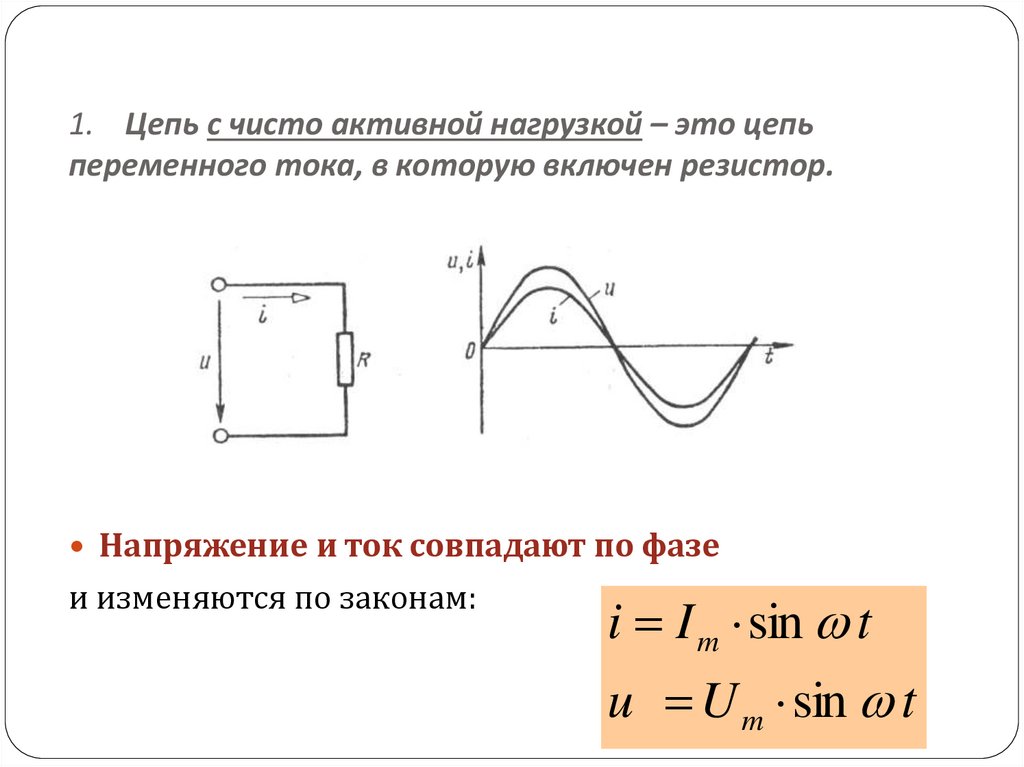 Фильтры имеют частоту (точку) среза между частотами, которые пропускаются, и частотами, которые ослабляются. Наиболее широко используются два типа фильтров: фильтры нижних частот и фильтры верхних частот. Фильтр нижних частот пропускает низкие частоты и ослабляет верхние. Фильтр верхних частот пропускает частоты, находящиеся выше частоты среза, и ослабляет частоты ниже частоты среза.
Фильтры имеют частоту (точку) среза между частотами, которые пропускаются, и частотами, которые ослабляются. Наиболее широко используются два типа фильтров: фильтры нижних частот и фильтры верхних частот. Фильтр нижних частот пропускает низкие частоты и ослабляет верхние. Фильтр верхних частот пропускает частоты, находящиеся выше частоты среза, и ослабляет частоты ниже частоты среза.
Фильтр нижних частот (рис. 15-2) состоит из конденсатора и резистора, включенных последовательно.
Рис. 15-2. RC фильтр нижних частот.
Входное напряжение приложено к последовательной цепочке из конденсатора и резистора. Выходное напряжение снимается с конденсатора. На низких частотах емкостное сопротивление больше, чем сопротивление резистора, так что большая часть напряжения падает на конденсаторе. Следовательно, большая часть напряжения появляется и на выходе. При повышении частоты входного напряжения емкостное сопротивление уменьшается, и на конденсаторе падает меньшее напряжение. Следовательно, на резисторе падает большее напряжение, и выходное напряжение уменьшается. Частота среза не является резкой границей. Чем выше частота входного сигнала, тем больше он ослабляется. На рис. 15-3 показана амплитудно-частотная характеристика RC фильтра нижних частот.
Следовательно, на резисторе падает большее напряжение, и выходное напряжение уменьшается. Частота среза не является резкой границей. Чем выше частота входного сигнала, тем больше он ослабляется. На рис. 15-3 показана амплитудно-частотная характеристика RC фильтра нижних частот.
Рис. 15-3. Амплитудно-частотная характеристика RC фильтра нижних частот.
Фильтр верхних частот также состоит из резистора и конденсатора, включенных последовательно (рис. 15-4).
Рис. 15-4. RC фильтр верхних частот.
Однако выходное напряжение снимается с резистора. На высоких частотах емкостное сопротивление низкое и большая часть напряжения падает на резисторе. При уменьшении частоты емкостное сопротивление увеличивается и на конденсаторе падает большее напряжение. В результате уменьшается выходное напряжение на резисторе. И опять уменьшение выходного напряжения является постепенным. На рис. 15-5 показана амплитудно-частотная характеристика RC фильтра верхних частот.
На рис. 15-5 показана амплитудно-частотная характеристика RC фильтра верхних частот.
Рис. 15-5. Амплитудно-частотная характеристика RC фильтра верхних частот.
Большинство электронных цепей используют как переменное, так и постоянное напряжения. Это приводит к тому, что сигнал переменного тока накладывается на сигнал постоянного тока. Если постоянный ток используется для питания оборудования, то желательно удалить из него сигналы переменного тока. Для этой цели можно использовать фильтр нижних частот. Развязывающая цепь (рис. 15-6) пропускает сигнал постоянного тока и ослабляет или устраняет сигнал переменного тока.
Рис. 15-6. Развязывающая RC цепочка.
Сигнал переменного тока может иметь форму колебаний, шумов или переходных импульсов. Путем подбора частоты среза большинство сигналов переменного тока может быть отфильтровано, и останется только постоянное напряжение на конденсаторе.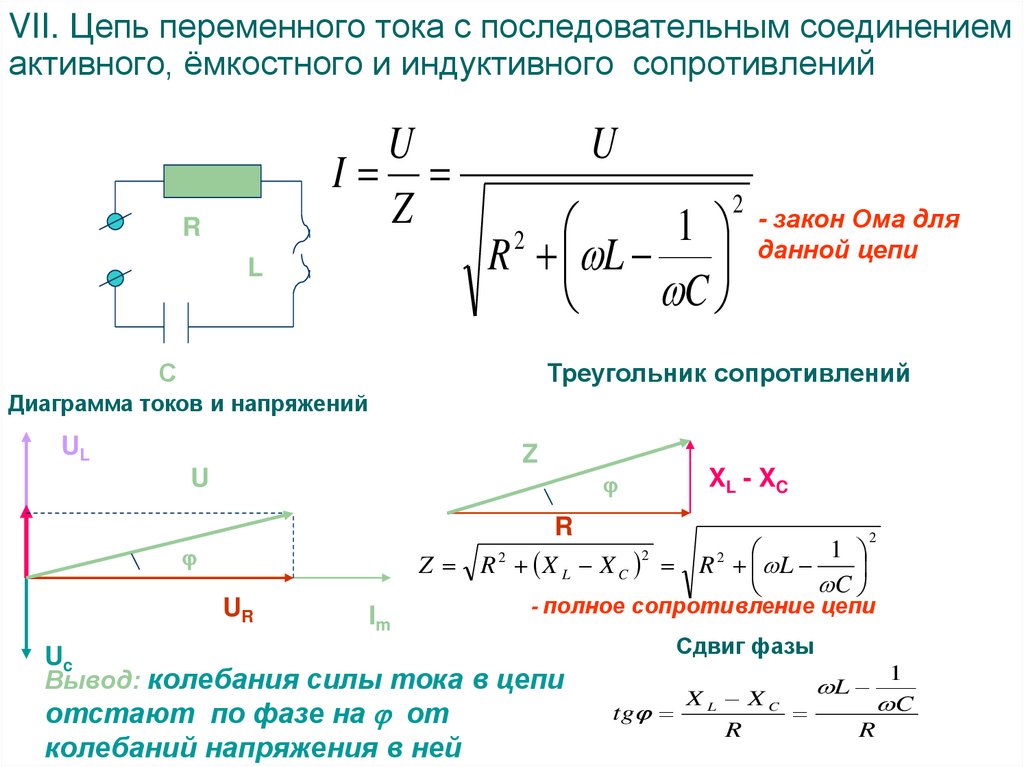
В других случаях желательно пропустить сигнал переменного тока и блокировать постоянное напряжение. Цепи этого типа называются связывающими (рис. 15-7). Для этих цепей можно использовать RC фильтр верхних частот.
Рис. 15-7. RC цепочка связи.
Сначала конденсатор заряжается до уровня постоянного напряжения. Когда конденсатор зарядится, постоянный ток уже не сможет течь по цепи. Источник переменного напряжения заставит конденсатор заряжаться и разряжаться с частотой переменного тока, создавая ток через резистор. Номинальные значения конденсатора и резистора выбираются таким образом, чтобы сигнал переменного тока проходил без затухания.
Иногда бывает необходимо сдвинуть фазу выходного сигнала переменного тока по отношению к входному сигналу. Для сдвига фазы могут также использоваться RC цепи. RC цепи фазового сдвига используются только тогда, когда желателен небольшой сдвиг фаз, порядка 60 градусов.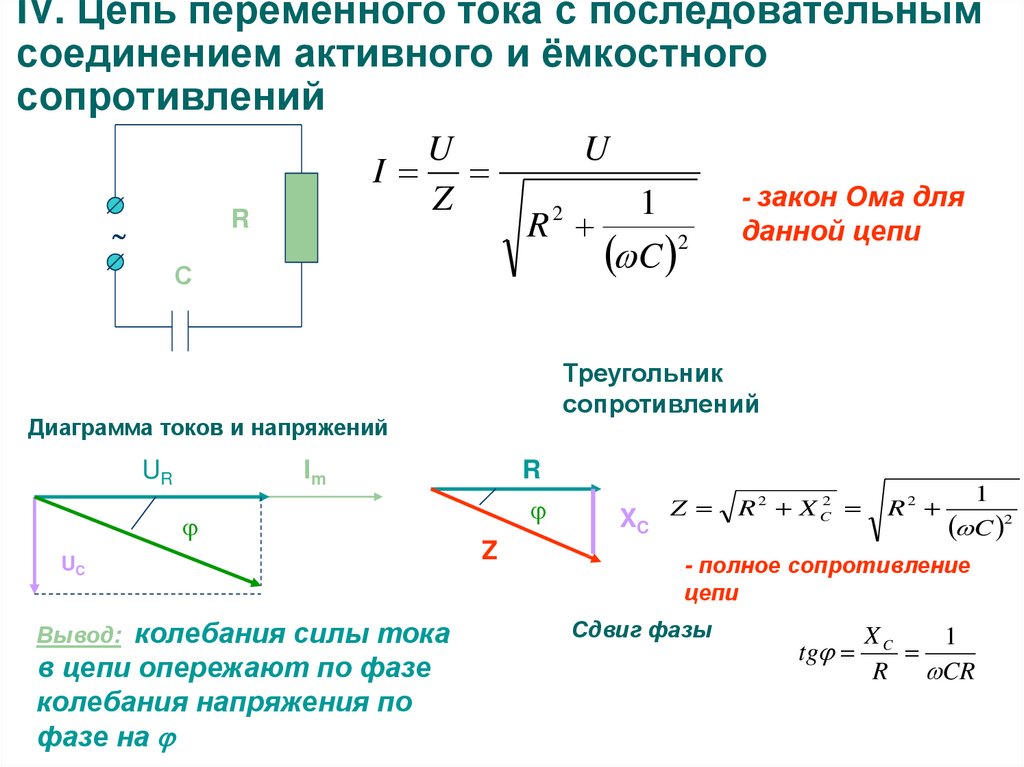
На рис. 15-8 показана цепь фазового сдвига, в которой входное напряжение приложено к комбинации резистор-конденсатор, а выходное напряжение снимается с резистора. Ввиду наличия конденсатора в этой цепи ток опережает напряжение. Напряжение на резисторе находится в фазе с током. Это приводит к тому, что выходное напряжение опережает по фазе входное.
Рис. 15-8. Цепь фазового сдвига, в которой выходное напряжение опережает по фазе входное.
На рис. 15-9 выходное напряжение снимается с конденсатора. Ток в цепи опережает приложенное напряжение. Однако напряжение на конденсаторе отстает от приложенного напряжения.
Рис. 15-9. Цепь фазового сдвига, в которой выходное напряжение на конденсаторе отстает от приложенного напряжения.
Для достижения большего сдвига фаз несколько фазосдвигающих RC цепочек можно включить последовательно (каскадно) (рис. 15–10). Однако каскадное включение цепочек уменьшает выходное напряжение. Для повышения выходного напряжения до необходимого уровня нужен усилитель.
15–10). Однако каскадное включение цепочек уменьшает выходное напряжение. Для повышения выходного напряжения до необходимого уровня нужен усилитель.
Фазосдвигающие цепочки пригодны только на одной частоте, так как емкостное сопротивление изменяется с частотой. Изменение емкостного сопротивления приводит к различным фазовым сдвигам.
Рис. 15–10. Каскадные фазосдвигающие RC цепи.
15-2. Вопросы
1. Каковы три основных применения резистивно-емкостных цепочек в электронных цепях?
2. Нарисуйте амплитудно-частотную характеристику фильтра нижних частот и расскажите, как он работает.
3. Нарисуйте амплитудно-частотную характеристику фильтра верхних частот и расскажите, как он работает.
4. Для чего предназначена развязывающая цепь?
5. Где используются фазосдвигающие RC цепочки?
РЕЗЮМЕ
• Когда к конденсатору приложено переменное напряжение, появляется ток.
• Зарядка и разрядка конденсатора создает впечатление протекания тока.
• В емкостной цепи ток опережает по фазе приложенное напряжение на 90 градусов.
• Емкостное сопротивление — это противодействие заряженного конденсатора изменению приложенного напряжения.
• Емкостное сопротивление обозначается Хс.
• Емкостное сопротивление измеряется в омах.
• Емкостное сопротивление может быть вычислено по формуле:
Хс = 1/2πfc
• RC цепочки используются для фильтрации, связи и сдвига фаз.
• Фильтр — это цепь, которая ограничивает пропускание некоторых частот.
• Фильтр нижних частот пропускает частоты ниже частоты среза. Он состоит из резистора и конденсатора, соединенных последовательно.
• Фильтр верхних частот пропускает частоты выше частоты среза. Он состоит из резистора и конденсатора, соединенных последовательно.
• Цепочки связи пропускают сигналы переменного тока и блокируют сигналы постоянного тока.
Глава 15. САМОПРОВЕРКА
1. Каково фазовое соотношение между током и приложенным напряжением в емкостной цепи?
2. Чему равно емкостное сопротивление конденсатора емкостью 1000 мкФ на частоте 60 герц?
3. Чему равен ток, текущий через конденсатор, указанный в предыдущем вопросе, при приложенном напряжении 12 вольт?
4. Перечислите три основных применения емкостных цепей.
5. Почему важны емкостные цепочки связи?
Формула емкостного сопротивления
После замыкания электрической цепи начинается зарядка, после чего конденсатор сразу же становится источником тока и напряжения, в нем возникает электродвижущая сила – ЭДС. Одно из основных свойств конденсатора очень точно отражает формула емкостного сопротивления.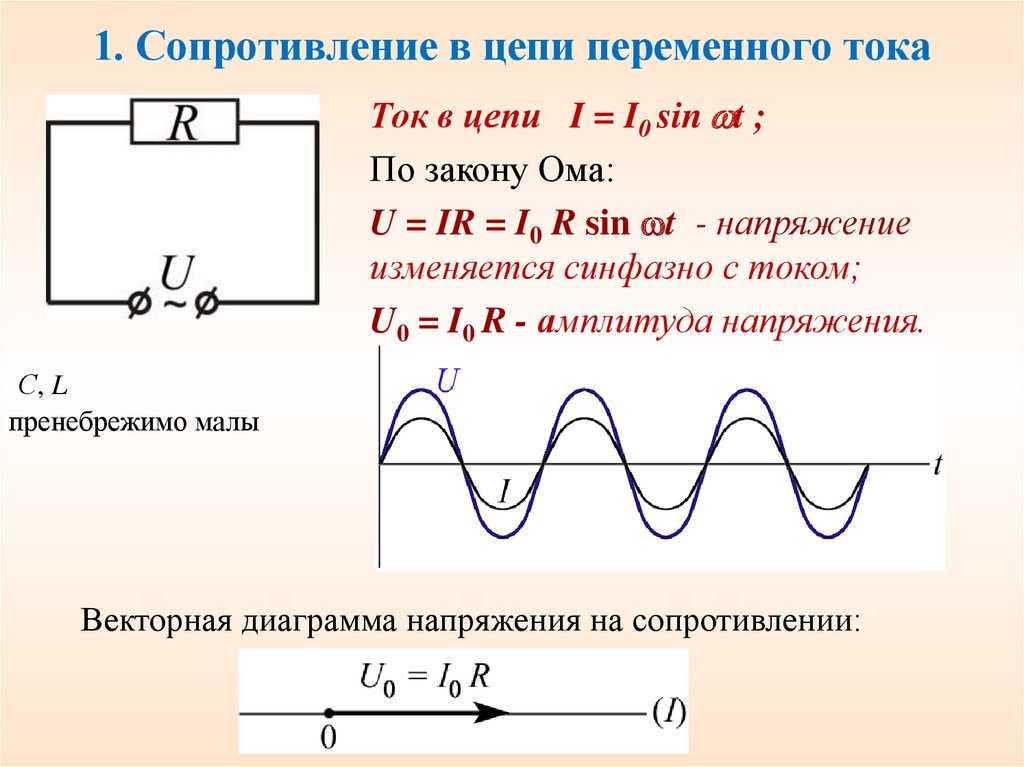 Данное явление возникает в результате противодействия ЭДС, направленного против источника тока, используемого для зарядки. Источник тока может преодолеть емкостное сопротивление лишь путем существенных затрат его собственной энергии, которая становится энергией электрического поля конденсатора. При разрядке конденсатор вся энергия возвращается обратно в цепь, превращаясь в энергию электрического тока.
Данное явление возникает в результате противодействия ЭДС, направленного против источника тока, используемого для зарядки. Источник тока может преодолеть емкостное сопротивление лишь путем существенных затрат его собственной энергии, которая становится энергией электрического поля конденсатора. При разрядке конденсатор вся энергия возвращается обратно в цепь, превращаясь в энергию электрического тока.
Емкостное сопротивление конденсатора
Конденсаторы относятся к наиболее распространенным элементам, используемым в различных электронных схемах. Они разделяются на типы, обладающие характерными особенностями, параметрами и индивидуальными свойствами. Простейший конденсатор состоит из двух металлических пластин – электродов, разделенных слоем диэлектрика. На каждом из них имеется собственный вывод, через который осуществляется подключение к электрической цепи.
Емкостное сопротивление можно отнести к реактивному, не вызывающему безвозвратных энергетических потерь. Зарядка конденсатора происходит до того уровня напряжения, которое отдается источником питания.
Существуют качества, присущие только конденсаторам. Например, они совершенно не пропускают через себя постоянный ток, хотя и заряжаются от него. После полной зарядки емкости, течение тока полностью прекращается, а внутреннее сопротивление устройства принимает бесконечно высокое значение.
Совершенно по-другому на конденсатор воздействует переменный ток, вполне свободно протекающий через емкость. Подобное состояние объясняется постоянными процессами зарядки-разрядки элемента. В этом случае действует не только активное сопротивление проводников, но и емкостное сопротивление самого конденсатора, возникающее как раз в результате его постоянной зарядки и разрядки.
Электрические параметры и свойства конденсаторов могут отличаться, в зависимости от различных факторов. В первую очередь они зависят от размеров и формы изделия, а также от типа диэлектрика. В разных типах устройств диэлектриком может служить бумага, воздух, пластик, стекло, слюда, керамика и другие материалы. В электролитических конденсаторах используются алюминий-электролит и тантал-электролит, что обеспечивает им повышенную емкость.
Названия других элементов определяются материалами обычных диэлектриков. Поэтому они относятся к категории бумажных, керамических, стеклянных и т.д. Каждый из них, в соответствии с характеристиками и особенностями, применяется в конкретных электронных схемах, с разными параметрами электротока.
В связи с этим, применение керамических конденсаторов необходимо в тех цепях, где требуется фильтрация высокочастотных помех. Электролитические устройства, наоборот, фильтруют помехи при низких частотах. Если же соединить параллельно оба типа конденсаторов, получится универсальный фильтр, широко применяемый во всех схемах. Несмотря на то, что их емкость является фиксированной величиной, существуют устройства с переменной емкостью, которая достигается путем регулировок за счет изменение взаимного перекрытия пластин. Типичным примером служат конденсаторы для подстройки, используемые при регулировке радиоэлектронной аппаратуры.
Емкостное сопротивление в цепи переменного тока
При включении конденсатора в цепь постоянного тока, на протяжении короткого периода времени будет наблюдаться течение по цепи зарядного тока. По окончании зарядки, когда напряжение конденсатора будет соответствовать напряжению источника тока, кратковременное течение тока в цепи прекратится. Таким образом, полностью заряженный конденсатор при постоянном токе будет своеобразным разрывом цепи или сопротивлением с бесконечно большим значением. При переменном токе конденсатор будет вести себя совершенно иначе. Его зарядка в такой цепи будет осуществляться поочередно в разных направлениях. Течение переменного тока в цепи в это время не прерывается.
По окончании зарядки, когда напряжение конденсатора будет соответствовать напряжению источника тока, кратковременное течение тока в цепи прекратится. Таким образом, полностью заряженный конденсатор при постоянном токе будет своеобразным разрывом цепи или сопротивлением с бесконечно большим значением. При переменном токе конденсатор будет вести себя совершенно иначе. Его зарядка в такой цепи будет осуществляться поочередно в разных направлениях. Течение переменного тока в цепи в это время не прерывается.
Более подробное рассмотрение этого процесса указывает на нулевое значение напряжения в конденсаторе в момент его включения. После поступления к нему переменного напряжения сети начнется зарядка. В это время сетевое напряжение будет возрастать на протяжении первой четверти периода. По мере того как на обкладках накапливаются заряды, происходит увеличение напряжения самого конденсатора. После того как сетевое напряжение в конце первой четверти периода станет максимальным, зарядка прекращается и значение тока в цепи станет равным нулю.
Существует формула для определения тока в цепи конденсатора: I = ∆q/∆t, где q является количеством электричества, протекающим по цепи в течение промежутка времени t. В соответствии с законами электростатики, количество электричества в устройстве составит: q = C x Uc = C x U. В этой формуле С будет емкостью конденсатора, U – напряжением сети, Uc – напряжением на обкладках элемента. В окончательном виде формула тока в цепи будет выглядеть следующим образом: i = C x (∆Uc/∆t) = C x (∆U/∆t).
При наступлении второй четверти периода произойдет уменьшение сетевого напряжения и начнется разрядка конденсатора. Ток в цепи изменит свое направление и будет течь в обратную сторону. В следующей половине периода направление сетевого напряжения изменится, наступит перезарядка элемента, а потом он вновь начнет разряжаться. Ток, присутствующий в цепи с конденсаторной емкостью, будет опережать по фазе напряжение на обкладках на 90 градусов.
Установлено что изменения тока конденсатора происходят со скоростью, находящейся в пропорциональной зависимости с угловой частотой ω. Поэтому в соответствии с уже известной формулой тока в цепи i = C x (∆U/∆t), аналогично получается, что действующее значение тока также будет представлять собой пропорцию между скоростью изменения напряжения и угловой частотой ω: I = 2π x f x C x U.
Поэтому в соответствии с уже известной формулой тока в цепи i = C x (∆U/∆t), аналогично получается, что действующее значение тока также будет представлять собой пропорцию между скоростью изменения напряжения и угловой частотой ω: I = 2π x f x C x U.
Далее уже совсем несложно установить значение емкостного сопротивления или реактивного сопротивления емкости: xc = 1/2π x f x C = 1/ ω x C. Данный параметр вычисляется, когда конденсаторная емкость включается в цепь переменного тока. Поэтому в соответствии с законом Ома в цепи переменного тока с включенным конденсатором, значение силы тока будет следующим: I = U/xc, а напряжение на обкладках составит: Uc = Ic x xc.
Часть сетевого напряжения, приходящаяся на конденсатор, получила название емкостного падения напряжения. Она известна также, как реактивная слагающая напряжения, обозначаемая символом Uc. Величина емкостного сопротивления хс, так же, как и значение индуктивного сопротивления xi напрямую связана с частотой переменного тока.
Емкость и импеданс в цепи переменного тока | Блог Advanced PCB Design
Ключевые выводы
Узнайте об импедансе конденсатора.
Получите более полное представление о важности импеданса конденсатора при анализе цепей переменного тока.
Узнайте, как рассчитать импеданс конденсатора.
Конденсаторы — чрезвычайно распространенные компоненты почти в каждой электронной схеме.
Область электроники содержит различные параметры, которые измеряют, помогают и влияют на функциональность и производительность каждого электронного устройства. Одним из важнейших параметров является импеданс в цепи переменного тока. В процессе проектирования необходимо точно оценивать импеданс, вызванный различными компонентами, чтобы принимать обоснованные проектные решения.
Одним из важнейших параметров является импеданс в цепи переменного тока. В процессе проектирования необходимо точно оценивать импеданс, вызванный различными компонентами, чтобы принимать обоснованные проектные решения.
Кроме того, такие параметры, как емкость и импеданс, должны оставаться в допустимых проектных пределах, иначе даже точные конструкции могут не обеспечить желаемую функциональность. Также бывают случаи, когда требуется преобразование одного параметра в эквивалент другого. Более того, преобразование таких параметров, как емкость, в импеданс необходимо при выполнении подробного анализа цепи переменного тока. Поэтому очень важно, чтобы разработчики понимали взаимосвязь между емкостью и импедансом в цепях переменного тока.
Что такое емкость?
Ниже приведено полезное определение емкости:
Емкость мы связываем, конечно же, с конденсаторами. Мы называем способность системы накапливать электрический заряд «емкостью». |
Теперь, когда мы определили емкость, давайте посмотрим на роль конденсатора в цепи переменного тока.
Функция конденсатора в цепи переменного тока
Конденсаторы представляют собой пассивные электронные компоненты, обеспечивающие накопление энергии в виде электростатического поля. Конденсатор заряжается, когда переменный ток достигает своего пика в цепи переменного тока, и разряжается, когда переменный ток уменьшается. Такое поведение позволяет конденсатору действовать как временное хранилище, в котором ток опережает напряжение на 90 градусов.
Инженеры-электрики используют конденсаторы для улучшения коэффициента мощности в цепи переменного тока. Например, цепь переменного тока, питающая индуктивные нагрузки, такие как двигатель, приводит к запаздывающему току.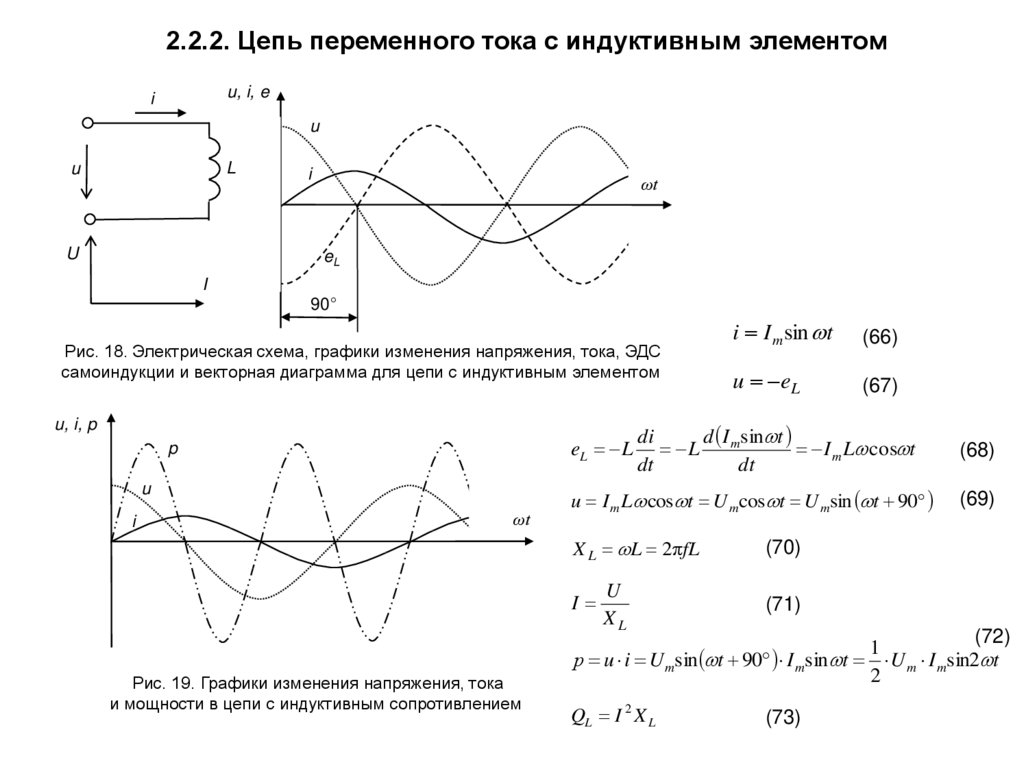 Добавление конденсатора помогает компенсировать отстающий ток и приближает коэффициент мощности к единице. Коррекция коэффициента мощности повышает эффективность использования энергии и снижает счета за электроэнергию.
Добавление конденсатора помогает компенсировать отстающий ток и приближает коэффициент мощности к единице. Коррекция коэффициента мощности повышает эффективность использования энергии и снижает счета за электроэнергию.
Конденсаторы в фильтрах нижних частот
В конструкции печатных плат конденсаторы часто используются в фильтрах нижних или верхних частот. Это связано с тем, что импеданс конденсатора зависит от частоты сигнала переменного тока, проходящего через него. Конденсатор обычно блокирует низкочастотные сигналы, пропуская более высокочастотные сигналы.
Фильтр низких частот RC. Источник
На приведенной выше диаграмме показан RC-фильтр нижних частот. Конденсатор зашунтирован на землю. Таким образом, высокочастотные сигналы направляются на землю. Это предотвращает попадание высокочастотного шума выше частоты среза на нагрузку.
Частота среза RC-фильтра нижних частот определяется следующим уравнением.
Вы можете лучше понять поведение фильтра по его передаточной функции с помощью следующего преобразования Лапласа.
Конденсаторы в фильтрах верхних частот
Конденсатор подключается последовательно с входным сигналом, образуя фильтр верхних частот. Судя по приведенной ниже диаграмме, конденсатор блокирует передачу постоянного тока или низкочастотных сигналов на нагрузку. Допускаются только сигналы выше частоты среза.
Фильтр высоких частот RC. Источник
Частота среза фильтра верхних частот RC следующая:
Передаточная функция RC-фильтра верхних частот определяется следующим уравнением.
Емкость конденсатора
.
Анатомия конденсатора.
Конденсатор состоит из двух проводящих пластин, разделенных изолирующим материалом, называемым диэлектриком. Емкость конденсатора прямо пропорциональна площади поверхности его пластины и обратно пропорциональна расстоянию между пластинами. Емкость также зависит от диэлектрической проницаемости вещества, разделяющего эти пластины.
Емкость конденсатора прямо пропорциональна площади поверхности его пластины и обратно пропорциональна расстоянию между пластинами. Емкость также зависит от диэлектрической проницаемости вещества, разделяющего эти пластины.
Емкость выражается следующим уравнением:
Где C — емкость, q — электрический заряд, а V — дифференциальный потенциал между проводящими пластинами.
Теперь, когда мы лучше понимаем емкость, давайте взглянем на импеданс в цепи переменного тока.
Общие сведения об импедансе в цепи переменного тока
Полное сопротивление — это активное сопротивление электрической цепи или компонента переменному току, возникающее в результате комбинированного воздействия реактивного сопротивления и омического сопротивления. Другими словами, импеданс — это просто расширение принципов сопротивления в цепях переменного тока. Мы также определяем его как любое препятствие или меру противодействия электрического тока потоку энергии при подаче напряжения.
Более техническое определение — это противопоставление электрической цепи потоку переменного тока одной частоты. Таким образом, это комбинация реактивного сопротивления и сопротивления, которую мы измеряем в омах, представляя ее символом Z.
Однако реактивное сопротивление (X) выражает сопротивление компонента переменному току, тогда как полное сопротивление (Z) представляет собой сумму сопротивления реактивное сопротивление. Мы показываем его как комплексное число, используя следующую формулу:
Z = R + jX
Здесь комплексное сопротивление равно Z.
Обозначаем сопротивление как R (реальный аспект).
Мы представляем реактивное сопротивление как X (воображаемый аспект).
Имейте в виду, что реактивное сопротивление может быть как отрицательным, так и положительным, тогда как сопротивление всегда положительное. Кроме того, реактивное сопротивление накапливает энергию в магнитном или электрическом поле, а сопротивление внутри цепи рассеивает энергию в виде тепла.
Теперь, когда мы изучили импеданс в цепи переменного тока, давайте посмотрим, как рассчитать импеданс конденсатора.
Как рассчитать импеданс конденсатора
Конденсатор создает в цепи определенный уровень емкости. Функционально конденсатор обеспечивает временное хранение электрической энергии в виде электрического потенциала, при котором ток конденсатора опережает его напряжение на 90°. Формула импеданса конденсатора выглядит следующим образом:
Z C = -jX CXC — емкостное реактивное сопротивление, характеризующее, какое сопротивление будет иметь конденсатор на определенной частоте.
Приведенное выше уравнение может быть дополнительно расширено следующим образом:
Z C = 1/j ω CЗдесь полное сопротивление конденсатора равно ZC.
Угловая частота равна ω, которую мы рассчитываем как:
ω = 2πf Мы представляем частоту сигнала как f и емкость конденсатора как C.
С точки зрения параметров конденсатора, сопротивление идеального конденсатора равно нулю. Однако реактивное сопротивление и импеданс реального конденсатора отрицательны для всех значений емкости и частоты. Эффективное сопротивление (абсолютное значение) конденсатора зависит и уменьшается с частотой.
Из приведенных выше уравнений видно, что реактивное сопротивление конденсатора обратно пропорционально емкости и частоте. Следовательно, более высокая емкость и более высокая частота приводят к более низкому реактивному сопротивлению. Это позволяет использовать конденсаторы с другими компонентами в конструкциях фильтров нижних или верхних частот и блокирует избирательные частоты.
Хотя емкость в цепи переменного тока легко различима, параметр импеданса в цепи переменного тока требует тщательного анализа цепи. Имея это в виду, получение более глубокого понимания взаимосвязи между емкостью и импедансом имеет первостепенное значение.
Правильное использование конденсаторов и уверенность в том, что их влияние на импеданс в цепи переменного тока предсказуемо и приемлемо, требует хорошего программного обеспечения для проектирования и анализа печатных плат. Если вы хотите узнать больше о том, как у Cadence есть решение для вас, поговорите с нашей командой экспертов или подпишитесь на наш канал YouTube.
Если вы хотите узнать больше о том, как у Cadence есть решение для вас, поговорите с нашей командой экспертов или подпишитесь на наш канал YouTube.
Свяжитесь с нами
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на Linkedin Посетить сайт Больше контента от Cadence PCB Solutions
Загрузка, подождите
Ошибка — что-то пошло не так!
Хотите последние новости о печатных платах?
Подпишитесь на нашу ежемесячную рассылку новостей
Спасибо!
Объяснение урока: Полное сопротивление цепей переменного тока
В этом объяснении мы узнаем, как рассчитать импеданс простых резистивно-емкостно-индуктивных цепей, используя емкостные и индуктивные реактивные сопротивления.
Реактивное сопротивление имеет конкретное, точно определенное значение и определено для цепей, подключенных к источникам переменной разности потенциалов.
Прежде чем рассматривать точное значение реактивного сопротивления, мы можем сначала сказать, что это свойство, которое можно сравнить с сопротивлением, но со значительными отличиями от него.
То, чем реактивное сопротивление похоже на сопротивление, заключается в том, что они оба уменьшают ток в цепи.
Дроссель с индуктивностью 𝐿 реагирует на изменение тока Δ𝐼 в интервале времени Δ𝑡 путем создания противодействующей ЭДС, 𝜀, где 𝜀=−𝐿Δ𝐼Δ𝑡.
Наведенная противодействующая ЭДС уменьшает мгновенный ток через катушку индуктивности. Уменьшенный мгновенный ток создает меньшую противодействующую ЭДС. и поэтому меньший противоток. Противоположный ток со временем уменьшается.
Чтобы показать, как индуктивность связана с реактивным сопротивлением, мы должны рассмотреть цепь, содержащую катушку индуктивности, подключенную к непрерывно меняющемуся источнику.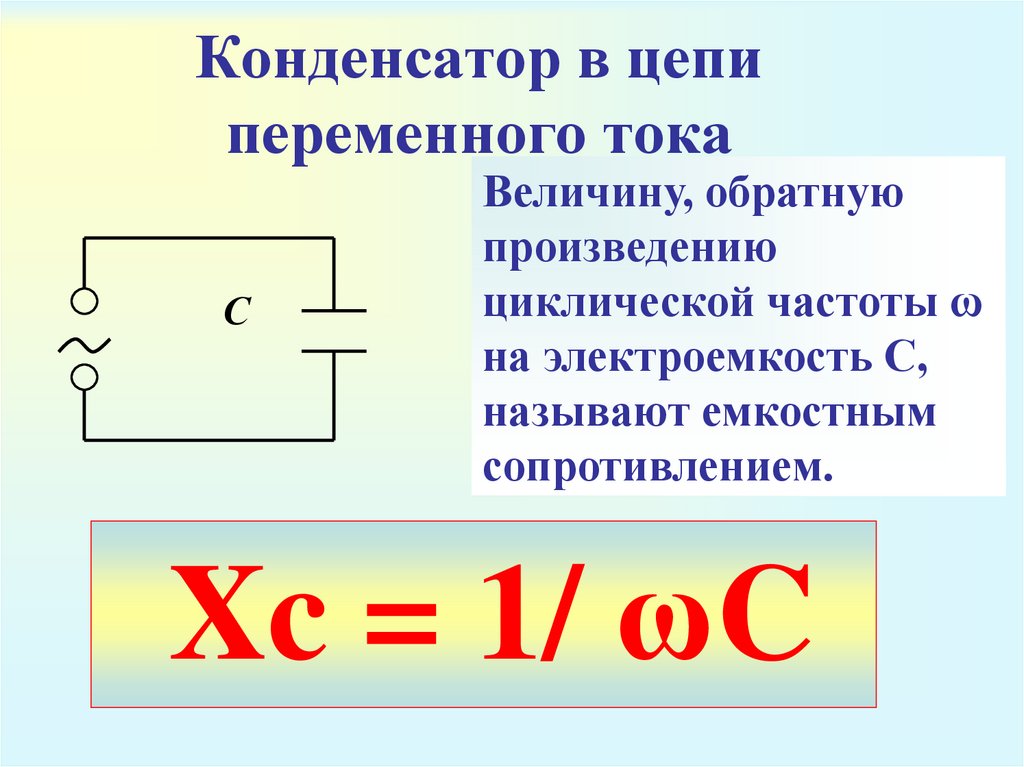 разности потенциалов, например, генератор, который создает переменную ЭДС с некоторой частотой 𝑓.
разности потенциалов, например, генератор, который создает переменную ЭДС с некоторой частотой 𝑓.
Независимо от того, имеет ли такая цепь индуктивность, ток в цепи изменяется синусоидально.
Для такой цепи мы можем определить ее индуктивное сопротивление, 𝑋. Мы можем назвать максимальное значение тока в цепи 𝐼max.
Напомним, что 𝜀=−𝐿Δ𝐼Δ𝑡.
Дело в том, что Δ𝐼Δ𝑡∝𝐼.max
Мы можем видеть эту пропорциональность, продемонстрированную на следующем графике двух синусоидальных токов с одинаковой частотой.
Чем больше индуктивность индуктора, тем медленнее может изменяться ток в индукторе.
Тогда мы видим, что чем больше значение 𝐿, тем меньше значение Δ𝐼Δ𝑡.
Отсюда следует, что для данного значения 𝑓, чем больше значение 𝐿, тем меньше должно быть максимальное значение 𝐼.
Также важно отметить, что частота синусоидального переменного тока должна определять скорость изменения этого тока.
Также должно быть так, что
Δ𝐼Δ𝑡∝𝑓.
На следующем графике показаны три синусоидальных тока.
Мы видим, что максимальное значение тока 𝐼 совпадает с максимальным значением тока 𝐼.
Мы также видим, что частота 𝐼 больше, чем частота 𝐼; следовательно, значение Δ𝐼Δ𝑡 из 𝐼 при 𝑡=0 больше, чем значение Δ𝐼Δ𝑡 из 𝐼 при 𝑡=0.
Ток 𝐼 имеет ту же частоту, что и ток 𝐼, но меньшее максимальное значение.
При 𝑡=0 текущий 𝐼 имеет то же значение Δ𝐼Δ𝑡, что и текущий 𝐼.
Это неравенство максимальных значений 𝐼 и 𝐼 необходимо для того, чтобы 𝐼 имел одинаковое значение Δ𝐼Δ𝑡 как 𝐼 при 𝑡=0, а также иметь ту же частоту, что и 𝐼.
Тогда мы видим, что чем больше значение 𝑓, тем меньше максимальное значение 𝐼.
Рассматривая зависимость 𝜀 от 𝐼max, 𝐿 и 𝑓, видим, что 𝜀∝−𝐿𝐼𝑓.max
Значение 𝑋 определяется как отношение 𝜀 к 𝐼макс.
Из этого мы видим, что 𝜀𝐼∝−𝐿𝑓𝑋∝−𝐿𝑓.max
Реактивное сопротивление не имеет направления, поэтому отрицательный знак не имеет значения, и поэтому можно точно так же сказать, что
𝑋∝𝐿𝑓.
Из этих соотношений можно вывести формулу для индуктивного сопротивления.
Формула: индуктивное реактивное сопротивление
Индуктивное реактивное сопротивление 𝑋 цепи с индуктивностью 𝐿, по которой течет переменный ток с частотой 𝑓 определяется выражением 𝑋=2𝜋𝑓𝐿.
Единицей измерения индуктивного сопротивления является ом. Это показано следующим образом: ГцVsAVAVAAΩAΩ×⋅==×=.
Мы видим, что индуктивное сопротивление имеет те же единицы измерения, что и сопротивление. Индуктивное реактивное сопротивление — это фактически сопротивление, которое применимо только к переменному току. токовые цепи, содержащие катушки индуктивности.
Мы видим, что увеличение индуктивности цепи увеличивает ее индуктивное сопротивление. Мы видим также, что увеличение частоты переменного ток увеличивает индуктивное сопротивление цепи.
Давайте рассмотрим пример с индуктивным реактивным сопротивлением.
Пример 1: Определение индуктивного сопротивления
Источник переменного напряжения с частотой 75 Гц подключен к
дроссель 35 мГн. Чему равно реактивное сопротивление цепи? Дайте ответ с точностью до двух знаков после запятой.
Чему равно реактивное сопротивление цепи? Дайте ответ с точностью до двух знаков после запятой.
Ответ
Индуктивное сопротивление 𝑋 цепи с индуктивностью 𝐿, по которой течет переменный ток с частота 𝑓 определяется выражением 𝑋=2𝜋𝑓𝐿.
Подставляя значения, указанные в вопросе, получаем 𝑋=2𝜋×75×0,035,HzH
С точностью до двух знаков после запятой 𝑋 равно 16,49 Ом.
Наряду с резисторами и катушками индуктивности в цепи могут быть конденсаторы. Конденсаторы также имеют реактивное сопротивление, называемое емкостным реактивным сопротивлением, 𝑋.
Прежде чем определить емкостное реактивное сопротивление, давайте рассмотрим, как действует емкость на уменьшение среднего тока в цепи.
Рассмотрим цепь, содержащую последовательно соединенные резистор и конденсатор.
Конденсатор может накапливать заряд, который накапливается на конденсаторе за счет тока в цепи, в которой находится конденсатор. Максимальный заряд, 𝑄,
который может храниться конденсатором с емкостью 𝐶, подключенным к разности потенциалов 𝑉, определяется выражением
𝑄=𝐶𝑉.
Конденсатор изначально хранит нулевой заряд и, следовательно, имеет нулевую разность потенциалов на нем. Чем больше заряд хранится в конденсаторе, тем больше потенциал разница по нему.
Чем больше заряд хранится в конденсаторе, тем меньше ток в цепи. Когда конденсатор накапливает максимальный заряд, он может храниться, ток в цепи, содержащей конденсатор, должен быть равен нулю.
Связь между разностью потенциалов на конденсаторе и током в цепи, содержащей конденсатор, может быть выражена как Δ𝑄Δ𝑡=𝐼=𝐶Δ𝑉Δ𝑡.
Если конденсатор имеет нулевую емкость, при подключении к цепи он изначально сохраняет свой максимальный заряд, поэтому ток в цепи должен быть равен нулю. Чем больше емкость конденсатора, тем больший заряд может быть перенесен током в цепи до того, как ток станет равным нулю.
Отсюда видно, что когда цепь, содержащая конденсатор, подключается к источнику разности потенциалов в течение определенного интервала времени,
ток в цепи уменьшится меньше, если использовать конденсатор большей емкости.
Из этого мы видим, что конденсатор также может уменьшать ток в цепи подобно тому, как это может делать катушка индуктивности. Однако, чем больше емкость конденсатора, тем меньше уменьшается ток.
Емкостное сопротивление имеет конкретное, точно определенное значение.
Чтобы показать, как емкость связана с емкостным реактивным сопротивлением, мы должны рассмотреть цепь, содержащую последовательно соединенные резистор и конденсатор. к непрерывно изменяющемуся источнику разности потенциалов, такому как генератор, который подает переменную ЭДС на некоторой частоте 𝑓.
Независимо от того, имеет ли такая цепь емкость, ток в цепи изменяется синусоидально.
Для такой цепи мы можем определить ее емкостное сопротивление, 𝑋. Максимальное значение разности потенциалов можно назвать через конденсатор 𝑉макс.
Напомним, что Δ𝑄Δ𝑡=𝐼=𝐶Δ𝑉Δ𝑡.
Дело в том, что Δ𝑉Δ𝑡∝𝑉.max
Также бывает, что Δ𝑉Δ𝑡∝𝑓.
Мы видим, что
𝐼∝𝐶𝑉𝑓. max
max
Значение 𝑋 определяется как отношение 𝑉max к 𝐼.
Из этого мы видим, что 𝐼𝑉∝𝐶𝑓𝑉𝐼∝1𝐶𝑓𝑋∝1𝐶𝑓.maxmax
Формула для емкостного реактивного сопротивления может быть получена из этих соотношений.
Формула: емкостное реактивное сопротивление
Емкостное реактивное сопротивление, 𝑋, цепи с емкостью 𝐶, по которой протекает переменный ток с частота 𝑓 определяется выражением 𝑋=12𝜋𝑓𝐶.
Единицей измерения емкостного сопротивления является ом. Это показано следующим образом: 1×===××××=××=.HzFsFsFsssAΩCsAΩCsΩCΩCVCVCs
Мы видим, что емкостное реактивное сопротивление имеет те же единицы измерения, что и сопротивление. Емкостное реактивное сопротивление — это фактически сопротивление, которое применимо только к переменному току. цепи, содержащие конденсаторы.
Мы видим, что увеличение емкости цепи уменьшает ее емкостное реактивное сопротивление. Мы видим также, что увеличение частоты переменного тока
уменьшает емкостное сопротивление цепи.
Полезно отметить, что отношение емкости и частоты к емкостному реактивному сопротивлению является обратным отношению индуктивности и частоты к индуктивному сопротивлению.
Давайте рассмотрим пример с емкостным реактивным сопротивлением.
Пример 2. Определение емкостного реактивного сопротивления
Источник переменного напряжения с частотой 50 Гц подключен к конденсатор 125 мкФ. Чему равно реактивное сопротивление конденсатора? Дай свой ответ с точностью до ома.
Ответ
Емкостное реактивное сопротивление 𝑋 цепи с емкостью 𝐶, по которой течет переменный ток с частотой 𝑓 определяется выражением 𝑋=12𝜋𝑓𝐶.
Подставляя значения, указанные в вопросе, получаем 𝑋=12𝜋×50×1,25×10,HzF
С точностью до ома, 𝑋 составляет 25 Ом.
Ток в цепи переменного тока в данный момент времени зависит от совместного действия сопротивления и реактивного сопротивления цепи. Это называется импедансом цепи 𝑍.
Это называется импедансом цепи 𝑍.
Цепь, содержащая резистор (R), катушку индуктивности (L) и конденсатор (C), подключенные к источнику переменной разности потенциалов, показана на следующем рисунке.
Резистор обеспечивает сопротивление цепи. Катушка индуктивности и конденсатор обеспечивают реактивное сопротивление цепи.
Для любой цепи переменного тока разность потенциалов 𝑉 в цепи меняется со временем. Мы можем обозначить через 𝑉 разность потенциалов на цепи в момент 𝑡.
Если такая цепь имеет сопротивление 𝑅, но не имеет реактивного сопротивления, то ток в данный момент 𝐼 определяется так, как это было бы в цепи постоянного тока по закону Ома. Мы можем выразить это как 𝐼=𝑉𝑅.
Однако, если цепь переменного тока имеет реактивное сопротивление, реактивное сопротивление цепи влияет на мгновенный ток в цепи. Мгновенный ток в такой цепи определяется выражением 𝐼=𝑉𝑍.
Емкостное и индуктивное сопротивления не просто суммируются, чтобы определить их вклад в импеданс.
Мгновенный ток, проходящий через конденсатор, не совпадает по фазе с мгновенной разностью потенциалов на конденсаторе. Текущие лиды разность потенциалов на фазовый угол 90∘.
Мгновенный ток, проходящий через индуктор, не совпадает по фазе с мгновенной разностью потенциалов на индукторе. ток отстает от потенциала разность на фазовый угол 90∘.
Эти соотношения фаз показаны на следующем рисунке.
Разность фаз между током и разностью потенциалов составляет 90∘ для обоих конденсаторов. и катушки индуктивности, но в противоположных направлениях.
Тогда мы можем видеть, что разность фаз между током и разностью потенциалов для конденсатора по сравнению с катушкой индуктивности составляет 90+90∘∘, что составляет 180∘.
Это означает, что влияние на мгновенный ток конденсатора и катушки индуктивности противоположно друг другу.
Отсюда видно, что если емкостное и индуктивное сопротивления цепи равны, то влияние общего реактивного сопротивления на ток равно нулю. В этом случае полное сопротивление цепи — это просто сопротивление цепи.
В этом случае полное сопротивление цепи — это просто сопротивление цепи.
Из этих соотношений можно получить формулу для импеданса.
Формула: Полное сопротивление
Полное сопротивление цепи 𝑍 определяется выражением 𝑍=𝑅+(𝑋−𝑋), где 𝑅 — сопротивление цепи, 𝑋 — индуктивное сопротивление цепи, 𝑋 — емкостное сопротивление цепи.
Сопротивление и реактивное сопротивление имеют единицу измерения Ом, поэтому единицей импеданса является является ом.
Важно отметить, что цепь может иметь ненулевое сопротивление, несмотря на нулевое сопротивление. Для цепи переменного тока, только реактивное сопротивление цепи может ограничивать значение тока. Это не относится к цепям, питаемым постоянной разностью потенциалов.
Рассмотрим пример с импедансом.
Пример 3: Определение импеданса
Цепь переменного тока содержит резистор сопротивлением 125 Ом, катушку индуктивности.
с индуктивным сопротивлением 450 Ом и конденсатором с сопротивлением 28 Ом. емкостное реактивное сопротивление. Каково сопротивление цепи? Дайте ответ с точностью до ома.
емкостное реактивное сопротивление. Каково сопротивление цепи? Дайте ответ с точностью до ома.
Ответ
Полное сопротивление цепи 𝑍 определяется выражением 𝑍=𝑅+(𝑋−𝑋), где 𝑅 — сопротивление цепи, 𝑋 — индуктивное сопротивление цепи, 𝑋 — емкостное сопротивление цепи.
Подставляя значения, указанные в вопросе, получаем 𝑍=(125)+(450−28).ΩΩΩ
С точностью до ома, 𝑍 составляет 440 Ом.
Давайте рассмотрим еще один такой пример.
Пример 4: Определение сопротивления, необходимого для конкретного полного сопротивления
Цепь переменного тока имеет полное сопротивление 750 Ом. В схеме есть резистор, катушка индуктивности с индуктивным сопротивлением 250 Ом и конденсатором с емкостное сопротивление 45,0 Ом. Каково сопротивление резистора? Дайте ответ с точностью до ома.
Ответ
Полное сопротивление цепи 𝑍 определяется выражением
𝑍=𝑅+(𝑋−𝑋),
где 𝑅 — сопротивление цепи, 𝑋 — индуктивное сопротивление цепи,
𝑋 — емкостное сопротивление цепи.
Подставляя значения, указанные в вопросе, получаем 750=𝑅+(250−45,0).ΩΩΩ
Это уравнение необходимо изменить, чтобы 𝑅 стало предметом, следующим образом: (750)=𝑅+(250−45,0)(750)=𝑅+(205)𝑅=(750)−(205)√𝑅=(750)−(205)𝑅=(750)−(205) .ΩΩΩΩΩΩΩΩΩΩΩ
С точностью до ома, 𝑅 составляет 721 Ом.
Рассмотрим пример, в котором определяются токи.
Пример 5. Определение мгновенных токов в цепи с сопротивлением, емкостью и индуктивностью
Цепь переменного тока содержит резистор с сопротивлением 25 Ом, катушку индуктивности с индуктивное сопротивление 32 Ом и конденсатор с сопротивлением 12,8 Ом. емкостное реактивное сопротивление. Пиковое напряжение, создаваемое источником переменного напряжения, питающим цепь, составляет 120 В.
- Каков пиковый ток в цепи? Дайте ответ с точностью до одного десятичного знака.
- Каково среднеквадратичное значение тока в цепи? Дайте ответ с точностью до одного десятичного знака.

Ответ
Часть 1
Пиковый ток 𝐼max определяется выражением 𝐼=𝑉𝑍.maxmax
Значение пикового напряжения источника переменного тока для схемы равно 120 В, поэтому мы видим, что 𝐼=120 𝑍.maxV
Полное сопротивление 𝑍 цепи определяется выражением 𝑍=𝑅+(𝑋−𝑋), где 𝑅 — сопротивление цепи, 𝑋 — индуктивное сопротивление цепи, 𝑋 — емкостное сопротивление цепи.
Подставляя значения, указанные в вопросе, получаем 𝑍=(25)+(32−12,8).ΩΩΩ
𝑍≈31,522Ω.
У нас есть то, что 𝐼≈12031.522.maxV
Пиковый ток равен 3,8 А с точностью до одного десятичного знака.
Часть 2
𝐼=𝐼√2.RMSmax
Используя полученное значение 𝐼max с точностью до одного десятичного знака, 𝐼RMS составляет 2,7 А.
Давайте теперь обобщим то, что было изучено в этом объяснителе.
Ключевые моменты
- Индуктивное сопротивление 𝑋 цепи с индуктивностью 𝐿, по которой протекает переменный ток
с частотой 𝑓 определяется выражением
𝑋=2𝜋𝑓𝐿.

Единицей индуктивного сопротивления является ом.
Единицей индуктивного сопротивления является ом. - Реактивное емкостное сопротивление, 𝑋, цепи с емкостью 𝐶, по которой протекает переменный ток с частотой 𝑓 определяется выражением 𝑋=12𝜋𝑓𝐶. Единицей емкостного сопротивления является ом.
- Полное сопротивление цепи 𝑍 определяется выражением
𝑍=𝑅+(𝑋−𝑋),
где 𝑅 — сопротивление цепи, 𝑋 — индуктивное сопротивление цепи,
𝑋 — емкостное сопротивление цепи.
Единицей импеданса является ом. - Мгновенный ток 𝐼 в цепи переменного тока определяется выражением 𝐼=𝑉𝑍, где 𝑉 — мгновенная разность потенциалов в цепи.
Объяснение урока: Резонанс в цепях переменного тока
В этом объяснении мы узнаем, как рассчитать резонансную частоту простых резистивно-емкостно-индуктивных цепей.
Цепь, содержащая резистор (R), катушку индуктивности (L) и конденсатор (C), подключенная к источнику переменной разности потенциалов
показано на следующем рисунке.
Переменный источник разности потенциалов изменяет определенную частоту 𝑓.
Полное сопротивление цепи зависит от частоты переменной разности потенциалов. Увеличение частоты переменной разности потенциалов увеличивает индуктивное сопротивление и уменьшает емкостное сопротивление (но не одинаково). Полное сопротивление цепи зависит от абсолютной разницы между индуктивным и емкостным сопротивлением цепи.
Полное сопротивление последовательной цепи переменного тока с индуктивностью и емкостью определяется по формуле.
Формула: Полное сопротивление
Полное сопротивление цепи 𝑍 определяется выражением 𝑍=𝑅+(𝑋−𝑋), где 𝑅 — сопротивление цепи, 𝑋 — индуктивное сопротивление цепи, 𝑋 — емкостное сопротивление цепи.
Резонансная частота цепи — это частота приложенной разности переменных потенциалов, которая создает наибольшую ток в цепи.
Частоты переменной разности потенциалов вблизи резонансной частоты генерируют токи, близкие по величине к резонансной
частотный ток, в то время как частоты дальше от резонансной частоты генерируют токи меньшей величины.
На следующем рисунке показано, как максимальный ток в цепи зависит от частоты.
Из формулы импеданса 𝑍=𝑅+(𝑋−𝑋), мы можем видеть это, когда 𝑋−𝑋=0, должно быть так, что 𝑍=𝑅, что соответствует минимальному импедансу цепи. Ток максимален для этого импеданса.
Значение емкостного сопротивления определяется по формуле.
Формула: емкостное реактивное сопротивление
Емкостное реактивное сопротивление, 𝑋, цепи с емкостью 𝐶, которая несет переменный ток с частотой 𝑓 определяется выражением 𝑋=12𝜋𝑓𝐶.
Значение индуктивного сопротивления находится по формуле.
Формула: индуктивное реактивное сопротивление
Индуктивное реактивное сопротивление 𝑋 цепи с индуктивностью 𝐿, по которой ток с частотой 𝑓 определяется выражением 𝑋=2𝜋𝑓𝐿.
Для минимального импеданса должно быть так, чтобы 2𝜋𝑓𝐿−12𝜋𝑓𝐶=0.
Это уравнение можно преобразовать следующим образом:
2𝜋𝑓𝐿=12𝜋𝑓𝐶2𝜋𝑓=12𝜋𝑓𝐿𝐶(2𝜋𝑓)=1𝐿𝐶2𝜋𝑓=1𝐿𝐶,
где 𝑓 — резонансная частота контура.
Отсюда получаем формулу для резонансной частоты.
Формула: Резонансная частота
Резонансная частота 𝑓 контура с индуктивностью 𝐿 и емкость 𝐶 определяется выражением 2𝜋𝑓=1𝐿𝐶.
Давайте теперь рассмотрим несколько примеров.
Пример 1. Определение резонансной частоты контура
Какова резонансная частота цепи, показанной на схеме? Дайте ответ с точностью до одного десятичного знака.
Ответ
Резонансная частота 𝑓 определяется выражением 2𝜋𝑓=1𝐿𝐶.
Подставляя значения, указанные в вопросе, получаем 2𝜋𝑓=17,5×3,5×10,HF
С точностью до одного десятичного знака 𝑓 равно 3,1 Гц.
Пример 2. Определение пикового тока в цепи, колеблющейся на резонансной частоте
Цепь, состоящая из последовательно соединенных резистора, конденсатора и катушки индуктивности, имеет резонансную частоту
372 Гц. Резистор имеет сопротивление
440 Ом, а конденсатор имеет емкость
112 мФ.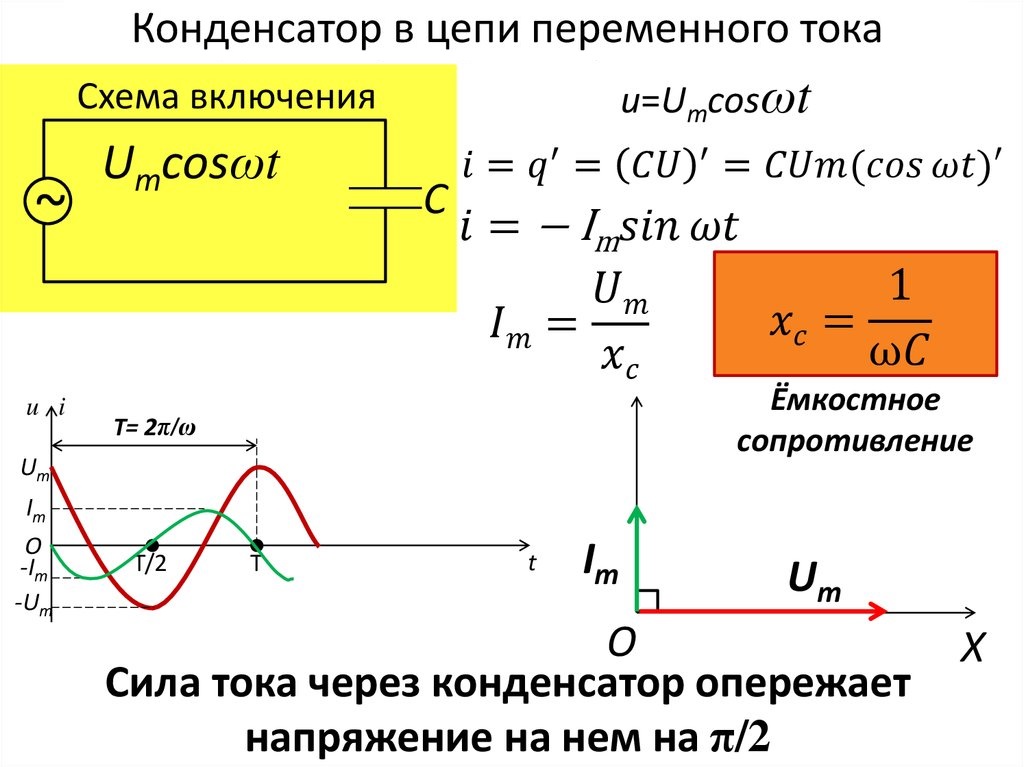 Пиковое напряжение в цепи
составляет 28 В. Каков пиковый ток в цепи при
переменный ток в цепи имеет частоту 372 Гц? Дайте ответ с точностью до двух знаков после запятой.
Пиковое напряжение в цепи
составляет 28 В. Каков пиковый ток в цепи при
переменный ток в цепи имеет частоту 372 Гц? Дайте ответ с точностью до двух знаков после запятой.
Ответ
Резонансная частота контура составляет 372 Гц.
Вопрос требует определения пикового тока.
Максимальная приложенная разность потенциалов составляет 28 В. Для определения пикового тока необходимо определить импеданс цепи.
Полное сопротивление 𝑍 цепи определяется выражением 𝑍=𝑅+(𝑋−𝑋), где 𝑅 — сопротивление цепи, 𝑋 — индуктивное сопротивление цепи, 𝑋 — емкостное сопротивление цепи.
Значения 𝑋 и 𝑋 не указаны. Эти значения мы можем найти по формулам для емкостного и индуктивного сопротивления цепи, 𝑋=12𝜋𝑓𝐶,𝑋=2𝜋𝑓𝐿, и резонансная частота контура, 2𝜋𝑓=1𝐿𝐶.
Однако, поскольку схема колеблется на своей резонансной частоте, должно быть так, что 𝑋−𝑋=0 и, следовательно, что 𝑍=𝑅.
Чтобы найти наибольший ток, нам нужно только разделить наибольшую разность потенциалов на нем на 𝑅:
𝐼=28440. ВОм
ВОм
С точностью до двух знаков после запятой 𝐼 равно 0,06 А.
Пример 3. Определение емкости цепи, колеблющейся на резонансной частоте
Цепь, содержащая последовательно конденсатор и катушку индуктивности, имеет резонансную частоту 575 кГц. Катушка индуктивности в цепи имеет индуктивность 1,25 Гн. Какова емкость конденсатора? Дайте ответ в экспоненциальном представлении с точностью до двух знаков после запятой.
Ответ
Емкость конденсатора связана с резонансной частотой контура, которая определяется выражением 2𝜋𝑓=1𝐿𝐶, где 𝐿 указано как 1,25 H, а 𝑓 указано быть 575 кГц, что составляет 5,75×10 Гц.
Формула должна быть изменена, чтобы 𝐶 стало предметом, следующим образом: (2𝜋𝑓)=1𝐿𝐶𝐶=1(2𝜋𝑓)𝐿.
Подставляя известные значения, получаем 𝐶=1(2𝜋×5,75×10)×1,25.HzH
В экспоненциальном представлении с точностью до двух знаков после запятой 𝐶
Пример 4. Определение индуктивного сопротивления цепи, колеблющейся на резонансной частоте 155 кГц.
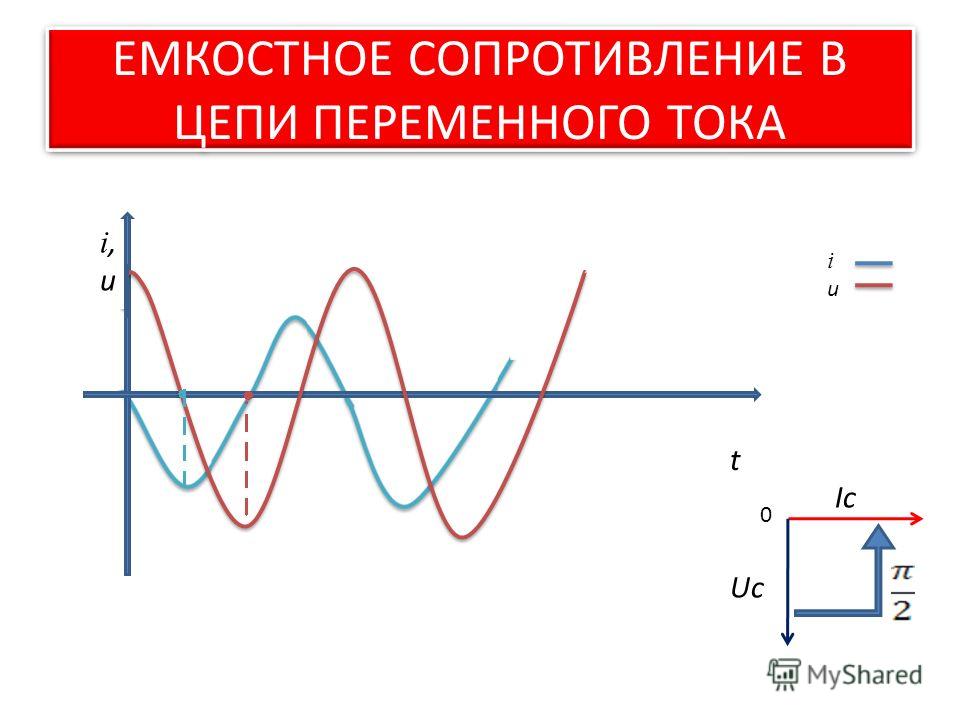 Конденсатор в цепи имеет емкость
215 мкФ. Чему равно индуктивное сопротивление цепи? Дайте ответ в экспоненциальном представлении с точностью до двух знаков после запятой.
Конденсатор в цепи имеет емкость
215 мкФ. Чему равно индуктивное сопротивление цепи? Дайте ответ в экспоненциальном представлении с точностью до двух знаков после запятой.Ответ
Индуктивное сопротивление цепи определяется выражением 𝑋=2𝜋𝑓𝐿, где 𝑓 заявлено как 155 кГц, что составляет 1,55×10 Гц, 𝐿 — индуктивность индуктора.
Значение 𝐿 не указано. Однако его можно найти, используя резонансную частоту контура, который дается 2𝜋𝑓=1𝐿𝐶, где 𝐶 заявлено как 215 мкФ, что составляет 2,15 × 10 F.
Формула резонансной частоты должна быть изменена, чтобы сделать 𝐿 предметом, следующим образом: (2𝜋𝑓)=1𝐿𝐶𝐿=1(2𝜋𝑓)𝐶.
Подставляя известные значения, получаем 𝐿=1(2𝜋×1,55×10)×2,15×10𝐿≈4,9×10.HzFH
Мы можем подставить это значение в 𝑋=2𝜋𝑓𝐿.
В экспоненциальном представлении с точностью до двух знаков после запятой 𝑋 составляет 4,78 × 10 Ом.
Этот вопрос также можно решить, если вспомнить, что на резонансной частоте цепи емкостная и индуктивная
реактивные сопротивления равны, поэтому вместо индуктивного реактивного сопротивления можно было бы рассчитать емкостное реактивное сопротивление.




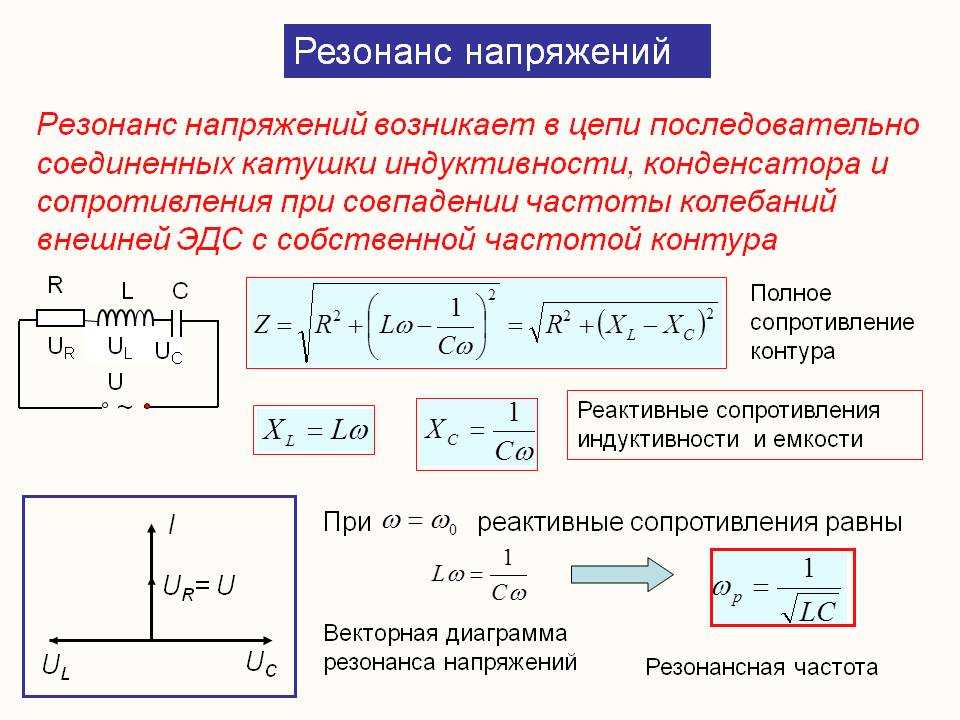 Однако в физике мы называем это отношением изменения электрического заряда в системе к изменению ее электрического потенциала. Фарад — стандартная единица измерения емкости.
Однако в физике мы называем это отношением изменения электрического заряда в системе к изменению ее электрического потенциала. Фарад — стандартная единица измерения емкости.

Единицей индуктивного сопротивления является ом.
Единицей индуктивного сопротивления является ом.