Компоненты вектора — формула, приложения, примеры
Компоненты вектора помогают разделить данный вектор на части по разным направлениям. Иногда возникает необходимость разбить вектор на его компоненты, чтобы облегчить выполнение многочисленных арифметических операций с векторами. Компоненты вектора представляют часть вектора относительно каждой из осей системы координат. Компоненты вектора также могут быть вычислены для вектора в трехмерной геометрической плоскости.
Давайте узнаем больше о компонентах вектора, о том, как найти компоненты вектора и о различных арифметических операциях с компонентами вектора.
| 1. | Каковы компоненты вектора? |
| 2. | Как найти компоненты вектора? |
| 3. | Алгебраические операции с использованием компонентов вектора |
| 4. | Примеры компонентов вектора |
5. | Практические вопросы |
| 6. | Часто задаваемые вопросы о компонентах вектора |
Что такое компоненты вектора?
Компоненты вектора дают разбиение вектора. Вектор разбивается относительно каждой из осей, и мы можем вычислить компоненты вектора. Отдельные компоненты вектора можно позже объединить, чтобы получить представление всего вектора. Векторы обычно представлены в двумерной координатной плоскости с осью x, осью y или трехмерным пространством, содержащим ось x, ось y, ось z соответственно. Векторы — это общие математические представления с направлением и величиной. 92}\)
Кроме того, векторы также представлены в виде \(\overrightarrow A = a\hat i + b \hat j + c \hat k\) в трехмерном пространстве. Здесь \(\hat i\), \(\hat j\), \(\hat k\) — единичные векторы вдоль оси x, оси y и оси z соответственно. Эти единичные векторы помогают идентифицировать компоненты векторов относительно каждой из осей.
Как найти компоненты вектора? 92}\)
Алгебраические операции с использованием компонентов вектора
Различные алгебраические операции над векторами можно легко выполнять, используя различные компоненты вектора. Рассмотрим два вектора \(\overrightarrow A = a_1\hat i + b_1 \hat j + c_1 \hat k\) и \(\overrightarrow B = a_2\hat i + b_2 \hat j + c_2 \hat k\ ).
- Для сложения двух векторов \(\overrightarrow A\) и \(\overrightarrow B\) имеем: \(\overrightarrow A + \overrightarrow B = (a_1 + a_2)\hat i + (b_1 + b_2 )\шляпа j + (c_1 + c_2)\шляпа k\).
- Для вычитания двух векторов \(\overrightarrow A\) и \(\overrightarrow B\) имеем: \(\overrightarrow A — \overrightarrow B = (a_1 — a_2)\hat i + (b_1 — b_2)\ шляпа j + (c_1 — c_2)\шапка k\).
- Два вектора \(\overrightarrow A\) и \(\overrightarrow B\) равны, если: \(a_1 = a_2\), \(b_1 = b_2\), \(c_1 = c_2\).
- Умножение вектора на скаляр λ дает: \(λ\overrightarrow A = λa_1\hat i + λb_1 \hat j + λc_1 \hat k\).
Связанные темы
Следующие темы полезны для лучшего понимания компонентов вектора.
- Векторы
- Единичный вектор
- Векторные формулы
- Векторные количества
- Типы векторов
- Перекрестное произведение двух векторов
Примеры компонентов вектора
Пример 1: Найдите компоненты x и y вектора, имеющего модуль 12 и образующего угол 45 градусов с положительной осью x.
Решение:
Дан вектор V= 12, образующий угол θ = 45º.
Компонент x вектора = \(V_x\) = VCosθ = 12.Cos45º = 12.(1/√2) = 6√2.
Y-компонента вектора = \(V_y\) = VSinθ = 12.Sin45º = 12.(1/√2) = 6√2.
Следовательно, компоненты x и компоненты y вектора равны 6√2.
Пример 2: Найдите вектор из компонентов вектора, имеющего x-компоненту из 5 единиц, y-компоненту из 12 единиц и z-компоненту из 4 единиц соответственно.
Решение:
Компонента X вектора = a = 5
Компонента Y вектора = b = 12
Компонента Z вектора = c = 4
Искомый вектор равен \(\overrightarrow V = a\hat i + b \hat j + c \hat k\)
Отсюда \(\overrightarrow V = 5\hat i + 12 \hat j + 4 \hat k\).
Следовательно, искомый вектор равен \(\overrightarrow V = 5\hat i + 12 \hat j + 4 \hat k\).
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Забронировать бесплатный пробный урок
Практические вопросы по компонентам вектора
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о компонентах вектора
Каковы три компонента вектора?
Тремя компонентами вектора являются компоненты вдоль оси x, оси y и оси z соответственно.
Для вектора \(\overrightarrow A = a\hat i + b \hat j + c \hat k\) a, b, c называются скалярными компонентами вектора A, а a\(\hat i\), b\(\hat j\), c\(\hat k\) называются компонентами вектора.
Являются ли компоненты вектора тоже вектором?
Компоненты вектора также являются векторами. Вектор \(\overrightarrow A = a\hat i + b \hat j + c \hat k\) имеет компоненты a, b, c вдоль осей x, y и z соответственно. Поскольку компоненты вектора имеют величину и аргумент, направленные вдоль соответствующих осей, эти компоненты также являются векторами.
Являются ли компоненты векторов скалярными?
Компоненты вектора не являются скалярами. Компоненты вектора также являются векторами и имеют величину и направление. Компоненты вектора также определяются относительно одной из осей в координатной плоскости или в трехмерном пространстве. 9{-1}\frac{V_y}{V_x}\).
Как определить коллинеарность векторов на основе компонентов вектора?
Коллинеарность двух векторов можно доказать, если один вектор получается умножением другого вектора с постоянным значением.
Также для двух коллинеарных векторов соответствующие компоненты двух векторов пропорциональны. Два вектора \(\overrightarrow A = a_1\hat i + b_1 \hat j + c_1 \hat k\) и \(\overrightarrow B = a_2\hat i + b_2 \hat j + c_2 \hat k\) называются быть коллинеарным, если \(\overrightarrow A\) = λ\(\overrightarrow B\), а также \(\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2 }\) = λ.
Компоненты вектора — для 2D и 3D с формулой и примером
Компоненты вектора в двухмерной системе координат обычно считаются компонентами x и y. Его можно представить как V = (v x , v y
Компоненты определения вектора
Предположим, что вектор V определен в двумерной плоскости. Вектор V разбит на две составляющие, такие как v x и v y
.
Теперь пусть угол θ образован между вектором V и x-компонентой вектора. Вектор V и его x-компонента (v x ) образуют прямоугольный треугольник, если провести прямую, параллельную y-компоненте (v
По тригонометрическим соотношениям мы знаем,
cos θ = смежная сторона/гипотенуза = v х /В
sin θ = Противоположная сторона/Гипотенуза = v y /V
, где V — величина вектора V.
Компоненты векторной формулы
Так как в предыдущем разделе мы получили выражение:
cos θ = v x /V
sin θ = v y /V
Таким образом, формула для нахождения компонентов любого заданного вектора принимает следующий вид:
v x = V cos θ
v y =Vsin θ
Где V — модуль вектора V, который можно найти с помощью теоремы Пифагора;
|В| = √(v x 2 , v y 2 )
Ортогональные векторы
Векторы могут быть легко представлены в трехмерной системе координат.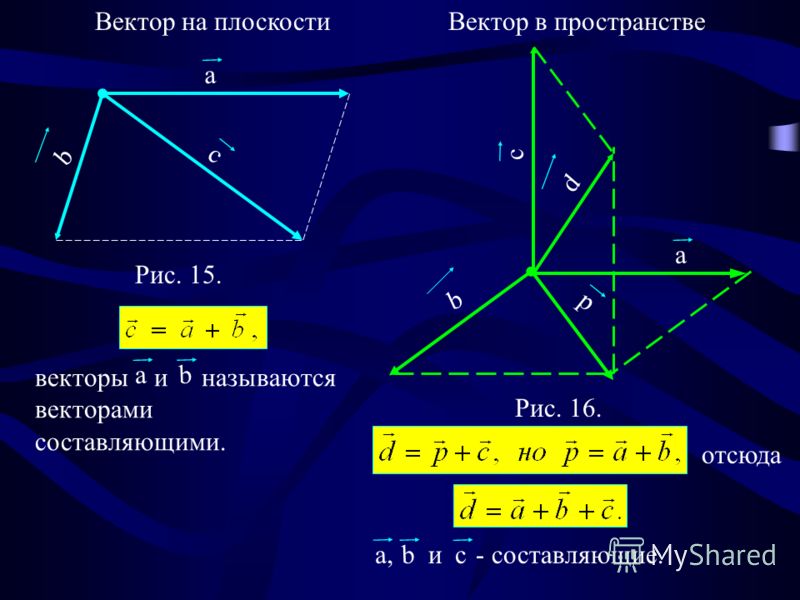
Прежде чем перейти к представлению векторов, давайте разберемся, что такое ортогональное представление.
В терминах координатной геометрии под ортогональным представлением мы понимаем параметры, находящиеся под прямым углом друг к другу. В ортогональной трехмерной системе у нас есть три оси, перпендикулярные друг другу, которые представляют оси x, y и z.
Единичные векторы: это векторы, имеющие величину единичной длины.
\(\begin{array}{l}\hat{x} = \frac{\overrightarrow{x}}{|\overrightarrow{x}|}\end{array} \)
Здесь
\(\begin{array}{l}\hat{x}\end{array} \)
представляет единичный вектор,\(\begin{array}{l}\overrightarrow{x}\ end{array} \)
представляет вектор и представляет величину вектора.В ортонормированных или ортогональных системах мы можем иметь три различных единичных вектора, по одному в каждом направлении. Его можно представить следующим образом:
Точка X(1, 1, 1) может быть представлена с помощью трех взаимно перпендикулярных осей как точки A(1, 0, 0), B(0, 1, 0) и C(0, 0, 1) на и оси соответственно.
Величина вектора
\(\begin{array}{l}\overrightarrow{OA}\end{array} \)
по оси равна 1. Точно так же величина векторов\(\begin{array }{l}\overrightarrow{OB}\end{array} \)
и\(\begin{array}{l} \overrightarrow {OC}\end{array} \)
также равно 1 по y и z оси соответственно. Эти векторы являются единичными векторами вдоль осей x, y и z и представлены\(\begin{array}{l}\hat{i}\end{array} \)
,\(\begin{array}{l} \hat{j}\end{array} \)
и\(\begin{array}{l}\hat{k}\end{array} \)
соответственно.Теперь с помощью единичных векторов мы можем представить любой вектор в трехмерной системе координат.
Компоненты вектора в 3D
Чтобы представить вектор в пространстве, мы разрешаем вектор по трем взаимно перпендикулярным осям, как показано ниже.
Вектор OM можно разложить по трем осям, как показано. Используя OM в качестве диагонали, строится параллелепипед, ребра которого OA, OB и OC лежат вдоль трех перпендикулярных осей.
Из приведенного выше рисунка можно сказать, что
\(\begin{array}{l}\overrightarrow{OA}\end{array} \)
=\(\begin{array}{l} x\hat{i}\end{array} \)
\(\begin{массив}{l}\overrightarrow{OB}\end{массив} \)
\(\begin{массив}{l} y\hat{j}\end{массив} \)
\(\begin{массив}{l}\overrightarrow{OC}\end{массив} \)
=\(\begin{массив}{l} z\hat{k}\end{массив} \)
Вектор может быть представлен как
\(\начало{массив}{l}r\конец{массив} \)
=\(\begin{array}{l}\overrightarrow{OM} = x\hat{i} + y \hat{j} + z \hat{k}\end{array} \)
Это известно как компонентная форма вектора.
Таким образом, вектор r может быть разрешен в направлениях i, j и k соответственно. Это представляет положение заданных векторов с точки зрения трех координатных осей.
Если вектор задан в форме, показанной выше, то величина такого вектора может быть найдена с помощью теоремы Пифагора на данном рисунке как , 92)}\конец{массив} \)
Сумма двух векторов a =
\(\begin{array}{l} a_1 \hat{i} + a_2 \hat{j} + a_3 \hat{k} \end{array} \)
и b =\(\begin{array}{l} b_1 \hat{i} + b_2 \hat{j} + b_3 \hat{k} \end{array} \)
получается путем сложения компонентов трех осей в отдельности.
т.е. a + b =
\(\begin{array}{l} a_1 \hat{i} + a_2\hat{j} + a_3\hat{k} + b_1 \hat{i} + b_2\hat{j } + b_3\шляпа{к} \конец{массив} \)
\(\begin{array}{l}\стрелка вправо a + b\end{массив} \)
=\(\begin{массив}{l}(a_1 + b_1)\шляпа{i} + (a_2 + b_2)\шляпа{j} + (a_3 + b_3)\шляпа{k}\end{массив} \)
Точно так же разница может быть представлена как:
a – b =
\(\begin{array}{l}(a_1 – b_1)\шляпа{i} + (a_2 – b_2)\шляпа{j} + (a_3 – b_3)\шляпа{k}\ конец{массив} \)
.Мы можем выполнять ряд математических операций над векторами, используя эту систему представления. Это и легко, и просто. Чтобы сделать наше понимание более ясным, давайте возьмем пример.
Проблема компонентов вектора
Пример: Два вектора задаются как a =
\(\begin{array}{l}5\hat{i} – 3\hat{j} + 4\hat{k}\end{array} \)
и b =\(\begin{array}{l}2\hat{i} – \hat{j} + \hat{k}\end{array} \)
. Найдите единичные векторы, а также сумму и разность обоих векторов.
