Сопротивление — Википедия

Материал из Википедии — свободной энциклопедии

Сопротивле́ние — многозначный термин. Общее значение — противодействие, воспрепятствование чему-либо.

• В электротехнике и электродинамике:
  • Сопротивление — простейшая модель резистора, в которой реальный резистор характеризуется только электрическим сопротивлением, а также некорректное название резистора (ранее применявшееся в русском языке как наименование электронного компонента).
  • Электрическое сопротивление — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока.
  • Волновое сопротивление линии передачи (волновое сопротивление) — величина, определяемая отношением электрического напряжения бегущей волны в линии передачи к силе тока этой волны (ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения).
  • Характеристическое сопротивление волны (характеристическое сопротивление) — величина, определяемая отношением поперечной составляющей напряженности электрического поля к поперечной составляющей напряженности магнитного поля бегущей волны.
• Термическое сопротивление — способность тела препятствовать распространению теплового движения молекул.
• Лобовое сопротивление — сила, препятствующая движению тел в жидкостях и газах.

• Движение сопротивления — организованные усилия части гражданского населения страны, направленные на сопротивление легитимной или оккупационной власти.
• Сопротивление (организация) — российская межрегиональная правозащитная общественная организация.
• Рутинное сопротивление — неявное противостояние действующей власти в форме мелкого саботажа, распространения критики власти и иных действий, не приводящих непосредственно к её свержению.

• Сопротивление — психический механизм, препятствующий психоаналитическому проникновению в бессознательное и мешающий возвращению вытесненного.
• Сопротивление — вымышленная организация вселенной Звёздных войн.

Основы радиотехники — электрическое сопротивление. Simpleinfo – все сложное простыми словами!

26 Декабря 2016

1926

И так, мы теперь знаем, как протекает электрический ток. Рассмотрели что такое сила и напряжение тока.
Еще раз  повторим:
Сила тока. Условное обозначение: I. Измеряется в амперах (А).

Напряжение тока. Условное обозначение: U. Измеряется в вольтах (В).

Давайте рассмотрим пример, замкнутой цепи:

наведите или кликните мышкой, для анимации

Если вы заметили, на этот раз мы добавили в цепь «нагрузку». Нагрузкой может быть любое устройство или элемент (например: лампочка, электродвигатель и т.д.). В этой замкнутой цепи, мы наблюдаем электрический ток, то есть движение заряженных частиц.

А так же есть, какие-то количественные показатели силы тока и напряжения.

При движение через проводник, заряженные частицы встречают сопротивление. Отсюда мы получаем новую для нас величину – сопротивление проводника или электрическое сопротивление.

Исходя из этого, сопротивление проводника – это физическая величина, которая характеризует свойство проводника препятствовать проводить электрический ток. Более простыми словами это величина, которая мешает проводить электрический ток.

Условное обозначение сопротивления: R.
Единица измерения сопротивления – это Ом.

Сопротивление проводника зависит от его материала, длины и площади поперечного сечения. Так же на сопротивление материала может повлиять окружающая среда (температура, свет и т.д.)

Давайте рассмотрим как взаимосвязаны сила тока, напряжение и сопротивление в замкнутой цепи. Мы видим как протекает ток по проводнику через нагрузку, цепь замкнутая. Сопротивление проводника на всем участке одинаковая, а сопротивление нагрузки отличается, оно выше чем у проводника. То есть движению заряженных частиц, в нагрузке препятствии больше, чем в проводнике.

Обратим внимание на движению частиц через проводник и нагрузку:

наведите или кликните мышкой, для анимации

Можно отметить, что движущихся частиц, через поперечное сечение нагрузки (за определенное время), проходит меньше, чем через проводник. Другими словами, чем больше сопротивление тем меньше сила тока. Что такое сила тока, мы рассмотрели в предыдущей статье.

Обратную картинку можно наблюдать с напряжением, сила с которой происходит движение частиц больше на участке нагрузки, чем в проводнике. Из этого мы получаем, что чем больше сопротивление, тем больше напряжение на участке этой нагрузке:

наведите или кликните мышкой, для анимации

Зависимость тока и напряжения от сопротивления нагрузки в последующих статьях будут рассмотрены подробнее.

Внутреннее сопротивление — Википедия

Двухполюсник и его эквивалентная схема

Вну́треннее сопротивле́ние двухполюсника — импеданс в эквивалентной схеме двухполюсника, состоящей из последовательно включённых генератора напряжения и импеданса (см. рисунок). Понятие применяется в теории цепей при замене реального источника идеальными элементами, то есть при переходе к эквивалентной схеме.

Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:

Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартёр потребляет ток порядка 250 А), а от батареи элементов стартёр вообще не станет вращаться, так как напряжение батареи при подключении к зажимам стартёра упадёт до долей вольта. Дело не в относительно небольшой электрической ёмкости батареек: запасённой в ней энергии и заряде в один ампер-час хватило бы для того, чтобы вращать стартёр в течение 14 секунд (при токе 250 А).

В соответствии с законом Ома в источниках с одинаковым напряжением ток в одинаковой нагрузке также должен быть одинаковым. В приведённом примере это не выполняется потому, что утверждение верно только для идеальных источников ЭДС; реальные же источники в той или иной степени отличаются от идеальных. Для описания степени отличия реальных источников от идеальных применяется понятие внутреннее сопротивление.

Эквивалентная схема активного двухполюсника[править | править код]

Реальные активные двухполюсники хорошо описываются математически, если их рассматривать как эквивалентную схему, состоящую из (см. рисунок) последовательно включённых генератора напряжения и сопротивления (в общем случае — импеданса). Генератор напряжения представляет собственно источник энергии, находящийся в этом двухполюснике. Идеальный генератор мог бы отдать в нагрузку сколь угодно большие мощность и ток. Однако сопротивление, включённое последовательно с генератором, ограничивает мощность, которую данный двухполюсник может отдать в нагрузку. Это эквивалентное сопротивление и называется

внутренним сопротивлением. Оно является лишь параметром абстрактной модели двухполюсника, то есть физического «резистора» как электронного компонента внутри двухполюсников обычно нет.

Формально, в реальных гальванических элементах это внутреннее сопротивление можно идентифицировать физически. Это суммарное сопротивление плюсового стержня (углерода, стали), самого корпуса (цинка и никеля), а также самого электролита (соли) и поглотителя водорода (в солевых элементах). Все эти материалы, как и поверхности раздела между ними, имеют конечное сопротивление, отличное от нуля.

В иных источниках это омическое сопротивление обусловлено сопротивлением обмоток и контактов, которое включено последовательно с собственно внутренним сопротивлением источника и снижают характеристики источников напряжения.

Контактные разности потенциалов имеют иную природу возникновения напряжения и являются неомическими, то есть здесь затраты энергии идут на работу выхода носителей заряда.

Сопротивление и внутреннее сопротивление[править | править код]

Основной характеристикой абстрактного двухполюсника является его внутреннее сопротивление (или, иначе, импеданс^[1]

). Однако, описать двухполюсник одним только сопротивлением не всегда возможно. Дело в том, что термин сопротивление примени́м только для чисто пассивных элементов, то есть, не содержащих в себе источников энергии. Если двухполюсник содержит источник энергии, то понятие «сопротивление» к нему просто не применимо, поскольку закон Ома в формулировке U=I·r не выполняется^[2].

Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников^[3], то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».

Если в какой-либо системе можно выделить вход и/или выход (пара электрических контактов), то часто употребляют следующие термины:

• Входное сопротивление, часто входной импеданс, — внутреннее сопротивление, проявляемое этой парой контактов как двухполюсника, которым является вход системы ^[4]
• Выходное сопротивление, часто выходной импеданс, — внутреннее сопротивление, проявляемое этой парой контактов как двухполюсника, которым является выход системы.

Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление, то есть резистор в нём присутствует обязательно), внутреннее сопротивление не обязательно сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности же, внутреннее сопротивление является внешним проявлением совокупности физических эффектов:

• Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление носит чисто активный характер (в низкочастотных цепях), и оно обусловлено физическими эффектами, которые не позволяют мощности, отдаваемой этим источником в нагрузку, превысить определённый предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в химическом источнике мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
• В случае двухполюсника, содержащего внутри электрическую схему, внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).

Отсюда также следуют некоторые особенности внутреннего сопротивления:

• Внутреннее сопротивление невозможно убрать из двухполюсника^[5]
• Внутреннее сопротивление не является стабильной величиной: оно может изменяться при изменении каких-либо внешних (нагрузка, ток) и внутренних (нагрев, истощение реагентов) условий.

Влияние внутреннего сопротивления на свойства двухполюсника[править | править код]

Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.

Если к источнику с ЭДС^[6] генератора напряжения E и активным внутренним сопротивлением r подключена нагрузка с сопротивлением R, то ток, напряжение и мощность в нагрузке выражаются следующим образом:

I=Er+R,UR=Er+RR,PR=E2(r+R)2R.{\displaystyle I={\frac {E}{r+R}},\quad U_{R}={\frac {E}{r+R}}{R},\quad P_{R}={\frac {E^{2}}{(r+R)^{2}}}{R}.}

Нахождение внутреннего сопротивления[править | править код]

Расчёт[править | править код]

Понятие расчёт применимо к схеме (но не к реальному устройству). Расчёт приведён для случая чисто активного внутреннего сопротивления (отличия реактивного сопротивления будут рассмотрены далее).

Примечание: Строго говоря, любой реальный импеданс (в том числе и внутреннее сопротивление) обладает некоторой реактивной составляющей, поскольку любой проводник имеет паразитную индуктивность и ёмкость. Когда мы говорим о чисто активном сопротивлении, то имеем в виду не реальную систему, а её эквивалентную схему, содержащую только резисторы: реактивность была отброшена как несущественная при переходе от реального устройства к его эквивалентной схеме. Если же реактивность существенна при рассмотрении реального устройства (например, при рассмотрении системы на высоких частотах), то эквивалентная схема составляется с учётом этой реактивности. Более подробно смотри в статье «Эквивалентная схема».

Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:

• ЭДС генератора напряжения U
• Внутреннее сопротивление r

В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов U_out = φ₂ − φ₁) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:

Uout1=U−rI1Uout2=U−rI2{\displaystyle {\begin{matrix}U_{out1}=U-rI_{1}\\U_{out2}=U-rI_{2}\end{matrix}}}

(Напряжения)

где U_out1 — выходное напряжение при токе I₁, U_out2 — выходное напряжение при токе I₂. Решая систему уравнений, находим искомые неизвестные:

r=Uout1−Uout2I2−I1,U=Uout1+I1Uout1−Uout2I2−I1=Uout1+I1r{\displaystyle r={\frac {U_{out1}-U_{out2}}{I_{2}-I_{1}}},\quad U=U_{out1}+I_{1}{\frac {U_{out1}-U_{out2}}{I_{2}-I_{1}}}=U_{out1}+I_{1}r}

(ОбщийСлучай)

Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система (Напряжения) записывается следующим образом:

Uoc=U−00=U−rIsc{\displaystyle {\begin{matrix}U_{oc}=U-0\\0=U-rI_{sc}\end{matrix}}}

где U_oc — выходное напряжение в режиме холостого хода (англ. open circuit), то есть при нулевом токе нагрузки; I_sc — ток нагрузки в режиме короткого замыкания (англ. short circuit), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:

r=UocIsc,U=Uoc{\displaystyle r={\frac {U_{oc}}{I_{sc}}},\quad U=U_{oc}}

(ВнутрСопр)

Таким образом, чтобы рассчитать внутреннее сопротивление и ЭДС эквивалентного генератора для двухполюсника, электрическая схема которого известна, необходимо:

• Рассчитать выходное напряжение двухполюсника в режиме холостого хода
• Рассчитать выходной ток двухполюсника в режиме короткого замыкания
• На основании полученных значений найти r и U по формуле (ВнутрСопр).

Измерение[править | править код]

Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение, которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.

Иногда применяется следующий простой способ измерения, не требующий вычислений:

• Измеряется напряжение холостого хода
• В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.

После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.

Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.

Реактивное внутреннее сопротивление[править | править код]

Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности, то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды, то есть расчет производится методом комплексных амплитуд.

Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией, а не скалярным значением:

• Можно искать различные параметры комплексного значения: модуль, аргумент, только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
• Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путём измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.

Измерение сопротивления петли фаза-нуль[править | править код]

Результат измерения сопротивления петли фаза-нуль в розетке бытовой электросети

Частным случаем измерения внутреннего сопротивления является измерение сопротивления петли фаза-нуль в электроустановках. Двухполюсником в этом случае является пара проводников электроустановки: фазный и рабочий нулевой проводники или два фазных проводника. На фотографии показан результат такого измерения в розетке бытовой электросети напряжением 220 вольт:

• активная составляющая: 0,49 Ом
• реактивная составляющая: 0,09 Ом
• модуль полного сопротивления: 0,5 Ом
• ожидаемый ток короткого замыкания: 440 А

Прибор находит внутреннее сопротивление путём косвенного измерения методом падения напряжения на нагрузочном сопротивлении. Этот метод рекомендуется к использованию в приложении D ГОСТ Р 50571.16-99. Метод описывается приведённой выше формулой (ОбщийСлучай) при I₁=0.

Результат измерения считается удовлетворительным, если ожидаемый ток короткого замыкания достаточно велик для надежного срабатывания аппарата, защищающего эту цепь от сверхтока.

В большинстве случаев следует говорить не о применении внутреннего сопротивления, а об учете его негативного влияния, поскольку внутреннее сопротивление является скорее негативным эффектом. Тем не менее, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто необходимым.

Упрощение эквивалентных схем[править | править код]

Представление двухполюсника как совокупность генератора напряжения и внутреннего сопротивления является наиболее простой и часто используемой эквивалентной схемой двухполюсника.

Согласование источника и нагрузки[править | править код]

Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника). Наиболее часто используются следующие типы согласования:

• Согласование по напряжению — получение в нагрузке максимального напряжения. Для этого сопротивление нагрузки должно быть как можно бо́льшим, по крайней мере, много больше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме холостого хода. При этом максимально достижимое в нагрузке напряжение равно ЭДС генератора напряжения E. Данный тип согласования применяется в электронных системах, когда носителем сигнала является напряжение, и его необходимо передать от источника к нагрузке с минимальными потерями.
• Согласование по току — получение в нагрузке максимального тока. Для этого сопротивление нагрузки должно быть как можно меньшим, по крайней мере, много меньше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме короткого замыкания. При этом максимально достижимый в нагрузке ток равен I_max=E/r. Применяется в электронных системах, когда носителем сигнала является ток. Например, при съеме сигнала с быстродействующего фотодиода целесообразно применять преобразователь ток-напряжение с минимальным входным сопротивлением. Малое входное сопротивление также решает проблему заужения полосы из-за паразитного RC-фильтра.
• Согласование по мощности — обеспечивает получение в нагрузке (что эквивалентно отбору от источника) максимально возможной мощности, равной P_max=E²/(4r)^[7]. В цепях постоянного тока: сопротивление нагрузки должно быть равно внутреннему сопротивлению r источника. В цепях переменного тока (в общем случае): импеданс нагрузки должен быть комплексно сопряженным внутреннему импедансу источника.
• Согласование по волновому сопротивлению — получение максимального коэффициента бегущей волны в линии передачи (в СВЧ технике и теории длинных линий). То же самое, что и согласование по мощности, но применительно к длинным линиям. Волновое сопротивление нагрузки должно быть равно внутреннему сопротивлению r. В СВЧ технике применяется практически всегда. Чаще всего термин согласованная нагрузка используется именно в этом смысле.

Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.

Понижение высоких напряжений[править | править код]

Иногда к источнику электропитания искусственно добавляют внешнее балластное сопротивление, соединённое последовательно с нагрузкой (оно суммируется с внутренним сопротивлением источника) для того, чтобы понизить получаемое от него напряжение, либо ограничить величину тока, отдаваемого в нагрузку. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор) во многих случаях неприемлемо, так как ведёт к бесполезному выделению значительной мощности на нём^[8]. Чтобы не расходовать энергию впустую и не решать проблему охлаждения дополнительного сопротивления, в системах переменного тока используют реактивные гасящие импедансы. На основе гасящего конденсатора может быть построен конденсаторный блок питания. Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств. Индуктивный балласт широко применяется для ограничения тока в цепи газоразрядных люминесцентных ламп.

Минимизация шума[править | править код]

При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители, которые могут быть как низкоомные, например, на биполярных транзисторах, так и высокоомными на полевых транзисторах, однако спроектированы они таким образом, что наименьший коэффициент шума достигается лишь при полном согласовании выходного сопротивления источника сигнала и входного сопротивления самого усилителя. Например, если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор, который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.

Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения, что и для применимости эквивалентных схем.

Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r. Тривиальные случаи двухполюсников без источников оговорены особо.

Малое внутреннее сопротивление[править | править код]

• Нулевым внутренним сопротивлением обладает только идеальный генератор напряжения. Если также рассматривать двухполюсники без источников, то сверхпроводящее короткое соединение тоже имеет нулевое внутреннее сопротивление (до величины токов, вызывающих потерю сверхпроводимости). Генератор со сверхпроводящей обмоткой при не слишком больших частотах и небольших токах также имеет активное внутреннее сопротивление, весьма близкое к нулю (индуктивный импеданс при определенных условиях может быть тоже довольно невелик).
• Автомобильная свинцово-кислотная стартёрная аккумуляторная батарея имеет r около 0,01 Ом. Благодаря столь низкому внутреннему сопротивлению ток, отдаваемый батареей при запуске двигателя, достигает 250 ампер и более (для легковых автомобилей).
• Бытовая сеть электроснабжения переменного тока в жилых помещениях имеет r от десятых долей Ом до 1 Ом и более (зависит от качества электропроводки). Высокое сопротивление соответствует плохой проводке: при подключении мощных нагрузок (например, утюга) напряжение падает, при этом заметно уменьшается яркость ламп освещения, подключенных к той же ветви сети. Повышается пожароопасность, поскольку на сопротивлении проводов выделяется значительная мощность. И наоборот, в хорошей сети с низким сопротивлением напряжение падает от допустимых нагрузок лишь незначительно. Ток при коротком замыкании в хорошей бытовой электросети достигает нескольких сотен ампер.
• Используя отрицательную обратную связь в электронных схемах, можно искусственно создавать источники, обладающие (при определённых условиях) очень низким внутренним сопротивлением. Такими свойствами обладают современные электронные стабилизаторы напряжения. Например, интегральный стабилизатор напряжения 7805 (выходное напряжение 5 В) имеет типичное выходное сопротивление менее 0,0009 Ома^[9]. Однако это вовсе не означает, что такой стабилизатор может отдать в нагрузку ток до 5500 А или мощность до 13 кВт при правильном согласовании. Характеристики стабилизатора нормированы только для рабочего диапазона токов, то есть в данном примере до 1,5 А. При превышении этого значения сработает защита, и стабилизатор отключится (при других конструкциях защиты ток ограничивается, а не отключается полностью).

Большое внутреннее сопротивление[править | править код]

Обычно двухполюсники с большим внутренним сопротивлением — это различного рода датчики, источники сигналов и т. п. Типичная задача при работе с такими устройствами — снятие с них сигнала без потерь из-за неправильного согласования. Для достижения хорошего согласования по напряжению сигнал с такого двухполюсника должен сниматься устройством, имеющим ещё большее входное сопротивление (как правило, сигнал с высокоомного источника снимается при помощи буферного усилителя).

• Бесконечным внутренним сопротивлением обладает только идеальный источник тока. Если также рассматривать двухполюсники без источников, то простой разрыв цепи (два вывода, ничем не соединённые) тоже имеет бесконечное внутреннее сопротивление.
• Конденсаторные микрофоны, пьезоэлектрические и пироэлектрические датчики, а также все остальные «конденсаторо-подобные» устройства имеют реактивное внутреннее сопротивление, модуль которого может достигать^[10] десятков и сотен мегаом. Поэтому такие источники требуют обязательного использования буферного усилителя для достижения согласования по напряжению. Конденсаторные микрофоны, как правило, уже содержат встроенный буферный усилитель, собранный на полевом транзисторе.
• Для измерения электрических потенциалов внутри живых клеток применяются электроды, представляющие собой стеклянный капилляр, заполненный проводящей жидкостью. Толщина такого проводника может быть порядка сотен ангстрем. Вследствие чрезвычайно малой толщины проводника такой «двухполюсник» (клетка с присоединёнными электродами) имеет внутреннее сопротивление порядка 100 мегаом. Высокое сопротивление и малое напряжение делают измерение напряжений внутри клетки непростой задачей.

Отрицательное внутреннее сопротивление[править | править код]

Существуют двухполюсники, внутреннее сопротивление которых имеет отрицательное значение. В обычном активном сопротивлении происходит диссипация энергии, в реактивном сопротивлении энергия запасается, а затем выделяется обратно в источник. Особенность отрицательного сопротивления в том, что оно само является источником энергии. Поэтому отрицательное сопротивление в чистом виде не встречается, оно может быть только имитировано электронной схемой, которая обязательно содержит источник энергии. Отрицательное внутреннее сопротивление может быть получено в схемах путём использования:

Системы с отрицательным сопротивлением потенциально неустойчивы и поэтому могут быть использованы для построения автогенераторов.

Входной импеданс антенны

• Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей. — М. — Л.: Энергия, 1965. — 892 с.
• Джонс М. Х. Электроника — практический курс. — М.: Техносфера, 2006. — 512 с. ISBN 5-94836-086-5
• Tildon H. Glisson. Introduction to Circuit Analysis and Design. — Springer, 2011. — P. 768. — ISBN 9789048194421.

1. ↑ Импеданс является обобщением понятия сопротивление для случая реактивных элементов. Более подробно смотри в статье Электрический импеданс
2. ↑ Применять закон Ома в такой формулировке к двухполюсникам с внутренними источниками некорректно, необходимо учитывать источники: U=Ir+ΣU_int, где ΣU_int — алгебраическая сумма ЭДС внутренних источников.
3. ↑ Отсутствие источников выражается в том, что напряжение на выводах двухполюсника при отсутствии нагрузки равно нулю. Сюда же относится случай, когда источники есть, но не влияют на выходное напряжение («никуда не подключены»).
4. ↑ Реза Ф., Сили С.Современный анализ электрических цепей Энергия, M.-Л., 1964 г., 480 с. с черт.
5. ↑ Исключение составляют случаи применения стабилизаторов компенсационного типа. Например, двухполюсник, содержащий батарею и ОУ, на некотором участке ВАХ может иметь как сколь угодно малое, так и отрицательное выходное сопротивление — до тех пор, пока избытка энергии в батарее хватает для компенсации.
6. ↑ То же самое, что и напряжение
7. ↑ 7.6. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ В ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА (неопр.). Дата обращения 6 апреля 2014.
8. ↑ Тем не менее, гасящие резисторы широко применяются для ограничения пускового тока тяговых электродвигателей постоянного тока на электротранспорте.
9. ↑ Изменение выходного напряжения не более 1,3 мВ в диапазоне выходных токов 0,005÷1,5 А. В более узком диапазоне токов 0,25÷0,75 А типичное выходное сопротивление ещё меньше — 0,0003 ома.
10. ↑ В рабочем диапазоне частот

Волновое сопротивление — Википедия

Материал из Википедии — свободной энциклопедии

Волновое сопротивление — характеристика среды распространения волны.

Волновое сопротивление в газе и жидкости — отношение звукового давления в бегущей плоской звуковой волне к колебательной скорости частиц среды. Также волновое сопротивление равно произведению плотности среды на скорость звука в ней.

Волновое сопротивление в твёрдых телах для продольных волн — отношение механического напряжения, взятого с обратным знаком, к колебательной скорости частиц среды.

См. также удельное акустическое сопротивление.

Волновое сопротивление в гидромеханике — часть гидро- и аэродинамического сопротивления, характеризующая затраты энергии на образование волн, например:

• волн, образующихся на поверхности воды при движении корабля;
• ударных волн, возникающих при сверхзвуковом полете самолёта;
• и т. д.

В электродинамике волновое сопротивление линии передачи (коротко — волновое сопротивление) — величина, определяемая отношением напряжения падающей волны к току этой волны в линии передачи (по закону Ома)^[1].

При определении волнового сопротивления может использоваться также напряжение и ток отражённой или бегущей волн.

Единица измерения — Ом.

При расчёте волнового сопротивления по методу комплексных амплитуд используют амплитуды напряжения и силы тока. При наличии потерь в линии передачи значение становится комплексным.

Волновое сопротивление линии передачи зависит от её конструкции и электрофизических параметров применяемых материалов (ε, μ, σ), что совместно определяет погонные параметры линии передачи (ёмкость, индуктивность, сопротивление и проводимость на единицу длины), а также от типа волны, при наличии дисперсии — от частоты электромагнитных колебаний.

Волновое сопротивление часто путают с характеристическим сопротивлением волны — величиной, определяемой отношением поперечной составляющей напряженности электрического поля к поперечной составляющей напряженности магнитного поля бегущей волны^[1].

В длинной линии волновое сопротивление равно (по закону Ома):

Z0=UmIm,{\displaystyle Z_{0}={U_{m} \over I_{m}},}

где:

В бесконечно длинных линиях нагрузка имеет чисто активный характер, поэтому энергия, запасаемая в индуктивности и ёмкости, одинаковая.

L1XIm22=C1XUm22,{\displaystyle {L_{1}XI_{m}^{2} \over 2}={C_{1}XU_{m}^{2} \over 2},}

где:

Поэтому волновое сопротивление в бесконечно длинных линиях определяется погонными индуктивностью и ёмкостью:

L1C1=UmIm=Z0.{\displaystyle {\sqrt {L_{1} \over C_{1}}}={U_{m} \over I_{m}}=Z_{0}.}

Волновое сопротивление среды — отношение амплитуд электрического и магнитного полей электромагнитных волн, распространяющихся в среде:

Z=E0−(x)H0−(x).{\displaystyle Z={E_{0}^{-}(x) \over H_{0}^{-}(x)}.}

Если волновые сопротивления двух сред, имеющих границу раздела, одинаковы, то на этой границе не происходит отражения электромагнитных волн, даже если диэлектрическая и магнитная проницаемости в средах различны.

При распространении электромагнитной волны в среде с диэлектрической ε{\displaystyle \varepsilon } и магнитной μ{\displaystyle \mu } проницаемостями амплитудные и мгновенные значения напряжённости электрического E{\displaystyle E} и магнитного H{\displaystyle H} полей связаны соотношением: ε0εE=μ0μH{\displaystyle {\sqrt {\varepsilon _{0}\varepsilon }}E={\sqrt {\mu _{0}\mu }}H}. Это выражение можно представить в виде: EH=μ0με0ε{\displaystyle {\frac {E}{H}}={\sqrt {\frac {\mu _{0}\mu }{\varepsilon _{0}\varepsilon }}}}. Отношение EH{\displaystyle {\frac {E}{H}}} принято называть волновым сопротивлением среды, поскольку существует формальная аналогия между уравнением EH=μ0με0ε{\displaystyle {\frac {E}{H}}={\sqrt {\frac {\mu _{0}\mu }{\varepsilon _{0}\varepsilon }}}} и законом Ома^[2]. Для вакуума μ=ε=1{\displaystyle \mu =\varepsilon =1}, поэтому его волновое сопротивление ρv=μ0ε0=376,73{\displaystyle \rho _{v}={\sqrt {\frac {\mu _{0}}{\varepsilon _{0}}}}=376,73} Ом.

1. ↑ ^{1 2} ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения.
2. ↑ Сена Л.А. Единицы физических величин и их размерности. — М., Наука, 1977. — С. 226-227

Удельное сопротивление. Реостаты — урок. Физика, 8 класс.

Соберём цепь, изображённую на рисунке. Силу тока в цепи измеряют амперметром, напряжение — вольтметром. Зная напряжение на концах проводника и силу тока в нём, по закону Ома можно определить сопротивление каждого из проводников.

 

 

В цепь источника тока по очереди будем включать различные проводники, например, никелиновые проволоки одинаковой толщины, но разной длины. Выполнив указанные опыты, мы установим, что из двух никелиновых проволок одинаковой толщины более длинная проволока имеет большее сопротивление.
В следующем эксперименте по очереди будем включать никелиновые проволоки одинаковой длины, но разной толщины (разной площади поперечного сечения). Установим, что из двух никелиновых проволок одинаковой длины большее сопротивление имеет проволока, поперечное сечение которой меньше.
В третьем эксперименте по очереди будем включать никелиновую и нихромовую проволоки одинаковой длины и толщины. Установим, что никелиновая и нихромовая проволоки одинаковых размеров имеют разное сопротивление.
Зависимость сопротивления проводника от его размеров и вещества, из которого изготовлен проводник, впервые на опытах изучил Ом. Он установил:

Сопротивление прямо пропорционально длине проводника, обратно пропорционально площади его поперечного сечения и зависит от вещества проводника.

 

Обрати внимание!

Сопротивление проводника прямо пропорционально его длине, т.е. чем длиннее проводник, тем больше его электрическое сопротивление.
Сопротивление проводника обратно пропорционально площади его поперечного сечения, т.е. чем толще проводник, тем его сопротивление меньше, и, наоборот, чем тоньше проводник, тем его сопротивление больше.

Чтобы лучше понять эту зависимость, представьте себе две пары сообщающихся сосудов, причём у одной пары сосудов соединяющая трубка тонкая, а у другой — толстая. Ясно, что при заполнении водой одного из сосудов (каждой пары) переход её в другой сосуд по толстой трубке произойдёт гораздо быстрее, чем по тонкой, т.е. толстая трубка окажет меньшее сопротивление течению воды. Точно так же и электрическому току легче пройти по толстому проводнику, чем по тонкому, т.е. первый оказывает ему меньшее сопротивление, чем второй.

Причиной наличия сопротивления у проводника является взаимодействие движущихся электронов с ионами кристаллической решётки проводника. Из-за различия в строении кристаллической решётки у проводников, выполненных из различных веществ, сопротивления их отличаются друг от друга. Для характеристики материала вводят величину, которую называют удельным сопротивлением.

Удельное сопротивление — это физическая величина, которая определяет сопротивление проводника из данного вещества длиной \(1\) м и площадью поперечного сечения \(1\) м².

Введём буквенные обозначения: \(ρ\) — удельное сопротивление проводника, \(l\) — длина проводника, \(S\) — площадь его поперечного сечения. Тогда сопротивление проводника \(R\) выразится формулой:

R=ρ⋅lS.

 

Из этой формулы можно выразить и другие величины:

 

l=R⋅Sρ, S=ρ⋅lR, ρ=R⋅Sl.

 

Из последней формулы можно определить единицу удельного сопротивления. Так как единицей сопротивления является \(1\) Ом, единицей площади поперечного сечения — \(1\) м², а единицей длины — \(1\) м, то единицей удельного сопротивления будет:

 

1 Ом ⋅1м21 м=1 Ом ⋅1 м, т.е. Ом⋅м.

 

Удобнее выражать площадь поперечного сечения проводника в квадратных миллиметрах, так как она чаще всего бывает небольшой. Тогда единицей удельного сопротивления будет:

 

1 Ом ⋅1мм21 м, т.е. Ом⋅мм2м.

 

В таблице приведены значения удельного сопротивления некоторых веществ при \(20\) °С.

 

 

Обрати внимание!

Удельное сопротивление с изменением температуры меняется.

Опытным путём было установлено, что у металлов, например, удельное сопротивление с повышением температуры увеличивается.

 

Обрати внимание!

Из всех металлов наименьшим удельным сопротивлением обладают серебро и медь. Следовательно, серебро и медь — лучшие проводники электричества.

При проводке электрических цепей используют алюминиевые, медные и железные провода.
Во многих случаях нужны приборы, имеющие большое сопротивление. Их изготавливают из специально созданных сплавов — веществ с большим удельным сопротивлением. Например, как видно из таблицы, сплав нихром имеет удельное сопротивление почти в \(40\) раз большее, чем алюминий.

 

Обрати внимание!

Стекло и дерево имеют такое большое удельное сопротивление, что почти совсем не проводят электрический ток и являются изоляторами.

 

На практике часто приходится менять силу тока в цепи, делая её то больше, то меньше. Так, изменяя силу тока в динамике радиоприёмника, мы регулируем громкость звука. Изменением силы тока в электродвигателе швейной машины можно регулировать скорость его вращения.
 

Для регулирования силы тока в цепи применяют специальные приборы — реостаты.

Простейшим реостатом может служить проволока из материала с большим удельным сопротивлением, например, никелиновая или нихромовая. Включив такую проволочку в цепь источника электрического тока через контакты А и С и передвигая подвижный контакт С, можно уменьшать или увеличивать длину включённого в цепь участка АС. При этом будет меняться сопротивление цепи, а следовательно, и сила тока в ней, это покажет амперметр.

 

Реостатам, применяемым на практике, придают более удобную и компактную форму. Для этой цели используют проволоку с большим удельным сопротивлением. Один из реостатов (ползунковый реостат) изображён на рисунке.

 

 

В этом реостате никелиновая проволока намотана на керамический цилиндр. Проволока покрыта тонким слоем не проводящей ток окалины, поэтому витки её изолированы друг от друга. Над обмоткой расположен металлический стержень, по которому может перемещаться ползунок. Своими контактами он прижат к виткам обмотки. От трения ползунка о витки слой окалины под его контактами стирается, и электрический ток в цепи проходит от витков проволоки к ползунку, а через него в стержень, имеющий на конце зажим \(1\). С помощью этого зажима и зажима \(2\), соединённого с одним из концов обмотки и расположенного на корпусе реостата, реостат подсоединяют в цепь. Перемещая ползунок по стержню, можно увеличивать или уменьшать сопротивление реостата, включённого в цепь.
Условное обозначение реостата в схемах показано на рисунке:

 

Каждый реостат рассчитан на определённое сопротивление и на наибольшую допустимую силу тока, превышать которую не следует, так как обмотка реостата накаляется и может перегореть. Сопротивление реостата и наибольшее допустимое значение силы тока указаны на нём.

 

Обрати внимание!

Реостат нельзя полностью выводить, так как сопротивление его при этом становится равным нулю, и если в цепи нет других приёмников тока, то сила тока может оказаться очень большой и амперметр испортится.

На рисунке изображён реостат, с помощью которого можно менять сопротивление в цепи не плавно, а ступенями — скачками, т.к. каждая спираль реостата имеет определённое сопротивление.

 

Источники:

Пёрышкин А.В. Физика. 8 класс// ДРОФА, 2013.

http://class-fizika.narod.ru/8_31.htm
http://electricalschool.info/main/osnovy/394-jelektricheskojj-soprotivlenie.html
http://xn--h2adlho.xn--g1ababalj7azb.xn--p1ai/%D1%83%D0%B4%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5-%D1%81%D0%BE%D0%BF%D1%80%D0%BE%D1%82%D0%B8%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5/
http://xn--h2adlho.xn--g1ababalj7azb.xn--p1ai/%D1%83%D1%80%D0%BE%D0%BA-38-%D1%80%D0%B5%D0%BE%D1%81%D1%82%D0%B0%D1%82%D1%8B/
http://mugo.narod.ru/Fiziks/15.html

 

Что такое сопротивление?

Этот сайт никак не мог обойтись без статьи про сопротивление. Ну никак! Есть в электронике самое фундаментальное понятие, которое является к тому же физическим свойством. Ты наверно уже знаком с вот этими друзьями: 

Напряжение	В	Вольт	Потенциальная сила воздействия электронов
Ток	I	Ампер	Поток электронов
Сопротивление	R	Ом	Физическое свойство материала
Мощность	P	Ватт	Поток электронов через сопротивление

Сопротивление — это свойство материала мешать потоку электронов. Материал как бы сопротивляется, препятствует этому потоку, как паруса фрегата сильному ветру!

В мире практически всё имеет свойство сопротивляться: воздух сопротивляется потоку электронов, вода тоже сопротивляется потоку электронов, но они всё равно проскальзывают. Медные провода тоже сопротивляются потоку электронов, но лениво. Так что они очень хорошо пропускают такой поток. 

Не имеют сопротивления только сверхпроводники, но это уже другая история, так как раз у них нет сопротивления, то сегодня они нам не интересны. 

Кстати, поток электронов — это и есть электрический ток. Формальное определение более педантичное, так что ищи его сам в такой же сухой книге. 

И да, электроны между собой взаимодействуют. Сила такого взаимодействия измеряется в Вольтах и называется напряжением. Скажешь, что странно звучит? Да ничего странного. Электроны напрягаются и двигают другие электроны с усилием. Несколько по-деревенски, зато понятен основной принцип. 

Осталось упомянуть про мощность. Мощность — это когда ток, напряжение и сопротивление собираются за одним столом и начинают работать. Тогда и появляется мощность — энергия, которую теряют электроны, проходя через сопротивление. Кстати:

I = U/R          P = U * I

Есть у тебя, к примеру, лампочка на 60Вт с проводом. Втыкаешь её в розетку на 220В. Что дальше? Лампочка оказывает потоку электронов с потенциалом в 220В некоторое сопротивление. Если сопротивление слишком мало — бум, сгорела. Если слишком большое — нить накала будет светиться очень слабо, если вообще будет. А вот если оно будет «в самый раз», тогда лампочка скушает 60Вт и превратит эту энергию в свет и тепло.

Тепло при этом побочный эффект и называется «потерей» энергии, так как вместо того, что бы светить ярче лампочка тратит энергию на нагрев. Пользуйтесь энергосберегающими лампами! Кстати, провод тоже обладает сопротивлением и если поток электронов будет слишком большим, то он также нагреется до заметной температуры. Тут можно предложить почитать заметку про то, зачем спользуются высоковольтные линии

Уверен, теперь ты понимаешь о сопротивлении больше. При этом мы не свалились в детали подобные удельному сопротивлению материала и формулы типа 

где ρ — удельное сопротивление вещества проводника, Ом·м, l — длина проводника, м, а S — площадь сечения, м².

Немного  анимашек для полноты картины

И наглядно о том, как поток электронов меняется от в зависимости от температуры проводника и его толщины 

Электрический импеданс — Википедия

Электри́ческий импеда́нс (ко́мплексное электри́ческое сопротивле́ние^[1]) (англ. impedance от лат. impedio «препятствовать») — комплексное сопротивление между двумя узлами цепи или двухполюсника для гармонического сигнала.

Это понятие и термин ввёл физик и математик О. Хевисайд в 1886 году^[2][3].

Резистор — пассивный элемент, обладающий чисто активным сопротивлением. Реактивная составляющая комплексного сопротивления резистора равна нулю, так как соотношение между напряжением на резисторе и током через него не зависит от частоты тока/напряжения и является пассивным элементом, поскольку не содержит внутренних источников энергии. Если к его концам приложить некоторое напряжение U (подсоединить источник напряжения), то через резистор пойдёт электрический ток I. Если через резистор пропустить электрический ток I (подсоединить источник тока), то между концами резистора возникнет падение напряжения U. Резистор характеризуется электрическим сопротивлением, которое равно отношению напряжения U, к току I (см. закон Ома для участка цепи):

R=UI.{\displaystyle R={\frac {U}{I}}.}

Применение понятия «электрическое сопротивление» к реактивным элементам (катушка индуктивности и конденсатор) при постоянном токе приводит к тому, что:

• сопротивление идеальной катушки индуктивности стремится к нулю:

если пропустить через идеальную катушку индуктивности некоторый постоянный ток I, то при любом значении I, падение напряжения на катушке будет нулевым:

U=0;{\displaystyle U=0;}

R=UI=0I=0;{\displaystyle R={\frac {U}{I}}={\frac {0}{I}}=0;}

если приложить к конденсатору некоторое постоянное напряжение U, то при любом значении U, ток через конденсатор будет нулевым:

I=0;{\displaystyle I=0;}

R=UI=U0=∞.{\displaystyle R={\frac {U}{I}}={\frac {U}{0}}=\infty .}

Это справедливо лишь для постоянного тока и напряжения. В случае же приложения к реактивному элементу переменного тока и напряжения, свойства реактивных элементов существенно иные:

• напряжение между выводами катушки индуктивности не равно нулю;
• ток, протекающий через конденсатор, не будет равен нулю.

Такое поведение не может быть описано в терминах активного сопротивления для постоянного тока, поскольку активное сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов между током и напряжением.

Было бы удобно иметь некоторый параметр аналогичный активному сопротивлению и для реактивных элементов, который бы связывал ток и напряжение на них подобно активному сопротивлению в формуле закона Ома для постоянного тока.

Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при воздействиях на них гармонических сигналов. В этом случае ток и напряжение оказываются связаны некой константой (подобной в некотором смысле активному сопротивлению), которая и получила название «электрический импеданс» (или просто «импеданс»). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно в таком представлении одновременно учитывается и амплитудные, и фазовые характеристики гармонических сигналов и откликов систем на гармоническое воздействие.

Импедансом z^(jω){\displaystyle {\hat {z}}(j\omega )\;} называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник в установившемся режиме, то есть после завершения переходных процессов. Для линейных пассивных цепей с постоянными параметрами в установившемся режиме импеданс не зависит от времени. Если время t в математическом выражении для импеданса не сокращается, значит, для данного двухполюсника понятие импеданса неприменимо.

z^(jω)=u^(jω,t)i^(jω,t)=U(ω)ej(ωt+ϕu(ω))I(ω)ej(ωt+ϕi(ω))=U(ω)ejϕu(ω)I(ω)ejϕi(ω)=U^(jω)I^(jω){\displaystyle {\hat {z}}(j\omega )\;={\frac {{\hat {u}}(j\omega ,t)\;}{{\hat {i}}(j\omega ,t)\;}}={\frac {U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}}{I(\omega )e^{j(\omega t+\phi _{i}(\omega ))}}}={\frac {U(\omega )e^{j\phi _{u}(\omega )}}{I(\omega )e^{j\phi _{i}(\omega )}}}={\frac {{\hat {U}}(j\omega )\;}{{\hat {I}}(j\omega )\;}}}

(1)

Здесь:

Исторически сложилось, что в электротехнике обозначение импеданса, комплексных амплитуд и других комплексных функций частоты записывают как f(jω){\displaystyle f(j\omega )}, а не f(ω){\displaystyle f(\omega )}. Такое обозначение подчёркивает, что используются комплексные представления гармонических функций вида ejωt{\displaystyle e^{j\omega t}}. Кроме того, над символом, обозначающим комплексный сигнал или комплексный импеданс, обычно ставят «домик» или точку: U˙(jω){\displaystyle {\dot {U}}(j\omega )\;} чтобы отличать от соответствующих действительных величин.

Алгебраическая форма[править | править код]

Если рассматривать комплексный импеданс как комплексное число в алгебраической форме, то действительная часть соответствует активному сопротивлению, а мнимая — реактивному. То есть двухполюсник с импедансом z^(jω){\displaystyle {\hat {z}}(j\omega )\;} можно рассматривать как последовательно соединенные резистор с сопротивлением ℜ(z^(jω)){\displaystyle \Re ({\hat {z}}(j\omega ))} и чисто реактивный элемент с импедансом ℑ(z^(jω)){\displaystyle \Im ({\hat {z}}(j\omega ))}

Рассмотрение действительной части полезно при расчёте мощности, выделяемой в двухполюснике, поскольку мощность выделяется только на активном сопротивлении.

Тригонометрическая форма[править | править код]

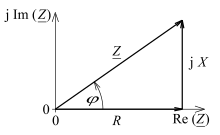
Если рассматривать импеданс как комплексное число в тригонометрической форме, то модуль соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а аргумент — сдвигу фазы между током и напряжением, то есть на сколько фаза тока отстаёт от фазы напряжения или опережает.

Понятие импеданса в классической форме применимо, если при приложении к двухполюснику гармонического напряжения, ток, вызванный этим напряжением, также гармонический той же частоты. Для этого необходимо и достаточно, чтобы двухполюсник был линейным и его параметры не менялись со временем и закончились переходные процессы. Если это условие не выполнено, то импеданс не может быть найден по следующей причине: невозможно получить выражение для импеданса, не зависящее от времени t, поскольку при вычислении импеданса множитель ejωt{\displaystyle e^{j\omega t}} в (1) не сокращается.

• Однако и для линейных двухполюсников (для которых зависимость от времени сокращается) импеданс всё же зависит от частоты (за исключением случая когда двухполюсник сводится к схеме из одних резисторов и импеданс оказывается действительной величиной).

Практически это означает, что импеданс может быть вычислен для любого двухполюсника, состоящего из резисторов, катушек индуктивности и конденсаторов, то есть из линейных пассивных элементов. Также импеданс хорошо применим для активных цепей, линейных в широком диапазоне входных сигналов (например, цепи на основе операционных усилителей). Для цепей, импеданс которых не может быть найден в силу указанного выше ограничения, бывает полезным найти импеданс в малосигнальном приближении — для бесконечно малой амплитуды сигнала для конкретной рабочей точки. Для этого необходимо перейти к эквивалентной схеме и искать импеданс для неё.

Обобщенный импеданс в s-плоскости и преобразование Лапласа[править | править код]

Импедансы, определённые через комплексную частоту jω{\displaystyle j\omega }, позволяют вычислять частотный отклик некоторой линейной цепи, возбуждаемой гармоническим сигналом, причём только в установившемся режиме. Для расчёта отклика цепи на сигнал, произвольно изменяющийся во времени применяется обобщенный импеданс — функции комплексной переменной s=σ+jω{\displaystyle s=\sigma +j\omega } и отклик цепи во временно́й области вычисляется через обратное преобразование Лапласа, причем в таких вычислениях возбуждающий сигнал fin(t){\displaystyle f_{in}(t)} из временного представления должен быть предварительно преобразован в комплексное представление Ft(s){\displaystyle F_{t}(s)} через прямое преобразование Лапласа:

Ft(s)=∫0∞fin(t)e−stdt.{\displaystyle F_{t}(s)=\int _{0}^{\infty }f_{in}(t)e^{-st}\,dt.}

Комплексный отклик системы выражается обычным способом через преобразованное комплексное представление возбуждающего сигнала и комплексную передаточную функцию системы H(s){\displaystyle H(s)}:

Ft,H(s)=H(s) Ft(s).{\displaystyle F_{t,H}(s)=H(s)\ F_{t}(s).}

Двухполюсник	Обобщённый импеданс
Резистор	R{\displaystyle R\,}
Катушка индуктивности	sL{\displaystyle sL\,}
Конденсатор	1sC{\displaystyle {\frac {1}{sC}}\,}

Комплексная передаточная функция вычисляется обычным методом расчёта электрических цепей, например, по правилам Кирхгофа, в формулы в качестве сопротивлений подставляются обобщённые импедансы. Обобщённые импедансы пассивных двухполюсников приведены в таблице. Например, обобщённый импеданс цепи, состоящей из последовательно включённых резистора и катушки индуктивности будет R+sL{\displaystyle R+sL}.

Отклик цепи во временно́й области вычисляется обратным преобразованием Лапласа:

fF,H(t)=L−1[H(s) Ft(s)]=12πi∫σ1−j⋅∞σ1+j⋅∞estH(s) Ft(s)ds,{\displaystyle f_{F,H}(t)={\mathcal {L}}^{-1}[H(s)\ F_{t}(s)]={\frac {1}{2\pi i}}\int \limits _{\sigma _{1}-j\cdot \infty }^{\sigma _{1}+j\cdot \infty }e^{st}H(s)\ F_{t}(s)\,ds,}

где σ1 {\displaystyle \sigma _{1}\ } — некоторое вещественное число, выбираемое из условий сходимости интеграла.

Пример вычисления временно́го отклика RC-фильтра нижних частот на ступенчатое возмущение

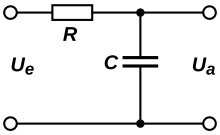Пассивный RС-фильтр нижних частот 1-го порядка

Простейший фильтр нижних частот 1-го порядка изображён на рисунке и состоит из последовательно соединённых резистора и конденсатора, образующего делитель напряжения для входного сигнала где выходной сигнал снимается с конденсатора, обобщённый комплексный коэффициент передачи HRC(s){\displaystyle H_{RC}(s)} такого делителя:

HRC(s)=1/sCR+1/sC=1sRC+1=1sT+1,{\displaystyle H_{RC}(s)={\frac {1/sC}{R+1/sC}}={\frac {1}{sRC+1}}={\frac {1}{sT+1}},}

где обозначено T=RC{\displaystyle T=RC} — постоянная времени RС-цепи.

Ступенчатый входной сигнал можно выразить через функцию Хевисайда h(t){\displaystyle h(t)}:

Uin(t)=U0 h(t),{\displaystyle U_{in}(t)=U_{0}\ h(t),}

где U0{\displaystyle U_{0}} — амплитуда ступеньки.

Преобразование Лапласа входного сигнала:

Fin(s)=L[U0 h(t)]=∫0∞e−stU0h(t)dt=U0/s.{\displaystyle F_{in}(s)={\mathcal {L}}[U_{0}\ h(t)]=\int \limits _{0}^{\infty }e^{-st}\,U_{0}\,h(t)\,dt=U_{0}/s.}

Uout(t)=L−1[HRC(s) Fin(s)]=12πi∫σ1−j⋅∞σ1+j⋅∞est1sT+1⋅U0sds=U0(1−e−t/T).{\displaystyle U_{out}(t)={\mathcal {L}}^{-1}[H_{RC}(s)\ F_{in}(s)]={\frac {1}{2\pi i}}\int \limits _{\sigma _{1}-j\cdot \infty }^{\sigma _{1}+j\cdot \infty }e^{st}{\frac {1}{sT+1}}\cdot {\frac {U_{0}}{s}}\,ds=U_{0}(1-e^{-t/T}).}

Таким образом, получен отклик цепи при нулевом начальном условии (UC=0{\displaystyle U_{C}=0} при t=0{\displaystyle t=0}), такой же, как и при применении другого метода расчёта, например, из решения обыкновенного дифференциального уравнения.

Для практического применения расчета цепей (и других расчётов) составлены подробные таблицы прямого и обратного преобразования Лапласа многих часто встречающихся при расчётах функций.

Комбинируя преобразование Лапласа с использованием его свойств и интеграл Дюамеля обычно относительно легко найти отклики во временной области самых различных линейных электрических цепей.

Идеальные элементы[править | править код]

Резистор[править | править код]

Для резистора импеданс всегда равен его сопротивлению R и не зависит от частоты:

zR=R{\displaystyle z_{R}=R}

(2)

Конденсатор[править | править код]

Ток и напряжение для конденсатора связаны соотношением:

i(t)=CdUdt.{\displaystyle i(t)=C{\frac {dU}{dt}}.}

(3)

Отсюда следует, что при напряжении

u^(jω,t)=U(ω)ej(ωt+ϕu(ω)){\displaystyle {\hat {u}}(j\omega ,t)=U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}}

(4)

ток, текущий через конденсатор, будет равен:

i^(jω,t)=Cddt(U(ω)ej(ωt+ϕu(ω)))=jωCU(ω)ej(ωt+ϕu(ω)).{\displaystyle {\hat {i}}(j\omega ,t)=C{\frac {d}{dt}}\left(U(\omega )e^{j(\omega t+\phi _{u}(\omega ))}\right)=j\omega CU(\omega )e^{j(\omega t+\phi _{u}(\omega ))}.}

(5)

После подстановки (4) и (5) в (1) получаем:

z^C(jω)=1jωC=−jωC.{\displaystyle {\hat {z}}_{C}(j\omega )={\frac {1}{j\omega C}}=-{\frac {j}{\omega C}}.}

(6)

Катушка индуктивности[править | править код]

Аналогичное рассмотрение для катушки индуктивности приводит к результату:

z^L(jω)=jωL.{\displaystyle {\hat {z}}_{L}(j\omega )\;=j\omega L.}

(7)

Общий случай[править | править код]

Для произвольного двухполюсника, состоящего из элементов с известным импедансом, нет необходимости производить приведенные выше вычисления с целью нахождения импеданса. Импеданс находится по обычным правилам расчёта сопротивления сложной цепи, то есть используются формулы для сопротивления при параллельном и последовательном соединении резисторов. При этом все математические операции производятся по правилам действий над комплексными числами. Например, импеданс идеальных последовательно соединенных резистора, конденсатора и катушки индуктивности будет равен:

Z^(jω) =R+1jωC+jωL=R−jωC+jωL=R+j(−1ωC+ωL).{\displaystyle {\hat {Z}}(j\omega )\ =R+{\frac {1}{j\omega C}}+j\omega L=R-{\frac {j}{\omega C}}+j\omega L=R+j\left(-{\frac {1}{\omega C}}+\omega L\right).}

(8)

Экспериментальное измерение импеданса[править | править код]

Прямое измерение импеданса требует измерения амплитуд синусоидальных напряжения и тока изучаемого двухполюсника, и одновременного измерения сдвига фазы между ними.

Импеданс также часто измеряют компенсационными методами с помощью мостов переменного тока, подобными мосту Уитстона для постоянного тока, при таких измерениях мост балансируют изменением эталонных реактивного и активного элементов, по величине реактивного и активного сопротивления эталонных элементов, требуемого для балансировки моста, определяется измеряемый импеданс.

В силовых устройствах измерение импеданса может потребовать одновременного измерения и подачи питания на работающее устройство.

Измерение импеданса устройств и линий передач является практической задачей в радиотехнике и других областях.

Измерения импеданса обычно проводятся на одной частоте, но если требуется определить зависимость импеданса от частоты, то измерения проводят на нескольких частотах в нужном диапазоне частот.

Активная и реактивная составляющие импеданса обычно выражают в омах, но могут использоваться связанные с импедансом величины, например, в радиотехнике, линиях передачи, коэффициент стоячей волны или коэффициент отражения имеют бо́льшее удобство.

Сопротивление устройства можно рассчитать путем деления комплексных напряжения и тока. Полное сопротивление устройства рассчитывается путем подачи синусоидального напряжения на устройство последовательно с эталонным резистором и измерения напряжений на резисторе и на самом устройстве. Выполнение этого измерения на нескольких частотах тестирующего сигнала обеспечивает определение фазового сдвига и величины импеданса^[5].

Измерение отклика исследуемой цепи на импульсный тестирующий сигнал можно использовать в сочетании с быстрым преобразованием Фурье для измерения импеданса различных электрических устройств^[5].

LCR-измеритель (индуктивность L, емкость C и сопротивление R) или измеритель иммитанса — это устройство, обычно используемое для измерения индуктивности, сопротивления и ёмкости компонента. Из этих значений можно рассчитать полное сопротивление на любой частоте.

Введение импеданса позволяет описывать поведение двухполюсника с реактивными свойствами при воздействии на него гармонического сигнала. Кроме того, в случае негармонического сигнала импеданс применяется столь же успешно. Для этого сигнал раскладывается на спектральные компоненты при помощи ряда Фурье или преобразования Фурье и рассматривается воздействие каждой спектральной компоненты. Вследствие линейности двухполюсника сумма откликов на спектральные компоненты равна отклику на исходный негармонический сигнал или применять преобразование Лапласа.