Сопротивление меди в зависимости от температуры. Зависимость сопротивления нихрома от температуры
Основными характеристиками проводниковых материалов являются:
- Теплопроводность;
- Контактная разность потенциалов и термоэлектродвижущая сила;
- Временное сопротивление разрыву и относительное удлинение при растяжении.
ρ — величина, характеризующая способность материала оказывать сопротивление электрическому току. Удельное сопротивление выражается формулой:
Для длинных проводников (проводов, шнуров, жил кабелей, шин) длину проводника l обычно выражают в метрах, площадь поперечного сечения S — в мм², сопротивление проводника r — в Ом, тогда размерность удельного сопротивления

Данные удельных сопротивлений различных металлических проводников приведены в статье «Электрическое сопротивление и проводимость «.
α — величина, характеризующая изменение сопротивления проводника в зависимости от температуры.

Данные температурных коэффициентов сопротивления различных проводниковых материалов приведены ниже в таблице.
Значение температурных коэффициентов сопротивления металлов
Теплопроводность
λ — величина, характеризующая количество тепла, проходящее в единицу времени через слой вещества. Размерность теплопроводности


Теплопроводность имеет большое значение при тепловых расчетах машин, аппаратов, кабелей и других электротехнических устройств.
Значение теплопроводности λ для некоторых материалов
| Серебро Медь Алюминий Латунь Железо, сталь Бронза Бетон Кирпич Стекло Асбест Дерево Пробка | 350 — 360 340 180 — 200 90 — 100 40 — 50 30 — 40 0,7 — 1,2 0,5 — 1,2 0,6 — 0,9 0,13 — 0,18 0,1 — 0,15 0,04 — 0,08 |
Из приведенных данных видно, что наибольшей теплопроводностью обладают металлы. У неметаллических материалов теплопроводность значительно ниже. Она достигает особенно низких значений у пористых материалов, которые применяю специально для тепловой изоляции. Согласно электронной теории высокая теплопроводность металлов обусловлена теми же электронами проводимости, что и электропроводность.
Контактная разность потенциалов и термоэлектродвижущая сила
Как было указано в статье «Металлические проводники «, положительные ионы металла расположены в узлах кристаллической решетки, образующей как бы ее каркас. Свободные электроны заполняют решетку наподобие газа, который называют иногда «электронным газом». Давление электронного газа в металле пропорционально абсолютной температуре и числу свободных электронов в единице объема, которое зависит от свойств металла. При соприкосновении двух разнородных металлов в месте соприкосновения происходит выравнивание давления электронного газа. В результате диффузии электронов металл, у которого число электронов уменьшается, заряжается положительно, а металл, у которого число электронов увеличивается, заряжается отрицательно. В месте контакта возникает разность потенциалов. Эта разность пропорциональна разности температур металлов и зависит от их вида. В замкнутой цепи возникает термоэлектрический ток. Электродвижущая сила (ЭДС), которая создает этот ток, называется
Явление контактной разности потенциалов применяется в технике для измерения температуры при помощи термопар. При измерении малых токов и напряжений в цепи в местах соединения различных металлов может возникнуть большая разность потенциалов, которая будет искажать результаты измерений. В этом случае необходимо подобрать материалы так, чтобы точность измерений была высокой.
Временное сопротивление разрыву и относительное удлинение при растяжении
При выборе проводов, помимо сечения, материала проводов, изоляции необходимо учитывать их механическую прочность. Особенно это касает
6. Температурный коэффициент сопротивления | 11. Физика проводников и диэлектриков | Часть1
6. Температурный коэффициент сопротивления
Температурный коэффициент сопротивления
Как вы могли заметить, значения удельных электрических сопротивлений в таблице из предыдущей статьи даны при температуре 20 ° Цельсия. Если вы предположили, что они могут измениться при изменении температуры, то оказались правы.
Зависимость сопротивления проводов от температуры, отличной от стандартной (составляющей обычно 20 градусов Цельсия), можно выразить через следующую формулу:
Константа «альфа» (α) известна как температурный коэффициент сопротивления, который равен относительному изменению электрического сопротивления участка электрической цепи или удельного сопротивления вещества при изменении температуры на единицу. Так как все материалы обладают определенным удельным сопротивлением (при температуре 20 ° С), их сопротивление будет изменяться на определенную величину в зависимости от изменения температуры. Для чистых металлов температурный коэффициент сопротивления является положительным числом, что означает увеличение их сопротивления с ростом температуры. Для таких элементов, как углерод, кремний и германий, этот коэффициент является отрицательным числом, что означает уменьшение их сопротивления с ростом температуры. У некоторых металлических сплавов температурный коэффициент сопротивления очень близок к нулю, что означает крайне малое изменение их сопротивления при изменении температуры. В следующей таблице приведены значения температурных коэффициентов сопротивления нескольких распространенных типов металлов:
| Проводник | α, на градус Цельсия |
| Никель | 0,005866 |
| Железо | 0,005671 |
| Молибден | 0,004579 |
| Вольфрам | 0,004403 |
| Алюминий | 0,004308 |
| Медь | 0,004041 |
| Серебро | 0,003819 |
| Платина | 0,003729 |
| Золото | 0,003715 |
| Цинк | 0,003847 |
| Сталь (сплав) | 0,003 |
| Нихром (сплав) | 0,00017 |
| 0,00013 | |
| Манганин (сплав) | 0,000015 |
| Константан (сплав) | 0,000074 |
Давайте на примере нижеприведенной схемы посмотрим, как температура может повлиять на сопротивление проводов и ее функционирование в целом:
Общее сопротивление проводов этой схемы (провод 1 + провод 2) при стандартной температуре 20 ° С составляет 30 Ом. Проанализируем схему с помощью таблицы напряжений токов и сопротивлений:
При 20 ° С мы получаем 12,5 В на нагрузке, и в общей сложности 1,5 В (0,75 + 0,75) падения напряжения на сопротивлении проводов. Если температуру поднять до 35 ° С, то при помощи вышеприведенной формулы мы легко сможем рассчитать изменение сопротивления на каждом из проводов. Для медных проводов (α = 0,004041) это изменение составит:
Пересчитав значения таблицы, мы можем увидеть к каким последствиям привело изменение температуры:
Сравнив эти таблицы можно прийти к выводу, что напряжение на нагрузке при увеличении температуры снизилось (с 12,5 до 12,42 вольт), а падение напряжения на проводах увеличилось (с 0,75 до 0,79 вольт). Изменения на первый взгляд незначительны, но они могут быть существенны для протяженных линий электропередач, связывающих электростанции и подстанции, подстанции и потребителей.
Как влияет нагрев на величину сопротивления. Как изменится сопротивление металлического проводника. Сопротивление меди в зависимости от температуры
Каждое вещество имеет свое удельное сопротивление. Причем сопротивление будет зависеть от температуры проводника. Убедимся в этом, проведя следующий опыт.
Пропустим ток через стальную спираль. В цепи со спиралью подключим последовательно амперметр . Он покажет некоторое значение. Теперь будем нагревать спираль в пламени газовой горелки. Значение силы тока, которое покажет амперметр, уменьшится. То есть, сила тока будет зависеть от температуры проводника.
Изменение сопротивления в зависимости от температуры
Пусть при температуре 0 градусов, сопротивление проводника равняется R0, а при температуре t сопротивление равно R, тогда относительное изменение сопротивления будет прямо пропорционально изменению температуры t:
В данной формуле а — коэффициент пропорциональности, который называют еще температурным коэффициентом. Он характеризует зависимость сопротивления, которым обладает вещество, от температуры.
Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании его на 1 Кельвин.
Для всех металлов температурный коэффициент больше нуля. При изменениях температуры он будет незначительно меняться. Поэтому, если изменение температуры невелико, то температурный коэффициент можно считать постоянным, и равным среднему значению из этого интервала температур.
Растворы электролитов с ростом температуры сопротивление уменьшается. То есть для них температурный коэффициент будет меньше нуля.
Сопротивление проводника зависит от удельного сопротивления проводника и от размеров проводника. Так как размеры проводника при нагревании меняются незначительно, то основной составляющей изменения сопротивления проводника является удельное сопротивление.
Зависимость удельного сопротивления проводника от температуры
Попытаемся найти зависимость удельного сопротивления проводника от температуры.
Подставим в полученную выше формулу значения сопротивлений R=p*l/S R0=p0*l/S.
Получим следующую формулу:
Данная зависимость представлена на следующем рисунке.
Попробуем разобраться, почему увеличивается сопротивление
Когда мы повышаем температуру, то увеличивается амплитуда колебаний ионов в узлах кристаллической решетки. Следовательно, свободные электроны будут чаще с ними сталкиваться. При столкновении они будет терять направленность своего движения. Следовательно, сила тока будет уменьшаться.
При нагревании увеличивается в результате увеличения скорости движения атомов в материале проводника с возрастанием температуры. Удельное сопротивление электролитов и угля при нагревании, наоборот, уменьшается, так как у этих материалов, кроме увеличения скорости движения атомов и молекул, возрастает число свободных электронов и ионов в единице объема.
Некоторые сплавы, обладающие большим , чем составляющие их металлы, почти не меняют удельного сопротивления с нагревом (константан, манганин и др.). Это объясняется неправильной структурой сплавов и малым средним временем свободного пробега электронов.
Величина, показывающая относительное увеличение сопротивления при нагреве материала на 1° (или уменьшение при охлаждении на 1°), называется .
Если температурный коэффициент обозначить через α , удельное сопротивление при to =20 о через ρ o , то при нагреве материала до температуры t1 его удельное сопротивление p1 = ρ o + αρ o (t1 — to) = ρ o(1 + (α (t1 — to))
и соответственно R1 = Ro (1 + (α (t1 — to))
Температурный коэффициент а для меди, алюминия, вольфрама равен 0,004 1/град. Поэтому при нагреве на 100° их сопротивление возрастает на 40%. Для железа α = 0,006 1/град, для латуни α = 0,002 1/град, для фехрали α = 0,0001 1/град, для нихрома α = 0,0002 1/град, для константана α = 0,00001 1/град, для манганина α = 0,00004 1/град. Уголь и электролиты имеют отрицательный температурный коэффициент сопротивления. Температурный коэффициент для большинства электролитов равен примерно 0,02 1/град.
Свойство проводников изменять свое сопротивления в зависимости от температуры используется в термометрах сопротивления . Измеряя сопротивление, определяют расчетным путем окружающую температуру.Константан, манганин и другие сплавы, имеющие очень небольшой т
Как изменится сопротивление металлического проводника. Сопротивление меди в зависимости от температуры
При нагревании увеличивается в результате увеличения скорости движения атомов в материале проводника с возрастанием температуры. Удельное сопротивление электролитов и угля при нагревании, наоборот, уменьшается, так как у этих материалов, кроме увеличения скорости движения атомов и молекул, возрастает число свободных электронов и ионов в единице объема.
Некоторые сплавы, обладающие большим , чем составляющие их металлы, почти не меняют удельного сопротивления с нагревом (константан, манганин и др.). Это объясняется неправильной структурой сплавов и малым средним временем свободного пробега электронов.
Величина, показывающая относительное увеличение сопротивления при нагреве материала на 1° (или уменьшение при охлаждении на 1°), называется .
Если температурный коэффициент обозначить через α , удельное сопротивление при to =20 о через ρ o , то при нагреве материала до температуры t1 его удельное сопротивление p1 = ρ o + αρ o (t1 — to) = ρ o(1 + (α (t1 — to))
и соответственно R1 = Ro (1 + (α (t1 — to))
Температурный коэффициент а для меди, алюминия, вольфрама равен 0,004 1/град. Поэтому при нагреве на 100° их сопротивление возрастает на 40%. Для железа α = 0,006 1/град, для латуни α = 0,002 1/град, для фехрали α = 0,0001 1/град, для нихрома α = 0,0002 1/град, для константана α = 0,00001 1/град, для манганина α = 0,00004 1/град. Уголь и электролиты имеют отрицательный температурный коэффициент сопротивления. Температурный коэффициент для большинства электролитов равен примерно 0,02 1/град.
Свойство проводников изменять свое сопротивления в зависимости от температуры используется в термометрах сопротивления
. Измеряя сопротивление, определяют расчетным путем окружающую температуру.Константан, манганин и другие сплавы, имеющие очень небольшой температурный коэффициент сопротивления применяют для изготовления шунтов и добавочных сопротивлений к измерительным приборам.
Пример 1. Как изменится сопротивление Ro железной проволоки при нагреве ее на 520°? Температурный коэффициент а железа 0,006 1/град. По формуле R1 = Ro + Ro α (t1 — to) = Ro + Ro 0,006 (520 — 20) = 4Ro , то есть сопротивление железной проволоки при нагреве ее на 520° возрастет в 4 раза.
Пример 2. Алюминиевые провода при температуре -20° имеют сопротивление 5 ом. Необходимо определить их сопротивление при температуре 30°.
R2 = R1 — αR1 (t2 — t1) = 5 + 0 ,004 х 5 (30 — (-20)) = 6 ом.
Свойство материалов изменять свое электрическое сопротивление при нагреве или охлаждении используется для измерения температур. Так, термосопротивления , представляющие собой проволоку из платины или чистого никеля, вплавленные в кварц, применяются для измерения температур от -200 до +600°. Полупроводниковые термосопротивления с большим отрицательным коэффициентом применяются для точного определения температур в более узких диапазонах.
 Полупроводниковые термосопротивления, применяемые для измерения температур называют термисторами
.
Полупроводниковые термосопротивления, применяемые для измерения температур называют термисторами
.
Термисторы имеют высокий отрицательный температурный коэффициент сопротивления, то есть при нагреве их сопротивление уменьшается. выполняют из оксидных (подвергнутых окислению) полупроводниковых материалов, состоящих из смеси двух или трех окислов металлов. Наибольшее распространение имеют медно-марганцевые и кобальто-марганцевые термисторы. Последние более чувствительны к температуре.
В этой статье мы рассмотрим резистор и его взаимодействие с напряжением и током, проходящим через него. Вы узнаете, как рассчитать резистор с помощью специальных формул. В статье также показано, как специальные резисторы могут быть использованы в качестве датчика света и температуры.
Представление об электричестве
Новичок должен быть в состоянии представить себе электрический ток. Даже если вы поняли, что электричество состоит из электронов, движущихся по проводнику, это все еще очень трудно четко представить себе. Вот почему я предлагаю эту простую аналогию с водной системой, которую любой желающий может легко представить себе и понять, не вникая в законы.
Обратите внимание, как электрический ток похож на поток воды из полного резервуара (высокого напряжения) в пустой(низкое напряжение). В этой простой аналогии воды с электрическим током, клапан аналогичен токоограничительному резистору.
Из этой аналогии можно вывести некоторые правила, которые вы должны запомнить навсегда:
— Сколько тока втекает в узел, столько из него и вытекает
— Для того чтобы протекал ток, на концах проводника должны быть разные потенциалы.
— Количество воды в двух сосудах можно сравнить с зарядом батареи. Когда уровень воды в разных сосудах станет одинаковым, она перестанет течь, и при разряде аккумулятора, разницы между электродами не будет и ток перестанет течь.
— Электрический ток будет увеличиваться при уменьшении сопротивления, как и скорость потока воды будет увеличиваться с уменьшением сопротивления клапана.
Я мог бы написать гораздо больше умозаключений на основе этой простой аналогии, но они описаны в законе Ома ниже.
Резистор

Резисторы могут быть использованы для контроля и ограничения тока, следовательно, основным параметром резистора является его сопротивление, которое измеряется в Омах . Не следует забывать о мощности резистора, которая измеряется в ваттах (Вт), и показывает, какое количество энергии резистор может рассеять без перегрева и выгорания. Важно также отметить, что резисторы используются не только для ограничения тока, они также могут быть использованы в качестве делителя напряжения для получения низкого напряжения из большего. Некоторые датчики основаны на том, что сопротивление варьируется в зависимости от освещённости, температуры или механического воздействия, об этом подробно написано в конце статьи.
Закон Ома
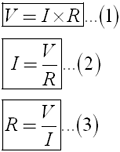
Понятно, что эти 3 формулы выведены из основной формулы закона Ома, но их надо выучить для понимания более сложных формул и схем. Вы должны быть в состоянии понять и представить себе смысл любой из этих формул. Например, во второй формуле показано, что увеличение напряжения без изменения сопротивления приведет к росту тока. Тем не менее, увеличение тока не увеличит напряжение (хотя это математически верно), потому что напряжение — это разность потенциалов, которая будет создавать электрический ток, а не наоборот (см. аналогию с 2 емкостями для воды). Формула 3 может использоваться для вычисления сопротивления токоограничивающего резистора при известном напряжении и токе. Это лишь примеры, показывающие важность этого правила. Вы сами узнаете, как использовать их после прочтения статьи.
Последовательное и параллельное соединение резисторов
Понимание последствий параллельного или последовательного подключения резисторов очень важно и поможет вам понять и упростить схемы с помощью этих простых формул для последовательного и параллельного сопротивления:
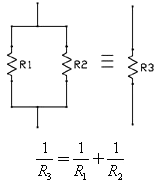
В этом примере схемы, R1 и R2 соединены параллельно, и могут быть заменены одним резистором R3 в соответствии с формулой:
В случае с 2-мя параллельно соединёнными резисторами, формулу можно записать так:
Кроме того, что эту формулу можно использовать для упрощения схем, она может быть использована для создания номиналов резисторов, которых у вас нет.
Отметим также, что значение R3 будет всегда меньше, чем у 2 других эквивалентных резисторов, так как добавление параллельных резисторов обеспечивает дополнительные пути
электрическому току, снижая общее сопротивление цепи.
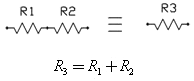
Последовательно соединённые резисторы могут быть заменены одним резистором, значение которого будет равно сумме этих двух, в связи с тем, что это соединение обеспечивает дополнительное сопротивление тока. Таким образом, эквивалентное сопротивление R3 очень просто вычисляется: R 3 =R 1 +R 2
В интернете есть удобные он-лайн калькуляторы для расчета и соединения резисторов.
Токоограничивающий резистор
Самая основная роль токоограничивающих резисторов — это контроль тока, который будет протекать через устройство или проводник. Для понимания их ра
|
Зависимость сопротивления от температуры — Знаешь как
Повышение температуры металлического проводника вызывает увеличение числа столкновений свободных электронов с атомами, вследствие чего уменьшается средняя скорость направленного движения электронов, что соответствует увеличению сопротивления. Таким образом, изменение сопротивления проводника от температуры зависит от строения материала проводника.

Относительное приращение сопротивления многих металлических проводников при изменении температуры в пределах 100° С пропорционально изменению температуры.
Таким образом,
Δr : r1 = (r2 — r1) : r1 = α(02 — 01)
откуда
r2 = r1+ r1α(02 — 01)
или окончательно
r2 = r1[1+α(02 — 01)]
где r1 и r2 — сопротивления при температурах 01 и 02;
α — температурный коэффициент сопротивления — относительное изменение сопротивления при повышении температуры на 1 °С.
Температурный коэффициент меди α = 0,004 1/град. Это обозначает, что при изменении температуры медного провода на 1 °С сопротивление его изменится на 0,4%.
Формулу можно использовать для измерения температуры O2 провода (обмотки машины), для чего при известных r1 α и 01 следует измерить сопротивление r2 и искомую температуру найти по формуле
02 = (r2 — r1) : αr1 + 01
Формула получена путем несложных преобразований из формулы.
Пример 1-3. Определить сопротивление проводов воздушной линии при температурах +20 и —10° С, если сечение медных проводов S = 10 мм2, длина линии 200 м.
Сопротивление двух проводов линии при температуре +20° С:
r1 = ρ(l : S) = 0,0175((2 • 200) : 10) = 0,7 ом
Сопротивление тех же проводов при температуре —10° С: r2 = r1[1 + α(02 — 01)] = 0,7[1+0,004 (— 30)] = 0,616 ом.
Пример 1-4. При температуре 01 = 20° С сопротивление медной обмотки электродвигателя r1 = 2,24 ом. После двух часов работы электродвигателя сопротивление той же обмотки r2 = 2,8 ом. Определить температуру обмотки электродвигателя после двух часов работы:
02 = (r2 — r1) : αr1 + 01 = (2,8 -2,4) : 0,004 • 2,4 + 20 ≈ 62° С
Статья на тему Зависимость электрического сопротивления от температуры
Удельное сопротивление и сверхпроводимость
Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.
На опыте установлено, что сопротивление R металлического проводника прямо пропорционально его длине L и обратно пропорционально площади его поперечного сечения А:
R = ρL/А (26.4)
где коэффициент ρ называется удельным сопротивлением и служит характеристикой вещества, из которого изготовлен проводник. Это соответствует здравому смыслу: сопротивление толстого провода должно быть меньше, чем тонкого, поскольку в толстом проводе электроны могут перемещаться по большей площади. И можно ожидать роста сопротивления с увеличением длины проводника, так как увеличивается количество препятствий на пути потока электронов.
Типичные значения ρ для разных материалов приведены в первом столбце табл. 26.2. (Реальные значения зависят от чистоты вещества, термической обработки, температуры и других факторов.)
|
Таблица 26.2. Удельное сопротивление и температурный коэффициент сопротивления (ТКС) (при 20 °С) |
||
| Вещество | Удельное сопротивление ρ,Ом·м | ТКС α,°C-1 |
| Проводники | ||
| Серебро | 1,59·10-8 | 0,0061 |
| Медь | 1,68·10-8 | 0,0068 |
| Алюминий | 2,65·10-8 | 0,00429 |
| Вольфрам | 5,6·10-8 | 0,0045 |
| Железо | 9,71·10-8 | 0,00651 |
| Платина | 10,6·10-8 | 0,003927 |
| Ртуть | 98·10-8 | 0,0009 |
| Нихром (сплав Ni, Fe, Сг) | 100·10-8 | 0,0004 |
| Полупроводники 1) | ||
| Углерод (графит) | (3-60)·10-5 | -0,0005 |
| Германий | (1-500)·10-5 | -0,05 |
| Кремний | 0,1 — 60 | -0,07 |
| Диэлектрики | ||
| Стекло | 109 — 1012 | |
| Резина твердая | 1013 — 1015 | |
| 1) Реальные значения сильно зависят от наличия даже малого количества примесей. | ||

Самым низким удельным сопротивлением обладает серебро, которое оказывается, таким образом, наилучшим проводником; однако оно дорого. Немногим уступает серебру медь; ясно, почему провода чаще всего изготовляют из меди.
Удельное сопротивление алюминия выше, чем у меди, однако он имеет гораздо меньшую плотность, и в некоторых случаях ему отдают предпочтение (например, в линиях электропередач), поскольку сопротивление проводов из алюминия той же массы оказывается меньше, чем у медных. Часто пользуются величиной, обратной удельному сопротивлению:
σ = 1/ρ (26.5)
σ называемой удельной проводимостью. Удельная проводимость измеряется в единицах (Ом·м) -1.
Удельное сопротивление вещества зависит от температуры. Как правило, сопротивление металлов возрастает с температурой. Этому не следует удивляться: с повышением температуры атомы движутся быстрее, их расположение становится менее упорядоченным, и можно ожидать, что они будут сильнее мешать движению потока электронов. В узких диапазонах изменения температуры удельное сопротивление металла увеличивается с температурой практически линейно:

где ρT — удельное сопротивление при температуре Т, ρ0 — удельное сопротивление при стандартной температуре Т0, а α — температурный коэффициент сопротивления (ТКС). Значения а приведены в табл. 26.2. Заметим, что у полупроводников ТКС может быть отрицательным. Это очевидно, поскольку с ростом температуры увеличивается число свободных электронов и они улучшают проводящие свойства вещества. Таким образом, сопротивление полупроводника с повышением температуры может уменьшаться (хотя и не всегда).
Значения а зависят от температуры, поэтому следует обращать внимание на диапазон температур, в пределах которого справедливо данное значение (например, по справочнику физических величин). Если диапазон изменения температуры окажется широким, то линейность будет нарушаться, и вместо (26.6) надо использовать выражение, содержащее члены, которые зависят от второй и третьей степеней температуры:
ρT = ρ0(1+αТ+ + βТ 2 + γТ 3),
где коэффициенты β и γ обычно очень малы (мы положили Т0 = 0°С), но при больших Т вклад этих членов становится существенным.
При очень низких температурах удельное сопротивление некоторых металлов, а также сплавов и соединений падает в пределах точности современных измерений до нуля. Это свойство называют сверхпроводимостью; впервые его наблюдал нидерландский физик Гейке Камер-линг-Оннес (1853-1926) в 1911 г. при охлаждении ртути ниже 4,2 К. При этой температуре электрическое сопротивление ртути внезапно падало до нуля.
Сверхпроводники переходят в сверхпроводящее состояние ниже температуры перехода, составляющей обычно несколько градусов Кельвина (чуть выше абсолютного нуля). Наблюдался электрический ток в сверхпроводящем кольце, который практически не ослабевал в отсутствие напряжения в течение нескольких лет.
В последние годы сверхпроводимость интенсивно исследуется с целью выяснить ее механизм и найти материалы, обладающие сверхпроводимостью при более высоких температурах, чтобы уменьшить стоимость и неудобства, обусловленные необходимостью охлаждения до очень низких температур. Первую успешную теорию сверхпроводимости создали Бардин, Купер и Шриффер в 1957 г. Сверхпроводники уже используются в больших магнитах, где магнитное поле создается электрическим током (см. гл. 28), что значительно снижает расход электроэнергии. Разумеется, для поддержания сверхпроводника при низкой температуре тоже затрачивается энергия.
Продолжение следует: Мощность.
Альтернативные статьи: Электрический ток, Закон Ома.
Замечания и предложения принимаются и приветствуются!

