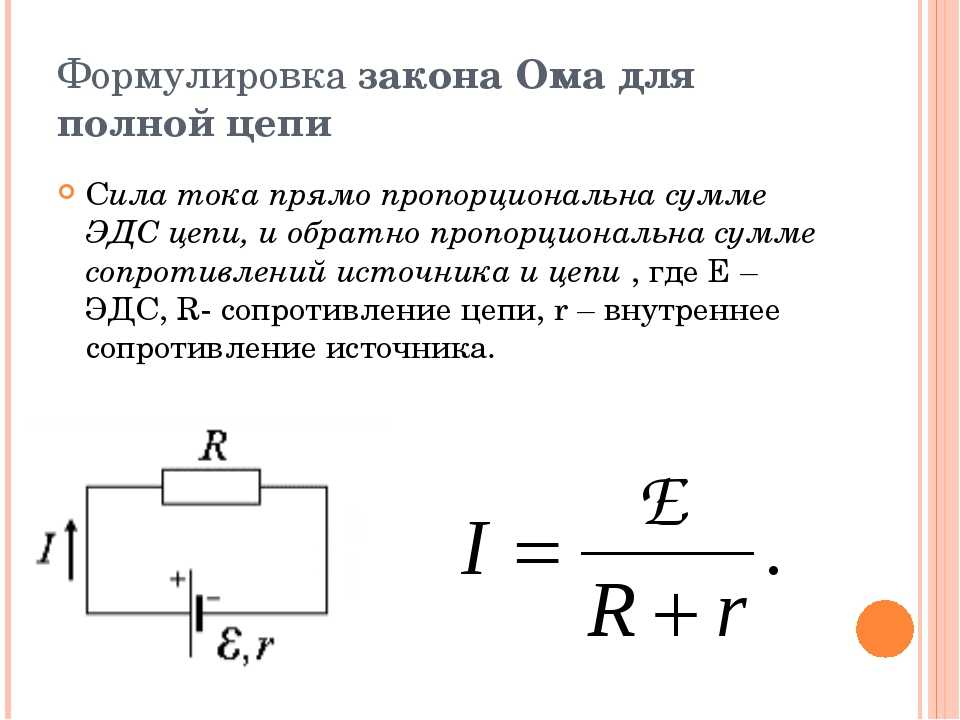
Определение внутреннего сопротивления и ЭДС источника электрического тока. — КиберПедия

Приборы и принадлежности, используемые в работе:

1. Источник электрической энергии.
2. Амперметр.
3. Вольтметр.
4. Реостат.
5. Ключ.
6. Соединительные провода.

 

Цель работы:

1. Научится собирать, заданную электрическую схему.

2. Используя закон ОМА для всей цепи, определить опытным путём величину внутреннего сопротивления и ЭДС источника электрической цепи.

 

1.ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ.

Формула закона Ома для всей цепи имеет вид:

, (1)

 

где:

Е — ЭДС источника электрической энергии

R — сопротивление внешней части цепи

r — внутреннее сопротивление источника

I — сила тока в цепи.

Перепишем формулу (I) в виде:

(2)

 

Величина является напряжением на внешней части цепи. Тогда формула (2) примет вид:

(3)

 

Если в полной цепи менять внешнее сопротивление, то будут меняться величины I и U (ток в цепи и напряжение на внешней её части). Пусть при силе тока в цепи , напряжение на внешней цепи равно , а при силе тока равно . Тогда дважды запишем формулу (3).

(4)

 

Левые части у уравнений одинаковые, поэтому приравняем правые части:

откуда:

и получим формулу для нахождения г внутреннего сопротивления источника:

(5)

 

Подставив (5) в одно из уравнений системы (4), получим формулу для нахождения Е ЭДС источника:

;

(6)

 

2. ХОД РАБОТЫ.

1. Определить цену деления амперметра и вольтметра.

 

2. Собрать следующую схему:

При сборке схемы соблюдать следующие требования:

— Собирать схему только при разомкнутом ключе К.

— Приступать к включению схемы и измерениям только после того, как преподаватель или лаборант проверят, правильно ли собрана Ваша схема.

— При замыкании ключа особое внимание обратить на показания амперметра — он не должен зашкаливать.

3. Изменяя величину внешнего сопротивления реостатом, получить 7 различных значений силы тока и напряжения во внешней цепи.

4. По формуле (5) вычислить 7 различных значений внутреннего сопротивления источника.

5. По формуле (6) вычислить 7 различных значений ЭДС источника электрической энергии.

6. Результаты измерений I и U, а также вычислений r и Е занести в таблицу.

В таблице n— число делений, на которое отклонилась стрелка амперметра или вольтметра при очередном измерении.

В следующую колонку после n записывается сила тока или напряжение в цепи, которые вычисляются по формуле:

(цена деления);

U = n_V × (цена деления).

Таблица результатов измерений и вычислений

Цена одного деления амперметра = …

Цена одного деления вольтметра =. ..

№

Сила тока

Напряжение

Внутренние сопротивление

ЭДС источника

Дел

I

Дел

U

r

sr

E

sЕ

n

А

n

B

Ом

Ом

Ом

Ом

%

В

В

В

В

%

7. Вычислить погрешности с которыми определены внутреннее сопротивление и ЭДС источника электрической энергии, по формулам:[13]

; s_r = D r_ср/ r_ср × 100%

;

8. Значение погрешностей занести в таблицу и по результатам, полученным в лабораторной работе сделать вывод[14].

 

 

КОНТРОЛЬНЫЕ ВОПРОСЫ ПЕРВОГО УРОВНЯ.

1. Закон Ома для всей цепи (формула и формулировка).

2.Закон Ома при параллельном, последовательном и смешанном соединении одинаковых источников электрической энергии (формулы, схемы).

3. Определение цены деления многопредельного прибора.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ ВТОРОГО И ТРЕТЬЕГО УРОВНЯ.

 

4.Закон Ома для участка цепи с ЭДС (3 случая и общий закон) и для всей цепи при нескольких ЭДС.

5.Что называется ЭДС источника электрической энергии? Единицы ЭДС.

6. Понятие внутреннего сопротивления источника.

7.Измерительные приборы вольтметр и амперметр[15].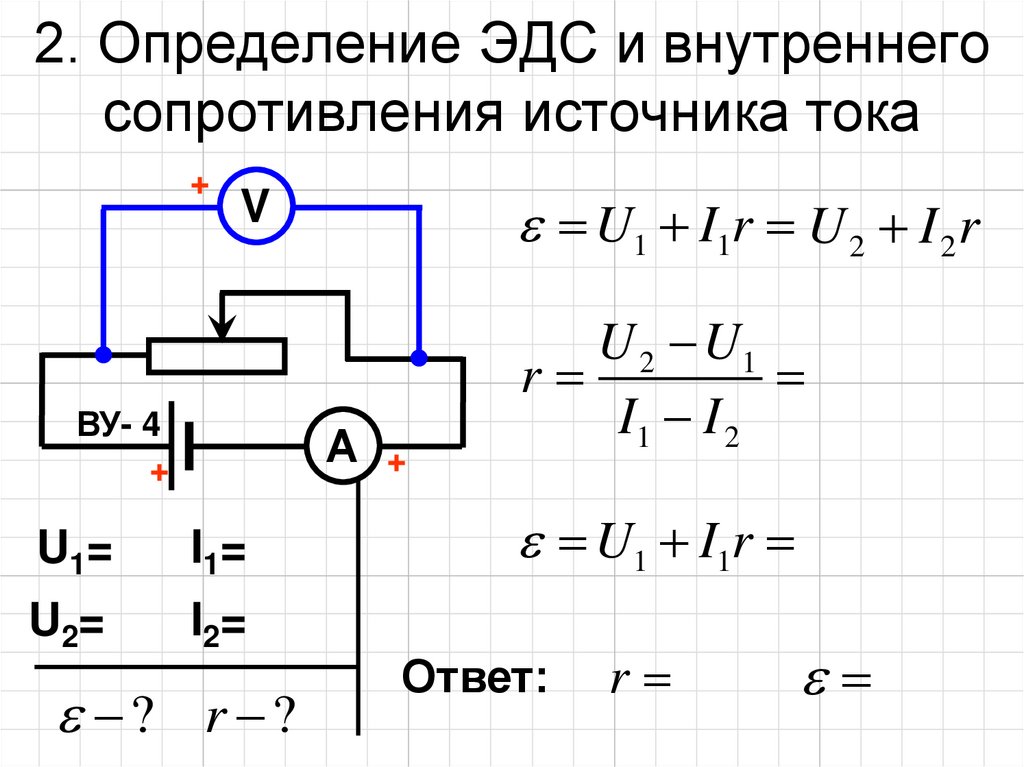

Лабораторная работа № 8.

Mr Toogood Physics — ЭДС и внутреннее сопротивление

Внутреннее сопротивление

Элементы и батареи преобразуют химическую энергию в электрический потенциал, который затем расходуется по цепи. Однако ни одна ячейка не эффективна при таком переносе на $100\%$. Никакая передача энергии не является эффективной на $100\%$, и электрические элементы и блоки питания не являются исключением. Электрический элемент состоит из трех частей: анода, катода и электролита. Анод и катод сделаны из двух разных металлов или из одного металла и углеродной пленки, а электролит представляет собой ионную жидкость, такую ​​как гидроксид калия. Когда ячейка включается в цепь, начинают происходить химические реакции на аноде и катоде. На аноде реакция окисления удаляет электроны из металла, и они начинают поступать в цепь. Это оставляет анод заряженным положительно, что притягивает больше электронов из электролита. Анод в отрицательной клемме ячейки. Возвращающиеся электроны собираются на катоде и он восстанавливается.

Катод является положительным полюсом. Через некоторое время анод потеряет почти все свои электроны, и электролит больше не сможет их поставлять, поэтому реакция замедлится, и ЭДС ячейки упадет.

Рисунок 1:  Упрощенный пример работы ячейки.

Когда происходят химические реакции, а также вырабатывается электричество, элемент выделяет небольшое количество тепла, которое излучается из системы и теряется. Поскольку энергия, теряемая ячейкой, представляет собой тепло, ее можно смоделировать так, как если бы она была резистором, генерирующим тепло, и называется внутренним сопротивлением

( r ) ячейки. Скорость потери энергии ячейкой, конечно же, измеряется в $\units{ваттах}$, и для ее описания можно использовать уравнения мощности для резистора.

Рисунок 2:  Когда ячейка генерирует ток, она также выделяет тепло.

Иногда на принципиальных схемах резистор изображается последовательно с ячейкой для представления внутреннего сопротивления; конечно, на самом деле внутри ячейки нет резистора, это просто полезный способ описания энергии, теряемой в цепи.

Внутреннее сопротивление является аналогом эффективности ячейки. Чем больше внутреннее сопротивление, тем больше тепла он выделяет при производстве электричества и тем менее эффективен. Внутреннее сопротивление также будет иметь разность потенциалов на нем, а это означает, что напряжение, измеренное на клеммах при протекании тока, ниже фактического истинного значения ЭДС элемента. Истинная ЭДС клетки составляет эти «потерянные вольты» плюс напряжение на клеммах .

э.д.с. = клемма p.d. + потеряно

вольт Рисунок 3:  ЭДС равна клемме p.d. плюс «потерянные вольты».

Математически это можно выразить так:

$$ε=ИК+Ир$$

Где:

• ε — ЭДС в $\units{V}$
• I ток в $\units{A}$
• R — полное сопротивление цепи в $\units{Ом}$
• r — внутреннее сопротивление элемента в $\units{Ом}$

Термин $IR$ представляет окончание p.d. а член $Ir$ – это потерянные вольты. Приведенное выше уравнение можно упростить до:

$$\большой ε=I\влево(R+r\вправо)$$

Часто в примерах цепей внутренним сопротивлением пренебрегают и предполагают идеальную ячейку без внутреннего сопротивления. Однако на уровне A от вас ожидают выполнения расчетов в цепях со значительным внутренним сопротивлением. Типичные внутренние сопротивления для современных аккумуляторов находятся в диапазоне от $\quantity{100}{мОм}$ до $\quantity{900}{мОм}$.

Вернуться к началу

---

Рабочий пример

Батарея соединена последовательно с резистором $\quantity{10}{Ω}$ и переключателем. Вольтметр подключен параллельно аккумулятору. Когда переключатель разомкнут (выключен), вольтметр показывает $\quantity{1.45}{V}$. Когда переключатель замкнут, показание равно $\quantity{1,26}{V}$.

Каково внутреннее сопротивление батареи?

1. $\количество{0,66}{Ом}$
2. $\количество{0,76}{Ом}$
3. $\количество{1.3}{Ω}$
4. $\количество{1,5}{Ом}$

Этот вопрос с несколькими вариантами ответов включает в себя относительно простой расчет, но важно, чтобы эти вопросы с несколькими вариантами ответов работали эффективно, чтобы вы не теряли время впустую.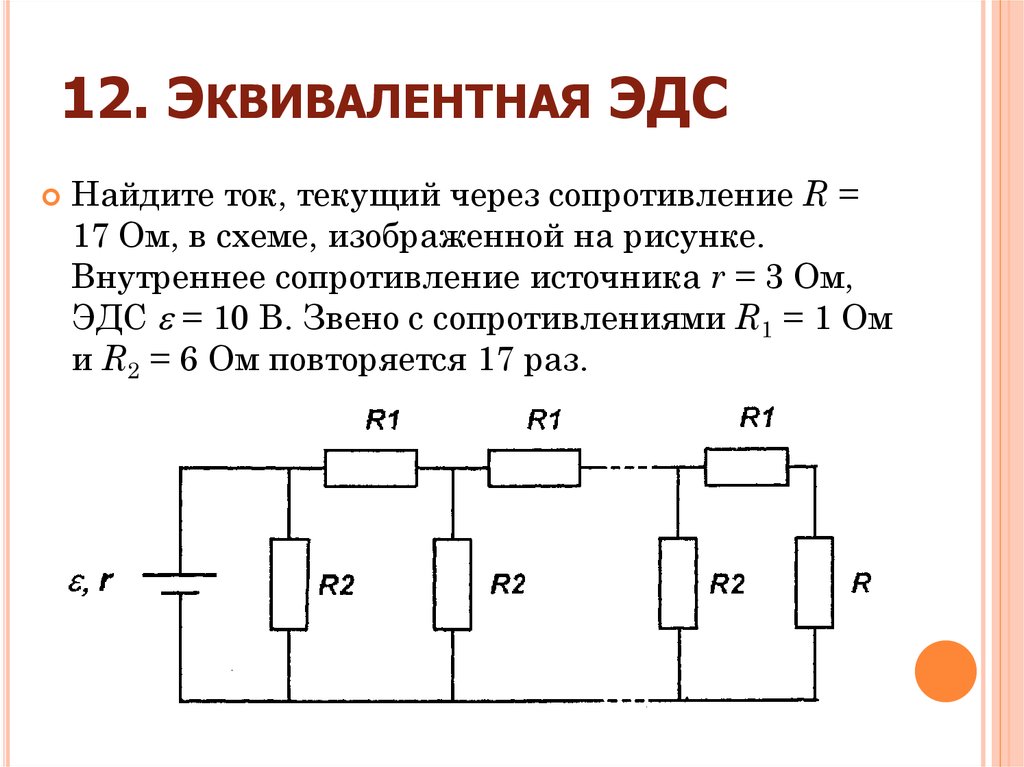

Мы знаем, что ЭДС ячейки равна $\quantity{1.45}{V}$, а конечный p.d. падает до $\quantity{1,26}{V}$, когда ток протекает через резистор $\quantity{10}{Ω}$, поэтому ток через резистор можно рассчитать как:

\начать{выравнивать} I&=\frac{V}{R}\\ I & = \ гидроразрыва {\ количество {1,26} {V}} {\ количество {10} {Ω}} \\ \\ I&=\количество{0,126}{A} \end{выравнивание}

Разность потенциалов на внутреннем сопротивлении составляет $\количество{1,45}{В} — \количество{1,45}{В} = \количество{0,19}{В}$

Теперь мы можем использовать это значение тока и значение потерянных вольт, чтобы найти значение внутреннего сопротивления:

$ $ R = \ гидроразрыва {V} {I} = {\ количество {0,19}{V}}{\количество{0,126}{A}}=\количество{1,5}{Ω}$$

Вернуться к началу

---

Внутреннее сопротивление и протекание тока

Чем больше ток протекает от элемента, тем выше скорость реакции в элементе и выделяется больше тепла, и, соответственно, тем выше потерянных вольт . Между током и энергией, теряемой на внутреннем сопротивлении, существует прямо пропорциональная зависимость.

Когда ток не течет, нет потерь энергии на внутреннее сопротивление и клемму p.d. будет равна ЭДС. На практике ЭДС ячейки можно определить с помощью мультиметра, который обычно имеет очень высокое сопротивление, и измерения на клемме pd, которая будет являться ЭДС, поскольку через измеритель не будет протекать ток.

Чем больше ток, протекающий через ячейку, тем больше разница между ЭДС и конечной p.d.. Если график клеммной p.d. и ток нанесен на график, ЭДС можно найти из точки пересечения с осью y, а градиент будет представлять внутреннее сопротивление.

Рисунок 4:  График терминала p.d. против тока для ячейки. Внутреннее сопротивление можно найти по градиенту.

Вы выполните это практическое задание для своего CAP, но вам нужно будет спроектировать схему и предложить подходящий диапазон сопротивлений для проверки.

Вернуться к началу

---

Рабочий пример

Учащийся исследует, как мощность, рассеиваемая на переменном резисторе Y, изменяется при изменении сопротивления.

На приведенной ниже схеме показана схема, которую использует учащийся. Y подключен к батарее с ЭДС ε и внутренним сопротивлением r .

Рисунок 5:  Простая схема с ячейкой и переменным резистором.

На графике показаны результаты, полученные студентом при изменении сопротивления Y от $\quantity{0,5}{Ω}$ до $\quantity{6,5}{Ω}$.

Рисунок 6:  График, показывающий, как мощность, рассеиваемая переменным резистором, изменяется в зависимости от его сопротивления.

1. Опишите, как мощность, рассеиваемая в Y, изменяется при увеличении его сопротивления от $\quantity{0,5}{Ω}$ до $\quantity{6,5}{Ω}$.

Ключевое слово в этом вопросе — описать , поэтому нам просто нужно сказать, что мы видим, но чтобы получить полную оценку, мы должны использовать данные из графика. Как мы видим, мощность увеличивается до тех пор, пока сопротивление не станет равным $\quantity{3}{Ω}$ и $\quantity{3}{W}$, а затем начинает уменьшаться по мере того, как сопротивление продолжает расти. 9{2}}{R}$. Когда внешнее сопротивление меньше внутреннего сопротивления, он будет иметь меньшую p.d. через него, поэтому он будет иметь меньшую мощность, чем внутреннее сопротивление. Когда внешнее сопротивление равно внутреннему сопротивлению, они оба будут иметь одинаковую разность потенциалов, и, следовательно, они будут иметь одинаковую мощность. Когда переменный резистор увеличивается настолько, что становится больше внутреннего сопротивления, мощность снова уменьшается, так как мощность обратно пропорциональна сопротивлению.

Это известно как теорема о максимальной мощности, т. е. максимальная мощность от источника (в данном случае от элемента) получается, когда нагрузка или внешнее сопротивление равны внутреннему сопротивлению источника питания.

2. ЭДС батареи равна $\quantity{6,0}{В}$, а сопротивление Y равно $\количество{0,80}{Ом}$.
1. Используйте данные из графика для расчета тока через батарею.

При чтении данных с графика рекомендуется тщательно аннотировать диаграмму карандашом и линейкой, чтобы убедиться, что значения, которые вы читаете, точны. 9{2}R$, чтобы найти текущий:

\начать{выравнивать} I & = \ sqrt {\ гидроразрыва {P} {R}} \\ I & = \ sqrt {\ frac {\ количество {1,95} {Вт}} {\ количество {0,80} {Ω}}} \\ \\ I&=\количество{1.56}{A} \end{выравнивание}

В таком вопросе легко забыть найти квадратный корень из $\frac{P}{R}$, поэтому будьте особенно осторожны при использовании калькулятора.

2. Рассчитать напряжение на Y.

Теперь, когда мы знаем ток и сопротивление, мы можем использовать закон Ома, $V=IR$, чтобы найти напряжение или p.d. по Ю.

$$V=\количество{1,56}{A}\times\количество{0,80}{Ω}=\количество{1,2}{V}$$
3. Рассчитайте внутреннее сопротивление батареи.

Это можно либо рассчитать по уравнению $ε=V+Ir$, либо прочитать по графику, используя теорему о максимальной мощности, как описано выше. Мы уже вычислили значения $V$ и $I$, используя уравнение и сделав $r$ субъектом:

\начать{выравнивать} г & = \ гидроразрыва {\ влево (ε-V \ вправо)} {I} \\ r&=\frac{\left(\quantity{6.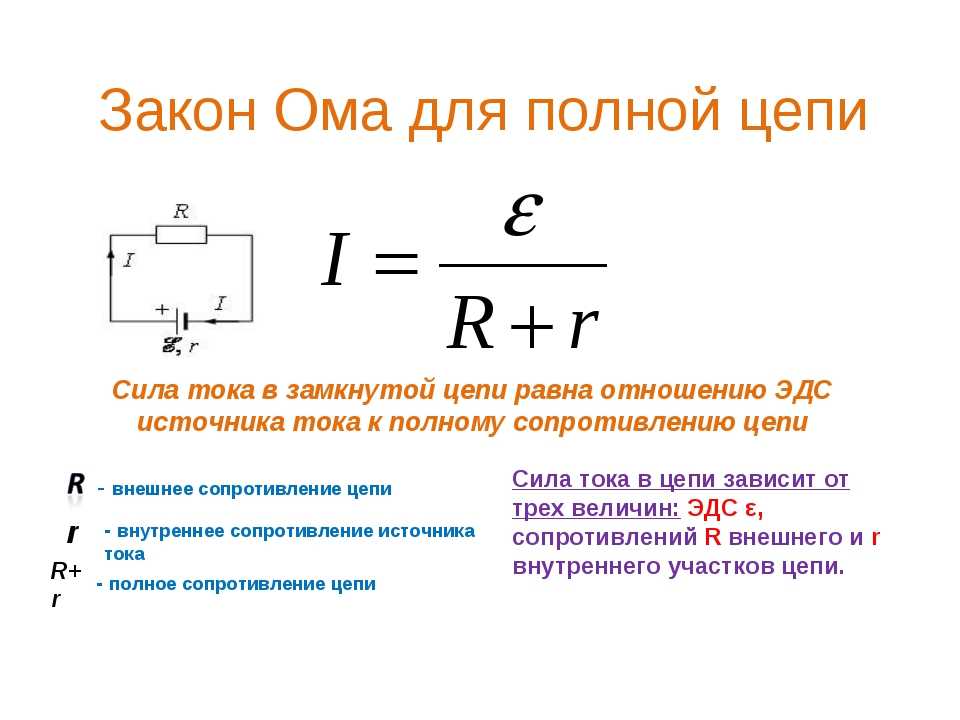 0}{V}-\quantity{1.2}{V}\right)}{\quantity{1.56}{A}}\\ \\ r&=\количество{3.1}{Ω} \end{выравнивание}

Даже если вы не смогли рассчитать прежние значения тока и разности потенциалов, вы можете прочитать значение сопротивления на пике графика, если вы указываете, что максимальная мощность будет рассеиваться, когда $Y=r $ и четко аннотировать график.

3. Учащийся повторяет эксперимент с батареей с той же ЭДС, но пренебрежимо малым внутренним сопротивлением. Сформулируйте и объясните, как теперь вы ожидаете, что мощность, рассеиваемая в Y, изменится при увеличении сопротивления Y от $\quantity{0,5}{Ω}$ до $\quantity{6,5}{Ω}$.

При незначительном внутреннем сопротивлении p.d. через Y будет равна ЭДС ячейки. Поскольку p.d. теперь постоянна, а соотношение между мощностью и сопротивлением, поскольку постоянное напряжение является обратным, мощность будет уменьшаться по мере увеличения значения Y.

Это вопрос, на который учащиеся обычно отвечают очень плохо, и легко предположить, что форма графика будет аналогичной, но иметь более низкое или более высокое значение пиковой мощности.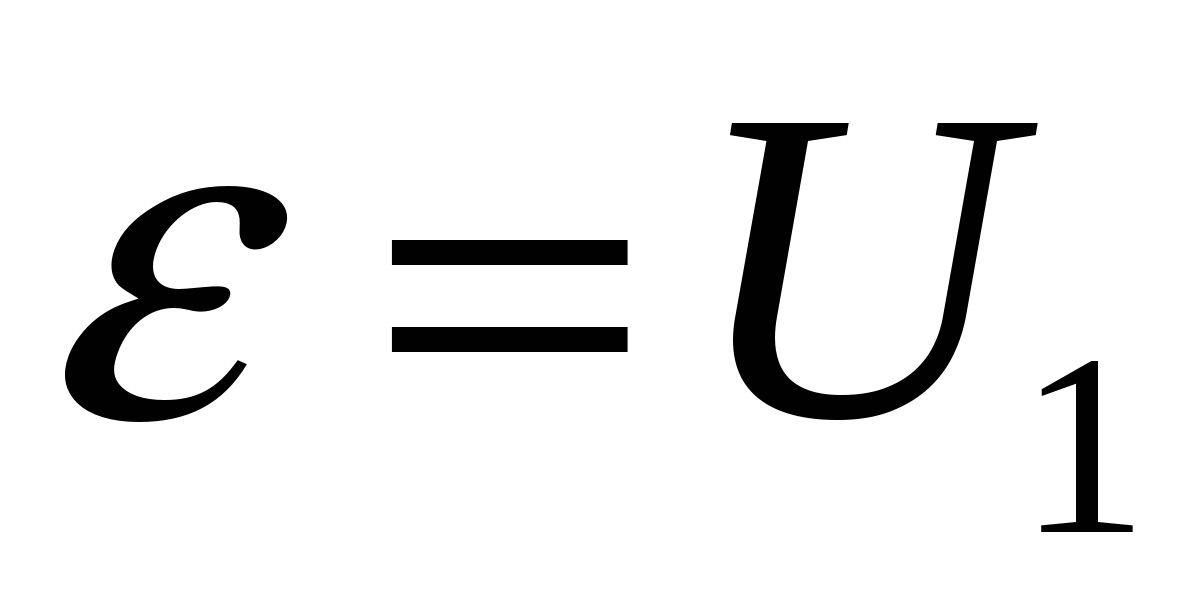 {2}}{R}$, поэтому по мере увеличения ресурса мощность уменьшается, и график будет выглядеть следующим образом:

Рисунок 8:  График, показывающий, как мощность, рассеиваемая переменным резистором, изменяется в зависимости от его сопротивления, когда внутренним сопротивлением ячейки можно пренебречь.

Наверх

---

Ресурсы

• Презентация
• Домашнее задание
• Рабочий набор CAP
• Пример данных CAP

---

Предыдущая тема

Следующая тема

Как ЭДС элемента не зависит от внешнего сопротивления (сопротивления цепи) и потребляемого тока?

спросил 2 года, 8 месяцев назад

Изменено 1 год, 8 месяцев назад

Просмотрено 571 раз

$\begingroup$

ЭДС — это работа, совершаемая для перемещения заряда по всей цепи. Если у меня есть резистор, не увеличится ли работа, проделанная для перемещения единичного заряда?

• электрические цепи
• электрические токовые
• электрические сопротивления

$\endgroup$

$\begingroup$

Как ЭДС ячейки не зависит от внешнего сопротивления (сопротивления цепь) и потребляемый ток?

ЭДС клетки представляет собой электрический потенциал (напряжение), возникающий внутри клетки в результате электрохимических реакций. Он идеально не зависит от внешнего сопротивления цепи и потребляемого тока. Напряжение на клеммах ячейки, $V_T$, не равно. Это потому, что все настоящие батареи имеют внутреннее сопротивление $r_b$. Когда ток потребляется цепью, происходит падение напряжения на внутреннем сопротивлении, что приводит к более низкому напряжению на клеммах.

На верхней диаграмме ниже показана «идеальная» батарея, то есть батарея с нулевым внутренним сопротивлением. Напряжение на клеммах $V_T$ равно ЭДС внутренней батареи независимо от сопротивления внешней нагрузки $R_L$ и потребляемого тока.

На нижней диаграмме показана «настоящая» батарея с внутренним сопротивлением $r_b$. Когда потребляется ток $I$, происходит падение напряжения $Ir_b$ на внутреннем сопротивлении, что приводит к более низкому напряжению на клеммах батареи. Аккумулятор должен совершить внутреннюю работу, чтобы преодолеть свое внутреннее сопротивление.

Надеюсь, это поможет.

$\endgroup$

$\begingroup$

ЭДС идеальной батареи постоянна, произойдет то, что ток через резистор уменьшится.

$\endgroup$

$\begingroup$

Если V=IR — это p.d на резисторе, то это то же самое для ЭДС $\epsilon=IR$, если только резистор подключен к батарее и в идеальных условиях.