Физика, 9 кл. (Буховерцев Б.Б.)
Физика, 9 кл. (Буховерцев Б.Б.)
ОглавлениеТЕПЛОВЫЕ ЯВЛЕНИЯ. МОЛЕКУЛЯРНАЯ ФИЗИКАГлава I. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ.  2. МАССА МОЛЕКУЛ. ПОСТОЯННАЯ АВОГАДРО 3. БРОУНОВСКОЕ ДВИЖЕНИЕ. 4. СИЛЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ 5. СТРОЕНИЕ ГАЗООБРАЗНЫХ, ЖИДКИХ И ТВЕРДЫХ ТЕЛ 6. ИДЕАЛЬНЫЙ ГАЗ В МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 7. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ I Глава II. ТЕМПЕРАТУРА. ЭНЕРГИЯ ТЕПЛОВОГО ДВИЖЕНИЯ МОЛЕКУЛ 8. ТЕПЛОВОЕ РАВНОВЕСИЕ. ТЕМПЕРАТУРА 9. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ 10. АБСОЛЮТНАЯ ТЕМПЕРАТУРА. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ 11. ИЗМЕРЕНИЕ СКОРОСТЕЙ МОЛЕКУЛ ГАЗА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ II Глава III. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ 13. ПРИМЕНЕНИЕ УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА К РАЗЛИЧНЫМ ПРОЦЕССАМ 14. ПРИМЕНЕНИЕ ГАЗОВ В ТЕХНИКЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ III Глава IV. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 16. РАБОТА В ТЕРМОДИНАМИКЕ 17.  КОЛИЧЕСТВО ТЕПЛОТЫ18. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 19. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ К РАЗЛИЧНЫМ ПРОЦЕССАМ 20. НЕОБРАТИМОСТЬ ПРОЦЕССОВ В ПРИРОДЕ 21. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ 22. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ (КПД) ТЕПЛОВОГО ДВИГАТЕЛЯ. ТЕПЛОВЫЕ ДВИГАТЕЛИ И ОХРАНА ПРИРОДЫ КРАТКИЕ ИТОГИ ГЛАВЫ IV Глава V. ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ 23. НАСЫЩЕННЫЙ ПАР 24. ЗАВИСИМОСТЬ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА ОТ ТЕМПЕРАТУРЫ. КИПЕНИЕ. КРИТИЧЕСКАЯ ТЕМПЕРАТУРА 25. ВЛАЖНОСТЬ ВОЗДУХА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ V Глава VI. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ 27. СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ 28. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ VI Глава VII. ТВЕРДЫЕ ТЕЛА 29. КРИСТАЛЛИЧЕСКИЕ ТЕЛА 30. АМОРФНЫЕ ТЕЛА 31. ДЕФОРМАЦИЯ. ВИДЫ ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ 32. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДИАГРАММА РАСТЯЖЕНИЯ 33. ПЛАСТИЧНОСТЬ И ХРУПКОСТЬ КРАТКИЕ ИТОГИ ГЛАВЫ VII ОСНОВЫ ЭЛЕКТРОДИНАМИКИ 34.  ЧТО ТАКОЕ ЭЛЕКТРОДИНАМИКА?Глава VIII. ЭЛЕКТРОСТАТИКА 35. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 36. ЗАРЯЖЕННЫЕ ТЕЛА. ЭЛЕКТРИЗАЦИЯ ТЕЛ 37. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА 38. ОСНОВНОЙ ЗАКОН ЭЛЕКТРОСТАТИКИ — ЗАКОН КУЛОНА 39. ЕДИНИЦА ЭЛЕКТРИЧЕСКОГО ЗАРЯДА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 40. БЛИЗКОДЕЙСТВИЕ И ДЕЙСТВИЕ НА РАССТОЯНИИ 41. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 42. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ 43. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ 45. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ РАВНОМЕРНО ЗАРЯЖЕННОГО ПРОВОДЯЩЕГО ШАРА И БЕСКОНЕЧНОЙ ПЛОСКОСТИ 46. ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ДВА ВИДА ДИЭЛЕКТРИКОВ 47. ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ 48. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 49. ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ 50. ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА 51. СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ.  ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ52. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ 53. ЭЛЕКТРОЕМКОСТЬ. ЕДИНИЦЫ ЭЛЕКТРОЕМКОСТИ 54. КОНДЕНСАТОРЫ. ЭЛЕКТРОЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА 55. ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА. ПРИМЕНЕНИЯ КОНДЕНСАТОРОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава IX. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК 56. ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА 57. УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА 58. ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ 59. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ПРОВОДНИКА ОТ ТЕМПЕРАТУРЫ 60. СВЕРХПРОВОДИМОСТЬ 61. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ 62. ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ 63. РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 65. ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ IX Глава X. ЭЛЕКТРИЧЕСКИЙ ТОК В РАЗЛИЧНЫХ СРЕДАХ 66. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ РАЗЛИЧНЫХ ВЕЩЕСТВ 67. 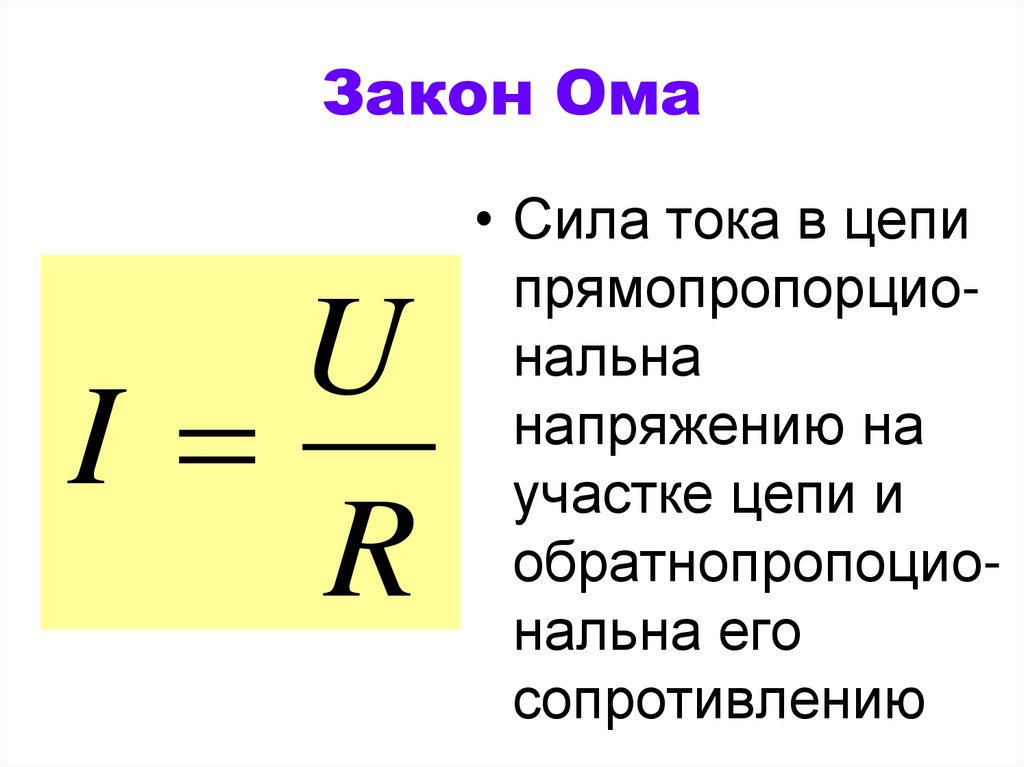 ЭЛЕКТРОННАЯ ПРОВОДИМОСТЬ МЕТАЛЛОВ68. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ 69. ЗАКОН ЭЛЕКТРОЛИЗА 70. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ 71. НЕСАМОСТОЯТЕЛЬНЫЙ И САМОСТОЯТЕЛЬНЫЙ РАЗРЯДЫ 72. РАЗЛИЧНЫЕ ТИПЫ САМОСТОЯТЕЛЬНОГО РАЗРЯДА И ИХ ТЕХНИЧЕСКИЕ ПРИМЕНЕНИЯ 73. ПЛАЗМА 74. ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ 75. ДВУХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА-ДИОД 77. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ 78. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ ПРИ НАЛИЧИИ ПРИМЕСЕЙ 79. ЭЛЕКТРИЧЕСКИЙ ТОК ЧЕРЕЗ КОНТАКТ ПОЛУПРОВОДНИКОВ p- И n- ТИПОВ 80. ПОЛУПРОВОДНИКОВЫЙ ДИОД 81. ТРАНЗИСТОР 82. ТЕРМИСТОРЫ И ФОТОРЕЗИСТОРЫ ПРИМЕР РЕШЕНИЯ ЗАДАЧИ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава XI. МАГНИТНОЕ ПОЛЕ 83. ВЗАИМОДЕЙСТВИЕ ТОКОВ. МАГНИТНОЕ ПОЛЕ 84. ВЕКТОР МАГНИТНОЙ ИНДУКЦИИ 85. ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ 86. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ 87. МОДУЛЬ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. МАГНИТНЫЙ ПОТОК 88. ЗАКОН АМПЕРА 89. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД.  90. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XI Глава XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ 91. ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 92. НАПРАВЛЕНИЕ ИНДУКЦИОННОГО ТОКА. ПРАВИЛО ЛЕНЦА 93. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 94. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 95. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ 96. САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ 97. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА 98. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ И ИХ ТЕХНИЧЕСКОЕ ПРИМЕНЕНИЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XII ЗАКЛЮЧЕНИЕ ЛАБОРАТОРНЫЕ РАБОТЫ |
Закон Ома для участка цепи. Видеоурок и разноуровневые самостоятельные работы. 10 класс. Физика. — Объяснение нового материала.
Комментарии преподавателяВ предыдущих параграфах были рассмотрены три величины, с которыми мы имеем дело в любой электрической цепи, — это сила тока, напряжение и сопротивление.
Эти величины связаны между собой. Зависимость силы тока от напряжения мы уже установили.
При проведении физических опытов, в которых определяют зависимость одной величины от другой, все остальные величины должны быть постоянными. Если они будут изменяться, то установить зависимость будет сложнее.
Поэтому, определяя зависимость силы тока от сопротивления, напряжение на концах проводника надо поддерживать постоянным.
Чтобы ответить на вопрос, как зависит сила тока в цепи от сопротивления, обратимся к опыту.
Магазин сопротивлений
На рисунке изображена электрическая цепь. В эту цепь по очереди включают проводники, обладающие различными сопротивлениями. Напряжение на концах проводника во время опыта поддерживается постоянным. За этим следят по показаниям вольтметра. Силу тока в цепи измеряют амперметром.
Рис. Зависимость силы тока от сопротивления
В таблице приведены результаты опытов с тремя различными проводниками.
Таблица
В первом опыте сопротивление проводника 1 Ом и сила тока в цепи 2 А. Сопротивление второго проводника 2 Ом, т. е. в два раза больше, а сила тока в два раза меньше. И наконец, в третьем случае сопротивление цепи увеличилось в четыре раза и во столько же раз уменьшилась сила тока. Напомним, что напряжение на концах проводников во всех трёх опытах было одинаковое, равное 2 В.
Обобщая результаты опытов, приходим к выводу, что сила тока в проводнике обратно пропорциональна сопротивлению проводника.
Ом Георг (1787—1854)
Немецкий физик.
Он вывел теоретически и подтвердил на опыте закон, выражающий связь между силой тока в цепи, напряжением и сопротивлением.
Зависимость силы тока от напряжения на концах участка цепи и сопротивления этого участка называется законом Ома по имени немецкого учёного Георга Ома, открывшего этот закон в 1827 г. Закон Ома читается так: сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
I = U / R
здесь I — сила тока в участке цепи, U — напряжение на этом участке, R — сопротивление участка.
Закон Ома — один из основных физических законов.
На рисунке зависимость силы тока от сопротивления проводника при одном и том же напряжении на его концах показана графически. На этом графике по горизонтальной оси в условно выбранном масштабе отложены сопротивления проводников в омах, по вертикальной — сила тока в амперах.
Рис, График зависимости силы тока в цепи от сопротивления
Из формулы I = U / R — следует, что
U = I • R и R = U / I
Следовательно, зная силу тока и сопротивление, можно по закону Ома вычислить напряжение на участке цепи, а зная напряжение и силу тока — сопротивление участка.
Сопротивление проводника можно определить по формуле R = U / I, однако надо понимать, что R — величина постоянная для данного проводника и не зависит ни от напряжения, ни от силы тока. Если напряжение на данном проводнике увеличится, например в три раза, то во столько же раз увеличится и сила тока в нём, а отношение напряжения к силе тока не изменится.
К занятию прикреплен файл «Это интересно!». Вы можете скачать файл в любое удобное для вас время.
. Действительно ли диод следует закону Ома?
Это действительно не черно-белый вопрос, и многие люди будут утверждать, что он не следует «Закону Ома», и в зависимости от того, как вы это аргументируете, они могут быть правы.
Однако на самом деле сопротивление диода изменяется в зависимости от приложенного тока или напряжения. Таким образом, вы не можете просто посмотреть сопротивление диода и использовать «закон Ома», чтобы определить соотношение между напряжением и током по старой доброй формуле V = IR, как вы можете это сделать с резистором. Из этого аргумента ни один диод, а точнее, полупроводник, похоже, не подчиняется закону Ома.
Однако, если у вас есть цепь с диодом, смещенным при напряжении V или с током смещения I, сопротивление диода в этих условиях остается постоянным. То есть формула Ома по-прежнему применяется, когда диод находится в устойчивом состоянии.
Если вы пытаетесь рассчитать выходной импеданс вашей схемы в этом состоянии, это важно знать, при этом признавая, что импеданс будет другим, когда схема находится в другом состоянии.
На самом деле, я бы даже сказал, что диод всегда подчиняется формуле Ома. Да V=ИК. Однако в случае диода R следует довольно сложному уравнению, включающему V или I в качестве переменных.0003
То есть для диода
\$V = I.R_D\$ Где
\$R_D = F(I,V)\$
\$V = I.F(I,V)\$
Итак, да, математически он следует формуле Ома, просто не в такой форме, которая вам очень полезна, за исключением очень специфических статических условий.
Для тех, кто утверждает, что «Закон Ома неприменим, если сопротивление непостоянно», я боюсь, что это неверная цитата Максвелла. Намерение Ома заключалось в том, что сопротивление должно быть постоянным во времени при стабильных условиях возбуждения. То есть сопротивление не может измениться самопроизвольно без изменения приложенного напряжения и тока.
Правда в том, что ничто не имеет фиксированного сопротивления. Даже ваш скромный резистор на четверть ватта изменит сопротивление при нагревании и старении.
Если вы думаете, что это всего лишь мнение одного человека, вы будете правы, его зовут
Георг Саймон Ом
Скорее всего, вы никогда не читали его работы, а если читали по-немецки, то оригинальную версию. Если вы когда-нибудь это сделаете, и я предупреждаю вас, что на 281 странице устаревшей английской и электрической терминологии это очень трудно читать, вы обнаружите, что он действительно охватывал нелинейные устройства, и поэтому они должны быть включены в законе Ома. На самом деле есть целое Приложение, около 35 страниц, полностью посвященное этой теме. Он даже признает, что там еще есть что обнаружить, и оставляет это открытым для дальнейшего расследования.
Закон Ома гласит.. согласно Максвеллу..
«Электродвижущая сила, действующая между концами любой части цепи, является произведением силы тока и сопротивления этой части цепи».
Это, однако, является лишь частью тезиса Ома и определяется словами Ома утверждением «гальваническая цепь… которая приобрела свое постоянное состояние» , которое определено в статье, и я перефразирую, как любое Элементу, сопротивление которого зависит от приложенного напряжения, тока или чего-то еще, необходимо дать возможность прийти в сбалансированное состояние. Далее, после любого изменения возбуждения цепи в целом, прежде чем формула начнет действовать, должна произойти перебалансировка. Максвелл, с другой стороны, квалифицировал это так: R не должно меняться с V или I.
Возможно, это не то, чему вас учили в школе, или даже то, что вы слышали, цитировали или читали из многих авторитетных источников, но это от самого Ома. Настоящая проблема заключается в том, что многие люди воспринимают или понимают лишь очень упрощенную интерпретацию тезиса Ома, написанную Максвеллом, которая, возможно, ошибочно распространялась десятилетиями с тех пор, как великий человек фактически выполнил свою работу под названием «Закон Ома».
Что, конечно, оставляет вас с парадоксом.
Дело в том, что Ом просто сформулировал: как только он установится в стабильное состояние, напряжение в цепи будет суммой тока, умноженного на сопротивления частей.
смоделируйте эту схему. Схема создана с помощью CircuitLab
\$E = I.R1 + I.R2 + I.R3\$
Где R3 — сопротивление диода. Таким образом, не имеет значения, является ли R3 диодом или нет. Что конечно правильно. Максвелл, с другой стороны, подразумевает, что, поскольку схема содержит нелинейный элемент, формула неприменима, что, конечно же, неверно.
Итак, полагаем ли мы, что то, что написал Максвелл, было ошибкой чрезмерного упрощения, и придерживаемся того, что на самом деле сказал Ом, или мы отбрасываем то, что на самом деле сказал Ом, и придерживаемся упрощения Максвелла, которое оставляет нелинейные части в стороне?
Если вы считаете, что диод не соответствует вашей ментальной модели закона Ома, то ваша модель закона Ома на самом деле является законом Максвелла.
Что-то, что нужно квалифицировать как подмножество тезиса Ома. Если вы считаете, что диод соответствует модели, то вы действительно цитируете тезис Ома.
Как я уже сказал, это не черное и белое. В конце концов, это не имеет большого значения, поскольку ничего не меняет.
Что произойдет, если студент при изучении зависимости силы тока от разности потенциалов будет держать длительное время замкнутой цепь для измерения силы тока и разности потенциалов?
Книга: Идея Xam — Наука
Глава: Бумага для тестирования модели
Тема: — Класс 10
йQ. № 24 Модельного теста 4
Слушайте аудиокниги NCERT, чтобы повысить производительность и удержание 2Х.
24
Что произойдет, если студент при изучении зависимости силы тока от разности потенциалов будет держать длительное время замкнутой цепь для измерения силы тока и разности потенциалов?
Согласно закону Ома, разность потенциалов (V) на концах резистора прямо пропорциональна току (I) через него при условии, что его температура остается неизменной.
это
Здесь R — постоянная для данного резистора при данной температуре и называется его сопротивлением. Единицей сопротивления в системе СИ является ом (Вт). График между разностью потенциалов на двух концах резистора и током через него представляет собой прямую линию, проходящую через начало координат. Наклон этого графика дает сопротивление R резистора. Чтобы проверить закон Ома, мы измеряем разность потенциалов на двух концах резистора при различных токах через него в электрической цепи. Ток через резистор измеряют, подключив к нему последовательно амперметр. Разность потенциалов на двух концах резистора измеряют, подключив к нему параллельно вольтметр.
Отсюда, Если студент при изучении зависимости силы тока от разности потенциалов держит цепь длительное время замкнутой для измерения силы тока и разности потенциалов, то:
(а) Погрешность нуля амперметра изменится
(b) Амперметр будет давать больше показаний
(c) Вольтметр будет показывать все более высокие показания
(d) Резистор будет нагреваться, и его значение будет меняться
При длительном протекании тока , резистор будет нагреваться, и его значение будет меняться, так как сопротивление зависит от температуры.
Упражнения по главам
6
При смешивании гранул твердого вещества A с порошком другого твердого вещества B не происходит химической реакции. Однако при нагревании смеси между ее компонентами происходит реакция. Один из продуктов, C, представляет собой металл и оседает в расплавленном состоянии, в то время как другой продукт, D, плавает над ним. Было замечено, что реакция сильно экзотермична.
и. На основании данной информации сделайте предположение об А и В и напишите химическое уравнение химической реакции с указанием условий реакции, физического состояния реагентов и продуктов и термического состояния реакции.
ii. Укажите любые два типа реакций, к которым можно отнести вышеперечисленные химические реакции.
8
Атомы восьми элементов A, B, C, D, E, F, G и H имеют одинаковое количество электронных оболочек, но разное количество электронов в самой внешней оболочке.
