Момент инерции твердого тела относительно постоянной оси вращения. Определение.

Момент инерции материальной точки относительно оси вращения определяется как величина, равная произведению массы материальной точки на квадрат расстояния от этой точки до оси вращения: .

Момент инерции твердого тела относительно оси вращения – мера инертности твердого тела во вращательном движении (аналог массы в поступательном движении), определяется как величина, равная сумме моментов инерции достаточно малых фрагментов твердого тела. Достаточно малым фрагментом твердого тела является фрагмент, размеры которого малы по сравнению с расстоянием от фрагмента до оси вращения. Таким образом, этот фрагмент может быть назван материальной точкой и его момент инерции подсчитывается по формуле: ,

а момент инерции всего твердого тела относительно постоянной оси вращения, по формуле: .

Для вычисления интеграла необходимо свести подинтегральное выражение к одной переменной величине.

Это достигается, в частности, учетом как характера распределения массы тела по его объему, так и симметрии формы тела.

Момент инерции твердого тела относительно постоянной оси вращения. Теорема о параллельных осях (теорема Штейнера).

Теорема связывает момент инерции относительно произвольной оси с моментом инерции относительно параллельной ей оси, проходящей через центр масс твердого тела: . Здесь m — масса тела, a – расстояние между осями.

Момент инерции твердого тела относительно постоянной оси вращения. Теорема о взаимно перпендикулярных осях.

Момент инерции плоского тела относительно произвольной оси

Z, перпендикулярной его плоскости, равен сумме моментов инерции относительно двух взаимно перпендикулярных осей X и Y, лежащих в плоскости тела и пересекающихся с осью Z: .

Уравнение вращательного движения твердого тела вокруг постоянной оси.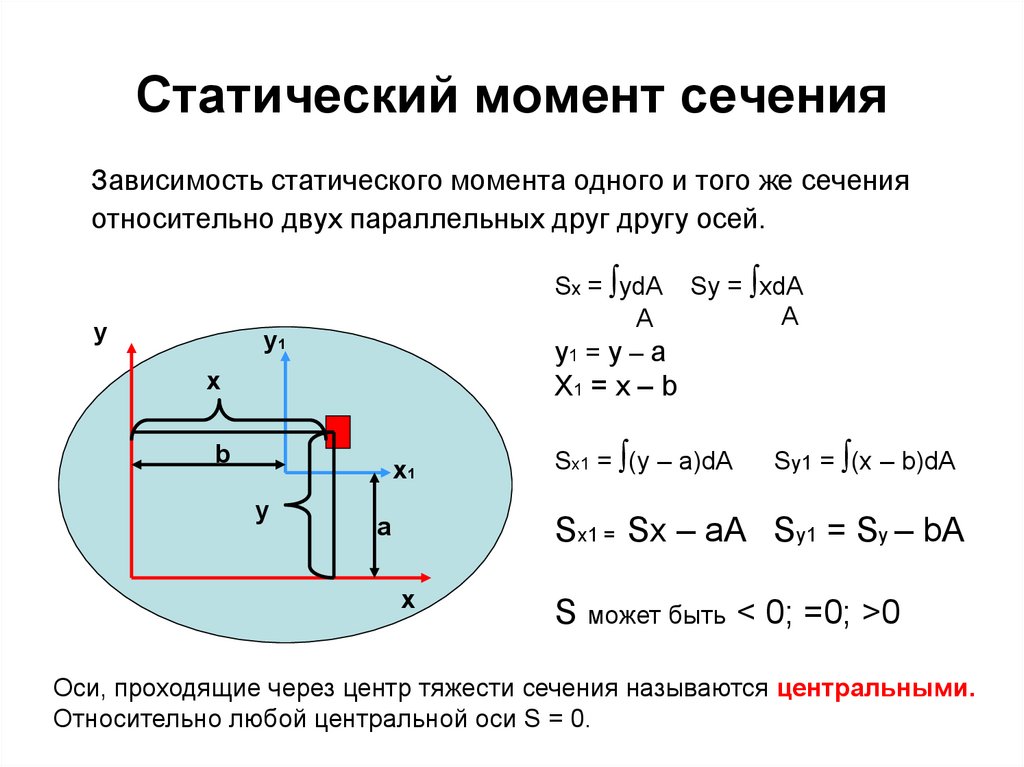

Уравнение записано в проекции на совмещенную с осью вращения координатную ось Z.

СЕМИНАР 5 МЕХАНИКА ТВЕРДОГО ТЕЛА. ЗАКОНЫ СОХРАНЕНИЯ.

Момент импульса твердого тела.

Момент импульса твердого тела относительно неподвижной оси Z, или проекция вектора момента импульса на координатную ось Z, совпадающую с осью вращения, равен произведению момента инерции тела относительно этой оси вращения на проекцию вектора угловой скорости на координатную ось Z.

Сохранение момента импульса системы твердых тел.

Для того чтобы момент импульса системы тел относительно некоторой оси сохранялся, необходимо чтобы суммарный момент внешних сил относительно этой оси был равен нулю.

Собственный момент импульса твердого тела относительно постоянной оси вращения.

-вычисляется относительно системы отсчета центра масс.

Кинетическая энергия твердого тела вращающегося вокруг постоянной оси.

Кинетическая энергия твердого тела в случае плоского движения.

В этом случае кинетическая энергия складывается из собственной энергии вращения вокруг оси, проходящей через центр масс и энергии поступательного движения со скоростью центра масс.

СЕМИНАР 6 ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ.

Собственные колебания

Гармоническими колебаниями материальной точки называется движение, при котором смещение x от положения устойчивого равновесия зависит от времени по закону , или .

Здесь .

Определение амплитуды смещения и начальной фазы колебаний смещения через начальное смещение и начальную скорость.

Если используется закон движения в виде , то .

Если же закон движения имеет вид , то .

Определение частоты или периода колебаний смещения колеблющегося тела от положения устойчивого равновесия.

Сначала убеждаемся в том, что у рассматриваемого тела или системы тел имеется положение устойчивого равновесия. Для этого положения записываем условие статики. Далее используем уравнение движения или закон сохранения механической энергии. В итоге приходим к уравнению гармонического осциллятора

Затухающие колебания Уравнение затухающих колебаний

.

Здесь , .

Решение уравнения .

Амплитуда затухающих колебаний . Коэффициент затухания и циклическая частота затухающих колебаний . Время релаксации , декремент и логарифмический декремент . Число колебаний за время релаксации .

Добротность . Зависимость энергии затухающих колебаний от времени .

Вынужденные колебания

Уравнение вынужденных колебаний

Решение уравнения .

Амплитуда вынужденных колебаний

Тангенс разности фаз колебаний вынуждающей силы и колебаний смещения материальной точки от положения равновесия .

Частота колебаний вынуждающей силы, при которой наблюдается резонанс смещения .

Добротность, как отношение смещения при резонансе к смещению при постоянной вынуждающей силе .

Задачи на геометрические характеристики | ПроСопромат.ру

Определить главные центральные моменты инерции, осевые моменты сопротивления  сечения, составленного из стандартных профилей проката.

Сечение состоит из двух неравнополочных уголков 75×50х5 (маркировка в мм) и швеллера № 16 (№ швеллера говорит о его высоте в см).

1. Определим положение центра тяжести сечения.

Сечение симметрично относительно оси у, проводим её как ось – главную и центральную. Координата х_С=0. Для нахождения у

С проводим случайную ось х′ (выбранную случайным образом). Обозначим центры тяжести всех профилей и выпишем необходимые характеристики профилей из сортамента прокатной стали.

Фигуры 1,2 – уголки 75×50х5

А₁=А₂=6,11 см²

I_х1= I_х2=34,8 см⁴

I_у1= I_у2

=12,5 см⁴

Фигура 3 – швеллер №16

А₃=18,1 см²,    

I_х3=747 см⁴, 

I_у3=63,3 см⁴.

Покажем на схеме и определим координаты у для профилей

у₁ = у₂ = у₀ =2,39 см,

у₁= —z₀ =-1,8 см.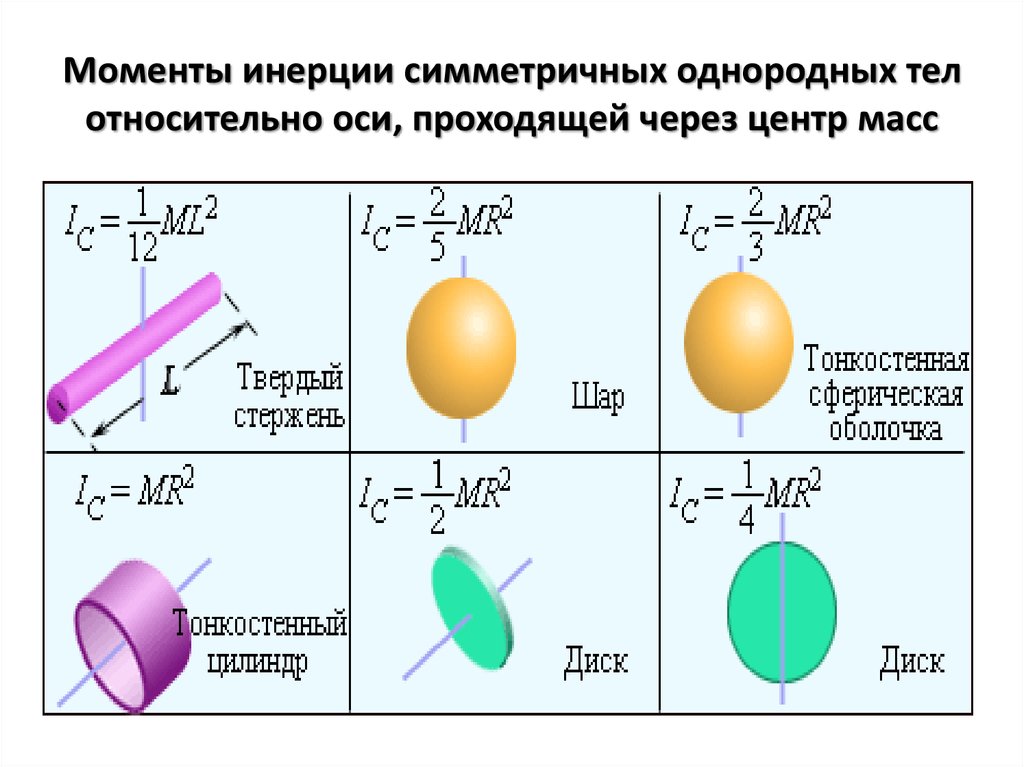

Определим координату у_С по формуле

 ,

где А_i – площадь каждого профиля,

      у_i – координата.

Проводим главную центральную ось х вниз от оси х′ на 0,11 см, наносим т.С – центр тяжести всего сечения.

2. Определяем главные центральные моменты инерции по формулам перехода:

,

где I_xi , I_yi — моменты инерции каждой фигуры;

А_i – площадь сечения каждой фигуры;

а_i – расстояние от центра тяжести

каждой фигуры до главной центральной оси х;

b_i – расстояние от центра тяжести каждой фигуры до главной центральной оси у.

Определяем а_i (смотрим схему)

а₁ = а₂ = у₁+|у_С|= 2,39 + 0,11 = 2,5см,

а₃= — (|у₃|-|у_С|) = -1,69см.

Определяем I_х. Следует обратить внимание на то, что фигура 3 – швеллер – повернут, поэтому, для определения I_х следует из сортамента взять I_у швеллера.

I_х3=63,3см⁴

Определяем I_у.  Для швеллера (повернут)  I_у3 =  I_х = 747см⁴.

Определим размеры b_i, показываем на схеме.

b₁= —х₀ = -1,17см,

b₂= х₀ = 1,17см,

b₃=0, т. к. центр тяжести швеллера лежит на оси у.

3. Определим осевые моменты сопротивления сечения по формулам:

Из схемы видно ,что

Тогда

Запись опубликована 08.09.2016 автором admin в рубрике Задачи на геометрические характеристики.

Определить главные центральные моменты инерции сечения геометрической формы.

1. Определим положение центра тяжести сечения.

Сечение симметрично относительно оси у, поэтому нанесем ось у – ось, на которой находится центр тяжести всего сечения. Координата х_С=0, значит, следует определить координату у_С.

Выберем случайную ось х′ — внизу сечения.

Разобьем сечение на простые фигуры:

фигура 1 – прямоугольник с основанием 8 см и высотой 6 см, отмечаем центр тяжести прямоугольника – т. С₁

фигура 2 – равнобедренный треугольник с основанием 8 см и высотой 3 см, отмечаем его центр тяжести – т. С₂.

Теперь  вычислим площади каждой фигуры и определим  координаты у каждой фигуры, затем координаты нанесем на схему

Прямоугольник

Треугольник

Теперь определим координату центра тяжести всего сечения по формуле:

Тогда

Отмечаем у_С на схеме, центр тяжести всего сечения – т. С — и проводим через эту точку главную центральную ось х.

По формулам перехода определяем главные центральные моменты инерции сечения:

,

где I_xi  , I_yi  — моменты инерции каждой фигуры;

А_i– площадь сечения каждой фигуры;

а_i – расстояние от центра тяжести каждой фигуры до главной центральной оси х;

b_i – расстояние от центра тяжести каждой фигуры до главной центральной оси у.

Фигура 1 – прямоугольник

Расстояние а₁ от С₁ до оси х покажем на схеме. Из схемы видно, что а₁=- ( у_С — у₁ )= -0,8 см. Так как С₁находится на оси у, то b₁=0.

Фигура 2 – треугольник

Находим а₂ =  у₂ — у_С = 7 — 3,8= 3,2 см, отмечаем на схеме.

b₂=0, т.к. С₂ находится на оси у.

Подставляем значения в формулы перехода и определяем:

— главный центральный момент инерции сечения относительно оси х

— главный центральный момент инерции сечения относительно оси у

Таким образом,

Запись опубликована 06. 09.2016 автором admin в рубрике Задачи на геометрические характеристики.

Для заданного поперечного сечения, состоящего из швеллера и равнобокого (равнополочного) уголка   требуется определить главные центральные моменты инерции

1)  Вычерчиваем сечение в масштабе.

2)  Разбиваем на простейшие фигуры:

       1. Швеллер №30 (пользуемся сортаментом прокатных профилей):

   2. Уголок :

3)  В каждой фигуре найти собственный центр тяжести С₁ и С_{2   ,}провести собственные оси.

4)  Выбрать вспомогательные оси  .

5) Относительно вспомогательных осей определить центр тяжести всей фигуры:

Через найденный центр тяжести проводим центральные оси.

6) Находим моменты инерции всей фигуры относительно центральных осей, используя формулы перехода между параллельными осями

При определении центробежного момента инерции следует помнить ,что если фигура имеет хотя бы одну ось симметрии, то эта ось является главной, вторая ось, перпендикулярная ей, тоже главная. Центробежный момент относительно главных осей равен 0. Таким образом, для швеллера  

Для уголка  см⁴,  знак зависит от расположения уголка (см. Таблицы «Знак центробежного момента для уголков»). В нашем случае он положительный.

Здесь: а_i – расстояния между центральной осью Х и собственным центром тяжести каждой фигуры,

b_i – расстояние между центральной осью Y и собственным центром тяжести каждой фигуры 

Как видим из вычислений, центробежный момент инерции сечения значит, центральные оси Х;Y не являются главными!

7) Определим положение главных осeй через угол α₀:

Знак «-» означает, что надо повернуть оси Х, У по часовой стрелке.

8) Определим главные моменты инерции сечения

 9) Проверка: Сумма моментов инерции относительно любых двух взаимно перпендикулярных осей есть величина постоянная:

Проверка выполняется.

 

Запись опубликована 06.12.2014 автором admin в рубрике Задачи на геометрические характеристики.

Найти главные центральные моменты инерции.

 

1. Подготовка исходных данных.

Из сортамента выписываем:

— для двутавра №10:

— для швеллера №20:

Нумеруем составные части, показываем их центры тяжести (С₁, С₂, С₃) и собственные центральные оси каждой из них (х₁,у₁; х₂,у₂; х₃,у₃).

2.  Поскольку сечение имеет одну ось симметрии, то она – одна из главных центральных (у₀). Найдем положение центра тяжести на этой оси. Для этого выберем вспомогательную ось х‘, перпендикулярную оси симметрии, и реализуем формулу:

которая и определит расстояние от оси х‘ до искомого центра тяжести.

Тогда А=А₁+А₂+А₃=2×20+14,3+28,83=83,15 см²,

тогда

Показываем на схеме центр тяжести «С» и проводим вторую главную центральную ось х₀.

Ординаты собственных центров тяжести простых фигур в системе главных центральных осей:

3. Вычисляем главные центральные моменты инерции

Итак, 

 

 

 

Запись опубликована 20. 09.2014 автором admin в рубрике Задачи, Задачи на геометрические характеристики.

Определить главные центральные моменты инерции сечения.

Составные простые части сечения: прямоугольник 100×60см (I),  полукруг r=30см  (IIи III), треугольник 100×30см (IV). 

Вертикальная ось симметрии у₀ является одной из главных центральных осей.

1. Найдем положение центра тяжести сечения на оси симметрии. Для этого выберем вспомогательную ось х‘, перпендикулярную оси симметрии. Пусть она совпадает с осями: х₁, х₂, х₃

.

 

Общая площадь А = А₁ — А₂ — А₃ + А₄ = 6000 – 1415 – 1415 + 1500 = 4670см².

Статический момент относительно вспомогательной оси х‘:

Тогда

значит, центр тяжести сечения располагается на 12,8см выше вспомогательной оси х‘.

 

2. Вычисляем осевые моменты инерции    

Они и будут главными центральными моментами инерции сечения.

Здесь применялись формулы:

 

 

 

Запись опубликована 20.09.2014 автором admin в рубрике Задачи, Задачи на геометрические характеристики.

Найти главные центральные моменты инерции сечения, состоящего из листа 40×2см и двух уголков №14/9.

Исходные данные из сортамента для неравнобокого уголка №14/9.

Сечение имеет одну ось симметрии. Она – одна из главных центральных. Обозначаем её х₀. Чтобы показать вторую главную центральную ось, надо найти положение центра тяжести на оси симметрии:

Выбираем вспомогательную ось у‘, перпендикулярную к оси симметрии и вычисляем статический момент сложного сечения относительно этой оси:

Проводим главную центральную ось у₀ через найденный центр тяжести.  

Вычисляем непосредственно главные центральные моменты инерции:

Таким образом, 

 

Запись опубликована 20.09.2014 автором admin в рубрике Задачи, Задачи на геометрические характеристики.

Требуется найти главные центральные моменты инерции.

Сечение имеет две оси симметрии. Следовательно, центр тяжести совпадает с точкой пересечения этих осей, а сами они оказываются главными центральными осями.

Остается лишь вычислить осевые моменты инерции относительно осей х₀ и у₀.

«Разбиваем» сечение на простые фигуры: прямоугольник 6×8см и два круга r=1см. Тогда:

Итак

,

 

 

Запись опубликована 20. 09.2014 автором admin в рубрике Задачи, Задачи на геометрические характеристики.

Требуется определить величины главных центральных моментов инерции.

Сечение имеет одну ось  симметрии.

На основании первого признака главных осей для симметричных сечений можно утверждать, что ось симметрии является одной из главных центральных осей. Обозначаем ее «у₀». Значит, вторая главная центральная ось, перпендикулярная оси симметрии, должна проходить через центр тяжести сечения.

Следовательно, нам достаточно только найти положение центра тяжести на оси симметрии, а для этого необходимо вычислить одну лишь координату его по формуле:

С этой целью выбираем вспомогательную ось х‘, «разбиваем» сложное сечение на прямоугольник со сторонами 10 и 4см и треугольник с основанием 4см и высотой 3см.

Тогда:

Проводим через найденный центр тяжести вторую главную центральную ось х₀.

Расстояние между осями х₁ и х₀: а₁=5 — 4,3 =0,7см, а расстояние между осями х₂ и х₀: а₂=10 – 1 — 4,3 = 4,7см.

Таким образом, положение главных центральных осей найдено, осталось вычислить величины главных центральных моментов инерции:

 

Запись опубликована 20.09.2014 автором admin в рубрике Задачи, Задачи на геометрические характеристики.

х‘, у‘ – вспомогательные оси при определении положения центра тяжести сечения,

S_х’, S_у’ – статические моменты относительно вспомогательных осей,

х_с, у_с – координаты центра тяжести сечения, а также и обозначение случайных (т. е. не главных) центральных осей,

х₀, у₀ – главные центральные оси,

α₀– угол поворота главных центральных осей от случайных центральных осей х_с и у_с,

, — главные центральные моменты инерции,

с_i – центры тяжести отдельных фигур, из которых состоит сечение сложной формы,

х_i, у_i – собственные центральные оси отдельных фигур, а также и координаты центров тяжести отдельных фигур в системе вспомогательных осей х‘, у‘,

а_i, в_i – расстояния между собственными центральными осями отдельных фигур х_i, у_i и случайными центральными осями всего сечения х_с, у_с.

 

Запись опубликована 12. 09.2014 автором admin в рубрике Задачи, Задачи на геометрические характеристики.

Требуется определить положение главных центральных осей и величины главных центральных моментов инерции.

Сечение имеет сложную форму, состоит их 4^х простых фигур:

I – швеллера №30^а,

II – прямоугольника 2×40см,

III – двутавра №20^а,

IV – равнобокого уголка №12 (d=10мм).

Всё начинается с подготовки исходных данных. С этой целью необходимо сделать выписки из таблиц Сортамента прокатных сечений (см. рубрику «Таблицы»).

Этап 0. Подготовительный

Фигура I. Швеллер №30^а

Фигура II – прямоугольник 2×40см, В сортаменте прокатной стали этой фигуры нет, поскольку все геометрические характеристики ее свободно вычисляются

Фигура III. Двутавр №20^а.

Фигура IV. Равнобокий уголок №12 (d=10мм).

Пользуясь данными сортамента, на схеме сечения, вычерченной в достаточно крупном масштабе, показываем положение центров тяжести каждой из фигур и собственные центральные оси х_i, у_i.

Этап 1. Определение положения центра тяжести сечения. Сечение не имеет осей симметрии. Поэтому придётся определять две координаты центра тяжести, используя формулы:

Для реализации этих формул выбираем вспомогательные оси х‘ и у‘ (см.схему сечения).

Площади отдельных фигур: А₁=43,89см², А₂=2×40=80см²,

А₃=35,5см², А₄=23,3см².

Координаты центров тяжести отдельных фигур:

Площадь всего сечения А=182,7см².

Тогда координаты собственных центров тяжести отдельных фигур в системе случайных центральных осей х_с, у_сбудут:

а₁=2,66см,                            b₁=-7,5см

а₂=-2,34см,                           b₂=-1,93см

а₃=-7,34см,                           b₃=9,07см

а₄=14,33см,                           b₄=2,4см.

Этап 2.  Определение моментов инерции относительно случайных центральных осей  х_с, у_с.

Справочные сведения о знаке собственного центробежного момента инерции уголка (равнобокого и неравнобокого):

Справочные сведения для определения собственного центробежного момента инерции неравнобокого уголка:  

Этап 3. Определение положения главных центральных осей

Положительный угол  α₀ соответствует повороту против часовой стрелки главных осей относительно случайных (см.схему).

Этап 4. Определение величин главных центральных моментов инерции

Правило: Ось с максимальным главным моментом инерции «тяготеет» к более тяжелой случайной оси. Поэтому в нашем случае:

тогда 

 

Проверки.

1. Выполнение закона суммы осевых моментов инерции.

Для этого сравним

.

 

получаем:

Разница в последней цифре дает незначительную погрешность <<5%, что вполне допустимо в инженерных расчетах.

2. Проверка правильности вычислений.

Суть ее в том, что если все сделано правильно, то центробежный момент инерции сечения относительно найденных нами главных осей должен равняться нулю.

Подставляя сюда    и sin13˚20’=0,2306,                                                    cos13˚20’=0,9730,имеем

погрешность составляет:

И эта проверка выполняется.

 

 

Запись опубликована 11.09.2014 автором admin в рубрике Задачи, Задачи на геометрические характеристики.

Moment of Inertia Lab — Физика B. Karpowicz

Название: Moment of Inertia Lab
Дата: 3/3/15
Партнер: Steph Kinsella

Цель

Цель этой лаборатории заключалась в том, чтобы определить момент инерции объекта, используя как геометрические формулы, так и величины углового движения.

Теория

Момент инерции — это свойство любого катящегося или вращающегося объекта, которое измеряет сопротивление объекта изменению направления вращения.

Чтобы вычислить момент инерции геометрически, необходимо идентифицировать формы объектов. Поскольку объект состоит из двух одинаковых форм (полого цилиндра или кольца и сплошного цилиндра или диска), можно использовать следующие уравнения для однородных объектов. Момент инерции предназначен для расчета всего объекта, поэтому уравнения складываются вместе, чтобы получить:

Используя величины углового движения, необходимо вывести дополнительное уравнение. Используя взаимосвязь между крутящим моментом и моментом инерции, а также диаграмму свободного тела для устройства и отметив, что сила, вызывающая крутящий момент, является натяжением, верно следующее: Тогда, просуммировав силы и подставив величину натяжения обратно в вышеприведенное уравнение, получим:

Наконец, подставив соотношение между угловым и тангенциальным ускорением в исходное соотношение, мы получим окончательное уравнение.

Экспериментальная техника

После расчетов необходимо измерить массы и радиусы диска и кольца, а также радиусы основания датчика вращательного движения. Устройство, установленное, как показано ниже, должно иметь диск, плотно сидящий на датчике движения, и кольцо, закрепленное на диске. Нить плотно обматывается вокруг основания системы и подводится к шкиву под параллельным углом, чтобы уменьшить ненужное трение.

К концу струны прикреплена подвеска, которая может упасть, заставляя систему наверху вращаться. Массы меняются с каждым испытанием эксперимента, чтобы получить множество различных точек данных.

С помощью Data Studio измеряется скорость вращения и определяется ускорение вращения путем нахождения наклона графика зависимости скорости от времени.

Данные

Измеренная масса кольца составила 0 . 122 кг .
Измеренная масса диска составила 0 ,465 кг .
Измеренный внутренний диаметр кольца составил 5,070 см, что дает внутренний радиус 0,02535 м .
Внешний диаметр кольца составил 7,335 см, что делает внешний радиус 0,03668 м .
Измеренный диаметр диска составил 9,230 см, что делает радиус диска 0,04615 м .
Диаметр части датчика вращательного движения, вокруг которой вращается система, был измерен и составил 4,520 см, что составляет ее радиус 0,0226 м 92.   Пример расчета также показан ниже.

Наконец, процентная разница между геометрическими и измеренными значениями составила 0,647%.

Заключение

Целью данной лабораторной работы было определение момента инерции системы кольцо-диск двумя методами. Геометрически момент инерции оказался равным 92.   Процентная разница между двумя значениями составила 0,647% .

Небольшая ошибка может быть связана с нашей классификацией шкива. Мы рассматривали шкив как невесомую систему без трения, хотя на самом деле это не так. Шкив создает небольшое трение о струну. Он также имеет свою массу и, следовательно, свой момент инерции, который должен быть включен в геометрический расчет, но для наших целей его не было.

Ссылки

Джанколи, Д. (2009). Физика для ученых и инженеров  (4-е изд.). Река Аппер-Сэдл, Нью-Джерси: Pearson Prentice Hall.
Lahs Physics (без даты). Получено 6 октября 2014 г. с сайта www.lahsphysics.weebly.com
Момент инерции. (н.д.). Получено 8 марта 2015 г. с http://www.engineeringtoolbox.com/moment-inertia-torque-d_913.html

Примечания по расчету момента инерции полого цилиндра

В этой статье мы раскроем интересную главу. в физике: момент инерции. Сегодня мы специально сосредоточимся на моменте инерции полого цилиндра. Теперь все энтузиасты физики могут знать, что эта тема чрезвычайно важна, но многие студенты путаются, изучая ее.

Это потому, что в момент инерции есть много технических деталей. Хотя, если вы правильно понимаете основную концепцию и формулы, то эта тема не доставит вам головной боли. Итак, берите ручку и бумагу и давайте разбираться, как рассчитать момент инерции полого цилиндра без каких-либо сложностей.

Что такое момент инерции?

Момент инерции можно определить, используя концепцию оси вращения, как величину, которая помогает измерить величину крутящего момента (силы, которая может заставить объект вращаться вокруг оси), необходимой для желаемого углового ускорения. Он также широко известен как момент инерции массы или момент инерции вращения.

Теперь значение момента инерции может варьироваться в зависимости от того, какое положение оси выбрано. Единицей СИ момента инерции является кг. м².

Посетите, чтобы узнать больше о Как подготовиться к UPSC без инструктажа

Момент инерции полого цилиндра:

Здесь мы рассмотрим момент инерции полого цилиндра, который вращается вокруг оси, проходящей через центр цилиндра. Для этого расчета мы будем использовать внутренний радиус r1 и внешний радиус r2. Поскольку мы знаем, что момент инерции не является полным без массы M, поэтому мы также будем использовать его. Итак, окончательное уравнение, которое мы получаем, выглядит следующим образом:

I= 1 ⁄ 2 M (r2² + r1²) 

Аналогично можно получить момент инерции полого цилиндра с тонкой стенкой;

I=Mr²

Я знаю, что у вас много путаницы относительно вывода этих уравнений. Не волнуйтесь, продолжайте читать статью, так как ниже мы подробно расскажем вам, как рассчитать момент инерции полого цилиндра.

Читайте также Учебный план UPSC скачать в формате pdf

Расчет момента инерции полого цилиндра:

Разберем компоненты полого цилиндра: внутренний радиус r¹, внешний радиус r² с массой M и длиной L.