Влияние геомагнитных бурь на здоровье человека
Статья опубликована на с. 16-17 (Мир)
К числу физических факторов окружающей природной среды, влияющих на здоровье человека, относятся и периодические возмущения магнитного поля Земли, геомагнитные бури.
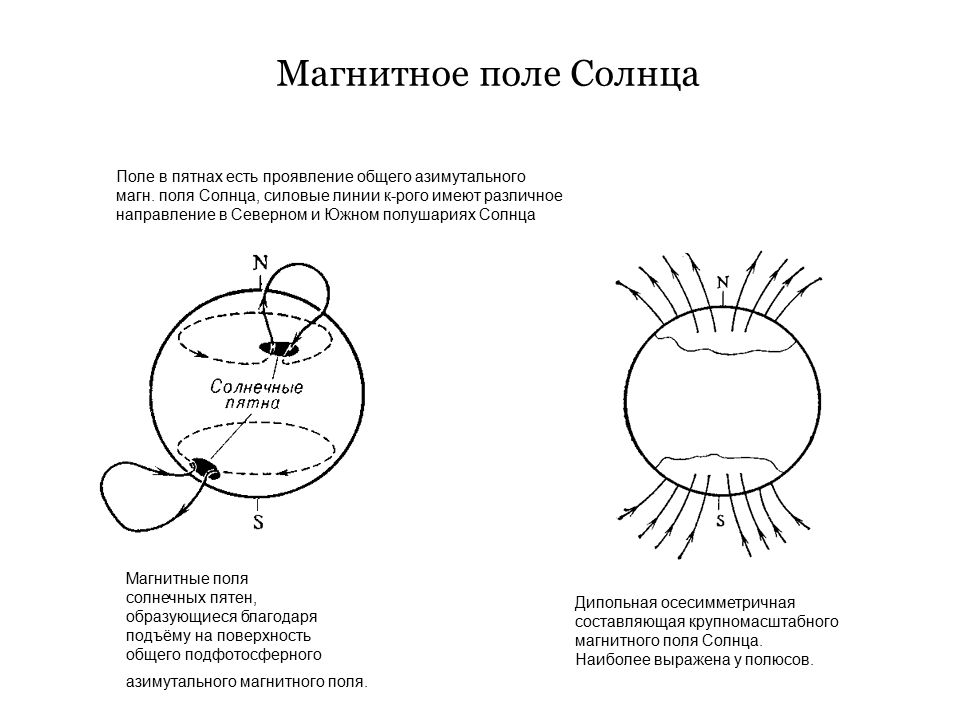
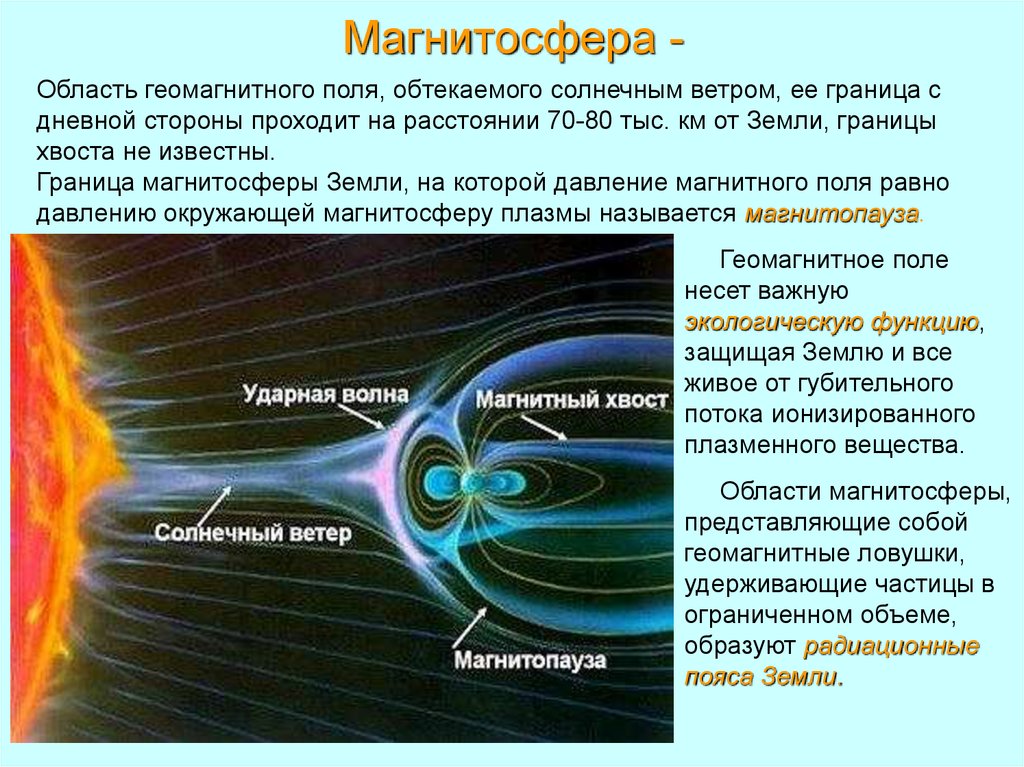
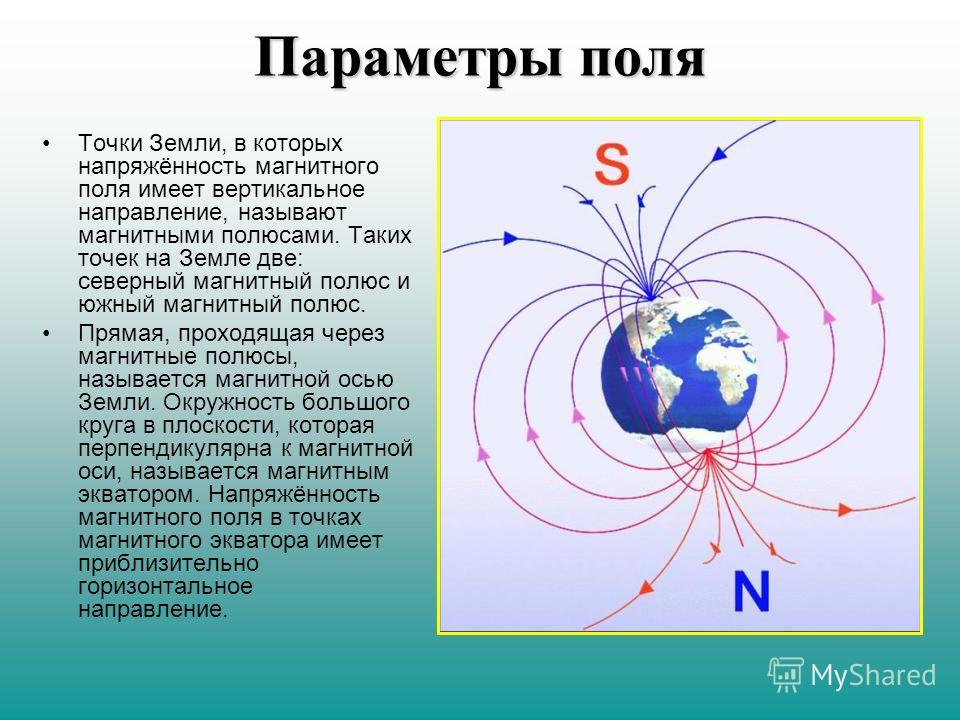
Как известно, Земля представляет собой гигантский магнит, имеющий магнитные полюса в Северном и Южном полушарии, с небольшим отклонением от их географических полюсов. По мнению большинства ученых, своим существованием геомагнитное поле (ГМП) обязано круговым токам, порождаемым жидким, состоящим в основном из железа ядром Земли. Конфигурация ГМП неравномерна: оно сжато со стороны видимого Солнца и хвостообразно вытянуто с противоположной. Это поле имеет конусообразную форму и простирается вокруг Земли на значительное расстояние — до 70–80 тысяч километров по направлению к Солнцу и в десятки раз больше в сторону от него (что примерно составляет 10 земных радиусов в первом и более 1000 радиусов — во втором случае).


В плане осведомленности населения наиболее часто используется так называемый K-индекс, характеризующий отклонение магнитного поля Земли от нормы в течение трехчасового интервала. Он имеет значения от 0 до 9 для каждого трехчасового интервала (0–3, 3–6, 6–9 и т.д.) мирового времени. Эти значения вычисляются как среднее из показаний нескольких геомагнитных обсерваторий, расположенных между 44 и 60 градусами северной и южной геомагнитных широт.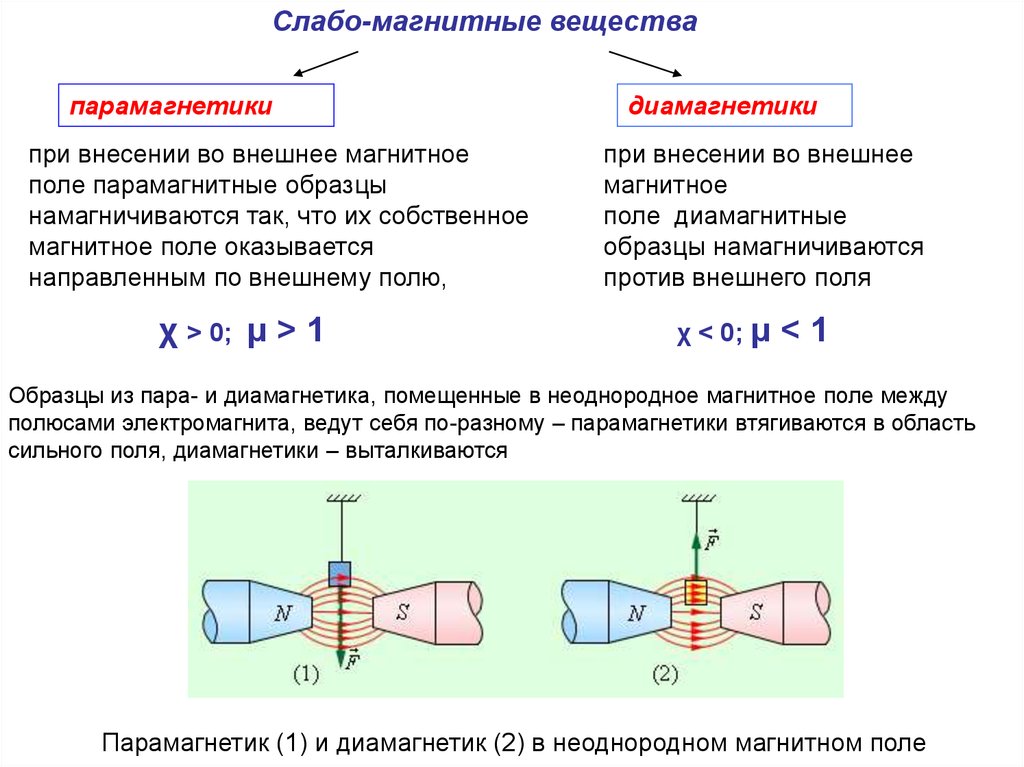



 Повышается уровень холестерина в крови. Многие ученые обращают внимание на близость параметров геомагнитных колебаний к частоте сердечных сокращений, а следовательно, вероятна опасность наслоения внешнего физического ритма на внутренний, что провоцирует возникновение аритмий, спазмы сердечных сосудов. Когда речь идет о влиянии ГМБ на функции организма, нередко высказывается мнение, что энергия магнитного поля мала и вряд ли способна восприниматься чувствительными системами и клетками организма. Некоторые ученые считают, что чувствительность человека к ГМБ природного происхождения уменьшает техногенный электромагнитный фон, формируемый многочисленными производственными и электробытовыми устройствами, контакт с которыми все более возрастает (чувствительность к ГМБ как бы ослабляется повседневными техногеннми электромагнитными шумами). Обращается внимание, например, на магнитные поля в метро, связанные с движением поездов и др. Убедительный ответ был дан в свое время (1967 г.) Г.В. Плехановым.
Повышается уровень холестерина в крови. Многие ученые обращают внимание на близость параметров геомагнитных колебаний к частоте сердечных сокращений, а следовательно, вероятна опасность наслоения внешнего физического ритма на внутренний, что провоцирует возникновение аритмий, спазмы сердечных сосудов. Когда речь идет о влиянии ГМБ на функции организма, нередко высказывается мнение, что энергия магнитного поля мала и вряд ли способна восприниматься чувствительными системами и клетками организма. Некоторые ученые считают, что чувствительность человека к ГМБ природного происхождения уменьшает техногенный электромагнитный фон, формируемый многочисленными производственными и электробытовыми устройствами, контакт с которыми все более возрастает (чувствительность к ГМБ как бы ослабляется повседневными техногеннми электромагнитными шумами). Обращается внимание, например, на магнитные поля в метро, связанные с движением поездов и др. Убедительный ответ был дан в свое время (1967 г.) Г.В. Плехановым. Он показал, что энергетический уровень магнитных бурь действительно невелик, но все же он примерно в 100 раз выше пороговых значений клеточной восприимчивости и реакции клеточных структур человека и животных (кстати, многие животные весьма чувствительны). В биологических системах, в том числе в организме человека, существуют упорядоченные движения электрических зарядов (электронов и ионов), определяющие основные процессы жизнедеятельности клеток. Кроме токов и зарядов, в живом организме имеются маленькие «магнитики» — это молекулы различных веществ, прежде всего молекулы воды, в эритроцитах и некоторых тканях содержится железо. Меняющееся геомагнитное поле вызывает переориентацию маленьких «магнитиков» в организме, меняя их первоначальное расположение. В организме возникают дополнительно к существующим в нем биотокам иные электрические токи, что еще больше нарушает его нормальную жизнедеятельность. Временной разрыв между хромосферными вспышками и связанными с ними ГМБ и проявлениями неблагоприятных реакций на них со стороны здоровья человека имеет существенные различия.
Он показал, что энергетический уровень магнитных бурь действительно невелик, но все же он примерно в 100 раз выше пороговых значений клеточной восприимчивости и реакции клеточных структур человека и животных (кстати, многие животные весьма чувствительны). В биологических системах, в том числе в организме человека, существуют упорядоченные движения электрических зарядов (электронов и ионов), определяющие основные процессы жизнедеятельности клеток. Кроме токов и зарядов, в живом организме имеются маленькие «магнитики» — это молекулы различных веществ, прежде всего молекулы воды, в эритроцитах и некоторых тканях содержится железо. Меняющееся геомагнитное поле вызывает переориентацию маленьких «магнитиков» в организме, меняя их первоначальное расположение. В организме возникают дополнительно к существующим в нем биотокам иные электрические токи, что еще больше нарушает его нормальную жизнедеятельность. Временной разрыв между хромосферными вспышками и связанными с ними ГМБ и проявлениями неблагоприятных реакций на них со стороны здоровья человека имеет существенные различия.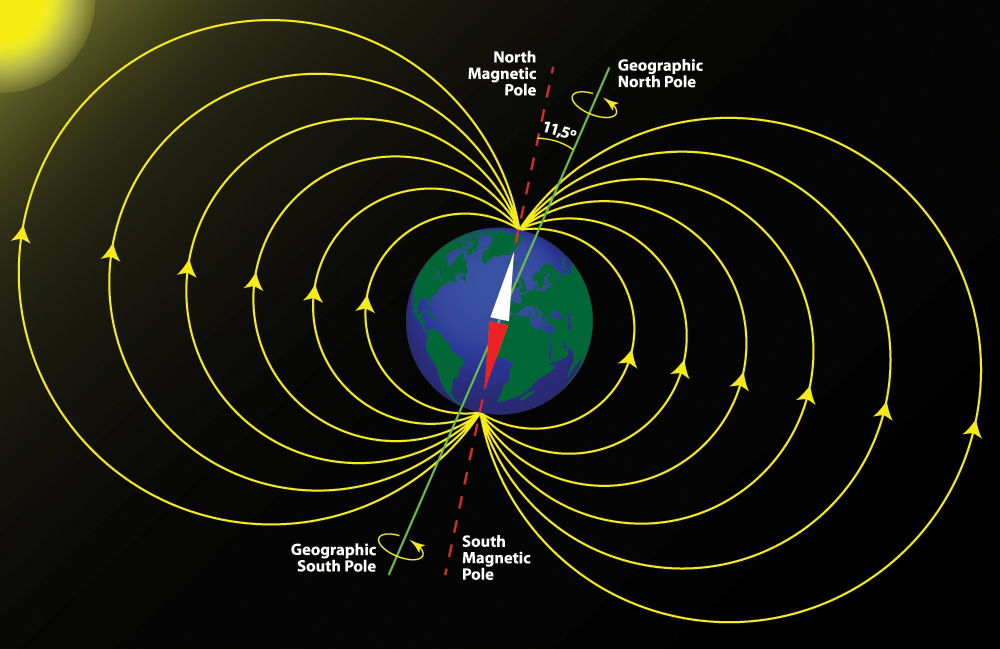 Большинство людей ощущает такие реакции на 2–3-й день после вспышки на Солнце, т.е. с момента начала ГМБ. Однако отмечено, что у некоторых людей подобная реакция возникает и за 1–2 дня до ГМБ, совпадая с появлением вспышек на Солнце. Солнечное излучение многокомпонентно, его составляющими являются корпускулярные потоки электронов, протонов, ядер гелия, рентгеновское и электромагнитное излучение, выбросы так называемой «корональной массы» и др. Возможно, реакция на хромосферные вспышки, предшествующие ГМБ, обусловлена тем, что рентгеновское и электромагнитное излучение достигает Земли через 8–10 минут от начала вспышки, а корпускулярные потоки — лишь через 24–30 часов после нее. Степень субъективных и объективных проявлений воздействия ГМБ зависит от общего состояния организма и его адаптационных резервов. У одних такие проявления слабо выражены, у других могут стать очень опасными, даже угрожающими жизни. Также различаются реакции во времени: у некоторых они проявляются в начале бури, иногда даже в канун ее, у других — в разгар или на финальной ее стадии.
Большинство людей ощущает такие реакции на 2–3-й день после вспышки на Солнце, т.е. с момента начала ГМБ. Однако отмечено, что у некоторых людей подобная реакция возникает и за 1–2 дня до ГМБ, совпадая с появлением вспышек на Солнце. Солнечное излучение многокомпонентно, его составляющими являются корпускулярные потоки электронов, протонов, ядер гелия, рентгеновское и электромагнитное излучение, выбросы так называемой «корональной массы» и др. Возможно, реакция на хромосферные вспышки, предшествующие ГМБ, обусловлена тем, что рентгеновское и электромагнитное излучение достигает Земли через 8–10 минут от начала вспышки, а корпускулярные потоки — лишь через 24–30 часов после нее. Степень субъективных и объективных проявлений воздействия ГМБ зависит от общего состояния организма и его адаптационных резервов. У одних такие проявления слабо выражены, у других могут стать очень опасными, даже угрожающими жизни. Также различаются реакции во времени: у некоторых они проявляются в начале бури, иногда даже в канун ее, у других — в разгар или на финальной ее стадии. Высказывается предположение, что люди, рожденные в период максимумов солнечной активности, более устойчивы к ГМБ, чем рожденные в годы спокойного Солнца. В системе медицинской профилактики последствий влияния ГМБ на здоровье и самочувствие человека могут быть использованы геофизические прогнозы солнечной активности и реакции магнитного поля Земли на нее. Поскольку геомагнитным бурям предшествуют интенсивные хромосферные вспышки на Солнце, а порожденный ими солнечный ветер доходит до Земли за один-два дня, появляется возможность заблаговременного прогнозирования предстоящей геомагнитной бури. Существуют долгосрочные и более достоверные (на несколько дней) краткосрочные прогнозы. Последние наиболее целесообразны для применения в целях оперативной медицинской профилактики. Установлено, что в отличие от слабовероятных долговременных прогнозов, имеющих лишь общеинформационный ориентировочный характер, надежность двухсуточного прогноза приближается к 50 %, а 1–2-часового — до 90 % и более. Может ли человек ослабить неблагоприятное действие ГМБ, усилить свою сопротивляемость к ним? Прежде всего напомним, что мощным и эффективным путем повышения сопротивляемости организма к любым неблагоприятным внешним воздействиям является повседневное соблюдение основных правил индивидуального здорового образа жизни (рациональное питание, личная гигиена, закаливание и физическая активность, отказ от вредных привычек, физиологический режим дня, чередование трудовых процессом с разумным отдыхом и т.
Высказывается предположение, что люди, рожденные в период максимумов солнечной активности, более устойчивы к ГМБ, чем рожденные в годы спокойного Солнца. В системе медицинской профилактики последствий влияния ГМБ на здоровье и самочувствие человека могут быть использованы геофизические прогнозы солнечной активности и реакции магнитного поля Земли на нее. Поскольку геомагнитным бурям предшествуют интенсивные хромосферные вспышки на Солнце, а порожденный ими солнечный ветер доходит до Земли за один-два дня, появляется возможность заблаговременного прогнозирования предстоящей геомагнитной бури. Существуют долгосрочные и более достоверные (на несколько дней) краткосрочные прогнозы. Последние наиболее целесообразны для применения в целях оперативной медицинской профилактики. Установлено, что в отличие от слабовероятных долговременных прогнозов, имеющих лишь общеинформационный ориентировочный характер, надежность двухсуточного прогноза приближается к 50 %, а 1–2-часового — до 90 % и более. Может ли человек ослабить неблагоприятное действие ГМБ, усилить свою сопротивляемость к ним? Прежде всего напомним, что мощным и эффективным путем повышения сопротивляемости организма к любым неблагоприятным внешним воздействиям является повседневное соблюдение основных правил индивидуального здорового образа жизни (рациональное питание, личная гигиена, закаливание и физическая активность, отказ от вредных привычек, физиологический режим дня, чередование трудовых процессом с разумным отдыхом и т. п.). Выше уже указывалось, что субъективная и объективная реакция на неблагоприятные внешние воздействия сугубо индивидуальна и может иметь разные проявления. Более того, есть немало людей (в основном молодых), которые субъективно вообще не реагируют на такие воздействия. Поэтому весьма важно, чтобы каждый человек, особенно страдающий какими-либо хроническими заболеваниями, в пожилом возрасте, знал, чувствителен ли он к изменению внешних (в том числе геомагнитных) воздействий, каких именно, и как такая чувствительность проявляется. Ориентировочный ответ на этот вопрос можно получить путем самонаблюдений. Для этого следует завести «Дневник самонаблюдения» и в течение хотя бы 3–4 месяцев ежедневно фиксировать в нем такие показатели своего самочувствия: общее самочувствие, артериальное давление, наличие или отсутствие болей в сердце, головной боли, тревожного настроения, уровень работоспособности, обострения имеющегося заболевания, показатели самочувствия и состояния здоровья, а также нарушения режима привычного режима дня, трудовой активности, питания и т.
п.). Выше уже указывалось, что субъективная и объективная реакция на неблагоприятные внешние воздействия сугубо индивидуальна и может иметь разные проявления. Более того, есть немало людей (в основном молодых), которые субъективно вообще не реагируют на такие воздействия. Поэтому весьма важно, чтобы каждый человек, особенно страдающий какими-либо хроническими заболеваниями, в пожилом возрасте, знал, чувствителен ли он к изменению внешних (в том числе геомагнитных) воздействий, каких именно, и как такая чувствительность проявляется. Ориентировочный ответ на этот вопрос можно получить путем самонаблюдений. Для этого следует завести «Дневник самонаблюдения» и в течение хотя бы 3–4 месяцев ежедневно фиксировать в нем такие показатели своего самочувствия: общее самочувствие, артериальное давление, наличие или отсутствие болей в сердце, головной боли, тревожного настроения, уровень работоспособности, обострения имеющегося заболевания, показатели самочувствия и состояния здоровья, а также нарушения режима привычного режима дня, трудовой активности, питания и т. п. За каждый день надо записывать основные погодные (метеорологические и гелиофизические) показатели, в т.ч. показатели возмущенности геомагнитного поля, наличие и уровень ГМБ (все эти показатели сейчас нетрудно найти в Интернете, многие из них публикуются в местной печати). Для большей объективности лучше эту группу показателей записать ретроспективно, т.е. после того, как будут зафиксированы показатели самочувствия и здоровья. Затем следует выделить дни и периоды ухудшения самочувствия и сопоставить их с гелиогеофизическими и метеорологическими показателями в эти же дни и периоды, в канун и после их наступления. Такое сопоставление позволит выявить наличие или отсутствие индивидуальной чувствительности к тем или иным факторам внешних погодных воздействий и характер проявлений этой чувствительности. Располагая такими сведениями, с помощью лечащего врача можно определиться, что надо изменять в режиме своего дня, в дозировках и времени приема лекарств в канун неблагоприятных погодных условий и предстоящих ГМБ (прогноз их регулярно публикуется в интернете, в частности на интернет-сайте Института земного магнетизма АН России).
п. За каждый день надо записывать основные погодные (метеорологические и гелиофизические) показатели, в т.ч. показатели возмущенности геомагнитного поля, наличие и уровень ГМБ (все эти показатели сейчас нетрудно найти в Интернете, многие из них публикуются в местной печати). Для большей объективности лучше эту группу показателей записать ретроспективно, т.е. после того, как будут зафиксированы показатели самочувствия и здоровья. Затем следует выделить дни и периоды ухудшения самочувствия и сопоставить их с гелиогеофизическими и метеорологическими показателями в эти же дни и периоды, в канун и после их наступления. Такое сопоставление позволит выявить наличие или отсутствие индивидуальной чувствительности к тем или иным факторам внешних погодных воздействий и характер проявлений этой чувствительности. Располагая такими сведениями, с помощью лечащего врача можно определиться, что надо изменять в режиме своего дня, в дозировках и времени приема лекарств в канун неблагоприятных погодных условий и предстоящих ГМБ (прогноз их регулярно публикуется в интернете, в частности на интернет-сайте Института земного магнетизма АН России). Поскольку одним из отрицательных последствий воздействия ГМБ является усиление тромбообразовательной функции крови, для ослабления этого и при отсутствии противопоказаний (гастрит, язвенная болезнь желудка), предварительно посоветовавшись со своим лечащим врачом, целесообразно принять 100–300 мг аспирина. Тем, кто реагирует на геомагнитные неурядицы нервозностью, тревогой, бессонницей, помогут простые успокоительные средства — настойки валерианы, пиона, эвкалипта (по 15 капель три раза в день после еды), сок из свежих листьев алоэ. Желательно в эти периоды несколько откорректировать свое питание. Специфической «противомагнитной» диеты не существует. Но соблюдение некоторых правил, несомненно, полезно и усиливает устойчивость к воздействию ГМБ. Прежде всего — умеренность в пищевой нагрузке (переедание ослабляет приток крови, а следовательно, и кислородное обеспечение мозга). Рацион питания должен включать в себя каши (гречневую, овсяную), приготовленные на воде или нежирном молоке. В нем должны быть богатые микроэлементами и витаминами свежие овощи и фрукты (в частности, бананы), отварная рыба.
Поскольку одним из отрицательных последствий воздействия ГМБ является усиление тромбообразовательной функции крови, для ослабления этого и при отсутствии противопоказаний (гастрит, язвенная болезнь желудка), предварительно посоветовавшись со своим лечащим врачом, целесообразно принять 100–300 мг аспирина. Тем, кто реагирует на геомагнитные неурядицы нервозностью, тревогой, бессонницей, помогут простые успокоительные средства — настойки валерианы, пиона, эвкалипта (по 15 капель три раза в день после еды), сок из свежих листьев алоэ. Желательно в эти периоды несколько откорректировать свое питание. Специфической «противомагнитной» диеты не существует. Но соблюдение некоторых правил, несомненно, полезно и усиливает устойчивость к воздействию ГМБ. Прежде всего — умеренность в пищевой нагрузке (переедание ослабляет приток крови, а следовательно, и кислородное обеспечение мозга). Рацион питания должен включать в себя каши (гречневую, овсяную), приготовленные на воде или нежирном молоке. В нем должны быть богатые микроэлементами и витаминами свежие овощи и фрукты (в частности, бананы), отварная рыба. В период ГМБ не переусердствуйте (особенно в пожилом возрасте, при болезнях сердца) с физической нагрузкой. Избегайте резкого подъема с постели после сна, который может ослабить приток крови к мозгу, провоцировать возникновение обморока, головокружения. Перед вставанием полежите спокойно несколько минут, затем не спеша вставайте и одевайтесь. И проследите за тем, чтобы был обеспечен полноценный ночной сон. При необходимости не бойтесь использовать для этого лекарственные препараты (вновь напомним: все лекарства и их дозировки — только после предварительной консультации со своим врачом!). Соблюдение этих простых и доступных каждому человеку мер позволит ослабить или вовсе предотвратить неблагоприятное влияние геомагнитных бурь на здоровье человека.
В период ГМБ не переусердствуйте (особенно в пожилом возрасте, при болезнях сердца) с физической нагрузкой. Избегайте резкого подъема с постели после сна, который может ослабить приток крови к мозгу, провоцировать возникновение обморока, головокружения. Перед вставанием полежите спокойно несколько минут, затем не спеша вставайте и одевайтесь. И проследите за тем, чтобы был обеспечен полноценный ночной сон. При необходимости не бойтесь использовать для этого лекарственные препараты (вновь напомним: все лекарства и их дозировки — только после предварительной консультации со своим врачом!). Соблюдение этих простых и доступных каждому человеку мер позволит ослабить или вовсе предотвратить неблагоприятное влияние геомагнитных бурь на здоровье человека. КАЛЕНДАРЬ МАГНИТНЫХ БУРЬ В ДЕКАБРЕ 2021 ГОДА: ОПАСАТЬСЯ НУЖНО НЕ ТОЛЬКО МЕТЕОЗАВИСИМЫМ ЛЮДЯМ
Рождественские и новогодние праздники не будут спокойными. В последний месяц уходящего 2021 года на Землю обрушатся сразу несколько магнитных бурь. На пике своей активности они достигнут красной отметки в 6-7 баллов. Спастись от магнитных бурь невозможно, но если подготовиться и быть во всеоружии, то удастся смягчить их воздействие на организм человека.
На пике своей активности они достигнут красной отметки в 6-7 баллов. Спастись от магнитных бурь невозможно, но если подготовиться и быть во всеоружии, то удастся смягчить их воздействие на организм человека.
Чем опасны магнитные бури?
Появление магнитных бурь на Земле провоцируют вспышки на Солнце. Активность небесного светила и «возмущенное» магнитное поле влияют на только на бытовые электрические приборы, работу спутников, качество передачи GPS-сигнала, но и состояние здоровья людей.
Магнитные бури вызывают перебои в работе сердца, повышают давление, нарушают сон, провоцируют ломоту в суставах, ухудшают настроение, приводят к депрессии. Особенно тяжело их переносят люди, которые страдают сердечно-сосудистыми заболеваниями, вегетососудистой дистонией, с избыточным весом. Они становятся невнимательными, конфликтными, беспокойными.
Больше всего подвержены воздействию бурь метеозависимые люди, а это каждый третий житель земли. Также геомагнитные возмущения могут плохо влиять на людей с пониженным иммунитетом, с хроническими болезнями, беременных, детей и пожилых граждан.
Самая сильная магнитная буря в истории человечества произошла 1 сентября 1859 года. Ночное небо над Северным полушарием Земли озарилось яркими вспышками, отдаленно похожими на Северное сияние. Увидеть явление можно было в разных частях света, даже на Гавайских островах.
Когда в декабре 2021 года ждать магнитных бурь
Знание точных дат магнитных бурь помогает подготовиться к негативному воздействию. Для этого нужно пересмотреть свой рацион и привычки.
Первый в декабре геоудар Земля приняла с 1 по 4 число. Его интенсивность в первые дни зимы оценивалась в 4 балла. Магнитная буря могла сказаться на тех, кто страдает от хронических головных болей и сердечно-сосудистых заболеваний.
Вторую волну магнитных «волнений», по мнению синоптиков и метеорологов, следует ожидать с 9 по 13 декабря. Интенсивность магнитной бури ожидается невероятно высокой — 7 баллов. Это значит, что ее эффект на себе почувствуют даже здоровые люди.
Третья магнитная буря с интенсивностью в 6 баллов придет на Землю в период с 18 по 22 декабря. Ее пик придется на День святого Николая Чудотворца, который отмечают 19 декабря. Поскольку это будет воскресенье, то метеозависимые люди смогут отлежаться. Врачи рекомендуют эти дни посвятить спокойным видам деятельности, свести к минимуму физические нагрузки, избегать эмоциональных перепадов.
Сюрприз в виде магнитной бури накроет земной шар и в последние дни уходящего 2021 года. По прогнозам ученых, 30 и 31 декабря ожидается буря интенсивностью в 4 балла. Это может привести к повышенной усталости и испорченному предновогоднему настроению. В связи с этим врачи советуют отказаться от обильного новогоднего застолья, ограничится легкими закусками вместо жирной пищи, алкоголь тоже желательно исключить либо употреблять его умеренно.
Кстати, согласно лунному календарю, неблагоприятными днями в декабре для метеочувствительных людей являются 6, 7, 13, 16, 19, 20, 22, 23 и 27 декабря.
Как пережить магнитные бури в декабре 2021 года
Накануне опасных для здоровья дат и в период магнитных «волнений» постарайтесь не переутомляться, больше гуляйте на свежем воздухе, чаще проветривайте комнаты, делайте влажную уборку. Хорошо высыпайтесь, делайте утреннюю гимнастику.
Добавьте в рацион легкую пищу, а также продукты, которые укрепляют стенки сосудов и позитивно влияют на кровоток и обмен веществ – например, морковь, цитрусовые фрукты, яйца и т.д. Пейте достаточное количество воды и следите за соблюдением здорового водного баланса. Откажитесь от копченостей, острых, жареных и соленых блюд, которые задерживают в организме воду.
В этот период также стоит ограничить употребление кофе, курение, прием алкоголя, отказаться от поездок за рулем автомобиля. Людям с хроническими болезнями следует запастись необходимыми медикаментами.
Важно сохранять спокойствие, не поддаваться панике и избегать конфликтных ситуаций. Снизить тревогу, стресс и бессонницу помогут йога, медитация, приятное общение.
Что делать, если во время магнитной бури повысилось давление, ранее мы уже рассказывали. Прочитать об этом вы можете здесь.
Подготовила Анжела ЛЮДЫНО
Фото из открытых интернет-источников
Вырождение в магнитоактивной плотной плазме
На этой странице
РезюмеВведениеРезультаты и выводыДоступность данныхКонфликты интересовБлагодарностиСсылкиАвторское правоСтатьи по теме Такая плазма вызвала большой интерес в последнее десятилетие из-за ее важности во многих областях физики, таких как полупроводники, металлы, микроэлектроника, углеродные нанотрубки, квантовые точки и квантовые ямы. Кроме того, вырожденная плазма представляет очень интересные особенности для зажигания и распространения волн термоядерного горения. В данной работе мы исследовали влияние постоянного магнитного поля на энергетические состояния и вырождение электронов в плотной плазме. С помощью теории возмущений рассматриваются два случая: сильно и слабо намагниченные электроны. Сильное магнитное поле не устранит полностью вырождение, но оно уменьшает вырождение. Собственные значения возмущенной энергии рассчитываются с высокой точностью. Кроме того, независимо от того, является ли возмущенное состояние вырожденным или нет, энергия определяется путем рассмотрения среднего значения орбитальной и спиновой связи по отношению к собственной функции . Здесь – вектор углового момента, – вектор спина электронов, – энергия связи спин-орбит в плазме, играющая решающую роль при изучении энергетических состояний и вырождения электронов плазмы.
Сильное магнитное поле не устранит полностью вырождение, но оно уменьшает вырождение. Собственные значения возмущенной энергии рассчитываются с высокой точностью. Кроме того, независимо от того, является ли возмущенное состояние вырожденным или нет, энергия определяется путем рассмотрения среднего значения орбитальной и спиновой связи по отношению к собственной функции . Здесь – вектор углового момента, – вектор спина электронов, – энергия связи спин-орбит в плазме, играющая решающую роль при изучении энергетических состояний и вырождения электронов плазмы.
1. Введение
При достаточном увеличении плотности плазмы квантовые эффекты становятся очень интересными. Сюда входят эффекты вырождения, которые становятся важными, когда , – температура плазмы, – температура Ферми, определяемая в энергии Ферми как , – постоянная Больцмана, – приведенная постоянная Планка. В этой модели эффекты рассеивания частиц имеют тенденцию быть важными для коротких масштабов (сравнимых с характерной длиной де Бройля), когда , является плазменной частотой.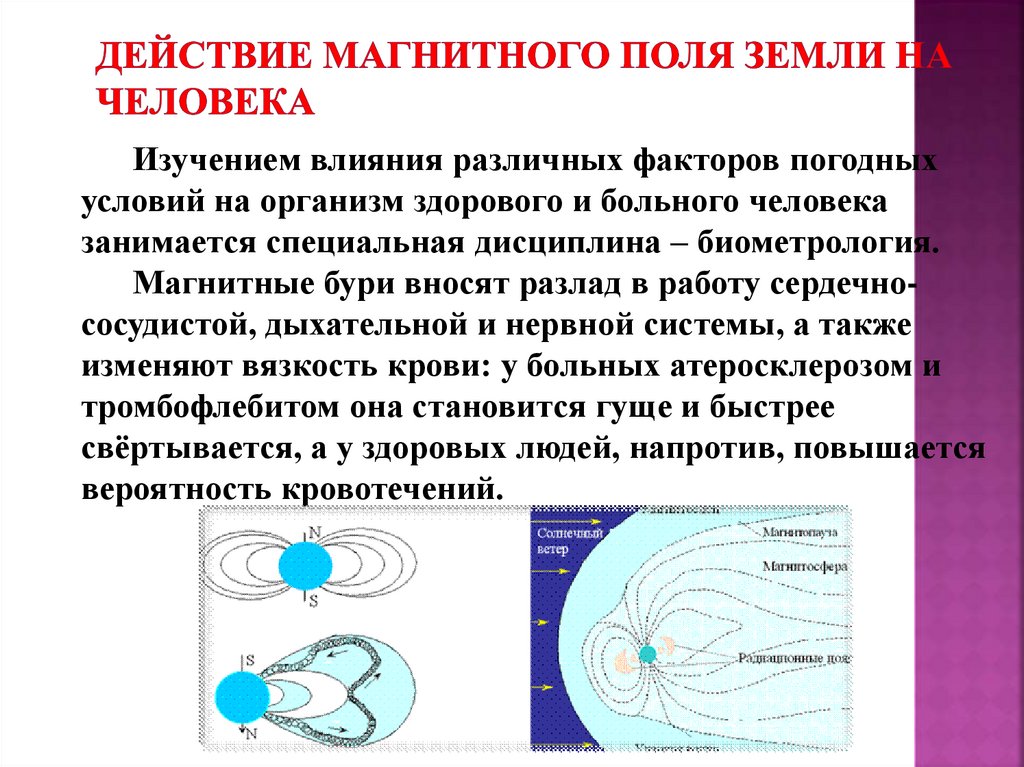 В квантовой кинетической теории эти эффекты хорошо моделируются с помощью теории возмущений.
В квантовой кинетической теории эти эффекты хорошо моделируются с помощью теории возмущений.
В плазме для дальнейшего совершенствования этих моделей учитывается спин электрона, который вводит в картину магнитную дипольную силу, прецессию спина и токи намагничивания спина [1–4].
На самом деле, наблюдается растущий интерес к плазме с низкой температурой и высокой плотностью, где важны квантовые свойства [5–8]. Перспективные приложения включают квантовые ямы [9], спинтронику [10] и плазмонику [11]. Квантовые плазменные эффекты могут представлять интерес и в экспериментах с твердотельными мишенями [12]. Важные классификации плотной плазмы включают в себя, являются ли они сильно или слабо связанными, а также являются ли они вырожденными или невырожденными [1]. В нескольких работах [5, 13–15] применялись квантовые плазменные эффекты, например, в томсоновском рентгеновском рассеянии в плазме с высокой плотностью энергии, а также экспериментальные методы для доступа к узкополосным спектральным линиям [2] для обнаружения частотных сдвигов, вызванных квантовые эффекты [13] и эксперименты следующего поколения по интенсивному взаимодействию лазера с плазмой плотности твердого тела [14].
Кроме того, квантовая или вырожденная плазма представляет большой интерес в связи с ее важными приложениями в современной технике и астрофизике. Такая плазма вызвала большой интерес в последнее десятилетие из-за ее важности во многих областях физики, таких как полупроводники, металлы, микроэлектроника [16], углеродные нанотрубки, квантовые точки и квантовые ямы [17–19]. Вырожденная плазма также играет важную роль в плотных астрофизических объектах, таких как плазма недр звезд и нейтронных звезд [20]. Исследуемый в плазме эффект захвата вырожденных электронов и невырожденных ионов в присутствии квантующего магнитного поля [4].
Обычная пертурбативная трактовка магнитных эффектов, таких как зеемановское расщепление атомных энергетических уровней в режиме сильного поля, в такой ситуации неприменима, вместо этого кулоновские силы действуют как возмущение магнитных сил.
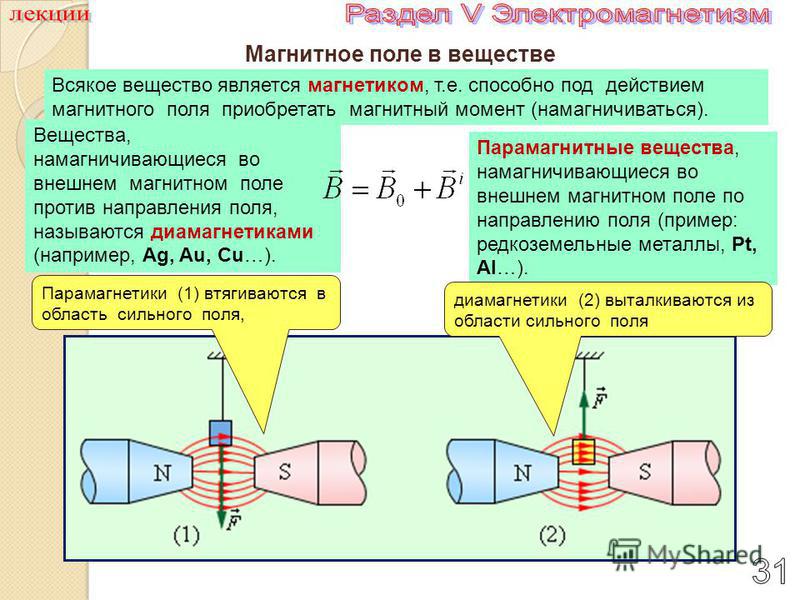
Благодаря крайнему ограничению электронов в поперечном направлении кулоновская сила становится гораздо более эффективной в связывании электронов вдоль направления магнитного поля [21]. Как известно, намагниченность электронного газа в слабом магнитном поле имеет две независимые части; (i) парамагнитные и (ii) диамагнитные части. Собственный или спиновой магнитный момент электронов порождает парамагнетизм Паули. Диамагнитная часть связана с тем, что орбитальное движение электронов квантуется в магнитном поле.
Как известно, намагниченность электронного газа в слабом магнитном поле имеет две независимые части; (i) парамагнитные и (ii) диамагнитные части. Собственный или спиновой магнитный момент электронов порождает парамагнетизм Паули. Диамагнитная часть связана с тем, что орбитальное движение электронов квантуется в магнитном поле.
Действительно, область квантовой физики плазмы становится все более актуальной [22–25], что обусловлено ее потенциальными приложениями в современных технологиях (например, металлические и полупроводниковые наноструктуры, такие как металлические наночастицы, металлические кластеры, тонкие металлические пленки, спинтроника, нанотрубки, квантовые ямы и квантовые точки, наноплазмонные устройства, квантовые рентгеновские лазеры на свободных электронах и др.). В плотной квантовой плазме и в ферми-газе металлов плотности вырожденных электронов чрезвычайно велики, так что их волновые функции перекрываются, и поэтому электроны подчиняются статистике Ферми-Дирака. Ферми-вырожденная плотная плазма может также возникать, когда пуля водорода сжимается до плотности, во много раз превышающей плотность твердого тела, в сценарии быстрого воспламенения для термоядерного синтеза с инерционным удержанием (ICF) [26, 27].
Ферми-вырожденная плотная плазма может также возникать, когда пуля водорода сжимается до плотности, во много раз превышающей плотность твердого тела, в сценарии быстрого воспламенения для термоядерного синтеза с инерционным удержанием (ICF) [26, 27].
Наша работа представляет большой интерес в настоящее время для экспериментов, и становится возможным сравнение теории и эксперимента, например, с помощью томсоновского рассеяния с использованием лазеров на свободных электронах, например, [5]. Повышение точности этих экспериментов станет движущей силой для развития теории в ближайшем будущем.
В настоящей работе мы ограничиваемся рассмотрением только слабосвязанной вырожденной плазмы, где эффекты ионной вязкости не учитываются, поскольку вязкостью ионов обычно можно пренебречь, пока период волны много больше временного масштаба ионной корреляции и скорость затухания за счет вязкостей много меньше рабочей частоты волны [28].
Мы исследовали влияние постоянного магнитного поля на энергетические состояния и вырождение электронов в плотной плазме. С помощью теории возмущений рассматриваются два случая: сильно и слабо намагниченные электроны. Собственные значения возмущенной энергии рассчитываются с высокой точностью. Рассчитана также энергия спин-орбитального взаимодействия в плазме, играющая решающую роль при изучении энергетических состояний электронов плазмы.
С помощью теории возмущений рассматриваются два случая: сильно и слабо намагниченные электроны. Собственные значения возмущенной энергии рассчитываются с высокой точностью. Рассчитана также энергия спин-орбитального взаимодействия в плазме, играющая решающую роль при изучении энергетических состояний электронов плазмы.
2. Базовый набор уравнений
В вырожденной плазме физические параметры, такие как плотность, магнитное поле и температура, изменяются в широком диапазоне значений. Например, плотность вырожденных электронов может на много порядков превышать плотность твердого вещества в белых карликах, нейтронных звездах и в следующем поколении инерционно сжатых материалов в экспериментах по интенсивному лазерному взаимодействию с твердой мишенью.
Представленная здесь теория представляет наибольший интерес для систем, где хотя бы один из параметров или не слишком мал. Примеры включают, например, лазерно-плазменные взаимодействия, твердотельную плазму и сильно намагниченные системы.
Следующие параметры могут использоваться для экспериментальных приложений. Численная плотность и магнитное поле имеют значения порядка 10 26 см −3 и 10 10 соответственно [4]. Эти числа использовались для расчета энергии Ферми и температуры Ферми как K и принимали температуру электронов [29].].
Мы предполагаем, что электроны в плазме принадлежат квантовой среде многочастичной системы. Такое предположение связано с тем, что полученные решения имеют характерные размеры порядка атомов.
Предположим, что у нас есть магнитное поле, приложенное к невозмущенной квантовой плазменной системе с гамильтонианом, определяемым:
где, — вектор углового момента, — вектор спина электронов, и — энергия спин-орбитальной связи в плазме, которому принадлежит существенная роль в изучении энергетических уровней электронов плазмы. является типом потенциала в системе.
При наличии магнитного поля мы должны ввести в (1) как (i) как энергию взаимодействия между орбитальным магнитным моментом электронов и магнитной индукцией,
, так и (ii) как энергию взаимодействия между спиновый магнитный момент и магнитная индукция,
Для простоты рассмотрим статическое магнитное поле, направленное в -направлении .
Полный гамильтониан (1) для вращающихся электронов имеет вид:
где, , , – циклотронная частота электрона, а .
и теперь рассматриваются как два возмущенных члена, и определим теперь уровни энергии уравнения на собственные значения для гамильтониана (4) с помощью теории возмущений, рассмотрев и задав относительные значения между и .
Будут рассмотрены два случая, т. е. (i) сильно намагниченные электроны и (ii) слабо намагниченные электроны.
3. Сильно намагниченная плазма
Если магнитное поле очень сильное такое, что его правомерно рассматривать только как возмущенную величину, а невозмущенный гамильтониан имеет вид:
Легко проверить, что все операторы , и коммутируют с невозмущенным гамильтонианом (5), поэтому собственная функция, соответствующая (5), может быть представлена в виде .
Соответственно, уравнение Шредингера может иметь вид:
где
– собственное значение невозмущенного гамильтониана .
Для значений ; и ; , то для обоих случаев и имеем вырождение второго порядка.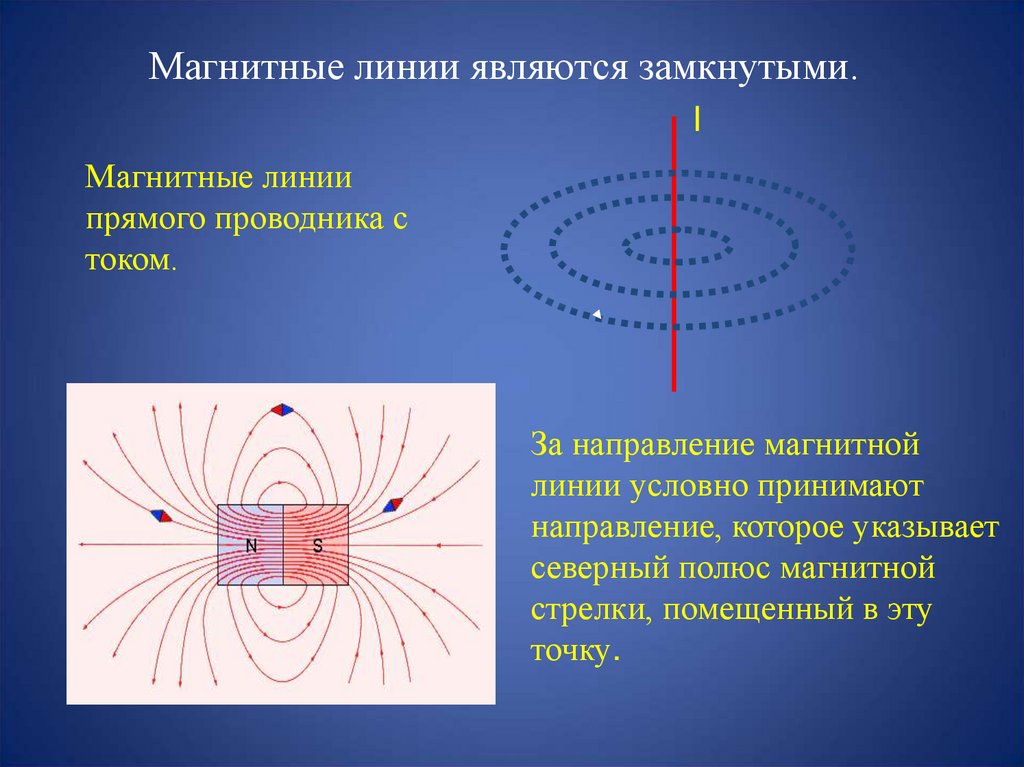 Для фиксированных состояний ; , у нас есть шесть возможных состояний, соответствующих ; . Эти шесть состояний определяют шесть возможных различных собственных функций, две из которых являются вырожденными, а остальные невырожденными, как показано в таблице 1.
Для фиксированных состояний ; , у нас есть шесть возможных состояний, соответствующих ; . Эти шесть состояний определяют шесть возможных различных собственных функций, две из которых являются вырожденными, а остальные невырожденными, как показано в таблице 1.
Из (7) видно, что использование сильного магнитного поля для удержания плазмы не устраняет полностью вырождение, но уменьшает вырождение.
Рассмотрим теперь теорию возмущений для расчета уровней энергии электронов в плазме, будет очень важно знать, является ли исследуемое состояние вырожденным или нет. Это связано с тем, что методика расчета для обоих случаев различна.
Возмущенные собственные значения энергии четырех невырожденных состояний равны
Для вырожденных состояний воспользуемся описанным выше случаем.
Пусть ; и ;
и примем вырожденные состояния
Кроме того, определим
Для вырожденного случая , теория возмущений требует обращения в нуль определителя невозмущенного гамильтониана , который представляет собой матрицу, состоящую из различных собственных функций невозмущенных членов соответствующей одной и той же энергии, т. е.
е.
Соотношение (11) определяет возможные значения для вырожденного состояния. Используемые функции являются собственными функциями для , т. е. имеет собственные функции
Соответственно, недиагностические члены (11) обращаются в нуль из-за ортогональности волновых функций, т.е. Кроме того, всякий раз, когда возмущенное состояние является вырожденным или нет; дается средним значением в состоянии .
Из вышеизложенного видно, что теории возмущений, при наличии внешнего магнитного поля удалось полностью устранить вырождение, т. е. только одну собственную функцию для каждого собственного значения . Кроме того, независимо от того, является возмущенное состояние вырожденным или нет, энергия определяется путем рассмотрения среднего значения по отношению к собственной функции .
Из (13) легко оценить как
где,
Теперь к (7) следует добавить возмущенную энергию (14), т. е.
, что показывает полную невырожденность конечного состояния из-за третий член в правой части (16).
4. Слабо намагниченная плазма
В этом случае предполагается, что электронная спин-орбитальная связь намного больше, чем , и возмущенный гамильтониан имеет вид:
, а невозмущенный гамильтониан:
Из спиновой теории Паули, имеющей тот же гамильтониан (18), константы движения равны, а собственные функции и собственные значения (18) будут иметь вид:
Оба собственных значения в (20) имеют вырождение порядка , а поскольку операторы .
Коммутирует с гамильтонианом, поэтому разрешенные собственные значения в функции состояния будут иметь ту же энергию, что и (20). Кроме того, коммутирует с и, следовательно, матрица возмущения, определяющая возмущенную энергию, и в этом случае будет диагональной. Соответственно, обращение в нуль его элементов дает:
Ясно, что появление первого члена в правой части (21), , связано с внешним постоянным магнитным полем, функционирующим для полного снятия вырождения.
Для вычисления заметим, что это не собственная функция для или. Следовательно, мы можем использовать следующее математическое правило:
Следовательно, мы можем использовать следующее математическое правило:
где, — произвольный оператор, любое дополнительное квантовое число, и — собственный набор операторов, что и .
Взяв -компоненту как , тогда
Подставляем произведение рассеяния в (23), получаем
Подставляем (24) в (21) получаем сдвиг энергетических уровней в виде: и 2), который измеряет уровни энергии электронов плазмы. , играет решающую роль в вырожденной плазме при рассмотрении зажигания и распространения волн термоядерного горения.
Однако результат волн термоядерного горения в невырожденной плазме ограничен силой ионно-электронных кулоновских столкновений и последующими механизмами потери энергии, такими как электронная теплопроводность и излучение (тормозное излучение).
Соотношение (26) согласуется с (37) согласно [30].
Ясно, что сдвиг энергетических уровней зависит от квантового числа , что снимает упомянутое ранее вырождение. Также сильно зависят от фактора Ланде , отсюда и квантовые числа электронных состояний плазмы.
Для мгновений рассмотрим следующие два случая, т. е.
Следовательно, при наличии слабого магнитного поля имеем следующие энергетические состояния:
наконец, энергия электрона плазмы уменьшается до
5. Результаты и выводы
В данной работе мы исследовали влияние постоянного магнитного поля на энергетические состояния и вырождение электронов в квантованной плотной плазме. С помощью теории возмущений рассматриваются два случая: сильно и слабо намагниченные электроны. Собственные значения возмущенной энергии рассчитываются аналитически с высокой точностью в обоих случаях. Подытожим основные результаты, полученные в данной работе:
5.1. В сильном магнитном поле
(i) Собственные значения невозмущенного гамильтониана
, отношение (7). Сильное магнитное поле не устранит полностью вырождение, но оно способно уменьшить его. (ii) Шесть состояний определяют шесть возможных различных собственных функций, две из которых являются вырожденными, а остальные невырожденными, как показано в таблице 1. (iii) Возмущенная энергия собственные значения четырех невырожденных состояний задаются формулами (13), (14). (iv) Общее конечное энергетическое состояние для невырожденных и вырожденных состояний определяется формулой (16).
(iii) Возмущенная энергия собственные значения четырех невырожденных состояний задаются формулами (13), (14). (iv) Общее конечное энергетическое состояние для невырожденных и вырожденных состояний определяется формулой (16).
5.2. В слабом магнитном поле
(i) Собственные функции и собственные значения невозмущенного гамильтониана (18) задаются формулами (19) и (20) соответственно. Оба собственных значения в (20) имеют вырождение порядка
. (ii) Возмущенная энергия
вычисляется и дается выражением (21). (iii) Появление первого слагаемого в правой части (21) полностью устраняет вырождения. (iv) Возмущенная энергия
просто вычисляется согласно (25), что строго пропорционально фактору Ланде. (v) Соотношения (28), (29) дают расчетные энергетические состояния. Если пренебречь спином электрона, оба энергетических состояния равны и задаются формулой (30).
Когда электроны плазмы становятся вырожденными, длина волны де Бройля для электронов становится больше по сравнению со средним расстоянием между частицами, и квантово-механические соображения приобретают первостепенное значение.
Из (7) видно, что использование сильного магнитного поля для удержания плазмы не устраняет полностью вырождение, но уменьшает вырождение, а из (13) теория возмущений устранила плазменное вырождение электрона по собственным функциям
Кроме того, независимо от того, является ли возмущенное состояние вырожденным или нет, энергия определяется путем рассмотрения среднего значения относительно собственной функции .
Из вышеизложенного видно, что теории возмущений при наличии внешнего магнитного поля удалось полностью устранить вырождение, т. е. только одну собственную функцию для каждого собственного значения .
Для слабо намагниченной плазмы энергетическая поправка зависит от квантового числа , что снимает вырождение. Кроме того, также сильно зависит от фактора Ланде , отсюда и квантовые числа электронного состояния плазмы.
Представленная здесь теория представляет наибольший интерес для систем, где хотя бы один из параметров или не слишком мал. Примеры включают, например, лазерно-плазменные взаимодействия, астрофизические объекты, твердотельную плазму и сильно намагниченные системы.
Как мы видели выше, добавление магнитного поля приводит к двум дополнительным слагаемым в гамильтониане. Первый возникает из-за того, что электрон заряжен. Второй член, возникающий из-за магнитного поля, — это связь со спином. Объединение двух членов, линейных по , дает так называемый плазменный гамильтониан Зеемана.
Используя представленные здесь результаты, становится возможным унифицированное рассмотрение эффекта Зеемана во всем диапазоне магнитных полей, используемых в настоящее время, например, в термоядерной плазме, где было продемонстрировано влияние эффекта Зеемана на измерения температуры плазмы. существенным во многих случаях.
Авторы очень заинтересованы в изучении в свое время применения их методов к (i) релятивистской плотной плазме, погруженной в колеблющееся неоднородное магнитное поле.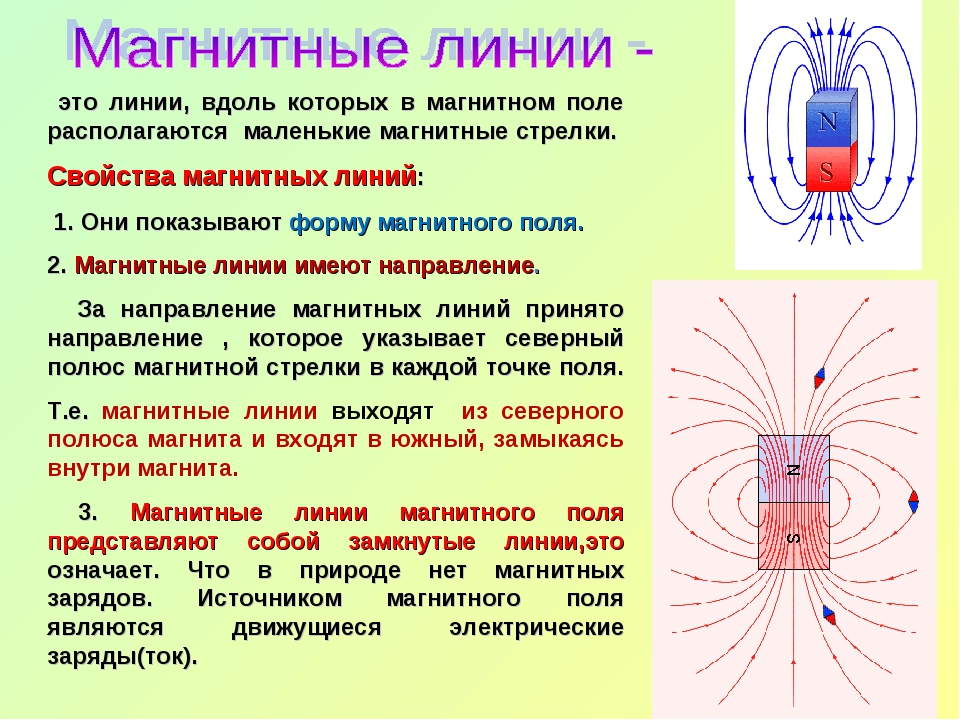 (ii) вырождению плазмы в присутствии электрического поля.
(ii) вырождению плазмы в присутствии электрического поля.
Доступность данных
Данные, использованные для поддержки результатов этого исследования, включены в статью (см. ссылки). Дополнительные данные, использованные для подтверждения результатов этого исследования, можно получить у соответствующего автора (Ш. М. Халил, [email protected]) по запросу.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Благодарности
Это исследование финансировалось деканатом научных исследований Университета принцессы Нуры бинт Абдулрахман в рамках программы ускоренного финансирования исследований.
Ссылки
М. Бониц, «Квантовая кинетическая теория», Springer, 2-е издание, 2016 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ф. А. Асенджо, Дж. Заманян, М. Марклунд, Г. Бродин и П. Йоханссон, «Полурелятивистские эффекты в квантовой плазме со спином 1/2», New Journal of Physics , vol.
 14, нет. 7, с. 073042, 2012.
14, нет. 7, с. 073042, 2012.Посмотреть по адресу:
Сайт издателя | Google Scholar
Экман Р., Заманян Дж., Бродин Г. Обменные поправки в низкотемпературной плазме, Physics Review E , vol. 92, нет. 1, 2015.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Шах Х. А., Икбал М. Дж., Цинцадзе Н., Масуд В., Куреши М. Н. С. Эффект захвата вырожденной плазмы в присутствии квантующего магнитного поля // Физика плазмы. 19, нет. 9, с. 092304, 2012.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Д. А. Чепмен и Д. О. Герике, «Анализ томсоновского рассеяния от неравновесной плазмы», Physics Review Letters , vol. 107, нет. 16, с. 165004, 2011.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Г.
 Манфреди, «Квантовые эффекты на неустойчивость Рэлея-Тейлора модели вязкоупругой плазмы через пористую среду», Fields Institute Communications Series , vol. 46, стр. 263–287, 2005.
Манфреди, «Квантовые эффекты на неустойчивость Рэлея-Тейлора модели вязкоупругой плазмы через пористую среду», Fields Institute Communications Series , vol. 46, стр. 263–287, 2005.Посмотреть по адресу:
Сайт издателя | Google Scholar
П. К. Шукла и Б. Элиассон, «Нелинейные аспекты квантовой физики плазмы», Успехи физики , вып. 53, нет. 1, стр. 51–76, 2010.
Посмотреть по адресу:
Сайт издателя | Google Scholar
П. К. Шукла и Б. Элиассон, «Коллоквиум: нелинейные коллективные взаимодействия в квантовой плазме с вырожденными электронными жидкостями», Reviews of Modern Physics , vol. 83, нет. 3, стр. 885–906, 2011.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Г. Манфреди и П.
 А. Эрвьё, «Авторезонансное управление многоэлектронной динамикой в непараболических квантовых ямах», Письма по прикладной физике , том. 91, нет. 6, с. 061108, 2007.
А. Эрвьё, «Авторезонансное управление многоэлектронной динамикой в непараболических квантовых ямах», Письма по прикладной физике , том. 91, нет. 6, с. 061108, 2007.Посмотреть по адресу:
Сайт издателя | Google Scholar
С. А. Вольф, Д. Д. Авшалом, Р. А. Бурман и др., «Спинтроника: взгляд на спиновую электронику в будущем», Science , vol. 294, нет. 5546, стр. 1488–1495, 2001.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. А. Этуотер, «Обещание плазмоники», Scientific American , том. 296, нет. 4, стр. 56–62, 2007 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
С. Х. Гленцер и Р. Редмер, «Рентгеновское томсоновское рассеяние в плазме с высокой плотностью энергии», Reviews of Modern Physics , vol.
 81, нет. 4, стр. 1625–1663, 2009.
81, нет. 4, стр. 1625–1663, 2009.Посмотреть по адресу:
Сайт издателя | Google Scholar
N. Crouseilles, P.-A. Hervieux, и G. Manfredi, «Квантовая гидродинамическая модель для нелинейной электронной динамики в тонких металлических пленках», Physical Review B , vol. 78, нет. 15, ID статьи 155412, 2008 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Марклунд, Г. Бродин, Л. Стенфло и К. С. Лю, «Новые квантовые пределы в плазмонных устройствах», Europhysics Letters , vol. 84, нет. 1, с. 17006, 2008.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Бродин Г., Мишра А.П., Марклунд М. Вклад спина в пондеромоторную силу в плазме.0217 Physical Review Letters , vol. 105, нет.
 10, ID статьи 105004, 2010.
10, ID статьи 105004, 2010.Посмотреть по адресу:
Сайт издателя | Google Scholar
А. Маркович, К. А. Рингхофер и К. Шмайсер, Полупроводниковые уравнения , Springer, Вена, 1990.
Л. К. Анг, Т. Дж. закона в квантовом режиме», Physical Review Letters , vol. 91, нет. 20, ID статьи 208303, 2003.
Вид:
Сайт издателя | Google Scholar
Т. К. Киллиан, «Плазма приведена в порядок», Nature (London) , vol. 441, с. 297, 2006.
Посмотреть по адресу:
Google Scholar
Ю. Д. Юнг, «Квантово-механические эффекты на электрон-электронное рассеяние в плотной высокотемпературной плазме», Physics of Plasmas , vol. 8, с. 3842, 2001.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М.
 Офер, Л. О. Сильва, Д. Э. Догер, В. К. Децик и Дж. М. Доусон, «Скорости ядерных реакций и энергия в звездной плазме: влияние сильно затухающих мод», Физика плазмы , вып. 8, нет. 5, стр. 2454–2460, 2001.
Офер, Л. О. Сильва, Д. Э. Догер, В. К. Децик и Дж. М. Доусон, «Скорости ядерных реакций и энергия в звездной плазме: влияние сильно затухающих мод», Физика плазмы , вып. 8, нет. 5, стр. 2454–2460, 2001.Посмотреть по адресу:
Сайт издателя | Google Scholar
Б. Элиассон и П. К. Шукла, «Формирование электростатических ударов в квантовой плазме с релятивистски вырожденными электронами», Europhysics Letters , vol. 97, нет. 1, с. 15001, 2012.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Дж. П. Митен, Дж. Далиго и Г. Грегори, «Степень достоверности гидродинамического описания ионов в плотной плазме», Physical Review E , vol. 83, нет. 1, ID статьи 015401, 2011.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Д.
 Лай, «Вещество в сильных магнитных полях», Reviews of Modern Physics , vol. 73, нет. 3, с. 629, 2001.
Лай, «Вещество в сильных магнитных полях», Reviews of Modern Physics , vol. 73, нет. 3, с. 629, 2001.Посмотреть по адресу:
Сайт издателя | Google Scholar
Бониц М., Молдабеков З.А., Рамазанов Т.С. Квантовая гидродинамика плазмы. Physics of Plasmas , vol. 26, нет. 9, п. 090601, 2019.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Сербето А., Мендонса Дж. Т., Цуй К. Х., Бонифачо Р. Квантовая волновая кинетика лазеров на свободных электронах с высоким коэффициентом усиления // Physics of Plasmas . vol. 15, нет. 1, с. 013110, 2008.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Д. Шайх и П. К. Шукла, «Турбулентность жидкости в квантовой плазме», Physical Review Letters , vol.
 99, нет. 12, ID статьи 125002, 2007 г.
99, нет. 12, ID статьи 125002, 2007 г.Посмотреть по адресу:
Сайт издателя | Google Scholar
П. К. Шукла, «Новый взгляд на квантовую плазму», Nature Physics , vol. 5, нет. 2, стр. 92-93, 2009.
Посмотреть по адресу:
Сайт издателя | Google Scholar
H. Azechi and F. Project, «Современное состояние программы FIREX для демонстрации воспламенения и горения», Plasma Physics and Controlled Fusion , vol. 48, нет. 12B, стр. B267–B275, 2006.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Шах Х.А., Куреши М.Н.С., Цинцадзе Н.Л. Эффект захвата в вырожденной квантовой плазме. Physics of Plasmas . vol. 17, нет. 3, с. 032312, 2010.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Сон С.
 и Фиш Н. Дж., «Эффективность привода тока в вырожденной плазме», Physical Review Letters , vol. 95, нет. 22, статья ID 225002, 2005.
и Фиш Н. Дж., «Эффективность привода тока в вырожденной плазме», Physical Review Letters , vol. 95, нет. 22, статья ID 225002, 2005.Посмотреть по адресу:
Сайт издателя | Google Scholar
Copyright
Copyright © 2020 H. Al-Yousef and Sh. М. Халил. Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Связь астрофизической турбулентности и магнитного пересоединения
Связь астрофизической турбулентности и магнитного пересоединения — Эксперты МакМастерПоиск
‘; nsldiv.innerHTML = nsldiv.innerHTML + nslink;
‘; nsldiv. innerHTML = nsldiv.innerHTML + nslink;
innerHTML = nsldiv.innerHTML + nslink;- Обзор
- Исследования
- Личность
- Дополнительная информация о документе
- Просмотреть все
реферат
- Астрофизические жидкости обычно турбулентны, и это необходимо учитывать.
приходится на большинство транспортных процессов. Мы обсуждаем, как ранее существовавшая турбулентность
изменяет магнитное пересоединение и как магнитное пересоединение влияет на МГД
турбулентный каскад. Мы показываем внутреннюю взаимозависимость и взаимосвязь
магнитная турбулентность и магнитное пересоединение, в частности, сильное
магнитная турбулентность в 3D требует пересоединения и 3D магнитная турбулентность
влечет за собой быстрое повторное подключение.
 Мы следуем подходу Эйинка, Лазаряна и Вишняка
2011, чтобы показать, что выражения быстрого магнитного пересоединения в Лазаряне и
Вишняк 1999 может быть восстановлено, если диффузия Ричардсона турбулентных течений
используется вместо обычной омической диффузии. Однако это не оживляет
концепция магнитной турбулентной диффузии, которая предполагает, что магнитные поля могут
смешиваться пассивным образом вплоть до очень малых масштабов диссипации. На
напротив, мы имеем дело с пересоединением динамически важных магнитных
пучки полей, которые сильно сопротивляются изгибу и имеют хорошо определенное среднее
направление, слабо возмущенное турбулентностью. Мы утверждаем, что в присутствии
турбулентности сама концепция замораживания потока требует модификации.
диффузию, возникающую из-за магнитной турбулентности, можно назвать пересоединением
диффузия, поскольку она основана на пересоединении силовых линий магнитного поля. Воссоединение
диффузия имеет важные последствия для непрерывных транспортных процессов в
намагниченной плазмы и для звездообразования.
Мы следуем подходу Эйинка, Лазаряна и Вишняка
2011, чтобы показать, что выражения быстрого магнитного пересоединения в Лазаряне и
Вишняк 1999 может быть восстановлено, если диффузия Ричардсона турбулентных течений
используется вместо обычной омической диффузии. Однако это не оживляет
концепция магнитной турбулентной диффузии, которая предполагает, что магнитные поля могут
смешиваться пассивным образом вплоть до очень малых масштабов диссипации. На
напротив, мы имеем дело с пересоединением динамически важных магнитных
пучки полей, которые сильно сопротивляются изгибу и имеют хорошо определенное среднее
направление, слабо возмущенное турбулентностью. Мы утверждаем, что в присутствии
турбулентности сама концепция замораживания потока требует модификации.
диффузию, возникающую из-за магнитной турбулентности, можно назвать пересоединением
диффузия, поскольку она основана на пересоединении силовых линий магнитного поля. Воссоединение
диффузия имеет важные последствия для непрерывных транспортных процессов в
намагниченной плазмы и для звездообразования.



 14, нет. 7, с. 073042, 2012.
14, нет. 7, с. 073042, 2012. Манфреди, «Квантовые эффекты на неустойчивость Рэлея-Тейлора модели вязкоупругой плазмы через пористую среду», Fields Institute Communications Series , vol. 46, стр. 263–287, 2005.
Манфреди, «Квантовые эффекты на неустойчивость Рэлея-Тейлора модели вязкоупругой плазмы через пористую среду», Fields Institute Communications Series , vol. 46, стр. 263–287, 2005. А. Эрвьё, «Авторезонансное управление многоэлектронной динамикой в непараболических квантовых ямах», Письма по прикладной физике , том. 91, нет. 6, с. 061108, 2007.
А. Эрвьё, «Авторезонансное управление многоэлектронной динамикой в непараболических квантовых ямах», Письма по прикладной физике , том. 91, нет. 6, с. 061108, 2007. 81, нет. 4, стр. 1625–1663, 2009.
81, нет. 4, стр. 1625–1663, 2009. 10, ID статьи 105004, 2010.
10, ID статьи 105004, 2010.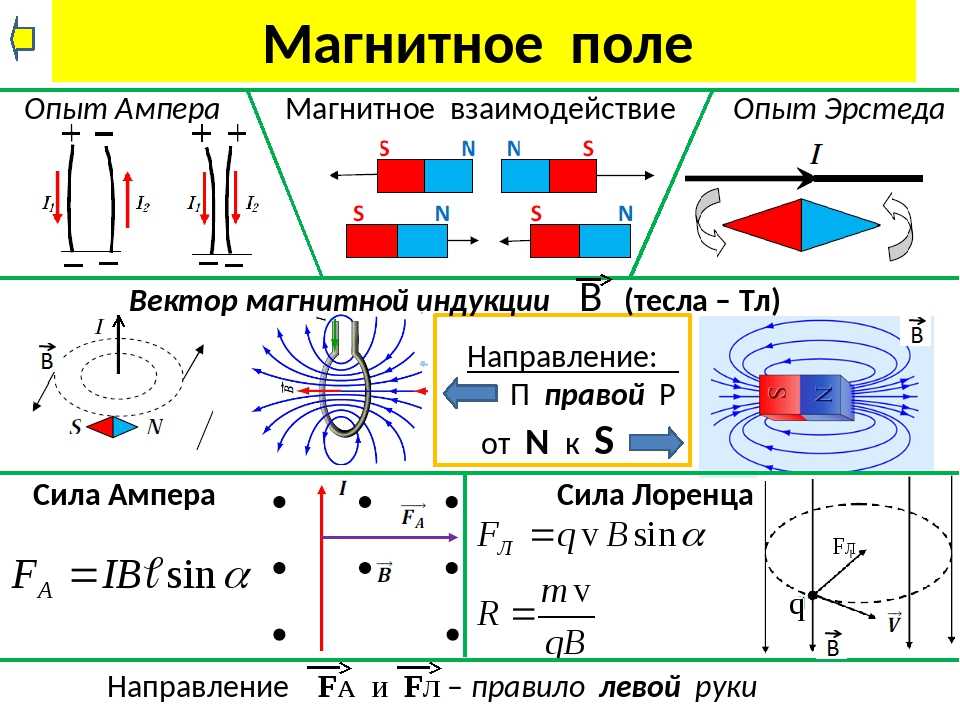 Офер, Л. О. Сильва, Д. Э. Догер, В. К. Децик и Дж. М. Доусон, «Скорости ядерных реакций и энергия в звездной плазме: влияние сильно затухающих мод», Физика плазмы , вып. 8, нет. 5, стр. 2454–2460, 2001.
Офер, Л. О. Сильва, Д. Э. Догер, В. К. Децик и Дж. М. Доусон, «Скорости ядерных реакций и энергия в звездной плазме: влияние сильно затухающих мод», Физика плазмы , вып. 8, нет. 5, стр. 2454–2460, 2001. Лай, «Вещество в сильных магнитных полях», Reviews of Modern Physics , vol. 73, нет. 3, с. 629, 2001.
Лай, «Вещество в сильных магнитных полях», Reviews of Modern Physics , vol. 73, нет. 3, с. 629, 2001. 99, нет. 12, ID статьи 125002, 2007 г.
99, нет. 12, ID статьи 125002, 2007 г. и Фиш Н. Дж., «Эффективность привода тока в вырожденной плазме», Physical Review Letters , vol. 95, нет. 22, статья ID 225002, 2005.
и Фиш Н. Дж., «Эффективность привода тока в вырожденной плазме», Physical Review Letters , vol. 95, нет. 22, статья ID 225002, 2005.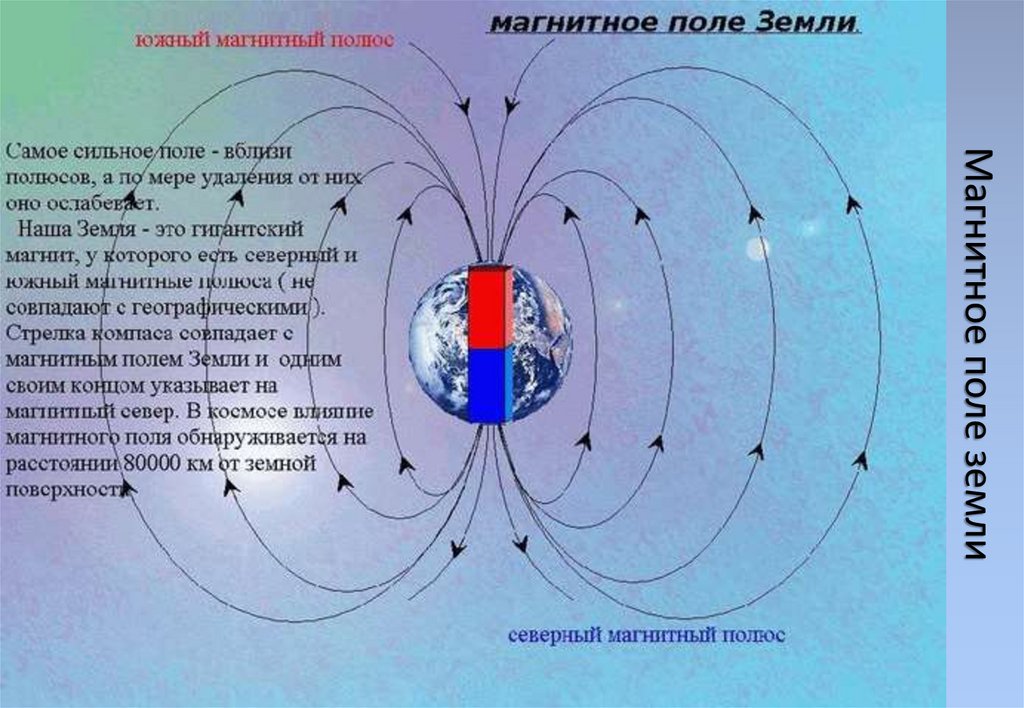 Мы следуем подходу Эйинка, Лазаряна и Вишняка
2011, чтобы показать, что выражения быстрого магнитного пересоединения в Лазаряне и
Вишняк 1999 может быть восстановлено, если диффузия Ричардсона турбулентных течений
используется вместо обычной омической диффузии. Однако это не оживляет
концепция магнитной турбулентной диффузии, которая предполагает, что магнитные поля могут
смешиваться пассивным образом вплоть до очень малых масштабов диссипации. На
напротив, мы имеем дело с пересоединением динамически важных магнитных
пучки полей, которые сильно сопротивляются изгибу и имеют хорошо определенное среднее
направление, слабо возмущенное турбулентностью. Мы утверждаем, что в присутствии
турбулентности сама концепция замораживания потока требует модификации.
диффузию, возникающую из-за магнитной турбулентности, можно назвать пересоединением
диффузия, поскольку она основана на пересоединении силовых линий магнитного поля. Воссоединение
диффузия имеет важные последствия для непрерывных транспортных процессов в
намагниченной плазмы и для звездообразования.
Мы следуем подходу Эйинка, Лазаряна и Вишняка
2011, чтобы показать, что выражения быстрого магнитного пересоединения в Лазаряне и
Вишняк 1999 может быть восстановлено, если диффузия Ричардсона турбулентных течений
используется вместо обычной омической диффузии. Однако это не оживляет
концепция магнитной турбулентной диффузии, которая предполагает, что магнитные поля могут
смешиваться пассивным образом вплоть до очень малых масштабов диссипации. На
напротив, мы имеем дело с пересоединением динамически важных магнитных
пучки полей, которые сильно сопротивляются изгибу и имеют хорошо определенное среднее
направление, слабо возмущенное турбулентностью. Мы утверждаем, что в присутствии
турбулентности сама концепция замораживания потока требует модификации.
диффузию, возникающую из-за магнитной турбулентности, можно назвать пересоединением
диффузия, поскольку она основана на пересоединении силовых линий магнитного поля. Воссоединение
диффузия имеет важные последствия для непрерывных транспортных процессов в
намагниченной плазмы и для звездообразования.