Вычитание векторов – примеры по правилу треугольника

4.6

Средняя оценка: 4.6

Всего получено оценок: 170.

4.6

Средняя оценка: 4.6

Всего получено оценок: 170.

Вычитание векторов часто вызывает проблемы у учеников. Это связано с тем, что вычитание в геометрии нужно выполнять очень осторожно, чтобы не получалось отрицательных чисел. А вектор может быть отрицательным, положительным, нулевым – это вызывает много ошибок, которых можно избежать просто один раз разобравшись в вопросе.

Вектор

Вектор – одно из самых интересных явлений в математике. Это первая величина во всем школьном курсе, которая имеет две характеристики: направление и размер. Вектором называют направленный отрезок, то есть отрезок, у которого стрелкой указали направление движения.

Представьте, вы прошли километр от дома до парка. Если поставить точку в начальном положении и стрелку в конечном, то результат движениям будет являться вектором. Ведь он имеет направление: от дом до парка.

При этом у результата движения есть и размер, в нашем случае это один километр.

Ученики часто пугаются отрицательных векторов, но в этом нет ничего страшного. Вектор это направление некого движения, а любое движение относительно, то есть зависит от системы отсчета.

В любую систему отчета входит точка отчета, система координат и прибор для измерения времени.

Если вектор поместить в любую систему координат, даже если это будет простой координатный луч, то вектор может быть направлен в одну сторону с системой координат, но может и в разные. Если вектор и система координат направлены в разные стороны, то вектор будет отрицательным.

Рис. 1. Вектор в системе координат.

При этом противоположным направлением считается любое в половине плоскости, в другую сторону которой направлен вектор.

Особые случаи векторов

Первый вопрос, который возникает у множества учеников, это возможность существования нуля в системе векторов. Ноль у векторов есть, только это не число, а точка.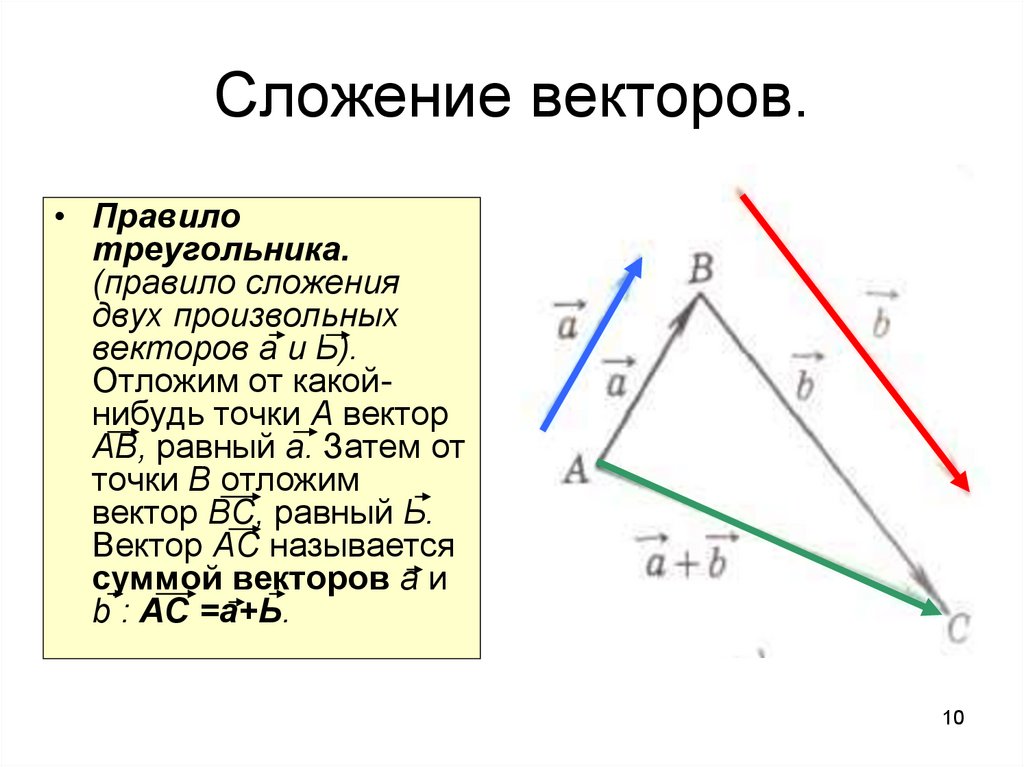 Любую точку можно считать нулевым вектором. Нулевой вектор появляется в результате сложения коллинеарных разнонаправленных векторов.

Рис. 2. Нулевой вектор.

Коллинеарными называют вектора, которые лежат на одной прямой. Эти векторы могут быть сонаправлены или противоположно направлены. При этом векторы, которые лежат на одной прямой так же считаются коллинеарными, так как любая прямая параллельна самой себе. Это не трудно понять, но запомнить название лучше наизусть, так как в тематике векторов, это определение встречается довольно часто.

Результат сложения или вычитания коллинеарных векторов будет коллинеарным для каждого из начальных построений. Поэтому найти результат такой операции можно арифметически, да и построить треугольник или параллелограмм из коллинеарных векторов не получится.

Вычитание векторов

Результатом вычитания векторов может быть:

• Вектор. Если вычитание производилось в системе координат, то результат может быть положительным или отрицательным
• Нулевой вектор или точка
• Никаких других результатов быть не может

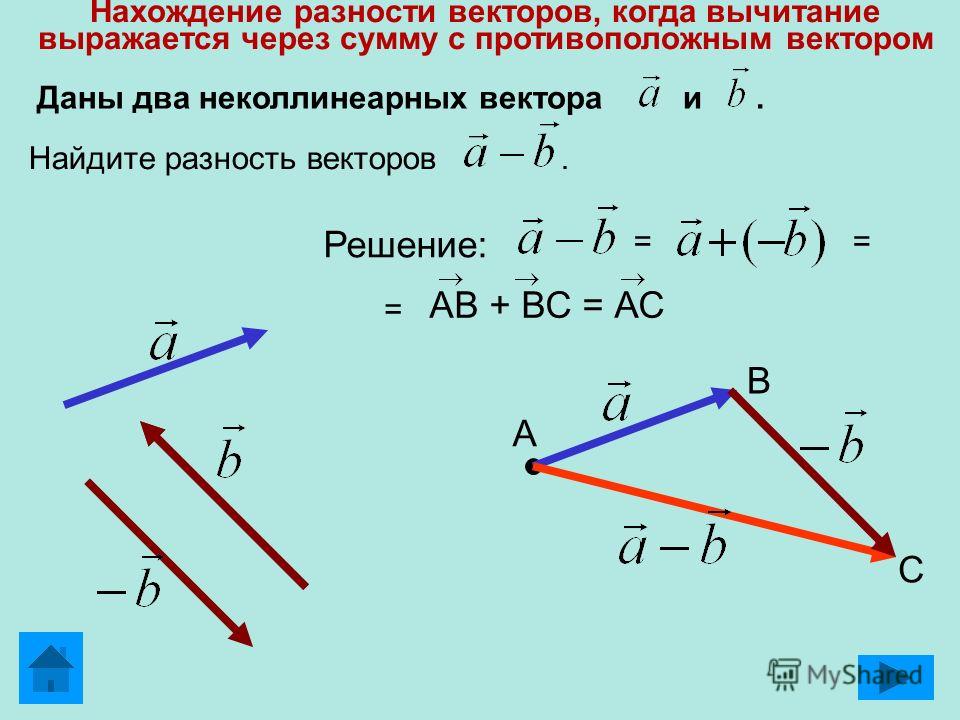
Рис. 3. Вычитание векторов.

Для того, чтобы вычесть один вектор из другого, любой из векторов заменяется на противоположный и выполняется сложение по правилу треугольника или параллелограмма. Таким образом, меняется знак вектора.

В математической записи это выглядит так:

АВ-МР=АВ+РМ – в математической записи первая буква означает начало вектора, вторая – конец. Так можно без чертежа обозначить направление.

Что мы узнали?

Мы поговорили о векторах и их частных случаях. Обсудили, как правильно вычитать вектора и что может получиться в результате такого вычитания. Привели пример правильной записи вычитания 2 векторов.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Руслан Галандских

  10/10

• Нина Трофимова

  5/10

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 170.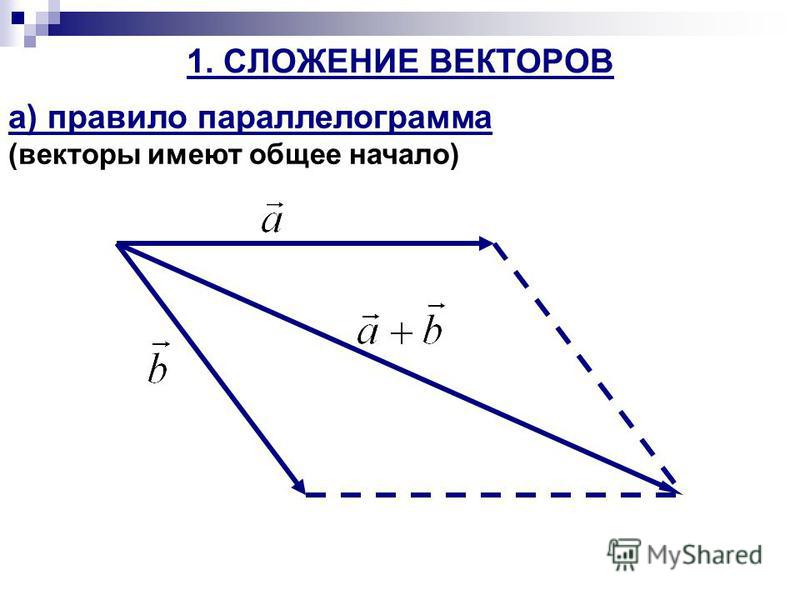

---

А какая ваша оценка?

в чем оно состоит, примеры решения задач

Основные понятия

Определение 1

Направленный вектор — это отрезок, для которого указано, какая из его граничных точек является началом, а какая концом.

Обозначается следующим образом:

 

Коллинеарность векторов означает: ненулевые векторы, которые лежат на одной прямой или на параллельных прямых. Нулевой вектор (вектор нулевой длины) является коллинеарным любому вектору.

Определение 2

Сонаправленные векторы — векторы, направленные в одну сторону.

Определение 3

Противонаправленные векторы — векторы, направленные в разные стороны.

 

Определение 4

Равные векторы — векторы, которые коллинеарны, сонаправлены и имеют одинаковую длину.

Формулировка компланарности векторов: векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.

Три вектора, среди которых имеются два коллинеарных, также компланарны.

Некомпланарный вектор не имеет равный ему вектор, лежащий в одной плоскости.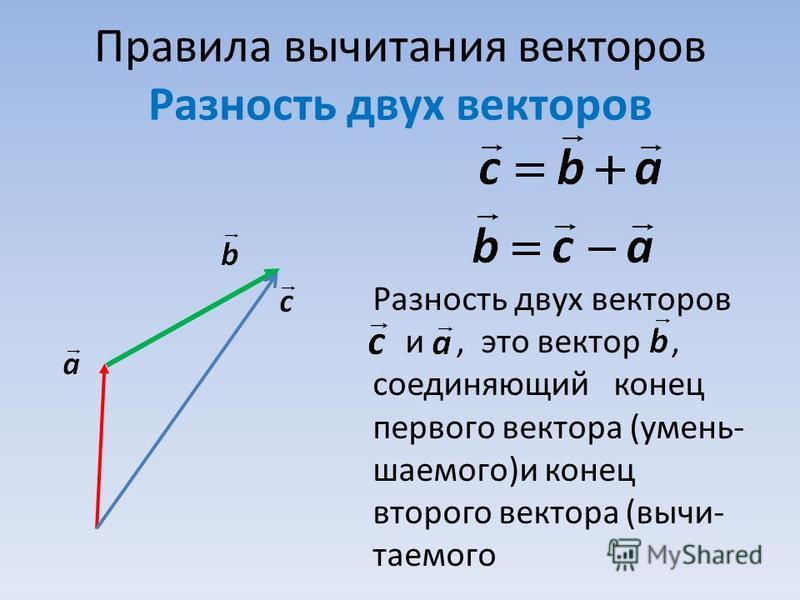

Складывать векторы можно несколькими способами. Мы рассмотрим сложение векторов методом параллелограмма.

Сложение векторов по правилу параллелограмма

Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти векторы и построить на них параллелограмм. Диагональ параллелограмма, исходящая из этой точки, и будет суммой векторов.

На рисунке все наглядно проиллюстрировано.

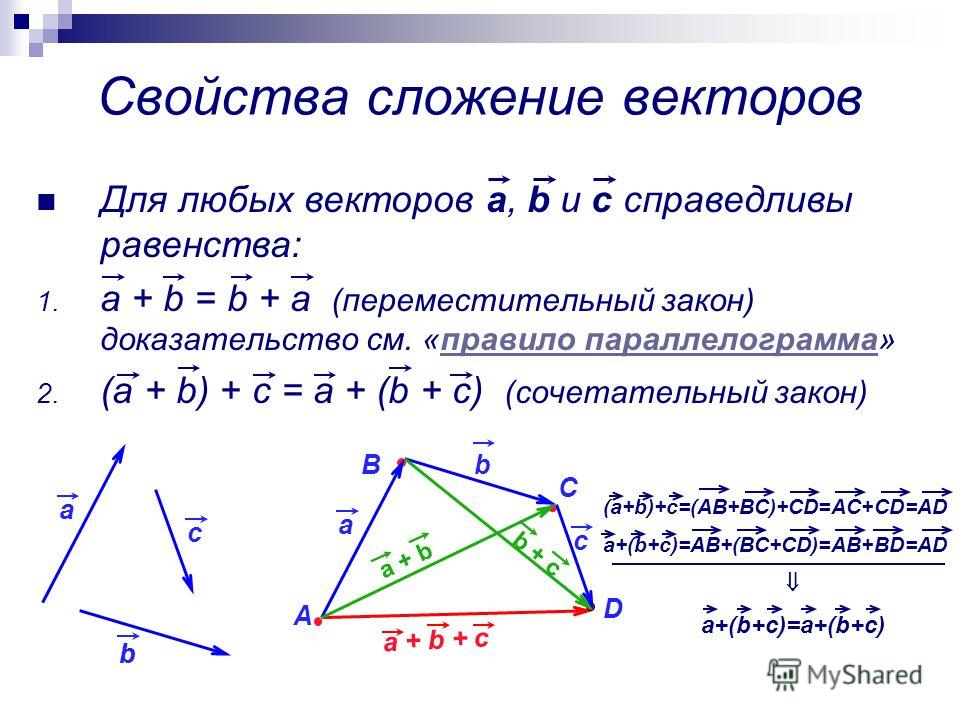
сочетательный закон:

 

Из произвольной точки А отложим вектор , прибавим к нему вектор , получим их сумму . К этой сумме прибавим вектор , получим результат:

 

В правой части выражения мы сначала получили сумму векторов , после прибавили ее к вектору  и получили результат: 

Таким образом, мы провели доказательство сочетательного закона сложения векторов.

Когда векторы расположены в пространстве и они не компланарны, для их сложения применяется правило параллелепипеда.

Для начала проводят построение:

1. Векторы приводят к общему началу А.

    2. На этих трех ребрах строиться параллелепипед.

    3. Диагональ параллелепипеда, которая выходит из этой же точки, изображает суммы векторов АВ, AD, AA1.

Примеры решения задач

Пример 1

Определить вид четырехугольника ABCD, если:

 

 

Решение:

Данный четырехугольник — ромб. Обоснуем это.

Мы знаем, что векторы  и  равны, отсюда следует, что равны их модули — то есть длины отрезков.

Векторы по условию сонаправлены и коллинеарны, то есть принадлежат параллельным прямым. Таким образом, заданный четырехугольник — параллелограмм.

Данный факт обоснован признаком параллелограмма: если две стороны четырехугольника принадлежат параллельным прямым и длины их равны, то данный четырехугольник — параллелограмм.

Согласно второму условию: , соседние стороны параллелограмма равны друг другу, а такой параллелограмм является ромбом.

Пример 2

Дан параллелепипед ABCDА1B1С1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов: AB+AD+AА1.

Решение:

AB+AD=AC, AC+AA1=AC1

Ответ: AC1.

Задания для самостоятельной работы

Задание 1

Дан параллелограмм ABCD. Найдите сумму векторов CD+DB+BA.

Задание 2

Дан параллелепипед ABCDА1B1С1D1. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов: DA+DC+DD1.

Сложение векторов — математика GCSE

Введение

Что такое сложение векторов?

Как добавить векторы

Лист сложения векторов

Распространенные заблуждения

Практические вопросы по сложению векторов

Добавление вектора Вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Теперь доступны еженедельные онлайн-уроки повторения математики GCSE

Узнать больше

Введение

Что такое сложение векторов?

Как добавить векторы

Лист сложения векторов

Распространенные заблуждения

Практические вопросы по сложению векторов

Сложение векторов Вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Здесь мы узнаем о сложении векторов.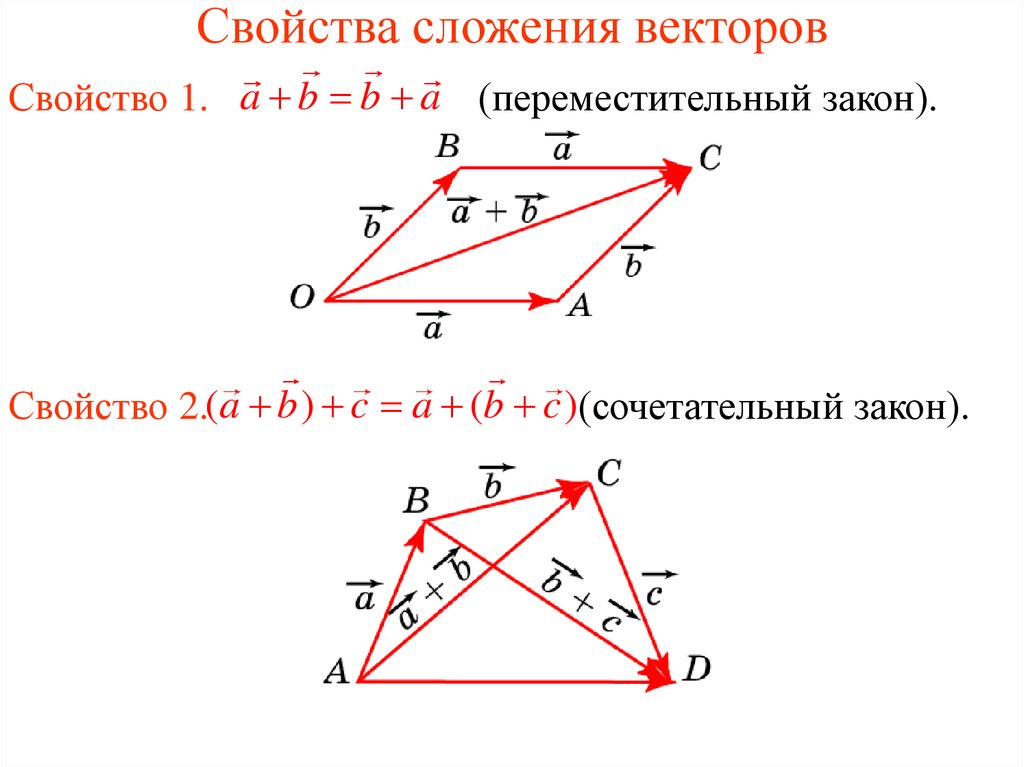

Существуют также векторные рабочие листы на основе экзаменационных вопросов Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое сложение векторов?

Добавление вектора — добавление одного вектора к другому вектору. Это иногда называют векторной суммой.

Для этого добавляем отдельные компоненты первого вектора ко второму вектору.
Сначала мы складываем горизонтальные компоненты вектора (верхние числа), а затем складываем вертикальные компоненты вектора (нижние числа).

Давайте рассмотрим несколько примеров векторов: вектор a и вектор b .

\[\textbf{а}= \left(\begin{массив}{1} 3\\ 2\\ \конец{массив}\справа) \четверка \textbf{b}= \left(\begin{массив}{1} 1\\ 4\\ \конец{массив}\справа)\]

Вот векторы, представленные схематически:

Для сложения векторов a + b мы добавляем вектор b в конец вектора a .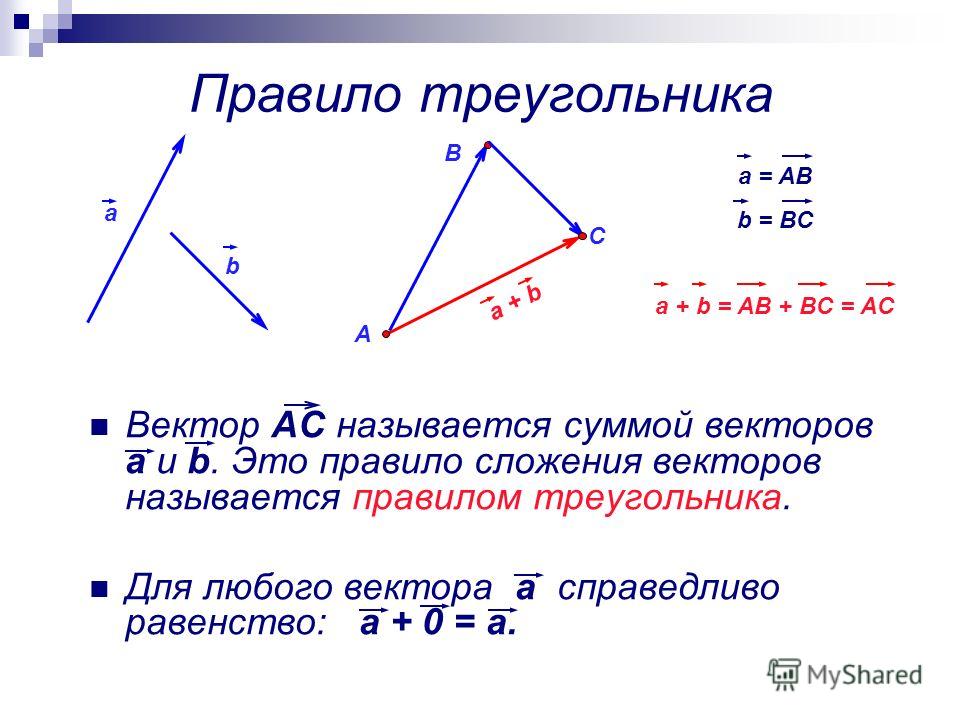

\[\textbf{a} +\textbf{b}= \left(\begin{массив}{1} 3\\ 2\\ \конец{массив}\справа) + \left(\begin{массив}{1} 1\\ 4\\ \end{массив}\right)\]

\[\textbf{a} +\textbf{b}= \left(\begin{массив}{1} 3\\ 2\\ \конец{массив}\справа) + \left(\begin{массив}{1} 1\\ 4\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 4\\ 6\\ \конец{массив}\справа)\]

При нахождении векторной суммы нам не нужно рисовать диаграмму. Мы можем просто добавить компоненты вектора. Сначала добавьте компоненты x (верхние числа), а затем добавьте компоненты y (нижние числа)

\[\textbf{a} +\textbf{b} = \left(\begin{массив}{1} 3\\ 2\\ \конец{массив}\справа) +\ \left(\begin{массив}{1} 1\\ 4\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 3+1\\ 2+4\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 4\\ 6\\ \end{array}\right)\]

Новый вектор, полученный в результате сложения двух данных векторов, известен как результирующий вектор .

Добавление векторов коммутативно , что означает, что порядок, в котором мы добавляем векторы, не важен. Другими словами, мы получим тот же результат, если начнем с вектора b и добавим вектор a.

\textbf{a} +\textbf{b}= \textbf{b} +\textbf{a}

Диаграмма представляет собой параллелограмм. Результирующий вектор является диагональю параллелограмма.

Что такое сложение векторов?

Как сложить векторы

Чтобы сложить векторы, чтобы найти векторную сумму:

1. Добавьте компоненты x .
2. Добавьте компоненты и .
3. Запишите результирующий вектор.

Как добавить векторы

Лист сложения векторов

Получите бесплатный лист сложения векторов, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКОРО

Икс

Лист сложения векторов

Получите бесплатный лист сложения векторов, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКОРО

Связанные уроки по векторам

Добавление вектора является частью нашей серии уроков по поддержке пересмотра векторов . Возможно, вам будет полезно начать с урока по основным векторам, чтобы получить общее представление о том, чего ожидать, или воспользоваться пошаговыми руководствами, приведенными ниже, для получения более подробной информации по отдельным темам. Другие уроки в этой серии включают в себя:

• Vectors
• Magnitude of a vector 
• Column vector
• Vector notation
• Vector multiplication
• Vector subtraction
• Vector problems

Vector addition examples

Example 1: add vectors

Add the given векторы

\[\left(\begin{массив}{1} 2\\ 4\\ \конец{массив}\справа) \текст{и}\ \left(\begin{массив}{1} 5\\ 1\\ \конец{массив}\справа)\]

1. Добавьте компоненты x
   .

Добавьте два верхних числа исходных векторов

2+5=7

2 Добавьте компоненты y.

4+1=5

3 Запишите результирующий вектор.

\[\left(\begin{массив}{1} 2\\ 4\\ \конец{массив}\справа) + \left(\begin{массив}{1} 5\\ 1\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 7\\ 5\\ \end{array}\right)\]

Пример 2: добавить векторы

Добавить заданные векторы

\[\left(\begin{массив}{1} 4\\ 2\\ \конец{массив}\справа) \текст{и}\ \left(\begin{массив}{1} 1\\ 7\\ \end{массив}\right)\]

Добавьте компоненты x .

Добавьте два верхних числа исходных векторов

4+1=5

Добавьте компоненты и .

Добавьте два нижних числа

2+7=9

Запишите результирующий вектор.

Запишите два ответа в виде вектор-столбца

\[\left(\begin{массив}{1} 4\\ 2\\ \конец{массив}\справа) + \left(\begin{массив}{1} 1\\ 7\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 5\\ 9\\ \end{array}\right)\]

Пример 3: добавить векторы

Добавить заданные векторы

\[\left(\begin{array}{1} 4\\ 1\\ \конец{массив}\справа) \текст{и}\ \left(\begin{массив}{1} -2\\ 3\\ \end{массив}\right)\]

Добавьте компоненты x .

Добавьте два верхних числа исходных векторов

4+-2=2

Добавьте компоненты и .

Добавьте два нижних числа

1+3=4

Запишите результирующий вектор.

Запишите два ответа в виде вектор-столбца

\[\left(\begin{array}{1} 4\\ 1\\ \конец{массив}\справа) + \left(\begin{массив}{1} -2\\ 3\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 2\\ 4\\ \end{array}\right)\]

Пример 4.

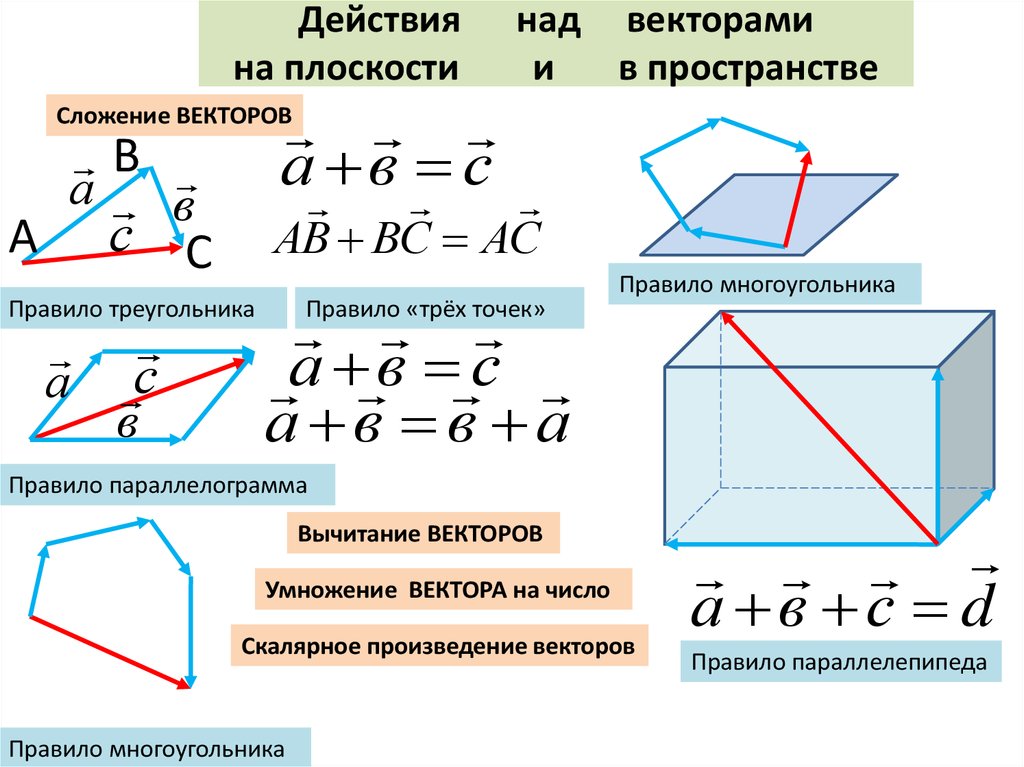Сложение векторов

Сложение заданных векторов

\[\left(\begin{массив}{1} -5\\ 2\\ \конец{массив}\справа) \текст{и}\ \left(\begin{массив}{1} 2\\ -4\\ \end{массив}\right)\]

Добавьте компоненты x .

Добавьте два верхних числа исходных векторов

-5+2=-3

Добавьте компоненты и .

Добавьте два нижних числа

2+-4=-2

Запишите результирующий вектор.

Запишите два ответа в виде вектор-столбца

\[\left(\begin{массив}{1} -5\\ 4\\ \конец{массив}\справа) + \left(\begin{массив}{1} 2\\ -4\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} -3\\ -2\\ \end{array}\right)\]

Пример 5: Добавить векторы

Добавить заданные векторы

\[\left(\begin{array}{1} 7\\ 3\\ \конец{массив}\справа) \текст{и}\ \left(\begin{массив}{1} -3\\ -4\\ \end{массив}\right)\]

Добавьте компоненты x .

Добавьте два верхних числа исходных векторов

7+-3=4

Добавьте компоненты и .

Добавьте два нижних числа

3+-4=-1

Запишите результирующий вектор.

Запишите два ответа в виде вектор-столбца

\[\left(\begin{array}{1} 7\\ 3\\ \конец{массив}\справа) + \left(\begin{массив}{1} -3\\ -4\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 4\\ -1\\ \end{array}\right)\]

Пример 6. Сложение векторов

Сложение заданных векторов

\[\left(\begin{массив}{1} -3\\ -1\\ \конец{массив}\справа) \текст{и}\ \left(\begin{массив}{1} -2\\ 4\\ \end{массив}\right)\]

Добавьте компоненты x .

Добавьте два верхних числа исходных векторов

-3+-2=-5

Добавьте компоненты и .

Добавьте два нижних числа

-1+4=3

Запишите результирующий вектор.

Запишите два ответа в виде вектор-столбца

\[\left(\begin{массив}{1} -3\\ -1\\ \конец{массив}\справа) + \left(\begin{массив}{1} -2\\ 4\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} -5\\ 3\\ \end{array}\right)\]

Распространенные заблуждения

• Сложение отрицательных целых чисел

При сложении положительного и отрицательного чисел легко допустить ошибку.

Убедитесь, что навыки работы с отрицательными числами хорошо отработаны.

3+-4=3-4=-1

• Обозначение векторов-столбцов

Векторы-столбцы имеют только 2 числа в квадратных скобках, у них есть верхний номер и нижний номер.

Нет необходимости в каких-либо других знаках препинания, таких как запятые или точки с запятой, и нет необходимости в черте для разделения чисел.

Практические вопросы по сложению векторов

\begin{pmatrix} \; 3 \;\\ \; 10 \; \end{pmatrix}

\begin{pmatrix} \; 2 \;\\ \; -3\; \end{pматрица}

\begin{pmatrix} \; 4 \;\\ \; 7\; \end{pmatrix}

\begin{pmatrix} \; 4 \;\\ \; -3\; \end{pmatrix}

\begin{pmatrix} \; 3 \;\\ \; 2\; \end{pmatrix} + \begin{pmatrix} \; 1 \;\\ \; 5 \; \end{pmatrix} = \begin{pmatrix} \; 3+1 \;\\ \; 2+5 \; \end{pmatrix} = \begin{pmatrix} \; 4 \;\\\; 7\; \end{pmatrix}

\begin{pmatrix} \; 5 \;\\ \; 8\; \end{pmatrix}

\begin{pmatrix} \; 4 \;\\ \; -15 \; \end{pmatrix}

\begin{pmatrix} \; 4 \;\\ \; 2\; \end{pматрица}

\begin{pmatrix} \; 5 \;\\ \; 2\; \end{pmatrix}

\begin{pmatrix} \; 4 \;\\\; 5 \; \end{pmatrix} + \begin{pmatrix} \; 1 \;\\ \; -3\; \end{pmatrix} = \begin{pmatrix} \; 4+1 \;\\ \; 5+-3\; \end{pmatrix} = \begin{pmatrix} \; 5 \;\\\; 2\; \end{pmatrix}

\begin{pmatrix} \; 3 \;\\ \; 11\; \end{pmatrix}

\begin{pmatrix} \; -3 \;\\ \; 11\; \end{pmatrix}

\begin{pmatrix} \; 3 \;\\ \; 5 \; \end{pmatrix}

\begin{pmatrix} \; -3 \;\\ \; -11\; \end{pматрица}

\begin{pmatrix} \; -2 \;\\\; 8\; \end{pmatrix} + \begin{pmatrix} \; -1 \;\\\; 3 \; \end{pmatrix} = \begin{pmatrix} \; -2+-1 \;\\ \; 8+3 \; \end{pmatrix} = \begin{pmatrix} \; -3 \;\\\; 11\; \end{pmatrix}

\begin{pmatrix} \; 2 \;\\ \; -4\; \end{pmatrix}

\begin{pmatrix} \; 2 \;\\ \; 4\; \end{pmatrix}

\begin{pmatrix} \; -2 \;\\ \; -4\; \end{pmatrix}

\begin{pmatrix} \; -2 \;\\ \; 4\; \end{pmatrix}

\begin{pmatrix} \; -2 \;\\\; 3 \; \end{pmatrix} + \begin{pmatrix} \; 4 \;\\\; -7\; \end{pmatrix} = \begin{pmatrix} \; -2+4\;\\\; 3+-7 \; \end{pmatrix} = \begin{pmatrix} \; 2 \;\\\; -4\; \end{pматрица}

\begin{pmatrix} \; 5 \;\\ \; 8\; \end{pmatrix}

\begin{pmatrix} \; 6 \;\\ \; 12\; \end{pmatrix}

\begin{pmatrix} \; 6 \;\\ \; 8\; \end{pmatrix}

\begin{pmatrix} \; -5 \;\\ \; 8\; \end{pmatrix}

\begin{pmatrix} \; -3 \;\\\; 6\; \end{pmatrix} + \begin{pmatrix} \; -2 \;\\\; 2\; \end{pmatrix} = \begin{pmatrix} \; -3+-2\;\\\; 6+2 \; \end{pmatrix} = \begin{pmatrix} \; -5 \;\\\; 8\; \end{pmatrix}

\begin{pmatrix} \; -7 \;\\ \; -3\; \end{pматрица}

\begin{pmatrix} \; 7 \;\\ \; -3\; \end{pmatrix}

\begin{pmatrix} \; -7 \;\\ \; 3 \; \end{pmatrix}

\begin{pmatrix} \; 7 \;\\ \; 3 \; \end{pmatrix}

\begin{pmatrix} \; -4\;\\\; -1\; \end{pmatrix} + \begin{pmatrix} \; -3 \;\\\; 4\; \end{pmatrix} = \begin{pmatrix} \; -4+-3\;\\\; -1+4 \; \end{pmatrix} = \begin{pmatrix} \; -7\;\\\; 3 \; \end{pmatrix}

Сложение векторов Вопросы GCSE

1. Какой из приведенных ниже векторов является суммой

 

\begin{pmatrix} \; 5 \;\\ \; 3 \; \end{pmatrix} \; а также \; \begin{pmatrix} \; 2 \;\\ \; -5 \; \end{pматрица} ?

 

А	\четверка \четверка	Б	\четверка \четверка	С	\четверка \четверка	Д
\begin{pmatrix} \; 7 \;\\ \; 2\; \end{pmatrix}	\четверка \четверка	\begin{pmatrix} \; 10 \;\\ \; -15 \; \end{pmatrix}	\квадратный \четверный	\begin{pmatrix} \; 7 \;\\ \; -2\; \end{pmatrix}	\четверка \четверка	\begin{pmatrix} \; 3 \;\\ \; 8\; \end{pmatrix}

 

(1 балл)

Показать ответ

2. Вот два вектора.

 

\textbf{a}= \begin{pmatrix} \; -3 \;\\ \; 4\; \end{pmatrix} \; а также \; \textbf{b}= \begin{pmatrix} \; 2 \;\\ \; 1 \; \end{pматрица}

 

Вычислить \textbf{a}+\textbf{b}
 

(2 балла)

Показать ответ

\begin{pmatrix} \; -1 \;\\ \; 5 \; \end{pматрица}

 

Для компонента x (верхнее число)

(1)

Для компонента y (нижнее число)

(1)

Сумма векторов.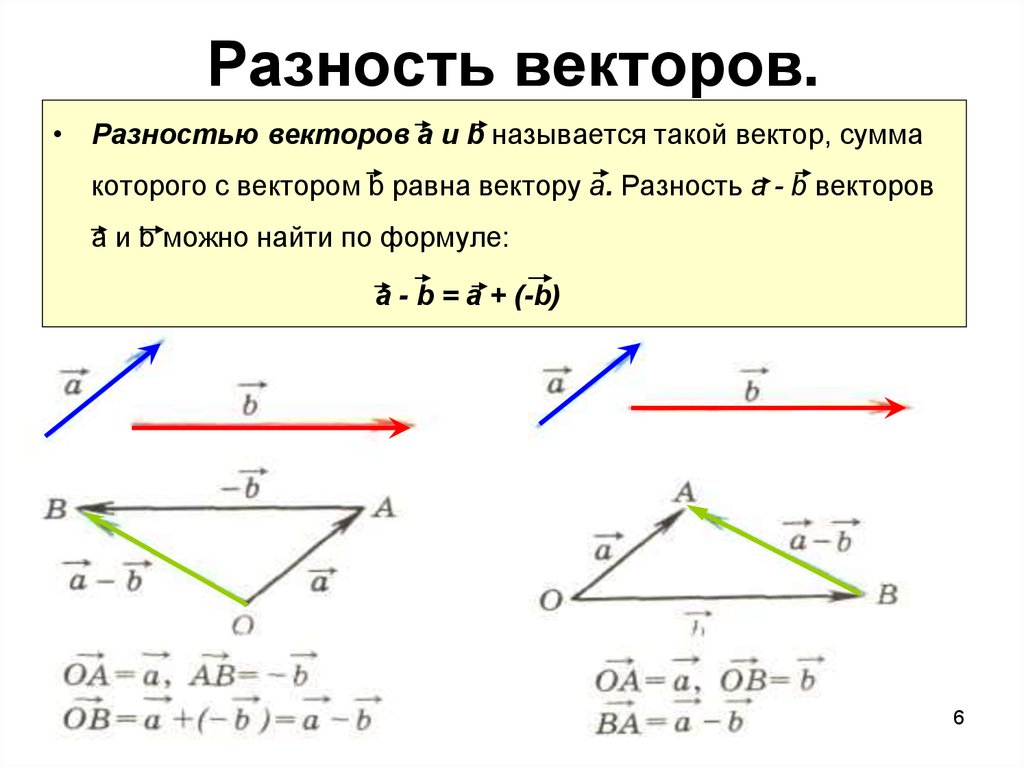

 

\begin{pmatrix} \; \текст{а} \;\\ \; 3 \; \end{pматрица} + \begin{pmatrix} \; 2 \;\\ \; \текст{б} \; \end{pматрица} знак равно \begin{pmatrix} \; 7 \;\\ \; -1\; \end{pматрица}

 

(a) Найдите значение a .

 

(b) Найдите значение b .

 

(2 балла)

Показать ответ

(a)

 

а=5

(1)

 

(б)

 

б=-4

(1)

Учебный контрольный список

Теперь вы научились:

• Складывать векторы

Следующие уроки

• Локусы и построение
• Преобразования
• Теоремы о кругах

Все еще застряли?

Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.

Узнайте больше о нашей программе повторения GCSE по математике.

Нахождение суммы двух векторов — Криста Кинг Математика

Что значит найти сумму двух векторов?

Когда мы хотим найти комбинацию двух векторов, мы просто совмещаем начальную точку второго вектора с конечной точкой первого вектора, а затем рисуем новый третий вектор из начальной точки первого в конечный пункт второго.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Другими словами, сочетание серого и синего — фиолетовое:

По сути, объединение двух векторов дает нам тот же результат, что и сложение векторов. В приведенном выше примере серый + синий = фиолетовый. Мы также можем вычитать векторы. Если вычитается вектор, мы движемся точно в направлении, противоположном исходному вектору. В приведенном ниже примере серый — синий = фиолетовый. Сплошной синий вектор — исходный вектор, но поскольку мы вычитаем, мы движемся в противоположном направлении.

Когда нам заданы числовые значения для векторов, мы просто суммируем ???x???-координаты, чтобы получить новую ???x???-координату, и суммируем ???y???? ?-координаты, чтобы получить новую ???y???-координату.

Как найти сумму векторов, в том числе когда векторы заданы в разных формах

Пройти курс

Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂

Еще два примера суммирования векторов

Пример

Найти сумму векторов.

???u=\langle2,1\rangle??? и ???v=\langle-1,5\rangle???

???u=2i-3j??? и ???v=6i+2j???

Для ???u=\langle2,1\rangle??? и ???v=\langle-1,5\rangle???:

Суммировать векторы ???u=\langle2,1\rangle??? и ???v=\langle-1,5\rangle???, мы просто суммируем ???x???-координаты, чтобы получить новую ???x???-координату, а затем делаем то же самое для ???y???-координат.