сложение, вычитание, умножение вектора на число. Схематические изображения. — КиберПедия

Вектор – это направленный отрезок.

Векторы могут обозначаться как 2-мя прописными буквами, так и одной строчной с чертой или стрелкой.

Длина вектора называется его модулем и обозначается

Если

Если

Векторы, лежащие на одной прямой или на параллельных прямых, называют коллинеарными.

Если начало и конец вектора совпадают , то такой вектор называется нулевым и обозначается Длина нулевого вектора равна нулю: , а направление – неопределенно.

Сложение векторов

 

Суммой двух векторов и называется вектор , начало которого совпадает с началом вектора , а конец – с концом вектора , отложенного из конца вектора (правило треугольника).

Суммой векторов и называется такой третий вектор , что при совмещенных началах этих трех векторов, векторы и служат сторонами параллелограмма, а вектор – его диагональю (называется сложением по правилу параллелограмма).

Сумма любого конечного числа векторов может быть найдена по правилу многоугольника: чтобы построить сумму конечного числа векторов, достаточно совместить начало каждого последующего вектора с концом предыдущего и построить вектор, соединяющий начало первого вектора с концом последнего.

При сложении векторов выполняется переместительныйзакон, т.е. + = +

 

и сочетательныйзакон, т.е. ( + )+ = +( + )

Вычитание векторов

Под разностью векторов и понимается вектор такой, что (см. рис. 5).

 

Умножение вектора на число

Произведением вектора на число k называется такой вектор , длина которого равна |k|⋅| |, причем векторы сонаправлены, если k>0, и противоположно направлены, если k<0.

Произведение нулевого вектора на любое число есть нулевой вектор.

Обозначение

Вектора и коллинеарны для любого k. Если два вектора и коллинеарны – то существует такое число k, что =k .
Произведение любого вектора на число нуль есть нулевой вектор.

Для любых векторов и и чисел k и l справедливы следующие законы:

Сочетательный: (kl)a→=k(l )

Первый распределительный: k(

+ )=k +k

Второй распределительный: (k+l) =k +l

 

Разложение вектора по базисным ортам. Направляющие косинусы. Длины векторов. Примеры.

Единичные векторы выходящие из начала координат в положительных направлениях осей OX, OYи OZназываются ортами этих осей.

Любой вектор можно разложить по ортам осей координат: , или

(на плоскости).

Пример:

Задание. Вектор задан своими координатами: . Записать разложение данного вектора по ортам осей координат.

Решение.

Числа называются направляющими косинусами вектора .

 

Направляющие косинусы вектора определяются соотношениями:

, ясно что

Пример: а = (3; -6; 2).

Длина вектора называется его модулем и обозначается

Если

Если

Пример: а = (3; -6; 2).

 

 

17. Ортогональные, коллинеарные и компланарные векторы: определения и примеры. Условия ортогональности, коллинеарности и компланарности.

Два вектора называются ортогональными, если в пересечении они образуют прямой угол, т.е. угол в 90^о.

Два вектора называются коллинеарными, если они лежат на одной прямой либо на параллельных прямых.

Три вектора называются компланарными , если они лежат в одной плоскости либо в параллельных плоскостях.

Условие ортогональности векторов. Два вектора и ортогональны (перпендикулярны), если их скалярное произведение равно нулю. · = 0

Условия коллинеарности

Ø Два вектора a и b коллинеарны, если существует число n такое, что

a = n · b

Ø Два вектора коллинеарны, если отношения их координат равны.

Ø Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.

 

Условия компланарности векторов

Ø Три вектора компланарны если их смешанное произведение равно нулю.

Ø Три вектора компланарны если они линейно зависимы.

Ø Для n векторов. Вектора компланарны если среди них не более двух линейно независимых векторов.

 

 

(НУЖНЫ ПРИМЕРЫ)

 

 

Сложение и вычитание векторов. Умножение вектора на число

1.	Выражение, содержащее векторы	1 вид — рецептивный	лёгкое	2 Б.	Упрощение выражения, содержащего векторы.
2.	Сумма векторов	1 вид — рецептивный	среднее	3 Б.	Вычисление суммы векторов, которые отложены на сторонах параллелепипеда.
3.	Сумма и разность векторов	1 вид — рецептивный	лёгкое	2 Б.	Сложение и вычитание векторов.
4.	Сложение и вычитание векторов	1 вид — рецептивный	лёгкое	2 Б.	Отработка простых операций с векторами.
5.	Арифметические операции с векторами	1 вид — рецептивный	лёгкое	2 Б.	Простейшие операции с векторами.
6.	Выражение вектора суммы	1 вид — рецептивный	среднее	3 Б.	Выражение вектора суммы через данный вектор.
7.	Выражение вектора разности	1 вид — рецептивный	среднее	3 Б.	Выражение вектора разности через данный вектор.
8.	Выражение с векторами	2 вид — интерпретация	среднее	5 Б.	Выполнение арифметических действий с векторами.
9.	Сложение и вычитание векторов	2 вид — интерпретация	среднее	4 Б.	Сложение и вычитание нескольких векторов.
10.	Сумма нескольких векторов	1 вид — рецептивный	среднее	3 Б.	Вычисление суммы нескольких векторов.
11.	Умножение вектора на число	2 вид — интерпретация	среднее	4 Б.	Нахождение числового коэффициента, выражающего отношение векторов.
12.	Сложение и умножение на число	3 вид — анализ	сложное	10 Б.	Вычисление результата нескольких операций с векторами.
13.	Арифметические действия с векторами, длина вектора	3 вид — анализ	сложное	8 Б.	Вычисление результата нескольких операций с векторами.
14.	Уравнение с векторами	3 вид — анализ	сложное	8 Б.	Нахождение неизвестного слагаемого.

Сложение и вычитание векторов. Умножение вектора на число

1. Сложение векторов. Векторы складываются геометрически по правилу параллелограмма или многоугольника.
Правило параллелограмма. Суммой двух векторов 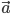и 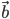называют такой третий вектор 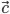, выходящий из их общего начала, который служит диагональю параллелограмма, сторонами которого являются сами векторы (рис.1) и обозначают так: .

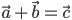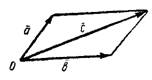
Рис.1

Правило многоугольника. Чтобы построить сумму любого конечного числа векторов, нужно в конце первого слагаемого вектора построить второй, в конце второго построить третий и т. д. Вектор, замыкающий полученную ломаную линию, представляет собой искомую сумму. Начало его совпадает с началом первого слагаемого вектора, а конец — с концом последнего.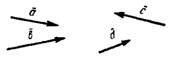

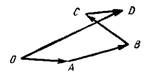
Рис.2

Например, сумма векторов 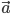, , 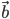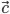и d получается так (рис.2). Строим векторы

Тогда вектор суммы

Два вектора и , имеющие равные длины, но противоположные направления, называются противоположными векторами (рис.3).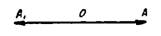

Рис.3

Если вектор , противоположен вектору , то можно записать:

.
Сумма противоположных векторов равна нуль-вектору:

Сумма векторов удостоверяет:
а) закону переместительности:

б) закону сочетательности:

2. Вычитание векторов. Вычитание двух векторов определяется как действие, обратное сложению.
Разностью двух векторов 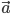и 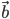называется такой третий вектор 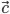, который нужно сложить с вектором 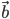, чтобы получить вектор 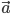, т. е. , если .
Чтобы из вектора 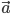вычесть вектор 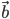, нужно отнести их к общему началу и провести вектор из конечной точки вектора-вычитаемого 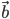конечную точку вектора-уменьшаемого 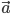(рис.4).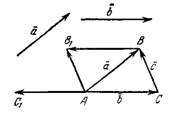

Рис.4

То же действие вычитания двух векторов можно произвести иначе.
Чтобы вычесть из вектора 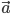вектор 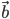, надо прибавить к вектору 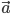равный и противоположно направленный вектору 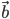вектор (- ).
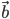Построим вектор , длина которого равна длине вектора , а направление его противоположно направлению вектора .
Кроме того, дополним треугольник ABC до параллелограмма АСВВ₁.
Очевидно равно . Следовательно, (рис.4).
Искомая разность

Мы получим следующее равенство:

3. Умножение вектора на скаляр. При умножении вектора 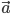на скаляр n получим вектор 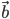, коллинеарный с вектором 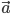и имеющий длину в n раз больше, чем . Этот новый вектор
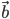
имеет одинаковое направление с вектором , если n>0, и противоположное с ним направление, если n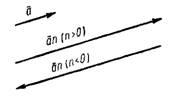

Рис.5

Если обозначить одноименной буквой с нуликом вверху вектор длины, равной 1, и того же направления, что и вектор 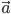, то из определения умножения вектора на скаляр следует

Единичный вектор направления вектора 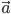называется его ортом.

12.Линейные операции над векторами. Сложение, вычитание и умножение вектора на число.

Сложение векторов

В алгебраическом представлении при сложении векторов с = a + b проекция результирующего вектора на оси координат является суммой соответствующих проекций складываемых векторов с учётом их знака:

с_x = a_x + b_x ; с_y = a_y + b_y ; с_z = a_z + b_z .

Если точка привязки не важна, а важна лишь величина (длина и направление) результирующего вектора, то сложение векторов можно считать коммутативной операцией (от перемены мест слагаемых сумма не меняется). В противном случае точка привязки результирующего вектора определяется исходя из физического смысла производимой операции (как правило, в физике точки привязки всех складываемых векторов и суммарного вектора совпадают, — то есть и все слагаемые, и их сумма применимы к одной и той же точке пространства или материальной точке).

Вычитание векторов

Вычитание векторов с = a – b можно представить как 2.narod.ru/info/vectors.htm»сложение уменьшаемого вектора с вектором, противоположным вычитаемому по направлению и равным ему по величине. Таким образом, в агебраическом представлении проекции вычитаемого вектора на оси координат меняют свой знак:

с_x = a_x – b_x ; с_y = a_y – b_y ; с_z = a_z – b_z .

Умножение вектора на число

При умножении вектора на число b = k · a в алгебраическом виде достаточно все его проекции умножить на это число:

b_x = k · a_x ; b_y = k · a_y ; b_z = k · a_z .

В строго геометрическом смысле при умножении на число начало вектора остаётся на месте, а «удлиняется» его конец. Однако на физических иллюстрациях часто остаётся на месте точка конца вектора, скажем точка приложения силы, хотя в общем случае этот вопрос всегда определяется физическим смыслом решаемой задачи.

Операция умножения на число является коммутативной  a · k = k · a  (от перемены мест сомножителей результат не меняется). При положительном множителе результирующий вектор сонаправлен с исходным, при отрицательном направление меняется на строго противоположное. Поэтому результат умножения вектора на число всегда 2.narod.ru/info/vectors.htm»коллинеарен с исходным вектором, за исключением случая, когда множитель или исходный вектор являются нулевыми — тогда результатом будет 2.narod.ru/info/vectors.htm»нулевой вектор, говорить о направлении которого некорректно.

Операция умножения на число является дистрибутивной  k · (a + b) = k · a + k · b  (произведение суммы векторов на число равно сумме произведений слагаемых на это же число).

Скалярное произведение векторов

Результатом скалярного перемножения векторов является число, равное произведению их модулей, умноженному на косинус угла между ними.

Вычисление скалярного произведения

В алгебраической форме скалярное произведение  d = a · b  вычисляется как

d = a_x · b_x + a_y · b_y + a_z · b_z .

Свойства скалярного произведения

Коммутативность:  a · b = b · a .

Дистрибутивность:  a · (b + c) = a · b + a · c .

Сочетательность (линейность) относительно скалярного множителя:  k · (a · b) = (k · a) · b = a · (k · b) .

Скалярный квадрат вектора равен квадрату его 2.narod.ru/info/vectors.htm»модуля:  a · a = |a|²  (норма вектора).

Векторное произведение

.Вычисление векторного произведения

В алгебраической форме векторное произведение  c = [a × b]  в правой системе координат вычисляется как

с_x = a_y · b_z – a_z · b_y ; с_y = a_z · b_x – a_x · b_z ; с_z = a_x · b_y – a_y · b_x .

В левой системе координат знаки слагаемых меняются на противоположные.

Свойства векторного произведения

Антикоммутативность:  [a × b] = –[b × a] .

Дистрибутивность:  [a × (b + c)] = [a × b] + [a × c] .

Сочетательность относительно скалярного множителя:  k · [a × b] = [(k · a) × b] = [a × (k · b)] .

Смешанное произведение:  a · [b × c] = [a × b] · c .

Векторный квадрат вектора всегда является 2.narod.ru/info/vectors.htm»нулевым вектором:  [a × a] = 0 . Поэтому, когда говорят о «квадрате вектора» без уточнения типа перемножения, имеют в виду скалярный квадрат (квадрат модуля вектора).