3 Сложение векторов
Определение
3.1. Суммой
двух векторов 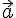 и
и 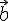 называется
вектор
называется
вектор  ,
где
,
где 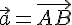 ,
, 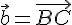 ,
, 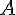 —
произвольная точка,
—
произвольная точка, 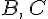 — точки,
полученные после откладывания
векторов
— точки,
полученные после откладывания
векторов 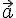
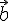 .
.Покажем,
что сумма векторов не зависит от выбора
точки 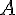 . Действительно,
пусть
. Действительно,
пусть 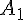 —
любая точка, отличная от точки
—
любая точка, отличная от точки 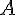 .
Строим векторы
.
Строим векторы 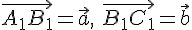 .
Докажем, что
.
Докажем, что 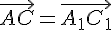 . Так
как
. Так
как 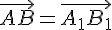
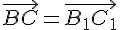 ,
то по
лемме 2.1.
,
то по
лемме 2.1. 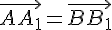 и
и 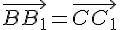 ,
то есть
,
то есть 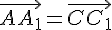 .
Следовательно, по той же лемме
.
Следовательно, по той же лемме 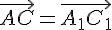 . Замечание
3.1. Для
нахождения суммы неколлинеарных векторов
приходится строить треугольник
. Замечание
3.1. Для
нахождения суммы неколлинеарных векторов
приходится строить треугольник 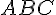
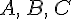 справедливо
равенство
справедливо
равенство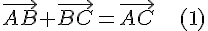
В частности, это правило справедливо и для коллинеарных точек.
Свойства сложения векторов.
ТЕОРЕМА
3.1. Для
произвольных векторов 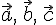
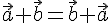 — коммутативность
сложения векторов. 2.
— коммутативность
сложения векторов. 2. 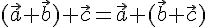 — ассоциативность
сложения
векторов. 3. . 4.
— ассоциативность
сложения
векторов. 3. . 4. 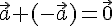 . Доказательство. 1. Пусть
. Доказательство. 1. Пусть 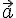 и
и 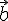
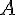 отложим
векторы
отложим
векторы 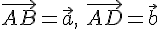 ,
а затем от точки
,
а затем от точки 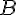 отложим
вектор
отложим
вектор  .
Согласно построению
.
Согласно построению 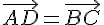 ,
поэтому по
лемме 2.1. получаем
,
поэтому по
лемме 2.1. получаем 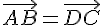 ,
т.е.
,
т.е. 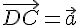
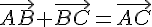 и
и 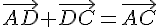 ,
следовательно,
,
следовательно, 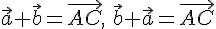 .
Отсюда получаем, что
.
Отсюда получаем, что 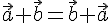 . 2. Пусть и
. 2. Пусть и  —
произвольные векторы. Возьмем какую-нибудь
точку
—
произвольные векторы. Возьмем какую-нибудь
точку 
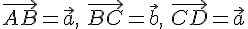 .
По
правилу треугольника
.
По
правилу треугольника 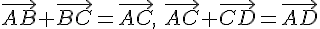 ,
поэтому
,
поэтому 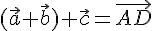 .
С другой стороны
.
С другой стороны 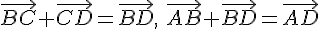 ,
поэтому
,
поэтому 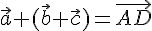 .
Отсюда получаем требуемое. 3. Применим
правило
.
Отсюда получаем требуемое. 3. Применим
правило 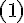
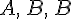 получим
получим 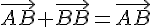 . Значит,
. Значит, 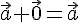 . 4. Применим
правило
. 4. Применим
правило  к
точкам
к
точкам  получим
получим 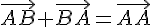 .
Значит,
.
Значит, 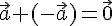
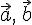 и
и  будем
считать вектор
будем
считать вектор 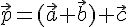 .
На основании доказанной теоремы
.
На основании доказанной теоремы 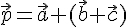 ,
поэтому при записи суммы трех векторов
можно опустить скобки и писать просто
,
поэтому при записи суммы трех векторов
можно опустить скобки и писать просто 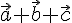 .
Более того, можно доказать, что сумма
трех векторов не зависит от порядка
слагаемых. В самом деле, докажем, например,
что
.
Более того, можно доказать, что сумма
трех векторов не зависит от порядка
слагаемых. В самом деле, докажем, например,
что 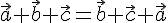
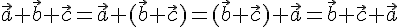 . 2. Аналогично
можно определить сумму
. 2. Аналогично
можно определить сумму  векторов,
где
векторов,
где  .
Пусть
.
Пусть 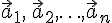 —
произвольные векторы. Их суммой называется
вектор
—
произвольные векторы. Их суммой называется
вектор 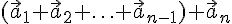
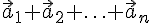 .
Из
второго свойства можно получить правило
многоугольника для нахождения суммы
любого конечного числа векторов. Оно
таково: Суммой
конечного числа векторов называется
вектор, идущий из начала первого в конец
последнего, при условии, что каждый
последующий вектор отложен из конца
предыдущего. Нетрудно
убедиться в том, что сумма
.
Из
второго свойства можно получить правило
многоугольника для нахождения суммы
любого конечного числа векторов. Оно
таково: Суммой
конечного числа векторов называется
вектор, идущий из начала первого в конец
последнего, при условии, что каждый
последующий вектор отложен из конца
предыдущего. Нетрудно
убедиться в том, что сумма 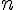 векторов
не зависит от порядка слагаемых. 3. Для
неколлинеарных векторов при их сложении
можно пользоваться правилом
параллелограмма: Суммой
двух неколлинеарных векторов является
диагональ параллелограмма, построенного
на этих векторах как на сторонах, при
условии, что начало искомого вектора
совпадает с началом данных векторов.
векторов
не зависит от порядка слагаемых. 3. Для
неколлинеарных векторов при их сложении
можно пользоваться правилом
параллелограмма: Суммой
двух неколлинеарных векторов является
диагональ параллелограмма, построенного
на этих векторах как на сторонах, при
условии, что начало искомого вектора
совпадает с началом данных векторов.4 Разность векторов.
Определение
4.1. Разностью
векторов 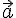 и
и 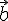 ,
взятых в данном порядке, называется
такой вектор
,
взятых в данном порядке, называется
такой вектор 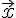 ,
который в сумме со вторым вектором дает
первый вектор. Докажем существование
и единственность разности. Существование. Отложим
векторы
,
который в сумме со вторым вектором дает
первый вектор. Докажем существование
и единственность разности. Существование. Отложим
векторы 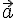
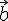 от
одной и той же точки
от
одной и той же точки  :
: 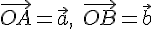 Применяя
равенство
Применяя
равенство 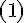 для
точек
для
точек 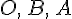 получаем
получаем 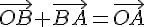 Полагая
Полагая  ,
будем иметь
,
будем иметь 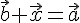 .
Этим доказано существование
разности. Единственность. Пусть
существует еще вектор
.
Этим доказано существование
разности. Единственность. Пусть
существует еще вектор 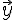 такой,
что
такой,
что 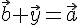 .
Тогда
.
Тогда 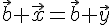 .
Прибавим к обеим частям этого равенства
вектор
.
Прибавим к обеим частям этого равенства
вектор 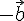 .
Получим
.
Получим 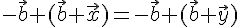
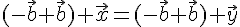
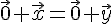
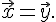 Таким
образом, доказано существование и
единственность разности любых двух
векторов, при этом эта разность
обозначается
Таким
образом, доказано существование и
единственность разности любых двух
векторов, при этом эта разность
обозначается 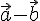 . Замечание
4.1. Из
доказательства существования разности
векторов можно сформулировать правило
нахождения разности двух векторов: Разностью
двух данных векторов, отложенных из
одной точки является вектор, идущий из
конца второго в конец первого.
. Замечание
4.1. Из
доказательства существования разности
векторов можно сформулировать правило
нахождения разности двух векторов: Разностью
двух данных векторов, отложенных из
одной точки является вектор, идущий из
конца второго в конец первого.Отметим
еще равенство 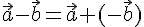 В
самом деле,
В
самом деле, 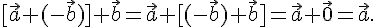
Глава 1. Векторная алгебра
§ 1. Линейные операции над векторами. Базис. Координаты вектора
Основные теоретические сведения
Линейные операции над векторами
Сложение векторов. Суммой векторов 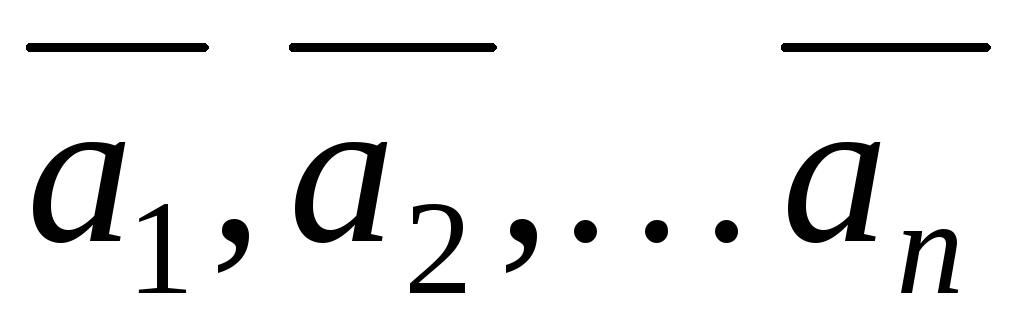 называется вектор
называется вектор  (рис.1.1), представляющий замыкающую
многоугольника, построенного на слагаемых
векторах (правило многоугольника). Из
этого правила для суммы двух векторов
получается правило параллелограмма
(рис. 1.2).
(рис.1.1), представляющий замыкающую
многоугольника, построенного на слагаемых
векторах (правило многоугольника). Из
этого правила для суммы двух векторов
получается правило параллелограмма
(рис. 1.2).

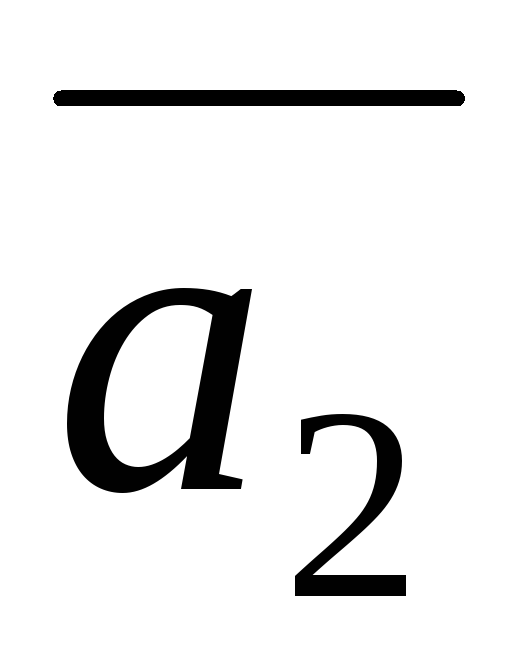


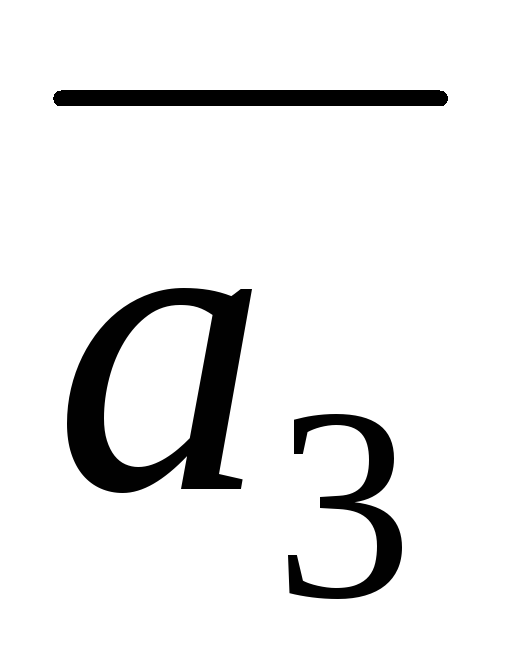
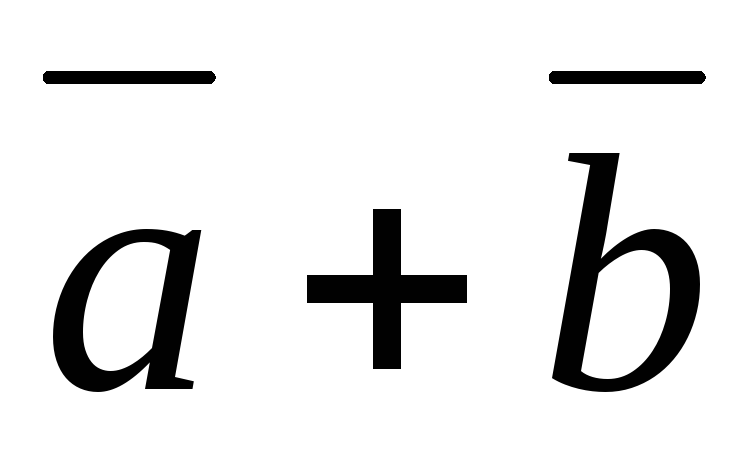
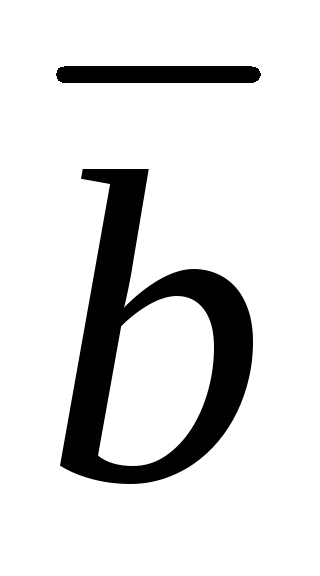
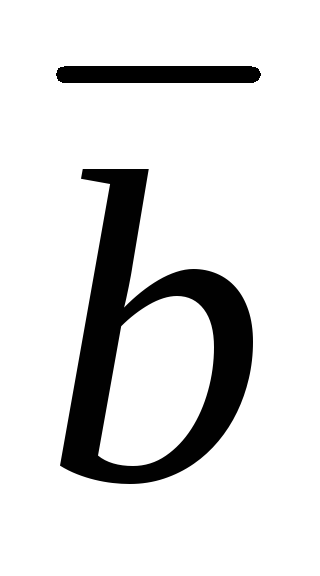
Рис. 1.1 Рис. 1.2
Свойства суммы векторов:
1. 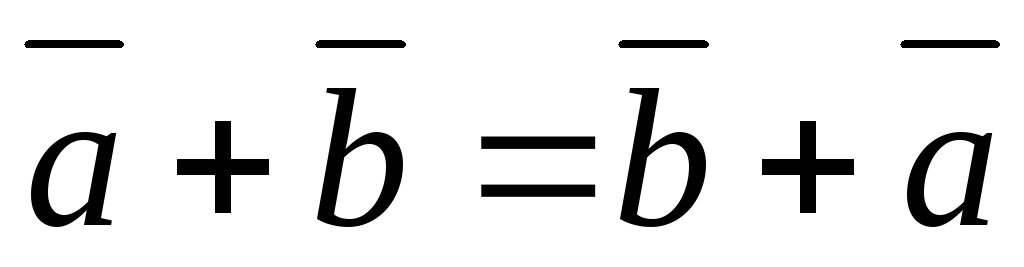 .
.
2. 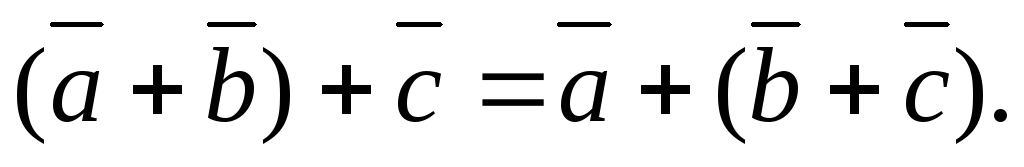
В ычитание
векторов: Разностью
ычитание
векторов: Разностью 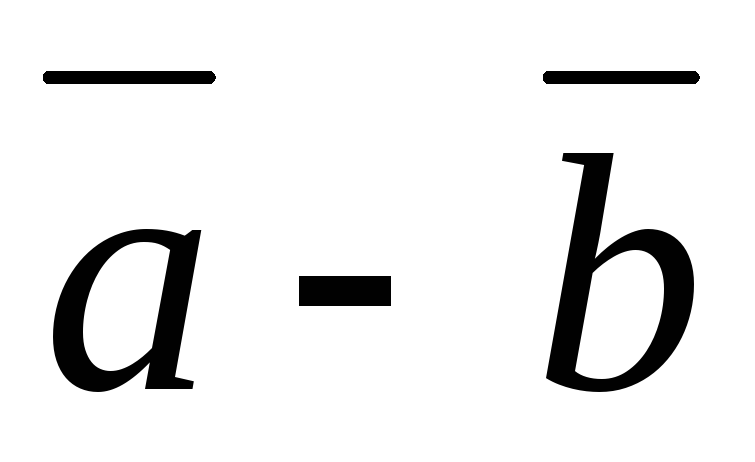 называется вектор
называется вектор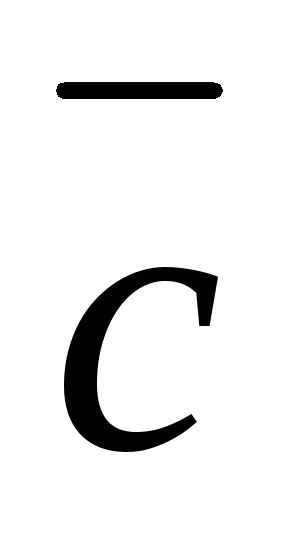 ,
такой что
,
такой что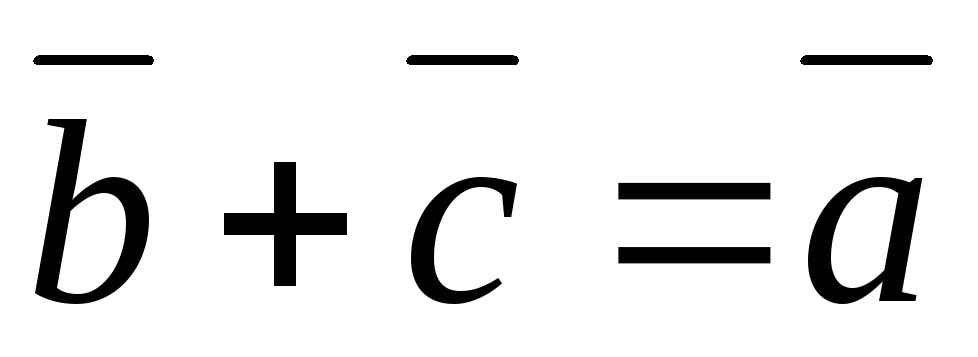 .
Для построения вектора
.
Для построения вектора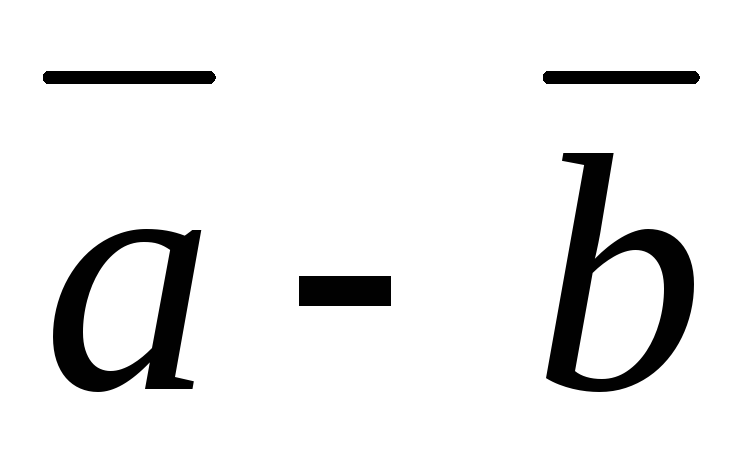 приводим к общему началу
приводим к общему началу
векторы  и
и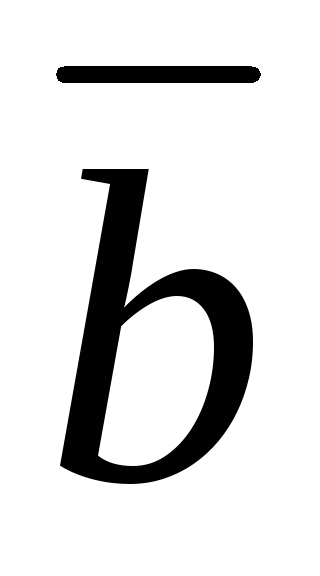 ,
затем по правилу многоугольника находим
,
затем по правилу многоугольника находим
 так, чтобы
так, чтобы  (рис. 1.3)
(рис. 1.3)
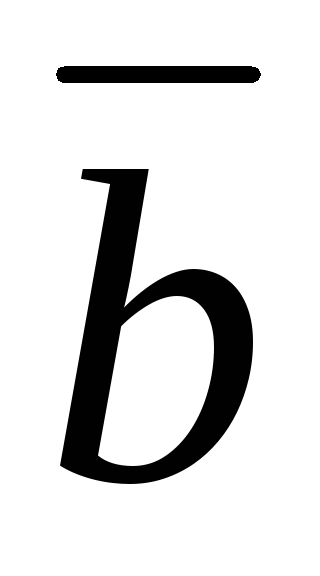
Рис. 1.3
Замечания
1. Вектор 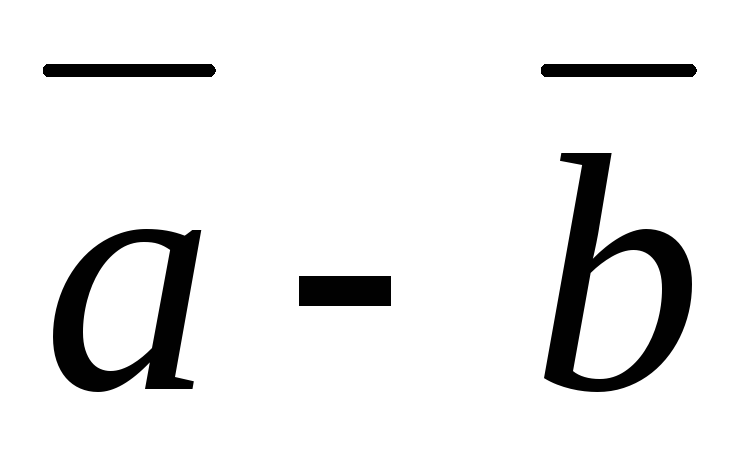 направлен от конца вычитаемого вектора
к концу уменьшаемого вектора.
направлен от конца вычитаемого вектора
к концу уменьшаемого вектора.
2. Векторы 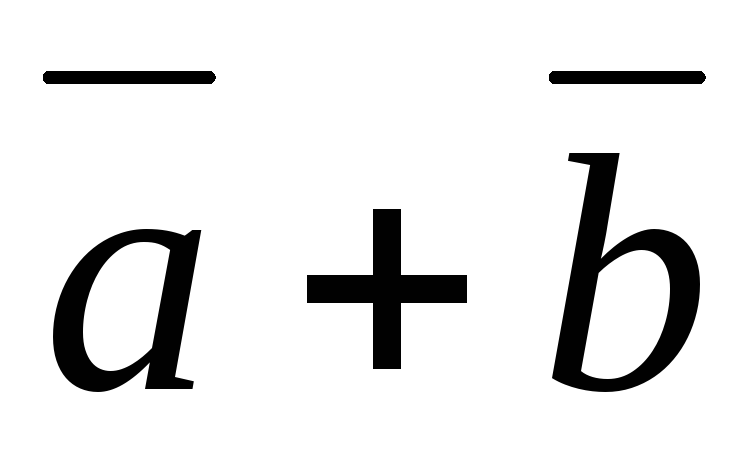 и
и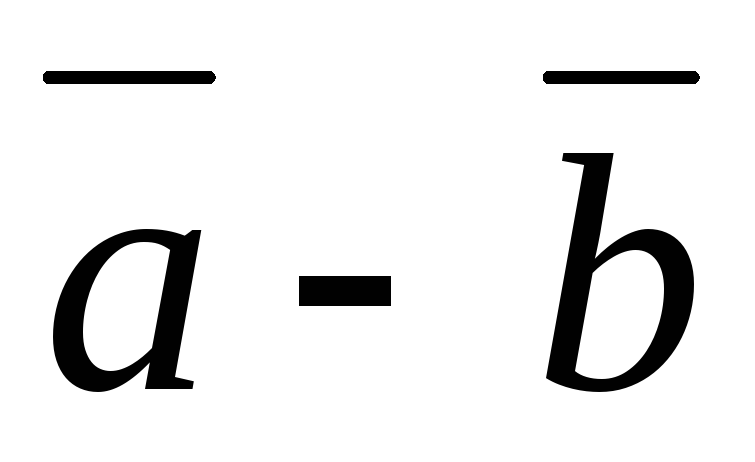 совпадают с диагоналями параллелограмма,
построенного на векторах
совпадают с диагоналями параллелограмма,
построенного на векторах и
и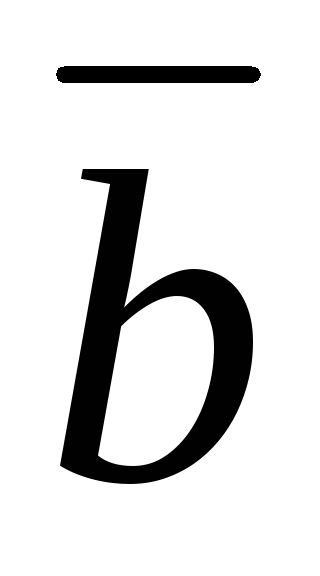 (рис. 1.2, рис. 1.3)
(рис. 1.2, рис. 1.3)
Умножение вектора
на число (скаляр). Произведением вектора  на число
на число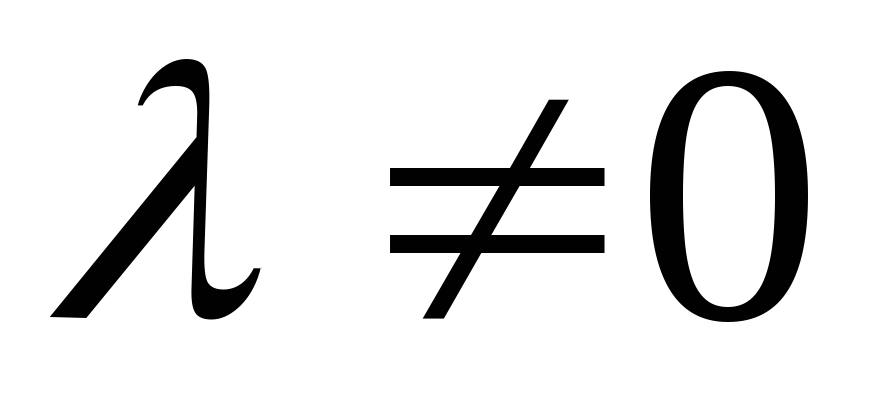 называется новый вектор
называется новый вектор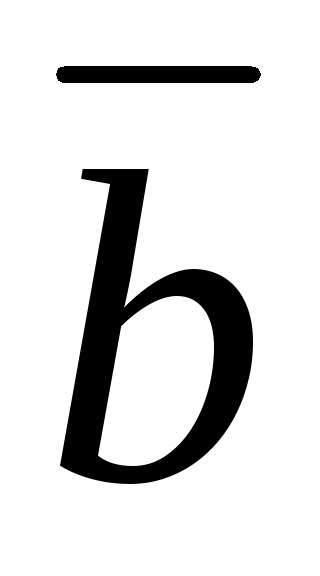 такой, что
такой, что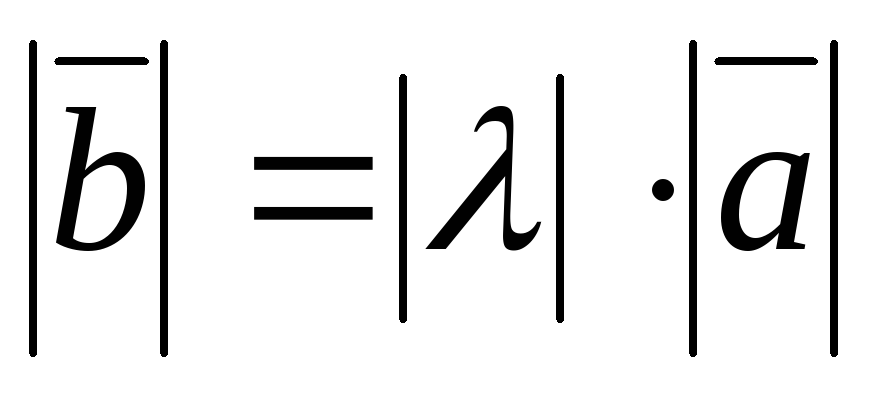 и
и при
при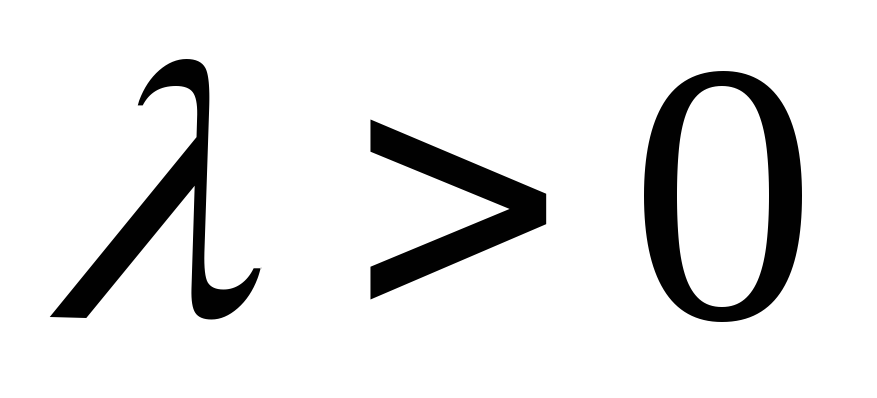 (вектора сонаправлены),
(вектора сонаправлены),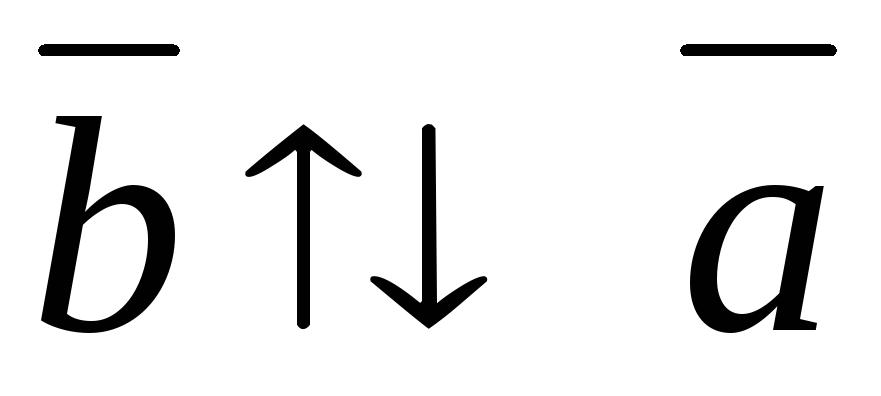 при
при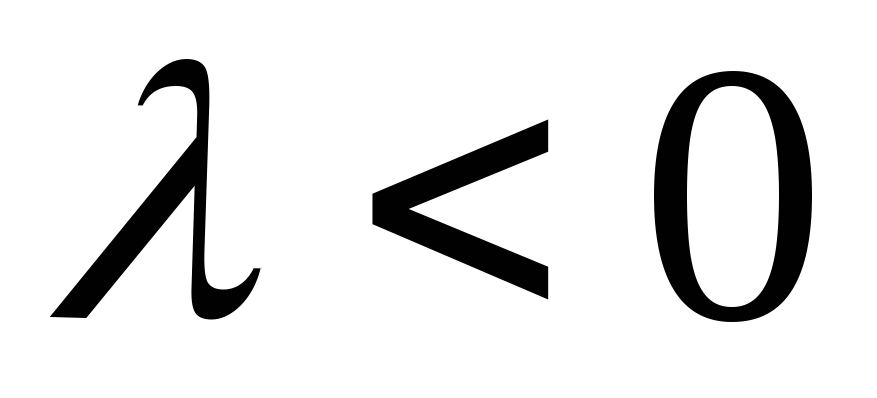 (вектора противоположно направлены).
(вектора противоположно направлены).
В частном случае
при 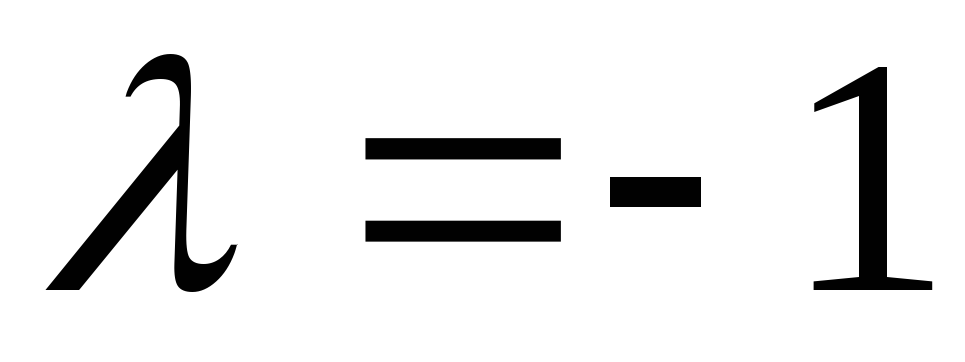 вектор
вектор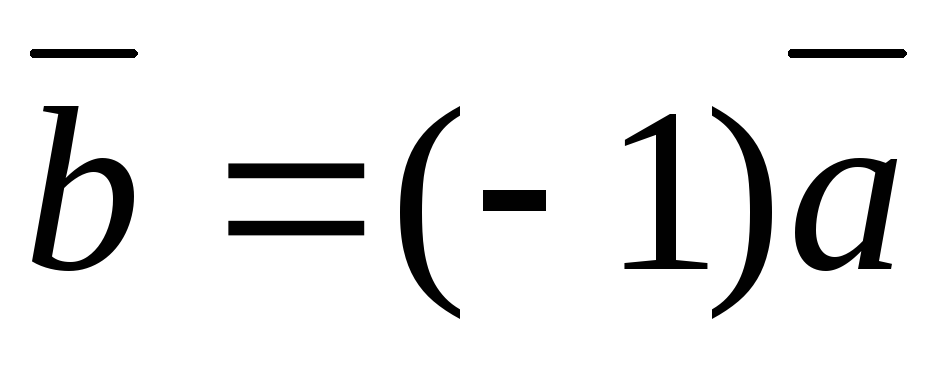 называется противоположным вектору
называется противоположным вектору и обозначается
и обозначается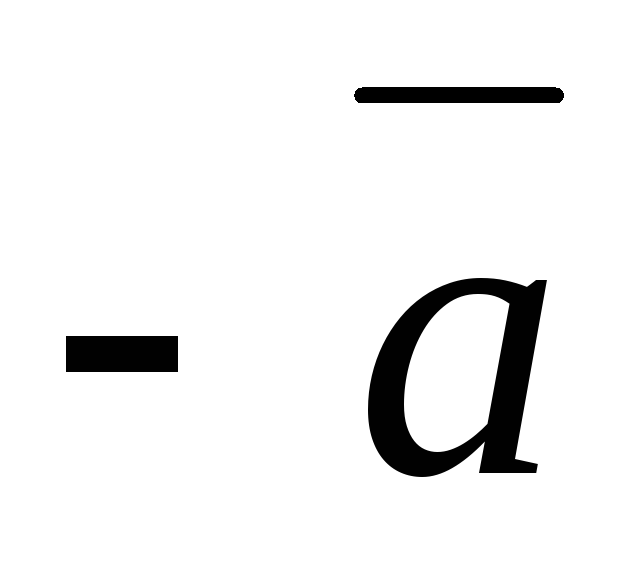 .
.
Свойства умножения вектора на скаляр:
1. 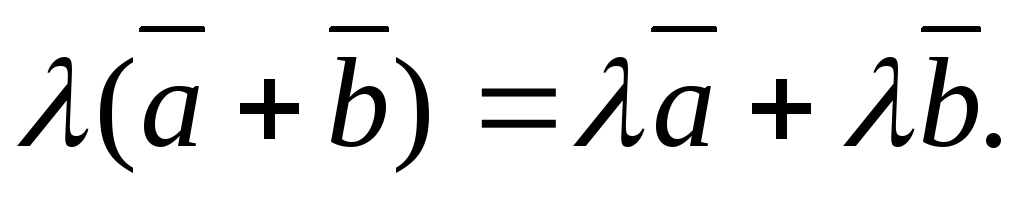
2. 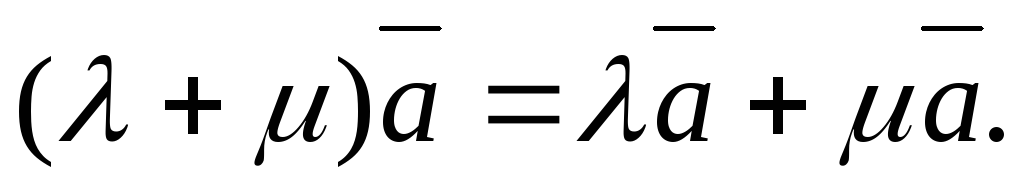
Имеет место
утверждение: 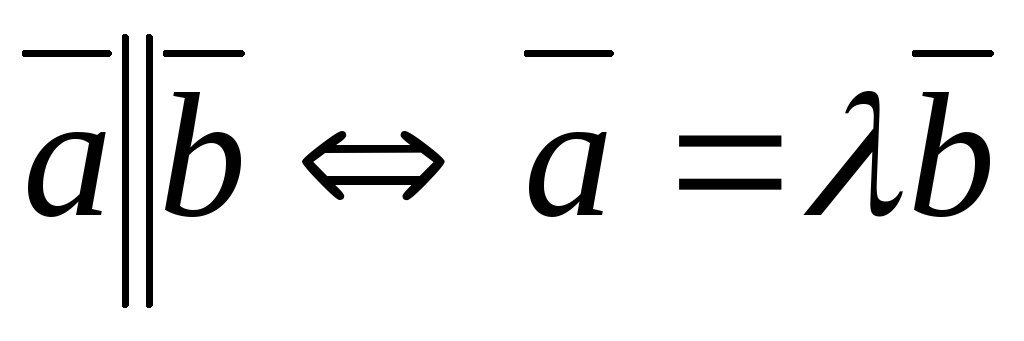 ,
где
,
где –
число.
–
число.
Линейная
зависимость векторов. Сумма 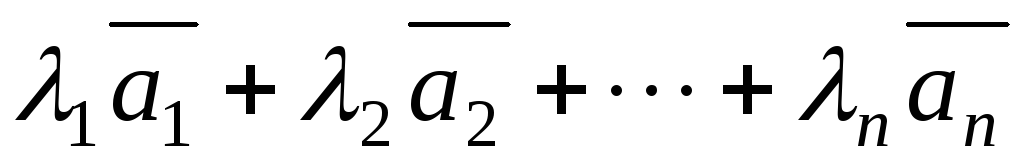 называется линейной комбинацией векторов
называется линейной комбинацией векторов ;
числа
;
числа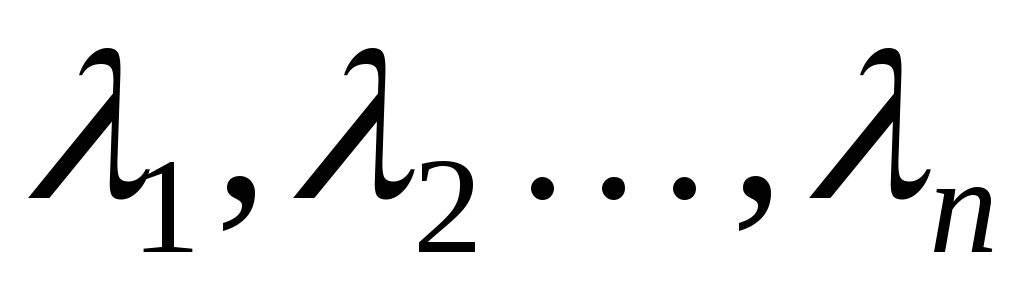 называются коэффициентами линейной
комбинации.
называются коэффициентами линейной
комбинации.
Векторы 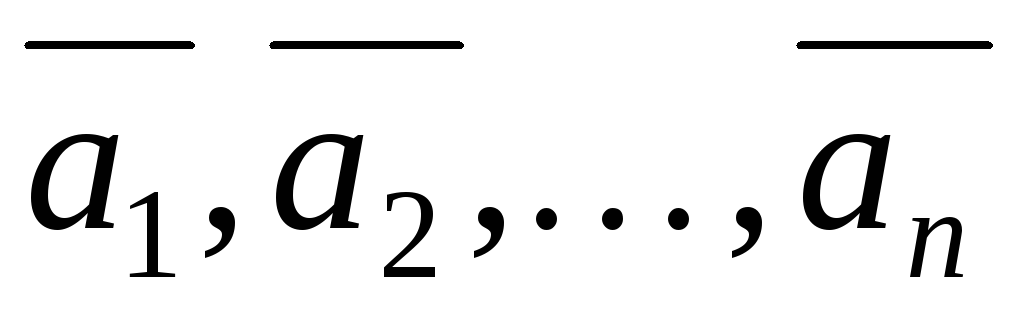 называютсялинейно
зависимыми,
если существуют числа
называютсялинейно
зависимыми,
если существуют числа 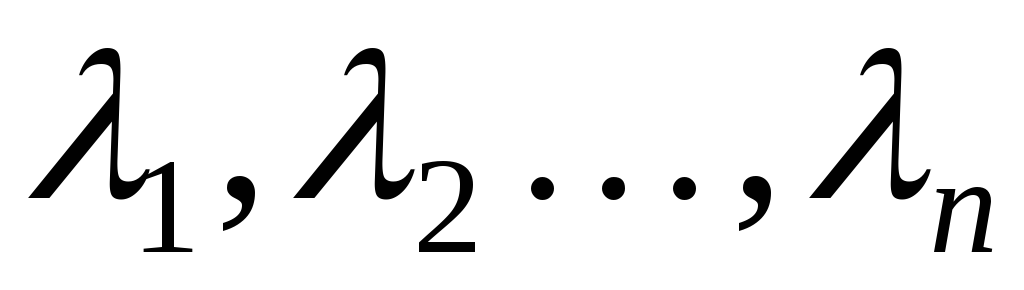 такие, что
такие, что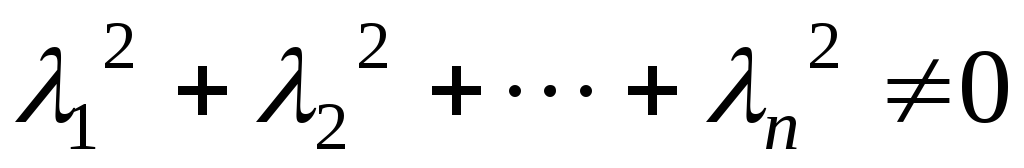 и
и .
.
Векторы 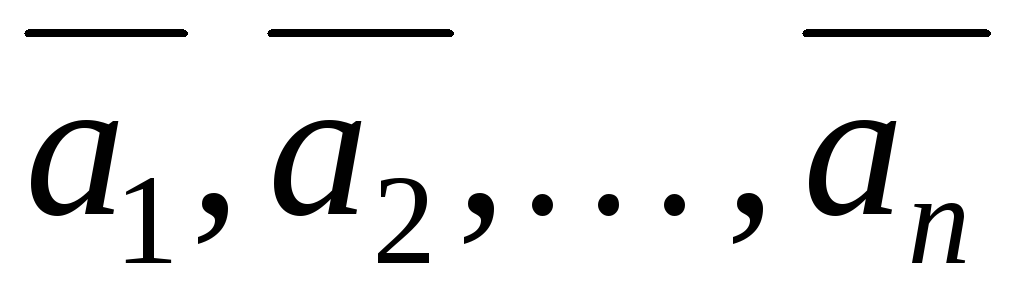 называютсялинейно
независимыми,
если
называютсялинейно
независимыми,
если 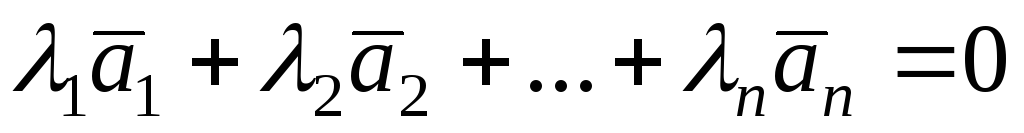 только при
только при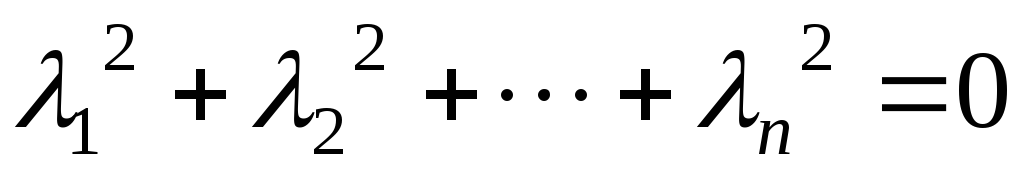 .
.
Два вектора зависимы тогда и только тогда, когда они коллинеарны. Три вектора зависимы тогда и только тогда, когда они компланарны. Четыре вектора всегда линейно зависимы.
Разложение
вектора на составляющие. Если  и
и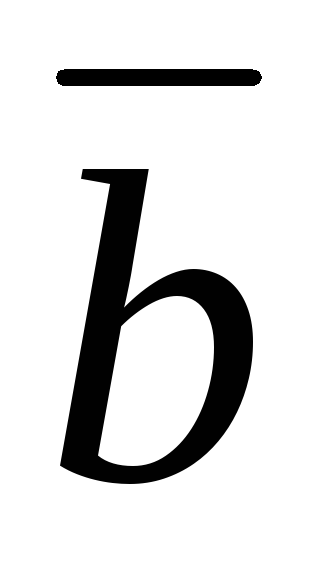 независимы (неколлинеарны), то любой
третий вектор
независимы (неколлинеарны), то любой
третий вектор ,
лежащий в плоскости
,
лежащий в плоскости и
и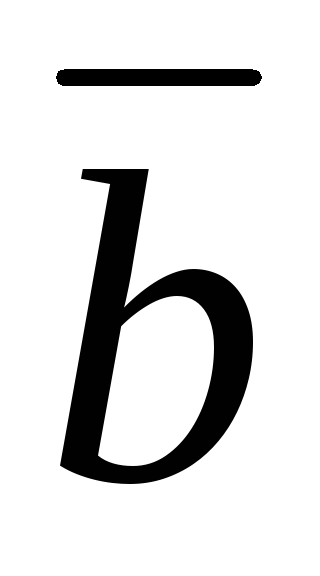 ,
единственным образом раскладывается
на составляющие по направлениям
,
единственным образом раскладывается
на составляющие по направлениям и
и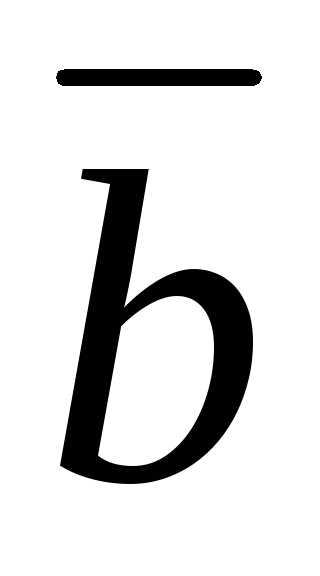 :
: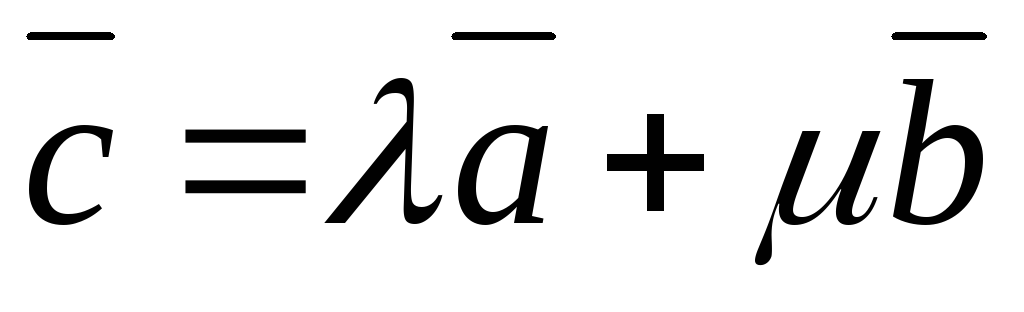 .
Если
.
Если независимы (некомпланарны), то любой
четвертый вектор
независимы (некомпланарны), то любой
четвертый вектор единственным образом раскладывается
по направлениям векторов
единственным образом раскладывается
по направлениям векторов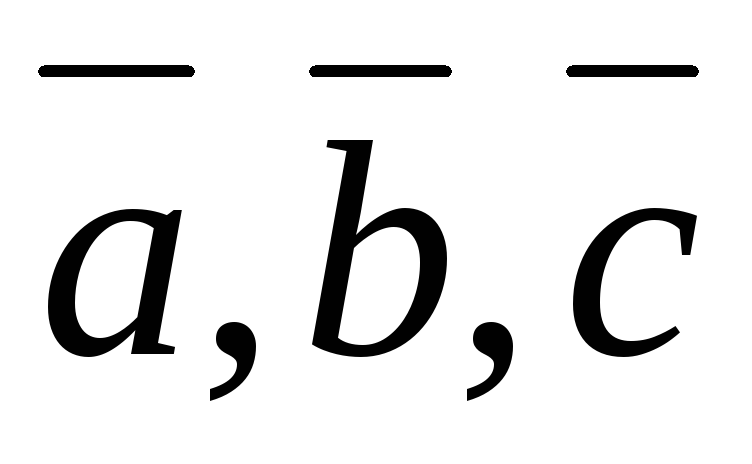 :
: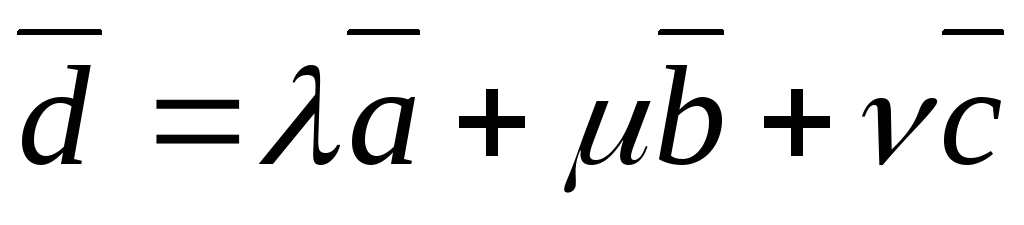 .
.
Векторный базис
и координаты вектора. Упорядоченная система любых трех линейно
независимых векторов называется базисом
трехмерного пространства. Предположим,
что в качестве базиса выбраны 3
некомпланарных вектора  ,
тогда любой вектор
,
тогда любой вектор можно представить в виде:
можно представить в виде: .
.
Числа 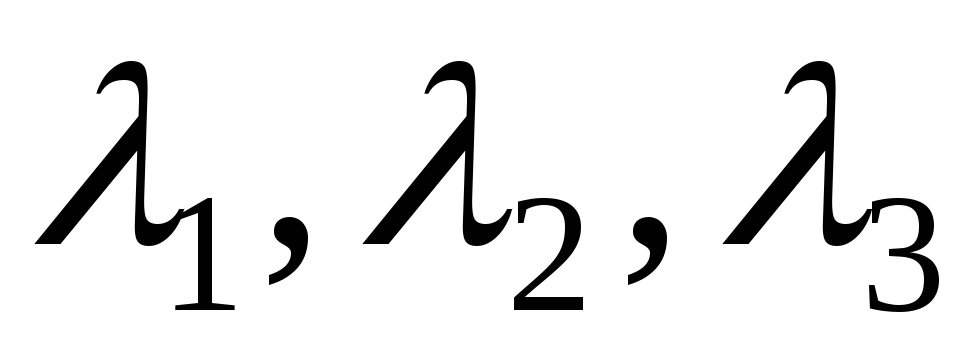 называются координатами вектора
называются координатами вектора в выбранном базисе. Наряду с записью
в выбранном базисе. Наряду с записью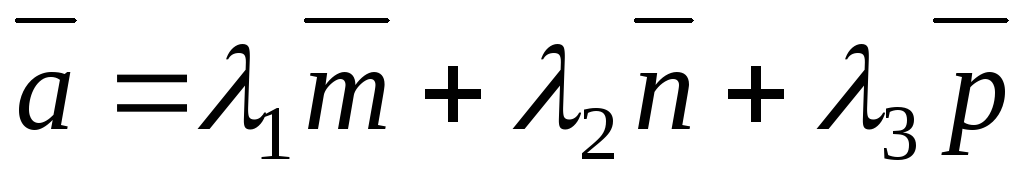 будем пользоваться символической
записью:
будем пользоваться символической
записью: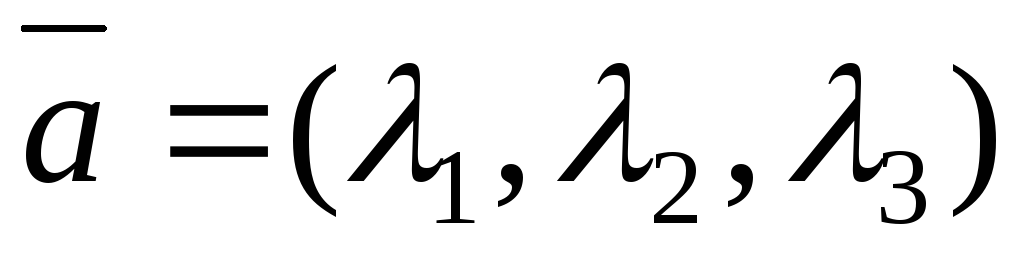 .
.
Аналогично, упорядоченная пара линейно независимых векторов называется базисом двухмерного пространства.
Базис называется
ортонормированным, если базисные векторы
являются взаимно перпендикулярными
ортами. В этом случае базисные векторы
обозначаются буквами 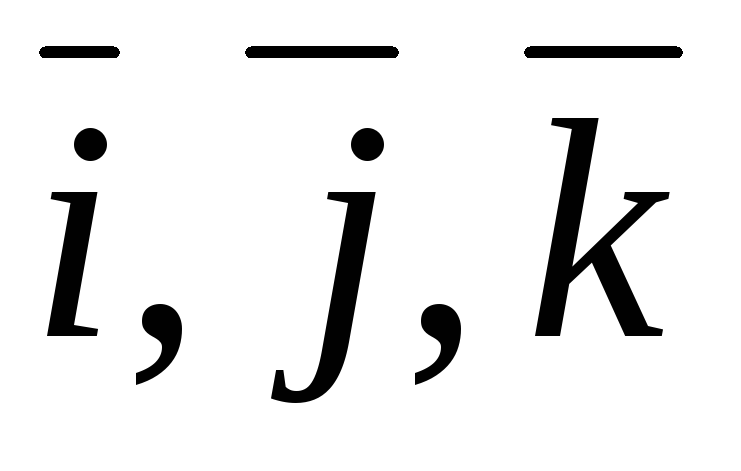 и наряду с записью
и наряду с записью пользуются символической записью:
пользуются символической записью: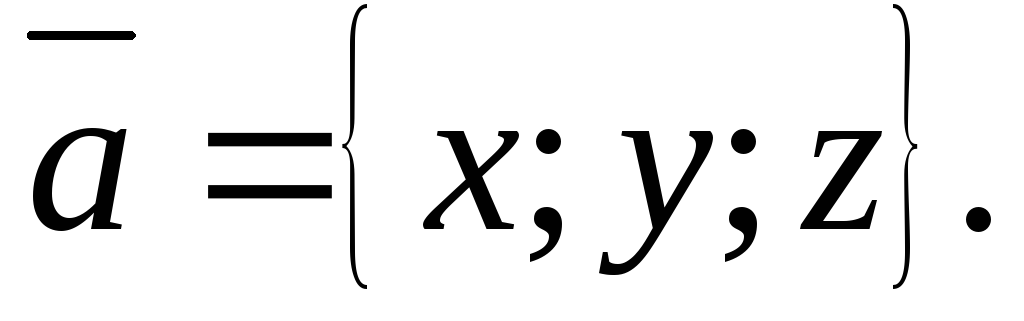 В ортонормированном базисе координаты
вектора совпадают с проекциями этого
вектора на направления базисных векторов:
В ортонормированном базисе координаты
вектора совпадают с проекциями этого
вектора на направления базисных векторов: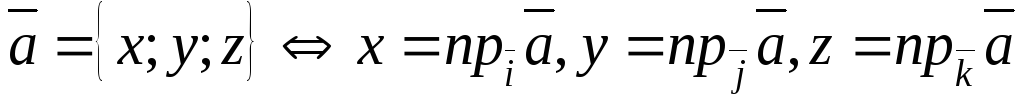 .
.
В любом базисе при сложении векторов их соответствующие координаты складываются, при умножении вектора на число все его координаты умножаются на это число.
Прямоугольная система координат и радиус-вектор.
Если в пространстве выбрана прямоугольная система координат, (рис. 1.4), то координатами точки называются координаты радиус-вектора этой точки.
M 0 y x Рис. 1.4 | Если вектор Если
даны две точки |
2. Простейшие операции над векторами
К простейшим операциям над векторами относится сложение и вычитание векторов и умножение вектора на скаляр. Все эти операции называются линейными.
1) Сложение векторов.
Определение
1. Чтобы найти
сумму двух векторов  и
и ,
необходимо конец вектора
,
необходимо конец вектора совместить с началом
совместить с началом .
Вектор
.
Вектор ,
соединяющий точки
,
соединяющий точки и
и ,
будет их суммой.
,
будет их суммой.
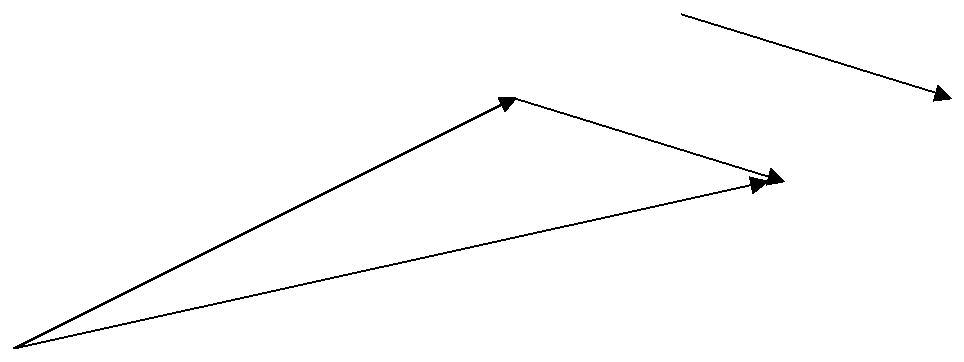
Обозначается
сума следующим образом: 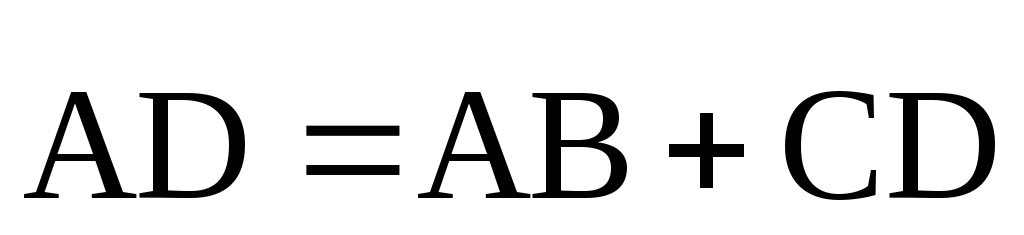 .
Величину ее можно найти и другим способом.
Начала векторов
.
Величину ее можно найти и другим способом.
Начала векторов и
и совмещаются и на них как на сторонах
строится параллелограмм. Диагональ
параллелограмма и будет суммой векторов.
совмещаются и на них как на сторонах
строится параллелограмм. Диагональ
параллелограмма и будет суммой векторов.
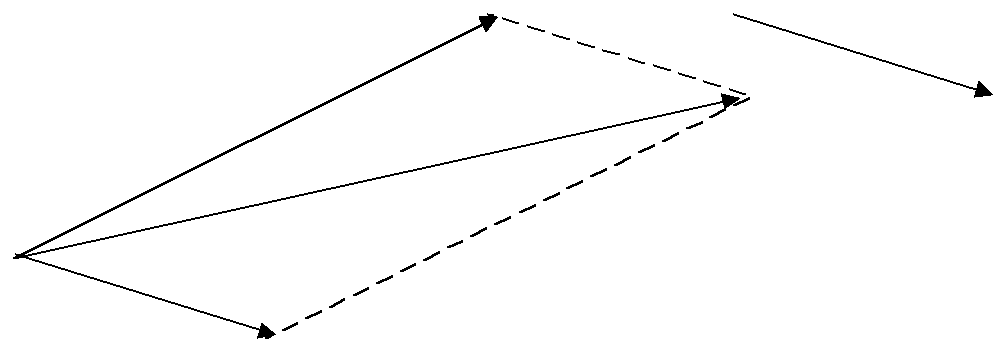

Из правила параллелограмма видно, что сумма векторов обладает переместительным свойством
. 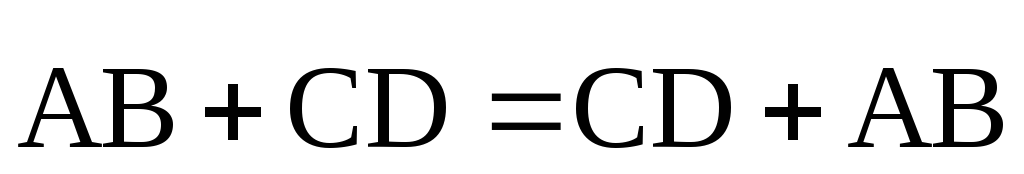
Если
слагаемых больше, например, три: 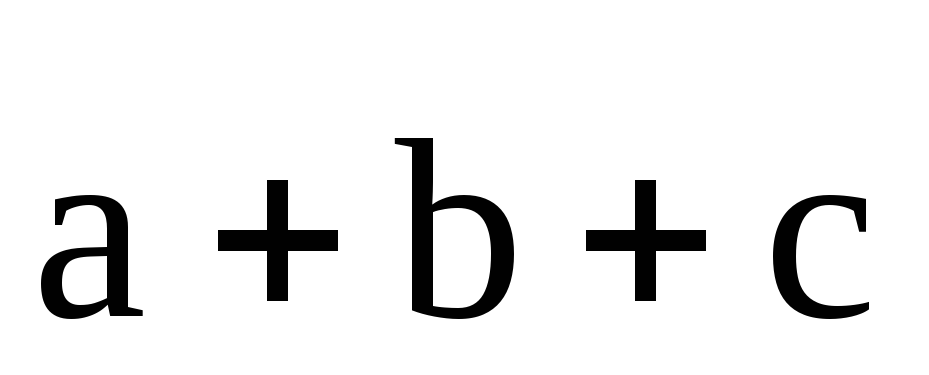 ,
поступают следующим образом. Строят
вначале сумму
,
поступают следующим образом. Строят
вначале сумму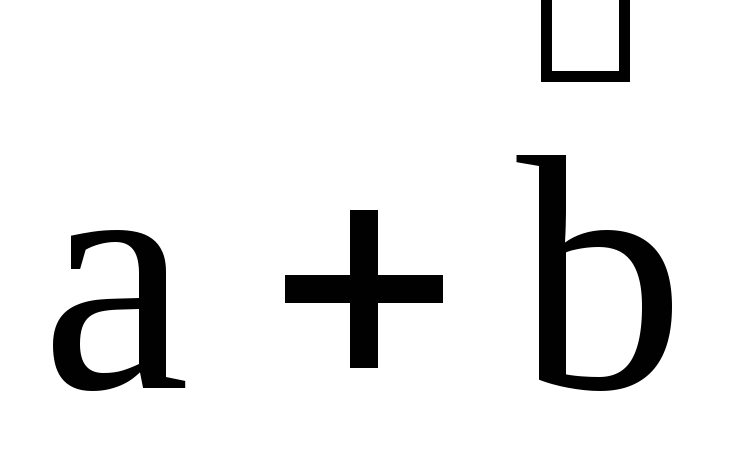 ,
а затем, прибавляя
,
а затем, прибавляя ,
получают вектор
,
получают вектор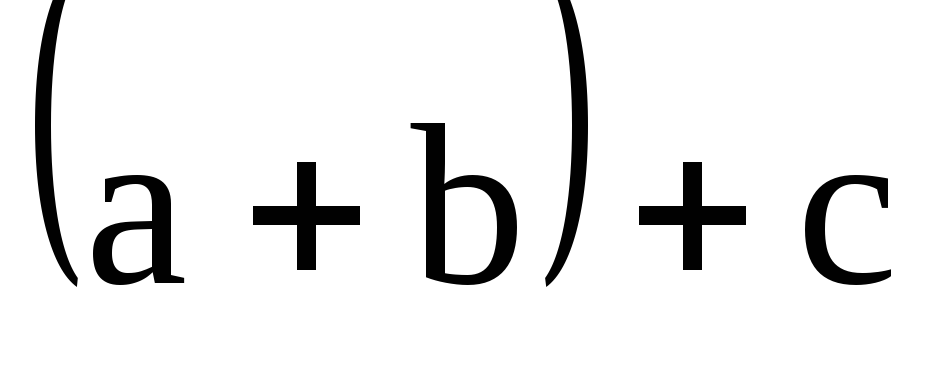 .
.


Из
рисунка видно, что тот же результат
будет, если сложить вначале 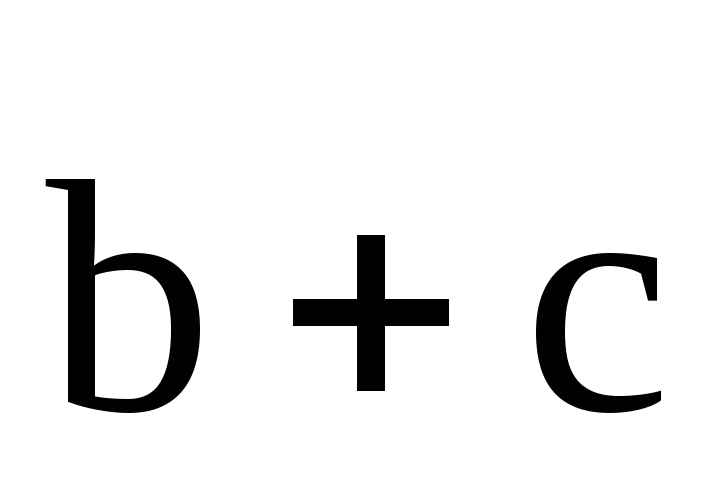 ,
а затем прибавить
,
а затем прибавить ,
то есть сумма векторов обладает
сочетательным свойством:
,
то есть сумма векторов обладает
сочетательным свойством:
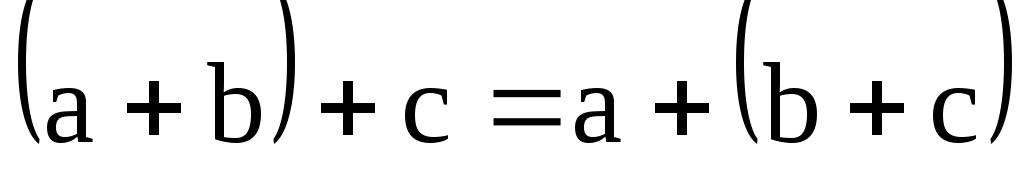 .
.
Если
при сложении нескольких векторов конец
последнего совпадает с началом первого,
то сумма равна ноль вектору 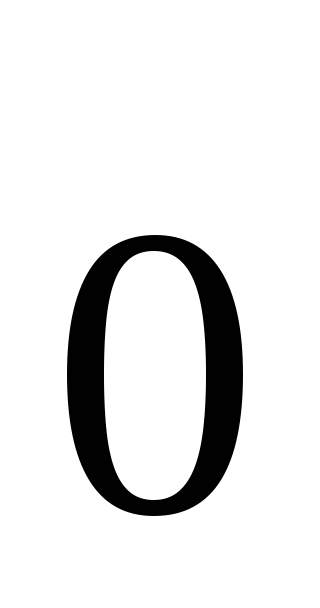 .
Очевидно,
.
Очевидно,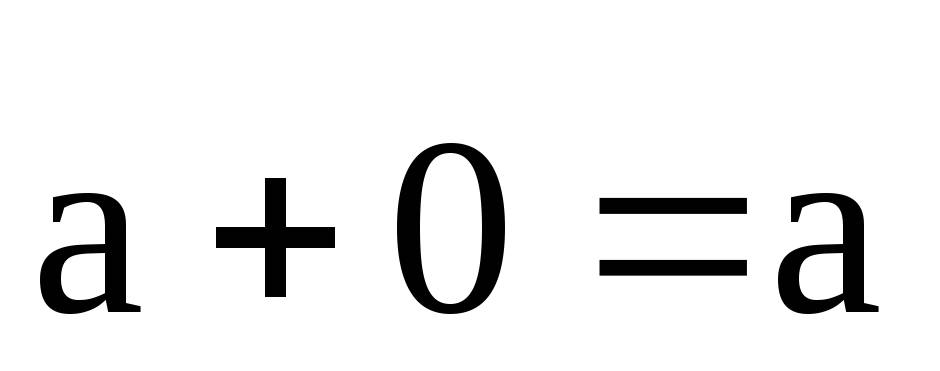 .
.
2) Разность векторов.
Определение
2. Разностью
двух векторов  и
и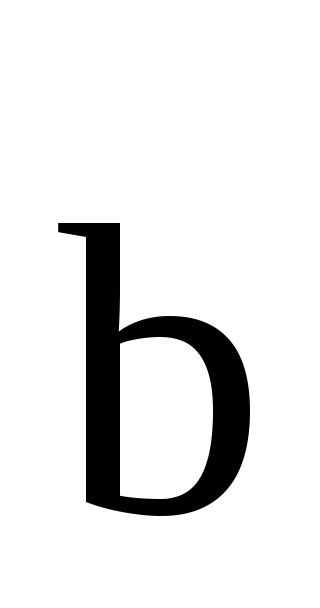 называется такой вектор
называется такой вектор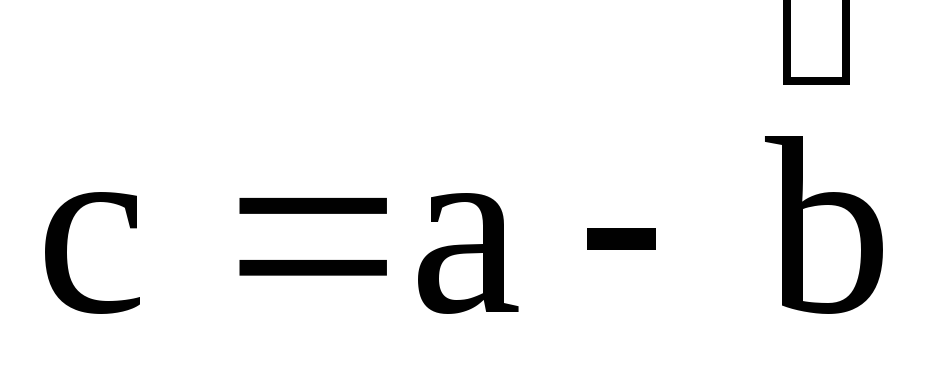 ,
сумма которого с вычитаемым
,
сумма которого с вычитаемым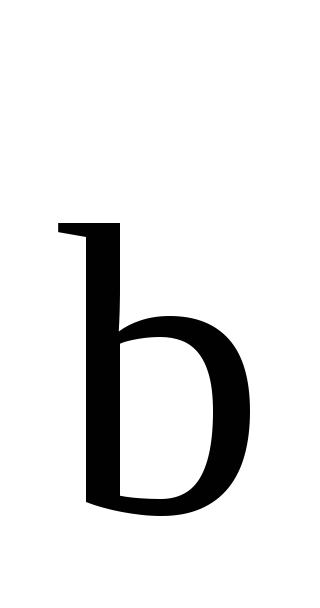 дает вектор
дает вектор .
.
Значит,
если 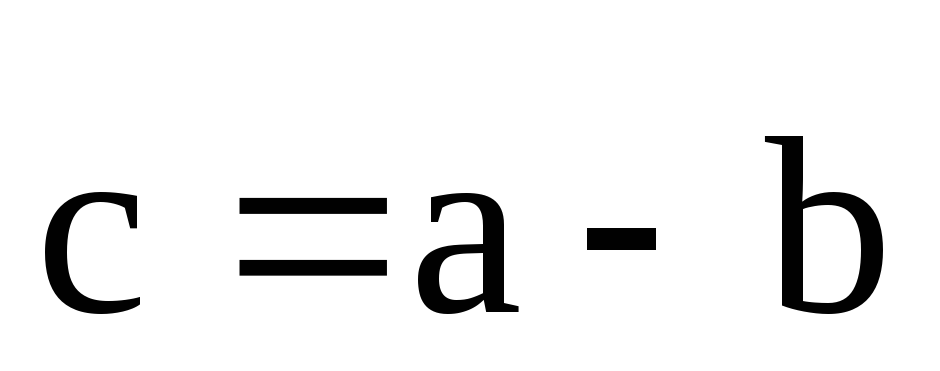 ,
то
,
то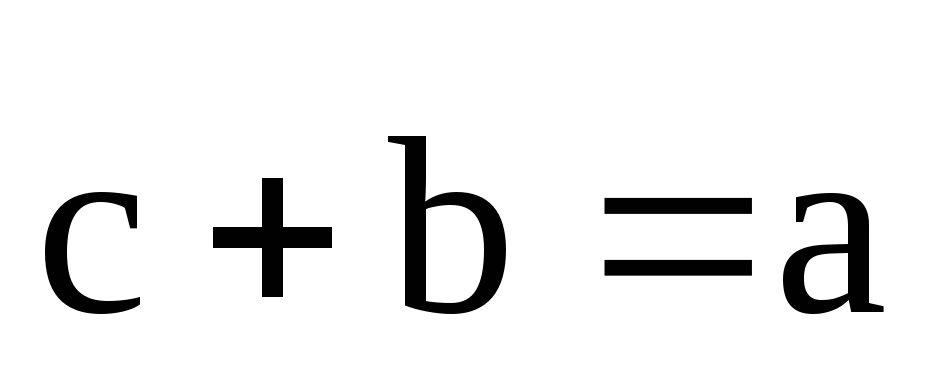 .
.
Из
определения суммы двух векторов вытекает
правило построения разности. Откладываем
из общей точки векторы  и
и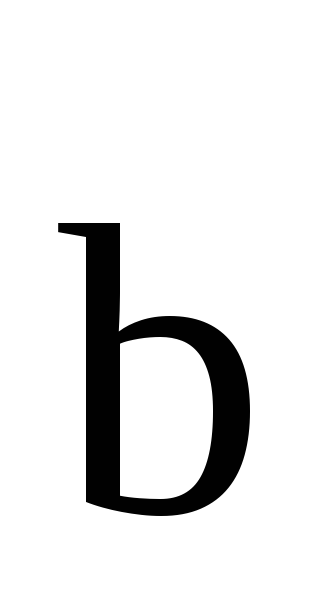 .
Вектор
.
Вектор соединяет концы векторов
соединяет концы векторов и
и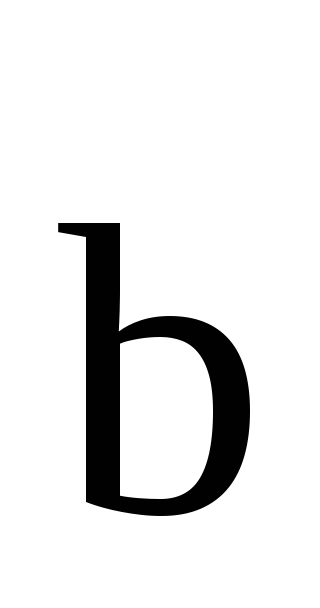 и направлен от вычитаемого к уменьшаемому.
и направлен от вычитаемого к уменьшаемому.

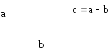
Видно,
что если на векторах  и
и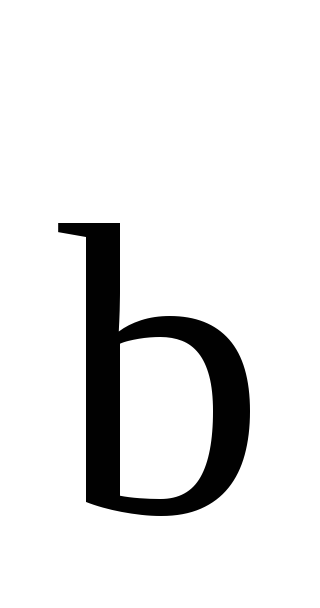 построить параллелограмм, то одна его
диагональ соответствует их сумме, а
вторая — разности.
построить параллелограмм, то одна его
диагональ соответствует их сумме, а
вторая — разности.
3) Умножение вектора на число.
Определение
3. Произведением
вектора  на число
на число называется вектор
называется вектор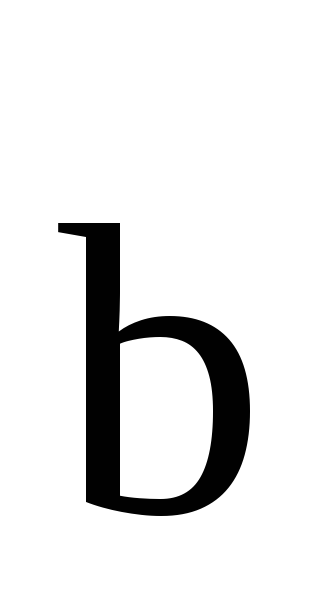 ,
определенный следующими условиями:
,
определенный следующими условиями:
1)  ;
;
2)
вектор  коллинеарен
вектору
коллинеарен
вектору ;
;
3)
векторы  и
и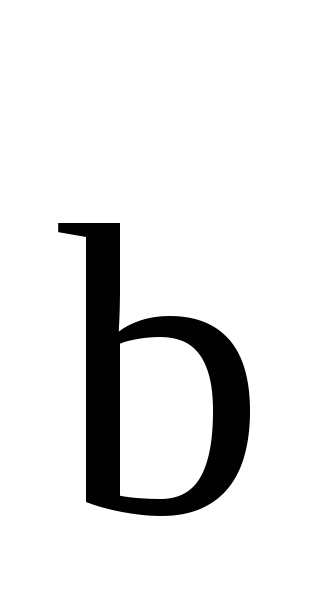 направлены одинаково, если
направлены одинаково, если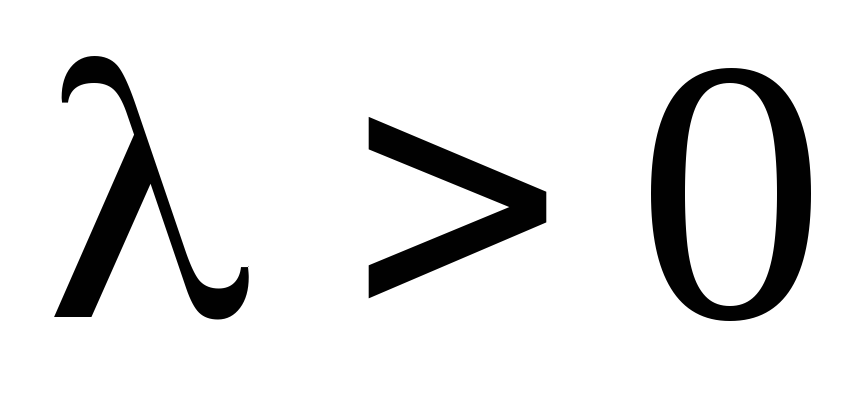 ,
и противоположно, если
,
и противоположно, если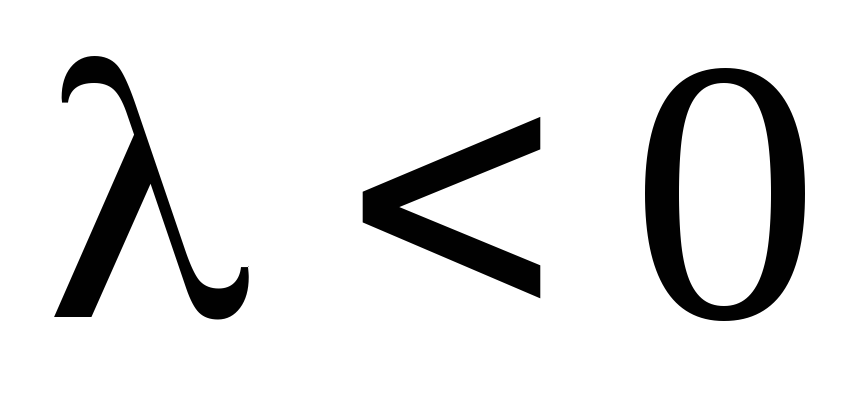 .
.
Очевидно,
что операция умножения вектора на число
приводит к его растяжению или сжатию.
Противоположный вектор 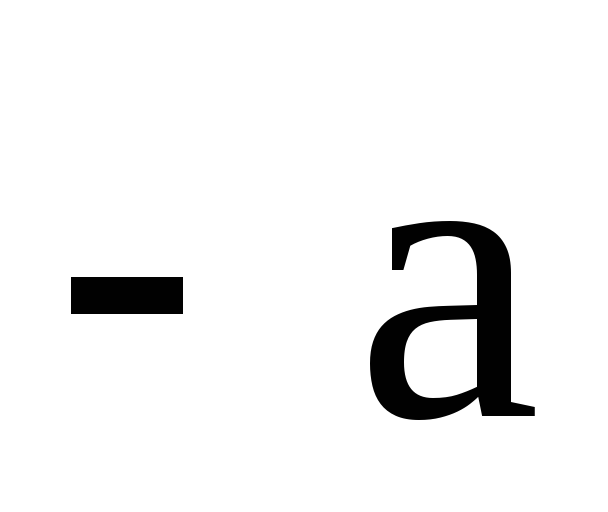 можно рассматривать как результат
умножения вектора
можно рассматривать как результат
умножения вектора на
на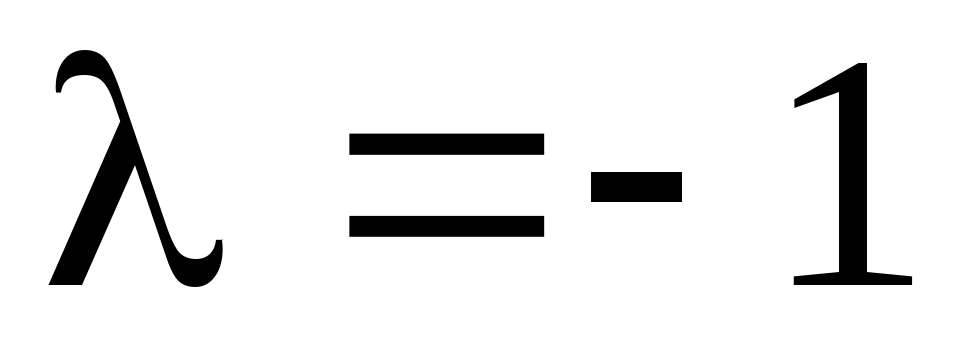 .
Отсюда,
.
Отсюда,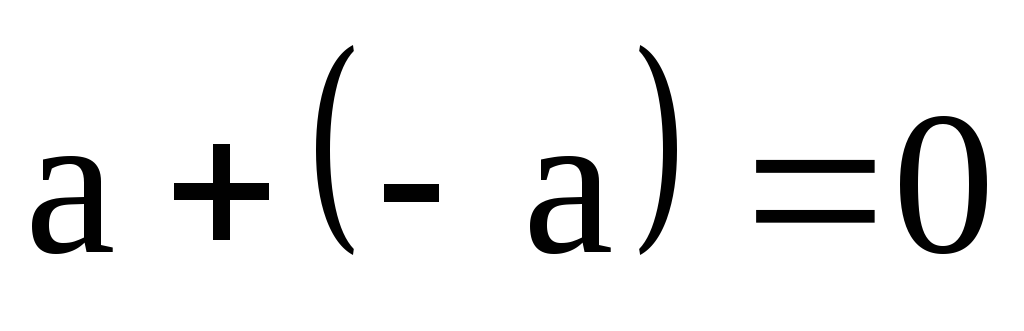 .
.
Из
определения 3 следует, что если 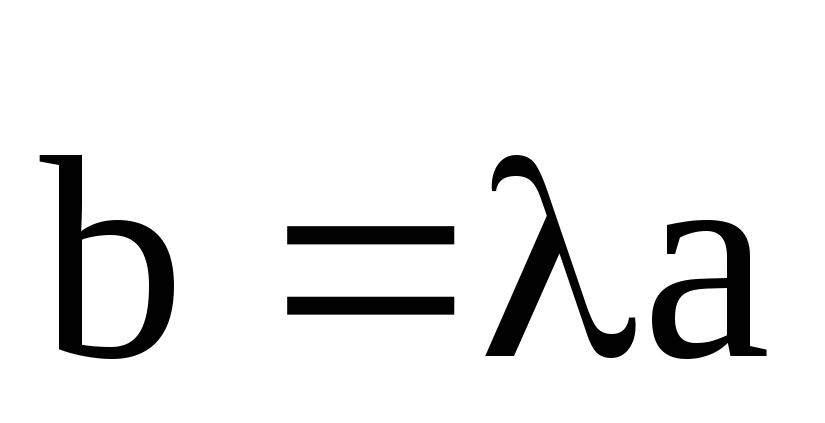 ,
то векторы
,
то векторы и
и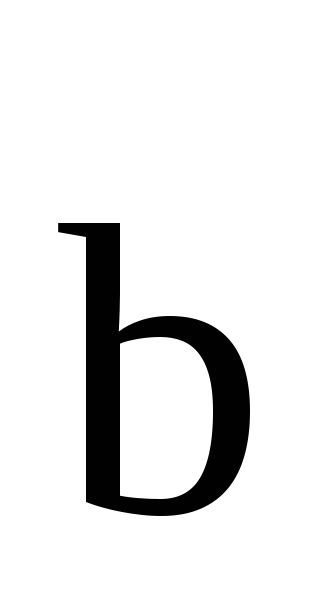 коллинеарны. Отсюда вытекает определение
коллинеарности векторов.
коллинеарны. Отсюда вытекает определение
коллинеарности векторов.
Определение
4. Любые два вектора  и
и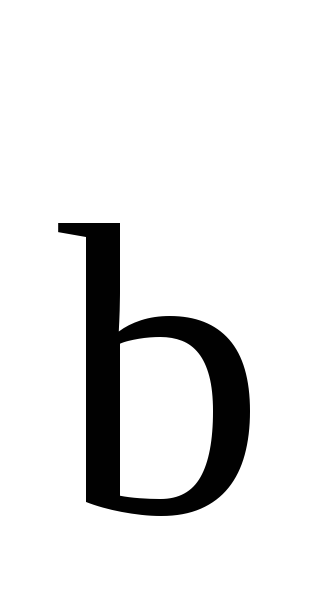 коллинеарны, если связаны соотношением
коллинеарны, если связаны соотношением ,
где
,
где — некоторое число.
— некоторое число.
Величину  можно определить из отношения
можно определить из отношения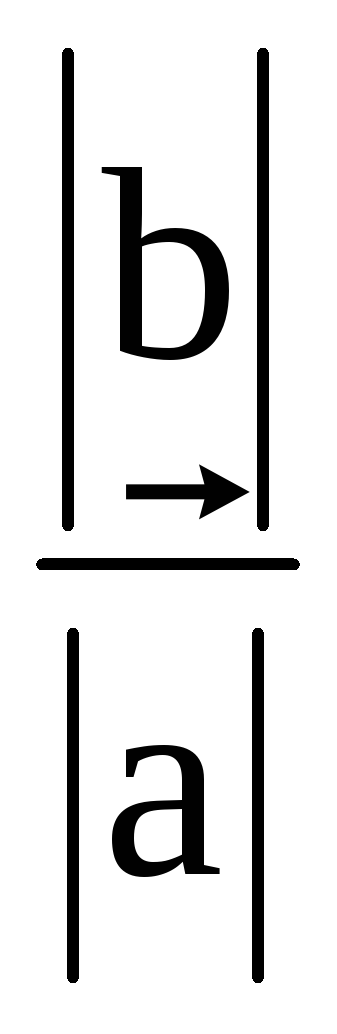 .
Оно положительно, если векторы направлены
в одну сторону, и наоборот отрицательно,
если направление векторов противоположно.
.
Оно положительно, если векторы направлены
в одну сторону, и наоборот отрицательно,
если направление векторов противоположно.
Из построения параллелограмма легко убедиться, что умножение вектора на число обладает распределительным свойством:
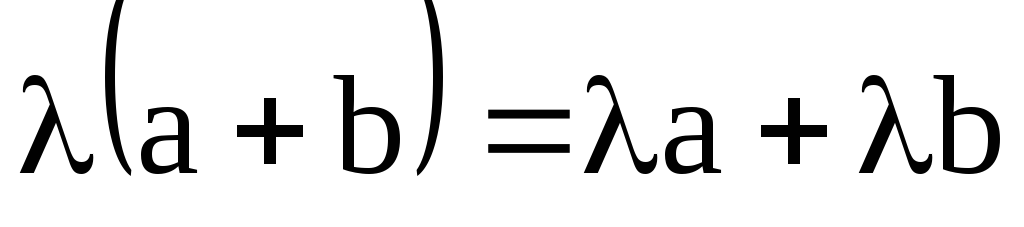 ;
; 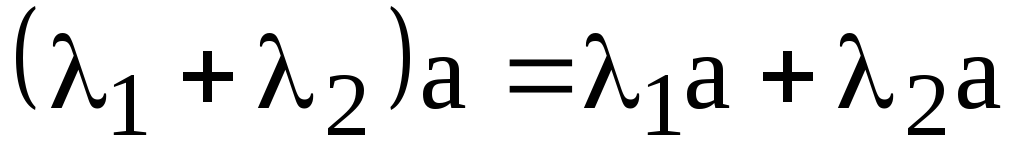
и сочетательным свойством
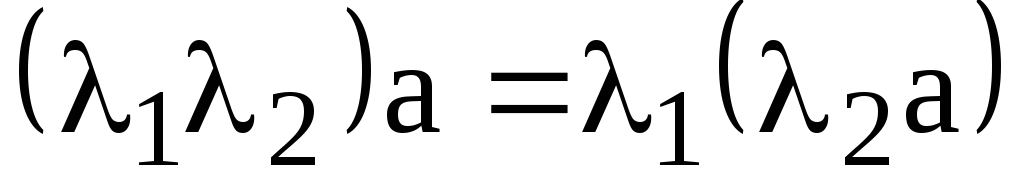 .
.
Определение 5. Вектор, длина которого равна единице, называется единичным вектором или ортом.
Обозначаются
единичные векторы символами 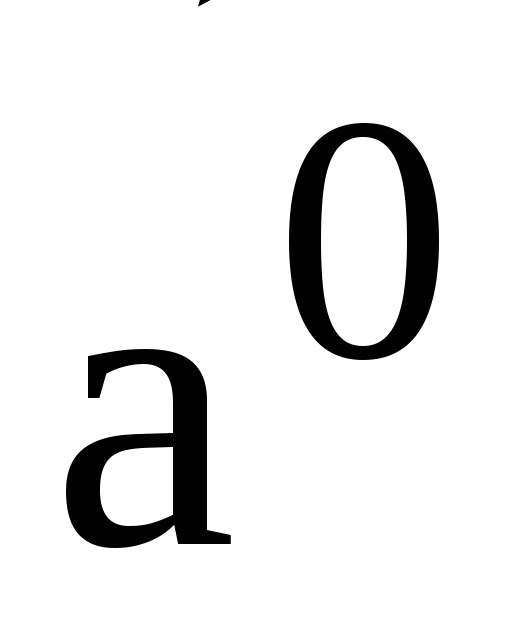 или
или .
.
Используя
понятие единичного вектора, любой вектор
можно представить следующим образом: 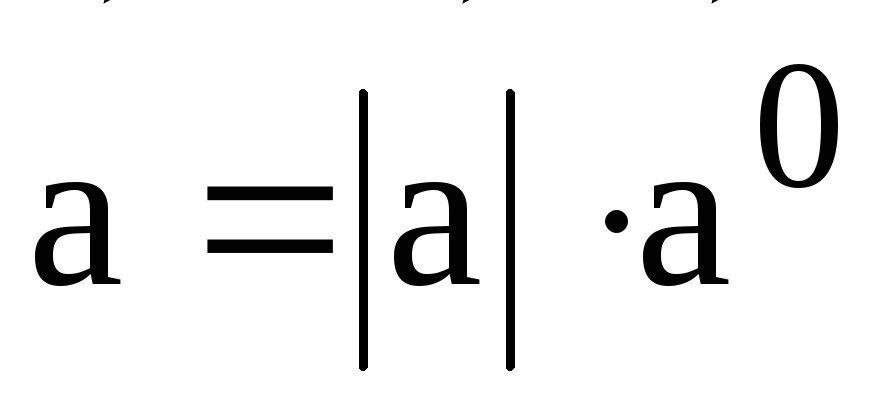 .
.
Числовые матрицы.
Ма́трица —
математический объект, записываемый в
виде прямоугольной таблицы чисел и
допускающий алгебраические операции
(сложение, вычитание, умножение) между
ним и другими подобными объектами.
Обычно матрицы представляются двумерными
(прямоугольными) таблицами. Иногда
рассматривают многомерные матрицы или
матрицы непрямоугольной формы. Обычно
матрицу обозначают заглавной буквой
латинского алфавита и выделяют круглыми
скобками «(…)» (встречается также
выделение квадратными скобками «[…]»
или двойными прямыми линиями «||…||»).
Числа, составляющие матрицу (элементы
матрицы), часто обозначают той же буквой,
что и саму матрицу, но строчной (к примеру a11 является элементом матрицы А).
У каждого элемента матрицы есть 2 нижних
индекса (aij) —
первый «i»
обозначает номер строки, в которой
находится элемент, а второй «j» —
номер столбца. Говорят «матрица размера 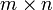 »,
подразумевая, что в матрице m строк и n столбцов. В одной матрице всегда
»,
подразумевая, что в матрице m строк и n столбцов. В одной матрице всегда  ,
, 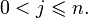
История
Понятие матрицы впервые появилось в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрасссу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г.
Операции над матрицами
Пусть aij — элементы матрицы A, а bij — элементы матрицы B.
Линейные операции:
Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен
bij = λaij
Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен
cij = aij + bij

Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой
cij = aij — bij
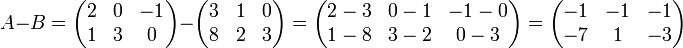
Сложение и вычитание допускается только для матриц одинакового размера.
Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть
A + Θ = A
Все элементы нулевой матрицы равны нулю.
Нелинейные операции:
Умножение
матриц
(обозначение: AB,
реже со знаком умножения 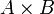 ) —
есть операция вычисления матрицы C,
элементы которой равны сумме произведений
элементов в соответствующей строке
первого множителя и столбце второго.
) —
есть операция вычисления матрицы C,
элементы которой равны сумме произведений
элементов в соответствующей строке
первого множителя и столбце второго.
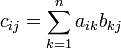
В
первом множителе должно быть столько
же столбцов, сколько строк во втором.
Если матрица A имеет размерность 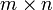 , B —
, B — 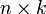 ,
то размерность их произведения AB = C есть
,
то размерность их произведения AB = C есть 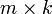 .
.
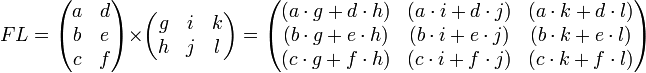


Возводить в степень можно только квадратные матрицы.
Транспонирование матрицы (обозначение: AT) — операция, при которой матрица отражается относительно главной диагонали, то есть
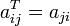
Если A —
матрица размера 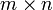 ,
то AT —
матрица размера
,
то AT —
матрица размера 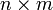
Свойства операций над матрицами
Ассоциативность сложения: A + (B + C) = (A + B) + C.
Коммутативность сложения: A + B = B + A.
Дистрибутивность умножения относительно сложения:
A(B + C) = AB + AC;
(B + C)A = BA + CA.
Свойства операции транспонирования матриц:
(AT)T = A
(AB)T = BTAT
(A − 1)T = (AT) − 1, если обратная матрица A — 1 существует.
Квадратная матрица и смежные определения
Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.
Для квадратных матриц существует единичная матрица E (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно
EA = AE = A
У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю
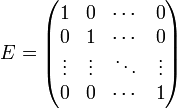
Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица A — 1 такова, что если умножить матрицу на неё, то получится единичная матрица:
AA − 1 = E
Общее определение абстрактного векторного пространства.
V
≠  ;a,
b,
c
є V;
P-числовое
поле.
;a,
b,
c
є V;
P-числовое
поле.
Пусть: 1. Задана операция ∆, которая каждому a є V и каждому λ є P ставит в соответствие элемент λ∆a є V.
2. ∀ a,b є V задана операция □, которая каждой упорядоченной паре a,b є V ставит в соответствие единственный элемент a□b є V.
При этом выполняются 8 свойств (аксиом).
1. a□(b□c)=(a□b)□c
2. Ǝ z є V | ∀ a є V |a□z=z□a=a
3. ∀ a Ǝ n | n□a=a□n=z
4. a□b=b□a
5. (α+β)∆a=(α∆a)□(β∆a)
6. α∆(a□b)= (α∆a)□(α∆ b)
7. α∆(β∆a)= (αβ)∆a
8.1∆a=a
∀ a, b є V; α,β є P; 1 є P
Тогда множество V называется векторным пространством над полем Р, операция □=+, ∆=умножение вектора на число, z-единичный элемент=0, а его элементы-векторы.
Перестановки и подстановки из n символов.
Перестановкой чисел 1, 2,…, n называется любое расположение этих чисел в определенном порядке. В элементарной алгебре доказывается, что число всех перестановок, которые можно образовать из n чисел, равно 12…n = n!. Например, из трех чисел 1, 2, 3 можно образовать 3!=6 перестановок: 123, 132, 312, 321, 231, 213. Говорят, что в данной перестановке числа i и j составляют инверсию (беспорядок), если i>j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего.
Перестановка называется четной (или нечетной), если в ней соответственно четно (нечетно) общее число инверсий. Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n-ой степени.
Подстановка,
переводящая одну перестановку в другую,
записывается двумя строками в общих
скобках, причем числа, занимающие
одинаковые места в рассматриваемых
перестановках, называются соответствующими и пишутся одно под другим. Например,
символ 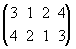 обозначает
подстановку, в которой 3 переходит в 4,
1
2, 2
1, 4
3. Подстановка называется четной (или нечетной),
если общее число инверсий в обеих строках
подстановки четно (нечетно). Всякая
подстановка n-ой степени может быть
записана в виде
обозначает
подстановку, в которой 3 переходит в 4,
1
2, 2
1, 4
3. Подстановка называется четной (или нечетной),
если общее число инверсий в обеих строках
подстановки четно (нечетно). Всякая
подстановка n-ой степени может быть
записана в виде 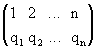 ,т.е.
с натуральным расположением чисел в
верхней строке.
,т.е.
с натуральным расположением чисел в
верхней строке.
Пусть нам дана квадратная матрица порядка n
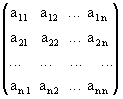 .
.
Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:
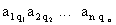 ,
,
где индексы q1,q2,…,qn составляют некоторую перестановку из чисел 1, 2,…, n. Число таких произведений равно числу различных перестановок из n символов, т.е. равно n!. Знак произведения равен (- 1)q, где q — число инверсий в перестановке вторых индексов элементов.
Свойства линейных операций над векторами.
Сложение векторов коммутативно, т.е. для любых векторов
 и
и  выполнено
выполнено  .
.Сложение векторов ассоциативно, т.е. для любых векторов
 ,
, и
и  выполнено
выполнено .
.Прибавление нулевого вектора
 к любому вектору
к любому вектору ,
не меняет последнего:
,
не меняет последнего: .
.Для любого вектора
 вектор
вектор является противоположным, т.е.
является противоположным, т.е. .
.Умножение вектора на число ассоциативно, т.е. для любых чисел
 и
и и любого вектора
и любого вектора ,
выполнено
,
выполнено .
.Умножение вектора на число дистрибутивно по отношению к сложению чисел:
 .
.Умножение вектора на число дистрибутивно по отношению к сложению векторов:
 .
.Умножение вектора на единицу не меняет вектора:
 .
.
3. Понятие линейной зависимости векторов.
Определение
9. Пусть
дана система векторов  1,
1,  2,
…,
2,
…, n и совокупность вещественных чисел
n и совокупность вещественных чисел  .
Тогда выражение вида
.
Тогда выражение вида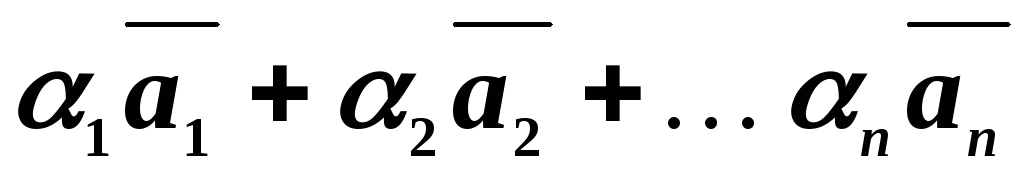 называетсялинейной
комбинацией векторов,
а числа
называетсялинейной
комбинацией векторов,
а числа 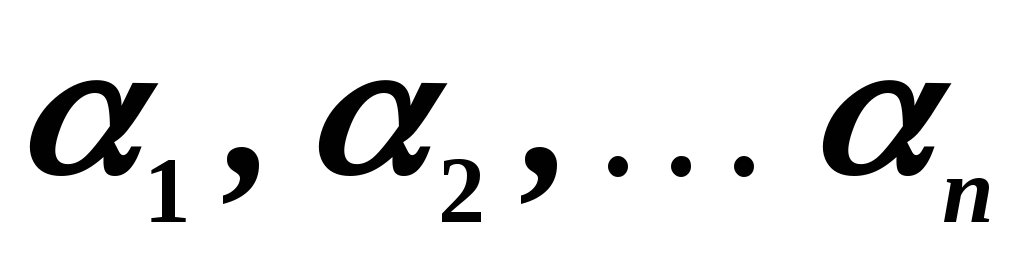 называются коэффициентами линейной
комбинации. Если некоторый вектор
называются коэффициентами линейной
комбинации. Если некоторый вектор  представлен как линейная комбинация
векторов
представлен как линейная комбинация
векторов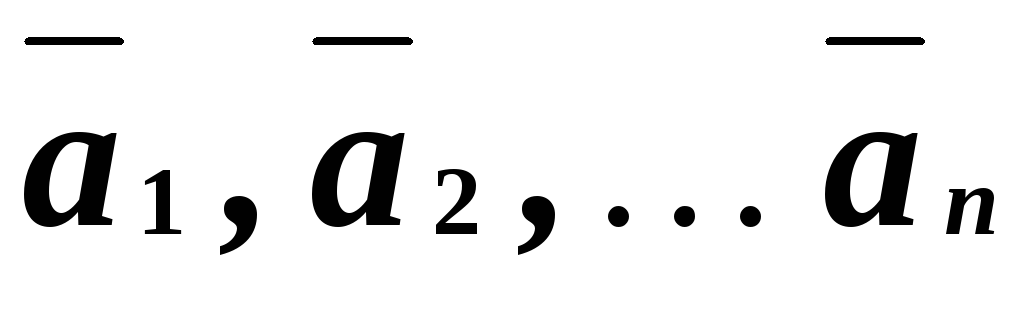 ,
т.е. в виде:
,
т.е. в виде: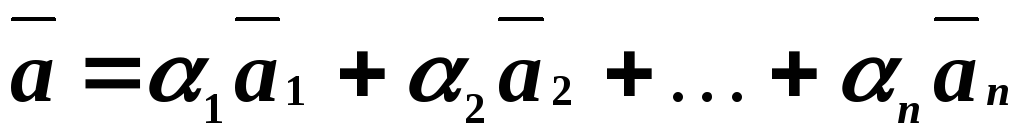 ,
то говорят, что вектор
,
то говорят, что вектор разложен по этим векторам.
разложен по этим векторам.
Определение
10. Векторы 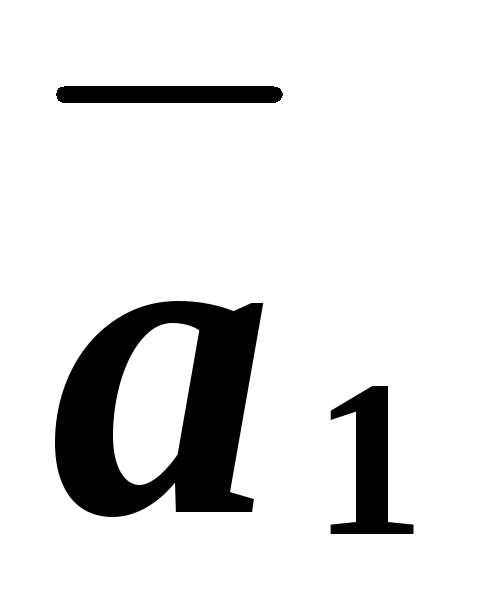 ,
, ,
…,
,
…,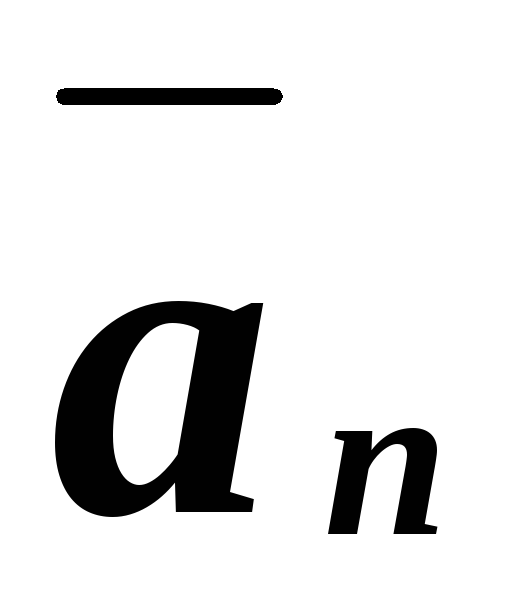 называютсялинейно
зависимыми, если существует набор коэффициентов
называютсялинейно
зависимыми, если существует набор коэффициентов 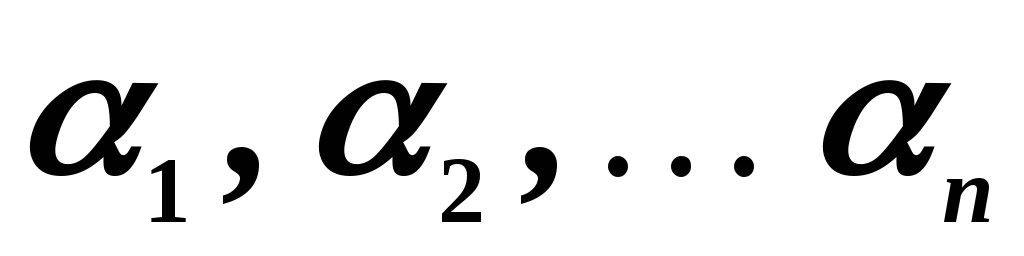 ,
одновременно не равных нулю
,
одновременно не равных нулю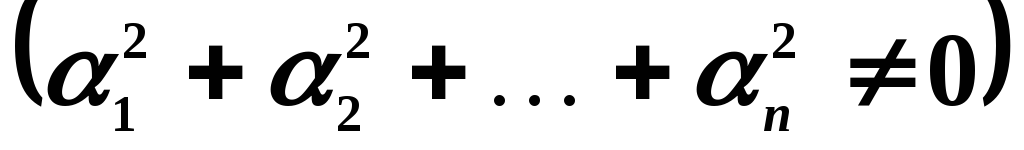 и таких, что
и таких, что
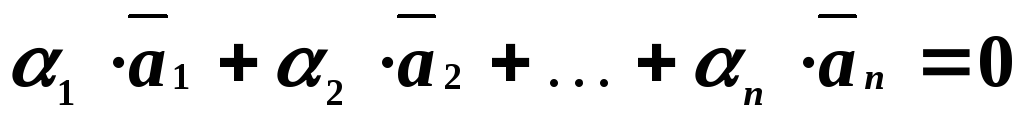 .
.
Определение
11. Векторы 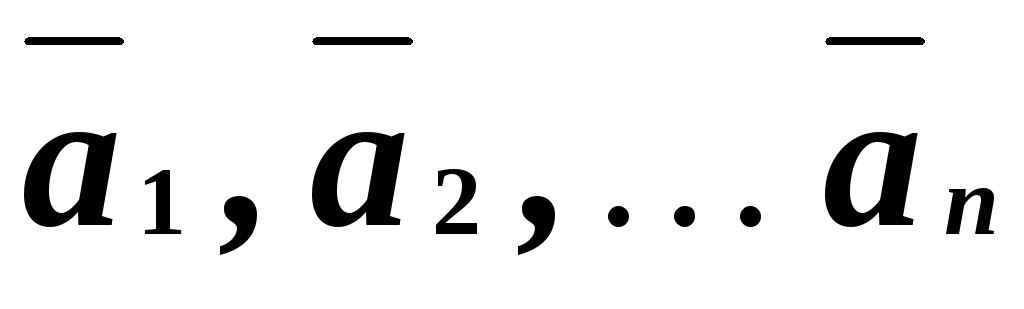 называютсялинейно
независимыми, если равенство нулю линейной комбинации
этих векторов возможно лишь при всех
коэффициентах одновременно равных
нулю.
называютсялинейно
независимыми, если равенство нулю линейной комбинации
этих векторов возможно лишь при всех
коэффициентах одновременно равных
нулю.
Определение 12. Базисом на прямой называется любой ненулевой вектор на этой прямой.
Определение 13. Базисом на плоскости называются два неколлинеарных вектора на этой плоскости, взятые в определенном порядке.
Определение
14. Базисом
в пространстве  называются три линейно независимые
вектора в этом пространстве, взятые в
определенном порядке.
называются три линейно независимые
вектора в этом пространстве, взятые в
определенном порядке.
Теорема 1 (о разложении вектора по базису в пространстве R3)
Пусть
даны три некомпланарные вектора: 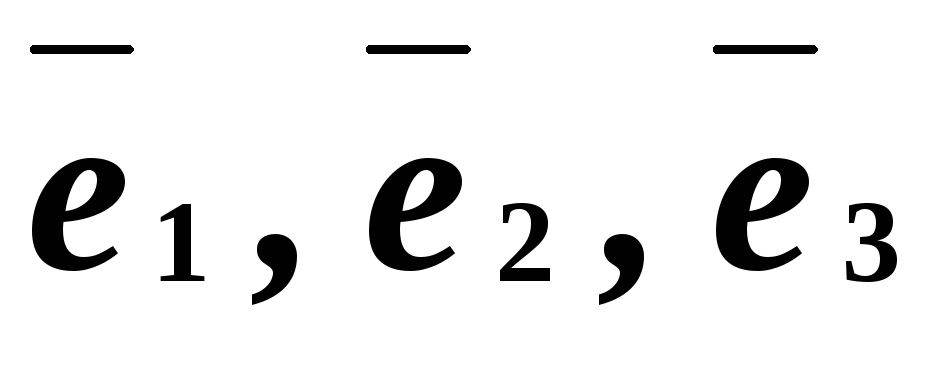 .
Любой вектор
.
Любой вектор раскладывается по ним. Такое разложение
единственно. Существует набор чисел
раскладывается по ним. Такое разложение
единственно. Существует набор чисел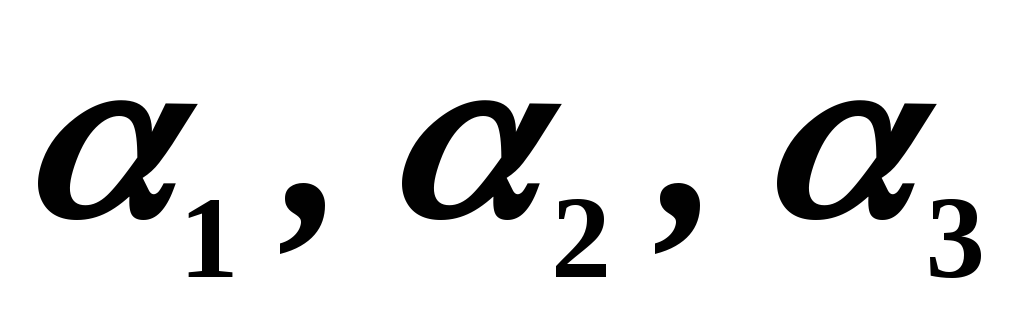 такой,
что:
такой,
что:
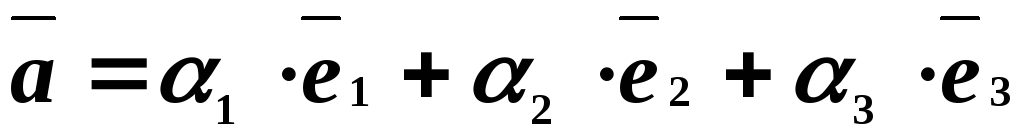 .
.
Свойства линейно зависимой и линейно независимой системы векторов:
Если хотя бы один из
 векторов есть нуль вектор, то все
векторов есть нуль вектор, то все векторов линейно зависимы.
векторов линейно зависимы.Если среди
 векторов какие-либо
векторов какие-либо векторов линейно зависимы, то все
векторов линейно зависимы, то все векторов линейно зависимы.
векторов линейно зависимы.Для того чтобы два ненулевых вектора были линейно зависимы необходимо и достаточно, чтобы они были коллинеарными.
Пусть
 — два неколлинеарных вектора плоскости.
Любой компланарный с ними вектор
— два неколлинеарных вектора плоскости.
Любой компланарный с ними вектор раскладывается по ним:
раскладывается по ним: .
Такое разложение единственно.
.
Такое разложение единственно.Три компланарных вектора линейно зависимы. Три некомпланарных вектора пространства линейно независимы.
Любые четыре вектора пространства
 линейно зависимы.
линейно зависимы.Система векторов
 1,
1,  2,
…,
2,
…, n линейно зависима тогда и только тогда,
когда один из них раскладывается в
линейную комбинацию остальных.
n линейно зависима тогда и только тогда,
когда один из них раскладывается в
линейную комбинацию остальных.
4. Понятие о проекциях.
П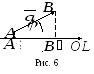 усть
дан вектор
усть
дан вектор и ось
и ось ,
, — угол между вектором
— угол между вектором и положительным направлением оси
и положительным направлением оси .
. и
и  —
основания перпендикуляров, опущенных
из точек
—
основания перпендикуляров, опущенных
из точек  и
и соответственно (см. рис. 6).
соответственно (см. рис. 6).
Определение
15. Проекцией вектора на ось называется длина отрезка
оси 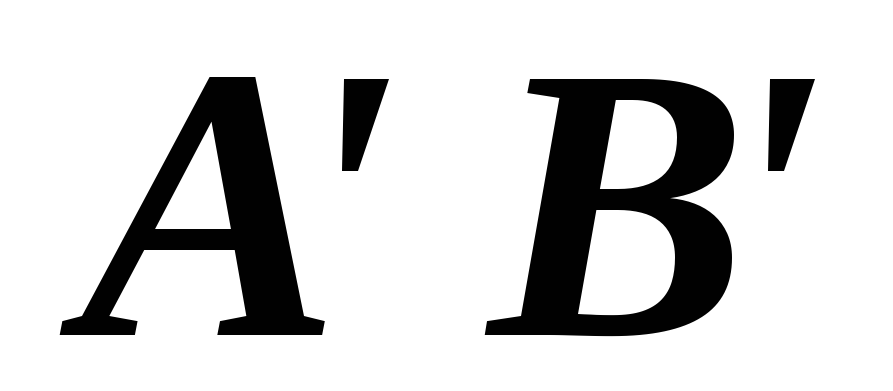 ,
взятая со знаком плюс, если вектор
,
взятая со знаком плюс, если вектор образует острый угол с направлением
оси, и со знаком минус в противоположном
случае.
образует острый угол с направлением
оси, и со знаком минус в противоположном
случае.
Теорема
2. Проекция
вектора  на ось
на ось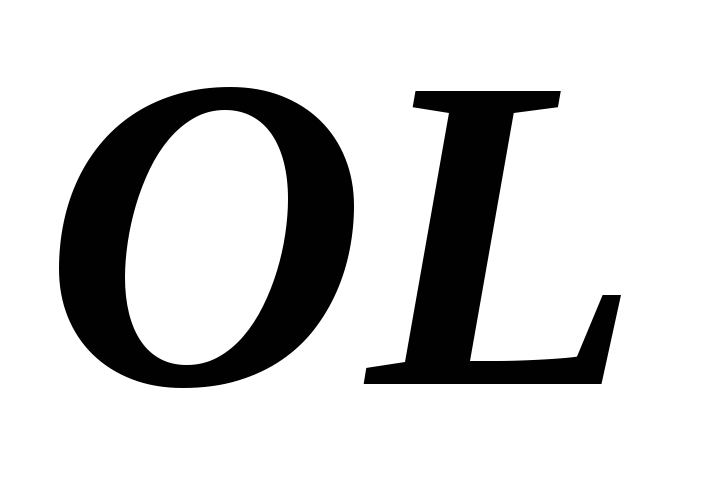 равна произведению длины вектора на
косинус угла между вектором и осью:
равна произведению длины вектора на
косинус угла между вектором и осью: 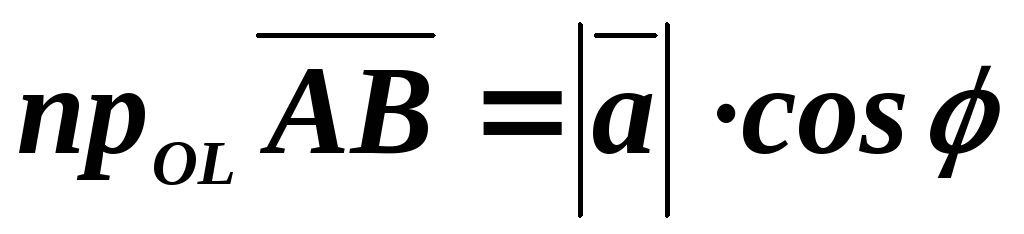 .
.
Следствие. При умножении вектора  на некоторое число
на некоторое число его проекция умножается на это же число:
его проекция умножается на это же число: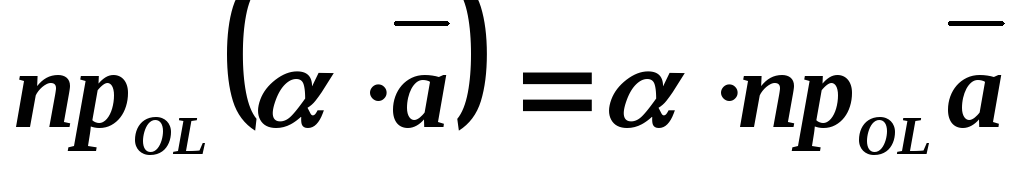 .
.
Теорема
3 (о проекции суммы). Проекция
суммы некоторого числа векторов на ось 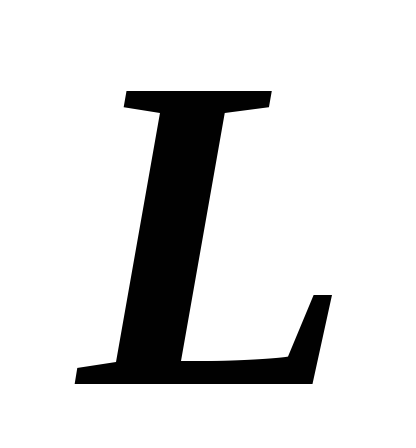 равна сумме проекций слагаемых векторов:
равна сумме проекций слагаемых векторов: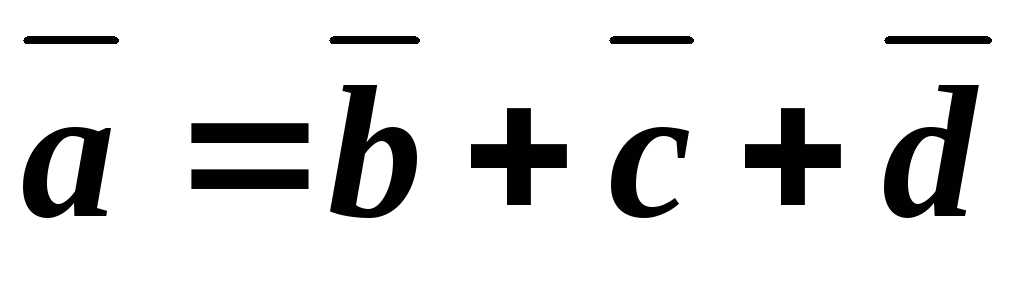 ,
, .
.
Действия над векторами и свойства векторов — справочник для студентов и школьников
В этом разделе мы обобщим раздел векторов, опишем все действия, которые можно выполнять над векторами, и какие у них свойства.
Действия по векторам
Определение
Вектор — это направленный сегмент \(\ \overline{A B} \), где точка \(\ A \) — это начало, а точка \(\ B \) — конец вектора.
Сумма \(\ \overline{a}+\overline{b} \) векторов \(\ \overline{a} {и} \overline{b} \) называется таким третьим вектором \(\ \overline{c} \), начало которого совпадает с началом \(\ \overline{a} \) , а конец с концом \(\ \overline{b} \), при условии, что конец вектора \(\ \overline{a} \) и начало вектора \(\ \overline{b} \) совпадают.
Свойства операции сложения:
1. – \(\ \overline{a}+\overline{b}=\overline{b}+\overline{a} \)коммутативность
2. – \(\ (\overline{a}+\overline{b})+\overline{c}=\overline{a}+(\overline{b}+\overline{c}) \) ассоциативность
3. \(\ \overline{a}+\overline{0}=\overline{a} \)
4. \(\ \overline{a}+(-\overline{a})=\overline{0} \)
Определение
Разница \(\ \overline{a}-\overline{b} \) векторов \(\ \overline{a} и \overline{b} \) называется вектором \(\ \overline{c} \) таким, что условие: \(\ \overline{b}+\overline{c}=\overline{a} \)
Произведение \(\ \alpha \overline{a} \) вектора \(\ \overline{a} \) на число \(\ \alpha \) представляет собой вектор \(\ \overline{b} \) , удовлетворяющий условиям:
1. \(\ \overline{b}\|\overline{a} \)
2. \(\ |\overline{b}|=|\alpha||\overline{a}| \)
3.\(\ \overline{a} \uparrow \uparrow \overline{b}, \operatorname{если} \alpha>0, \overline{a} \uparrow \rfloor \overline{b}, \operatorname{если} \alphaСвойства умножения вектора на число:
1. \(\ (\alpha \pm \beta) \overline{a}=\alpha \overline{a} \pm \beta \overline{a} \)
2. \(\ \alpha(\overline{a} \pm \overline{b})=\alpha \overline{a} \pm \alpha \overline{b} \)
3. \(\ \alpha(\beta \overline{a})=(\alpha \beta) \overline{a}=\beta(\alpha \overline{a}) \)
4. \(\ 1 \cdot \overline{a}=\overline{a} \)
5.\(\ -1 \cdot \overline{a}=-\overline{a} \)
6. \(\ 0 \cdot \overline{a}=\overline{0} \)
Определение
Скалярное произведение двух ненулевых векторов \(\ \overline{a} {и} \overline{b} \) представляет собой число, равное произведению длин этих векторов и косинуса угла между ними: \(\ \overline{a} \overline{b}=\overline{a} \cdot \overline{b}=(\overline{a}, \overline{b})=|\overline{a}||\overline{b}| \cos (\overline{a}, \overline{b}) \)
Свойства точечного продукта:
1. \(\ (\overline{a}, \overline{b})=(\overline{b}, \overline{a}) \) — симметрия.
2 \(\ (\overline{a}, \overline{a})=|\overline{a}|^{2} \) Обозначается \(\ (\overline{a}, \overline{a})=\overline{a}^{2} \) и называется скалярным квадратом.
3. Если \(\ \overline{a} \neq \overline{0} \), то \(\ (\overline{a}, \overline{b})=|\overline{a}| \cdot \Pi p_{\overline{a}} \overline{b} \)
4. Если \(\ \overline{a} \neq \overline{0} \quad{и}\quad \overline{b} \neq \overline{0} \quad{и}\quad(\overline{a}, \overline{b})=0 \) Обратное также верно.
5. \(\ (\overline{a}+\overline{b}, \overline{c})=(\overline{a}, \overline{c})+(\overline{b}, \overline{c}) \)
6. \(\ (\lambda \overline{a}, \overline{b})=\lambda(\overline{a}, \overline{b}) \)
7. \(\ (\alpha \overline{a}+\beta \overline{b}, \gamma \overline{c}+\delta \overline{d})=\alpha \gamma(\overline{a}, \overline{c})+\alpha \delta(\overline{a}, \overline{d})+\beta \gamma(\overline{b}, \overline{c})+\beta \delta(\overline{b}, \overline{d}) \)
Определение
Векторное произведение ненулевых векторов \(\ \overline{a} и \overline{b} \) представляет собой вектор \(\ \overline{c} \), обозначаемый символом \(\ [\overline{a}, \overline{b}] \) или \(\ \overline{a} \times \overline{b} \), длина которого равна \(\ |\overline{c}|=|\overline{a}||\overline{b}| \sin (\overline{a}, \overline{b}) \)
Свойства векторного произведения:
1. \(\ [\overline{a}, \overline{b}]=\overline{0} \) если и только если \(\ \overline{a}\|\overline{b} \)
2. \(\ [\overline{a}, \overline{b}]=-[\overline{b}, \overline{a}] \)
3. Модуль векторного произведения \(\ |[\tilde{a}, \overline{b}]| \) равен площади параллелограмма, построенного на указанных векторах \(\ \overline{a} {и} \overline{b} \) (рис. 2), т.е.
\(\ S=|[\overline{a}, \overline{b}]|=|\overline{a}||\overline{b}| \sin (\overline{a}, \overline{b}) \)
4. \(\ [\lambda \overline{a}, \overline{b}]=[\overline{a}, \lambda \overline{b}]=\lambda[\overline{a}, \overline{b}] \)
5. \(\ \left[\tilde{a}_{1}+\overline{a}_{2}, \overline{b}\right]=\left[\overline{a}_{1}, \overline{b}\right]+\left[\overline{a}_{2}, \overline{b}\right] ;\left[\overline{a}, \overline{b}_{1}+\overline{b}_{2}\right]=\left[\overline{a}, \overline{b}_{1}\right]+\left[\overline{a}, \overline{b}_{2}\right] \)
Определение
Смешанное произведение трех векторов \(\ \overline{a}, \overline{b}, \overline{c} \) , это число, равное скалярному произведению вектора \(\ \overline{a} \times \overline{b} \) на вектор \(\ (\overline{a}, \overline{b}, \overline{c})=([\overline{a}, \overline{b}], \overline{c}) \):
Свойства смешанного продукта:
1. \(\ (\overline{a}, \overline{b}, \overline{c})=(\overline{a},[\overline{b}, \overline{c}]) \)
2. \(\ (\overline{a}, \overline{b}, \overline{c})=(\overline{b}, \overline{c}, \overline{a})=(\overline{c}, \overline{a}, \overline{b})=-(\overline{b}, \overline{a}, \overline{c})=-(\overline{c}, \overline{b}, \overline{a})=-(\overline{a}, \overline{c}, \overline{b}) \)
3. Три вектора копланарны тогда и только тогда, когда \(\ (\overline{a}, \overline{b}, \overline{c})=0 \)
4. Три вектора правильны тогда и только тогда, когда \(\ (\overline{a}, \overline{b}, \overline{c})>0 \). Если \(\ (\overline{a}, \overline{b}, \overline{c})5. \(\ (\lambda \overline{a}, \overline{b}, \overline{c})=(\overline{a}, \lambda \overline{b}, \overline{c})=(\overline{a}, \overline{b}, \lambda \vec{c})=\lambda(\overline{a}, \overline{b}, \overline{c}) \)
6. \(\ \left(\overline{a}_{1}+\overline{a}_{2}, \overline{b}, \overline{c}\right)=\left(\overline{a}_{1}, \overline{b}, \overline{c}\right)+\left(\overline{a}_{2}, \overline{b}, \overline{c}\right) \)
7. \(\ \left(\overline{a}, \overline{b}_{1}+\overline{b}_{2}, \overline{c}\right)=\left(\overline{a}, \overline{b}_{1}, \overline{c}\right)+\left(\overline{a}, \overline{b}_{2}, \overline{c}\right) \)
8. \(\ \left(\overline{a}, \overline{b}, \overline{c}_{1}+\overline{c}_{2}\right)=\left(\overline{a}, \overline{b}, \overline{c}_{1}\right)+\left(\overline{a}, \overline{b}, \overline{c}_{2}\right) \)
9. \(\ ([\overline{a}, \overline{b}], \overline{c})=\overline{b}(\overline{a}, \overline{c})-\overline{a}(\overline{b}, \overline{c}) ;(\overline{a},[\overline{b}, \overline{c}])=\overline{b}(\overline{a}, \overline{c})-\overline{c}(\overline{a}, \overline{b}) \)
10. Личность Якоби: \(\ (\overline{a},[\overline{b}, \overline{c}])+(\overline{b},[\overline{c}, \overline{a}])+(\overline{c},[\overline{a}, \overline{b}])=0 \)


 z
z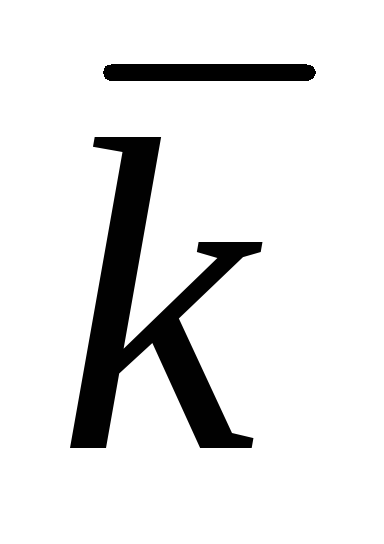
 имеет координатыx, y, z,
то координатами точки М будут числа x, y, z,
что записывается в виде М(x,y,z).
имеет координатыx, y, z,
то координатами точки М будут числа x, y, z,
что записывается в виде М(x,y,z).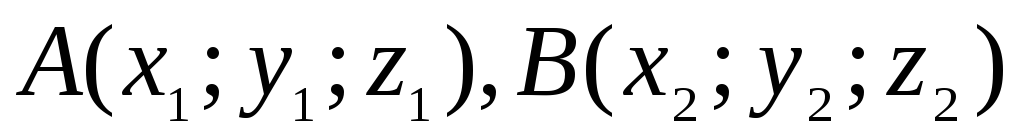 ,
то
,
то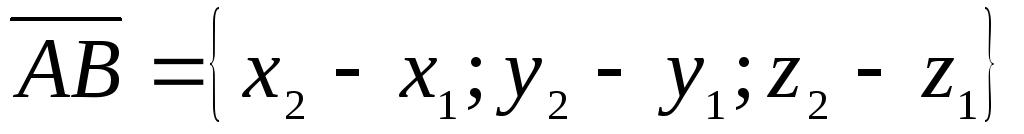 и
и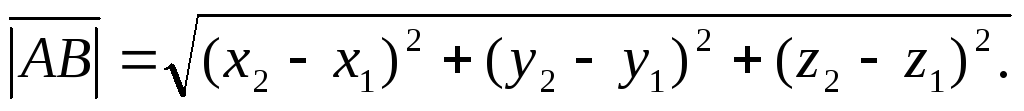
 и
и 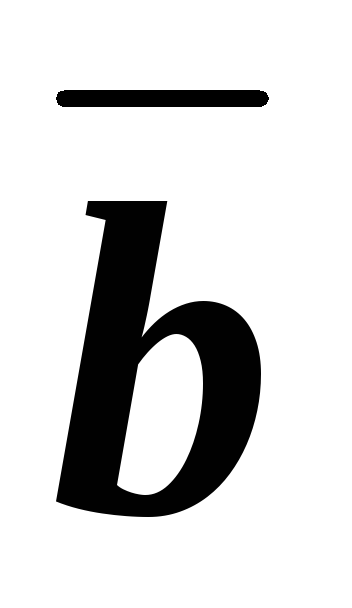 выполнено
выполнено 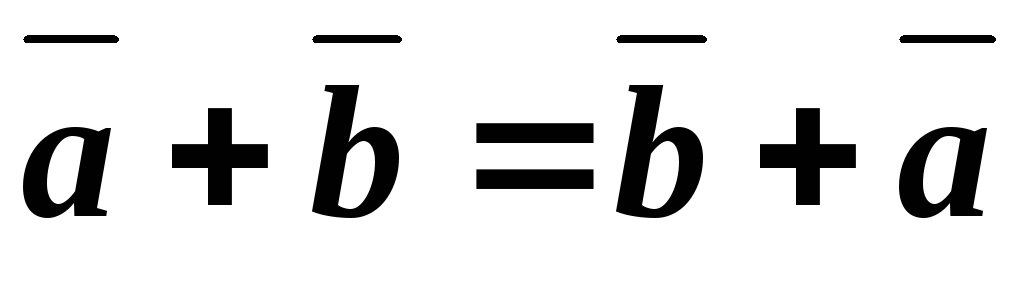 .
. ,
,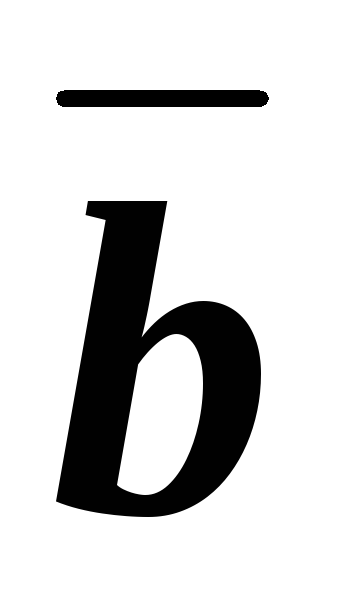 и
и  выполнено
выполнено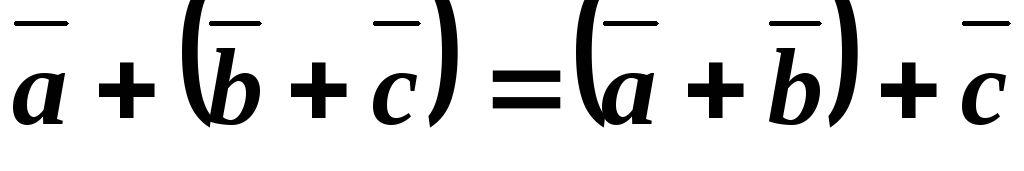 .
.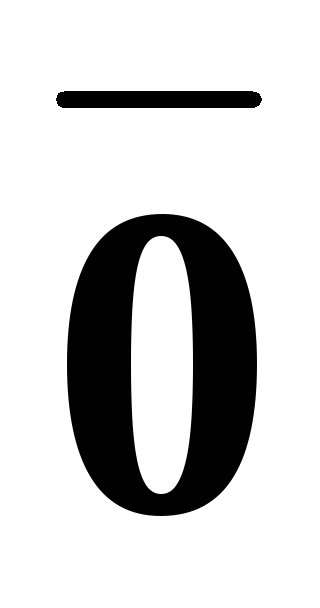 к любому вектору
к любому вектору ,
не меняет последнего:
,
не меняет последнего: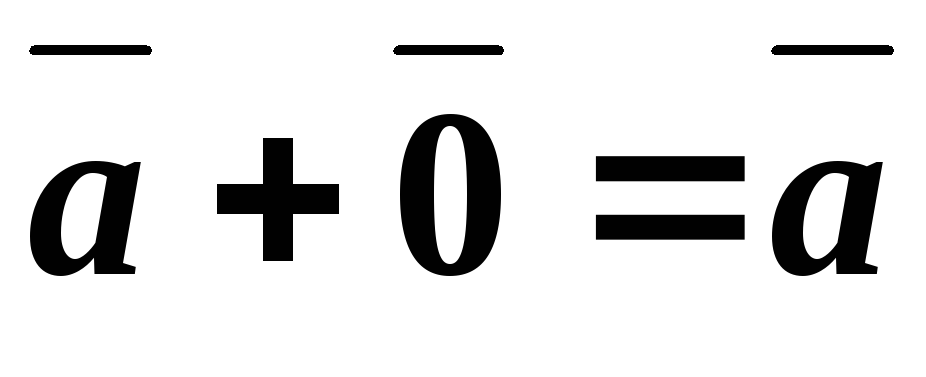 .
. вектор
вектор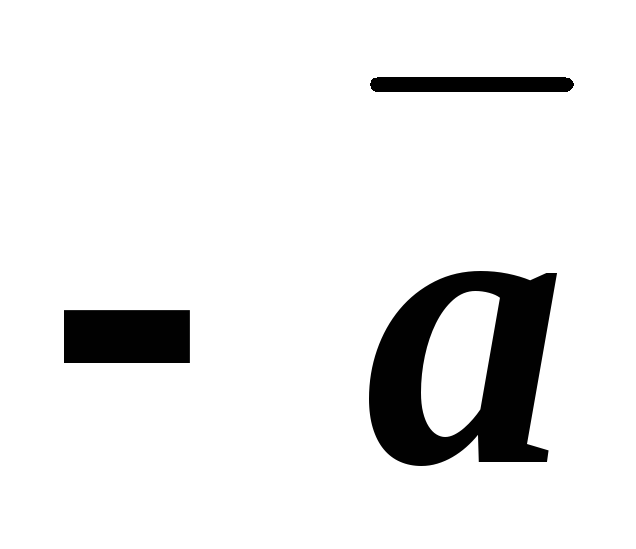 является противоположным, т.е.
является противоположным, т.е. .
. и
и и любого вектора
и любого вектора ,
выполнено
,
выполнено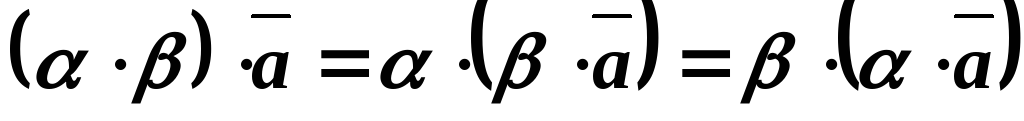 .
.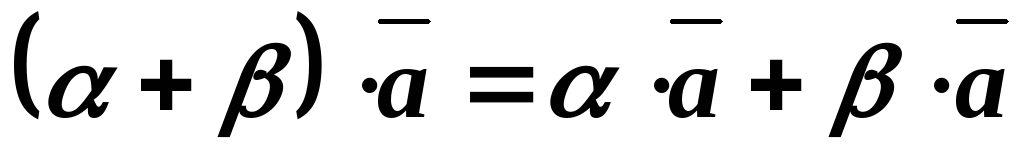 .
.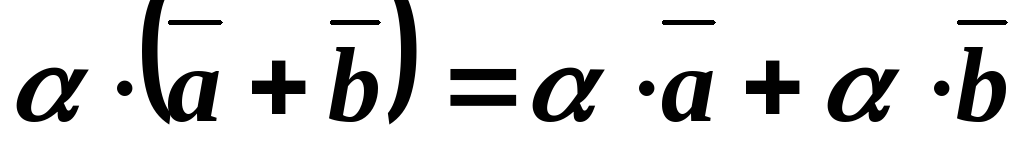 .
.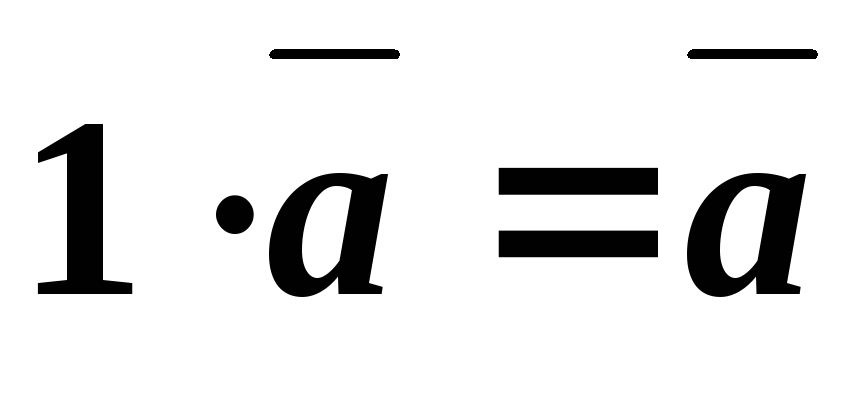 .
. векторов есть нуль вектор, то все
векторов есть нуль вектор, то все векторов линейно зависимы.
векторов линейно зависимы. векторов какие-либо
векторов какие-либо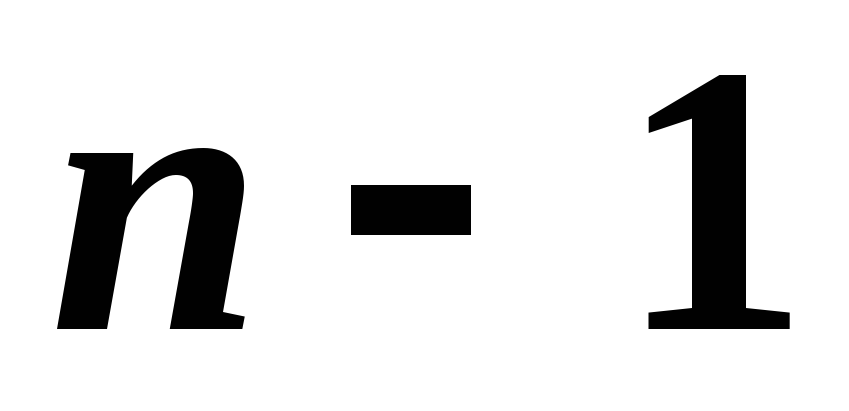 векторов линейно зависимы, то все
векторов линейно зависимы, то все векторов линейно зависимы.
векторов линейно зависимы.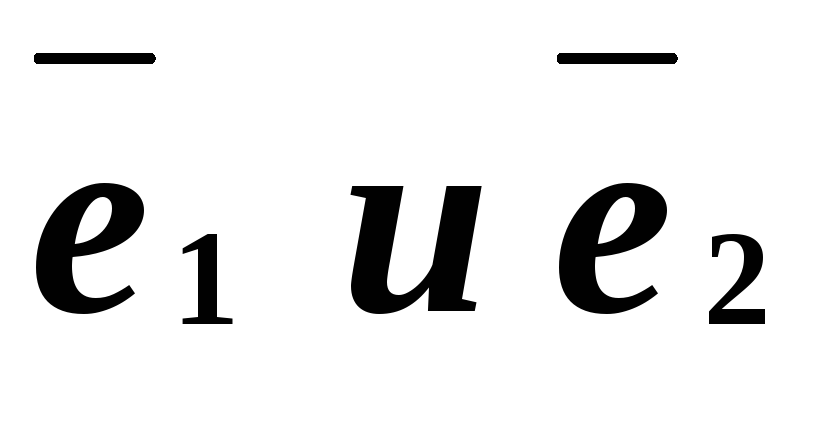 — два неколлинеарных вектора плоскости.
Любой компланарный с ними вектор
— два неколлинеарных вектора плоскости.
Любой компланарный с ними вектор раскладывается по ним:
раскладывается по ним: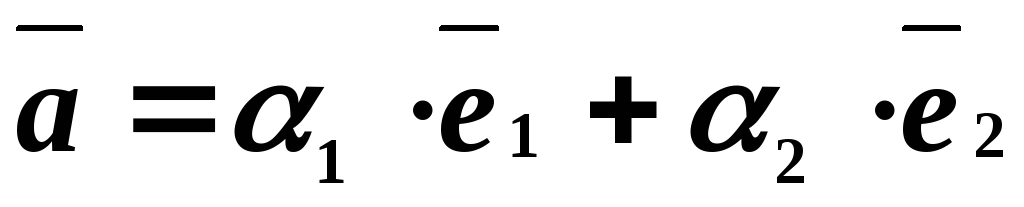 .
Такое разложение единственно.
.
Такое разложение единственно. линейно зависимы.
линейно зависимы. 1,
1,  2,
…,
2,
…, n линейно зависима тогда и только тогда,
когда один из них раскладывается в
линейную комбинацию остальных.
n линейно зависима тогда и только тогда,
когда один из них раскладывается в
линейную комбинацию остальных.