Напряжённость электрического поля. Силовые линии
Напряжённость электрического поля. Силовые линии
«Физика — 10 класс»
Что является посредником, осуществляющим взаимодействие зарядов?
Как определить, какое из двух полей более сильное? Предложите пути сравнения полей.
Напряжённость электрического поля.
Электрическое поле обнаруживается по силам, действующим на заряд. Можно утверждать, что мы знаем о поле всё, что нам нужно, если будем знать силу, действующую на любой заряд в любой точке поля. Поэтому надо ввести такую характеристику поля, знание которой позволит определить эту силу.
Если поочерёдно помещать в одну и ту же точку поля небольшие заряженные тела и измерять силы, то обнаружится, что сила, действующая на заряд со стороны поля, прямо пропорциональна этому заряду. Действительно, пусть поле создаётся точечным зарядом q1. Согласно закону Кулона (14.2) на точечный заряд q действует сила, пропорциональная заряду q. Поэтому отношение силы, действующей на помещаемый в данную точку поля заряд, к этому заряду для каждой точки поля не зависит от заряда и может рассматриваться как характеристика поля.
Подобно силе, напряжённость поля — векторная величина; её обозначают буквой :
Отсюда сила, действующая на заряд q со стороны электрического поля, равна:
=q. (14.8)
Направление вектора совпадает с направлением силы, действующей на положительный заряд, и противоположно направлению силы, действующей на отрицательный заряд.
Единица напряжённости в СИ — Н/Кл.
Силовые линии электрического поля.
Электрическое поле не действует на органы чувств. Его мы не видим. Однако мы можем получить некоторое представление о распределении поля, если нарисуем векторы напряжённости поля в нескольких точках пространства (рис. 14.9, а). Картина будет более наглядной, если нарисовать непрерывные линии.
Линии, касательная в каждой точке которых совпадает с вектором напряжённости электрического поля, называют силовыми линиями или линиями напряжённости поля (рис. 14.9, б).
Направление силовых линий позволяет определить направление вектора напряжённости в различных точках поля, а густота (число линий на единицу площади) силовых линий показывает, где напряжённость поля больше. Так, на рисунках 14.10—14.13 густота силовых линий в точках А больше, чем в точках В. Очевидно, что
Не следует думать, что линии напряжённости существуют в действительности вроде растянутых упругих нитей или шнуров, как предполагал сам Фарадей. Линии напряжённости помогают лишь наглядно представить распределение поля в пространстве. Они не более реальны, чем меридианы и параллели на земном шаре.
Силовые линии можно сделать видимыми. Если продолговатые кристаллики изолятора (например, хинина) хорошо перемешать в вязкой жидкости (например, в касторовом масле) и поместить туда заряженные тела, то вблизи этих тел кристаллики выстроятся в цепочки вдоль линий напряжённости.
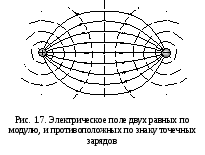
На рисунках приведены примеры линий напряжённости: положительно заряженного шарика (см. рис. 14.10), двух разноимённо заряженных шариков (см. рис. 14.11), двух одноимённо заряженных шариков (см. рис. 14.12), двух пластин, заряды которых равны по модулю и противоположны по знаку (см. рис. 14.13). Последний пример особенно важен.
На рисунке 14.13 видно, что в пространстве между пластинами силовые линии в основном параллельны и находятся на равных расстояниях друг от друга: электрическое поле здесь одинаково во всех точках.
Электрическое поле, напряжённость которого одинакова во всех точках, называется однородным.
В ограниченной области пространства электрическое поле можно считать приближённо однородным, если напряжённость поля внутри этой области меняется незначительно.
Силовые линии электрического поля не замкнуты, они начинаются на положительных зарядах и оканчиваются на отрицательных. Силовые линии непрерывны и не пересекаются, так как пересечение означало бы отсутствие определённого направления напряжённости электрического поля в данной точке.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Электростатика — Физика, учебник для 10 класса — Класс!ная физика
Что такое электродинамика — Электрический заряд и элементарные частицы. Закон сохранения заряд — Закон Кулона. Единица электрического заряда — Примеры решения задач по теме «Закон Кулона» — Близкодействие и действие на расстоянии — Электрическое поле — Напряжённость электрического поля. Силовые линии — Поле точечного заряда и заряженного шара. Принцип суперпозиции полей — Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» — Проводники в электростатическом поле — Диэлектрики в электростатическом поле — Потенциальная энергия заряженного тела в однородном электростатическом поле — Потенциал электростатического поля и разность потенциалов — Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности — Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» — Электроёмкость. Единицы электроёмкости. Конденсатор — Энергия заряженного конденсатора. Применение конденсаторов — Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»
Силовые линии электрического поля
Величина или сила электрического поля в пространстве, окружающем заряд, который является источником, прямо пропорционально количеству этого заряда и обратно квадрату расстояние от этого заряда. Направление электрического поля согласно принятым правилам всегда от положительного заряда в сторону отрицательного заряда. Это можно представить как если поместить пробный заряд в область пространства электрического поля источника и этот пробный заряд будет либо отталкиваться, либо притягиваться (в зависимости от знака заряда). Электрическое поле характеризуется напряженностью, которое являясь векторной величиной может быть представлено графически в виде стрелки имеющей длину и направление. В любом месте направление стрелки указывает направление напряженности электрического поля
Более полезным средством визуального представления векторного характера электрического поля является использование такого понятия как силовые линии электрического поля, или просто — силовые линии. Вместо того, чтобы изображать бесчисленные векторных стрелки в пространстве, окружающие заряд-источник, оказалось полезным объединить их в линии, где сами вектора являются касательными к точкам на таких линиях.
В итоге с успехом для представления векторной картины электрического поля применяют силовые линии электрического поля, которые выходят из зарядов положительного знака и заходят в заряды отрицательного знака, а также простираются до бесконечности в пространстве. Такое представление позволяет увидеть умом невидимое человеческому глазу электрическое поле. Впрочем, такое представление удобно также и для гравитационных сил и любых других бесконтактных дальнодействующих взаимодействий.
Модель электрических силовых линий включает в себя бесконечное их количество, но слишком высокая плотность изображения силовых линий снижает возможность чтения узоров поля, поэтому их число ограничивается удобочитаемостью.
Правила рисования силовых линий электрического поля
Есть множество правил составления таких моделей электрических силовых линий. Все эти правила созданы для того, чтобы сообщить наибольшую информативность при визуализации (рисовании) электрического поля. Один из способов — это изображение силовых линий. Один из самых распространенных способов — это окружить более заряженные объекты большим количеством линий, то есть большей плотностью линий. Объекты с большим зарядом создают более сильные электрические поля и потому плотность (густота) линий вокруг них больше. Чем ближе к заряду источнику, тем выше плотность силовых линий, и чем больше величина заряда, тем гуще вокруг него линии.
Второе правило для рисования линий электрического поля включает в себя изображение линий другого типа, таких, которые пересекают первые силовые линии перпендикулярно. Такой тип линий именуется эквипотенциальными линиями, а при объемном представлении следует говорить об эквипотенциальных поверхностях. Этот тип линий образует замкнутые контуры и каждая точка на такой эквипотенциальной линии имеет одинаковое значение потенциала поля. Когда какая либо заряженная частица пересекает такие перпендикулярные силовым линиям линии (поверхности), то говорят о совершении зарядом работы. Если же заряд будет двигаться по эквипотенциальным линиям (поверхностям), то хотя он и движется, но работы при этом никакой не совершается. Заряженная частица, оказавшись в электрическом поле другого заряда начинает двигаться, но в статическом электричестве рассматриваются только неподвижные заряды. Движение зарядов называется электрическим током, при этом носителем заряда может совершатся работа.
Важно помнить, что силовые линии электрического поля не пересекаются, а линии другого типа — эквипотенциальные, образуют замкнутые контуры. В том месте, где имеет место пересечение линий двух типов, касательные к этим линиям взаимно перпендикулярны. Таким образом получается нечто вроде искривленной координатной сетки, или решетки, ячейки которой, а также точки пересечения линий разных типов характеризуют электрическое поле.
Пунктирные линии — эквипотенциальные. Линии со стрелками — силовые линии электрического поля
Электрическое поле состоящее из двух и более зарядов
Для уединенных отдельно взятых зарядов силовые линии электрического поля представляют собой радиальные лучи выходящие из зарядов и идущие в бесконечность. Какова будет конфигурация силовых линий для двух и более зарядов? Для выполнения такого узора необходимо помнить, что мы имеем дело с векторным полем, то есть с векторами напряженности электрического поля. Чтобы изобразить рисунок поля, нам необходимо выполнить сложение векторов напряженности от двух и более зарядов. Результирующие векторы будут представлять собой суммарное поле нескольких зарядов. Как в этом случае можно построить силовые линии? Важно помнить, что каждая точка на силовой линии — это единственная точка соприкосновения с вектором напряженности электрического поля. Это следует из определения касательной в геометрии. Если от начала каждого вектора построить перпендикуляр в виде длинных линий, тогда взаимное пересечение многих таких линий изобразит ту самую искомую силовую линию.
Для более точного математического алгебраического изображения силовых линий необходимо составить уравнения силовых линий, а вектора в этом случае будут представлять первые производные, линии первого порядка, которые и есть касательные. Такая задача порой является чрезвычайно сложной и требует компьютерных вычислений.
В первую очередь важно помнить, что электрическое поле от многих зарядов представлено суммой векторов напряженности от каждого источника заряда. Это основа для выполнения построения силовых линий для того чтобы визуализировать электрическое поле.
Каждый внесенный в электрическое поле заряд приводит к изменению, пусть даже незначительному, узора силовых линий. Такие изображения бывают порой очень привлекательными.
Силовые линии электрического поля как способ помочь уму увидеть реальность
Майкл Фарадей
Понятие электрического поля возникло когда ученые пытались объяснить дальнодействие, которое происходит между заряженными объектами. Представление об электрическом поле было впервые введено физиком 19-го века Майклом Фарадеем. Это был результат восприятия Майклом Фарадеем невидимой реальности в виде картины силовых линий характеризующих дальнодействие. Фарадей не стал размышлять в рамках одного заряда, а пошел дальше и расширил границы ума. Он предположил, что заряженный объект (или масса в случае с гравитацией) влияют на пространство и ввел понятие поля такого влияния. Рассматривая такие поля он смог объяснить поведение зарядов и тем самым раскрыл многие секреты электричества.
Электрическое поле относится к такой категории вещей, которые видятся не глазами, а умом. Изображение силового взаимодействия в виде линий разных типов, а также в виде различных цветовых раскрасок — всего лишь способ помочь уму увидеть невидимое. Электростатика изучает неподвижные заряды, но на практике, в реальной жизни, заряды находятся в постоянном движении, что гораздо сложнее для представления картины поля. Получается так, что необходимо видеть в динамике всё то, чем определяется и изображается электрическое поле, но в этом случае больше подходят не отдельно взятые рисунки, а их последовательная анимация.
Дата: 29.04.2015
© Valentin Grigoryev (Валентин Григорьев)
Силовые линии электростатического поля
Теорема Остроградского–Гаусса, которую мы докажем и обсудим позже, устанавливает связь между электрическими зарядами и электрическим полем. Она представляет собой более общую и более изящную формулировку закона Кулона.
| Остроградский Михаил Васильевич (1801 – 1862) отечественный математик и механик. Учился в Харьковском ун-те (1816 – 1820), совершенствовал знания в Париже (1822 – 1827). Основные работы в области математического анализа, математической физики, теоретической механики. Решил ряд важных задач гидродинамики, теории теплоты, упругости, баллистики, электростатики, в частности задачу распространения волн на поверхности жидкости (1826 г.). Получил дифференциальное уравнение распространения тепла в твердых телах и жидкостях. Известен теоремой Остроградского-Гаусса в электростатике (1828 г.). |
| Гаусс Карл Фридрих (1777 – 1855) – немецкий математик, астроном и физик. Исследования посвящены многим разделам физики. В 1832 г. создал абсолютную систему мер (СГС), введя три основных единицы: единицу времени – 1 с, единицу длины – 1 мм, единицу массы – 1 мг, и в 1833 г. совместно с В. Вебером построил первый в Германии электромагнитный телеграф. Еще в 1845 г. пришел к мысли о конечной скорости распространения электромагнитных взаимодействий. |
В принципе, напряженность электростатического поля, создаваемого данным распределением зарядов, всегда можно вычислить с помощью закона Кулона. Полное электрическое поле в любой точке является векторной суммой (интегральным) вкладом всех зарядов, т.е.
| или | (2.1.1) |
Однако, за исключением самых простых случаев, вычислить эту сумму или интеграл крайне сложно.
Здесь приходит на помощь теорема Остроградского-Гаусса, с помощью которой гораздо проще удается рассчитать напряженность электрического поля, создаваемая данным распределением зарядов.
Основная ценность теоремы Остроградского-Гаусса состоит в том, что она позволяет глубже понять природу электростатического поля и устанавливает более общую связь между зарядом и полем.
Но прежде, чем переходить к теореме Остроградского-Гаусса необходимо ввести понятия: силовые линии электростатического поля и поток вектора напряженности электростатического поля.
Для того чтобы описать электрическое поле, нужно задать вектор напряженности в каждой точке поля. Это можно сделать аналитически или графически. Для этого пользуются силовыми линиями – это линии, касательная к которым в любой точке поля совпадает с направлением вектора напряженности (рис. 2.1).
Рис. 2.1
Силовой линии приписывают определенное направление – от положительного заряда к отрицательному, или в бесконечность.
Рассмотрим случай однородного электрического поля.
Однородным называется электростатическое поле, во всех точках которого напряженность одинакова по величине и направлению, т.е. Однородное электростатическое поле изображается параллельными силовыми линиями на равном расстоянии друг от друга (такое поле существует, например, между пластинами конденсатора) (рис. 2.2).
В случае точечного заряда, линии напряженности исходят из положительного заряда и уходят в бесконечность; и из бесконечности входят в отрицательный заряд. Т.к. то и густота силовых линий обратно пропорциональна квадрату расстояния от заряда. Т.к. площадь поверхности сферы, через которую проходят эти линии сама возрастает пропорционально квадрату расстояния, то общее число линий остается постоянным на любом расстоянии от заряда.
Для системы зарядов, как видим, силовые линии направлены от положительного заряда к отрицательному (рис. 2.2).
Рис. 2.2
Из рисунка 2.3 видно, так же, что густота силовых линий может служить показателем величины .
Густота силовых линий должна быть такой, чтобы единичную площадку, нормальную к вектору напряженности пересекало такое их число, которое равно модулю вектора напряженности , т.е.
Пример 1: если на рисунке 2.3 выделить площадку, то напряженность изображенного поля будет равна
| Рис. 2.3 | Рис. 2.4 |
Пример 2: площадка находится в однородном поле Сколько линий пересекает эту площадку, если угол составляет 30º (рис. 2.4).
, отсюда линий.
1.5. Графическое изображение электрических полей. Силовые линии и эквипотенциальные поверхности

Силовые линии – это непрерывные линии, касательные к которым в каждой точке, через которую они проходят, совпадают с вектором напряженности электрического поля (рис. 1.5). Густота силовых линий (число силовых линий, проходящих через единицу площади) пропорциональна напряженности электрического поля.
Эквипотенциальные поверхности (эквипотенциали) – поверхности равного потенциала. Это поверхности (линии), при движении по которым потенциал не меняется. Иначе, разность потенциалов между двумя любыми точками эквипотенциальной поверхности равна нулю. Силовые линии перпендикулярны эквипотенциальным поверхностям и направлены в сторону наиболее резкого убывания потенциала. Этот факт следует из уравнения (1.10) и доказывается в курсе математического анализа разделе «Скалярные и векторные поля».
Рассмотрим
в качестве примера электрическое поле,
создаваемое на расстоянии 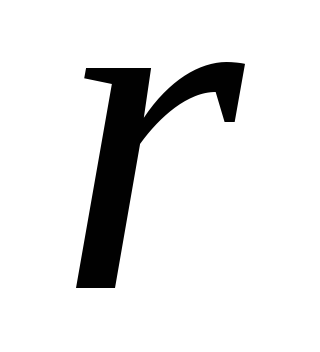 от точечного заряда. Согласно (1.11,б)
вектор напряженности совпадает с
направлением вектора
от точечного заряда. Согласно (1.11,б)
вектор напряженности совпадает с
направлением вектора ,
если заряд положительный, и противоположен
ему, если заряд отрицательный.
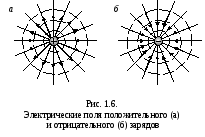
Следовательно, силовые линии расходятся
радиально от заряда (рис. 1.6, а, б). Густота
силовых линий, как и напряженность,
обратно пропорциональна квадрату
расстояния (
,
если заряд положительный, и противоположен
ему, если заряд отрицательный.
Следовательно, силовые линии расходятся
радиально от заряда (рис. 1.6, а, б). Густота
силовых линий, как и напряженность,
обратно пропорциональна квадрату
расстояния (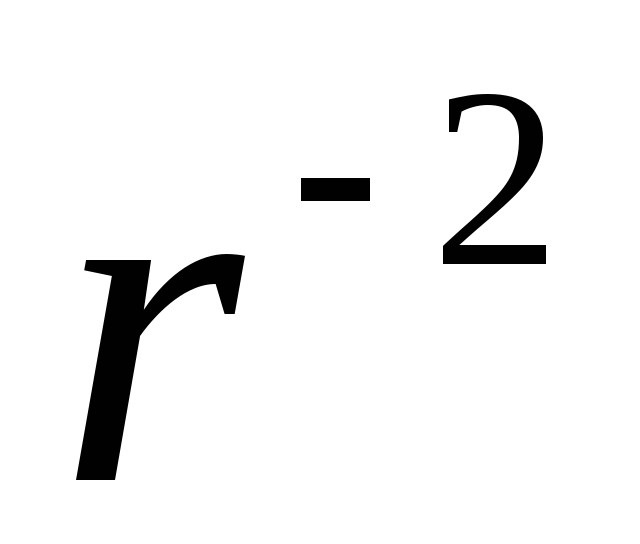 )
до заряда. Эквипотенциальные поверхности
электрического поля точечного заряда
представляют собой сферы с центром в
месте расположения заряда.
)
до заряда. Эквипотенциальные поверхности
электрического поля точечного заряда
представляют собой сферы с центром в
месте расположения заряда.
1.6. Теорема Гаусса для электрического поля в вакууме
Основной задачей электростатики является задача о нахождении напряженности и потенциала электрического поля в каждой точке пространства. В п. 1.4 мы решили задачу о поле точечного заряда, а также рассмотрели поле системы точечных зарядов. В этом параграфе речь пойдет о теореме, позволяющей рассчитывать электрическое поле более сложных заряженных объектов. Например, заряженной длинной нити (прямой), заряженной плоскости, заряженной сферы и других. Рассчитав напряженность электрического поля в каждой точке пространства, используя уравнения (1.12) и (1.13), можно вычислить потенциал в каждой точке или разность потенциалов между двумя любыми точками, т.е. решить основную задачу электростатики.
Для
математического описания введем понятие
потока вектора напряженности или потока
электрического поля. Потоком (Ф) вектора  электрического поля через плоскую
поверхность площади
электрического поля через плоскую
поверхность площади называется величина:
называется величина:
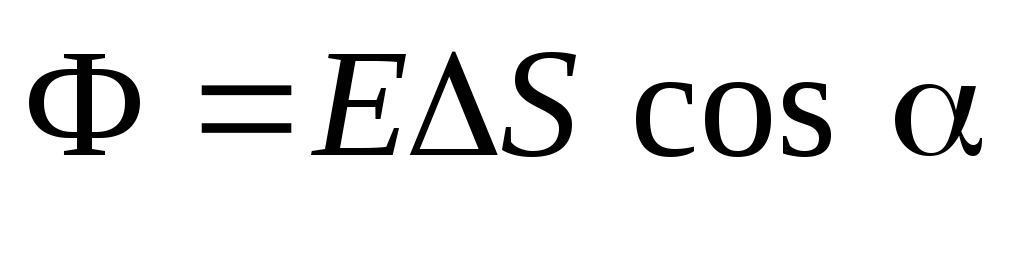 ,
(1.16)
,
(1.16)
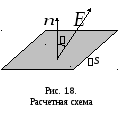
 – напряженность электрического поля,
которая предполагается постоянной в
пределах площадки
– напряженность электрического поля,
которая предполагается постоянной в
пределах площадки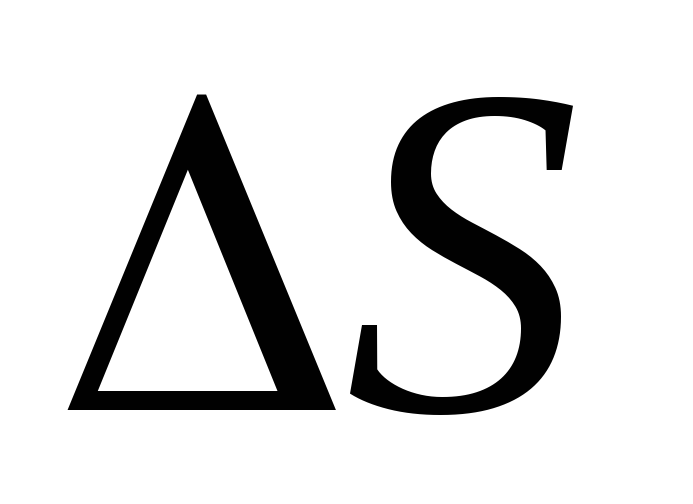 ;
; –
угол между направлением вектора
–
угол между направлением вектора и единичного вектора нормали
и единичного вектора нормали к площадке
к площадке (рис. 1.8). Формулу (1.16) можно записать,
используя понятие скалярного произведения
векторов:
(рис. 1.8). Формулу (1.16) можно записать,
используя понятие скалярного произведения
векторов:  . (1.15,а)
. (1.15,а)
В
случае, когда поверхность  не плоская, для вычисления потока ее
необходимо разделить на малые части
не плоская, для вычисления потока ее
необходимо разделить на малые части ,
которые можно приблизительно считать
плоскими, а затем записать выражение
(1.16) или (1.16,а) для каждого куска поверхности
и сложить их. В пределе, когда поверхностьSi очень мала (
,
которые можно приблизительно считать
плоскими, а затем записать выражение
(1.16) или (1.16,а) для каждого куска поверхности
и сложить их. В пределе, когда поверхностьSi очень мала (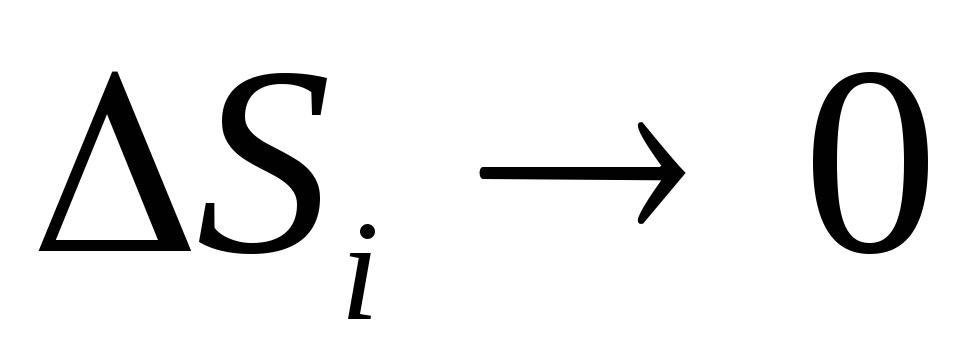 ),
такую сумму называют поверхностным
интегралом и обозначают
),
такую сумму называют поверхностным
интегралом и обозначают .
Таким образом, поток вектора напряженности
электрического поля через произвольную
поверхность
.
Таким образом, поток вектора напряженности
электрического поля через произвольную
поверхность определяется выражением:
определяется выражением:
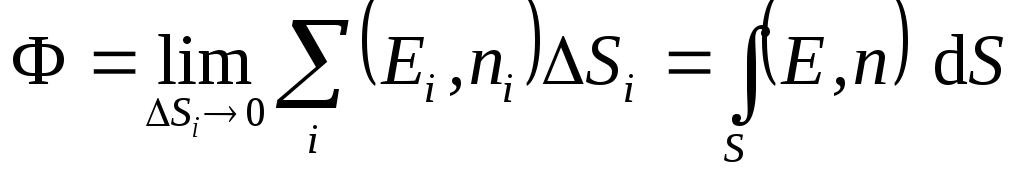 .
(1.17)
.
(1.17)
В
качестве примера рассмотрим сферу
радиуса 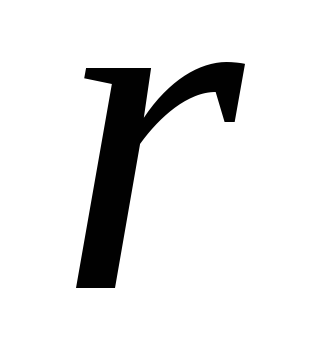 ,
центром которой служит положительный
точечный заряд
,
центром которой служит положительный
точечный заряд  ,
и определим поток электрического поля
через поверхность этой сферы. Силовые
линии (см., например, рис.1.6, а) выходящие
из заряда, перпендикулярны поверхности
сферы, и в каждой точке сферы модуль
напряженности поля один и тот же
,
и определим поток электрического поля
через поверхность этой сферы. Силовые
линии (см., например, рис.1.6, а) выходящие
из заряда, перпендикулярны поверхности
сферы, и в каждой точке сферы модуль
напряженности поля один и тот же
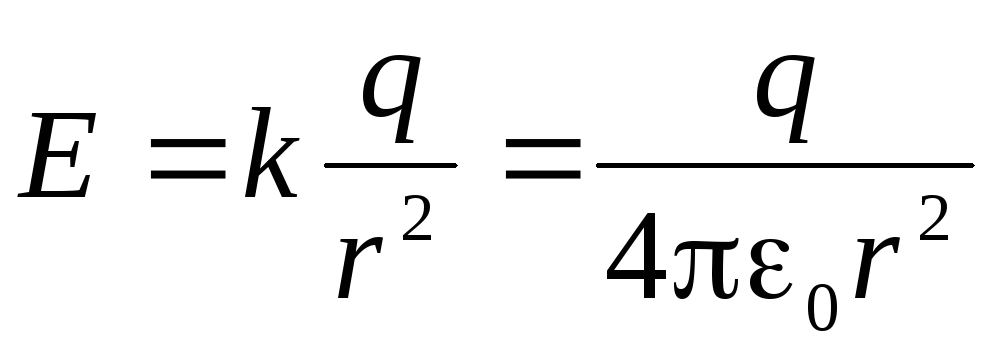 .
.
Площадь
сферы  ,
,
тогда 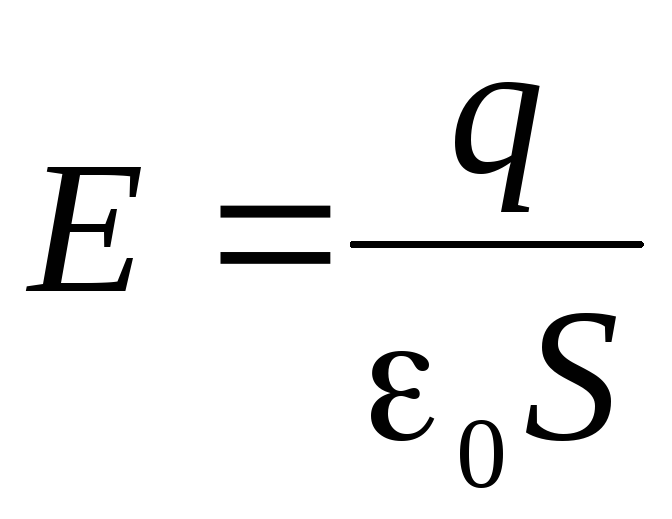

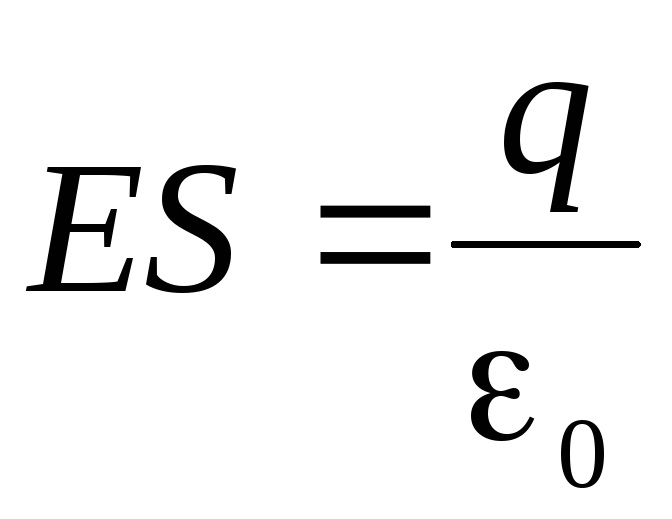 .
.
Величина  и представляет собой поток электрического
поля через поверхность сферы. Таким
образом, получаем
и представляет собой поток электрического
поля через поверхность сферы. Таким
образом, получаем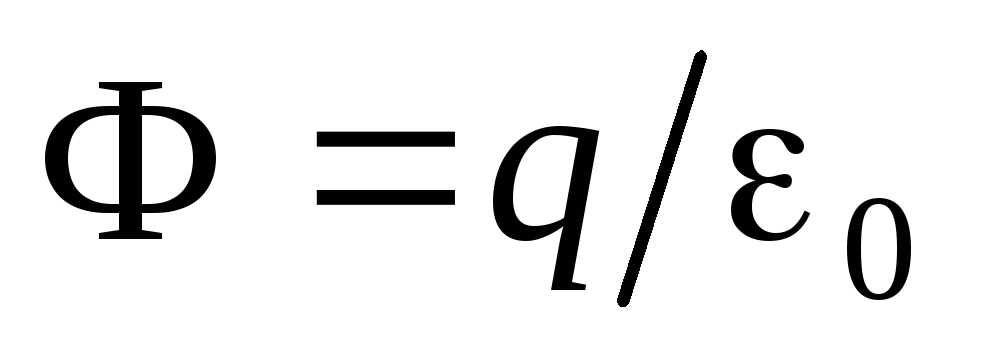 .
Видно, что поток через поверхность сферы
электрического поля не зависит от
радиуса сферы, а зависит только от самого
заряда
.
Видно, что поток через поверхность сферы
электрического поля не зависит от
радиуса сферы, а зависит только от самого
заряда .
Поэтому, если провести ряд концентрических
сфер, то поток электрического поля через
все эти сферы будет одинаковым. Очевидно,
что число силовых линий, пересекающих
эти сферы, тоже будет одинаковым.
Условились число силовых линий, выходящих
из заряда, принимать равным потоку
электрического поля:
.
Поэтому, если провести ряд концентрических
сфер, то поток электрического поля через
все эти сферы будет одинаковым. Очевидно,
что число силовых линий, пересекающих
эти сферы, тоже будет одинаковым.
Условились число силовых линий, выходящих
из заряда, принимать равным потоку
электрического поля: .
.
Если
сферу заменить любой другой замкнутой
поверхностью, то поток электрического
поля и число силовых линий, пересекающих
ее, не изменятся. Кроме того, поток
электрического поля через замкнутую
поверхность, а значит и число силовых
линий, пронизывающих эту поверхность,
равняется 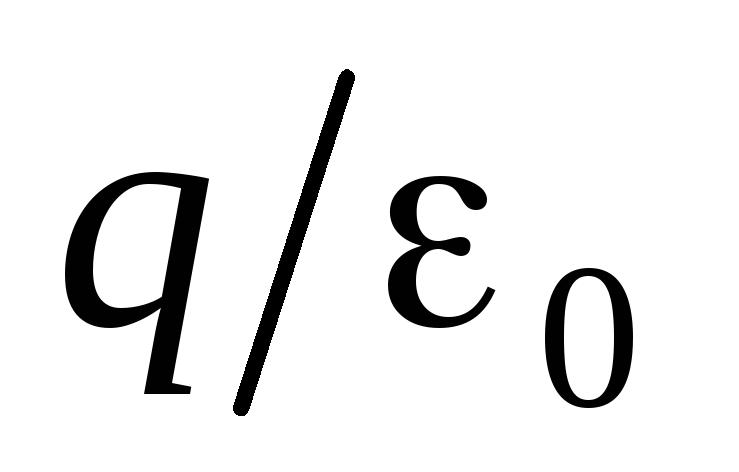 не только для поля точечного заряда, но
и для поля, создаваемого любой совокупностью
точечных зарядов, в частности – заряженным
телом. Тогда величину
не только для поля точечного заряда, но
и для поля, создаваемого любой совокупностью
точечных зарядов, в частности – заряженным
телом. Тогда величину следует считать как алгебраическую
сумму всей совокупности зарядов,
находящихся внутри замкнутой поверхности.
В этом и состоит суть теоремы Гаусса,
которая формулируется так:
следует считать как алгебраическую
сумму всей совокупности зарядов,
находящихся внутри замкнутой поверхности.
В этом и состоит суть теоремы Гаусса,
которая формулируется так:
Поток
вектора напряженности электрического
поля через произвольную замкнутую поверхность
равняется 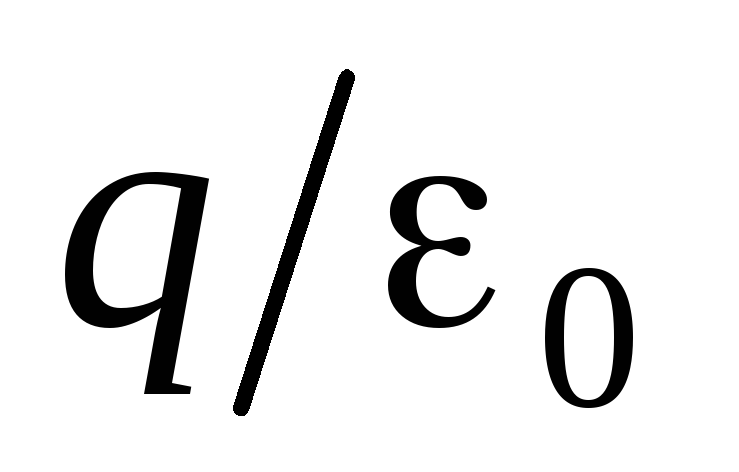 ,
где
,
где  алгебраическая сумма зарядов, заключенных внутри этой
поверхности.
алгебраическая сумма зарядов, заключенных внутри этой
поверхности.
Математически теорему можно записать в виде
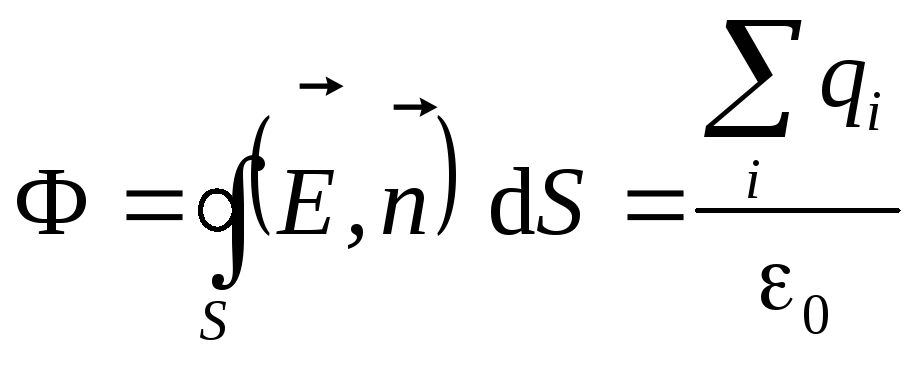 .
(1.18)
.
(1.18)
Отметим,
что если на некоторой поверхности S вектор  постоянен и параллелен вектору
постоянен и параллелен вектору ,
то поток через такую поверхность
,
то поток через такую поверхность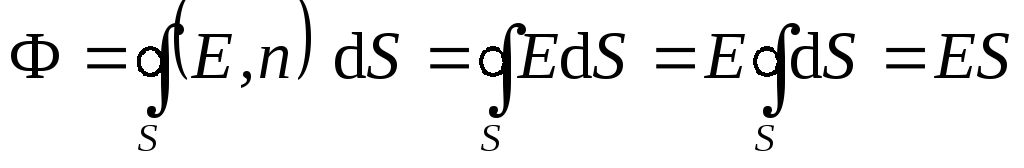 .
Преобразуя первый интеграл, мы сначала
воспользовались тем, что векторы
.
Преобразуя первый интеграл, мы сначала
воспользовались тем, что векторы и
и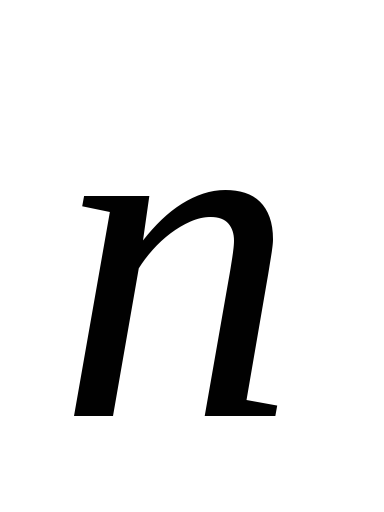 параллельны, а значит
параллельны, а значит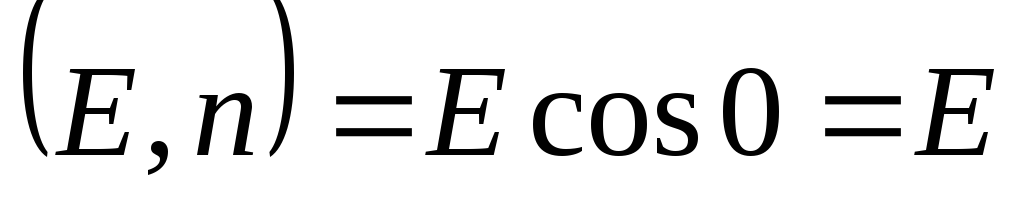 .
Затем вынесли величину
.
Затем вынесли величину за знак интеграла в силу того, что она
постоянна в любой точке сферы
за знак интеграла в силу того, что она
постоянна в любой точке сферы .
Применяя теорему Гаусса для решения
конкретных задач, специально в качестве
произвольной замкнутой поверхности
стараются выбирать поверхность, для
которой выполняются описанные выше
условия.
.
Применяя теорему Гаусса для решения
конкретных задач, специально в качестве
произвольной замкнутой поверхности
стараются выбирать поверхность, для
которой выполняются описанные выше
условия.
Приведем несколько примеров на применение теоремы Гаусса.
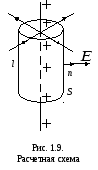
Решение. Предположим для определенности, что
нить заряжена положительно. В силу
симметрии задачи можно утверждать, что
силовые линии будут радиально расходящимися
от оси нити прямыми (рис.1.9), густота
которых по мере удаления от нити
уменьшается по какому-то закону. По
этому же закону будет уменьшаться и
величина электрического поля 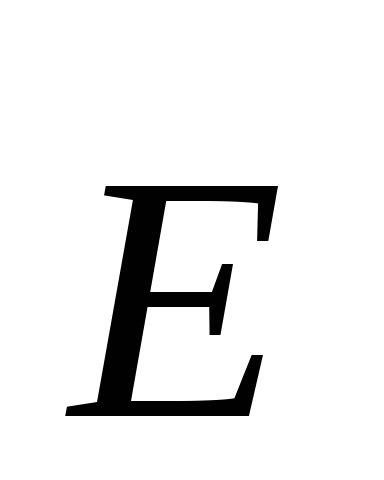 .
Эквипотенциальными поверхностями
будут цилиндрические поверхности с
осью, совпадающей с нитью.
.
Эквипотенциальными поверхностями
будут цилиндрические поверхности с
осью, совпадающей с нитью.
Пусть
заряд единицы длины нити равен  .
Эта величина называется линейной
плотностью заряда и измеряется в СИ в
единицах [Кл/м]. Для расчета напряженности
поля применим теорему Гаусса. Для этого
в качестве произвольной замкнутой
поверхности
.
Эта величина называется линейной
плотностью заряда и измеряется в СИ в
единицах [Кл/м]. Для расчета напряженности
поля применим теорему Гаусса. Для этого
в качестве произвольной замкнутой
поверхности выберем цилиндр радиуса
выберем цилиндр радиуса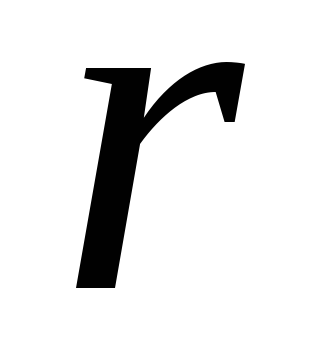 и длины
и длины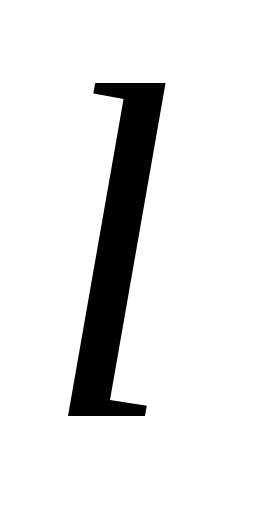 ,
ось которого совпадает с нитью (рис.1.9).
Вычислим поток электрического поля
через площадь поверхности цилиндра.
Полный поток складывается из потока
через боковую поверхность цилиндра и
потока через основания
,
ось которого совпадает с нитью (рис.1.9).
Вычислим поток электрического поля
через площадь поверхности цилиндра.
Полный поток складывается из потока
через боковую поверхность цилиндра и
потока через основания
 .
.
Однако,  ,
поскольку в любой точке на основаниях
цилиндра
,
поскольку в любой точке на основаниях
цилиндра .
Это значит, что
.
Это значит, что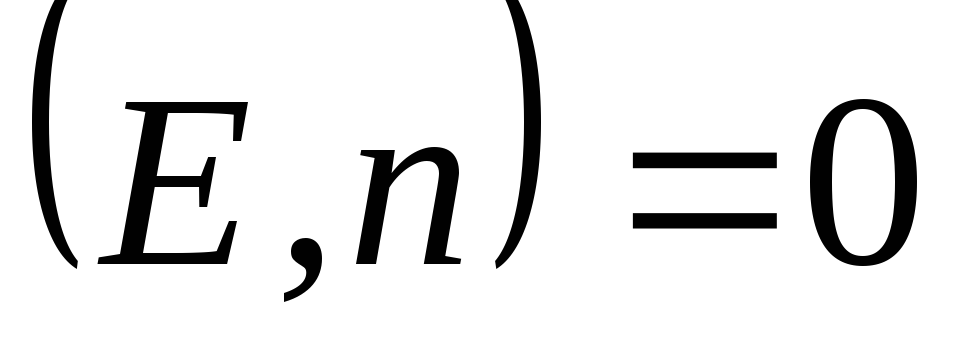 в этих точках. Поток через боковую
поверхность
в этих точках. Поток через боковую
поверхность .
По теореме Гаусса этот полный поток
равен
.
По теореме Гаусса этот полный поток
равен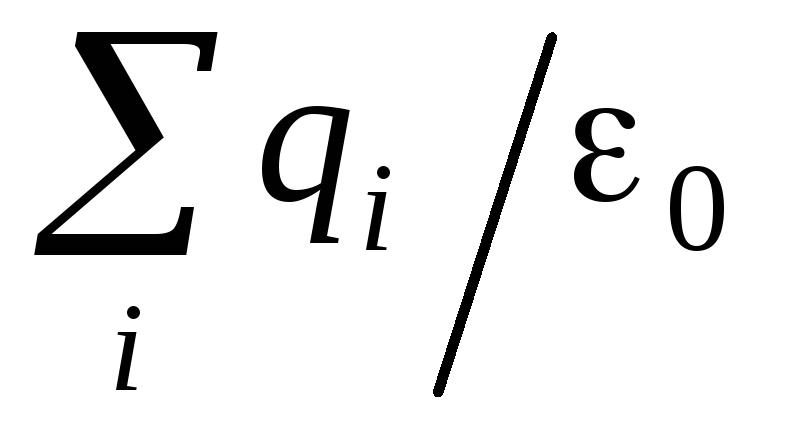 .
Таким образом, получили
.
Таким образом, получили
 .
.
Сумма
зарядов, находящихся внутри цилиндра,
выразим через линейную плотность заряда  :
: .
Учитывая, что
.
Учитывая, что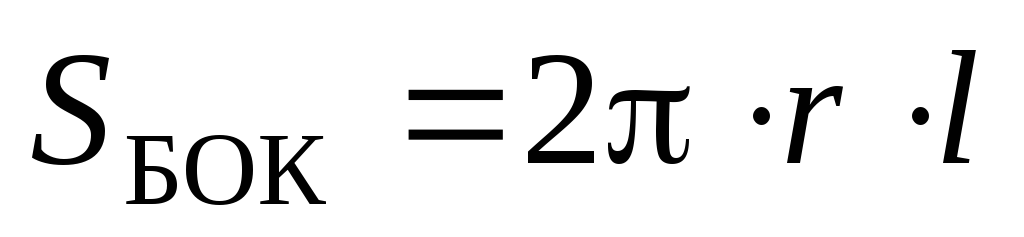 ,
получим
,
получим
 ,
,
откуда:
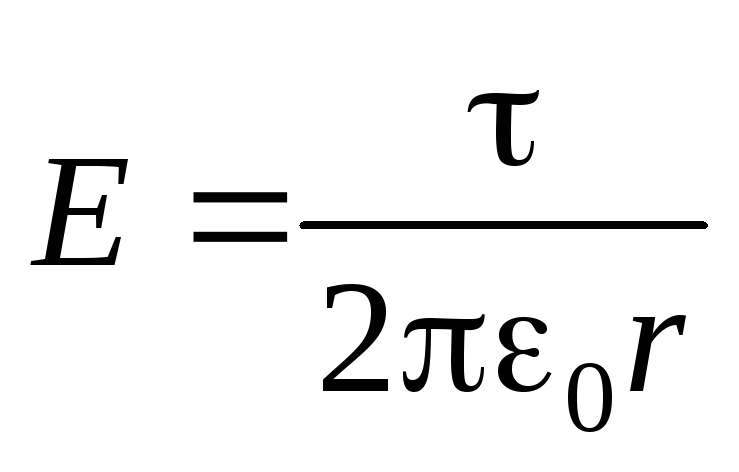 ,
(1.19)
,
(1.19)
т.е.
напряженность и густота силовых линий
электрического поля равномерно заряженной
бесконечной нити убывает обратно
пропорционально расстоянию (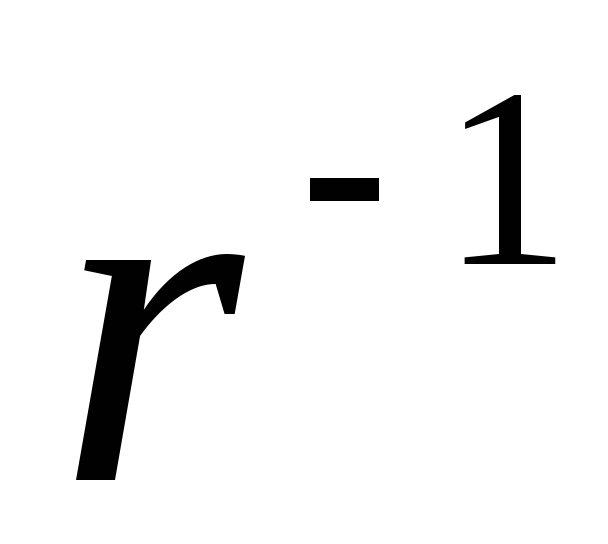 ).
).
Найдем
разность потенциалов между точками,
находящимися на расстояниях  и
и от нити (принадлежащими эквипотенциальным
цилиндрическим поверхностям с радиусами
от нити (принадлежащими эквипотенциальным
цилиндрическим поверхностям с радиусами и
и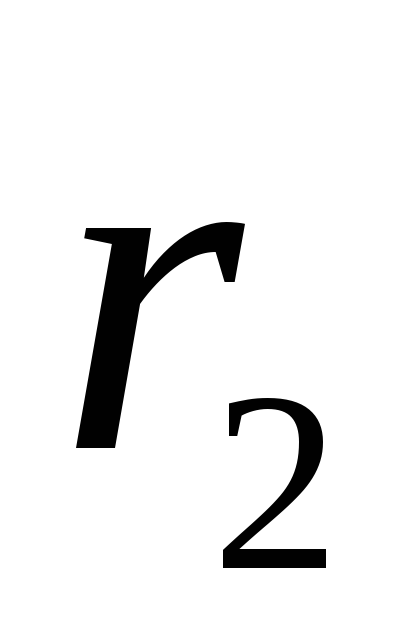 ).
Для этого воспользуемся связью
напряженности электрического поля с
потенциалом в виде (1.9,в):
).
Для этого воспользуемся связью
напряженности электрического поля с
потенциалом в виде (1.9,в): .
Учитывая выражение (1.19), получим
дифференциальное уравнение с разделяющимися
переменными:
.
Учитывая выражение (1.19), получим
дифференциальное уравнение с разделяющимися
переменными:
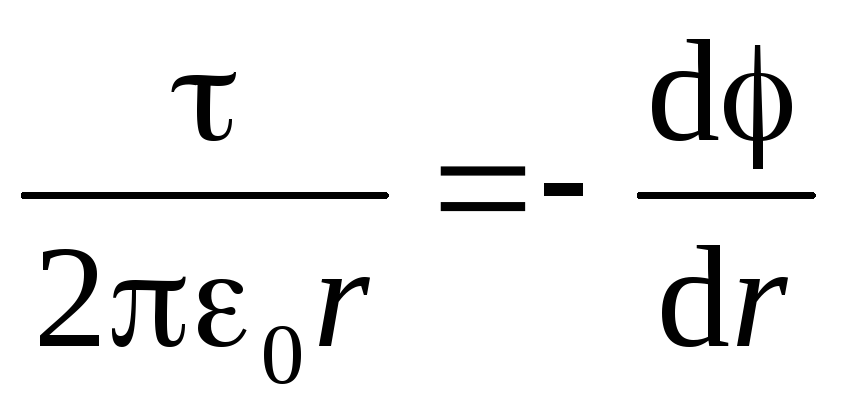





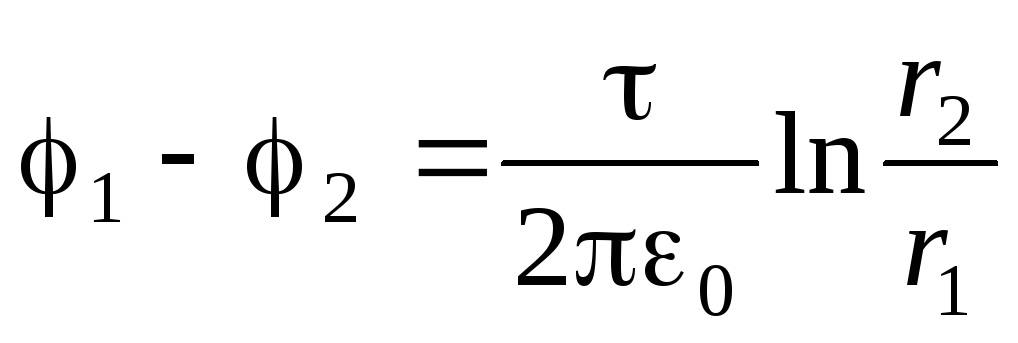 .
.

Решение. Электрическое поле равномерно
заряженной плоскости показано на рис.
1.10. В силу симметрии силовые линии должны
быть перпендикулярны плоскости. Поэтому
сразу можно сделать вывод о том, что
густота линий, а, следовательно,
и напряженность электрического поля
при удалении от плоскости меняться не
будут. Эквипотенциальные поверхности
представляют собой плоскости,
параллельные данной заряженной плоскости.
Пусть заряд единицы площади плоскости
равен  .
Эта величина называется поверхностной
плотностью заряда и измеряется в СИ в
единицах [Кл/м2].
.
Эта величина называется поверхностной
плотностью заряда и измеряется в СИ в
единицах [Кл/м2].
Применим
теорему Гаусса. Для этого в качестве
произвольной замкнутой поверхности  выберем цилиндр длиной
выберем цилиндр длиной ,
ось которого перпендикулярна плоскости,
а основания равноудалены от нее
(рис.1.10). Общий поток электрического
поля
,
ось которого перпендикулярна плоскости,
а основания равноудалены от нее
(рис.1.10). Общий поток электрического
поля .
Поток через боковую поверхность равен
нулю. Поток через каждое из оснований
равен
.
Поток через боковую поверхность равен
нулю. Поток через каждое из оснований
равен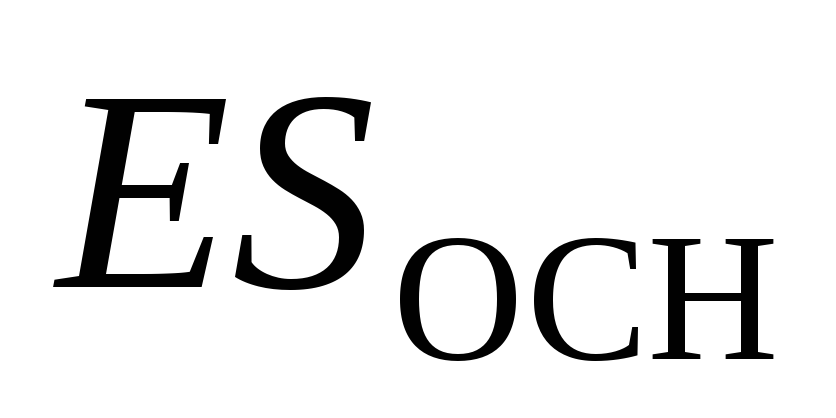 ,
поэтому
,
поэтому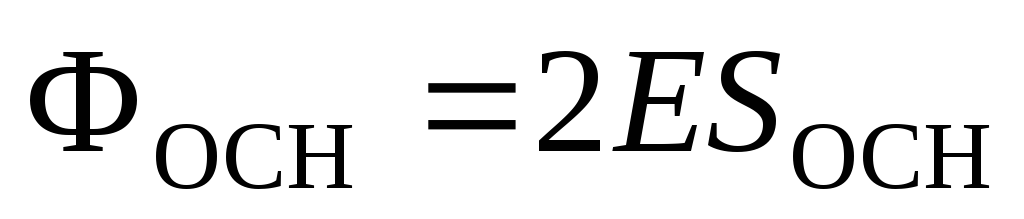 .
По теореме Гаусса получим:
.
По теореме Гаусса получим:
 .
.
Сумму
зарядов, находящихся внутри цилиндра  ,
найдем через поверхностную плотность
заряда
,
найдем через поверхностную плотность
заряда :
: .
Тогда
.
Тогда ,
откуда:
,
откуда:
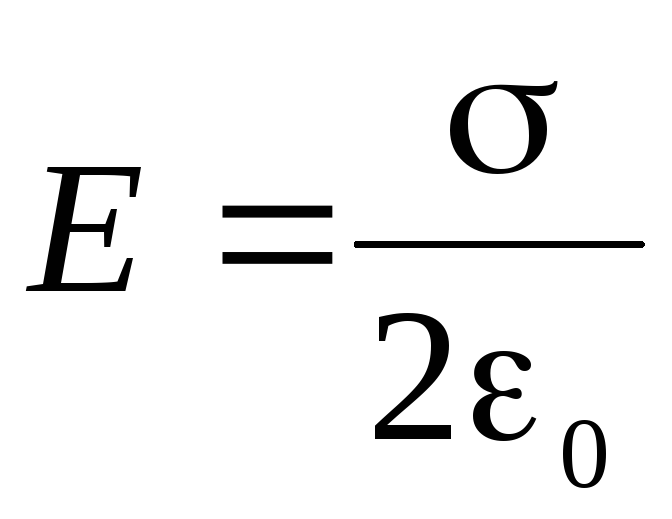 .
(1.20)
.
(1.20)
Из полученной формулы видно, что напряженность поля равномерно заряженной плоскости не зависит от расстояния до заряженной плоскости, т.е. в любой точке пространства (в одной полуплоскости) одинакова и по модулю, и по направлению. Такое поле называется однородным. Силовые линии однородного поля параллельны, их густота не меняется.
Найдем
разность потенциалов между двумя точками
однородного поля (принадлежащим
эквипотенциальным плоскостям  и
и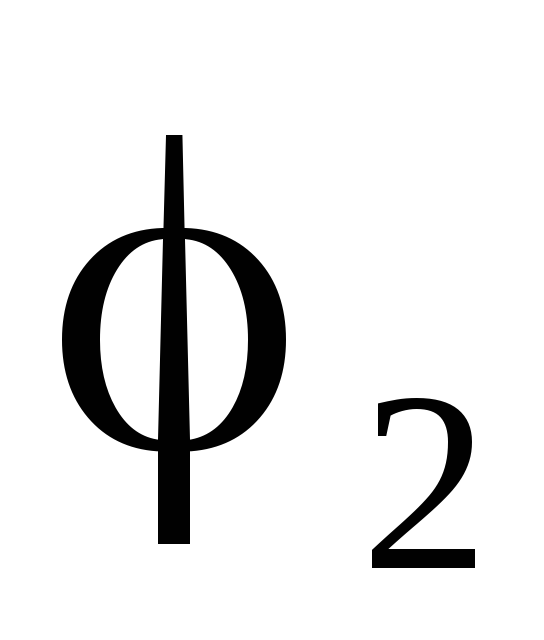 ,
лежащим в одной полуплоскости относительно
заряженной плоскости (рис.1.10)). Направим
ось
,
лежащим в одной полуплоскости относительно
заряженной плоскости (рис.1.10)). Направим
ось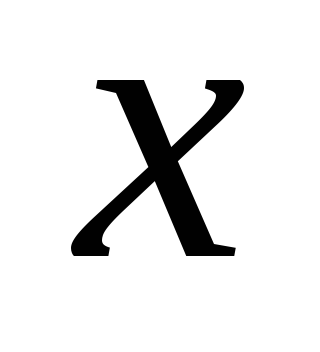 вертикально вверх, тогда проекция
вектора напряженности на эту ось равна
модулю вектора напряженности
вертикально вверх, тогда проекция
вектора напряженности на эту ось равна
модулю вектора напряженности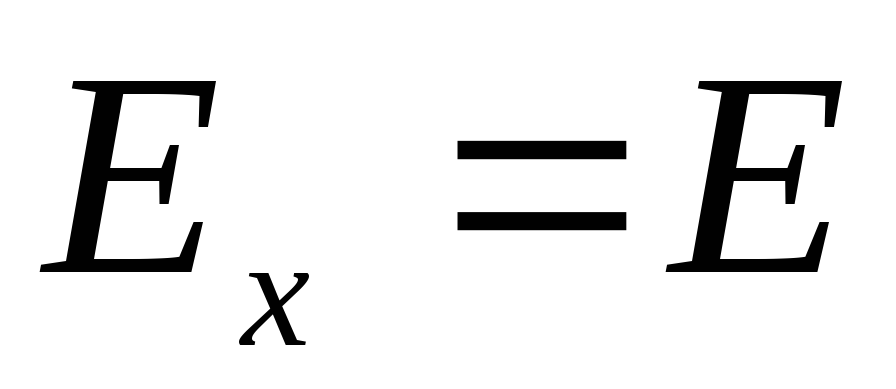 .
Воспользуемся уравнением (1.9):
.
Воспользуемся уравнением (1.9):
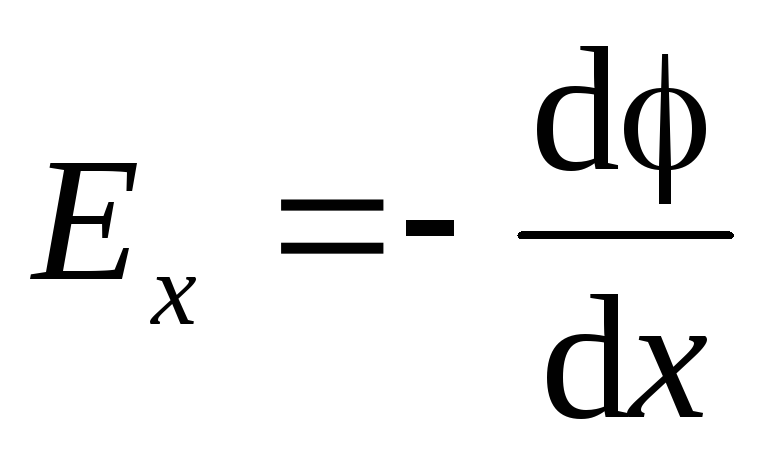

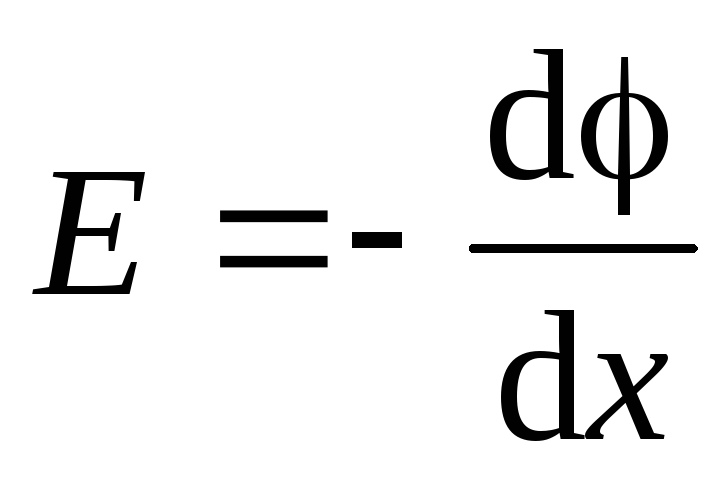



 .
.
Постоянную
величину  (поле однородно) можно вынести из под
знака интеграла:
(поле однородно) можно вынести из под
знака интеграла: 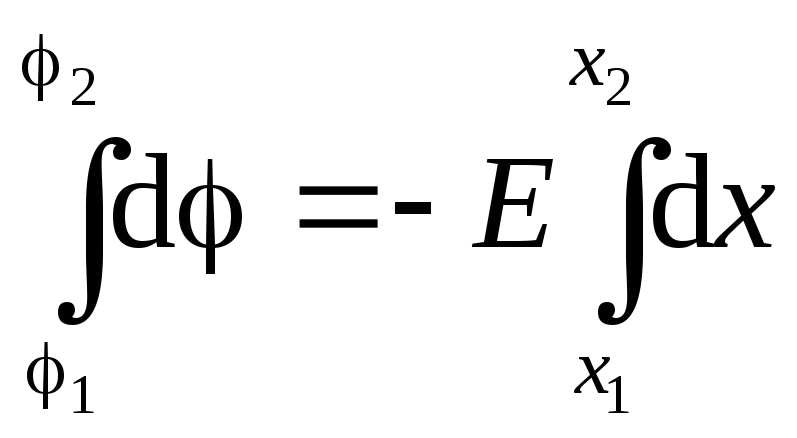 .
Интегрируя, получаем:
.
Интегрируя, получаем:  .
Итак, потенциал однородного поля линейно
зависит от координаты.
.
Итак, потенциал однородного поля линейно
зависит от координаты.
Разность
потенциалов между двумя точками
электрического поля – есть напряжение
между этими точками (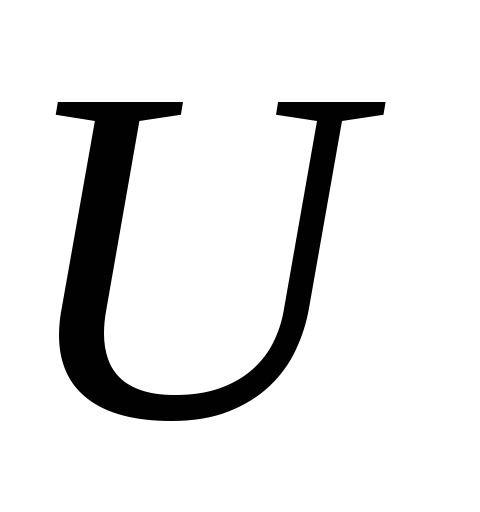 ).
Обозначим расстояние между эквипотенциальными
плоскостями
).
Обозначим расстояние между эквипотенциальными
плоскостями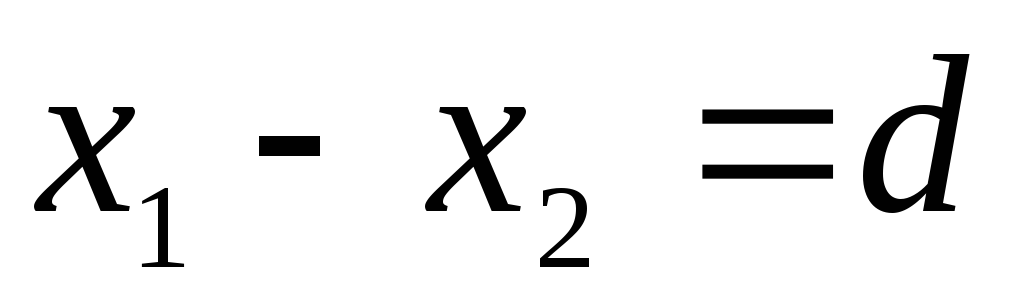 .
Тогда можно записать, что в однородном
электрическом поле:
.
Тогда можно записать, что в однородном
электрическом поле:
 .
(1.21)
.
(1.21)
Еще
раз подчеркнем, что при использовании
формулы (1.21) нужно помнить, что величина 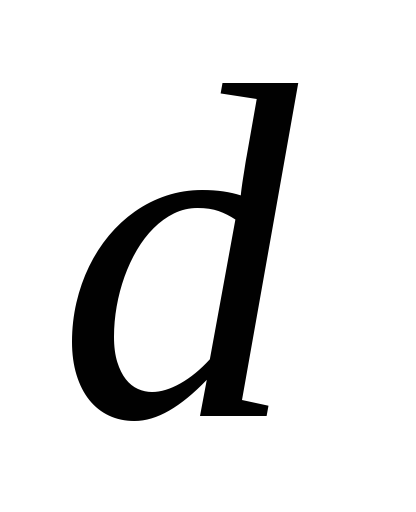
не расстояние между точками 1 и 2, а
расстояние между эквипотенциальными
плоскостями, которым эти точки принадлежат.
не расстояние между точками 1 и 2, а
расстояние между эквипотенциальными
плоскостями, которым эти точки принадлежат.
 и
и .
. Решение. Воспользуемся
результатом примера 1.3 и принципом
суперпозиции. Согласно этому
принципу результирующее электрическое
поле в любой точке пространства 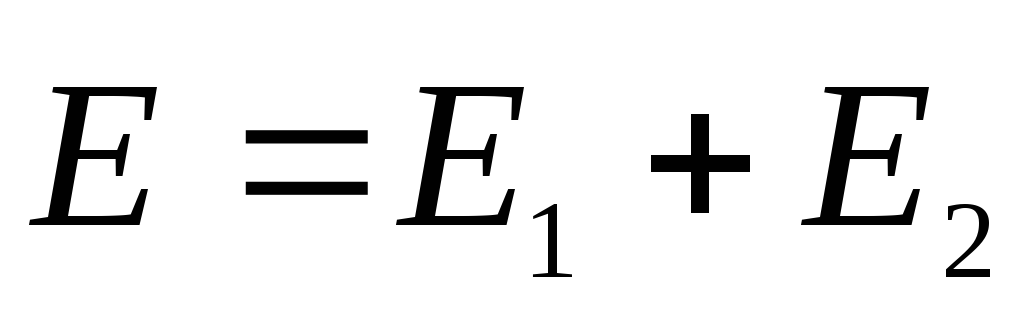 ,
где
,
где и
и — напряженности электрических полей
первой и второй плоскости. В пространстве
между плоскостями вектора
— напряженности электрических полей
первой и второй плоскости. В пространстве
между плоскостями вектора и
и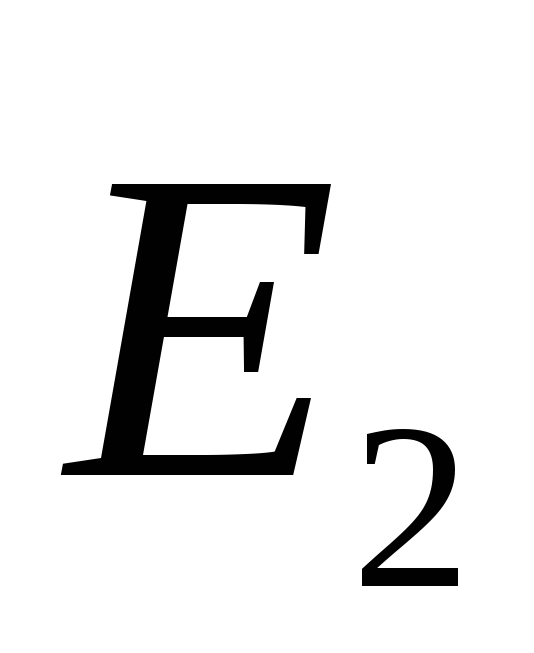 направлены в одну сторону, поэтому
модуль напряженности результирующего
поля
направлены в одну сторону, поэтому
модуль напряженности результирующего
поля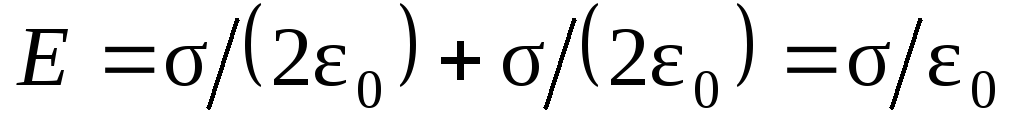 .
Во внешнем пространстве вектора
.
Во внешнем пространстве вектора и
и направлены в разные стороны, поэтому
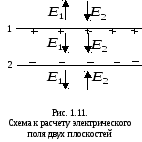
направлены в разные стороны, поэтому (рис. 1.11). Таким образом, электрическое
поле есть только в пространстве между
плоскостями. Оно однородно, так как
является суммой двух однородных полей.
(рис. 1.11). Таким образом, электрическое
поле есть только в пространстве между
плоскостями. Оно однородно, так как
является суммой двух однородных полей.
Пример
1.5. Найти
напряженность и потенциал электрического
поля равномерно заряженной сферы.
Суммарный заряд сферы равен  ,
а радиус сферы –
,
а радиус сферы –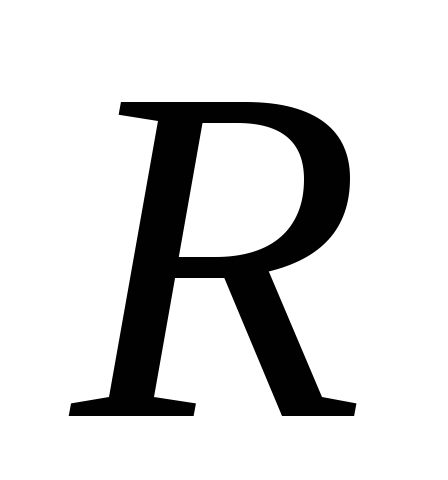 .
.
Решение. В силу симметрии распределения заряда силовые линии должны быть направлены вдоль радиусов сферы.
Рассмотрим
область внутри сферы. В качестве
произвольной поверхности  выберем сферу радиуса
выберем сферу радиуса ,
центр которой совпадает с центром
заряженной сферы. Тогда поток электрического
поля через сферуS:
,
центр которой совпадает с центром
заряженной сферы. Тогда поток электрического
поля через сферуS:  .
Сумма зарядов внутри сферы
.
Сумма зарядов внутри сферы радиуса
радиуса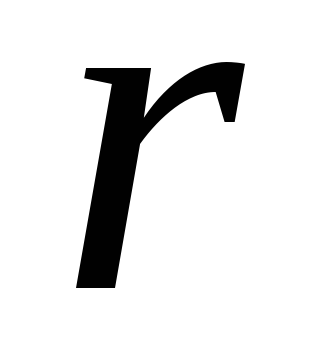 равна нулю, поскольку все заряды
располагаются на поверхности сферы
радиуса
равна нулю, поскольку все заряды
располагаются на поверхности сферы
радиуса  .
Тогда по теореме Гаусса:
.
Тогда по теореме Гаусса: 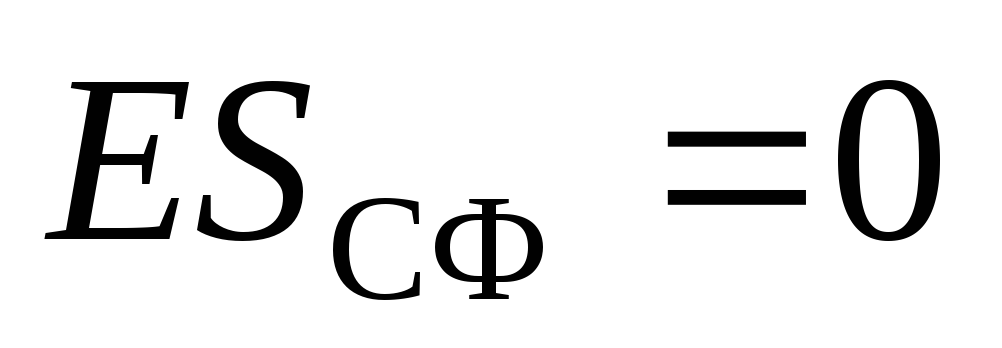 .
Поскольку
.
Поскольку ,
то
,
то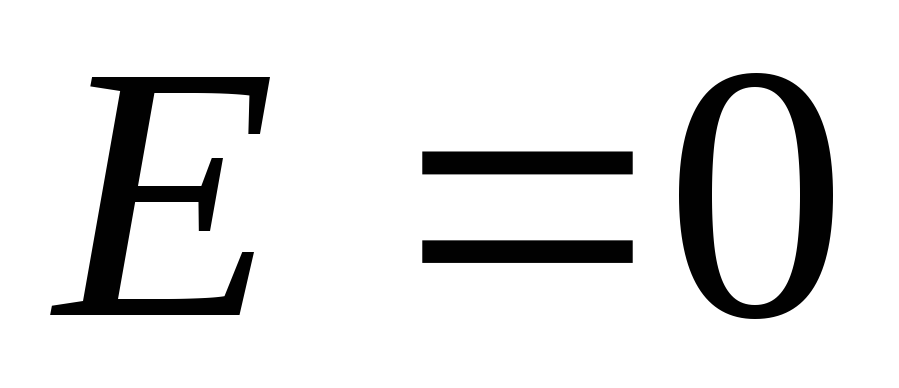 .
Таким образом внутри равномерно
заряженной сферы поля нет.
.
Таким образом внутри равномерно
заряженной сферы поля нет.
Рассмотрим
область вне сферы. В качестве произвольной
поверхности  выберем сферу радиуса
выберем сферу радиуса ,
центр которой совпадает с центром
заряженной сферы. Поток электрического
поля через сферу
,
центр которой совпадает с центром
заряженной сферы. Поток электрического
поля через сферу :
: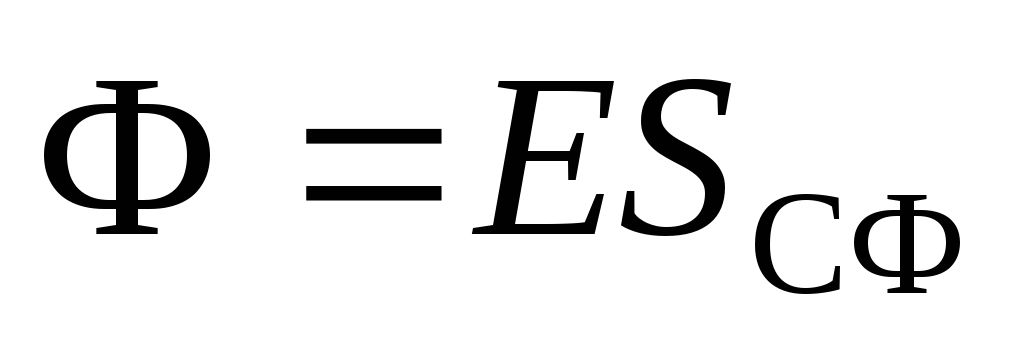 .
Сумма зарядов внутри сферы равна полному
заряду
.
Сумма зарядов внутри сферы равна полному
заряду заряженной сферы радиуса
заряженной сферы радиуса .
Тогда по теореме Гаусса:
.
Тогда по теореме Гаусса: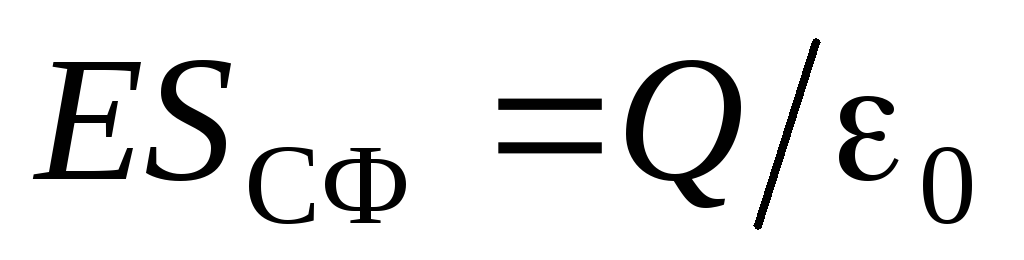 .
Учитывая, что
.
Учитывая, что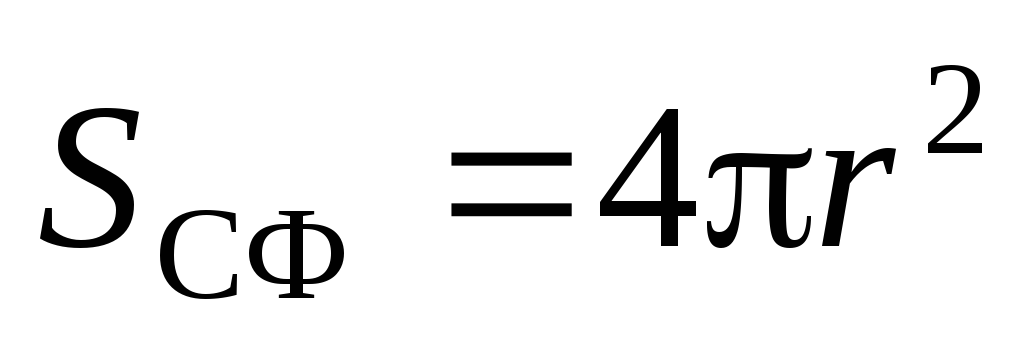 ,
получим:
,
получим:
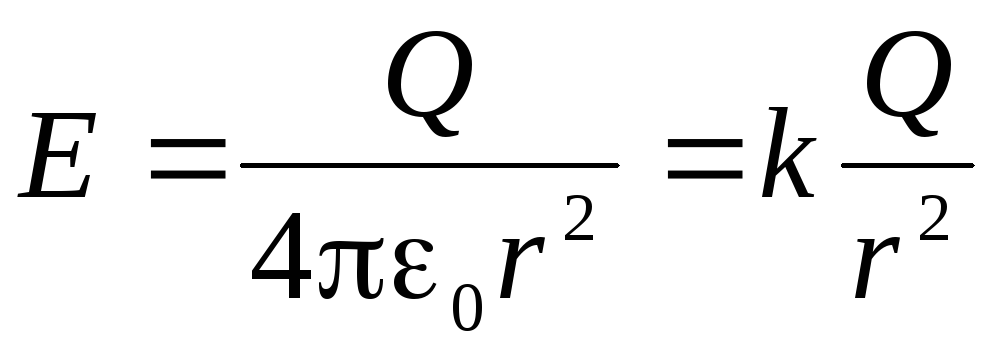 .
.
Рассчитаем потенциал электрического поля. Удобнее начать с внешней области , поскольку мы знаем, что на бесконечном расстоянии от центра сферы потенциал принимается равным нулю. Используя уравнение (1.11,а) получаем дифференциальное уравнение с разделяющимися переменными:




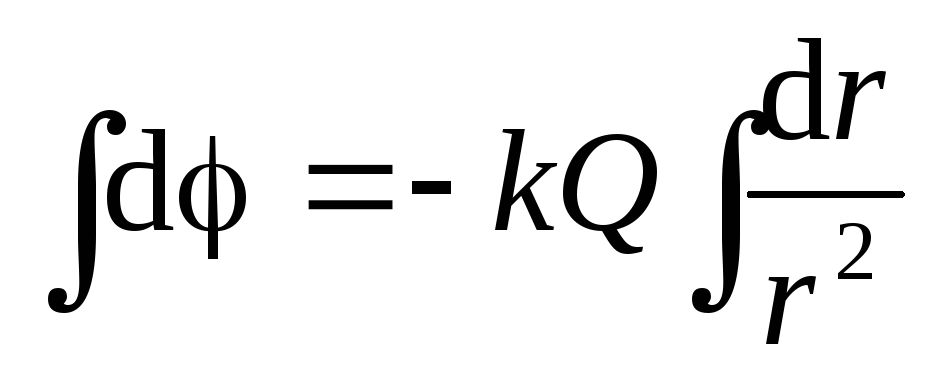

 .
.
Константа  ,
поскольку
,
поскольку при
при .
Таким образом, во внешнем пространстве
(
.
Таким образом, во внешнем пространстве
( ):
):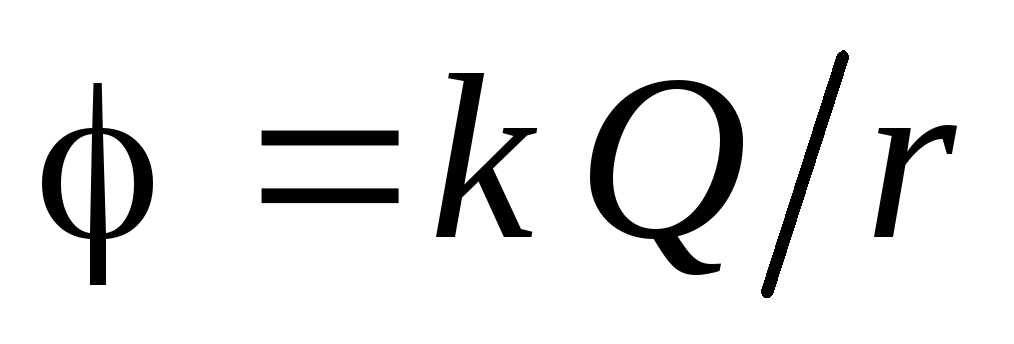 .
.
Точки
на поверхности заряженной сферы (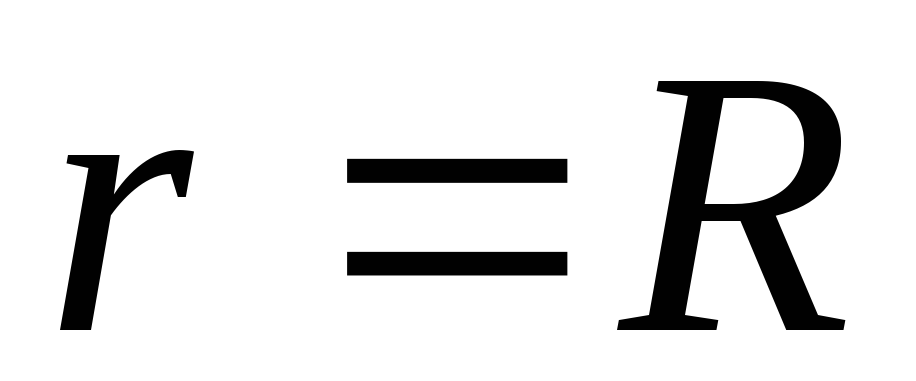 )
будут иметь потенциал
)
будут иметь потенциал .
.
Рассмотрим
область  .
В этой области
.
В этой области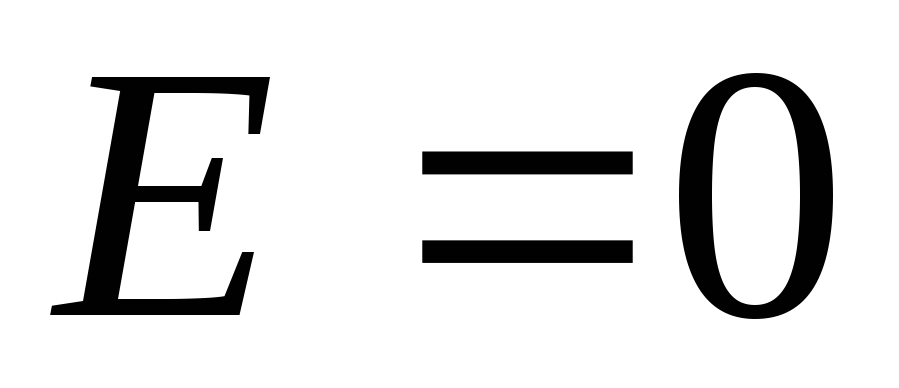 ,
поэтому из уравнения (1.11,а) получаем:
,
поэтому из уравнения (1.11,а) получаем: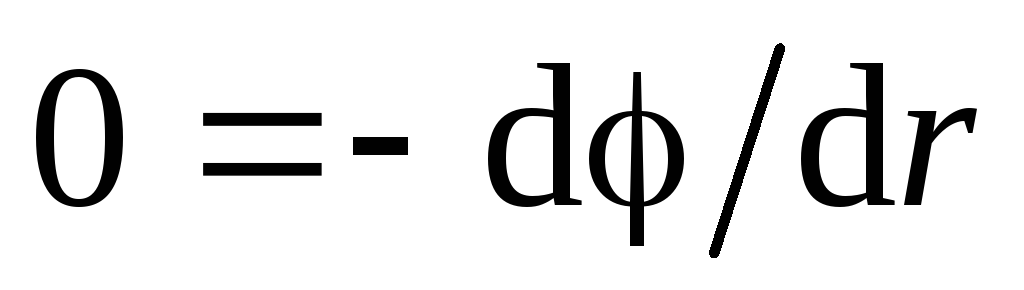

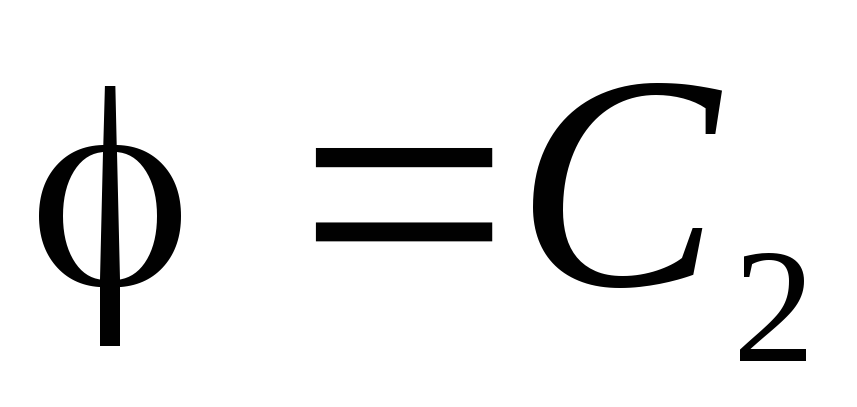 .
В силу непрерывности функции
.
В силу непрерывности функции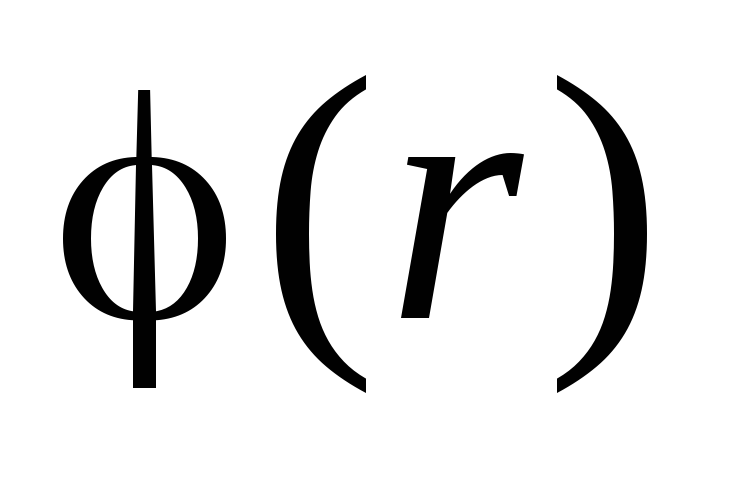 константа
константа должна быть равна значению потенциала
на поверхности заряженной сферы:
должна быть равна значению потенциала
на поверхности заряженной сферы: .
Таким образом, потенциал во всех точках
внутри сферы:
.
Таким образом, потенциал во всех точках
внутри сферы: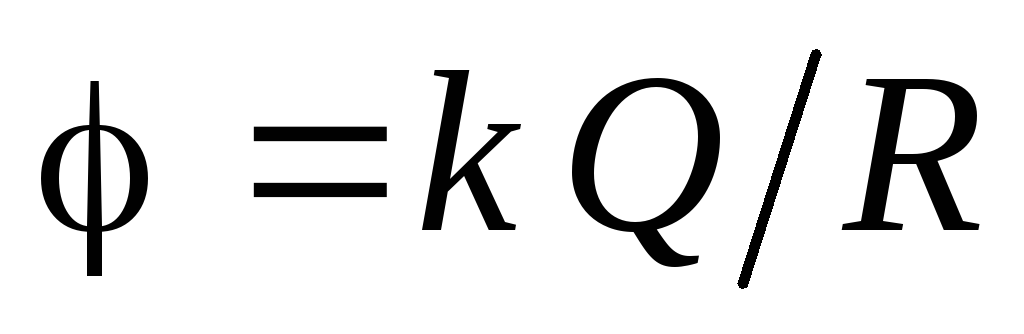 .
.

 ,
что и заряд сферы, помещенным в центр
сферы. Во внутреннем пространстве поле
отсутствует, а потенциал во всех
точках одинаков. Электрическое поле
(силовые линии и эквипотенциальные
поверхности) заряженной сферы изображены
на рис. 1.12. Предполагается, что сфера
заряжена положительно. Вне сферы силовые
линии и распределены в пространстве
точно так же, как и силовые линии точечного
заряда.
,
что и заряд сферы, помещенным в центр
сферы. Во внутреннем пространстве поле
отсутствует, а потенциал во всех
точках одинаков. Электрическое поле
(силовые линии и эквипотенциальные
поверхности) заряженной сферы изображены
на рис. 1.12. Предполагается, что сфера
заряжена положительно. Вне сферы силовые
линии и распределены в пространстве
точно так же, как и силовые линии точечного
заряда.
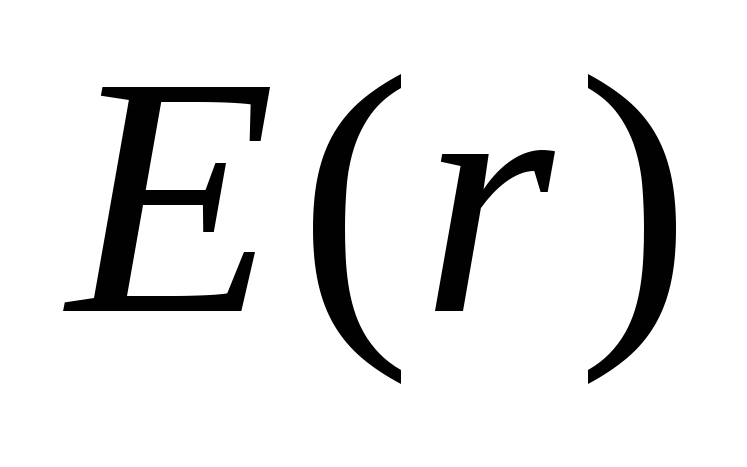 и
и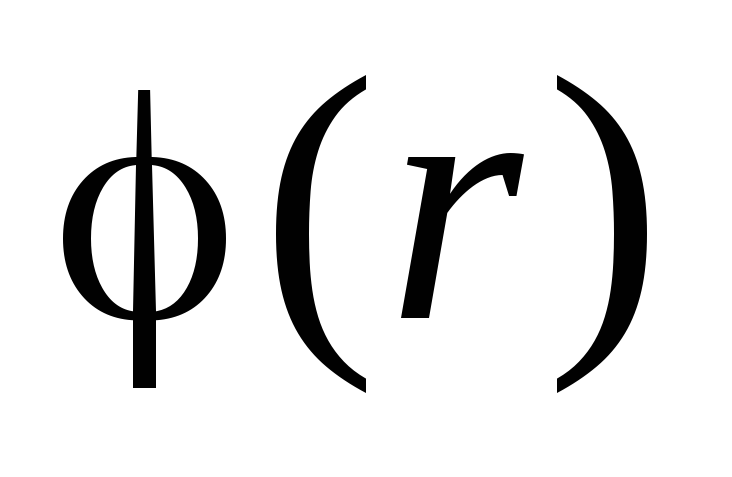 .
Функция
.
Функция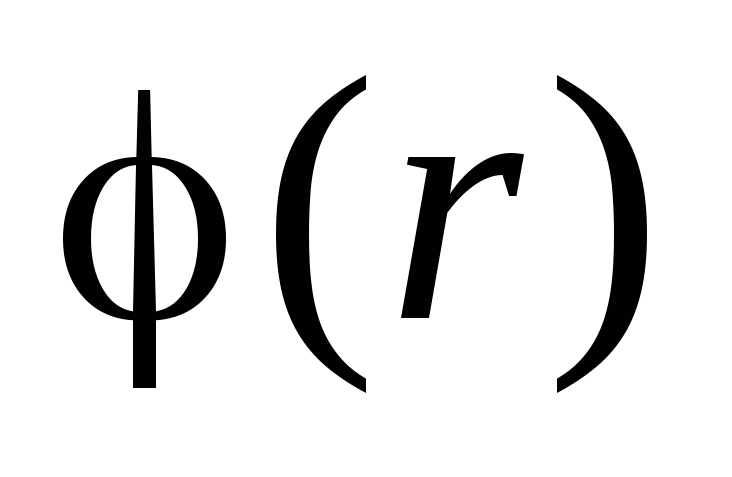 непрерывна, а функция
непрерывна, а функция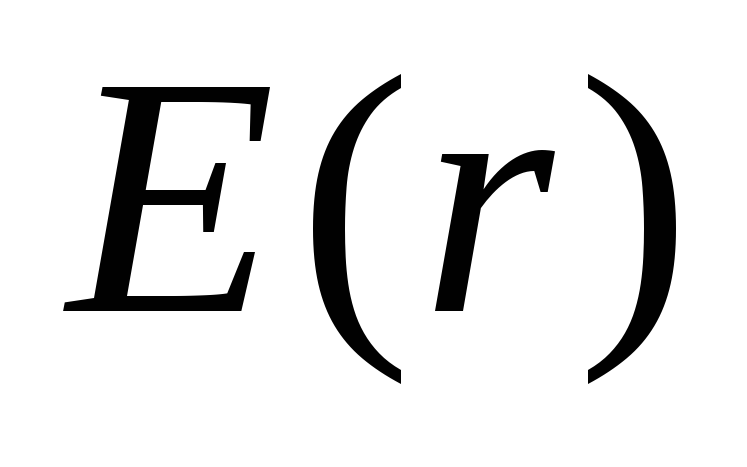 скачкообразно меняется при переходе
через границу заряженной сферы. Величина
скачка равна
скачкообразно меняется при переходе
через границу заряженной сферы. Величина
скачка равна .
Действительно, вблизи заряженной сферы
(
.
Действительно, вблизи заряженной сферы
( )
напряженность поля во внешнем пространстве
)
напряженность поля во внешнем пространстве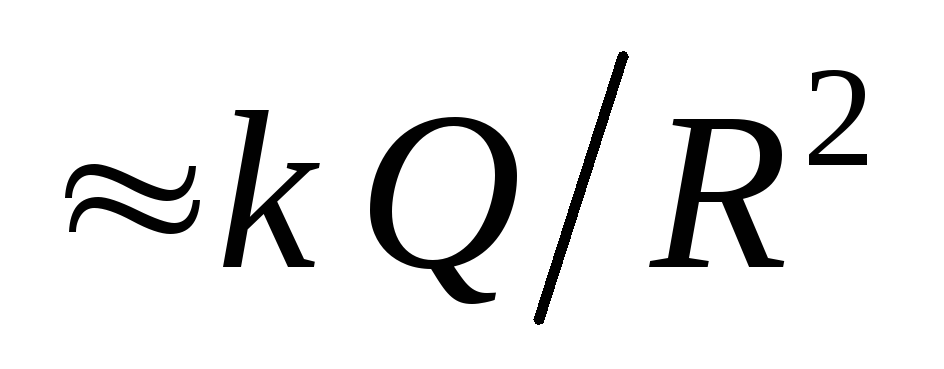 ,
а внутри равна нулю.
,
а внутри равна нулю.Величину скачка можно выразить через поверхностную плотность заряда на сфере:
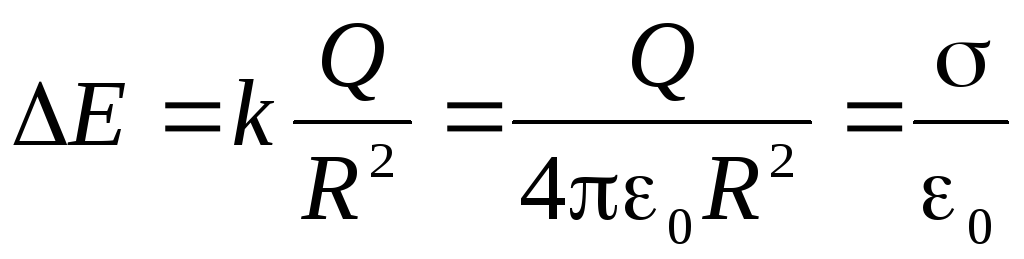 .
.
Заметим,
что это общее свойство электростатического
поля: на заряженной поверхности проекция
напряженности на направление нормали
всегда испытывает скачок  независимо от формы поверхности.
Рекомендуем проверить этот принцип для
поля равномерно заряженной плоскости
и поля двух параллельных заряженных
плоскостей (примеры 1.3, 1.4).
независимо от формы поверхности.
Рекомендуем проверить этот принцип для
поля равномерно заряженной плоскости
и поля двух параллельных заряженных
плоскостей (примеры 1.3, 1.4).
С
точки зрения математики непрерывность
потенциала в точках заряженной поверхности
означает, что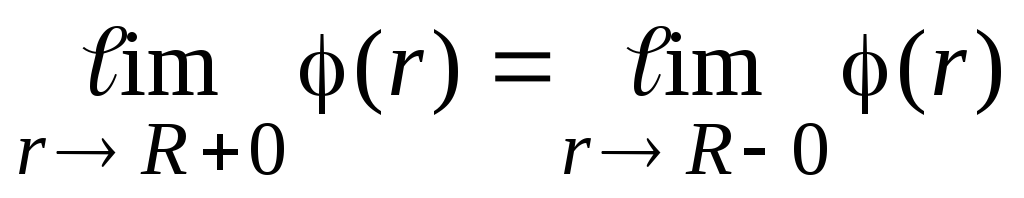 .
С точки зрения физики непрерывность
функции
.
С точки зрения физики непрерывность
функции можно объяснить следующим образом. Если
бы потенциал на границе некоторой
области имел бы скачок (разрыв), то при
бесконечно малом перемещении некоторого
заряда
можно объяснить следующим образом. Если
бы потенциал на границе некоторой
области имел бы скачок (разрыв), то при
бесконечно малом перемещении некоторого
заряда из точки 1, лежащей с одной стороны
границы, в точку 2, лежащую на другой ее
стороне, совершалась бы конечная работа
из точки 1, лежащей с одной стороны
границы, в точку 2, лежащую на другой ее
стороне, совершалась бы конечная работа ,
где
,
где и
и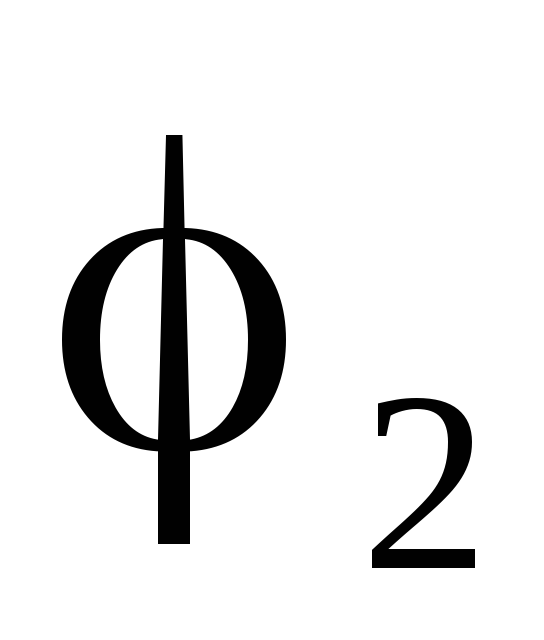
потенциалы точек 1 и 2 соответственно,
а величина
потенциалы точек 1 и 2 соответственно,
а величина  равна величине скачка потенциала на
границе области. Конечная работа,
совершенная на бесконечно малом
перемещении, означает, что на границе
раздела бы действовали бесконечно
большие силы, что невозможно.
равна величине скачка потенциала на
границе области. Конечная работа,
совершенная на бесконечно малом
перемещении, означает, что на границе
раздела бы действовали бесконечно
большие силы, что невозможно.
Напряженность электрического поля, в отличие от потенциала, на границе области может меняться очень резко (скачкообразно).
Пример 1.6.Две концентрические сферы
радиусов и
и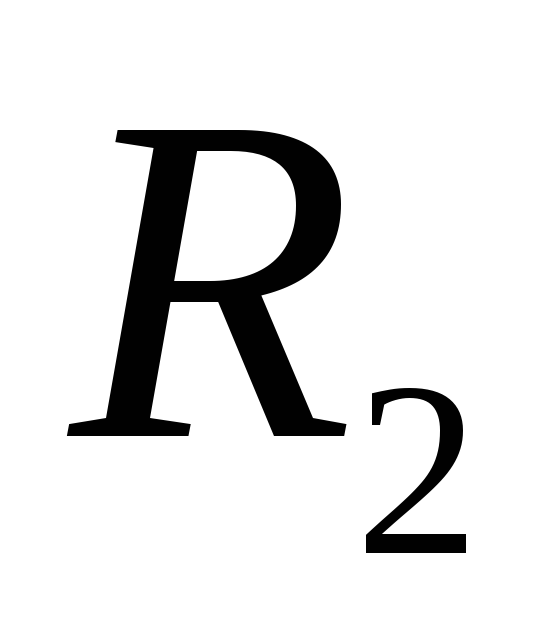 (
(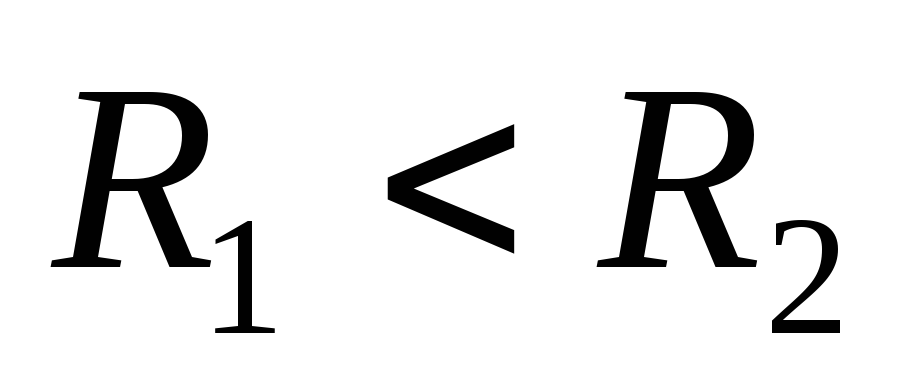 )
равномерно заряжены равными по модулю,
но противоположными по знаку зарядами
)
равномерно заряжены равными по модулю,
но противоположными по знаку зарядами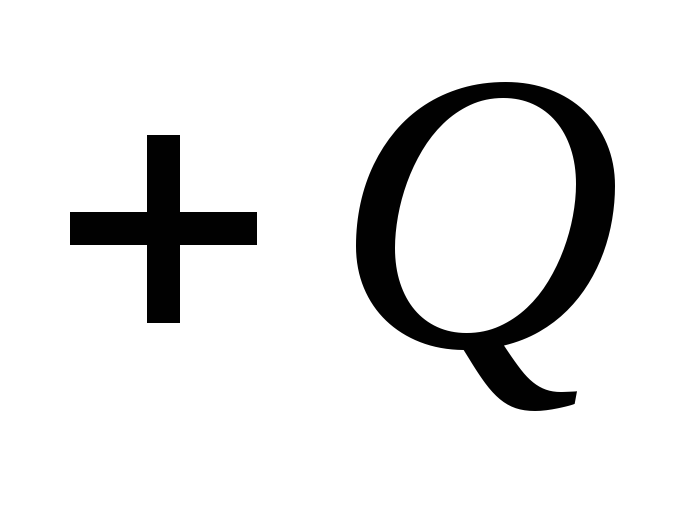 и
и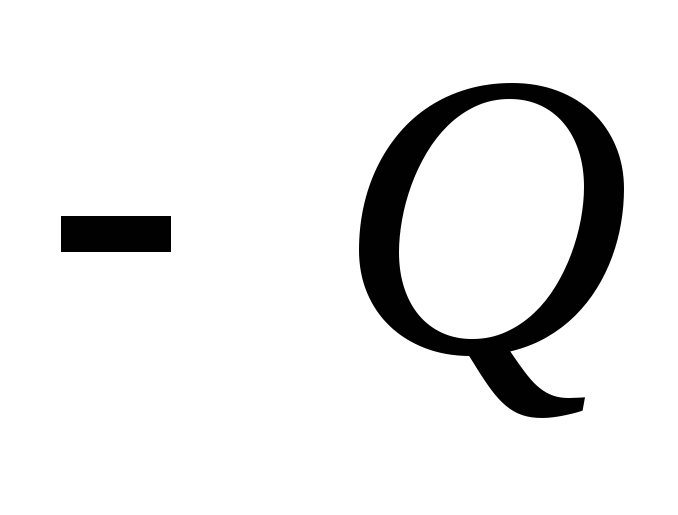 (сферический конденсатор). Определить
напряженность и потенциал электрического
поля во всем пространстве.
(сферический конденсатор). Определить
напряженность и потенциал электрического
поля во всем пространстве.
Решение. Решение этой задачи можно было бы также начать с применения теоремы Гаусса. Однако, используя результаты предыдущего примера и принцип суперпозиции (1.13, 1.14), ответ можно получить быстрее.
Во
внешних точках пространства ( )
электрическое поле создается зарядами
обеих сфер. Величина напряженности поля
первой сферы
)
электрическое поле создается зарядами
обеих сфер. Величина напряженности поля
первой сферы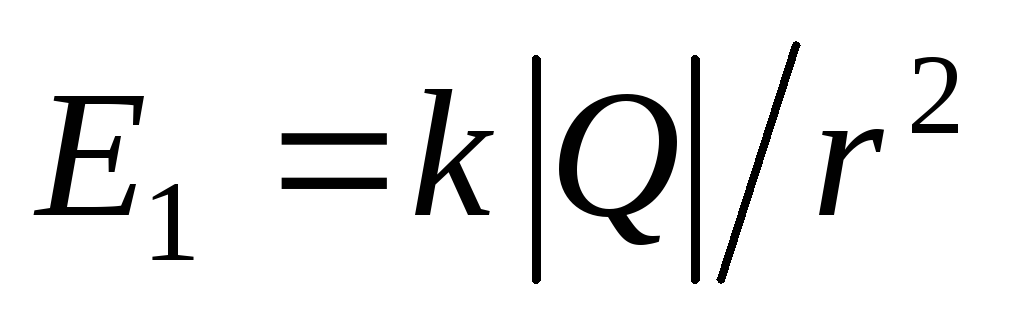 и направлена от сфер вдоль радиусов.
Величина напряженности поля второй
сферы такая же
и направлена от сфер вдоль радиусов.
Величина напряженности поля второй
сферы такая же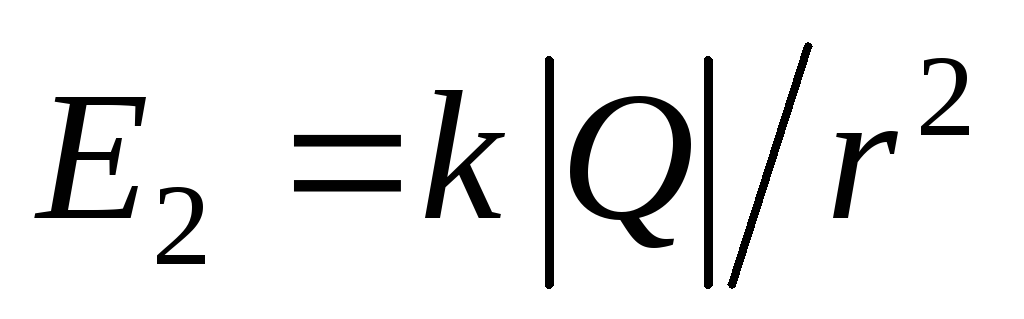 ,
но направлена противоположно.
Следовательно, согласно принципу
суперпозиции, во всех внешних точках
пространства электрическое поле будет
отсутствовать
,
но направлена противоположно.
Следовательно, согласно принципу
суперпозиции, во всех внешних точках
пространства электрическое поле будет
отсутствовать .
.
Рассмотрим
точки пространства между сферами ( ).
Эти точки являются внутренними для
отрицательно заряженной сферы, поэтому
в этой области
).
Эти точки являются внутренними для
отрицательно заряженной сферы, поэтому
в этой области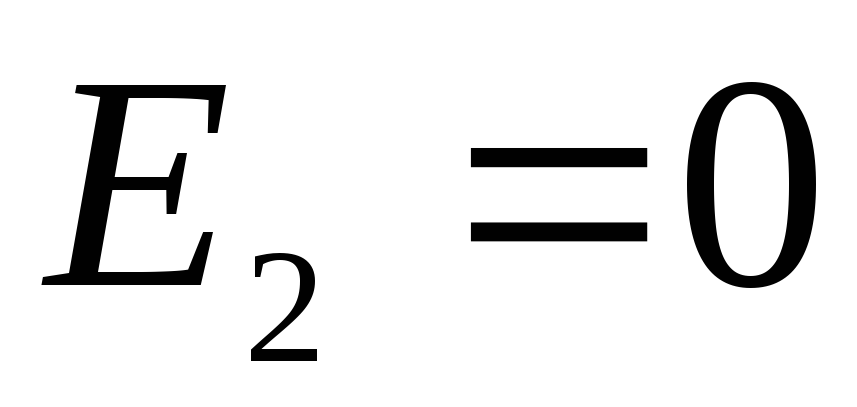 (см. пример 1.5). Для положительно заряженной
сферы эти точки являются внешними,
поэтому
(см. пример 1.5). Для положительно заряженной
сферы эти точки являются внешними,
поэтому .
Таким образом, величина напряженности
поля в этой области
.
Таким образом, величина напряженности
поля в этой области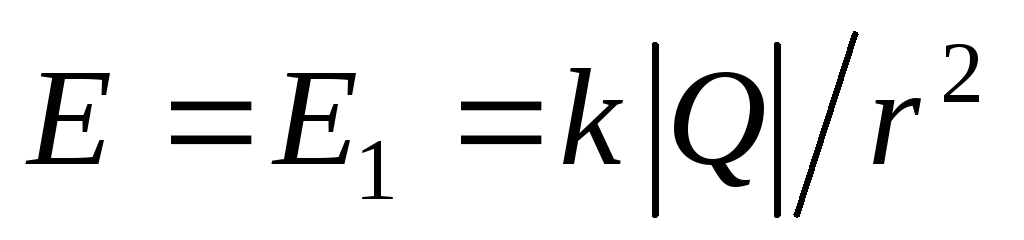 .
Здесь поле создают только заряды меньшей
сферы.
.
Здесь поле создают только заряды меньшей
сферы.
Наконец,
во внутренних точках пространства (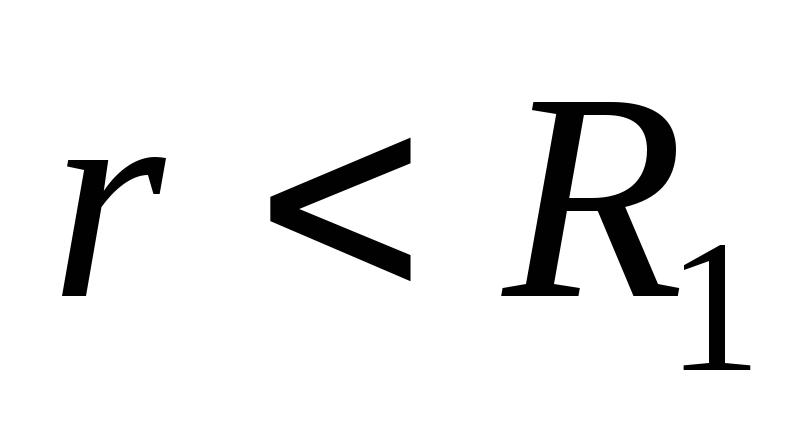 )
)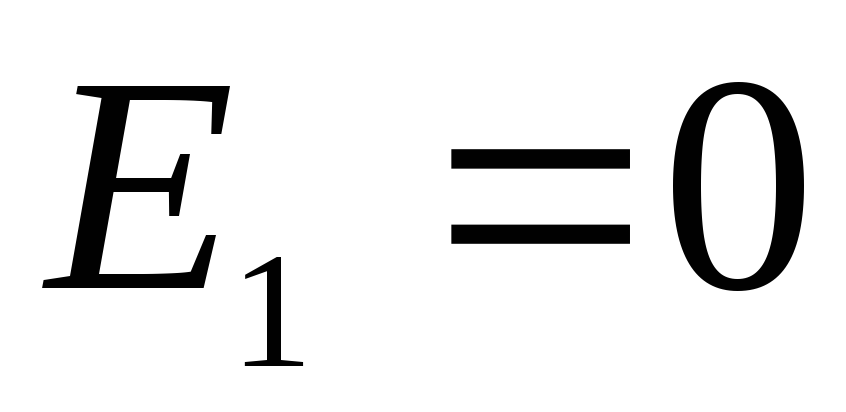 и
и ,
поэтому электрического поля в этих
точках нет.
,
поэтому электрического поля в этих
точках нет.
Аналогично можно применить принцип суперпозиции и для потенциалов. Получаются следующие результаты:
 :
: 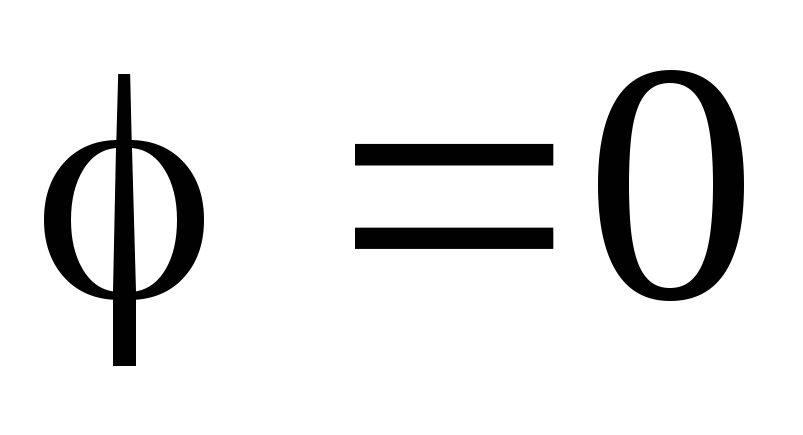 ;
;
 :
: 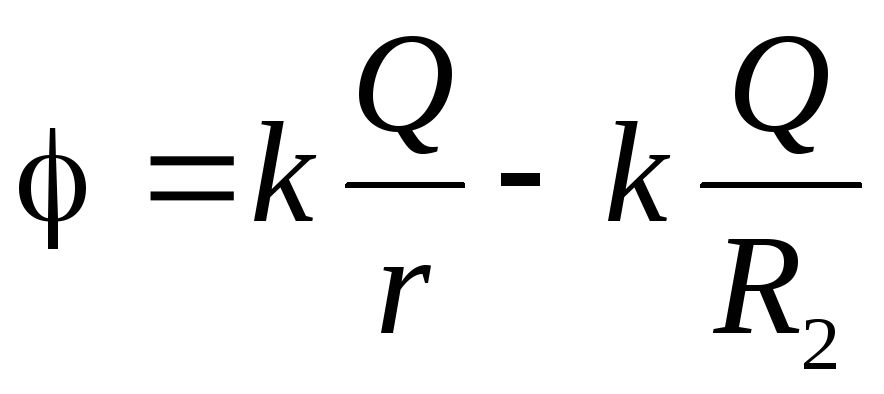 ;
;
 :
:  .
.
Рекомендуем
самостоятельно получить эти результаты,
а также схематически изобразить
электрическое поле и построить графики  и
и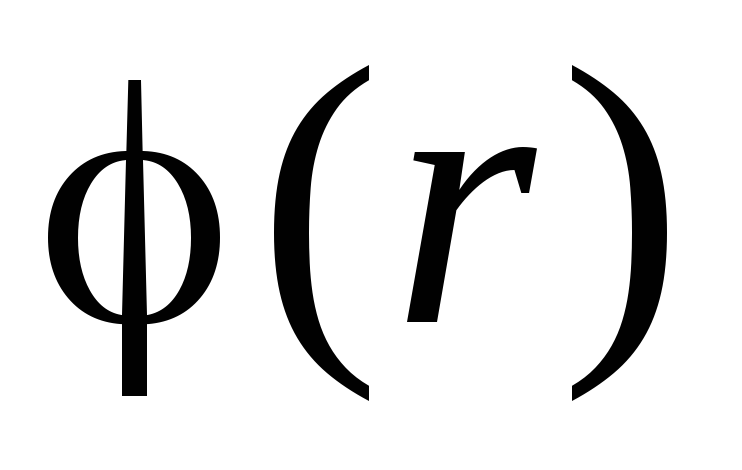 .
.
силовые линии — это… Что такое силовые линии?
СИЛОВЫ́Е ЛИ́НИИ, линии, проведенные в каком-либо силовом поле (см. СИЛОВОЕ ПОЛЕ) (электрическом, магнитном, гравитационном), касательные к которым в каждой точке поля совпадают по направлению с вектором, характеризующим данное поле (вектор напряженности (см. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ) электрического или гравитационного полей, вектор магнитной индукции (см. МАГНИТНАЯ ИНДУКЦИЯ)). Силовые линии — только наглядный способ изображения силовых полей. Впервые понятие «силовые линии» для электрических и магнитных полей ввел М.Фарадей (см. ФАРАДЕЙ Майкл).Так как напряженности полей и магнитная индукция — однозначные функции точки, то через каждую точку пространства может проходить только одна силовая линия. Густота силовых линий обычно выбирается так, чтобы число силовых линий, пересекающих единичную площадку, перпендикулярную к силовым линиям, было пропорционально напряженности поля (или магнитной индукции) на этой площадке. Т. о., силовые линии дают наглядную картину распределения поля в пространстве, характеризуя величину и направление напряженности поля.
Силовые линии электростатического поля (см. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ) всегда незамкнуты: они начинаются на положительных зарядах и оканчиваются на отрицательных (или уходят на бесконечность). Силовые линии нигде не пересекаются, так как в каждой точке поля его напряженность имеет одно единственное значение и определенное направление. Густота силовых линий больше вблизи заряженных тел, где напряженность поля больше.
Силовые линии электрического поля в пространстве между двумя положительными зарядами расходятся; можно указать нейтральную точку, в которой поля сил отталкивания обоих зарядов гасят друг друга.
Силовые линии одиночного заряда представляют собой радиальные прямые, которые расходятся от заряда лучами, подобно силовым линиям гравитационного поля точечной массы или шара. Чем дальше от заряда, тем меньше густота линий — это иллюстрирует ослабление поля с увеличение расстояния.
Силовые линии, исходящие от заряженного проводника неправильной формы, сгущаются вблизи любого выступа или острия, вблизи вогнутостей или полостей густота силовых линий уменьшается.
Если силовые линии исходят от положительно заряженного острия, находящегося вблизи отрицательно заряженного плоского проводника, то они сгущаются вокруг острия, где поле очень сильное, и расходятся в большую область вблизи плоскости, на которой оканчиваются, входя в плоскость перпендикулярно.
Электрическое поле в пространстве между параллельными заряженными пластинами однородно. Линии напряженности в однородном электрическом поле параллельны друг другу.
Если в силовое поле попадает частица, например электрон, то он под действием силового поля приобретает ускорение, и направление его движения не может точно следовать по направлению силовых линий, он будет двигаться в направлении вектора количества движения.
Магнитное поле (см. МАГНИТНОЕ ПОЛЕ) характеризуют линии магнитной индукции, в любой точке которых вектор магнитной индукции направлен по касательной.
Линии магнитной индукции магнитного поля прямого проводника с током представляют собой окружности, лежащие в плоскостях, перпендикулярных проводнику. Центры окружности находятся на оси проводника. Силовые линии вектора магнитной индукции всегда замкнуты, т. е. магнитное поле является вихревым. Железные опилки, помещенные в магнитное поле, выстраиваются вдоль силовых линий; благодаря этому можно экспериментально определять вид силовых линий магнитной индукции. Вихревое электрическое поле, порождаемое изменяющимся магнитным полем, также имеет замкнутые силовые линии.
основное свойство электрического поля. Силовые линии электростатического поля и их свойства.
По современным представлениям, электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела. Электрическое поле, окружающее заряженное тело, можно исследовать с помощью так называемого пробного заряда – небольшого по величине точечного заряда, который не вносит заметного перераспределения исследуемых зарядов. Для количественного определения электрического поля вводится силовая характеристика напряженность электрического поля. Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда. Напряженность электрического поля рассчитывается по формуле: Е=F/q, E=K|q|/r2 <a rel=»nofollow» href=»http://www.sch50.mccme.ru/sch/fizik/napr_electric_pole.htm» target=»_blank»>http://www.sch50.mccme.ru/sch/fizik/napr_electric_pole.htm</a> Поле напряженности является векторным. Чтобы наглядно представить это поле необходимо в каждой точке пространства провести вектор, длинна которого в установленных ед-ах равна силе, действующей на ед-ный положительный заряд, помещенный в эту точку. Такое представление очень удобно. Для большей наглядности эл. поле изображают семейством силовых линий, указывающих направление напряженности поля в каждой точке пространства. Эти силовые линии проводят так, чтобы указывать направление силы, действующей в данном поле на положительный пробный заряд. Непрерывные линии, касательные к которым в каждой точке, через которую они проходят, совпадают с вектором напряженности, называются силовыми линиями электрического поля или линиями напряженности. Густота линий больше там, где напряженность поля больше. Силовые линии электрического поля, созданного неподвижными зарядами не замкнуты: они начинаются на положительных зарядах и заканчиваются на отрицательных. Электрическое поле, напряженность которого одинакова во всех точках пространства, называется однородным. Густота линий больше вблизи заряженных тел, где напряженность больше. Силовые линии одного и того же поля не пересекаются. На любой заряд в электрическом поле действует сила. Если заряд под действием этой силы перемещается, то электрическое поле совершает работу. Работа сил по перемещению заряда в электростатическом поле не зависит от траектории движения заряда и определяется только положением начальной и конечной точек. <a rel=»nofollow» href=»http://www.sch50.mccme.ru/sch/fizik/sil_lines.htm» target=»_blank»>http://www.sch50.mccme.ru/sch/fizik/sil_lines.htm</a>
Электростатическое поле, напряженность, силовые линии, их свойства. Принцип суперпозиции, сумма векторов
Тестирование онлайн
Электростатическое поле
Электростатическое поле — это особая форма материи, которая возникает вокруг неподвижного электрического заряда. Это поле нет возможности увидеть, понюхать. Поле можно представить при помощи линий напряженности (силовых линий).
На рисунке видно, какое условное направление имеют силовые линии: начинаются на положительных зарядах и заканчиваются на отрицательных. Изображено и то, как линии напряженности распределяются при взаимодействии одноименных и разноименных зарядов.В реальности силовые линии можно увидеть при помощи железных опилок.
Чем дальше удаляться от заряда, тем меньше сила поля (силовые линии редеют), тем слабее взаимодействуют заряженные тела, посредством создаваемого ими поля.
Поле бывает однородным. В этом случае линии напряженности параллельные.
Поле однородное между пластинами в центре
Напряженность поля
Как оценить силу поля вокруг некоторого заряда? Для этого используют пробный заряд q0. Пробный заряд — это всегда положительный заряд, его собственное электростатическое поле ничтожно мало, относительно исследуемого поля.
Сила, с которой поле действует на пробный заряд в данной точке поля, называется напряженностью электростатического поля в этой точке
Напряженность поля — векторная величина. Вектора — это касательная к линиям напряженности в данной точке поля. Направлен вектор туда же, куда силовая линия (линия напряженности).
Вектор напряженности в различных точках поля: А, B, C и D
Вектор напряженности в точках 1, 2 и 3
Можно вывести формулу
— напряженность поля точечного заряда q на расстоянии r от него.
Принцип суперпозиции
Если поле создается несколькими зарядами, то напряженность в некоторой точке равна векторной сумме напряженностей каждого из полей в отдельности

