Операции над векторами в прямоугольной системе координат, сложение векторов по координатам

Если задана плоскость Oxy с векторами a→=ax, ay и b→=(bx, by), то мы можем разложить их по координатным векторам i→ и j→. Тогда это будет иметь вид a→=ax·i→+ay·j→ и b→=bx·i→+by·j→. Чтобы найти сумму a→ и b→ и произведение a→ на λ, рассмотрим:

a→+b→=ax·i→+ay·j→+bx·i→+by·j→=(ax+bx)·i→+(ay+by)·j→

λ·a→=λ·(ax·i→+ay·j→)=(λ·ax)·i→+(λ·ay)·j→

Это равенство справедливо по свойству операций над векторами.

Определение 1

Разложение векторов – это a→+b→ и λ·a→, представленное в частях неравенства по i→ и j→ координатам. Координаты векторов a→+b→ и λ·a→ равны соответственно (ax+bx, ay+by) и (λ·ax, λ·ay).

Таким же образом a→=(ax, ay, az) и b→=(bx, by, bz) записываются как a→+b→=ax·i→+ay·j→+az·k→+bx·i→+by·j→+bz·k→=(ax+bx)·i⇀+(ay+by)·j→+(az+bz)·k→λ·a→=λ·(ax·i→+ay·j→+az·k→)=(λ·ax)·i→+(λ·ay)·j→+(λ·az)·k→

а значит a→+b→=(ax+bx, ay+by, az+bz),  λ·a→=(λ·ax, λ·ay, λ·az)

Отсюда делаем вывод, что координаты векторов a→ и b→ равны сумме соответствующих координат векторов a→и b→, координаты произведения вектора a→ на λ приравниваются к соответствующим координатам вектора a→, умноженным на число в заданной системе координат.

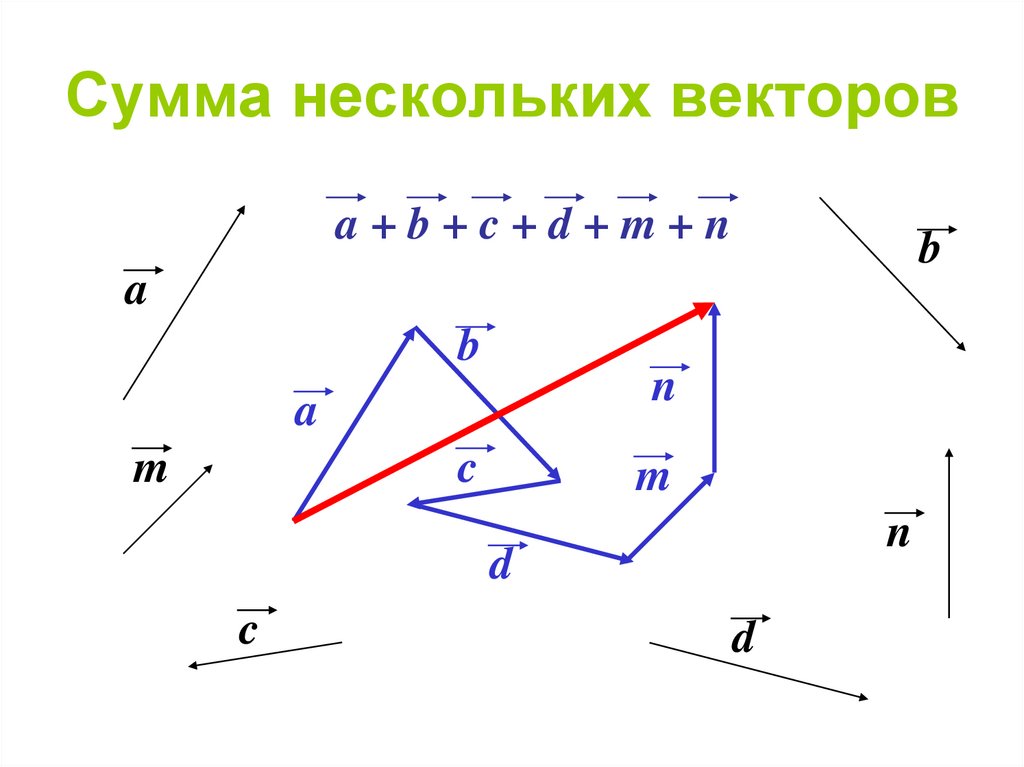
При необходимости нахождения координат суммы нескольких векторов, необходимо сложить координаты каждого вектора соответственно. Рассмотрим примеры.

Пример 1

Нужно выполнить сложение a→=(2, 3-13)  и b→=(-1,-13). Чему равны координаты произведения вектора a→ на 3.

Решение 

Из определения имеем, что сумма векторов равна сумме их координат соответственно, тогда a→+b→=(2+(-1),3-13+(-13))=(1, -13).

Числовое значение умножается на каждую координату: 3·a→=(3·2, 3·3-13)=23,3-33.

Ответ: a→+b→=(1, -13),   3·a→=(23, 3-33)

Пример 2

Заданы векторы a→=(0, 1, -2), b→=(-1, -1, 3), c→=(4, -3, 2) .

Каковы координаты вектора 2·a→+3·(b→-c→)=2·a→+3·b→+(-3)·c→.

Решение 

Применяя свойства векторов, получим: 2·a→+3·(b→-c→)=2·a→+3·b→+(-3)·c→.

Подставляем значения координат и получаем: 2·a→+3·b→+(-3)·c→=2·(0,1,-2)+3·(-1,-1, 3)+(-3)·(4,-3, 2)=

=(2·0, 2·1, 2·(-2))+(3·(-1), 3·(-1), 3·3)+((-3)·4,(-3)·(-3)·2)=

=(0, 2, -4)+(-3, -3, 9) + (-12, 9 -6)=

=(0+(-3)+(-12), 2+(-3)+9, -4+9+(-6))=(-15, 8, -1)

Можно решить другим способом.

Обратим внимание на разложение a→, b→ и c→ :

a→=0·i→+1·j→+(-2)·k→=j→-2·k→

b→=(-1)·i→+(-1)·j→+3 ·k→=-i→-j→+3·k→

c→=4·i→+(-3)·j→+2·k→=4·i→-3·j→+2·k→

Исходя из свойств векторов, видим, что: 2·a→+3·(b→-c→)=2·(j→-2·k→)+3·(-i→-j→+3·k→-(4·i→-3·j→+2·k→))==2·j→-4·k→+3·(-5·i→+2·j→+1·k→)=-15·i→+8·j→-k→

 Значит, координаты вектора 2·a→+3·(b→-c→) равны (-15, 8, -1).

Ответ: 2·a→+2·(b→-c→)=(-15, 8, -1)

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Навигация по статьям

Предыдущая статья

Нахождение середины отрезка

Следующая статья

Расстояние между точками

• Векторное произведение
• Векторное пространство
• Векторы на плоскости и в пространстве
• Геометрическая фигура угол
• Деление отрезка в заданном соотношении
• Все темы по математике

• Дипломные работы
• Курсовые работы
• Рефераты
• Контрольные работы
• Отчет по практике
• Эссе

Узнать подробнее

Система автоматизированного документооборота

• Вид работы:

  Реферат

• Выполнена:

  23 декабря 2022 г.

• Стоимость:

  1 000 руб

Заказать такую же работу

Расчет параметров Тобразной схемы замещения трансформатора по паспортным данным

• Вид работы:

  Контрольная работа

• Выполнена:

  14 октября 2022 г.

• Стоимость:

  2 900 руб

Заказать такую же работу

Свойства информационных поводов применительно к организациям использующих религиозный фактор

• Вид работы:

  Курсовая работа

• Выполнена:

  24 сентября 2022 г.

• Стоимость:

  2 200 руб

Заказать такую же работу

Основы информационных технологий в строительстве

Заказать такую же работу

расчет схемы каскада РПУ

• Вид работы:

  Домашняя работа

• Выполнена:

  23 июня 2022 г.

• Стоимость:

  3 000 руб

Заказать такую же работу

Цифровые двойники технологического оборудования

• Вид работы:

  Реферат

• Выполнена:

  6 мая 2022 г.

• Стоимость:

  2 000 руб

Заказать такую же работу

Смотреть все работы по информационным технологиям

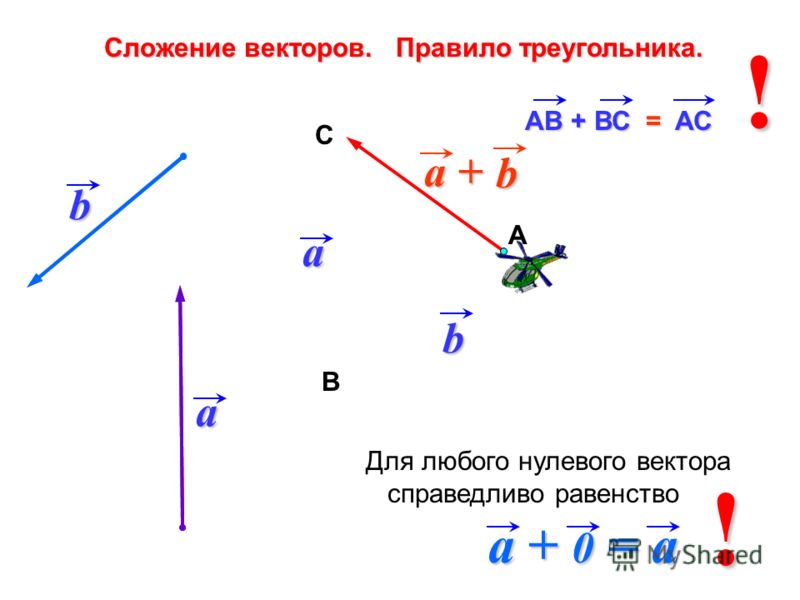
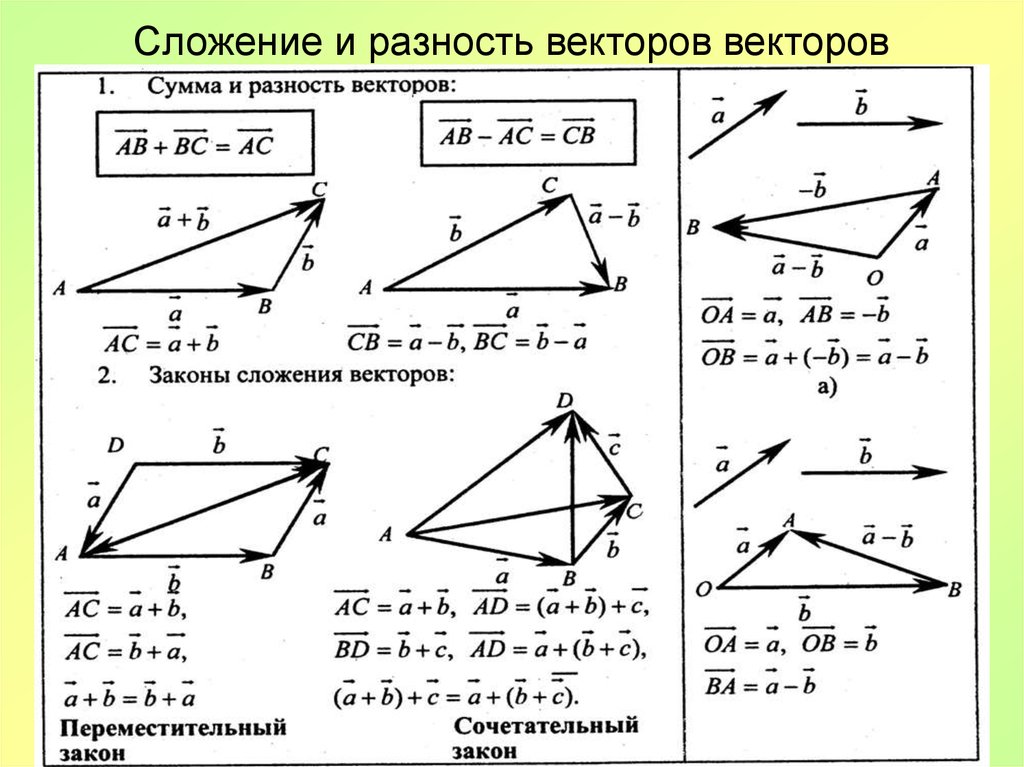
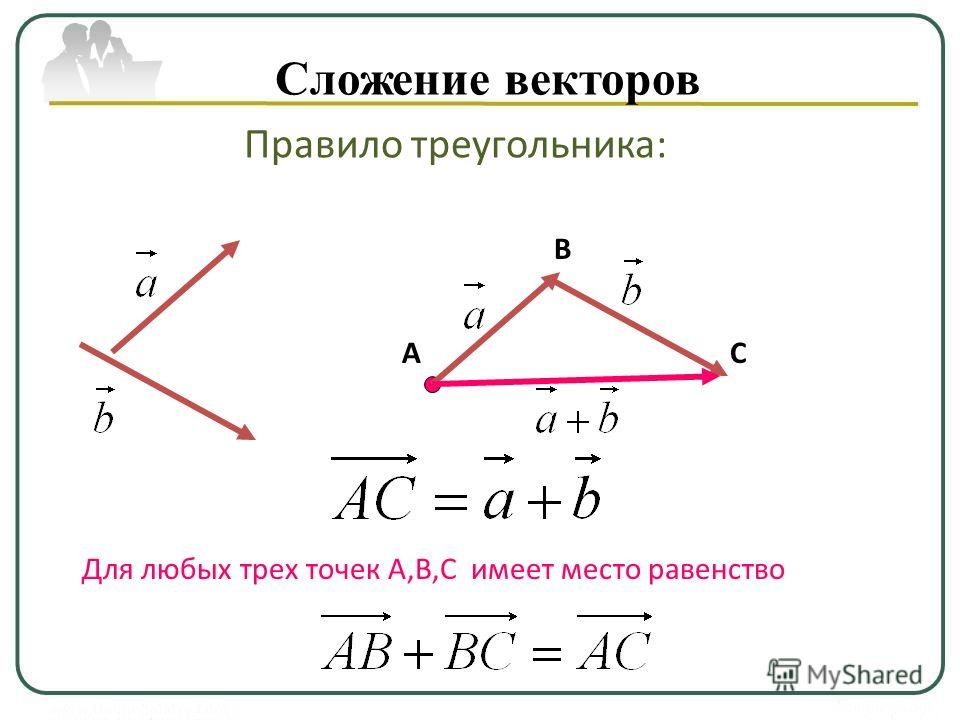
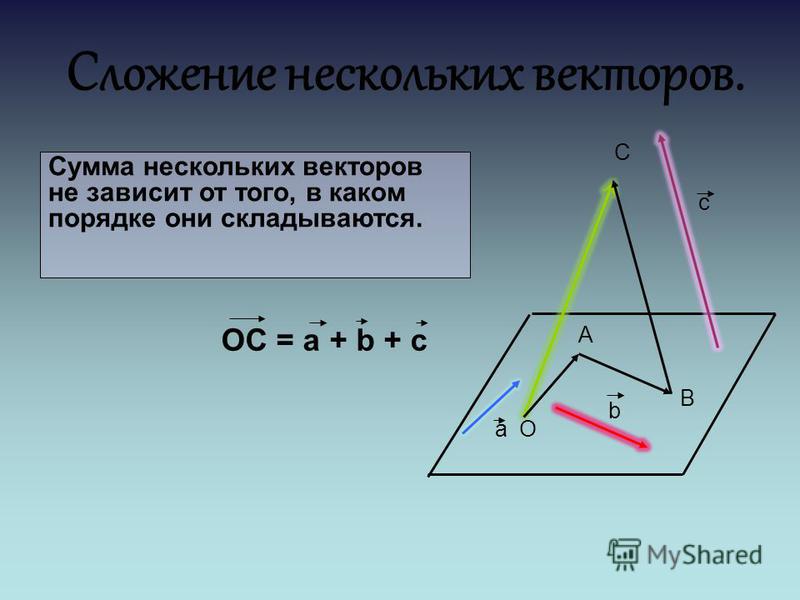
Сложение векторов.

С уммой двух векторов и называется вектор , соединяющий начало вектора с концом вектора , отложенного от конца вектора .

Произведение вектора на число.

Произведение м вектора на число называется вектор, который имеет длину и который имеет направление вектора в случае и противоположное направление в случае .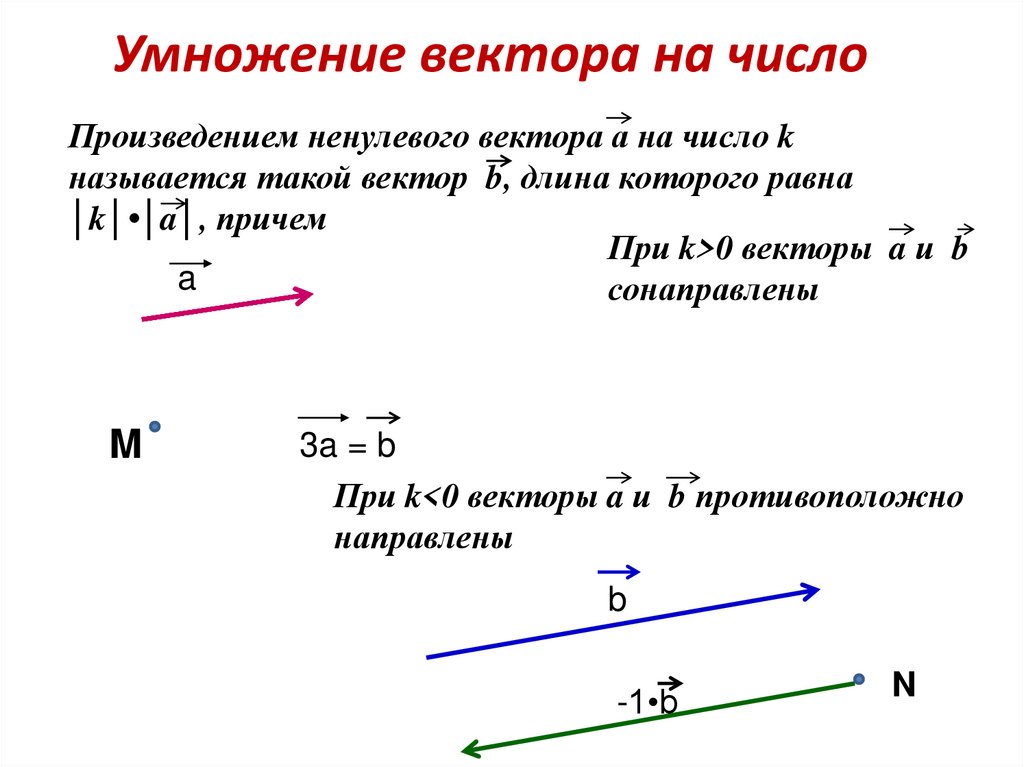

Пример 3.1. Даны векторы и .

П остройте векторы: 1) ;

2) .

§ 2. Декартовы прямоугольные координаты вектора. Длина вектора.

Пусть вектор составляет угол с осью .

П роекцией вектора на ось называется число, равное длине вектора (рис.3.1), взятой со знаком «плюс», если направление вектора совпадает с направлением оси и со знаком «минус» в противном случае.

П роекцию вектора на ось можно вычислить по формуле:

.

Д екартовыми прямоугольными координатами вектора называются его проекции на соответствующие координатные оси .

В ектор с координатами записывают в виде или , где — единичные векторы координатных осей соответственно. Длина вектора определяется по формуле:

.

Если вектор задан точками и , то его координаты вычисляются по формулам:

.

Пример 3.2. Даны две точки и . Найдите координаты и длину вектора .

П о условию задачи , , , , , . Значит, .

.

Пример 3.3. Даны два вектора и . Найдите координаты и длину вектора .

; ;

;

.

С овместим параллельным переносом начало некоторого вектора с началом координат прямоугольной системы координат . Пусть — углы, которые образует вектор с осями координат соответственно (рис.3.2). Направление вектора определяется с помощью направляющих косинусов , , , для которых справедливы равенства:

§ 3. Скалярное произведение векторов.

С калярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними (см. рис.3.3):

.

И з рис. 3.3 видно, что .

Поэтому или . (*)

Свойства скалярного произведения.

1. — переместительный закон.

2. — распределительный закон.

3. Е сли то .

4. (или или ).

В частности, скалярное произведение единичных векторов (ортов) удовлетворяет равенствам:

5. Е сли векторы заданы координатами , или , , то

.

6. У гол между векторами и определяется по формуле:

.

1. В екторы и коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.:

.

2. У словие перпендикулярности векторов и :

.

Пример 3.4. Векторы и образуют угол . Зная, что и , вычислите .

.

П ример 3.5. Даны вершины треугольника , и . Найдите: 1) внутренний угол при вершине ;

2) .

Д ля нахождения угла найдём векторы и .

;

.

Тогда Т.е.

Согласно формуле (*)

.

ЧТО ДОЛЖЕН ЗНАТЬ СТУДЕНТ

1. Понятие вектора.

2. Понятие единичного и нулевого вектора.

3. Модуль вектора, формула расстояния между двумя точками.

4. Понятие коллинеарности векторов.

5. Линейные операции над векторами.

6. Понятие проекции вектора на ось.

7. Скалярное произведение векторов.

Вектор координат

Марко Табога, доктор философии

В векторном пространстве любой вектор можно представить в виде линейной комбинации основа. Коэффициенты линейной комбинации называются координатами вектора относительно базиса.

Содержание

1. Мотивация

2. Определение

3. Примеры

   91
   1
   1

   Пример 2

4. Добавление координатных векторов

5. Умножение координатных векторов на скаляре

6. Массивы координатных векторов1110111111111111111111111111111111111111 годы. 1

7. Упражнение 2

Мотивация

Ранее мы предоставили два определения векторного пространства:

• неформальное определение: вектор — это конечный массив чисел, и множество таких массивы называются векторным пространством тогда и только тогда, когда они замкнуты относительно принимать линейные комбинации;

• формальное определение: векторное пространство — это множество, снабженное двумя операциями, называется векторным сложением и скалярным умножением, которые удовлетворяют ряду аксиомы.

Более простое неформальное определение вполне совместимо с более формальным. определение, как множество числовых массивов удовлетворяет всем свойствам векторное пространство при условии, что векторное сложение и скалярное умножение определяется обычным образом и что множество замкнуто относительно линейных комбинации.

Теперь мы вводим новое понятие, понятие вектора координат, которое делает два определения почти эквивалентны: если мы имеем дело с аннотация векторное пространство , но его размерность конечна и мы можем идентифицировать базис для пространства, то мы можем записать каждый вектор в виде линейной комбинации основы; как следствие, мы можем представить вектор как массив , называемый вектором координат, который содержит коэффициенты линейная комбинация.

Как только мы получили это простое представление, мы можем применить обычные правила матричной алгебры к координатным векторам, даже если мы имеем дело с абстрактное векторное пространство.

Это не только очень удобно, но и стирает различия между двумя подходы к определению векторов и векторных пространств (по крайней мере, для конечномерный случай).

Определение

Теперь мы готовы дать определение вектора координат.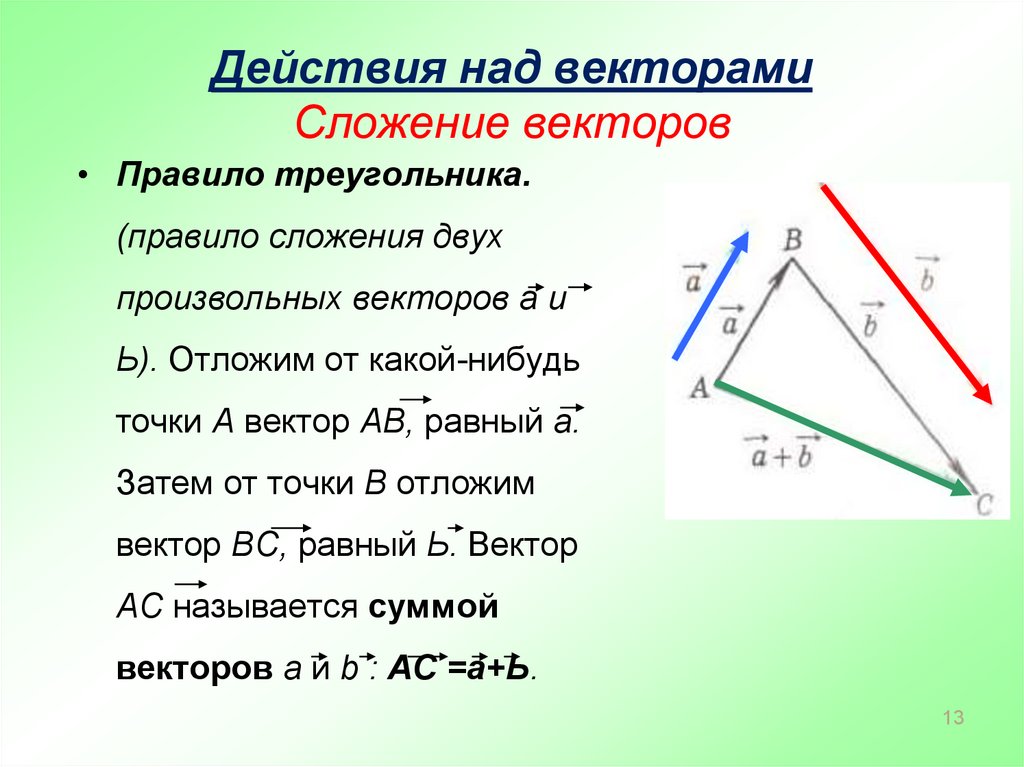

Определение Позволять — конечномерное линейное пространство. Позволять быть основой для . Для любого , взять уникальный набор скаляры такой чтоЗатем, в векторис называется координатный вектор из по отношению к основе .

Заметим, что единственность скаляров гарантируется уникальность представления в терминах базиса.

Примеры

Приведем несколько примеров.

Пример 1

Позволять быть векторным пространством и основу для него.

Предположим, что вектор можно записать в виде линейной комбинации базиса как следует:

Тогда координатный вектор в отношении

Пример 2

Рассмотрите пространство второго порядка полиномыгде коэффициенты и аргумент являются скалярами.

Как мы уже говорили в лекции о линейные пространства, является векторным пространством при условии, что сложение полиномов и их умножение на скаляры производится обычным образом.

Рассмотрим полиномы

Эти три полинома образуют базис для потому что они линейны независимыми (никакая их комбинация не равна нулю ни при каком ) и их можно линейно комбинировать так, чтобы получить любой формы выше:

Координатный вектор относительно базиса, который мы только что нашли is

Сложение векторов координат

Добавление двух векторов можно выполнить, выполнив обычный операция сложения векторов на соответствующие им координатные векторы.

Предложение Позволять быть линейным пространством и основа для . Позволять . Тогда координатный вектор относительно базиса равна сумме координатных векторов и по тому же основанию, что есть,

Доказательство

Предположим, что представления в терминах основа так что координатные векторы по коммутативные и дистрибутивные свойства векторного сложения и скалярного умножение в абстрактных векторных пространствах, мы имеем чтоТаким образом, координатный вектор is

Умножение векторов координат на скаляры

Умножение вектора на скаляр можно выполнить, выполнив обычная эксплуатация умножение скаляром на его координатном векторе.

Предложение Позволять быть линейным пространством и основа для . Позволять и разреши быть скаляром. Тогда координатный вектор по базе равен произведению и координатный вектор , что есть,

Доказательство

Предположим, что представление в терминах основа Иссо что вектор координат это по ассоциативные и дистрибутивные свойства скалярного умножения в абстрактные векторные пространства, мы имеем чтоТаким образом, координатный вектор

Числовые массивы представляют собой векторы координат относительно каноническая основа

Когда элементы линейного пространства представляют собой одномерные массивы чисел (векторы в простейшем смысле терм), то они совпадают со своими координатными векторами относительно стандартная основа.

Пример Позволять быть пространством всех векторы-столбцы. Позволять — его каноническая основа, где вектор, элементы которого все , кроме -й, что равно : Брать любой Затем, совпадает с его вектором координат относительно базиса , что это потому что

Решенные упражнения

Ниже вы можете найти несколько упражнений с поясненными решениями.

Упражнение 1

Позволять — векторное пространство всех полиномов третьего порядка.

Выполнить сложение двух многочленыandby используя их координатные векторы относительно базис

Убедитесь, что результат тот же, что и при суммировании двух полиномы напрямую.

Решение

Представления в терминах основы Таким образом, два координатных вектора их сумма Иссо что это тот же результат, который мы получаем, выполняя добавление напрямую:

Упражнение 2

Позволять быть пространством всех векторы.

Рассмотрим основу где

Найдите координатный вектор с отношении к данному основанию.

Решение

У нас есть чтоПоэтому, координатный вектор

Как цитировать

Пожалуйста, указывайте как:

Taboga, Marco (2021). «Координатный вектор», Лекции по матричной алгебре. https://www.statlect.com/matrix-алгебра/координата-вектор.

Вектор координат

Марко Табога, доктор философии

В векторном пространстве любой вектор можно представить в виде линейной комбинации основа. Коэффициенты линейной комбинации называются координатами вектора относительно базиса.

СОДЕРЖАНИЕ

1. Мотивация

2. Определение

3. . координатные векторы скалярами

4. Числовые массивы являются координатными векторами относительно канонического базиса

5. Решенные упражнения

   1. Упражнение 1

   2. Упражнение 2

Мотивация

Ранее мы предоставили два определения векторного пространства:

• неформальное определение: вектор — это конечный массив чисел, и множество таких массивы называются векторным пространством тогда и только тогда, когда они замкнуты относительно принимать линейные комбинации;

• формальное определение: векторное пространство — это множество, снабженное двумя операциями, называется векторным сложением и скалярным умножением, которые удовлетворяют ряду аксиомы.

Более простое неформальное определение вполне совместимо с более формальным. определение, как множество числовых массивов удовлетворяет всем свойствам векторное пространство при условии, что векторное сложение и скалярное умножение определяется обычным образом и что множество замкнуто относительно линейных комбинации.

Теперь мы вводим новое понятие, понятие вектора координат, которое делает два определения почти эквивалентны: если мы имеем дело с рефератом векторное пространство , но его размерность конечна и мы можем идентифицировать базис для пространства, то мы можем записать каждый вектор в виде линейной комбинации основы; как следствие, мы можем представить вектор как массив , называемый вектором координат, который содержит коэффициенты линейная комбинация.

Как только мы получили это простое представление, мы можем применить обычные правила матричной алгебры к координатным векторам, даже если мы имеем дело с абстрактное векторное пространство.

Это не только очень удобно, но и стирает различия между двумя подходы к определению векторов и векторных пространств (по крайней мере, для конечномерный случай).

Определение

Теперь мы готовы дать определение вектора координат.

Определение Позволять — конечномерное линейное пространство. Позволять быть основой для . Для любого , взять уникальный набор скаляры такой чтоЗатем, в векторис называется координатным вектором по отношению к основе .

Заметим, что единственность скаляров гарантируется уникальность представления в терминах базиса.

Примеры

Приведем несколько примеров.

Пример 1

Позволять быть векторным пространством и основу для него.

Предположим, что вектор можно записать в виде линейной комбинации базиса как следует:

Тогда координатный вектор в отношении

Пример 2

Рассмотрите пространство второго порядка полиномыгде коэффициенты и аргумент являются скалярами.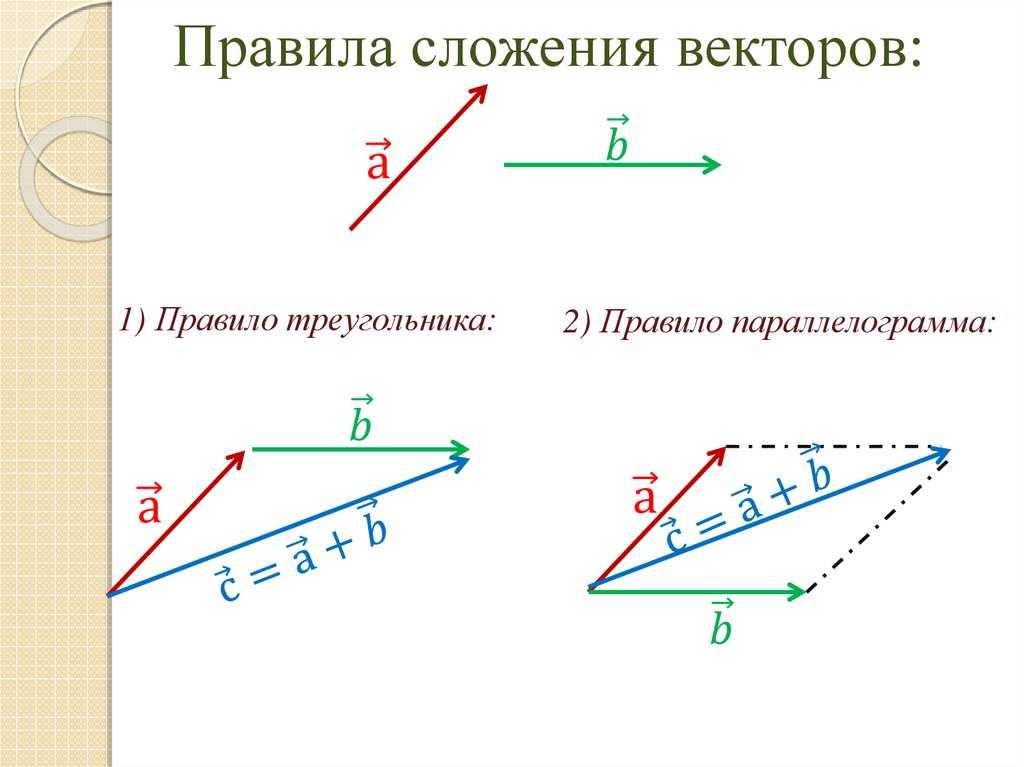

Как мы уже говорили в лекции о линейные пространства, является векторным пространством при условии, что сложение полиномов и их умножение на скаляры производится обычным образом.

Рассмотрим полиномы

Эти три полинома образуют базис для потому что они линейны независимыми (никакая их комбинация не равна нулю ни при каком ) и их можно линейно комбинировать так, чтобы получить любой формы выше:

Координатный вектор относительно базиса, который мы только что нашли is

Сложение векторов координат

Добавление двух векторов можно выполнить, выполнив обычный операция сложения векторов на соответствующие им координатные векторы.

Предложение Позволять быть линейным пространством и основа для . Позволять . Тогда координатный вектор относительно базиса равна сумме координатных векторов и по тому же основанию, что есть,

Доказательство

Предположим, что представления в терминах основа так что координатные векторы по коммутативные и дистрибутивные свойства векторного сложения и скалярного умножение в абстрактных векторных пространствах, мы имеем чтоТаким образом, координатный вектор is

Умножение векторов координат на скаляры

Умножение вектора на скаляр можно выполнить, выполнив обычная эксплуатация умножение скаляром на его координатном векторе.

Предложение Позволять быть линейным пространством и основа для . Позволять и разреши быть скаляром. Тогда координатный вектор по базе равен произведению и координатный вектор , что есть,

Доказательство

Предположим, что представление в терминах основа Иссо что вектор координат это по ассоциативные и дистрибутивные свойства скалярного умножения в абстрактные векторные пространства, мы имеем чтоТаким образом, координатный вектор

Числовые массивы представляют собой векторы координат относительно каноническая основа

Когда элементы линейного пространства представляют собой одномерные массивы чисел (векторы в простейшем смысле терм), то они совпадают со своими координатными векторами относительно стандартная основа.

Пример Позволять быть пространством всех векторы-столбцы. Позволять — его каноническая основа, где вектор, элементы которого все , кроме -й, что равно : Брать любой Затем, совпадает с его вектором координат относительно базиса , что это потому что

Решенные упражнения

Ниже вы можете найти несколько упражнений с поясненными решениями.

Упражнение 1

Позволять — векторное пространство всех полиномов третьего порядка.

Выполнить сложение двух многочленыandby используя их координатные векторы относительно базис

Убедитесь, что результат тот же, что и при суммировании двух полиномы напрямую.

Решение

Представления в терминах основы Таким образом, два координатных вектора их сумма Иссо что это тот же результат, который мы получаем, выполняя добавление напрямую:

Упражнение 2

Позволять быть пространством всех векторы.