Шестнадцатеричные числа | это… Что такое Шестнадцатеричные числа?
ТолкованиеПеревод
- Шестнадцатеричные числа
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.
Содержание
- 1 Применение
- 2 Способы записи
- 2.1 В математике
- 2.2 В языках программирования
- 3 Перевод чисел из одной системы счисления в другую
- 3.1 Перевод чисел из шестнадцатеричной системы в десятичную
- 3.2 Перевод чисел из двоичной системы в шестнадцатеричную
- 3.3 Таблица перевода чисел
- 4 См.
 также
также - 5 Ссылки
Применение
Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Способы записи
В математике
В математике систему счисления принято писать в подстрочном знаке. Например, десятичное число 1443 можно записать как 1443
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и
- В Си и языках схожего синтаксиса, например, в
- В некоторых ассемблерах используют букву «h», которую ставят после числа.
 Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510) - Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бэйсика используют префикс «$». Например, «$5A3».
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т.д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
- Другие версии Бэйсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как \xCC, где CC — шестнадцатеричный код символа.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316=5·162+10·161+3·160
=5·256+10·16+3·1=1280+160+3=144310Перевод чисел из двоичной системы в шестнадцатеричную
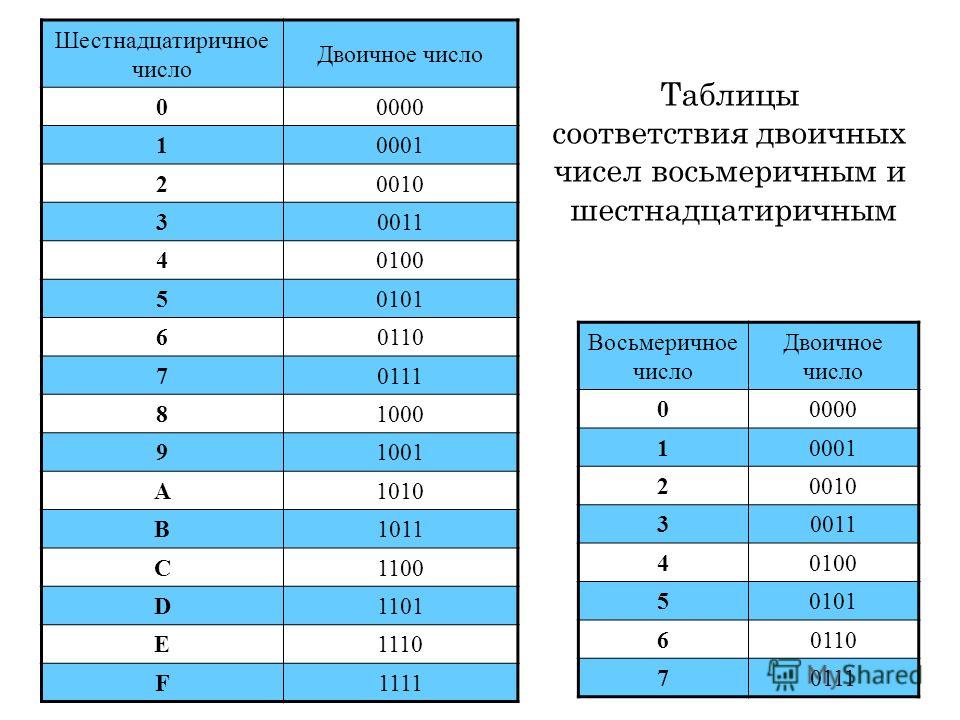
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.
Например:
101101000112=0101 1010 0011=5A316 Таблица перевода чисел
0hex = 0dec = 0oct 0 0 0 0 1hex = 1dec = 1oct 0 0 0 1 2hex = 2dec = 2oct 0 0 1 0 3hex = 3dec = 3oct 0 0 1 1 4hex = 4dec = 4oct 0 1 0 0 5hex = 5dec = 5oct 0 1 0 1 6hex = 6dec = 6oct 0 1 1 0 7hex = 7dec = 7oct 0 1 1 1 8hex = 8dec = 10oct 1 0 0 0 9hex = 9dec = 11oct 1 0 0 1 Ahex = 10dec = 12oct 1 0 1 0 Bhex = 11dec = 13oct 1 0 1 1 Chex = 12dec = 14oct 1 1 0 Dhex = 13dec = 15oct 1 1 0 1 Ehex = 14dec = 16oct 1 1 1 0 Fhex = 15dec = 17oct 1 1 1 1 См.
 также
также- Система счисления
- Двоичные приставки
- Шестнадцатеричный редактор
Ссылки
- Шестнадцатеричные числа и операции с ними
- Таблица порядков двоичных, шестнадцатеричных и десятичных чисел
- Онлайн калькулятор для перевода чисел из одной системы счисления в другую
Wikimedia Foundation. 2010.
Игры ⚽ Поможем решить контрольную работу
- Шестнадцатиричная система счисления
- Шестнадцать
Полезное
Шестнадцатеричные числа | это… Что такое Шестнадцатеричные числа?
ТолкованиеПеревод
- Шестнадцатеричные числа
 Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.
Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.Содержание
- 1 Применение
- 2 Способы записи
- 2.1 В математике
- 2.2 В языках программирования
- 3 Перевод чисел из одной системы счисления в другую
- 3.1 Перевод чисел из шестнадцатеричной системы в десятичную
- 3.2 Перевод чисел из двоичной системы в шестнадцатеричную
- 3.3 Таблица перевода чисел
- 4 См. также
- 5 Ссылки
Применение
Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, БЭСМ-6) использовали восьмеричную систему.

В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Способы записи
В математике
В математике систему счисления принято писать в подстрочном знаке. Например, десятичное число 1443 можно записать как 144310 или как 5A316.
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и
- В Си и языках схожего синтаксиса, например, в
- В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
- Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бэйсика используют префикс «$». Например, «$5A3».
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т.
 д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3. - Другие версии Бэйсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как \xCC, где CC — шестнадцатеричный код символа.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316=5·162+10·161+3·160
=5·256+10·16+3·1=1280+160+3=144310Перевод чисел из двоичной системы в шестнадцатеричную
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.

Например:
101101000112=0101 1010 0011=5A316 Таблица перевода чисел
0hex = 0dec = 0oct 0 0 0 0 1hex = 1dec = 1oct 0 0 0 1 2hex = 2dec = 2oct 0 0 1 0 3hex = 3dec = 3oct 0 0 1 1 4hex = 4dec = 4oct 0 1 0 0 5hex = 5dec = 5oct 0 1 0 1 6hex = 6dec = 6oct 0 1 1 0 7hex = 7dec = 7oct 0 1 1 1 8hex = 8dec = 10oct 1 0 0 0 9hex = 9dec = 11oct 1 0 0 1 Ahex = 10dec = 12oct 1 0 1 0 Bhex = 11dec = 13oct 1 0 1 1 Chex = 12dec = 14oct 1 1 0 0 Dhex = 13dec = 15oct 1 1 0 1 Ehex = 14dec = 16oct 1 1 1 0 Fhex = 15dec = 17oct 1 1 1 1 См.
 также
также- Система счисления
- Двоичные приставки
- Шестнадцатеричный редактор
Ссылки
- Шестнадцатеричные числа и операции с ними
- Таблица порядков двоичных, шестнадцатеричных и десятичных чисел
- Онлайн калькулятор для перевода чисел из одной системы счисления в другую
Wikimedia Foundation. 2010.
Игры ⚽ Поможем решить контрольную работу
- Шестнадцатиричная система счисления
- Шестнадцать
Полезное
Преобразование шестнадцатеричных чисел в десятичные – x-engineer.org
Прежде чем приступить к преобразованию шестнадцатеричных чисел в десятичные, ознакомьтесь со следующими статьями:
- Системы представления чисел – десятичная, двоичная, восьмеричная и шестнадцатеричная: в этой статье объясняются различные типы систем представления чисел: десятичная, двоичная, шестнадцатеричная и восьмеричная
- Преобразование десятичного числа в шестнадцатеричное: в этой статье объясняется, как преобразовать десятичное число в шестнадцатеричное число 93 &= 4096
\end{split}\]Например, давайте преобразуем шестнадцатеричное число 0xFACE в десятичное число.

Метод 1
Этот метод прост и использует степень числа 16.
Шаг 1 . Преобразуйте каждый из шестнадцатеричных символов в десятичные следующим образом:
Шестнадцатеричное F A C E 4 15 10 12 14 Шаг 2 . Multiply each of the decimal numbers with the corresponding power of 16, as follows:
Decimal 15 10 12 14 Powers of 16 16 3 16 2 16 1 16 0 Multiplication 15·16 3 10·16 2 12·16 1 14·16 0 Step 3 .
 Сложите произведения всех операций умножения. Результатом будет десятичное число.
Сложите произведения всех операций умножения. Результатом будет десятичное число.\[\bbox[#FFFF9D]{15 \cdot 4096 + 10 \cdot 256 + 12 \cdot 16 + 14 \cdot 1 = 64206}\]
Шестнадцатеричное число 0xFACE , преобразованное в десятичное, равно 640020 .
Метод 2
Этот метод не такой прямой, как первый, но его проще выполнить, поскольку он не требует сложных операций умножения. Это также может быть выполнено без калькулятора или программного обеспечения. Принцип этого метода заключается в использовании преобразования из шестнадцатеричной системы в двоичную в первую очередь и из двоичной системы в десятичную во вторую.
Шестнадцатеричное число может быть представлено 4 битами. Например, старший символ в шестнадцатеричной системе счисления равен 9.0020 F , что в двоичном виде равно 0b1111 .
Шаг 1 . Convert the hexadecimal numbers into binary, as follows:
90Hexadecimal F A C E Decimal 15 10 12 14 Binary 1111 1010 1100 1110
\end{split} \]Шаг 4 .
 Выполните сумму умножений, чтобы получить десятичное число
Выполните сумму умножений, чтобы получить десятичное число\[32768+16384+8192+4096+2048+512+128+64+8+4+2=64206\]
Как видите, мы получили тот же результат с обоими методами. Преимущество второго заключается в том, что он имеет дело с более простыми умножениями и может выполняться без карманного калькулятора или программного обеспечения.
Конечно, мы также можем использовать функцию Scilab
hex2dec()для преобразования из шестнадцатеричного в десятичное.--> hex2dec('FACE')ans =
64206.-->.
Не забудьте поставить лайк, поделиться и подписаться!
Эквиваленты десятичных и шестнадцатеричных чисел Десятичные числа от 0 до 255; От 00 до FF
Эквиваленты десятичных (DEC) и шестнадцатеричных (HX) чисел
DEC HX 000 00 001 01 002 02 003 03 004 04 005 05 006 06 007 07 008 08 009 09 010 0А 011 0Б 012 0С 013 0Д 014 0Е 015 0F ДЕК HX 016 10 017 11 018 12 019 13 020 14 021 15 022 16 023 17 024 18 025 19 026 1А 027 1Б 028 1С 029 1Д 030 1Э 031 1F ДЕК HX 032 20 033 21 034 22 035 23 036 24 037 25 038 26 039 27 040 28 041 29 042 2А 043 2Б 044 2С 045 2Д 046 2Е 047 2F ДЕК HX 048 30 049 31 050 32 051 33 052 34 053 35 054 36 055 37 056 38 057 39 058 3А 059 3Б 060 3С 061 3Д 062 3Е 063 3F ДЕК HX 064 40 065 41 066 42 067 43 068 44 069 45 070 46 071 47 072 48 073 49 074 4А 075 4Б 076 4С 077 4Д 078 4Е 079 4F ДЕК HX 080 50 081 51 082 52 083 53 084 54 085 55 086 56 087 57 088 58 089 59 090 5А 091 5Б 092 5С 093 5Д 094 5Е 095 5F ДЕК HX 096 60 097 61 098 62 099 63 100 64 101 65 102 66 103 67 104 68 105 69 106 6А 107 6Б 108 6С 109 6Д 110 6Е 111 6F ДЕК HX 112 70 113 71 114 72 115 73 116 74 117 75 118 76 119 77 120 78 121 79 122 7А 123 7Б 124 7С 125 7Д 126 7Э 127 7F ДЕК HX 128 80 12981 130 82 131 83 132 84 133 85 134 86 135 87 136 88 137 89 138 8А 139 8Б 140 8С 141 8Д 142 8Е 143 8F ДЕК HX 144 90 145 91 146 92 147 93 148 94 149 95 150 96 151 97 152 98 153 99 154 9А 155 9Б 156 9С 157 9Д 158 9Е 159 9F ДЕК HX 160 А0 161 А1 162 А2 163 А3 164 А4 165 А5 166 А6 167 А7 168 А8 169 А9 170 АА 171 АВ 172 АС 173 г.  н.э.
н.э.174 АЕ 175 АФ ДЕК HX 176 Б0 177 Б1 178 Б2 179 Б3 180 В4 181 В5 182 В6 183 В7 184 В8 185 В9 186 БА 187 ББ 188 г. до н.э. 189 БД 190 БЭ 191 БФ ДЕК HX 192 С0 193 С1 194 С2 195 С3 196 С4 197 С5 198 С6 199 С7 200 С8 201 С9 202 КА 203 КБ 204 СС 205 компакт-диск 206 СЕ 207 ЦФ ДЕК HX 208 Д0 209 Д1 210 Д2 211 Д3 212 Д4 213 Д5 214 Д6 215 Д7 216 Д8 217 Д9 218 ДА 219 ДБ 220 пост. 


 также
также Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
 также
также Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.
Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.
 д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
 также
также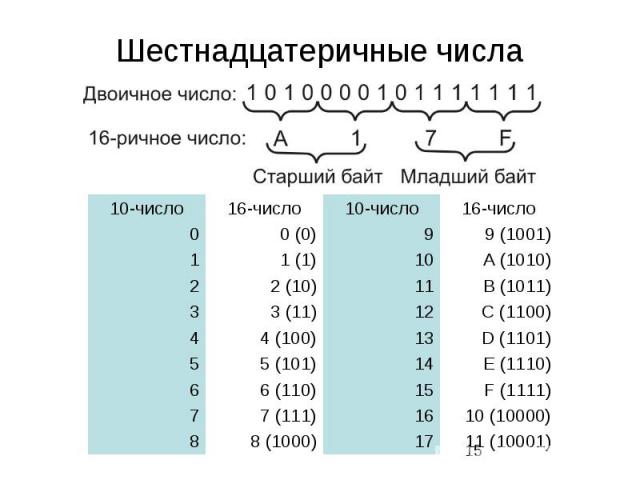
 Сложите произведения всех операций умножения. Результатом будет десятичное число.
Сложите произведения всех операций умножения. Результатом будет десятичное число. Выполните сумму умножений, чтобы получить десятичное число
Выполните сумму умножений, чтобы получить десятичное число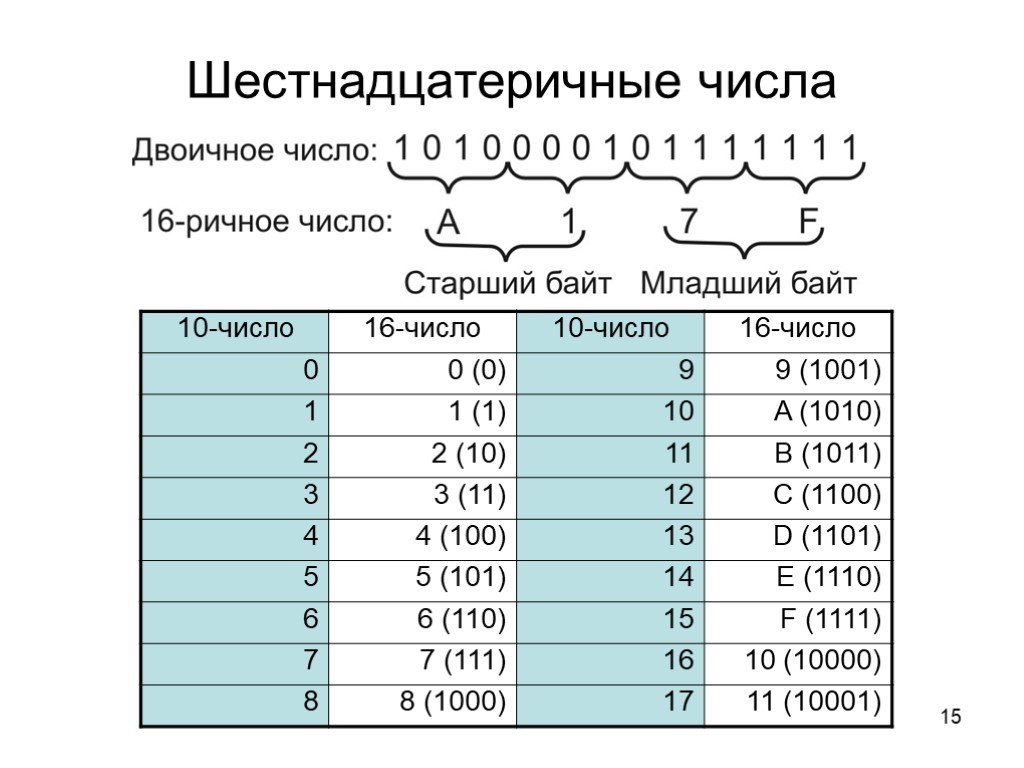 н.э.
н.э.