Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса — ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший «Салат из свеклы с чесноком» Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д. Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. |
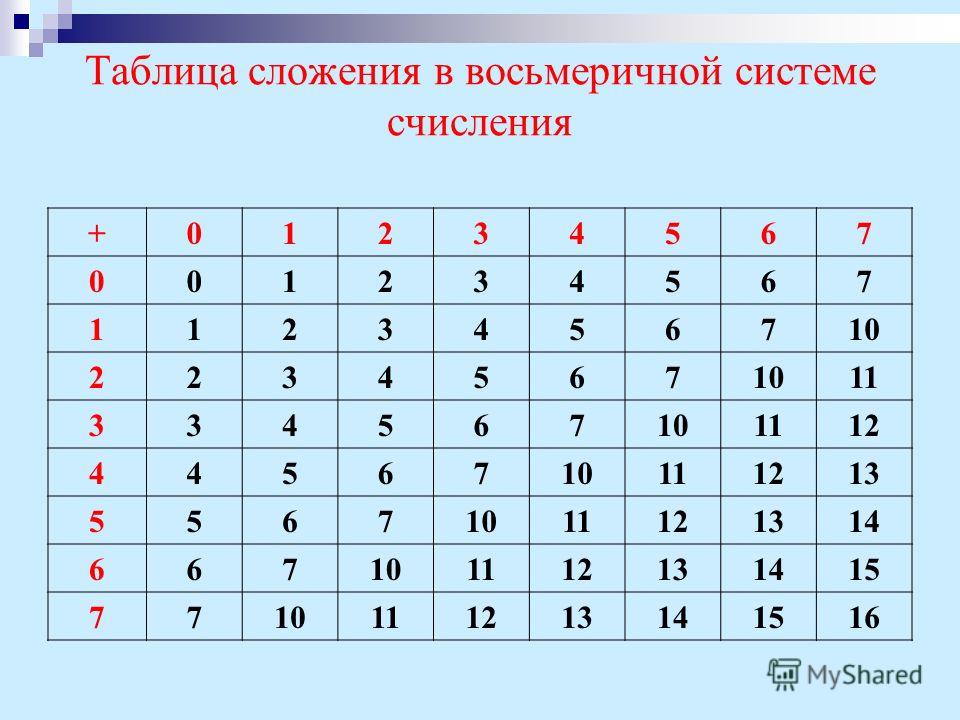
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
Пример 1. Сложим числа 15 и 6 в различных системах счисления.
Пример 2. Сложим числа 15, 7 и 3.
Пример 3. Сложим числа 141,5 и 59,75.
Ответ: 141,5 + 59,75 = 201,2510 = 11001001,01 Проверка. Преобразуем полученные суммы к десятичному виду: 311,28 = 3*82 + 1•81 + 1*80 + 2*8-1 = 201,25 C9,416 = 12*161 + 9*160 + 4*16-1 = 201,25
Вычитание Пример 4. Вычтем единицу из чисел 102, 108 и 1016 Пример 5. Вычтем единицу из чисел 100 Пример 6.Вычтем число 59,75 из числа 201,25. Ответ: 201,2510 – 59,7510 = 141,510 = 10001101,12 = 215,48 = 8D,816. Проверка. Преобразуем полученные разности к десятичному виду: 215,48 = 2*82 + 1*8 8D,816 = 8*161 + D*160 + 8*16–1 = 141,5.
Умножение Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям. Пример 7. Перемножим числа 5 и 6. Ответ: 5*6 = 3010 = 111102 = 368. Проверка. Преобразуем полученные произведения к десятичному виду: 368 = 3•81 + 6•80 = 30. Пример 8. Ответ: 115*51 = 586510 = 10110111010012 = 133518. Проверка. Преобразуем полученные произведения к десятичному виду: 133518 = 1*84 + 3*83 + 3*82 + 5*81 + 1*80 = 5865. Деление Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей. Пример 9. Разделим число 30 на число 6. Ответ: 30 : 6 = 510 = 1012 = 58. Пример 10. Разделим число 5865 на число 115. Восьмеричная: 133518 :1638 Ответ: 5865 : 115 = 5110 = 1100112 = 638. Проверка. Преобразуем полученные частные к десятичному виду: Пример 11. Восьмеричная: 438 : 168 Ответ: 35 : 14 = 2,510 = 10,12 = 2,48. Проверка. Преобразуем полученные частные к десятичному виду:
Упражнения 2.1. Переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы: (№ варианта соответствует № рабочего места)
2. (№ варианта соответствует № рабочего места)
2.3. Переведите в двоичную и восьмеричную системы шестнадцатеричные числа: (№ варианта соответствует № рабочего места)
2. а) от 1011012 до 1100002 в двоичной системе; б) от 2023 до 10003 в троичной системе; в) от 148 до 208 в восьмеричной системе; г) от 2816 до 3016 в шестнадцатеричной системе.
2.5. Составьте таблицы сложения однозначных чисел в троичной и пятеричной системах счисления.
2.6. Составьте таблицы умножения однозначных чисел в троичной и пятеричной системах счисления.
2.7. Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения: (№ варианта соответствует № рабочего места)
2.8. В каких системах счисления выполнены следующие сложения? Найдите основания каждой системы:
2.9. Разделите 100101102 на 10102 и проверьте результат, умножая делитель на частное.
2.10. Разделите 100110101002 на 11002 и затем выполните соответствующее десятичное и восьмеричное деление.
Доверь свою работу ✍️ кандидату наук! Имя Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое Нажимая кнопку «Продолжить», я принимаю политику конфиденциальности |
16 системы счисления сложение
Вы искали 16 системы счисления сложение? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и в сложение чисел в системах счисления, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «16 системы счисления сложение».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 16 системы счисления сложение,в сложение чисел в системах счисления,вычитание и сложение в системах счисления,вычитание и сложение систем счисления,как складывать в системе счисления,как складывать в шестнадцатиричной системе счисления,как складывать системы счисления,как складывать числа в десятичной системе счисления,как складывать числа в разных системах счисления,как складывать числа в шестнадцатеричной системе счисления,как складывать шестнадцатиричные числа,как сложить шестнадцатеричные числа,онлайн сложение чисел в восьмеричной системе счисления,онлайн сложение чисел в разных системах счисления,онлайн сложение чисел в шестнадцатеричной системе счисления,онлайн сложение шестнадцатиричных чисел,систем счисления сложение,система счисления вычитание и сложение,система счисления сложение,системы счисления 16 сложение,системы счисления как складывать,системы счисления сложение,сложение 16 ричных чисел,сложение 16 ричных чисел онлайн,сложение 16 системы счисления,сложение 2 системы счисления,сложение в 16 системе счисления,сложение в 2 системе счисления,сложение в 8 системе счисления,сложение в разных системах счисления,сложение в системах счисления,сложение в системе счисления,сложение в шестнадцатеричной системе,сложение в шестнадцатеричной системе счисления,сложение восьмеричных чисел калькулятор,сложение и вычитание в разных системах счисления,сложение и вычитание в системах счисления,сложение и вычитание в шестнадцатеричной системе счисления,сложение и вычитание систем счисления,сложение и вычитание чисел в разных системах счисления,сложение и вычитание шестнадцатеричных чисел,сложение разных систем счисления,сложение систем счисления,сложение систем счисления с решением онлайн сложение,сложение система счисления,сложение системы счисления,сложение системы счисления 16,сложение сс,сложение чисел в восьмеричной системе счисления онлайн,сложение чисел в разных системах счисления,сложение чисел в разных системах счисления онлайн,сложение чисел в системах счисления,сложение чисел в шестнадцатеричной системе,сложение чисел в шестнадцатеричной системе счисления,сложение чисел в шестнадцатеричной системе счисления онлайн,сложение шестнадцатеричной системы счисления,сложение шестнадцатеричных чисел,сложение шестнадцатиричной системы,сложение шестнадцатиричной системы счисления,сложение шестнадцатиричных чисел онлайн,сложения в шестнадцатеричной в системе счисления,сложения систем счисления,сложить числа в восьмеричной системе счисления онлайн,сложить шестнадцатеричные числа,таблица сложения 16 ричной системы счисления.
Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 16 системы счисления сложение,в сложение чисел в системах счисления,вычитание и сложение в системах счисления,вычитание и сложение систем счисления,как складывать в системе счисления,как складывать в шестнадцатиричной системе счисления,как складывать системы счисления,как складывать числа в десятичной системе счисления,как складывать числа в разных системах счисления,как складывать числа в шестнадцатеричной системе счисления,как складывать шестнадцатиричные числа,как сложить шестнадцатеричные числа,онлайн сложение чисел в восьмеричной системе счисления,онлайн сложение чисел в разных системах счисления,онлайн сложение чисел в шестнадцатеричной системе счисления,онлайн сложение шестнадцатиричных чисел,систем счисления сложение,система счисления вычитание и сложение,система счисления сложение,системы счисления 16 сложение,системы счисления как складывать,системы счисления сложение,сложение 16 ричных чисел,сложение 16 ричных чисел онлайн,сложение 16 системы счисления,сложение 2 системы счисления,сложение в 16 системе счисления,сложение в 2 системе счисления,сложение в 8 системе счисления,сложение в разных системах счисления,сложение в системах счисления,сложение в системе счисления,сложение в шестнадцатеричной системе,сложение в шестнадцатеричной системе счисления,сложение восьмеричных чисел калькулятор,сложение и вычитание в разных системах счисления,сложение и вычитание в системах счисления,сложение и вычитание в шестнадцатеричной системе счисления,сложение и вычитание систем счисления,сложение и вычитание чисел в разных системах счисления,сложение и вычитание шестнадцатеричных чисел,сложение разных систем счисления,сложение систем счисления,сложение систем счисления с решением онлайн сложение,сложение система счисления,сложение системы счисления,сложение системы счисления 16,сложение сс,сложение чисел в восьмеричной системе счисления онлайн,сложение чисел в разных системах счисления,сложение чисел в разных системах счисления онлайн,сложение чисел в системах счисления,сложение чисел в шестнадцатеричной системе,сложение чисел в шестнадцатеричной системе счисления,сложение чисел в шестнадцатеричной системе счисления онлайн,сложение шестнадцатеричной системы счисления,сложение шестнадцатеричных чисел,сложение шестнадцатиричной системы,сложение шестнадцатиричной системы счисления,сложение шестнадцатиричных чисел онлайн,сложения в шестнадцатеричной в системе счисления,сложения систем счисления,сложить числа в восьмеричной системе счисления онлайн,сложить шестнадцатеричные числа,таблица сложения 16 ричной системы счисления. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 16 системы счисления сложение. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычитание и сложение в системах счисления).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 16 системы счисления сложение. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычитание и сложение в системах счисления).
Решить задачу 16 системы счисления сложение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Назначение
НазначениеНазначение
Прочтите рецензии на «Основы счисления:»
Шестнадцатеричный учебник
Двоичные числа
Номер системы
Ниже приведены два примера, показывающие, как выполнить сложение чисел, один для
числа в двоичном формате, другой для чисел в шестнадцатеричном формате. Это
параллели с тем, как это делается в десятичном виде.
Это
параллели с тем, как это делается в десятичном виде.
Назначение:
Выполните следующие задачи на сложение в двоичном и шестнадцатеричном формате.
ДВОИЧНЫЙ:
1) 0101 2) 0101
3) 0111
+1010 +1011 +0111
ШЕСТНАДЦАТЕРИЧНЫЙ:
4) 4817 5) 4817
6) 4817 7) 4817
+3172 +3173 +3179 +317F
8) 4817 9) 4817 10) B4AC
+B172 +B972 +FD86
Для каждой из приведенных выше сумм определите, какой из предоставленных ответов является правильный:
1. 0101 + 1010
а. 1000
б. 10000
в. 0001
д. 1110
е. 1111
2. 0101 + 1011
а. 1000
б. 10000
в. 0001
д. 1110
е. 1111
3. 0111 + 0111
а. 1000
б. 10000
10000
в. 0001
д. 1110
е. 1111
4. 4817 + 3172
а. 7990
б. 1Б232
в. F989
д. 10189
е.798А
ф. 7996
грамм. 7989
5. 4817 + 3173
а. 7990
б. 1Б232
в. F989
д. 10189
е.798А
ф. 7996
грамм. 7989
6. 4817 + 3179
а. 7990
б. 1Б232
в. F989
д. 10189
е.798А
ф. 7996
грамм. 7989
7. 4817 + 317F
а. 7990
б. 1Б232
в. F989
д. 10189
е.798А
ф. 7996
грамм. 7989
8. 4817 + B172
а. 7990
б. 1Б232
в. F989
д. 10189
е.798А
ф. 7996
грамм. 7989
9. 4817 + В972
а. 7990
б. 1Б232
в. F989
д. 10189
е.798А
ф. 7996
грамм. 7989
10. B4AC + FD86
а. 7990
б. 1Б232
в. F989
д. 10189
е.798А
ф. 7996
7996
грамм. 7989
Примеры:
ДВОИЧНЫЙ ПРИМЕР ДОПОЛНЕНИЯ
0111
+1110
Действуем по столбцам, справа налево, так же, как и в десятичном, отмечая несет там, где они происходят. Итак, сначала мы позаботимся о самом правом столбце ( свою колонку).
0111
+1110
1 плюс 0 равно 1. Запишите это.
0111
+1110
1
Теперь перейдите ко второму справа столбцу (столбец двойки).
0111
+1110
1
1 плюс 1 это… Ну, для нас это 2. Но в двоичной системе счисления нет
«2»!! У них только 0 и 1. Вот так они пишут этот номер
«2» равно 10 (один в столбце двоек и ни одного в столбце единиц—
в сумме два). Но это число, 10, занимает два столбца и поэтому не помещается
во 2-й столбец суммы. Итак, мы поместили туда только «0» часть 10,
и перенесите «1» часть 10 в следующий столбец. (Это именно
аналогична операции переноса в десятичном виде, с которой вы знакомы.)
(Это именно
аналогична операции переноса в десятичном виде, с которой вы знакомы.)
1
0111
+1110
01
Теперь перейдите к 3-му столбцу справа (столбец четверки).
1
0111
+1110
01
1 плюс 1 плюс 1 это… Ну, для нас это 3. Но двоичная система счисления не имеет «3»!! У них только 0 и 1. Так они кстати напишите это число «3» равно 11 (один в двойке плюс один в одна колонка — всего три). Но это число, 11, занимает два столбца. и поэтому не может вписаться в 3-й столбец суммы. Итак, мы поместили туда только самый правый «1» часть из 11 и нести крайнюю левую «1» часть из 11. к следующему столбцу.
1
0111
+1110
101
Теперь перейдите к четвертой справа колонке (восьмерке).
1
0111
+1110
101
1 плюс 0 плюс 1 это. .. Ну, 2. Но 2 в этой системе счисления равно 10. Но это
число 10 занимает два столбца и поэтому не может вписаться в четвертый столбец суммы. Так
ставим туда только «0» часть 10, а переносим «1» часть
из 10 в следующую колонку.
.. Ну, 2. Но 2 в этой системе счисления равно 10. Но это
число 10 занимает два столбца и поэтому не может вписаться в четвертый столбец суммы. Так
ставим туда только «0» часть 10, а переносим «1» часть
из 10 в следующую колонку.
1
0111
+1110
10101
10101 — это окончательная сумма. 0111 плюс 1110 равно 10101. Один из способов проверить это состоит в том, чтобы преобразовать каждое из этих чисел в десятичное число и посмотреть, работает ли оно. 0111 это Семь. 1110 — это четырнадцать. Поэтому мы надеемся, что 10101 — это двадцать один. Это?
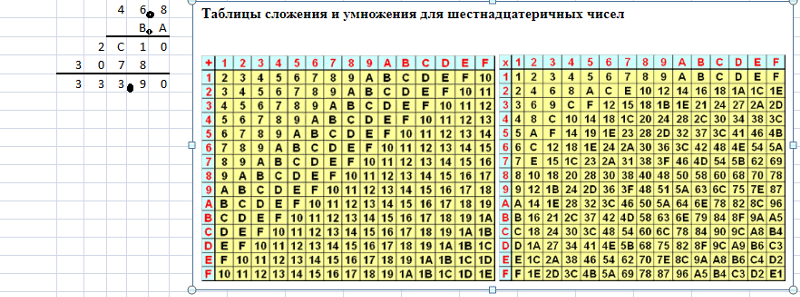
ПРИМЕР ШЕСТНАДЦАТЕРИЧНОГО СЛОЖЕНИЯ
У нас есть обычные цифры от 0 до 9, плюс 6 других. Они есть A представляет десять, B представляет одиннадцать, C представляет двенадцать, D представляет тринадцать, E означает четырнадцать, а F означает пятнадцать.
4817
+792Б
Действуем по столбцам, справа налево, так же, как и в десятичном, отмечая
несет там, где они происходят. Итак, сначала мы позаботимся о самом правом столбце (
свою колонку).
Итак, сначала мы позаботимся о самом правом столбце (
свою колонку).
4817
+792Б
7 плюс B означает 7 плюс одиннадцать. Это восемнадцать. В шестнадцатеричном виде мы пишем, что как двузначное число, с одной цифрой в шестнадцатеричном столбце, а другой в свою колонку. Давайте использовать цифру 1 в столбце шестнадцати. Затем, представляя баланс в колонке единиц, мы ставим 2. 7 плюс B равно 12 в шестнадцатеричном виде (это НЕ двенадцать, в разговоре вы бы произнесли «один два»). Мы введите 2 в 1-й столбец суммы и перенесите 1 во 2-й.
1
4817
+792Б
2
Теперь перейдите ко второй справа колонке (шестнадцатая колонка).
1
4817
+792Б
2
1 плюс 1 плюс 2 равно 4. Введите 4 в столбце суммы 2-й справа.
1
4817
+792Б
42
Теперь перейдите к 3-му столбцу справа (столбец двести пятьдесят шестой).
4817
+792Б
42
9 плюс 8 будет семнадцать. В шестнадцатеричном виде мы записываем это как двузначное число, с одна цифра в столбце шестнадцати, а другая в столбце единиц. Давайте использовать цифра 1 в шестнадцатеричной колонке. Затем, представляя баланс в столбец, ставим 1. 8 плюс 9равно 11 в шестнадцатеричном формате (это НЕ одиннадцать, вы бы произносить в разговоре «one one»). Вводим первую 1 в поле сумма 3-го столбца, а вторую 1 перенести в 4-й столбец.
1
4817
+792Б
142
Теперь перейдите к четвертой справа колонке (четыре тысячи девяносто шестой).
1
4817
+792Б
142
1 плюс 4 плюс 7 равно двенадцати в десятичном виде. В шестнадцатеричном виде у нас есть цифра для то, а именно C. Так что поместите C в 4-й столбец суммы.
1
4817
+792B
C142
C142 является окончательной суммой.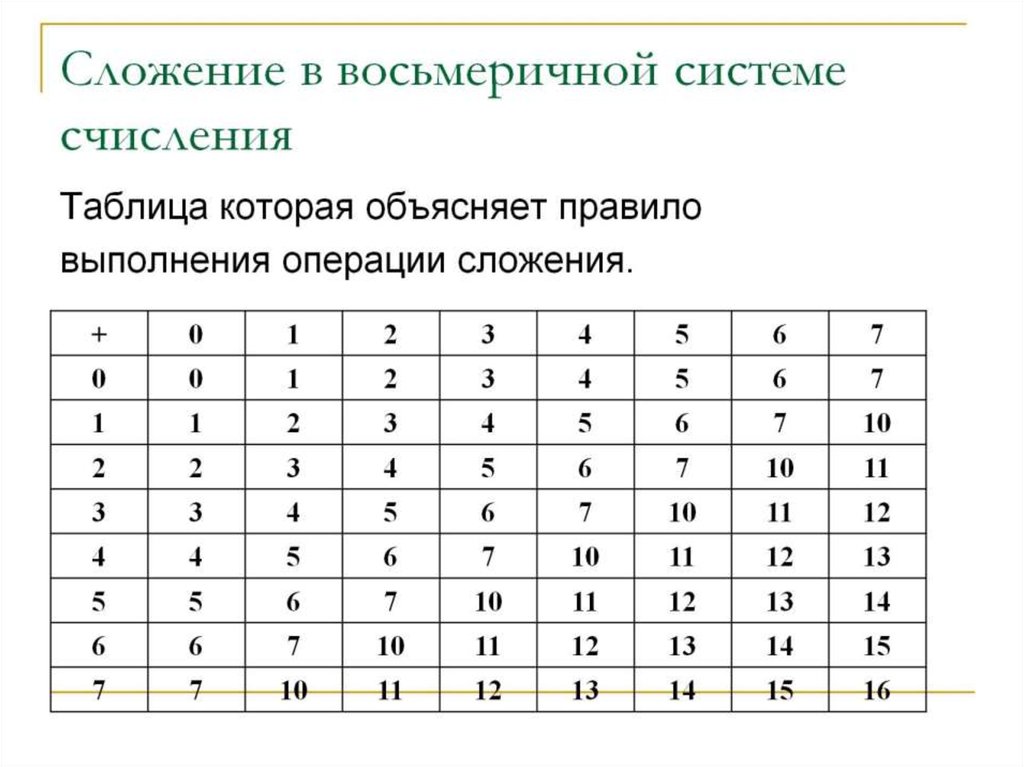 4817 плюс 392В представляет собой C142. Один из способов проверить это
состоит в том, чтобы преобразовать каждое из этих чисел в десятичное число и посмотреть, работает ли оно.
4817 плюс 392В представляет собой C142. Один из способов проверить это
состоит в том, чтобы преобразовать каждое из этих чисел в десятичное число и посмотреть, работает ли оно.
4817 в шестнадцатеричном виде равно (7 x 1) + (1 x 16) + (8 x 256) + (4 x 4096) = 18 455 дюймов.
десятичный.
792B в шестнадцатеричном виде равно (11 x 1) + (2 x 16) + (9 x 256) + (7 x 4096) = 31019 дюймов.
десятичный.
Десятичная сумма равна 18455 + 31090 = 49474. Поэтому мы надеемся, что шестнадцатеричная C142 — это десятичное число 49474. Так ли это?
Шестнадцатеричный калькулятор — Лучший онлайн-калькулятор базы чисел
Что такое шестнадцатеричное число?
Шестнадцатеричное (Hex) число — это число, выраженное в системе счисления с основанием 16 (шестнадцатеричная система счисления). Шестнадцатеричные числа представлены 16 символами. Символы «0»–«9» для представления значений от 0 до 9 и «A»–«F» для представления значений от 10 до 15.
Шестнадцатеричные арифметические операции — сложение, вычитание, умножение и деление
Сложение
Сложение шестнадцатеричных чисел аналогично десятичному сложению.
Когда результат сложения цифр превышает максимально допустимые значения, вы должны перенести избыточную сумму, разделенную по основанию (16), на цифру слева, чтобы ее можно было добавить к следующему разрядному значению.
8AC 16 + B7E 16
| 1 | 1 | ||
| 8 | A | C | |
| + | B | 7 | E |
| 1 | 4 | 2 | A |
- C 16 + E 16 = 1A 16 1 будет перенесен на следующую колонку
- 1 16 + A 16 + 7 16 = 12 16 1 будет перенесен на следующий столбец
- 1 16 + 16966 + 16 3666 + 16.
 + 16 3666 + 16 3666. + B 16 = 14 16
+ 16 3666 + 16 3666. + B 16 = 14 16
Вычитание
Вычитание шестнадцатеричного аналогично сложению, вместо переноса числа берутся из левого столбца (более значащая цифра).
8AC 16 + B7E 16
| A | 16 | ||
| B | A | 3 | |
| — | 8 | B | 3 |
| 2 | F | 0 |
- 3 16 — 3 16 = 0
- A 16 — B 16 = F 16 Поскольку A меньше, чем B, требуется заимствование, поэтому мы вычтем 1 из более значимой цифры и добавим десятичную цифру 16 к заимствуемой цифре.

- Как мы позаимствовали из B 16 , так что он станет 16 , поэтому 16 — 8 16 = 2 16
= от другого нумера. Десятичный
Обратитесь к нашему конвертеру числовой базы, чтобы узнать о преобразовании из десятичного в шестнадцатеричный. Преобразование шестнадцатеричной системы счисления в десятичную (из базы 16 в базу 10) является просто обратным процессу преобразования десятичной системы в шестнадцатеричную.
Умножьте цифры (биты) шестнадцатеричного числа, начиная с младшего (крайнего правого) бита, на 16 n , а затем сложите их все. Здесь n — позиция цифры, начиная справа, при условии, что крайняя правая цифра равна 0.
Преобразование 15A из шестнадцатеричной системы счисления в десятичную ) * 16 0 = 346 в десятичном виде
Шестнадцатеричное число в двоичное
Шестнадцатеричное число можно преобразовать в двоичное путем преобразования шестнадцатеричного числа в десятичное, а затем преобразования десятичного числа в двоичное.
Поскольку шестнадцатеричное основание 16 является степенью числа 2, шестнадцатеричное число также можно преобразовать непосредственно в двоичное. Чтобы преобразовать шестнадцатеричное число в двоичное, вам нужно просто заменить соответствующие двоичные цифры каждого шестнадцатеричного бита.
3C 16 = 0011 1100 = 111100 2
Обратитесь к нашему Калькулятору двоичной базы и преобразованию, чтобы узнать о преобразовании из двоичного в шестнадцатеричное.
Шестнадцатеричное число в восьмеричное
Шестнадцатеричное число можно преобразовать в восьмеричное путем преобразования шестнадцатеричного числа в десятичное, а затем преобразования десятичного числа в восьмеричное.
Поскольку и шестнадцатеричное основание 16, и восьмеричное основание 8 являются степенью двойки, шестнадцатеричное число также можно преобразовать в восьмеричное путем предварительного преобразования в двоичное.
Преобразуйте шестнадцатеричное число в двоичное указанным выше методом, а затем, чтобы преобразовать двоичное число в восьмеричное, разделите двоичное число на группы по 3 бита, начиная слева.


 Завет мужчины с женщиной
Завет мужчины с женщиной



 Разделим число 35 на число 14.
Разделим число 35 на число 14. 2. Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:
2. Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы: 4. Выпишите целые числа:
4. Выпишите целые числа:
 ru Все права принадлежат авторам размещенных материалов. Обратная связь…
ru Все права принадлежат авторам размещенных материалов. Обратная связь…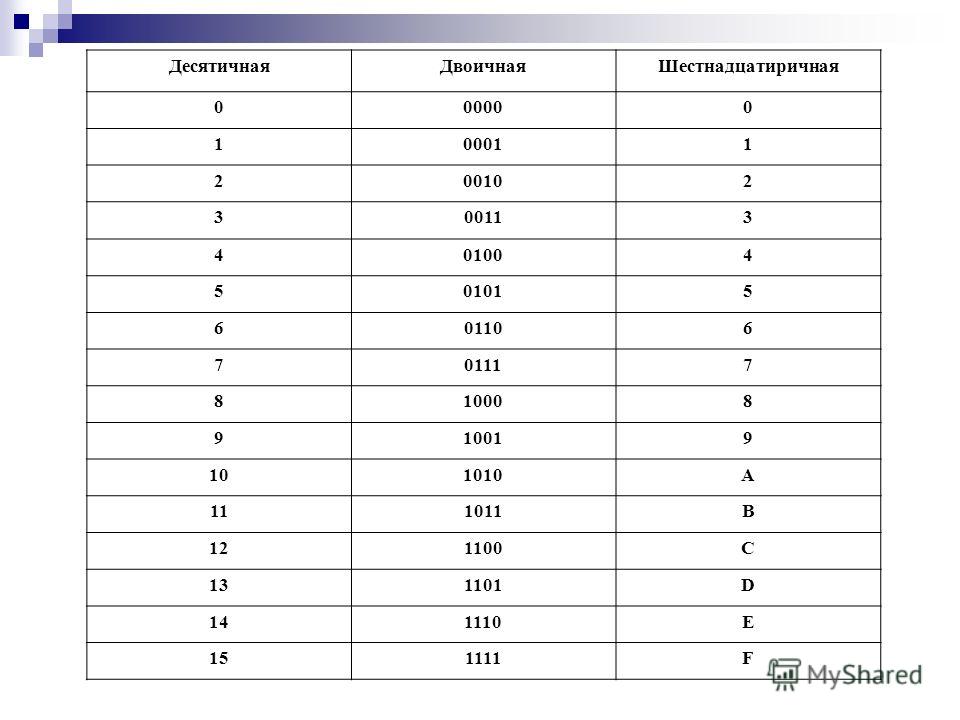 + 16 3666 + 16 3666. + B 16 = 14 16
+ 16 3666 + 16 3666. + B 16 = 14 16 