Скорость волны в физике, теория и онлайн калькуляторы

Скорость волны в физике, теория и онлайн калькуляторы

Определение скорости волны

Геометрическое место точек среды, для которых в некоторый момент времени фаза волны имеет одно и то же значение, называют волновой поверхностью или фронтом волны.

Определение

Скорость перемещения фронта волны называется скоростью волны.

Если рассматривается одномерный случай гармонической волны, то уравнение волновой поверхности имеет вид:

\[Ф_s=\omega t-kx+\varphi \ \left(1\right),\]

где${\ Ф}_s$ — фаза волны; $k=\frac{2\pi }{\lambda }$ — волновое число; $\lambda $ — длина волны; $\omega $ — циклическая частота; $\varphi $ — начальная фаза. Условию (1) в каждый момент времени соответствует только одна точка оси X c координатой, равной:

\[x=\frac{\omega t+\varphi -Ф_s}{k}\left(2\right).\]

Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне вырождается в точку.

Из выражения (2) видно, что волновые поверхности с течением времени перемещаются в веществе со скоростью:

\[\frac{dx}{dt}=\frac{\omega }{k}=\frac{\lambda }{T}=v\ \left(3\right).\]

Для гармонических волн скорость движения поверхности волны совпадает со скоростью распространения волны. Скорость, определенная выражением (3) называют фазовой скоростью.

В случае гармонической волны скорость распространения энергии совпадает с фазовой скоростью волны.

Скорость волны зависима от среды и типа волны. Скорость волны не надо путать со скоростью колебания частиц среды в волне.

Фазовая скорость распространения продольных волн

Скорость распространения продольных упругих волн в однородных в газах или жидкостях равна:

\[v=\sqrt{\frac{K}{\rho }}\left(4\right),\]

где $K$ — модуль объемной упругости вещества; $\rho =const$ — плотность среды. В газах формула (4) справедлива, если избыточное давление много меньше, чем равновесное давление невозмущенного газа.

Для определения скорости распространения продольных волн в газе используют формулу:

\[v=\sqrt{\frac{\gamma p}{\rho }}\left(5\right),\]

где $\gamma $ — показатель адиабаты; $p$ — давление газа.

Фазовая скорость распространения продольных волн в твердом теле:

\[v=\sqrt{\frac{E}{\rho }}\left(6\right),\]

где $E$ — модуль Юнга вещества стержня.

Фазовая скорость распространения поперечных волн

Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде можно вычислить как:

\[v=\sqrt{\frac{G}{\rho }\left(7\right),}\]

где $G$ — модуль сдвига среды; $\rho $ — плотность вещества.

Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.

Групповая скорость волн

Для диспергирующих волн помимо фазовой скорости волны следует использовать такое понятие как групповая скорость. Если фазовая скорость зависит от частоты и в среде распространяются волны сложного негармонического характера, то при помощи групповой скорости характеризуют распространение волн.

Групповой скоростью называют скорость движения группы (цуга) волн, которые создают в каждый момент времени локализованный в пространстве волновой пакет. Любая реальная волна является суперпозицией гармонических волн. Скорость с которой такая волна распространяется в веществе, имеющем дисперсию на равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.

Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой:

\[u=v-\frac{dv}{d\lambda }\left(8\right).\]

Если дисперсия отсутствует, то $\frac{dv}{d\lambda }=0$, тога фазовая и групповая скорости равны и не зависят от длины волны. {-3}}}\approx 350\ \left(\frac{м}{с}\right).\]

Ответ: $v=350\frac{м}{с}$

   

Пример 2

Задание: Какова скорость распространения волны в упругой среде, если разность фаз точек, которые находятся на расстоянии $\Delta x,$ равна $\Delta \varphi $ при частоте колебаний равной $\nu $?

Решение: Рассмотрим уравнение одномерной плоской волны:

\[s=A{\cos \left[\omega t-kx+\varphi \right]\ }\left(2.1\right).\]

где

\[k=\frac{2\pi }{\lambda }=\frac{\omega }{v}\left(2.2\right).\]

Фазы колебаний двух точек в этой волне равны:

\[{\varphi }_1=\omega t-kx_1+\varphi ;;\ {\varphi }_2=\omega t-kx_2+\varphi \left(2.3\right).\]

Найдем их разность:

\[\Delta \varphi =\omega t-kx_2+\varphi -\left(\omega t-kx_1+\varphi \right)=k\left(x_2-x_1\right)=\frac{\omega }{v}\Delta x\left(2.

4\right).\]

Выразим циклическую частоту ($\omega $) через частоту $\nu $:

\[\omega =2\pi \nu \ \left(2.5\right).\]

Выражение (2.4) преобразуем к виду:

\[\Delta \varphi =\frac{\omega}{v} \Delta x=\frac{2 \pi \nu}{v} \Delta x\left(2.6\right).\]

Из (2.6) выразим искомую скорость:

\[v=\frac{2 \pi \nu \Delta x}{\Delta \varphi }(\frac{м}{с}).\]

Ответ: $v=\frac{2 \pi \nu \Delta x}{\Delta \varphi }\frac{м}{с}$

   

Читать дальше: скорость движения.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Длина волны. Скорость распространения волны (Ерюткин Е.С.) 9 класс онлайн-подготовка на Ростелеком Лицей

Тема 12: Механические колебания и волны. Звук

• Видео
• Тренажер
• Теория

Заметили ошибку?

Введение

 

Для начала вспомним, что механическая волна – это колебание, которое распространяется с течением времени в упругой среде. Раз это колебание, волне будут присущи все характеристики, которые соответствуют колебанию: амплитуда, период колебания и частота.

 

 

Длина волны

 

 

Кроме этого, у волны появляются свои особые характеристики. Одной из таких характеристик является длина волны. Обозначается длина волны греческой буквой  (лямбда, или говорят «ламбда») и измеряется в метрах. Перечислим характеристики волны:

 

Что такое длина волны?

Длина волны – это наименьшее расстояние между частицами, совершающими колебание с одинаковой фазой.

Рис. 1. Длина волны, амплитуда волны

Говорить о длине волны в продольной волне сложнее, потому что там пронаблюдать частицы, которые совершают одинаковые колебания, гораздо труднее. Но и там есть характеристика – длина волны, которая определяет расстояние между двумя частицами, совершающими одинаковое колебание, колебание с одинаковой фазой.

Также длиной волны можно назвать расстояние, пройденное волной, за один период колебания частицы (рис. 2).

Рис. 2. Длина волны

 

Скорость волны

 

 

Следующая характеристика – это скорость распространения волны (или просто скорость волны). Скорость волны обозначается так же, как и любая другая скорость, буквой  и измеряется в . Как наглядно объяснить, что такое скорость волны? Проще всего это сделать на примере поперечной волны.

 

Поперечная волна – это волна, в которой возмущения ориентированы перпендикулярно направлению ее распространения (рис. 3).

Рис. 3. Поперечная волна

Представьте себе летящую над гребнем волны чайку. Ее скорость полета над гребнем и будет скоростью самой волны (рис. 4).

Рис. 4. К определению скорости волны

 

Связь длины волны и ее скорости

 

 

Скорость волны зависит от того, какова плотность среды, каковы силы взаимодействия между частицами этой среды. Запишем связь между скоростью волны, длиной волны и периодом волны: .

 

Скорость можно определить, как отношение длины волны, расстояние, пройденное волной за один период, к периоду колебания частиц среды, в которой распространяется волна. Кроме этого, вспомним, что период связан с частотой следующим соотношением:

Тогда получим соотношение, которое связывает скорость, длину волны и частоту колебаний: .

Мы знаем, что волна возникает в результате действия внешних сил. Важно заметить, что при переходе волны из одной среды в другую изменяются ее характеристики: скорость движения волн, длина волны. А вот частота колебания остается прежней.

 

Список литературы

1. Соколович Ю. А., Богданова Г. С. Физика: справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: издательство «Ранок», 2005. – 464 с.
2. Перышкин А. В., Гутник Е. М., Физика. 9 кл.: учебник для общеобразоват. учреждений / А. В. Перышкин, Е. М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «eduspb» (Источник)
2. Интернет-портал «eduspb» (Источник)
3. Интернет-портал «class-fizika.narod.ru» (Источник)

 

Домашнее задание

1. Поплавок совершает колебания на волнах. За 10 с он совершил 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?
2. Тело совершает гармонические колебания по закону  м. Определите амплитуду, период, частоту, смещение и скорость в момент времени 0,1 с.
3. Определите длину звуковой волны ноты, если ее частота колебаний 430 Гц, а скорость звука в воздухе 340 м/с?

 

Заметили ошибку?

Расскажите нам об ошибке, и мы ее исправим.

Видеоурок: Длина волны. Скорость распространения волны (Ерюткин Е.С.) по предмету Физика за 9 класс.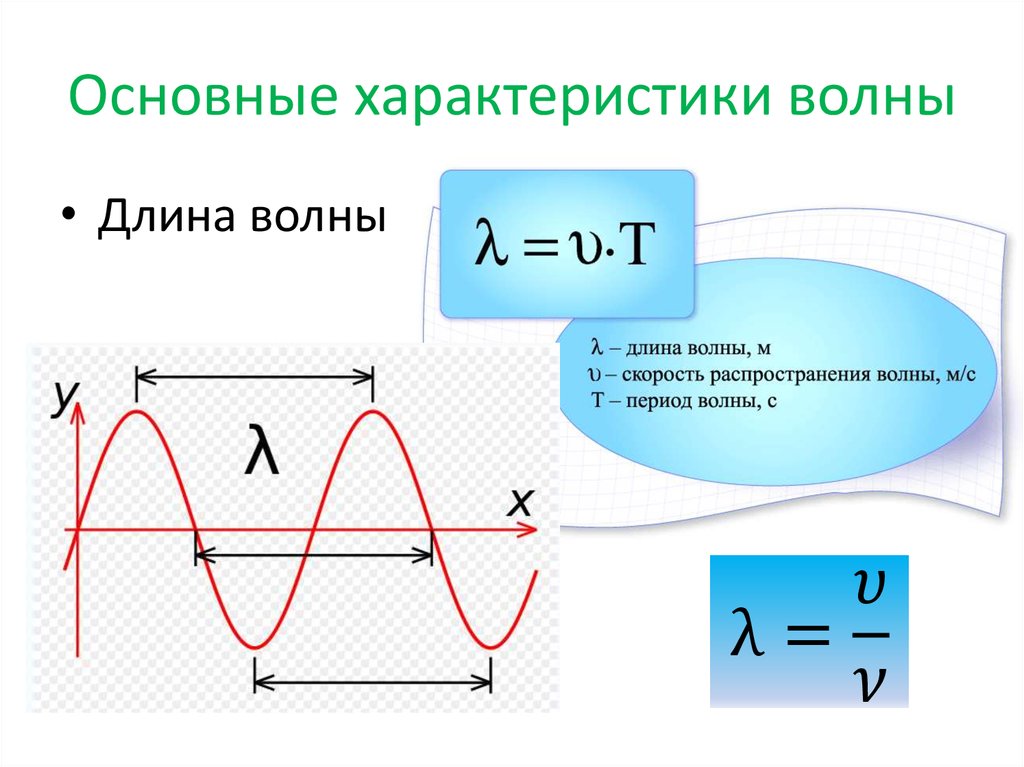

Скорость волны — Видео по физике от Brightstorm

Хорошо. Поговорим о скорости волны. И особенно его отношение к частоте и длине волны. Это действительно самое важное, что вы увидите в подобных задачах по вводной физике.

Хорошо. Итак, движение волны, поскольку волна — это то, что создается возмущением, а затем просто распространяется по своей воле через среду, движение волны зависит только от свойств самой среды. А это значит, что его скорость может зависеть только от среды. Но это не означает, что он не зависит от длины волны и периода. Это зависит от длины волны и периода. Просто по стандартной формуле. Скорость равна расстоянию, деленному на время. Теперь, если у меня есть периодическая волна, которая распространяется через среду, как далеко она распространяется? Ну, если я про одно из возмущений, то расстояние равно длине волны. Сколько времени это занимает? Ну, если я говорю об одном из возмущений, то время равно периоду. А это значит, что скорость равна длине волны, деленной на период.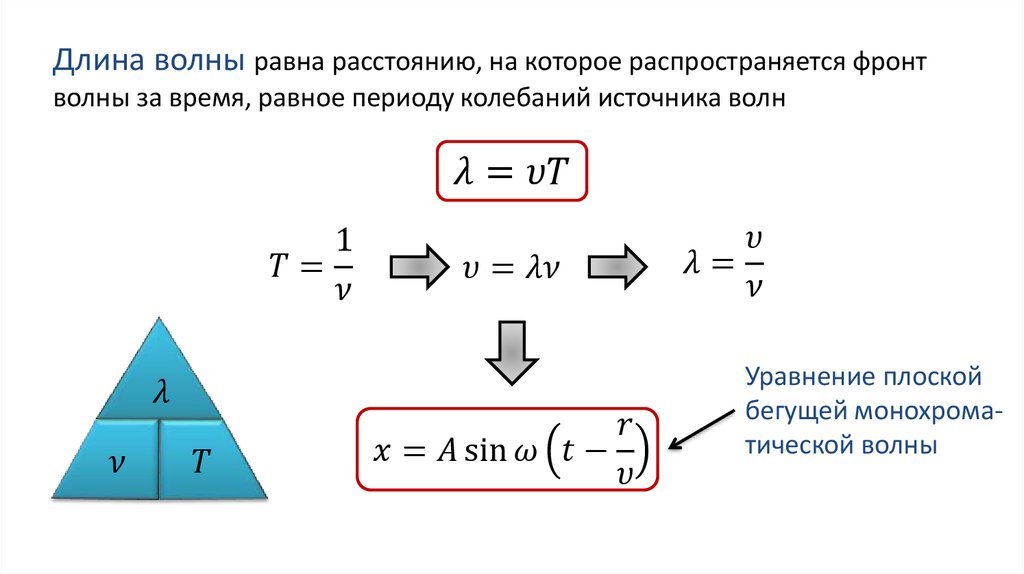

Теперь мы можем записать это в более привычной форме, просто взяв коэффициент [IB] и вспомнив, что единица за период равна частоте. Это означает, что скорость равна длине волны, умноженной на частоту. Это уравнение чрезвычайно распространено. вы будете видеть это все время в этом разделе физики. Хорошо. Итак, давайте посмотрим, что это значит.

Если я говорю о волнах, распространяющихся через одну и ту же среду, то скорость должна быть постоянной. Это означает, что длина волны, умноженная на частоту, постоянна. Это означает, что если длина волны увеличивается, частота должна уменьшаться. Наоборот. Если длина волны уменьшается, то частота увеличивается. Итак, длинноволновые волны имеют очень-очень малые частоты, тогда как коротковолновые волны тоже очень быстрые и имеют высокие частоты. Хорошо. Давайте посмотрим, как мы можем использовать эту идею для решения некоторых проблем.

Процедура довольно проста, но я хотел проиллюстрировать пару распространенных ошибок, которые совершают люди. Хорошо. Итак, номер один, очень прямолинейно, волна имеет длину волны два сантиметра и частоту 300 герц. Какова его скорость? Итак, v равно лямбда f. Итак, я собираюсь сказать, хорошо, хорошо, v равно лямбда f. Таким образом, лямбда составляет 2 сантиметра, а f — 300 герц. Итак, когда я умножаю 2 на 300, я получаю 600, но какая теперь единица измерения? Хорошо, хорошо, если я просто сделаю это напрямую, это будут сантиметры. Герц — это количество волн в секунду. Так что это будет в секунду. Но это конечно не СИ. Что мне действительно нужно сделать, так это впитать эти 100 в сенте и записать ответ как 6 метров в секунду. И если я это сделаю, вообще никаких проблем. И если я не помню, чтобы сделать это, и это проблема со свободным ответом, я в порядке. Пока я писал это в сантиметрах в секунду, это правильно. Абсолютно прав. Но если это задача с множественным выбором, скорее всего, ответ будет таким, и я должен быть в состоянии распознать это.

Хорошо. Задача 2. В среде распространяется волна с длиной волны 20 мм. Итак, теперь я хочу знать, какова длина волны, частота которой вдвое больше. Хорошо. Сейчас. Я не знаю, какая здесь скорость. Так что я действительно не могу, я не могу получить частоту. Но дело в том, что мне это не нужно. Потому что я знаю, что длина волны, умноженная на частоту, постоянна. Итак, я умножаю частоту на 2. Так что же это означает для длины волны? Что ж, если произведение постоянное, а здесь я получил 2, то здесь я должен получить половину. Итак, я собираюсь умножить длину волны на половину с половиной от 20, 10. Вот и все. Хорошо? Теперь идея в том, что мне не нужно было иметь номера для всего. Часто задачи так задаются в подобных подразделениях, так что надо просто знать, как это настроить. Это не сложно, но вам просто нужно знать, как это сделать, и это требует некоторой практики. Хорошо.

Итак, давайте посмотрим на последний. Волна с длиной волны 21 миллиметр движется в среде со скоростью, равной одной трети скорости волны. Хорошо. Что-то здесь происходит. Мы больше не в одной среде. Хорошо. Итак, мы должны помнить кое-что, когда переходим к другой среде. Частота не может измениться, как и период. В остальном все ставки сняты, частота и период должны оставаться прежними. Пока это одна и та же волна, частота и период одинаковы. Все остальное может измениться, ясно?

Итак, входит в среду со скоростью, равной одной трети скорости волны, и я хочу узнать новую длину волны. Хорошо. Вот идея. Скорость равна длине волны, умноженной на частоту. Мы сказали, что частота не может измениться, скорость упала в 3 раза. Частота та же. Не могу изменить. Так что же это означает в отношении длины волны? Это означает, что длина волны должна уменьшиться в три раза, потому что длина волны может изменяться. Поэтому, как только мы признаем это, проблема становится легкой. 21 разделить на 3 равно 7. Готово. Но нам нужно понять этот простой факт. Сейчас я видел много задач, которые написаны еще проще, чем эта, где будет сказано, какая новая частота? Вместо этого он даст нам частоты, или частота будет повышаться, понижаться или останется прежней? Частота должна оставаться неизменной, потому что частота не может измениться. И как только мы признаем это и что это уравнение всегда верно, длина волны и скорость должны делать одно и то же.

Хорошо. Это скорость волны.

Руководство по изучению скорости волны | Inspirit

Инструменты для творчества скоро появятся, чтобы вдохновить!

Присоединяйтесь к списку рассылки, чтобы узнать, когда мы запустимся.

Физика

Общая физика

Гармоническое движение и волны

Учебное пособие по скорости волн

Джессика

MS-PS4-1

Расстояние, пройденное волной за определенный промежуток времени, называется скоростью волны.

Что такое скорость волны?

Расстояние, которое волна проходит за определенное время, например количество метров, которое волна проходит за секунду, называется скоростью волны. Защипывание гитарной струны является примером скорости волны.

Если кто-то дернет гитарную струну, кажется, что струны движутся в виде поперечной волны. Хотя звуковая волна представляет собой продольную волну, волна на гитаре поперечная. Частицы в струне движутся перпендикулярно направлению распространения волны.

ФОРМУЛА СКОРОСТИ ВОЛНЫ

Уравнение скорости волны (скорость = длина волны x частота) связывает скорость волны с длиной волны и частотой. Когда длина волны и частота известны, это уравнение можно использовать для расчета скорости волны.

Частота волн — это количество волн, которые движутся в секунду. Кроме того, продолжительность рассчитывается как обратная величина частоты волны. Длина волны — это расстояние между соответствующими точками двух последовательных волн.

ПЕРЕМЕННЫЕ, ВЛИЯЮЩИЕ НА СКОРОСТЬ ВОЛНЫ

• Длина волны
• Скорость
• Расстояние
• Частота

Вышеуказанные четыре переменные влияют на скорость волны.

ЗАВИСИМОСТЬ СРЕДЫ

• Скорость большинства волн зависит от среды, через которую распространяется волна.
• Волны обычно быстрее всего проходят через твердые тела и медленнее всего через газ.
• Это потому, что частицы ближе всего друг к другу в твердом теле, а частицы ближе всего друг к другу в газе.
• Если частицы находятся дальше друг от друга, распределению энергии потребуется больше времени, чтобы пройти через среду от одной частицы к другой.

###Свойства волн

__1. Амплитуда __

Во время волнового движения частицы колеблются вокруг своего среднего положения или положения равновесия, создавая звуковые волны. Максимальное смещение частиц выше или ниже среднего положения называется амплитудой, или можно сказать, что Амплитуда — это максимальная высота выше или ниже среднего положения. Амплитуда обозначается X0, а единицей амплитуды в системе СИ является метр.

__2. Длина волны __

Поперечные волны распространяются в последовательных или последовательных гребнях и впадинах, в то время как продольные волны распространяются в последовательном сжатии и разрежении.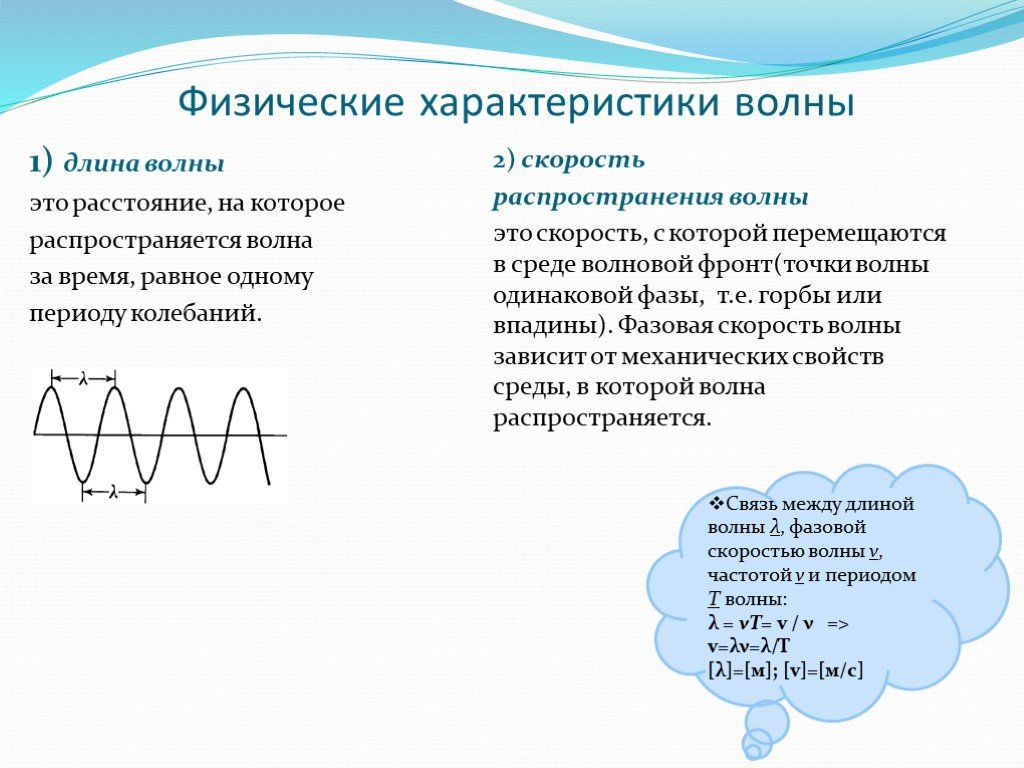 В случае поперечных волн длина последовательной коры и впадины называется ее длиной волны. В то время как в случае продольных волн длина последовательного сжатия и разрежения называется ее длиной волны. Длина волны обозначается греческой буквой лямбда (λ), а ее единицей СИ является метр.

3. Период времени

Чтобы понять концепцию периода времени, мы должны понять концепцию волнового цикла. В случае поперечных волн одна кора и одна впадина образуют один волновой цикл или одно колебание, а в случае продольных волн одно сжатие и одно разрежение образуют один волновой цикл или одно колебание. Общее число волновых циклов зависит от количества корок и впадин в поперечных волнах, тогда как в случае продольных волн оно зависит от числа сжатий и разрежений. Время, за которое колеблющееся тело совершает один волновой цикл или одно колебание, называется периодом времени. Период времени обозначается буквой Т, а его единицей СИ является секунда. Например, если волна завершает свое колебание или один волновой цикл за две секунды, то ее период времени составляет T = 2 секунды.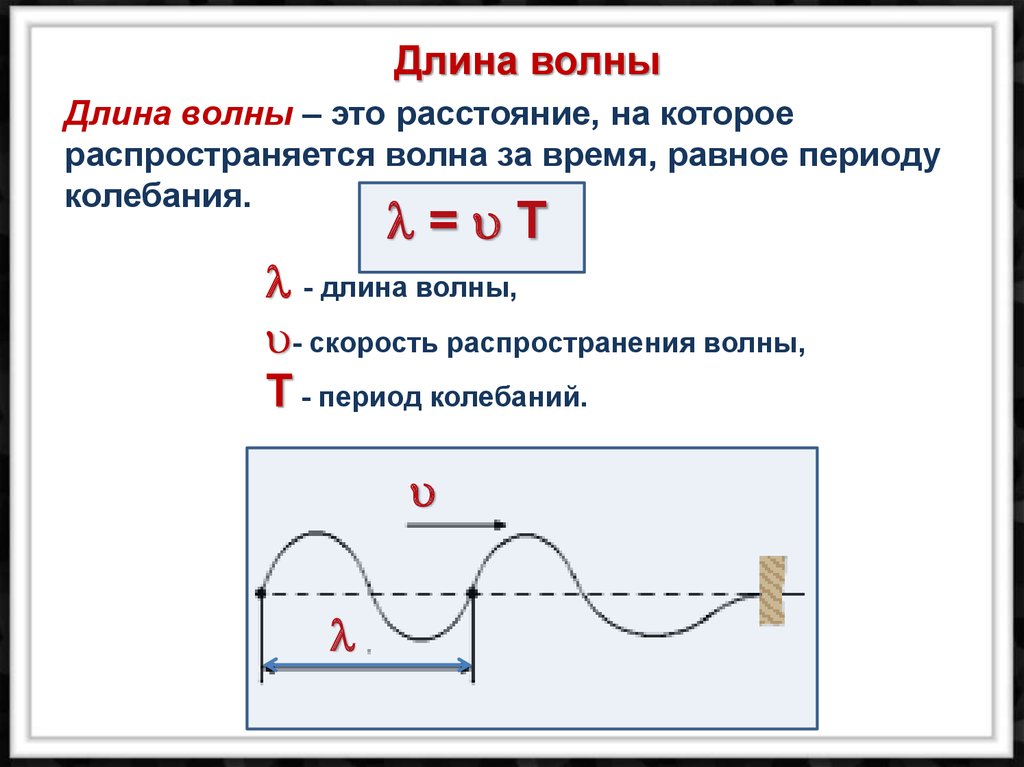

4. Частота Количество волновых циклов или количество колебаний, совершенных за одну секунду. Частота обозначается f. Единицей частоты в системе СИ является герц. Например, если волна совершает три колебания за одну секунду, то частота этой волны равна трем герцам. Частота обратно пропорциональна периоду времени.

Пример скорости волны

Резюме

• Уравнение скорости волны (скорость = длина волны x частота) связывает скорость волны с длиной волны и частотой.
• Когда длина волны и частота известны, это уравнение можно использовать для расчета скорости волны.
• Частота волны — это количество волн, которые движутся за одну секунду.
• Кроме того, период времени рассчитывается как величина, обратная частоте волны.
• Длина волны — это расстояние между соответствующими точками любых двух последовательных волн.

Часто задаваемые вопросы

В. Что такое скорость волны?

Расстояние, пройденное данной точкой (например, вершиной) волны за данный интервал времени, является скоростью в случае волны.