Сила трения скольжения — это… Что такое Сила трения скольжения?

Сила трения скольжения — силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.

Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения и не зависит от площади соприкосновения. (Это можно объяснить тем, что никакое тело не является абсолютно ровным. Поэтому истинная площадь соприкосновения гораздо меньше наблюдаемой. Кроме того, увеличивая площадь, мы уменьшаем удельное давление тел друг на друга.) Величина, характеризующая трущиеся поверхности, называется коэффициентом трения, и обозначается чаще всего латинской буквой «k» или греческой буквой «μ». Она зависит от природы и качества обработки трущихся поверхностей. Кроме того, коэффициент трения зависит от скорости. Впрочем, чаще всего эта зависимость выражена слабо, и если большая точность измерений не требуется, то «k» можно считать постоянным.

В первом приближении величина силы трения скольжения может быть рассчитана по формуле:

, где

 — коэффициент трения скольжения,

 — сила нормальной реакции опоры.

По физике взаимодействия трение принято разделять на:

• Сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазками — очень редко встречающийся на практике случай. Характерная отличительная черта сухого трения — наличие значительной силы трения покоя.
• Сухое с сухой смазкой (графитовым порошком)
• Жидкостное, при взаимодействии тел, разделённых слоем жидкости или газа (смазки) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость;
• Смешанное, когда область контакта содержит участки сухого и жидкостного трения;
• Граничное, когда в области контакта могут содержатся слои и участки различной природы (окисные плёнки, жидкость и т. д.) — наиболее распространённый случай при трении скольжения.

В связи со сложностью физико-химических процессов, протекающих в зоне фрикционного взаимодействия, процессы трения принципиально не поддаются описанию с помощью методов классической механики.

При механических процессах всегда происходит в большей или меньшей степени преобразование механического движения в другие формы движения материи (чаще всего в тепловую форму движения). В последнем случае взаимодействия между телами носят названия сил трения.

Опыты с движением различных соприкасающихся тел (твёрдых по твёрдым, твёрдых в жидкости или газе, жидких в газе и т. п.) с различным состоянием поверхностей соприкосновения показывают, что силы трения проявляются при относительном перемещении соприкасающихся тел и направлены против вектора относительной скорости тангенциально к поверхности соприкосновения. При этом всегда происходит нагревание взаимодействующих тел.

Силами трения называются тангенциальные взаимодействия между соприкасающимися телами, возникающие при их относительном перемещении. Силы трения возникающие при относительном перемещении различных тел, называются силами внешнего трения.

Силы трения возникают и при относительном перемещении частей одного и того же тела. Трение между слоями одного и того же тела называется внутренним трением.

В реальных движениях всегда возникают силы трения большей или меньшей величины. Поэтому при составлении уравнений движения, строго говоря, мы должны в число действующих на тело сил всегда вводить силу трения F тр.

Тело движется равномерно и прямолинейно, когда внешняя сила уравновешивает возникающую при движении силу трения.

Для измерения силы трения, действующей на тело, достаточно измерить силу, которую необходимо приложить к телу, чтобы оно двигалось без ускорения.

Движение тела под действием силы трения

Ускорение тела, возникающее вследствие силы трения

Известно, что сила трения скольжения направлена в сторону, противоположную направлению относительной скорости движения трущихся тел.

Отсюда следует, что ускорение, которое такая сила сообщает движущемуся телу, тоже направлено против относительной скорости. А это значит, что действие силы трения приводит к уменьшению абсолютного значения скорости тела относительно того тела, по которому оно скользит.

Если на тело, которое скользит по неподвижной поверхности, никакие силы, кроме силы трения не действуют, то оно, в конце концов, останавливается. Рассмотри этот часто встречающийся случай.

Представим себе, что перед движущимся поездом неожиданно появилось некоторое препятствие и машинист отключил двигатель и включил тормоз. Начиная с это момента, на поезд действует только сила трения, так как сила тяжести скомпенсирована реакцией рельсов, а сила сопротивления воздуха мала. Через некоторое время $t$ поезд, пройдя расстояние $l$ — тормозной путь, остановится. Найдем время $t$, нужное для остановки, и расстояние $l$, которое поезд пройдет за это время.

Под действием сила трения $\overline{F}_{mp} $поезд будет двигаться с ускорением, равным:

Выберем координатную ось $x$ так, чтобы ее положительное направление совпадало с направлением скорости движения поезда.

Рисунок 1.

Так как сила трения $\overline{F}_{mp} $направлена в противоположном направлении, ее проекция на ось х отрицательна. Отрицательна и проекция вектора ускорения на ось $x$. Поэтому если абсолютное значение силы трения равно $\left|\overline{F}_{mp} \right|$, то:

Но ускорение определяется также формулой:

где $v_{0} $- скорость поезда до начала торможения.

Время торможения при движении тела под действием силы трения

Так как нас интересует промежуток времени $t$ от начала торможения до остановки поезда, то конечная скорость $v=0$. Тогда:

Таким образом:

Получим выражения для времени торможения:

Нахождение пути, пройденного телом под действием силы трения

А теперь найдем тормозной путь $l$. Для этого воспользуемся формулой:

Так как $v=0$, то:

Так как $\overline{a}=-\frac{\left|\overline{F}_{mp} \right|}{m} $, получим:

Из этой формулы видно, что пройденный до остановки путь пропорционален квадрату скорости. Если увеличить скорость вдвое, то потребуется вчетверо больший путь для остановки.

Пример 1

С какой скоростью двигался автомобиль, если после выключения двигателя он прошел до остановки путь равный $80$ м? Коэффициент трения принять равным $0,25$.

Дано: $l=80$м, $\mu =0,25$.

Найти: $v$-?

Решение:

Воспользуемся раннее выведенными формулами для нахождения тормозного пути:

$l=\frac{mv_{0}^{2} }{2\overline{\left|F_{mp} \right|}} $. (1)

Так как $F_{mp} =\mu mg$, подставим в формулу (1) и получим:

$l=\frac{mv_{0}^{2} }{2\mu mg} $. (2)

Выразив из формулы (2) $v_{0} $найдем величину искомой скорости:

$v_{0} =\sqrt{2\mu gl} =20$м/с

Ответ: Скорость автомобиля до выключения двигателя $v_{0} =20$ м/с.

Пример 2

Сноубордист массой $80$ кг, имеющий в конце спуска скорость $20$ м/с, останавливается через $40$ с после окончания спуска. Определите силу трения и коэффициент трения.

Дано: $m=80$кг, $v_{0} =20$м/с, $t=40$с.

Найти: $F_{mp} $, $\mu $-?

Решение:

Уравнение движения сноубордиста будет иметь вид:

\[ma=F_{mp} .\]

Используя выражения для нахождения ускорения (конечная скорость $v=0$), получим:

\[a=-\frac{v_{0} }{t} .\]

Тогда:

$F_{mp} =ma=-m\frac{v_{0} }{t} =40H$.

Так как сила трения $\overline{F}_{mp} $равна $F_{mp} =\mu Bg$, находим коэффициент трения $\mu $:

\[\mu =\frac{F_{mp} }{mg} =0,05.\]

Ответ: $F_{mp} =40H$, $\mu =0,05$.

Пример 3

Сани массой $16$ кг перемещают по горизонтальной плоскости под действием силы $180 H$, направленной под углом $30^\circ$ к горизонтали. Коэффициент терния саней о плоскость $0,5$. Определить ускорения, с которым движутся сани.

Дано: $m=16$кг, $F=180 H$, $\alpha =30^\circ$, $\mu =0,5$.

Найти: $a$-?

Решение:

Рисунок 2.

Уравнение движения тела:

\[m\overline{a}=m\overline{g}+\overline{N}+\overline{F}+\overline{F}_{mp} .\]

Выберем направление осей $x$ и $y$ и спроецируем на них силы и ускорение:

\[\begin{array}{l} {ma=F\cos \alpha -F_{mp} } \\ {0=-Bg+N+F\sin \alpha } \end{array}\]

Поскольку $F_{mp} =\mu N$, а из второго уравнения $N=mg-F\sin \alpha $, то $F_{mp} =\mu (mg-F\sin \alpha )$. Тогда из первого уравнения ускорение:

$a=\frac{1}{m} [F\cos \alpha -\mu (mg-F\sin \alpha )]\approx 7,6м/с^2$

Ответ: $a$=$7,6м/с^2$

Силы трения

Классифицируя силы трения, прежде всего, разделяют сухое и вязкое трение (рис. 3.6).Первое возникает между сухими твёрдыми поверхностями тел, а второе — при движении в вязкой среде, либо при относительном движении тел, разделённых смазочным слоем.

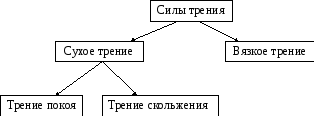
Рис. 3.6

При сухом трении, в свою очередь, различают трение покоя и трение скольжения.

3. Сухое трение

Приложим «небольшую» силу к телу, лежащему на горизонтальной поверхности. «Небольшую» — то есть, недостаточную для начала движения. Тело будет оставаться в покое, потому что кроме приложенной нами силы 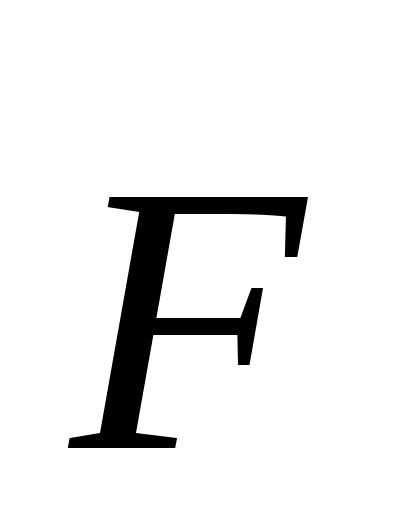на тело будет действовать равная и противоположно направленная сила трения. Это и есть «сила трения покоя» (рис. 3.7). Тело будет оставаться в покое при изменении направления приложенной силы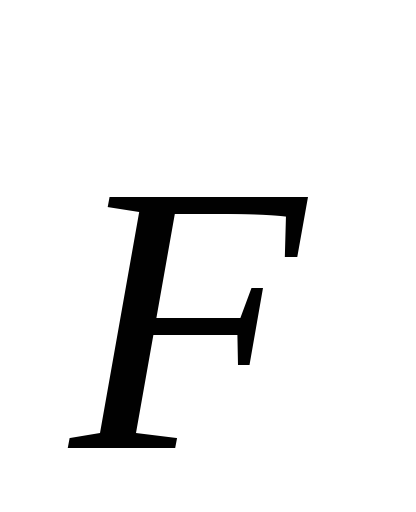и, в известных пределах, её величины. Это означает, что с изменением силыбудет меняться величина и направление силы трения покоя.

Увеличивая приложенное усилие 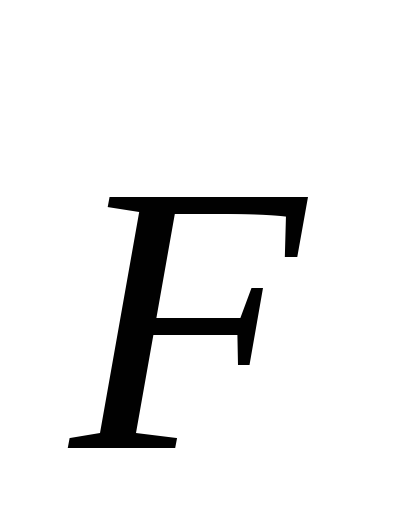, мы будем наблюдать рост силы трения покоя. Однако, этот рост не безграничен. Когда сила трения покоя достигнет своего предельного значения, начнётся скольжение тела по поверхности. Максимальная сила трения покоя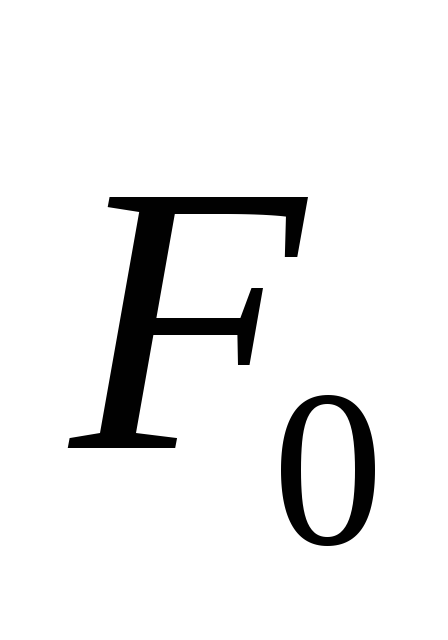зависит от материала контактирующих поверхностей, качества их обработки и от величины силы, прижимающей тело к поверхности — силы нормального давленияN.

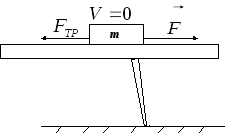
Рис. 3.7

Если приложенная сила FпревышаетF₀, тело будет двигаться с ускорением, пропорциональным равнодействующей силыFи силы трения — теперь уже скольжения —F_тр.

Согласно опытному закону Амонтона (1699) максимальное значение силы трения покоя F₀и сила трения скольжения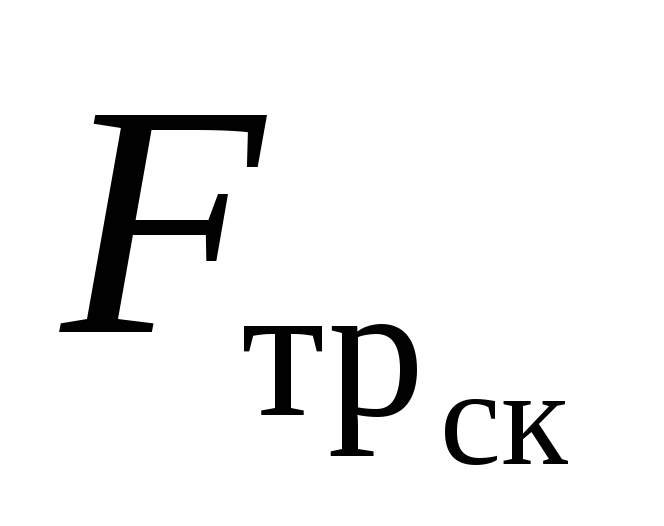пропорциональны величине силы нормального давления, прижимающей трущиеся поверхности друг к другуN:

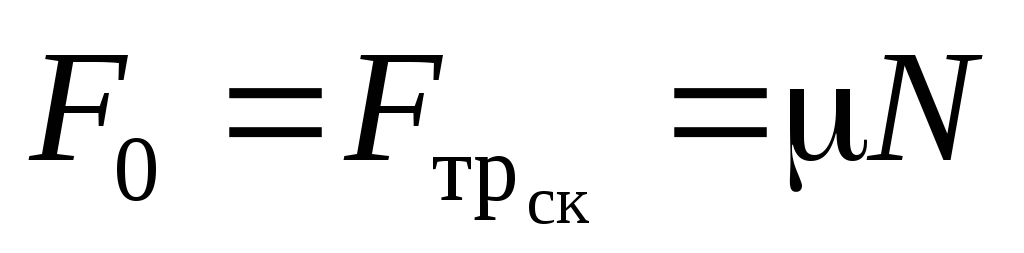. (3.11)

Здесь — коэффициент сухого трения. Это табличная величина, связанная как уже отмечалось, с материалом трущихся поверхностей и качеством их обработки.

Сила трения скольжения не зависит от площади поверхности соприкосновения тел.

4. Вязкое трение

Сила вязкого трения действует на тело, движущееся в вязкой среде (жидкой или газообразной). Она зависит от формы и размеров тела, скорости его движения, а также от физических свойств среды: в частности — от плотности и вязкости.

Н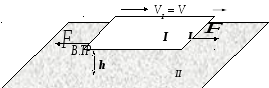ьютон экспериментально исследовал силу вязкого трения, возникающую при относительном скольжении двух поверхностей I и II, разделённых слоем жидкости (рис. 8).

Рис. 3.8

Эта сила оказалась пропорциональной скорости Vподвижной пластины I, её площадиSи обратно пропорциональной толщинеhразделительного слоя жидкости:

. (3.12)

Здесь — вязкость жидкости, [Пас].

В 1851 году английский физик Джордж Стокс рассчитал силу вязкого сопротивления, действующую на твёрдый шар радиуса rпри его медленном поступательном движении в неограниченной вязкой среде:

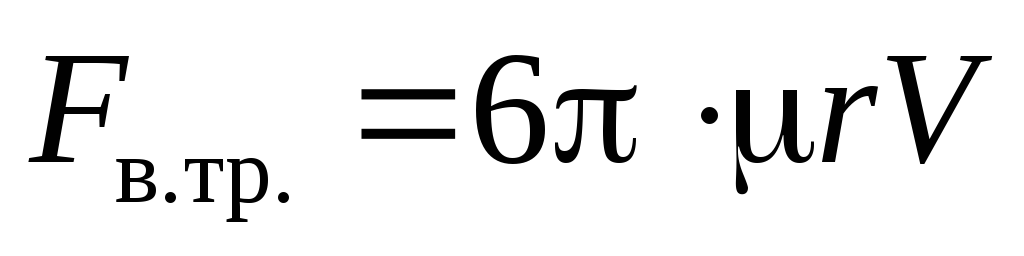. (3.13)

Эта формула известна как закон Стокса.

Покажем, как, используя этот закон, можно экспериментально определить вязкость жидкости .

На шар радиуса r, падающий в вязкой среде будут действовать три силы (рис. 9): сила тяжестиP=_тgV, сила вязкого сопротивленияF_в.тр.= 6rv и сила гидростатического выталкивания (Архимеда)F_Арх.=_жgV. Здесь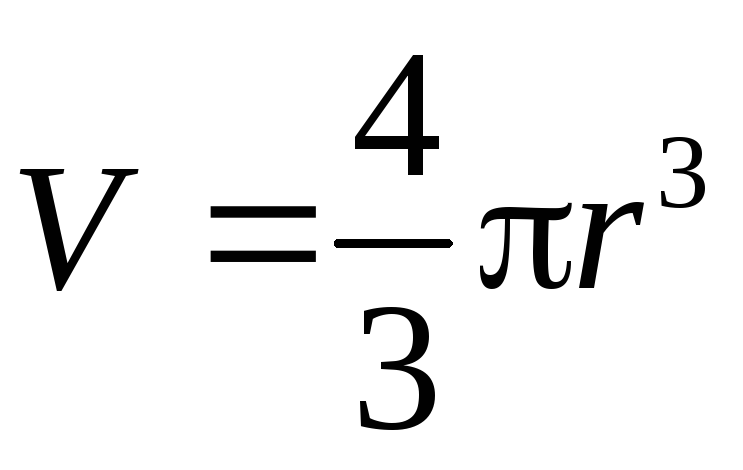— объём шара.

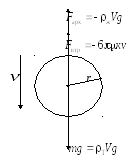
Рис. 3.9

Под действием этих сил движение шара будет происходить с ускорением:

.

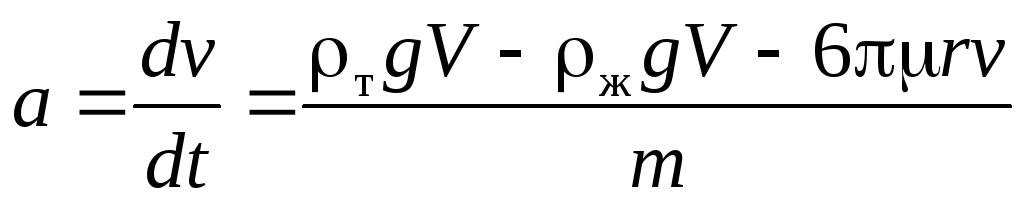Важно подметить, что в числителе этого выражения первые два слагаемых остаются постоянными, а третье в процессе движения увеличивается по мере роста скорости шара v.

При этом ускорение будет уменьшаться и станет равным нулю, когда равнодействующая сил (числитель) обратится в ноль:

_тgV –_жgV – 6rv₀=0 (3.14)

Далее движение будет происходить с неизменной скоростью v₀.

Решим последнее уравнение относительно коэффициента вязкости :

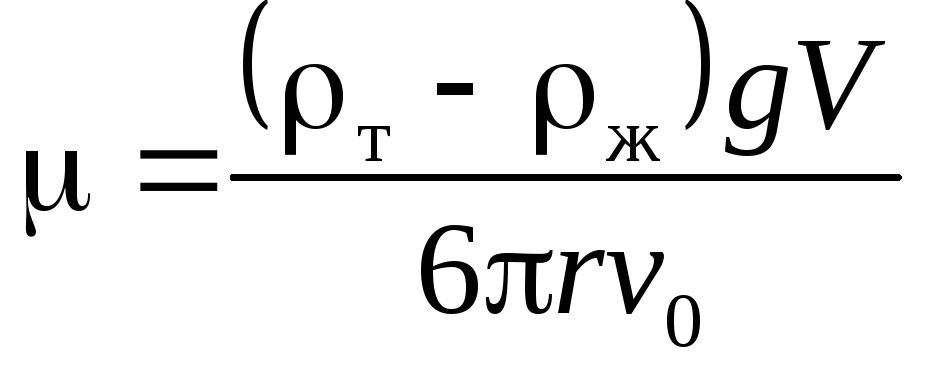(3.15)

Для вычисления вязкости жидкости нужно измерить_ти_ж— плотность вещества шара и жидкости;rиv₀— радиус шара и скорость его равномерного падения в среде. Конечно, придётся вычислить и объём шараV=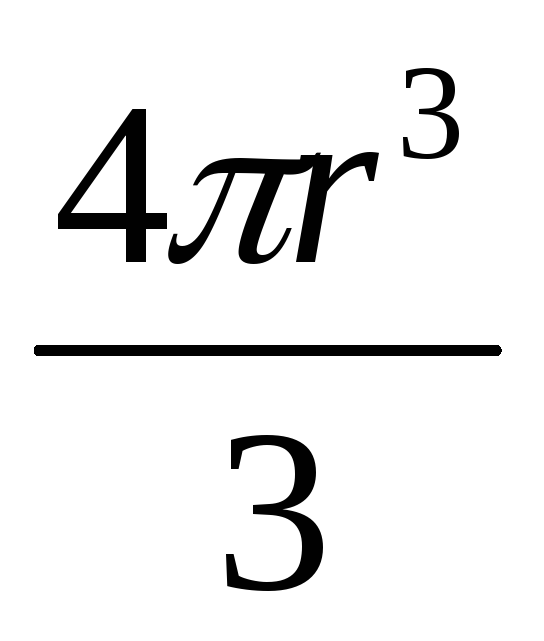. Эта простая методика измерения вязкости и сегодня широко используется в «вискозиметрах Стокса».

Движение по наклонной плоскости тела: скорость, трение, время

Динамика и кинематика — это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.

Основная формула динамики

Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:

F¯ = m*a¯

Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.

В случае движения вращения второй закон Ньютона записывается в виде:

M = I*α

Здесь M и I — моменты силы и инерции, соответственно, α — угловое ускорение.

Формулы кинематики

Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:

a = Δv/Δt;

v = v₀ ± a*t;

S = v₀*t ± a*t²/2

Здесь v₀ — значение начальной скорости тела, S — пройденный за время t путь вдоль прямолинейной траектории. Знак «+» следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак «-«. Это важный момент.

Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:

α = Δω/Δt;

ω = ω₀ ± α*t;

θ = ω₀*t ± α*t²/2

Здесь α и ω — угловые ускорение и скорость, соответственно, θ — угол поворота вращающегося тела за время t.

Линейные и угловые характеристики друг с другом связаны формулами:

a = α*r;

v = ω*r

Здесь r — радиус вращения.

Движение по наклонной плоскости: силы

Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.

Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:

• тяжести;
• реакции опоры;
• трения качения и/или скольжения;
• натяжение нити;
• сила внешней тяги.

Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.

Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.

Методика решения

Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.

Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:

F_f = µ*N

Где N — реакция опоры, µ — коэффициент трения, не имеющий размерности.

Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:

F = m*g*sin(φ) — µ*m*g*cos(φ) = m*g*(sin(φ) — µ*cos(φ)) = m*a

Здесь φ — это угол наклона плоскости к горизонту.

Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.

В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:

F = m*g*sin(φ) — F_r = m*a

Где F_r — сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, F_r создает следующий момент:

M = F_r*r = I*α

Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.

Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.

Задача на движение бруска по наклонной плоскости

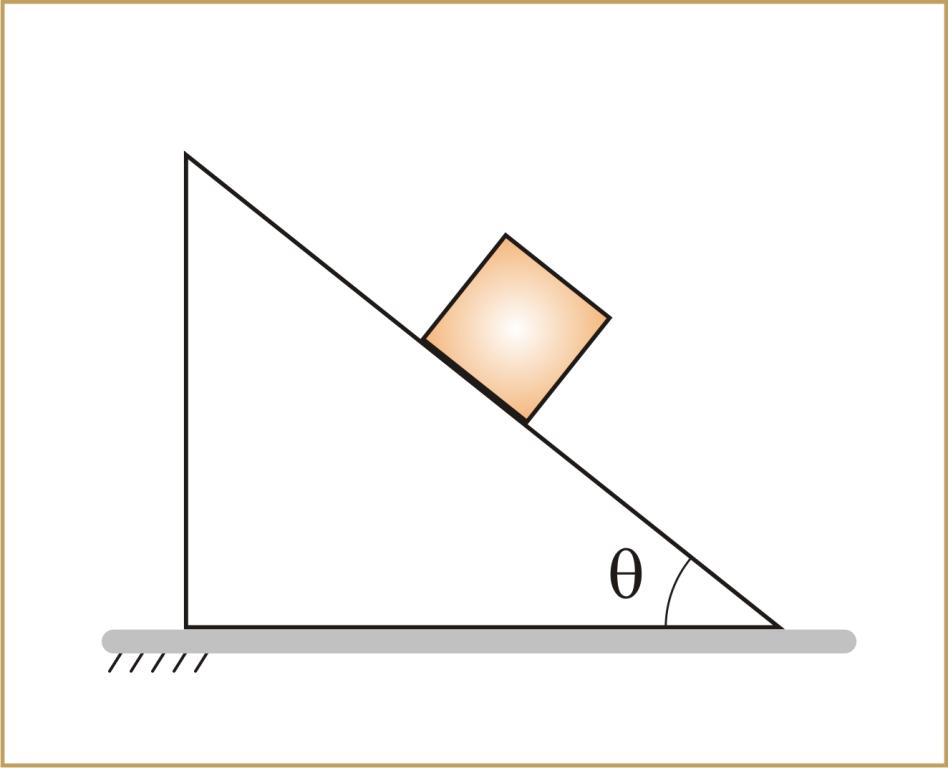
Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45^o. Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.

Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:

m*g*(sin(φ) — µ*cos(φ)) = m*a =>

a = g*(sin(φ) — µ*cos(φ)) ≈ 4,162 м/с²

Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:

S = a*t²/2

Откуда следует выразить время, и подставить известные значения:

t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 с

Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.

Задача со скатывающимся по плоскости цилиндром

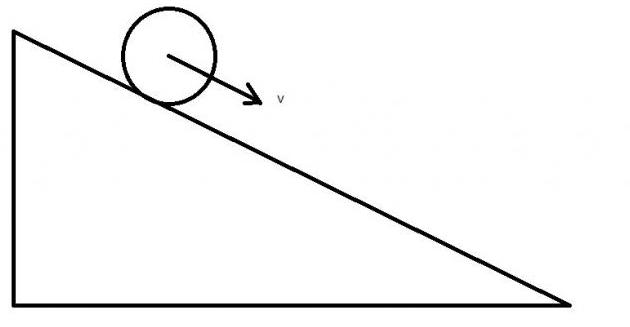
Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30^o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.

Запишем соответствующие уравнения:

m*g*sin(φ) — F_r = m*a;

F_r*r = I*α = I*a/r

Момент инерции I цилиндра вычисляется по формуле:

I = 1/2*m*r²

Подставим это значение во вторую формулу, выразим из нее силу трения F_r и заменим полученным выражением ее в первом уравнении, имеем:

F_r*r = 1/2*m*r²*a/r = >

F_r = 1/2*m*a;

m*g*sin(φ) — 1/2*m*a = m*a =>

a = 2/3*g*sin(φ)

Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.

Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:

S = a*t²/2 =>

t = √(2*S/a)

Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:

v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))

Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.

Вязкое трение и сопротивление среды

Отличие вязкого трения от сухого заключается в том, что оно способно обращаться в ноль одновременно со скоростью. Даже при малой внешней силе может быть сообщена относительная скорость слоям вязкой среды.

Сила сопротивления при движении в вязкой среде

Замечание 1

Кроме сил трения при движении в жидких и газообразных средах возникают силы сопротивления среды, которые проявляются намного значительней, чем силы трения.

Поведение жидкости и газа по отношению к проявлениям сил трения не отличаются. Поэтому, приведенные ниже характеристики, относят к обоим состояниям.

Определение 1

Действие силы сопротивления, возникающей при движении тела в вязкой среде, обусловлено ее свойствами:

• отсутствие трения покоя, то есть передвижение плавающего многотонного корабля при помощи каната;
• зависимость силы сопротивления от формы движущегося тела, иначе говоря, от ее обтекаемости для уменьшения сил сопротивления;
• зависимость абсолютной величины силы сопротивления от скорости.

Сила вязкого трения

Определение 2

Существуют определенные закономерности, которым подчинены и силы трения и сопротивления среды с условным обозначением суммарной силы силой трения. Ее величина находится в зависимости от:

• формы и размеров тела;
• состояния его поверхности;
• скорости относительно среды и ее свойства, называемого вязкостью.

Для изображения зависимости силы трения от скорости тела по отношению к среде используют график рисунка 1.

Рисунок 1. График зависимости силы трения от скорости по отношению к среде

Если значение скорости мало, то сила сопротивления прямо пропорциональна относительно υ, а сила трения линейно увеличивается со скоростью:

Fтр=-k1υ (1).

Наличие минуса означает направление силы трения в противоположную сторону относительно направления скорости.

При большом значении скорости происходит переход линейного закона в квадратичный, то есть рост силы трения пропорционально квадрату скорости:

Fтр=-k2υ2 (2).

Если в воздухе уменьшается зависимость силы сопротивления от квадрата скорости, говорят о скоростях со значениями нескольких метров в секунду.

Величина коэф

Трение, его виды. Трение скольжения и трение качения. Сила и коэффициент трения. Борьба с износом трущихся деталей

материал предоставил СИДОРОВ Александр Владимирович

Трение (фрикционное взаимодействие) – процесс взаимодействия тел при их относительном движении (смещении) либо при движении тела в газообразной или жидкой среде.

Изучением процессов трения занимается раздел физики, который называется трибология (механика фрикционного взаимодействия).

Трение принято разделять на:

• сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями / смазками (в том числе и твёрдыми смазочными материалами) – очень редко встречающийся на практике случай; характерная отличительная черта сухого трения – наличие значительной силы трения покоя;
• граничное, когда в области контакта могут содержаться слои и участки различной природы (окисные плёнки, жидкость и так далее) – наиболее распространённый случай при трении скольжения;
• жидкостное (вязкое), возникающее при взаимодействии тел, разделённых слоем твёрдого тела (порошком графита), жидкости или газа (смазки) различной толщины – как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость, величина вязкого трения характеризуется вязкостью среды;
• смешанное, когда область контакта содержит участки сухого и жидкостного трения;
• эластогидродинамическое (вязкоупругое), когда решающее значение имеет внутреннее трение в смазывающем материале. Возникает при увеличении относительных скоростей перемещения.

Сила трения – это сила, возникающая в месте соприкосновения тел и препятствующая их относительному движению.

Причины возникновения силы трения:

• шероховатость соприкасающихся поверхностей;
• взаимное притяжение молекул этих поверхностей.

Трение скольжения

– сила, возникающая при поступательном перемещении одного из контактирующих / взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения.

Трение качения – момент сил, возникающий при качении одного из двух контактирующих / взаимодействующих тел относительно другого.

Трение покоя – сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга.

Сила трения прямо пропорциональна силе нормальной реакции, то есть зависит от того, насколько сильно тела прижаты друг к другу и от их материала, поэтому основной характеристикой трения является

коэффициент трения, который определяется материалами, из которых изготовлены поверхности взаимодействующих тел. [1]

Износ – изменение размеров, формы, массы или состояния поверхности изделия вследствие разрушения (изнашивания) поверхностного слоя при трении. [2]

Работа любой машины неизбежно сопровождается трением при относительном движении её частей, поэтому полностью устранить износ невозможно. Величина износа при непосредственном контакте поверхностей прямо пропорциональна работе сил трения.

Абразивный износ частично вызывается действием пыли и грязи, поэтому очень важно содержать оборудование в чистоте, особенно её трущиеся части.

Для борьбы с износом и трением заменяют одни металлы другими, более устойчивыми, применяют термическую и химическую обработку трущихся поверхностей, точную механическую обработку, а также заменяют металлы различными заменителями, изменяют конструкцию, улучшают смазку (изменяют вид, вводят присадки) и т.д.

В машинах стремятся не допускать непосредственного трения скольжения твёрдых поверхностей, для чего или разделяют их слоем смазки (жидкостное трение), или же вводят между ними добавочные элементы качения (шариковые и роликовые подшипники).

Основное правило конструирования трущихся деталей машин состоит в том, что более дорогой и трудно заменяемый элемент трущейся пары (вал) изготовляют из более твёрдого и более износоустойчивого материала (твёрдая сталь), а более простые, дешёвые и легко заменяемые части (вкладыши подшипников) изготовляют из сравнительно мягкого материала с небольшим коэффициентом трения (бронза, баббит).

Большинство деталей машин выходят из строя именно вследствие износа, поэтому уменьшение трения и износа даже на 5-10% даёт огромную экономию, что имеет исключительное значение. [3]

Перечень ссылок

1. Трение // Википедия. – http://ru.wikipedia.org/wiki/Трение.
2. Износ (техника) // Википедия. – http://ru.wikipedia.org/wiki/Износ_(техника).
3. Трение в машинах, трение и износ в машиностроении // Проект-Технарь. Прогрессивные авто-технологии. – http://www.studiplom.ru/Technology/Trenie.html.

Вопросы для контроля

1. Что такое трение?
2. Какие существуют разновидности трения?
3. Что приводит к возникновению силы трения?
4. Как классифицируют трение в зависимости от действующих сил?
5. Что такое износ и как с ним борются?

Силы трения. Коэффициент трения. Движение тела с учетом силы трения

«Любую задачу реально выполнить,

если разбить ее на выполнимые части»

Данная тема будет посвящена решению задач на силы трения и изучению движение тела с учетом сил трения.

Задача 1. Упряжка ездовых собак может тянуть по снегу сани с максимальной силой 500 Н. Какой массы саней с грузом может перемещать данная упряжка собак, двигаясь равномерно, если коэффициент трения саней о снег составляет 0,1?

ДАНО:	РЕШЕНИЕ: Запишем второй закон Ньютона В проекциях на ось Ох: В проекциях на ось Оу: Сила трения: Тогда искомая масса равна

Ответ: 500 кг.

Задача 2. Мальчик начинает тянуть санки по снегу, прилагая силу 20 Н, направленную под углом 30^о к горизонту. Определите ускорение, с которым движутся санки, если их масса равна 4 кг, а коэффициент трения между санками и снегом равен 0,01.

ДАНО:	РЕШЕНИЕ: Запишем второй закон Ньютона В проекциях на ось Ох: В проекциях на ось Оу: Из последнего уравнения выразим значение силы нормальной реакции опоры Сила трения определяется по формуле Тогда Тогда ускорение санок равно

Ответ: 4,3 м/с².

Задача 3. Определите наименьший радиус поворота, который может сделать автомобиль, движущийся со скоростью 15 м/с, если коэффициент трения между шинами автомобиля и дорогой равен 0,1.

ДАНО:	РЕШЕНИЕ: Запишем второй закон Ньютона для рассматриваемого случая В проекциях на ось Ох: В проекциях на ось Оу: Сила трения определяется по формуле Центростремительное ускорение определяется по формуле С учётом последней формулы получаем

Ответ: 225 м.

Задача 4. Автомобиль массой 3500 кг, разгоняясь из состояния покоя, достигает скорости 10 м/с, а затем продолжает движение с выключенным двигателем до полной остановки. Определите весь путь, пройденный автомобилем за время движения, если сила тяги двигателя составляет 3500 Н, а коэффициент трения шин о дорогу равен 0,02.

ДАНО:

РЕШЕНИЕ: Запишем второй закон Ньютона В проекциях на ось Ох: В проекциях на ось Оу: Сила трения определяется по формуле Тогда получаем Путь, пройденный автомобилем на разгонном участке Перейдем к рассмотрению второго участка движения автомобиля — участка торможения Запишем второй закон Ньютона для второго участка В проекциях на ось Ох: В проекциях на ось Оу: Сила трения определяется по формуле Тогда получаем Длина участка торможения: Весь путь, пройденный автомобилем, складывается из длин участков разгона и торможения

Ответ: 312,5 м.