Скалярный квадрат вектора
Что будет, если вектор 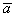 умножить на самого себя?
умножить на самого себя?
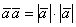
Или: 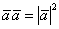
Число 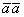 называется скалярным квадратом вектора
называется скалярным квадратом вектора 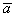 , и обозначатся как
, и обозначатся как  .
.
Таким образом,скалярный квадрат вектора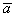 равен квадрату длины данного вектора:
равен квадрату длины данного вектора: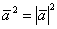
Из данного равенства можно получить формулу для вычисления длины вектора: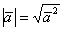
Свойства скалярного произведения.
Для произвольных векторов 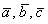 и любого числа
и любого числа 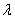 справедливы следующие свойства:
справедливы следующие свойства:
1) 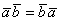
2) 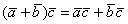 – распределительный или дистрибутивный закон скалярного произведения. Попросту, можно раскрывать скобки.
– распределительный или дистрибутивный закон скалярного произведения. Попросту, можно раскрывать скобки.
3) 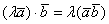 – сочетательный или ассоциативный закон скалярного произведения. Константу можно вынести из скалярного произведения.
– сочетательный или ассоциативный закон скалярного произведения. Константу можно вынести из скалярного произведения.
Пример
Найти скалярное произведение векторов 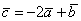
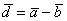 , если известно, что
, если известно, что 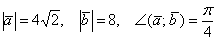 .
.
Решение:
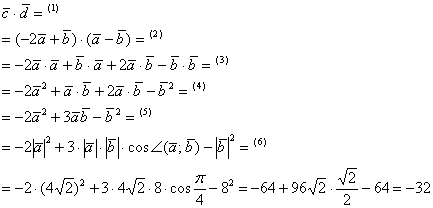
(1) Подставляем выражения векторов 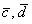 .
.
(2) Раскрываем скобки по правилу умножения многочленов. Раскрыть скобки нам позволяет дистрибутивное свойство скалярного произведения.
(3) В первом и последнем слагаемом компактно записываем скалярные квадраты векторов: 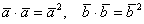 . Во втором слагаемом используем перестановочность скалярного произведения:
. Во втором слагаемом используем перестановочность скалярного произведения: 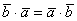 .
.
(4) Приводим подобные слагаемые: 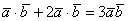 .
.
(5) В первом слагаемом используем формулу скалярного квадрата 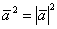 , о которой не так давно упоминалось. В последнем слагаемом, соответственно, работает та же штука:
, о которой не так давно упоминалось. В последнем слагаемом, соответственно, работает та же штука: 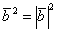
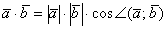 .
.
(6) Подставляем данные условия  , и ВНИМАТЕЛЬНО проводим окончательные вычисления.
, и ВНИМАТЕЛЬНО проводим окончательные вычисления.
Ответ: 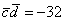
Пример
Найти длину вектора 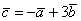
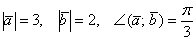 .
.
Решение:
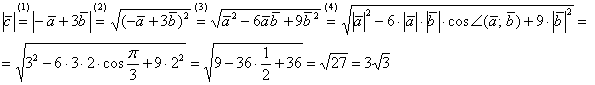
(1) Поставляем выражение вектора  .
.
(2) Используем формулу длины: 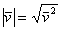 , при этом в качестве вектора «вэ» у нас выступает целое выражение
, при этом в качестве вектора «вэ» у нас выступает целое выражение 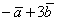 .
.
(3) Используем школьную формулу квадрата суммы 
(4) Дальнейшее аналогично действиям из двух предыдущих задач.
Ответ: 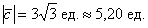
Угол между векторами
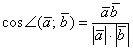
Если известны длины двух векторов и их скалярное произведение, то можно вычислить косинус угла между данными векторами, а, следовательно, и сам угол.
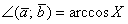
Пример
Найти угол между векторами 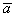 и
и 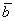 , если известно, что
, если известно, что 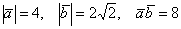 .
.
Решение: Используем формулу: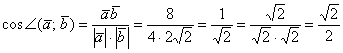
На заключительном этапе вычислений использован технический приём – устранение иррациональности в знаменателе. В целях устранения иррациональности я домножил числитель и знаменатель на 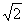
Итак, если 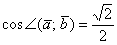 , то:
, то: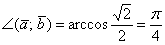
Ответ: 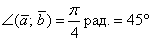
Не забываем указывать размерность – радианы и градусы.
Пример
Даны 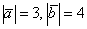
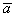 ,
, 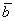 и угол между ними
и угол между ними 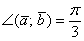 . Найти угол между векторами
. Найти угол между векторами 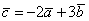 ,
, 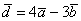 .
.
Алгоритм решения:
1) По условию требуется найти угол между векторами 
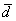 , поэтому нужно использовать формулу
, поэтому нужно использовать формулу 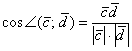 .
.
2) Находим скалярное произведение 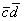 .
.
3) Находим длину вектора  и длину вектора
и длину вектора 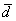 .
.
4) Нам известно число 
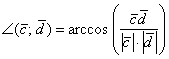
Сделайте самостоятельно и сравните с решением.
Решение: Найдём скалярное произведение:

Найдём длину вектора  :
:
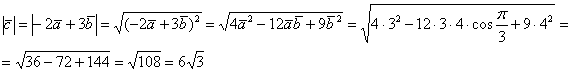
Найдём длину вектора 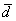

Таким образом:
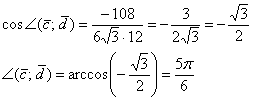
Ответ:
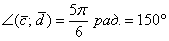
Скалярное произведение векторов,
заданных координатами в ортонормированном базисе
В данном разделе рассматриваются только ортонормированные базисы плоскости и пространства.
Скалярное произведение векторов 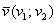 и
и 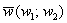 , заданных в ортонормированном базисе
, заданных в ортонормированном базисе 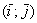 , выражается формулой
, выражается формулой 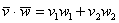
Скалярное произведение векторов 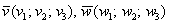 , заданных в ортонормированном базисе
, заданных в ортонормированном базисе 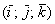 , выражается формулой
, выражается формулой 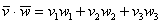
То есть, скалярное произведение равно сумме произведений соответствующих координат векторов.
Пример
Найти скалярное произведение векторов:
а) 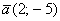 и
и 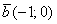
б) 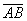 и
и 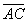 , если даны точки
, если даны точки 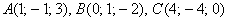
Решение:
а) Здесь даны векторы плоскости. По формуле 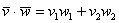 :
: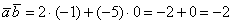
б) Сначала найдём векторы: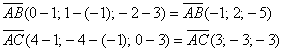
По формуле  вычислим скалярное произведение:
вычислим скалярное произведение: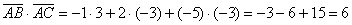
Ответ: 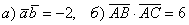
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
Тема_02_СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
14
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
I. Определение скалярного произведения. Понятие о евклидовом пространстве.
Введем
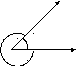
понятие угла между векторами. Пусть
даны два ненулевых вектора и 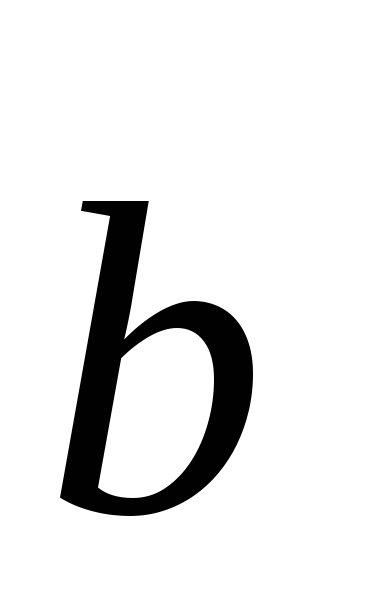 . После совмещения их начал они образуют
на плоскости два угла
. После совмещения их начал они образуют
на плоскости два угла 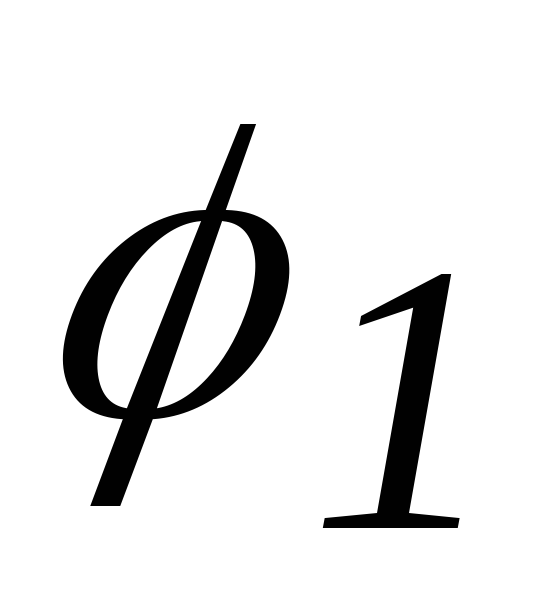 и
и 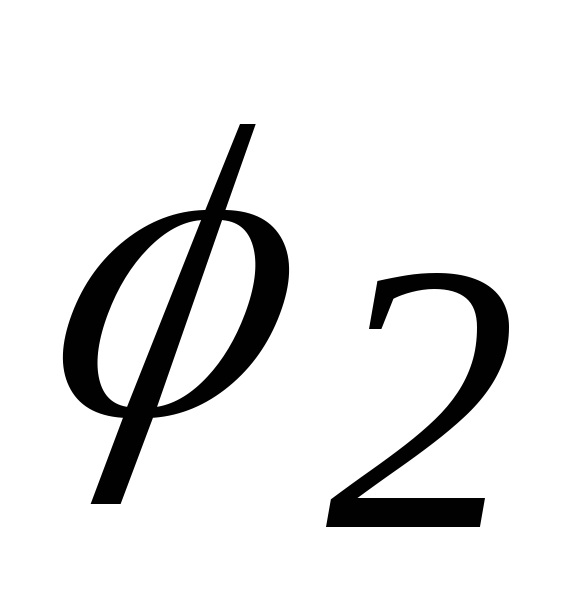 . Углом между векторами называют тот
из углов, который не превосходит
. Углом между векторами называют тот
из углов, который не превосходит  .
.
На
рисунке это угол 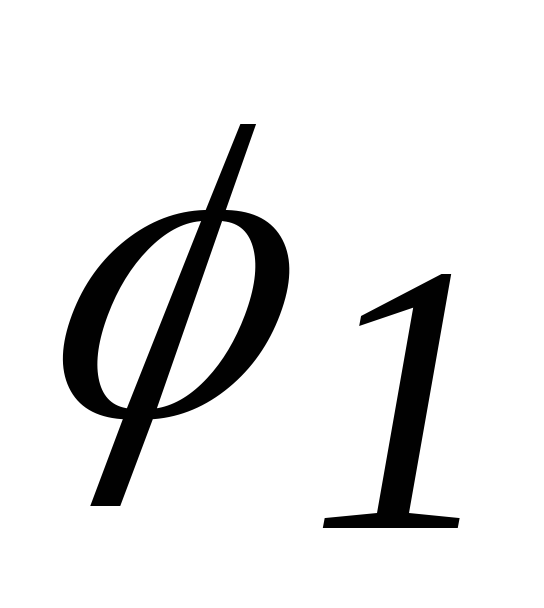 .
.

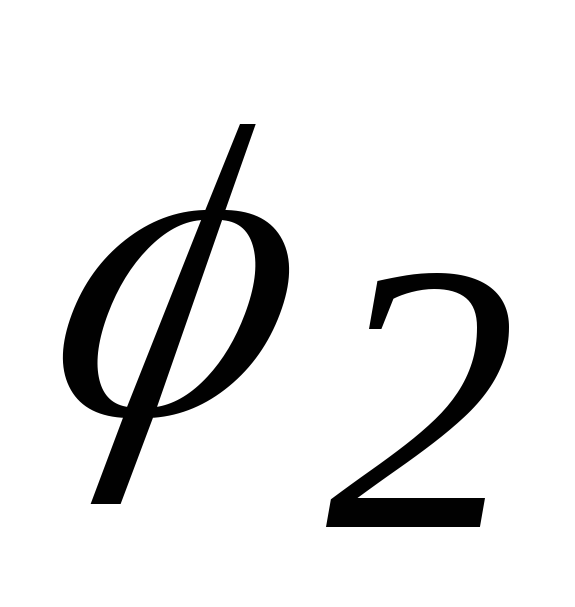
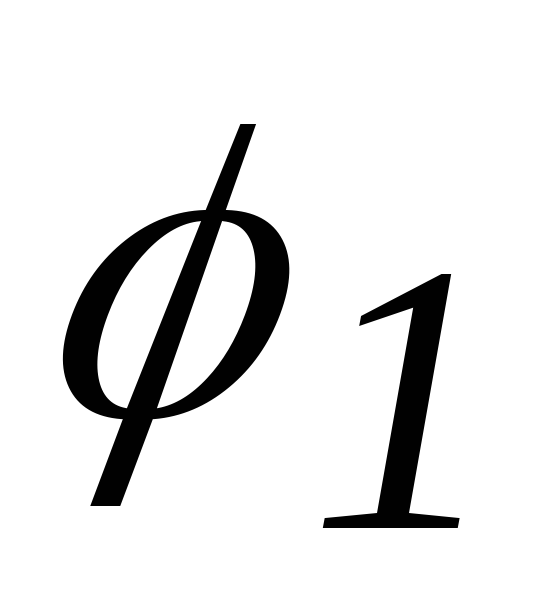
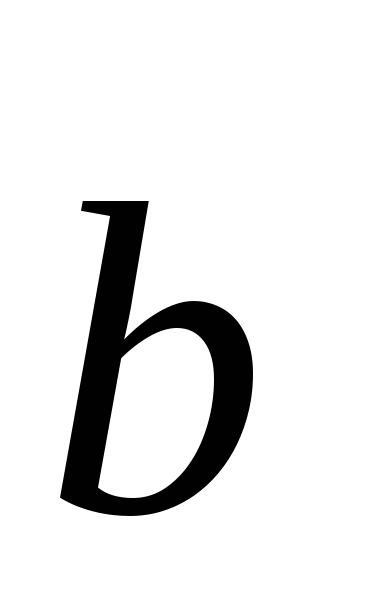
Определение: скалярным
произведением векторов  и
и 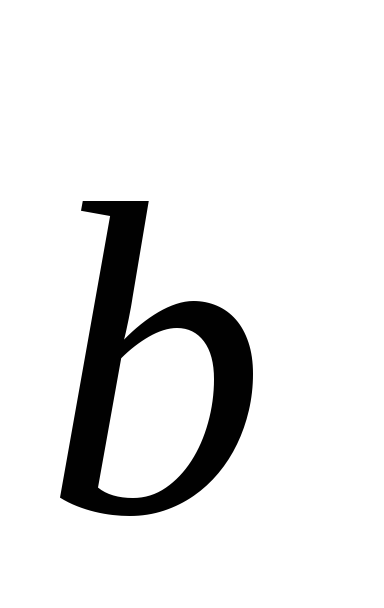 называется число, равное произведению
длин этих векторов на косинус угла между
ними:
называется число, равное произведению
длин этих векторов на косинус угла между
ними:
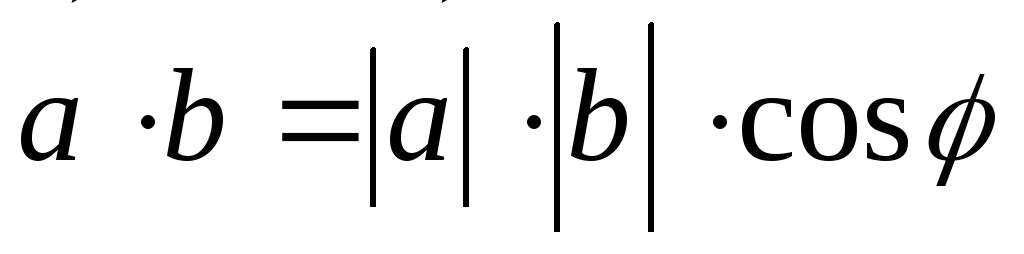 .
(1)
.
(1)
Если
один из векторов  или
или 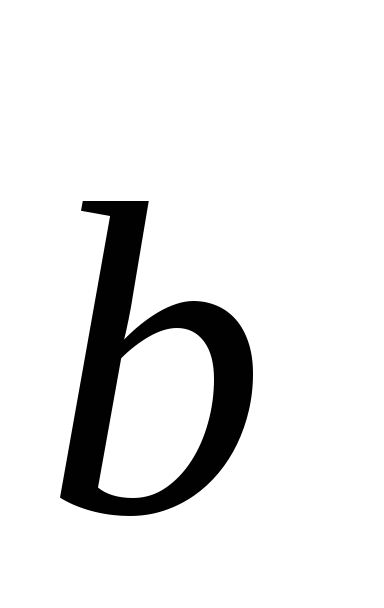 нулевой,
то угол между векторами не определен,
а скалярное произведение считается
равным нулю.
нулевой,
то угол между векторами не определен,
а скалярное произведение считается
равным нулю.
Линейное
пространство, для элементов которого
определена операция скалярного
произведения, называют евклидовым
пространством.
Евклидово пространство размерностью n принято обозначать буквой 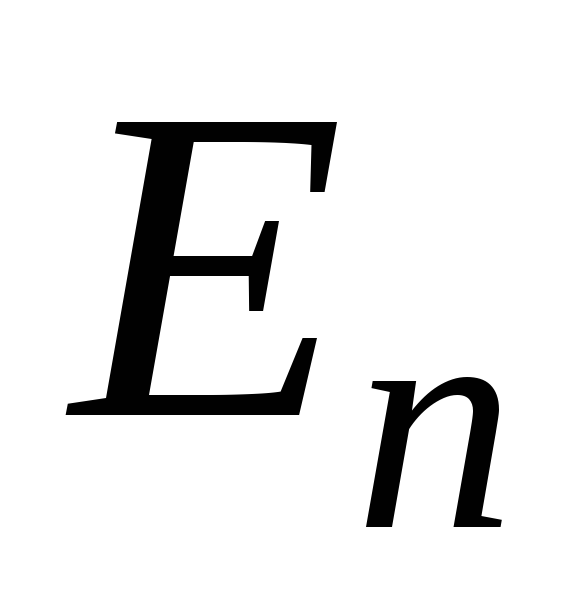 .
.
II. Геометрические свойства скалярного произведения.
Условия перпендикулярности двух векторов.
Знак скалярного произведения позволяет оценить взаимное расположение перемножаемых векторов, если среди них нет нулевых.
Если 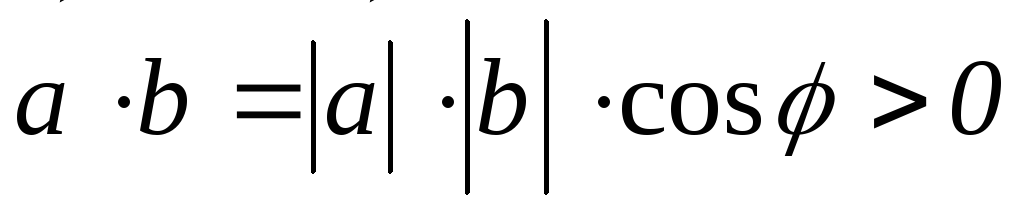 ,
то, поскольку
,
то, поскольку 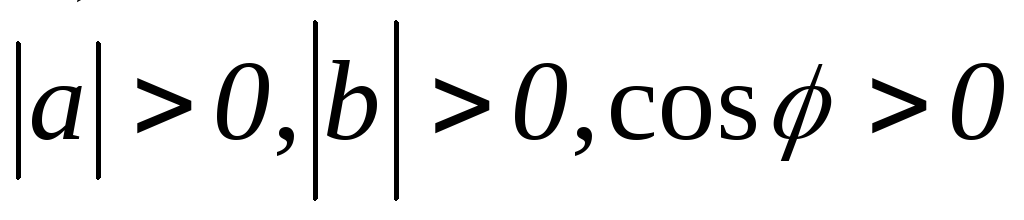 ,
и, следовательно,
угол между векторами острый (
,
и, следовательно,
угол между векторами острый (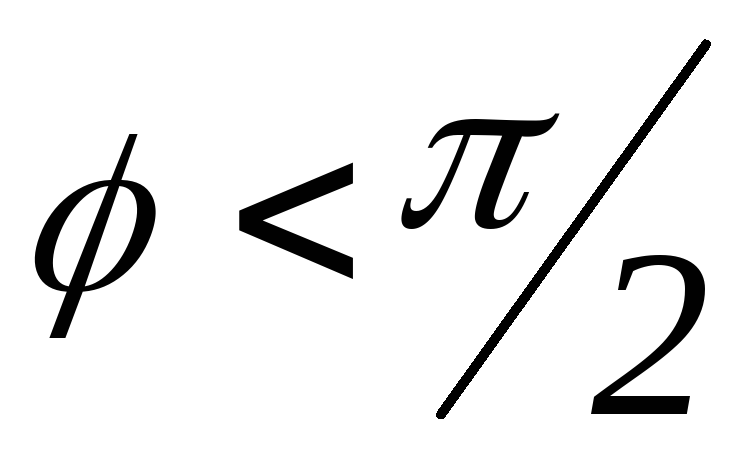 ).
).
Если
же
,
то 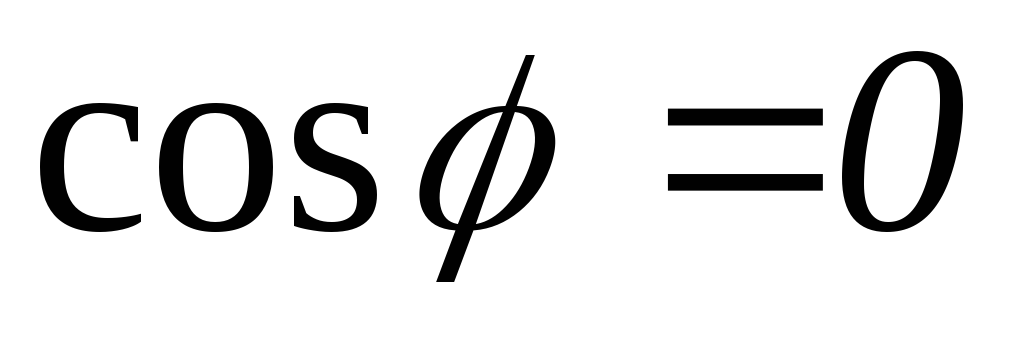 ,
т.к.
,
т.к. 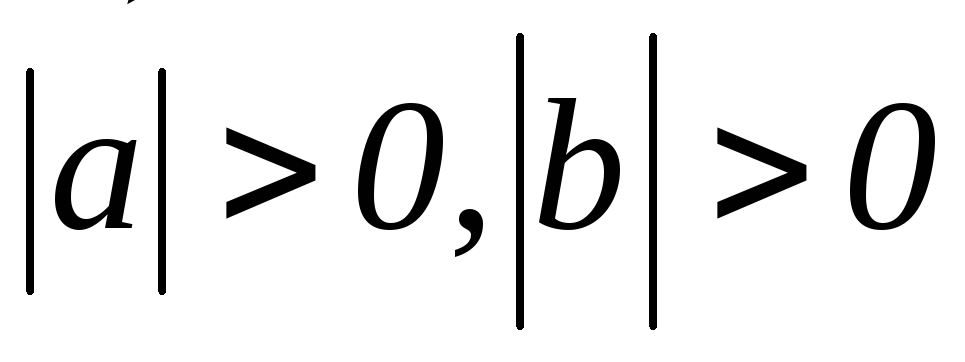 ,
т.е. векторы ортогональны (
,
т.е. векторы ортогональны (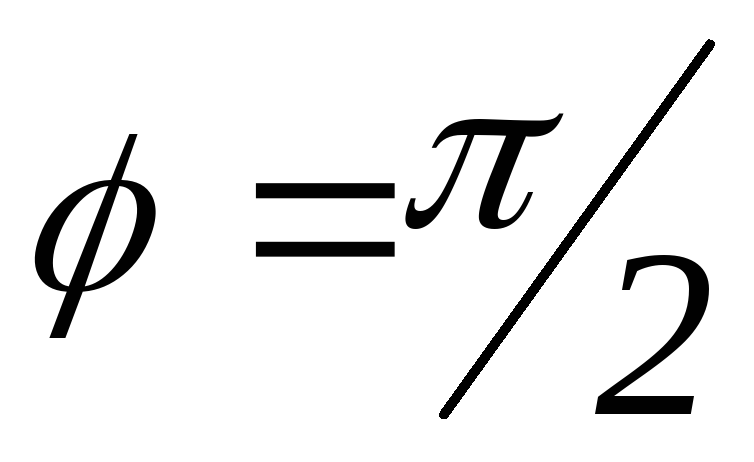 ).
).
И
обратно, если векторы ортогональны, то 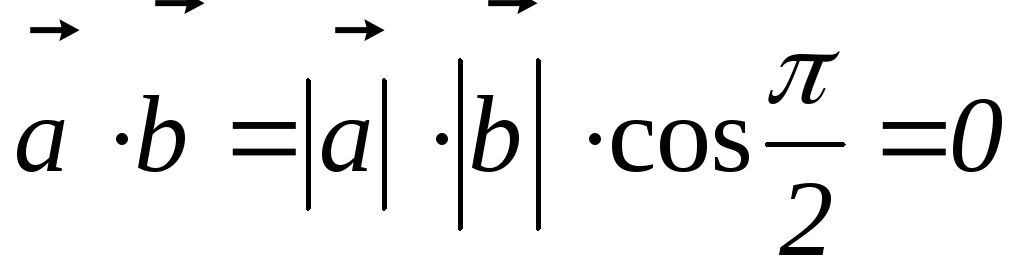 .
.
Таким образом, нами доказана следующая теорема:
необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.
Указанное геометрическое свойство скалярного произведения проиллюстрировано следующим примером из механики.
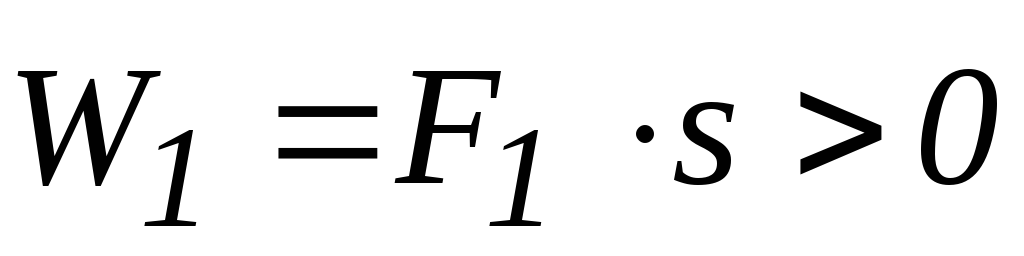 —
движущая сила
—
движущая сила
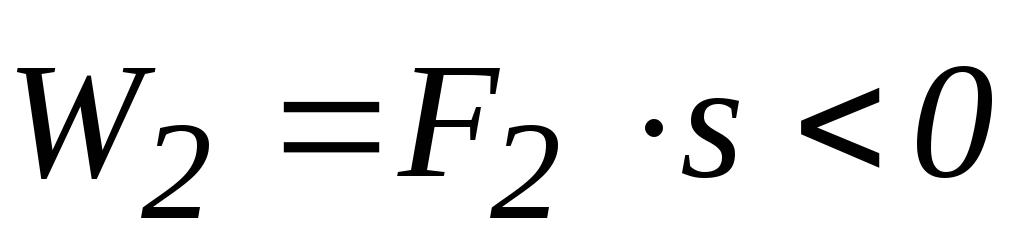 —
сила сопротивления
—
сила сопротивления
 —
сила не производит работу
—
сила не производит работу

III. Алгебраические свойства скалярного произведения.
К алгебраическим свойствам скалярного произведения относятся следующие:
1)
коммутативность 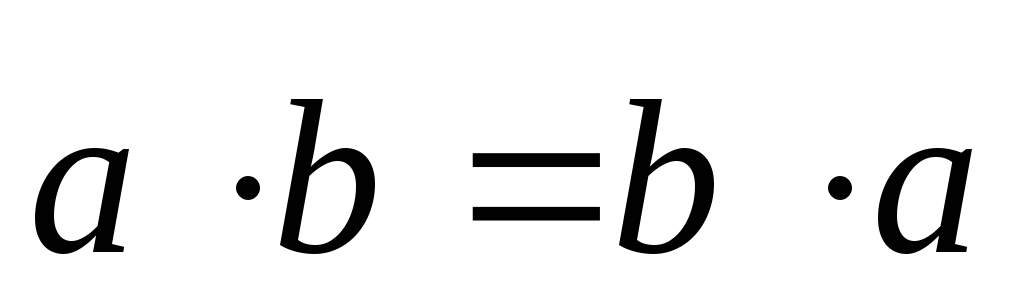 — непосредственно следует из определения,
т.к. не различаются углы между векторами
— непосредственно следует из определения,
т.к. не различаются углы между векторами  и
и 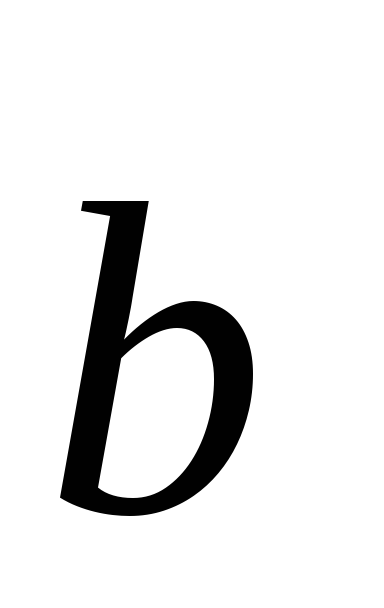 и векторами
и векторами 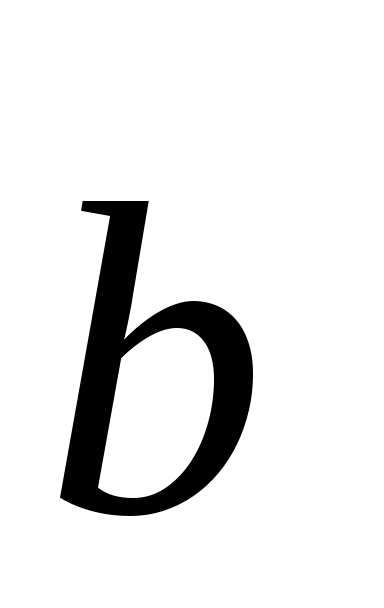 и
и  ;
;
2)
ассоциативность: 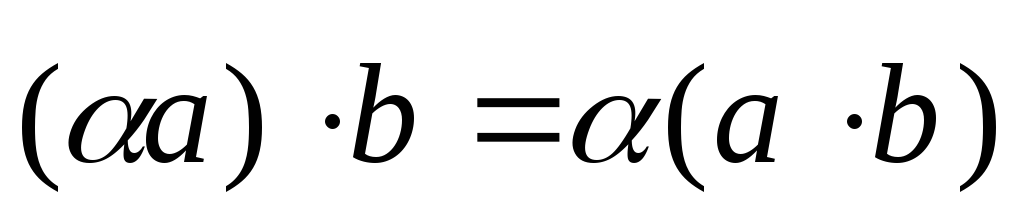
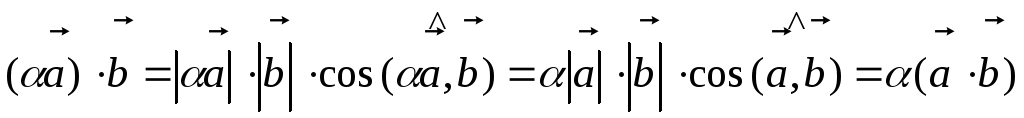 ,
,
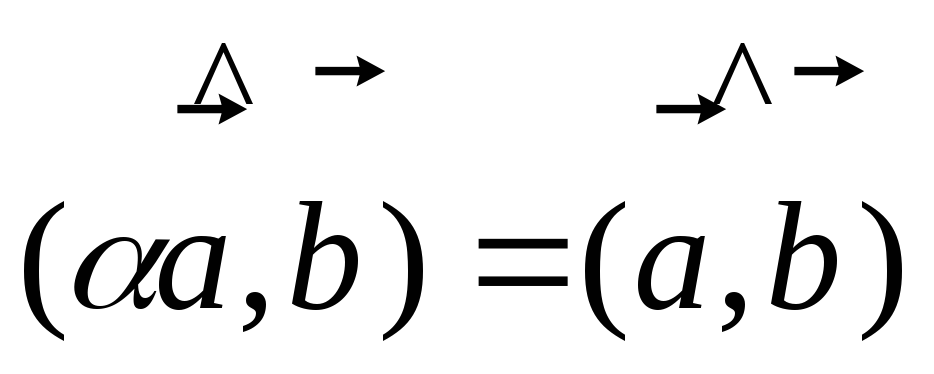 ,
т.к. векторы
,
т.к. векторы  и
и  коллинеарны;.
коллинеарны;.
3)
дистрибутивность: 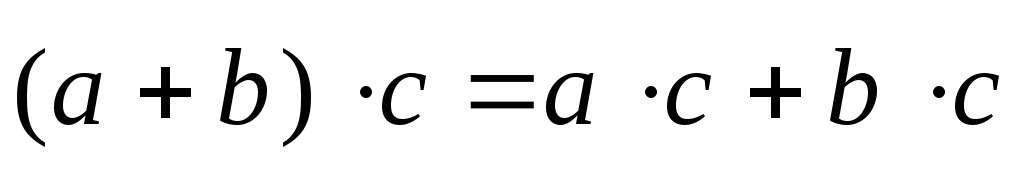 .
.
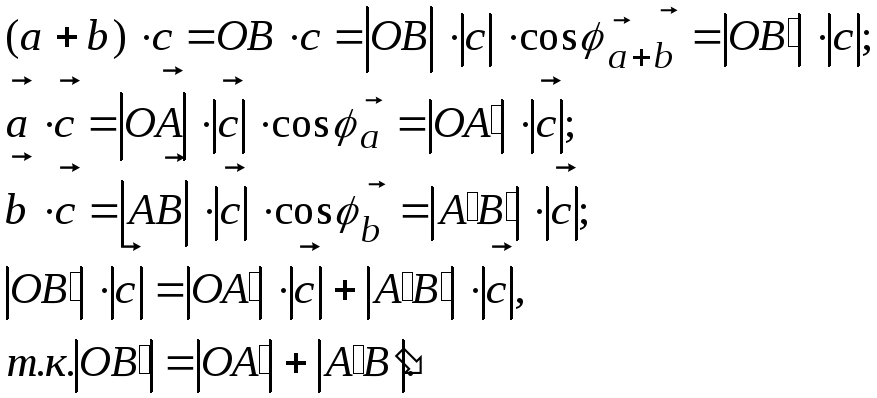

4) , если  —
ненулевой вектор
—
ненулевой вектор
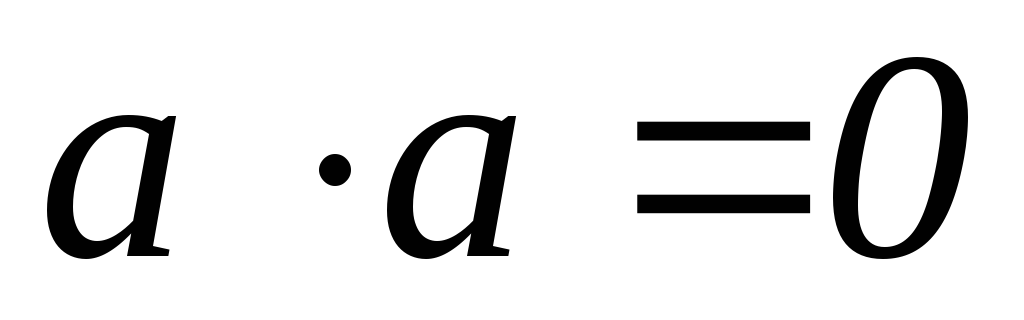 ,
если
,
если  — нулевой вектор.
— нулевой вектор.
Из
формулы (1) 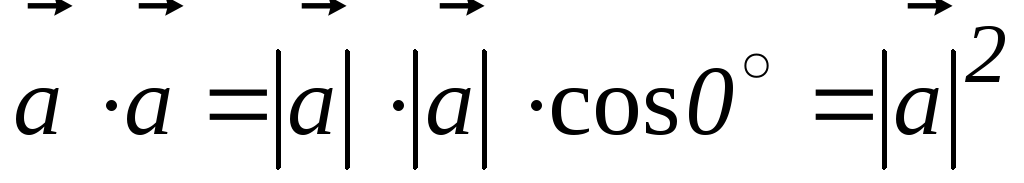 — скалярный квадрат вектора равен
квадрату его длины. Отсюда и вытекает
справедливость свойства (4).
— скалярный квадрат вектора равен
квадрату его длины. Отсюда и вытекает
справедливость свойства (4).
Свойства (2) и (3) отражают линейность скалярного произведения и имеют фундаментальное значение, т.к. позволяют проводить операции с векторными многочленами по обычным правилам алгебры.
Пример .
Вычислить 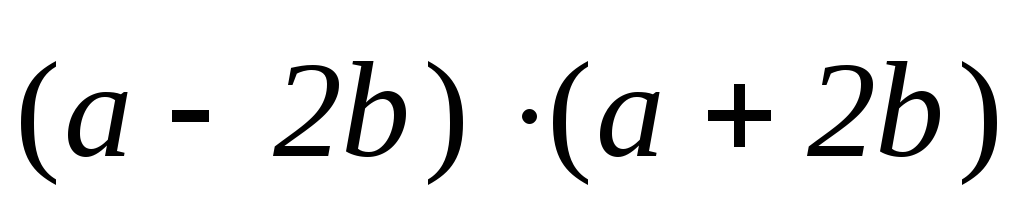 , если
, если 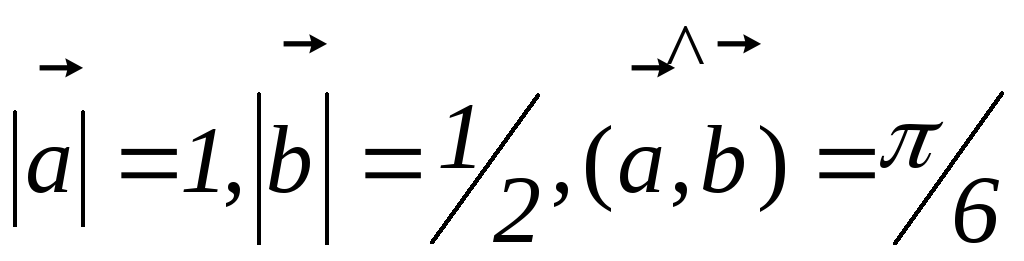
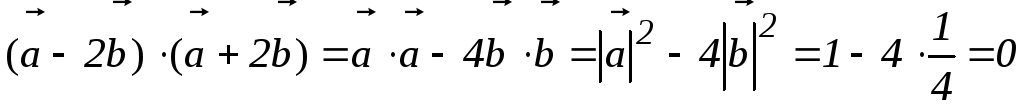 .
.
IV. Выражение скалярного произведения через координаты.
Пусть
векторы  и
и 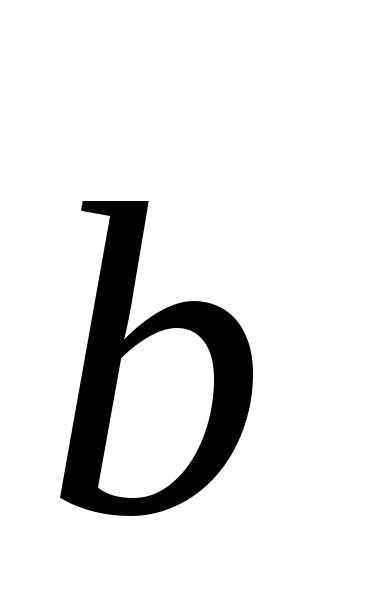 заданы своими координатами в
ортонормированном базисе
заданы своими координатами в
ортонормированном базисе 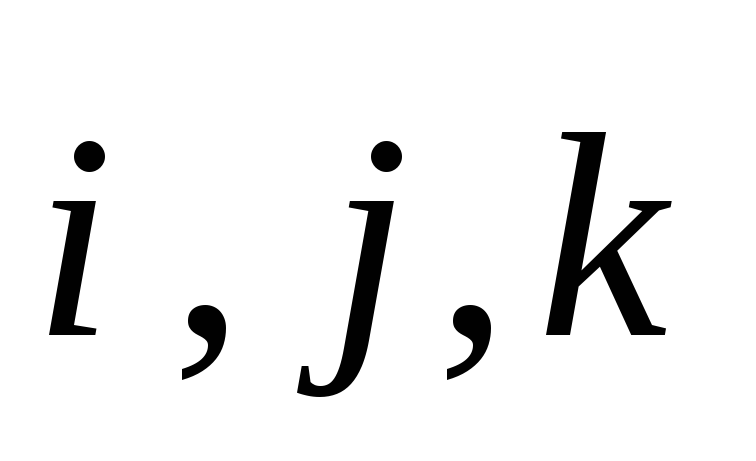 .
Это значит, что могут быть записаны
следующие разложения
.
Это значит, что могут быть записаны
следующие разложения
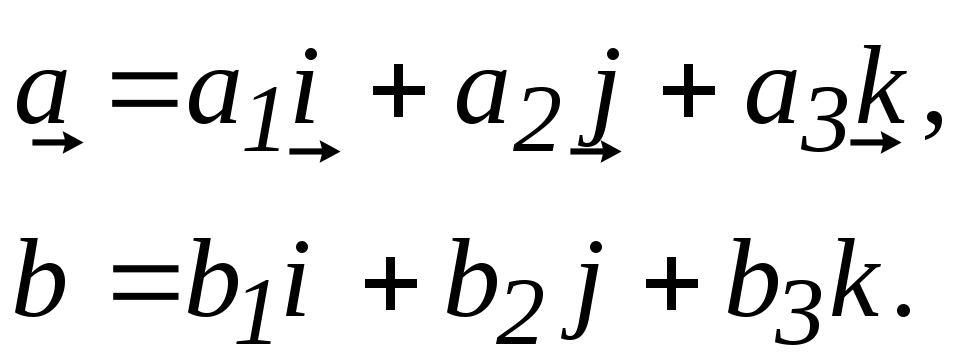
Найдем скалярное произведение векторов:
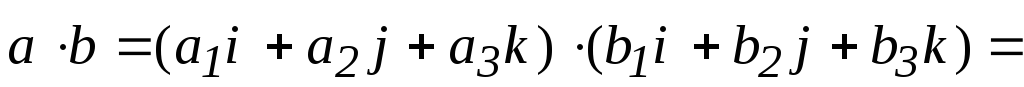
в силу свойств (2) и (3) можно раскрыть скобки и записать
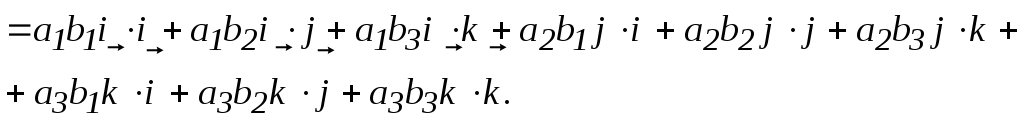
Вычислим
скалярные произведения базисных
векторов. Поскольку базис ортонормированный,
то длины векторов 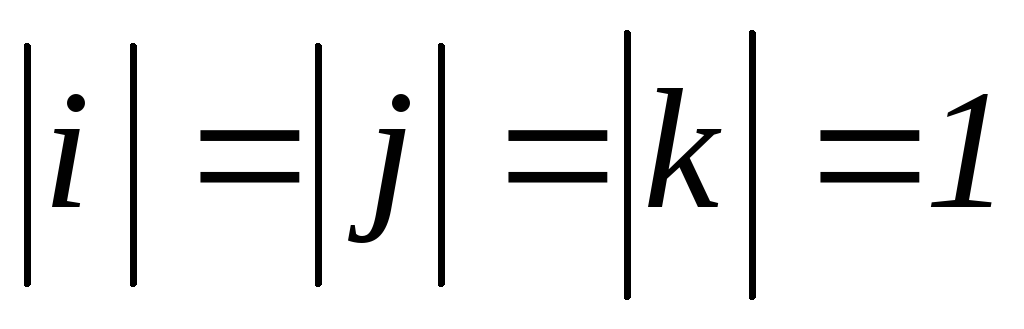 ,
а углы между ними
,
а углы между ними 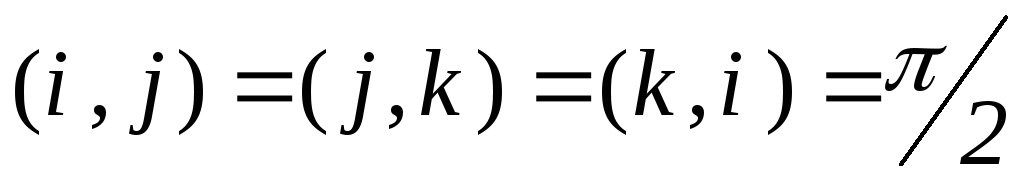 .
.

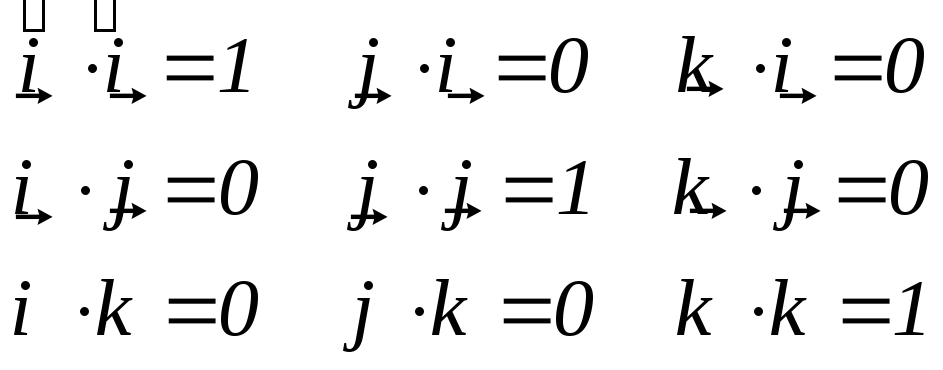
В общем случае условием ортонормированности базиса является требование
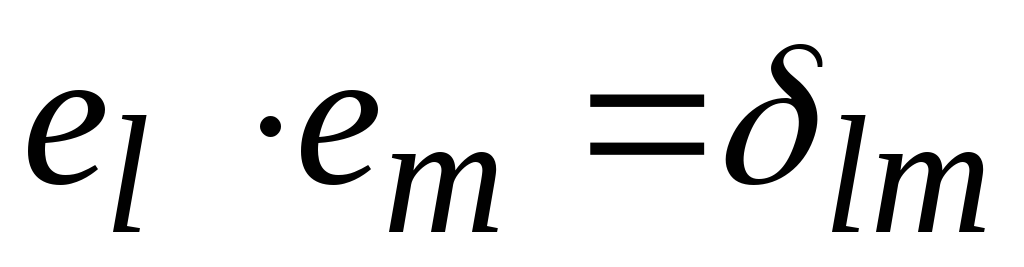 ,
где символ Кронекера
,
где символ Кронекера 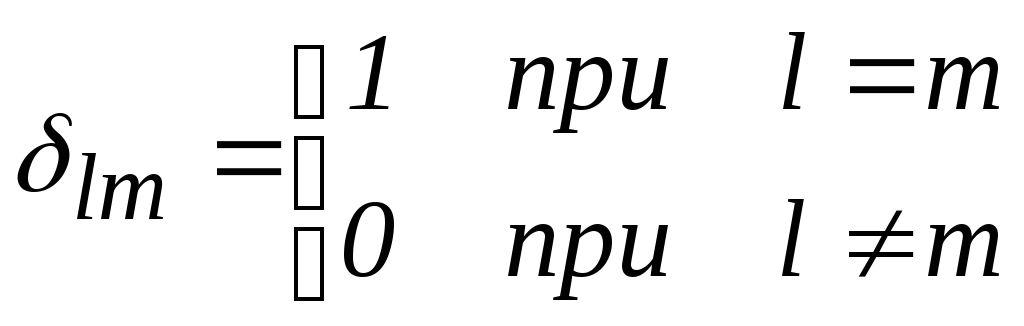 .
.
Тогда скалярное произведение векторов через их координаты можно записать
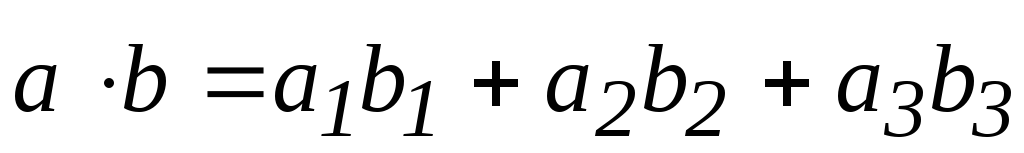 .
(2)
.
(2)
Все выкладки можно записать с помощью так называемых «немых» индексов:
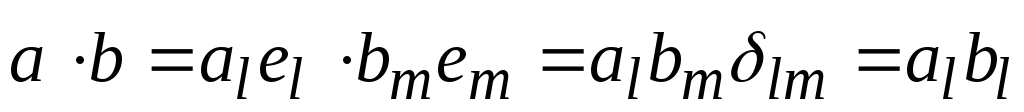 .
.
Итак, скалярное произведение векторов равно сумме произведений их соответствующих координат в ортонормированном базисе.
V. Длина вектора, угол между векторами. Проекция вектора на ось.
Полученное выражение скалярного произведения через координаты векторов в ортонормированном базисе (2) и знание геометрических свойств скалярного произведения позволяют получить выражения через координаты векторов для их длин и углов между ними.
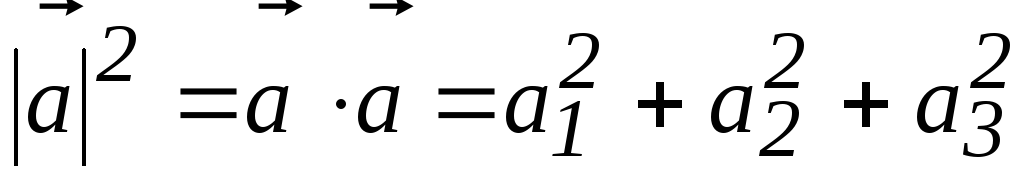 .
.
Тогда
длина вектора 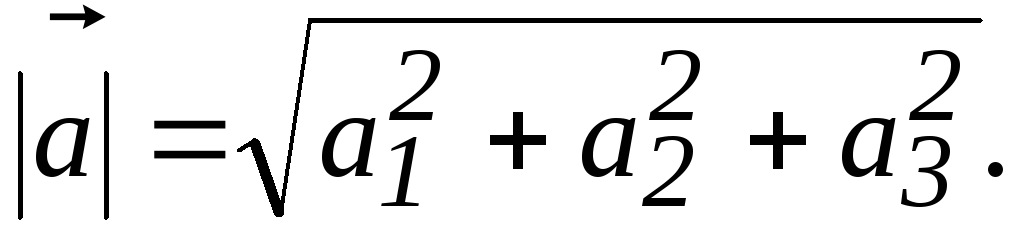 (3)
(3)
Из определения скалярного произведения (1) можно получить выражение для косинуса угла между векторами
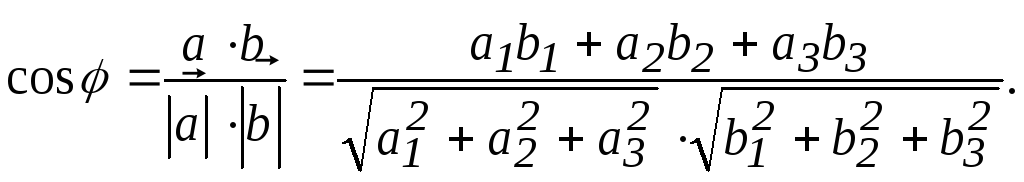 (4)
(4)
Условие
ортогональности векторов  и
и  может быть записано в виде
может быть записано в виде
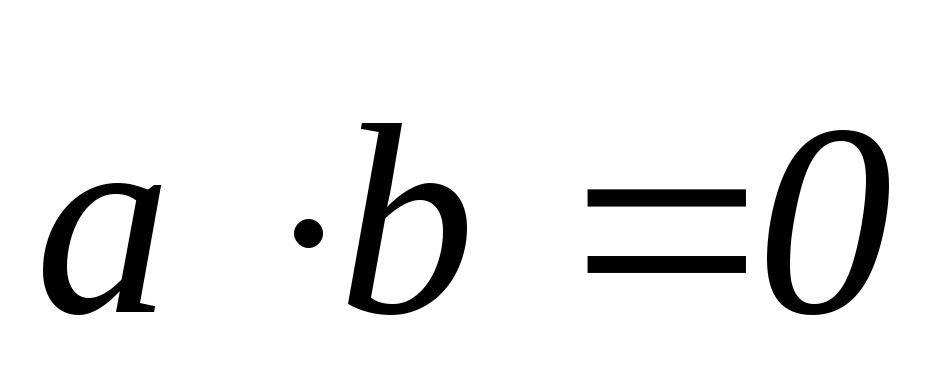 или
или 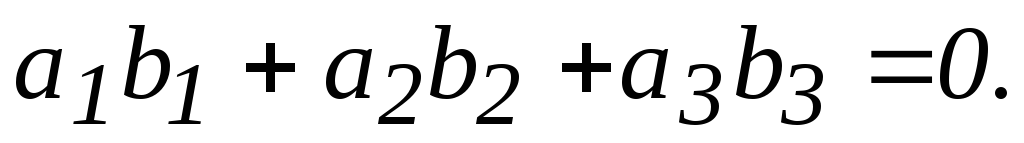
В
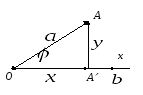
Если
через конец вектора  про- вести
прямую, перпендикулярную оси Ox,
то получившийся вектор
про- вести
прямую, перпендикулярную оси Ox,
то получившийся вектор 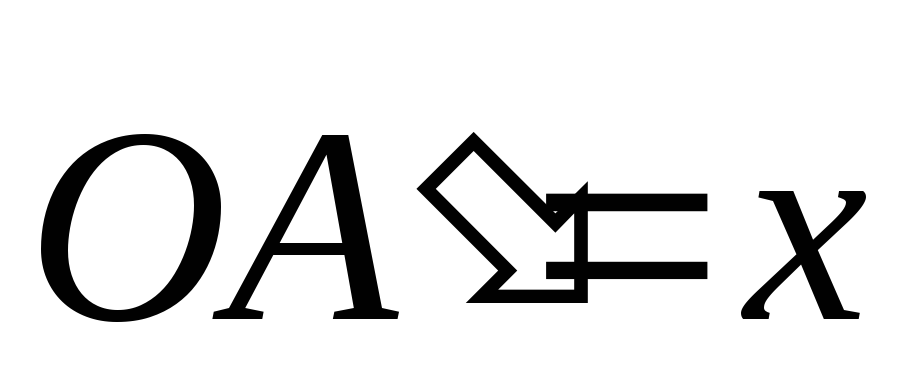 называется ортогональной проекцией
вектора
называется ортогональной проекцией
вектора  на ось Ox,
а вектор
на ось Ox,
а вектор 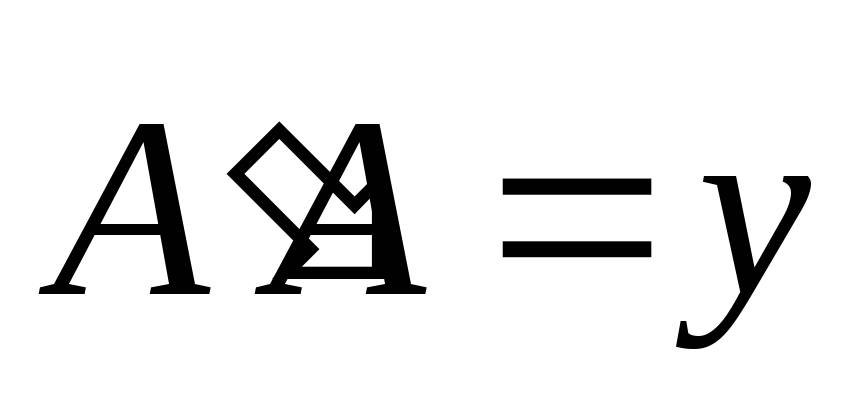 — ортогональной составляющей вектора
— ортогональной составляющей вектора  ,
причем
,
причем 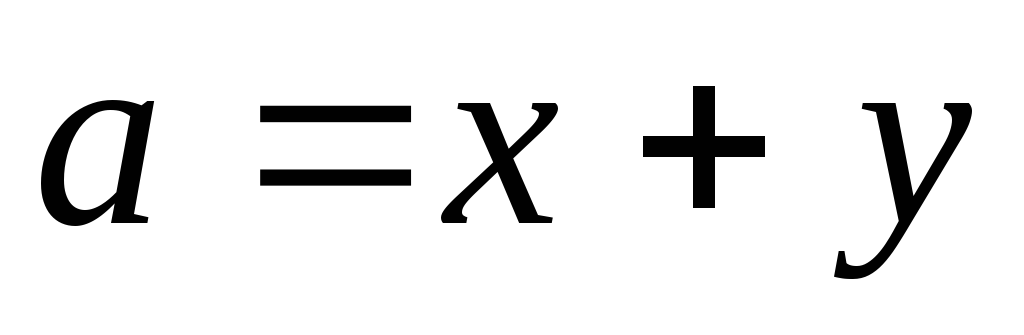 .
.
Если
ось Ox задается некоторым вектором 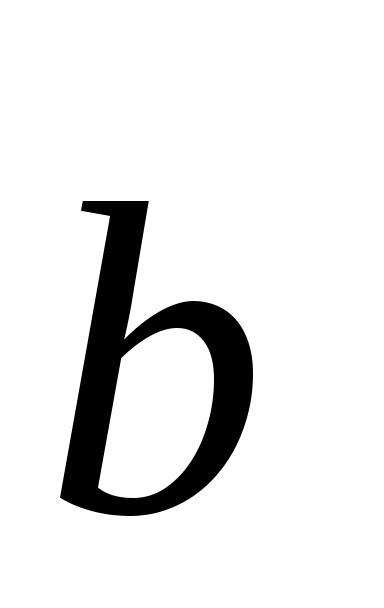 ,
то ортогональная проекция вектора
,
то ортогональная проекция вектора 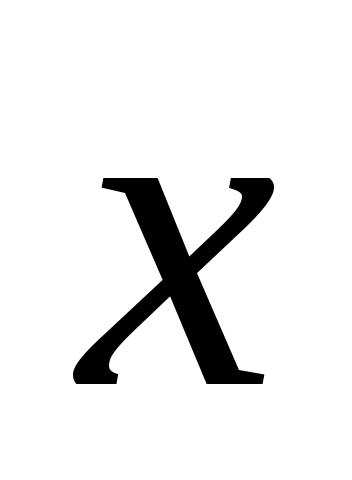 на эту ось может быть найдена с помощью
скалярного произведения. Из
на эту ось может быть найдена с помощью
скалярного произведения. Из  получим
получим 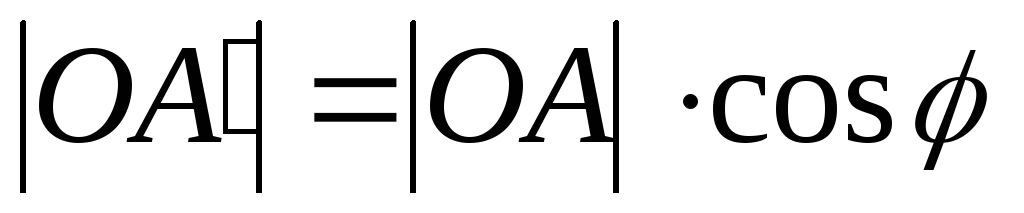 ,
тогда
,
тогда
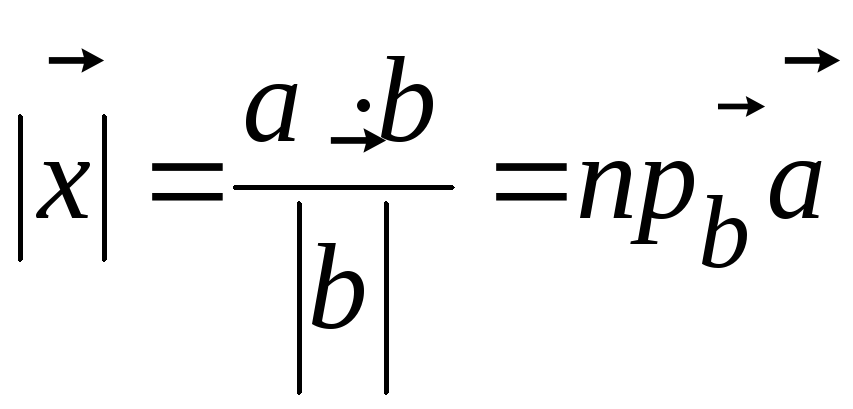 .
(5)
.
(5)
Вектор  коллинеарен вектору
коллинеарен вектору  и имеет длину равную
и имеет длину равную 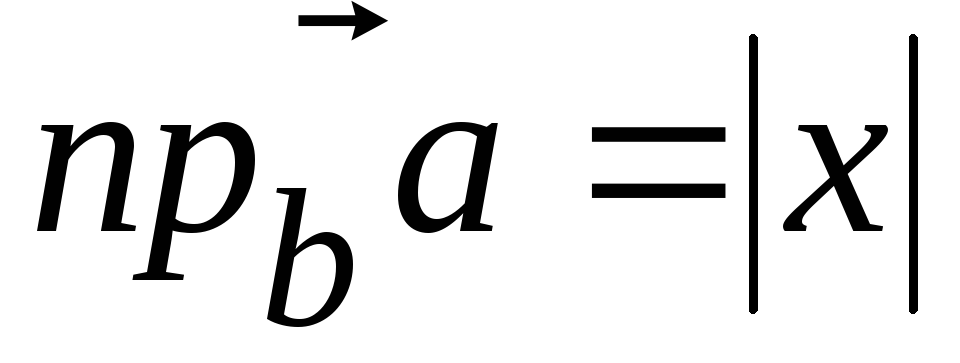 и может быть представлен в виде
и может быть представлен в виде 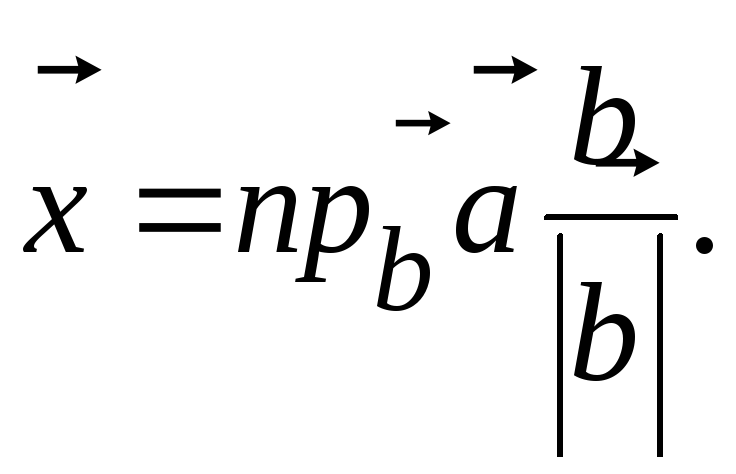 Здесь вектор
Здесь вектор 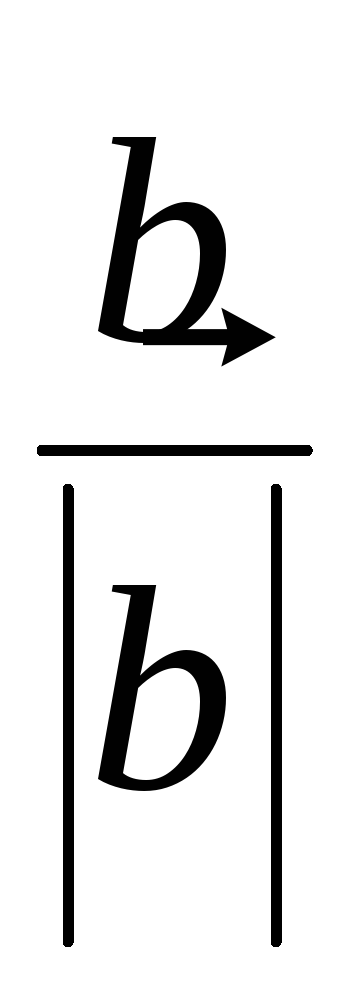 — единичный вектор в направлении оси Ox .
— единичный вектор в направлении оси Ox .
Необходимо
еще раз подчеркнуть, что соотношения
(2), (3), (4) и (5) получены нами в предположении,
что векторный базис 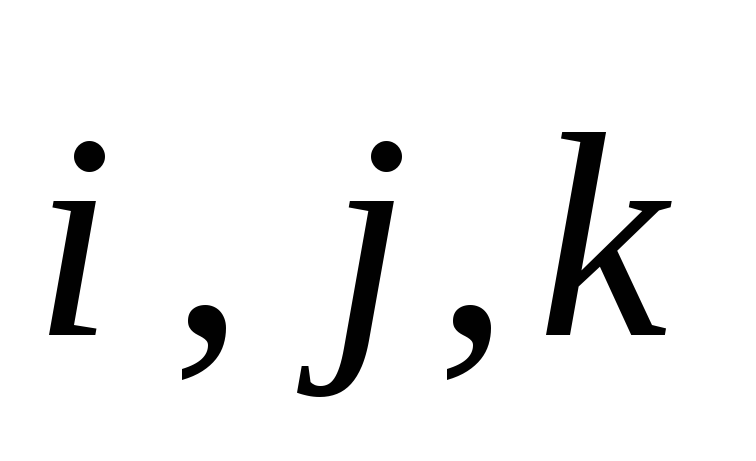 является ортонормированным. В противном
случае эти соотношения недействительны.
является ортонормированным. В противном
случае эти соотношения недействительны.
Пример:
Пусть 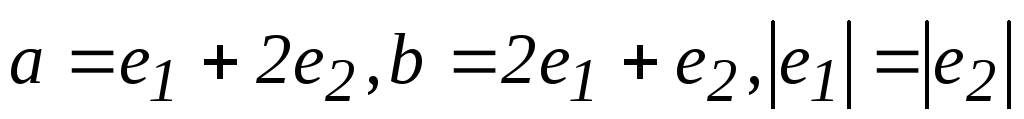 (базис нормирован), но
(базис нормирован), но  .
Тогда
.
Тогда
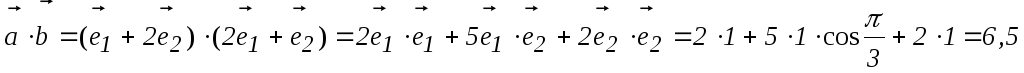 Найдем,
чему равны проекции вектора
Найдем,
чему равны проекции вектора  на оси прямоугольной декартовой системы
координат:
на оси прямоугольной декартовой системы
координат:

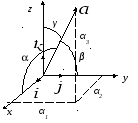
Таким образом, координаты вектора в ортонормированном базисе равны ортогональным проекциям этого вектора на соответствующие оси координат.
Косинусы
углов между вектором  и базисными векторами называют
направляющими косинусами, они могут
быть найдены по следующим формулам:
и базисными векторами называют
направляющими косинусами, они могут
быть найдены по следующим формулам:
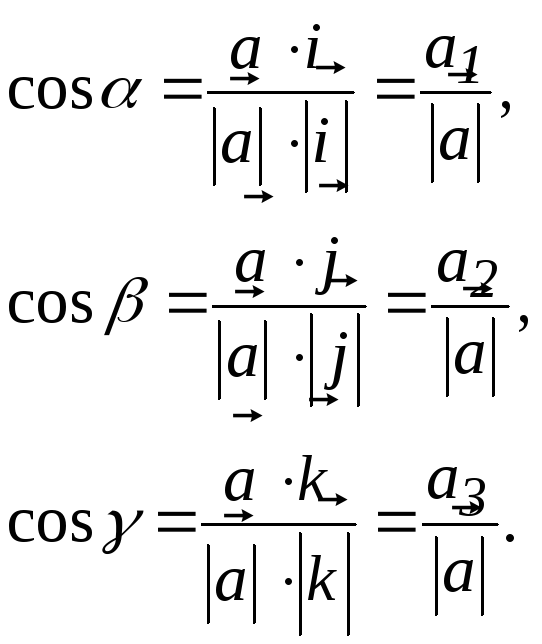 (6)
(6)
Скалярное произведение векторов. Он-лайн калькуляторы скалярного произведения и угла между векторами по координатам.
Скалярное произведение векторов.Скалярное произведение векторов. Он-лайн калькуляторы скалярного произведения и угла между векторами по координатам.
Скалярное произведение векторов — это операция над двумя векторами, результатом которой является число (не вектор).
Определяется скалярное произведение, как правило, следующим образом:
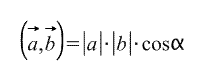 |
Иными словами, скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними . Необходимо заметить, что угол между двумя векторами — это угол, который они образуют, если отложить их от одной точки, то есть начала векторов должны совпадать.
Непосредственно из определения следуют следующие простейшие свойства:
1. Скалярное произведение произвольного вектора а на себя же (скалярный квадрат вектора а) всегда неотрицательно, и равно квадрату длины этого вектора. Причем скалярный квадрат вектора равен нулю тогда и только тогда, когда данный вектор — нулевой.
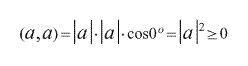
2.Скалярное произведение любых перпендикулярных векторов a и b равно нулю.
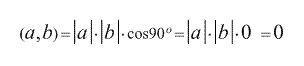
3. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда они перепендикулярны или хотя бы один из них — нулевой.
4. Скалярное произведение двух векторов a и b положительно тогда и только тогда, когда между ними острый угол.
5.Скалярное произведение двух векторов a и b отрицательно тогда и только тогда, когда между ними тупой угол.
Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами.
(Вычислить координаты вектора, если заданы координаты его начала и его конца очень просто —
Пусть есть вектор AB, А — начало вектора, В — конец, и координаты этих точек
А=(a1,a2,a3), В=(b1,b2,b3)
Тогда координаты вектора АВ:
АВ={b1-a1, b2-a2, b3-a3}.
Аналогично в двухмерном пространстве — просто отсутствуют третьи координаты)
Итак, пусть даны два вектора, заданные набором своих координат:
а) В двухмерном пространстве(на плоскости).
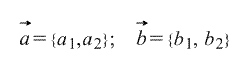
Тогда их скалярное произведение можно вычислить по формуле:
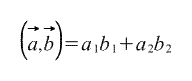
б) В трехмерном пространстве
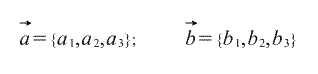
Аналогично двухмерному случаю, их скалярное произведение вычисляется по формуле:
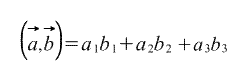
Вычисление угла между векторами с помощью скалярного произведения.
Самое распространенное математическое приложение скалярного произведения двух векторов — это вычисление угла между векторами, заданными своими координатами. Для примера возьмем трехмерный случай. (Если вектора заданы на плоскости, то есть двумя координатами, во всех формулах просто отсутствуют третьи координаты.)
Итак, пусть у нас есть два вектора:
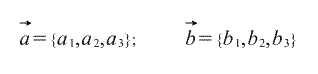
И нам нужно найти угол между ними. С помощью их координат найдем их длины, а затем просто приравняем две формулы для скалярного произведения. Таким образом мы получим косинус искомого угла.
Длина вектора а вычисляется как корень из скалярного квадрата вектора а, который мы вычислим по формуле для скалярного произведения векторов, заданных координатами:
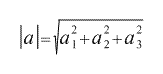
Аналогично вычисляется длина вектора b.
Итак,
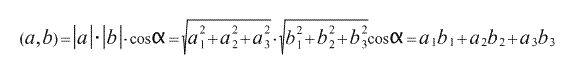
Значит,
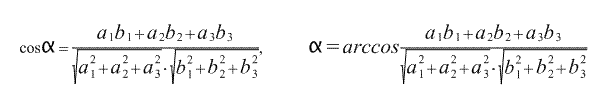
Искомый угол найден.
Он-лайн калькулятор скалярного произведения двух векторов.
Чтобы найти скалярное произведение двух векторов с помощью данного калькулятора, нужно ввести в первую строку по порядку координаты первого вектора, во вторую- второго. Координаты векторов могут быть вычислены по координатам их начала и конца (см. выше Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами. )
Если вектора заданы двумя координатами, то на месте третьей координаты каждого вектора нужно поставить ноль.
Он-лайн калькулятор угла между векторами.
Аналогично предыдущему калькулятору, необходимо ввести координаты обоих векторов по порядку, и если вектора заданы двумя координатами — на месте третьих координат следует поставить ноль.
Скалярное произведение векторов. Он-лайн калькуляторы скалярного произведения и угла между векторами по координатам.
Скалярное произведение векторов. Он-лайн калькуляторы скалярного произведения и угла между векторами по координатам.
Скалярное произведение векторов — это операция над двумя векторами, результатом которой является число (не вектор).
Определяется скалярное произведение, как правило, следующим образом:
Иными словами, скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними . Необходимо заметить, что угол между двумя векторами — это угол, который они образуют, если отложить их от одной точки, то есть начала векторов должны совпадать.
Непосредственно из определения следуют следующие простейшие свойства:
1. Скалярное произведение произвольного вектора а на себя же (скалярный квадрат вектора а) всегда неотрицательно, и равно квадрату длины этого вектора. Причем скалярный квадрат вектора равен нулю тогда и только тогда, когда данный вектор — нулевой.
2.Скалярное произведение любых перпендикулярных векторов a и b равно нулю.
3. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда они перепендикулярны или хотя бы один из них — нулевой.
4. Скалярное произведение двух векторов a и b положительно тогда и только тогда, когда между ними острый угол.
5.Скалярное произведение двух векторов a и b отриц
Свойства скалярного произведения. Скалярное произведение векторов и его свойства. Скалярный квадрат вектора.
Напомним, векторы — это величины, которые описываются как величиной, так и направлением.
Скалярное произведение \( \overline{a }\) и \( \overline{b }\) определяется как
\( \overline{a }· \overline{b }\) \(= |a| |b|· ∠ (\overline{a }\overline{b })\)
где \(| a |-\) модуль, или величина \( a\),
\(| b |-\) модуль \(b\),
\(∠ (\overline{a }\overline{b })\)-угол между \(a\) и \(b\):
Если два вектора сонаправены, то \( ∠cos (\overline{a }\overline{b })= ∠cos \;0=1\) скалярное произведение равно \( \overline{a }· \overline{b }\)\(=\)\( \overline{|a| }· \overline{|b| }\).
1 свойство. Умножим вектор сам на себя:
- \( ( \overline{a }· \overline{a }\)\(= \overline{|a| }^2) \) в результате мы получаем скалярный квадрат вектора.
2 свойство. Скалярный квадрат вектора всегда больше нуля или равен нулю:
- \(\)\( \overline{a }· \overline{a }\geq0\)
3 свойство. Произведение вектора само на себя равно нулю тогда и только тогда, когда вектор является нулевым вектором:
- \( \overline{a }· \overline{a }=0\) если \( \overline{a }= \overline{0 }\)
4 свойство. Переместительное или коммутативное свойство :
- \( \overline{a }· \overline{b }= \overline{b }· \overline{a }\)
5 свойство. Распределительное или дистрибутивное свойство:
- \(( (\overline{a }+\overline{b })\overline{с }= \overline{a }· \overline{c }+\overline{b }· \overline{c })\)
6 свойство. Cочетательное или ассоциативное свойство:
- \((\lambda \overline{a })· \overline{b }= \lambda(\overline{b }· \overline{a })-\) выносим константу
7 свойство. Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы перпендикулярны:
- \(a ≠ 0, b ≠ 0, a · b = 0 <=> a ┴ b\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Скалярное произведение векторов
Для начала вспомним, какие действия над векторами вам известны.
Итак,
это сложение двух векторов по правилу треугольника или параллелограмма и
нескольких векторов по правилу многоугольника. Вектор разности векторов  мы
получали как вектор суммы векторов
мы
получали как вектор суммы векторов  .
.

Также вам знакомо правило умножение вектора на число.

Сегодня вы познакомитесь с ещё одним действием над векторами — скалярным умножением векторов.
Определение. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
Скалярное
произведение векторов  обозначают
так
обозначают
так  .
.
Или возможна запись без знака умножения.
Оно равно произведению длин данных векторов на косинус угла между ними.

Стоит вспомнить, что угол между векторами получают, откладывая данные векторы от одной точки. При этом выбирают угол меньший 180°
Обратите внимание, ранее, при выполнении сложения, вычитания векторов и умножения вектора на число, результатом каждого из этих действий мы получали некоторый вектор.
Результатом же скалярного произведения векторов является число.
Сейчас подробнее рассмотрим случай, когда скалярное произведение векторов равно 0.
Понятно, что для этого хотя бы один из множителей должен быть равен нулю.
Такими будут случаи, когда хотя бы один из векторов в произведении является нулевым.
Если
же векторы  ненулевые,
то косинус угла между ними должен быть равен 0.
ненулевые,
то косинус угла между ними должен быть равен 0.
Среди возможных значений градусной меры угла между двумя векторами только лишь косинус угла в 90° равен 0.
Отсюда
получаем, что векторы  перпендикулярны.
перпендикулярны.

Подытожим. Скалярное произведение равно нулю, если хотя бы один из векторов сомножителей является нулевым.
Ну, а скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Из
формулы скалярного произведения также можно заметить, что, если векторы  не
нулевые, то их длины всегда больше нуля, поэтому их произведение тоже
положительно. А вот значение косинуса угла между ними может принимать как
положительные, так и отрицательные значения.
не
нулевые, то их длины всегда больше нуля, поэтому их произведение тоже
положительно. А вот значение косинуса угла между ними может принимать как
положительные, так и отрицательные значения.
Можно
сказать, что скалярное произведение двух ненулевых векторов больше нуля, если
угол между векторами острый. Равно нулю, если угол между ним прямой. И меньше
нуля, если угол между данными векторами тупой. Ещё раз обратим внимание на то,
что эти заключения верны для ненулевых векторов  .
.
Задача.
Найти скалярное произведение векторов  и
и
 ,
пользуясь данными рисунков.
,
пользуясь данными рисунков.


Решение.
а)
б)
в)
г)
Мы рассмотрели примеры применения формулы скалярного произведения двух векторов и убедились, что скалярное произведение ненулевых векторов больше нуля, если угол между ними является острым, равно нулю — если векторы перпендикулярны, и меньше нуля — если угол между векторами тупой.
А
сейчас рассмотрим сонаправленные векторы  и
и
 .
Запишем формулу их скалярного произведения.
.
Запишем формулу их скалярного произведения.

Вы должны помнить с прошлых уроков, что угол между сонаправленными векторами равен нулю. А косинус угла в 0° равен 1. Тогда получаем, что скалярное произведение сонаправленных векторов равно произведению их длин.
Говоря о противоположно направленных векторах, можно вспомнить, что угол между ними равен 180°. Значит, косинус равен -1.
Тогда
скалярное произведение противоположно направленных векторов равно  .
.

Что касается, скалярного произведения вектора на самого себя, то его называют скалярным квадратом вектора. Этот случай можно рассматривать в контексте сонаправленных векторов. Действительно, ведь векторы равны, а значит, и сонаправлены. Такое произведение равно произведению длин данного вектора.
Тогда получаем, что скалярный квадрат вектора равен квадрату его длины.

Задача.
Найдём скалярные квадраты векторов  ,
,
 ,
,
 и
и
 .
.

Решение.




Скалярное
произведение векторов применяется не только в математике. Например, из курса
механики известно, что работа постоянной силы F
при перемещении из точки М в точку Н равна  .
.
Тем
самым получаем, что работа силы F
равна скалярному произведению вектора силы  и
вектора перемещения
и
вектора перемещения  .
.
Вернёмся к скалярному произведению в математике и решим несколько задач.
Задача.
К одной и той же точке приложены  и
и
 ,
действующие под углом в
,
действующие под углом в  друг
к другу.
друг
к другу.  ,
,
 .
Найти величину равнодействующей силы
.
Найти величину равнодействующей силы  .
.
Решение.

1 способ





 ,
,

2 способ





 ,
,

Ответ:
 .
.
Задача.
В  ,
, где
где
 ,
проведена высота
,
проведена высота  .
Вычислить
.
Вычислить  ,
,
 ,
,
 ,
,
 .
.
Решение



 ,
так как
,
так как 


Подведём итоги нашего урока.
Сегодня вы познакомились с новым действием над векторами — скалярным умножением векторов.
Скалярным произведением двух векторов называют произведение длин данных векторов на косинус угла между ними.
Проанализировав эту формулу, мы заметили, что скалярное произведение равно нулю, если хотя бы один из векторов сомножителей является нулевым. Ну, а скалярное произведение ненулевых векторов рано нулю, тогда и только тогда, когда данные векторы перпендикулярны.
Также, пользуясь знаниями об углах между сонаправленными и противоположно направленными векторами, мы выяснили, что скалярное произведение сонаправленных векторов равно произведению их длин, а скалярное произведение противоположно направленных векторов противоположно произведению их длин.
Введя понятия скалярного квадрата вектора, мы получили, что он равен квадрату длины данного вектора.
Знания о скалярном произведении векторов можно применять не только на уроках математики. Так же они широко используются в физике.
Вычислительная геометрия, или как я стал заниматься олимпиадным программированием.Часть 1
Здравствуйте, уважаемые хабравчане! Это моя вторая статья, и мне хотелось бы поговорить о вычислительной геометрии.Немного истории
Я являюсь студентом уже 4 курса математического факультета, и до того как я начал заниматься программированием, я считал себя математиком на 100 процентов.
В конце первого курса мой преподаватель по информатике, который занимается олимпиадным программированием, обратил на меня внимание. Им как раз не хватало одного математика в команду. Так потихоньку меня начали приучать к олимпиадному программированию. Скажу честно, для меня это было очень сложно: для человека, который узнал слово Delphi на первом курсе. Однако мой преподаватель оказался очень грамотным специалистом и нашел хороший подход ко мне. Он начал давать мне математические задачи, который я сначала решал чисто математически, а уже потом писал код (с грехом пополам).
Мне очень нравится подход моего преподавателя: «разберись с этой темой, а потом расскажи нам, да так чтоб мы все поняли».
Итак, первой на самом деле важной задачей, с которой мне поручили разобраться, было именно вычислительная геометрия, необходимо было разобраться в типичных задач этого раздела информатики. И я решил подойти к этой задаче со всей ответственностью.
Я помню, как долго мучился с этими задачами, чтобы они прошли все тесты на сайте informatics.mccme. Зато теперь я очень рад, что прошел через все испытания и знаю, что же такое задачи вычислительной геометрии.
Вступление
«Вычислительная геометрия – это раздел информатики, изучающий алгоритмы решения геометрических задач. Такие задачи возникают в компьютерной графике, проектировании интегральных схем, технических устройств и др. Исходными данными в такого рода задачах могут быть множество точек, набор отрезков, многоугольники и т.п. Результатом может быть либо ответ на какой-то вопрос, либо какой-то геометрический объект».
Поскольку статья является достаточно большой я решил разбить ее на две части: первая часть посвящена многоугольникам, вторая – взаимному расположению различных геометрических объектов.
Немного теории о векторах
Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.
Длиной ненулевого вектора AB называется длина отрезка AB. Длина нулевого вектора считается равной нулю.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора AB и CD коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы AB и CD называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы AB и CD называются противоположно направленными. Нулевой вектор принято считать сонаправленным с любым вектором.
Скалярное произведение векторов
Скалярное произведение векторов — это число, равное произведению длин этих векторов на косинус угла между ними.
(a, b) = |a||b|cos∠(a, b)
Если векторы заданы своими координатами a(x1, y1), b(x2, y2) то скалярное произведение (a, b) = x1x2 + y1y2.
Косое произведение векторов
Псевдоскалярным или косым произведением векторов на плоскости называется число
[a, b] = |a||b|sinθ
где — угол вращения (против часовой стрелки) от a к b. Если хотя бы один из векторов a и b нулевой, то полагают [a, b] = 0.
Если векторы заданы своими координатами a(x1, y1), b(x2, y2) то косое произведение [a, b] = x1y2 — x2y1.
Геометрически косое произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора.
Косое произведение векторов в задачах вычислительной геометрии занимает такое же почетное место, как рекурсии в комбинаторике. Это своего рода жемчужина вычислительной геометрии. Практически каждая задача вычислительной геометрии имеет более простое решение с помощью косового произведение вместо лобового решения.
А теперь займемся практикой
Начнем с треугольников
Задача №1
Задача очень простая, а именно: по введенным трем числам a, b, c определить существует ли треугольник с такими сторонами.
Решение
Понятно, что здесь нужно только проверить неравенство треугольника: a + b > c, a + c > b, b + c > a. Интересно, при изучении неравенства треугольника только ли у меня возник вопрос: не могут ли отрицательные числа тоже удовлетворять этим трем неравенствам? Оказывается, нет! Если мы сложим каждое неравенство, то получим a > 0, b > 0, c > 0. Поэтому неравенство треугольника является необходимым и достаточным условием существования треугольника.
Задача №2
Задача является очень похожей на предыдущую с той разницей, что треугольник задан не сторонами, а координатами вершин.
Решение
С первого взгляда решение кажется очевидным: вычислить стороны треугольника и свести задачу к предыдущей. Однако поскольку расстояние между двумя точками A(x1, y1), B(x2, y2) вычисляется по формуле √(x1-x2)2+(y1-y2)2 то при извлечении корня возможна потеря точности, что плохо скажется на проверке неравенства треугольника. Оказывается, что если треугольник задан координатами своих вершин, то вычислять длины его сторон и проверять неравенство треугольника не требуется. В этом случае треугольника не существует тогда и только тогда, когда данные три точки лежат на одной прямой. А это легко проверяется через косое произведение векторов. Если оно равно нулю, то векторы коллинеарные, то есть все три точки лежат на одной прямой.
Во всех следующих задачах будем считать, что треугольник существует, поскольку процедуру проверки существования треугольника мы только что рассмотрели.
Задача №3
Треугольник задан своими сторонами. Определить тип треугольника: тупоугольный, прямоугольный или остроугольный.
Решение
Вспомним, что представляют собой каждый вид треугольника.
Из курса геометрии известно, что напротив большей стороны лежит больший угол (он нам и нужен). Поэтому если мы выясним чему равен больший угол, то поймем тип треугольника:
- Угол больше 90° – треугольник тупоугольный
- Угол меньше 90°– треугольник остроугольный
- Угол равен 90°– треугольник прямоугольный
Очевидно, что если косинус угла больше нуля то угол меньше 90°, если он равен нулю, то угол равен 90°, если он меньше нуля, то угол больше 90°. Однако немного поразмыслив можно понять, что вычислять косинус угла не обязательно, необходимо учесть лишь его знак:
- Если cosα > 0, то a2 < b2 + c2 – треугольник остроугольный
- Если cosα = 0, то a2 = b2 + c2 – треугольник прямоугольный
- Если cosα < 0, то a2 > b2 + c2 – треугольник тупоугольный
Задача №4
Задача аналогична предыдущей задаче, только треугольник задан не своими сторонами, а координатами вершин.
Решение
Аналогично задаче 2 можно сказать, что эта задача полностью сводится к предыдущей задаче (так оно и есть). Однако, как и во второй задаче, решение можно упростить. Вообще, если треугольник задан координатами своих вершин, то всегда легче работать с ним через вектора, нежели вычислять стороны. Аналогично предыдущей задаче, необходимо определить каким является наибольший из углов треугольника. Вид угла легко определяется по знаку скалярного произведения образующих его векторов: оно положительно для острого угла, равно нулю для прямого угла и отрицательно для тупого угла. Поэтому необходимо посчитать все три скалярных произведения и перемножить их и по знаку данного числа можно судить о типе треугольника.
Задача №5
По данным сторонам треугольника найти его площадь.
Решение
Очевидно решение, заключается в применение формулы Герона.
Кстати, никого не интересовало доказательство этой формулы?
Вот и все!
Задача №6
Вычислить площадь треугольника заданного координатами своих вершин.
Решение
Не будем говорить о решении, которое сводится к предыдущей задачи, а попробуем воспользоваться геометрическим смыслом косового произведения. Геометрически косое произведение двух векторов определяет ориентированную площадь параллелограмма натянутого на эти вектора. Поскольку диагональ параллелограмма разбивает его на два равновеликих треугольника, то можем найти площадь нашего треугольника, как половину площади параллелограмма.
Для векторов a(x1, y1), b(x2, y2)
S = (x1y2 — x2y1) / 2 — ориентированная площадь треугольника
Задача №7
Дана точка и треугольник заданный координатами своих вершин. Определить лежит ли точка внутри, на границе или вне этого треугольника.
Решение
У этой задачи есть два принципиально разных решения. Начнем с наименее привлекательного.
Метод площадей
Если сумма площадей треугольников AKB, AKC, BKC (не ориентированных, а «обычных») больше площади треугольника ABC точка лежит вне треугольника. Если же сумма первых трех площадей равна четвертой, то нужно проверить, не равна ли нулю одна из трех площадей. Если равна, то точка лежит на границе треугольника, иначе – внутри.
Вычислять площади треугольников, естественно, надо через косое произведение векторов. Этот метод не очень хороший. Поскольку здесь используются сравнение чисел с плавающей точкой, а это в свою очередь может привести к принятию неверного решения при сравнении. Второй метод опять таки опирается на вектора, он намного эффективнее во всех отношениях.
Проверка полуплоскостей
Если хотя бы одна из сторон треугольника «разводит» противолежащую ей вершину и точку по разным полуплоскостям, то точка лежит вне треугольника. Иначе, если точка принадлежит хотя бы одной из прямых, содержащих стороны треугольника, то она находится на границе треугольника. Иначе точка лежит внутри треугольника.В первом примере сторона AB разводит вершину C и точку K по разным полуплоскостям, поэтому точка лежит снаружи.
Задача №8
Вычисление площади многоугольника заданного координатами своих вершин.
Решение
Под многоугольником будем подразумевать простой многоугольник, то есть без самопересечений. При этом он может быть как выпуклым, так и не выпуклым.
Данную задачу можно решить двумя способами: вычисляя ориентированные площади трапеций и треугольников.
Метод трапеций
Для того чтобы посчитать площадь многоугольника нужно разбить его на трапеции, так как это показано на рисунке, а затем сложить ориентированные площади полученных трапеций это будет ориентированной площадью исходного многоугольника.
S = SA1A2 B2 B1 + SA2 A3 B3B2 + SA3A4B5B3 + SA4A5B6B5 + SA5A6B4 B6 + SA6A1 B1 B4
Площади трапеций считаем по известной формуле: полусумма оснований на высоту
SA1A2 B2 B1 = 0.5 * (A1B1 + A2B2) *(B2 — B1)
Поскольку полученная площадь является ориентированной, необходимо вычислить ее модуль.
Метод треугольников
Аналогично предыдущему методу можно разбивать многоугольник не на трапеции, а на треугольники, как показано на рисунке. В результате, сложив ориентированные площади этих треугольников, мы получим опять-таки ориентированную площадь многоугольника.
S = SOA1A2 + SOA2A3 + SOA3A4 + SOA4A5 + SOA5A6 + SOA6A1
Как вы видите задача вычисления площади многоугольника достаточна проста. Не знаю, почему, но мне больше нравится решать эту задачу методом разбиения на трапеции (наверно потому, что на всех олимпиадах я ее так решал). Тем более, что при втором решении площади треугольников надо вычислять через косое произведение. О формуле Герона надо забыть!!!
Задача №9
Многоугольник задан координатами своих вершин в порядке его обхода. Необходимо проверить является ли многоугольник выпуклым.
Решение
Напомню, что многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.
Задача опять сводится к вычислению косового произведения векторов, а именно у выпуклого многоугольника знаки косых произведений [Ai Ai+1, Ai+1 Ai+2] либо положительны, либо отрицательны. Поэтому если мы знаем направление обхода, то знак косых произведений для выпуклого многоугольника одинаков: он неотрицателен при обходе против часовой стрелки и неположителен при обходе по часовой стрелки.
Задача №10
Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).
Решение
Для решения этой задачи рассмотрим вспомогательную задачу: отрезок задан координатами своих концов, являющихся целыми числами. Необходимо посчитать количество целочисленных точек лежащих на отрезке. Понятно, что если отрезок вертикальный или горизонтальный, то необходимо вычесть координаты концов и добавить единицу. Интерес представляет случай, когда отрезок не является вертикальным или горизонтальным. Оказывается в этом случае необходимо достроить отрезок до прямоугольного треугольника и ответом будет число равное наибольшему общему делителю длин катетов этого треугольника плюс единица.
Для любого многоугольника с целочисленными координатами вершин справедлива формула Пика: S = n + m/2 — 1, где S – площадь многоугольника, n – количество целых точек лежащих строго внутри многоугольника, m – количество целых точек лежащих на границе многоугольника. Поскольку площадь многоугольника мы знаем как вычислять, то S известно. Так же мы можем вычислить количество целых точек лежащих на границе многоугольника, поэтому в формуле Пика остается лишь одна искомая неизвестная которую мы можем найти.
Рассмотрим пример:
S = 16 + 4 + 4,5 + 6 + 1 + 2 = 33,5
m = 15
n = 33,5 – 7,5 +1 = 27 — точек лежит строго внутри многоугольника
Вот так вот решается эта задачка!
Вот и все! Надеюсь, Вам понравилась статья, и я напишу ее вторую часть.

