Свойства скалярного произведения. Кратко, с примерами
Для произвольных векторов и любого числа справедливы следующие свойства:
1) – переместительный или коммутативный закон
2) – распределительный или дистрибутивный закон скалярного произведения. Попросту, можно раскрывать скобки.
3) – сочетательный или ассоциативный закон скалярного произведения относительно множителя (константу можно вынести из скалярного произведения)
Зачастую всевозможные свойства (которые ещё и доказывать надо!) воспринимаются студентами как ненужный хлам, который лишь
необходимо вызубрить и сразу после экзамена благополучно забыть. Казалось бы, чего тут важного – все и так с первого класса
знают, что от перестановки множителей произведение не меняется: . Должен предостеречь, в высшей математике с подобным подходом легко «наломать
дров».
Задача 17
Найти скалярное произведение векторов и , если известно, что
Решение: сначала проясним ситуацию с вектором . Что это вообще такое? Сумма векторов и представляет собой вполне определенный вектор, который и обозначен через . Такая же история с вектором – это сумма векторов и
Итак, по условию требуется найти скалярное произведение . По идее, нужно применить рабочую формулу , но беда в том, что нам неизвестны длины векторов и угол между ними. Зато в условии даны аналогичные параметры для векторов , поэтому мы пойдём другим путём:
(1) Поставляем выражения векторов .
(2) Используя дистрибутивное свойство, раскрываем скобки по правилу умножения многочленов: чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена
(3) В первом и последнем слагаемом компактно записываем скалярные квадраты векторов: . Во втором слагаемом используем перестановочность скалярного произведения: .
(4) Приводим подобные слагаемые: .
(5) В первом слагаемом используем формулу скалярного квадрата . В последнем слагаемом работает та же штука: . Второе слагаемое раскладываем по стандартной формуле .
(6) Подставляем исходные данные и ВНИМАТЕЛЬНО проводим окончательные вычисления.
Ответ:
Отрицательное значение скалярного произведения констатирует тот факт, что угол между векторами является тупым.
Задача типовая, вот пример для самостоятельного решения:
Задача 18
Найти скалярное произведение векторов и , если известно, что .
Теперь ещё одно распространённое задание, как раз на новую формулу длины вектора . Обозначения тут будут совпадать, поэтому для ясности я перепишу её с другой буквой:
Задача 19
Найти длину вектора , если .
Сначала решение, затем комментарии:
(1) Поставляем выражение вектора .
(2) Используем формулу длины: , при этом в качестве вектора «вэ» у нас выступает целое выражение .
(3) Используем школьную формулу квадрата суммы :
– обратите внимание, как она здесь любопытно
сработала, фактически это квадрат разности , и, по
сути, так оно и есть. Переставим векторы местами: – получилось то же самое с точностью до перестановки слагаемых.
(4) Дальнейшее уже знакомо из двух предыдущих задач.
Ответ:
Коль скоро речь шла о длине, то не забываем указать размерность – «единицы».
Найти длину вектора , если .
Это пример для самостоятельного решения.
Продолжаем выжимать полезные вещи из скалярного произведения:
1.6.5. Как найти угол между векторами?
1.6.3. Скалярный квадрат вектора
| Оглавление |
Автор: Aлeксaндр Eмeлин
Скалярное произведение векторов. Примеры решения задач
Решения типовых задач по теме: «Скалярное произведение векторов»
Задача № 1. Векторы
и образуют угол . Зная,
что , вычислить:
Решение. Так как скалярное произведение двух векторов равно произведению их длин, умноженному на косинус угла между ними, и скалярный квадрат вектора равен квадрату его длины, будем иметь:
Ответ: 1) 428; 2) 804.
Задача № 2. Определить, при каком значении векторы и будут взаимно перпендикулярными, если
Решения этих задач подробно изложено в следующем видео
youtube.com/embed/SyA8k1vrrbg» frameborder=»0″ allowfullscreen=»allowfullscreen»> Задача № 3. Вычислить тупой угол, образованный медианами, проведенными из вершин острых углов равнобедренного прямоугольного треугольника.
Задача № 4. Зная одну из вершин треугольника А (1; —6; — 3) и векторы, совпадающие с двумя его сторонами
{0; 3; 5} и {4; 2; —1}, найти остальные вершины и сторону .
Решение. Найдем координаты вершины В, исходя из формул, что проекции вектора равны:
Откуда
Таким образом,
В( 1; -3; 2).
Аналогично найдем координаты точки С:
С(5; -1; 1).
Теперь найдем вектор :
Ответ: B(1; -3; 2), С(5; -1; 1), {—4; -5; -4}.
Решения этих задач подробно изложено в следующем видео
youtube.com/embed/fhwGqRo-PPw?list=PLk91qesJngSK-fpBM4iu3CGyDAugw6n0A» frameborder=»0″ allowfullscreen=»allowfullscreen»> Задача № 5. В плоскости yOz найти вектор
, перпендикулярный вектору {12;-3;4} и имеющий одинаковую с ним длину.
Задача № 6. Вычислить, какую работу производит сила {6; — 2; 1}, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения А(3;4;—2) в положение В (4;-2;-3).
Решение. Найдем проекции вектора , по которому перемещается точка приложения силы , по фомулам
т. е.
Следовательно, имеем
={1;-6;-1}.
Так как работа численно равна скалярному произведению производящей ее силы на пройденный путь, то найдем скалярное произведение векторов и :
Ответ: А = 17 (единиц работы).
Решения этих задач подробно изложено в следующем видео
youtube.com/embed/nzWvFpt4DIw» frameborder=»0″ allowfullscreen=»allowfullscreen»> Задача № 7. Дан треугольник с вершинами А (- 2; 3; 1), В (-2; -1; 4) и С (- 2; -4; 0). Определить его внутренний угол при вершине С.
Задача № 8. Даны три вектора
{ 1; —4; 8}, {4; 4: -2}, {2; 3; 6}.
Вычислить проекцию вектора на вектор .
Решения этих задач подробно изложено в следующем видео
Скаляр, Вектор, Тензор [Encyclopedia Magnetica]
Содержание
Скаляр, Вектор, Тензор
Обзор
Скаляр
Вектор
Вектор нормали
Тензор
Единичный вектор
Скалярная, векторная и тензорная запись
Векторные операции
Сложение, вычитание, умножение
Векторное исчисление
Набла ∇ оператор
Скалярные и векторные поля
Система координат
См.
такжеКаталожные номера
такжеСкаляр, вектор, тензор — математическое представление физического объекта, которое может быть характеризуется величиной и/или направлениями, связанными с ним. Скаляры, векторы и тензоры — это величины, которые не меняются при изменении системы координат (например, между декартовой, цилиндрической, сферической).
Скаляры, векторы и тензоры широко используются в математической обработке электромагнитных задач, а также в том, как обычно формулируются уравнения Максвелла.
Векторное исчисление (а также тензорное исчисление) можно использовать с аналитическими уравнениями, а также с численными расчетами, такими как моделирование методом конечных элементов.
Векторы можно анализировать с точки зрения ковариантных и контравариантных компонент, а также преобразовывать между различными системами координат, в том числе неортогональными. Существует множество подробных следствий, касающихся векторов и расчетов на их основе, и лучше всего изучить соответствующие учебники и литературу, а также попрактиковаться на более простых случаях, прежде чем выполнять более сложные расчеты.
Обзор
| Скаляр (Тенсор Рейнг 0) | Vector (Tensor Rank 1) | TENSOR (Tens 2) 9044 40106 (Tens 2). | |
|---|---|---|---|
| типичные примеры в декартовой системе | | ||
| математическое представление с x, y, z | $(x)$ | $(x, y, z)$ или $\left( \begin{array}{c} x \\ y \\ z \end{массив} \right)$ | $\left( \begin{array}{c} x_{xx} & x_{xy} & x_{xz} \\ y_{yx} & y_{ yy} & y_{yz} \\ z_{zx} & z_{zy} & z_{zz} \end{array} \right)$ |
| математическое представление с x я \\ x_3 \end{массив} \right)$ | $\left( \begin{array}{c} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22 } & x_{23} \\ x_{31} & x_{32} & x_{33} \end{массив} \right)$ | ||
| количество | 1 | 3 | 9 |
| значение значений | величина (без направления) | величина в одном направлении | величина взаимодействия в нескольких направлениях |
Скаляр
Пример скаляра : длина некоторого элемента
Скалярное значение имеет только амплитуду без направления, но может быть положительным, нулевым или отрицательным. Математически можно показать, что скаляр является тензором нулевого ранга или вектором в одномерном пространстве, так что его амплитуда может быть положительной или отрицательной. Скаляры можно использовать и в пространствах с большим количеством измерений (2D, 3D, 4D). Например, масса покоя — это скаляр в четырехмерном пространстве-времени. ВекторПример вектора в трехмерном пространстве с тремя ортогональными координатами ( x , y , z 9960169 )
Векторы могут представлять такие «направленные» величины, как: сила (действующая по заданному направлению), скорость или скорость (движение в заданном направлении), ориентация поверхности (путем определения перпендикулярного к ней вектора) и т. В декартовой системе координат вектор можно разложить на набор ортогональных компонентов, число которых равно количеству измерений пространства. Значение, связанное с каждым направлением, представляет собой числовой множитель длины для каждого единичный вектор $\hat{\imath}, \hat{\jmath}, \hat{k}$ (более подробно поясняется ниже). Векторы и компоненты векторов можно переводить между различными системами координат без изменения их смысла или значения представляемой физической величины. Такие преобразования математически строги, если выполняются аналитическим способом. В 2D-пространстве есть 2 компонента, поэтому можно выполнять вычисления, аналогичные векторным задачам, но с использованием инструмента комплексных чисел. Векторы также можно использовать в четырехмерных пространствах и в любом произвольном количестве измерений, если это необходимо. «Хиральность» системы координат важна для векторов из-за таких последствий, как правило правой руки. Векторы могут быть представлены несколькими способами, некоторые примеры показаны в таблице.
Вектор нормали Векторы также можно использовать для представления компонентов поверхности. Можно определить тип вектора, перпендикулярного плоской плоскости, которая касается данной поверхности в данной точке. Если этот вектор затем выражается как единичный вектор , то он известен как вектор нормали $\hat{n}$ («нормальный» означает «перпендикулярный»). Векторы нормалей полезны в векторном исчислении , особенно при расчете и измерении потока векторного поля (электрического потока и магнитного потока). В правосторонней системе координат полярность вектора нормали в системе определяется правилом правой руки (как показано). В левосторонней системе полярность была бы обратной. Точно так же может быть определен тангенциальный вектор . Тангенциальные составляющие полезны в некоторых случаях измерения напряженности магнитного поля. Положительное направление движения вектора по траектории C также определяется правой рукой в правой системе; вектор нормали $\mathbf{\hat{n}}$ обозначает вектор нормали (перпендикулярный) к поверхности $a$ Векторы нормалей (синие) для каждого бесконечно малого фрагмента поверхности можно использовать для извлечения перпендикулярной составляющей векторного поля (красные) — это позволяет вычислить поток векторного поля TensorExample of a tensor — with a set of 3 orthogonal vectors interacting with the three orthogonal surfaces ( нормальные векторы не показаны)
Тензор представляет собой более общий способ обработки различных компонентов в математике. Скаляр — это тензор ранга 0, поэтому требуется только одно независимое значение, связанное с ним, независимо от количества измерений данного пространства, поэтому для 3D это 3 0 =1. Тензор ранга 1 является вектором и требует столько компонентов, сколько измерений в данном пространстве, таким образом, для 3D это 3 1 = 3. Для тензора ранга 2 требуется больше компонентов, для трехмерного пространства это 3 2 = 9, а для тензора ранга 3 потребуется 27 значений (3 3 ). Векторы (тензорный ранг 1) могут представлять действия и взаимодействия в одном направлении. Однако тензоры ранга 2 можно использовать для представления действий и взаимодействий в нескольких направлениях в пространстве. Например, силы могут действовать вдоль анализируемого направления (сжатие или растяжение), а также перпендикулярно ему (срез или скручивание). Эти различные направления взаимодействия не могут быть представлены одним вектором. Но если на единицу объема материала действуют силы, эти взаимодействия можно представить, приняв во внимание каждую сторону бесконечно малого куба и выразив взаимодействия между всеми трехмерными направлениями. Следовательно, тензоры необходимы для захвата анизотропного поведения во всех направлениях, и, следовательно, тензорная проницаемость может потребоваться в сильно анизотропных трехмерных случаях. Математически обработка тензоров аналогична обработке векторов, потому что в матричных обозначениях используется несколько ортогональных компонентов. Однако сложность значительно возрастает из-за большого количества независимых компонентов, необходимых для таких вычислений. Тензорное поле имеет тензорное значение в каждой точке пространства . б) сплюснутый эллипсоид ($k_1 < k_2 = k_3$)в) вытянутый эллипсоид ($k_1 > k_2 = k_3$) г) трехосный эллипсоид ($k_1 \neq k_2 \neq k_3$)
Единичный вектор Единичные векторы — это инструмент, полезный в векторном исчислении. Например, для главного вектора, который может быть описан значениями координат $\vec{F}$ = ( x , y , z ) = (2, 3, 4), числа обозначают произведение для каждого из единичных векторов (длина 2 в направлении x , 3 в y и 4 в z ). Пример вектора F и его отношение к единичным векторам ф Это эквивалентно геометрическому сложению векторов трех компонентов, так что:
$\vec{F} = 2 ·\hat{i} + 3 ·\hat{j} + 4 ·\hat{k}$, где единичные векторы $\hat{i}, \hat{j}, \ hat{k}$ находятся в направлениях x , y , z соответственно. Обозначение «шляпа» $\hat{k}$ используется вместо обозначения «стрелка» $\vec{k}$ просто для того, чтобы подчеркнуть, что единичные векторы составляют основы направлений, хотя они также являются «обычными» векторами, просто с длиной или модулем, равным 1 в данной системе координат. Единичные векторы $\hat{i}, \hat{j}$ имеют шляпу над точкой, поэтому часто пишутся без точки, только со шляпой: $\hat{\imath}, \hat{\jmath }$. При использовании понятия единичного вектора неявно понимается, что запись $\vec{F} = (2, 3, 4)$ означает $\vec{F} = 2 ·\hat{\imath} + 3 ·\hat {\jmath} + 4 ·\hat{k}$, и аналогично для другого числа измерений. Вычисления, выполненные с единичными векторами, математически эквивалентны тем, в которых используются «полные» векторы. Форма диктуется в основном предпочтениями авторов данного издания. Поэтому уравнения, эквивалентные математически, могут различаться в разных публикациях по способу выражения компонентов из-за подхода, принятого при их выводе. Скалярная, векторная и тензорная нотация
Существует несколько способов представления векторов в математических уравнениях. Обычно скаляры обозначаются обычным шрифтом, используемым для имен переменных. Векторы могут быть обозначены «стрелкой» (для полных векторов) или «шляпой» (для единичных векторов), чтобы включить явную информацию о том, что данная величина действительно является вектором. Однако для удобства векторы можно обозначать просто полужирным шрифтом, что широко используется в научной литературе. Это продиктовано в основном простотой и ясностью обозначений, поскольку, как правило, меньшее количество четких символов легче понять. Не существует определенного способа обозначения тензоров, и поэтому можно использовать векторную форму, если только нет необходимости убедиться, что следует избегать путаницы. Векторные операции Векторами можно математически манипулировать, в некотором смысле подобно скалярам, но сложность операций увеличивается из-за количества компонентов, участвующих в таких вычислениях. Сложение, вычитание, умножениеВекторное исчисление позволяет анализировать электромагнитные явления в трехмерном пространстве в соответствии с уравнениями Максвелла. Векторами можно манипулировать алгебраически (сложение, вычитание, отрицание), с обработкой, аналогичной скалярным значениям, но, конечно, с учетом угла между ними. Например, скалярное сложение означает простую арифметическую сумму компонентов, а векторное сложение означает геометрическую сумму. Определение левосторонней и правосторонней системы координат, с векторное произведение $\vec{c}=\vec{a} × \vec{b}$, выраженное пальцами, вытянутыми под прямым углом Векторы можно перемножать, но есть три операции:
$$\mathbf{A} × \mathbf{B} = \left(\begin{array}{c} \hat{\imath} & \hat{\jmath} & \hat{k} \\ A_x & A_y & A_z \\ B_x & B_y & B_z \end{array} \right) = ( A_y B_z — A_z B_y ) \hat{\imath} + ( A_z B_x — A_x B_z ) \ hat{\jmath} + ( A_x B_y — A_y B_x ) \шляпа{k} $$ Точечные и перекрестные произведения можно комбинировать, например, тройное скалярное произведение возвращает скалярное значение, пропорциональное объему (параллелепипеду), растянутому между всеми тремя входными векторами: $$ \mathbf{A} · ( \mathbf{B} × \mathbf{C}) = \left( \begin{array}{c} A_x & A_y & A_z \\ B_x & B_y & B_z \\ C_x & C_y & C_z \end{array} \right) = A_x ( B_y C_z — B_z C_y ) + A_y ( B_z C_x — B_x C_z ) + A_z ( B_x C_y — B_y C_x ) $$ Кроме того, 9Тройное векторное произведение 0079 можно рассчитать аналогичным образом, но с использованием более утомительных уравнений из-за количества задействованных компонентов, и поэтому обычно проще использовать эквивалентное тождество, в котором вместо этого используются скалярные произведения: $$\mathbf{A} × (\mathbf{B} × \mathbf{C}) = \left(\begin{array}{c} \hat{\imath} & \hat{\jmath} & \hat{ k} \\ A_x & A_y & A_z \\ ( B_y C_z — B_z C_y ) & ( B_z C_x — B_x C_z ) & ( B_x C_y — B_y C_x ) \end{массив} \right) = \mathbf{B} (\ mathbf{A} ·\mathbf{C}) — \mathbf{C}( \mathbf{A} · \mathbf{B})$$ Интересно, что деление вектора на не может быть легко определено и поэтому не используется в векторном исчислении. Векторное исчисление
Исчисление включает производные и интегралы, а векторное исчисление включает производные и интегралы векторов, которые могут представлять функции или поля в трехмерном пространстве. Оператор набла ∇ позволяет значительно упростить обозначения.
Набла ∇ оператор Такой оператор, как квадратный корень $\sqrt{F}$, сообщает, что необходимо выполнить операцию над переменной F , следующей за оператором. В трехмерном пространстве векторы могут быть разделены на ортогональные компоненты, и частные производные могут быть рассчитаны соответственно для каждого компонента направления. Специальный символ ∂ используется для обозначения того, что производные являются частичными, поэтому для одного компонента это может быть $\frac{∂F}{∂x} = \frac{∂}{∂x}(F)$ и более компонентов. можно использовать соответственно. Таким образом, в трехмерном пространстве оператор может быть определен с тремя компонентами направленного единичного вектора ($\hat{\imath}, \hat{\jmath}, \hat{k}$), а для простоты записи — только с одним символ с именем набла или del , обозначенный перевернутым треугольником $\vec{∇} ≡ \mathbf{∇} ≡ ∇$ (стрелка или жирный шрифт обычно опускаются), может использоваться для представления вся операция. $$ \vec{∇} ≡ \mathbf{∇} ≡ ∇ ≡ \hat{\imath} \frac{∂}{∂x} + \hat{\jmath} \frac{∂}{∂y} + \hat {k} \frac{∂}{∂z} $$ 92} $$ Скалярное и векторное поляПлотность электрического потока D увеличивается, если площадь диэлектрика с высокой диэлектрической проницаемостью уменьшается в том же электрическом поле (векторном поле) В физике поле — это такая область пространства, в которой каждой точке такого пространства приписывается некоторое значение. Стрелки компаса следуют направлению магнитного поля ( B или H ) вокруг провода с током I — магнитное поле «циркулирует» вокруг провода с током Если значения скалярные, то это скалярное поле (такое распределение температуры внутри тела). Если значения являются векторами, то это векторное поле (например, распределение скорости газа внутри некоторого контейнера). Векторное исчисление можно использовать для выполнения расчетов полей, а также для вычисления таких векторных и скалярных величин, как: магнитный поток, плотность магнитного потока, электрический поток, плотность электрического потока и т. д. Система координатВекторы и тензоры могут быть определены или выражены в различных системах координат, которые используются для уменьшения сложности вычислений некоторых задач. Это связано с тем, что математические уравнения могут иметь немного различную форму в каждой из таких систем, и поэтому их может быть легче решить аналитически (или численно) в данной системе. Три наиболее важные системы: декартова , цилиндрическая и сферическая . Если они трехмерные, то каждому из них требуется три уникальных значения для идентификации уникального вектора или расстояния от некоторой контрольной точки, например. Пример представления одного и того же вектора в трех разных системах координат: декартовой ( x , y , z ), цилиндрической ( r , φ , z ) и сферические ( r , φ , θ ) В декартовой системе есть три ортогональных направления, например ( x , y , z ), и поэтому каждый вектор может быть объединен из трех компонентов, каждый из которых выражает линейное расстояние от контрольной точки (0 , 0, 0). Расстояния также могут быть представлены в относительном смысле, определяющем длину и угол вектора, но не его местоположение как таковое. В цилиндрической системе также есть три компонента. Но расположение данной точки внутри цилиндра может быть выражено радиусом r , углом φ и высотой z цилиндра, поэтому такой набор значений однозначно идентифицирует данную точку или вектор. В сферической системе компоненты обозначают радиус r и два угла φ и θ . Такая система полезна для выполнения расчетов в сферической или эллиптической геометрии. Конкретные компоненты различаются между системами, но они могут быть преобразованы между ними посредством строгих математических соотношений. Конечно, имена переменных компонентов (для длин и углов) могут быть выбраны произвольно, в зависимости от предпочтений в данном подходе. См. также
Каталожные номера1) , 1) , 1) , 1) , 1) , 1) , 1) , 1) , 1) , 1) , 1) , 1) , 1) , 1) , 1) , 1) , 1) , 1) , 1) Дэниел Флейш, Руководство для студентов по векторам и тензорам, Cambridge University Press, Кембридж, 2012, ISBN 9780521171908 2) , 2) , 2) E. 3) , 3) Дэниел Флейш, Руководство для студентов по уравнениям Максвелла, издательство Кембриджского университета, Кембридж, 2008, ISBN 9780521877619 4) Physics, PDEs, Mathematical and Numerical Modeling, COMSOL, март 2019 г. , Метод конечных элементов Magnetics: документация, {дата обращения: 25.06.2021} 6) , 6) , 6) Ричард Фейнман, Роберт Лейтон, Мэтью Сэндс, Ферромагнетизм, Фейнмановские лекции по физике, Vol. II, Основные книги, ISBN: 9780465079988 8) Дэвид С. Джилс, Введение в магнетизм и магнитные материалы, второе издание, Chapman & Hall, CRC, 1998, ISBN 9780412798603 7798603 9987777777777777777 .7777777777777 904.77777777 777777777777 . 10) Роберт С. Вреде, Введение в векторный и тензорный анализ, Courier Corporation, 2013 г., ISBN 048661879X Scalar Вектор, Тензор, скалярное поле, Векторное поле, тензорное поле, тензор ранга 2, Тензорный ранг 1, Тензорный ранг 0, Счетчик Скалары и векторы — Pickman PhysicsСкалярные и векторные цели обучения
Физика — это математическая наука, используемая для объяснения и предсказания природных явлений в окружающем вас мире. Мы используем уравнения, чтобы ответить на вопросы, используя измеряемые переменные в эксперименте или заданные переменные в вопросе. Важно знать переменные, которые использует ваш класс, и единицы измерения, которые помогут вам определить используемые уравнения. В то время как физика остается прежней, в другом учебнике могут использоваться две разные буквы для обозначения переменных одного и того же уравнения. Например, смещение может быть представлено переменной d в одной книге или X в другой. Мы будем использовать X для смещения на наших страницах. Первое уравнение, которое мы будем использовать: скорость равна смещению, деленному на время. Это представлено уравнением v=X/t. Это было бы то же самое, что v = d/t, если бы ваш учитель использовал d для представления смещения. Базовая скорость и переменные скорости
Скаляр в физике включает только величину. Вектор в физике включает в себя величину и направление. Два общих вектора: смещение , например, 5 метров на восток, и , скорость , например 5 метров в секунду на восток. Скаляр против вектора Перемещение Чем расстояние отличается от смещения?Расстояние (скаляр) — это мера между двумя точками. Поскольку у расстояния нет направления, вы суммируете все пройденные сегменты. Смещение (вектор) — это мера того, где вы находитесь от исходной точки или начальной точки и в каком направлении. Расстояние составляет Смещение при повороте Скалярное расстояние и векторное смещение Как рассчитать расстояние и смещение? Посмотрите на разницу между в том, как рассчитываются расстояние и перемещение . Для вектора смещения вы превратить направление в математический знак и добавить векторы. Обратите внимание на изображение справа, на котором показаны общие знаки, заменяющие направления. Поэтому мы называем правую положительную, а левую отрицательную. Следовательно, 6 метров справа становятся +6 метрами, а 4 метра слева становятся -4 метрами. Теперь добавьте векторы, но включите знаки (+6) + (-4) = +2. Водоизмещение = (+6) + (-4) = +2. Как только вы получите окончательный ответ, поверните знак обратно в направлении, а затем включите устройство. Общие знаки, которые заменяют направление в вычислениях Вычисление скалярной скорости и векторной скоростиСкаляры используются со скалярами, поэтому используйте расстояние для расчета скорости , как показано в уравнении справа. Векторы идут вместе с векторами, поэтому используйте смещение для расчета скорости , как показано в уравнении справа. Формулы скорости и скорости Уравнение на анимации справа (v = Δx/t, а также представленное в двух формах на изображении выше) будет использоваться в примерах для расчета скорости или скорости, но я буду использовать расстояние при расчете скорость и смещение при расчете скорости.
Обратите внимание: на картинке справа стикмен останавливается и движется с разной скоростью. Чем мгновенная скорость отличается от средней скорости?
Скорость равна как далеко вы проедете от начальной точки за период времени включая направление . Если ваша скорость никогда не меняется, вы движетесь с постоянной скоростью . Ускорение описывает, как скорость изменяется от начальной скорости в течение периода времени . Вы можете ускориться, двигаясь быстрее, двигаясь медленнее (это также называется замедлением) и меняя направление. С ускорение описывает изменение скорости во времени, единица измерения ускорения включает единицу измерения скорости ( м/с ) за другой период времени ( с ) . Следовательно, единицей измерения ускорения является м/с/с или чаще м/с 2 . Ускорение также является вектором и включает направление изменения скорости.
Когда мы заканчиваем этот раздел, важно, чтобы вы запомнили свои единицы измерения. (Полезны карточки для заметок)
В следующем разделе этого модуля вы узнаете о различных способах расчета ускорения. Посмотрите на анимацию ниже, чтобы увидеть, как измеряются смещение и расстояние. Затем наблюдайте, как 9Векторная скорость 0079 использует смещение в расчете , а скалярная скорость использует расстояние . Если бы объект никогда не менял направления, величина скорости и скорости была бы одинаковой. Что происходит со смещением после того, как крупье меняет направление и продолжает движение? После смены направления смещение уменьшается по мере приближения к начальной точке Что происходит с пройденным расстоянием после того, как крупье меняет направление и продолжает движение? После изменения направления пройденное расстояние продолжает складываться Решение для других, отличных от v, уравнений постоянной скоростиСколько времени требуется, чтобы пройти 500 метров со скоростью 20 м/с? x = 500 м v = 20 м/с t = ? v = x/t преобразуется в t = x/v t = x/v t = 500/20 t = 25 с Пример 1 скалярного вектора 30 90 90 право на следующие вопросы. Томас во время обеденного перерыва потратил 30 минут, чтобы сходить в библиотеку, а затем в кафе. 1. Какое расстояние проехал Томас за обедом? Расстояние это сумма всех измерений, пройденных здесь. 100 в кафе, потом еще 45 в библиотеку, потом 45 обратно в кафе. Так что сложите все это. 100 + 45 + 45 = 190 метров 2. Каково было его водоизмещение ? Смещение – это расстояние, на котором находится Томас от исходной точки (начала), указанное в направлении от исходной до конечной точки. (100 м вправо) + (45 м вправо) + (45 м влево) Поскольку мы не можем вычислить направления в калькуляторе, право становится (+), а лево становится (-) (+100) + (+45) + (-45) = +100 Наконец, мы добавляем единицу и превращаем знак обратно (здесь +) в направление. +100 = 100 м вправо 3. расстояние = 190 м время = 1800 с скорость = ? Используйте расстояние для определения скорости в уравнении скорость = расстояние/время скорость = 190/1800 скорость = 0,1056 м/с ? перемещение = 100 м вправо время = 1800 с скорость = ? Использование смещения для определения скорости в уравнении скорость = перемещение/время скорость = 100/1800 скорость = 0,0556 м/с вправо там же.) См. страницу решения Викторина по скалярным векторам Знаете ли вы разницу между скалярами и векторами? Пройдите этот тест, чтобы узнать. 1 / 11 Что это за направление 15 метров на север ? 15 15 метров 15 метров на север метров север 2 / 11 Что это за единица измерения 15 метров на север ? 15 15 метров 15 метров на север метров север 3 / 11 Какова величина 15 метров на север ? 15 15 метров 15 метров на север метров север 4 / 11 Каково ваше перемещение после прохождения 1 0 метров на восток а затем 20 метров на запад за 80 секунд ? 0 метров 10 метров East 10 метров West 30 метров восток 30 метров West 30 метров 5 /11 .  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
д.
В большинстве расчетов в литературе, если не указано иное, то неявно предполагается правосторонняя система.
0 
Единичный вектор параллелен некоторому главному вектору, но имеет длину, равную единице, если выражается в тех же единицах, что и главный вектор.
Особенно важно проводить различие между скалярами и векторами, потому что некоторые операции не могут выполняться одинаковым образом со скалярами и векторами, или порядок компонентов может иметь значение в векторных операциях. 
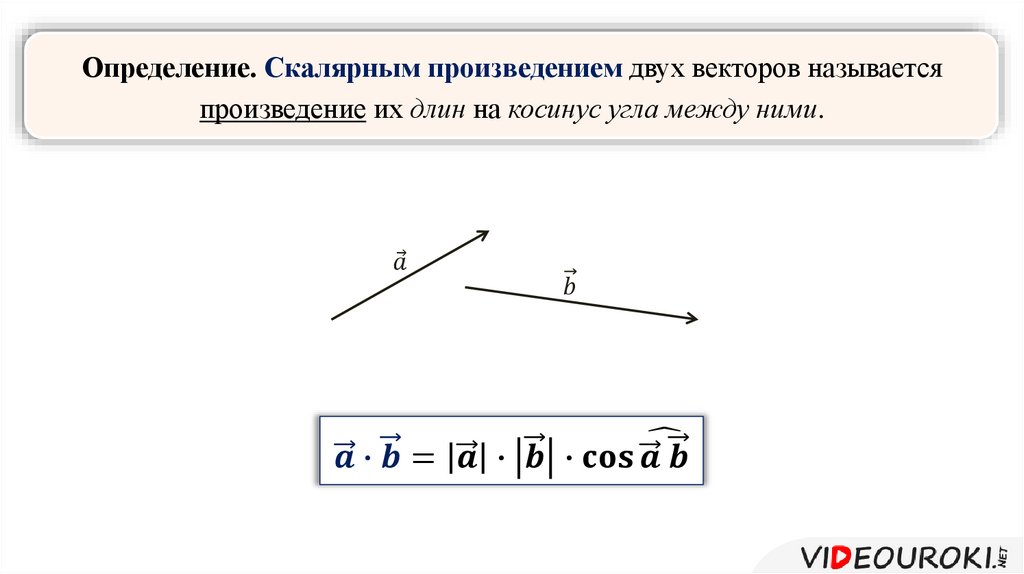Во избежание путаницы в большинстве публикаций точка скалярного умножения не используется (просто опущен). Однако это упущение не является строго необходимым, поскольку операция диктуется типом входных значений.
Порядок входных векторов имеет значение, так что: $\mathbf{A} × \mathbf{B} = — \mathbf{B} × \mathbf{A} = \mathbf{C}$. Также важна хиральность системы координат, поскольку результат может менять знак, если вычисления производить в правой или левой системе. 
Вместо этого в некоторых случаях, например, в 2D-анализе, гораздо выгоднее изменить представление на комплексные числа, которые позволяют выполнять деление и, следовательно, получать правильный результат с более простыми вычислениями.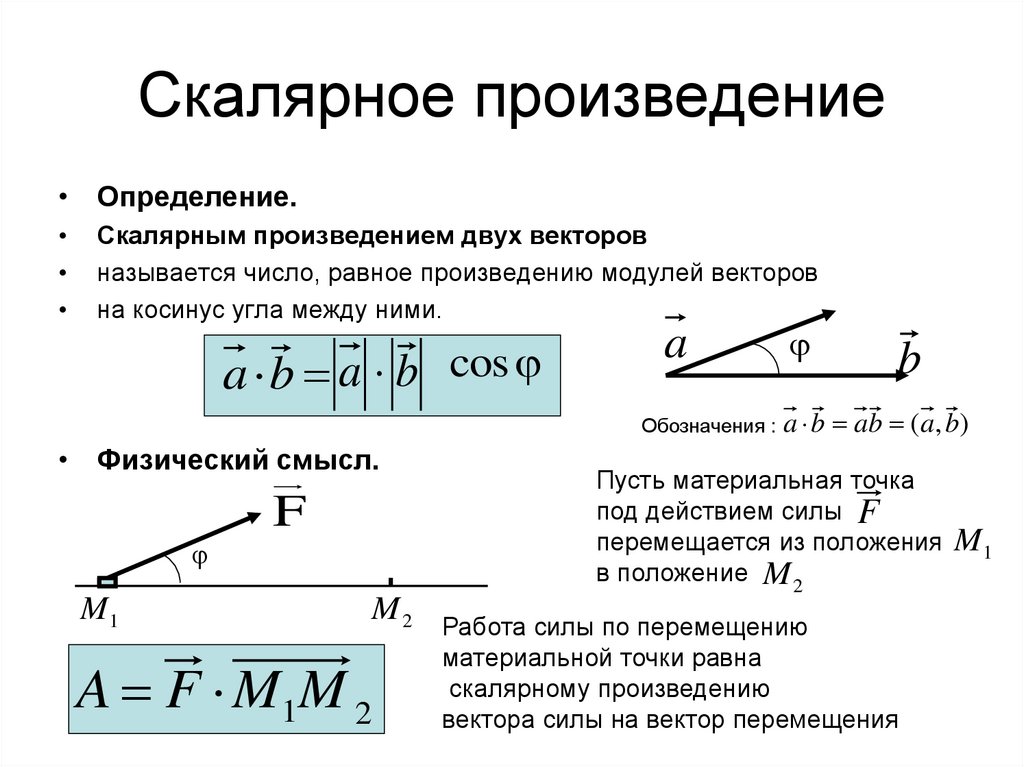 
Точно так же оператор производной $\frac{dF}{dx} = \frac{d}{dx}(F)$ информирует о том, что производная должна быть произведена над величиной F , приведенной ниже.
В декартовой системе: 
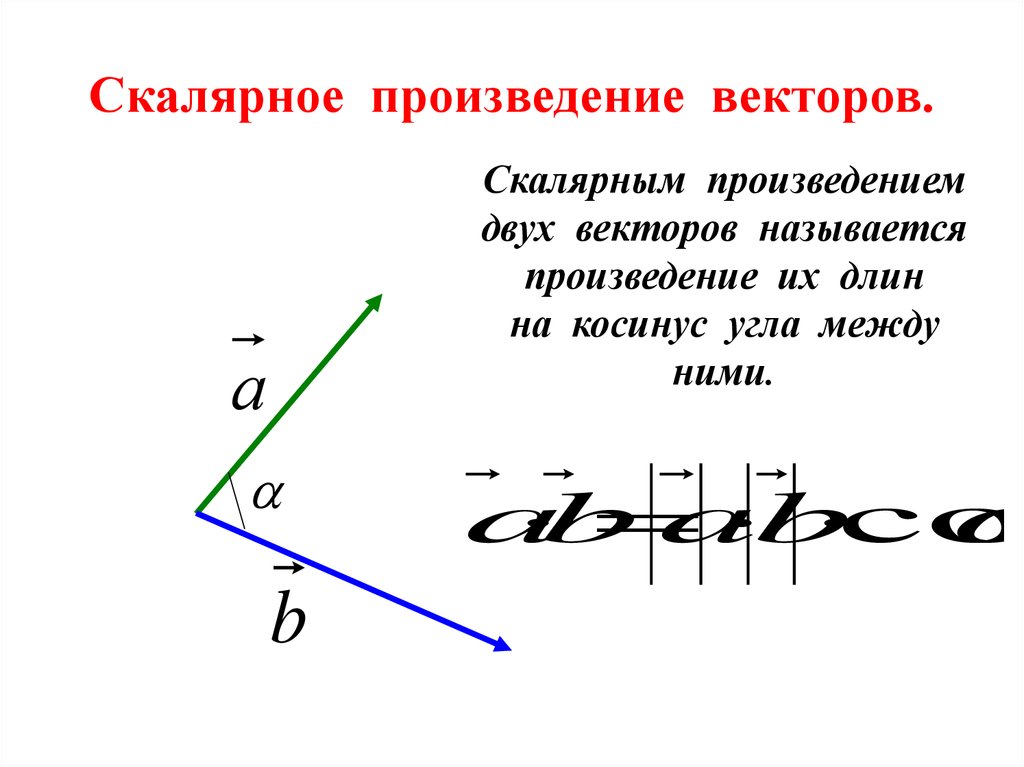(0, 0, 0).
Такая система полезна для выполнения расчетов с геометрией, которая имеет одну ось вращательной симметрии.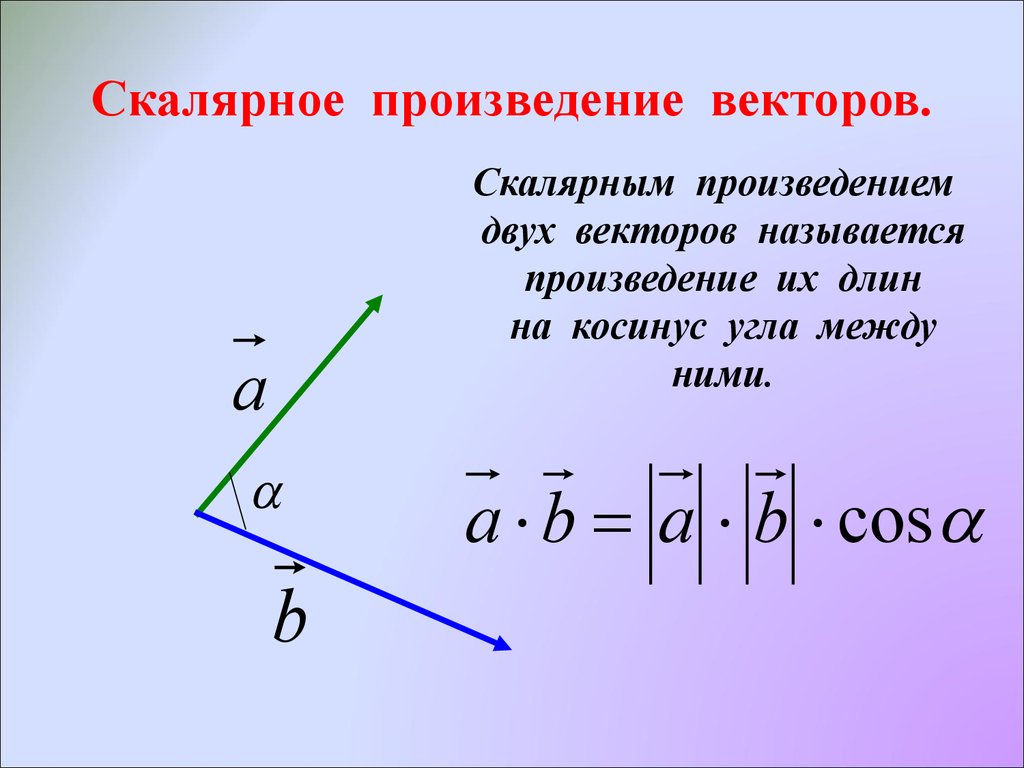
M. Purcell, D.J. Морин, Электричество и магнетизм, 3-е издание, Cambridge University Press, 2013, ISBN 9781107014022
, 4-е изд., Пирсон, Бостон, 2013 г., ISBN 0321856562
Мы начнем наши уроки с кинематики, изучения движения.
Величина — это число и единица измерения. Два общих скаляра: расстояние , например 5 метров, и скорость , например 5 метров в секунду. Скорость является скалярной, потому что она использует скалярное расстояние, пройденное за время.
Стикмен на картинке идет прямо от начала координат (0 метров) до 6 метров. Затем он поворачивает налево и проходит 4 метра назад. Поскольку направление не имеет значения, для расстояния вы добавляете каждый метр, пройденный в любом направлении вверх. Итак 6 метров + 4 метра.
Таким образом, +2 становится 2 метрами правильно.
Вы должны знать свою начальную скорость, чтобы определить конечную скорость. Ускорение 2 со скоростью 5 м/с означает, что вы каждую секунду изменяете свою скорость на пять метров в секунду.
Прежде чем мы начнем, давайте посмотрим, как выполнять вычисления с использованием скаляров и векторов.
Определить скорость Томаса во время 30-минутного (1800-секундного) обеда?