Скалярные и векторные величины
Даны определения и приведены примеры скалярных и векторных величин. Описаны математические операции над векторными величинами.
Физические величины бывают скалярными и векторными
Скалярные величины
Скалярная величина (от лат. scalaris – ступенчатый) в механике – величина, каждое значение которой может быть выражено одним числом.
Примеры скалярных величин: масса тела, время, температура, длина, путь, площадь.
Более подробно функционирование опорно-двигательного аппарата человека и биомеханика мышц описаны в книге:
Биомеханика опорно-двигательного аппарата человека
Векторные величины
Если величина, кроме числового значения характеризуется еще и направлением, то она называется векторной величиной или просто вектором. То есть вектор определяется численным значением и направлением.
Примеры векторных величин: перемещение, скорость, ускорение, сила, момент силы, импульс тела.
Обозначение векторных величин
На рисунках и схемах вектор отображается отрезком прямой со стрелкой на одном конце.
Длина отрезка в выбранном масштабе выражает числовое значение векторной величины (его модуль), а стрелка указывает ее направление.
На рисунках, схемах и в тексте векторные величины обозначают несколькими способами:
1 способ. Векторная величина обозначается строчной или заглавной буквой со стрелкой или чертой над ней (рис. 1).
Рис.1. Вектор и его обозначение2 способ. Векторная величина обозначается заглавными буквами, обозначающими начало и конец вектора с чертой или стрелками над ними (рис. 1).
3 способ. Иногда векторные величины в формулах обозначаются жирным шрифтом, а скалярные — обычным. Например: F=ma
Операции над векторными величинами (векторами)
Над векторными величинами возможны следующие математические операции:
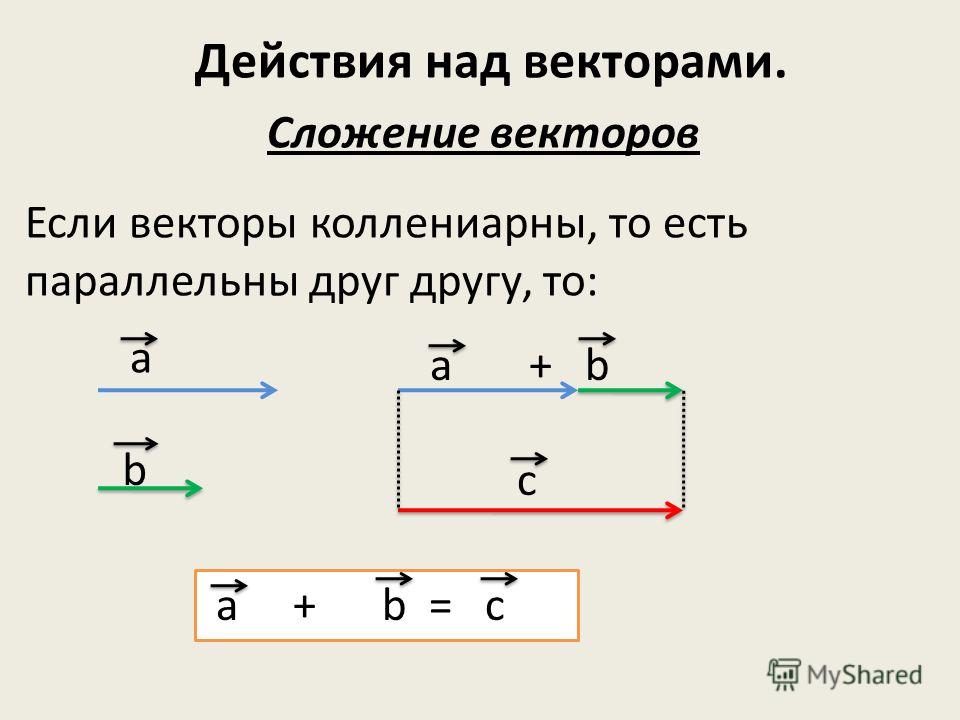
- Сложение и вычитание векторов.
- Умножение вектора на скаляр.
- Произведение векторов (скалярное и векторное).
Литература
- Петров В.А., Гагин Ю.А. Механика спортивных движений.
– М: Физкультура и спорт, 1974. – 232 с.
– М: Физкультура и спорт, 1974. – 232 с.С уважением, А.В. Самсонова
Похожие записи:
Сила
Дано определение силы в механике. Описаны факторы, определяющие действие на тело силы: направление, точка приложения и численное значение.
Звенья тела человека как рычаги
Дано описание опорно-двигательного аппарата (ОДА) человека как системы рычагов. Приведен пример расчета силы двуглавой мышцы плеча…
Способ определения положения центров масс (центров тяжести) звеньев тела человека
Описан способ определения положения центров масс (центров тяжести, ЦТ) звеньев тела человека по Вильгельму Брауне и…
Распределение масс в теле человека
Описаны особенности распределения масс в теле человека. Дано понятие геометрии масс тела человека. Показано, что на…
Центр масс и центр тяжести тела
Описаны: центр масс (ЦМ) и центр тяжести (ЦТ) твердого тела. Приведены различные определения ЦМ и ЦТ тела.
Показано…
Момент силы и плечо силы
Дано определение момента силы и плеча силы. Определение плеча и момента силы рассмотрено на примерах ОДА человека при…
28. Элементы векторной алгебры. Скалярные и векторные величины
Если физическая или геометрическая величина характеризуется только одним неотрицательным числом, то она называется скалярной. Например, длина отрезка, площадь фигуры, объем тела, масса тела и т. д. скалярные величины.
Если физическая или геометрическая величина характеризуется не только и численным значением и направлением, то она называется Векторной. Например, скорость, ускорение, сила и т. д. векторные величины.
2. Сонаправленность лучей. Любая точка A принадлежащая прямой A Делит ее на две части. Лучом называется часть прямой A, расположенная по одну сторону от точки A. Точка A называется Началом луча. Если точка B Принадлежит лучу, то он обозначается двумя точками AB.
Определение 1. Два луча AB и CD называются Сонаправленными, если либо один из лучей содержится в другом луче, либо они лежат на параллельных прямых по одну сторону от прямой
На рис 1. лучи AB, CD, EF сонаправленные, а лучи AB, KL — противоположно направленные.
Теорема 1. Отношение сонаправленности лучей есть отношение эквивалентности, т. е. для любых лучей AB, CD, EF выполняются свойства:
1) — рефлексивность,
2) Þ
3) & CD EF Þ AB EF — транзитивнсть.
Доказательство. Первое и второе свойства, непосредственно следуют из определения сонаправленных лучей. Докажем третье свойство.
Пусть AB CD & CD EF. Рассмотрим только один случай, когда лучи AB, CD, EF не лежат в одной плоскости (остальные случаи предоставляем рассмотреть самостоятельно).
Из условия следует, что лучи AB, CD
Таким образом лучи 2. Лучи AB, CD, EF лежат в одной плоскости b, на разных параллельных прямых. Рассмотрим тогда четвертый луч KL, сонаправленный с лучом CD и не лежащий в плоскости b. Так как AB CD & CD KL, то по случаю 1 AB KL. По свойству 2, KL CD.Так как KL CD & CD EF, то по случаю 1 KL EF. Так как
Так как отношение сонаправленности лучей является отношением эквивалентности, то множество всех лучей разбивается на классы эквивалентности, каждый из которые состоят из всех лучей сонаправленных друг другу, и называется Направлением.
3. Направленные отрезки. Пусть A и B Различные точки принадлежащие прямой A. Отрезком AB называется часть прямой A, расположенная между точками A и B. Точка A и B Называется Концами отрезка
Определение 3. Направленным отрезком Называется отрезок AB, обозначаемый символом , у которого один конец A считается первым, а конец В вторым. Первый конец называется началом, А второй — концом направленного отрезка.
На чертеже направленный отрезок изображается стрелкой, идущей из точки A в точку B.
Если конец и начало направленного отрезка совпадают, то он называется Нулевым направленным отрезком и изображается на чертеже точкой.
Определение 3. Два направленных отрезка и называются Сонаправленными (Противоположно направленными), если лучи AB и CD сонаправлены (противоположно направлены), обозначаем символом ( ¯).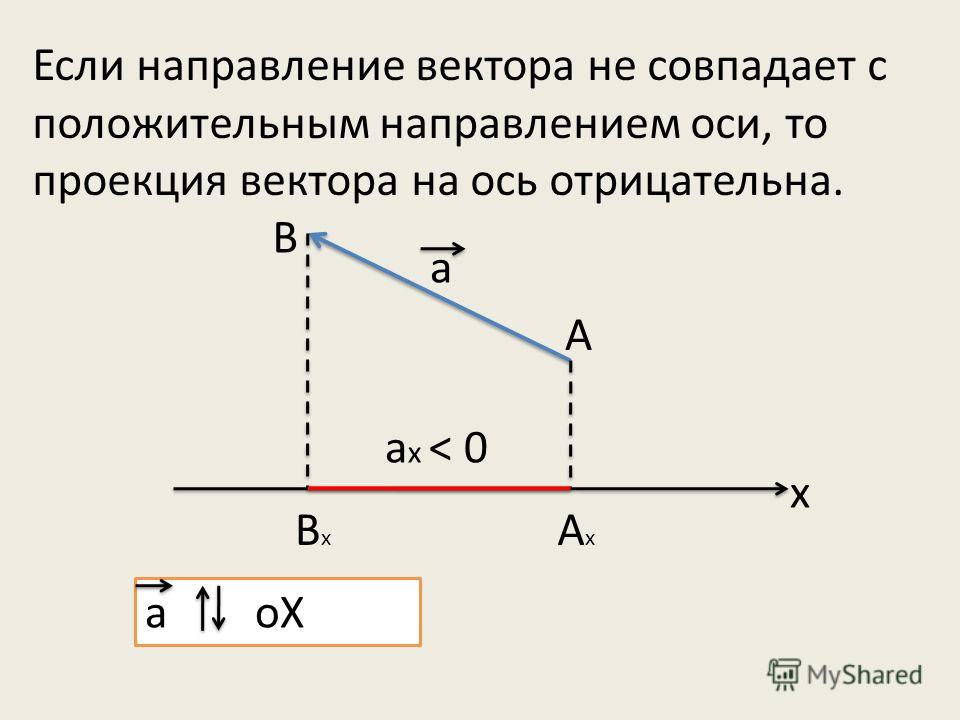
Определение 4. Длиной или Модулем направленного отрезка называется отрезка AB, обозначается символом
Определение 5. Два направленных отрезка и называются равными, если они сонаправлены, , и их длины равны, =, обозначается символом =
Теорема 2. Отношение равенства направленных отрезков есть отношение эквивалентности, т. е. для любых направленных отрезков , , Выполняются свойства:
1) = — рефлексивность,
2) = Þ = — симметричность,
3) = &
Доказательство. Докажем свойство 3, первое и второе свойства доказываются аналогично. По условию = & = . Тогда по определениям 3-5 имеем AB CD, CD EF И =, =. По теореме 1 и по свойству длины отрезка имеем AB EF и =. Отсюда, по определению, .
Имеют место следующие утверждения равносильные определению равенства направленных отрезков.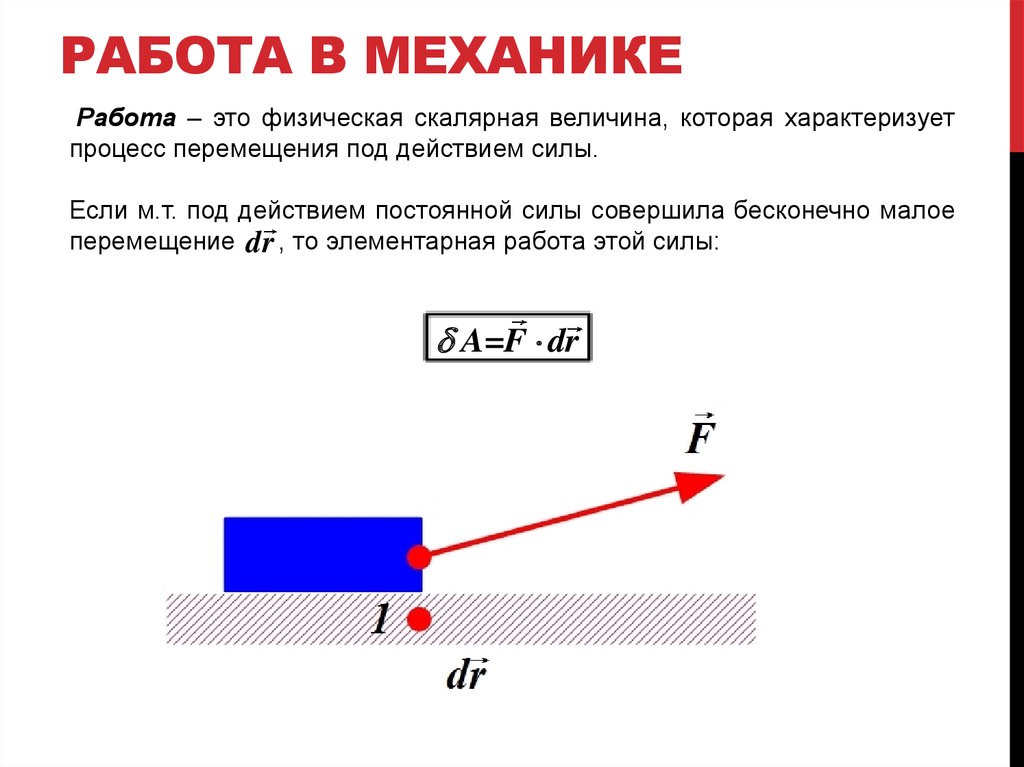
Теорема 3. Два направленных отрезка И
Доказательство. Если отрезки , лежат на одной прямой, то утверждение следует из рис. 3. Поэтому рассмотрим случай, когда отрезки AB и CD лежат на разных прямых.
Пусть = . Так как лучи AB и CD сонаправлены, то точки D, B лежат по одну сторону от прямой AC. Так как AB||CD, |AB|= |CD|, то четырехугольник ADBC — параллелограмм. По свойству диагоналей параллелограмма середины его диагоналей AD И CB Совпадают.
Если середины отрезков
Следствие 1. Два направленных отрезка И Не лежащие на одной прямой равны тогда и только тогда, когда четырехугольник ADBC — параллелограмм.
Следствие 2. Два направленных отрезка И Не лежащие на одной прямой равны тогда и только тогда, когда равны направленные отрезки И .
Доказательство. Утверждения
| < Предыдущая | Следующая > |
|---|
Видео урок: Скалярные и векторные величины
Стенограмма видео
В этом видео наша тема скалярная
и векторные величины. Мы научимся определять
эти два термина, а также различные способы объединения скалярных и векторных
количества.
Мы видим, что этот эскиз здесь
намекая на разницу между ними. Но чтобы прояснить ситуацию, когда мы получаем
начнем, давайте определим эти два термина.
Скалярная величина или скаляр для Короче говоря, это количество или количество чего-то, что полностью описывается величину или размер. В качестве простого примера этого, если мы было, скажем, пять яблок, то скалярная величина, описывающая количество яблок, равна просто пять яблок. В общем случае скалярная величина может просто быть чистым числом само по себе. В данном случае это было бы пять. Или это может быть число вместе с Ед. изм. И в этом примере мы можем думать слова «яблоки» как единицы, типа вещей, которые мы измеряем.
Но давайте подумаем о другом
примеры скалярных величин. Допустим, нам нужно было отправиться в
продовольственный магазин, а магазин находился в 1,3 км.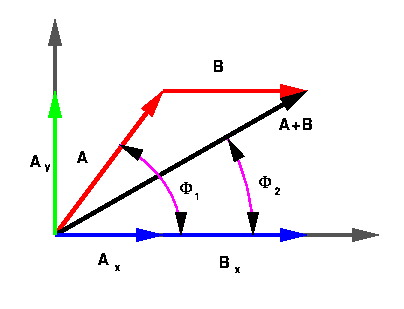
Это скалярная величина. И вообще, это относится к любому
расстояние. Или как насчет того, если бы мы планировали
встретиться с другом через 30 минут? Это время, и все ценности времени
являются скалярами. То же самое и с температурами
а также скорости. На этом этапе мы можем начать
интересно, какие величины не являются скалярами. То есть то, что осталось для вектора
количества для описания? Но сначала определение.
Можно сказать, что векторные величины,
или векторы для краткости, это величины, которые полностью описываются величиной
и направление. Вспоминая наш пример
открывая экран этих двух хищных птиц, если бы они знали, что кролик был не просто
в пяти километрах отсюда, но в пяти километрах к востоку, тогда они узнают
смещение кролика от себя. Мы видим, что это смещение имеет
величина, это пять километров, а также направление, это восток, и
поэтому является вектором.
Все смещения разделяют это
качество.
Другой тип векторной величины
все силы. Полное описание силы
включает его величину, в данном случае семь ньютонов, а также направление
действует сила. Итак, сила — это вектор, как и
ускорение. Всякий раз, когда мы полностью определяем
ускорение, мы описываем его величину, часто в метрах в секунду в квадрате. И мы также рассказываем, как это
указывая. И, как последний пример, все
скорости также являются векторами. И обратите внимание, что в этом случае мы
выбрал величину скорости, которая соответствует нашей скорости. Таким образом, скорость, которая является вектором, равна
скорость, скалярная величина, в каком-то направлении. Кстати, вектор смещения
и скалярное расстояние работают так же. Векторное смещение состоит из
расстояние, скаляр, в каком-то направлении, в данном случае на восток.
Теперь, когда мы поняли, что скалярные и векторные величины, давайте рассмотрим различные способы, которыми мы могли бы объединить их. Для начала представим, что мы хотели бы объединить некоторую скалярную величину с другой величиной, которая также является скаляр. Предположим, что эти две величины с одной стороны пять метров, расстояние, а с другой 13 кельвинов, температура. Мы сразу видим, что даже хотя обе эти величины являются скалярами, нет смысла их складывать или вычитать одно от другого. Мы могли бы сделать это, только если бы наши двое скалярные величины имели тот же тип единицы измерения. Например, скажем, мы хотели объедините пять метров с 27 метрами. Это и скаляры, и, в в этом случае не возникнет проблем со сложением их вместе или вычитанием единицы из другой.
Мы можем сказать, что в целом, если бы мы
например, объединить две скалярные величины, пока единицы измерения совпадают, мы можем сложить или
вычесть их.
И если мы затем рассмотрим объединение
две векторные величины, мы получим аналогичный результат. Скажем, например, что мы хотели бы
объединить эти два вектора: сила в восемь ньютонов на запад со скоростью
три метра в секунду вправо. Так же, как с нашими двумя скалярами
величин такого же типа, мы не можем сложить эти векторы вместе или
вычесть одно из другого, потому что они тоже разных типов. Самый быстрый способ увидеть это —
обратите внимание, что они имеют разные единицы измерения, ньютоны и метры в секунду.
Итак, несмотря на то, что оба эти
количества являются векторами, мы не можем складывать и вычитать их из-за единиц
несоответствие. Но если бы у них был такой же сорт
единиц, скажем, эта сила здесь и эта, которую мы только что определили, затем объедините их
через сложение или вычитание будет иметь смысл. Итак, если мы хотим объединить
скаляр со скаляром или вектор с вектором, мы можем сложить или вычесть эти пары
величин, если их единицы совпадают.
А теперь рассмотрим третий
возможность объединения скаляров и векторов.
Что, если бы мы захотели объединить
скалярная величина с векторной величиной? Например, скажем, мы хотели
объединить время, скажем, 16 секунд, с вектором ускорения, скажем, в два метра
за секунду в квадрате влево. На этих примерах понятно
нам сразу же, что мы не можем просто сложить или вычесть эти скалярные и векторные
количества. Но чтобы немного изучить эту идею,
допустим, скалярная величина и векторная величина, которые мы выбрали, на самом деле имели
однотипные единицы. Например, что, если мы хотим
объедините скорость, которая является скаляром с единицами измерения в метрах в секунду, со скоростью,
который является вектором, но имеет те же единицы измерения? Оказывается, даже в этом случае
согласования единиц, мы не можем складывать или вычитать скаляр и вектор.
Представьте, например, что вы пытаетесь добавить от трех метров в секунду до четырех метров в секунду на север. Поскольку наша векторная величина имеет направлении, мы действительно не знали бы, как совместить этот аспект направления с ненаправленный скаляр. просто у нас нет такой информации о скорости, и поэтому мы не можем добавить его к скорости. Как ни странно, это не означают, что нет никакого способа объединить скалярную величину с векторной величиной. Это потому, что математическое операции умножения и деления все еще открыты для нас.
И как ни странно,
эти операции между скаляром и вектором, вообще говоря, разрешены. Например, скажем, что мы делим
наше ускорение, вектор, на это количество времени, скаляр. Результатом этого будет
дробь, две шестнадцатых или, что то же самое, одна восьмая метра на секунду в квадрате
в секунду, действуя влево.
Теперь метр в секунду в квадрате на
секунда также может быть записана как метр в секунду в кубе. И так, что мы имеем здесь
по сути, скорость изменения ускорения во времени, то есть насколько
ускорение в метрах в секунду в квадрате меняется каждую секунду.
Это определенно странно.
единицей, а не той, с которой мы обычно сталкиваемся, но это не значит, что она запрещена или
невозможно. Мы могли бы представить сценарий, в котором
ускорение изменяется в течение некоторого промежутка времени. И поэтому, хотя, может быть, и очень
редко, такой способ объединения этих двух величин допускается. Дальнейшие примеры могут показать нам, что
как разрешено деление, так и умножение между скаляром и вектором
количество. Итак, мы подведем итог этому
путь. Когда мы хотим объединить скаляр
с вектором мы не можем складывать или вычитать их, но мы можем умножать или делить.
И последнее, что мы можем сделать. о комбинировании скаляров и векторов заключается в том, что когда мы рассматриваем возможность получения вектора и вектор вместе, объединяя их либо сложением, либо вычитанием, затем если это разрешено — то есть если единицы совпадают — то мы можем сделать это графически так и арифметически. Чтобы увидеть, как это работает, давайте очистим немного места на экране, а затем нарисуйте пару осей координат. Теперь, что мы хотим сделать здесь, это графически соедините два вектора, которые будем называть векторами сил. У нас уже есть одна сила восемь ньютонов на запад, и поэтому давайте определим другое. Скажите, что это два ньютона на юг.
Эти единицы измерения ньютонов и
направления, прикрепленные к ним, запад и юг, показывают нам, как мы можем обозначить оси на
наш график. Допустим, это направление
север, это направление на восток и что наши оси отмечены в единицах
таких ньютонов.
Теперь, когда мы начнем строить наш вектор
восьми ньютонов на запад на этом графике, мы сразу видим, что нам нужно будет
расширить нашу ось на запад. Но как только мы это сделали, мы можем
затем начертите нашу силу в восемь ньютонов, направленную на запад. Он начинается в начале, а затем
идет восемь единиц, восемь ньютонов, в западном направлении. Далее мы можем сделать набросок в нашем
сила в два ньютона на юг. Это будет выглядеть так на нашем
график.
Итак, мы сказали ранее, что если мы
есть два вектора и их единицы совпадают, то мы можем сложить или вычесть их. Поскольку эти векторы оба
силы, они отвечают этому условию иметь одинаковые подразделения. Таким образом, мы должны быть в состоянии, для
например, сложите их вместе. И когда векторы построены
вместе на одном и том же графике, как эти, мы используем то, что называется от кончика к хвосту
способ сделать это.
Этот метод работает так. Начиная с любого из наших двух
векторов, мы находим вершину этого вектора. Допустим, мы начинаем с нашего
восьминьютонный вектор на запад, что означает, что вершина находится прямо здесь. Итак, это наш совет в
метод «кончик к хвосту».
Затем мы находим хвост
другого вектора. Это тот самый момент. И мы переводим или сдвигаем
второго вектора так, чтобы его хвост лежал поверх кончика первого. Таким образом, это потребует перемещения нашего
Золотой вектор, тот, который указывает на два ньютона на юг, вот так. Теперь, когда наши векторы расположены
кончик к хвосту, мы начинаем с самого начала, хвост самого первого, это в
Происхождение. И мы рисуем вектор из этого
указать на кончик нашего второго вектора. Таким образом, мы можем сказать, что если наш первый
вектор был вектором 𝐀, а второй был вектором 𝐁, тогда этот зеленый вектор мы
только что нарисованное равно 𝐀 плюс 𝐁.
Итак, когда мы объединяем
векторов можно не только алгебраически, но и графически.
Зная все это о скалярных и векторные величины, давайте немного попрактикуемся в этих идеях с помощью пример.
Что из следующего является вектором количество? (А) Энергия, (Б) давление, (С) разность потенциалов, (D) сила, (E) заряд.
Итак, идея вот в чем
из этих пяти величин является вектором. И мы можем вспомнить, что вектор
количество определяется как имеющее как величину, так и направление. И конкретно это факт
что вектор имеет связанное с ним направление, которое отличает его от того, что
называется скалярной величиной, которая является величиной, которая имеет только величину. Итак, когда мы рассматриваем наши различные
вариантов ответа, давайте рассмотрим примеры каждой из этих величин и посмотрим,
мы находим любые направления вместе с величинами.
Начиная с выбора (А), энергии, например, количество энергии может быть таким: 12 джоулей. Что касается давления, то стандартной единицей измерения давления в дюйме является паскаль. Стандартная единица для сообщения разность потенциалов равна вольту. У нас может быть, скажем, 32 вольта. В то время как единица силы на основе СИ ньютон, мы могли бы иметь силу, скажем, на 13 ньютонов вправо. И суммы заряда, как правило, выражается в единицах кулонов. У нас может быть 0,3 кулона обвинять.
Во всех этих примерных количествах
мы видим, что есть величины: 12 джоулей, 3,1 паскаля, 32 вольта и так далее. Но по нашему определению того, что
количество векторов, одной только величины недостаточно для создания вектора. Нам также нужно направление, связанное
с такой величиной. Требуя, чтобы это было правдой, мы видим
что только один из наших пяти вариантов имеет направление.
Это сила, которая является силой
на 13 ньютонов вправо. Здесь у нас есть величина, 13
Ньютоны и направление. И никакие другие величины
иметь направление. Итак, мы выберем вариант ответа (D),
сила, как единственная векторная величина, указанная здесь.
Давайте теперь посмотрим на второй пример упражнение.
Если площадь умножить на длина, является ли результирующая величина векторной величиной или скалярной величиной?
Итак, мы говорим о
умножение площади на длину. И мы могли бы представить, скажем, что
это наш район и вот это наша длина. Когда мы умножаем эту площадь на это
длина, мы собираемся получить какой-то результат, и мы хотим знать, является ли это вектором
количество или скалярное количество. Вот разница между
два. Скалярная величина или скаляр для
Короче говоря, имеет только величину, в то время как векторная величина, или вектор, имеет и то, и другое.
величину и направление. Итак, чтобы выяснить, является ли наша область
умноженное на длину является скаляром или вектором, нам нужно посмотреть, имеет ли оно
только величина или величина вместе с направлением.
Продукт нашего района и нашего
длина это объем 𝑉. И вот теперь мы спрашиваем себя, действительно ли
этот объем имеет только величину или имеет величину вместе с
направление? Таким образом, мы можем видеть, что это
объем действительно имеет величину, то есть размер, равный любому 𝐴, умноженному на 𝐿
является. Но нет определенного направления
в котором этот объем или любой объем точек. Итак, здесь у нас есть величина,
но у нас нет направления. Основываясь на наших определениях скаляра
и векторные величины, что и отвечает на наш вопрос. Если площадь умножить на
длина, результирующая величина является скалярной величиной.
Подведем итог тому, что у нас есть узнал о скалярных и векторных величинах. В этом уроке мы определили скаляр и векторные величины. И мы увидели, что жизненно важное разница между ними в том, что скалярная величина имеет только величину, а векторная величина имеет как величину, так и направление. Далее мы видели, что скаляр и скаляр или вектор и вектор можно складывать или вычитать, если их единицы измерения совпадают. В связи с этим мы увидели, что скалярная величина может умножать или делить вектор. И, наконец, мы увидели, что два или более векторы можно комбинировать графически, используя так называемый метод «кончик к хвосту». Это краткое изложение скалярных и векторные величины.
7.3: Векторы, скаляры и системы координат
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 200151
- OpenStax
- OpenStax
Направление вектора в одномерном движении задается просто знаком плюс (+) или минус (-).
Векторы представлены графически стрелками. Стрелка, используемая для представления вектора, имеет длину, пропорциональную величине вектора (например, чем больше величина, тем больше длина вектора) и указывает в том же направлении, что и вектор.
Некоторые физические величины, такие как расстояние, либо не имеют направления, либо не указаны. Скаляр – это любая величина, имеющая величину, но не имеющую направления. Например, температура 20ºC, 250 килокалорий (250 калорий) энергии в шоколадном батончике, 9Ограничение скорости 0 км/ч, рост человека 1,8 м и расстояние 2,0 м — все это скаляры — величины без определенного направления. Обратите внимание, однако, что скаляр может быть отрицательным, например, температура -20ºC. В этом случае знак минус указывает точку на шкале, а не направление. Скаляры никогда не изображаются стрелками.
Системы координат для одномерного движения
Чтобы описать направление векторной величины, вы должны указать систему координат в системе отсчета.
Для одномерного движения это простая система координат, состоящая из одномерной координатной линии. В общем, при описании горизонтального движения движение вправо обычно считается положительным, а движение влево считается отрицательным. При вертикальном движении движение вверх обычно положительное, а движение вниз отрицательное. Однако в некоторых случаях, как в случае со струей на рисунке \PageIndex{2}\), удобнее поменять местами положительное и отрицательное направления. Например, если вы анализируете движение падающих объектов, может быть полезно определить положительное направление вниз. Если люди в гонке бегут налево, полезно определить лево как положительное направление. Это не имеет значения, пока система ясна и последовательна. Как только вы задаете положительное направление и начинаете решать проблему, вы не можете изменить его.
Рисунок \(\PageIndex{2}\): обычно удобно рассматривать движение вверх или вправо как положительное (+), а движение вниз или влево как отрицательное (-).
Упражнение \(\PageIndex{1}\)
Скорость человека может оставаться неизменной, когда он поворачивает за угол и меняет направление. Учитывая эту информацию, является ли скорость скалярной или векторной величиной? Объяснять.
- Ответить
Скорость является скалярной величиной. Он совсем не меняется при смене направления; следовательно, он имеет только величину. Если бы это была векторная величина, она менялась бы при изменении направления (даже если бы ее величина оставалась постоянной).
Резюме
- Вектор — это любая величина, имеющая величину и направление.
- Скаляром называется любая величина, имеющая величину, но не имеющую направления.
- Перемещение и скорость являются векторами, тогда как расстояние и скорость являются скалярами.
- В одномерном движении направление задается знаком плюс или минус для обозначения влево или вправо, вверх или вниз и т.
