Скалярное умножение Википедия

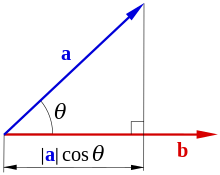Скалярное произведение векторов (a,b){\displaystyle (\mathbf {a} ,\mathbf {b} )} равно произведению |a||b|cos⁡(θ){\displaystyle |\mathbf {a} ||\mathbf {b} |\cos(\theta )}

Скаля́рное произведе́ние (иногда называемое внутренним произведением) — операция над двумя векторами, результатом которой является скаляр, то есть число, не зависящее от выбора системы координат.

Обычно для скалярного произведения векторов a{\displaystyle \mathbf {a} } и b{\displaystyle \mathbf {b} } используется одно из следующих обозначений.

(a,b){\displaystyle (\mathbf {a} ,\mathbf {b} )}

a⋅b, a→⋅b→{\displaystyle \mathbf {a} \cdot \mathbf {b} ,\ {\vec {a}}\cdot {\vec {b}}} или просто ab{\displaystyle \mathbf {a} \mathbf {b} }

⟨a,b⟩{\displaystyle \langle \mathbf {a} ,\mathbf {b} \rangle } или (обозначение Дирака, применяемое в квантовой механике для векторов состояния ^[1]): ⟨a|b⟩{\displaystyle \langle a|b\rangle }

В простейшем случае обычного пространства скалярное произведение ненулевых векторов a{\displaystyle \mathbf {a} } и b{\displaystyle \mathbf {b} } определяется как произведение длин этих векторов на косинус угла между ними^[2]:

(a,b)=|a

Скалярное произведение — Вики

Скалярное произведение векторов (a,b){\displaystyle (\mathbf {a} ,\mathbf {b} )} равно произведению |a||b|cos⁡(θ){\displaystyle |\mathbf {a} ||\mathbf {b} |\cos(\theta )}

Скаля́рное произведе́ние (иногда называемое внутренним произведением) — операция над двумя векторами, результатом которой является скаляр, то есть число, не зависящее от выбора системы координат.

Обычно для скалярного произведения векторов a{\displaystyle \mathbf {a} } и b{\displaystyle \mathbf {b} } используется одно из следующих обозначений.

(a,b){\displaystyle (\mathbf {a} ,\mathbf {b} )}

a⋅b, a→⋅b→{\displaystyle \mathbf {a} \cdot \mathbf {b} ,\ {\vec {a}}\cdot {\vec {b}}} или просто ab{\displaystyle \mathbf {a} \mathbf {b} }

⟨a,b⟩{\displaystyle \langle \mathbf {a} ,\mathbf {b} \rangle } или (обозначение Дирака, применяемое в квантовой механике для векторов состояния ^[1]): ⟨a|b⟩{\displaystyle \langle a|b\rangle }

В простейшем случае обычного пространства скалярное произведение ненулевых векторов a{\displaystyle \mathbf {a} } и b{\displaystyle \mathbf {b} } определяется как произведение длин этих векторов на косинус угла между ними^[2]:

(a,b)=|a||b|cos⁡(θ){\displaystyle (\mathbf {a} ,\mathbf {b} )=|\mathbf {a} ||\mathbf {b} |\cos(\theta )}

Равносильное определение: скалярное произведение есть произведение длины

Скалярное умножение — это… Что такое Скалярное умножение?



Скалярное умножение

Wikimedia Foundation. 2010.

• Скалярное произведение векторов
• Скалярные величины

Смотреть что такое «Скалярное умножение» в других словарях:

• Скалярное произведение — (в зарубежной литературе scalar product, dot product, inner product )  операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов сомножителей и угол между… …   Википедия

• Умножение матриц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведением матриц. Содержание 1 Определение 2 Иллюстрация 3 Мотивировка …   Википедия

• Векторное умножение — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства …   Википедия

• ВЕКТОР — В физике и математике вектор это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент,… …   Энциклопедия Кольера

• Позиционные коды векторов — Содержание 1 Специальная алгебра многомерных векторов[1] 1.1 Специальное умножение …   Википедия

• SSE4 — SSE4  новый набор команд микроархитектуры Intel Core, впервые реализованный в процессорах серии Penryn (не следует путать с SSE4A от AMD)[1]. Он был анонсирован 27 сентября 2006 года, однако детальное описание стало доступно только весной… …   Википедия

• SSE4.1 — SSE4 это новый набор команд Intel Core микроархитектуры, впервые реализованный в процессорах серии Penryn (не следует путать с SSE4A от AMD). Он был анонсирован 27 Сентября 2006, однако детальное описание стало доступно только весной 2007, свежее …   Википедия

• SSE4.2 — SSE4 это новый набор команд Intel Core микроархитектуры, впервые реализованный в процессорах серии Penryn (не следует путать с SSE4A от AMD). Он был анонсирован 27 Сентября 2006, однако детальное описание стало доступно только весной 2007, свежее …   Википедия

• Прямоугольная система координат — Прямоугольная система координат  прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для… …   Википедия

• Алгебра —          Общие сведения          Алгебра один из больших разделов математики (См. Математика), принадлежащий наряду с арифметикой (См. Арифметика) и геометрией (См. Геометрия) к числу старейших ветвей этой науки. Задачи, а также методы А.,… …   Большая советская энциклопедия

Скаляр — Википедия

Скаля́р (от лат. scalaris — ступенчатый) — величина, полностью определяемая в любой координатной системе одним числом или функцией, которое не меняется при изменении пространственной системы координат. В математике под «числами» могут подразумеваться элементы произвольного поля, тогда как в физике имеются в виду действительные или комплексные числа. О функции, принимающей скалярные значения, говорят как о скалярной функции.

Скаляр всегда описывается одним числом, а вектор может описываться двумя или более числами.

При смене системы координат скаляр остаётся неизменным (инвариантным), в отличие, например, от компонентов вектора, которые могут быть разными у одного и того же вектора в разных базисах.

В общей и линейной алгебре скаляр — элемент основного поля. При этом, любой элемент линейного пространства может быть умножен на скаляр и результатом будет другой, коллинеарный элемент линейного пространства.

В тензорном исчислении скалярами являются тензоры валентности (0,0).

Примерами скаляров являются длина, площадь, время, масса, плотность, температура, поток и т. п.^[1]

Важно заметить, что понятие скаляра довольно сильно связано с контекстом. Так, в общепринятом контексте современной физики часть приведённых величин скалярными не являются.

[1]

В современной физике, подразумевающей пространственно-временной подход, под скаляром обычно имеется в виду скалярное поле, то есть пространственно-временной скаляр, лоренц-инвариантная величина, не меняющаяся при переходе от одной инерциальной системы отсчёта к другой (а в общей теории относительности и других метрических теориях гравитации — скаляр остается неизменным также и при переходе к неинерциальным системам отсчёта). В этом отличие от ньютоновской физики, где под скаляром понимается обычный скаляр обычного трёхмерного пространства (так, энергия в ньютоновском смысле — скаляр, а в пространственно-временном — лишь компонента четырёхмерного вектора).

Ошибочные примеры скаляров и нескалярные величины[править | править код]

Типичным примером величины, выражающейся одним числом, но

не являющейся скаляром, является одна из координат вектора в каком-то произвольно выбранном базисе (при почти любом изменении базиса координата не останется неизменной, она, таким образом, не инвариант)^[2].

То же касается координаты тензора любой другой валентности (кроме нулевой).

Можно проиллюстрировать неинвариантность нескалярной величины на угловых координатах, ограниченных диапазоном в один оборот. В случае, если отсчёт ведётся от 0 до 2π (предел 2π не включается в диапазон и соответствует 0), угловое расстояние между 1,7π и 0,2π по модулю составит 1,5π, а если аналогичный отсчёт ведётся от –π до π (здесь предел π также не включается в диапазон), то угловое положение 1,7π предыдущего примера будет соответствовать –0,3π, и угловое расстояние между 0,2π и –0,3π по модулю составит 0,5π с отличием в половину диапазона. Так же учитывается возможная смена координат и в задачах с повторяющимися диапазонами, которые кратны обороту (или периоду) или используют часть оборота (половина оборота достаточна для определения углового положения симметричных тел и явлений).

Ещё одним примером величины, не являющейся, строго говоря, скаляром, является псевдоскаляр (хотя на практике иногда, исходя из соображений удобства или краткости, разграничения между скалярами и псевдоскалярами могут и не проводить, если это не существенно для изложения).

1. ↑ ^{1 2} Среди приведённых величин большинство являются скалярами лишь в весьма ограниченных контекстах. Так, хотя длина или площадь, понимаемые как длина и площадь, определённые для основного пространства рассматриваемой теории, несомненно, являются хорошими примерами скаляров, тем не менее, обычные (то есть рассматриваемые в рамках обычного трёхмерного пространства) длина и площадь, а также время — являются скалярами только в классической (ньютоновской) физике (см. замечание о современной физике), так как основное пространство современных физических теорий по умолчанию обычно включает как минимум четырёхмерное пространство-время. В общеупотребительном современном понимании скалярами из перечисленного являются масса, 4-мерная длина — интервал (а трёхмерная длина — нет!), 4-мерная (но не трёхмерная!) площадь, также — «инварианты» электромагнитного поля: E² − H², E⋅H. А время и энергия, например, являются не скалярами, первое — компонентой вектора 4-мерного перемещения, вторая — компонентой 4-вектора энергии-импульса. Вообще же говоря, если идёт речь о физике, чтобы не ошибиться в понимании применения термина скаляр надо выяснить контекст: идёт ли речь об «обычном» трёхмерном пространстве или о пространственно-временной формулировке.
2. ↑ Речь идёт именно о координате в произвольном базисе, который можно менять. Тем не менее, координата определённого вектора в определённом фиксированном базисе — скаляр. Это внешне немного напоминает казуистику, но на самом деле просто подчёркивает тот факт, что настоящий скаляр остаётся инвариантным при любом изменении базиса (иногда класс преобразований базиса, для которых требуется инвариантность скаляра, ограничивают, но всё же этот класс остаётся достаточно широким; строго же говоря, даже если этот класс широк, если речь идёт об инварианте ограниченного класса преобразований, обычно его именно так и называют, не употребляя термина «скаляр».

скалярное умножение — это… Что такое скалярное умножение?



скалярное умножение

scalar multiplication

Большой англо-русский и русско-английский словарь. 2001.

• скалярное произведение
• скалярное уравнение

Смотреть что такое «скалярное умножение» в других словарях:

• Скалярное умножение — …   Википедия

• Скалярное произведение — (в зарубежной литературе scalar product, dot product, inner product )  операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов сомножителей и угол между… …   Википедия

• Умножение матриц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведением матриц. Содержание 1 Определение 2 Иллюстрация 3 Мотивировка …   Википедия

• Векторное умножение — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства …   Википедия

• ВЕКТОР — В физике и математике вектор это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент,… …   Энциклопедия Кольера

• Позиционные коды векторов — Содержание 1 Специальная алгебра многомерных векторов[1] 1.1 Специальное умножение …   Википедия

• SSE4 — SSE4  новый набор команд микроархитектуры Intel Core, впервые реализованный в процессорах серии Penryn (не следует путать с SSE4A от AMD)[1]. Он был анонсирован 27 сентября 2006 года, однако детальное описание стало доступно только весной… …   Википедия

• SSE4.1 — SSE4 это новый набор команд Intel Core микроархитектуры, впервые реализованный в процессорах серии Penryn (не следует путать с SSE4A от AMD). Он был анонсирован 27 Сентября 2006, однако детальное описание стало доступно только весной 2007, свежее …   Википедия

• SSE4.2 — SSE4 это новый набор команд Intel Core микроархитектуры, впервые реализованный в процессорах серии Penryn (не следует путать с SSE4A от AMD). Он был анонсирован 27 Сентября 2006, однако детальное описание стало доступно только весной 2007, свежее …   Википедия

• Прямоугольная система координат — Прямоугольная система координат  прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для… …   Википедия

• Алгебра —          Общие сведения          Алгебра один из больших разделов математики (См. Математика), принадлежащий наряду с арифметикой (См. Арифметика) и геометрией (См. Геометрия) к числу старейших ветвей этой науки. Задачи, а также методы А.,… …   Большая советская энциклопедия

скалярное умножение — с английского на русский

См. также в других словарях:

• Скалярное умножение — …   Википедия

• Скалярное произведение — (в зарубежной литературе scalar product, dot product, inner product )  операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов сомножителей и угол между… …   Википедия

• Умножение матриц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведением матриц. Содержание 1 Определение 2 Иллюстрация 3 Мотивировка …   Википедия

• Векторное умножение — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства …   Википедия

• ВЕКТОР — В физике и математике вектор это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент,… …   Энциклопедия Кольера

• Позиционные коды векторов — Содержание 1 Специальная алгебра многомерных векторов[1] 1.1 Специальное умножение …   Википедия

• SSE4 — SSE4  новый набор команд микроархитектуры Intel Core, впервые реализованный в процессорах серии Penryn (не следует путать с SSE4A от AMD)[1]. Он был анонсирован 27 сентября 2006 года, однако детальное описание стало доступно только весной… …   Википедия

• SSE4.1 — SSE4 это новый набор команд Intel Core микроархитектуры, впервые реализованный в процессорах серии Penryn (не следует путать с SSE4A от AMD). Он был анонсирован 27 Сентября 2006, однако детальное описание стало доступно только весной 2007, свежее …   Википедия

• SSE4.2 — SSE4 это новый набор команд Intel Core микроархитектуры, впервые реализованный в процессорах серии Penryn (не следует путать с SSE4A от AMD). Он был анонсирован 27 Сентября 2006, однако детальное описание стало доступно только весной 2007, свежее …   Википедия

• Прямоугольная система координат — Прямоугольная система координат  прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для… …   Википедия

• Алгебра —          Общие сведения          Алгебра один из больших разделов математики (См. Математика), принадлежащий наряду с арифметикой (См. Арифметика) и геометрией (См. Геометрия) к числу старейших ветвей этой науки. Задачи, а также методы А.,… …   Большая советская энциклопедия

Скалярное умножение — с русского на все языки

См. также в других словарях:

• Скалярное умножение — …   Википедия

• Скалярное произведение — (в зарубежной литературе scalar product, dot product, inner product )  операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов сомножителей и угол между… …   Википедия

• Умножение матриц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведением матриц. Содержание 1 Определение 2 Иллюстрация 3 Мотивировка …   Википедия

• Векторное умножение — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства …   Википедия

• ВЕКТОР — В физике и математике вектор это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент,… …   Энциклопедия Кольера

• Позиционные коды векторов — Содержание 1 Специальная алгебра многомерных векторов[1] 1.1 Специальное умножение …   Википедия

• SSE4 — SSE4  новый набор команд микроархитектуры Intel Core, впервые реализованный в процессорах серии Penryn (не следует путать с SSE4A от AMD)[1]. Он был анонсирован 27 сентября 2006 года, однако детальное описание стало доступно только весной… …   Википедия

• SSE4.1 — SSE4 это новый набор команд Intel Core микроархитектуры, впервые реализованный в процессорах серии Penryn (не следует путать с SSE4A от AMD). Он был анонсирован 27 Сентября 2006, однако детальное описание стало доступно только весной 2007, свежее …   Википедия

• SSE4.2 — SSE4 это новый набор команд Intel Core микроархитектуры, впервые реализованный в процессорах серии Penryn (не следует путать с SSE4A от AMD). Он был анонсирован 27 Сентября 2006, однако детальное описание стало доступно только весной 2007, свежее …   Википедия

• Прямоугольная система координат — Прямоугольная система координат  прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для… …   Википедия

• Алгебра —          Общие сведения          Алгебра один из больших разделов математики (См. Математика), принадлежащий наряду с арифметикой (См. Арифметика) и геометрией (См. Геометрия) к числу старейших ветвей этой науки. Задачи, а также методы А.,… …   Большая советская энциклопедия