Найдите скалярное произведение векторов a и b: a = 2p + 3q, b = 3p − 4… — Учеба и наука

Ответы

a*b=(2p+3q)(3p−4q)=6p^2-12q^2+pq=6|p|^2-12|q|^2+|p|*|q|cos(π/4)= =6*3^2-12*(√2)^2+3*√2*√2/2=54-24+3=33 29. 10.15

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

15)Скалярное произведение векторов.

Геометрический и механический смысл. Свойства. Таблица умножения ортов. Угол между векторами.

Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними:

ab = |a||b| cosφ . (5.4)

Обозначения скалярного произведения: ab, (ab), a·b .

Свойства скалярного произведения:

1. ab = |a| пр_аb.

Доказательство. По свойству проекции пр_аb = |b| cosφ, следовательно, ab = |a| пр

аb.

2. ab = 0 a b. 3. ab = ba .

4. (ka)b = k(ab). 5. (a + b)c = ac + bc .

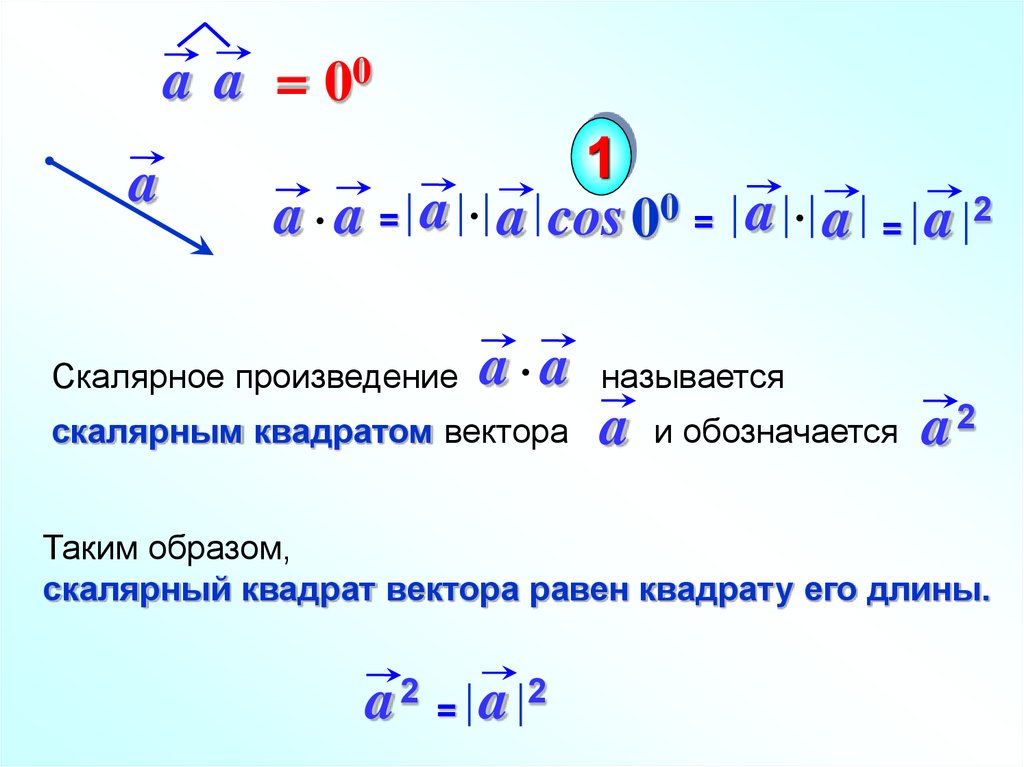
6. a² = aa = |a|² , где а² называется скалярным квадратом вектора

а.

7. Если векторы а и b определены своими декартовыми координатами

a = {X₁, Y₁, Z₁}, b = {X₂, Y₂, Z₂}, (5.5)

то ab = X₁X₂ + Y₁Y₂ + Z₁Z₂ .

(5. 6)

Доказательство. Используя формулу (5.3), получим:

ab = (X₁i + Y₁j + Z₁k)(X₂i + Y₂j + Z₂k) .

Используя свойства 4 и 5, раскроем скобки в правой части полученного равенства:

ab = X₁X₂ii +Y₁Y₂jj + Z₁Z₂

kk + X₁Y₂ij +X₁Z₂ik + Y₁X₂ji + Y₁Z₂jk + Z₁X₂ki + Z₁Y₂kj.

Но ii = jj = kk = 1 по свойству 6,

ij = ji = ik = ki = jk = kj = 0 по свойству 2, поэтому

ab = X₁X₂ + Y₁Y₂ + Z₁Z₂ .

8. cosφ = . (5.6)

Замечание. Свойства 2, 3, 4 доказываются из определения 5.14, свойства 5, 6 – из свойств проекции, свойство 8 – из свойства 7 и свойств направляющих косинусов.

Пример.

a = {1, -5, 12}, b = {1, 5, 2}. Найдем скалярное произведение векторов а

и b :

ab = 1·1 + (-5)·5 + 12·2 = 1 – 25 + 24 = 0. Следовательно, векторы а и b ортогональны.

-Механический смысл скалярного произведения векторов. Скалярное произведение силы F на вектор перемещения S равно работе А этой силы при перемещении материальной точки по вектору S: A = FS.

-Геометрический смысл — произведение длины одного вектора на проекцию на него второго вектора.

-Таблица скалярного умножения ортов i, j, k

Используя определение скалярного произведения векторов,

получим:

1 i

× i = i i cos0 = 1 × 1 × 1 = 1 .

Значит, j × j = k × k = 1 .

2 i × j = i × j 90 = 1× 1× 0 = 0

—Угол между векторами

     

16)Понятие тройки векторов. Левая, правая тройка, Определение векторного произведения. Геометрический смысл. Свойства. Векторное произведение в декартовых координатах.

Тройка некомпланарных векторов abc называется правой (левой), если после приведения к общему началу вектор с располагается по ту сторону от плоскости, определяемой векторами а и b, откуда кратчайший поворот от а к b кажется совершающимся против часовой стрелки (по часовой стрелке).

с с

b a

a b

abc – правая тройка abc – левая тройка

Замечание. В дальнейшем будем рассматривать только правые системы координат, т.е. системы, базисные векторы которых образуют правую тройку.

Векторное произведение векторов.

Вектор с называется векторным произведением векторов а и b, если:

1. |c| = |a||b|sinφ, где φ – угол между а и b.

2. c a, c b.

3. Тройка векторов abc является правой.

Обозначения векторного произведения: c = [ab], c = a b.

Свойства векторного произведения.

1. [ba] = — [ab].

Доказательство. Вектор —с удовлетворяет первым двум условиям определения векторного произведения и образует с векторами b и а правую тройку векторов.

2. [ab] = 0 a ║ b.

Доказательство. Из первого пункта определения 6.2 следует, что модуль векторного произведения ненулевых векторов равен нулю только при sinφ = 0, что соответствует коллинеарности векторов а и b.

3. Модуль векторного произведения |[ab]| равняется площади S параллелограмма, построенного на приведенных к общему началу векторах а и b.

Доказательство следует из первого пункта определения 6.2.

Орт е_а произвольного вектора а – это вектор единичной длины, коллинеарный а и одинаково с ним направленный ( | е_а| = 1, е_а || a).

Cледствие из свойства 3. [ab] = Se, где е – орт вектора [ab].

4. [(ka)b] = k[ab].

5. [(a + b)c] = [ac] + [bc].

6. Если в декартовой системе координат a = {X_a, Y_a, Z_a}, b = {X_b, Y_b, Z_b}, то

7. [ab] =

8. Доказательство.

Представим векторы а и b в виде: a = X_ai + Y_aj +Z_ak, b = X_bi + Y_bj +Z_bk. Отметим, что [ij] = k, [jk] = i, [ki] = j, [ii] = [jj] = [kk] = 0. Тогда с использованием свойств 4 и 5 получим:

[(X_ai + Y_aj + Z_ak)(X_bi + Y_bj + Z_bk)] =(Y_aZ_b – Y_bZ_a)i + (X_bZ_a – X_aZ_b)j + (X_aY_b – X_bY_a)k, что доказывает свойство 6.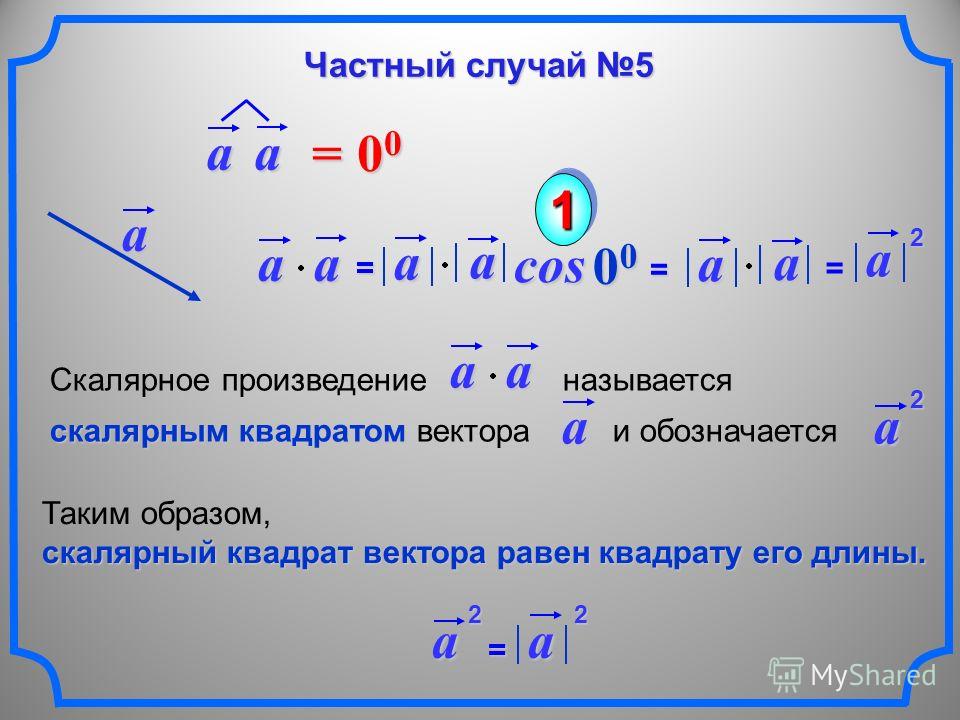

Пример. Вычислим векторное произведение векторов а = {3, -4, 2} и b = {1, 5, 1}.

[ab] = ={-14, -1, 19}.

Скалярное произведение двух векторов: определение, формула и свойства

Векторы — это величины, которые имеют как величину, так и направление, а операции, которые можно выполнять над векторами, — это сложение и умножение. Умножение векторов можно выполнить двумя способами, а именно скалярным произведением векторов и перекрестным произведением векторов. Скалярное произведение — это один из способов умножения двух или более векторов. Результат скалярного произведения векторов является скалярной величиной. Следовательно, скалярное произведение векторов также известно как скалярное произведение. Скалярное произведение векторов имеет различные приложения в геометрии, механике, технике, астрономии и т. д.

Что такое скалярное произведение двух векторов?

Скалярное произведение двух векторов равно произведению величины и направления и косинуса угла между двумя векторами. Результат скалярного произведения двух векторов, лежащих в одной плоскости двух векторов. Скалярный продукт двух векторов может быть положительным действительным числом, отрицательным действительным числом или нулем.

В векторной алгебре, если два вектора заданы как \(x=(x_{1},x_{2},x_{3},…..,x_{n})\) и \(y= (y_{1},y_{2},y_{3},…..,y_{n})\), то их скалярное произведение равно: 9{n}x_{i}y_{i}\)

Определение скалярного произведения векторов можно дать двумя способами: алгебраическим и геометрическим. Алгебраическим способом скалярное произведение является суммой произведений соответствующих элементов двух последовательностей чисел. С геометрической точки зрения скалярное произведение — это произведение евклидовой величины двух векторов и косинуса угла между ними.

Проекция векторов: Скалярное произведение векторов полезно при определении компонента одного вектора в направлении другого вектора. Проекция одного вектора на другой вектор — это ширина тени представленного вектора на другой вектор.

Проекция векторов достигается путем умножения величины представленных векторов на косинус угла между двумя векторами. Результатом формулы векторной проекции является скалярное значение.

Предположим, OA = x , OB = y , два вектора и \(\theta\) угол между x и y .

Проведите линию AL перпендикулярно OB.

Из прямоугольного треугольника OAL,

\(cos\theta=\frac{OL}{OA}\)

\(OL=OA cos\theta=\left|x\right|cos\theta\)

OL указывает на векторную проекцию x на y .

x \(\cdot\) y = \(\left|x\right|\left|y\right|cos\theta\)

x \(\cdot\) y = \(\left|y\right|OL\)

x \(\cdot\) y = \(\left|y\right|\) (проекция x на y ) .

Таким образом, проекция х на y = \(\frac{x\cdot y}{\left|y\right|}\).

Аналогично, проекция y на x = \(\frac{x\cdot y}{\left|x\right|}\).

Скалярное произведение двух векторов Формула

Предположим, что x и y — два ненулевых вектора, а \(\theta\) — это угол между двумя векторами, затем скалярное произведение (или скалярное произведение) двух векторов обозначается как x \(\cdot\) y , что определяется как

x \(\cdot\) y = \(\left|x\right|\left|y\right|cos\theta\),

где

• \(\left|x\right |\) = величина x ,
• \(\left|y\right|\) = величина y ,
• \(\theta\) = угол между векторами x и y .

Примечание: \(\theta\) не определено, если модуль любого из векторов равен нулю, т. е. a = 0 или b = 0.

Как найти скалярное произведение двух векторов?

Предположим, что если два вектора выражаются через единичные векторы i, j, k вдоль осей x, y и z, то скалярное произведение двух векторов получается следующим образом:

Шаг 1: Если \(x=x_{1}\шляпа{i}+x_{2}\шляпа{j}+x_{3}\шляпа{k}\) и \(y=y_{1}\шляпа{i} +y_{2}\hat{j}+y_{3}\hat{k}\), то скалярное произведение x и y равно

x \(\cdot\) y = \((x_{1}\шляпа{i}+x_{2}\шляпа{j}+x_{3}\шляпа{k})\cdot(y_{1}\шляпа{i}+y_{ 2}\шляпа{j}+y_{3}\шляпа{k})\).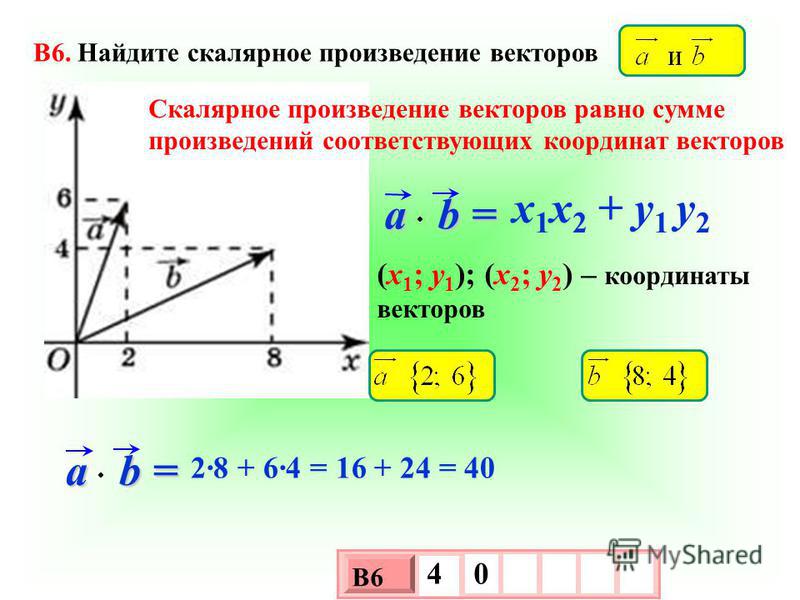

Шаг 2: x \(\cdot\) y = \((x_{1}y_{1})(\hat{i}\cdot\hat{i})+(x_{ 1}y_{2})(\шляпа{i}\cdot\шляпа{j})+(x_{1}y_{3})(\шляпа{i}\cdot\шляпа{k})+(x_{ 2}y_{1})(\шляпа{j}\cdot\шляпа{i})+(x_{2}y_{2})(\шляпа{j}\cdot\шляпа{j})+(x_{ 2}y_{3})(\шляпа{j}\cdot\шляпа{k})+(x_{3}y_{1})(\шляпа{k}\cdot\шляпа{i})+(x_{ 3}y_{2})(\шляпа{k}\cdot\шляпа{j})+(x_{3}y_{3})(\шляпа{k}\cdot\шляпа{k})\).

Шаг 3: Точечные отношения единичных векторов по трем осям следующие: шляпа{k}\cdot\шляпа{i}=0\) и

\(\шляпа{i}\cdot\шляпа{i}=\шляпа{j}\cdot\шляпа{j}=\шляпа{k}\cdot\шляпа{k}=1\).

Шаг 4: Используя точечное отношение единичных векторов, мы имеем

x \(\cdot\) y = \(x_{1}y_{1}+x_{2}y_{2} +x_{3}y_{3}\).

Примеры скалярного произведения двух векторов

Ниже приведены некоторые примеры скалярного произведения двух векторов:

• Скалярное произведение двух единичных векторов: Скалярное произведение двух единичных векторов равно единице. Предположим, что для двух единичных векторов 9{\circ}\) = ab (0) = 0.

Свойства скалярного произведения векторов

Рассмотрим a , b и c — действительные векторы и ‘x’ y’ является скаляром, то скалярное произведение удовлетворяет следующим свойствам:

Свойство 1: Коммутативное свойство: Скалярное произведение векторов коммутативно, т.е. (\cdot\) a,

Это следует из определения (\(\theta\) угол между a и b ):

a \(\cdot\) b  = \(\left|a\right|\left|b\right|cos\theta=\left|b\right |\left|a\right|cos\theta\) = b \(\cdot\) a .

Свойство 2: Распределительное свойство:  Скалярное произведение векторов является дистрибутивным по отношению к сложению векторов, т.е. \) б + а \(\cdot\) в.

Свойство 3: Билинейность Свойство: Скалярное произведение векторов является билинейным, т.е. ) b ) + ( a \(\cdot\) c ).

Свойство 4: скалярное умножение Свойство: Скалярное умножение векторов определяется выражением ) б ).

Свойство 5: Неассоциативность Свойство: Скалярное произведение векторов неассоциативно, потому что скалярное произведение между скаляром ( a \(\cdot\) b ) и вектором ( c ) не определено, это означает, что выражения ( a \(\cdot\) b )\(\cdot\) c или a \(\cdot\)( b \(\cdot\) c ) не определены. Свойство скалярного умножения иногда называют «ассоциативным законом для скаляра и скалярного произведения» или «скалярное произведение ассоциативно по отношению к скалярному умножению», потому что c( a \(\cdot\) b ) = (c a )\(\cdot\) b = a \(\cdot\)(c b ).

Свойство 6: Ортогональность Свойство: Два ненулевых вектора a и b ортогональны тогда и только тогда, когда a \(\cdot\) b = 0,

Произведение разницы между 9005t Векторы и векторное произведение векторов

Скалярное произведение двух векторов

• Скалярное произведение двух векторов A и B определяется как скалярная величина AB\(\cos\theta\), где \(\theta\) — угол между ними, такой что \(0\leq \theta \leq \pi\) .

• Обозначается A \(\cdot\) B путем помещения между векторами точки.
• Итак, у нас есть уравнение: A \(\cdot\) B = AB\(\cos\theta\).

• Скалярное произведение векторов также известно как скалярное произведение двух векторов.

Перекрестное произведение двух векторов

• Перекрестное произведение двух векторов A и B определяется как AB\(\sin\theta\) с направлением, перпендикулярным A и B в правой системе, где \(\theta\) — угол между ними такой, что \(0\leq \theta \leq \pi\).

• Обозначим A \(\times\) B , поставив знак креста между векторами. 9{\circ}\)

  = (2)(3)(1/2)

  = 3.

  Пример 2: Вычислить скалярное произведение двух векторов a = (1, 2, 3) и б = (4, -5, 6).

  Решение: Даны векторы a = (1, 2, 3) и b = (4, -5, 6) соответственно.

  a \(\cdot\) b = (1, 2, 3)\(\cdot\)(4, -5, 6)

  a \(\cdot\) b = (1)(4)+(2)(-5)+(3)(6)

  a \(\cdot\) b = 4 – 10 + 18

  a \(\cdot\) b = 12.

  Мы надеемся, что приведенная выше статья поможет вам понять и сдать экзамен приготовления. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.

  Часто задаваемые вопросы о скалярном произведении двух векторов

  В.1 Что такое скалярное произведение двух взаимно перпендикулярных векторов? 9{2}\).

  Q.5 Что такое скалярное произведение двух векторов?

  Ответ 5 Скалярное произведение двух векторов равно произведению величины и направления и косинуса угла между двумя векторами. Результат скалярного произведения двух векторов, лежащих в одной плоскости двух векторов. Скалярный продукт двух векторов может быть положительным действительным числом, отрицательным действительным числом или нулем.

  Скачать публикацию в формате PDF

  Читать больше сообщений

  Законы сложения векторов со свойствами треугольника, параллелограмма, многоугольника с примерами
  Уравнение сферы: длина окружности, площадь поверхности и формула объема	Центробежная сила: узнайте ее формулу, единицу измерения, примеры и области применения
  Деструктивная перегонка: узнайте ее процесс, продукты и области применения

  Калькулятор скалярного произведения

  Введите значения векторов a и b и нажмите кнопку расчета, чтобы найти a. b с помощью калькулятора скалярного произведения

  Содержание:

  • Что такое скалярное произведение?
  • Формула скалярного произведения
  • Как вычислить скалярное произведение двух векторов?

  Дайте нам отзыв

  ✎

  ✉

  Калькулятор скалярного произведения используется для нахождения скалярного произведения двух векторов. Он вычисляет скалярное произведение двумерных и трехмерных векторов. Калькулятор предоставляет пошаговое решение поставленных задач.

  Что такое скалярный продукт?

  Скалярное произведение — это основной способ объединения двух векторов. Он используется, чтобы узнать направление двух векторов. Скалярное произведение двух векторов также известно как результат и является скалярной величиной.
  Скалярное произведение обозначается буквой a.b и читается как «a dot b».

  Формула скалярного произведения

  Формула скалярного произведения:

  a.b = |a||b| cos(θ) … (i)

  • a и b — два вектора.
  • |а| & |б| — величины векторов a и b.
  • «θ» — это угол между a и b.

  В математике мы можем вывести другую форму скалярного произведения. Пусть a = (a ₁ , a ₂ , a ₃ ) & b = (b ₁ , b ₂ , b ₃ ) — два вектора. Теперь по закону косинусов

  |a – b| ² = |а| ² + |б| ² – 2|а||б| cos(θ)

  Упростим приведенное выше выражение с помощью величины векторной формулы.

  (A ₁ — B1) ² + (A ₂ — B ₂ ) ² + (A ₃ — B ₃ ) ^{2 — B ₃ ) 2 — B ₃ ) 2 — B ₃ ) 2 — B ₂ + a ₂ 2 + a ₃ 2 ) + (b ₁ 2 + b ₂ 2 + b ₃ 2 ) – 2|a| |б| cos(θ)}

  Откройте квадрат каждого члена.

  (а ₁ ² — 2а ₁ б ₁ + B ₁ ² ) + (A ₂ ² — 2A ₂ B ₂ + B ₂ ^{2 + B ₂ 2 + B _{2 2} + B _{2 2} + B ₂ . B ₃ + B ₃ 2 ) = (A ₁ 2 + ₂ 2 + A ₃ 2 + A ₃ 2 + A ₃ 2 + A ₃ 2 + A 2 2 2 2 2 2 + 2 . б ₂ 2 + б ₃ 2 ) – 2|а||б| cos(θ)}

  Теперь возьмем аналогичные члены в той же части уравнения.

  (A ₁ ² — 2A ₁ B ₁ + B ₁ ² ) + (A ₂ ² ) + (A ₂ ² ) (A ₂ ² ) + (A ₂ ² ) + (A ₂ ² ). ² ) + (A ₃ ² — 2A ₃ B ₃ + B ₃ ² ) — ( ² ) — ( ₃ ² ) — ( ₃ ² ) — ( ₃ ² ) — (A ₃ ² ) — ( ₃ ² ) — ( ₃ ² ). а ₃ ² ) — (б ₁ ² + б ₂ ² + б ₃ ² ) = – 2|a||b| cos(θ)

  После вычитания подобных членов получаем

  — 2a ₁ b ₁ + (-2a ₂ b ₂ ) + (-2a _{1 b 3} ) – 2|а||б| cos(θ)

  — 2(a ₁ b ₁ + a ₂ b ₂ + a ₃ b ₃ ) = – 2|a||b| cos(θ)

   (а ₁ б ₁ + а ₂ б ₂ + а ₃ б ₃ ) = |а||б| cos(θ) … (ii)

  Теперь подставим уравнение (ii) в (i), получим

  a.