Скалярное произведение векторов — Студопедия
Поделись
| Определение скалярного произведения векторов на плоскости | Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними: Важно! Произведение вектора на число – это вектор Произведение двух векторов, — это число ( числа часто называют скалярными) |
| Угол между векторами на плоскости | Угол между векторами острый Угол между векторами тупой Угол между векторами – прямой ( векторы перпендикулярны) Угол между векторами равен 00 Векторы сонаправлены Угол между векторами равен 1800 Векторы противоположно направлены Если один из векторов или оба вектора нулевые, то угол между ними будет равен 0°. |
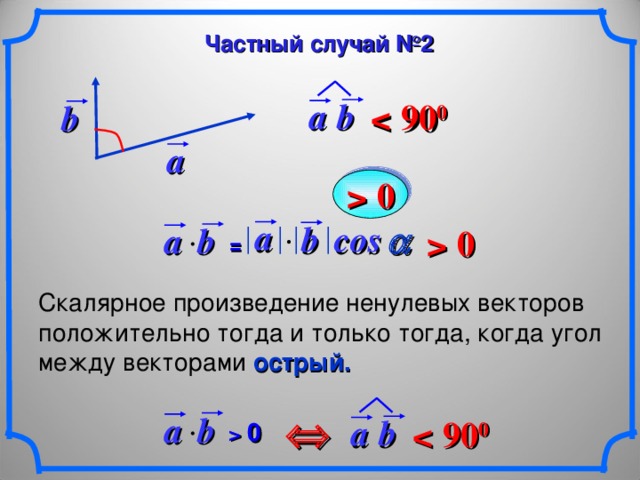
| Знак скалярного произведения | 1. Если угол между векторами острый, то скалярное произведение будет положительным числом (так как косинус острого угла — положительное число).
Если векторы сонаправлены, то угол между ними будет равен 0°, а косинус равен 1, скалярное произведение также будет положительным.
2. Если угол между векторами тупой, то скалярное произведение будет отрицательным (так как косинус тупого угла — отрицательное число).
Если векторы направлены противоположно, то угол между ними будет равен 180°. Скалярное произведение также отрицательно, так как косинус этого угла равен −1.
Справедливы и обратные утверждения:
1. Если скалярное произведение векторов — положительное число, то угол между данными векторами острый.
2. Если скалярное произведение векторов — отрицательное число, то угол между данными векторами тупой.
|
| Особенный третий случай | 3. Если угол между векторами прямой, то скалярное произведение векторов равно нулю, так как косинус прямого угла равен 0.
Обратное суждение: если скалярное произведение векторов равно нулю, то эти векторы перпендикулярны.
|
| Квадрат вектора | Вектор, умноженный на самого себя будет числом, которое называется скалярным квадратом вектора.
Скалярный квадрат вектора равен квадрату длины данного вектора и обозначается как a⃗ |
| Свойства скалярного произведения | |
| Направляющие векторы | Вектор называют направляющим вектором прямой, если он находится на прямой или параллелен этой прямой. |
| Координаты произведения вектора на число | Если векторы заданы координатами:
a⃗ {x1;y1;z1}, b⃗ {x2;y2;z2},
то скалярное произведение векторов вычисляется по правилу:
a⃗ |
| Основные формулы скалярного произведения в пространстве | Если векторы заданы координатами: a⃗ {x1;y1;z1}, b⃗ {x2;y2;z2}, |
9 класс.
Геометрия. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов. — Решение задач по теме «Скалярное произведение векторов».Комментарии преподавателяПовторение теории начнем с перечня основных теорем.
Рис. 1. Иллюстрация к теоремам
1. Площадь треугольника:
,
площадь треугольника равна половине произведения двух сторон на синус угла между ними.
2. Теорема синусов и следствие из неё:
,
сторона а относится к синусу противолежащего угла α так же, как сторона b относится к синусу противолежащего угла β так же, как сторона с относится к синусу своего противолежащего угла γ. Все эти отношения равны 2R, где R – это радиус описанной окружности.
Чтобы найти радиус, достаточно знать сторону и синус противолежащего угла.
3. Теорема косинусов:
,
квадрат стороны равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
В основных теоремах фигурирует синус и косинус угла треугольника. Но угол треугольника может быть тупым. Поэтому вспомним определение синуса и косинуса для угла .
На рисунке 2 изображена полуокружность радиусом 1, угол α острый, точка М соответствует этому углу. У точки М есть две координаты ().
Можно дать определение синуса и косинуса. Рассмотрим прямоугольный треугольник (выделенный на рис. 2) с гипотенузой 1. Синусом угла называется отношение катета противолежащего к гипотенузе, т. е. это, ордината точки М. Косинусом угла называется отношение прилежащего катета к гипотенузе, т. е. , абсцисса точки М.
Рис. 8. Иллюстрация к примеру
Рис.
3. Иллюстрация к примеру
На рисунке 3 угол α тупой. У точки М есть две координаты ().
Следовательно, , т. е. абсцисса точки, а , то есть ордината точки. Таким образом, мы распространили синус и косинус угла от 0 до 180 градусов.
Исходя из этого, координаты какой-либо точки А будут следующими:
Дано: в треугольнике АВС сторона АВ=8см, угол А=, угол В= (рис. 4).
Найти: сторону АС и ВС, угол С, то есть решить треугольник.
Решение:
Рис. 4. Иллюстрация к задаче
Так как сумма углов треугольника равна , угол С равен минус 2 известных угла:
С=
Все углы известны.
Далее используем теорему синусов:
, где 8 – длина стороны АВ, то есть стороны с.
Получили уравнение относительно a
а=
=
Сторона ВС4 см
По теореме синусов находим сторону b=AC
b
Сторона АС6 см
Ответ: угол С=105, сторона ВС4 см, сторона АС6 см.
Треугольники входят в состав многих фигур, например трапеций, параллелограммов. Поэтому решение треугольников позволяет решать задачи с этими фигурами.
Дано: смежные стороны параллелограмма равны а и b, один из углов равен γ (рис. 5).
Найти: диагонали параллелограмма.
Решение:
Рис. 5. Иллюстрация к задаче
АВСD – параллелограмм, сторона АВ=b, сторона AD=a, угол γ – угол между сторонами a и b (рис. 5). Следовательно, треугольник ABD задан полностью. Найти BD и AC.
Решение данной задачи для параллелограмма полностью основано на теореме косинусов для треугольника. Диагональ BD входит в треугольник АВD. В этом треугольнике известны две стороны и угол между ними. Следовательно:
Одна диагональ найдена.
Вторая диагональ АС входит в треугольник АСD.
Используем свойство параллелограмма. Противоположные стороны параллелограмма равны. AB=CD=b. Сумма углов, прилежащих к одной стороне, равна 180º. Cледовательно, ∠ADC=180.
Применяем теорему косинусов для треугольника ACD:
AC=
Задача решена.
Теорема косинусов для треугольника позволяет вывести важное метрическое свойство для параллелограмма.
Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Рис. 6. Иллюстрация к задаче
Дано: ABCD-параллелограмм, =BD и =AC — его диагонали, a=BC=AD и b=AB=DC – cтороны параллелограмма, ∠BAD=γ, ∠ADC=180 (рис. 6).
Доказать:
Доказательство:
Найдём из треугольника ABD, то есть выпишем для этого треугольника теорему косинусов. найдём из треугольника ADC, также выписав для него теорему косинусов.
,
Складываем два равенства:
Задача решена, свойство доказано.
Из предыдущей задачи мы увидели, что свойство треугольника позволяет решать задачи для параллелограмма и даже устанавливает свойство параллелограмма. Это свойство параллелограмма позволяет решать задачи для треугольника.
Рис. 7. Иллюстрация к задаче
Дано:Треугольник АВС, АВ=с, CA=b, BC=a.
Найти: Медиану А= треугольника АВС.
Решение:
Проведём прямую = (рис. 7). Получили четырёхугольник ABDC. Докажем, что он параллелограмм.
В этом четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, следовательно, этот четырёхугольник – параллелограмм. Поэтому воспользуемся свойством параллелограмма:
Получили уравнение для искомой медианы:
Ответ:
Докажите:
1.
Медиана рассекает треугольник на 2 равновеликих треугольника. Равновеликих – значит, имеющих одинаковую, равную площадь.
2. Три медианы рассекают треугольник на 6 равновеликих треугольников.
Рис. 8. Иллюстрация к задаче
Дано: треугольник АВС, – середины сторон (рис. 8)
Доказать: 1.,
2. .
Доказательство:
– медианы, следовательно, используя свойства медианы, имеем:
1. Рассмотрим треугольники (рис. 9). Каждый из них имеет сторону и одинаковую высоту h. Следовательно, площадь каждого:
,
Рис. 9. Иллюстрация к задаче
площадь треугольника АВС, поэтому площади треугольников равны
половине площади треугольника АВС. Следовательно, медиана рассекает треугольник на два равновеликих треугольника.
2. Рассмотрим треугольник : угол γ – угол между сторонами , где .
Найдём отношение этих площадей:
= =
Следовательно:
А так как:
,
То:
Получаем, что медианы рассекают треугольник на 6 равновеликих треугольников.
На данном уроке мы повторили теорию по теме соотношение сторон и углов в треугольнике и решили типовые задачи по данной теме.
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/9-klass/skalyarnoe-proizvedenie-vektorov/reshenie-zadach-po-teme-razdela-2
http://interneturok.ru/ru/school/geometry/9-klass/skalyarnoe-proizvedenie-vektorov/prosteyshie-zadachi-po-teme-razdela
http://interneturok.ru/ru/school/geometry/9-klass/skalyarnoe-proizvedenie-vektorov/reshenie-zadach-po-teme-razdela-prodolzhenie-1
http://interneturok.ru/ru/school/geometry/9-klass/skalyarnoe-proizvedenie-vektorov/reshenie-zadach-po-teme-razdela-prodolzhenie-2
http://www.
youtube.com/watch?v=DIeo71CR4fY
линейная алгебра. Почему скалярное произведение вектора и само по себе равно длине вектора в квадрате?
Задать вопрос
спросил
Изменено 1 год, 8 месяцев назад
Просмотрено 1к раз
$\begingroup$
Итак, интуитивно понятно, что скалярное произведение двух векторов показывает, насколько один вектор движется в направлении другого.
Следуя этой логике, можно было бы подумать, что скалярное произведение вектора а и самого себя будет равно длине заданного вектора, поскольку вектор движется полностью в своем собственном направлении, но это не похоже на то, что дело.
Кто-нибудь, пожалуйста, объясните ошибку в моей логике, и, пожалуйста, не используйте алгебраические доказательства, потому что их трудно понять интуитивно. Я благодарю вас заранее! 92$, длина в квадрате. В $2$-мерном случае мы снова получаем квадрат длины по теореме Пифагора. Каждый раз, когда размерность увеличивается на $1$, это остается верным, опять же по теореме Пифагора. Например, если $x$ является трехмерным вектором, его можно рассматривать как самую длинную диагональ прямоугольного треугольника и, следовательно, как гипотенузу прямоугольного треугольника, две другие стороны которого являются ребром и гипотенузой прямоугольного треугольника. еще один прямоугольный треугольник.
Интуитивная причина, по которой длина возводится в квадрат, заключается в том, что $x\cdot x$ является произведением двух $x$s и имеет единицы длины, возведенные в квадрат. У него может быть не больше единиц длины, чем у площади основания и высоты прямоугольника. Еще один способ понять это: если $x$ удваивается, $x\cdot x$ становится $$(2x)\cdot(2x)=4x\cdot x.
$$Удвоение вектора увеличивает его квадрат вчетверо, а не сама длина.
Как заметил @Joe, проекция $x$ на $y$ имеет длину $\frac{x\cdot y}{\Vert y\Vert}$ и равна $\frac{x\cdot y}{\ Vert y\Vert}\frac{y}{\Vert y\Vert}=\frac{x\cdot y}{y\cdot y}y$, поэтому проекция $x$ на себя равна $\frac{x \cdot x}{x\cdot x}x=x$. Обратите внимание, что $x\cdot x$ здесь не имеет значения.
$\endgroup$
$\begingroup$
Здесь может быть полезно различать три разные вещи:
Скалярное произведение $A$ и $B$ равно $A\cdot B = |A||B| \cos\тета$.
векторная проекция $B$ на $A$ равна $|B| \cos \theta \cdot \frac{A}{|A|} = |B| \cos\theta\cdot\hat A$.
Скалярная проекция
Если у вас есть два вектора, указывающих в одном направлении, скажем, $A = (3,0)$ и $B = (5,0)$, их скалярное произведение равно $15$, то есть произведению их величин.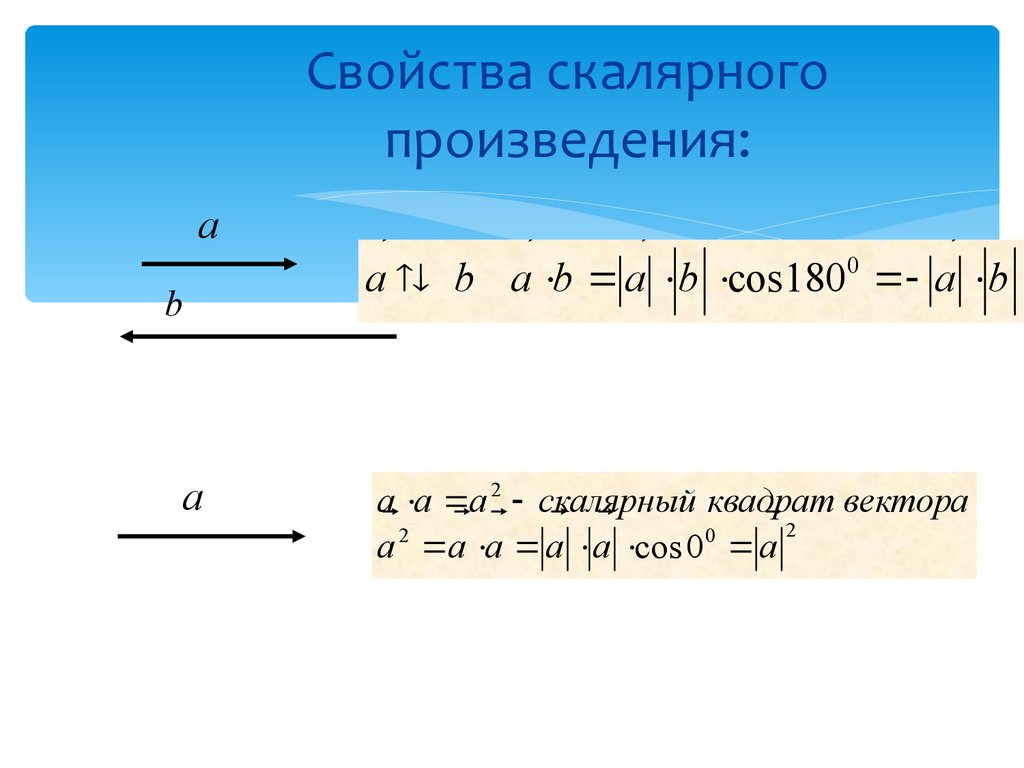
Векторная проекция $B$ на $A$ будет равна $(5,0)$. Скалярная проекция будет $5$.
$\endgroup$
Для любых двух чисел a и b произведение a−b на себя равно a2−2ab+b2. Справедлив ли этот знакомый алгебраический результат для скалярных произведений вектора u − v с самим собой?
РЕШЕНИЕ: Для любых двух чисел a и b произведение a−b на себя равно a2−2ab+b2. Справедлив ли этот знакомый алгебраический результат для скалярных произведений вектора u − v с самим собой?Алгебра -> Настраиваемые средства решения задач Word -> Геометрия -> РЕШЕНИЕ: Для любых двух чисел a и b произведение a−b на себя равно a2−2ab+b2. Справедлив ли этот знакомый алгебраический результат для скалярных произведений вектора u − v с самим собой? Войти
|
com
|
