Компьютерные системы счисления — презентация онлайн

Похожие презентации:

Пиксельная картинка

Информационная безопасность. Методы защиты информации

Электронная цифровая подпись (ЭЦП)

Этапы доказательной медицины в работе с Pico. Первый этап

История развития компьютерной техники

От печатной книги до интернет-книги

Краткая инструкция по CIS – 10 шагов

Информационные технологии в медицине

Информационные войны

Моя будущая профессия. Программист

СИСТЕМЫ
СЧИСЛЕНИЯ
МАТЕМАТИЧЕСКИЕ ОСНОВЫ
ИНФОРМАТИКИ
Общие сведения
Система счисления — это знаковая система, в которой
приняты определённые правила записи чисел.
Цифры — знаки, при помощи которых записываются числа.
Алфавит системы счисления — совокупность цифр.
Простейшая и самая древняя система — унарная система
счисления. В ней для записи любых чисел используется всего
один символ — палочка, узелок, зарубка, камушек.

Система счисления называется непозиционной, если
количественный эквивалент (количественное значение)
цифры в числе не зависит от её положения в записи числа.
Система счисления называется позиционной, если
количественный эквивалент цифры в числе зависит от её
положения в записи числа.
Основание позиционной системы счисления равно
количеству цифр, составляющих её алфавит.
Узловые и алгоритмические числа
Узловые числа обозначаются цифрами.
Римская система счисления
1
5
10
50
I
V
X
L
100
500
1000
C
D
M
Десятичная система счисления
Цифры 1234567890 сложились в Индии около 400 г. н. э.
Арабы стали пользоваться подобной
нумерацией около 800 г. н. э.

Примерно в 1200 г. н. э. эту
нумерацию начали применять в
Европе.
Основная формула
В позиционной системе счисления с основанием q любое число
может быть представлено в виде:
Aq =±(an–1 qn–1+ an–2 qn–2+…+ a0 q0+ a–1 q–1+…+ a–m q–m)
Здесь:
А — число;
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы
счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
qi — «вес» i-го разряда.
Такая запись числа называется развёрнутой формой записи.
Развёрнутая форма
Aq =±(an–1 qn–1+ an–2 qn–2+…+ a0 q0+ a–1 q–1+…+ a–m q–m)
Примеры записи чисел в развёрнутой форме:
2012=2 103 +0 102 +1 101 +2 100
0,125=1 10-1 +2 10-2 +5 10–3
14351,1=1 104 +4 103 +3 102 +5 101 +1 100 +1 10–1
Устное повторение:
1. Где применяется двоичная
система счисления?
2. Каков ее алфавит и основание?
3. Как записать двоичное число в
развернутой форме?
Двоичная
система счисления
Двоичной системой счисления называется позиционная
система счисления с основанием 2.
Двоичный алфавит: 0 и 1.
Для целых двоичных чисел можно записать:
an–1an–2…a1a0 = an–1 2n–1 + an–2 2n–2 +…+ a0 20
Например:
100112 =1 24+0 23+0 22+1 21+1 20 = 24 +21 + 20 =1910
Правило перевода двоичных чисел в десятичную систему счисления:
Вычислить сумму степеней двойки, соответствующих единицам в
свёрнутой форме записи двоичного числа
Свяжи
цифры
8 экономии
и 16памяти
с названием
Сколько
разрядов
ПК в
Придумай
способ
места
займет
двоичное
памяти
ПК. число?
систем
счисления.
1110111000101110000111110000002
73427037008
3B8B87C016
«Компьютерные» системы счисления
Двоичная система используется в компьютерной технике,
так как:
двоичные числа представляются в компьютере с
помощью простых технических элементов с двумя
устойчивыми состояниями;
представление информации посредством только двух
состояний надёжно и помехоустойчиво;
двоичная арифметика наиболее проста;
существует математический аппарат, обеспечивающий
логические преобразования двоичных данных.
Двоичный код удобен для компьютера.
Человеку неудобно пользоваться длинными и
однородными
кодами.
Специалисты
заменяют
двоичные коды на величины в восьмеричной или
шестнадцатеричной системах счисления.
Восьмеричная система
счисления
Восьмеричной системой счисления называется
позиционная система счисления с основанием 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
an–1an–2…a1a0 = an–1 8n–1+an–2 8n–2+…+a0 80
Пример: 10638 =1 83 +0 82+6 81+3 80=56310.
Для перевода целого восьмеричного числа в десятичную
систему счисления следует перейти к его развёрнутой
записи и вычислить значение получившегося выражения.
Шестнадцатеричная
система счисления
Основание: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
3АF16 =3 162+10 161+15 160 =768+160+15=94310.
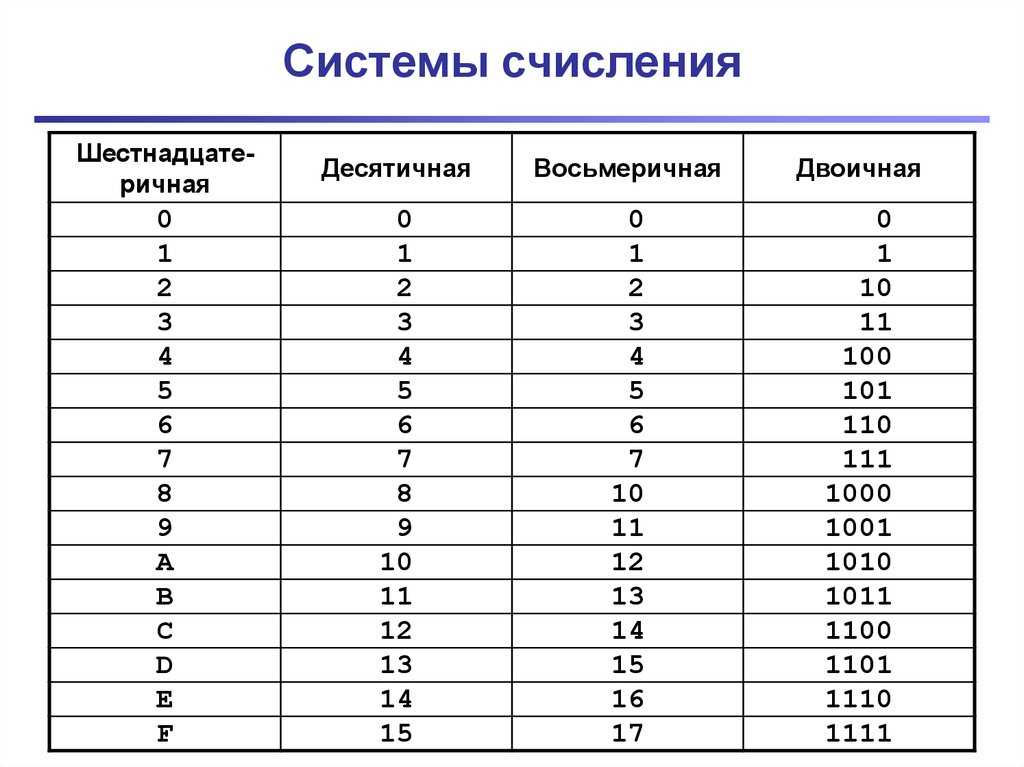
Таблица соответствия 10-х, 2-х, 8-х и 16-х чисел от 0 до 16
Десятичная
система
Двоичная
система

Восьмеричная
система
Шестнадцатеричная
система
0
0
0
0
1
1
1
1
2
10
2
2
3
11
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
111
7
7
8
1000
10
8
9
1001
11
9
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
16
10000
20
10
17
10001
21
11
18
10010
22
12
Задания для выполнения на уроке
Самостоятельно выполнить задания
Домашнее задание

English     Русский Правила

Восьмеричная и шестнадцатеричные системы счисления.

Компьютерные системы счисления. Правило перевода целых десятичных чисел

Похожие презентации:

Пиксельная картинка

Информационная безопасность. Методы защиты информации

Электронная цифровая подпись (ЭЦП)

Этапы доказательной медицины в работе с Pico. Первый этап

История развития компьютерной техники

От печатной книги до интернет-книги

Краткая инструкция по CIS – 10 шагов

Информационные технологии в медицине

Информационные войны

Моя будущая профессия. Программист

Восьмеричная и
шестнадцатеричные системы
счисления. Компьютерные системы
счисления.
Правило перевода целых
десятичных чисел в систему
счисления с основанием q.

Цели урока:
образовательные – выяснить, почему именно двоичная
система счисления используется в компьютере, показать
связь между двоичной, восьмеричной и
шестнадцатеричной системами счисления;
сформировать знания и умения перевода небольших
десятичных и двоичных чисел в восьмеричную и
шестнадцатеричную системы счисления.
развивающие – умение анализировать любую
позиционную систему счисления как знаковую систему;
воспитательные – понимание роли фундаментальных
знаний как основы современных информационных
технологий.
Задачи:
1) рассмотрение восьмеричной системы счисления как
знаковой системы;
2) рассмотрение правила перевода целых десятичных
чисел в восьмеричную систему счисления
3) рассмотрение шестнадцатеричной системы
счисления как знаковой системы;
4) рассмотрение правила перевода целых десятичных
чисел в шестнадцатеричную систему счисления;
5) рассмотрение правила перевода двоичных чисел в
шестнадцатеричную и восьмеричную системы
счисления;
6) характеристика двоичной, восьмеричной и
шестнадцатеричной систем счисления с точки зрения их
использования в компьютерной технике.
Восьмеричная система
счисления
Восьмеричной системой счисления называется
позиционная система счисления с основанием 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
an–1an–2…a1a0 = an–1 8n–1+an–2 8n–2+…+a0 80
Пример: 10638 =1 83 +0 82+6 81+3 80=56310.
Для перевода целого восьмеричного числа в десятичную
систему счисления следует перейти к его развёрнутой
записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную
систему счисления следует последовательно выполнять
деление данного числа и получаемых целых частных на 8 до
тех пор, пока не получим частное, равное нулю.
Шестнадцатеричная
система счисления
Основание: q = 16.

Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
3АF16 =3 162+10 161+15 160 =768+160+15=94310.
Переведём десятичное число 154 в шестнадцатеричную
систему счисления:
154 16
-144
9
16
10
(А)
9
0
15410 = 9А16
Правило перевода целых десятичных чисел
в систему счисления с основанием q
1) последовательно выполнять деление данного числа и
получаемых целых частных на основание новой системы
счисления до тех пор, пока не получим частное, равное нулю;
2) полученные остатки, являющиеся цифрами числа в
новой системе счисления, привести в соответствие с
алфавитом новой системы счисления;
3) составить число в новой системе счисления, записывая
его, начиная с последнего полученного остатка.
Цифровые весы
Таблица соответствия 10-х, 2-х, 8-х и 16-х чисел от 1 до 16
Десятичная
система
Двоичная
система
Восьмеричная
система
Шестнадцатеричная
система
1
1
1
1
2
10
2
2
3
11
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
111
7
7
8
1000
10
8
9
1001
11
9
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
16
10000
20
10
17
10001
21
11
18
10010
22
12
Двоичная арифметика
Арифметика двоичной системы счисления основывается
на использовании следующих таблиц сложения и
умножения:
+
0
1
0
1
0
0
1
0
0
0
1
1
10
1
0
1
«Компьютерные» системы счисления
Двоичная система используется в компьютерной технике,
так как:
двоичные числа представляются в компьютере с
помощью простых технических элементов с двумя
устойчивыми состояниями;
представление информации посредством только двух
состояний надёжно и помехоустойчиво;
двоичная арифметика наиболее проста;
существует математический аппарат, обеспечивающий
логические преобразования двоичных данных.
Двоичный код удобен для компьютера.
Человеку неудобно пользоваться длинными и
однородными
кодами.
Специалисты
заменяют
двоичные коды на величины в восьмеричной или
шестнадцатеричной системах счисления.

English     Русский Правила

типов систем номера компьютеров: двоичный и десятичный десятичный цвет

под редакцией TheGuyLoveny, Jen Moreau, Sarmal, SharingKnowledge

9 Части:

Бинарные номера

‘Десятичные номера

Hexadecimal Числа

БИАРИАНСКИЕ ДАМЕНИ 9000 2

2

СПОРТА.

Двоичное вычитание

Эта статья является частью серии статей об организации компьютера и языке ассемблера (COAL). Прочитайте полную серию здесь

Ссылка на эту статью

…Подробнее

Содержание

• 1 Двоичные числа
• 2 ‘ Десятичные числа
• 3 Шестнадцатеричные числа
• 4 Двоичное сложение
• 5 Дополнение до 2
• 6 Двоичное вычитание
• 7 Эта статья является частью серии статей о Компьютерная организация и язык ассемблера (COAL) . Полную серию читайте здесь
• 8 Ссылка на эту статью
• 9 комментариев

Двоичные числа

Двоичные числа имеют базовое число, состоящее из единиц или нулей. Компьютеры сильно ограничены двоичными цифрами или битами. Память также представлена ​​в битах, например, КБ, МБ, ГБ, ТБ, ПБ. Интересно, что компьютеры имеют только два состояния: ВКЛ и ВЫКЛ. Эти состояния представлены цифрами 1 (ВКЛ) и 0 (ВЫКЛ). Когда число передается из ячейки памяти в другую, скажем, например, a = 4, десятичное число 1 присваивается переменной a. Это десятичное число преобразуется в биты : (0100)2 . CPU сигнализирует о передаче памяти. В этом случае перейти в память, где находится переменная a . 0100 бит присваивается переменной a.

Было ли это полезно? Да | Нет| Мне нужна помощь

Ну, это было легко, но реальный вопрос в том, как компьютер узнает, что такое 1 и 0? Тот факт, что компьютер является электронным устройством, когда возникает мощность или электричество, представлен. Отсутствие электрического тока означает 0 (ВЫКЛ.). При назначении (0100) «a» должно быть (OFF ON OFF OFF).

Было ли это полезно? Да | Нет| мне нужна помощь

‘

Десятичные числа

Мы используем десятичные числа повсюду в нашей повседневной жизни. Цифры от 0 до 9 — это десятичные числа, также известные как десятеричные. Люди работают с десятичными числами, а компьютеры — нет. Как объяснялось выше, компьютеры работают только с двоичными числами. Десятичные числа преобразуются в двоичные числа для хранения их на компьютерах. Всякий раз, когда они отображаются на экране, они преобразуются из двоичных в десятичные числа.

Было ли это полезно? Да | Нет| мне нужна помощь

Шестнадцатеричные числа

Шестнадцатеричные числа — это числа с основанием 16 или шестнадцатеричные. Они чаще всего используются программистами. Он имеет 0-9 цифр, и оттуда он представлен как A для 10, B для 11 и так далее до F для 15.

Было ли это полезно? Да | Нет| Мне нужна помощь

Вот таблица преобразования шестнадцатеричных чисел в двоичные:

Двоичное сложение

Двоичное сложение довольно просто. Два двоичных числа складываются побитно.

• 1 + 1 = 0, 1 заимствуется на следующий бит.
• 0 + 1 = 1
• 1 + 0 = 1
• 0 + 0 = 0

Пример 1: Добавьте (110 110)2 и (1110001)2

Результат : (1101111)2

Дополнение до 2

Дополнение до 2 используется для представления отрицательных двоичных чисел в памяти компьютера. Положительные числа представляются как есть, а отрицательные числа представляются с использованием дополнения до 2. Дополнение до 2 использует дополнение до 1.

Было ли это полезно? Да | Нет| Мне нужна помощь

2 Дополнение работает: Примените дополнение 1. Добавьте 1 бит к битам. Теперь дополнение до 1 — это не что иное, как инвертирование битов, то есть от 1 до 0 и наоборот.

Например: Представьте (1101111)2 в дополнении до 2.

• Шаг 1: Инвертировать все биты (дополнение до 1).

(1101111)2 >>>>> (0010000)2

• Шаг 2: Добавьте 1 бит к битам.

Дополнение до 2 (1101111)2 равно (0010001)2

Двоичное вычитание

Двоичное вычитание немного отличается в битах. Шаги в двоичном вычитании:

Шаг 1: преобразовать биты секунды в дополнение до 2. Шаг 2: Добавьте два бита. Шаг 3: Отбросить лишний бит из результата (если он есть).

Пример 1:

Вычесть (10101)2 и (01110)2

• Шаг 1: Возьмите дополнение до 2 от 2-го значения.

Инвертировать все биты и добавить к ним 1 бит.

01110 >>>>>>>>> 10001

(10001)2 + (00001)2 = (10010)2

• Шаг 2 : Добавьте оба бита.

Результат: (00111)2

Пример 2. Выполнение двоичного вычитания 010101 и 101010

• Шаг 1: Применение дополнения до 2 ко вторым битам.

Инвертировать все биты : (101010) >>>>>>> (010101)

Теперь добавьте к результату 1 бит : (010101) + (000001) = (010110)

• Шаг 2 : Добавьте оба бита.

(010101)2 + (010110)2

Не было лишнего бита для отбрасывания, поэтому Результат: (101011)2

Эта статья является частью серии статей о

Компьютерная организация и язык ассемблера (COAL) . Полную серию читайте здесь

1) Компьютерная организация и язык ассемблера (COAL)

2) Системы счисления

3) Обзор иерархии компьютерных языков

Ссылка на эту статью

Если вам нужно сослаться на эту статью в своей работе, вы можете скопировать и вставить следующее в зависимости от требуемого формата:

АПА (Американская психологическая ассоциация)
Типы компьютерных систем счисления: двоичная и десятичная. (2017). В ScienceAid . Получено 10 февраля 2023 г. с https://scienceaid.net/Number_Systems 9.0003

MLA (Ассоциация современного языка) «Типы компьютерных систем счисления: двоичные и десятичные». ScienceAid , scienceaid.net/Number_Systems Дата обращения 10 февраля 2023 г.

Чикаго/Турабиан ScienceAid.net. «Типы компьютерных систем счисления: двоичные и десятичные». По состоянию на 10 февраля 2023 г. https://scienceaid.net/Number_Systems.

Комментарии

Категории : Организация компьютера и язык ассемблера

Недавние правки: SarMal, Jen Moreau, TheGuyLoveNY

Системы счисления | 4 основных типа систем счисления (примеры)

Мы, люди, используем слова, числа и символы для общения друг с другом. Однако компьютеры не могут понять этот язык. Следовательно, данные преобразуются в электронный сигнал, когда мы получаем данные. Каждый импульс известен как код, и ASCII переводит код в числовой формат. Он создает числовое значение, состоящее из цифр для каждой цифры, символа и символа, понятных системе. Числовое значение цифры в числе можно указать с помощью Число, Положение цифры в числе, Основание системы. Поэтому, чтобы понимать компьютерный язык или общаться с системой, нужно знать системы счисления.

Типы систем счисления

Системы счисления в компьютерах следующие:

1. Двоичная система счисления

Двоичная система использует только две цифры «0» и «1», следовательно, основание равно 2. Таким образом, она также известна как система счисления с основанием 2.
В этой системе есть два типа электронных импульсов. Если электронный импульс отсутствует, цифра представлена ​​«0», а если электронный импульс присутствует, то это 1 ′. Одна двоичная цифра — это бит. Последовательность из четырех битов (1001) является полубайтом, а последовательность из восемь бит (11001010) называется байтом. Двоичный представляет собой определенную степень основания (2) системы счисления.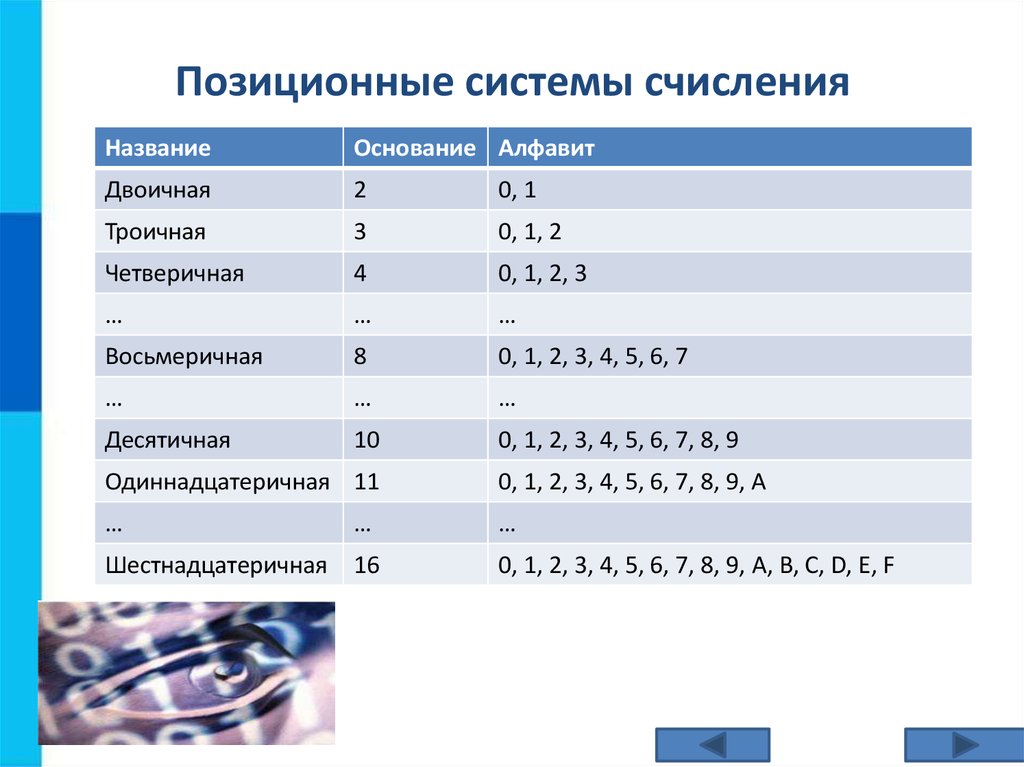 Например, 2 ₀ . Последняя позиция в двоичном числе представляет степень x основания (2). Пример, 2 _x , где x представляет последнюю позицию -1.

Пример

Здесь мы увидим пример расчета десятичного эквивалента двоичного числа
Двоичное число: 11001 ₂

11001 ₂ можно записать как 11001
Шаг 1: ((1 x 24) + (1 x 23) + (0 x 22) + (0 x 21) + (1 x 20)) ₁₀
Шаг 2 : (16 + 8 + 0 + 0 + 2) ₁₀
Шаг 3: 2610

2. Восьмеричная система счисления

Восьмеричная система использует восемь цифр 0, 1, 2, 3, 4, 5, 6 , 7, следовательно, основание равно 8. Каждая позиция в восьмеричном числе указывает на нулевую степень основания (8). Поэтому она также известна как система счисления с основанием 8. Например. 8 ₀ . Последняя позиция в восьмеричном числе представляет степень x основания (8). Например, 8x, где x представляет последнюю позицию -1.

Пример

Здесь мы увидим пример того, как вычислить десятичный эквивалент восьмиугольника
Октальный номер: 120718

12071 ₈ может быть написано как 12071

Шаг 1: (1 x 844) (1 x 844). + (2 x 83) + (0 x 82) + (7 x 81) + (1 x 80)) ₁₀

Шаг 2: (4096 + 1024 + 0 + 56 + 1) ₁₀

Шаг 3: 5177

3. Десятичная система счисления

Десятичная система использует восемь цифр 0, 1, 2, 3, 4, 5, 6, 7, 8,9следовательно, основание равно 10. В этой системе счисления 9 является самым высоким цифровым значением, тогда как 0 является самым низким цифровым значением. Положение каждой цифры в десятичном числе указывает на определенную степень основания (10) системы. В повседневной жизни мы используем десятичную систему счисления. Десятичная система счисления способна указывать любое числовое значение.

Пример

Здесь мы увидим пример расчета десятичного эквивалента десятичного числа
Десятичное число: 1237 ₁₀

1237 ₁₀ можно записать как 1237

Шаг 1: (1 x 103)+ (2 x 102)+ (3 x 101)+ (7 x 100) ₁₀

9003 900 (1 x 1000)+ (2 x 100)+ (3 x 10)+ (7 x 1) ₁₀

Шаг 3: (1000 + 200 + 30 + 7) ₁₀

82 Шаг 4: 1237

4.

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления использует 10 цифр и 6 букв, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D , E, F. Следовательно, его основание равно 16. Каждая позиция в восьмеричном числе указывает на нулевую степень основания (8). Таким образом, она также известна как система счисления с основанием 16, а также буквенно-цифровая система счисления, потому что она использует как числовые цифры, так и алфавиты.
Буквы представляют числа, начинающиеся с 10. A = 10. B = 11, C = 12, D = 13, E = 14, F = 15. Каждая позиция в шестнадцатеричном числе указывает на нулевую степень основания (16). Последняя позиция в шестнадцатеричном числе представляет степень x основания (16). Пример 16x, где x представляет собой последнюю позицию -1.

Пример

Здесь мы увидим пример расчета десятичного эквивалента шестнадцатеричного числа
Шестнадцатеричное число: 19FDA ₁₆

9 ₁₀

Шаг 2: ((1 x 164) + (9 x 163) + (15 x 162) + (13 x 161) + (10 x 160)) ₁₀

Шаг 3: ( 65536+ 36864 + 3840 + 208 + 10) ₁₀

Шаг 4: 106458

Заключение

В этой статье мы рассмотрели систему счисления, которая используется для обмена данными с компьютером преобразования.