Как объяснить двоичную систему счисления детям

Как компьютер считает

Когда в древности люди только изобретали счёт, они, как сейчас маленькие дети, считали на пальцах. Пальцев на руках – десять, поэтому и система счисления у нас – десятичная. Однако наша система счёта компьютеру не слишком-то понятна: ему ближе двоичная. У компьютера нет десяти пальцев, но, с другой стороны, и двух тоже нет. Откуда тогда взялась двоичная система, что это за ноль и единица, которыми думает компьютер? И как из них получаются обычные, понятные цифры?

Для того чтобы в общих чертах понять, как думает компьютер, начнём с самого начала. Компьютер, по сути, – это много всякой электроники, собранной вместе в правильном порядке. А электроника (до того, как к ней добавили программу) понимает только одно: включена она или выключена, есть сигнал или нет сигнала.

Обычно «есть сигнал» обозначают единицей, а «нет сигнала» – нулём: отсюда и выражение, что «компьютер говорит на языке нулей и единиц».

Этот язык нулей и единиц называют ещё двоичной системой счисления – потому что в ней всего две цифры. Наша привычная система счисления – десятичная, в ней десять цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Но есть и множество других – восьмеричная, пятеричная, одиннадцатиричная и какая угодно ещё.

У нас с вами нет цифры «десять», правда? Число 10 состоит из двух цифр – 1 и 0.

Точно так же в пятеричной системе счисления не будет цифры «5», только 0, 1, 2, 3 и 4.

Посчитаем в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30, 31, 32, 33, 34, 40, 41, 42, 43, 44, 100 (!!!), 101, 102 и так далее. Можно сказать, что как система счисления называется, такой цифры в ней и нет. В нашей десятичной нет цифры «10», в пятеричной нет цифры «5» (и всех, которые после неё), в восьмеричной – «8» и так далее.

А в шестнадцатиричной «16», например, есть! Поэтому нам шестнадцатиричную систему понять ещё сложнее. Давайте посчитаем в шестнадцатиричной:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21, 22…97, 98, 99, 9A, 9B, 9C, 9D, 9E, 9F, A0, A1, A2… F7, F8, F9, FA, FB, FC, FD, FE, FF, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 10A, 10B, 10C и так далее.

Двоичная система счисления, впрочем, тоже выглядит странновато для непривычного взгляда:

0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001…

Вот примерно такими числами и думает компьютер где-то внутри себя. Но человеку такими числами думать совершенно неудобно, поэтому мы преобразуем числа из двоичной в более удобную систему счисления.

В компьютерных программах часто используют восьмеричную и шестнадцатиричную системы: компьютеру легко их понять (потому что 8=2*2*2, 16=2*2*2*2, а с двоичной системой компьютер знаком изначально), а для людей это удобно, потому что поближе к привычной десятичной.

Как переводить числа из одной системы счисления в другую

Чтобы понять принцип, будем, как мы с вами любим, разбираться на конфетах.

И на конфетах мы с вами будем переводить число 33 в восьмеричную систему счисления. Мы решим, что единицы – это сами конфеты, а десятки – это коробки, в каждой из которых лежит по десять конфет. Вот и получится, что 33 – это 3 коробки по 10 конфет и ещё 3 конфеты где-то сбоку.

Но мы переводим наше конфетное богатство в восьмеричную систему счисления, а это значит, что нам надо вытряхнуть все конфеты из коробочек по 10, сложить в коробочки по 8 и посмотреть, что из этого выйдет.

Из 33 получится 4 полных восьмеричных коробочки и 1 конфета останется сама по себе, так как 33/8=4 (ост. 1). То есть 33=8*4+1 – так в восьмеричной системе счисления получается число 41.

33 в десятичной – это 41 в восьмеричной. Это одно и то же число, просто разложенное по разным коробочкам, переведённое в разное основание.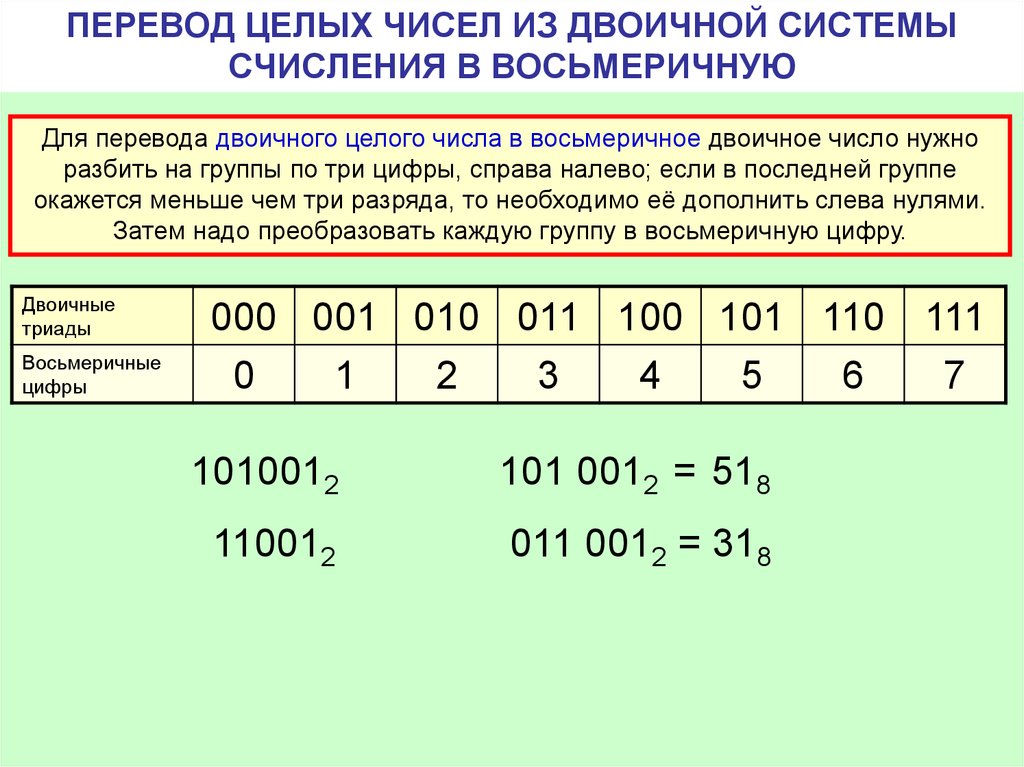

Количество конфет не поменялось, мы просто считали их по-разному!

Двоичная система, как мы уже выяснили, более странная и непривычная для человеческого взгляда. Давайте попробуем перевести 33 в двоичную – получится аж 16 коробочек по 2! И что же делать? Писать 16 как-то странно, помня о том, что в двоичной системе есть только ноль и единица, а шестёрки, которая нам нужна для шестнадцати, совершенно точно нет!

Посмотрим на нашу десятичную систему. В ней мы считаем десятки – 10, 20, 30, 40, 50, 60, 70, 80, 90 – а когда у нас набирается десять десятков, мы достаём большую коробку – 100.

У нас 100 – это 10*10, 1000 – 10*10*10, 10 000 – 10*10*10*10 и так далее. Для других систем счисления это работает точно так же! В восьмеричной системе 100=8*8, 1000=8*8*8; в двоичной 100=2*2, а 1000=2*2*2; а в шестнадцатиричной (есть и такая, помните?) 100=16*16, 1000=16*16*16.

Здесь нам пригодятся степени. Если вы их ещё не проходили в школе, не пугайтесь, степени – это очень просто. Число в степени – это число, сколько-то раз умноженное на само себя. То есть 5³=5*5*5 (пять в третьей степени – это пять, три раза умноженная сама на себя: 5*5*5), или 8

5=8*8*8*8*8 (восемь в пятой степени – это восемь, пять раз умноженная на саму себя: 8*8*8*8*8).

Если мы вспомним про наши 10 000=10*10*10*10 в десятичной и 1000=8*8*8 в восьмеричной, то можно легко заметить, что сколько нулей, столько раз и умножаем на само себя. Другими словами, количество символов в числе минус один – это степень, в которую надо возвести основание. В числе 1000 у нас четыре символа, значит умножать надо 4–1, то есть 3 раза. Если основание 10, то тысяча – это 10, три раза умноженная сама на себя: 10*10*10. Если основание 8, то тысяча – это 8, три раза умноженная сама на себя: 8*8*8.

Обо всём этом мы заговорили, пытаясь перевести 33 в двоичную систему. Просто так поделить это число на коробочки по 2 оказалось затруднительным. Но если вспомнить про наши сотни-тысячи, можно задуматься: а ведь в двоичной 100=2*2, 1000=2*2*2, 10 000=2*2*2*2 и так далее.

Для перевода из десятичной системы в двоичную удобно помнить степени двойки. Даже можно сказать, что без этой хитрости со степенями мы устанем, умаемся и немножко сойдем с ума. А степени двойки выглядят как-то так:

Теперь, глядя на табличку, мы видим, что 33=2⁵+1, то есть 33=2*2*2*2*2+1. Вспоминаем – сколько раз умножаем, столько будет нулей – то есть наше 2*2*2*2*2 в двоичной системе будет 100000. Не забудем оставшуюся в стороне единичку, и получится, что 33 в десятичной – это 100001 в двоичной. Правильно и красиво это записывают так:

33₁₀=100001₂

Давайте (чтобы совсем хорошо понять) переведём в двоичную систему число 15.

1. В первую очередь – смотрим в табличку.

а) Какое самое близкое к 15 число в ней? Нет, 16 не подходит, оно больше, а нам нужно самое близкое, которое меньше.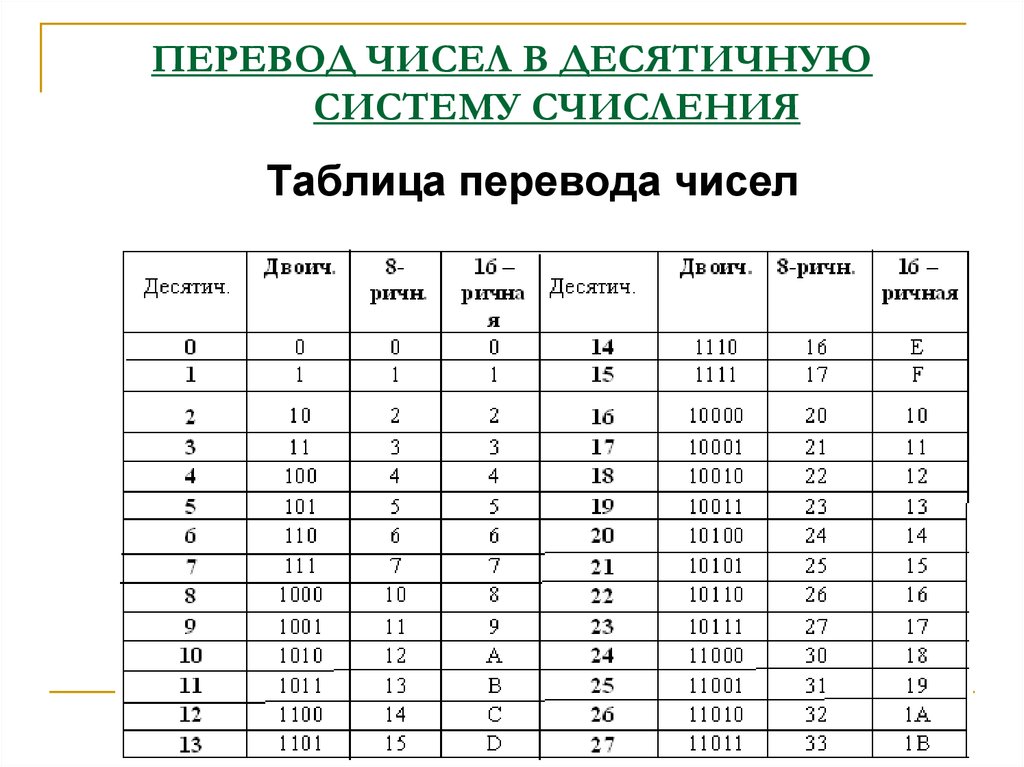 Получается, что это 8, то есть 2³

, то есть 2*2*2.

б) Восемь конфет из 15 разобрали, осталось – 15-8 – семь. Какое ближайшее число из таблички? Нет, восемь снова не подойдет, см. выше. Подойдет четыре, то есть 2², то есть 2*2.

в) Четыре из семи конфет разобрали, осталось – 7-4 – три. Из таблички понимаем, что самое близкое число – 2, то есть 2¹, то есть просто 2.

г) Три минус два – осталась 1 конфета, тут уже табличка не понадобится. В таблички такого рода можно не смотреть, когда ваш остаток меньше основания, а наша единица точно меньше двойки.

2. Собираем всё найденное в табличке вместе: 15=2³ + 2² + 2¹ + 1, оно же: 15=2*2*2 + 2*2 + 2 + 1.
3. В двоичной системе 2*2*2=1000, 2*2=100, 2=10, помните? И у нас получается 1000+100+10+1, то есть 1111.
4. Итак,

15₁₀=1111₂

Когда просто смотришь на все эти шаги, кажется, что это просто свалка из Кучи Разных Странно Написанных Цифр. И запутаться во всём этом в первый раз – нормально. И во второй, и в третий. Просто попробуйте сделать это ещё и ещё раз – по шагам, как написано выше, и всё получится.

И наоборот это тоже работает! Например, число 11010101₂ – как из него сделать понятное десятичное? Точно так же, при помощи таблички. Пойдем с конца:

1*2⁰+0*2¹+1*2²+0*2³+1*2⁴+0*2⁵+1*2⁶+1*2⁷=

1*1+0*2+1*4+0*8+1*16+0*32+1*64+1*128=

1+0+4+0+16+0+64+128=213

То есть,

11010101₂ = 213₁₀

Вот примерно так компьютер понимает привычные нам числа.

Когда смотришь на это в первый раз, кажется, что это, во-первых, совершенно непостижимо, а, во-вторых, вообще не сработает. Поэтому сейчас мы с вами сделаем немножко математической магии, чтобы убедиться, что системы счисления – это такая же реальная вещь, как, например, задача «раздать пятерым детям пятнадцать печенек поровну».

Итак, возьмем пример 15+6 и решим его в разных системах счисления. Понятно, что в нашей, десятичной, получится 21. А что выйдет, например, в восьмеричной?

Переводим 15 в восьмеричную систему счисления. Первый шаг у нас при переводе в другую систему – посмотреть в табличку степеней. 8² – это уже 64, и в 15 оно точно уже никак не влезет, поэтому берем 8¹ – то есть просто 8. 15–8=7, оно меньше нашего основания 8, поэтому с ним мы ничего не делаем.

Итак, получилось, что 15=8¹+7.

В восьмеричной системе логика точно такая же, как, например, в двоичной: 8³ – это 1000, 8² – это 100, 8¹ – это 10. Получилось, что:

15₁₀=17₈

Напомню, наш пример был 15+6. 15 мы перевели в восьмеричную систему, как же перевести 6? Она меньше 8, нашего основания, поэтому ответ – оставить как есть. Наш пример сейчас выглядит так:

15₁₀+6₁₀=17₈+6₈

Теперь мы будем складывать в восьмеричной системе счисления. Как это делается? Так же, как и в десятичной, но надо помнить, что десяток в восьмеричной системе – это восемь, а не десять, и что 8 и 9 в ней не существует.

Когда мы считаем в десятичной системе, по сути, мы делаем так:

15+6=15+5+1=20+1=21

Попробуем проделать тот же фокус в восьмеричной системе:

17₈+6₈=17₈+1₈+5₈=20₈+5₈=25₈

Почему 17+1? Потому что 7+1=8, а 8 – это наш десяток! В восьмеричной системе 7+1=10, а значит, 17+1=20. Если на этом месте ваш мозг начинает бить тревогу и рассказывать, что здесь что-то не так, вернитесь в начало статьи, где мы с вами считали в разных системах счисления.

Теперь наш пример выглядит как

15₁₀+6₁₀=17₈+6₈=25₈

Переведем 25₈ обратно в нашу систему счисления. В десятичной мы бы, увидев число 25, могли сказать, что в нём две десятки и пять единиц. В восьмеричной, как вы, наверное, уже догадались, число 25₈  – это две восьмерки и пять единиц. То есть 25₈=2*8+5=21₁₀.

Итак, наш пример целиком:

15₁₀+6₁₀=17₈+6₈=25₈=21₁₀

Получилось точно такое же 21, какое вышло у нас в самом начале, когда мы посчитали 15+6 привычным нам способом в десятичной системе.

Арифметические правила не меняются от того, что мы выбрали другую систему счисления. Поэтому и компьютер, переводя всё в нули и единицы, которые для нас выглядят непонятно и бессмысленно, не теряет при этом информацию, которую мы ему дали, и может, посчитав в удобной ему форме, выдать результат, переведя его обратно в привычный нам вид.

Кодирование информации в информатике

Мы обсуждили, как компьютер понимает числа. Они получаются из других чисел – двоичных, которые компьютер понимает. А как быть с буквами? Картинками? Играми?

Какие вообще бывают виды кодирования информации в науке обращения с компьютером – информатике?

Тут надо на секунду задуматься, как общаются сами люди. Мы используем слова, из слов делаем предложения, из предложений – текст, рассказ, диалог. Но чтобы сделать слово, мы используем буквы, которых всего-навсего 33 штуки!

Просто представьте: все книги, которые вы когда-либо читали – это лишь разные сочетания одних и тех же 33 букв.

Но мы делаем из букв слова по определённым правилам, а словами обозначаем предметы, свойства, действия, эмоции, фантазии. Буквы – это кубики, из которых мы строим слова. А слова – это код, которым мы обозначаем всё, что встречается в нашей жизни, чтобы потом об этом кому-нибудь рассказать.

Точно так же происходит и с компьютером. При помощи цифр мы объясняем компьютеру, что у него есть монитор, мышка, клавиатура и другие детали, рассказываем, как с ними обращаться и как реагировать, когда что-то делаем мы.

Но сейчас мы с вами поговорим о более конкретных и практических кодах. И начнём с того, как компьютер понимает буквы.

Раз компьютер знает только цифры, значит и буквы он видит через цифры. Это, примерно, как если бы мы букву А записали как 1, Б как 2, В как 3, и так далее.

Примерно такие таблицы (только больше и сложнее) компьютер и использует, чтобы понимать буквы.

Представьте себе: кто-то записал анекдот на компьютер и прислал вам. Вы открываете документ, а там ничего непонятно. Примерно вот так:

 Р§РµР”овек сейчас СѓРІРёРґРёС‚ Дишь то, что ожидает увидеть.

Это компьютер ошибся с кодировкой. Что такое кодирование в информатике? Так обычно называют присвоение каждому символу (букве, знакам препинания и так далее) определённого кода согласно специальной табличке. Кодировка – это способ, которым зашифровывает и расшифровывает буквы компьютер, можно сказать, табличка, которую он выбирает. Табличек у него на такой случай много, и надо знать, по какой расшифровывать, иначе получится белиберда.

Давайте немножко побудем компьютером. У нас с вами будет две таблички: в одной сначала будет идти алфавит, а потом знаки препинания, в другой – наоборот.

Кодировочная Таблица 1:

Кодировочная Таблица 2:

Зашифруем с вами фразу «Пароль – три зелёных свистка». Зашифровывать мы будем по первой таблице, а расшифровывать – по второй.

Первая буква – П. В первой таблице у неё номер 17. Дальше буква А. У неё номер 1. Продолжите сами и проверьте себя, правильно ли у вас получится!

А получилась в итоге вот такая строчка:

17-1-18-16-13-30 38 20-18-10 9-6-13-6-15-29-23 19-3-10-19-20-12-1

Теперь попробуем расшифровать её при помощи второй таблицы.

Во второй таблице цифра 17 у буквы И, цифра 1 у точки и так далее (расшифруйте сами).

У нас получилось:

И.йзех э лйв(жфо к?вклд

Итак, результат, во-первых, непонятный, а, во-вторых, совершенно не похож на ту фразу, которую мы хотели передать. И получилось это из-за того, что таблица для шифровки и таблица для дешифровки не совпали.

Точно так же с фразой и с текстом вроде «Р§РµР”РѕРІРµРє сейчас» – так получается, когда компьютер пытается расшифровать текст не по той таблице, по которой он был зашифрован. Ещё в таких случаях говорят, что «в тексте неправильная кодировка». Сам текст от этого не испортился, просто программе где-нибудь в настройках надо указать, какой кодировкой воспользоваться (обычно это utf8, или UNICODE, или как в этом случае Windows-1251).

Давным-давно, когда компьютеры были большими, а жёсткие диски в них –маленькими, придумали кодировку ASCII (читается как «аскИ»).

Это табличка, где зашифрованы буквы латинского алфавита (мы обычно привыкли о них думать, как об английских буквах), знаки препинания и некоторые служебные символы (например, символ, который обозначает, что надо продолжить с нового абзаца).

Когда в компьютерах придумывают что-то новое, однажды бывает очень важно, чтобы кто-то сказал: «А теперь ВОТ ЭТО мы все делаем одинаково». Например, весь вай-фай в мире работает примерно одинаково, поэтому почти любой телефон может подключиться почти к любой точке вай-фай.

Точно так же произошло и с кодировочной таблицей. Мы с вами раньше уже убедились, что она обязательно должна быть одинаковая у отправителя и получателя, и этой одинаковой таблицей стала ASCII аж в 1963 году.

Сначала всё было замечательно, но потом компьютеры стали становиться меньше и удобнее, ими стали пользоваться разные люди, в том числе не знающие английского. А русский, например, алфавит (который также называют «кириллица») в ASCII не входит. Как быть? Куда бежать? И в 1991 году был придуман UNICODE (читается как «Юникод» или «Уникод» – почти как «Универмаг», но не магазин).

Юникод может закодировать очень большое число символов из разных письменностей: китайские иероглифы, математические символы, буквы греческого алфавита, латиницы и кириллицы.

ASCII стала первой частью Юникода, и специальные договоренности в программах позволяют читать при помощи Юникода текст, который был закодирован в ASCII.

Когда вы сохраняете файл в том же «Блокноте», вы можете выбрать кодировку и при выборе заметить, что их гораздо больше, чем мы разобрали в статье.

В заключение давайте поговорим, где какая кодировка нужна.

Обычно выбором кодировки занимаются люди, работающие с компьютерами профессионально – при написании программ, настройки баз данных и т. п. Мы с вами не будем вникать во все тонкости, и рассмотрим этот вопрос в общих чертах:

– Windows-1251

Как видно из названия, это основная кодировка операционных систем семьи Windows. Когда вы точно знаете, что все компьютеры, которые будут работать с файлами, используют Windows – она отличный выбор. Если же нет, могут возникнуть проблемы с невидимыми символами. Потому что Windows-1251 их считает служебными, а многие другие кодировки решают, что это такие буквы непонятные, и в результате случается неразбериха.

– ASCII

Старая, но надёжная. Подойдёт, если ваш текст на английском, а компьютер, где надо открыть файл – очень, очень старый.

– UNICODE

Это рекомендуемая кодировка для всех систем! Если друг прислал вам файл, а у вас в нём кракозябры, попросите его пересохранить файл с кодировкой unicode, и, скорее всего, проблема будет решена.

– UTF-8

Вариант записи того же Юникода. Он специфический, и обычно используется программами при общении внутри себя самих (например, общение программы со своей базой данных).

Итак, кодированием текста в информатике обычно называют способ компьютера перевести текст в понятный ему вид по одной из общепринятых табличек. Если файл был сохранён в одной кодировке, а открыт в другой – обычно получается белиберда вместо текста.

Все компьютеры знают одни и те же кодировки, чтобы понимать файлы, сделанные другими компьютерами, но кодировки существуют разные – под разные цели. Лучше всего сохранять файлы в кодировке UNICODE –  так больше всего шансов, что у другого человека этот файл откроется.

Как можно увидеть, криптография – это не только наука про тайны и не только детская игра. У этой науки есть множество простых практических точек приложения, и если ребёнок знаком с её концепциями, то многое, что может испугать, сбить с толку и привести в отчаяние, для него будет просто задачей, к которой надо найти правильное решение.

Дневники чайника

Дневники чайника

Про цифры, числа и верёвки

Я сделал всё, чтобы статья была понятна и интересна всем читателям.

Но если для вас здесь всё ясно, как 2×2, — не обижайтесь.

Ведь не все же такими умными сразу родились. ;)

Итак, система счисления — это всего лишь письменный и устный способ представления чисел.

Про устную составляющую мы говорить вообще не будем, займёмся правилами записи чисел. То есть главный предмет — цифры и отношения между ними.

Хорошо бы ещё понять, что такое число, номер, цифра, количество…

Начнём с самого простого.

Цифра

Одна цифра есть один условный письменный знак, который представляет число.

«0,1,2,3,4,5,6,7,8,9» — это цифры, принятые для нашей системы счисления.

«A,B,C,D,E,F» — это цифры, принятые в шестнадцатиричной системе для представления чисел 10d,11d,12d,13d,14d,15d.

Номер

Ещё совсем недавно большинство людей не имели представления об отвлечённых числах. Посмотрите, даже Даль в своём словаре толкует номер как число, и это отражает язык бытовых понятий, но сейчас взглянем на вопрос по-другому.

Мы привыкли думать, что номер выдаётся конкретному объекту, например: маршрут автобуса, место в театре или даже телефон обладают номером. То есть номер не существует вне связи с конкретным объектом, а это очень важное отличие от современного понятия числа.

Номер — это именование объекта в числовом виде.

Количество

Вот тут я на 100% согласен с Далем. Мы говорим: количество и качество чего-либо. Таким образом, говоря о количестве, мы измеряем свойство объекта. Выразить количество (веса, объёма, штук…) можно только через число, но не всякое число можно использовать для выражения количества. Простой пример: +20 градусов и -20 градусов есть одинаковое количество от нуля, но разные числа.

А от номера количество отличается тем, что оно есть у любого объекта, это обязательное свойство предмета.

Число

Необъяснимое понятие.

Человечество только начало постигать эту загадочную субстанцию. Всё, чему мы научились, — выражать числа через отношения к единице или другим числам. С точки зрения науки нельзя определять понятие через само себя. А других способов я не знаю.

Чтобы не сильно мудрить, сразу ограничим разговор целыми числами, и по большей части речь пойдёт о натуральных (положительных целых) числах. Однако нужно сознавать, что бывают и более сложные виды чисел: рациональные, иррациональные, мнимые и даже те, которые мы ещё никак не называем, потому что просто ничего о них не знаем.

Мне кажется, для простого объяснения хотя бы натуральных чисел будет полезно быстренько пройтись по цепочке развития от обезьяны до Битфрая (поверьте, цепочка не очень длинная =).

Счёт

Наш мозг имеет множество подходов к обработке чисел. Главным образом их можно разделить по таким свойствам:

дискретный счёт — выделение объектов в единицы или их части,

и чувственный счёт — восприятие изменений целиком.

Изначально для вычислений цифры были не нужны. Потому что никто даже не разделял предметы на единицы. Чтоб вы точно поняли, о чём я говорю, приведу пример:

\
 \
  \
   \
    \

Любой трезвый человек безошибочно определит, что эта «палка» расположена не вертикально (при наличии некоторой базы). Однако у нас нет транспортира. Как мы это делаем? Проводим цифровые вычисления? Или используем шаблон?

Нет, просто у каждого из нас есть свой хитрый компьютер для подобных целей. Результатом действий этого компьютера будет чувство разности — в данном случае чувственная разность между запомненной вертикалью (от видимой базовой линии) и положением этой «палки».

Большинство животных умеют выделять объекты, и они прекрасно чувствуют количество этих объектов. Научных доказательств у меня нет, но что-то подсказывает: некоторые животные всё-таки могут считать дискретно и даже передавать друг другу цифровую информацию (те же пчёлы).

Давайте предположим, как могли быть осознаны целые единицы и как возникли специальные знаки для их представления.

Как появились цифры

В одной умной книге (см. Историю математики, том I) написано, что первым шагом к цифровому счёту было установление «взаимно однозначного соответствия» между разными предметами.

Даже обезьяны могут разделить бананы среди детёнышей по штукам. Каждому малышу мама отдаёт один банан.

Таким образом, она неосознанно проводит «взаимно однозначное соответствие» между разными объектами (бананами и малышами).

Для того чтобы сделать самый элементарный выбор, желательно произвести осознанный прогноз. Счёт здесь просто необходим.

Нужно знать: сколько воды взять с собой в дорогу, сколько дней пути, сколько камней обработать для топоров… Так что совсем не удивительно, что через некоторое время появились существа, до которых дошло простейшее осознание постоянно повторяющегося вокруг них процесса.

Они специально начали выставлять предметы счёта друг перед другом, для того чтобы узнать, каких меньше.

Видимо, так и выглядел первый шаг к осознанию понятия числа.

Следующий шаг, очевидно, сделали люди. Они усовершенствовали этот метод.

«Колдуны», самые умные представители древних общин, выделили особые предметы для счёта.

Возможно, изначально это были камушки, возможно палочки, а может быть, и косточки врагов. Но со временем у большинства такими предметами стали части тела (ведь оно всегда с собой), в частности, пальцы.

Спустя некоторое время появился знак «I». Предположим, в виде зарубки на стволе дерева или угольной чёрточки на скале. Так числа обрели письменную форму.

Уже здесь можно говорить о принятии самой простой системы счисления.

Это система, основанная на сложении (аддитивная). Система с одним символом.

I    = 1
II   = 2
III  = 3
IIII = 4
...

Даже такой способ записи из одного символа (и счёт сложением) очень помог рассмотреть мир вокруг, а это позволило выжить и развиться.

Давайте рассмотрим эту систему по элементам.

Такая система счисления может представлять только целые положительные числа (натуральные).

Метод представления — сложение единственного символа в системе с другими такими же.

Отвлечённые числа

Параллельно с предметным счётом стали развиваться абстрактные категории.

Люди осознали, что число может быть не только предметным, то есть три стрелы, три собаки, три дня, но и отвлечённым — просто III.

По самым скромным подсчётам, от обезьяны с бананами до восприятия отвлечённых целых чисел прошло ~2,5 миллиона лет =).

Насколько мне известно, отвлечённые числа пришли к нам через геометрию, но об этом я писать не буду, хотя тема очень интересная. Почитайте сами в учебнике про то, как из условной записи геометрических задач началась алгебра.

Естественная потребность развития языка — называть всё, что видишь. Очень быстро каждая следующая единица обрела своё собственное имя. У разных народов этот процесс, видимо, происходил по-разному. Кто-то называл единицы как части тела (один — нос, два — глаза, или один — палец, два — кулак, три — локоть…), кто-то — как природные явления или предметы, а некоторые вперемешку. С развитием письменности стали возникать и соответствующие знаки (цифры).

Здесь, пожалуй, стоит посмотреть на римскую систему записи чисел.

I   II   III

IV  V    VI   VII   VIII

IX  X    XI   XII   XIII

XIV XV   XVI  XVII  XVIII
. ..

Что же мы видим?

Всё та же арифметика, натуральные числа.

Но теперь цифр много, и число формируется не только сложением, а ещё и вычитанием. В некотором роде прогресс.

Восприятие такого числа начинается не слева направо или наоборот, а с младшей цифры в числе.

Если она стоит слева от следующей по старшинству цифры, то её нужно отнимать, а если справа — то прибавлять.

Такая система даёт возможность относительно коротко записывать большие натуральные числа.

Однако здесь не хватает ещё одной мелочи, можно сказать, ничтожной мелочи, да нет, это даже не мелочь, это просто ничего — ноль.

0

Вы, наверное, слышали, что слово цифра — искажённый перевод древнего арабского слова со значением «пустое», так когда-то именовали ноль. Да и в русском языке слово цифра раньше означало именно ноль.

Как же люди могли додуматься использовать такую совершенно абстрактную категорию?

С одной стороны, при вычитании бОльшего числа из меньшего возникает странная субстанция, назовём её долг.

Она не давала покоя многим учёным, и не только им. Ведь ни один ростовщик никогда не смирится с тем, что долг считать нельзя.

C другой стороны — интерес к познанию мира.

На тот момент центром развития оказался Восток (главным образом, Индия и Китай). Заметьте, именно там люди особенно много думают о гармонии. Мудрецы всю свою жизнь ищут баланс, центр сил, точку равновесия. Найденные ответы выражаются самыми разными способами и один из них — математика.

Примерно в нулевом году (+-~300 лет) ноль-таки был обозначен известными нам цивилизациями.

«0» — made in China =)

Не удивляйтесь. Вполне возможно, запись числа ноль пришла из Китая.

Во всяком случае, насколько мне известно, самые древние записи нуля (маленькая точка) были найдены именно на территории тогдашней Китайской империи. Книги свидетельствуют, что китайцы сначала использовали пустую ячейку для представления числа ноль.

Хотя данный вопрос не так принципиален.

Намного интереснее, что можно сделать, зная о таком числе и имея подобную цифру?

Очень много. Ноль — самая могущественная сила во Вселенной, он может всё!

Ноль создаёт порядок в математике, и он же вносит в неё хаос… Впрочем, об этом можно рассуждать до бесконечности и даже дальше — до нуля :).

Применительно к нашей теме ноль позволил повсеместно использовать позиционную систему счисления.

Отдохните перед главными мыслями этой статьи.

Позиционные системы счисления

Теперь рекомендую долго и старательно медитировать в процессе чтения.

Тем, кто не поймёт вопроса, дальше идти некуда. =(

Представьте такую незамысловатую верёвку.

Верёвка наглядно демонстрирует нашу систему счёта.

Что здесь есть?

Во-первых — направление счёта. Очень важный фактор для наглядного представления.

Во-вторых — 10 узелков

Ну и, конечно, нельзя забывать про 10 отрезков.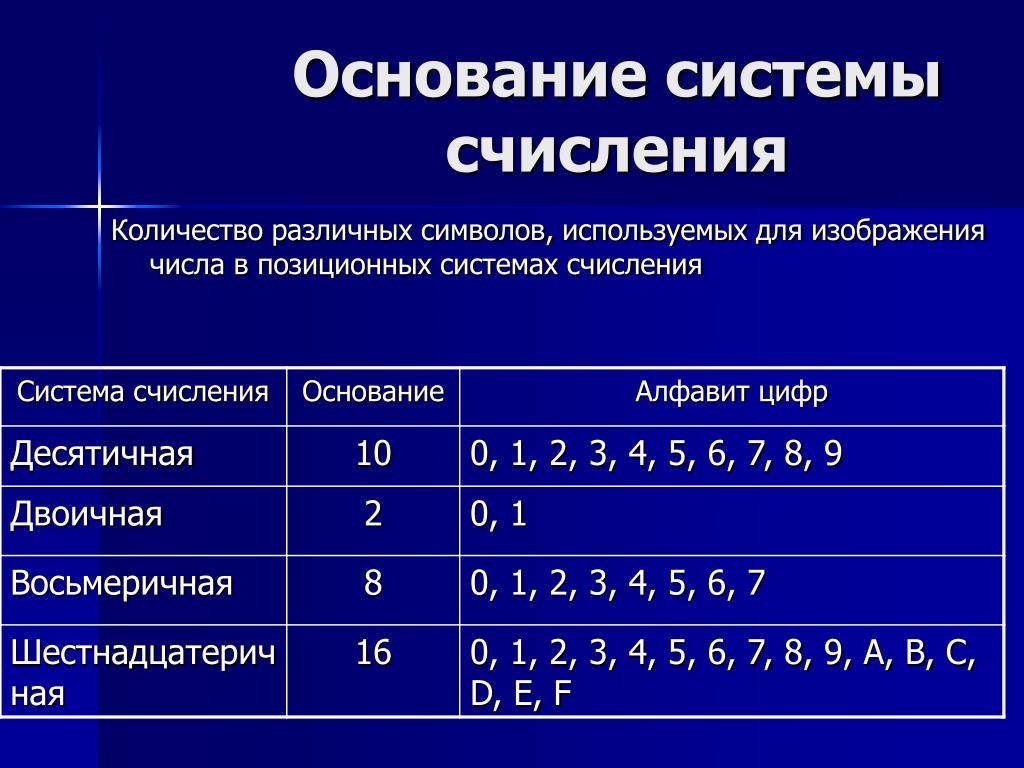

На рисунке выше пронумерованы отрезки.

Целью счёта мы определим именно отрезки.

Отрезки — предметы измерения.

Но что тогда будут символизировать узелки?

А вот что:

Ведь на нижнем узелке ещё нет отрезков.

Значит, туда мы поставим цифру 0.

А узел с цифрой 9 сообщает, что посчитано девять отрезков.

Таким образом, можно сказать:

узлы — «цифры»,

отрезки — «числа».

Вообразите, что мы измеряем этой верёвкой размер земельного участка, фундамент будущего дома, оконные проёмы и мелкую мебель внутри.

Верёвка должна быть длиннее участка, но ведь при десяти узелках на такой длиннющей верёвке небольшие предметы измерять не получится. Что же делать?

Можно измерять маленькие предметы частями одного отрезка между целыми узелками (дробями). Не самый удобный способ (я дроби вообще не очень люблю =), но довольно долго мы так и делали. И вот наконец-таки для удобства маленькие отрезки мы тоже обозначили более мелкими узелками. Задумайтесь над этим.

Есть и другой способ. Сразу завести маленькую верёвку для небольших предметов…

Если при измерении большой верёвкой остался неизмеренный кусок меньше целого отрезка, можно там приложить эту маленькую верёвку и домерить.

Короче говоря, решений очень много, но все они рано или поздно приведут к позиционной системе счисления.

Так же, как и счёт: горшками, бочками, телегами и любыми более крупными объектами, чем конечные предметы счёта.

Вот как можно представить позиционный принцип записи чисел через наши верёвки:

Маленькая верёвка ровно умещается в одном отрезке большой верёвки.

Люди сообразили, что удобнее, когда на всех верёвках равное количество узелков.

Каждая следующая верёвка в 10 раз больше предыдущей.

10*10=100, столько маленьких отрезков во второй верёвке.

Давайте попробуем записать цифрами результат подсчёта ширины будущей дороги.

Три отрезка большой верёвки и один отрезок маленькой.

Запишем это так же, как на рисунке. Каждая бОльшая верёвка будет слева (дело было на Востоке =):

Выходит 31.

Но, как всегда, мы решили сэкономить на дороге. Ну, пусть не будет этого маленького отрезка.

Вот тут и пригодится запись цифры ноль.

Три отрезка большой верёвки и нет отрезков на маленькой, получается = 30.

Это и называется позиционный метод записи чисел.

Позиция здесь — очередное место для цифры (слева).

Конечно, можно записывать числа таким же методом, не используя цифру 0, но всё равно в позиции, где нет отрезков, будет хотя бы пустое место. Например, сверху мы пишем номер позиции, а снизу её значение:

Номер позиции - 4321
Значение      - 4 3

Так я записал число 4030.

А можно записать, как в древности это делали китайцы:

В любом случае, экономия средств (речевых и письменных) — одна из важнейших сил развития языка. Ноль просто обязан был обзавестись собственным символом. А нам остаётся только радоваться, что это уже произошло.

Основные характеристики позиционных систем

Рассмотрим систему, получившуюся с верёвками.

Опять только целые числа, однако теперь к положительным (1,2,3…) прибавился ещё и ноль.

Как и раньше, система не ограничена, но направленна. Ведь мы можем предположить сколько угодно верёвок и все будем складывать только «вперёд».

Система построена на умножении, а не на сложении, как более древние.

И наконец-таки, важнейшая характеристика подобного представления.

Каждая следующая верёвка в P раз больше предыдущей.

Узелков на всех верёвках одинаковое количество = P.

P — это основание.

Основание — главная характеристика позиционной системы счисления. Оно равно количеству символов в системе.

Ещё нам пригодится такой термин, как разряд.

Разряд = номер позиции цифры минус один.

Разряд — положение цифры в числе за вычетом единицы. Рост разрядов у нас принят влево и считается от нуля.

Перевод чисел в разные системы счисления

Чтоб не запутаться в разных основаниях, назовём в этой статье количество предметов измерения просто количеством.

Количество — реальное число измеряемых предметов или отвлечённое число.

Выражать в тексте количество будем в системе с основанием 10d, так как она наша родная.

Но само количество не зависит от записи чисел, это вы должны хорошо понимать. Ведь как бы мы ни записывали, а от этого реальное число предметов совершенно не изменится.

Составим формулу, опираясь на верёвки (рисуйте их сами, если такой образ помогает).

Возьмём верёвки с четырьмя узелками и отрезками на каждой (основание — 4).

Измерим что-нибудь и получим такой результат:

3 самых маленьких отрезка, 2 отрезка из следующей верёвки, 0 отрезков из верёвки ещё большего размера и 2 самых больших отрезка.

То есть в четверичной системе счисления мы получаем:

2023

Основание = 4, значит, каждая следующая верёвка в 4 раза больше предыдущей.

Или по-другому: каждый следующий разряд в 4 раза больше.

Наша задача найти общую сумму самых маленьких отрезков (то есть количество).

Начиная с младшего разряда, мы будем складывать количества.

3 — уже определено, это и есть количество 3.

2 — это два отрезка по четыре маленьких в каждом 2*4= количество 8

0 — он и в Африке ноль

2 — это два отрезка, в которых 4 более маленьких, в которых 4 более маленьких, в которых 4 самых маленьких =).

Можно сначала посчитать количество в старшем разряде так:

2 *4=8. Мы узнали, сколько в четвёртой верёвке отрезков из третьей.
8 *4=32, теперь перевели в отрезки второй верёвки. И вот, наконец: 
32*4= количество 128

Запишем по-человечески:

2*43=128

Все количества по отдельности мы узнали.

Очевидно, что если просто сложить количества, то получится искомый результат.

128+0+8+3=139

Если взять ещё несколько примеров из этой серии и чуть-чуть подумать, то записать красиво наш пример можно так:

2*4³ + 0*4² + 2*4¹ + 3*4⁰ = 139

Суть вот в чём:

значение цифры * основание, возведённое в степень разряда = количество за этой цифрой в данной позиции.

За базовую систему взята привычная нам dec. Поэтому, сложив все количества вместе, мы имеем десятичную запись числа.

Но если бы расчёты проводились, например, в hex-системе, мы получили бы шестнадцатиричное представление.

Обобщённый вид этой формулы вы уже видели, и теперь она не должна показаться такой страшной.

Есть ещё один забавный вопрос, вызывающий некоторые сложности при нулевом знакомстве с нашей системой счёта.

А почему старшая цифра — «9»?

Все, наверное, знают, что десятичная система связана с пальцами рук, но, возможно, не все могут сказать, почему она не одиннадцатиричная. Ведь по сути каждый палец обозначает один предмет, а как я уже сказал, в позиционной системе основание равно количеству цифр. Значит, десять пальцев — это десять предметов плюс цифра ноль, получается = 11. Некоторые народы так и считали, но почему же десятичная система оказалась устойчивей?

Ответ кроется в кулаках =).

Возможно, на кулаках и была построена древнейшая позиционная система.

Дело в том, что загибая десятый палец, мы получаем два кулака.

Так вот, если два сжатых кулака становятся следующим разрядом, то можно сказать, что десятый палец и кулак — одна сущность = 10.

Давайте представим это в наших верёвочных образах.

Вы, наверное, заметили: на верхнем конце верёвок нет узелка.

Значит, старшая цифра 9 обозначает, что посчитано девять предметов счёта.

Куда же делся верхний узелок?

Хм… Попробуем доработать верёвку, замкнув её. Вот так:

Смотрите, как красиво получилось.

Всё сошлось — десять узелков, десять отрезков и нет никаких «обрезков».

Мы ведь на самом деле ведём счёт от нуля до нуля.

То есть в позиционной системе счисления цифра 0 одновременно и самая младшая, и самая старшая!

Пройдя круг, сделаем +1 к следующему разряду, создавая, таким образом, бесконечный цикл.

Из такого представления вытекает много интересных закономерностей.

Например, запись «10»:

цифра «0» и слева стоящая цифра «1» всегда будут выражать основание.

Ведь на верёвке может быть сколько угодно узелков (от двух до бесконечности) и каждый из них может иметь цифру, но при этом мы всегда будем прибавлять единицу к следующему разряду только когда пройдём ноль.

Допустим, двоичная система может быть представлена так:

Да, круга не получилось. =/

Тут вообще на глаз один отрезок. Однако если мы вспомним про направление счёта, то станет понятно:

надо дойти до единицы и затем вернуться к нулю, только после этого выполняется +1 к следующему разряду.

Значит, мы были правы, 10b= количество 2.

Запомните это равенство:

10 = основание,

а по правилам современной математической записи:

10_(p)=P,

где P — основание.

В позиционных системах оно будет выполняться всегда, пока мы используем для записи единичного количества и отсутствия предмета цифры 1 и 0 соответственно.

Теперь очень легко можно решать простые задачки вроде этой:

110=35+42

В какой системе это записано?

Достаточно сложить младший разряд:

5+2= количество 7

Затем старший:

3+4= количество 7

Получилось равенство:

110= количество 77

Осталось только сократить:

10= количество 7

Ответ: в семеричной системе.

Ах да, чуть не забыл, уроки-то про Ассемблер =).

Всё! Сворачиваем отвлечение и возвращаемся к практике программирования.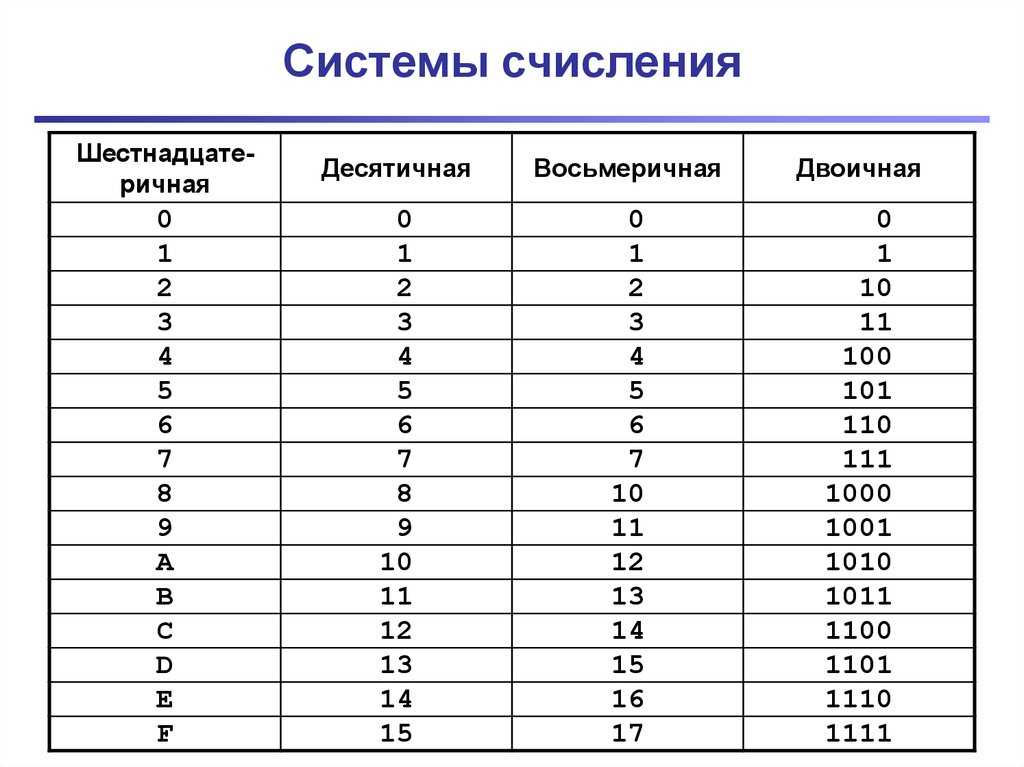

Больше не будем говорить о математике. Сдалась она нам вообще? ;)

Bitfry

---

А для тех, кто серьёзно заинтересовался темой систем счисления, приведу полезную ссылку на статью «Система счисления» из Википедии.

Именно эта статья указана по нескольким причинам. Во-первых, она постоянно обновляется, во-вторых, там довольно интересный список литературы и ссылки уже долго «живут». Начать рекомендую с брошюрки «Популярные лекции по математике», выпуск 40.

Хотя я бы включил в список обязательного прочтения ещё одну книгу:
«История математики с древнейших времён до начала XIX столетия» (в трёх томах, под редакцией А. П. Юшкевича, изд-во «Наука», М., 1970).

Сам сейчас читаю ещё только первый том, и больше всего для этой статьи я почерпнул именно оттуда.

Впрочем, смотрите сами, что вам будет интересно.

Системы счисления для чайников — Электротехника 123

Зачем изучать системы счисления?

Когда люди разговаривают друг с другом, они говорят на определенном языке. Этот язык состоит из слов и букв.

Хотя мы печатаем слова и буквы на компьютере, компьютер не понимает слова и буквы. Скорее, эти слова и буквы переводятся в числа.

Компьютеры «разговаривают» и понимают числа. Как программист или ИТ-специалист, вы должны понимать три наиболее распространенные системы счисления, которые часто используются в компьютерах.

Эти системы счисления:

1. Десятичная
2. Шестнадцатеричный
3. Двоичный

Если вы разбираетесь в системах счисления, вы разберетесь в следующих разделах информатики:

• Вы поймете, как вычислять сетевые адреса
• Вы поймете, как читать адреса памяти в дампах ядра
• Вы поймете определения цветов в веб-программировании и программировании приложений
• Вы поймете многие другие понятия

Десятичная система счисления

Десятичная система счисления — это система, которая широко известна людям, потому что она наиболее часто используется в арифметике и в повседневной жизни.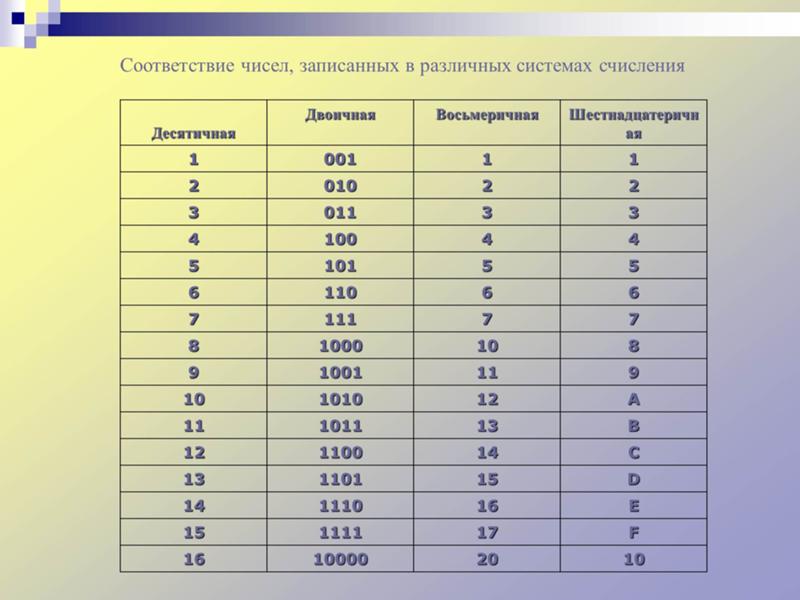

Десятичная система счисления также известна как система счисления с основанием 10, поскольку каждая позиция в числе представляет собой возрастающее число с основанием 10.

Например, первая позиция (крайняя справа) представлена ​​​​как 10 ⁰ .

Вторая позиция (одна справа) представлена ​​как 10 ¹ и так далее.

Чтобы определить, какое действительное число находится в каждой позиции, возьмите число, которое появляется в этой позиции, и умножьте его на 10 ^x , где x — представление мощности.

Например, если число находится в крайнем правом положении, возьмите число в крайнем правом положении и умножьте его на 10 ⁰ .

Если в числе несколько позиций (например, 1374), сложите все результаты вместе.

Так как система счисления представлена ​​в «десятках», есть только 10 чисел, которые могут быть значением в каждой позиции числа с основанием 10. Каждая позиция может содержать только число от 0 до 9.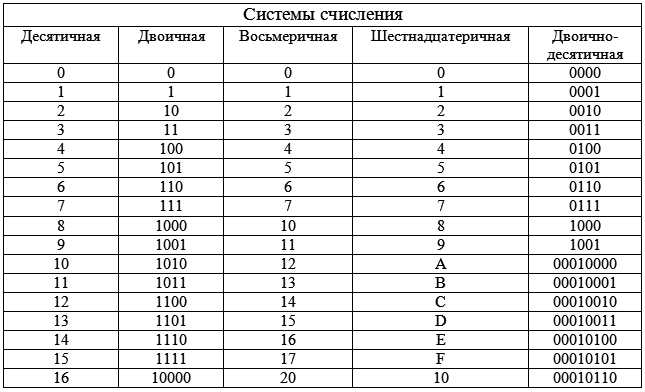

Давайте рассмотрим пример интерпретации числа с основанием 10. Пример числа в десятичной системе — 1374. Мы знаем это число как «одна тысяча триста семьдесят четыре». Вот как интерпретировать десятичное число:

Число 1374 на самом деле является представлением десятичных разрядов. Первая крайняя правая позиция числа представляет 10 ⁰ .

Следующая позиция представляет 10 ¹ .

Следующая позиция представляет 10 ² .

По мере того, как мы продвигаемся дальше влево от числа, каждая степень увеличивается на 1.

Чтобы определить, какое число на самом деле находится в позиции, возьмите число, которое появляется в позиции, и умножьте его на 10 ^x , где x представляет мощность.

Сложите все числа из каждой позиции, чтобы узнать, что это за число.

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления используется в компьютерах в качестве промежуточной системы, например, для представления адресов памяти или представления цветов.

Шестнадцатеричная система счисления также известна как система счисления с основанием 16, поскольку каждая позиция в числе представляет собой возрастающее число с основанием 16.

Например, первая позиция (крайняя справа) представлена ​​​​как 16 ⁰ . Вторая позиция (одна крайняя справа) представлена ​​как 16 ¹ и т. д.

Чтобы определить, каково действительное число в «десятичном» представлении, возьмите число, которое появляется в позиции, и умножьте его на 16 ^x , где x — представление в степени.

Например, если число находится в крайнем правом положении, возьмите число в крайнем правом положении и умножьте его на 16 ⁰ . Если в числе несколько позиций (например, 17AF), сложите все результаты вместе.

Поскольку система счисления представлена ​​в «шестнадцатерках», в каждой позиции числа с основанием 16 может быть значение только 10 цифр и 5 букв. Ниже приведены числа, которые может содержать каждая позиция:

Шестнадцатеричное представление	«Десятичное» значение
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
А	10
Б	11
С	12
Д	13
Е	14
Ф	15

Давайте рассмотрим пример интерпретации числа с основанием 16.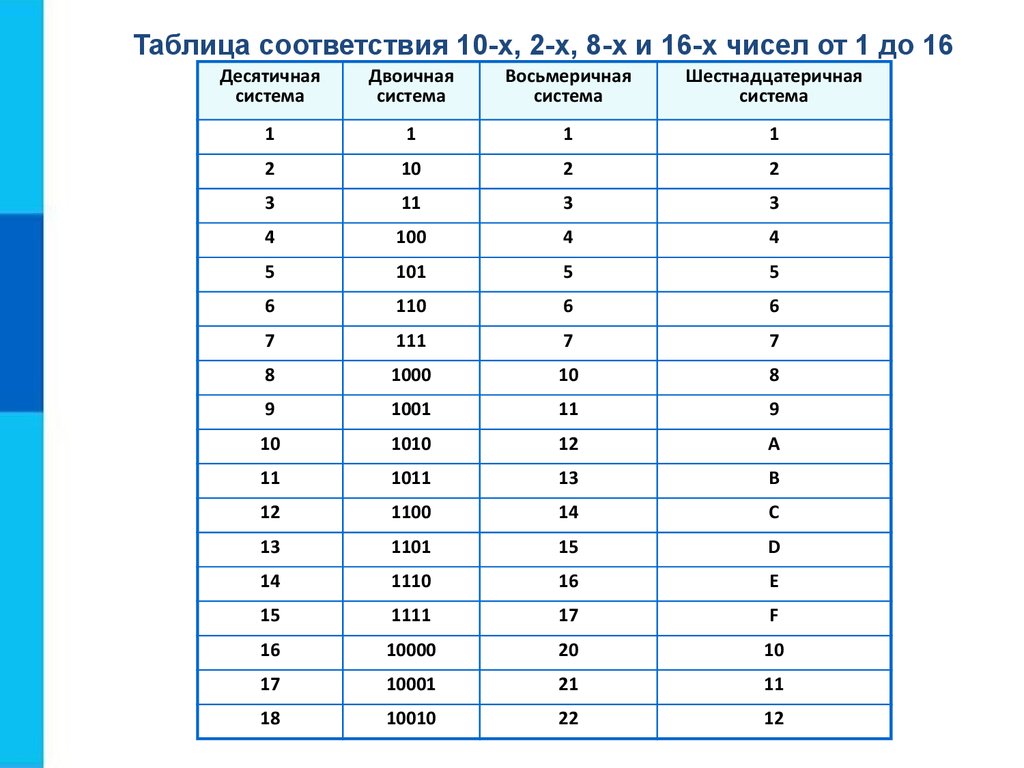 Пример номера в шестнадцатеричном формате: 17AF. Вот как «интерпретировать» число в десятичном формате:

Число 17AF является шестнадцатеричным числом. Первая крайняя правая позиция числа представляет 16 ⁰ .

Следующая позиция представляет 16 ¹ .

Следующая позиция представляет 16 ² .

По мере того, как мы продвигаемся дальше влево от числа, каждая степень увеличивается на 1.

Чтобы определить, какое число на самом деле находится в позиции, возьмите число, которое появляется в позиции, и умножьте его на 16 ^x , где x представляет мощность.

Обратите внимание, что в шестнадцатеричной системе счисления буквы от A до F обозначают числа от 10 до 15 соответственно.

Сложите вместе все числа из каждой позиции, чтобы узнать, что такое десятичное число.

Двоичная система счисления

Двоичная система счисления — это основная система счисления, которую использует большинство машин (и электрических устройств) для связи. Двоичная система счисления также известна как система счисления с основанием 2, потому что каждая позиция в числе представляет возрастающее число с основанием 2.

Например, первая позиция (крайняя справа) представлена ​​как 2 ⁰ .

Вторая позиция (одна справа) представлена ​​как 2 ¹ и так далее. Чтобы определить, какое фактическое число находится в каждой позиции, возьмите число, которое появляется в этой позиции, и умножьте его на 2 ^x , где x – это представление степени 90 315.

Например, если число находится в крайнем правом положении, возьмите число в крайнем правом положении и умножьте его на 2 ⁰ .

Если в числе несколько позиций (например, 10011), сложите все результаты вместе.

Поскольку система счисления представлена ​​«двойками», есть только 2 числа, которые могут иметь значение в каждой позиции числа с основанием 2. Каждая позиция может содержать только 0 или 1.

Давайте рассмотрим пример интерпретации числа с основанием 2. Пример числа в десятичной системе — 100101. Вот как «интерпретировать» число в десятичном формате:

Число 100101 является двоичным числом. Первая крайняя правая позиция числа представляет 2 ⁰ .

Следующая позиция представляет 2 ¹ .

Следующая позиция представляет 2 ² .

По мере того, как мы продвигаемся дальше влево от числа, каждая степень увеличивается на 1.

Чтобы определить, какое число на самом деле находится в позиции, возьмите число, которое появляется в позиции, и умножьте его на 2 ^x , где x представляет мощность.

Обратите внимание, что в двоичной системе счисления в каждом разряде могут стоять только два числа: 0 или 1.

Сложите все числа из каждого разряда, чтобы узнать, что такое десятичное число.

Нравится:

Нравится Загрузка…

10 Альтернативные системы счисления и счисления

Различие между числами и числами тонкое, но важное.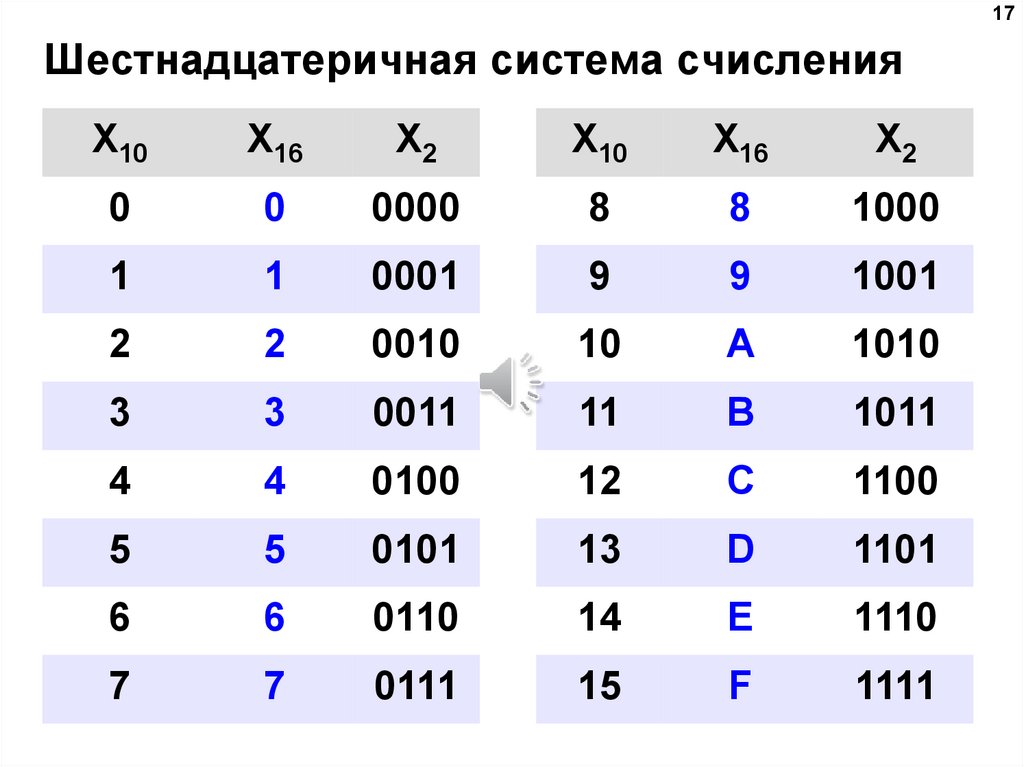 Число — это идея, которая выражает сколько или сколько. Числительное – это письменный знак, который выражает число. Вот десять способов представления чисел, которые отличаются от индийско-арабской (десятичной) системы.

Учетные отметки

Числа — это абстракции, обозначающие реальные вещи. Первые известные числа появились с ростом торговли и коммерции — людям нужно было отслеживать такие товары, как животные, собранный урожай или инструменты. Сначала торговцы использовали глиняные или каменные жетоны, чтобы упростить работу по подсчету. Со временем жетоны заменили счетные метки, выцарапанные на кости или на глине.

Учетные метки в комплекте

По мере того, как ранние люди привыкали к тому, что метки для подсчета обозначают объекты реального мира, следующим шагом в развитии чисел, вероятно, стали метки, нацарапанные в связки по 5 (пальцы одной руки), 10 (пальцы обеих рук) или 20 (пальцы рук и ног). Объединение предоставило простой способ более легкого подсчета больших чисел.

Конечно, эту систему гораздо легче читать, чем несвязанные скретчи — вы можете легко умножить или посчитать на пять, чтобы получить сумму. Даже сегодня люди отслеживают очки в играх, используя такие пакеты.

Египетские цифры

Древнеегипетские цифры — одна из старейших систем счисления, используемых до сих пор. Египетские цифры используют семь символов.

Египетские цифры

Номер	Символ
1	Ход
10	Хомут
100	Катушка веревки
1000	Лотос
10 000	Палец
100 000	Лягушка
1 000 000	Мужчина с поднятыми руками

Числа формируются путем накопления необходимого количества символов. Например,

7 = 7 ходов

24 = 2 вилки, 4 такта

1,536 = 1 лотос, 5 мотков веревки, 3 ярма, 6 ударов

Вавилонские цифры

Вавилонские цифры, появившиеся около 4000 лет назад, используют два символа:

.

1 = Д

10 = <

Для чисел меньше 60 числа формируются путем накопления достаточного количества необходимых вам символов. Например,

6 = ГГГГГГ

34 = <<

Для чисел от 60 и выше в вавилонских числительных используется разрядное значение, основанное на числе 60.

61 = Г Д	(один 60 и один 1)
124 = ГГ ГГГГ	(две 60 и четыре единицы)
611 = <	(десять 60 и одиннадцать единиц)

Древнегреческие цифры

Древнегреческие цифры были основаны на греческих буквах. Цифры от 1 до 999 были сформированы с использованием показанных символов:

Римские цифры

Хотя римским цифрам более 2000 лет, люди все еще используют их сегодня либо в декоративных целях (например, на часах, краеугольных камнях и памятных вещах Суперкубка), либо когда необходимы цифры, отличные от десятичных чисел (например, в контурах). Римские цифры используют семь символов, все из которых являются заглавными буквами латинского алфавита (который также является английским алфавитом):

Я = 1	В = 5	Х = 10	Д = 50
С = 100	Д = 500	М = 1000

Цифры майя

Цифры майя появились в Южной Америке примерно в тот же период, что и римские цифры в Европе. Цифры майя используют два символа: точки и горизонтальные полосы. Полоса равна 5, а точка равна 1. Числа от 1 до 19 образуются путем накопления точек и полос. Например,

3 = 3 точки

7 = 2 точки на 1 полосе

19 = 4 точки на 3 полосах

Числа от 20 до 399 формируются из тех же комбинаций, но подняты вверх для обозначения разрядности. Например,

21 = поднятая 1 точка, 1 точка (одна 20 + одна 1)

399 = поднятые 4 точки над 3 полосами, 4 точки над 3 полосами (девятнадцать 20-х + три пятерки + четыре единицы)

Базовые 2 (двоичные) числа

Двоичные числа используют только два символа: 0 и 1. Эта простота делает двоичные числа полезными в качестве системы счисления, которую компьютеры используют для хранения данных и вычислений.

Как и в знакомой вам десятичной системе, в двоичных числах используется разрядное значение. В отличие от десятичной системы, двоичная разрядность основана не на степенях десяти (1, 10, 100, 1000 и т. д.), а на степенях двойки (20, 21, 22, 23, 24, 25, 26, 27, 28, 29 и т. д.), как показано здесь:

.

Двоичные разрядные значения

512с

256с

128с

64с

32с

16с

8 с

4с

2 с

1с

Числа с основанием 16 (шестнадцатеричные)

Первым языком компьютера являются двоичные числа. Но на практике люди находят двоичные числа любой значительной длины практически не поддающимися расшифровке. Шестнадцатеричные числа, однако, удобочитаемы для человека и по-прежнему легко переводятся в двоичные числа, поэтому программисты используют шестнадцатеричные числа как своего рода общий язык при взаимодействии с компьютерами на самом глубоком уровне, на уровне аппаратного и программного обеспечения.

Шестнадцатеричная система счисления использует все десять цифр от 0 до 9 из десятичной системы счисления. Кроме того, он использует еще шесть символов:

.

А = 10	Б = 11	С = 12
Д = 13	Е = 14	Ф = 15

Шестнадцатеричная система с разрядными значениями, основанная на степенях числа 16.

Шестнадцатеричные разряды

1 048 576 с

65 536 с

4096 с

256с

16с

1с

Как видите, каждое число в таблице ровно в 16 раз больше числа, стоящего справа от него.

Числа, основанные на простых числах

Одним из дурацких способов представления чисел, в отличие от других, являются числа, основанные на простых числах. Числа, основанные на простых числах, аналогичны десятичным, двоичным и шестнадцатеричным числам в том, что они используют разрядное значение для определения значения цифр.