Двоичная система счисления – таблица последовательности, примеры (8 класс, информатика)

4.7

Средняя оценка: 4.7

Всего получено оценок: 249.

4.7

Средняя оценка: 4.7

Всего получено оценок: 249.

Информация в компьютере обрабатывается в цифровом формате, в виде набора нулей и единиц, поэтому все числа переводятся в двоичный вид. Система счисления, в которой для обозначения чисел применяется всего два знака, называется двоичной. Метод представления чисел в двоичном формате изучается в курсе информатики 8 класса.

Двоичная система

Система счисления, которая в своем арсенале использует только две цифры, то есть имеющая основание два, называется двоичной или бинарной. В такой системе числа заменяются последовательностью нулей и единиц. Например, десятичное число 134 в двоичном формате выглядит как 10000110. Для того чтобы понять, как это работает, следует придерживаться правил перевода чисел из одной системы счисления в другую.

Рис. 1. Двоичная система счисления.

Перевод чисел из десятичной системы счисления в двоичную

Перевод целой части десятичного числа производится путем поочередного деления частного на основание двоичной системы, то есть на два. В остатке от деления останется либо ноль, либо единица. Эти остатки записываются, начиная с последнего частного в направлении слева направо. Это и будет двоичным представлением десятичного числа.

Рассмотрим примеры.

Для перевода десятичного числа 29 в двоичный формат:

Делят 29 на два, получают 14 и в остатке 1. Остаток следует запомнить.

Затем частное от деления, то есть число 14 снова делят на два, получено 7 и в остатке 0 (ноль).

Разделим 7 на два, получим частное 3 и остаток 1.

Три делят на два, получено в частном 1 и остаток 1.

Так как последнее частное 1 меньше основания системы счисления, то есть числа 2, то последовательное деление прекращают.

Затем записывают остатки, начиная с последнего частного, и получают последовательность чисел: 11101. Таким образом, десятичное число 29 в двоичной системе счисления равно 11101.

Еще один пример: перевод числа 37 в двоичный формат.

37 / 2 = 18 (1)

18 / 2 = 9 (0)

9 / 2 = 4 (1)

4 / 2 = 2 (0)

2 / 2 = 1 (0)

Получен результат: 100101.

Если десятичные числа расположить последовательно и сопоставить с их двоичными эквивалентами, то можно увидеть некоторую закономерность.

Таблица двоичной системы счисления

0	0	8	1000
1	01	9	1001
2	10	10	1010
3	11	11	1011
4	100	12	1100
5	101	13	1101
6	110	14	1110
7	111	15	1111

Как видно из таблицы, после 11 в числовом ряду двоичных чисел идет число 100.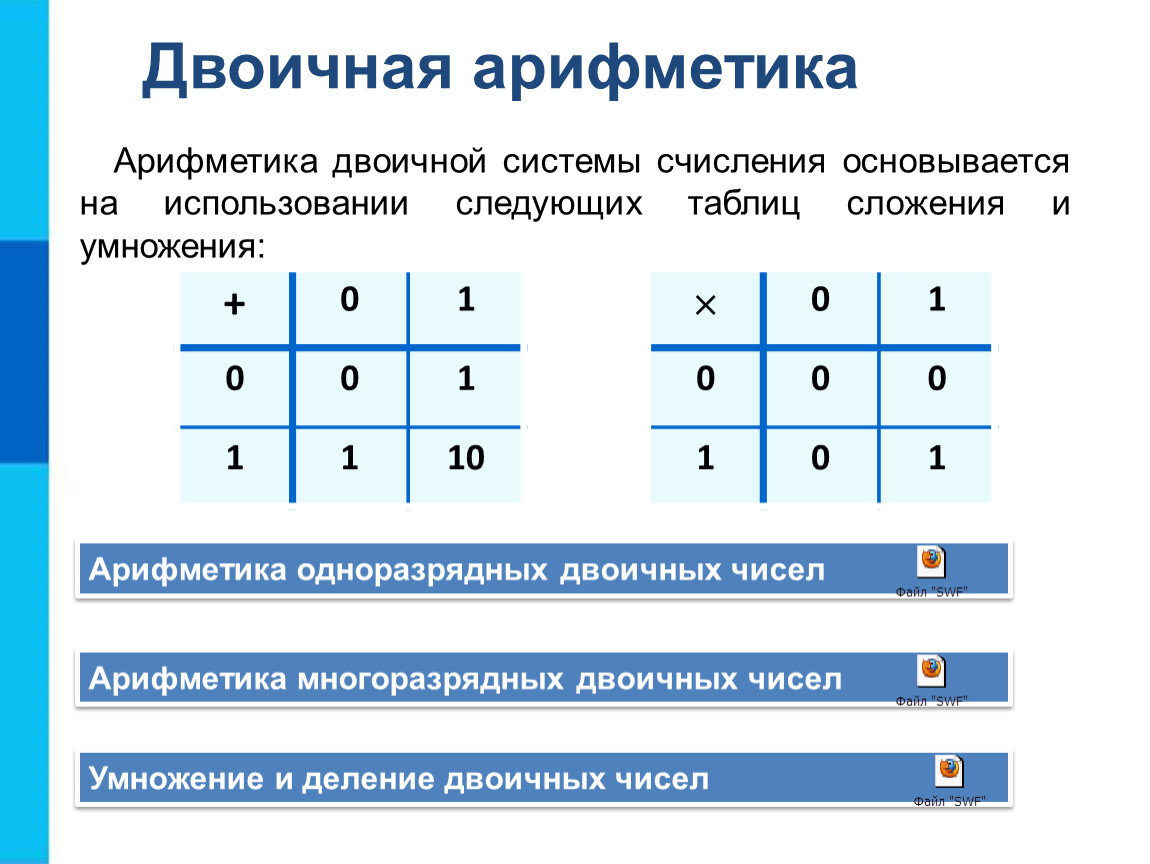 Так как в двоичной системе счисления только два знака 0 и 1 для обозначения числа, то происходит сдвиг разрядной сетки влево. После двузначного числа 11 идет трехзначное число 100.

Таблицей двоичной системы удобно пользоваться для перевода только небольших десятичных чисел. Ее даже рекомендуется запомнить, как таблицу умножения в математике. Но ни в коем случае нельзя по таблице переводить отдельные цифры числа в десятичный формат. Это приведет к ошибке. Например, десятичное число 15 это не 1 и 101, (вместе 1101), а все-таки 1111.

Перевод двоичных чисел в десятичную систему счисления

Обратный перевод двоичного числа в десятичную систему производится также строго по правилу перевода.

Рис. 2. Портрет Г. В. Лейбница.

Сначала нумеруются разряды двоичного числа справа налево, начиная с нулевого, а затем каждая цифра двоичного числа умножается на основание двоичной системы, то есть на два, возведенной в степень соответствующего разряда. Полученные произведения суммируются, и получается десятичное число.

Например: двоичное число 1110001 в десятичной системе равно 113.

Нумеруем разряды числа, начиная с нуля: 1(6) 1(5) 1(4) 0(3) 0(2) 0(1) 1(0).

Каждую цифру двоичного числа умножаем на два в степени разряда и суммируем:

1*2⁶ + 1*2⁵ + 1*2⁴ +0*2³ + 0*2² + 0*2¹ + 1*2⁰ = 64 + 32 + 16 + 0 + 0 + 0 +1 = 113

Следует помнить, что любое число в степени ноль равно единице.

Двоичная система счисления была описана Готфридом Вильгельмом Лейбницем в 18 веке. На это его вдохновили гексограммы из китайской книги Перемен, которые соответствовали двоичным числам от 0 до 111111.

Рис. 3. Гексаграммы книги перемен.

Что мы узнали?

Данные в ЭВМ представляются в двоичном формате. Двоичная система счисления оперирует для записи чисел только двумя символами 0 и 1. Перевод десятичных чисел в двоичную систему и обратно производится строго по правилам.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Альбина Авезова

  5/10

Оценка статьи

4.7

Средняя оценка: 4.7

Всего получено оценок: 249.

---

А какая ваша оценка?

Двоичная система счисления, 0 и 1, двоичные числа

Содержание:

1. Общая форма записи двоичных чисел
2. Правила сложения двоичных чисел
3. Вычитание методом заимствования
4. Вычитание методом дополнения
5. Правила умножения двоичных чисел

Вспомним материал по системам счисления. В нём говорилось, что наиболее удобной системой счисления для компьютерных систем является двоичная система. Дадим определение этой системе:

Двоичной системой счисления называется позиционная система счисления, у которой основанием является число 2.

Для записи любого числа в двоичной системе счисления используются всего лишь 2 цифры: 0 и 1.

Общая форма записи двоичных чисел

Для целых двоичных чисел можно записать:

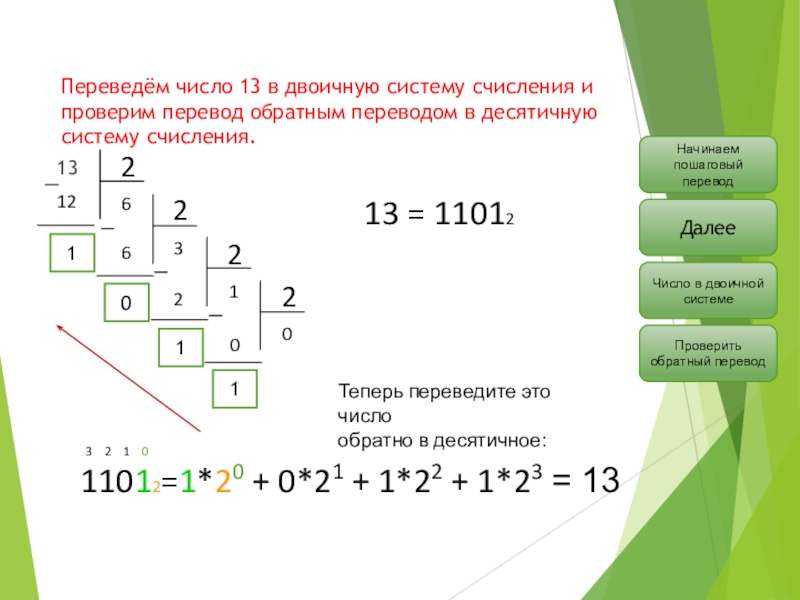a_n−1a_n−2. ..a₁a₀=a_n−1⋅2ⁿ⁻¹+a_n−2⋅2ⁿ⁻²+…+a₀⋅2⁰

Данная форма записи числа «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: требуется вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.

Правила сложения двоичных чисел

Основные правила сложения однобитовых чисел

0+0=0
0+1=1
1+0=1
1+1=10

Отсюда видно, что и, как и в десятичной системе счисления, числа, представленные в двоичной системе счисления, складывают поразрядно. Если разряд переполняется, единица переносится в следующий разряд.

Пример сложения двоичных чисел

Правила вычитания двоичных чисел

0-0=0
1-0=0
10-1=1

Но как быть с 0-1=? Вычитание двоичных чисел немного отличается от вычитания десятичных чисел. Для этого используется несколько способов.

Вычитание методом заимствования

Запишите двоичные числа друг под другом – меньшее число под большим. Если меньшее число имеет меньше цифр, выровняйте его по правому краю (так, как вы записываете десятичные числа при их вычитании).
Некоторые задачи на вычитание двоичных чисел ничем не отличаются от вычитания десятичных чисел. Запишите числа друг под другом и, начиная справа, найдите результат вычитания каждой пары чисел.

Вот несколько простых примеров:

1 — 0 = 1
11 — 10 = 1
1011 — 10 = 1001

Рассмотрим более сложную задачу. Вы должны запомнить только одно правило, чтобы решать задачи на вычитание двоичных чисел. Это правило описывает заимствование цифры слева, чтобы вы могли вычесть 1 из 0 (0 — 1).

110 — 101 = ?

В первом столбце справа вы получаете разность 0 — 1. Для ее вычисления необходимо позаимствовать цифру слева (из разряда десятков).

Во-первых, зачеркните 1 и замените ее на 0, чтобы получить такую задачу: 1010 — 101 = ?
Вы вычли («позаимствовали») 10 из первого числа, поэтому вы можете написать это число вместо цифры, стоящей справа (в разряд единиц). 101100 — 101 = ?
Вычтите цифры в правом столбце. В нашем примере:

101100 — 101 = ?

Правый столбец: 10 — 1 = 1.
102 = (1 x 2) + (0 x 1) = 210 (цифры нижнего регистра обозначают систему счисления, в которой записаны числа).

12 = (1×1) = 110.

Таким образом, в десятичной системе эта разность записывается в виде: 2 — 1 = 1.

Вычтите цифры в оставшихся столбцах. Теперь это легко сделать (работайте со столбцами, двигаясь, справа налево):

101100 — 101 = __1 = _01 = 001 = 1.

Вычитание методом дополнения

Запишите двоичные числа друг под другом так, как вы записываете десятичные числа при их вычитании. Этот метод используется компьютерами для вычитания двоичных чисел, так как он основан на более эффективном алгоритме.

Однако простому человеку, привыкшему вычитать десятичные числа, этот метод может показаться более сложным (если вы программист, обязательно познакомьтесь с этим методом вычитания двоичных чисел).

Рассмотрим пример: 101100₂ — 11101₂= ?

Если значность чисел разная, к числу с меньшей значностью слева припишите соответствующее количество 0.

101100₂ — 011101₂= ?

В вычитаемом числе поменяйте цифры: каждую 1 поменяйте на 0, а каждый 0 на 1.

011101₂ → 100010₂.

На самом деле мы «забираем дополнение у единицы», то есть вычитаем каждую цифру из 1. Это работает в двоичной системе, так как у такой «замены» может быть только два возможных результата: 1 — 0 = 1 и 1 — 1 = 0.

К полученному вычитаемому прибавьте единицу.

100010₂+ 1₂ = 100011₂

Теперь вместо вычитания сложите два двоичных числа.

101100₂ +100011₂= ?

Проверьте ответ. Быстрый способ – откройте двоичный онлайн калькулятор и введите в него вашу задачу. Два других метода подразумевают проверку ответа вручную.

1) Переведем числа в двоичную систему счисления:
Допустим, что из числа 101101₂ нужно вычесть 11011₂

2) Обозначим как A число 101101₂ и как B число 11011₂.

3) Запишем числа A и B столбиком, одно под другим, начиная с младших разрядов (нумерация разрядов начинается с нуля).

Разр.	6	5	4	3	2	1	0
A		1	0	1	1	0	1
B			1	1	0	1	1

 

4) Вычтем разряд за разрядом из числа A число B записывая результат в C начиная с младших разрядов. Правила поразрядного вычитания, для двоичной системы счисления представлены в таблице ниже.

Заем из текущего разряда Oi-1	Ai	Bi	Ci	Заем из следующего разряда Oi+1
	0	0	0
	0	1	1	1
	1	0	1
	1	1	0
1	0	0	1	1
1	0	1	0	1
1	1	0	0
1	1	1	1	1

 

Весь процесс сложения наших чисел выглядит следующим образом:

(красным шрифтом показаны заёмы из соответствующего разряда)

Получилось 101101₂ — 11011₂ = 10010₂
или в десятичной системе счисления: 45₁₀ — 27₁₀ = 18₁₀

Правила умножения двоичных чисел.

В целом эти правила очень просты и понятны.

0*0=0
0*1=0
1*0=0
1*1=1

Умножение многоразрядных двоичных чисел происходит точно также как и обычных. Каждое значащий разряд умножаем на верхнее число по приведенным правилам, соблюдая позиции. Умножать просто — так как умножение на единицу даёт одно и тоже число.

×				1	1	1	0
					1	0	1
+				1	1	1	0
		1	1	1	0
	1	0	0	0	1	1	0

 

Система счисления Методы перевода десятичного числа в двоичное

Двоичная система счисления – Математические тайны

Определение

Согласно цифровой электронике и математике, двоичное число определяется как число, выраженное в двоичной системе счисления или системе счисления с основанием 2. Он описывает числовые значения двумя отдельными символами; 1 (один) и 0 (ноль). Система с основанием 2 — это позиционная система счисления с основанием 2.

Двоичная система применяется внутри почти всех новейших компьютеров и компьютерных устройств из-за ее непосредственной реализации в электронных схемах с использованием логических вентилей. Каждая цифра обозначается как бит . ¹

Одна двоичная цифра — это бит. Последовательность из четырех битов (1001) называется полубайтом, а последовательность из восьми битов (11001010) называется байтом. Двоичный представляет собой определенную степень основания (2) системы счисления.

Пример

Здесь мы увидим пример того, как вычислить десятичный эквивалент двоичного числа.
Двоичный номер: 11001 ₂

11001 ₂  можно записать как 11001
Шаг 1:  (1 × 2⁴) + (1 × 2³) + (0 × 2²) + (0 × 2¹) + (1 × 2⁰)
Шаг 2:  (16 + 8 + 0 + 0 + 1)  ₁₀
Шаг 3:  (25) ₁₀ или 25

«Би» в двоичном формате означает «два». Следовательно, это возвращает линию к представлению числа только с точки зрения 0 и 1. Можно легко выразить десятичные числа в терминах двоичной системы счисления. Десятичные числа и двоичные числа имеют разные обозначения. Десятичное число представлено с основанием 10, а двоичное число представлено с основанием 2. Например, 2 в десятичной записи представлено как (2)10(2)10. Двоичное число для 2 представлено как (10)2(10)2. Следовательно, 10 — это двоичное представление числа 2. ²

Ссылки

¹ «Двоичная система счисления – определение, преобразование и примеры». 2022.  BYJUS . https://byjus.com/maths/binary-number-system/.

² «Двоичная система счисления – схема, преобразование и операции». 2022.  КУЕМАТ . https://www.cuemath.com/numbers/binary-number-system/.

Дополнительное чтение

«Двоичная система счисления — определение, преобразование, примеры — GeeksForGeeks». 2022. КомпьютерщикиДляГиков . https://www.geeksforgeeks.org/binary-number-system-definition-conversion-examples/.

Эрен, Ильнур. «Двоичная система счисления». 2018.  Средний . https://ilknureren.medium.com/binary-number-system-c1015a413b75.

Видео

Двоичные числа – БЫСТРО и ПРОСТО! Представление чисел и букв в двоичном формате: ускоренный курс информатики №4 Двоичная система счисления

---

⭐ Советую прочитать весь справочник. Другие ссылки можно прочитать полностью, но я оставляю это на ваше усмотрение.

Двоичная система счисления

Двоичная система счисления — это позиционная система счисления с основанием 2, изобретенная Готфридом Вильгельмом Лейбницем в 17 веке. В системе счисления с основанием 2 основание равно 2, поскольку только две цифры, 0 и 1, используются для представления всех возможных чисел.

Две цифры 0 и 1 часто называют битами, что является сокращением слова «двоичные цифры».

Например, 11001 ₂ — это двоичное число.

• Количество битов равно 5, так как 11001 ₂ имеет 5 цифр.
• Таким образом, каждая цифра двоичного числа является битом. Например, 1 слева — это бит в числе 11001 ₂ .
• 1 справа называется наименее значащим битом (LSB)
• 1 слева называется самым значащим битом (MSB)

Как преобразовать десятичную систему в двоичную

Метод №1:

11001 ₂ — это 25 в виде десятичного числа. Чтобы преобразовать 25 в двоичную систему счисления, нам нужно записать 25 в расширенной форме, убедившись, что каждое слагаемое можно записать как степень двойки.

25 = 16 + 8 + 1 = 2 ⁴ + 2 ³ + 2 ⁰

, чтобы сделать 25, нам нужна 1 группа из 16, 1 группа 8, 0 Группа 4, 0 Группа 2 и 1.

Начиная справа налево, 1 идет на первом месте (2 ⁰ ), 0 идет на втором месте (2 ¹ ), 0 занимает третье место (2 ² ), 1 занимает четвертое место (2 ³ ) и 1 занимает пятое место (2 ⁴ ), как показано на рисунке ниже. .

25 в двоичном формате равно 11001 ₂

Обратите внимание, что нет группировок по двойке и четвёрке. В итоге поставьте нули на второе и третье место.

Как производится группировка в двоичной системе счисления. Общие рекомендации, которым необходимо следовать при преобразовании с основанием 10 на основание 2

Группа с энного места на первое. Это означает, что вы должны сначала создать группу с максимально возможной степенью числа 2.

Например, я пытаюсь преобразовать 45 в двоичную систему счисления. Спросите себя: «Какова наибольшая степень числа 2 меньше 45?»

2 ⁶ = 64. 2 ⁵ = 32. Таким образом, наибольшая степень числа 2 меньше 45 равна 2 ⁵ = 32

Поскольку 32 стоит на шестом месте, поместите 1 в число . шестое место . Затем попытайтесь выяснить, что входит в значение места раньше.

45 — 32 = 13 

Спросите себя: «Какова наибольшая степень числа 2 меньше 13?»

2 ⁴ = 16. 2 ³ = 8. Таким образом, наибольшая степень числа 2 меньше 13 равна 2 ³ = 8

Поскольку 8 стоит на четвертом месте, поместите 1 на четвертое место. . Затем попытайтесь выяснить, что входит в значение места раньше.

13 — 8 = 5

Спросите себя: «Какова наибольшая степень числа 2, меньшего, чем 5?»

2 ³ = 8. 2 ² = 4. Таким образом, наибольшая степень числа 2 меньше 5 равна 2 ² = 4

Поскольку 4 идет на третьем месте, поместите 1 на третье место . Затем попытайтесь выяснить, что входит в значение места раньше.

5 — 4 = 1 и 1 занимает первое место .

Обратите внимание, что вы ничего не ставите на пятое и второе место, поэтому в этих местах стоят нули.

Следовательно, 45, переведенное в двоичную систему счисления, равно 101101.

Можно также написать 45 _десять  или 101101 _два

Будьте очень внимательны, когда читаете  101101 _два !

101101 ₂  читается один ноль один один ноль один по основанию 2.

Метод №2:

Шаг 1

Разделите делимое 25 на 2 и запишите алгоритм деления.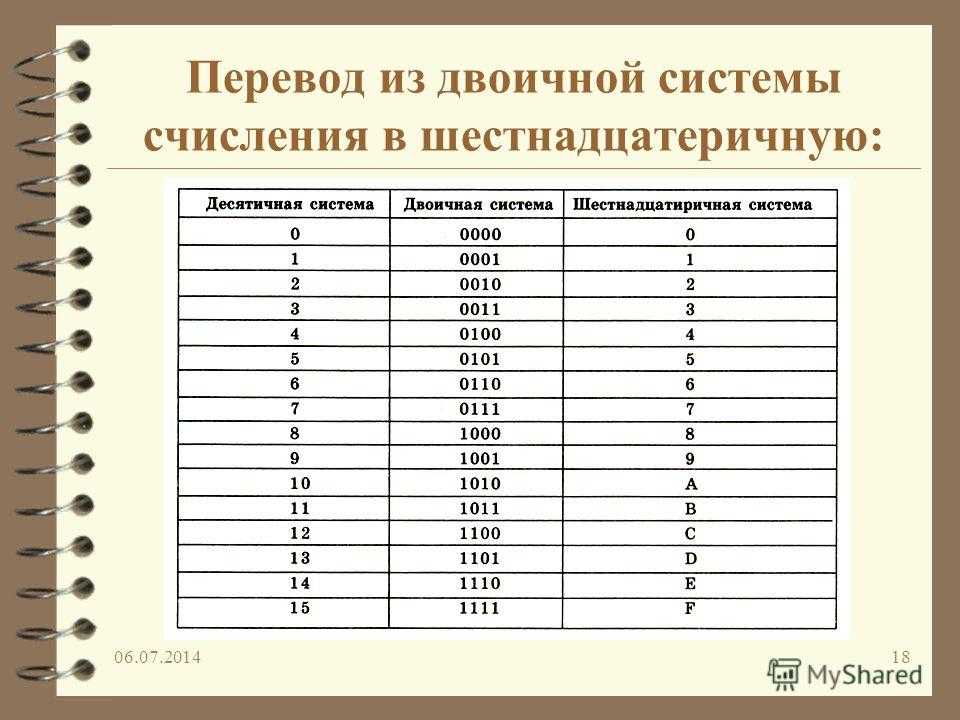

Шаг 2

Используйте частное, полученное на шаге 1, в качестве нового делимого. Разделите новое делимое на 2 и снова напишите алгоритм деления. Продолжайте делать это, пока частное не станет равным 0,9.0005

Используя метод № 2, вот как преобразовать десятичное число 25 в двоичное число.

25 = 2 x 12 + 1

12 = 2 x 6 + 0

6 = 2 x 3 + 0

3 = 2 x 1 + 1

1 = 2 x 0 + 1 900 05

Напишите все остатки, полученные снизу вверх, как 110001 ₂

Таблица преобразования двоичных чисел в десятичные
Двоичный	Десятичный	Двоичный	Десятичный
0	0	10000	16
1	1	10001	17
10	2	10010	18
11	3	10011	19
100	4	10100	20
101	5	10101	21
110	6	10110	22
111	7	10111	23
1000	8	11000	24
1001	9	11001	25
1010	10	11010	26
1011	11	11011	27
1100	12	11100	28
1101	13	11101	29
1110	14	11110	30
1111	15	11111	31

Сходство и различие между десятичной системой счисления и двоичной системой счисления

Основное различие между двоичной системой счисления и знакомой нам системой счисления с основанием 10 заключается в том, что группировка выполняется группами по 2, а не по 10. десять и 4, как показано ниже.

Есть кое-что важное, о чем следует помнить, и это ключ к полному пониманию этого урока!

• Цифры 0,1,2,3,4,5,6,7,8,9 используются для представления всех возможных чисел. Обратите внимание, что основание 10 состоит из 10 цифр, поэтому основание равно 10.

• В зависимости от того, насколько велико число, мы делаем группы по десять, сто, тысяча, десять тысяч и т. д. (Это степень 10: 10 ¹ = 10, 10 ² = 100 , 10 ³ = 1000)

• Если число меньше 10, например 8 и 9, то число будет занимать разряд единиц.

• Если число больше 9 и меньше 100, например 10, 55 и 98, группа(ы) из десяти будет занимать разряд десятков.

• Если число больше 99 и меньше 1000, например 100, 255 и 999, группа(ы) из сотен будет занимать разряд сотен.

• И так далее…

Например, внимательно изучите следующий номер, чтобы увидеть, как он был организован.

Так как число больше 99, нам пришлось сделать группы по сто десять. Обратите также внимание на то, как группы сотен помещаются в разряд сотен, а группы из десяти помещаются в разряд десятков.

Аналогичным образом, двоичная система счисления имеет собственное разрядное значение.

• Цифры 0,1 используются для представления всех возможных чисел в двоичной системе счисления. Обратите внимание, что в базе 2 есть 2 цифры для представления всех возможных чисел.

• В зависимости от того, насколько велико число, мы делаем группы по 2, 4, 8, 16, 32 и т. д. (это степень числа 2: 2 ¹ = 2, 2 ² = 4, 2 ³ = 8)

• Если число меньше 2, например 1, создавать группы не нужно. И это число будет занимать значение первого места . Это разрядное значение соответствует разряду единиц в системе счисления с основанием 10. На самом деле эта единица одинакова в двоичной системе и в системе с основанием 10.


• Если число больше 1 и меньше 4, например, 2 и 3, одна группа из двух будет занимать второе значение разряда . Вы также можете назвать это «двухзначным» значением.

• Если число больше 3 и меньше 8, например 4 и 7, одна группа из четырех будет занимать третье место . Вы также можете назвать это «четыре» разряда

• Если число больше 7 и меньше 16, например 8, 11 и 14, одна группа из восьми будет занимать четвертое разрядное значение . Вы также можете назвать это «восьмой» разрядностью.

• Если число больше 15 и меньше 32, например 16, 21 и 30, одна группа из шестнадцати будет занимать значение пятого разряда . Вы могли бы также назвать его «шестнадцать» разряда.

• Если число больше 31 и меньше 64, например, 32, 45 и 63, одна группа из тридцати двух займет шестое разрядное значение . Вы также можете назвать это значением «тридцать два».

• И так далее. ..

Поскольку мы используем только 0 и 1 для представления чисел, невозможно записать двоичные числа, используя число 2 или любое число больше 2.

Применение двоичная система счисления

Система счисления с основанием 2 имеет множество применений в компьютерных технологиях. Например, каждый когда-либо построенный компьютер хранит такие данные, как числа, графики и буквы, внутри, используя двоичную систему счисления.

В каждом компьютере обычно существует максимальное количество битов, которые используются для хранения целых чисел. В настоящее время значение обычно составляет 16, 24 или 32 бита. Однако многие из компьютеров, выпущенных в 1970-х годах, использовали только 8 бит для хранения данных.

8 бит имеет восемь единиц и является двоичным числом 2 ⁵ + 2 ⁴ + 2 ³ + 2 ² + 2 ¹ + 2 ⁰ = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255.

На 8-битном компьютере любая операция на компьютере, которая возвращает целочисленное значение больше 255, вызовет ошибку, поскольку все ячейки памяти израсходованы. Однако 16-разрядный компьютер может выдать целое число с максимальным значением 65535. Вы можете понять, почему возникла необходимость в создании компьютеров, которые могут хранить больше данных.

Калькулятор преобразования десятичного числа в двоичный

Например, введите 45 в калькулятор, и вы увидите, что ответ равен 101101, как уже было показано выше.

основать

1. Математический тест SAT: как подготовиться к встрече с ним и выжить

   9, 23 июня 12:04

   Математический раздел SAT известен своей сложностью. Но это не обязательно. Узнайте, как подготовиться и уверенно заполнить раздел, здесь.

   Подробнее

2. Фундаментальный принцип счета

   06, 23 июня 07:32

   В этом уроке представлен фундаментальный принцип счета. Научитесь считать с принципом умножения и принципом сложения.