Контрольная работа «ЛОГИКА» (10 класс)
контрольная работа «ЛОГИКА»
1 вариант
1. Для какого названия животного ложно высказывание:
Четвертая буква гласная → ¬ (Вторая буква согласная)?
1. собака 2. жираф 3. верблюд 4. страус
2. Для какого Х истинно высказывание:
(Х >2) V (Х> 5)→ (Х< 3)?
1.5 2.2 3.3 4.4
3. Символом F обозначена логическая функция от двух аргументов (А и В), заданная таблицей истинности. Какое выражение соответствует F?
А
В
F
1) А → ( ¬А V ¬ В)
0
0
1
2) А ᴧ В
0
1
1
3) ¬ А → В
1
0
1
4) ¬ А ᴧ ¬ В
1
1
0
4. Какое логическое выражение эквивалентно выражению ¬( А ᴧ¬ В ᴧ¬ С)?
1. ¬А V В V С 2. ¬А V В V¬ С 3. ¬А ᴧ Вᴧ С 4. А ᴧВ ᴧ ¬ С
5. Укажите значения переменных K, L, M, N при которых ложно логическое выражение: (K →¬ M) V (¬L ᴧ M ᴧK) V ¬N.
Ответ запишите в виде строки из четырех символов — значений переменных K, L, M, N ( в указанном порядке).
контрольная работа «ЛОГИКА»
2 вариант
1. Для какого слова ложно высказывание:
Первая буква слова согласная → (Вторая буква гласная ᴧ последняя буква согласная)?
1. жара 2. орда 3. огород 4. парад
2. Для какого из значений Z будет ложным высказывание:
(Z >2) V (Z > 4)→ (Z > 3)?
1.1 2.2 3.3 4.4
3. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов (X , Y, Z). Дан фрагмент таблицы истинности выражения F . Какое выражение соответствует F?
X
Y
Z
F
1) X ᴧY ᴧZ
0
0
0
0
2) ¬X V Y V ¬ Z
1
1
0
1
3) X ᴧ(Y V Z)
1
0
0
1
4) (X VY)ᴧ¬ Z
4. Какое логическое выражение эквивалентно выражению ¬(¬ А V В) ᴧ С?
1. ¬А ᴧВ ᴧ¬ С 2. (А ᴧ ¬В) V С 3. (А ᴧ В) V С 4. А ᴧ¬В ᴧ С
5. Укажите значения переменных P, Q, S, T при которых ложно логическое выражение: (P V¬ Q) V (Q →( S VT))
Ответ запишите в виде строки из четырех символов — значений переменных P, Q, S, T ( в указанном порядке).
контрольная работа «ЛОГИКА»
3 вариант
1. Для какого имени животного истинно высказывание:
¬ (первая буква гласная → Вторая буква гласная) ᴧ последняя буква гласная?
1. Ирина 2. Максим 3. Артем 4. Мария
2. Для какого из значений Y будет истинно высказывание:
(Y <5) ᴧ ((Y > 1)→ (Y > 5)) ?
1.1 2.2 3.3 4.4
3. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов (X , Y, Z). Дан фрагмент таблицы истинности выражения F . Какое выражение соответствует F?
X
Y
Z
F
1) X V Y ᴧZ
0
0
0
1
2) X V Y V Z
0
0
1
1
3) X ᴧY V Z
0
1
0
1
4) ¬X V ¬Yᴧ¬ Z
4. Какое логическое выражение эквивалентно выражению ¬(¬ А ᴧ¬ В) ᴧ С?
1. ¬А V В V¬ С 2. А ᴧ В ᴧ С 3. (А V В) ᴧ С 4. (¬А ᴧ¬В) V¬ С
5. Укажите значения переменных K, L, M, N при которых ложно логическое выражение: (¬ K V M) → (¬L V M V N) .
Ответ запишите в виде строки из четырех символов — значений переменных K, L, M, N ( в указанном порядке).
Логические функции и логические выражения — урок. Информатика, 10 класс.
Логической функцией или, по-другому, предикатом на множестве \(M\) называют такую функцию от нескольких аргументов, которая при любом наборе значений этих аргументов из множества \(M\) принимает только одно из двух значений.
В языках программирования часто используются английские слова того же смысла True и False. Нередко предикат называют еще высказывательной формой, поскольку после подстановки вместо переменных элементов множества получается некое утверждение об этом наборе элементов, которое является либо истинным, либо ложным. Например, предикат «сумма \(x\) и \(y\) равна \(z\)» от трех аргументов \(x, y и z\), рассматриваемый на множестве натуральных чисел, принимает значение Истина при \(x = 3, y = 4, z = 7\) и значение Ложь при \(x = 2, y = 2, z = 5\). По аналогии с общим обозначением в математике функции как fx1,x2,…,xn в качестве общего обозначения предиката мы будем использовать запись Px1,x2,…,xn. Впрочем, вместо \(P\) можно использовать любую букву латинского алфавита.
В приведенном примере переменные \(x, y\) и \(z\) свободны в том смысле, что могут принимать любые значения из множества натуральных чисел. Поэтому данная логическая функция имеет три аргумента. Но не всегда число аргументов логической функции совпадает с числом фигурирующих в ее описании переменных. Рассмотрим, такой предикат: «существует \(x\), для которого сумма \(x\) и \(y\) равна \(z\)». Хотя в описании фигурируют три переменные \(x, y\) и \(z\), подставлять числа можно только вместо двух из них — \(y\) и \(z\). Так что здесь только два аргумента: \(y\) и \(z\). В таблице \(1\) приведены значения данной логической функции для некоторых наборов значений аргументов \(y\) и \(z\) (этот предикат мы рассматриваем на множестве натуральных чисел).
Таблица 1

Обрати внимание!
Переменная \(x\) в такой функции называется связанной. При этом говорят, что переменная \(x\) связана квантором существования. Для него есть специальное обозначение: ∃.
Происхождение этого знака простое: в английском слове «Exist» — существовать — взята первая буква и симметрично отражена относительно вертикальной оси. С помощью этого символа рассматриваемый нами предикат записывается так: ∃x(x+y=z).Впрочем, переменная может быть связанной и по-другому. Рассмотрим, для примера, на множестве натуральных чисел предикат «для любого \(y\) выполнено неравенство \(x+y>z\)». Здесь связанной переменной является \(y\). Примеры значений этого предиката приведены в таблице \(2\).
Таблица 2

Обрати внимание!
В этом случае говорят, что переменная связана квантором всеобщности, который обозначают символом ∀.
Его происхождение аналогично: от слова «All» (все) взята первая буква и симметрично отражена относительно горизонтальной оси. С помощью этого квантора данный предикат запишется так: ∀yx+y>z.
В предикате могут оказаться связанными не одна, а несколько переменных. Например, можно рассматривать предикат ∀y∃xx+y=z — для любого \(y\) существует \(x\), такой, что выполняется равенство \(x+y=z\). Или другой предикат: ∃x∀yx+y=z — существует \(x\), такой, что для любого \(y\) выполняется равенство \(x+y=z\). Каждый из них является логической функцией от одного аргумента \(z\), но это разные функции. Например, на множестве целых чисел первая из этих функций при любом значении аргумента \(z\) принимает значение Истина, в то время как вторая функция на том же множестве при любом значении аргумента \(z\) принимает значение Ложь. Как видите, порядок, в котором употреблены кванторы, имеет принципиальное значение.
Если в предикате все переменные оказались связанными, то такой предикат является высказыванием.
Например, предикат ∀z∀y∃xx+y=z — это высказывание, утверждающее, что для любых чисел \(z\) и \(y\) существует их разность (она обозначена пере-менной \(x\)). Это высказывание истинно на множестве целых чисел, но ложно на множестве натуральных чисел. Поэтому, обсуждая свойства того или иного предиката, надо всегда указывать множество, на котором он рассматривается. Впрочем, и для числовых функций, которые вы уже много лет изучаете на уроках математики, самое первое, о чем идет речь, — это их область определения.
При словесном описании логической функции построение отрицания к какому-либо утверждению можно выполнить добавлением словосочетания «Неверно, что…», после чего следует исходное утверждение. Например, отрицание высказывания «Я пошел в кино» можно выразить так: «Неверно, что я пошел в кино». IIpaвда, таким образом свою мысль выражают крайне редко. Обычно говорят: «Я не пошел в кино». Но заметьте, что ни одна из фраз «Не я пошел в кино» и «Я пошел не в кино» не является отрицанием исходного высказывания. А теперь рассмотрим, как строится отрицание высказывания, полученного связыванием переменной при помощи квантора. Вот пример высказывания: «Все ученики нашего класса имеют дома компьютер». Его отрицанием является высказывание «Неверно, что все ученики нашего класса имеют дома компьютер». Но каждому ясно, что это высказывание равносильно такому: «Существует ученик нашего класса, у которого дома нет компьютера». Как видите, при построении отрицания квантор всеобщности преобразуется в квантор существования. Более точно, если через \(P(x)\) обозначить предикат «ученик \(x\) имеет дома компьютер», то исходное высказывание запишется так: ∃xP(x). А его отрицание запишется как ∃xP(x)¯. Аналогично можно объяснить, почему при построении отрицания квантор существования заменяется квантором всеобщности. Итак, для логических функций, имеющих вид Q1x1Q2x2…QkxkPx1,x2,…,xk,y1,y2,…,yk, где Q1,Q2,…Qk — символы ∀ или ∃, x1,x2,…,xk — связанные переменные, y1,y2,…,yk — свободные переменные предиката \(P\), справедливо следующее правило построения отрицания. Чтобы получить отрицание логической функции, надо каждый квантор всеобщности заменить квантором существования и наоборот, а предикат \(P\) заменить его отрицанием.
Гейн А. Г., Ливчак А. Б., Сенокосов А. И. Информатика и ИКТ. 10 класс. М. : Просвещение, 167 с.
Логика и компьютер. Логические операции. Диаграммы Эйлера-Венна
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 10 классы | Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, сокращенный курс, 2 часа в неделю) | Логика и компьютер. Логические операции. Диаграммы Эйлера-Венна
Содержание урока
§18. Логика и компьютер
§19. Логические операции
Введение
Операция «НЕ»
Операция «И»
Операция «ИЛИ»
Операция «исключающее ИЛИ»
Импликация
Эквивалентность
Другие логические операции
Логические выражения
Вопросы и задания, Задачи
§20. Диаграммы
§19. Логические операции
Вопросы и задания
Задачи
1. Даны два высказывания: А — «В Африке водятся жирафы» и В — «В Мурманске идёт снег». Постройте из них различные сложные высказывания.
2. Дано высказывание «Винни-Пух любит мёд, и дверь в дом открыта». Как бы вы сформулировали отрицание этого высказывания?
3. Что такое таблица истинности?
4. Почему таблица истинности для операции «НЕ» содержит две строки, а таблицы для других изученных операций — четыре? Сколько строк в таблице истинности выражения с тремя переменными? С четырьмя? С пятью?
5. В каком порядке обычно записываются значения переменных в таблице истинности? Зачем это нужно?
6. Когда истинно высказывание А И В? А ИЛИ В?
7. Какие электрические схемы можно использовать для иллюстрации операций «И» и «ИЛИ»?
8. Какие знаки применяют для обозначения операций «НЕ», «И», «ИЛИ»?
9. Почему операция «И» называется логическим умножением, а «ИЛИ» — логическим сложением?
10. В чём различие арифметического и логического сложения?
11. Сколько можно определить различных логических функций с двумя переменными? С тремя переменными?
12. Чем отличается операция «исключающее ИЛИ» от операции «ИЛИ»?
13. Почему операция «исключающее ИЛИ» называется сложением по модулю 2?
14. Как записать выражение А ⊕ В с помощью базового набора операций (НЕ, И, ИЛИ)?
15. Как можно доказать или опровергнуть логическое равенство?
16. Какими интересными свойствами обладает операция «исключающее ИЛИ»?
17. Что значит выражение «обратимая операция»? Какие изученные логические операции являются обратимыми?
18. Какое свойство операции «исключающее ИЛИ» позволяет использовать ее для простейшего шифрования?
19. Чем отличается смысл высказывания «если А, то В» в обычной речи и в математической логике?
20. Запишите в виде логической формулы высказывание «Если утюг горячий, то лоб холодный».
21. Запишите в виде логической формулы высказывание «Неверно, что если утюг горячий, то лоб холодный». Можно ли в этом случае сразу сказать, каким является утюг и каким — лоб?
22. Как выразить импликацию через операции «НЕ» и «ИЛИ»? Докажите полученное тождество.
23. Как выразить эквивалентность через операции «НЕ», «И» и «ИЛИ»? Докажите полученное тождество.
24. Чем интересны операции «штрих Шеффера» и «стрелка Пирса»?
25. Докажите тождества, позволяющие представить базовые логические операции через штрих Шеффера. Попробуйте построить и доказать аналогичные тождества для операции «стрелка Пирса».
26. Что такое формализация?
27. В каком порядке выполняются действия в логических выражениях?
28. Что можно сделать для того, чтобы изменить естественный порядок действий?
29. Какие операции называются бинарными и унарными? Приведите примеры унарных и бинарных операций в математике.
30. Поясните разницу между терминами «логическое выражение» и «логическая функция».
31. Можно ли сказать, что таблица истинности однозначно определяет:
а) логическое выражение;
б) логическую функцию?
32. Что такое вычислимое логическое выражение?
33. Что такое тавтология? Противоречие? Приведите примеры.
34. Что такое равносильные выражения?
Подготовьте сообщение
а) «Логическая операция «Штрих Шеффера”»
б) «Логическая операция “Стрелка Пирса»»
в) «Шифрование с помощью операции «исключающее ИЛИ»»
Задачи
1. Составьте деревья для вычисления логических выражений и табли цы истинности этих выражений:
2. Составьте деревья для вычисления логических выражении и табли цы истинности этих выражений:
3. Символом F обозначено одно из указанных ниже логических выражений от трёх аргументов: X, У, Z. Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F?
4. Для предыдущего задания определите, сколько различных логических функций соответствует заданной частичной таблице истинности.
5. Задано 5 строк таблицы истинности некоторого логического выражения с тремя переменными. Сколько различных логических функций ей соответствуют?
6. Символом F обозначено одно из указанных ниже логических выражений от трёх аргументов: X, У, Z. Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F7
7. Символом F обозначено одно из указанных ниже логических выра жений от трёх аргументов: X, У, Z. Дан фрагмент таблицы истин ности выражения F. Какие из этих выражений могут соответство вать F?
8. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F?
9. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F?
10. Определите значение логического выражения (X > 2) → (X > 3) для X = 1, 2, 3, 4.
11. Определите значение логического выражения ((X < 5) → (Х < 3)) • ((Х < 2) → (Х < 1)) для X = 1, 2, 3, 4.
12. Определите значение логического выражения ((X > 3) + (Х < 3)) → (Х < 1) для X = 1, 2, 3, 4.
13. Определите значение логического выражения ((X < 4) → (Х < 3)) • ((X < 3) → (Х < 1)) для X = 1, 2, 3, 4.
14. Определите значение логического выражения (X • (X — 8) < 2 • X — 25) → (X > 7) для X = 4, 5, 6, 7.
15. Найдите все целые значения X, при которых логическое выражение (X > 2) → (X > 5) ложно.
16. Найдите все целые значения X, при которых логическое выражение ((X > 0) + (X > 4)) → (X > 4) ложно.
17. Автопилот может работать, если исправен главный бортовой компьютер или два вспомогательных. Выполните формализацию и запишите логические формулы для высказываний «Автопилот работоспособен» и «Автопилот неработоспособен».
18. Каково наибольшее целое положительное число X, при котором истинно утверждение: (Х(Х + 3) > Х2 + 9) → (Х(Х + 2) ≤ Х2 + 11)?
19. Каково наибольшее целое положительное число X, при котором истинно утверждение: (121 < Х2) → (Х > Х + 5)?
20. Каково наибольшее целое положительное число X, при котором ложно утверждение: (X (X + 6) + 9 > 0) → (X2 > 45)?
21. Каково наибольшее целое положительное число X, при котором истинно утверждение: (Х2 -1 > 100) → (Х(Х — 1) < 100)?
22. Каково наибольшее целое положительное число X, при котором ложно утверждение: (7Х -3 < 75) → (Х(Х — 1) > 65)?
23. Известно, что для чисел А, В и С истинно утверждение ((С < А) + (С < В)) • ((С + 1) < А) • ((С + 1) < В).
а) Чему равно С, если А = 25 и В = 48?
б) Чему равно С, если А = 45 и В = 18?
24. Известно, что для чисел А, В и С истинно утверждение (А = В) • ((В < А) → (2С > А)) • ((А < В) → (А > 2С)).
Чему равно А, если С = 10 и В = 22?
Следующая страница  §20. Диаграммы
§20. Диаграммы
Cкачать материалы урока
Элементарные логические функции одного аргумента
При синтезе логических схем широко применяются элементы с одним и двумя входами.
При одном аргументе n = 1 количество различных наборов равно двум: 0 и 1, а число различных переключательных функций – четырем. Их перечень приведен в таблице 1.7.
Число различных логических функций очень быстро растет с увеличением числа переменных (N = 22n, где n — число переменных), поэтому все их изучить невозможно. Любая логическая функция, зависящая от n-переменных (n>2), выражается через функции, зависящие от одной или двух переменных. Поэтому логические функции, зависящие от одной и двух переменных, занимают особое место в теории логических функций. Их называют элементарными логическими функциями или базовыми (основными).
Рассмотрим эти функции.
При n = 0 имеются две различные функции f0 = 0 и f1 = 1. Функция f0 = 0 называется константой 0, а функция f1 = 1 называется константой 1.
Таблица 1.7
Х | 0 | 1 | Условное обозначение | Название функции |
f0 (Х) f1 (Х) f2 (Х) f3 (Х) | 0 0 1 1 | 0 1 0 1 | 0 Х 1 | Константа 0 Переменная Х Инверсия Х Константа 1 |
Функция f0 (X) тождественно равна 0. Эту функцию называют константой нуля и обозначают f0 (X) = 0.
Функция f3 (X) тождественно равна единице. Эту функцию называют константой единицы и обозначают f3 (Х) = 1.
Функция f1 (X) повторяет значение аргумента и потому тождественно равна переменной Х.
Функция
f2 (X) принимает значения, противоположные
значениям аргумента: если Х=0, f2 (X) = 1; если Х = 1, f2 (X) = 0. Эту функцию называют инверсией
переменной Х или отрицанием Х и обозначают
f2 (X) =  .
.
На рисунке 1.5 приведены электрические схемы, реализующие переключательные функции одного аргумента, в которых нуль представляется низким потенциалом (потенциалом “земли”) (рис. 1.15а), а единица — высоким потенциалом +Е (рис. 1.15б). Константа нуля и единицы реализуется подключением выхода “земля” к источнику питания +Е соответственно, а переменная Х – отрезком проводника (рис. 1.15в). Переключательная функция “инверсия” требует для реализации электрическую схему инвертора (рис.1.15 г).

Рисунок 1.15 — Реализация логических функций от одного аргумента
Логические функции двух аргументов
При
двух аргументах X1 и X2 количество различных функций равно
шестнадцати (таблица 1.8). В число их
входят функции, равные константам 0 и
1, переменным X1 и X2,
а также их инверсиям  1 и
1 и  2:
2:
f0 (X1, X1) = 0 — константа нуль;
f3 (X1, X2) = X1 — аргумент X1;
f5 (X1, X2) = X2 — аргумент X2;
f10(X1,
X2)
= 2 —
отрицание X2;
2 —
отрицание X2;
f12(X1,
X2)
= 1 —
отрицание X1;
1 —
отрицание X1;
f15(X1, X2) = 1 — константа единица.
Особенностью этих функций является то, что их значения зависят не от всех переменных (аргументов). Такие функции называются вырожденными. Они сводятся к рассмотренным ранее функциям одного аргумента и к тем же методам схемной реализации. Остальные переключательные функции двух аргументов являются невырожденными.
Таблица 1.8
Х1 | 0 | 0 | 1 | 1 | Наименование функции | Условное обозначение |
Х2 | 0 | 1 | 0 | 1 | ||
f0 (X1, X1) | 0 | 0 | 0 | 0 | Константа нуль | 0 |
f1 (X1, X1) | 0 | 0 | 0 | 1 | Конъюнкция & | Х1 & Х2 |
f2 (X1, X1) | 0 | 0 | 1 | 0 | Запрет по Х2 (НЕТ) | Х1 ∆ Х2 |
f3 (X1, X1) | 0 | 0 | 1 | 1 | Аргумент Х1 | Х1 |
f4 (X1, X1) | 0 | 1 | 0 | 0 | Запрет по Х1 (НЕТ) | Х2 ∆ Х1 |
f5 (X1, X1) | 0 | 1 | 0 | 1 | Аргумент Х2 | Х2 |
f6 (X1, X1) | 0 | 1 | 1 | 0 | Логич. неравнозначные | Х1 |
f7 (X1, X1) | 0 | 1 | 1 | 1 | Дизъюнкция | Х1 |
f8 (X1, X1) | 1 | 0 | 0 | 0 | Стр. Пирса (ИЛИ-НЕ) | Х1 ↓ Х2 |
f9 (X1, X1) | 1 | 0 | 0 | 1 | Логич. равнозначные | Х1 = Х2 |
f10 (X1, X1) | 1 | 0 | 1 | 0 | Отрицание Х2 (НЕ) | Х2 |
f11 (X1, X1) | 1 | 0 | 1 | 1 | Импликация от Х2 и Х1 | Х2 → Х1 |
f12 (X1, X1) | 1 | 1 | 0 | 0 | Отрицание Х1 (НЕ) | Х1 |
f13 (X1, X1) | 1 | 1 | 0 | 1 | Импликация от Х1 и Х2 | Х1 → Х2 |
f14 (X1, X1) | 1 | 1 | 1 | 0 | Штрих Шеффера | Х1 ׀ Х2 |
f15 (X1, X1) | 1 | 1 | 1 | 1 | Константа единицы | 1 |
1. Функция f1 (X1,X2) совпадает с таблицей умножения двух одноразрядных двоичных чисел (таблица 1.9). Она носит название логического умножения, конъюнкции или функции “И”.
f1 (X1,X2)
= X1 X2 = X1 X2.
X2 = X1 X2.
Таблица 1.9 — Обозначение на схемах по ЕСКД
Х1
Х2
X
 1
1 X2
X20
0
0
0
1
0
1
0
0
1
1
1
2. Функция f2 (X1,X2) = 1 только в случае, если X1=1, а X2=0. Появление сигнала Х2 = 1 как бы запрещает прохождение сигнала Х1 на выход схемы. Поэтому данная функция называется функцией запрета или функцией “НЕТ” (таблица 1.10).
Таблица 1.10 — Обозначение на схемах по ЕСКД
Х1
Х2
X
 1 ∆
X2
1 ∆
X20
0
0
0
1
0
1
0
1
1
1
0
3. Функция f4 (X1,X2) аналогична функции f2 (X1,X2) с той лишь разницей, что здесь роли переменных X1 и X2 поменялись.
4. Функция f9 (X1,X2) равна 1, когда значения аргументов X1 и X2 совпадают, т.е. равнозначны. Отсюда вытекает название — логическая равнозначность (Таблица 1.11).
Таблица 1.11 — Обозначение на схемах по ЕСКД
Х1
Х2
X
 1 =
X2
1 =
X20
0
1
0
1
0
1
0
0
1
1
1
5. Поскольку функция f6 (X1,X2) противоположна f9 (X1,X2), то ей присвоено название логическая неравнозначность и, кроме того, эта функция совпадает с таблицей сложения одноразрядных двоичных чисел по модулю 2, что обусловило второе название — ”сложение по модулю два” (таблица 1.12).
Таблица 1.12 — Обозначение на схемах по ЕСКД
Х1
Х2
f
 6(X1,X2)
6(X1,X2)0
0
0
0
1
1
1
0
1
1
1
0
6. Функция f7 (X1,X2) — логическое сложение или дизъюнкция (функция “ИЛИ”) (таблица 1.13).
Таблица 1.13 — Обозначение на схемах по ЕСКД
Х1
Х2
X
 1
1 X2
X20
0
0
0
1
1
1
0
1
1
1
1
7. Функция f8 (X1,X2) — отрицание дизъюнкции носит название “Стрелка Пирса”, функция Вебба (Даггера) (ИЛИ-НЕ) (табл. 1.14).
f8 (X1,X2)
= X1 ↓ X2 = X1 X2
X2
Таблица 1.14 — Обозначение на схемах по ЕСКД
Х1
Х2
X
 1 ↓ X2
1 ↓ X20
0
1
0
1
0
1
0
0
1
1
0
8.
Функция f4 (X1,X2)
= X1│X2 = 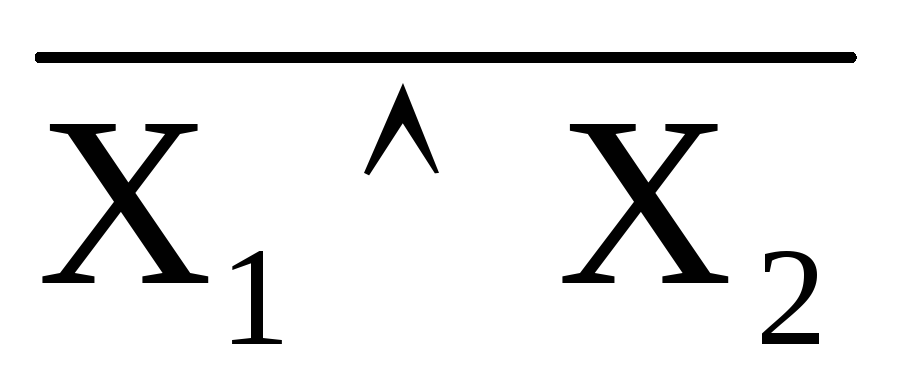 носит
название “Штрих
Шеффера” или отрицание конъюнкции
(И-НЕ) (табл. 1.15).
носит
название “Штрих
Шеффера” или отрицание конъюнкции
(И-НЕ) (табл. 1.15).
Таблица 1.15 — Обозначение на схемах по ЕСКД
Х1
Х2
X
 1 | X2
1 | X20
0
1
0
1
1
1
0
1
1
1
0
Необходимо отметить, что функции f8 и f14 в отдельности являются функционально полными, т.е. с их помощью можно выразить любую сколь угодно сложную функцию путем суперпозиции.
9. Функции f13 (X1,X2) и f11 (X1,X2) носят название “импликация” и записываются f13 (X1,X2) = X1→X2, и f8 (X1,X2) = X2→X1 (таблицы 1.16-1.17).
Таблица 1.16 Таблица 1.17
Х1
Х2
X1 → X2
Х1
Х2
X2 → X1
0
0
1
0
0
1
0
1
1
0
1
0
1
0
0
1
0
1
1
1
1
1
1
1
Если X1 = 1, то X2 = 0, f13 (X1,X2) = 0.
Если X2 = 1, то X1 = 0, f8 (X1,X2) = 0.
Высказывание Х1 называется посылкой, а Х2 — следствием.
На первый взгляд таблица истинности для импликации может показаться несколько странной, так как из нее следует, что истинным является сложное высказывание, составленное из двух ложных высказываний. Например, высказывание “если дважды два – пять, то снег – черный”, следует считать истинным, хотя никакой логической связи между простым высказыванием, составляющим данное предложение, нет. Это связано с тем, что в алгебре логики любое простое высказывание рассматривают только с точки зрения его свойства быть истинным или ложным, а содержанием высказывания не интересуются. Поэтому логическими связями могут объединяться высказывания, не связанные между собой по смыслу. Тот факт, что высказывание Х1 → Х2 истинно при Х1 = 0 и любое значение Х2 означает, что, исходя из ложной посылки (Х1), можно прийти к любому следствию (Х2) как истинному, так и ложному. УГО по госту приведены соответственно на рис. 1.23 и 1.24.

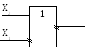
Рисунок 1.23 — Логическая схема Рисунок 1.24 — Логическая схема импликации Х1 ® X2 импликации Х2 ® X1
Логические операции отрицания выполняются над одним аргументом. Логические операции логической равнозначности, запреты, импликации выполняются над двумя аргументами.
Логические операции дизъюнкции, конъюнкции, сложение по модулю 2, “Штрих Шеффера”, “Стрелка Пирса” могут выполняться над двумя и более аргументами. Значение рассмотренных функций состоит в том, что из них может быть построена произвольная логическая функция, зависящая более чем от двух переменных. Логические функции, зависящие более чем от двух переменных, называются сложными логическими функциями.



 Х2
Х2 Х2
Х2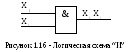 1
1 X2
X2 1 ∆
X2
1 ∆
X2 1 =
X2
1 =
X2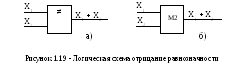 6(X1,X2)
6(X1,X2) 1
1 X2
X2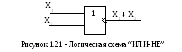 1 ↓ X2
1 ↓ X2 1 | X2
1 | X2